Demolition of concrete by thermal shock spallation: a mesoscopic numerical study based on embedded discontinuity finite elements

Abstract

This paper deals with 2D (plane strain) and axisymmetric numerical modelling of concrete fracture processes under mechanical and thermal loading. A mesoscopic modelling approach with an explicit representation of aggregates as Voronoi polygons is chosen while the concrete fracture model is based on rate-dependent embedded discontinuity finite elements with Rankine criterion indicating a new crack initiation. This choice enables the study of the effects of inherent crack populations on the response of concrete under mechanical and thermal loading. In the numerical examples, the performance of the present modelling approach is first demonstrated in the uniaxial compression and tension tests under plane strain conditions. Then, the problem of thermal spallation of concrete surface under dry conditions due to a high intensity, short duration heat flux is simulated under axisymmetric conditions. The underlying uncoupled thermo-mechanical problem is solved with an explicit time marching scheme based on the staggered approach. Different heat flux intensities and heating times as well as combined effect of surface roughness and pre-stress field are tested. The simulation results suggest that demolition of concrete structures by heat shock is a viable method.

1 Introduction

Understanding concrete fracture processes under thermal and thermo-mechanical loading conditions is of substantial practical importance in structural engineering. Fire induced concrete spalling, for example, is a problem encountered with concrete structures under fire (Lottman 2017; Liu et al. 2018; Fu and Li 2011). This phenomenon is characterized by, often violent, ejection of chunks of concrete, called spalls, from heated concrete. While the occurrence of this kind of concrete spalling is an undesired event leading to a loss of load bearing capacity, spalling can also be a desired event to be exploited in drilling and demolition of concrete structures. In the present paper, this latter kind of concrete spalling, which is exploited in thermal jet rock drilling (Kant et al. 2017), is considered. Naturally, there are numerous studies on thermo-mechanical modelling of concrete in general (Gawin et al. 2003, 2011; Caggiano and Guillermo 2015; Schrefler et al. 2002) and concrete spalling under fire in particular (Fu and Li 2011; Tenchev and Purnell 2005; Ju et al. 2016; Caldas et al. 2013; Ozbolt and Bosnjak 2013; Zhao et al. 2017). However, the numerical studies on demolition or drilling of concrete by exploiting the spalling phenomenon or heat shocks seem extremely rare or nonexistent, as the author could not find any of the kind.

When the spalling phenomenon is exploited for demolition of concrete structures, e.g. by drilling, the surface area affected by the heat flux is local while the intensity of the flux, or the heating rate, is much higher than in the fire-induced spalling. Indeed, if the drilling by thermal spalling is to be competitive with purely mechanical drilling, the heating time leading to spalling should be of the order of fractions of a second, while the heating times in fire-induced spalling vary from tens of minutes to hours (Liu et al. 2018).

Concerning the mechanisms behind concrete spalling, the two main theories are pore pressure spalling and thermal stress spalling (Fu and Li 2011). The former, occurring typically between 220 and $320\,^{\circ }\hbox {C}$, is induced by moisture clogging and pore pressure build up inside the heated concrete, while the latter is caused by thermal stresses induced by the thermal gradient and occurs within $430\,^{\circ }\hbox {C}$ and $660\,^{\circ }\hbox {C}$ (Liu et al. 2018). Thermal stress spalling is facilitated by the local concrete inhomogeneities causing strain incompatibilities between the cement matrix and aggregates (Fu and Li 2011). Moreover, the favorably oriented inherent microcracks also enhance the spalling by the wing crack-growth mechanism (Kant et al. 2017; Walsh and Lomov 2013; Kant and von Rohr 2016). In the present study, the thermal stress spalling is taken as the mechanism that drives the phenomenon and motivates the model development.

The traditional approach on concrete modelling is to homogenize the aggregate-mortar bi-phasic structure and to use phenomenological constitutive models, based on plasticity theory and/or damage mechanics, implemented in the finite element method (FEM) (Barpi 2004; Winnicki et al. 2001; Grassl and Jirásek 2006; Feenstra and De Borst 1996; Jason et al. 2006; Hofstetter and Meschke 2011). This approach can realistically predict the concrete structural response and is still of great importance in structural design. However, homogenized approach is inadequate when heterogeneous mesostructure of concrete needs to be taken into account. This is especially true in the present case of modelling concrete spalling where the inherent microcracks and the aggregate-induced heterogeneity have a major effect on the behavior. Moreover, as aggregates introduce various fracture toughening mechanisms, such as crack stopping, redirection and branching (Landis and Bolander 2009), their explicit description is crucial. For this reason, mesomechanical approach explicitly representing the aggregate-mortar structure has been a topic of many numerical studies [see Tang et al. (2007), Pulatsu et al. (2019), Pieralisi et al. (2016), Etse et al. (2012), Tang et al. (2016), Wu et al. (2019), Nitka and Tejchman (2015, (2020)), Gangnant et al. (2016), Pedersen et al. (2013), Snozzi et al. (2011, (2012) and Saksala (2018b) for example].

As for the fracture or cracking description in concrete, the discrete element or particle methods would be a natural choice due to their inherent superiority, in this regard, over the continuum methods. However, particle methods are computationally at least one order of magnitude more demanding due the need to track the particle configurations and their contacts. Therefore, the embedded discontinuity finite elements approach is (see Simo et al. (1993) and Simo and Oliver (1994) for original developments) chosen here to describe the concrete fracture processes. This approach was successfully applied in modelling concrete cracking by Sancho et al. (2007) and by Huespe and Oliver (2011) for example.

Within these guidelines, a numerical study on the demolition of concrete by thermal spalling with high intensity and short duration heat shocks is attempted in this paper. A mesomechanical approach based on embedded discontinuity finite elements for numerical modelling of concrete fracture processes under mechanical and thermal loading is developed and tested for this purpose. There are, of course, numerous previous studies considering thermo-mechanical cracking with discontinuity finite elements approach, see e.g. Ngo et al. (2014, (2013), Pressacco and Saksala (2020) using the embedded discontinuity FEM, and Jung et al. (2016), Habib et al. (2018), and Liu et al. (2013) using the extended FEM. However, none of them deal with short duration, high intensity heat shocks on brittle materials. To the best of the author’s knowledge, this is the first numerical study of this kind. The main novelty of the present study is not so much in the numerical method developed, which is actually a new combination of the existing components, but in the fact that it represents innovative applications-oriented research that uses numerical methods to investigate the feasibility of new technologies.

2 Theory of the numerical model

The theory of the chosen concrete modelling approach is explained in this section. First, the constitutive model for concrete fracture based on the embedded discontinuity finite element method is outlined. Then, the concrete mesostructure modelling is given. Finally, an explicit staggered scheme to solve the underlying thermo-mechanical problem of concrete under external heating is specified. At this preliminary level of developments, dry conditions of concrete are assumed meaning that the hygro-thermal effects are ignored.

2.1 Concrete fracture model based on the embedded discontinuity FEM

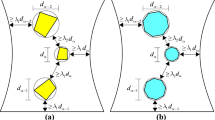
Concrete fracture is modelled by the embedded discontinuity approach. Only the finite element implementation of the embedded discontinuity kinematics is presented here. For a detailed treatment of the topic, see Simo et al. (1993), Simo and Oliver (1994), Huespe and Oliver (2011) and Jirásek (2000). According to this method, the crack is represented by a displacement discontinuity embedded inside a finite element. For the constant strain triangle (CST) with a discontinuity ${\Gamma }_{d}$ (see Fig. 1), the displacement and strain fields can be written as

$$\begin{aligned}&{\mathbf {u}}\left( {\mathbf {x}} \right) =N_{i}\left( {\mathbf {x}} \right) {\mathbf {u}}_{i}^{e}\nonumber \\&\qquad \qquad +M_{{\Gamma }_{d}}\left( {\mathbf {x}} \right) {{{\varvec{\upalpha }} }}_{d}\hbox { with }M_{{\Gamma }_{d}}\left( {\mathbf {x}} \right) =H_{{\Gamma }_{d}}\left( {\mathbf {x}} \right) -\varphi \left( {\mathbf {x}} \right) \end{aligned}$$

(1)

$$\begin{aligned}&{{{{\varvec{\upvarepsilon }}}}\left( {\mathbf {x}} \right) =\left( {\nabla }N_{i}{\otimes }{\mathbf {u}}_{i}^{e} \right) }^{sym}-\left( {\nabla }\varphi \left( {\mathbf {x}} \right) {\otimes }{{{\varvec{\upalpha }}}}_{d} \right) ^{sym}\nonumber \\&\qquad \qquad +\delta _{{\Gamma }_{d}}\left( {\mathbf {n}}\otimes {{{\varvec{\upalpha }}}}_{d} \right) ^{sym} \end{aligned}$$

(2)

where $N_{i}$ and ${\mathbf {u}}_{i}^{e}$ are the standard interpolation functions and nodal displacements ($i = 1,2,3$ with summation on repeated indices), respectively, and the displacement jump is denoted by ${{{\varvec{\upalpha }} }}_{d}$. Moreover, $H_{{\Gamma }_{d}}$ and $\delta _{{\Gamma }_{d}}$ are the Heaviside function and its gradient, the Dirac delta function at the discontinuity. Finally, the usual assumption with low order elements that ${\nabla }{{{\varvec{\upalpha }} }}_{d}{\equiv \mathbf{0} }$ was made in arriving at the expression for the strain in (2). This means that the displacement jump is elementwise constant, similarly as the ordinary strain for a CST element.

The reason for using function $M_{\varGamma _{d}}$ in (1) is that is restricts the effect of ${{{\varvec{\upalpha }} }}_{d}$ inside the corresponding finite element, i.e. ${{{\varvec{\upalpha }}}}_{d}{\equiv \mathbf{0}}$ outside that element, see Fig. 1. From the practical point of view, this decomposition of the displacement facilitates the handling of the essential boundary conditions (Huespe and Oliver 2011; Jirásek 2000; Saksala et al. 2015). Function $\varphi$ appearing in $M_{\Gamma _{d}}$ is chosen, from among the possible combinations of the shape functions, so that its gradient is as parallel as possible to the crack normal ${\mathbf {n}}_{d}$:

$$\begin{aligned} \nabla \varphi =\mathrm {arg}\left( \mathop {\max }\limits _{k=1,2} \frac{\left| \sum _{i=1}^{k}\nabla N_{i}\cdot {\mathbf {n}}_{d} \right| }{\left\| \sum _{i=1}^{k}{\nabla }N_{i} \right\| } \right) \end{aligned}$$

(3)

This choice has proved to be computationally robust, and it gives good results (Sancho et al. 2007). For the case in Fig. 1, criterion (3) gives the interpolation function $N^{sol}$ of the solitary node as function $\varphi$.

Fig. 1

Illustration of a CST element with an embedded discontinuity line

An essential component of the finite element implementations of the embedded discontinuity theory is the imposition of the traction discontinuity over a discontinuity. Here, the enhanced assumed strains concept is chosen for this purpose (Radulovic et al. 2011). Accordingly, the variation of the enhanced part of the strain in (1) is constructed in the strain space orthogonal to the stress field. Applying the $L_{\mathrm {2}}$-orthogonality condition with a special Petrov–Galerkin formulation, gives the following expression for the weak form of the traction balance (Radulovic et al. 2011; Mosler 2005):

$$\begin{aligned} \frac{1}{A_{e}}\int _{\Omega _{e}{\setminus }\varGamma _{d}}{{{{\varvec{\upsigma }} \cdot }}{\mathbf {n}}_{d}d{\Omega -}\frac{1}{l_{d}}} \int _{\varGamma _{d}} {\mathbf {t}}_{\varGamma _{d}}d{\Gamma }_{d}=0 \end{aligned}$$

(4)

where ${{{\varvec{\upsigma }} }}$ is the stress tensor, ${\mathbf {t}}_{\varGamma _{d}}$ is the traction vector, $A_{e}$is the area of the element, and $l_{d}$ is the length of the discontinuity ${\Gamma }_{d}$. As the integrands in (4) are constants for the CST element, the weak traction continuity reduces to the strong (local) form of traction continuity:

$$\begin{aligned} {\mathbf {t}}_{\varGamma _{d}}={{{\varvec{\upsigma }} \cdot }}{\mathbf {n}}_{d}=\left( {\mathbf {E}}(\theta ):\left( \hat{{\varvec{\upvarepsilon }}}-\left( {\nabla }\varphi \left( {\mathbf {x}} \right) {\otimes }{{{\varvec{\upalpha }}}}_{d} \right) ^{sym} \right) \right) \cdot {\mathbf {n}}_{d}\nonumber \\ \end{aligned}$$

(5)

where E is the elasticity tensor depending on temperature $\theta$ and ${\hat{{\varvec{\upvarepsilon }}}=\left( {\nabla }N_{i}{\otimes }{\mathbf {u}}_{i}^{e} \right) }^{sym}$ . It is worth noting that such an EAS concept based formulation results in a simple implementation without the need to know explicitly neither the exact position of the discontinuity within the element nor its length. However, this, along with the criterion (3) for choosing the ramp function, leads to discontinuous crack path, which in turn results in locking problems. A remedy to alleviate locking is presented below in Sect. 2.2. Moreover, only the regular part, $\left( {\nabla }\varphi \left( {\mathbf {x}} \right) {\otimes }{{{\varvec{\upalpha }}}}_{d} \right) ^{sym}$, of the enhanced strain (2) appears in the stress–strain relationship and the final discretized equations since the singular part, $\delta _{{\Gamma }_{d}}\left( {\mathbf {n}}\otimes {{{\varvec{\upalpha }} }}_{d} \right) ^{sym}$, is nonzero only at the discontinuity while the regular part is valid for the bulk material. Moreover, this procedure is in agreement with the EAS concept (Mosler 2005).

The formal similarity of expression (5) to that of the stress-elastic strain relation in computational plasticity suggests that a similar formulation, i.e. a traction-separation law with loading functions indicating crack opening, as in plasticity could be used here for solving the irreversible crack opening increments. As this is indeed the case (Mosler 2005), a computational multisurface plasticity inspired model based on the classical elastic predictor-plastic corrector split is employed here.

As for the loading functions indicating the stress states leading to crack opening in tension (mode I) or shear (mode II) modes, there are basically two options: the effect of shear and tension components of the traction can be combined into a single loading function (Saksala 2018b; Mosler 2005) or divided into separate loading functions (Saksala et al. 2015; Brancherie and Ibrahimbegovic 2009). As a single discontinuity per element is allowed in the present approach, the separation of shear and tension modes does not result in computationally inconvenient scheme, as it would in multiple discontinuity per element case. Moreover, separation of the modes alleviates the shear parameter problem inherent in the combined modes loading function approach (Saksala 2018b). Namely, when both modes are combined in a single loading function and the crack opening direction is defined as a gradient of the loading function, the opening direction may not be parallel to the loading axis even in uniaxial tension if the local stress state is disturbed by inhomogeneities of concrete. This problem can partially be alleviated by the shear retention parameter, as was shown by Saksala (2018b). However, separation of the modes I and II into their respective loading functions solves the problem in a more satisfactory manner. Therefore, this approach is chosen here. The relevant model components, i.e. the loading functions, softening rules and evolution laws are defined as (Saksala et al. 2015)

$$\begin{aligned}&\phi _{\mathrm {t}}\left( {\mathbf {t}}_{{\Gamma }_{d}},\kappa ,\dot{\kappa } \right) ={\mathbf {n}}{\cdot }{\mathbf {t}}_{{\Gamma }_{d}}-\left( \sigma _{\mathrm {t}}(\theta )+q\left( \kappa ,\dot{\kappa } \right) \right) \end{aligned}$$

(6)

$$\begin{aligned}&\phi _{\mathrm {s}}\left( {\mathbf {t}}_{{\Gamma }_{d}},\kappa ,\dot{\kappa } \right) =\left| {\mathbf {m}}\cdot {\mathbf {t}}_{{\Gamma }_{d}} \right| -\left( \sigma _{\mathrm {s}}(\theta )+\frac{\sigma _{\mathrm {s}}}{\sigma _{\mathrm {t}}}q\left( \kappa ,\dot{\kappa } \right) \right) \nonumber \\ \end{aligned}$$

(7)

$$\begin{aligned}&q=h\kappa +s\dot{\kappa }, h=-g\sigma _{\mathrm {t}}\exp \left( -g\kappa \right) , g=\frac{\sigma _{\mathrm {t}}}{G_{\mathrm {Ic}}} \end{aligned}$$

(8)

$$\begin{aligned}&\dot{{\mathbf{t}}}_{{\Gamma }_{d}}=-{\mathbf {E}}(\theta )\mathrm {:}\left( {\nabla }\varphi \left( {\mathbf {x}} \right) {\otimes }\dot{{\varvec{\upalpha }} }_{d} \right) {\cdot }{\mathbf {n}} \end{aligned}$$

(9)

$$\begin{aligned}&\dot{{\varvec{\upalpha }}}_{d}=\dot{{\varvec{\upalpha }}}_{\mathrm {I}}+\dot{{\varvec{\upalpha }} }_{\mathrm {II}}=\dot{\lambda }_{\mathrm {t}}\frac{\partial \phi _{\mathrm {t}}}{\partial {\mathbf {t}}_{{\Gamma }_{d}}}\nonumber \\&\qquad \qquad +\dot{\lambda }_{\mathrm {s}}\frac{\partial \phi _{\mathrm {s}}}{\partial {\mathbf {t}}_{{\Gamma }_{d}}}, \dot{\kappa }=-\dot{\lambda }_{\mathrm {t}}\frac{\partial \phi _{\mathrm {t}}}{\partial q}-\dot{\lambda }_{\mathrm {s}}\frac{\partial \phi _{\mathrm {s}}}{\partial q} \end{aligned}$$

(10)

$$\begin{aligned}&\dot{\lambda }_{i}\geqslant 0, \phi _{i}\leqslant 0, \dot{\lambda }_{i}\phi _{i}=0 (i=\mathrm {t,s}) \end{aligned}$$

(11)

where ${\mathbf {m}}$ denotes the unit tangent of a discontinuity, $\kappa , \dot{\kappa }$ are the internal variable and its rate related to the softening law for a discontinuity, and $\sigma _{\mathrm {t}}$ and $\sigma _{\mathrm {s}}$ are the temperature, $\theta$, dependent tensile and shear strength, respectively. Moreover, parameter h is the softening modulus of the exponential softening rule while parameter g controls the initial slope of the softening curve and is calibrated by the mode I fracture energy $G_{\mathrm {Ic}}$. Equation (9) is obtained from (5) by taking into account that at the material point level temperature and the total stain are constants. Moreover, the Koiter’s rule for bi-surface plasticity is applied in (10)$_{\mathrm {1}}$ where the total displacement jump is a sum of the contributions from mode I and mode II increments, while $\dot{\lambda }_{\mathrm {t}}{\mathbf {,}\dot{\lambda }}_{\mathrm {s}}$ are the corresponding crack opening and sliding increments. The evolution law (10)$_{\mathrm {2}}$ for the internal variable $\kappa$consists also of the contributions from the mode I and mode II components. Note also that the material rate-sensitivity is accommodated by adding a constant viscosity term, withs being viscosity modulus, to the uniaxial tensile strength. However, strain rate effects are not studied in this paper. In addition to accommodation of rate effects, the introduction of viscosity enhances the robustness of the integration of Eqs. (6)–(11). This can be seen as follows. Assume, for simplicity, the 1D case with the tensile loading function being violated. Now, the corresponding opening increment is solved by $\delta \lambda _{\mathrm {t}}=\phi _{\mathrm {t}}/(E\mathrm {+}h\mathrm {+}s\mathrm {/\Delta }t)$ where E is the elastic modulus. If the softening modulus is negative enough, as it may be for deep softening curves, the divisor here can become negative, and the computations consequently halt, in the inviscid case. In the viscid case, the time step ${\Delta }t$ is usually so small for explicit time stepping that the term $s\mathrm {/\Delta }t$ secures the positivity of the divisor and thus enhances the robustness.

The Eqs. (11) are the classical Kuhn–Tucker conditions imposing the consistency. This means that the viscosity is included with the viscoplastic consistency approach by Wang et al. (1997). The solution of the model in (6)–(11), i.e. the stress return mapping, is described by Wang et al. (1997) and Saksala et al. (2015), and summarized for the convenience of the reader in Appendix B.

At the local level, the material behavior is isotropic and linearly elastic until the tensile strength is reached. When the tensile strength in an element is reached, a discontinuity is embedded with a normal parallel to the first principal direction. A discontinuity, once embedded, cannot rotate. This criterion to introduce crack based on the principal stress (Rankine) criterion is suitable for modelling concrete fracturing under thermal loading since thermal strains are volumetric in nature. However, it will be demonstrated in the numerical simulations that this criterion is sufficient to predict the concrete failure mode and compressive strength of the specimen in purely mechanical uniaxial compression test as well. Finally, it should be noted that cracks appear naturally in each element where the Rankine criterion is violated and, thus, no crack path tracking algorithms are used. This, however, leads to discontinuous crack path, which may cause locking problems dealt with next.

2.2 Isotropic damage model to alleviate locking problems

The FE formulations of embedded discontinuity kinematics with low-order elements suffer from crack locking (spurious stress transfer over the crack) and spreading (i.e. the crack dispersion over a wide zone) problems (Sancho et al. 2007; Radulovic et al. 2011). Some remedies, such as the rotating discontinuity approach (Sancho et al. 2007) and the multiple intersecting discontinuities (Radulovic et al. 2011) have been developed to alleviate the locking problem with linear elements. However, the rotating discontinuity approach is not physically sound (cracks do not rotate in reality), while the multiple intersecting discontinuity approach results in considerably more complicated stress return mapping algorithm. Therefore, a simple isotropic damage model, which has been used by Jirásek and Zimmermann (1998) with the rotating crack models to prevent spurious stress generation, is employed to alleviate these problems. Accordingly, a transition from embedded discontinuity model to isotropic damaging is triggered in an element with a discontinuity after the displacement jump has reached certain threshold opening. The damage variable is defined as

$$\begin{aligned} \omega= & {} 1-\exp \left( -g\left( {\upalpha }_{d}-{\upalpha }_{tr} \right) \right) \mathrm {with } \end{aligned}$$

(12)

$$\begin{aligned} \alpha _{\mathrm {tr}}= & {} -\mathrm {ln}(q_{\mathrm {tr}}/q_{\mathrm {0}})/g \end{aligned}$$

(13)

where g is defined in the previous section, ${\alpha }_{d}$ is the history variable for the damage model being defined as the maximum value reached (during the loading process) by the norm of the displacement jump ${{\alpha }}_{d}$. Moreover, $\alpha _{tr}$ is the threshold value indicating the transition to the damage model. Finally, $q_{\mathrm {tr}}$/$q_{\mathrm {0}}$ represents the ratio of the final (softened) and initial strength. The value of this parameter should be small enough so as not to affect the softening process too early. In the simulations presented later, a value of 0.1 is used, which means that the damage model is activated when 90of the strength is exhausted. By this model, spurious stress generation is effectively eliminated, as the stress multiplied with (1$-\omega )$ as

$$\begin{aligned} {{{\varvec{\upsigma }}}}= & {} (1-\omega ){\mathbf {E}}(\theta ):( \hat{{\varvec{\upvarepsilon }} }-({\nabla }\varphi ( {\mathbf {x}} ){\otimes }{{{\varvec{\upalpha }}}}_{d} )^{sym}\nonumber \\&-{{{\varvec{\upvarepsilon }}}}_{\theta } ), {{{\varvec{\upvarepsilon }}}}_{\theta }=\alpha \Delta \theta {\mathbf {I}} \end{aligned}$$

(14)

where ${{\varepsilon }}_{\theta }$ is the thermal strain due to the external heat flux to be explained later in Sect. 2.4.

2.3 Mesoscopic description of concrete

Concrete is described mesoscopically as a bi-phasic material with explicit aggregate grains in a mortar matrix similarly as in Saksala (2018b). Thereby, in the numerical concrete, the aggregates are generated by shrinking Voronoi polygons from a Voronoi tessellation. However, here a random shrinkage (the shrinkage parameter being uniformly distributed between 0.2 and 0.6) is applied and the aggregates are also randomly rotated (with the rotation angle uniformly distributed between 0 and $\pi$/4) in order to obtain a more realistic mesostructure. The resulting mortar-aggregate structure is meshed with ordinary CST elements. Another new feature in the present study is to include an initial randomly oriented microcrack population in the cement matrix, see Fig. 2. Concrete contains inherent microcrack populations induced by hydration processes, for example. These cracks have, expectedly, a non-negligible influence on the concrete failure processes.

Fig. 2

Numerical concrete mesostructure (aggregates in mortar matrix containing microcracks)

In the numerical concrete mesostructure in Fig. 2, the aggregates are represented by 50 Voronoi polygons of different shapes and sizes. The blue lines (598 in total) represent the inherent microcrack population with random orientation (i.e. their alignment angle is uniformly distributed between $-\pi$/2 and $\pi$/2). Their locations are obtained by random permutation of an array of mortar element numbers having 598 tags signifying the initial cracks. It is assumed that only the cement matrix contains initial cracks. It should finally be stressed that this numerical concrete do not necessarily correspond to any real concrete but is generated for demonstrative purposes only.

2.4 Explicit solution scheme for solving the underlying uncoupled thermo-mechanical problem

The starting point for developing a time stepping solution scheme for the heat shock induced fracturing of concrete is the fully coupled localized thermo-mechanical problem. Here, “localized” means that a discontinuity (crack) is included. However, in the present approach the crack surface is not a traction-free surface with explicit topological features, such as doubled nodes as in the cohesive zone interface elements (see Willam et al. (2014) for example), but an embedded cohesive crack governed by the model in Eqs. (6)–(11). Thereby, the temperature over the discontinuity is taken to be continuous while the heat flux, being defined by the Fourier’s law, has a discontinuity. The justification for this assumption is that generally, the material properties are temperature dependent so that the crack surface acts as a material interface. With a temperature difference over the nodes of an element with a crack, the material properties are also different over the crack leading to a jump in flux at the crack surface while still having continuity in temperature over the crack (Ngo et al. 2014, 2013). This being the setting, the local, strong form of the balance equations can be written for present purposes as (Pressacco and Saksala 2020)

$$\begin{aligned}&\left\{ \begin{array}{l} \rho \ddot{\mathbf{u}}={\nabla }\cdot {{{\varvec{\upsigma }} }+\mathbf {b}\hbox { for }\mathbf {x}\in }{\Omega }_{e}{\setminus }{\Gamma }_{d} \\ {\varvec{\upsigma }} \cdot {\mathbf {n}}_{d}={\mathbf {t}}_{\varGamma _{d}} \hbox { for }\,\,\mathbf {x}\in {\Gamma }_{d} \end{array} \right. \hbox { mechanical part }\nonumber \\ \end{aligned}$$

(15)

$$\begin{aligned}&\left\{ \begin{array}{l} \rho c\dot{\theta }=-{\nabla }\cdot {\mathbf {q}}+Q_{\mathrm {mech}}\hbox { for }\mathbf {x}\in {\Omega }_{e}{\setminus }{\Gamma }_{d} \\ \llbracket {\mathbf {q}} \rrbracket \cdot {\mathbf {n}}_{d}={\mathbf {t}}_{\varGamma _{d}}\cdot \dot{{\varvec{\upalpha }}}_{d}+h\kappa \dot{\kappa } \hbox { for } \mathbf {x}\in {\Gamma }_{d} \end{array} \right. \hbox { thermal part }\nonumber \\ \end{aligned}$$

(16)

where $Q_{\mathrm {mech}}$ is the mechanical heating due to thermo-elasticity effects in the bulk material and $\llbracket {\mathbf {q}} \rrbracket$ is the jump in the heat flux defined by the Fourier’s law ${\mathbf {q=-}}k{\nabla }\theta$ with k being the conductivity of the material. Moreover, $\rho$ and c are the density and the specific heat capacity of the material, $\dot{\theta }$ is the rate of change of temperature in Eq. (16). Finally, $\ddot{\mathbf{u}}$ is the acceleration vector.

Now, this coupled thermo-mechanical problem can be significantly simplified based on the nature of the application in mind in the present work. Namely, the thermal fracturing of concrete under transient, i.e. high intensity and short duration, heat fluxes is considered. The related order of magnitude of the temperature rise at the surface under the exposure of heat flux is hundreds of degrees centigrade, $\sim 500\,^{\circ }\hbox {C}$. Therefore, the thermo-elastic effects in the bulk continuum material can be ignored as their order of magnitude is about $10^{-1\circ }\hbox {C}$ (Ottosen and Ristinmaa 2005). Hence, $Q_{\mathrm {mech}}{\equiv 0}$ hereafter. Moreover, the mechanical dissipation effects at the discontinuity, i.e. the right-hand side of Eq. (16)$_{\mathrm {2}}$, are also considered as insignificant in comparison to the external heat flow (Ngo et al. 2013). Therefore, the problem to be solved defined by (15) and (16)$_{\mathrm {1}}$ accompanied with suitable initial and boundary conditions, becomes uncoupled. That means the only information transfer between thermal and mechanical parts being the thermal strain defined in Eq. (14) and temperature dependence of the mechanical properties of concrete.

At this point, it should be noted that no reference to any thermodynamic framework has been made above. The reason for this is that the mechanical part of the problem, i.e. model in Eqs. (6)–(11), was formulated analogously to the associated plasticity. Furthermore, the thermodynamic coupling was shown to be negligible in the present application and the problem became thus uncoupled. However, it is still instructive to derive the state equations from a free energy potential and show that the model fulfils the dissipation inequality. These aspects are treated at some length in Appendix A (for more details in thermodynamic aspects of embedded discontinuity models and coupled thermo-mechanical models can be found in Radulovic et al. (2011), Mosler (2005), Brancherie and Ibrahimbegovic (2009), Willam et al. (2014), Ngo et al. (2014, (2013) and Ottosen and Ristinmaa (2005)).

The finite element discretized version of Eqs. (15) and (16) are (Ottosen and Ristinmaa 2005)

$$\begin{aligned}&\mathbf{M }_{u}\ddot{{\varvec{u}}}_{t}+\mathbf{f }_{t}^{int}\nonumber \\&\quad =\mathbf{f }_{t}^{ext} \quad { with}\; \mathbf{f }_{t}^{int}=\mathbf{A }_{e=1}^{N_{el}}\int _\Omega ^{\mathbf {e}} {\mathbf{B }_{u}^{e,T}{{\varvec{\sigma }}}_{t}d\Omega } \end{aligned}$$

(17)

$$\begin{aligned}&\mathbf{M }_{\theta }\dot{{\varvec{\theta }} }_{t}+\mathbf{K }_{\theta }{{\varvec{\theta }}}_{t}=\mathbf{f }_{t}^{q}{ }{} { with} \nonumber \\&{\mathbf {M}}_{{\uptheta }}={\mathbf {A}}_{e=1}^{N_{el}}\int _{\Omega ^{{{{\varvec{e}}}}}} {\rho c{\mathbf {N}}_{{\uptheta }}^{e,T}{\mathbf {N}}_{{\uptheta }}^{e}{\Omega }^{e}}, \nonumber \\&{\mathbf {K}}_{{\uptheta }}={\mathbf {A}}_{e\mathrm {=1}}^{N_{el}}\int _{\Omega ^{{{\varvec{e}}}}} {k{\mathbf {B}}_{{\uptheta }}^{e,T}{\mathbf {B}}_{{\uptheta }}^{e}{d{\Omega }}^{e}} , {\mathbf {f}}_{t}^{\mathrm {q}}\nonumber \\&={\mathbf {A}}_{e\mathrm {=1}}^{N_{el}}\int _{\Gamma _{q}^{e}} {{\mathbf {N}}_{{\theta }}^{e}q_{n}d\varGamma } { } \end{aligned}$$

(18)

where, u, $\mathbf{M} _{\mathrm {u}}$, $\mathbf{f} ^{\mathrm {int}}$, $\mathbf{f} ^{\mathrm {ext}}$ are the nodal displacement vector, the (lumped) mass matrix, the internal and external force vectors, respectively. Moreover, ${\varvec{\uptheta }}$, $\mathbf{M} _{\theta }$, $\mathbf{K} _{\theta }$, $\mathbf{f} ^{q}$, and $q_{n}$ are the nodal temperature vector, the capacitance matrix, the conductivity matrix, the external heat vector, and the heat flux (normal to surface), respectively. ${\mathbf {A}}$ is the standard finite element assembly operator, ${\mathbf {N}}_{\theta }^{e}$ and ${\mathbf {B}}_{\theta }^{e}$ are the temperature interpolation matrix and its gradient matrix and, finally, ${\mathbf {B}}_{\mathrm {u}}^{e}$ is the standard kinematic matrix mapping the nodal displacement vector into the element strains.

Since the present paper considers concrete under transient thermal loading, the governing equations of motion and heat are solved with an explicit time integrator. The explicit modified Euler method is chosen for time integration of the mechanical part and thermal parts. For mechanical part, it is a second order method (in convergence) having the same critical time step as the central difference scheme (Hahn 1991). The system response is calculated by equations (Saksala 2018a)

$$\begin{aligned}&{\mathbf {M}}_{\mathrm {u}}\ddot{\mathbf{u}}_{t}={\mathbf {f}}_{t}^{\mathrm {ext}}-{\mathbf {f}}_{t}^{\mathrm {int}}{\rightarrow }\ddot{\mathbf{u}}_{t} \end{aligned}$$

(19)

$$\begin{aligned}&\dot{\mathbf{u}}_{t+\Delta t}=\dot{\mathbf{u}}_{t}+{{\Delta }t\ddot{\mathbf{u}}}_{t} \end{aligned}$$

(20)

$$\begin{aligned}&{\mathbf {u}}_{t+\Delta t}={\mathbf {u}}_{t}+\Delta t\dot{\mathbf{u}}_{t+\Delta t} \end{aligned}$$

(21)

$$\begin{aligned}&{\mathbf {M}}_{\theta }{{{\varvec{\uptheta }} }}_{t+\Delta t}{\mathbf {=}}\left( {\mathbf {M}}_{\theta }{\mathbf {-}}{\Delta t{\mathbf {K}}}_{\theta ,t} \right) {{{\varvec{\uptheta }} }}_{t}{\mathbf {+}}\Delta t{\mathbf {f}}_{t}^{q} \end{aligned}$$

(22)

where $\Delta t$ is the time step. Unfortunately, the drawback of this scheme (as well as all other explicit schemes) is the conditional stability with respect to the time step. For the mechanical part, the time step is restricted by the Courant limit $\Delta t =$$\alpha l_{\mathrm {emin}}$/c where $l_{\mathrm {emin }}$is the dimension of the smallest element in the mesh, c is the dilatation wave speed, and $\alpha < 1$ is a security coefficient. Thermal part allows usually time steps several orders of magnitude larger than the mechanical one. Fortunately, the inertia effects in the thermal cracking problem of concrete are so mild that the problem is particularly amenable to the mass scaling technique.

The solution of the uncoupled thermo-mechanical problem of concrete cracking under intensive external heat influx is as follows. First, the temperature field is solved with Eq. (22) while ignoring convection at the boundaries of the concrete domain due to the short heating time ($< 1\hbox { s}$). Then, having the thermal strain due to the new temperature field as a loading (Eq. 14), the model described in Eqs. (6)–(11) is solved at the element level resulting in a new internal force vector for the mechanical part. Finally, the mechanical part is solved by (19)–(21). The solution process is presented as a flow chart in Appendix B.

Finally, the simplifying assumptions and techniques facilitating the formulation of the present modelling approach merit a brief discussion before presenting the numerical simulations. First, the embedded discontinuity kinematics were implemented with the linear triangular element without imposing the crack path continuity over the boundaries of adjacent elements. This approach results in locking problems under certain loading types (mixed mode I/II opening). A remedy of activating a scalar damage model at the later stage of the crack opening process was employed. This remedy, however, generates an undesired side effect of destroying the crack induced anisotropy in the elements where applied. Nevertheless, this shortcoming comes into play only in cyclic or highly rotated stress states. Second, the coupled thermo-mechanical problem related to an element with a discontinuity was simplified by setting thermo-elasticity effects in the bulk material and mechanical dissipation effects at the discontinuity to zero. This assumption, while justified by the governing nature of the external heat influx, makes the modelling approach suitable only for problems of the present class of applications. Third, due to the chosen explicit time marching approach to solve the global system of equations, mass scaling of the mechanical part of the solution scheme (Eqs. 19–22) must be applied in order to increase the critical time step so that practical heating times can be simulated. This choice restricts even more the applicability of the present modelling approach to applications with relatively short time duration. Moreover, as the mass of the mechanical part is scaled, the inertia effects must be negligible.

3 Numerical examples

The above presented numerical method is applied here in modelling concrete fracture in mechanical, thermal and thermo-mechanical loading conditions. First, the boundary conditions and material properties as well as model parameters are specified. Then, the model is tested first in a purely mechanical uniaxial compression and tension tests. Finally, the thermal spalling problem of concrete is simulated under axisymmetric conditions. The effect of lateral mechanical confinement and the surface roughness is also tested. All the simulations are carried out with a self-written Matlab code.

Due to the unfortunate fact that no experiments on spalling of concrete under short duration and high intensity thermal jets were available, a proper model validation is postponed to future studies of the method. However, the model is tested under mechanical loading and the results are discussed in reference to the literature. Moreover, the simulation results are discussed in reference to experiments on plasma shock induced damage on granite rock by Mardoukhi et al. (2017). Finally, there are many numerical studies on thermo-mechanical problems without validation against experiments, see Willam et al. (2014) and Ngo et al. (2014) for example.

3.1 Boundary conditions and material parameters for simulations

The material properties, the values given in Table 1 for the mortar and the aggregates are used if not otherwise explicitly stated. The mechanical and thermal properties of the mortar are the averages of the range given for Portland cement in the site www.engineeringtoolbox.com while the values for aggregates are valid for quartzite rock (Mahabadi 2012). As for the density, a homogeneous value, $2400\,\hbox {kg/m}^{\mathrm {3}}$, is used in all simulations. The viscosity values in Table 1 are chosen small enough so as not to cause notable strain rate hardening at low strain rates in tension and high enough to guarantee the robustness of the simulations, as discussed in Sect. 2.1. Finally, the damage transition parameter, $q_{\mathrm {tr}}/q_{\mathrm {0}}$ representing the ratio of the final (softened) and initial strength, is set to 0.1, which means that the damage model is activated when 90% of the strength is exhausted (Sect. 2.2).

Table 1 Material properties and model parameter values used in simulations

As the focus in this paper is primarily on the mechanical response, only some of the key properties affecting the mechanical response within the present uncoupled modelling are assumed temperature dependent. Namely, for the sake of simplicity, the Young’s modulus, tensile and shear strength are assumed to depend linearly on temperature so that their values at $500\,^{\circ }\hbox {C}$ are 50 % of the corresponding values at room temperature ($293\, ^{\circ }\hbox {K}$) (Ottosen and Ristinmaa 2005; Tufail et al. 2017; Heuze 1983). At $500\, ^{\circ }\hbox {C}$, the thermal expansion coefficient is assumed to increase 1.5 times the value it has at room temperature. Mathematically, the temperature dependence of a property x is thus of form $x\left( \theta \right) =x\left( \theta _{\mathrm {ref}} \right) +K_{x}^{500}(\theta -\theta _{\mathrm {ref}})$ where $K_{x}^{500}$ is the modulus of temperature dependence and $\theta _{\mathrm {ref}}$ is reference temperature. This simplified assumption is sufficient for the present purpose to reveal the effect of temperature dependence in general, not its exact quantification for a specific concrete. It is noted that cracking affects the thermal conductivity. Unlike the temperature dependence of the thermal properties, which is ignored, this effect is tested here in the numerical simulations for the bulk conductivity.

The initial cracks, represented by randomly oriented pre-embedded discontinuities, are assumed to have insignificant tensile and shear strength, say 0.1 MPa. Moreover, the elements in the Interfacial Transition Zone (ITZ) modelled as a strip of elements around the aggregates have strength 50% of the mortar strength. The tensile strength distribution of the numerical concrete is illustrated in Fig. 3b. Moreover, the finite element mesh and the boundary conditions for mechanical and thermo-mechanical simulations are illustrated in Fig. 3a. It is reminded here that the boundaries are thermally insulated.

Fig. 3

Boundary conditions for thermo-mechanical test simulations and the CST mesh with 16,662 elements (a), and tensile strength distribution of numerical concrete (b)

The volume fraction of aggregates in the numerical concrete sample in Fig. 3b is 0.289, a value that does not necessarily represent any real concrete.

3.2 Uniaxial tension test

A uniaxial tension test simulation under plane strain conditions is carried out first. The material and model data given in Table 1 are used. Due to the explicit time stepping, truly quasi-static simulations are beyond any practical convenience. Thereby, a constant boundary velocity condition with $v_{x} = 0.01\hbox { m/s}$, resulting in a strain rate of $0.1\hbox { s}^{\mathrm {-1}}$, is applied. This value is small enough so as not to induce any inertia effects or, with the low viscosity values in Table 1, notable strain rate hardening effects. Neither the initial microcrack population shown in Fig. 2 nor the ITZ by lowering the strengths of the elements surrounding the aggregates are applied here in order to reveal the effect of the aggregates only. The simulation results are shown in Fig. 4.

As the aggregates cause stress perturbations due to the mismatch in elasticity coefficients, they also serve as natural sites for crack initiation. This is indeed the case, as can be observed in Fig. 4a, b. Here, the aggregate edges that are perpendicular to the loading have most of the cracks (note that no ITZ is modelled here). As expected, the aggregates themselves, due to their higher strength, have a small number of cracks. At the post-peak part of the loading process, crack openings localize into a final macro failure mode shown in Fig. 4c. This is the transversal splitting mode with double crack system [see van Mier (1996) and Zhou and Qiao (2020)] for experimental instances of this failure mode). It appears quite commonly in numerical simulations (Nitka and Tejchman 2015; Tang et al. 2016). The corresponding tensile strength of the specimen is 3.4 MPa (Fig. 4d), which is close to the value given to the mortar in Table 1. A notable feature in the stress–strain curve is the non-linear pre-peak part, which is caused by the heterogeneity-induced microcracking.

Fig. 4

Simulation results for uniaxial tension test (without initial cracks and ITZ): Crack distribution (a), a detailed view on cracks (b), failure mode (in terms of crack opening magnitudes) (c), and the corresponding stress–strain curve (d) at the end of simulation

Next, the effect of the ITZ scheme and the initial microcrack population (Fig. 1) is tested. The simulation results are shown in Fig. 5.

Fig. 5

Simulation results for uniaxial tension test (with initial cracks and ITZ): Crack distribution (a), failure mode (in terms of crack opening magnitudes) (b), and the corresponding stress-strain curve (c) at the end of simulation

When the ITZ and the initial microcrack population are included, the crack pattern due to uniaxial tension loading in Fig. 5a is considerably different from that in Fig. 4a. Namely, there are much more new cracks around the aggregates due the ITZ having lowered tensile strength, as can be observed upon comparison of Figures 4a and  5a. Moreover, the initial cracks serve as stress concentrations facilitating thus the initiation of new cracks. The failure mode is the single transversal split mode exhibited in Fig.  5b. As expected, the tensile strength of the specimen is lower, 2.15 MPa to be exact. A notable feature of the stress–strain response in Fig. 5c is the pronounced pre-peak nonlinear part due cracking in the ITZ.

Before moving on, it is interesting to calculate the upper-bound elastic moduli with the rule of mixtures and compare it to the one realized in the simulation (i.e. the slope of the stress–strain curves. The rule of mixtures gives ($E_{\mathrm {ub}} \quad =$$f_{\mathrm {agg}}E_{\mathrm {agg}} \quad +$$f_{\mathrm {mor}}E_{\mathrm {mor}})$ 36.8 GPa while the realized one is 35 GPa.

3.3 Uniaxial compression test

As the present model use the first principal stress criterion as the failure criterion, the uniaxial compressive strength of the numerical concrete is likely to be overpredicted (a homogeneous sample would never fail). The heterogeneities introduced by the aggregates, the initial microcracks and the ITZ surely mitigate this problem by inducing local, short-range tensile stresses. However, if the orientation of the introduced crack is nearly parallel to the loading axis, which is the major principal direction, the required shear component of the traction over the crack may still not be enough to trigger the shear band formation and, consequently, the resulting compressive strength will be overestimated. With a non-structured mesh, a remedy is to reorient the crack by setting it parallel to the element edge whose normal is the most parallel to the first principal (of the stress state in that element) direction. This scheme, which has certain computational benefits (Radulovic et al. 2011; Mosler 2005), is tested here.

In passing, it is interesting to note here that the present principal stress criterion for uniaxial compression test simulation works very well, when heterogeneity is taken into account in some form, with crystalline rocks (e.g. Kuru granite) for which the compressive/tensile strength ratio is about 20 or even more (Saksala 2016). With these rocks, the very existence of mode II as a primary fracture mechanism has been questioned (Doz and Riera 2000).

Uniaxial compression test is next simulated with the present principal stress criterion with the material data in Table 1 and with the reorientation of the crack normal mentioned above. With the latter method, the crack shear strength for mortar is set to 11.5 MPa, which is the average of the values given for the cohesion of Portland cement in www.engineeringtoolbox.com. Moreover, the initial crack population and the ITZ are ignored. The simulation results with the crack reorientation scheme applying a constant boundary velocity of 0.1 m/s (corresponding to a strain rate of 1 $\hbox {s}^{\mathrm {-1}})$ are shown in Fig. 6. The reasons for using this loading rate are the same as for the uniaxial tension test above. Moreover, the compressive strength is expected to be ten times higher than the tensile strength—hence the ten times higher loading rate. This value is still small enough so as not to induce any inertia effects (which start to be significant at $\sim$ 100 $\hbox {s}^{\mathrm {-1}})$. Moreover, with the low viscosity values in Table  1, no notable strain rate hardening effects are produced. Finally, it is noted that the experimental dynamic increase factor at this rate is less than 1.5 (Barpi 2004; Winnicki et al. 2001).

Fig. 6

Simulation results for uniaxial compression test with the crack normal reorientation: Crack distribution (a), detailed view on cracks (b), final failure mode (in terms of crack opening magnitudes) (c), and the corresponding stress–strain curve (d) at the end of simulation

According to the results in Fig. 6a, there are cracks nearly everywhere in the mortar matrix. Some of these cracks traverse the aggregates as well (see Fig. 6a). The reorientation of crack normals facilitates the mobilization of the shear strength, which results, through the localization of crack opening deformation, in a typical experimentally observed shear failure mode (van Mier 1996) in Fig.  6c. The corresponding compressive strength is 33.4 MPa giving the uniaxial compressive/tensile strength ratio 9.8 (33.4/3.4), which is experimentally acceptable (van Mier 1996). It should be stressed here that this reorientation of the crack normal is a numerical trick which of course do not have a counterpart in nature since there are no finite elements in real materials. However, given that the brittle materials have grains and grain boundaries and the fact that a crack path usually follows randomly oriented grain boundaries, i.e. the microcracks are not fully parallel to loading axis in uniaxial compression, this approach is not alien to nature (compare to the rock mechanics implementations of the cohesive zone element method and the discrete element method where cracking takes place along the randomly oriented boundaries of the discrete polygons).

As the final purely mechanical numerical test, the compression test is simulated with the original crack orientation scheme. This time, the ITZ and the initial crack population (in Fig. 1) are included. The simulation results for the values given in Table 1 are shown in Fig. 7.

Fig. 7

Simulation results for uniaxial compression test with the initial microcrack population (blue lines) and ITZ (${{\varvec{n}}}_{d} = {{\varvec{n}}}_{1}$): Crack distribution just before the peak stress (a), at the end of loading (b), final failure mode (in terms of crack opening magnitude) (c), and the corresponding stress-strain curve (d) at the end of simulation

When the crack normal vectors are oriented parallel to the first principal direction, the resulting failure mode changes substantially from the reorientation scheme above. More specifically, the macrocracks are more axially oriented and there are many more cracks in the aggregates (Fig. 7b). As observed in Fig. 7a showing the crack distribution just before the peak stress, the aggregate boundaries, now weakened by the ITZ scheme and the pre-existing microcracks, serve as the initiation sites for new cracks. The corresponding compressive strength is about 54 MPa (the compressive/tensile strength ratio is 25 (52/2.15)), which is about 62% larger than that with the crack reorientation scheme. In any case, it can be concluded that the main features of pure mechanical behavior concrete can be captured with the present modelling approach.

3.4 Thermal and thermo-mechanical loading cases

Thermal cracking test simulations are carried out here with the boundary conditions described in Fig. 3a. Three different heating time/heat flux intensity combinations are tested. These combinations are: (LC1) $T_{\mathrm {heat}} \quad =$ 0.03 s, $q_{n} \quad =$ 1E7 W/m$^{\mathrm {2}}$; (LC2) $T_{\mathrm {heat}} \quad =$ 0.2 s, $q_{n} \quad =$ 2E6 W/$\hbox {m}^{\mathrm {2}}$; (LC3) $T_{\mathrm {heat}} \quad =$ 1 s, $q_{n} \quad =$ 4.5E5 W/$\hbox {m}^{\mathrm {2}}$. Moreover, the effect of surface roughness and the lateral confining pressure are tested. As mentioned, mass scaling must be used in order to keep the simulation times feasible with longer heating durations

3.4.1 LC1: Temperature distribution and stress components for linear elastic material

Before showing the results for thermal cracking, it is instructive to see the stress component distributions in the linear elastic case resulting from the heating. These, along with temperatures, are shown in Fig. 8.

Fig. 8

Simulations results for LC1 with linear elastic material: Temperature distribution (a), temperature–time evolution at the flux nodes (b), and the stress components (c) at the end of simulation

The temperatures at the surface under the heat flux vary between 300 anf $900\,^{\circ }\hbox {C}$ at the end of heating, as shown in Fig. 8b. Due to the very short heating time, the changes in temperature have restricted into a very narrow strip adjacent to the surface. The steep temperature gradient generates a compressive stress state in a narrow strip adjacent to the surface. In this strip, the compressive stress varies between $-50$ to $-250$ MPa. Beneath the compressive stress zone, the radial stress component displays values exceeding the tensile strength of the mortar matrix, see Fig. 8c. It should also be observed that the heterogeneities, i.e. the different mechanical and thermal properties of the matrix and the aggregates, produce stress concentrations as well as shear stresses of considerable magnitude. This is the case at the edge of the thermal jet, $r \quad =$ 0.05 mm, where the vertical ($\sigma _{\mathrm {z}})$ and shear stress ($\sigma _{\mathrm {rz}})$ components have considerable values inside an aggregate located here. These stress component fields help to understand the basic mechanism of the thermal spallation phenomenon: the tensile stresses below the highly compressed disc-shaped layer lead the tensile cracking therein enabling thus the buckling of the compressed surface layer outwards.

3.4.2 LC1: Effect of mass scaling

It appears that the present problem is amenable to extreme mass scaling in the mechanical part. The density for the mass matrix is multiplied with factors of 100 and 10,000, which results, respectively, in 10-fold and 100-fold critical time steps. The simulation results are presented in Fig. 9 for different mass scaling factors. First, the general features of the results are discussed. The induced cracks are parallel to the concrete surface in the compressive stress zone but below it, their orientation is, complying with the tensile stress state therein, perpendicular to the surface. Moreover, the cracks traverse the aggregates as well in the compressive stress zone. The mismatch in the mechanical and thermal properties of the mortar and the aggregates has generated a considerable number of cracks in the ITZ around the aggregates. However, the cracks are restricted quite close to the concrete surface due to the short heating time. Local spalling is predicted here at the elements adjacent to the concrete surface with $r < 0.01\hbox { m}$ (Fig. 9d). It should be noted that the crack opening magnitude is plotted in the deformed meshes without magnification.

Fig. 9

Simulations results for LC1 with different mass scaling: Cracks for no mass scaling (a), for 100-fold density (b), for 10,000-fold density (c), crack opening magnitude without mass scaling (deformed mesh) (d), 100-fold density (e), for 10,000-fold density (f) at the end of simulations

As for the mass scaling effects, the results with no mass scaling and with 100-fold density are virtually identical (compare Fig. 9a and d to b and e). In contrast, when the density is 10,000-fold, local differences appear, as can be observed in Fig. 9c and f. The most notable difference is that the heavy deformation of the surface elements is predicted at different locations with the larger mass scaling. However, these differences are not so dramatic as to invalidate the results computed with this extreme mass scaling altogether.

Fig. 10

Simulations results for LC1 with different mass scaling: Details of cracks without mass scaling (left), for 10,000-fold density (right)

Finally, a detail of cracks for the case without mass scaling and for the case with 10,000-fold density is shown in Fig. 10. As can be observed, there are more cracks in the mass scaled results than in the solution without mass scaling.

3.4.3 LC2: Influence of ITZ, initial cracks, and temperature dependence of material properties

Due to the longer heating time, simulations for this load case are carried out with the milder mass scaling, which gave results almost identical to the case without mass scaling. The simulation results are shown first in Fig. 11 for the case where the ITZ, initial crack distribution, and temperature dependence of the material properties (see Sect. 3.1) are included. Then, these features are ignored in another simulation to see their effect.

Fig. 11

Simulations results for LC2 (100-fold density): Cracks (a), temperature–time evolution at the flux nodes (b), crack opening magnitude (deformed mesh, no magnification) (c), and a detail with different scale (d), and isotropic damage (e) at the end of simulation

The temperature reaches $600\,^{\circ }\hbox {C}$ in some of the surface nodes under the thermal flux at the end of exposure. It should be noted that this temperature is enough for spalling to occur in granitic rocks (Kant and von Rohr 2016) so that the aggregate cracking visible in Fig. 11a is realistic. There are also more cracks here than in LC1 between the aggregates adjacent to the surface (Fig.  11a). Moreover, the crack openings display considerably more pronounced values so that spalling is predicted in a wider area (note the different scale of crack opening norm in Fig. 11d). Indeed, the isotropic damage variable approaches unity at many elements (see Fig. 11e) meaning that the tensile strength at the cracks in those elements is totally exhausted. Considering the temperature range (from 430 to $660 \,^{\circ }\hbox {C}$ (Liu et al. 2018)) within which the concrete spalling has been observed, this prediction is in accordance with the experiments.

Next, the ITZ, the initial crack population, and the temperature dependence are ignored in order to see their joint effect on the thermal cracking. The results are shown in Fig. 12.

Fig. 12

Simulations results for LC2 (100-fold density) without ITZ, initial cracks and temperature dependence of the material properties: Cracks (a) and crack opening magnitude (b) at the end of simulation

The results in Fig. 12 display many fewer cracks and the opening magnitudes are modest. Definitely, no spalling is expected here. The effect, combined or individual, of the initial cracks and the ITZ is less pronounced than that of the temperature dependent material parameters.

3.4.4 LC2: Influence of surface roughness and confining pressure

In reality, concrete structures (e.g. circular slab of a footing under lateral confinement at depth) are subjected to loading and their surfaces are not perfectly smooth as in the simulations above. Therefore, it is important here to test the combined effect of surface roughness and radial confinement stress on the crack pattern and damage induced by the heat shock. Moreover, it is interesting to see the effect of the lateral confinement as it adds to the compressive stress state due to temperature gradient. The surface roughness is accounted for by adding a random perturbation vector with an average component of 0.25 mm to the y-coordinates of the mesh surface (upper edge) nodes. Moreover, a radial initial stress of 5 MPa is applied gradually (i.e. increasing from 0 to 5 MPa during a rise time of 0.05 s) before the application of the heat flux (see Fig. 3a). The simulation results are shown in Fig. 13.

Fig. 13

Simulations results for LC2 (100-fold density): Cracks (a), crack opening magnitudes (undeformed mesh) (b), isotropic damage variable distribution (c), temperature–time evolution at the flux nodes (d), radial stress component (deformed mesh) (e), and temperature distribution (f) at the end of simulation

The combined effect of the surface roughness and the confining pressure is notable (see Fig. 13). To some extent, the confinement suppresses cracking at the non-favorably oriented edges of the ITZs around the aggregates (compare Figs. 11a, c to  13a, b). However, it should be noted that the results for the crack opening magnitude distribution in Fig. 13b are plotted in the undeformed mesh due to heavy deformation of some of the elements adjacent to the concrete surface shown in Fig. 13e. This behavior did not affect the computation due to the explicit solution scheme employed. Moreover, the isotropic damage parameter approaches unity at these elements (see Fig. 13c). Consequently, the nominal stress components at these heavily damaged elements is close to zero, as can be observed in Fig. 13e, meaning an insignificant contribution to the internal force vector (17). It can be concluded that a combination of surface roughness and lateral (to the heat flux direction) confinement facilitates the thermal spalling by amplifying the buckling mechanism of the surface cracks.

It should be noted here that spalling is not predicted in the simulations above as it appears in reality, i.e. buckling and ejection of rock chips from the surface. The main reason is the switching on of the isotropic damage model, which eliminates all the stresses (spurious and real ones alike) in the element by Eq. (14). Consequently, the highly damaged elements cannot bear any compressive stresses and the buckling, and hence the ejection of the strip of elements adjacent to the surface is prevented. Another reason is that hygro-thermal effects, especially the pore pressure, which enhance the spalling phenomenon, are not accounted for at the present stage of the model.

3.4.5 LC3

The third load case with the longest heating time and lowest flux magnitude is applied here. As the heating time is 1 s, the simulation is carried out with the larger, 10,000-fold mass scaling. The simulation results are shown in Fig. 14.

Fig. 14

Simulations results for LC3 (10,000-fold density): Cracks (a), crack opening magnitudes (b), temperature–time evolution at the flux nodes (c),and temperature distribution (d) at the end of simulation

With LC3, as the final temperature levels reached at the surface nodes are considerably lower than those in previous loading cases, the resulting crack opening magnitudes in the elements adjacent to the concrete surface also remained substantially lower than those in LC2. Nevertheless, there are four elements even here (adjacent to the surface with $r \quad \sim$ 7 mm) where the isotropic damage variable approaches unity. Therefore, spalling, albeit very local, is predicted here as well. Moreover, the crack opening magnitudes around the aggregates are similar or even slightly larger than in the previous loading cases.

3.4.6 Mesh size effect

The effect of mesh size is tested. For simplicity, the ITZ and the microcrack distribution are ignored here. Loading case 2 is applied with the 10,000-fold mass scaling. The simulation results for the original mesh (16,662 elements with average element size 1 mm) and for a finer mesh with 39,569 elements (average element size 0.65 mm) are shown in Fig. 15.

Fig. 15

Simulations results for mesh refinement test (LC2, 10,000-fold density) without ITZ, initial cracks and temperature dependence of the material properties: Cracks with the original mesh (a), finer mesh (b), crack opening magnitudes with the original mesh (c), finer mesh (d), and temperature–time evolution at the flux nodes with the original mesh (e) and the finer mesh (f)

The results with the original and refined meshes show similar general features but the details deviate to some extent. The temperature evolutions at the flux nodes in Fig. 15e, f are reasonably similar. Moreover, the number of cracks is naturally higher with the finer mesh, and the details of the crack opening magnitude patterns in Fig. 15c, d differ as well. However, these deviations are not severe enough to disqualify the results obtained with the original mesh.

3.4.7 Effect of cracking on thermal conductivity of the bulk material

The final simulation tests the effect of cracking on the thermal conductivity of the material. For this end, following Willam et al. (2014), an exponential degradation of the thermal conductivity as a function of crack opening magnitude is employed as

$$\begin{aligned} k\left( \left\| {{{\varvec{\upalpha }}}}_{d} \right\| \right) =k_{0}\mathrm {exp}(-g\left\| {{{\varvec{\upalpha }}}}_{d} \right\| ) \end{aligned}$$

(23)

where $k_{\mathrm {0}}$ is the initial value of thermal conductivity and g is defined in Sect. 2.2. This choice actually synchronizes the degradation of the conductivity with the traction-separation law in Sect. 2.1. Note also that the norm of the displacement jump is used in (23) instead of the history variable ${\alpha }_{d}$ of the isotropic damage model since, upon crack closure, the thermal conductivity recovers.

This setting renders the global thermo-mechanical problem coupled, i.e. there is two-way information flow between the mechanical and the thermal parts. However, no modifications are needed in the global solution scheme due to its explicit nature. Simulation results for LC2 are shown in Fig. 16.

Fig. 16

Simulations results for cracking dependent conductivity (LC2, 100-fold density): Cracks (a), temperature–time evolution at the flux nodes (b), crack opening magnitude (deformed mesh, no magnification) (c), and isotropic damage (d) at the end of simulation

Comparing the results in Fig. 16 to those in Fig. 11, it can observed that the effect of cracking on thermal conductivity is considerable. Namely, the temperature evolution at the flux nodes, solved from Eq. (22), is now reaching much higher values at the end of simulation. This can be understood after noting that the entries of the conductivity matrix in (22) approach zero as the crack opening increases (in the failed elements). This leads to a linear temperature evolution, as Eq. (22) becomes linear with a constant external heat vector. The difference in the temperature evolution is naturally reflected in the details of the final failure modes in Figs. 11c and  16c.

4 Discussion

A mesoscopic numerical method for concrete under thermal and mechanical loadings based on embedded discontinuity finite elements was developed in this paper. This approach describes the concrete mesostructure explicitly by modelling the aggregates as randomly shrunken and rotated Voronoi polygons. The mortar and the aggregates were meshed with linear triangle elements which allows the interfacial transition zones to be accounted for as strips of weaker elements around the aggregates. With the chosen first principal stress (Rankine) criterion, the accommodation of heterogeneity is indispensable to have any fracturing in uniaxial compression test simulations. This approach is also suitable to account for the inherent microcrack populations in concrete cement matrix as pre-embedded discontinuities with lowered strengths.

As for the thermal cracking, the model was designed to simulate concrete demolition by high intensity, short duration heat shocks exploiting the thermal spalling phenomenon. Due to the highly dominating role of the external heating (heat shock), the mechanical heating effects were neglected and, consequently, the underlying thermo-mechanical problem was solved as an uncoupled problem. An explicit time marching with mass scaling was employed for this purpose. Due to the heavy deformation of the elements during the spalling stage and almost perpendicular crack orientations in adjacent elements close to the specimen surface, an implicit solution scheme would face insurmountable convergence difficulties. On the other hand, in the explicit method the mechanical part suffers from the conditional (time step) stability, which is a serious drawback in thermo-mechanical problems.

In the axisymmetric simulations of a numerical concrete plate subjected to local surface heat shocks of various intensity and duration were tested. However, spalling was not predicted in the simulations above as it appears in reality, i.e. buckling and ejection of concrete chips from the surface. The main reason is the switching on of the isotropic damage model, which eliminates all the stresses (spurious and real ones alike) in the element by Eq. (14). Consequently, the highly damaged elements cannot bear any compressive stresses and the buckling, and hence the ejection, of the strip of elements adjacent to the surface is prevented. Another reason is that hygro-thermal effects, especially the pore pressure, which enhance the spalling phenomenon, are not accounted for at the present stage of the model. Instead of the ejection of concrete chips, spalling was predicted as highly damaged elements.

Finally, the reliability of the results is addressed. As already mentioned, the mechanical part does predict the realistic failure modes of concrete under uniaxial tension and compression. Moreover, spalling in the numerical simulations was predicted within the temperature range of the experiments, i.e. from 430 to $660\,^{\circ }\hbox {C}$ (Liu et al. 2018). As for the evaluation of spalling depth, no experiments were available to the author. However, experiments on granite rock based on a plasma torch treatment do exist. Mardoukhi et al. (2017) performed heat shock experiments on Kuru granite with a plasma torch. In their setup, the plasma torch (with a nominal power or 50 kW and a jet diameter of 20 mm) was moved at a constant velocity of 50 mm/s at a distance 6.5 cm over a Kuru granite sample. An example of the resulting damage patterns is shown in Fig. 17.

Fig. 17

Optical images (under UV light) of a Kuru granite surface before (a) and after (b), and identified cracks/craters before (c) and after (d), the plasma jet treatment, and the surface of a specimen in the normal light after the experiment (the arrow indicates the direction of the movement of the plasma torch, and the dashed lines in (e) marks the border of the affected zone)

In this setup, the heating time of a rock surface points under the circular jet varied from a negligible time (at the outer edge) to 0.4 s (at the center), which is of the same order of magnitude as in the simulations presented here. Figure 17 shows clear damage due to thermal spalling. The depth of the craters thus induced ranged from 0.2 to 0.8 mm, which does not deviate too much from the thickness of the damaged layer in the present simulations. However, it should be noted that the Kuru granite has the tensile strength of about 10 MPa, which is more than twice the mortar tensile strength (3.5 MPa) used here but equal to the tensile strength of the aggregates (which also failed in some of the simulations here). Moreover, it should be mentioned that the plasma torch gases have a large flow velocity (about 50–100 m/s at the distance applied in these experiments), which contributed to the removal of the loose spalls from the rock surface. Furthermore, the surface temperatures during the heating or after it were not determined. It was also impossible to evaluate the heat flux to the rock surface at the distance of 6.5 cm. Despite these shortcomings, these experimental results provide some credibility and qualitative validation for the present thermal spalling simulations.

Another aspect of the validity of the results concerns the fact that the mesostructure of the numerical concrete was generated by some random processes (location of initial cracks and their location, the shrinkage of aggregates and their rotation) and yet only a single sample was considered. Now, this issue is more relevant concerning the mechanical simulations where stress state is global and different mesostructures lead to different details of the failure mode and to deviation of the peak strength, see Saksala (2018a, (2018b) for an example. However, the influence of mesostructural architecture is far less pronounced in the heat shock simulations where the stress state is more local. Moreover, the numerical concrete mesostructure was so designed that the area subjected to the heat flux has all the relevant features of the numerical concrete. Indeed, there are aggregates having a common edge with the free rock surface subjected to the heat flux, and aggregates with only a vertex touching the heated part of the free surface. Moreover, there is plain mortar as well as the mortar with initial cracks on the heated surface. Therefore, as simulations on different mesostructures did not result in drastic deviations, it can be concluded that the heat shock simulation results are representative while the mechanical test simulations may have deviations in detail, depending on the particular mesostructure.

5 Conclusions

The present numerical study on the demolition of concrete by high intensity, short duration thermal shocks involved the development of a suitable numerical approach and its application in both purely mechanical and thermo-mechanical problems. Concerning the mechanical constitutive tests, the following conclusions on the present approach can be cautiously drawn:

• 1. The salient features of concrete behavior in uniaxial compression and tension tests, including the global pre-peak and post-peak nonlinearities, can be captured by an embedded discontinuity FEM model having a linear elastic behavior up to fracture (introduction of a crack) at the material point level, if heterogeneity description due to aggregates (modelled here as Voronoi polygons), the ITZ (modelled here as a narrow strip of elements with lowered strength around the aggregates) and inherent microcracks (modelled here as a pre-embedded randomly oriented discontinuity population) is included.

• 2. The typical failure modes of low and high strength concretes can be predicted with the embedded discontinuity FEM, having the first principal stress criterion as the crack initiation criterion, when a crack re-orientation scheme is employed: If the crack normal is parallel to the first principal direction, high strength concrete behavior with the multiple axial splitting mode is realized. When the crack is re-oriented parallel to the element edge, which is most parallel to the first principal direction, the typical shear banding of low strength concrete samples results.

Concerning the uncoupled explicit thermo-mechanical solution scheme and its application in simulations of concrete demolition heat shocks, the following conclusions can be drawn:

• 1. Due to the quasi-static nature of thermally induced cracking, the mechanical part of the explicit thermo-mechanical solution scheme is amenable to extreme mass scaling by which the critical time step can increase to 100-fold without losing the overall quality of the solution.

• 2. The axisymmetric simulations of a numerical concrete plate subjected to local surface heat shocks demonstrated that concrete demolition by short duration and high intensity thermal jet is a viable method: In the simulations, the most pronounced spalling was predicted in the case with 0.2 s of duration and 2E6 W/m$^{\mathrm {2}}$ of flux intensity, with the surface temperature reaching $600\,^{\circ }\hbox {C}$.

• 3. As the present method is able to account for various environmental conditions, such as the ITZ, inherent microcracks, surface roughness and confining pressure, it could serve as a tool in the development of the thermal shock based concrete demolition techniques, especially after an extension to include hygro-thermal effects and to genuine 3D setting.

Appendices

Appendix A

The thermodynamic aspects of the model are considered here. The starting point is the postulation of a free energy potential. Before that, however, the continuum mechanics counterparts of Eqs. (1) and (2) are written in form

$$\begin{aligned}&{\mathbf {u}}\left( {\mathbf {x}} \right) =\bar{\mathbf{u}}\left( {\mathbf {x}} \right) \nonumber \\&\qquad \qquad +M_{{\Gamma }_{d}}\left( {\mathbf {x}} \right) {{{\varvec{\upalpha }} }}_{d}\hbox { with }M_{{\Gamma }_{d}}\left( {\mathbf {x}} \right) =H_{{\Gamma }_{d}}\left( {\mathbf {x}} \right) -\varphi \left( {\mathbf {x}} \right) \nonumber \\ \end{aligned}$$

(A1)

$$\begin{aligned}&{\varvec{\upvarepsilon }}\left( {\mathbf{x}} \right) = \mathop {\underbrace{{{{\nabla ^s}{{\bar{{\mathbf{u}}}}}\left( {\mathbf{x}} \right) - {{\left( {\nabla \varphi \left( {\mathbf{x}} \right) \otimes {{\varvec{\upalpha }}_d}} \right) }^s}}}}}\limits _{{{\bar{\varvec{\upvarepsilon }}}}\left( {\mathbf{x}} \right) }\nonumber \\&\qquad \qquad + \delta _{{{{\Gamma }}_d}} \mathop {\underbrace{{\left( {{\mathbf{n}} \otimes {{\varvec{\upalpha }}_d}} \right) }^s}}\limits _{{{{\varvec{\upvarepsilon }}_\delta }\left( {\mathbf{x}} \right) }} \end{aligned}$$

(A2)

where $\bar{\mathbf{u }}$ is the regular displacement, and ${\varvec{\alpha }}_{d}$ is the displacement jump over the discontinuity ${\Gamma }_{d}$. Moreover, ${(\cdot )}^{s}$ denotes the symmetric part of $\left( \cdot \right)$ while $\bar{\varvec{\upvarepsilon } }\mathbf {(}{\mathbf {x}}\mathbf {)}$ (${\mathbf {x}\in }{\Omega }_{e}{\setminus }{\Gamma }_{d})$ and ${{\varvec{\upvarepsilon }}}_{\delta }({\mathbf {x}})$ (${\mathbf {x}\in }{\Gamma }_{d})$ in (A2) are the regular and irregular (singular) parts of the strain, respectively. In addition, under the infinitesimal deformation assumption the strain can be additively split into mechanical and thermal parts by

$$\begin{aligned} {\varvec{\upvarepsilon }} ={{{\varvec{\upvarepsilon }} }}_{m}+{{{\varvec{\upvarepsilon }}}}_{\theta }=\bar{{\varvec{\upvarepsilon }} }+ \mathop {\underbrace{{{\varvec{\upvarepsilon }}}_{\delta }\delta _{\Gamma _d}}}\limits _{\bar{\bar{{\varvec{\upvarepsilon }}}}} +{{\upvarepsilon }}_{\theta } \end{aligned}$$

(A3)

where thermal strain is ${{\varepsilon }}_{\theta }\mathbf {=}\alpha (\theta )(\theta -\theta _{0}){\mathbf {I}}$ (as in Eq. (14)). Now, the free energy per unit volume for the present model is defined by (compare to Grassl and Jirásek (2006); Ngo et al. (2013, (2014)

$$\begin{aligned}&\rho \psi \left( {{{\varvec{\upvarepsilon }}}},\kappa ,\omega ,\theta \right) \nonumber \\&\quad =\frac{1}{2}\left( 1-\omega \right) \left( {{{\varvec{\upvarepsilon }} }}-{{{\varvec{\upvarepsilon }} }}_{\theta } \right) :\mathbf {E}(\theta ):({\varvec{\upvarepsilon }} -{{{\varvec{\upvarepsilon }}}}_{\theta } )\nonumber \\&\quad +\psi _{p}\left( \kappa \right) +\rho c\left( \left( \theta -\theta _{0} \right) -\theta \ln \left( \frac{\theta }{\theta _{0}} \right) \right) \nonumber \\&\quad = \mathop {\underbrace{{{1 \over 2}\left( {1 - \omega } \right) \left( {{{\bar{\varvec{\upvarepsilon }}}} - {{{{\varvec{\upvarepsilon }}}}_\theta }} \right) :\mathbf{{E}}\left( \theta \right) :\left( {{{\bar{\varvec{\upvarepsilon }} }} - {{{{\varvec{\upvarepsilon }}}}_\theta }} \right) }}}_{{{\psi _m}}}\nonumber \\&\qquad + \mathop {\underbrace{{\rho c\left( {\left( {\theta - {\theta _0}} \right) - \theta \ln \left( {{\theta \over {{\theta _0}}}} \right) } \right) }}}\limits _{{\psi _\theta }}\nonumber \\&\qquad +\mathop {\underbrace{{1 \over 2}\left( {1 - \omega } \right) {\bar{\bar{\varvec{\upvarepsilon }}}}:\mathbf{E}\left( \theta \right) : {\bar{\bar{\varvec{\upvarepsilon }}}}+ {\psi _p}\left( \kappa \right) }}\limits _{{\psi _d}} \end{aligned}$$

(A4)

where, $\psi _{\theta }$ and $\psi _{m}$ are the thermal and regular mechanical part of the free energy defined for ${\mathbf {x}\in }{\Omega }_{e}{\setminus }{\Gamma }_{d}$, and $\psi _{d}$ is singular part of the free energy defined for ${\mathbf {x}\in }{\Gamma }_{d}$ with ${ \psi }_{p}$ being the “plastic” part governing the softening at the discontinuity by ${q=- \partial \psi }_{p}/\partial \kappa$, where q is the stress like softening variable in Eq. (8).

Now, the stress–strain relation (14) and the thermodynamic force conjugate to the damage variable, i.e. the damage energy release rate Y, can be obtained by the standard procedure as

$$\begin{aligned}&{{{\varvec{\sigma }}}}=\rho \frac{\partial \psi }{\partial {{{\varvec{\upvarepsilon }}}}}=\rho \frac{\partial \psi _{m}}{\partial \bar{{\varvec{\upvarepsilon }}}}\nonumber \\&\quad =\left( 1-\omega \right) {\mathbf {E}}(\theta ):\left( \bar{{\varvec{\upvarepsilon }} }-{{{\varvec{\upvarepsilon }}}}_{\theta } \right) ,\quad Y=-\rho \frac{\partial \psi }{\partial \omega }\nonumber \\&\quad =\frac{1}{2}\left( {{{\varvec{\upvarepsilon }} }}-{{{\varvec{\upvarepsilon }}}}_{\theta } \right) :{\mathbf {E}}(\theta ):\left( {{{\varvec{\upvarepsilon }}}}-{{{\varvec{\upvarepsilon }}}}_{\theta }\right) \end{aligned}$$

(A5)

Next, the dissipation inequality for deriving Eq. (10) is needed. As the model is linear elastic up to fracture, all the dissipative processes, save the thermal dissipation, take place in the discontinuity. Hence, under the present assumption of negligible thermo-elastic effects in the bulk continuum material, the dissipation inequality can be written as (Ottosen and Ristinmaa 2005)

$$\begin{aligned} {{{\mathcal {D}}}} = \mathop {\underbrace{{\mathbf{{t}}_{{\Gamma _d}}}\cdot {{{{\dot{\varvec{\upalpha }}}}}_d} - q{\dot{\kappa }} + Y{\dot{\omega }} }}\limits _{{\mathcal{D}_m}} - \mathop {\underbrace{\mathbf{{q}}\cdot \nabla \theta /\theta }}\limits _{{{{{\mathcal {D}}}}_\theta }} \ge 0 \end{aligned}$$

(A6)

where ${\mathcal {D}}_{\theta }$ is the thermal dissipation with the flux vector being ${\mathbf {q=-}}k{\nabla }\theta$ (Fourier’s law), as defined earlier. It is straightforward to show that the present model fulfills the dissipation inequality. By the Fourier’s law, the last term is nonpositive and hence its negation always nonnegative. Moreover, as E is positive definite, Y in (A5) is always nonnegative. In addition, as $\dot{\omega }$ is always nonnegative by construction, the damage dissipation$Y\dot{\omega }$ is always nonnegative. As for the product $q\dot{\kappa }$, it is clearly nonpositive for pure softening “plasticity” ($h\leqslant )$ as $\dot{\kappa }$ is nonnegative by Eq. (10). Therefore, the negation of this product is always nonnegative. Finally, the first term ${\mathbf {t}}_{\Gamma _{d}}\cdot \dot{\alpha }_{d}$ is shown to be nonnegative as follows:

$$\begin{aligned}&{\mathbf {t}}_{\Gamma _{d}}\cdot \dot{{\varvec{\upalpha }}}_{d}=\left( {{{\varvec{\upsigma }} \cdot }}{\mathbf {n}}_{d} \right) \cdot \left( \dot{\lambda }_{\mathrm {t}}{\mathbf {n}}_{d}+\dot{\lambda }_{\mathrm {s}}\mathrm {sgn}\left( {\mathbf {m}}_{d}\cdot {\mathbf {t}}_{{\Gamma }_{d}} \right) {\mathbf {m}}_{d} \right) \\&\quad =\dot{\lambda }_{\mathrm {t}}{\mathbf {t}}_{{\Gamma }_{d}}{{\cdot }}{\mathbf {n}}_{d}\mathbf {+}\dot{\lambda }_{\mathrm {s}}\mathop {\underbrace{\mathrm{{sgn}}\left( {{\mathbf{{m}}_d}\cdot {\mathbf{{t}}_{{{{\Gamma }}_d}}}} \right) {\mathbf{{m}}_d}\cdot {\mathbf{{t}}_{{{{\Gamma }}_d}}}}}\limits _{\left| {\mathbf{{m}}\cdot {\mathbf{{t}}_{{{{\Gamma }}_d}}}} \right| } \ge 0 \end{aligned}$$

where Eqs. (5) and (10) have been used. Moreover, $\dot{\lambda }_{\mathrm {t}}$ and $\dot{\lambda }_{\mathrm {s}}$ are nonnegative by Eq. (11). Finally, term ${\mathbf {t}}_{{\Gamma }_{d}}{{\cdot }}{\mathbf {n}}_{d}{\geqslant }$ for all ${\mathbf {t}}_{{\Gamma }_{d}}$ such that $\phi _{\mathrm {t}}={\mathbf {n}}{\cdot }{\mathbf {t}}_{{\Gamma }_{d}}-\left( \sigma _{\mathrm {t}}\left( \theta \right) +q\left( \kappa ,\dot{\kappa } \right) \right) =0$, since $\sigma _{\mathrm {t}}\left( \theta \right) +q\left( \kappa ,\dot{\kappa } \right)$ is always positive. Thus, the dissipation inequality is fulfilled.

Actually, as the model is formulated analogously to the associated plasticity models, the mechanical dissipation inequality without damage is automatically fulfilled by Eq. (10) (Ottosen and Ristinmaa 2005) due to the convexity of the loading functions. Therefore, it remains to be shown that these evolution equations can be derived by the postulate of maximum dissipation. This is done as follows [see Mosler (2005); Ngo et al. (2013, (2014)]. The solution for the maximum of the constraint maximum dissipation problem is equivalent to the Kuhn–Tucker conditions of the free optimization problem of the Lagrangian

$$\begin{aligned} {\mathcal {L}}\left( {\mathbf {t}}_{\Gamma _{d}},q,Y,\theta ,\dot{\lambda }_{\mathrm {t}},\dot{\lambda }_{\mathrm {s}} \right) =-{\mathcal {D}}+\dot{\lambda }_{\mathrm {t}}\phi _{\mathrm {t}}\mathbf {+}\dot{\lambda }_{\mathrm {s}}\phi _{\mathrm {s}} \end{aligned}$$

(A7)

from which Eqs. (10) and (11) follow as the stationary conditions, e.g.

$$\begin{aligned}&\frac{\partial L}{\partial {\mathbf {t}}_{\Gamma _{d}}}=-\frac{\partial D}{\partial {\mathbf {t}}_{\Gamma _{d}}}+\dot{\lambda }_{\mathrm {t}}\frac{{\partial \phi }_{\mathrm {t}}}{\partial {\mathbf {t}}_{\Gamma _{d}}}+\dot{\lambda }_{\mathrm {s}}\frac{{\partial \phi }_{\mathrm {s}}}{\partial {\mathbf {t}}_{\Gamma _{d}}}\nonumber \\&\quad \Rightarrow \dot{{\varvec{\upalpha }} }_{d}\mathbf {=}\dot{\lambda }_{\mathrm {t}}\frac{{\partial \phi }_{\mathrm {t}}}{\partial {\mathbf {t}}_{\Gamma _{d}}}\mathbf {+}\dot{\lambda }_{\mathrm {s}}\frac{{\partial \phi }_{\mathrm {s}}}{\partial {\mathbf {t}}_{\Gamma _{d}}} \end{aligned}$$

(A8)

$$\begin{aligned}&\frac{\partial L}{\partial q}=-\frac{\partial D}{\partial q}+\dot{\lambda }_{\mathrm {t}}\frac{{\partial \phi }_{\mathrm {t}}}{\partial q}\mathbf {+}\dot{\lambda }_{\mathrm {s}}\frac{{\partial \phi }_{\mathrm {s}}}{\partial q}\nonumber \\&\quad \Rightarrow \dot{\kappa }\mathbf {=-}\dot{\lambda }_{\mathrm {t}}\frac{{\partial \phi }_{\mathrm {t}}}{\partial q}\mathbf {-}\dot{\lambda }_{\mathrm {s}}\frac{{\partial \phi }_{\mathrm {s}}}{\partial q} \end{aligned}$$

(A9)

which are Eq. (10). This concludes the thermodynamic considerations of the present model.

Appendix B

A flow chart for the solution process of the problem of heat shock induced cracking of concrete is presented here (Fig. 18).

Fig. 18

Flow of the thermo-mechanical solution process

The stress return mapping is performed by the following update formulae (valid when both $\phi _{\mathrm {t}}>0$ and $\phi _{\mathrm {s}}>0)$:

$$\begin{aligned} \begin{aligned} \lambda _{\mathrm {t},k+1}&=\lambda _{\mathrm {t},k}+\delta \lambda _{\mathrm {t},k}, \lambda _{\mathrm {s},k+1}=\lambda _{\mathrm {s},k}+\delta \lambda _{\mathrm {s},k} \\ {\Delta }\lambda _{\mathrm {t,}k\mathrm {+1}}&={\Delta }\lambda _{\mathrm {t,}k}+\delta \lambda _{\mathrm {t},k}, {\Delta }\lambda _{\mathrm {s,}k\mathrm {+1}}={\Delta }\lambda _{\mathrm {s,}k}+\delta \lambda _{\mathrm {s},k} \\ \delta {{\varvec{\upalpha }}}_{\mathrm {I},k+1}&=\delta {{\varvec{\upalpha }} }_{\mathrm {I},k}+\delta \lambda _{\mathrm {t},k}{{\varvec{n}}}, \delta {{\varvec{\upalpha }}}_{\mathrm {II,}k\mathrm {+1}}\\&=\delta {{\varvec{\upalpha }}}_{\mathrm {II,}k}+\mathrm {sgn}({\mathbf {t}}_{\Gamma _{d}}\cdot {{\varvec{m}}})\delta \lambda _{\mathrm {s},k}{{\varvec{m}}} \\ \delta {{\varvec{\upalpha }}}_{d,k+1}&=\delta {{\varvec{\upalpha }}}_{\mathrm {I},k+1}+\delta {{\varvec{\upalpha }} }_{\mathrm {II,}k\mathrm {+1}}, {{\varvec{\upalpha }} }_{d,k+1}\\&\quad ={\alpha }_{d,k}+\delta {{\varvec{\upalpha }} }_{d,k+1} \\ \mathbf {t}_{{\Gamma }_{d},k+1}&=\mathbf {t}_{{\Gamma }_{d},k}-\mathbf {n}\cdot {\mathbf {E}}(\theta ):(\nabla \varphi \otimes \delta {{\varvec{\upalpha }}}_{d,k+1})^{sym} \\ \kappa _{k+1}&=\lambda _{\mathrm {t},k+1}+\frac{\sigma _{\mathrm {s}}}{\sigma _{\mathrm {t}}}\lambda _{\mathrm {s},k+1}. \dot{\kappa }_{k+1}\\&={\Delta }\lambda _{\mathrm {t},k+1}+\frac{\sigma _{\mathrm {s}}}{\sigma _{\mathrm {t}}}{\Delta }\lambda _{\mathrm {s},k+1} \end{aligned} \end{aligned}$$

where the crack opening increments $\delta \lambda _{\mathrm {t},k}$ and $\delta \lambda _{\mathrm {s},k}$ are solved by

$\mathbf{G }\delta {{\varvec{\lambda }} }=\mathbf{F }$ with

$$\begin{aligned} {\varvec{G}}= & {} \left[ {\begin{array}{*{20}c} \mathbf{n} \cdot \left( \mathbf{n} \cdot {\mathbf {E}}\left( \theta \right) \cdot \nabla \varphi \right) \cdot \mathbf{n}+ h\\ +\frac{s}{{\Delta }t} \frac{\partial \varphi _{s}}{\partial \mathbf{t} _{\Gamma _{d}}}{} \mathbf{n} \cdot (\mathbf{n} \cdot {\mathbf {E}}(\theta )\cdot \nabla \varphi )\cdot \mathbf{m} +\frac{\sigma _{\mathrm {s}}}{\sigma _{\mathrm {t}}}(h+\frac{s}{{\Delta }t})\\ \frac{\partial \phi _{\mathrm {s}}}{\partial \mathbf{t} _{\Gamma _{d}}}{} \mathbf{m} \cdot (\mathbf{n} \cdot {\mathbf {E}}(\theta )\cdot \nabla \varphi )\cdot \mathbf{n} \\ +\frac{\sigma _{\mathrm {s}}}{\sigma _{\mathrm {t}}}(h+\frac{s}{{\Delta }t}) \mathbf{m} \cdot (\mathbf{n} \cdot {\mathbf {E}}(\theta )\cdot \nabla \varphi )\cdot \mathbf{m} +(\frac{\sigma _{\mathrm {s}}}{\sigma _{\mathrm {t}}})^{2}(h+\frac{s}{{\Delta }t})\\ \end{array} } \right] \\ \delta {{\varvec{\lambda }} }= & {} \left( {\begin{array}{*{20}c} \delta \lambda _{\mathrm {t}}\\ \delta \lambda _{\mathrm {s}}\\ \end{array} } \right) , \mathbf{F} =\left( {\begin{array}{*{20}c} \phi _{\mathrm {t}}\\ \phi _{\mathrm {s}}\\ \end{array} } \right) \end{aligned}$$

After the convergence is reached, i.e. $\phi _{\mathrm {t}}({{\varvec{\sigma }} }_{k+1},\kappa _{k+1},\dot{\kappa }_{k+1})<TOL$ and $\phi _{\mathrm {s}}({{\varvec{\sigma }} }_{k+1},\kappa _{k+1},\dot{\kappa }_{k+1})<TOL$, the new stress is calculated with Eq. (14).