1 Introduction

The field of cyclic mechanical fatigue is one of the most important branches of post and current research in engineering. Catastrophic failures of different types of technical structures like trains, airplanes, bridges, turbine rotors, pressure vessels and others, occurred as consequence of the fatigue of materials. Accordingly, this phenomenon must be kept in the focus of present studies. From a material science perspective, the fatigue mechanism principles are mostly understood and explained in several textbooks by e.g. Dowling (2013), Schijve (2009), Haibach (2006). The total fatigue life of a structure is generally divided into two phases. The crack nucleation phase describes the period in which a microcrack is initiated as a consequence of irreversible cyclic slip in grains with proper orientation and the growth of this microcrack to an order where it is visible with the naked eye or at least by utilizing a low rate magnifying glass. The second period contains the propagation of the macrocrack until final failure. For both of these periods different phenomenological prediction frameworks exist. The total life time approach is mainly based on so-called Wöhler curves or S-N curves, respectively. These curves assign a certain number of bearable load cycles to a certain load amplitude. The particular cycle numbers may serve as input for damage accumulation laws, where the linear accumulation hypothesis referred to as the Miner rule (Miner 1945) is widely applied. The most popular method to describe macrocrack growth is Paris’ law (Paris and Erdogan 1963). Within this method the cyclic crack growth rate \( \mathrm {d}a/\mathrm {d}N\) is described as a function of the cyclic stress intensity factor \({\Delta } K\), which basically incorporates effects of external load, actual crack length and geometry. It was found that, at least within the region of sub critical crack extension, this function plotted on a double logarithmic scale is a straight line. Accordingly the crack growth rate is approximated by a power law. Extensions of this law were proposed to include effects like mean stress or stress ratio (see e.g. Dowling 2013). Paris’ law is also the basis for the most widely used numerical tool for fatigue crack growth simulations namely NASGRO (Forman et al. 2005).

Essential studies attempt to model cyclic fatigue failure using the framework of Continuum Damage Mechanics (CDM), which was comprehensively outlined by Lemaitre (1992) to describe the evolution of a damage variable, were presented by e.g. Marigo (1985) or Chow and Wei (1991). However, within these models, the fatigue life is modeled only for the period until crack nucleation. A numerical model for the simulation of fatigue crack growth was introduced by Fish and Oskay (2005). The damage evolution within this work is modeled by the growth of the void volume fraction, which is governed by extensions of Gurson’s failure model. To obtain a crack or its sharp interfaces, respectively, finite elements are deleted once a critical void volume fraction is reached.

As an alternative to conventional crack growth simulation techniques, phase field modeling for fracture has gained attention within the past decade. This method provides a very useful tool for the numerical simulation of problems dealing with sharp interfaces, as it does not require procedures for mesh disconnection, element deletion, and re-meshing for an explicit modeling of the interfaces. The phase at a certain location is incorporated by introducing additional degrees of freedom. In the context of fracture, the framework was applied to dynamic fracture (see e.g. Schlüter et al. 2014), and quasi static brittle fracture in e.g. Kuhn and Müller (2010); Borden et al. (2014); Miehe et al. (2010). Extensions of these model exist for ductile fracture (e.g. Kuhn et al. 2016; Borden et al. 2016) and also effects like anisotropic fracture resistance were studied by e.g. Teichtmeister et al. (2017), Schreiber et al. (2017), Hakim and Karma (2009). Models for fatigue damage were so far presented by Alessi et al. (2017) and Seiler et al. (2018). In these models the phase field is driven by degrading the energy release rate once a damage parameter increases.

In this work, the fatigue mechanisms occurring in a material are interpreted as additional driving force contribution, contribution that originates from cyclically accumulated deformation work. The formulation is an extension of the model proposed by Kuhn and Müller (2010) for brittle fracture and as a linear elastic material model is considered within our work, the range of validity in terms of the number of cycles to failure \(N_F\) may be restricted to high cycle fatigue, which covers \(N_F \ge 1000\) for many metallic materials. The driving force for the phase field variable \(s({{\varvec{\mathrm {x}}}},t)\) incorporates an additional energy contribution accounting for fatigue damage accumulation due to an increasing number of load cycles.

2 Phase field model for fatigue fracture

2.1 The regularized model for brittle fracture

The core idea of a phase field fracture model is to introduce an additional field variable to represent cracks. A continuous transition of this field variable \(s({{\varvec{\mathrm {x}}}},t)\) within the interval [0, 1] approximates the crack faces. The crack field is 1 as long as the material remains undamaged and drops once fracturing occurs, where the lower limit \(s=0\) represents cracks. The phase field model from Kuhn and Müller (2010) uses the regularized formulation of a variational model for brittle fracture (Bourdin et al. 2000). As an extension of Griffith’s theory, which states that a crack propagates once the energy release rate reaches a certain critical value, it is postulated that the displacement field \({{\varvec{\mathrm {u}}}}\) and the fracture field s locally minimize the total energy E within a loaded body.

$$\begin{aligned} \begin{aligned} E(\nabla {{\varvec{\mathrm {u}}}},s,\nabla s)=&\int _{{\Omega }} \psi (\nabla {{\varvec{\mathrm {u}}}},s,\nabla s) \, \mathrm {d}V \\ =&\int _{{{\Omega }}} \left[ (g(s)+\eta )W(\nabla {{\varvec{\mathrm {u}}}}) + {\Gamma }(s,\nabla s) \right] \; \mathrm {d}V. \end{aligned} \end{aligned}$$
(1)

In Eq. (1) W is the elastic strain energy density, which is multiplied by a degradation function g(s) to account for the stiffness reduction in cracked regions. The surface energy density contribution \({\Gamma }\) accounts for the energy required for the formation of a crack surface. The parameter \(\eta \) shall be chosen \(0<\eta \ll 1\) to avoid numerical problems within the static solution scheme. The elastic strain energy density

$$\begin{aligned} W&=\frac{1}{2}{{\varvec{\varepsilon }}}({{\varvec{\mathrm {u}}}})^T {\mathbb {C}} {{\varvec{\varepsilon }}}({{\varvec{\mathrm {u}}}}) \end{aligned}$$
(2)

can be formulated in terms of the infinitesimal strain tensor

$$\begin{aligned} {{\varvec{\varepsilon }}}({{\varvec{\mathrm {u}}}})&= \frac{1}{2}\left( \nabla {{\varvec{\mathrm {u}}}}+ \left( \nabla {{\varvec{\mathrm {u}}}}\right) ^T \right) , \end{aligned}$$
(3)

where \(\nabla {{\varvec{\mathrm {u}}}}\) is the spacial gradient of the displacements. In Eq. (2) the Voigt notation for symmetric tensors is used for the linearized strain tensor \({{\varvec{\varepsilon }}}\) and the stiffness tensor \({\mathbb {C}}\) . The second energy contribution in Eq. (1) is the fracture energy density

$$\begin{aligned} {\Gamma }(s,\nabla s)={\mathcal {G}}_c\left( \frac{(1-s)^2}{4\epsilon }+ \epsilon |\nabla s|^2 \right) , \end{aligned}$$
(4)

which besides a local part, further consists of a non-local part, characterized by the spacial gradient of s. The two contributions are multiplied by the critical energy release rate \({\mathcal {G}}_c\). The length scale \(\epsilon \) controls the width of the transition zone between undamaged and broken material. This crack surface contribution regularizes Griffith’s theory, which proposes the proportionality of the fracture energy and the crack surface. Assuming a hyperelastic material, the stresses can be derived from the potential \(\psi \) by

$$\begin{aligned} {{\varvec{\sigma }}}=\frac{\partial \psi }{\partial {{\varvec{\varepsilon }}}}= (g(s)+\eta ){\mathbb {C}}{{\varvec{\varepsilon }}}. \end{aligned}$$
(5)

Different types of degradation functions g(s) are proposed in the literature (Bourdin et al. 2000; Kuhn et al. 2015; Borden et al. 2016). However, this function has to fulfill several criteria as \(g(0)=0\), \(g(1)=1\) and also \(g'(0)=0\). These requirements are satisfied by the quadratic function

$$\begin{aligned} g_b(s)=s^2, \end{aligned}$$
(6)

which is used in the original regularized formulation proposed by Bourdin et al. (2000). Discussions about a quadratic and a cubic degradation function are given in Kuhn et al. (2015). These functions were shown to shift the stress level at which crack initiation occurs to higher stresses and also to conserve the linear elastic stress strain behavior until crack initiation. A mixed formulation for the degradation function

$$\begin{aligned} g_{\beta }(s)=\beta (s^3-s^2)+3s^2-2s^3 \end{aligned}$$
(7)

was proposed by Borden et al. (2016). Notice, that for \(\beta =2\), \(g_\beta \) becomes \(g_b\) and for \(\beta \rightarrow 0\), \(g_{\beta }\) becomes the cubic degradation function introduced by Kuhn et al. (2015). Accordingly, the model behavior is effected by varying the parameter \(\beta \).

A generalized Ginzburg-Landau equation (Gurtin 1996) is used to obtain the time evolution of the phase field s via

$$\begin{aligned} \begin{aligned} {\dot{s}}&=-M \underbrace{\left\{ \frac{\partial \psi }{\partial s}- \nabla \cdot \left( \frac{\partial \psi }{\partial \nabla s} \right) \right\} }_{{\delta } \psi /{\delta } s} \\&=-\frac{M}{2}\left\{ g'(s) {{\varvec{\varepsilon }}}^T {\mathbb {C}} {{\varvec{\varepsilon }}}- {\mathcal {G}}_c \left( 4\epsilon {\Delta } s+ \frac{1-s}{\epsilon }\right) \right\} \end{aligned} \end{aligned}$$
(8)

where \({\Delta }\) is the Laplace operator. The scalar mobility parameter M in Eq. (8) acts as a viscous control parameter to approach the stationary limit, which is specified by \(\frac{{\delta } \psi }{{\delta } s}=0\). The limit case \(M \rightarrow \infty \) approximates quasi static conditions.

2.2 Phase field formulation for cyclic fatigue

To provide a correct understanding of the model described in the following, it is important to comment on the interpretation of the phase field variable s. In particular the transition zone between the two phases broken and intact (\(0<s<1\)) requires special consideration. A possible interpretation is to connect s to the fraction of micro voids within a representative volume element, as it was proposed by Voyiadjis and Mozaffari (2013). Here, s is brought in direct connection with the damage variable from the CDM framework (Lemaitre 1992). On the other hand, the phase field variable in Bourdin’s original model (Bourdin et al. 2000) did not have a physical interpretation at all, but the scalar phase field s was rather incorporated in the energy formulation of a fractured body to enable a regularization of the crack energy. According to this explanation, the meaning of s results from the phase field philosophy itself, which is to approximate sharp interfaces by a smooth transition of an order parameter for numerical reasons. In the phase field model presented within this work, we follow this second interpretation. The term damage refers to fatigue damage, which will be applied to drive the phase field, but it is not explicitly connected to it. Specifically, s is driven by a proper estimate for the fatigue damage increment \(\mathrm {d}D_\text {f}\) occurring in the material within a certain cycle interval.

2.2.1 Phase field fracture model for fatigue failure

As explained in Sect. 2.1, a sequence of local minimizers of the total internal energy, depending on displacement and fracture fields, has to be found in order to obtain the correct crack pattern, or in other words information for crack initiation, kinking or branching, respectively. Suppose a sample is exposed to a monotonically increasing load. In that case the solution reveals an evolution of the crack field, since at some point the surface part of Eq. (1) will increase as it becomes energetically more favorable to form a crack, which means to decrease s, than to allow for more strain energy. Within the regime of cyclic fatigue the load maximums are rather small to very small compared to quasi static fracture loads. Presuming such a small load and a constant \({\mathcal {G}}_c\), the solution will not yield a decline of s in case of the classical model (Kuhn and Müller 2010), as energy consumed by irreversible processes associated with an increasing state of fatigue is not taken into account. Accordingly, crack growth would be too costly with respect to the total internal energy. A modification of the total energy formulation has been proposed by Alessi et al. (2017) in order to enable crack growth driven by cyclic fatigue. The modification basically applies to the crack energy \(\int _{{\Omega }} {\Gamma } \, \mathrm {d}V\), where the fracture resistance \({\mathcal {G}}_c\) is degraded by a function of a plastic strain variable, which is accumulated over an increasing number of load cycles.

Within this work we present an alternative approach for a regularized formulation of the total energy

$$\begin{aligned} \begin{aligned}&E^{\text {f}}(\nabla {{\varvec{\mathrm {u}}}},s,\nabla s, D_\text {f})=E+E^{\text {ac}}\\&\quad =\int _{{{\Omega }}} \left[ (g(s)+\eta )W+ {\Gamma } \right] \; \mathrm {d}V + \int _{{\Omega }} h(s) P(D_\text {f}) \; \mathrm {d}V, \end{aligned} \end{aligned}$$
(9)

where an additional energy density contribution P is introduced to account for the sum of additional driving forces associated with the mechanism of cyclic mechanical fatigue. The function h(s) degrades P in a similar way as W is degraded by g(s) once a crack propagates. The energy contribution \(E^{\text {ac}}\) is governed by a piece-wise defined function

$$\begin{aligned} P(D_\text {f})=\left\{ \begin{array}{l c r} 0 &{} \text {for} &{} D_\text {f}<D_{\text {fc}}\; \\ q(D_\text {f}-D_{\text {fc}})^b &{} \text {for} &{} D_\text {f} \ge D_{\text {fc}},\\ \end{array} \right. \end{aligned}$$
(10)

with the threshold value \(D_{\text {fc}}\). According to this definition the amount of additional energy to enter Eq. (9) remains zero until a certain critical value \(D_{\text {fc}}\) of the accumulated damage \(D_\text {f}\) is reached and increases rapidly (governed by the model parameters q and b) after this limit is exceeded. The actual accumulated fatigue damage is in general described as

$$\begin{aligned} D_\text {f}=D_0+\mathrm {d}D_\text {f}(\sigma _a,{\bar{\sigma }},R,{\dot{\varepsilon }},D_0), \end{aligned}$$
(11)

which is the sum of the previous damage state \(D_0\) and the damage increment \(\mathrm {d}D_\text {f}\) as a function of the amplitude \(\sigma _a\), the mean value of the stress \({\bar{\sigma }}\), the load ratio R, the stain rate \({\dot{\varepsilon }}\), and the damage history or the previous damage state, respectively. The main task in this context is to find an accurate formula for the increment \(\mathrm {d}D_\text {f}\). Equation (11) indicates that, generally, several effects have to be considered for an estimate of the damage increment. However, the choice has to be made also in consideration of computational effort, which a certain model may cause. Straightforward approaches for the fatigue lifetime estimation of a component, which are commonly used and were also incorporated within approaches for numerical fatigue estimations (see e.g. Bograd et al. 2008) are Miner’s rule (Miner 1945) and the fatigue damage model proposed by Chaboche and Lesne (1988). The main difference between these two approaches is that Miner’s rule does not consider the effect of the current state of damage \(D_0\) on the increment, which is formulated as

$$\begin{aligned} \mathrm {d}D_{\text {f}_i}=\frac{1}{N_{F_i}} \mathrm {d}N , \end{aligned}$$
(12)

with the number of bearable load cycles \(N_{F_i}\) and the cycle increment \(\mathrm {d}N\). Considering Eq. (12) it becomes clear that the damage accumulation is linear and accordingly the influence of load sequence on the fatigue life is not cough. Within this work we primarily want to give a principal description of the proposed modification of the phase field model. Hence, only the Miner rule was so far incorporated for the evaluation of the damage increment, as it provides an easy and very stable way of implementation. However, it shall be outlined at this point, that other approaches, as e.g. the model for fatigue damage from Chaboche, could also be incorporated within the presented framework.

Fig. 1
figure 1

Schematic illustration of a S-N line

Full size image

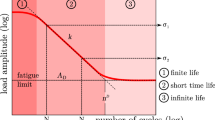
The particular critical cycle number \(N_{F_i}\) can be obtained by an appropriate S-N curve. These curves (see Fig. 1) are plots, obtained within fatigue experiments, of the stress magnitude for cyclic loading depending on the corresponding number of bearable load cycles \(N_F\). A straight line is obtained using a double logarithmic scale.

With Eq. (12) and an appropriate S-N curve, the total internal Energy \(E^\text {f}\) of a component that may contain cracks caused by quasi static or by cyclic loading is then

$$\begin{aligned} \begin{aligned} E^{\text {f}}&=\int _{{\Omega }} (g(s)+\eta )\frac{1}{2}{{\varvec{\varepsilon }}}^T {\mathbb {C}} {{\varvec{\varepsilon }}}\; \mathrm {d}V \\&\quad + \int _{{\Omega }} {\mathcal {G}}_c\left( \frac{(1-s)^2}{4\epsilon }+ \epsilon |\nabla s|^2 \right) \; \mathrm {d}V\\&\quad + \int _{{\Omega }} h(s) q\left\langle D_0+\frac{\mathrm {d}N}{n^D} \left( \frac{\sigma _A}{A_D}\right) ^k-D_\mathrm{c} \right\rangle ^b \; \mathrm {d}V, \end{aligned} \end{aligned}$$
(13)

with the driving force quantity \(\sigma _A\), which is related to a stress amplitude. This variable will be explained within the next section. Other quantities introduced in Eq. (13) are the fatigue limit \(A_D/2\), the knee point cycle number \(n^D\) and the slope factor k of the S-N curve. The \(\langle \cdot \rangle ^n\) denote Macauley brackets with the definition

$$\begin{aligned} \langle \cdot \rangle ^n= \left\{ \begin{array}{l c r} 0 &{} \text {for} &{} (\cdot ) \le 0\; \\ (\cdot )^n &{} \text {for} &{} (\cdot ) > 0.\\ \end{array} \right. \end{aligned}$$
(14)

Considering the energy in Eq. (13) the stresses become

$$\begin{aligned} {{\varvec{\sigma }}}= \underbrace{(g(s)+\eta ){\mathbb {C}}{{\varvec{\varepsilon }}}}_{{{\varvec{\sigma }}}^\text {e}} +\underbrace{h(s)q b\langle D_\text {f}-D_\text {fc} \rangle ^{(b-1)}\frac{\partial D_\text {f}}{\partial {{\varvec{\varepsilon }}}}}_{{{\varvec{\sigma }}}^\text {ac}}. \end{aligned}$$
(15)

The first term in Eq. (15) is the usual degraded stress tensor and the second term may be considered an additional stress component accounting for accumulated micro stresses as consequence of the fatigue mechanism.

2.2.2 Cycle resolved simulation scheme

Depending on the magnitude of the load cycles, the fatigue mechanism may require a very large number of cycles before consequences on a macro level like crack nucleation or extension can be observed. Accordingly, an efficient scheme is required to integrate large numbers of cycles with respect to a characteristic cycle number, otherwise simulation times cannot be kept within a reasonable limit. Even for conventional fatigue life approaches certain amounts of similar cycles are summarized to blocks, where the connection of all these blocks represents the whole load history called load collective. Fish and Yu (2002) proposed a scheme called “cycle jump”, where the damage at the end of a simulation step including a certain number of cycles \(D_{(i+{\Delta } N_i)}\) is calculated via

$$\begin{aligned} D_{(i+{\Delta } N_i)}=D_i+{\Delta } N_i \cdot {\Delta } D_i. \end{aligned}$$
(16)

The damage at the previous step is \(D_i\) and the particular \({\Delta } D_i\) values are obtained by an explicit Euler method. Within this simulation scheme the block size summarizing several cycles, \({\Delta } N_i\) is chosen adaptive.

The time-cycle transfer scheme presented within this work is quite similar. Suppose a constant block size or number of cycles per time \(\frac{{\Delta } N}{{\Delta } t}\), respectively, leads to a certain evolution of damage. By utilizing Eq. (12), the damage of the actual time is

$$\begin{aligned} D_i=D_{i-1}+\mathrm {d}D_{\text {fMiner}}({\Delta } t_i). \end{aligned}$$
(17)

The phase field evolution Eq. (8) can be transferred to the cycle domain using the chain rule. Accordingly, the evolution of the phase field can be reformulated in terms of cycles

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}s}{\mathrm {d}N}=&-{\hat{M}} \left\{ g'(s) \frac{1}{2} {{\varvec{\varepsilon }}}^T{\mathbb {C}}{{\varvec{\varepsilon }}}+h'(s)P(D_\text {f}) \right. \quad \; \\&\left. -{\mathcal {G}}_c \left( 2 \epsilon {\Delta } s -\frac{s-1}{ 2 \epsilon } \right) \right\} , \end{aligned} \end{aligned}$$
(18)

with \({\hat{M}}\) denoted the mobility in the cycle domain. The damage will be updated within every simulation step according to the change caused by a chosen cycle number. To ensure good convergence even for a rapid increase of P, adaptive step size adjustment must be implemented.

3 Numerical implementation

For the evaluation of the enhancement of this phase field model for fatigue failure the quadratic degradation function from Eq. (6) is chosen for g(s) and h(s). If volume forces are neglected within the mechanical equilibrium and the modified evolution equation for the phase field Eq.  (18) is utilized, the governing set of differential equations for the unknown displacements \({{\varvec{\mathrm {u}}}}\) and the order parameter s is given by

$$\begin{aligned} \begin{bmatrix} \nabla \cdot &{} 0 \\ 0 &{} \frac{1}{{\hat{M}}}\frac{\mathrm {d}\;\;\;}{\mathrm {d}N} + 2(W + P) + \frac{{\mathcal {G}}_c}{2\epsilon } - {\mathcal {G}}_c2\epsilon {\Delta } \end{bmatrix} \begin{bmatrix} {{\varvec{\sigma ({{\varvec{\mathrm {u}}}})}}} \\ s \end{bmatrix} = \begin{bmatrix} {{\textit{\textbf{0}}}} \\ \frac{{\mathcal {G}}_c}{2\epsilon } \end{bmatrix} \end{aligned}$$
(19)

where \(\nabla \cdot \) is used as divergence operator. Multiplying both equations with the respective virtual quantities \(\delta {{\varvec{\mathrm {u}}}}\) and \(\delta s\) and integration by parts, the particular weak forms are obtained

$$\begin{aligned} 0=-\int _{{\Omega }} {{\varvec{\sigma }}}^T \cdot \delta {{\varvec{\varepsilon }}} \; \mathrm {d}V+\int _{\partial {\Omega }_t} \delta {{\varvec{\mathrm {u}}}}^T \cdot {{\varvec{\mathrm {t}^*}}} \; \mathrm {d}S \end{aligned}$$
(20)

with the prescribed traction vector \({{\varvec{\mathrm {t}}}}^*\) on \(\partial {\Omega }_t\) and

$$\begin{aligned} \begin{aligned} 0=-&\int _{{\Omega }} \delta s {\hat{M}}^{-1} \frac{\mathrm {d}s}{\mathrm {d}N} \;\; \mathrm {d}V \\ -&\int _{{\Omega }} \delta s \left( s {{\varvec{\varepsilon }}}^T {\mathbb {C}} {{\varvec{\varepsilon }}}+2P(D_\text {f}) + {\mathcal {G}}_c\frac{s-1}{2\epsilon } \right) \;\; \mathrm {d}V \\ -&\int _{{\Omega }} 2 \mathrm {G}_c \epsilon \nabla s^T \nabla \delta s \;\; \mathrm {d}V, \end{aligned} \end{aligned}$$
(21)

where the homogeneous Neumann boundary condition \(\nabla s\cdot {{\varvec{\mathrm {n}}}}=0\) at \(\partial {\Omega }\) is used. The isoparametric concept is used in order to obtain a discrete description of the field quantities \({{\varvec{\mathrm {u}}}}\) and s by means of the shape functions \(H_I\) for the nodes \(I=1,\dots ,n\) with

$$\begin{aligned} {{\varvec{\mathrm {u}}}}({{\varvec{\mathrm {x}}}})=\sum _{I=1}^n H_I({{\varvec{\mathrm {x}}}}) \hat{{{\varvec{\mathrm {u}}}}}_I \end{aligned}$$
(22)

and

$$\begin{aligned} s({{\varvec{\mathrm {x}}}})=\sum _{I=1}^n H_I({{\varvec{\mathrm {x}}}}){\hat{s}}_I, \end{aligned}$$
(23)

where the denotation \(\hat{(\cdot )}\) indicates nodal values. By introducing the differential operator matrices for a two dimensional setting

$$\begin{aligned} {{\textit{\textbf{B}}}}_I^{{{\varvec{{{{\varvec{\mathrm {u}}}}}}}}}({{\varvec{\mathrm {x}}}})=\begin{bmatrix} H({{\varvec{\mathrm {x}}}})_{I,x} &{} 0\\ 0 &{} H({{\varvec{\mathrm {x}}}})_{I,y}\\ H({{\varvec{\mathrm {x}}}})_{I,y} &{}H({{\varvec{\mathrm {x}}}})_{I,x} \end{bmatrix} \end{aligned}$$
(24)

and

$$\begin{aligned} {{\textit{\textbf{B}}}}^s_I =\begin{bmatrix} H({{\varvec{\mathrm {x}}}})_{I,x}\\ H({{\varvec{\mathrm {x}}}})_{I,y} \end{bmatrix}, \end{aligned}$$
(25)

where \((\cdot ),_v\) indicates partial derivatives \(\frac{\partial (\cdot )}{\partial v}\), the values for \({{\varvec{\varepsilon }}}\) and \(\nabla s\) can be computed from

$$\begin{aligned} {{\varvec{\varepsilon }}}({{\varvec{\mathrm {x}}}})=\sum _{I=1}^n {{\textit{\textbf{B}}}}_I^{{{\varvec{{{{\varvec{\mathrm {u}}}}}}}}}({{\varvec{\mathrm {x}}}})\hat{{{\varvec{\mathrm {u}}}}}_I \end{aligned}$$
(26)

and

$$\begin{aligned} \nabla s ({{\varvec{\mathrm {x}}}})=\sum _{I=1}^n {{\textit{\textbf{B}}}}_I^s({{\varvec{\mathrm {x}}}}){\hat{s}}_I, \end{aligned}$$
(27)

where the Voigt notation is used. An analog discretization may be applied for the virtual quantities. Accordingly the contributions to the vector of the internal forces at node I become

$$\begin{aligned} {{\textit{\textbf{F}}}}^{{\varvec{{{{\varvec{\mathrm {u}}}}}}}}_I=\int _{{\Omega }} \left( {{\textit{\textbf{B}}}}_I^{{\varvec{{{{\varvec{\mathrm {u}}}}}}}}\right) ^T {{\varvec{\sigma }}} \;\mathrm {d}V \end{aligned}$$
(28)

and

$$\begin{aligned} \begin{aligned} F^s_I&=\int _{{\Omega }} H_I {\hat{M}}^{-1} \frac{\mathrm {d}s}{\mathrm {d}N} \; \mathrm {d}V \\&\quad + \int _{{\Omega }} H_I\left( s {{\varvec{\varepsilon }}}^T {\mathbb {C}} {{\varvec{\varepsilon }}} + 2sP(D_\text {f})+{\mathcal {G}}_c \frac{s-1}{2\epsilon } \right) \; \mathrm {d}V \\&\quad + \int _{{\Omega }} 2{\mathcal {G}}_c\epsilon \left( {{\textit{\textbf{B}}}}_I^s\right) ^T \nabla s \; \mathrm {d}V. \end{aligned} \end{aligned}$$
(29)

In the following, we denote by \(\sigma _A({{\varvec{\varepsilon }}})\) any representative component of the stress tensor or property of the stress tensor, chosen as the driving quantity for the fatigue mechanism. This work aims at investigating fundamentals of the integration of fatigue failure within a phase field formulation in terms of mode-I fracture. Accordingly, the normal stress component in loading direction

$$\begin{aligned} \sigma _A={{\textit{\textbf{ 1 }}}}^T{\mathbb {C}}{{\varvec{\varepsilon }}}, \end{aligned}$$
(30)

with \({{\textit{\textbf{ 1 }}}}=\left( 0,1,0\right) ^T\) is considered as appropriate stress measure for cyclic tensile loading in vertical direction. In order to find a solution \({{\textit{\textbf{U}}}}^*=\left( {{\varvec{\mathrm {u}}}}^*,s^*,{\dot{s}}^*\right) ^T\) of the nonlinear system, the Newton-Raphson scheme is applied. The particular components of the current stiffness matrix are found as

$$\begin{aligned} {{\textit{\textbf{K}}}}_{IJ}^{{{\varvec{{{{\varvec{\mathrm {uu}}}}}}}}}=&\frac{\partial {{\textit{\textbf{F}}}}_I^{{\varvec{{{{\varvec{\mathrm {u}}}}}}}}}{\partial {{\varvec{\mathrm {u}}}}_{J}}=\int _{{\Omega }} {{\textit{\textbf{B}}}}_I^{{\varvec{{{{\varvec{\mathrm {u}}}}}}}}(s^2+ \eta ){\mathbb {C}} {{\textit{\textbf{B}}}}_J^{{{\varvec{{{{\varvec{\mathrm {u}}}}}}}}} \nonumber \\&+ s^2 {{\textit{\textbf{B}}}}_I^{{\varvec{{{{\varvec{\mathrm {u}}}}}}}} \left( f_1+f_2 \right) {\mathbb {C}}{{\textit{\textbf{ 1 }}}} \left[ {\mathbb {C}}{{\textit{\textbf{ 1 }}}} \right] ^T {{\textit{\textbf{B}}}}_J^{{{\varvec{{{{\varvec{\mathrm {u}}}}}}}}} \; \mathrm {d}V, \end{aligned}$$
(31)
$$\begin{aligned} {{\textit{\textbf{K}}}}_{IJ}^{s{{\varvec{{{{\varvec{\mathrm {u}}}}}}}}}=&\frac{\partial {{\textit{\textbf{F}}}}_I^s}{\partial {{\varvec{\mathrm {u}}}}_{J}}= \int _{{\Omega }} H_I 2 s \left( {\mathbb {C}} {{\varvec{\varepsilon }}} + f_3\cdot {\mathbb {C}}{{\textit{\textbf{ 1 }}}} \right) ^T {{\textit{\textbf{B}}}}_J^{{\varvec{{{{\varvec{\mathrm {u}}}}}}}} \; \mathrm {d}V, \end{aligned}$$
(32)
$$\begin{aligned} {{\textit{\textbf{K}}}}_{IJ}^{{{\varvec{{{{\varvec{\mathrm {u}}}}}}}}s}=&\frac{\partial {{\textit{\textbf{F}}}}_I^{{\varvec{{{{\varvec{\mathrm {u}}}}}}}}}{\partial s_{J}}= \int _{{\Omega }} \left( {{\textit{\textbf{B}}}}_I^{{\varvec{{{{\varvec{\mathrm {u}}}}}}}} \right) ^T 2 s H_J \left( {\mathbb {C}} {{\varvec{\varepsilon }}} + f_3\cdot {\mathbb {C}}{{\textit{\textbf{ 1 }}}} \right) \mathrm {d}V, \end{aligned}$$
(33)
$$\begin{aligned} {{\textit{\textbf{K}}}}_{IJ}^{ss}=&\frac{\partial {{\textit{\textbf{F}}}}_I^s}{\partial s_{J}}= \int _{{\Omega }} H_I H_J \left( {{\varvec{\varepsilon }}}^T {\mathbb {C}} {{\varvec{\varepsilon }}} +2P +\frac{G_c}{2\epsilon } \right) \nonumber \\&+ 2{\mathcal {G}}_c \epsilon \left( {{\textit{\textbf{B}}}}_I^s \right) ^T {{\textit{\textbf{B}}}}_J^s \; \mathrm {d}V \end{aligned}$$
(34)

with

$$\begin{aligned} f_1&=\frac{\partial ^2 P(D_{i-1}+{\Delta } D_i)}{\partial D_i^2 } \cdot \left( \frac{k \sigma _A^{(k-1)}}{n^D A_D^k}\mathrm {d}N \right) ^2, \end{aligned}$$
(35)
$$\begin{aligned} f_2&=\frac{\partial P(D_{i-1}+{\Delta } D_i)}{\partial D_i } \cdot \frac{k(k-1)\sigma _A^{(k-2)}}{n^D A_D^k} \mathrm {d}N, \end{aligned}$$
(36)
$$\begin{aligned} f_3&=\frac{\partial P(D_{i-1}+{\Delta } D_i)}{\partial D_i } \cdot \frac{k \sigma _A^{(k-1)}}{n^D A_D^k}\mathrm {d}N \end{aligned}$$
(37)

and the damping matrix is zero, except for the component

$$\begin{aligned} D_{IJ}^{s{\dot{s}}}=\frac{\partial F_I^s }{\partial s,_N}= \int _{{\Omega }} H_I H_J {\hat{M}}^{-1} \; \mathrm {d}V. \end{aligned}$$
(38)

Using the implicit Euler method for the transient problem is sufficient as the number of cycles is directly proportional to time. However, automatic step size adjustment is applied to ensure a stable computation when the phase field decreases due to rapid increase of the fatigue damage.

4 Examples and validation

Fig. 2
figure 2

Set up for phase field simulation of C(T)-specimen

Full size image

For an experimental characterization of the fatigue crack growth behavior of materials the so-called compact tension (CT) specimen is, among others, frequently used. Accordingly, this specimen geometry was also chosen for the conducted simulations within this study, whose results are presented in the following. The definition of the geometry of the C(T)-specimen is given in the ASTM E 399 standard (ASTM 2009). For the simulations the software FEAP 8.4 was used. The model was implemented into a user element routine for a 4-node quadrilateral element. Figure 2 shows the setup for the mode-I simulations. For the simulations, force was used as control variable. The force transmission by a bolt was approximated by a distributed sinusoidal load across the upper semi-circle of the bolt hole. The pulsating load is approximated within the transient simulations by means of a ramp function, where each simulation step represents a certain increment of load cycles (see Fig. 3). As only constant amplitude loading was considered the applied force was kept constant after the maximum load was reached. For all numerical experiments a material with Young’s modulus \(E=2.1\cdot 10^5\,\hbox {MPa}\), Poisson’s ratio \(\nu =0.3\) and critical energy release rate \({\mathcal {G}}_c=2.33\cdot 10^3\,{\hbox {J/m}^2}\) was considered. Further, the parameters \(A_D= 200\,\hbox {MPa}\) and \(k=5\) were used.

Fig. 3
figure 3

Schematic illustration of the approximation of cyclic loading within simulation

Full size image

4.1 Crack initiation and model characteristics

Fig. 4
figure 4

Evaluation of stress contributions on a horizontal straight line at the crack tip after a 0 cycles, b \(1.4\cdot 10^5\) cycles, c \(1.66\cdot 10^5\) cycles, and d \(2.0\cdot 10^5\) cycles

Full size image

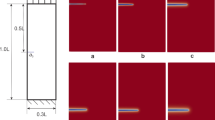
The main feature of the original phase field formulation for brittle fracture is a crack pattern that locally minimizes the total energy. The solution is allowed to yield cracks and cracks will appear once their formation is beneficial with respect to the total energy. However, as previously explained, the modified phase field model for fatigue fracture has an additional mechanism, which includes a fatigue related driving force. The plots in Fig. 4 show the evaluation of the stress contributions \(\sigma ^\text {e}\) and \(\sigma ^\text {ac}\) of Eq. (15) in vertical direction on a line, which extends in horizontal direction from the notch tip of the C(T)-specimen. Furthermore, the effective stress in vertical direction \(\sigma _A\) is indicated. For simplicity all stresses are normalized by the threshold stress \(A_D\). A corresponding contour plot of the phase field s within a square section (edge length approximately \(1\,\hbox {mm}\)) around the notch tip is indicated in every illustration. Note that for this simulation the initial s field was 1 over the whole specimen. In other words, the specimen was not pre-cracked and the crack initiation period will be illustrated in the following. The plot in Fig. 4a shows the situation after the initial ramp up, i.e. complete load applied. The phase field remains 1 indicating intact material everywhere. The stress at the notch tip is slightly above \(A_D\). This state stays unaltered until a number of approximately \(1.4\cdot 10^5\) cycles was applied (Fig. 4b). At this point an increase of the \(\sigma ^\text {ac}\) contribution can be recognized, which indicates that the damage at the notch tip has grown to a relevant amount such that the energy density contribution P significantly affects the energy functional. Consequently the phase field decreases and the stresses are degraded. After another \(0.3\cdot 10^5\) cycles the phase field at the notch tip is almost zero (Fig. 4c) and \(\sigma _A\) increases, while \(\sigma _y^\mathrm{e}\) decreases due to the degradation. This observation illustrates that \(\sigma _A\) rather than \(\sigma _y^\mathrm{e}\) is a suitable driving force, as otherwise the fatigue damage would stop to grow. A fatigue crack was initiated after a cycle number of approximately \(2.0\cdot 10^5\) (Fig. 4d). Both stress contributions are zero at the crack tip as they are fully degraded. Note that for the subsequent evolution of the energy density contribution P a higher stress is observed as driving force as for the crack nucleation. This will certainly lead to a smaller number of cycles until the next crack growth increment occurs, compared to the interval for crack initiation. This behavior is in agreement with experimental findings (see e.g. Haibach 2006).

Fig. 5
figure 5

Illustration of crack growth data from phase field simulation as a plot of the different energy contributions (left) and as a N-a plot (right)

Full size image

In order to assess the crack growth behavior, another simulation was set up and ran until a fatigue crack with a total length of \(15\,\hbox {mm}\) was generated. Figure 5 shows the results obtained from this simulation by means of different illustrations. The plot on the right shows the crack evolution with respect to the number of applied load cycles. For selected N-a states, contour plots, representing the phase field variable s over the specimen, are indicated among the line plot. The crack length is measured from the tip of the V-notch to the actual crack tip (maximum x-coordinate with \(s=0\)). A nonlinear function of the crack length with respect to the number of applied load cycles is obtained from the simulation. The steep gradient at the end of the simulation indicates high crack growth rates. This behavior is qualitatively in line with experimental findings (see e.g. Dowling 2013). An illustration of the particular energy contributions of the total energy (Eq. (9)) with respect to the number of load cycles for the same simulation is shown in the left diagram of Fig. 5. Note that for this simulation the node at the crack tip was initially set to \(s=0\). This explains the small deviation of \(E_{\varGamma }\) from zero at the beginning. However, this evaluation provides good insight into the mechanism of the proposed phase field model. The onset of crack growth is indicated in the plot by the first increase of the crack energy contribution \(E_{{\Gamma }}\). It may be recognized, that the energies \(E^{\text {ac}}\) representing the fatigue energy and \(E_W\) representing strain energy are small compared to \(E_{{\Gamma }}\). Accordingly for the illustration these contributions were factorized by 10. The fatigue energy \(E^{\text {ac}}\) increases as consequence of the rising fatigue damage induced by cyclic loading. Accordingly, s decreases, which yields an increase of \(E_{{\Gamma }}\) and a decrease of \(E^{\text {ac}}\) to compensate the additional crack energy and minimize the total energy. The energy contribution \(E^{\text {ac}}\) increases subsequently within another area according to the actual crack pattern and the process starts again. The strain energy contribution \(E_W\) is almost constant for the larger part of the simulation and increases with higher rates only after approximately \(2.5\cdot 10^5\) cycles due to higher stresses with increasing crack length.

4.2 Evaluation of crack growth rates

The growth behavior of a macro crack, which is exposed to cyclic loads is still mainly described by the a relation between the growth rate \(\mathrm {d}a/\mathrm {d}N\) and the cyclic stress intensity factor \({\Delta } K\), which represents the properties of crack length, loading conditions, and geometry. This law, denoted as Paris’ law, was first presented in Paris and Erdogan (1963) and is given by

$$\begin{aligned} \frac{\mathrm {d}a}{\mathrm {d}N}=C\left( {\Delta } K\right) ^m, \end{aligned}$$
(39)

were C and m are material dependent parameters. In a double logarithmic diagram one obtains the power law of Eq. (39) as a straight line. Within common experimental procedures for the identification of the crack growth behavior, a discrete form of the growth rate

$$\begin{aligned} \left( \frac{\mathrm {d}a}{\mathrm {d}N}\right) _p\approx \frac{a_p-a_{p-1}}{N_p-N_{p-1}} \end{aligned}$$
(40)

is utilized with p denoting the p-th data point. For the approximation of the \({\Delta } K\) values associated to the C(T)-specimen we stuck to Srawley (1976), who recommends:

$$\begin{aligned} \begin{aligned} {\Delta } K=&\frac{{\Delta } F}{B\sqrt{L}} \frac{2+\tfrac{a}{L}}{\left( 1-\tfrac{a}{L}\right) ^{3/2}}\cdot \\&\left[ 0.886 + 4.64\left( \tfrac{a}{L}\right) ^2 - 13.32\left( \tfrac{a}{L}\right) ^3 \right. \\&\left. + 14.72\left( \tfrac{a}{L}\right) ^4 - 5.69\left( \tfrac{a}{L}\right) ^5 \right] , \end{aligned} \end{aligned}$$
(41)

where the actual crack length a is considered as the horizontal distance from the center of the holes to the crack tip (see Fig. 2). According to this, for another assessment of the proposed phase field model several simulations with different maximum force values for the introduced mode-I test of the C(T)-specimen were performed. A fatigue crack was generated within every simulation and driven to a maximum length of approximately \(6\,\hbox {mm}\). Figure 6 summarizes the results of these simulations. Within a double logarithmic plot of the crack growth rates with respect to the stress intensity factor all the data points lie close to a straight line. This straight line, which confirms Eq. (39) with \(C=2.8\cdot 10^{-7}\,{\frac{\hbox {mm}/\hbox {cycle}}{(\hbox {MPa}\sqrt{\hbox {m}})^\textit{m}}}\) and \(m=2.5\) was estimated by means of a least square fit and reveals a coefficient of determination of 0.996. The associated N-a plots are presented in Fig. 6a. According to the different levels of the maximum load for each simulation, large differences are obtained for the number of cycles required to generate a certain crack length. However, all samples fit to the Paris parameters of Fig. 6a, which is indeed a very important property regarding a comparison with experimental findings.

Fig. 6
figure 6

Evaluated crack growth data from four different phase field simulations as a N-a plot and b double logarithmic diagram of crack growth rates vs. \(\varDelta K\) factors

Full size image

5 Concluding remarks

A phase field model, which is able to cover the phenomenon of cyclic mechanical fatigue, has been presented as enhancement of the model for brittle fracture from Kuhn and Müller (2010). The driving force for the fatigue mechanism was realized by a new energy contribution accounting for the irreversibility of mechanical fatigue. Numerical simulations show that our model generally yields reasonable results in terms of fatigue crack nucleation and growth and therefore describes the phenomenon. Simulated crack growth rates confirm the Paris law, which represents experimental findings. However, as fatigue of materials is a rather complex field, which is effected by many quantities like load ratio, load sequence, strain rate, temperature, environment and not forgetting the class of the material, further enhancement of the current phase field model has to be done in order to accomplish a comprehensive formulation.