An analytical model for DCB/wedge tests based on Timoshenko beam kinematics for accurate determination of cohesive zone lengths

Abstract

In this work, an analytical model consisting of Timoshenko beams coupled with a cohesive zone is used in order to analyze the extent of the cohesive fracture process zone within mechanical systems displaying beam-like features. This is the case, for example, for the double cantilever beam (DCB) specimen or for the wedge test specimen. The predictions of the model are displayed under the form of diagrams and formulas involving non-dimensional parameters, that can be readily used for example in the context of the identification of cohesive parameters from experimental data. The predictions are also compared to those of previous papers using beam models. It appears that in some configurations, for example soft materials with moderate toughness, the kinematic hypothesis of the Timoshenko beam is necessary in order to get accurate estimate of process zone lengths. The influence of the shape of the cohesive law is also discussed.

Appendices

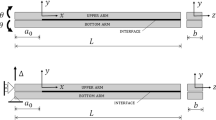
Appendix A: Equations for the Timoshenko beam model coupled with Dugdale type cohesive interaction

The Timoshenko beam theory accounts for shear stress in the beam. The bending moment M and shear force T in the beam are expressed as:

$$\begin{aligned}&\begin{aligned} M&= EI \frac{\partial \phi }{\partial x},\end{aligned} \end{aligned}$$

(7a)

$$\begin{aligned}&\begin{aligned} T = \kappa G S \left( \frac{\partial w}{\partial x} - \phi \right) ,\end{aligned} \end{aligned}$$

(7b)

where w is the deflection, S is the area of the cross section, $\phi$ is the rotation of the cross section, G is the shear modulus and $\kappa$ is a shear coefficient equal to 5/6 for a rectangular cross section (see Fig. 11).

With a distributed shear load q(x) along the beam, the equilibrium equations write:

$$\begin{aligned} \frac{\partial M}{\partial x} + T&= 0 \ , \end{aligned}$$

(8a)

$$\begin{aligned} \frac{\partial T}{\partial x} + q&= 0 \ . \end{aligned}$$

(8b)

Fig. 11

Timoshenko Beam kinematics

1.1 Solution for undamaged area (Region 1)

In region 1 ( $L_{cz} \le x \le a + L_{cz}$) of the DCB/Wedge test, only a load P or a displacement U is applied at the end of the specimen, with no distributed load applied to the beam ($q(x) = 0$). In this case, combining Eqs 7a and 8a simply leads to:

$$\begin{aligned} EI \frac{\partial ^4 w_1(x)}{\partial x^4} = 0, \end{aligned}$$

(9)

where $w_1(x)$ is the deflection of region 1 in z. Integration of this relation leads to an expression for $w_1$:

$$\begin{aligned} w_1(x)=A_1x^3+A_2x^2+A_3x+A_4, \end{aligned}$$

(10)

where $A_1 , A_2, A_3 \ \text {and} \ A_4$ are constants to be determined.

The cross section rotation along region 1 is also obtained:

$$\begin{aligned} \phi _1(x) = \frac{\partial w_1(x)}{\partial x} + C_1. \end{aligned}$$

(11)

1.2 Solution for damaged area (Region 2)

Along Region 2 ($0 \le x \le L_{cz}$) a cohesive zone is inserted between the two DCB/Wedge specimen. Hence, traction forces will develop along the interface in response to the beam displacement, creating a distributed shear load q(x) along the beam. Combining Eqs 7a and 8a this time leads to:

$$\begin{aligned} EI \frac{\partial ^4 w_2(x)}{\partial x^4} = q(x)-\frac{EI}{\kappa GS}\frac{\partial ^2 q(x)}{\partial x^2} \; , \end{aligned}$$

(12)

and

$$\begin{aligned} \phi _2(x)= \frac{\partial w_2(x)}{\partial x} - \frac{T(x)}{\kappa GS} = \frac{\partial w_2(x)}{\partial x} + \frac{\int _0^{x} q(\xi ) d\xi }{\kappa GS} . \end{aligned}$$

(13)

The traction-separation law governing the displacement of the beam along this region for a Dugdale type cohesive law, Dugdale (1960) is characterized by $q(x)=-T_{max}$. Replacing q(x) in Eqs. 12 and 13 respectively leads to:

$$\begin{aligned} EI \frac{\partial ^4 w_2(x)}{\partial x^4} = -T_{max} - \left[ \frac{EI}{\kappa GS}\frac{\partial ^2 (-T_{max})}{\partial x^2} =0 \right] , \end{aligned}$$

(14)

and

$$\begin{aligned} \phi _2(x)= \frac{\partial w_2(x)}{\partial x} - \frac{T_{max} \ x}{\kappa GS} +C_2, \end{aligned}$$

(15)

where $C_2$ is a constant to be determined.

Integration of Eq. 14 yields:

$$\begin{aligned} w_2(x)=\frac{-T_{max}\ x^4}{24D}+B_1x^3+B_2x^2+B_3x+B_4, \end{aligned}$$

(16)

where $B_1, B_2, B_3 \ \text {and} \ B_4$ are constants to be determined.

1.3 Solution for the contact region (Region 3)

As previously explained, in region 3 ($0 \le x \le -\infty$), there is a compression along the plane ($y=0$), which is a symmetry plane for the complete specimen, the half of which is represented in the model. The expression of the contact pressure $P_c(x)$ that has to be applied in this region can be obtained by using a modified version of Eq. 12, replacing q(x) by $P_c(x)$ and $w_2$ by $w_3 \equiv 0$:

$$\begin{aligned} P_c(x) - \frac{EI}{\kappa GS} \frac{{\partial ^2 P_c(x)}}{\partial x^2} =0 \ \ \mathrm {for} \ x \ \in [0,-\infty ]. \end{aligned}$$

(17)

Solving Eq. 17 yields:

$$\begin{aligned} P_c(x) = C_3 e^{\zeta x}, \end{aligned}$$

(18)

where $\zeta = \sqrt{\frac{\kappa G S}{EI}}$ and $C_3$ is the last constant of the problem to be determined.

Finally, the complete solutions of the displacement and rotation fields in the systems reads:

$$\begin{aligned} \left\{ \begin{array}{l} w_1(x)=A_1x^3+A_2x^2+A_3x+A_4 \\ \phi _1(x) = \frac{\partial w_1(x)}{\partial x} + C_1\\ w_2(x)=\frac{-T_{max}}{24D}+B_1x^3+B_2x^2+B_3x+B_4\\ \phi _2(x)= \frac{\partial w_2(x)}{\partial x} - \frac{T_{max} \ x}{\kappa GS} +C_2\\ P_c(x) = C_3 e^{\sqrt{\frac{\kappa G S}{EI}} x}. \end{array}\right. \end{aligned}$$

1.4 Continuity and boundary conditions

The 11 coefficients $A_i , \ B_i \ (i= 1,2,3,4)$ and $C_i(i=1,2,3)$ can be found from boundary conditions and continuity of displacement w(x), neutral axis rotation $\frac{\partial w(x)}{\partial x}$, cross section rotation $\phi (x)$, bending moment M(x) and shear force T(x).

• At $x = a + L_{cz}$:

  The bending moment is zero:

  $$\begin{aligned} M_1(a + L_{cz}) = \frac{EI \partial \ \phi _1(a + L_{cz})}{\partial x}=0. \end{aligned}$$

  In the case of the wedge test, the displacement at the end of the beam is constant and equal to:

  $$\begin{aligned} w_1(a+L_{cz})=U, \end{aligned}$$

  where U is half the thickness of the inserted wedge.

  Alternatively, in the case of the DCB test, the shear force at the end of the beam is equal to :

  $$\begin{aligned} \frac{EI\ \partial \phi _1^2(a+L_{cz})}{\partial x^2}=P, \end{aligned}$$

  where P is load applied to the end of the beam.

• At $x = L_{cz}$:

  the following continuity conditions are used:

  • Displacement: $\displaystyle w_1(L_{cz}) = w_2(L_{cz}).$

  • Cross section rotation: $\displaystyle \phi _1(Lcz) = \phi _2(Lcz).$

  • Bending moment: $\displaystyle \frac{ \partial \phi _1(L_{cz})}{\partial x}=\frac{ \partial \phi _2(L_{cz})}{\partial x.}$

  • Shear force :$\displaystyle \frac{ \partial \phi _1^2(L_{cz})}{\partial x^2}=\frac{ \partial \phi _2^2(L_{cz})}{\partial x^2}$

  • Beam profile slope: $\displaystyle \frac{\partial w_1(Lcz)}{\partial x} = \frac{\partial w_2(Lcz)}{\partial x}$.

• At $x =0$:

  The displacement and its first derivatives are zero:

  $$\begin{aligned} w_2(0)= \frac{\partial w_2(0)}{\partial x}=0. \end{aligned}$$

  In addition, using Eqs. 7a and 7b, the cross section rotation can be expressed as:

  $$\begin{aligned} \phi _2(0)=\frac{\partial w_2(0)}{\partial x} + \frac{EI }{\kappa GS}\frac{ \partial \phi _2^2(0)}{\partial x^2}, \end{aligned}$$

  which provides a way of getting the constant $C_2$.

  Finally, using the continuity of the bending moment between region 2 and 3 provides the equation used to determine $C_3$:

  $$\begin{aligned} \frac{\partial \phi _2(0)}{\partial x}= & {} \frac{\partial \phi _3(0)}{\partial x} = \left( \frac{\partial ^2 w_3(0)}{\partial x^2} - \frac{q(x)}{\kappa GS} \right) \\= & {} \frac{P_c(0)}{\kappa GS}. \end{aligned}$$

This makes 11 relations to determine the 11 coefficients $A_i$, $B_i$ and $C_i$.

1.5 Determination of the fracture process zone length $L_{cz}$

In order to is estimate the length of the process zone $L_{cz}$, one last condition is needed. Writing the equilibrium of the external loads applied to the beam in the y direction writes:

$$\begin{aligned} \int \limits _{-\infty }^{0} P_c(x)dx + \int \limits _{0}^{L_{cz}}q(x)dx + \ P \ = \ 0 , \end{aligned}$$

(19)

where P is the load applied to the extremity of the beam. Taking for example $q(x) = - T_{max}$ in the case of a Dugdale type cohesive zone then leads to:

$$\begin{aligned} \frac{C_3}{\zeta } \ - \ T_{max} \ L_{cz} + \ P \ = \ 0. \end{aligned}$$

(20)

Equation 20 thus provides a relationship to determine $L_{cz}$, for a given value of the loading parameter (U or P).

Finally, in order to find the critical value of the loading parameter at the onset of propagation ($U_{crit}$ or $P_{crit}$), one last relation is used:

$$\begin{aligned} w_2({L_{cz}) = \frac{\delta _{max}}{2}.} \end{aligned}$$

(21)

Appendix B: Example of an estimate of a process zone length from experimental data

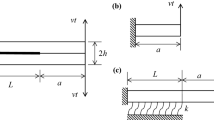
Finding reliable data on experimental cohesive zone lengths represents a challenge for the fracture mechanics community. The process zone length is usually very small compared to the test geometry, and it is difficult to obtain it by direct observation. However, long process zone lengths can be found in the case of fibrous composite materials where large scale bridging can be observed in front of the crack-tip during delamination. Thus, to validate our cohesive zone length estimation, we chose to apply our methodology, developed in Sect. 3, to Huang et al. (2018) who performed experimental DCB tests on a Bamboo-based composite, known as parallel strand bamboo or PSB. The material properties and the test geometry can be found in Table 5. A fracture toughness $G_c=145\; {\text {J/m}}^2 \ (0.145\;{\text {N/mm}})$ was calculated by the compliance method. A critical opening displacement $\delta _{max} =0.038$ mm was measured using a microscopic camera. The process zone length $L_{cz}$ was found to be equal to 12.1 mm.

We estimate the cohesive strength assuming a linear softening law: $T_{max} = 2 \times G_c/\delta _{max} = 7.63$ MPa. Injecting these values into our non-dimensional parameters, we find $X = 9000/7.63 \approx 1179$ and $Y = Gc/T_{max} \times h \approx 8 .10^{-4}$. Using the iso-values of $L_{cz} /h$ plotted in Fig.4b for the linear softening law with the values X and Y, we find $L_{cz} /h = 0.59$ which gives $L_{cz} = 14,16$ mm for $h=24$ mm (17$\%$ higher than the values provided by the authors). Using Eq. 1 with the linear softening law, we find $L_{cz} =$ 19,81 mm, (64% higher than the provided value). This illustrates how the Euler–Bernoulli based models can provide estimates that are noticeably different from our Timoshenko based model.

Table 5 Materials properties and geometry of the PSB specimen used by Huang et al. (2018)