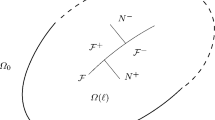
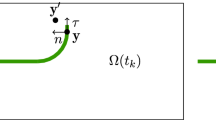
Abstract
Three-dimensional crack growth initiation is examined under the assumption that the crack front remains smooth. Two important modeling issues, specific to three-dimensional rather than two-dimensional cracks, are addressed. First, it is established that, at each point along the crack front, the velocity and configurational force are two-dimensional vectors, lying in the local normal plane. This allows one to generalize any two-dimensional crack growth criterion to three dimensions. Second, a simple mesoscopic model to account for along-the-front non-locality is proposed. This model eliminates pathological growth patterns ubiquitous to basic models applied to three-dimensional cracks. Further, the model is straightforward to use as it relies on standard fracture properties only.




Similar content being viewed by others
References
Antman SS (2005) Nonlinear problems of elasticity, 2nd edn. Springer, New York
Ballarini R, Royer-Carfagni G (2016) A Newtonian interpretation of configurational forces on dislocations and cracks. J Mech Phys Solids 95:602–620
Bigoni D, Dal Corso F, Bosi F, Misseroni D (2015) Eshelby-like forces acting on elastic structures: theoretical and experimental proof. Mech Mater 80(B):368–374
Broek D (1986) Elementary Engineering fracture mechanics. Kluwer Academic Publishers, Dordrecht
Castonguay ST, Mear ME, Dean RH, Schmidt JH (2013) Predictions of the growth of multiple interacting hydraulic fractures in three dimensions. In: SPE annual technical conference and exhibition, society of petroleum engineers, 2013. SPE-166259-MS
Cherepanov GP (1967) Crack propagation in continuous media. J Appl Math Mech 31(3):503–512
Cotterell B, Rice JR (1980) Slightly curved or kinked cracks. Int J Fract 16(2):155–169
Detournay E (2016) Mechanics of hydraulic fractures. In: Davis SH, Moin P (ed) Annual review of fluid mechanics, vol 48. Annual Reviews. pp 311–339
Eshelby JD (1951) The force on an elastic singularity. Philos Trans R Soc Lond A Math Phys Sci 244(877):87–112
Eshelby JD (1975) Elastic energy-momentum tensor. J Elast 5(3–4):321–335
Goldstein RV, Salganik RL (1974) Brittle fracture of solids with arbitrary cracks. Int J Fract 10(4):507–523
Gurtin ME (2000) Configurational forces as basic concepts of continuum physics. Springer, New York
Gurtin ME, Podio-Guidugli P (1996) Configurational forces and the basic laws for crack propagation. J Mech Phys Solids 44(6):905–927
Hakim V, Karma A (2009) Laws of crack motion and phase-field models of fracture. J Mech Phys Solids 57(2):342–368
Hodgdon JA, Sethna JP (1993) Derivation of a general 3-dimensional crack propagation law: a generalization of the principle of local symmetry. Phys Rev B 47(9):4831–4840
Hull D (1999) Fractography: observing, measuring and interpreting fracture surface topography. Cambridge University Press, Cambridge
Knauss WG (1970) An observation of crack propagation in anti-plane shear. Int J Fract 6(2):183–187
Knowles E, Sternberg JK (1972) On a class of conservation laws in linearized and finite elastostatics. Arch Ration Mech Anal 44(3):187–211
Lin B, Mear ME, Ravi-Chandar K (2010) Criterion for initiation of cracks under mixed-mode I plus III loading. Int J Fract 165(2):175–188
Mahajan RV, Ravichandar K (1989) An experimental investigation of mixed-mode fracture. Int J Fract 41(4):235–252
Movchan AB, Gao H, Willis JR (1998) On perturbations of plane cracks. Int J Solids Struct 35(26–27):3419–3453
Pressley A (2007) Elementary differential geometry. Springer, New York
Rice JR (1968) A path-independent integral and approximate analysis of strain concentration by notches and cracks. J Appl Mech 35(2):379–386
Rice JR (1984) Lecture notes on fracture mechanics. Division of Engineering and Applied Sciences, Harvard University, Cambridge
Rungamornrat J, Wheeler MF, Mear ME (2005) Coupling of fracture/non-newtonian flow for simulating nonplanar evolution of hydraulic fractures. In: SPE annual technical conference and exhibition, society of petroleum engineers, 2005. SPE 96968n
Shih CF, Moran B, Nakamura T (1986) Energy release rate along a three-dimensional crack front in a thermally stressed body. Int J Fract 30(2):79–102
Sommer E (1969) Formation of fracture ‘lances’ in glass. Eng Fract Mech 1(3):539–540
Xu G, Bower AF, Ortiz M (1994) An analysis of nonplanar crack-growth under mixed-mode loading. Int J Solids Struct 31(16):2167–2193
Acknowledgements
I am grateful to my colleagues and friends for helpful discussion. Those include Mark Mear, Charles Mood, K. Ravi-Chandar, Lorenzo Sadun, and Misha Vishik (University of Texas at Austin), David Parks (MIT), John Napier (University of Pretoria), Emmanuel Detournay (University of Minnesota), and John Bassani (University of Pennsylvania). This work was supported by a grant from the National Science Foundation (CMMI 1663551), MTS fellowship at the University of Minnesota, and Moncrief Grand Challenge Faculty Award from Institute for Computational Engineering and Sciences at University of Texas at Austin.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Rodin, G.J. Local and non-local modeling aspects of three-dimensional cracks growth initiation. Int J Fract 221, 211–220 (2020). https://doi.org/10.1007/s10704-020-00424-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10704-020-00424-8