On the applicability of linear elastic fracture mechanics scaling relations in the analysis of intergranular fracture of brittle polycrystals

Abstract

Crack propagation in polycrystalline specimens is studied by means of a generalized finite element method with linear elastic isotropic grains and cohesive grain boundaries. The corresponding mode-I intergranular cracks are characterized using a grain boundary brittleness criterion that depends on cohesive law parameters and average grain boundary length. It is shown that load–displacement curves for specimens with the same microstructure and for various cohesive law parameters can be obtained from a master load–displacement curve by means of simple linear elastic fracture mechanics scaling relations. This property is a consequence of the independence of intergranular crack paths from cohesive law parameters. Perfect scaling is obtained for cases characterized by the same grain boundary brittleness number, irrespective of its value, whereas scaling is approximated for cases with different but relatively large values of the grain boundary brittleness number. The former case corresponds to grain boundary traction profiles that are identical apart from a scale factor; in the latter case, a large grain boundary brittleness number implies similar, apart from a scale factor, traction profiles. By exploiting this property, it is demonstrated that computationally expensive simulations can be avoided above a certain grain boundary brittleness threshold value.

1 Introduction

Linear elastic fracture mechanics (LEFM) provides analytical solutions for the global mechanical response of homogeneous specimens and structures in terms of macroscopic load–displacement curves. Because of the linear dependence of these curves on the fracture toughness, they scale with it. The aim of this study is to show that such scaling holds in intergranular crack propagation in brittle polycrystalline specimens if certain conditions are met.

In polycrystalline materials, brittle intergranular failure is understood as failure that takes place along a single crack trajectory. A popular method to describe the mechanical response of a polycrystalline specimen is to define crack surfaces by means of cohesive discontinuities (Simonovski and Cizelj 2015; Ha et al. 2015). These cohesive discontinuities, through the cohesive law, are associated to a cohesive length scale that must be resolved by the discretization for the simulations to produce reliable results. The extent of this zone around a propagating crack tip depends on the cohesive law parameters (fracture energy or fracture toughness and tensile strength), and numerical simulations of brittle failure can be computationally demanding because of the stringent mesh requirements to adequately resolve it. A relative measure of the cohesive zone size is the brittleness number (Hillerborg et al. 1976; Carpinteri 1982; Bažant and Pfeiffer 1987; Carpinteri and Colombo 1989; Planas and Elices 1991; Abdel-Tawab and Rodin 1998; Bache 1985), a quantity that associates a characteristic dimension of the specimen to the cohesive length scale. Based on its definition, the higher the brittleness number, the smaller the element size, thus resulting into computationally expensive simulations. In cases with high brittleness numbers, LEFM can deliver practically acceptable results without the necessity to run accurate but expensive nonlinear finite element analyses (Confalonieri et al. 2014; Mulay et al. 2015; Lucas et al. 2015; Infuso et al. 2014; Gulizzi et al. 2018). The question addressed here is whether and to what extent LEFM scaling relations can be used to replace traditional, finite element-based numerical analysis of brittle failure in polycrystalline specimens.

In this work, variations of key cohesive law parameters are thoroughly investigated to study local and global responses of two-dimensional specimens employing different polycrystalline topologies with different grain sizes. To quantify the brittleness level in each simulation, a grain boundary brittleness number is proposed in Sect. 3. As shown in Sect. 3.1, when two material parameters share the same brittleness number value, the corresponding load–displacement curves can be scaled between each other in a (numerically) accurate manner using LEFM scaling relations. If the brittleness number values are different, Sect. 3.2 shows that scaling holds with pretty good accuracy only above a certain threshold value. The scaling relations hold even when the process zone at the crack tip is not negligibly small compared to the crack length. The result is quite beneficial for highly brittle polycrystals as load–displacement curves can be obtained at a relatively low computational cost. The proposed brittleness number provides a general basis for scaling in brittle polycrystals because of its insensitivity to material parameters and grain size variations as illustrated in Sect. 5. It is also shown that fracture toughness is the only important parameter in crack propagation in brittle polycrystals beyond a certain value of the brittleness number.

Fig. 1

A polycrystalline topology (a), superimposed on a background finite element mesh (b), results in a GFEM discretization for polycrystals (c). The accuracy of the solution can be improved through a mesh refinement procedure (d)

2 Method of analysis and assumptions

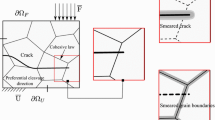
The study conducted in this paper relies on the analysis of the load–displacement curves of cracked polycrystalline specimens. These are obtained by performing numerical crack propagation analyses on the specimen depicted in Fig. 2.

Mode-I intergranular crack paths are obtained with a generalized finite element method (GFEM) for polycrystals (Simone et al. 2006; Shabir et al. 2011). A particular feature of this approach is that it does not require any mesh generator to mimic the polycrystalline topology. In fact, the GFEM discretization is obtained by superimposing a polycrystalline topology on a background finite element mesh as shown in Fig. 1a–c. Noteworthy, grain boundaries can cut elements, and junctions can be located within elements, thus facilitating the mesh generation process. The performance of the method in terms of accuracy of the solution can be improved by means of automatic mesh refinement, especially along grain boundaries and around junctions. In this work, constant strain triangular element background meshes are refined as shown in Fig. 1d using the algorithm proposed by Rivara (1989). According to Shabir et al. (2011), mesh independent results can be obtained if two conditions are met: (1) the length $l_\text {e}$ of the longest side of all the elements intersected by the grain boundaries, the average grain boundary length $l_\text {gb}$, and the characteristic length $l_\text {z}$ of the cohesive law are related through the inequality $l_\text {e} \le \min \left( {l_\text {z}/3, l_\text {gb}/2} \right)$, and (2) each grain boundary crosses at least four elements. These two heuristic criteria ensure that the stress field ahead a propagating crack tip is adequately represented.

Alumina, Al$_2$O$_{3}$, with Young’s modulus $E=384.6$ GPa and Poisson’s ratio $\nu =0.23$, is selected as a representative brittle polycrystalline material. Following Warner and Molinari (2006), the grains are considered as linear elastic and isotropic. Non-linearities are therefore confined to grain boundaries where the Xu and Needleman (1994) potential-based cohesive law, modified to reflect secant unloading and reloading behavior, is employed. In the Xu–Needleman cohesive law, the characteristic length $l_z$ (Palmer and Rice 1973) is given by

$$\begin{aligned} l_\text {z} = \frac{9\pi }{32}\frac{E}{1-v^2}\frac{G_\text {Ic}}{\sigma _\text {max}^2} = \frac{9\pi }{32} \left( {\frac{K_\text {Ic}}{\sigma _\text {max}}} \right) ^2, \end{aligned}$$

(1)

where $G_\text {Ic}=(1-\nu ^2)K^2_\text {Ic}/E$ is the fracture energy, $K_\text {Ic}$ the fracture toughness, and $\sigma _\text {max}$ the tensile or cohesive strength.

Mode-I load–displacement curves and crack paths are obtained considering the single edge notched four point bending specimen depicted in Fig. 2. For numerical convenience, the region outside the process zone is approximated as a linear elastic homogeneous material. The microstructure in the process zone is described using irregular hexagonal grain topologies, each comprising a variable number of grains as shown in Fig. 3. These irregular arrangements are obtained by perturbing the grain junctions of regular hexagonal topologies. The analyses are performed under plane strain conditions considering small elastic strains and rotations and mode-I loading conditions. The specimen is subjected to a quasi-static loading condition with an incrementally variable load P. Shabir et al. (2011) demonstrated that intergranular brittle cracking of polycrystalline aggregates is independent of key cohesive law parameters such as $G_\text {Ic}$ (or $K_\text {Ic}$) and $\sigma _\text {max}$ and depends only on the geometry of the polycrystalline microstructure. As a consequence, reliable crack paths for brittle polycrystals can be obtained using a convenient cohesive law parameter set.

Fig. 2

The test setup for the notched specimen used in the simulations. The process zone is described using the granular arrangements shown in Fig. 3. The specimen length $W=2400~\upmu$m

Fig. 3

Granular arrangements in the process zone of the test setup in Fig. 2. The blue line indicates the computed crack path while the thick black line indicates the traction-free notch from which the crack propagated

As a limit case (i.e., when there are only two grains as in Fig. 3a, and the material parameters correspond to brittle grain boundary behavior), the numerical solution converges to the analytical load–displacement curve derived by Corigliano and Mariani (1996) in the context of LEFM using the so-called compliance method [refer to Paris and Sih (1965, pp. 51–52), for more details]. The relation between force P per unit of beam width and displacement ${\varDelta }$ for a single edge notched four point bending specimen is expressed through

$$\begin{aligned} P = \sqrt{\frac{2DG_{\text {Ic}}}{\text {d}C / \text {d} \alpha }} \quad \text {and} \quad {\varDelta }=\frac{CP}{2} \end{aligned}$$

(2)

and is a function of the geometrical parameters defined in Fig. 2, the normalized crack length $\alpha =a/D$, the compliance

$$\begin{aligned} C\left( {\alpha } \right)= & {} \frac{12e^2}{ED^3} \left( W-\frac{4}{3}e \right) \nonumber \\&+\, \frac{24e^2}{ED^2} \left[ -\frac{d_1}{d_2 -2} \left( (1-\alpha )^{d_2 -2} -1 \right) \right. \nonumber \\&+ \,\frac{d_3}{2} \left( \frac{1}{(1-\alpha )^2} -1 \right) \nonumber \\&\left. + \,\frac{d_1}{d_2 +1} \left( (1-\alpha )^{d_2 +1} -1 \right) -d_3 \alpha \right] , \end{aligned}$$

(3)

and the constants $d_1$, $d_2$ and $d_3$ which are equal to 2.64, 6.65 and 1.32, respectively. Note that the normalized crack length $\alpha =0.5$ prior to fracture propagation.

3 Grain boundary brittleness number and scaling relations

The brittleness of a structural response can be identified by making use of the so-called brittleness number (Karihaloo et al. 1993). In the context of nonlinear fracture mechanics of ceramic materials such as concrete, Hillerborg et al. (1976) characterized the behavior of structural members through the ratio of a characteristic structural length (the fracture ligament length b) and the characteristic length $l_\text {z}$ of the cohesive law. The dimensionless parameter $b / l_{\text {z}}$ was subsequently termed the brittleness number. Closely related quantities were later defined by Carpinteri et al. (Carpinteri 1982; Carpinteri and Colombo 1989). As pointed out by Bažant and Pfeiffer (1987), these parameters indicate relative situations since they depend on the geometrical shape of the specimen and therefore cannot be used to define an absolute range of values over which LEFM can be used. These brittleness indicators are however defined under the assumption of a homogeneous material, with no information about the microstructure of the material, and relate the failure processes to a structural size (i.e., the fracture ligament length).

Fig. 4

Scaling of the load–displacement curve through the grain boundary brittleness number $\beta _\text {gb}$ for the two- (a) and 80- (b) grain topologies reported in Fig. 3. The label of the master curve is reported in bold typeface in the legend. The scaled curves (marked with symbols) have been obtained from the master curves (blue lines) using the scaling relations (5)

Similar concepts can be defined in brittle polycrystalline materials undergoing intergranular crack propagation where three relevant length scales can now be identified: the characteristic length of the cohesive law $l_\text {z}$, Eq. (1), the grain boundary length $l_\text {gb}$, and a specimen characteristic length such as the fracture ligament length b. If, however, the specimen characteristic dimensions are comparable to the average grain size, i.e., of the same order of magnitude or one order of magnitude larger as in, e.g., micro electro mechanical systems (MEMS) (Mullen et al. 1997; Corigliano et al. 2008), then only the first two length scales need to be considered. Thus, we define the non-dimensional grain boundary brittleness number as

$$\begin{aligned} \beta _\text {gb}=\frac{l_\text {gb}}{l_\text {z}} = \frac{32}{9 \pi } \left( {\frac{\sigma _\text {max}}{K_\text {Ic}}} \right) ^2 l_\text {gb}. \end{aligned}$$

(4)

This quantity can be understood as a local version (i.e., at the grain boundary level) of the expression $b / l_{\text {z}}$ proposed by Hillerborg et al. (1976). Since the failure processes studied in this document take place at the grain boundary level, this indicator can be considered of general validity, irrespective of the structure geometry (see the discussion in Bažant and Pfeiffer 1987).

Our numerical experiments indicate that for a given polycrystalline specimen, the brittleness number $\beta _\text {gb}$ can be employed to relate to each other load–displacement curves obtained with different sets of cohesive law parameters by means of the following scaling relations:

$$\begin{aligned} P=\frac{K_\text {Ic}}{\bar{K}_\text {Ic}} \, \bar{P} \quad \text {and} \quad {\varDelta }=\frac{K_\text {Ic}}{\bar{K}_\text {Ic}} \, \bar{{\varDelta }}. \end{aligned}$$

(5)

According to these relations, each point $\left( {P, {\varDelta }} \right)$ on the load–displacement curve related to a specimen with fracture toughness $K_{\text {Ic}}$ can be expressed through a master load–displacement curve $\left( {\bar{P}, \bar{{\varDelta }}} \right)$ related to the same specimen with fracture toughness $\bar{K}_\text {Ic}$. This implies that if two sets of cohesive law parameters ($G_\text {Ic}$, $\sigma _\text {max}$ or $K_\text {Ic}$, $\sigma _\text {max}$) have the same brittleness numbers, the corresponding load–displacement curves are related through the scaling relations (5) as discussed in Sect. 3.1. The scaling relations in (5) are reminiscent of LEFM. Indeed, they can also be derived from the analytical relations (2) and are valid for any specimen shape. As another application, it is shown in Sect. 3.2 that the scaling relation also holds when the brittleness numbers related to two cohesive law parameter sets are above a threshold.

3.1 Scaling of load–displacement curves with identical grain boundary brittleness number

When two sets of cohesive law parameters results in the same grain boundary brittleness number, it is possible to obtain the load–displacement curve corresponding to one set by simply scaling the response corresponding to the other set through the scaling relations (5). This is illustrated in Fig. 4 for the two- and 80-grain topologies in Fig. 3. The perfect scaling of the load–displacement curves originates from grain boundary traction profiles that are identical apart from a scale factor. A further consequence of this local behavior is that crack paths are identical (refer to the discussion in Shabir et al. 2011). In general, this property of the load–displacement curve holds for any number of grains and is independent of the value of $\beta _\text {gb}$.

Fig. 5

Two-grain specimen: a–c analytical and numerical load–displacement curves; b–d evolution of normal traction profiles versus the normalized coordinate s along the grain boundary sampled at points A, B and C on the corresponding load–displacement curves (the notch is located at $s=0$)

3.2 Scaling of load–displacement curves with different grain boundary brittleness number

The higher the grain boundary brittleness number, the more brittle the structural response—in a perfectly brittle material the grain boundary brittleness number is infinite and the plastic process zone collapses to a point. Next, we will define a threshold value of the grain boundary brittleness number above which scaling holds between two load–displacement curves with different values of $\beta _\text {gb}$ for a given microstructure. The threshold value will identify situations in which very expensive simulations, characterized by large values of $\beta _\text {gb}$, can be replaced by less expensive ones, i.e., with a lower $\beta _\text {gb}$, by considering the global response in terms of the load–displacement curves and making use of the scaling relations (5).

3.2.1 Two-grain arrangement

Consider the two-grain arrangement shown in Fig. 3a. The length of the grain boundary $l_{\text {gb}}$ (the ligament length in this case) between these two grains is $120~\upmu$m. Numerical load–displacement curves are compared to the corresponding analytical curves obtained using the LEFM relations (2). Figures 5 and 6 show the results of this investigation. It is evident from Fig. 5a, c that the numerical curve approaches the corresponding analytical curve only for high values of $\beta _\text {gb}$. The extent of non-linearity can be observed through the evolution of the traction profile in the normal direction along the grain boundary as shown in Fig. 5b, d.

When the scaling relations are applied to the numerical curves reported in Fig. 6a, it can be observed in Fig. 6b, c that the scaled curves follow the original curves only in an approximate manner. Important features such as the peak load and the elastic branch are grossly captured. Scaling does not hold in both cases, and the use of the scaling relations is therefore not recommended in this situation. Further investigations with grain boundary lengths between 120 and 4 $\upmu$m confirmed this behavior.

3.2.2 Multiple-grain arrangements

This section shows the applicability of the scaling relations (5) to polycrystalline specimens. We start with the topologies in Fig. 3b–e that represent the process zone of the specimen depicted in Fig. 2.

The load–displacement curves for the specimen with the 40-grain topology depicted in Fig. 3b are shown in Fig. 7. These curves (solid lines) are compared to the scaled curves obtained using the scaling relations (5). When a master curve (solid thick line) is tagged with a low brittleness number as in Fig. 7a, the master curve cannot generate other load–displacement curves by means of the scaling relations (5). When the master curve has a high brittleness number ($\beta _{\text {gb}} = 2.68$) as in Fig. 7b, scaling is effective only when the brittleness number of the curve that is to be scaled is relatively high ($\beta _{\text {gb}} \ge 1.65$). In both cases discussed so far, scaling holds only for the curves characterized by $\beta _{\text {gb}} \ge 1.65$. And indeed, although the curve with $\beta _{\text {gb}}=2.68$ is selected as the master curve in Fig. 7b, it is also possible to consider the curve with $\beta _{\text {gb}} = 1.65$ as master curve and with it obtain load–displacement curves related to higher values of $\beta _{\text {gb}}$.

The arguments about the numerical value of the brittleness number and its relation to the effectiveness of the scaling operation between load–displacement curves are confirmed by the curves Fig. 7c, d where scaling is always effective. These figures also show that the quality of the scaling improves with master curves characterized by high values of $\beta _{\text {gb}}$. At variance with the two-grain arrangement discussed in Sect. 3.2.1, the peak load is now adequately reproduced and all curves show the same elastic branch for a relatively low value of the grain boundary brittleness parameter. Based on these observations, we propose a conservative threshold value of 2 for $\beta _{\text {gb}}$ above which the scaling of load–displacement curves with different grain boundary brittleness value is possible.

Fig. 6

Scaling of the load–displacement curves using master curves with different $\beta _\text {gb}$ for the two-grain example. Panel b compares the load–displacement curves in a against the scaled up curves obtained using the curve with the highest grain boundary brittleness parameter; a similar operation is conducted in c where the load–displacement curves in a are compared against the scaled down curves obtained using the lowest grain boundary brittleness parameter. In both cases, scaling is unsatisfactory

Fig. 7

The load–displacement curves obtained from the numerical solution (solid lines) of the 40-grain topology in Fig. 3b are compared to the scaled curves obtained using the scaling relations (5). When the brittleness number is low the quality of the scaling is poor. Panel a shows that scaling a master curve (solid thick line) with a low brittleness number is not effective. Panel b indicates that when the master curve has a high brittleness number ($\beta _{\text {gb}} = 2.68$) scaling is effective only when done on cases with relatively high brittleness number ($\beta _{\text {gb}} \ge 1.65$). This is confirmed by the curves in c and d where scaling is always effective. Label “A” indicates the points that correspond to the same position of the crack tip using two different values of the tensile strength (refer to Fig. 8)

Fig. 8

von Mises stress plots for the 40-grain topology depicted in Fig. 3b. The plots a, b and c correspond to the same crack tip position and are indicated by point A in Fig. 7. These plots can be mutually scaled only for $\beta _\text {gb} \ge 2$. The differences of the stress fields b and c with respect to the master stress field a are presented in plots d and e, respectively, to show that they are moderate in case of $\beta _\text {gb} \ge 2$ (d)

To gain further insight into the observed scaling of the load–displacement curves for $\beta _\text {gb} \ge 2$, von Mises stress contour plots for various values of the grain boundary brittleness number are reported in Fig. 8a–c. The stress fields are sampled considering the same position of the crack tip—in our numerical simulations, a crack develops when the crack openings are larger than the corresponding characteristic separation values (Shabir et al. 2011); therefore, considering that the slope of the pre-peak part of the traction-separation curve depends on the cohesive law parameters, the actual crack opening related to the same crack tip position might correspond to visually different cracks. In Fig. 8, the differences of the stress fields in (b) and (c) with respect to the master stress field in (a) are shown in (d) and (e), respectively. It can be observed that the differences shown in (d) are small and confined along the crack path only, whereas in (e) they are large and spread over the process zone. The small differences in (d) justify the mutual scaling of corresponding load–displacement curves [i.e., related to (a) and (b)] for which $\beta _\text {gb} \ge 2$.

To determine whether the grain size has an effect on the threshold value for $\beta _{\text {gb}}$, we increased the number of grains to 80 by reducing the grain size to 21 $\upmu$m as shown in Fig. 3c. The corresponding load–displacement curves are reported in Fig. 9 where it can be observed that the mutual scaling of the load–displacement curves holds practically for $\beta _{\text {gb}} \ge 1.77$. It is important to mention here that for a given value of the fracture toughness, the load–displacement curves, obtained considering different values of cohesive strength, have negligible differences when $\beta _\text {gb} \ge 2$. Further analyses on a 190-grain topology with an average grain size of $\approx 13~\upmu$m (Fig. 3d) and a 665-grain topology with an average grain size of $\approx 7~\upmu$m (Fig. 3e) have been considered. The results reported in Figs. 10 and 11 support the proposed threshold value for $\beta _{\text {gb}}$. The scaling property of the load–displacement curves have been observed also in grain topologies generated with a centroidal Voronoi tessellation algorithm.

Fig. 9

The load–displacement curves obtained from the numerical solution (solid lines) of the 80-grain topology in Fig. 3c are compared to the scaled curves obtained using the scaling relations (5). When the brittleness number is low the quality of the scaling is poor. Panel a shows that when the master curve has a high brittleness number ($\beta _{\text {gb}} = 3.10$) scaling is effective only when scaling is done for cases with relatively high brittleness number ($\beta _{\text {gb}} \ge 1.77$). This is confirmed by the curves in b where scaling is always effective

Fig. 10

The load–displacement curves obtained from the numerical solution (solid lines) of the 190-grain topology in Fig. 3d are compared to the scaled curves obtained using the scaling relations (5). When the brittleness number is low the quality of the scaling is poor. Panel a shows that when the master curve has a low brittleness number scaling is not effective. Panel b indicates that scaling is always effective when the master curve has a high brittleness number ($\beta _{\text {gb}} = 2.00$) and scaling is done for cases with higher brittleness number

Fig. 11

The load–displacement curves obtained from the numerical solution (solid lines) of the 665-grain topology in Fig. 3e are compared to the scaled curves obtained using the scaling relations (5). When the brittleness number is low the quality of the scaling is poor. Panel a shows that when the master curve has a low brittleness number scaling is not effective. Panel b indicates that scaling is always effective when the master curve has a high brittleness number ($\beta _{\text {gb}} = 2.00$) and scaling is done for cases with higher brittleness number

Table 1 Cost of the simulations for the load–displacement curves shown in Fig. 11b for the 665-grain topology in Fig. 3e in terms of relative simulation time with respect to $\beta _\text {gb}=2$

Table 2 Brittleness number $\beta _\text {gb}$ considering various average grain boundary lengths with two sets of cohesive law parameters

Table 1 lists the simulation cost for the 665-grain topology in Fig. 3e for various values of $\beta _\text {gb}$. The corresponding load–displacement curves, along with the scaled curves, are reported in Fig. 11b. The results in Table 1 indicate that the load–displacement curve for the set of parameters corresponding to $\beta _\text {gb}=6.06$ can be obtained from the curve with $\beta _\text {gb}=2$ with a saving of almost 90% on the simulation time. it is important to note that the saving in computational costs is due to the less stringent mesh size requirements related to a less brittle material or, as evident from Table 1, to the reduction in the number of degrees of freedom and load increments. In general, the number of load increments is linked to the smoothness of the load–displacement curve. Smooth curves, such as that corresponding to $\beta _\text {gb}=0.1$ in Fig. 11, can be obtained when the cohesive length has been adequately resolved by the mesh. For relatively high values of the grain boundary brittleness number, such as those listed in Table 1, this is a difficult task as the meshing requirements are usually prohibitive. The results reported in Table 1 have been obtained using the meshing requirements reported in Sect. 2 which assure mesh independent results but yield ragged load–displacement curves. These ragged curves can be traced using a large number of load increments and are related to discretized systems with a computationally tractable number of degrees of freedom.

4 Effectiveness of the grain boundary brittleness number

The effectiveness of the grain boundary brittleness number $\beta _\text {gb}$ in identifying load–displacement curves amenable to be scaled can be further illustrated by comparing its value for cases with variable grain size whilst considering the same cohesive law parameters ($\sigma _{\text {max}}=0.6$ GPa and $K_{\text {Ic}}=1.7$ MPa$\sqrt{\text {m}}$) as shown in Table 2.

Borrowing from concepts of metal plasticity and according to the ASTM E399 standard (ASTM 2004), the validity of the small scale yielding condition, and thus of LEFM outside the process zone, is assured since $L_\text {y}\approx 20$ $\upmu$m and the minimum specimen dimension is the fracture ligament length equal to 120 $\upmu$m—the small scale yielding condition is valid when the minimum specimen size exceeds

$$\begin{aligned} L_\text {y} = 2.5 \left( {\frac{K_\text {Ic}}{\sigma _\text {max}}} \right) ^2, \end{aligned}$$

(6)

where here the cohesive strength $\sigma _\text {max}$ takes the place of the yield stress $\sigma _\text {y}$. Therefore, LEFM might be used to characterize, to a certain extent, the essential features of the mechanical response. However, the values listed in Table 2 and the corresponding load–displacement curves clearly show that only a grain-based parameter criterion, rather than one based on a characteristic structural length, gives valuable indications regarding the scaling of a load–displacement curve through the relations in (5). Similar conclusions hold for the results obtained with $\sigma _{\text {max}}=2$ GPa and $K_{\text {Ic}}=4$ MPa$\sqrt{\text {m}}$, for which $L_\text {y}\approx 10$ $\upmu$m.

Fig. 12

Scaling of the load–displacement curves considering two different materials and a fixed grain size of 100 $\upmu$m for the 40-grain topology shown in Fig. 3b. The curves show a scaling behavior similar to that presented in Fig. 7b, d for the corresponding $\beta _{\text {gb}}$ values

5 Generality of the grain boundary brittleness number

To strengthen the argument that the grain boundary brittleness number is insensitive to material parameters (as illustrated in Fig. 4 for cohesive parameters) and grain size variations (as presented in Sect. 3.2.2), the 40-grain topology depicted in Fig. 3b is scaled up from a grain size of 33 $\upmu$m to 100 $\upmu$m (here W changes to 7200 $\upmu$m in Fig. 2). The cohesive parameters are selected in such a way that the calculated values of $\beta _{\text {gb}}$ match with some of the values already considered for the 40-grain topology in Fig. 7. From the results presented in Fig. 12a, b, it can be easily observed that the curves show the same scaling behavior as reported in Fig. 7b, d for the same $\beta _{\text {gb}}$. This observation proves that the shape of the curves is insensitive to the grain size variations for identical values of $\beta _{\text {gb}}$. The same scaling behavior is observed for another set of simulations considering elastic properties of polycrystalline silicon—the modulus of elasticity E and Poisson’s ratio $\nu$ are set equal to 160 GPa and 0.25, respectively. The corresponding curves are reported in Fig. 12c, d exhibiting the same scaling behavior as reported above. These observations confirm that $\beta _\text {gb}$ is insensitive to the values of material parameters and grain size variations and provides a measure of brittleness that is valid in any brittle polycrystal undergoing intergranular crack propagation. This confirmation also validates $\beta _\text {gb} > 2$ as a range of validity for the mutual scaling of their load–displacement curves.

6 Discussion

Computationally expensive simulations of intergranular crack propagation in polycrystalline specimens are characterized by combinations of fracture toughness and tensile strength values that result in high values of the grain boundary brittleness number $\beta _\text {gb}$. Under certain circumstances, this computational effort can be strongly reduced, and global responses in terms of load–displacement curves can be obtained by simple scaling operations with reference to a less costly simulation. What makes scaling possible in the first place is the fact that mode-I intergranular crack paths in brittle polycrystals are independent of cohesive law parameters as shown by Shabir et al. (2011) (by analogy, this independence holds also in the case of realistic distributions of grain boundary properties). The shape of the load–displacement curve is a direct signature of the crack path if brittle failure, characterized by very large values of the brittleness number $\beta _\text {gb}$, is confined to a single crack as under quasi-static loading conditions. The load–displacement curve is serrated because each unloading and reloading branch indicates the opening of a grain boundary and therefore unequivocally identifies a failing grain boundary along the crack path. When failure is brittle, the deformation is confined to a small region around the propagating crack tip and the smaller this region the sharper the unloading and reloading branches. In such a situation, only the grain boundaries in the immediate proximity deform and, in the case of truly brittle failure, there is only one opening grain boundary. When the value of the brittleness number is relatively low, the unloading and reloading branch is smooth and there might be more than one grain boundary opening around a propagating crack tip. The sharpness of the unloading and reloading branches is identified by the value of the brittleness number $\beta _\text {gb}$. This number is therefore the other necessary component to characterize scaling as it identifies the extent of the failure region relative to the grain boundary. The results show that the global response in terms of the load–displacement curve of specimens with high grain boundary brittleness number can be approximated, to a high degree of accuracy, by choosing any convenient set of cohesive law parameters such that the grain boundary brittleness number $\beta _\text {gb} \ge 2$, and by scaling the global response with the corresponding values of fracture toughness.

Under the condition $\beta _\text {gb} \ge 2$, any load–displacement curve can be chosen as a master curve to scale the others. However, curves with high fracture toughness and low cohesive strength are to be preferred because of their low computational cost as relative coarse meshes suffice to resolve the cohesive zone along the grain boundaries. When the brittleness number $\beta _\text {gb} \ge 2$, the only relevant cohesive law parameter in brittle fracture of polycrystals becomes the fracture toughness (i.e., the load–displacement curves are not influenced by the value of the tensile strength). Further, the quality of the scaling for $\beta _\text {gb} \ge 2$ is not influenced by the grain arrangement. These conclusions hold also for specimens with different shape and boundary conditions. This has been confirmed considering the three 80-grain realizations studied in Shabir et al. (2011) in a single-edge-notch tension specimen (Fig. 2 in Shabir et al. 2011) and in the specimen described in Sect. 2 for various values of $\beta _\text {gb}$.

Considering the aforementioned independence of the crack path from cohesive law parameters (Shabir et al. 2011), the results obtained in this study allow to characterize the mode-I intergranular fracture response of brittle polycrystals in terms of crack path, load–displacement curve, and stress field employing inexpensive computations. The validity of the results is however restricted to cases in which failure processes are confined to a single grain boundary, a condition that has been formalized with reference to a range of values of the grain boundary brittleness number ($\beta _\text {gb} \ge 2$). As this condition is defined with reference to an average grain boundary length, scaling holds in an accurate manner for each portion of the load–displacement curve that corresponds to a grain boundary opening/closing process if the corresponding grain boundary length is smaller or equal to the average grain boundary length. In this sense, scaling holds irrespective of the grain shape. In situations with a wide distribution of grain sizes (and grain boundary length), the definition of a representative grain boundary length might not be trivial (the average grain boundary length is not a good choice as the length of some grain boundaries might be smaller that the process zone size, thus breaking down the scaling property).

As a final remark, when two material parameter sets yield the same value of the grain boundary brittleness number, the corresponding load–displacement curves can be scaled between each other in an accurate manner (irrespective of the value).