Elastic vortices and thermally-driven cracks in brittle materials with peridynamics

Abstract

Instabilities in thermally-driven crack growth in thin glass plates have been observed in experiments that slowly immerse a hot, pre-notched glass slide into a cold bath. We show that a nonlocal model of thermomechanical brittle fracture with minimal input parameters can predict the entire phase diagram of fracture measured in experiments for the low immersion speed regime. Geometrical restrictions to crack growth commonly found in other approaches are absent here. We discuss a method for determining the appropriate size of the peridynamic horizon based on a data point around a separating line between crack-type zones in the experimental phase diagram. Once the nonlocal size is smaller than the length-scale introduced by the thermal gradient, the computational results show that no fracture criterion is needed beyond Griffith’s criterion to capture the observed instabilities. The combination of thermal gradients and competing contraction forces on the two sides of the crack are behind the observed crack path instabilities. Elastic (velocity) vortices of material points show how and why the cracks develop along the observed paths. Our results demonstrate that thermally-driven fracture in brittle materials can be predicted with accuracy. We anticipate that this model will lead to design protocols for controlled fracture in brittle materials relevant in materials science and advanced manufacturing.

Appendices

Appendix A1: Mathematical expression of the analytical thermal field

An analytical expression, shown in Fig. 1, that approximates the thermal field from the water bath, across the gap, and into the oven, is (see Bouchbinder et al. 2003, Pham et al. 2008):

$$\begin{aligned} {\begin{array}{l} T\left( x \right) =\left\{ {\begin{array}{ll} T_{0}\quad &{} if \quad x\le -\,H,\\ T_{0}+\frac{1}{2}T_{\mathrm {gap}}\left( 1-\frac{1-exp\left( \frac{x}{L_{D}} \right) }{1-exp\left( -\frac{H}{L_{D}} \right) } \right) \quad &{} if - H<x\le 0,\\ T_{0}+\frac{1}{2}T_{\mathrm {gap}}\left( 1-\frac{1-exp\left( -\frac{x}{L_{D}} \right) }{1-exp\left( -\frac{H}{L_{D}} \right) } \right) \quad &{} if \quad 0<x\le H,\\ T_{0}+T_{\mathrm {gap}} \quad &{} if \quad x>H,\\ \end{array}} \right. \end{array}}\nonumber \\ \end{aligned}$$

(A1)

where $H=10$ mm (double of the gap length h) to have a transition of the temperature between three zones similar to that observed in the experiment (see Fig. 1 bottom panel), $T_{0}$ the temperature of the cold water bath, $T_{\mathrm {gap}}$ the temperature difference between water bath and oven, $L_{D}$ = 1 mm the diffusion length, and x the coordinate along length direction with the origin $(x = 0)$ placed at the interface between the water bath and the gap.

Appendix A2: Temperature dependent fracture energy

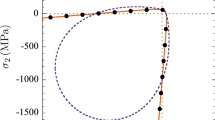
Experiments showed that the fracture energy decreases with the increase of the temperature at the crack tip (

dots and corresponding blue guideline in Fig. 12, digitizied from Fig. 11 in Ronsin and Perrin 1998). To take this effect into consideration in our simulation, the guideline is fitted using the equation:

$$\begin{aligned} G_{0}= & {} G_{\mathrm {0,min}}+\left( G_{\mathrm {0,max}}-G_{\mathrm {0,min}} \right) \nonumber \\&\cdot \exp \left[ -\beta \left( T-T_{0} \right) \right] , \end{aligned}$$

(A2)

where $G_{\mathrm {0,max}}=3.8\, \mathrm {J/}\mathrm {m}^{\mathrm {2}}$ and $G_{\mathrm {0,min}}=1.6\, \mathrm {J/}\mathrm {m}^{\mathrm {2}}$ correspond to the fracture energy at lower temperature limit temperature ($T_{0}=30\, \mathrm {^{\circ }C})$ and at higher temperature limit, respectively. $\beta =1/14$ is a fitting parameter. Equation A2 represents the experimental $G_{\mathrm {0}}$—T relation very well, for T above 45 $\mathrm {^{\circ }C}$. A slight deviation below 45 $\mathrm {^{\circ }C}$ has no impact on the crack growth because the crack tip never falls in this low temperature region.

Fig. 13

Crack paths for different horizon sizes $\delta$, while other parameters are fixed: a $\delta = 0.4$ mm; b $\delta = 0.3$ mm; c $\delta = 0.2$ mm; d $\delta = 0.15$ mm; e $\delta = 0.1$ mm. The m-ratio is 6

Fig. 14

Elastic vortices appear in the streamlines of the “velocity” field. Crack paths for different plate widths w, for the temperature gap $T_{\mathrm {gap}}=\, 135\, \mathrm {^{\circ }C}$, and plate immersion speed $v=0.5$ mm/s. a $w=10$ mm; b $w=13$ mm; c $w=16$ mm

Appendix A3: $\varvec{\delta }$-convergence

Figure 13 shows the crack path at different horizon size $\delta$ while other parameters are fixed: $T_{\mathrm {gap}} = 135$ $\mathrm {^{\circ }C}$, immersing velocity $v = 0.05$ mm/s, plate width $w = 15\,\hbox {mm}$, $m=\delta /\Delta x=6$. On the physical phase diagram, the physical parameters place this case near the transition zone between growth of a straight crack and an oscillatory crack (see Fig. 6). Branching cracks are observed at $\delta = 0.4$ and 0.3 mm, while oscillating crack is observed at $\delta = 0.2\,\hbox {mm}$ and lower. The horizon size influences the amount of damage along the crack path. For a larger horizon, a larger amount of material is damaged and any small imbalance between the amounts of material on the sides of the crack path gets amplified more. As the horizon decreases, this imbalance approaches the physical, real imbalance, that leads to thermal strain larger on one side than the other, which consequently results in contraction forces that pull the crack from its straight path into an oscillatory one. (see discussion in Sect. 4.3). Notice that for the oscillating crack case, the wavelength appears to be relatively insensitive to the horizon size, while the starting point of oscillations slightly moves farther from the notch tip the smaller the horizon is.

Appendix A4: Elastic vortex and instability of crack growth for ${\varvec{v}} = 0.5$ mm/s