Analysis of symmetric and skew-symmetric weight functions for a semi-infinite interfacial crack in transversely isotropic piezoelectric bimaterials

Abstract

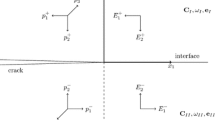
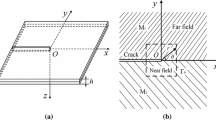
This paper presents an analysis of symmetric and skew-symmetric weight functions for in-plane interfacial crack problems in piezoelectric bimaterials. The symmetric weight function matrix is obtained by means of the solution of a Wiener–Hopf functional equation and the skew-symmetric weight function matrix is developed by the construction of a corresponding full field solution. The explicit expressions for the symmetric and skew-symmetric weight functions are given and applied to in-plane deformation problems for a semi-infinite crack between two dissimilar piezoelectric materials. The validity of the present method in the determination of the field intensity factors is demonstrated by illustrative examples, in which both piezoelectric bimaterials and piezoelectric/elastic bimaterials are considered. It is shown that, for the present interfacial crack problem, both symmetric and skew-symmetric weight function matrices are necessary in the general integral formula for the evaluation of field intensity factors, and that the contribution of the skew-symmetric element of the applied load is not negligible in fracture analysis.

Appendix A

Although for most $\varepsilon$-class piezoelectric bimaterials and piezoelectric/elastic bimaterials the eigenvectors $\mathbf{w}$ take the form set out in Eq. (49), a minority of $\varepsilon$-class bimaterials lead to eigenvectors w with the following structures (Ou and Wu 2003; Ou and Chen 2004)

$$\begin{aligned} \mathbf{w}=\left\{ {{\begin{array}{lll} {l_1 }&{} {\hbox {i}m_1 }&{} {\hbox {i}n_1 } \\ \end{array} }} \right\} ^{\mathrm{T}},\mathbf{w}_3 =\left\{ {{\begin{array}{lll} 0&{} {m_3 }&{} {n_3 } \\ \end{array} }} \right\} ^{\mathrm{T}}, \end{aligned}$$

(88)

where $l_1, m_i$ and $n_i \left( {i=1,3} \right)$ are real. Since $\mathbf{w}_3$ completely coincide with Eq. (49), all the variables related to $\mathbf{w}_3$ should have the same form as those in the previous section; for brevity, they will not be provided herein. Also, in this appendix, if no special explanation is given, all variables have the same form as those in the previous text.

Correspondingly, introducing $\mathbf{U}^{i}=\left\{ {{\begin{array}{lll} {U_1^i }&{} {U_2^i }&{} {U_3^i } \\ \end{array} }} \right\} ^{\mathrm{T}}$ and tractions $\varvec{\Sigma }^{i}=\left\{ {{\begin{array}{lll} {\Sigma _1^i }&{} {\Sigma _2^i }&{} {\Sigma _3^i } \\ \end{array} }} \right\} ^{\mathrm{T}} \quad \left( {i=1,2,3} \right)$ and taking $C_I =1, C_{II} =C_D =0$ and $C_{II} =1, C_I =C_D =0$ and $C_D =1, C_I =C_{II} =0$, respectively, one gets

$$\begin{aligned} \varvec{\Sigma }^{1}({x_1 })= & {} \frac{\left( {-x_1 } \right) ^{-\frac{3}{2}}}{\sqrt{2\pi }}\left\{ {\begin{array}{l} l_1 \left( {\left( {-x_1 } \right) ^{\mathrm{i}\varepsilon }+\left( {-x_1 } \right) ^{-{\mathrm{i}}\varepsilon }} \right) \\ -\hbox {i}m_1 \left( {\left( {-x_1 } \right) ^{\mathrm{i}\varepsilon }-\left( {-x_1 } \right) ^{-{\mathrm{i}}\varepsilon }} \right) \\ -\hbox {i}n_1 \left( {\left( {-x_1 } \right) ^{\mathrm{i}\varepsilon }-\left( {-x_1 } \right) ^{-{\mathrm{i}}\varepsilon }} \right) \\ \end{array}} \right\} ,\nonumber \\ \varvec{\Sigma }^{2}({x_1 })= & {} \frac{\left( {-x_1 } \right) ^{-\frac{3}{2}}}{\sqrt{2\pi }}\left\{ {\begin{array}{l} \hbox {i}l_1 \left( {\left( {-x_1 } \right) ^{\mathrm{i}\varepsilon }-\left( {-x_1 } \right) ^{-{\mathrm{i}}\varepsilon }} \right) \\ m_1 \left( {\left( {-x_1 } \right) ^{\mathrm{i}\varepsilon }+\left( {-x_1 } \right) ^{-{\mathrm{i}}\varepsilon }} \right) \\ n_1 \left( {\left( {-x_1 } \right) ^{\mathrm{i}\varepsilon }+\left( {-x_1 } \right) ^{-{\mathrm{i}}\varepsilon }} \right) \\ \end{array}} \right\} ,\nonumber \\ \end{aligned}$$

(89)

and their Fourier transforms are

$$\begin{aligned} \left( {\hat{\varvec{\Sigma }}^{1}} \right) ^{(-)}(\xi )= & {} \frac{2\xi _-^{\frac{1}{2}} }{1+4\varepsilon ^{2}}\left\{ {\begin{array}{l} \hbox {i}l_1 \left( {\omega +\rho } \right) \\ m_1 \left( {\omega -\rho } \right) \\ n_1 \left( {\omega -\rho } \right) \\ \end{array}} \right\} ,\nonumber \\ \left( {\hat{\varvec{\Sigma }}^{2}} \right) ^{(-)}(\xi )= & {} \frac{2\xi _-^{\frac{1}{2}} }{1+4\varepsilon ^{2}}\left\{ {\begin{array}{l} l_1 \left( {-\omega +\rho } \right) \\ \hbox {i}m_1 \left( {\omega +\rho } \right) \\ \hbox {in}_1 \left( {\omega +\rho } \right) \\ \end{array}} \right\} , \end{aligned}$$

(90)

where $\omega$ and $\rho$ have the same form as Eq. (52). The Fourier transforms of the three independent symmetric and skew-symmetric weight functions are consistent with Eqs. (53) and (54).

The symmetric weight function $[\mathbf{U}]({x_1 })$ is equal to zero for $x_1 <0$, and for $x_1 >0$ it takes the form

$$\begin{aligned} \left\{ {{\begin{array}{lll} {\left[ {\mathbf{U}^{1}} \right] ^{(+)}}&{} {\left[ {\mathbf{U}^{2}} \right] ^{(+)}}&{} {\left[ {\mathbf{U}^{3}} \right] ^{(+)}} \\ \end{array} }} \right\} =-\bar{\mathbf{H}}\left\{ {{\begin{array}{lll} {\varvec{\Xi }^{1}}&{} {\varvec{\Xi }^{2}}&{} {\varvec{\Xi }^{3}} \\ \end{array} }} \right\} ,\nonumber \\ \end{aligned}$$

(91)

where

$$\begin{aligned} \varvec{\Xi }^{1}= & {} \frac{x_1^{-\frac{1}{2}} }{\sqrt{2\pi }\left( {1+4\varepsilon ^{2}} \right) c_1 c_2 }\left\{ {\begin{array}{l} \hbox {i}l_1 \left( {\tilde{\omega }+\tilde{\rho }} \right) \\ m_1 \left( {\tilde{\omega }-\tilde{\rho }} \right) \\ n_1 \left( {\tilde{\omega }-\tilde{\rho }} \right) \\ \end{array}} \right\} ,\nonumber \\ \varvec{\Xi }^{2}= & {} \frac{x_1^{-\frac{1}{2}} }{\sqrt{2\pi }\left( {1+4\varepsilon ^{2}} \right) c_1 c_2 }\left\{ {\begin{array}{l} l_1 \left( {-\tilde{\omega }+\tilde{\rho }} \right) \\ \hbox {i}m_1 \left( {\tilde{\omega }+\tilde{\rho }} \right) \\ \hbox {in}_1 \left( {\tilde{\omega }+\tilde{\rho }} \right) \\ \end{array}} \right\} . \end{aligned}$$

(92)

The skew-symmetric weight function $\left\langle \mathbf{U} \right\rangle ({x_1 })$ is equal to $\mathbf{D}_1 [\mathbf{U}]^{(+)}({x_1 })$ for $x_1 >0$, and for $x_1 <0$ it takes the form

$$\begin{aligned} \left\{ {{\begin{array}{lll} {\left\langle {\mathbf{U}^{1}} \right\rangle }&{} {\left\langle {\mathbf{U}^{2}} \right\rangle }&{} {\left\langle {\mathbf{U}^{3}} \right\rangle }\\ \end{array} }} \right\} =\mathbf{D}_2 \left\{ {{\begin{array}{lll} {\varvec{\Pi }^{1}}&{} {\varvec{\Pi }^{2}}&{} {\varvec{\Pi }^{3}} \\ \end{array} }} \right\} , \end{aligned}$$

(93)

where

$$\begin{aligned} \varvec{\Pi }^{1}= & {} \frac{\left( {-x_1 } \right) ^{-\frac{1}{2}}}{\sqrt{2\pi }\left( {1+4\varepsilon ^{2}} \right) c_1 c_2 }\left\{ {\begin{array}{l} -l_1 \left( \mathop {\omega }\limits ^{\frown }+\mathop {\rho }\limits ^{\frown }\right) \\ \hbox {i}m_1 \left( \mathop {\omega }\limits ^{\frown }-\mathop {\rho }\limits ^{\frown }\right) \\ \hbox {i}n_1 \left( \mathop {\omega }\limits ^{\frown }-\mathop {\rho }\limits ^{\frown }\right) \\ \end{array}} \right\} ,\nonumber \\ \varvec{\Pi }^{2}= & {} \frac{\left( {-x_1 } \right) ^{-\frac{1}{2}}}{\sqrt{2\pi }\left( {1+4\varepsilon ^{2}} \right) c_1 c_2 }\left\{ {\begin{array}{l} \hbox {i}l_1 \left( -\mathop {\omega }\limits ^{\frown }+ \mathop {\rho }\limits ^{\frown }\right) \\ -m_1 \left( \mathop {\omega }\limits ^{\frown }+\mathop {\rho }\limits ^{\frown }\right) \\ -n_1 \left( \mathop {\omega }\limits ^{\frown }+{\mathop {\rho }\limits ^{\frown }} \right) \\ \end{array}} \right\} . \end{aligned}$$

(94)

The matrix $\hat{{\Upsilon }}_1 \left( {\xi _+ } \right)$ in Eq. (70a) becomes

$$\begin{aligned} \hat{{\Upsilon }}_1 \left( {\xi _+ } \right) =2\left( {{\begin{array}{l@{\quad }l@{\quad }l} {\hbox {i}l_1 \gamma }&{} {\hbox {i}l_1 \vartheta }&{} 0 \\ {-m_1 \gamma }&{} {m_1 \vartheta }&{} {m_3 \left( {1+\hbox {i}} \right) } \\ {-n_1 \gamma }&{} {n_1 \vartheta }&{} {n_3 \left( {1+\hbox {i}} \right) } \\ \end{array} }} \right) , \end{aligned}$$

(95)

and correspondingly, $\varvec{\Theta }_1$ in Eq. (73a) is replaced by

$$\begin{aligned} \varvec{\Theta }_1 =\left( {{\begin{array}{l@{\quad }l@{\quad }l} {\frac{\left( {1-2\hbox {i}\varepsilon } \right) \chi _1 }{2\left( {1+4\varepsilon ^{2}} \right) e^{\pi \varepsilon }c_1 c_2 }}&{}\quad {\frac{e^{\pi \varepsilon }\left( {1+2\hbox {i}\varepsilon } \right) \chi _2 }{2\left( {1+4\varepsilon ^{2}} \right) c_1 c_2 }}&{}\quad 0\\ {-\frac{\hbox {i}\left( {1-2\hbox {i}\varepsilon } \right) \chi _1 }{2\left( {1+4\varepsilon ^{2}} \right) e^{\pi \varepsilon }c_1 c_2 }}&{}\quad {\frac{\hbox {i}e^{\pi \varepsilon }\left( {1+2\hbox {i}\varepsilon } \right) \chi _2 }{2\left( {1+4\varepsilon ^{2}} \right) c_1 c_2 }}&{}\quad 0 \\ 0&{}\quad 0&{}\quad {-\hbox {i}\chi _3 } \\ \end{array} }} \right) ,\nonumber \\ \end{aligned}$$

(96)

where

$$\begin{aligned} \chi _1= & {} \Delta _{21} l_1 -\Delta _{22} m_1 -\Delta _{23} n_1 ,\nonumber \\ \chi _2= & {} \Delta _{11} l_1 +\Delta _{12} m_1 +\Delta _{13} n_1,\nonumber \\ \chi _3= & {} \Delta _{32} m_3 +\Delta _{33} n_3, \end{aligned}$$

(97a)

and

$$\begin{aligned} \left( {{\begin{array}{l@{\quad }l@{\quad }l} {\Delta _{11} }&{}\quad {\Delta _{12} }&{}\quad {\Delta _{13} } \\ {\Delta _{21} }&{}\quad {\Delta _{22} }&{}\quad {\Delta _{23} } \\ {\Delta _{31} }&{}\quad {\Delta _{32} }&{}\quad {\Delta _{33} } \\ \end{array} }} \right)&\quad =&\quad \left( {{\begin{array}{lll} {l_1 }&{}\quad {m_1 }&{}\quad {n_1 } \\ {l_1 }&{}\quad {-m_1 }&{}\quad {-n_1 } \\ 0&{}\quad {m_3 }&{}\quad {n_3 } \\ \end{array} }} \right) \nonumber \\&\left( {{\begin{array}{l@{\quad }l@{\quad }l} {H_{11} }&{}\quad {H_{12} }&{}\quad {H_{13} } \\ {H_{12} }&{}\quad {H_{22} }&{}\quad {H_{23} } \\ {H_{13} }&{}\quad {H_{23} }&{}\quad {H_{33} } \\ \end{array} }} \right) .\nonumber \\ \end{aligned}$$

(97b)