Simulation of mixed-mode I/III stable tearing crack growth events using the cohesive zone model approach

Abstract

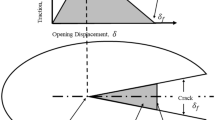
A cohesive zone model (CZM) approach is applied to simulate mixed-mode I/III stable tearing crack growth events in specimens made of 6061-T6 aluminum alloy and GM 6208 steel. The materials are treated as elastic–plastic following the $J_{2}$ flow theory of plasticity, and the triangular cohesive law is employed to describe the traction-separation relation in the cohesive zone ahead of crack front. A hybrid numerical/experimental approach is employed in simulations using 3D finite element method. For each material, CZM parameter values are chosen by matching simulation prediction with experimental measurement (Yan et al. in Int J Fract 144:297–321, 2009), of the crack extension-time curve for the $30^{\circ }$ mixed-mode I/III stable tearing crack growth test. With the same sets of CZM parameter values, simulations are performed for the $60^{\circ }$ loading cases. Good agreements are reached between simulation predictions of the crack extension-time curve and experimental results. The variations of CTOD with crack extension are calculated from CZM simulations under both $30^{\circ }$ and $60^{\circ }$ mixed-mode I/III conditions for the aluminum alloy and steel respectively. The predictions agree well with experimental measurements (Yan et al. in Int J Fract 144:297–321, 2009). The findings of the current study demonstrate the applicability of the CZM approach in mixed-mode I/III stable tearing simulations and reaffirm the connection between CTOD and CZM based simulation approaches shown previously for mixed-mode I/II crack growth events.