Abstract
Existing and emerging methods in computational mechanics are rarely validated against problems with an unknown outcome. For this reason, Sandia National Laboratories, in partnership with US National Science Foundation and Naval Surface Warfare Center Carderock Division, launched a computational challenge in mid-summer, 2012. Researchers and engineers were invited to predict crack initiation and propagation in a simple but novel geometry fabricated from a common off-the-shelf commercial engineering alloy. The goal of this international Sandia Fracture Challenge was to benchmark the capabilities for the prediction of deformation and damage evolution associated with ductile tearing in structural metals, including physics models, computational methods, and numerical implementations currently available in the computational fracture community. Thirteen teams participated, reporting blind predictions for the outcome of the Challenge. The simulations and experiments were performed independently and kept confidential. The methods for fracture prediction taken by the thirteen teams ranged from very simple engineering calculations to complicated multiscale simulations. The wide variation in modeling results showed a striking lack of consistency across research groups in addressing problems of ductile fracture. While some methods were more successful than others, it is clear that the problem of ductile fracture prediction continues to be challenging. Specific areas of deficiency have been identified through this effort. Also, the effort has underscored the need for additional blind prediction-based assessments.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Fracture of structural metals has been a pervasive engineering concern, dating back to the origins of metallurgy itself. There are numerous examples where structural metal failure has altered the course of human history, including notable examples such as the catastrophic failure of Liberty ships in World War II, and the failure of tin coat buttons which some believe halted the advance of Napoleon’s army into Russia in 1812. Modern engineering design against structural fracture is historically attributed to contributions by C. E. Inglis in the 1910s (Inglis 1913), A. A. Griffith in the 1920s (Griffith 1921) and G. R. Irwin in the 1950s (Irwin 1958). Today, most engineering classes on failure of structural materials focus on concepts around linear elastic fracture mechanics (Williams 1957) and elastoplastic fracture mechanics (Rice and Rosengren 1968; Rice 1967). However, courses and textbooks in fracture may foster misconceptions that fracture scenarios are all predictable and can be prevented using LEFM and EPFM tools. This is not the case. There are many realistic engineering circumstances where the fracture community’s collective knowledge-base can only provide “ball-park” estimates for the critical conditions that cause fracture. The purpose of the Sandia Fracture Challenge was to assess the fracture community’s current capabilities for predicting failure of a ductile structural metal. In this assessment, 13 computational teams representing academic, industry, and research labs reported blind predictions for a tearing scenario. While round-robin style computational assessments of ductile fracture have been performed previously, e.g. Bernauer and Brocks (2002), some important features of the present study were (1) the test geometry was heretofore unknown and significantly distinct from most existing test geometries, (2) the modeling teams all reported predictions that were blind to each other’s predictions and to the experimental outcome, (3) the teams were not given any instructions about what modeling approach was to be used, (4) details provided regarding the test geometry and material property data was commensurate with information that may be available in a typical ‘real-world’ engineering scenario, and (5) the teams were given the opportunity to bound their predictions, but were not instructed as to how to do so.
While many of the basic concepts in fracture are now over 50 years old, there has been a continued effort in the development of innovative methods to predict fracture behavior, especially in the numerical methodologies for predicting fracture in complex geometries, loading, and boundary conditions. Meshless computational methods, automated adaptive remeshing algorithms, microstructurally-informed multiscale models, and enriched/extended finite elements are just a few of the recent advances that have been applied to resolve longstanding issues in the computational prediction of fracture. Despite these advances, the evaluation of the true predictive ability of computational methods is lacking. In the early development of a modeling approach, developers usually test the method against certain standards and known cases. However, to evaluate a method’s true predictive ability it is necessary to probe the method beyond the investigator’s knowledge into problems whose outcome is unknown a priori. The approach taken in this work was to invent a never-seen-before scenario and collect blind predictions made without foreknowledge of the experimentally observed outcome. The scenario was the prediction of the crack initiation and propagation of a ductile structural stainless steel (15-5 PH) under quasi-static room temperature test conditions in a test specimen that possessed modest geometric simplicity, but challenging fracture conditions. The specimen geometry chosen for this study had never been studied before, either experimentally or computationally, but possessed some important similarities to a previous scenario involving many non-uniformly arranged interacting holes (Al-Ostaz and Jasiuk 1997; Li et al. 2000). The geometry was mechanically challenging because (1) it contained multiple holes that could potentially deflect the crack and influence the crack-tip stress state, (2) it did not contain a pre-existing sharp crack, (3) it was of a thickness somewhere between plane stress dominance and plane strain dominance, and (4) there was a competition between a tensile-dominated and shear-dominated failure mode. There was also limited standard experimental data provided on which to calibrate material model parameters. Tensile test data and sharp crack Mode-I fracture data were provided, as well as details of the material and even some limited microstructural information. Engineering drawings for all specimens were provided along with nominal tolerances. The experimental and computational results were presented at a special symposium at the ASME 2012 International Mechanical Engineering Congress and Exposition (IMECE) in Houston, TX on November 9-15, 2012. Another meeting was held in Albuquerque, NM on June 18-19, 2013 in order to coordinate the writing of this manuscript.
The outline of this article is given as follows. Section 2 is a review of the 2012 Sandia Fracture Challenge along with a detailed description of the problem. Test setup and results from three testing labs are given in Sect. 3. A brief summary of numerical methods provided by each of the thirteen (13) teams is given in Sect. 4 followed by a comparison of their predictions with the test data in Sect. 5. Finally, in Sect. 6, discussion and assessment of discrepancy between predictions and experiments are provided followed by a summary of the existing technology gap and future research and development efforts needed to enhance the fidelity of our modeling methodologies in ductile fracture. The “Appendix” contains short descriptions of the methods and blind prediction results of each team that participated in the Challenge. Some of the teams have presented a more complete description of their modeling efforts in articles that are included in this special volume of the International Journal of Fracture.
2 The Challenge
2.1 Concept for a challenge scenario
In recent years, Sandia National Laboratories has conducted a series of double-blind assessments of computational predictions in the area of ductile failure of structural alloys (Boyce et al. 2011). Based on these past efforts, it was clear that the double-blind evaluation methodology should be governed by some common constraints. First, this ‘toy problem’ or ‘puzzle’ should have no obvious or closed-form solution. It should be sufficiently distinct from other standard or known test geometries so that the outcome of the exercise is unknown to the participants. The scenario should be readily confirmed through experiments. This implies that the sample geometry is readily manufactured with easily measured geometric features. The manufacturing process should avoid unintentional complications such as significant residual stresses or non-negligible surface damage. The quantities of interest, such as forces and displacements, should be readily measurable with common instrumentation so that the tests can be repeated in numerous labs in a cost effective manner. The experiment should involve simple, uniaxial loading conditions that are readily tested with common lab-scale load frames and common grips. The sample and loading conditions should avoid unwanted modes of deformation such as buckling. Finally, it may be desirable for the challenge scenario to result in a single unambiguous repeatable experimental outcome, or as is the case for the present work, the scenario could be near a juncture of two competing outcomes. Since the challenge scenario involves a novel test geometry, the repeatability of the behavior may not be apparent until after significant experimental effort. In the present work and similar, prior efforts at Sandia, the experiments were not performed until after the computational challenge had been issued. This approach ensured that all participants (including the experimentalists) were not biased by any prior knowledge of the outcome.
2.2 The 2012 Sandia Fracture Challenge scenario
The fracture challenge was advertised to potentially interested parties through a mechanics weblog site, imechanica.org, and through an e-mail solicitation to many known researchers in the fracture community. The fracture challenge was issued via these same electronic formats on May 15, 2012; with final predictions all due on September 15, 2012, four months after the issuance of the challenge. The initial packet of information contained material processing and test data on mechanical properties, the test specimen geometry, the loading conditions, and instructions on how to report the predictions. The degree of detail provided was intended to be commensurate with the level of detail that is typically available in real engineering scenarios in industry. These details regarding the material, test geometry/loading conditions, and quantities of interest are described in the following three subsections.
2.2.1 Material
The alloy of interest was 15-5 PH, a precipitation hardened martensitic stainless steel. This alloy was chosen because it provided a useful representation of a moderately ductile structural alloy that would likely be unfamiliar to the participants. All test specimens were extracted from a single plate purchased from AK Steel (West Chester, Ohio) with a nominal thickness of 3.18 mm. The actual measured thickness was 3.124 mm. The original material certification was provided to the participants, and included the following chemical analysis (in wt%): C 0.04, Mn 0.48, P 0.019, S 0.0005, Si 0.40, Cr 15.21, Ni 4.19, Mo 0.12, Cu 3.39, Nb 0.32, Ta 0.001.
The plate was heat treated at Sandia National Labs with the intention of producing the H1100 heat treatment condition. Detailed furnace thermocouple records were provided to the participants, showing that the plate was heat treated at \(593\,^{\circ }\hbox {C} (1,100\,^{\circ }\hbox {F}\)) for 4 h followed by an inert gas flow cooling rate similar to that of a typical air cool. A detailed machining diagram was provided showing the location and orientation of the challenge test specimens as well as the tensile, compact tension C(T), and metallurgical witness coupons, as shown in Fig. 1.
The participants were also given detailed metallographic analysis of the microstructure of the martensitic stainless steel, provided by Drs. Yuxiong Mao and Mark Horstemeyer of Mississippi State University. These images show the equiaxed grain shape and 5–20 \(\upmu \hbox {m}\) grain size, occasional inclusions and longitudinal segregation/banding. Examples are shown in Fig. 2.
Examples of (upper) the polished surface showing inclusions indicated by circles, and (lower) an etched surface showing grain structure and banding. Both examples are taken along the longitudinal-short orientation to emphasize the features associated with rolling. Microstructural analysis was provided on all three planes, courtesy of Drs. Yuxiong Mao and Mark Horstemeyer of Mississippi State University
Four tensile coupons were tested, two oriented along the rolling direction and two oriented along the transverse-to-rolling plate direction. All tests were conducted according to ASTM E8 using the nominal geometry shown in Fig. 3. Strain was measured using an extensometer with a 25.4 mm gage length. Engineering stress–strain curves were provided as shown in Fig. 4, as well as the raw force-displacement data for each tensile test. The observed strength values were \(\sim \)8 % higher than is typically reported for the H1100 condition, and were more consistent with an H1075 condition. This discrepancy was noted to the participants. Images of the fracture surface morphology shown in Fig. 5 were also provided to the participants.
Three fracture toughness tests were performed on C(T) specimens (Fig. 6) extracted from the same plate of material used for the challenge tests and the tensile bars; due to insufficient plate thickness, these measurements were not performed under plane strain conditions. Force measurements were made with a load cell and load line displacement measurements were made with a crack opening displacement (COD) gauge inserted on the knife-edge features in the mouth of the C(T) specimens. The load cell capacity was 22.2 kN and the COD gauge had a range of 5.08 mm. The as-machined normalized notch length, taken as the ratio of notch length, a, to specimen width, W, was \(a/W = 0.5\). The specimens were fatigue precracked at a load ratio of \(R=P_\mathrm{min} / P_\mathrm{max}=0.1\) to a typical precrack length of \(a/W \approx 0.6\), with actual measured fatigue precrack lengths reported for each specimen. The observed force versus COD measurements are shown in Fig. 7. This type of data, while not valid for the determination of plane strain toughness, could be used to calibrate model parameters for tearing. The decision on if or how to use all of the material property data was left to the individual participants.
2.2.2 Fracture challenge geometry and loading condition
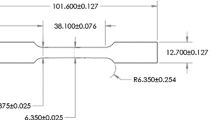
The Fracture Challenge specimen geometry is shown in Fig. 8 with detailed dimensions shown in Fig. 9. The specimen features a blunt notch, labeled ‘A’, with a diameter of 2.54 mm and three holes, labeled ‘B’, ‘C’, and ‘D’. Holes ‘B’ and ‘C’ are of equal diameter (1.78 mm), while hole ‘D’ has a larger diameter (3.05 mm). The holes are located approximately one plate thickness away from the tip of the blunt notch, with the goal of generating three separate potential localization paths.
Two pin holes were machined well away from the notch tip for insertion of loading pins. These pin holes provided for standard clevis grip loading in either a screw or hydraulic uniaxial load frame. The participants were instructed that the sample would be loaded at a loading rate of 0.0127 mm/s. No other details regarding the boundary conditions were provided. It is important to note that the primary test lab, Sandia’s Structural Mechanical Laboratory, was also provided this same level of detail regarding how the tests should be performed. No additional constraints were placed on the test lab’s decision of how to apply boundary conditions. Any undeclared aspects of loading that were salient to the outcome were considered as sources of potential uncertainty. This limited definition of the boundary conditions bears similarity to real world engineering problems, where the detailed boundary conditions are rarely well defined.
2.2.3 Quantities of interest
A set of quantitative questions were posed to the participants to facilitate comparing the analyses to the experimental results. These questions were meant to evaluate the robustness of the analysis technique in predicting specimen fracture behavior. All challenge participants were issued the following three questions:
-
(Q1) What is the force and COD displacement at which a crack first initiates?
-
(Q2) The starter notch, A, holes B–D, and the backside edge, E are labeled in the drawing. What is the path of crack propagation? i.e. a crack that initiated on the backside and propagated to hole D and then to notch A would be labeled “E–D–A”.
-
(Q3) If the crack does propagate to either holes B, C, or D, at what force and COD displacement does the crack re-initiate out of the first hole?
The crack opening displacement measurement was defined for the participants in the following way: “A Crack opening displacement (COD) gage will be used to monitor load-line displacement at the point of the ‘knife-edge’ features, akin to fracture toughness testing. Only \(\Delta \) COD will be measured (the test will begin with COD\(\,{=}\,\)0 mm)”. Also, the condition of crack initiation was defined for the participants: “For the purposes of this challenge, crack initiation will be defined as a crack \(\ge 100\,\upmu \hbox {m}\) on the sidewall surface of the sample, so as to be witnessed by in-situ microscope”.
All participants were also asked to report their entire predicted force-COD displacement curve. Ultimately, the comparison of this force-displacement curve between experiments and the model predictions was the most instructive quantity of interest.
3 Experimental method and results
A series of experiments were performed to observe the natural failure process for the challenge. Ideally, the experiments would provide an unambiguous, repeatable observation of failure. However, materials are rarely homogeneous, machined geometries always have dimensional variability, boundary conditions rarely mimic our idealized conceptions, and the intrinsic fracture process can be stochastic/chaotic. For these reasons, there is a need to repeat the experimental observation several times. It is also beneficial to repeat the experiments in multiple independent test labs to show the variation of results from one experimental setup to another. In the present work, Sandia’s Structural Mechanics Laboratory was chosen as the primary test lab to perform ten detailed repetitions of nominally identical tests. Two other labs performed a smaller set of experiments, intended to confirm the primary results, or reveal lab-to-lab variation: Sandia’s Materials Mechanics Laboratory and the laboratory of Prof. Ravi-Chandar at the University of Texas at Austin. All three labs utilized specimens machined in one batch from the same plate of material. The remainder of the experimental section contains details from the experiments for each of these three labs, with an emphasis on the core set of ten observations from the Sandia Structural Mechanics Laboratory.
3.1 Observations from the Sandia Structural Mechanics Lab
3.1.1 Test setup and methodology
Fabrication of all specimens occurred from the same lot of material by the same machine shop. In anticipation of the potential influence of small variations in the specimen dimensions on the failure, many measurements were taken of the specimens tested in both the Structural Mechanics Laboratory (specimens D1, D2, and S1–S8) and the UT-Austin laboratory (specimens S9–S11) prior to testing. Figure 10 identifies the locations of each measurement.
The blue circles represent thickness measurements taken using a 0–6.35 mm QuantuMike micrometer with a resolution of 1.27 \(\upmu \)m and an accuracy of \(\pm \)1.27 \(\upmu \)m. The measurement surfaces of the micrometer were circular thus spanning a larger measurement area compared to a point measurement. Ten thickness measurements were taken of each specimen. The orange lines represent length measurements taken with an optical Wild M3Z stereomicroscope with a 0.254-\(\upmu \)m resolution and an accuracy of \(\pm \)0.508 \(\upmu \)m. Twenty vertical and thirteen horizontal length measurements were taken. A zoomed-in view of the features B, C, and D in Fig. 11 illustrates the diametric measures of these holes.
The measured lengths and thicknesses for specimens D1, D2, and S1–S11 are included as Supplementary Information for this article. Specimens D1, D2, and S1–S8 were tested in the Sandia Structural Mechanics Laboratory. Specimens S9–S11 were tested at UT-Austin. Dimensional measurements revealed that some of the features were not manufactured within the specified tolerance of \(\pm \)50.8 \(\upmu \)m (detailed measurements for each test sample are shown in Supplementary Information). Specifically, the ratio of the vertical distance from Hole D to the notch divided by the horizontal distance from Hole C to the notch was below tolerance for all specimens except specimens D1, S9, and S10. The potential failure paths appear to be affected by the relative ligament lengths represented by this ratio.
All tests were performed at ambient temperature on an MTS servo-hydraulic 97.9-kN (22-kip) load frame at a displacement rate of 12.7 \(\upmu \)m/s, controlled by the MTS FlexTest Controller. The test setup consisted of a simple, well-defined uniaxial load imparted on the test specimens. The test was set up to meet the challenge of measuring force and COD at which the crack first initiated, to determine the crack path, and measure the force and COD if a crack reinitiated out of a hole. Crack initiation was defined as a crack 100 \(\upmu \)m in length on the sidewall surface of the specimen, visible by an in-situ microscope. For the test series, the Epsilon Tech Corp. COD gage (Jackson, WY) was situated on the knife-edges of the specimen and began with a reading of 0 mm. A photograph of the actual experimental setup is shown in Fig. 12.
Two load cells were connected to the upper, stationary crosshead. One load cell was a 97.9-kN (22-kip) load cell and the second load cell, referred to as an auxiliary load cell, had a rated capacity of 8.9-kN (2-kip). The actuator was located on the lower portion of the frame and moved in a downward direction to apply the required tensile load. The test specimen was attached to two clevis fixtures with round pin holes for metal pins. In turn, the clevises were threaded into the load cell and actuator using threaded adapters. These clevis fixtures were securely mounted to the load train without rotational degrees of freedom. Only the specimens were allowed to rotate through the pin joints. Three displacement measurements were recorded. The first was an internal LVDT monitoring the actuator stroke. The second displacement measurement came from an external \(\pm \)5.08-mm “grip” LVDT positioned between the clevis-pin fixtures, allowing displacement measurements closer to the test article. This LVDT from Macro Sensors (Pennsauken, NJ) was used for control at a rate of 12.7 \(\upmu \)m/s. The grip LVDT was calibrated at time of use with a Boeckeler Digital Micrometer, having \(\pm \)0.508-\(\upmu \)m resolution and repeatability within \(\pm \)0.508 \(\upmu \)m. The Epsilon COD gage was calibrated at the time of use with a Starret Micrometer. The COD gage measured the displacement change in the notch opening, having \(\pm \)0.508-\(\upmu \)m resolution and repeatability within \(\pm \)8.6 \(\upmu \)m.
Two cameras were used to capture visible cracks on the specimen surface, each with a different field of view. A 5-megapixel Point Grey Research (PGR) Grasshopper camera with a Navitar Zoom 6000 lens was used to view one side of the specimen. This zoom lens had a lens resolution of 102 line pairs per mm (lp/mm), and the pixels/\(\upmu \)m ratio ranged from 0.207 to 0.511. Images for this camera were acquired at an approximate rate of 1 Hz. The second camera employed was a Canon EOS Rebel T31 Digital Single Lens Relflex (DSLR) with a macro lens focused on the opposite side of the test specimen. This DSLR camera had a lens resolution of 36 lp/mm, and the pixels/\(\upmu \)m ratio ranged from 0.113 to 0.124. Images for this camera were acquired at an approximate rate of 0.25 Hz. These two cameras were situated perpendicular to the surfaces of the specimens; thus, they could not observe any crack initiation on the through-thickness faces of the features. The cameras were both triggered by the MTS FlexTest Controller, and the MTS FlexTest DAQ system simultaneously collected the time, force, grip LVDT displacement, and COD data corresponding to each image.
To situate all parts within the load train, the specimen was exercised in tension within the elastic region between 89 N and 445 N. Although not shown in Fig. 12, dial indicators were positioned in the test setup to measure the lateral displacement of the upper and lower clevises. The dial indicators measured less than 25 \(\upmu \)m of lateral displacement at maximum load.
Ten specimens were tested, each with one of three specific orientations in the grips. The purpose for the different specimen orientations was to assess if the experimental setup led to a preferential loading path rather than the specimen geometry and material properties alone. From the perspective of the PGR zoom camera with the lower MTS actuator moving down, the three orientations were (1) the notch on the right with hole D above (Specimens D1, D2, S1, S2, S3, and S7), (2) the notch on the right with hole B above (Specimens S4, S5, and S6), and (3) the notch on the left with hole D above (Specimen S8.)
After testing, the force and displacement data was correlated with the image sequences from the two cameras. While the cameras were supposed to be triggered at periodic intervals (every 1 s for PGR, every 4 s for DSLR), post-test analysis revealed that \(\sim \)2 % of the images had not been captured for each camera, presumably due to ineffective triggering. Embedded image timestamps and file timestamps were used to determine the times of the missing images for all DSLR image sequences and for the PGR camera sequences for specimens D2 and S1–S8. The only image sequence without embedded timestamps or useful file timestamps was for the PGR camera for specimen D1; here, visual cues such as camera motion, lighting changes, and large displacements from elastic recovery due to the load drops associated with crack formation were used to correlate the DSLR and PGR camera images in the vicinity of crack events only. This post-test data-image alignment allowed for the comparison of load versus COD profile and the visual observations of the surface cracks.
3.1.2 Test results and observations
Load versus COD profiles
Nine out of the ten specimens tested in the Structural Mechanics Laboratory exhibited crack path of A–D–C–E, while one specimen, labeled D1, exhibited a different crack path of A–C–E. Figure 13 is the load versus COD measurement plot with the post-test images of the ten specimens. The load versus COD curve for D1 has a different profile than the curves for the other nine specimens; specimen D1 had the highest peak load and the most delayed first load drop. The nine specimens with A–D–C–E crack path had similar peak load values and had small variations in load for load drops of each of the cracks, but with significant variation in the COD measurement at the load drops. Specimen D1 broke from A–C directly as opposed to A–D–C for the other specimens, but the overall load drop from A–C, regardless of crack path, is approximately the same for all ten specimens from around 8.0 to 5.3 kN. The cracks from A–D and D–C occurred in quick succession, with more overall total COD for a similar reduction in load as compared to the A–C crack in specimen D1. All ten specimens had a similar load plateau after the crack propagated from either D–C or A–C. The crack from C–E resulted in similar load versus COD profiles below 5.3 kN for all ten specimens. There was no apparent correlation between crack path and specimen orientation or between load versus COD profile and specimen orientation.
Table 1 includes the peak force of each specimen, as well as the force and COD measurements for the load drops in the load versus COD curves associated with each crack. These load drops corresponded to audible cracking sounds and were defined as a slope in the load versus COD profile of a magnitude greater than 17.5 N/\(\upmu \)m for cracks A–C, A–D and D–C and of a magnitude greater than 4.5 N/\(\upmu \)m for the C–E crack, but did not necessarily correspond to the appearance of a crack on the surface of the specimens. The peak load of the A–C–E crack path specimen was largest of all the specimens at 8,746 N. The average peak load for the A–D–C–E crack-path specimens was 8,500 N, ranging from 8,427 to 8,627 N. The first crack from A–C for specimen D1 occurred at a load of 8,066 N and a COD of 3.543 mm; the first crack from A–D occurred at an average load of 8,290 N, ranging from 8,127 to 8,416 N, and average COD measurement of 2.424 mm, ranging from 1.976 to 2.779 mm. The second crack from D–C for nine specimens occurred at an average load of 6,812 N, with a range of 5,589 to 7,359 N, and an average COD measurement of 2.691 mm, with a range of 2.080 to 3.173 mm. The crack between holes C and E from specimen D1 occurred at a COD measurement of 5.217 mm, which is close to the average COD measurement for the other nine specimens of 5.330 mm, (ranging from 4.853 to 5.768 mm), and slightly higher load of 5,128 N as compared to the other nine specimens, averaging 5,013 N (ranging from 4,962 to 5,091 N). The range of the COD measurement for each crack in the A–D–C–E specimens was large; the range of load for each crack was small for A–D and C–E, but large from D–C.
Visual observations of the crack paths on the specimen surfaces
One part of the Challenge was the prediction of the load and COD measurements at crack initiation of the first and second cracks, defined as a 100-\(\upmu \)m crack on the surface of the specimen. The intention behind this definition was to allow for an unambiguous criterion for crack initiation, not necessarily related to a load drop or unspecified crack length; but, this implicitly assumed that the cracks would initiate and grow as a 2D crack, through the thickness. Unexpectedly, in the experiments, subsurface cracks would initiate at the load drop in the load-COD profile, accompanied by an audible cracking noise, but nearly every crack would not appear on the surface of the specimens until the specimen had opened to an additional COD of \(\sim \)0.2–0.35 mm. The cracks usually appeared on the surface between features, not the feature edges. The camera setup did not allow for imaging of the through-thickness edges, but only the front and back surfaces. Due to the image resolution of the cameras and often shear-dominated crack paths, the cracks on the surface were not deterministically discernible, often appearing as dark regions on the length scale close to 100 \(\upmu \)m and then as a clear crack on larger length scales. Videos of the front and back surface images and corresponding load versus COD profile for the crack path of specimens D1 and S4 are available as Supplementary Information for this article.
Tables 2, 3 and 4 list the force and COD measurements associated with the range of images where cracks greater than 100 \(\upmu \)m on the surface of the specimen were clearly not present to where cracks were plainly visible, including the length of the cracks when they were plainly visible. The tables are separated by the first crack (A–C or A–D), the D–C cracks of nine of the specimens, and the C–E cracks, also listing the load drop data and time, showing that the cracks usually appear on the surface after the load drop. It is important to note that the crack could appear on either surface and did not necessarily appear on both surfaces at the same time, highlighting the three-dimensional and stochastic nature of the crack propagation through the specimen. For D1, the A–C crack on the surface was apparent in the Canon DSLR image immediately following the load drop, though not in the image of the PGR camera after the load drop; hence the large range in Table 2 over which the A–C crack could have appeared on the surface spans the DSLR images around the load drop. For all other nine specimens, the first crack A–D appeared on the surface much later than the load drop. For the D–C and C–E cracks of the A–D–C–E crack path specimens, the appearances of the cracks were after the load drops, and at a smaller force and larger COD measurements than the load drops. For specimen D1, the load drop was within the range of images where the C–E crack may have appeared on the surface. The appearance of the C–E crack in D1 was within the range of force and COD of the C–E crack of the other specimens.
Figure 14 shows two sequences of images from the DSLR camera and PGR camera for the A–C crack on the back and front of Specimen D1, respectively. In this specimen, the interior crack nucleation event at the load drop (8,066 N, 3.542 mm COD, 294.4 s) led to an immediate surface crack on the back, a crack on the front surface was not clear until several seconds later. For both front and back camera views, the crack did not first emerge at the edge of either notch A or hole C, but rather on the surface in between these two features and then propagated outward towards both features.
Specimen D1 images for crack A–C of back and front surfaces: a larger field of view of the back surface at t \(=\) 291.0 s, before the load drop, with smaller field of view indicated by dashed white box; b inset image of the back surface, before the load drop with no surface crack; c inset image of the back surface, when a 825-\(\upmu \)m crack is clearly visible; d inset image of the back surface when the back surface crack has fully bridged A–C; e same size inset image of the front surface immediately before the load drop; f inset image of the front surface after the load drop without a front surface crack; g inset image of the front surface when a 735-\(\upmu \)m crack is just discernible; and h inset image of the front surface, when the crack fully bridged A–C
In specimen D1, the second cracking event (path C–E) first appeared on the surface sometime between t = 432.6 and 435.7 s, while the load drop (5,128 N, 5.217 mm COD) occurred before this time range at t\(\,{=}\,\)423.5 s. Hence, the surface crack appeared after the load drop, again indicating that a subsurface crack had initated and only later did it propagate to the surface. Similar to the first crack in specimen D1, the crack between C and E appeared on the surface ahead of hole C, not starting at the edges. The crack first propagated towards C on the surface before propagating back towards E. The C–E crack behavior for specimen D1 is typical of all C–E cracks, though the precise timing of the appearance of the crack on the surface relative to the load drop varied, as listed in Table 4.
Figure 15 shows a sequence of images from the PGR camera for the A–D crack in specimen S4, which had a load drop at 8,305 N, 2.497 mm COD, and t\(\,{=}\,\)204.6 s. The visual appearance of the surface crack was more than 27 s and \(\sim \)0.35 mm COD after the main load drop for the subsurface crack. The crack propagated from the area between A and D outwards towards the edges of A and D, along a jagged path. The complete bridging of A–D did not occur until after the second load drop that was associated with the next subsurface crack between holes D and C that occurred at t\(\,{=}\,\)237.0 s.
Specimen S4 Images for Crack A–D: a larger field of view with smaller field of view indicated by dashed white box; b inset image just before load drop; c inset image after load drop without any visible surface crack; d inset image just before the surface crack appears in the dark region in between A and D; e inset image when a 560-\(\upmu \)m crack appeared; and f inset image when the crack fully bridged notch A and hole D
The second surface crack between D and C was also not visually observed until 30 s after the second load drop (5,496 N, 3.292 mm COD, 267.0 s). Also, the crack between D and C appeared on the surface between the holes, not starting at the edges. Crack bridging was evident during propagation between D and C. For the crack from hole C towards the edge of specimen S4 at E, the crack appeared on the back surface at t\(\,{=}\,\)456.4 s after the third load drop (t\(\,{=}\,\)441.0 s), ahead of the edge of C, and then propagated towards C on the surface before propagating back towards E. The crack behavior for specimen S4 was typical of the A–D–C–E crack-path specimens.
Fracture surfaces of the two crack paths
The fracture surfaces of the two observed crack paths are highly three-dimensional without through-thickness uniform flat fracture, but a combination of flat fracture, V-shear fracture, and slant fracture. Figure 16 contains a 3D reconstruction of a set of top-down white-light digital microscope images of the D1 fracture surfaces and surface height profiles of the A–C crack and of the first portion of the C–E crack from a laser scanning microscope. The A–C crack has a flat fracture surface in the middle of that crack; this flat fracture is slightly sloped between notch A and hole C in the overall crack propagation direction. The A–C crack also has the shear lips with approximately 40–55\(^{{\circ }}\) slopes in the y–z plane near the surfaces imaged during in the tests and in the x–z plane at the edge of notch A and at the edge of hole C. The C–E crack has a triangular flat-fracture region just ahead of hole C, and what appears to be a V-shear fracture on either side of the flat fracture; the two sides of the V-shear fracture are angled at an approximately \(45^{{\circ }}\) angle in the y–z plane relative to the flat fracture. The V-shear fracture becomes slightly steeper to \(55^{{\circ }}\) as the crack grows, and then it transitions to a slant fracture further from hole C and has an angle of approximately 40–45\(^{{\circ }}\) in the y–z plane. This behavior in the C–E crack is similar in all of the specimens, except specimen S6, which did not have a transition between the V-shear fracture and the slant fracture, but only the flat to V-shear fracture transition. Figure 17 has an angled view of the crack path in specimen S4 and a direct view of the A–D crack in specimen S4. The A–D and D–C cracks are shear-dominated, but they are not uniform through the thickness. These cracks slant towards the front and back surfaces and are jagged through the thickness at the edges of holes D and C. These fracture surfaces are rather different than the A–C crack in specimen D1, which has prominent shear lips far into the thickness, surrounding the flat fracture.
Fracture surface of specimen D1 with A–C–E crack path from left to right: crack path is three dimensional through the thickness; (Top) complete fracture surface of both halves of the specimen, where hole B is located in the upper half and hole D is located in the lower half of this image (image taken by a Keyence VHX-1000 digital microscope with 3D image stitching); (bottom left) A–C crack surface with height profiles (image constructed from a Zeiss LSM700 laser scanning microscope with 5X objective and 0.5 zoom factor); (bottom right) First portion of the C–E crack surface with height profiles (image constructed from the Zeiss LSM700)
3.2 Confirmation observations from Sandia’s Materials Mechanics Lab
The purpose of a second independent test lab was to confirm the reproducibility of the primary experimental observations from the Structural Mechanics Lab, described in the previous section. For this reason, only three tests were performed, and the focus was on measuring the force-COD response of the challenge specimen to confirm the results of the structural mechanics lab. Both labs were blind of the other labs measurement approach, to avoid bias in methodology.
The Sandia Materials Mechanics lab utilized a 100-kN MTS servo-hydraulic load frame with standard clevis grips and a 22-kN load cell. The COD gage was a 0 to 5.08-mm displacement gage calibrated against a micrometer-based calibrator at the time of use. The most significant difference between the two labs was that the Materials Mechanics lab utilized a universal joint between the upper grip and the load cell to partially compensate for minor misalignments. A single universal joint was deemed sufficient because of the additional rotational degrees of freedom afforded by the clevis pins. However, the Materials Mechanics lab did not utilize extra LVDTs to monitor in-test rotations as had been used by the Structural Mechanics lab.
The core comparison between the primary results of the Structural Mechanics Lab and the confirmation results of the Materials Mechanics lab is shown in Fig. 18. Note that the Materials Mechanics lab selection of a 5.08-mm range COD gage limited observation of the final stages of crack propagation. The load drop associated with crack initiation out of hole C was not captured due to the limitations of the COD gage used by this lab. Otherwise the two labs demonstrated strikingly comparable results. While 9 of the 10 tests from the Structural Mechanics lab failed along path A–D–C–E, 2 of the 3 tests failed in this same manner in the Materials Mechanics lab. The remaining 2 tests (one from each lab) failed along path A–C–E.
3.3 Further observations from the University of Texas
The University of Texas volunteered to perform additional tests that were not blind either to the test results from the Sandia Structural Mechanics Laboratory or to the predictions of all the teams. In fact, this group was motivated by the fact that two different failure paths were observed in the tests thereby implying non-uniqueness of the results. The additional observation that a rigid coupling had been used by the Sandia Structural Mechanics Lab in connecting the specimen to the test frame was used to postulate that there might have been loading imperfections that may result in nonunique response of nominally the same specimens. Therefore experiments were performed on three additional specimens S9–S11 at the University of Texas. These samples were obtained from the same sheet as the remaining specimens that were tested by the two Sandia groups and therefore are nominally the same material, with the same heat-treatment conditions.
The University of Texas experiments utilized a 100-kN Instron electromechanical load frame, with a 100-kN load cell. The crosshead rate was maintained at 12.7 \(\upmu \)m/s, the same rate used by the Sandia Structural Mechanics Laboratory. Two universal joints were placed, one each at the upper and lower grips in order to minimize the effect of loading misalignments. With two joints, the specimen can reorient itself to align with the load with a minimum of loading imperfections. In addition, the clevis holes where the pin connects the specimen to the loading frame were made to have a flat portion in order to permit large rotations that would arise in the pins; this is in accordance with the ASTM guidelines for fracture testing. Instead of using COD gages to measure the displacements of the loading points, a full-field three-dimensional image correlation (3D-DIC) method was used to determine the displacements over the entire specimen. Details of the experimental methods, sensitivity resolution, and results are described by Gross and Ravi-Chandar (2013).
The main comparison between the primary results of the University of Texas results and the results of the Sandia Structural Mechanics Laboratory is shown in Fig. 19, through the load-COD plot. The COD was determined through post-processing of the 3D-DIC data. The load-COD variation falls within the trends identified by the two Sandia groups. Two of the three samples (S09 and S10) failed along the path A–C–E while the third sample (S11) failed along A–D–C–E. Failure occurred abruptly with two audible ‘pops’ for specimen S11 and with an initial audible ‘pop’ and then a somewhat more gradual growth of the crack for specimens S09 and S10. It was also noted that in specimen S11, hole A was significantly misaligned with respect to the flat portion of the notch and made the ligament A–D smaller in this specimen than in the other two. These results suggest that while loading misalignments may be one contributing factor to the crack path selection, geometric imperfections may also play a significant role; these aspects are examined further in Sect. 6.1.3 in the present article, and through additional simulations by Gross and Ravi-Chandar (2013).
4 Brief team-by-team synopsis of modeling method
The following is a brief overview of the team-by-team modeling approaches; see “Appendix” for more detailed descriptions of each team’s approach and their respective references. Also, several teams contributed optional companion full-length articles within this Special Issue. The majority of teams used finite element methods with the exception of one team using Peridynamics, another using the Reproducing Kernel Particle Method, and one using the Material Point Method. Most also used fully three-dimensional models for the geometry with the exception of one team which used shell elements. The methods were calibrated with either the uniaxial tension test alone or the combination of uniaxial and compact tension tests. All of the teams used plasticity models with various modifications to capture failure.
Team 1 used a standard von Mises plasticity model for metals with user-prescribed hardening as a function of equivalent plastic strain. In addition to conventional plasticity, this model has an empirical tearing parameter for crack initiation and growth. The model was calibrated based on simulations of the uniaxial tension and compact tension experiments.
Team 2 used a plasticity model with scalar damage. A unique feature of this model is that with dependence on the invariants I1, J2, and J3 this model can distinguish between pressure-dominated and shear-dominated failure. Damage rate depends on plastic strain rate and a reference strain which depends on the three stress invariants. This model was calibrated by simulating the uniaxial tension test only.
Team 3 used Hill’s anisotropy for the plasticity model, with power-law hardening and a modified version of the Johnson-Cook strain-to-failure model. When the material failure criterion of equivalent plastic strain reaching a critical level was met, element stiffness was reduced to zero. Two of the three parameters for this model were calibrated with the tensile and compact tension test data. The final parameter requires a measurement of the failure strain at low triaxiality, and since this was not available it was simply estimated based on past experience.
Team 4 used the Reproducing Kernel Particle Method which is a mesh-free method with displacement enrichments for the crack surface and crack tip. A conventional J2 plasticity model was used and calibrated based on the uniaxial tension experiment. The maximum principal tensile strain is used as the crack initiation and propagation criterion.
Team 5 used plasticity with damage based on a classical Gurson–Tvergaard–Needleman (GTN) fracture model. Failure is modeled based on a void nucleation and growth criterion. This model was calibrated using both the uniaxial and compact tension data.
Team 6 developed a two-scale plasticity model, using Multiresolution Continuum Theory, in which the macro-scale is based on a Gurson type yield surface which is coupled to a modified Fleck–Hutchinson model at the micro-scale. The micro-scale considered both plastic and gradient-plastic mechanisms. An intrinsic length scale captures the inhomogeneous deformation between micro-voids. This model was calibrated based on the tensile test data.
Team 7 took three separate approaches using both Abaqus and FRANC3D software: a damage mechanics approach in Abaqus/Explicit, a cohesive zone approach in Abaqus/Standard with the PPR model, and an explicit geometric crack growth approach in FRANC3D. The given tensile (stress–strain), fracture toughness, and necking data were used to calibrate each model’s requisite material parameters to give three separate predictions of crack growth in the challenge specimen.
Team 8 used the Material Point Method instead of a finite element model. A plasticity model was used combined with the evolution of decohesion based on a discontinuous bifurcation analysis. The model parameters were obtained from simulations of the uniaxial and compact tension experiments.
Team 9 did not use finite elements and instead used Non-local Peridynamic Theory. This method naturally enables crack initiation and growth without an external failure criterion and without remeshing. The yield stretch in the plasticity model is calibrated against the tensile test data, and the critical stretch for material failure is calibrated against compact tension test.
Team 10 used an extended finite element (XFEM) method for shell element within Abaqus’ framework (XSHELL). A plane strain core approach has been developed to capture the thickness constraint induced stress triaxility and its effect on the ductile fracture in the vicinity of the crack tip. A mesh independent kinematic description of crack initiation and propagation is accomplished through an elementwise crack insertion with cohesive injection once its accumulative plastic strain reaches a critical value.
Team 11 used a Shear Modified Gurson (SM-G) plasticity model. The model was calibrated with a simulation of the uniaxial tension test and a comparison of the predicted reduction of area on the fracture surface with the experiment.
Team 12 used a von Mises plasticity model with user-prescribed hardening and non-linear elasticity. For one approach, failure was modeled using a cohesive surface model with an exponential potential for mixed mode crack propagation with cohesive surfaces placed along expected crack paths. A second approach used a damage model with damage dependent on the hydrostatic stress.
Team 13 used a von Mises plasticity model with a three-parameter Modified Mohr-Coulomb fracture model. With this failure model the strain to failure is based on stress triaxiality and the normalized Lode angle. Model parameters were calibrated based on the uniaxial tension test only.
5 Comparison of predictions and experiments
5.1 Comparison of Scalar Quantities of Interest and Crack Path
In real-world engineering scenarios, modeling is often used to predict scalar performance metrics such as the maximum allowable service load that a component can support or how far the component can be deformed before it will form a crack. Motivated by this, the challenge scenario specified certain scalar metrics to be reported. The teams were asked to predict the force and COD when a crack first initated, and then when a crack later reinitated from a second feature. The teams were given instructions to report single scalar values for their expected outcome and were also offered the opportunity to bound their predictions with lower and upper limits. This offered teams the possibility of performing uncertainty analyses.
The challenge problem statement specified that a \(100\,\upmu \hbox {m}\) surface crack was the defining characteristic for crack initiation. As described in the Experimental section, the audible crack nucleation event and associated load drop preceded the emergence of a visible surface crack, in some cases by several seconds, suggesting that the crack initiation event occurred entirely subsurface. There was significant quantitative variability in the experimental assessment of the emergence of the visual crack. In hindsight, the load drop would have been a metric that was easier to define and measure. Moreover, the teams may have not had the fidelity to distinguish between the nucleation event and the \(100\,\upmu \hbox {m}\) surface crack. For this reason, the experimental results presented in this section include both types of observations.
Table 5 provides a numerical comparison of the experimentally observed values from the Sandia Solid Mechanics lab to each of the 13 team predictions. The experimental results include 9 observations of path A–D–C–E and a single result for path A–C–E. The single observation from the Sandia Solid Mechanics lab of fracture path A–C–E, occurred for sample D1. Of all manufactured specimens, this particular sample, D1, had actual dimensions closest to the nominal dimensions of the challenge geometry, shown in Fig. 9. In fact, only sample D1 was within the requested \(\pm \)50.8 \(\upmu \hbox {m}\) machining tolerance for the placement of holes C and D relative to notch A. Samples S09 and S10, tested in the UT-Austin lab, were out of specified machining tolerance but had ratios of A–D to A–C ligament lengths closest to the nominal geometry. Samples S09 and S10 also followed crack path A–C–E. The other ten samples followed crack path A–D–C–E. The A–D–C–E crack path selection may be due, at least in part, to geometric deviations from the nominal dimensions. Material variability may also play a role in crack path selection, as well as its obvious role in causing scatter in the forces and displacements required for crack initiation. Based on the current experimental observations, it is not reasonable to eliminate the possibility that some subset of geometries manufactured within machining tolerances may still fail along path A–D–C–E.
Figure 20 provides a graphical representation of the comparison between computational predictions and the experimentally observed range of force and displacement values. This graph deviates slightly from the numbers reported in Table 5 in that the figure also includes the non-blind experimental data from the UT-Austin lab. The UT-Austin lab provided two additional observations of specimens that failed by the A–C–E crack path. These combined three observations help to set a more realistic range for the experimental scatter associated with the A–C–E crack path. Due to the differences in experimental results regarding the crack path selected, it may be more useful to compare predictions for crack path A–D–C–E to the experimental scatter for samples that followed crack path A–D–C–E, and likewise compare predictions of A–C–E to observations of A–C–E. For this purpose, both the experimental ranges and numerical predictions were color-coded in Fig. 20: red for crack path A–D–C–E and blue for crack path A–C–E.
Comparison of blind predictions to the experimental range of combined observations from the Sandia Solid Mechanics lab and the UT-Austin lab. Red points and lines correspond to observations and predictions of path A–D–C–E, whereas blue points and lines correspond to observations and predictions of path A–C–E. Data points represent the blind predictions for the expected outcome of the challenge and vertical bars represent each teams’ bounds on their predictions. The range of experimentally observed values are bounded by upper and lower horizontal lines
5.2 Comparison of force-COD curves
While the scalar metrics discussed in the previous section may provide the most realistic representation of common engineering problems, the force-displacement curve may provide the most insight into the efficacy of the various modeling approaches. Eachteam was asked to report their best prediction for the force-displacement behavior. The blind predictions for force-displacement behavior are compared to the experimentally observed force-displacement curves in Fig. 21. A detailed discussion comparing predictions to experiments is contained in the Sect. 6.
Comparison of force-COD predictions (colors) to experimental observations (gray lines). The solid gray lines represent the 10 experimental observations from the Sandia Structural Mechanics lab, and the dashed gray lines represent 3 non-blind experimental observations from the UT-Austin group. Path A–D–C–E experimental results are shown in lighter gray and the teams that predicted this path are underlined. Path A–C–E are shown in darker gray lines, and the corresponding team numbers are not underlined
6 Discussion
The goal of the present study was to evaluate ductile fracture prediction methods under pseudo-real-world conditions, replicating the conditions that are typical in an engineering environment. The challenge was open to the public so that a large number of participant teams would help represent the breadth of state-of-the-art capabilities across the mechanics community. As a collective effort, this body of work can be used to draw general conclusions about the fidelity of failure prediction, and the specific topic areas that require further investment.
6.1 Assessing agreement and discrepancy between predictions and experiments
6.1.1 Generic categorization of potential sources of discrepancy
Several sources of uncertainty and variability have been identified and categorized (Kennedy and O’Hagan 2001):
-
Parameter uncertainty—setting an input variable to a value that does not reflect nature.
-
Structural uncertainty/model inadequacy—the form of the governing constitutive equations are inaccurate.
-
Residual variability—additional variability in a natural process that is not captured within the fidelity of the model.
-
Parametric variability—allowing a parameter to ‘float’ due to insufficient knowledge of its true value(s).
-
Experimental uncertainty/observation error—calibration based on experiments that do not correctly reflect nature, or incorrectly represent the desired scenario.
-
Algorithmic/numerical/code uncertainty—improper numerical implementation of algorithms.
Systematic isolation and evaluation of each source of discrepancy is time-consuming and not routinely performed. The teams were each given the opportunity to bound their predictions. Most often, when teams did bound their predictions, they focused on parametric variability. They typically performed a sensitivity analysis on certain parameters that were deemed to be inadequately estimated based on the provided material property information. The modeling approaches taken were largely deterministic: calibration was typically done to average material property behavior, and the observed material property scatter was rarely taken into account. Also, no team systematically varied the dimensions of the geometric specimen features across the allowable machining tolerance ranges in the blind predictions. This sort of dimensional tolerance analysis was only performed after the conclusion of the blind phase of the predictions in an attempt to understand why certain specimens would ‘choose’ a particular crack path.
It is worth noting that the range of modeling methods used by the 13 teams represent differing levels of maturity. For example, the use of a Gurson model (Gurson 1977) within a finite element framework has seen many decades of prior development, and the teams that chose such an approach may benefit from the maturity of the technique and vast available literature from which to draw additional insight that can be brought to bear on the Challenge. In contrast, numerical methods such as Peridynamics have only recently emerged, and the proper application of these techniques to problems in ductile fracture has not been fully explored.
6.1.2 An assessment of the crack path ambiguity
An important ambiguity that arose from this challenge was in the observed crack path. In the experiments performed at three independent laboratories on the same nominal geometry, fabricated from the same sheet, the failure exhibited two different paths: A–C–E and A–D–C–E. There are at least three different approaches that one might adopt in interpreting these experiments prior to embarking on a comparison with the blind predictions. The first approach is purely statistical: nine out of the ten specimens tested as the primary data for this Challenge followed the path A–D–C–E, and therefore, statistically the path A–D–C–E is a higher probability event. In the absence of any additional information, one might be forced to act on such a proposition. However, this does not examine or consider causation; in the present example, additional information is available, both within the experimental results and the underlying theoretical framework within which these experiments were performed and interpreted, that allows additional considerations. The second approach is to take an engineering point of view: both solutions (paths A–C–E and A–D–C–E) were in fact realized in experiments, and could therefore be acceptable engineering solutions to nominally the same problem. If decisions are to be made concerning the reliability of the structure, a conservative approach can be established by using the lower bounds from the measurements for both the load-carrying capacity and the load-line displacement. Such decisions are commonly made in numerous engineering applications. However, they are not predictive since, once again, the underlying causation—why does the failure follow one path or the other—is not understood or examined closely. The third approach, and one that is perhaps the most difficult, but also the most satisfying, is to probe the problem further to determine the underlying reasons for the multiple solutions to the problem. It should also be noted that the distinction between these two paths is important, because the A–D fracture was shear dominated whereas the A–C fracture was tensile dominated. Shear versus tensile fracture is a known difficulty in computational predictions, and a phenomenological topic that has been of recent interest. For this reason, it was important to delve into the crack path ambiguity in more detail.
Nine of the ten specimens tested in the Structural Mechanics Laboratory followed crack path A–D–C–E, with only one specimen following path A–C–E. The load-COD profiles for the nine A–D–C–E crack-path specimens were similar, particularly in the characteristic features of the load drop with incremental COD. The magnitudes of load drop for propagating the crack to hole C were similar, regardless of whether the crack followed path A–D–C or went directly along path A–C, although the crack for path A–C occurred at significantly higher COD values. The conditions for crack re-initiation out of hole C were similar, regardless of whether the crack had followed path A–D–C–E or A–C–E. Two other labs performed these experiments, one blind set performed in the Sandia Materials Mechanics Laboratory before the predictions were returned and one set performed in Ravi-Chandar’s laboratory at the University of Texas at Austin after the predictions had been reported. These two labs only tested a small population of samples (3 each), yet both labs observed samples failing along both crack paths.
There are three different potential experimental imperfections that are the focus of discussions regarding crack path selection: (1) material inhomogeneities such as the observed banding, (2) load train alignment issues, and (3) specimen geometry deviations off of the nominal dimensions. While each of these could bear relevance, the effect of inhomogeneities has been reduced by using the same sheet of material for all specimens, and by specifying geometric feature sizes that were over an order of magnitude larger than the length scale of the sparsest inhomogeneity (spacing between bands). Tests performed at the different labs with different types of loading arrangements indicated similar trends in the failure paths, implying that the imperfections in the loading boundary condition may not be the primary determinant of path selection. This leaves the third source—geometric imperfections as the main suspected determinant of failure path selection. In this regard, an important quantitative correlation was found between the variations in the measured sample dimensions and the observed crack path. An obvious geometric feature of potential relevance to the crack path was the ligament distance between notch A and hole D; additionally, the ratio of the vertical distance between the notch edge A and hole D to the horizontal distance between the notch tip and hole C may reveal why the crack would prefer a given crack path. Table 6 lists relevant pre-test specimen geometry measurements based on the lengths labeled in Fig. 10, with the dimensions exceeding the prescribed tolerance of \(\pm \)0.0508 mm highlighted. The notch width (V10) is larger than the drawing tolerance for nearly all of the specimens; this led to a smaller vertical ligament distance between the notch edge A and hole D, given by V12-(V9+V10), for the majority of the specimens and for all but one of the specimens with crack path A–D–C–E. The horizontal ligament distance between the notch tip and hole C, given by H4-(H-C)-H5, was within tolerance; thus, hole C was located within tolerance for all of the specimens. The ratio of the vertical ligament between the notch edge A and hole D to the horizontal ligament distance between the notch tip and hole C is supposed to be two-thirds, but most specimens had a smaller ratio. Specimens with crack path A–C–E had a percent error in this ratio from \(-\)1.3 to +1.9 %, while specimens with crack path A–D–C–E had a percent error in this ratio of \(-\)5.4 to \(-\)2.2 %. In other words, the specimens where the ligament between A and D was significantly smaller than specified (relative to the length of the ligament between A and C) tended to fail along A–D–C–E. This exploration of the imperfections appears to indicate a systematic preference for one path to the other depending on the nature of the imperfections, and hence points not to a bifurcation, but to two solutions that are in close proximity.
6.1.3 Overview of agreement between predictions and experiments
As was the intention of this endeavor, the challenge scenario offered a problem in the area of ductile fracture that was not trivial to predict. In spite of the somewhat simplistic geometry, the common loading conditions, and the wealth of material property information provided, there was a wide range of predictions reported. While there was a wide range of experimental observations, there was a much broader band of computational predictions.
Most of the teams had elements of success in their prediction. From the perspective of crack path, all teams correctly predicted one of the two experimentally observed crack paths: A–C–E, or A–D–C–E. Elasticity, yielding, and work hardening regimes were predictable for a majority of the groups. The force-displacement curve in Fig. 21, seemed to show reasonable qualitative agreement for most of the groups, at least through the initial crack initiation load drop. For both crack path A–D–C–E and path A–C–E, nearly all of the teams were able to predict the force for first crack initiation within experimental scatter. Yet only a few teams were able to predict the COD value for first crack initiation. Force was much easier to predict that COD value for two reasons: (1) in the vicinity of first crack initiation, the force-displacement curve was nearly horizontal, and the force value was insensitive to the precise point of crack initiation whereas COD was highly sensitive, (2) there was a wide range of experimentally observed force values: the force value dropped rapidly as a result of the first crack initiation, leading to broad experimental scatter in the force value at which a visual crack was detected.
The second cracking event, either out of hole D for path A–D–C–E, or hole C for path A–C–E, was more difficult to predict quantitatively. Based on Fig. 20, only seven teams were able to predict the force at second crack initiation within the experimental error bounds associated with that predicted crack path. Only one team was able to predict the COD value for second crack initiation within experimental bounds for the predicted crack path.
Did any team get the entire challenge completely correct? While Team 2 was the only team that had predictions of the scalar quantities of interest (QoI’s) that were consistently within the experimental scatter (see Table 5), Team 2 was not able to maintain good agreement with the experimental load-COD curve across all cracking events. Specifically, Team 2 did not predict the broad plateau in load at \(\sim \)5,500 N (COD \(\sim \)4-6 mm) prior to crack initiation from hole C. This plateau was observed to be nearly identical for both experimentally observed crack paths, and Team 3 (who predicted crack path A–C–E) was able to predict the load-COD curve correctly through the end of the plateau in load. However, Team 3 did not predict the COD at which the second crack is initiated within the experimental scatter. Although Team 3 did not perform as well as Team 2 in answering the scalar metrics that are representative of engineering analyses, they predicted the load-COD response within experimental scatter over the widest range of COD. Crack initiation from hole C (as inferred from the final load drop) was difficult for all of the teams to predict. This, after all, was the final significant mechanical event, and the teams had to get all previous elasticity, yielding, work hardening, necking, crack initiation, and crack propagation correct to finally predict the correct loads and displacements at which a crack would emerge from hole C.
The challenge approach presented in this work provides a reasonable benchmark of state-of-the-art in ductile fracture prediction, at least within the capabilities represented by the 13 participant teams. However, the approach is limited in its ability to single out the precise strengths and weaknesses of different approaches. The approach intends to mimic that of a real-world engineering scenario, where the challenge does not isolate specific sources of error. Only a subsequent analysis by the participants can identify the specific elements that caused poor predictivity. Likewise, the approach may be insensitive to certain sources of prediction error that would become problematic in other scenarios. Moreover, the challenge scenario only assesses predictivity within the scope of the challenge problem: quasi-static room temperature deformation and fracture of a structural alloy with moderate ductility. For example, the results of this challenge do not speak to the ability of modeling methods to address problems in the area of dynamic fracture, coupled thermomechanical fracture, environmentally-accelerated fracture, etc.
6.2 Future needs for improving predictivity of computational models in the area of ductile fracture
6.2.1 Constitutive modeling
Computational models are dependent on the material characterization experiments that are used to calibrate the constitutive model(s). While there are many handbooks and databases for material property data, these databases often only include rudimentary property information such as yield strength and ultimate tensile strength. Even full stress–strain data is sometimes difficult to obtain. In some cases, even when stress–stain curves are available, crucial details of the tensile geometry are lacking. Mode-I plane strain fracture toughness data is sometimes available, and to a lesser extent, plane strain J\(_{IC}\) data is available, especially for alloys used in high-reliability structures such as nuclear reactors and aerostructures. However, the extension of sharp-crack plane strain fracture toughness values to realistic engineering structures is not always straightforward, as demonstrated in the current Challenge. For these reasons, computational efforts always require material property experiments. While these experiments are both costly and time consuming, there is no substitute: fracture properties in structural metals can not be obtained from first principles calculations. More efficient methods to gather a sufficient amount of material property information from a minimum number of experiments is needed. What is the minimum number of calibration tests that are needed for a model? Can emerging experimental techniques, such as digital image correlation, provide a richer material property dataset from fewer tests with which to populate model calibration?
One of the difficulties in predicting the Sandia Fracture Challenge was the lack of sufficient material property data to calibrate constitutive models for failure. The Challenge intentionally provided only material property data that would typically be available in a structural analysis for engineering problems. While extensive data was provided for tensile behavior and sharp-crack fracture toughness behavior, many prediction teams would have benefited from more detailed experimental measurements (such as details of 3-dimensional deformation during necking in the uniaxial tensile experiment, and crack extension data from the fracture tests), and more importantly from additional information regarding the shear deformation and shear failure behavior of the material. Currently, the fracture mechanics community lacks a widely-accepted criterion for failure. Moreover, the mechanics community lacks a widely-accepted, standardized test method to evaluate shear deformation and failure. There are several experimental methods that have been proposed for this problem, including the Iosopescu geometry (ASTM D5379), V-notched rail shear (ASTM D7078), the Butterfly geometry (Dunand and Mohr 2011), and punch geometry (ASTM D732). In addition, some sheet forming experiments such as mandrel forming involve extensive shear deformation, but are not loaded in pure shear. While these methods each have utility, the lack of shear material property data likely stems from a lack of standardization for shear test methods. Early modeling methods for ductile failure of metals, such as the Gurson method (Gurson 1977), did not take into account low triaxiality shear failure as a distinct mode of failure.
Another deficiency that some teams revealed was the lack of a material model that captured microstructure and macrostructure of the material. Microstructure includes aspects such as grain size, grain boundary arrangements, precipitate content, crystallographic texture etc., and macrostructure includes aspects such as macroscopic anisotropy (i.e. plate anisotropy), and inhomogeneous banding of the microstructure (stringers of precipitates). While optical micrographs were provided of the grain structure, none of the teams used this information in their modeling method. Multi-scale computational methods that incorporate the effects of microstructure are under development by a number of research groups (Allison et al. 2011; Horstemeyer 2012; McDowell 2010; Emery et al. 2009). However, these models remain largely developmental, in part due to the challenges of mapping measurable properties to model parameters. Explicit representation of microstructure is computationally expensive and data management is cumbersome. Techniques are needed to connect advances in homogenization theory with characterization of micro structural detail in order to develop continuum-scale constitutive and failure models in a rational way.
6.2.2 Failure modeling
The current challenge highlighted the lack of a widely-accepted criterion for the onset of failure (e.g. void nucleation). Some teams merely used critical strain, some teams used a more complex tearing parameter, and yet others used a modified Gurson model. Teams 2 and 3 reported predictions that were among the most successful, yet their failure models differed significantly: Team 2 used a recently developed pressure-dependent damage model that can distinguish shear- and tensile-contributions to failure, whereas Team 3 used equivalent plastic strain. These differences expose a lack of maturity or consensus with regard to failure models. While detailed mechanics models exist for void growth and coalescence, there is little agreement on the micro-scale conditions for void nucleation. Failure is generally thought to initiate at pre-existing defects, voids or inclusions; and by that rationale some of the most widely accepted mechanics models require that materials contain some seed volume fraction of voids or pre-existing inclusions. Early reviews of this topic (Goods and Brown 1979), suggested that void nucleation can occur not only at inclusions or second-phase particles, but also at grain boundaries which serve as sites for dislocation pile-up. High-purity single crystalline metals fail by a void nucleation process that is similar (or identical) to the failure process observed in many ductile metals. Deformation-induced subgrain structure may facilitate the nucleation of voids (Boyce et al. 2012). There is clearly a need for continued investigation regarding the critical conditions that lead to void nucleation, especially in the absence of pre-existing defects or hard particle interfaces. Most likely, emerging models for accurate prediction of void nucleation will need to be multiscale to capture details of the evolving microstructure while also capturing the macroscale boundary conditions.
6.2.3 Computational methods
There was a striking inconsistency in each of the teams approach to uncertainty quantification (UQ). All groups were asked to report not only the expected value for the forces and displacements at fracture, but they were also asked to report lower and upper bounds for these values. Some groups reported only deterministic predictions, and other teams reported large uncertainty bands, even larger than the significant experimental scatter. While UQ is a vibrant research area (Oberkampf and Roy 2010), the current effort demonstrates that UQ is far from mature, at least in the context of ductile fracture prediction. There are several possible explanations from the inconsistency in UQ methods. Most importantly, because this was essentially a volunteer effort on the part of participants, the time needed for detailed UQ analysis was not available. To make UQ a reality, the mechanics community will have to rely not only on improved probabilistic methods, but also on computationally efficient models so that multiple scenarios can be studied in a time- and cost-effective manner. In addition, there is very little guidance or standardization to improve consistency in performing UQ analysis. Moreover, there is similarly little guidance on the appropriate number of calibration experiments needed to quantify material variability.
A difficulty discussed among teams was the challenge of scalability. Ductile fracture is known to be a scale-sensitive problem. For this reason, lab-scale test coupons, such as those used in the present study may not represent fracture behavior in large-scale structure such as ships or buildings. Real world applications span many orders of magnitude in size, from micro- and nano-electronics to civil structures. However, experimental testing and standardization in fracture, such as ASTM E399, focus on lab-scale test specimens, with little guidance to scaling for other engineering scales. Even the Sandia Fracture Challenge geometry itself evaluates fracture modeling only at the lab scale—the material property coupons were of a similar scale to the challenge geometry, and would be relevant to structures where the dimension of critical features in on the scale of a few millimeters. In many large-scale or geometrically complex engineering structures, there is a limit to the number of elements that are computationally practical. The Challenge specimen was small and simple enough that the teams could expend a large number of elements in the features of concern. Team 3 appears to have used the largest number of elements in the prediction: 2 million elements were used to predict the Challenge. Because of this, team 3 was only able to run a small number of simulations to bound their predictions. In many engineering scenarios, the analyst must carefully trade-off computational cost with spatial and geometric accuracy. For example, in some large scale welded structures, even the geometric details of the weld must be ignored or homogenized for computational practicality.
With regard to scale, a pervasive problem in fracture prediction is mesh-size sensitivity and model regularization. It is interesting to note that none of the teams performed a mesh-convergence study on their predictions. Some groups used an extremely fine mesh, and other groups selected a similar mesh size for the material property calibration coupons and the Challenge specimen. The physical mechanisms of fracture possess several intrinsic length scales governing physical phenomena (dislocation core size, grain size, plastic zone size, shear band spacing, etc), but conventional continuum analysis is a scale-invariant approach. This challenge of incorporating length-scale dependence into continuum methods has been studied extensively for many years, e.g. Chen et al. (2000), Gao and Huang (2003), Needleman (2000). However, there is yet to be a consistent method for incorporating length-scale effects in fracture. One technique employed by some prediction teams to mitigate mesh dependency was to calibrate the material property tests with the same mesh scale as was used to predict the Challenge scenario. Other techniques like cohesive zones, peridynamics, and extended finite elements provide alternative methods to manage dissipation by incorporating additional knowledge of an intrinsic scale. It is possible that the regularization technique itself might depend on the type of fracture problem that is being addressed. The difficulties associated with regularization continue to impede predictivity.
6.3 Recommendations for future challenge scenarios
6.3.1 Specific topical areas in deformation and fracture where blind assessment is needed
A single Challenge such as the present study only provides limited insight into the predictivity of ductile failure. The efficacy or deficiency of a particular team’s modeling approach should not be overstated based on this single Challenge effort. Instead, additional Challenges will help illuminate methods that consistently produce the most reasonable predictions. A limitation to the blind fracture challenge as it was issued in the current study, was the difficulty in isolating individual sources of error. Prediction errors can stem from inadequate physics models, poor numerical methods, improper boundary conditions, and several other sources already discussed. A prediction that does not match experimental observations may stem from any one of these errors, and isolation requires subsequent studies. A future challenge could be issued to isolate specific effects, such as mesh dependency.
The Challenge presented in the current work only examines one narrow aspect of failure predictivity. The Challenge represents monotonic tearing failure of millimeter-scale geometric features under slow, quasi-static loading conditions in a plate that is in between plane stress and plane strain conditions, for a material that possesses low work hardening and modest ductility. The current Challenge does not necessarily reflect predicitivity in other scenarios. For example, dynamic crack propagation was not addressed in the current challenge. The instantaneous load drop and audible pop associated with a crack forming between notch A and hole D was at first a dynamic crack propagation event, but the crack became stable even before it had propagated to the visible sidewall surfaces. A different Challenge could be devised to more carefully interrogate the prediction of dynamic crack propagation, and the transition between stable and dynamic propagation. Or, even a switch to a more brittle material with the same challenge geometry might provide a better investigation of dynamic crack propagation prediction. The current study focused only on the general material class of ductile metals, but fracture prediction is a challenge for other material classes as well (composites, hierarchical materials, foams and porous materials, metallic glasses, graded materials, etc.) and those other material classes could benefit from a similar blind assessment.
There are several other conditions that would be interesting to evaluate using such a blind assessment technique such as, (1) high temperature or low temperature fracture crossing a ductile-to-brittle transition, (2) dynamic fracture, such as under quasi-adiabatic conditions, impact loading, etc., (3) fracture of a microstructurally-sensitive or intentionally defected material such as aluminum alloys where failure initiates at precipitate phase boundaries, (4) fracture prediction of a complex large-scale structure where lab-scale material properties must be extrapolated to the length scale of the challenge structure, such as emulating prediction of fracture in an airplane wing.
In addition, a future challenge could intentionally explore methods for uncertainty quantification. Such a challenge would require statistical details provided regarding the variability in a manufacturing process or observed variability in material.
6.3.2 Guidance for execution of a future challenge
The present work revealed several pitfalls in the execution of a blind assessment in the area of solid mechanics. These ‘lessons learned’ can help foster better Challenge exercises in the future. For example, there was a significant issue raised by the manufacture of specimens that were not only deviating from the nominal sample dimension, but also deviated slightly beyond the allowable manufacturing tolerances. While none of the groups used the dimensional tolerances in their initial blind predictions, the subsequent analysis of experimental data and discrepancies with computational predictions revealed that the out-of-tolerance specimens could have emphasized a crack path solution that was not the same as the crack path associated with nominal dimensions. In the future, the actual test articles could be manufactured before the beginning of the challenge and the as-measured dimensions of the actual articles could be provided to the prediction teams. This would be especially useful for an exercise evaluating uncertainty quantification methodologies. In addition, a second deficiency in the current exercise was the selection of a scalar metric for prediction that was not easily measured. Specifically, the initial blind challenge called on the teams to predict the onset of crack initiation as defined by a 100-\(\upmu \hbox {m}\) visible surface crack. This was not only difficult to observe experimentally, but the conditions were vastly different from those of the initial crack formation event, which was better evidenced by an audible signal and a distinct load drop. If more tests had been performed prior to the issuance of the Challenge, then the ambiguities raised by this problem may have been avoided. The additional advantage to running a series of experiments before the issuance of a challenge is that the repeatability of the measurements can be confirmed. In the present experiments, the observation of the two crack paths would have been discovered before the onset of the Challenge, and might have led to a modification of the test geometry so that only one crack path was preferred. A concern of performing the experiments before the issuance of the challenge lies in keeping the results confidential so that the prediction teams are blind and unbiased.
The current blind assessment methodology did not constrain the analysts to a particular method. Instead, the participant teams could utilize whatever methodologies within their capabilities that they deemed appropriate. In this way, the current Challenge replicated a pseudo-real-world engineering problem. However, in this approach, the isolation of specific sources of discrepancy between model and experiments can be difficult. There are many areas where discrepancies can arise, such as improper calibration to material properties, improper constitutive models, or numerical algorithm computational errors, to name a few. A sensitivity analysis performed after the comparison to experiments can help to isolate the most important sources of error.
The material property data that was provided to the teams is an important factor in their predictive success. The current challenge attempted to replicate pseudo-real-world engineering conditions by providing material property data that was commensurate with typical engineering scenarios, based on ASTM standard test methods. In many real engineering scenarios, even less material information is available. For example, in the current Challenge multiple full tensile engineering stress–strain curves provided for both the longitudinal and transverse plate directions, as well as the dimensions of the tensile bar, and shape of the post-fracture neck, were provided for ease of calibration to a material constitutive model. Often, in real engineering scenarios, details such as the tensile dimensions are not available, and this lack of information can cause problems in constitutive calibration. A future challenge could even explore how engineers and analysts approach problems with less material information or different material information, and how they use this lack of information to drive uncertainty quantification.
The results of this Challenge also bring out some pertinent questions related to the development of the Quantities of Interest (QoI’s). The selection of appropriate QoI’s is extremely important in interpreting the experiments and simulations. Typical engineering practice is to reduce the complexity of the problem by reducing the results of experiments and simulations to a few scalar metrics with which higher level decisions could be made. In this spirit, the current challenge posed a few scalar QoI’s: the load and COD at the onset of the first and second failure as well as the path of the crack. Difficulties associated with identifying the onset of failure and ambiguities in crack path selection have already been discussed. These difficulties suggest that while the QoI’s may be set a priori, one must be aware of their potential limitations and have in place procedures for generating alternate QoI’s a posteriori. In this regard, it might be useful to introduce conditional QoI’s; for example, in the present challenge, considering that there are four distinct phases in the response—elastic, elastic-plastic, localization, and failure—conditional QoI’s that present ‘go–no-go’ decision points along the response could be postulated:
-
First, was the elastic stiffness of the structure captured correctly by the model?
-
If yes, then, was the prediction of the stable plastic response up to the limit load within acceptable range of the experiments?
-
If yes, then, was the onset of any localization predicted correctly?
-
Finally, were the original QoI’s based on the onset of first and second failure predicted correctly?
The reason for positing the ‘go – no-go’ decision points is that there are some aspects of modeling that are well-established and that any new model that is unable to capture the more elementary features of the response may not provide reliable predictions of more complicated, and less well-established features of the response. The advantage of this procedure is that while simple scalar measures could be used at higher level decision-making, the validation of the scalar QoI’s must pass through a much greater detailed assessment at a lower-level.
One final aspect of the comparison of the experiments and predictions involves quantitative measures of comparison. In the present study, a rudimentary statistical comparison is made by comparing the range of the upper and lower bound predictions to the scatter in the experimentally measured response. More sophisticated measures based on Bayesian statistics have been developed in recent years to handle verification, validation and uncertainty quantification. Future challenges should consider implementing such measures to perform quantitative comparison.
7 Summary and conclusions
Sandia proposed a double blind fracture challenge to the international engineering community and thirteen teams submitted blind computational results, representing contributions from 22 institutions. The intent was to assess the predictive accuracy of current methods. It is clear that this blind assessment effort has helped make each of the modeling teams more acutely aware of some of the weaknesses of their methods. Many of these weaknesses are discussed in detail in the Appendices, and as a result of the present effort, many of the teams are working to address these weaknesses. One surprising source of error that became apparent through an honest evaluation of the capabilities was ‘operator’ error, such as misinterpreting the desired prediction quantities, misreporting the results, or making dubious assumptions. It appears that these mistakes can overwhelm any predictivity (or errors in numerics/physics/co) that may be present in the models. Even transcription errors can present real hurdles to reporting accurate predictions. These ‘simple’ mistakes are often quickly discounted after the fact. Yet they can have a quantitatively large effect on blind predictivity.
One common theme that appears to affect all of the modeling methods is the availability of calibration data on the particular alloy of interest. The current effort was restricted to readily available data, which included tensile and fracture test data. All of the methods would benefit from more extensive calibration data beyond traditional material property tests. For example, a suite of test geometries spanning different degrees of stress concentrations, stress state, mode mixity, post-necking behavior, etc. could be useful to calibrate models prior to using them on an ‘unknown’ problem. There already appear to be early discussions regarding the development of such a test suite. Nevertheless, it is important to remember that reliance on such a test suite would mean that each alloy of interest would require extensive experimental evaluation prior to modeling. At a time when high-throughput experimentation, data management, data mining, and exascale computing are becoming commonplace in other fields, it is important that the structural failure prediction community also develops new approaches to take advantage of these emerging capabilities.
In addition, there were several other known but unresolved issues in fracture prediction that were highlighted by the Challenge exercise: (1) in this specific Challenge, geometric uncertainties were shown to have a huge impact on crack path predictions, (2) mesh convergent methods remain an open issue, (3) effects of microstructure may be important but were not included by any of the teams, (4) improved physical descriptions of fracture are necessary to reduce dependence on empirical material testing, (5) there is a trade-off or balance that is necessary between physical realism and computational efficiency. This list only highlights those issues in fracture prediction that were brought to light by this particular Sandia Fracture Challenge. There are other known gaps in failure prediction, such as the need for microstructurally-informed models, which were not elucidated by the present exercise, but may be exposed by future challenges.
References
ABAQUS/6.12 Manual (2012) Simulia Inc., Providence, RI
Al-Ostaz A, Jasiuk I (1997) Crack initiation and propagation in materials with randomly distributed holes. Eng Fract Mech 58(5–6):395. doi:10.1016/s0013-7944(97)00039-8
Allison JE, Collins PM, Spanos G (2011) Proceedings of the 1st world congress on integrated computational materials engineering (ICME), Wiley.com
Bai Y, Wierzbicki T (2010) Application of extended Mohr–Coulomb criterion to ductile fracture. Int J Fract 161(1):1–20. doi:10.1007/s10704-009-9422-8
Bauvineau L, Burlet H, Eripret C, Pineau A (1996) Modelling ductile stable crack growth in a C-Mn steel with local approaches. J Phys IV France 06(C6):C3-633–C36-42
Beese AM, Luo M, Li Y, Bai Y, Wierzbicki T (2010) Partially coupled anisotropic fracture model for aluminum sheets. Eng Fract Mech 77(7):1128–1152. doi:10.1016/j.engfracmech.2010.02.024
Benseddiq N, Imad A (2008) A ductile fracture analysis using a local damage model. Int J Press Vessel Pip 85(4):219–227. doi:10.1016/j.ijpvp.2007.09.003
Bernauer G, Brocks W (2002) Micro-mechanical modelling of ductile damage and tearing—results of a European numerical round robin. Fatigue Fract Eng Mater Struct 25(4):363–384. doi:10.1046/j.1460-2695.2002.00468.x
Boyce BL, Cox JV, Wellman GW, Emery JM, Ostien JT, Foster JT, Cordova TE, Crenshaw TB, Mota A, Bishop JE, Silling SA, Littlewood DJ, Foulk JW, III, Dowding KJ, Dion K, Robbins JH, Spencer BW (2011) Ductile failure X-prize, Report Number SAND2011-6801. Sandia National Laboratories
Boyce BL, Clark BG, Lu P, Carroll JD, Weinberger CR (2012) The morphology of tensile failure in Tantalum. Metall Mater Trans A:1–14
Chen Z (1996) Continuous and discontinuous failure modes. J Eng Mech ASCE 122(1):80–82. doi:10.1061/(asce)0733-9399
Chen JS, Pan CH, Wu CT, Liu WK (1996) Reproducing kernel particle methods for large deformation analysis of non-linear structures. Comput Methods Appl Mech Eng 139(1–4):195–227. doi:10.1016/s0045-7825(96)01083-3
Chen J-S, Wu C-T, Belytschko T (2000) Regularization of material instabilities by meshfree approximations with intrinsic length scales. Int J Numer Methods Eng 47(7):1303–1322
Chen Z, Hu W, Shen L, Xin X, Brannon R (2002) An evaluation of the MPM for simulating dynamic failure with damage diffusion. Eng Fract Mech 69(17):1873–1890. doi:10.1016/s0013-7944(02)00066-8
Chen Z, Shen L, Mai YW, Shen YG (2005) A bifurcation-based decohesion model for simulating the transition from localization to decohesion with the MPM. Zeitschrift Fur Angewandte Mathematik Und Physik 56(5):908–930. doi:10.1007/s00033-005-3011-0
Decamp K, Bauvineau L, Besson J, Pineau A (1997) Size and geometry effects on ductile rupture of notched bars in a C-Mn steel: experiments and modelling. Int J Fract 88(1):1–18. doi:10.1023/a:1007369510442
Dunand M, Mohr D (2010) Hybrid experimental-numerical analysis of basic ductile fracture experiments for sheet metals. Int J Solids Struct 47(9):1130–1143. doi:10.1016/j.ijsolstr.2009.12.011
Dunand M, Mohr D (2011) Optimized butterfly specimen for the fracture testing of sheet materials under combined normal and shear loading. Eng Fract Mech 78(17):2919–2934. doi:10.1016/j.engfracmech.2011.08.008
Emery J, Hochhalter J, Wawrzynek P, Heber G, Ingraffea A (2009) DDSim: a hierarchical, probabilistic, multiscale damage and durability simulation system-Part I: methodology and Level I. Eng Fract Mech 76(10):1500–1530
Fleck NA, Hutchinson JW (1993) A phenomenological theory for strain gradient effects in plasticity. J Mech Phys Solids 41(12):1825–1857
Freund LB (1972) Crack-propagation in an elastic solid subjected to general loading—I. Constant rate of extension. J Mech Phys Solids 20(3):129–140. doi:10.1016/0022-5096(72)90006-3
Freund LB (1979) Mechanics of dynamic shear crack-propagation. J Geophys Res 84(NB5):2199–2209. doi:10.1029/JB084iB05p02199
Gao H, Huang Y (2003) Geometrically necessary dislocation and size-dependent plasticity. Scripta Materialia 48(2):113–118
Ghahremaninezhad A, Ravi-Chandar K (2012) Ductile failure behavior of polycrystalline Al 6061-T6. Int J Fract 174(2):177–202. doi:10.1007/s10704-012-9689-z
Ghahremaninezhad A, Ravi-Chandar K (2013) Ductile failure behavior of polycrystalline Al 6061-T6 under shear dominant loading. Int J Fract 180(1):23–39. doi:10.1007/s10704-012-9793-0
Goods SH, Brown LM (1979) The nucleation of cavities by plastic deformation—overview. Acta Metall 27(1):1–15
Griffith AA (1921) The phenomena of rupture and flow in solids. Philos Trans R Soc Lond Ser A Contain Papers Math Phys Character 221:163–198
Gross AJ, Ravi-Chandar K (2013) Prediction of ductile failure using a local strain-to-failure criterion. Int J Fract (submission to Sandia Fracture Challenge Special Issue)
Gurson AL (1977) Continuum theory of ductile rupture by void nucleation and growth. I. Yield criteria and flow rules for porous ductile media. Transactions of the ASME Series H. J Eng Mater Technol 99(1):2–15
Haltom SS, Kyriakides S, Ravi-Chandar K (2013) Ductile failure under combined shear and tension. Int J Solids Struct 50(10):1507–1522. doi:10.1016/j.ijsolstr.2012.12.009
Horstemeyer MF (2012) Integrated Computational Materials Engineering (ICME) for metals: using multiscale modeling to invigorate engineering design with science. Wiley.com
Inglis CE (1913) Stresses in a plate due to the presence of cracks and sharp corners. In: Transactions of the insititution of naval artchitects, vol. 55. pp 219–241
Irwin G (1958) handbuch der Physik, vol VI. Springer, Berlin
Kennedy MC, O’Hagan A (2001) Bayesian calibration of computer models. J R Stat Soc: Ser B Stat Methodol 63(3):425–464
Krysl P, Belytschko T (1997) Element-free Galerkin method: convergence of the continuous and discontinuous shape functions. Comput Methods Appl Mech Eng 148(3–4):257–277. doi:10.1016/s0045-7825(96)00007-2
Li SF, Hao W, Liu WK (2000) Mesh-free simulations of shear banding in large deformation. Int J Solids Struct 37(48–50):7185–7206. doi:10.1016/s0020-7683(00)00195-5
Liu WK, Jun S, Zhang YF (1995) Reproducing kernel particle methods. Int J Numer Methods Fluids 20(8–9):1081–1106. doi:10.1002/fld.1650200824
Luo M, Wierzbicki T (2010) Numerical failure analysis of a stretch-bending test on dual-phase steel sheets using a phenomenological fracture model. Int J Solids Struct 47(22–23):3084–3102. doi:10.1016/j.ijsolstr.2010.07.010
Luo M, Dunand M, Mohr D (2012) Experiments and modeling of anisotropic aluminum extrusions under multi-axial loading—Part II: Ductile fracture. Int J Plast 32–33:36–58. doi:10.1016/j.ijplas.2011.11.001
Macek RW, Silling SA (2007) Peridynamics via finite element analysis. Finite Elem Anal Des 43(15):1169–1178. doi:10.1016/j.finel.2007.08.012
McDowell DL (2010) A perspective on trends in multiscale plasticity. Int J Plast 26(9):1280–1309
McVeigh C, Liu WK (2008) Linking microstructure and properties through a predictive multiresolution continuum. Comput Methods Appl Mech Eng 197(41–42):3268–3290
McVeigh C, Liu WK (2010) Multiresolution continuum modeling of micro-void assisted dynamic adiabatic shear band propagation. J Mech Phys Solids 58(2):187–205
Moes N, Dolbow J, Belytschko T (1999) A finite element method for crack growth without remeshing. Int J Numer Methods Eng 46(1):131–150. doi:10.1002/(sici)1097-0207(19990910)46:1<131:aid-nme726>3.0.co;2-j
Nahshon K, Hutchinson JW (2008) Modification of the Gurson model for shear failure. Eur J Mech a-Solids 27(1):1–17. doi:10.1016/j.euromechso1.2007.08.002
Nahshon K, Xue Z (2009) A modified Gurson model and its application to punch-out experiments. Eng Fract Mech 76(8):997–1009. doi:10.1016/j.engfracmech.2009.01.003
Needleman A (2000) Computational mechanics at the mesoscale. Acta Materialia 48(1):105–124
Oberkampf WL, Roy CJ (2010) Verification and validation in scientific computing, vol 5. University Press Cambridge, Cambridge
Park K, Paulino GH, Roesler JR (2009) A unified potential-based cohesive model of mixed-mode fracture. J Mech Phys Solids 57(6):891–908. doi:10.1016/j.jmps.2008.10.003
Rice JR (1967) A path independent integral and the approximate analysis of strain concentration by notches and cracks. DTIC Document
Rice J, Rosengren G (1968) Plane strain deformation near a crack tip in a power-law hardening material. J Mech Phys Solids 16(1):1–12
Roe KL, Siegmund T (2003) An irreversible cohesive zone model for interface fatigue crack growth simulation. Eng Fract Mech 70(2):209–232. doi:10.1016/s0013-7944(02)00034-6
Rose JH, Ferrante J, Smith JR (1981) Universal binding-energy curves for metals and bimetallic interfaces. Phys Rev Lett 47(9):675–678. doi:10.1103/PhysRevLett.47.675
Schmitt W, Sun DZ, Blauel JG (1997) Damage mechanics analysis (Gurson model) and experimental verification of the behaviour of a crack in a weld-cladded component. Nuclear Eng Des 174(3):237–246. doi:10.1016/S0029-5493(97)00135-0
Siegmund T, Bernauer C, Brocks W (1998) Two models of ductile fracture in contest: porous metal plasticity and cohesive elements. ECF 12 Fract Defects 2:933–938
Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48(1):175–209. doi:10.1016/s0022-5096(99)00029-0
Skallerud B, Zhang ZL (1997) A 3D numerical study of ductile tearing and fatigue crack growth under nominal cyclic plasticity. Int J Solids Struct 34(24):3141–3161. doi:10.1016/S0020-7683(96)00137-0
Sulsky D, Chen Z, Schreyer HL (1994) A particle method for history-dependent materials. Comput Methods Appl Mech Eng 118(1–2):179–196. doi:10.1016/0045-7825(94)00033-6
Tvergaard V (1981) Influence of voids on shear band instabilities under plane-strain conditions. Int J Fract 17(4):389–407. doi:10.1007/bf00036191
Tvergaard V, Needleman A (1984) Analysis of the cup-cone fracture in a round tensile bar. Acta Metall 32(1):157–169. doi:10.1016/0001-6160(84)90213-X
Vernerey FJ, Liu WK, Moran B (2007) Multi-scale micromorphic theory for hierarchical materials. J Mech Phys Solids 55:2603–2651. doi:10.1016/j.jmps.2007.04.008
Wellman GW (2012) A simple approach to modeling Ductile fracture, Report Number SAND2012-1343. Sandia Report. Sandia National Laboratories, Albuquerque, NM
Williams M (1957) On the stress distribution at the base of a stationary crack. J Appl Mech 24(1):109–114
Xu XP, Needleman A (1994) Numerical simulations of fast crack-growth in brittle solids. J Mech Phys Solids 42(9):1397. doi:10.1016/0022-5096(94)90003-5
Xue L (2006) Void shearing effect in ductile fracture of porous materials. In: Besson J et al (eds) Local approach to fracture: EUROMECH-MECAMAT, (2006) 9th European mechanics of materials conference (EMMC9). Moret-sur-Loing, France, pp 483–488
Xue L (2007) Damage accumulation and fracture initiation in uncracked ductile solids subject to triaxial loading. Int J Solids Struct 44(16):5163–5181. doi:10.1016/j.ijsolstr.2006.12.026
Xue L (2008) Constitutive modeling of void shearing effect in ductile fracture of porous materials. Eng Fract Mech 75(11):3343–3366. doi:10.1016/j.engfracmech.2007.07.022
Xue L (2009) Stress based fracture envelope for damage plastic solids. Eng Fract Mech 76(3):419–438. doi:10.1016/j.engfracmech.2008.11.010
Xue L, Wierzbicki T (2009) Numerical simulation of fracture mode transition in ductile plates. Int J Solids Struct 46(6):1423–1435. doi:10.1016/j.ijsolstr.2008.11.009
Xue L, Mock W Jr, Belytschko T (2010a) Penetration of DH-36 steel plates with and without polyurea coating. Mech Mater 42(11):981–1003. doi:10.1016/j.mechmat.2010.08.004
Xue Z, Pontin MG, Zok FW, Hutchinson JW (2010b) Calibration procedures for a computational model of ductile fracture. Eng Fract Mech 77(3):492–509. doi:10.1016/j.engfracmech.2009.10.007
Acknowledgments
B.L.B. and H.E.F. would like to thank Dr. Steven Kempka for managing Sandia’s role in this work through the DOE Advanced Scientific Computing program. The Sandia authors would like to thank the following individuals for providing laboratory support of the experiments: Thomas Crenshaw, Alex Hielo, Jack Heister, John Laing, Cayetano Mendoza, and Alice Kilgo. The authors would also like to thank Dr. Yuxiong Mao and Prof. Mark Horstemeyer for providing metallographic analysis and SEM fractography. The University of Texas at Austin effort was performed during the course of an investigation into ductile failure under two related research programs funded by the Office of Naval Research: MURI project N00014-06-1-0505-A00001 and FNC project: N00014-08-1-0189. This support is gratefully acknowledged. D. T. O’Connor was supported by a National Physical Sciences Consortium Fellowship. Team 8 was supported in part by the National Natural Science Foundation of China under Grant Number 11232003, and the National Key Basic Research Special Foundation of China under Grant Number 2010CB832701 and 2010CB832704. Team 10 would like to gratefully acknowledge the support from the Office of Naval Research/Ship Systems and Engineering Research Division under the Contract N00014-11-C-0487. Sandia National Laboratories is a multi-program laboratory managed and operated by Sandia Corporation, a wholly owned subsidiary of Lockheed Martin Corporation, for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-AC04-94AL85000.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary material 1 (avi 30851 KB)
Supplementary material 2 (avi 42909 KB)
Appendix: Additional details on modeling approaches and results
Appendix: Additional details on modeling approaches and results
1.1 Team 1
Team Members: M. Neilsen, K. Dion, E. Fang, A. Kaczmarowski, E.Karasz; Sandia National Laboratories, New Mexico, USA
Predictions for the 2012 Sandia Fracture Challenge were generated using a transient-dynamic finite element code with a Multilinear Elastic Plastic Failure (MLEPF) model developed at Sandia (Wellman 2012). This model is a conventional, rate-independent, vonMises plasticity model for metals with user prescribed hardening as a function of equivalent plastic strain. In addition to conventional plasticity, this model has an empirical criterion for crack initiation and growth. Failure initiates when the tearing parameter, \(t_{p}\), given by the following equation reaches a critical level
where \(\sigma _{\max } \) is the maximum principal stress, \(\sigma _m\) is the mean stress, \(\varepsilon _p \) is the equivalent plastic strain and the Macaulay bracket, \(\left\langle {\bullet } \right\rangle \), indicates that the tearing parameter will only increase if the argument within the brackets is positive. After material failure is initiated, material strength is linearly reduced to zero over an increment of strain, the critical crack opening strain, in the crack opening direction and elements with no strength left are removed from the mesh.
The first step in these analyses was to obtain material parameters for the MLEPF model by simulating the uniaxial tension and fracture toughness experiments that were reported by the organizers of the Sandia Fracture Challenge. The initial part of the stress–strain curve can be captured from the reported stress strain behavior prior to necking. To capture the measured response after necking, the uniaxial tension test was simulated and points in the post-localization hardening regime were modified and simulations repeated until the predicted engineering stress versus engineering strain curve matched the experiment (Fig. 22). The critical tearing parameter was then selected such that the bar would tear at the last recorded point in the experiment when the load dropped. There was some variation in engineering strain associated with final load drop so values of 0.90 and 1.50 were chosen for the critical tearing parameter (Fig. 22). The fracture toughness test was modeled, and the critical crack opening strain was calibrated to 0.3 to bring the predicted load displacement curve close to the reported load displacement curve.
Finally, the challenge geometry was simulated using a finite element model with 125,916 elements and 12 elements through the thickness of the plate. The element size used in the challenge simulation was chosen to be close to the element size (0.25 mm edge length) used in the prior simulations of the uniaxial tension and fracture toughness tests. The challenge simulation ran in \(\sim \)20,000 s on 120 processors. This model captured the initial load plateau and drop to a lower plateau due to tearing between the notch and Hole C (Fig. 23). For the simulation with a critical tearing parameter of 1.50, a crack is predicted to first appear in Hole C at a crack opening displacement (COD) of 3.100 mm and force of 8,017 N. Crack re-initialization is predicted on the opposite side of Hole C at a COD of 3.481 mm and force of 5,410 N. Unfortunately the force and COD numbers originally submitted for entry into Table 5 and Fig. 20 were incorrect. At the peak force of 9,007 N recorded in Table 5, for the Sandia Team, Team 1, a crack is initiated in the ligament between Holes C and A, but a surface crack does not appear on the surface of Hole C until the load has dropped to 8,017 N. The COD numbers recorded in Table 5 for Team 1 were times in seconds in the transient dynamic simulations when the cracks appeared and not the COD in inches.
The MLEPF model predicts crack re-initialization and continued load drop much earlier than was observed in the experiments (Fig. 23). The A–C–E crack path predicted by this model matches only one of the ten experimental results and most experiments exhibited an A–D–C–E crack path. However, it was later found that many of the specimens deviated from the design geometry that the model was based on; thus, it would be interesting to rerun these simulations with some as-manufactured geometries to see if the MLEPF would predict the A–D–C–E crack path with the deviated geometries. Finally, the MLEPF model tends to predict a crack oriented perpendicular to the front face and a close examination of the experimental results reveals a crack that tends to form at an angle through the thickness of the plate. The coarseness or texture of the mesh used in these simulations may have prevented this model from capturing cracking at an angle through the thickness. We do not know if mesh refinement would improve predictions with this model. Also, since the model dissipates energy based on a user-prescribed critical crack opening strain, the energy dissipated by crack growth with this model is expected to be mesh size dependent. Modifications to reduce mesh size and texture dependence are currently being investigated. Additional information about predictions with the MLEPF model can be found in a companion paper published in this same special issue by Neilsen et al.
1.2 Team 2
Team Member: L. Xue; Schlumberger, Sugar Land, Texas
1.2.1 Approach to ductile fracture prediction
There are mainly two approaches to model damage plasticity of ductile materials: the micromechanical approach and the macroscopic approach. The micromechanical approach characterizes the damage of the material by some micro scale quantities, typically including void nucleation, growth, shearing and coalescence, for example, the Gurson–Tvergaard–Needleman–Xue model (Xue 2006, 2008). Micromechanical models usually require a large number of material parameters whose calibration is not trivial. On the other hand, macroscopic approaches avoid the overburdens of the details of microstructures and their interaction and, rather, aim at the overall measurable change of the mechanical response of the damaged material. In comparison of the two, the microscopic approach is a long shot due to the added difficulties to quantify the intermediate micro quantities and, furthermore, the modeling of the interactions between micro scale entities are still vague. On the contrary, the macroscopic approach is more straightforward—the reduction of ductility and the strength are quantified explicitly.
Ductile plates often fail in one of these two competing modes. In order to capture the pressure dependence and the Lode angle (or J3) dependence of the ductile fracture, the underlying damage accumulation of the two competing modes have to be properly modeled. It has become clear that the conventional I1-J2 models is inadequate in capturing three dimensional fracture patterns. Only recently, with the introduction of I1-J2-J3 models, the capturing of the damage evolution in three dimensional loadings became possible (Xue 2007, 2009; Xue and Wierzbicki 2009).
1.2.2 Fracture prediction with damage plasticity mode
The fracture strain envelope for ductile materials is usually non-linear. For instance, damage plasticity model proposed by Xue (2007) requires four parameters to depict the three-dimensional surface. Xue (2009) proposed a simplified Tresca type of fracture envelope in the stress space and developed an empirical relationship between the size of fracture envelope and the slope of pressure dependence by analyzing the Bridgman’s experimental data. Using a Swift relationship to fit the matrix material stress–strain curve, the Xue (2009) model can be described by the following set of expressions:
where \(p\) is the pressure and \(\theta _\mathrm{L}\) is the Lode angle of the current stress state. \(\sigma _\mathrm{y0}, \varepsilon _{0} \) and \(n\) are three Swift parameters to describe the relationship the matrix stress \(\sigma _\mathrm{M}\) and plastic strain \(\varepsilon _\mathrm{p}\). They were fit from the simple tension test results. \(\varepsilon _\mathrm{f} \) describes the fracture stress envelope by two parameters—a reference fracture stress \(\sigma _\mathrm{f0} \) (or equivalently a reference fracture strain \(\varepsilon _\mathrm{f0} =\varepsilon _0 \left[ {\left( {\frac{\sigma _{\mathrm{f0}} }{\sigma _{\mathrm{y0}} }} \right) ^{1/n}-1} \right] )\) and a pressure sensitivity parameter \(k_\mathrm{p}\). The two fracture stress envelope parameters can be related by an empirical expression given by Eq. (28) in Xue (2009), which is \(k_\mathrm{p} =\frac{n}{\sigma _{\mathrm{y0}} \varepsilon _{\mathrm{f0}} }\). And \(D\) is the damage which describes the deterioration of the material. From early studies, the two exponent parameters describing the damage accumulations and weakening, i.e. \(m\) and \(\beta \) are about 2.0 for many metals, which are adopted in the present case.
1.2.3 Calibration of material parameters
The simple tension coupon test by Sandia National Lab was first simulated using the Xue (2009) model. From the stress–strain curve given, it is clear that this stainless steel is less ductile than DH-36. The calibrated \(\varepsilon _{\mathrm{f0}} \) for DH-36 is about 2.5 (Xue et al. 2010a). Hence, the search for the reference fracture strain \(\varepsilon _{\mathrm{f0}} \) is narrowed down to below 2.5, i.e. to the left hand side of DH-36 on the log-log plot of the pressure sensitivity and the fracture strain (Fig. 24a). After several numerical tests, the \(\varepsilon _{\mathrm{f0}} \) value appears to be around 2.0. The plastic strain at fracture and the load-displacement curve is shown in Fig. 24b, c.
Numerical calibration of material parameters using the tensile coupon test. a search range of reference fracture strain \(\varepsilon _{\mathrm{f0}} \), b strain contours of test coupon after break; c the experimental (blue solid-line) and numerical (red dot line) results of the load-displacement curves
1.2.4 Simulation results with damage plasticity model
Eight-node brick elements with one-point integration are used in the simulation. Twenty element are used through the thickness and the in-plane element size is about the same as in the thickness direction in the area of interest. With the calibrated material parameter \(\varepsilon _{\mathrm{f0}} =2.0\), simulation of the three hole specimen is carried out. The predicted crack path is A–D–C–E as shown in Fig. 25a, which is observed in most physical experiments as reported by the Sandia team. The predicted modes of all the three segments of the crack path agrees with experiments: (a) both show in-plane mode II shear in A–D segment; (b) both show in-plane mode II shear in D–C segment; (c) both show out-of-plane mixed I/III shear mode or a “V” shaped double shear lip for C–E segment. The load-displacement prediction also matches experimental results very well except the plateau before final load drop is a little short.
Further parametric study reveals that the two competing modes: A–C–E and A–D–C–E are indeed very close to each other, although A–C–D–E appears to be the dominant mode. With little increase in the fracture strain, the A–D–C–E model can change to A–C–E mode. Not much change in the critical forces at the initiation of the first segment and the second segment of fracture is observed, but the initial CTOD increased by a third when the reference fracture strain of the material is increased from 2.0 to 2.2. Five strains (\(\varepsilon _{\mathrm{f0}} =2.0, 2.1, 2.2, 2.3\) and 2.5) were adopted in the simulation and their respective results are plotted in Fig. 25b. The two thick blue lines are the load-displacement curves for \(\varepsilon _{\mathrm{f0}} =2.0\) and 2.1, which show A–D–C–E paths. With increased fracture strains \(\varepsilon _{\mathrm{f0}} =2.2, 2.3\) or 2.5, the fracture path changes to A–C–E and their load-displacement curves are shown in thick red lines.
1.2.5 Conclusions
In this double-blind study, the damage-plasticity model with stress-based fracture envelop (Xue 2009) is used in the prediction. The fracture path and the overall load-displacement features are predicted very well. Moreover, it is the simplest possible method with only one parameter to calibrate besides the true stress–strain curve. This is mainly attributed to two aspects of the model: (a) the I1-J2-J3 nature of ductile fracture is correctly characterized by this simple model; (b) the empirical relationship eliminates the cumbersome of material calibration for multiple parameters and provides a quick assessment with reasonable accuracy to characterize the mechanical behavior of the material. These advantages are demonstrated by numerical results of the crack propagation in the three-hole specimen.
1.3 Team 3
Team Members: A. J. Gross, A. Ghahremaninezhad and K. Ravi-Chandar; The University of Texas
In some recent work we have identified that, for a class of ductile materials, plastic deformation proceeds without intervening damage until very large strain levels; this is confirmed through observations and measurements of deformation at multiple scales, from the macroscopic to the level of the grains (Ghahremaninezhad and Ravi-Chandar 2012, 2013; Haltom et al. 2013). The upshot of these investigations is twofold: first, it is essential that the plastic response of the material be calibrated to much larger strain levels than is usually achieved in a standard tensile test. Second, the mechanisms of final failure—void nucleation, growth and coalescence—occur within a highly localized zone in the plastically deformed material, and only at the very end of the material’s ability to withstand deformation. Thus, final failure may be implemented numerically by a simple damage criterion such as element deletion. However, it is necessary to perform a careful evaluation of the plastic strain levels at which damage may initiate under multiaxial loading. We have adopted this approach in formulating the simulation of the challenge problem.
The plastic constitutive properties of 15-5 PH stainless steel in the H1075 condition are modeled by the flow theory of plasticity with isotropic hardening. The slight anisotropy in yield observed from tensile tests in the longitudinal and transverse directions of the sheet is included with Hill’s 1948 yield criterion; in the absence of data corresponding to the thickness direction, normal anisotropy is assumed. It is evident that uniaxial tensile test results cannot be used to determine the stress–strain behavior beyond a logarithmic strain of \(\sim \)6 % because of the inhomogeneity of the deformation that occurs beyond the Considère strain. Therefore, we proceed as follows: the material behavior is assumed to be well-described by a general power law model: \(\sigma =C_1 +C_2 \left( {C_3 +\varepsilon ^{p}} \right) ^{C_4}\). The coefficients of the power law are then found through iterative finite element simulations of the tensile test with different trial coefficients and a nonlinear optimization scheme to minimize the squared-error between the net load in the experiment and each simulation. The final result is an accurate simulation of the tensile specimen’s global response, and an estimate of the stress–strain behavior determined far beyond the Considère strain.
Damage of the material is modeled by a modified version of the Johnson-Cook failure model: \(\varepsilon _f =D_1 +D_2 \exp \left( {D_3 \sigma ^{*}} \right) \), where \(\sigma ^{*}\) is the stress triaxiality. When an element in the FEM simulations meets the above damage initiation criterion, as implemented through the cumulative damage approach within ABAQUS, its stiffness is set to zero. The three coefficients of this model need to be calibrated but only two restrictions can be placed on the coefficients from the experimental results. The first is obtained from the tensile test simulation and the nominal strain at rupture from the experiments, providing an estimate of the failure strain at moderate triaxiality. The second is obtained from matching the global load-displacement response of the compact tension specimen test, providing an estimate of the failure strain at high triaxiality. A mesh size of 31.75 \(\upmu \)m was used in this simulation in regions where failure occurs; this dimension was maintained in the challenge simulation. One degree of freedom is left unconstrained in the failure model with no experimental result available for calibration. An approximation is made for failure at low triaxialities based on prior knowledge of other materials to complete the model (see companion article by Gross and Ravi-Chandar in this special issue) for details of calibration of this failure model).
The challenge geometry is simulated with an ABAQUS/Explicit FEM model. Mass scaling is used to increase the stable time step to make a quasi-static simulation feasible on a desktop computer. A uniform and highly refined mesh is used in the vicinity of the holes \(A\)–\(B\)–\(C\)–\(D\) in regions of anticipated strain localization. The smallest mesh dimension was about 31.75 \(\upmu \hbox {m}\), providing a high spatial resolution in the simulation. Eight-noded linear elements with reduced integration and hourglass control were used. A total of 2.25 million elements with seven million degrees of freedom were used; computations were performed in a Linux machine utilizing seven cores and typically required about 280 h of CPU time. Loading is applied by prescribing a zero displacement at the bottom loading pin and a quadratic displacement rate at the top loading pin location. The results are shown in Fig. 26, where the load-COD variation is shown along with selected deformed shapes. Initially, the equivalent plastic strain accumulates rapidly in the ligament \(A\)–\(D\), up to a magnitude of 0.4. Strain accumulation halts in ligament \(A\)–\(D\) when the limit load of 8.6 kN (1935 lbf) is reached, at a crack opening displacement (COD) of 2.33 mm (0.092 in). Thereafter localization occurs in the ligament \(A\)–\(C\), thus leading to its eventual failure. The failure of this ligament occurs over a small increase of COD in the simulation, raising the possibility of a dynamic event in the experiment. Due to the artificially increased mass, the simulation cannot capture dynamic events correctly. Therefore, this simulation does not provide a confident prediction just after the fracture of ligament \(A\)–\(C\) begins. The integrity of the simulation resumes shortly thereafter (at a COD increment of 263 \(\upmu \)m (0.0104 in) after first initiation), and shows a nearly constant load maintained over a large range of COD. On this load plateau, deformation is localizing on the surface of hole \(C\), in the large ligament \(C\)–\(E\). The final fracture is then initiated just off the surface of hole \(C\) and is accompanied by a rapid drop in load. With continued loading, the crack propagates towards the back edge of the specimen until the simulation is stopped. Therefore, the crack is predicted to propagate on path \(A\)–\(C\)–\(E\). The expected load and COD for first initiation were reported just prior to first element failure on ligament \(A\)–\(C\). This was chosen instead of the 100 \(\upmu \)m surface crack criterion, which was used as the lower bound, because failure of ligament \(A\)–\(C\)–\(E\) was predicted to be dynamic. It was assumed that the experimental setup would be incapable of tracking fast crack growth. The expected load and COD for second initiation was reported just before a surface crack 100 \(\upmu \)m in length was visible in the simulation. The upper bounds for second initiation were reported prior to first element failure on ligament \(C\)–\(E\).
Overall, the prediction from this modeling effort has very good agreement with the experimental results for specimen D1 which followed the crack path \(A\)–\(C\)–\(E\). Specifically, the following quantities show excellent agreement between the simulation and experiment: the load-COD variation prior to the onset of localization, the limit load, plateau load beyond failure of the ligament \(A\)–\(C\), and the rate at which load drops after both failures are initiated. The COD of second initiation is the weakest part of the prediction. We attribute this shortcoming to the fact that the triaxiality at the initiation site is much lower than any experimental result used to calibrate the failure model and consequently falling outside the region where the failure model is best matched to the material. The other issue for discussion is the predominant development of the fracture path \(A\)–\(D\)–\(C\)–\(E\) in the experiments. Additional experiments were performed on specimens provided by Sandia from the same stock as the challenge samples. The results from these and additional simulations, demonstrating that the same material model can be used to predict both experimentally observed crack paths by including proper geometric defects, are reported in another article (see Gross and Ravi-Chandar 2013).
1.4 Team 4
Team Members: S. P. Lin \(^{1}\), S.W. Chi \(^{2}\), J. S. Chen \(^{1}\), E. Yreux \(^{1}\), M. R \(\ddot{u}\) ter \(^{1}\); 1: Civil and Environmental Engineering Department University of California, Los Angeles (UCLA); 2: Civil and Materials Engineering Department University of Illinois at Chicago
1.4.1 Approach
We introduce a Reproducing Kernel Particle Method (RKPM) (Liu et al. 1995; Chen et al. 1996) with crack surface-tip discontinuity enrichment (Moes et al. 1999; Krysl and Belytschko 1997) for fracture mechanics based numerical simulation of the fracture challenge problem. Under this framework, the approximation of the displacement field is constructed as follows:
where \(\Psi _I \left( \mathbf{x} \right) \) is the reproducing kernel shape function of degree one, \(H_i \left( \mathbf{x} \right) \) and \(f_i \left( \mathbf{x} \right) \) are the Heaviside functions and the crack-tip visibility based discontinuous functions, respectively (Krysl and Belytschko 1997), \(N_{cut}\) are the enriched nodes with the crack surface cutting through their supports, \(N_{tip }\) are the near-tip enriched nodes, \(\mathbf{d}_I, \mathbf{a}_J \) and \(\mathbf{b}_K \) are the nodal coefficients, and \(N\) is the total node set. The enrichment functions are designed such that the enriched shape functions preserve the partition-of-unity property: \(H_1 \left( \mathbf{x} \right) +H_2 \left( \mathbf{x} \right) =1, f_1 \left( \mathbf{x} \right) +f_2 \left( \mathbf{x} \right) =1\). Since the partition of unity property is preserved, the nodal masses remain constant while other generalized enrichment schemes result in inconsistent nodal masses (the enriched nodes may have different units from non-enriched nodes and the nodal masses change as the crack propagates). As the discretization changes along with crack propagation, new bases for the approximation fields will be introduced. The coefficients of the new bases can be easily determined by imposing the conservation laws of linear momentum and kinetic energy on the enriched nodes. Consequently, the computational complexity can be reduced. The material under consideration is modeled by J2 elastoplasticity with the following hardening rule:
where \(H\) and \(K\) are the kinematic and isotropic hardening parameters, respectively, \(\bar{{e}}^{p}\) is the effective plastic strain, and \(Y\) is the yield stress.
1.4.2 Calibration of material model and failure parameters
From the tensile failure experimental data provided by Sandia shown in Fig. 27, the nominal stress–strain curve exhibits a noticeable change in slope after 0.08 nominal strain (point A) and ruptures at nominal strain of 0.16 (point B). The change in slope in Fig. 27 is primarily caused by the necking effect (see the numerical simulation in the inset of Fig. 27) and the evolution in the material hardening. We used the tensile test data to characterize the yield stress \(Y=0.99~\hbox {GPa}\) and the hardening parameters \(\alpha =8.6\) and \(\beta =122\). We assumed that the tensile failure is the dominant mode in the fracture challenge problem and adopted the maximum principle tensile strain \(\varepsilon _{cr} \) as the crack initiation and propagation criterion. We further assumed that the micro-cracks could initiate anywhere in the softening region up to the rupture point in Fig. 27 (from A to B). To determine the appropriate crack initiation threshold strain value, several local maximum principal tensile strains in the softening region (from A to B in Fig. 27) in the numerical tensile tests, corresponding to values from 0.246 and 1.106, respectively, were selected to study their effects on the predicted load-displacement behavior. In the transient crack propagation simulation, the crack propagation speed plays an important role and typically can be estimated by J-integral-based empirical laws in linear elastic fracture mechanics (Freund 1972). However, due to the strong ductility and the local irregularity of the geometry due to existence of holes in the specimen, it is difficult to perform the J-integral without interference from the three holes near the notch. Therefore, we numerically estimated the crack propagation speed through modeling the fracture toughness test as shown in Fig. 28, along with the guideline from an analytical and empirical investigation (Freund 1972, 1979) which identified that in the case of non-branching crack propagations, the crack propagation speed is much lower than the Rayleigh wave (RW) speed. The results suggest that by prescribing the crack propagation speed as 0.02 % of the Rayleigh wave speed, it yields the best agreement with the experimental data.
1.4.3 Modeling fracture challenge problem
A Lagrangian reproducing kernel formulation (Chen et al. 1996) with extrinsic enrichment scheme described in Eq. (6) was employed to model the fracture challenge problem. The RKPM discretization contained a total of 94,176 particles where 4 particles were used in the thickness direction. The mean nodal distance near the fracture zone is 0.2 mm, which is consistent with that being used in the fracture toughness modeling. As reported in the main body of this article, the blind predictions were not in good agreement with the experimental observations. This was due to the underestimation of the crack initiation threshold strain where a nominal strain 0.08 at the beginning of the softening region was chosen in the blind test, in addition to an inconsistent employment of nominal strain measure in experimental data and the local maximum principal tensile strain measure for \(\varepsilon _{cr} \) used in computation, causing premature crack formation. In the post-blind tests, it is assumed that the micro-cracks could initiate anywhere in the softening region up to the rupture point in Fig. 27 as discussed above in Sect. 8.4.2, and the numerical results associated with various \(\varepsilon _{cr} \) values within the softening region are compared with experimental load-COD curves as shown in Fig. 29a. For \(\varepsilon _{cr}\) less than 0.423, the crack path A–D–C–E as shown in Fig. 29b agrees well with the experimental observation. Three crack initiation points marked as A–D, C–D, and C–E in Fig. 29a are associated with crack paths from A to D, from C to D, and from C to E, respectively. As \(\varepsilon _{cr}\) becomes larger than 0.462, the crack path of A–C–E is observed as shown in Fig. 29, and this pattern of crack propagation has also been observed in the experiment.
1.4.4 Conclusions and remarks
The high sensitivity of crack initiation strains on the crack path and the corresponding Force-COD behavior as shown in the numerical experiment in Fig. 29 call for a multiscale verification and validation effort to identify crack initiation characteristics for enhanced reliability in the simulation of material defects and failures.
1.5 Team 5
Team members: D. Qian \(^{1}\), Z. Zhou \(^{1}\), S. Bhamare \(^{2}\); 1: University of Texas at Dallas; 2: University of Cincinnati
1.5.1 Simulation methodology
We have employed the commercial FEM code LS-DYNA incorporating the Gurson–Tvergaard–Needleman (GTN) model (Gurson 1977; Tvergaard and Needleman 1984) for the Sandia Fracture Challenge problem. Both geometric and material nonlinearities are considered in the simulation approach.
1.5.2 Material model
The GTN model takes into account the important link between macro- and micro-scale evolutions of damage. In GTN model, the yield condition is given by
in which \(\sigma _{eq} \) is the von Mises equivalent stress, \(\sigma _Y \)is the yield stress, \(q_1 \) and \(q_2 \) are material parameters for modeling low void volume fractions, \(\sigma _m \) is the mean stress. Here \(f^{*}(f)\) is a function of the void volume fraction \(f\) and represents the modified damage parameter, given as
\(f_F \) is the final void volume fraction at failure and \(f_c \) is critical void volume fraction corresponding to void coalescence.
1.5.3 Failure initiation and growth criteria
Material failure occurs when the void volume fraction \(f\) exceeds \(f_F \). The evolution of \(f\) consists of two contributions: void nucleation and growth which are given as
where the void nucleation depends exclusively on effective plastic strain \(\varepsilon _{eq}^p \), while the void growth is controlled by plastic volume strain \(\varepsilon _{kk}^p \). \(S_{N}, E_{N}\) and \(f_{N}\) are parameters for the Gaussian distribution that is assumed for the void nucleation rate.
1.5.4 Calibration of material model and failure parameters
In our simulations, the yield stress \(\sigma _Y \) in Eq. (8) as a function of plastic strain is obtained from the uniaxial tension test data provided by the experimental group. The initial GTN model parameters of steels are based on refs (Bauvineau et al. 1996; Decamp et al. 1997; Siegmund et al. 1998; Schmitt et al. 1997; Skallerud and Zhang 1997; Benseddiq and Imad 2008). \(q_{1}=1.5, q_{2}=1, E_{N}=0.3, S_{N}=0.1, f_{0}\approx 0\) and \(f_{F}\approx 0.2\) are the standard material parameters for steel. \(f_{N}\) is in the range of 0.002-0.02, and \(f_{c}\) is in the range of 0.004-0.06. Initial simulation indicates that the most sensitive parameters for crack initiation and propagation are \(f_{N}\) and \(f_{c}\), in which \(f_{N }\)controls the nucleation rate, while \(f_{c}\) is the critical value of void coalescence.
We first calibrate the GTN parameters based on the simulations of uniaxial tension test. From a series of simulations, two sets of parameters are determined as the lower bound (LB) and upper bound (UB), which are employed in the subsequent simulations. The LB parameter set (\(f_{N} =0.002, f_{c}=0.004\)) predicts faster void nucleation and propagation rates, while the UB (\(f_{N} =0.002, f_{c}=0.008\)) gives slower rates. The stress–strain response of uniaxial tension from simulations and experiments are plotted in Fig. 30a, in which UB yields better fit to experimental data on uniaxial tension. Another source for calibrating the material model is the fracture toughness test data, as shown in Fig. 30b. It can be seen that the agreement between the simulated force-COD curves and the experimental data is not as good as in the case of uniaxial tension. Based on the assumption that less uncertainty is involved in designing the uniaxial tension experiment, no further adjustment was made to the calibrated parameter sets.
1.5.5 Modeling details for the fracture challenge specimen
The FEM model for the fracture challenge problem is shown in Fig. 31a. The model is set up based on the standard drawing of the specimen without considering any variations in the actual geometry. The FEM discretization contains 171,825 8-noded brick elements and 190,528 nodes, and the characteristic element size in the critical region near the notch tip is \(0.05\,\hbox {mm}\times 0.05\,\hbox {mm}\times 0.21\,\hbox {mm}\). The loading pins are directly modeled through contact algorithm. The bottom pin is fixed and the top pin is displaced vertically at 0.0127 mm/s. Frictionless contacts are assumed between the pins and the sample. Dynamic simulation with a mass scaling time step of 0.001s is performed, and element deletion is used to simulate the crack propagation, once the void volume fraction reaches \(f_{F}\).
1.5.6 Predictions of the fracture challenge specimen
The typical A–C–E crack path from simulations is illustrated in Fig. 31b, and the force-COD responses are compared in Fig. 31c. From the simulation, we find that crack always nucleates in the subsurface and propagates to the inner surface of the holes in seconds. By averaging the results based on UB and LB parameters, several critical force and COD values are obtained. The force associated with first visible crack is 7,380 N (1659 lbf) compared to measurement of 5,996–7,469 N (1348–1679 lbf), and the corresponding COD is 4.7 mm (0.185 inch) compared to measurement of 2.235–3.480 mm (0.088–0.137 inch). The force associated with second visible crack is 5,725 N (1287 lbf).
1.5.7 Comments on methods and results
The force values obtained from simulations are in good agreement with experimental data. However, the COD values show a large discrepancy. In addition, majority of the experiments yield the crack path of A–D–C–E as opposed to A–C–E. These disagreements are thought to be caused by two important factors: First of all, the GTN parameter sets calibrated based on tensile test underestimate the void nucleation/growth rates, as evidenced by the comparison with the compact tension test data. This is further confirmed by the observation that the crack path will switch from A–C–E to A–D–C–E with reduced COD values if the GTN parameters are adjusted to give faster void nucleation and propagation rates. Secondly, the crack path is observed to be quite sensitive to the geometric variations that are not considered in the simulation. Additional simulations indicate that a switch from A–C–E to A–D–C–E can take place if hole D is moved towards notch A along the line of centers connecting notch A and hole D. Details on these studies will be described in a separate paper.
1.6 Team 6
Team Members: D. T. O’Connor \(^{1}\), S. Tang \(^{2}\), K. I. Elkhodary \(^{3}\), J. Zhao \(^{1}\); 1: Department of Mechanical Engineering, Northwestern University, Evanston, IL.; 2: Materials Science and Engineering, Chongqing University; 3: Department of Mechanical Engineering, The American University in Cairo.
1.6.1 Approach
For this challenge we employed the Multiresolution Continuum Theory (Vernerey et al. 2007; McVeigh and Liu 2010), which assumes N embedded length scales, to be able to model the multiple scale fracture behavior of the Sandia Fracture Challenge compact tension specimens. In this case, two scales are assumed to account for the ductile behavior at the coarse scale and micro-void formation at the micron-scale.
1.6.2 Simulation methodology
In the Multiresolution Continuum Theory (MCT) a rate formulation for multiscale microstructural mechanics is assumed. Linear superposition of multiple deformation rates, which evolve due to \(N\) imbedded microstructural length scales, is considered. Micro-stress and micro-double-stress are introduced for each imbedded scale to penalize resulting inhomogeneity of deformation. The corresponding internal power density is,
where \({\varvec{\sigma }}_0 \) is the Cauchy stress conjugate to a coarse-scale velocity gradient \(\mathbf{L} _0 \) and \(\mathbf{L}_n \) is the \(\hbox {n}^\mathrm{th}\) inhomogeneous deformation rate evolving in a sub-volume \(V_n \) of a material point \(V_0 \), i.e. \(V_n\subset V_{0}\), due to a micro-mechanism of the \(\hbox {n}^{\mathrm{th}}\) length scale. Conjugate penalty stresses are defined by volume averages,
where \({\varvec{\sigma }} _p^n \) is a penalty stress and \(\mathbf{y}_n \) is a local position vector. To solve for \(\mathbf{s}_n \) and \(\mathbf{ss}_n \) an additive elastic-plastic decomposition of the deformation rate \(\mathbf{D}_n \) and its gradient \({\varvec{\nabla }} \mathbf{D}_n \) is assumed,
The corresponding objective stress rate and double stress rate may be computed from the elastic part of the rate of deformation using a generalized Hooke’s law such that,
where \(\mathbf{C}_n \) is the elasticity tensor characterizing the properties of the microstructure of the \(n^\mathrm{th}\) sub-volume, and \(\mathbf{CC}_n \) is a sixth-order elastic tensor, typically computed from
To compute the objective stress rate of Eq. (16), it is required to calculate the plastic deformation rate \(\mathbf{D}_n^p \) and its gradient \({\varvec{\nabla }} \mathbf{D}_n^p \), which will be subtracted from the total rate according to Eq. (15). Typically, plastic potentials\(\phi _n,\phi \phi _n\) and an associative flow rule is used,
where \(\lambda \) is a plastic multiplier. The yield surfaces \(\phi _n \) and \(\phi \phi _n \) are of a pre-defined form so that only parameter-fitting from RVE results are needed (McVeigh and Liu 2008).
In this paper, two scales are assumed: coarse-scale ductile behavior and an imbedded micron-scale to account for micro-voiding. For the coarse scale, a Gurson-type yield surface is used,
where \(\sigma _{eq} \) is the von Mises stress, \(\bar{{\sigma }}\) is the flow stress, which evolves according to the power law \(\overline{\varvec{\sigma }} \,{=}\,{\varvec{\sigma }} _{y_0 } \left( {1+\varepsilon ^{p}\varepsilon _0^{-1} } \right) ^{n}\), where \({\varvec{\sigma }} _{y_0 } \) is the yielding stress, \(\varepsilon ^{p}\) is the equivalent plastic strain, and \(\varepsilon _0 \) the yielding strain. Continuing from Eq. (19), \(\sigma _m \) is the mean stress, and \(q_1 \), and \(q_2\) are constants. The void volume fraction,\(f\), evolves by \(\dot{f}=(1-f)D_{kk}^p +k_\omega fw(\sigma )S_{ij} D_{ij} ^{p}(\sigma ^{e})^{-1}\), where \(w(\sigma )=1-\left( {27J_3 (2\sigma _e ^{3})^{-1}} \right) ^{2}, S\) is the deviatoric stress, and \(k_\omega \) is a constant. For the imbedded micron-scale behavior, which results from micro-void interactions, the potentials for plastic and gradient-plastic mechanisms are coupled, and a single surface is used,
Equation (20) is a modified Fleck–Hutchinson model (Fleck and Hutchinson 1993), where \(a\) is a fitting parameter, \(l\) is the length scale of inhomogeneous deformation between micro-voids, and \(\sigma _y^H \) is the strength by which a material resists the onset of inhomogeneous deformation.
1.6.3 Modeling details for the challenge specimen
Before any full-scale analysis could be performed the appropriate parameters for the constitutive models (Modified Gurson and Fleck–Hutchinson) needed to be determined. This was done utilizing the data provided by the Sandia Fracture Challenge team at Sandia National Labs that included the material properties (AK Steel 15-5 PH H1075), tensile specimen geometry, and tensile test stress–strain data. The values for the parameters in the constitutive model that were found to best represent the tensile test stress–strain curve through failure can be seen in Table 7.
With the calculated parameters for the constitutive models found, the larger compact tension specimen was simulated next. First, using the geometry provided by the Sandia Fracture Challenge team, the compact tension specimen was meshed with approximately 140,000 elements and the results are seen in Fig. 32. The MCT simulation was performed using an LSDYNA user-element, with 8 nodes, full integration, and 6 extra degrees of freedom for the micro-deformation rate. During the simulation the bottom hole was held fixed while the top hole was pulled at a velocity of 2 m/s. The result of the simulation can be seen in Fig. 33, which shows a contour plot of equivalent plastic strain.
1.6.4 Blind predictions of the fracture challenge specimen
We found that the crack travels along the path A–D–C–E as labeled in Fig. 33, which corresponds to the crack path observed during the experiment. Subsequently, we also measured the force and crack opening displacement (COD). The force for the force-COD curve during the simulation was calculated by measuring the internal forces around the surface of the top hole.
Although the peak value for force in our simulation was off, the simulation results for the force when fracture initiates compared well with experiment but the subsequent behavior after initial fracture did not compare very well. We found that when we compared with the experiment of specimen 2, as seen in Fig. 34, at the onset of fracture our measured force of 9,190 N was 11 % higher and our measured COD of 1.11 mm was 43 % lower than the experimental values.
1.6.5 Comments on methods and results
The method used here, Multiresolution Continuum Theory, which is based on power equivalence, was capable of a good prediction of the force at initial fracture. The maximum force, however, was over-predicted, while strain was correspondingly under-predicted, especially during the crack propagation phase along path D–C–E. As a result, the predicted area under the force-displacement curve (toughness) is comparable to experiment for the crack initiation phase. Discrepancies in the initial loading portion of the curve, and the over-prediction of the maximum force, may be attributed to the fast loading rate. The loading rate used here was much faster than the quasi-static rate of the experiments and future work will include investigation into quasi-static models in an attempt to better match the experimental results. We are currently working on better constitutive modeling approaches to overcome the difficulty in load/displacement ratios. Furthermore, as element deletion was used in this model, it is expected that the thickness of the elements deleted was too coarse to yield convergent predictions and that their removal may have created stress concentration sites that diminished the strain at failure. Further study of crack-surface generation methods, e.g. XFEM, will thus be explored.
1.7 Team 7
Team Members: J. Hochhalter \(^{1}\), A. Cerrone \(^{2}\), A. R. Ingraffea \(^{2}\), P. Wawrzynek \(^{2}\), B. Carter \(^{2}\), J. Emery \(^{3}\), M. Veilleux \(^{3}\); 1: NASA LaRC; 2: Cornell University; 3: Sandia National Laboratories, Albuquerque, NM.
1.7.1 Approaches
Porous metal plasticity
A void-growth plasticity model (Gurson 1977) was used to model both the bulk behavior of the specimen as well as failure. In this model, the elastic response is restricted to the linear elastic isotropic condition while hardening is isotropic with a yield condition given by Tvergaard (1981). Damage is the product of void coalescence; when a critical void fraction has been met at a material point, it loses all capacity to carry stress.
Cohesive zone modeling
In a second approach, a potential-based cohesive-zone model was employed to model fracture in the challenge specimen. The PPR cohesive model (Park et al. 2009) was chosen as it gives the user relative freedom in defining the shape of the normal and tangential traction-separation laws; the PPR model accepts different cohesive strengths, fracture energies, and softening behaviors for each. It was assigned to a single layer of cohesive elements spanning the A–C–E crack path, an intrinsic approach in which the crack path is enforced a priori by the user.
Geometrically explicit, elasto-plastic crack growth
In a third approach, FRANC3D was coupled with Abaqus/Standard to grow a geometrically explicit crack in the elasto-plastic challenge specimen. Crack initiation was determined from the porous metal plasticity model, and the COD growth criterion was calibrated from the provided experimental data. The 3D crack evolved based on the maximum tensile stress criterion. The procedure is summarized below:
-
1.
Load the uncracked model until a 100 \(\upmu \hbox {m}\)-sized element was completely damaged at the notch root.
-
2.
Insert an initial crack in the location of the damaged element and remesh.
-
3.
Map the state-dependent variables from the uncracked configuration to the cracked configuration.
-
4.
Reapply load to the cracked model until the critical COD is reached.
-
5.
Grow the crack and remesh.
-
6.
Map the state-dependent variables from the previous cracked configuration to the new cracked configuration.
-
7.
Repeat steps 4-6 until failure.
1.7.2 Material parameters
Parameters for the porous metal plasticity (damage) modeling approach were first calibrated using the provided tensile-experiment data. The tensile specimen geometry model was generated in Abaqus/CAE, meshed with 200 \(\upmu \hbox {m}\)-sized tetrahedral elements, and simulated using Abaqus/Explicit (explicit solver) as it more accurately captured the softening stage of the material response near failure than did Abaqus/Standard (implicit solver). The calibration of the material parameters was separated into two stages. In the first stage, several sets of material parameters were identified that reproduced the measured stress–strain behavior of the material. The sets of material parameters that most accurately reproduced the reduction in cross-sectional area observed during the tensile test were kept. In the second stage, the fracture toughness specimen geometry model was generated, meshed, and simulated using the same tools and mesh size as with the tensile specimens. The set of material parameters that best reproduced the measured force versus opening were then used to model the fracture challenge specimen. In a similar manner, the parameters for the cohesive model were also calibrated from the given fracture toughness test data. Lastly, the critical COD parameters were also calibrated using the measured fracture toughness data. In this case, it was observed that a rising COD versus crack length was necessary to accurately reproduce the observed behavior.
1.7.3 Mesh refinement/sensitivity
Most of the efforts to model the fracture challenge specimen were spent on the porous metal plasticity approach since it appeared to provide the most promising results in the short amount of time provided. Since the material parameters were calibrated using a 200 \(\upmu \)m-sized tetrahedral elements, the same mesh characteristics were used near the notch root of the fracture challenge specimen model. The simulated crack path was found to be mesh-sensitive; depending on the mesh refinement level beyond the notch, the predicted crack path was either A–D–C–E or A–C–E, Fig. 35. In each case shown in Fig. 35, the element size along the notch is the same, but the coarsening away from the notch is much higher in the case on the right, and this was enough to cause a change in the predicted crack path. In general, it was observed that as the model became populated entirely with 200 \(\upmu \)m-sized elements, the predicted path was consistently A–C–E.
1.7.4 Blind predictions
The porous metal plasticity simulations of the challenge specimen fracture were run with Abaqus/Explicit. The porous metal plasticity model reproduced accurately the peak load carrying capacity of the specimen and the opening at which it occurred and qualitatively reproduced experimental load versus COD. However, it failed to capture the sharp drops in load-bearing capacity observed during the experiment and illustrated in Fig. 36. It is also noteworthy that for the “to spec” geometry, the model predicted A–C–E crack growth, which is consistent with the only experimental “to spec” crack path. Moreover, for the S5 geometry, a configuration exhibiting the largest deviations from spec, the porous metal plasticity model predicted A–D–C–E crack growth, which is consistent for all of the experimental “not to spec” crack paths.
With regards to the cohesive zone effort, simulations were conducted in Abaqus/Standard. The bulk material was assigned an elasto-plastic model with a user-defined hardening law. The PPR was exposed in a 12-noded triangular UEL. As with the void-growth plasticity model, the sharp drops in load-bearing capacity were not captured by the cohesive zone model, Fig. 36. Both approaches’ shortcomings motivate the need to model cracks in the specimen explicitly.
Load versus COD for geometrically explicit elasto-plastic crack growth is given in Fig. 36. It is noted that this approach is able to capture the aforementioned sharp drop in load-bearing capacity; however, these simulations are preliminary in that the critical COD was scaled back to prevent large amounts of crack tip blunting, which caused poor element quality upon remeshing. On-going simulations with mesh smoothing should provide more accurate predictions.
1.8 Team 8
Team Members: P. Yang \(^{1}\), Y. Gan \(^{2}\), X. Zhang \(^{1}\), Z. Chen \(^{3,4}\); 1: Department of Engineering Mechanics, Tsinghua University, Beijing 100084, China; 2: Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, China, 3: Department of Civil and Environmental Engineering, University of Missouri, Columbia, MO 65211, USA; 4: Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024, China
1.8.1 Approach
A combined elastoplasticity and decohesion model is used with the Material Pont Method (MPM) for the Sandia Fracture Challenge 2012 problem. Before the critical strength is reached, von Mises plasticity with a linear hardening rule models the inelastic material behavior. Based on the previous work (Chen 1996; Chen et al. 2005), the computational efficiency of decohesion modeling is improved by prescribing the critical normal and tangential decohesion strengths directly, without performing discontinuous bifurcation analysis in each time step, to predict the post-peak response with a single-processor personal computer. The MPM (Chen et al. 2002; Sulsky et al. 1994) is employed to simulate the three-dimensional evolution of failure from microcracking to macrocracking without the need for remeshing.
1.8.2 Model calibration
Based on the SNL data, Poisson’s ratio of 0.3, elasticity modulus of 195 GPa and yield strength of 1,100 MPa are used for the material model, while the tangent modulus for the von Mises linear hardening rule is determined with the uniaxial tensile test to be 1,150 MPa. Local Mode I failure is considered so that the decohesion model is active if the normal decohesion strength of 3,000 MPa is reached. The linear decohesion relation is adopted with the reference decohesion value of \(2\hbox {x}10^{-7}\) m for the given MPM discretization. Since an explicit time integrator is used in the three-dimensional MPM code, the loading rate of 5 m/s, instead of 0.0127 mm/s as used in the experiment, is chosen to save the computational time for the blind prediction exercise. As compared with the uniaxial tensile test data, the use of the above model parameter values and loading rate yields the reasonable constitutive response, as shown in Fig. 37 below.
1.8.3 Simulation procedure
A direct displacement control is used as the boundary condition with the loading rate of 5 m/s, which results in the oscillation of data due to the wave reflection in the finite specimen domain and to the use of explicit time integration without artificial damping. The MPM with a multi-level grid is adopted for the simulation, with a fine background grid (level 1) being used around the holes and a coarse grid (level 0) away from the holes. The cubic cell size in level 1 and level 0 is 0.25 and 0.50 mm, respectively. The number of material points in each cubic cell is 8 for both levels 1 and 0. The onset and evolution of failure from microcracking to macrocracking are predicted by the constitutive model and failure criterion, and could be simulated with the MPM code without remeshing or element erosion.
1.8.4 Mesh refinement
The MPM background cell size is corresponding to the reference decohesion value, which is related to the characteristic size of decohesion zone. Hence, no convergence study is required (Fig. 38).
1.8.5 Blind predictions
1.8.6 Concluding remarks
Due to the time limit, the constitutive model was calibrated only against the uniaxial tensile test so that the simulated post-peak response with a fixed failure mode is not satisfactory. As reported in the corresponding paper of the special issue, there is a transition between different failure modes along the cracking path, which depends on the stress distribution around the path due to the nonlocal nature of failure evolution. Based on a parametric study and available test data, the proposed model-based simulation procedure could be calibrated, without fixing the local failure mode, to predict the essential feature of the observed cracking response. The numerical oscillation with the explicit code appears to be large as compared with the experimental observation so that the implicit MPM code might be an alternative choice.
1.9 Team 9
Team Members: E. Madenci and B. Kilic; University of Arizona
1.9.1 Simulation methodology
The PeriDynamic (PD) theory was employed to simulate the deformation, crack initiation and crack propagation. The PD theory is concerned with the physics of a material body at a point that interacts with all points within its range. The peridynamic formulation starts with the equation of motion reformulated in integral form as Silling (2000)
in which \(\mathbf{x}\) is the material point within the domain \(\mathfrak {R}, \mathbf{u}\) is the displacement vector field, \(\mathbf{b}\) is a prescribed body-force density field, \(\rho \) is mass density in the reference configuration, \(\mathbf{f}\) is a response function whose value is the force vector per unit volume squared that the material at point \(\mathbf{{x}'}\) exerts on the material at point \(\mathbf{x}\), and \(t\) designates time.
1.9.2 Failure initiation and growth criteria
The bond stretch, \(s\), is defined in terms of relative position \(({\varvec{\upxi }}=\mathbf{x'}-\mathbf{x})\) and relative displacement \(({\varvec{\upeta }} =\mathbf{u'}-\mathbf{u})\) as \(s={\left( {\left| {\varvec{\upxi }}+{\varvec{\upeta }}\right| -\left| {\varvec{\upxi }}\right| } \right) }/{\left| {\varvec{\upxi }}\right| }\). When the stretch between two points exceeds the specified critical (failure) stretch, the interaction between these material points is terminated. The local damage at a point is the ratio of amount of broken interactions to total amount of interactions. The response function, which governs how the material points interact, contains the necessary constitutive information for the material. For an isotropic material, PD response function can be written as
in which \(H(s-s_0 )\) is the Heaviside step function, \(s_0 \) is the critical stretch, \(c\) is given in terms of bulk modulus \(\kappa \) and the horizon radius, \(\delta \) as Silling (2000) \(c=18\kappa /(\pi \delta ^{4})\). The critical stretch value can be obtained through an inverse approach by simulating fracture experiments. The specific form of \(f(s)\) is specified as
The bond stretch rate, \(\dot{s}\), is the time derivative of bond stretch, and \(\nu \) is the viscous damping coefficient.
1.9.3 Material model
The strain hardening behavior in PD theory can be achieved by defining each PD interaction as an elastic-perfectly plastic material (Macek and Silling 2007). Because all interactions do not result in yielding at the same time, the overall behavior of the material exhibits strain hardening. The function, \(g(s)\) in Eq. (23) can be expressed as
where \(s_Y \) represents the yield stretch and \(s^{*}\) represents the permanent stretch as a result of loading and unloading. Therefore, the value of the yield stretch, \(s_Y \) can be obtained by using the stress–strain response of the material in an inverse manner.
1.9.4 Calibration of parameters for material model and failure
With the initial guess for \(s_Y \), the uniaxial tensile test of the material is simulated by computing the applied force and the displacement field; leading to the computation of stress and strain. The simulation (case 1–4) is repeated with a different \(s_Y \) value until it matches with the data. Comparison of simulations to stress–strain relations data is shown in Fig. 39a. In a similar manner, the critical stretch value, \(s_0\) is determined through an inverse approach by simulating the compact tension tests. The simulation is repeated (cases 1–3) with a different \(s_0\) value until it matches with the force—crack opening displacement (COD) data as shown in Fig. 39b.
1.9.5 Modeling the fracture challenge specimen
While the blind predictions reported in the main body of the text did not show good agreement with the experimental results, post-blind analysis was able to better replicate the experiments. After determining the yield stretch, \(s_Y \) and the critical stretch, \(s_0 \), the PD simulation of the challenge problem under the assumption of perfectly aligned grips and with nominal geometric dimensions. The loading is applied through displacement constraints. The specimen was discretized with hexahedron regions with edge length of \(\sim \)0.63 mm based on a preliminary mesh convergence study. Also, adaptive dynamic relaxation technique is employed for time integration. The horizon was specified as 1.5621 mm.
The PD simulation led to the crack growth path of A–C–E, and maximum force of 7,495 N. The PD prediction of the crack growth in the challenge specimen is shown in Fig. 40a. As shown in Fig. 40b, the COD is 1.9 mm at first crack initiation, and the force and COD for subsequent crack initiation from a hole are 5,294 N and 2.85 mm.
1.9.6 Remarks
The PD simulation can be further refined by eliminating the possible sources of error due to discretization (refinement of grid), adaptive dynamic relaxation for time integration, and the plastic deformation model. The effect of geometric parameters and misalignment in loading can also be included, and possibly capture the propagation of path of A–D–C–E.
1.10 Team 10
Team Members: T. Zhang, E. Fang, P. Liu, and J. Lua; Global Engineering and Materials, Inc.
1.10.1 Summary of XSHELL methodology
We have used the XSHELL toolkit developed in-house to predict the fracture pattern and its associated load-deflection curve for the 2012 Sandia Fracture Challenge problem. Given the limitation of the plane stress approximation in the XSHELL modeling approach, a plane strain core approach has been developed to capture the thickness constraint induced stress triaxility and its effect on the ductile fracture in the vicinity of the crack tip. A rational mixture of plane strain and plane stress plasticity model was implemented via a calibration at the coupon level to evaluate the geometry dependent constraint. A mesh independent kinematic description of crack initiation and propagation is accomplished through an elementwise crack insertion with cohesive injection once its accumulative plastic strain reaches a critical value.
XSHELL is an extended finite element based toolkit for Abaqus, which is developed for dynamic failure prediction of a thin walled shell structure. Key solution modules in XSHELL consist of kinematic representation of a cracked shell via its phantom paired elements, crack initiation prediction using a triaxility and Lode angle dependent failure criterion, mesh independent crack insertion through a shell element, cohesive injection for characterization of the energy dissipation during crack growth, and a customized Abaqus CAE for display of the fractured pattern and its associated load displacement curve.
To capture the thickness dependent constraint on the ductile fracture, a plane strain core model was implemented within the XSHELL framework. Considering a plane strain core element with its plane strain portion of \(\alpha \) and the remaining plane stress portion of (1-\(\alpha \)), the resulting internal force (IF) including the change of the thickness associated with the plane stress portion can be determined by
where \(\bar{A}_{e} \) is the in-plane area of the element, B is the strain displacement matrix, \(\alpha \) is the composition of the plane strain portion of the plane strain core element and \(t_i \) is the layer thickness of the \(i\mathrm{th}\) integration point in the through the thickness direction before the deformation. Term \((1+\varepsilon _{33})\) in Eq. (25) is introduced here to account for the thickness shrinkage. \(\sigma _{p-\sigma }\) and \(\sigma _{p-\varepsilon }\) represent the plane stress and plane strain stress components of the corresponding layer in the plane strain core element.
1.10.2 Calibration of material model and failure parameters
To explore the applicability of XSHELL prediction of a 3D structure, a nonlinear stress strain behavior is calibrated first from the experimental force displacement curve of the simple tension coupon tested by Sandia National Lab using XSHELL. As shown in Fig. 41a, material softening behavior cannot be captured fully due to the incapability of XSHELL in characterization of the necking behavior. The load and crack opening displacement (P-COD) curve for the compact specimen with \(a/W\) of 13.82 was used next to determine the geometry dependent plane strain core parameters. The plane strain composition parameter \(\alpha \) and its steady state failure strain (\(\varepsilon _{p})\) were determined together from the best matching of XSHELL prediction with the P-COD curve of the compact specimen as shown in Fig. 41b. The determined \(\alpha \) and the steady state failure strain \(\varepsilon _{p}\) are 0.04 and 0.25, respectively. The plane strain core band width used in the calibration model is set to be twice of the plate thickness. The deviation shown in Fig. 41b is attributed to the blunt notch representation of a sharp crack in the XSHELL simulation model.
1.10.3 Application of XSHELL Model for the 2012 Sandia Fracture Challenge problem
After determination of both the stress strain behavior and the plane strain core parameters, an XSHELL model for the Sandia challenge problem was developed next. Given the location of the notch and holes in the Sandia challenge problem, a user-defined XSHELL zone denoted by the red box in Fig. 42 is used with the plane strain core option invoked. All the elements outside the red box are Abaqus’ shell elements. The resulting total numbers of Abaqus and XSHELL elements are 6354 and 2748, respectively. The loading pin is simulated using Multi-point constraints in Abaqus. In order to capture the crack initiation (crack size \(\ge 0.1\hbox { mm }\)), the element sizes at the critical region are around \(0.06\hbox { mm } \times 0.07\hbox { mm }\).
As shown in Fig. 42, the predicted failure sequence is given by the crack initiation at Point A followed by its growth to Hole D and a new crack initiation at Hole C followed by its growth to Hole D. Finally, a horizontal crack initiated at Hole C is propagated to the edge (Point E) of the specimen resulting in a complete failure. The predicted COD value at the instant of the first crack initiation is smaller than the test value, the simulated load is 7,139 N which is slightly higher than the average value 6,761 N for the occurrence of the first visible crack. A comparison of the fractured pattern and the force-crack opening displacement (COD) curve with the corresponding test data is given in Fig. 43.
1.10.4 Concluding remarks
Based on the exercise of the XSHELL toolkit for the ductile fracture prediction of the Sandia challenge problem, we can draw the following conclusions:
-
1.
Despite the use of a simplified 2D shell with a 9000-element model, both the failure sequence and the ductile fracture path have been correctly simulated.
-
2.
The force-COD curve predicted by the XSHELL toolkit has a discrepancy in comparison with the test data. This is mainly attributed to the use of
-
a.
a constant failure strain criterion that is independent of the triaxility and Lode angle;
-
b.
an assumption of the same geometry dependence of \(\alpha \) for the compact specimen as the challenge problem;
-
c.
use of XSHELL Model without iterative fitting process to get the stress strain curve from uniaxial tensile testing data; and
-
d.
use of through-the-thickness cracking without slanting in XSHELL modeling.
-
a.
A refined analysis along with a parametric study of plane strain core parameters was performed after this blind analysis.
1.11 Team 11
Team Members: K. Nahshon, M. Miraglia, J. Cruce, R. DeFrese, E. T. Moyer; Naval Surface Warfare Center Carderock Division
1.11.1 Introduction
Blind analyses of the Sandia Fracture Challenge (SFC) coupon were performed using a conventional non-linear explicit Finite Element (FE) approach along with a porous plasticity model. The Shear Modified Gurson (SM-G) model described in Nahshon and Hutchinson (2008) was utilized along with the calibration approach outlined by Xue et al. (2010b). The SM-G model is based on the Gurson porous plasticity model (Gurson 1977) with an additional term in the void evolution description to account for damage development under shear-dominated loading conditions. In contrast to other prediction approaches, this approach is highly mature from a numerical point of view. Hence, the primary focus here is on the careful calibration of model parameters from provided test data.
1.11.2 Numerical approach
Prior to performing predictions of the SFC coupon, the SM-G model was calibrated to uniaxial tensile test data. Below, a brief description of the SM-G model is provided, followed by a description of the model calibration process.
Shear-modified Gurson model
The yield surface of the SM-G model is taken as the original Gurson yield surface (Gurson 1977) along with the additional fitting terms and void coalescence and failure parameters developed by Tvergaard and Needleman (1984):
where \(\sigma _e \) and \(\sigma _M \) are the effective stress of the bulk, porous material, and the undamaged matrix material, respectively, and \(\sigma _m \) is the mean stress of the bulk material. The term \(f^{*}\) is equal to the current void volume fraction, \(f\), until it reaches a critical value for void coalescence, \(f_c \). Once reached, the voids grow at an increased rate as a result of coalescence until the void volume fraction at failure is reached.
The development of voids is given by:
where \(D_{ij}^P\) is the plastic strain-rate tensor. The invariant measure \(\upomega \), which is equal to zero for all axisymmetric stress states and unity for all stress states described by a combination of pure shear and hydrostatic tension, is given by:
where \(J_3 \) is the third invariant of the stress deviator tensor. The second term in Eq. (27), which accounts for the evolution of voids under shear dominated stress states, is the only modification the SM-G model makes to the Gurson model. The use of the SM-G model requires the fitting of two parameters, namely the initial void volume fraction, and \(k_\omega \). In addition, the uniaxial stress–strain behavior of the matrix material is required.
The SM-G model was previously implemented as a VUMAT user-material in the ABAQUS (ABAQUS/ 6.12 Manual 2012) code as described in Nahshon and Xue (2009). Here, all calculations presented were performed using the SIERRA/SM (formerly SIERRA Presto) FE code developed by Sandia National Labs utilizing the built-in VUMAT capability.
Calibration of SM-G model from tensile test data
Simulations of uniaxial tension tests were performed to obtain the necessary constitutive description of the steel of interest, namely the full uniaxial true stress–strain behavior prior to damage and the initial void volume fraction. These calculations were performed in two phases. First, calibration of the matrix hardening curve to uniaxial tension response was conducted using standard \(\hbox {J}_{2}\) plasticity. Second, calculations including damage were carried out in order to determine the initial value of void volume fraction. Utilizing the curve shown in Fig. 44, along with an initial void volume fraction of 0.005, it was found that the entire engineering stress–strain curve and final deformed shape were closely reproduced. As no shear-dominated test data was provided, it was assumed that \(k_\omega =2.5\), consistent with other ductile steels. A full list of model parameters is provided in Table 8.
1.11.3 Simulation of fracture challenge specimen
A finite element model of the Fracture Challenge specimen was developed using the constitutive parameters and hardening curve developed from the tensile test simulations along with the mesh illustrated in Fig. 45. The mesh consisted of 626,424 solid first-order eight-noded hexahedral elements with a nominal mesh size of \(25\times 100\times 100\,\upmu \)m in the refined region and \(500\times 500\times 100\,\upmu \)m in the coarse region. The element size in the refined region was maintained at the same size as the tensile coupon mesh presented earlier to avoid mesh size effects. Note that prior to determining the mesh region for refinement, calculations without the most refined region were performed to determine the localization path.
The predicted load-COD curve from the numerical simulations is shown in Fig. 45 along with the experimentally measured curves from all tests. The load is reproduced quite closely through peak load and the rapid drop in load associated with initial cracking is well within the experimental bounds. However, the subsequent load plateau is somewhat high and the drop in load associated with subsequent crack propagation occurs at a lower COD as compared to experimentally observed results. The predicted crack path is ‘C–A–E’ which is one of the paths observed in testing. Full comparison of numerical and experimental values at key points in the load-COD curve is shown in Table 9.
The selected approach was successful in predicting the load-COD response, within experimental bounds, but was not able to predict the ‘A–D–C–E’ localization path. While the SM-G model is able to predict shear-dominated fracture, no data on the shear-driven fracture of the selected alloy was available, thus introducing uncertainty to the model calibration. It is anticipated that, when correctly calibrated, and the effect of geometric and machining tolerances included, further simulations will indicate an ‘A–D–C–E’ localization path. An important caveat of this approach, as discussed in Xue et al. (2010b), is that the advantages of robustness and pedigree are balanced by the need for highly refined discretization on a sub-millimeter scale. Even with powerful computational resources, this limits predictions to the component and subassembly level where such fine discretization can be performed.
1.12 Team 12
Team Members: S. Brinckmann \(^{1}\) and Lukas Quinkert \(^{2}\); 1: Max-Planck Institut für Eisenforschung, Düsseldorf, Germany; 2: Chair of Industrial and Automotive Drivetrains, Ruhr-University Bochum, Germany.
The numerical model for ductile failure of the given specimen was divided into two modular parts. Having a modular structure, both parts could be used independently in other studies.
The first module is a conventional isotropic elastic—isotropic plastic material description with von Mises yielding and subsequent hardening, which readily exists in ABAQUS. A non-linear elastic material model was employed to mirror the experimental results of the uniaxial tension sample. The non-linear elastic material response was implemented as user property, that depends on the von Mises stress. The von Mises stress was chosen as dependent parameter because plasticity similarly depends on it. An alternative method, dependence on the hydrostatic stress, was rejected for the discrepancy with the plastic description although that method yielded similar global results (i.e. similar force-displacement curve) in the uniaxial tension loading condition. The elastic \(\mathbf{E}_{0}, \mathbf{E}_{1}, \varvec{\upnu }\) and plastic (i.e. flow curve) material parameters were inversely identified, i.e. fitted, with the use of a Java program that uses Abaqus to evaluate each material property configuration. For each material configuration the global force-displacement curve is numerically determined and compared with the experimental data. The material parameters are optimized such, as to minimize the difference between numerical and experimental curves.
The second module simulates metal separation. Generally, metal separation depends on the mode mixity between the three fracture modes. The mode mixity enters the fracture models as coupling parameter between normal and tangential direction. From the provided scanning electron microscopy images, the failure surface exhibited isotropic dimples with no preferred orientation and with no apparent shearing. Therefore, it was concluded that this material fractures by void initiation, spherical void growth, void coalescence which was assumed to arise from a large hydrostatic stress in 3D or a large first principle stress in 2D. It should be noted however, that the von Mises stress determines the evolution of plasticity.
Two alternative simulation methods were utilized to investigate the influence of each method. The cohesive surface approach uses additional elements which are placed along the expected crack path. These elements have initially zero thickness and the long corners of the element are opposite to each other. As the normal stresses increase the thickness of these elements increases and the cohesive elements simulate the opening of the crack. Similarly, an increasing shear stresses on the element leads to an increase in mode II opening. Rose et al. (1981) gave a universal binding energy relation for normal separation which is based on quantum mechanical simulations of metals. The present implementation uses the exponential potential according to Xu and Needleman (1994), which is based on the Rose et al. (1981) potential:
where the potential is denoted with \({\varvec{\Phi }}\). The normal and tangential tractions \(\mathbf{t}_\mathrm{n}\) and \(\mathbf{t}_\mathrm{t}\) are the spacial derivatives of the potential in the respective directions. The capital \({\varvec{\Delta }}\) denote the current opening and the lower-case \({\varvec{\updelta }}\) the characteristic separation in the respective directions. The coupling parameters q and r relate the normal and the tangential separation. The strength of the cohesive zone in the normal and tangential direction—which are defined by the \({\varvec{\Phi }}_\mathrm{n}, {\varvec{\updelta }}_\mathrm{n}\) and r—and the corresponding characteristic separations are material dependent properties. This cohesive surface law was implemented in a 2D plain strain formulation (Roe and Siegmund 2003).
An automatic crack path identification algorithm was implemented, which consists of the following steps:
-
1.
evaluation of the maximal principal stress, and determination whether the threshold is fulfilled
-
2.
evaluation of the normal direction to the maximal principle stress
-
3.
move the nodal points of the crack tip adjacent mesh to align an element boundary to the evaluated direction. Ensure during this step that the topology of the elements remains physical, i.e. the elements remain convex and non-overlapping.
-
4.
separate the identified element boundary and insert a cohesive element into the mesh
-
5.
restart the simulation from time \(\mathbf{t}\varvec{=} \mathbf{0}\)
Since the algorithm restarts after each successive cohesive surface insertion, a mapping of the state variables, i.e. equivalent plastic strain, can be avoided. The details of this algorithm are given in a forthcoming publication.
The second metal separation model uses a first order damage law; the material stiffness decreases linearly as damage accumulates. In the present implementation damage accumulation is based on the hydrostatic stress and not on the von Mises stress to decouple metal separation from plasticity, which is intrinsically based on the von Mises stress. The damage D is defined as
where \(\mathbf{p}_{\min }\) and \(\mathbf{p}_{\max }\) are the hydrostatic pressures at which damage accumulation initiates and completes, respectively. This time independent equation is augmented by an effective damage equation
where \(\mathbf{D}_{\mathbf{n}-1}\) is the effective damage of the previous time step, dt is the current time step duration and \(\mathbf{dt}_\mathbf{0}\) is a reference duration. As such, the effective damage ensures that a longer duration leads to an increased damage, i.e. it takes into account the viscous type of void growth. Attention was paid to prevent unphysical damage evolution: material healing was prevented. It should be noted that the implemented damage model uses the three dimensional stress state. As such this 3D model, predicts the damage initiation in the interior of a tensile specimen and the subsequent growth to the outside. The final phase of tensile bar failure is not well captured by the present model because it does not reproduce the experimentally observed bank development.
For the CT specimen, we compared the simulation results of the cohesive surface model, i.e. first fracture model, and the damage model, i.e. second fracture model. For both material models the fracture properties were manually optimized such as to reproduce the experimental load-displacement curve. Since the cohesive element approach adds elements of finite stiffness, this stiffness reduces the global stiffness which leads to a lower load-displacement curve during elastic loading.
For the sample that was used in the challenge, both models predicted a similar load at failure, as shown in Fig. 46a. However, the cohesive surface model predicted a substantially smaller displacement at failure than the damage model. We assume, that this difference is due to the difference in damage representation: according to the cohesive surface model, damage is localized in infinitely narrow band in the undeformed configuration; contrary the damage model assumes that damage is spread across multiple elements. Both models also differed in the site of first rupture. The hydrostatic failure mechanism of the damage model leads initially to crack initiation in the ligament between the holes. Final rupture however occurs first in the ligament between hole C and the backside E. Concluding the comparison of the fracture models, the damage spreading leads to a larger fracture toughness in the damage model. Since the microscopy images revealed a large amount of void growth which is better represented by the damage model, the predictions of the damage model were used in the challenge. The damage model exhibits a small element size effect: the finer mesh results in a lower load and displacement at failure.
a The force-displacement curves for both fracture models (cohesive zones (CZ), damage model) are given in SI units. The stiffness adjusted result for the cohesive surface model is added. b The von Mises stress distribution is given for the damage model with a medium element size distribution. The stress distribution is superimposed by the damage distribution SDV1
1.13 Team 13
Team Members: K. Pack, M. Luo, T. Wierzbicki; Impact and Crashworthiness Lab, Massachusetts Institute of Technology, Cambridge, MA, USA
1.13.1 Plasticity modeling
The plastic behavior of a metallic material is fully described by a yield function, hardening curve, and flow rule. Based on the negligible change in the engineering stress–strain curve between longitudinal and transverse directions provided by Sandia, we adopted the von-Mises isotropic yield function and obtained the true stress–strain curve up to the necking point from the data on longitudinal specimen #2. Since the fracture occurs after considerable necking, the inverse method was employed in order to identify the optimized true stress–strain curve in the post necking region. The stress–strain curve after necking was adjusted such that the engineering stress–strain curve predicted from the numerical simulation showed a good agreement with the one found in the experiment. A fine mesh of 0.15 mm was used at the critical region to capture the diffuse and localized necking. These optimized piecewise linear data were applied to subsequent finite element (FE) analysis. Isotropic hardening with the associated flow rule was assumed in light of the monotonically increasing loading program.
1.13.2 Fracture modeling and calibration
MIT team used the three-parameter Modified Mohr-Coulomb (MMC) fracture model developed by Bai and Wierzbicki (2010). The backbone of this model is the function in the form of Eq. 32, which describes the equivalent strain to fracture \(\bar{\varepsilon }_{f}\) for a proportional loading as a function of the stress triaxiality \(\eta \) and the normalized Lode angle \(\bar{\theta }\).
The model has three parameters of \(\hbox {c}_1,\hbox {c}_2\), and \(\hbox {c}_3\) to be determined from tests, thus requiring at least three experiments for calibration. In the special case where \(\hbox {c}_1 =0\) and \(\hbox {c}_3 =1\), the model reduces to the maximum shear stress criterion. To fully exploit the accuracy and predictive power of the MMC model, dense experimental programs covering a wide range of stress states are recommended, such as the ones shown in Beese et al. (2010) and Luo and Wierzbicki (2010). In addition, MIT team makes use of the inverse calibration (or so-called hybrid experimental-numerical) procedure that requires FE simulation of each test. This procedure is explained in detail in Dunand and Mohr (2010) and Luo et al. (2012). Sandia provided us with the result of the uniaxial tension and toughness tests. FE simulation of the toughness test with the pre-existing sharp crack introduces a very strong mesh dependency. Therefore, toughness tests were not used by MIT team for the model calibration. Two approaches were taken in this research. We first considered the maximum shear stress model with only one parameter to be found from the test. The stress state inside of the neck of the dog-bone specimen is not proportional (see Fig. 47). Hence, an incremental damage rule is needed in conjunction with the Eq. (32). It is assumed that fracture initiates when the function in Eq. (33) reaches unity.
To identify the unknown parameter, \(\hbox {c}_2\), a MATLAB-base optimization routine was built such that the damage value calculated with the history of \(\eta ,\bar{\theta }\), and \(\bar{\varepsilon }_{p}\) (equivalent plastic strain), which are extracted at the critical element from FE simulation up to the experimentally determined average displacement to fracture, is enforced to be one.
For the full three-parameter MMC model, two parameters \(\hbox {c}_1 \) and \(\hbox {c}_3 \) were estimated based on our experience in testing and calibrating many similar materials, and \(\hbox {c}_2 \) was determined using a similar procedure as described above. Figure 47 represents the constructed 3D fracture surface, and the black line indicates the history of stress parameters of the critical point in the dog-bone specimen up to fracture.
The calibrated model was verified by showing that the engineering stress–strain curve and the cross-sectional shape in the neck region after fracture were accurately predicted as shown in Fig. 48.
1.13.3 Blind fracture simulation for Sandia compact tension specimen
As for the FE model, reduced-integration eight-node 3D elements (type C3D8R of the Abaqus element library) of the same size as the one used in the calibration procedure were built up around the starter notch and three holes to minimize the mesh size effect. Twenty elements made up the whole thickness and the total number of elements was approximately 120,000. Two pins were considered to be rigid, and the surface to surface contact with zero friction coefficient was applied between the pins and the specimen. Fixed mass scaling of \(10^{8}\) was employed to reduce computation time with the confirmation of negligible ratio of kinetic energy to internal energy for whole model, and the element deletion technique was used with the user subroutine (VUMAT) of Abaqus/Explicit.
As illustrated in Fig. 49, the full MMC model predicted that the first crack initiates between the starter notch A and hole C, and after the ligament separates completely, another crack develops at the surface of hole C and propagates to the backside edge E.
Figure 50 represents the comparison of the force-COD curves from the MMC simulation (red line) and the experiments. We only presented the experimental results with the same crack path as ours. As summarized in Table 10, the maximum force and forces at the first and second crack initiation were accurately predicted. The COD at the first crack initiation was slightly over-predicted due to the over-adjusted stress–strain curve after necking although it was defined as the COD at which the first element was killed on the mid-plane, not on the surface. The COD at the second crack initiation was over-predicted as well partially due to the predicted stable crack growth during the first crack propagation (load drops with a gentle slope). A subsequent study on the mesh size effect revealed that the finer mesh is, the faster crack propagates, leading to the faster load drop. The result is discussed in detail in the full version paper. Blue line in Fig. 50 represents the simulation result using the maximum shear stress criterion. This criterion predicts better the second phase of the crack propagation, but worse the first phase.
1.13.4 Conclusion
Plasticity and fracture modeling based on only one calibration test already led to a reasonably acceptable prediction. However, more than one test is required to improve the plasticity and fracture model. Also, early shear localization and A–D–C–E crack path could be predicted by introducing the concept of ‘pre-damage’. This is also described in the full version paper.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Boyce, B.L., Kramer, S.L.B., Fang, H.E. et al. The Sandia Fracture Challenge: blind round robin predictions of ductile tearing. Int J Fract 186, 5–68 (2014). https://doi.org/10.1007/s10704-013-9904-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10704-013-9904-6