An efficient numerical method for the solution of the second boundary value problem of elasticity for 3D-bodies with cracks

Abstract

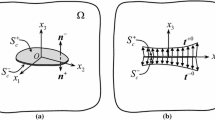
The second boundary value problem of elasticity for 3D-bodies containing cracks is considered. Presentation of the solution in the form of the double layer potential reduces the problem to a system of 2D-integral equations which kernels are similar for the body boundary and crack surfaces. For discretization of these equations, Caussian approximation functions centered at a set of nodes homogeneously distributed on the body and crack surfaces are used. For such functions, calculation of the elements of the matrix of the discretized problem is reduced to five standard 1D-integrals that can be tabulated. For planar cracks, these integrals are calculated in closed analytical forms. The method is mesh free, and for its performing, only node coordinates and surface orientations at the nodes should be defined. Calculation of stress intensity factors at the crack edges in the framework of the method is discussed. Examples of an elliptical crack, a lens-shaped crack, and a spherical body subjected to concentrated and distributed surface forces are considered. Numerical results are compared with the solutions of other authors presented in the literature. Convergence of the method with respect to the node grid steps is analyzed. An efficient algorithm of the node grid generation is proposed.

Appendix

Let a smooth surface $\Omega$ in 3D-space be described by an implicit equation

$$\begin{aligned} \Phi (\mathbf {x})=\Phi (x_{1},x_{2},x_{3})=0. \end{aligned}$$

(123)

For generation of a homogeneous node grid on this surface, an arbitrary point $\mathbf {x}\in \Omega$ is to be taken as an original node $\mathbf {x} ^{(1)}.$ The next node $\mathbf {x=x}^{(2)}$ is any solution of the equations

$$\begin{aligned} |\mathbf {x}^{(1)}\mathbf {-x}|=h,\quad \Phi (\mathbf {x})=0. \end{aligned}$$

(124)

The third node $\mathbf {x=x}^{(3)}$ is one of the two solutions of the following equations

$$\begin{aligned} |\mathbf {x}^{(1)}\mathbf {-x}|=h,\text { }|\mathbf {x}^{(2)}\mathbf {-x}|=h, \quad \Phi (\mathbf {x})=0. \end{aligned}$$

(125)

For calculation of the coordinates of the $s$th node $\mathbf {x=x}^{(s)} ( s=4,5,\ldots )$, we consider the system of equations

$$\begin{aligned} |\mathbf {x}^{(p)}\mathbf {-x}|&= h,\quad |\mathbf {x}^{(q)}\mathbf {-x}|=h, \quad \Phi (\mathbf {x})=0; \nonumber \\ p,q&= 1,2,\ldots ,s-1;\quad p\ne q; \end{aligned}$$

(126)

Among the solutions $\mathbf {x}=\mathbf {x}_{m}^{(s)}$ of this system we chose the one $\mathbf {x}^{(s)}$ that satisfies the conditions

$$\begin{aligned}&\!\!\! |\mathbf {x}^{(p)}\mathbf {-x}_{m}^{(s)}|\ge h,\text { }p=1,2,\ldots ,s-1;\nonumber \\&\!\!\!\min _{m}|\mathbf {x}_{m}^{(s)}-\mathbf {x}^{(1)}|=|\mathbf {x}^{(s)}-\mathbf {x} ^{(1)}|. \end{aligned}$$

(127)

In the case of a planar crack, this algorithm leads to a regular hexagonal node grid on the crack plane. For a spherical surface, an example of the generated node grid is presented in Fig. 21. The centers of small spheres shown in this figure compose a set of approximating nodes. Some defects of the grid where the distances between the neighbor nodes are more than $h$ do not affect practically the quality of the solution for sufficiently small grid steps $h$.

Fig. 21

The node grid on different sides of a spherical surface covered by a set of small spheres with constant radii $h/2$; the set of approximating nodes are the small sphere centers