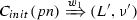Abstract
Static verification techniques are used to analyse and prove properties about programs before they are executed. Many of these techniques work directly on the source code and are used to verify data-oriented properties over all possible executions. The analysis is necessarily an over-approximation as the real executions of the program are not available at analysis time. In contrast, runtime verification techniques have been extensively used for control-oriented properties, analysing the current execution path of the program in a fully automatic manner. In this article, we present a novel approach in which data-oriented and control-oriented properties may be stated in a single formalism amenable to both static and dynamic verification techniques. The specification language we present to achieve this that of ppDATEs, which enhances the control-oriented property language of DATEs, with data-oriented pre/postconditions. For runtime verification of ppDATE specifications, the language is translated into a DATE. We give a formal semantics to ppDATEs, which we use to prove the correctness of our translation from ppDATEs to DATEs. We show how ppDATE specifications can be analysed using a combination of the deductive theorem prover KeY and the runtime verification tool LARVA. Verification is performed in two steps: KeY first partially proves the data-oriented part of the specification, simplifying the specification which is then passed on to LARVA to check at runtime for the remaining parts of the specification including the control-oriented aspects. We show the applicability of our approach on two case studies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Runtime verification has been touted as a practical verification technique, and although it does not provide program analysis before deployment, it can check correct behaviour post-deployment by observing whether actual execution paths at runtime conform to the specification. Runtime verification scales up much more effectively than static analysis both in terms of performance and in terms of applicability to diverse contexts in which a program may interact with various other systems, services, libraries and be deployed.
Despite the fact that overheads induced by runtime verification might be small when compared to the computational effort required for static analysis, the fact that is done while the software is live can be problematic and prohibitive for certain systems. In this paper we present an approach to address the issue of runtime overheads through the use of static, deductive verification—an approach which also has the benefit of being able to verify parts of the specification a priori for all potential execution paths, leaving only parts which could not be proved before deployment to be checked dynamically.
Apart from the computational power required to perform the analysis, deductive and runtime verification have largely been applied to disjoint areas—whereas deductive analysis has been extensively used to verify properties focusing on a system’s data, e.g., [2, 23, 28, 30], runtime verification has been extensively used to verify control-flow properties with reasonable overheads [11, 15, 18, 33]. Combining the two approaches has the additional benefit that static analysis might be more effective in proving the parts of a specification which dynamic analysis might struggle most with. The challenge is thus to design a specification language which allows the expression of combined data- and control-flow properties in such a manner that they can be effectively decomposed for the application of different verification techniques.
The StaRVOOrS framework [5] addresses these issues by identifying a specification notation for such properties and a verification methodology combining static and dynamic analysis to verify combined control- and data-oriented properties. Although one may envisage different ways to combine static and dynamic analysis tools, a crucial requirement is that the specification languages used in the tools chosen are either identical, or can be somehow combined to allow for rich specifications getting the best of both approaches. Similar to mode automata [31] we have chosen to adopt an automata-based specification language (for the control-flow properties) but extended with data-flow properties encoded in the different states of the formalism.
This article is a significantly extended and revised version of two papers. In [3] we introduced the formalism ppDATE, where parts of the syntax where left underspecified, and we gave a high-level description of the algorithm to translate ppDATE into DATE [18], the formalism used in the runtime verification tool Larva [19]. In [16] we presented the tool StaRVOOrS, a full implementation of the framework introduced in [3, 5].
The novel contributions of this paper, going beyond the results reported in [3] and [16] are the following: (i) We present a complete formal definition of ppDATE automata, including a formal semantics for the formalism (Sect. 5); (ii) A proof of soundness of the algorithm to translate from ppDATE specifications into DATE ones (Sect. 7). (iii) The application of our approach to SoftSlate Commerce, an open-source Java shopping cart web application (Sect. 9); (iv) A description of the results of the case study including an analysis of the verification process providing evidence that our approach reduces the overhead of the runtime monitoring (Sect. 9).
Structure of the paper Sect. 2 provides background information regarding the verification techniques used on this paper. Section 3 introduces informally the specification language ppDATE. Sect. 4 introduces the StaRVOOrS framework and provides a description of its workflow. Section 5 presents formally the specification language ppDATE, and Sect. 6 provides its operational semantics. Sect. 7 gives a translation algorithm from ppDATEs into DATEs, and provides a proof of correctness. Sect. 8 presents a fully automated tool which implements the StaRVOOrS framework. Sections 9 and 10 discuss two case studies which illustrate the benefits of using StaRVOOrS for verifying software. Sect. 11 discusses related work. We conclude this paper in Sect. 12.
2 Preliminaries
The work presented in this article is centred around static and runtime verification of Java systems. To implement these verification techniques, we use the deductive verifier KeY and the runtime verifier Larva. In this section, we introduce these tools at a high level of abstraction, but with sufficient detail to enable the understanding of the rest of the paper.
2.1 The deductive verifier KeY
KeY [2] is a deductive verification tool for data-centric functional correctness properties of Java source code. KeY generates proof obligations in dynamic logic (DL), a modal logic for reasoning about programs. DL extends first-order logic with two modalities,  and \({[p]}{\phi }\), where p is a program and \(\phi \) is another DL formula. The formula
and \({[p]}{\phi }\), where p is a program and \(\phi \) is another DL formula. The formula  is true in a state s if there exists a terminating run of p, starting in s, resulting in a state where \(\phi \) holds. The formula \({[p]}{\phi }\) holds in a state s if all terminating runs of p, starting in s, result in a state in which \(\phi \) holds. For deterministic programs p, the only difference between the two modalities is that termination is stated in
is true in a state s if there exists a terminating run of p, starting in s, resulting in a state where \(\phi \) holds. The formula \({[p]}{\phi }\) holds in a state s if all terminating runs of p, starting in s, result in a state in which \(\phi \) holds. For deterministic programs p, the only difference between the two modalities is that termination is stated in  , and assumed in \({[p]}{\phi }\).
, and assumed in \({[p]}{\phi }\).
KeY features (static) verification of Java source code annotated with specifications written in the Java Modelling Language (JML) [29]. JML allows for the specification of pre- and postconditions of method calls, and class/interface invariants. The main features of KeY are the translation of JML annotated Java programs to Java DL, and a theorem prover for validity of Java DL formulae, using a sequent calculus, covering almost all features of sequential Java (with the exception of generics and floating-point types currently). Given a set of formulae \(\varGamma \), the sequent  holds if p, when starting in a state fulfilling all formulae in \(\varGamma \), terminates in a state fulfilling \(\phi \). The calculus uses the symbolic execution paradigm. For that, DL is extended by explicit substitutions. During the symbolic execution of p, the effects of p are gradually, starting from the front, turned into explicit substitutions. Thereby, after some proof steps, a certain prefix of p has turned into a substitution \(\sigma \), representing the effects so far, while a remaining program \(p'\) is yet to be executed. While verifying p, an intermediate proof node may look like
holds if p, when starting in a state fulfilling all formulae in \(\varGamma \), terminates in a state fulfilling \(\phi \). The calculus uses the symbolic execution paradigm. For that, DL is extended by explicit substitutions. During the symbolic execution of p, the effects of p are gradually, starting from the front, turned into explicit substitutions. Thereby, after some proof steps, a certain prefix of p has turned into a substitution \(\sigma \), representing the effects so far, while a remaining program \(p'\) is yet to be executed. While verifying p, an intermediate proof node may look like  . It tells us that, if \(\varGamma \) was true before the original program p, and \(\sigma \) is the accumulated effect up to now, then \(\phi \) will be true after executing the remaining program \(p'\).
. It tells us that, if \(\varGamma \) was true before the original program p, and \(\sigma \) is the accumulated effect up to now, then \(\phi \) will be true after executing the remaining program \(p'\).
As an example, consider a proof of the following DL sequent:

(where \(p_1\), \(p_2\), and q are Java fragments and \(\phi \) is some postcondition). The sequent says that in each state where x and y are positive, the program given in the modality (which first swaps x and y using arithmetics) will terminate and result in a state where \(\phi \) holds. When proving this sequent, the KeY prover will first, in a number of steps, turn the three leading assignments into explicit substitutions, apply the first to the second, the result to the third, and perform arithmetic simplification, arriving at

where \((\texttt {x}\leftarrow \texttt {x+y}\,\Vert \,\texttt {y}\leftarrow \texttt {x}\,\Vert \,\texttt {x}\leftarrow \texttt {y})\) denotes the explicit (parallel) substitution resulting from symbolic execution of the first three statements. A ‘right-win’ semantics is adopted to resolve clashes in substitutions, such that the above simplifies to:

In general, most proofs branch over case distinctions, often triggered by Boolean decisions in the source code. The branching happens by applying rules like the following, simplifiedFootnote 1 if rule:

In our example, applying the if rule to the latest sequent results in splitting the proof into two branches, with the following sequents, respectively:

Applying the substitution on the left side of either sequent results in:


Note that in this step, by applying the swapping substitution, the branching condition (x being even or odd) on the state after swapping got translated into a condition on the prestate of the original program p, before the swapping. The resulting sequents tell us, among other things, that if y is even (respectively odd) in the prestate of p, then path \(p_1\) (respectively \(p_2\)) is taken in the execution of p. In general, when building a proof in such a symbolic manner, the left side of sequents accumulate conditions on the original prestate through a particular execution path.
Once all proof branches are closed, we have a complete proof of the root sequent. However, a proof attempt may result in a partial proof, only, where some proof branches are closed and others are not. Such partial proofs are important for the work presented in this article. In the above example, consider a partial proof where the left branch, i.e., the sub-proof for sequent (2), is closed, whereas the right branch, i.e., the sub-proof for sequent (3), is not closed. From this partial proof, we can conclude that the following modification of the root sequent (1) is valid:

(We added \(\texttt {y\%2} = \texttt {0}\) to the left side of (1), as additional assumption.) This sequent can be proven by replaying the original proof, where now both branches would close. The left branch closes as the sub-proof for (2) will replay identically. The right branch closes because the following variant of (3) can be closed immediately, due to contradicting assumptions:

2.2 The runtime verifier Larva
Larva
Footnote 2 [19] is an automata-based runtime verification tool for Java programs. As with many other runtime verifiers, Larva automatically generates a runtime monitor from a property written in a formal language, in its case using Dynamic Automata with Timers and Events (DATEs) [18]. Transitions in a DATE are of the form: \({event} \mid {condition} \mapsto {action}\), where event is what triggers the transition, the condition is checked and must hold in order the transition to take place, and the action is a code snippet to be performed when taking the transition (after checking the condition). DATEs are an extension of timed automata—they are effectively finite state automata, whose transitions are triggered by system events (primarily entry points  and exit points \(\texttt {f}^\uparrow \) of methods) and timers, but augmented with: (i) A symbolic state which may be used as conditions to guard transitions and can be modified via actions also specified on the transition; (ii) replication of automata, through which a new automaton is created for each discovered instance of an object; (iii) communication between automata using standard CCS-like channels with c! acting as a broadcast on channel c and which can be read by another automaton matching on event c? Full details of the formalisation of DATEs can be found in [19].
and exit points \(\texttt {f}^\uparrow \) of methods) and timers, but augmented with: (i) A symbolic state which may be used as conditions to guard transitions and can be modified via actions also specified on the transition; (ii) replication of automata, through which a new automaton is created for each discovered instance of an object; (iii) communication between automata using standard CCS-like channels with c! acting as a broadcast on channel c and which can be read by another automaton matching on event c? Full details of the formalisation of DATEs can be found in [19].
The automata illustrated in Fig. 1 represent an example of DATE automata describing a property which should hold during a connection. The first automaton ensures that if the connection drops (event  ) occurs five times, a message is broadcast (over channel \( unreliable \)) to highlight the fact that the connection port is unreliable. The second automaton (with the \( foreach \) keyword) ensures that every time a file transfer is initiated, an automaton is created to monitor that transfer. If during the transfer (i.e. between the events
) occurs five times, a message is broadcast (over channel \( unreliable \)) to highlight the fact that the connection port is unreliable. The second automaton (with the \( foreach \) keyword) ensures that every time a file transfer is initiated, an automaton is created to monitor that transfer. If during the transfer (i.e. between the events  and \(\texttt {end}^\downarrow \)) one receives event \( unreliable? \), no further transfers may occur.
and \(\texttt {end}^\downarrow \)) one receives event \( unreliable? \), no further transfers may occur.
In order to monitor a system using Larva, the user must provide the system to be monitored (a Java program) and a set of properties in the form of a Larva script (a textual representation of DATEs). Larva transforms the set of properties into monitoring code together with AspectJ code to link the system with the monitors. Since the Java byte code is used for instrumentation, it is possible to monitor third-party software with Larva, though knowledge of methods names is still required.
3 ppDATE: a specification language for data- and control-oriented properties
In many cases, verification tools perform more effectively on a particular style of specification. In combining two different verification tools which use very different analysis techniques, one challenge is that if we adopt an off-the-shelf language, we cannot expect to derive useful verification results from both tools. Given that deductive verification tools like KeY perform much better on data-centric properties, while runtime verification tools like Larva perform better on control-flow properties, we have defined a specification language to combine the two types of properties. In real scenarios, there is often a need to specify both, rich data constraints and legal execution sequences.
Data-oriented properties are typically written in expressive formalisms (like first-order logic), but typically give invariants about specific points in the execution of a system, rather than properties across traces of execution. JML is one such languages, which focuses primarily on pre/postconditions of method calls and class invariants, but is not well suited for specifying which sequences of events or states are correct. In contrast, control-oriented specification languages specialise primarily on identifying legal sequences of events or states, for instance using automata or temporal logics. Although constraints about the data are possible, they are usually cumbersome and greatly increase the computational complexity required to verify them. DATE is one such specification language.
Coding control-flow into data-centric languages, like coding legal execution traces via model/ghost fields in JML, or including data-flow information in control-centric languages, like considering variable updates as events in DATE specification, can lead to substantial increase in the complexity of the specification from an understandability and/or verification perspective.
In order to address this, we propose ppDATE, a formalism to deal with both types of properties ensuring understandability and tractability of analysis using the StaRVOOrS verification framework. ppDATE [3] is an automata-based formalism to specify both control- and data-oriented properties. ppDATEs are basically transition systems with states and transitions between states. Transitions are labelled by a trigger (tr), a condition (c), and an action (a). Together, the label is written \(tr \mid c \mapsto a\). A transition is enabled to be taken whenever its trigger is active and its condition holds. A trigger is activated by the occurrence of either a visible system event such as the invocation or termination of a method execution, or a ppDATE internal event generated by certain actions labelling other transitions. If a transition is taken, we will say that it fires. The conditions may depend on the values of system variables (i.e., variables of the system under scrutiny) and the values of ppDATE variables. The latter can be modified via actions in the transitions. ppDATE states represent the status of an observer of a system (rather then, directly, the status of a system itself). Note that each state essentially represents the set of observed system traces leading to that state. The language also offers parallelism on the specification side, in the sense that different ppDATEs run in parallel, possibly communicating which each other through events, and possibly creating new ppDATEs on demand. This parallelism allows for a strong separation of concerns in the specification.
In addition to the above, a particular feature of the ppDATE is that states may be tagged with any number of Hoare triples, to specify the computation of a method in a history-context sensitive way. For instance, assume that a ppDATE state q is tagged with the Hoare triple \(\{\pi \}{foo}\{\pi '\}\). This means that, if foo is invoked after a system trace which led the observer to q, and if furthermore \(\pi \) holds at the time of the invocation, then \(\pi '\) should be satisfied upon termination of this execution of foo. This allows for data-centric specification of individual methods’ behaviour (Hoare triple), however in a control sensitive manner (state).
Compared to usual automata based (or temporal logic based) specification approaches, ppDATE is more expressive concerning the computation on data. Compared to data-centric pre/post-specification (like, e.g., JML), ppDATE can avoid the coding of some notion of status into additional data and additional constraints in the pre/postconditions.
To write a ppDATE, a good approach may be to, first, define the control-oriented properties, i.e., the automata. Next, one shall proceed to define the different Hoare triples. Finally, one places the Hoare triples on the appropriate states of the ppDATE.
Below, we provide a few examples of ppDATE specifications. On this examples, \(tr^\downarrow \) means that the method associated to the trigger tr has just been called, and \(tr^\uparrow \) means that method associated to the trigger tr has terminated its execution.
Example 1
Let us consider a coffee machine system where after a certain amount of coffee cups are brewed, its filters have to be cleaned. If the limit of coffee cups is reached, the machine should not be able to brew any more coffee. In addition, while the coffee machine is active (a coffee cup is being brewed), it is not possible to start brewing another coffee, or to clean the filters.
Figure 2 illustrates a ppDATE describing this part of the system. In other words, whenever the coffee machine is not active, i.e., the machine is not brewing a cup of coffee, and the method brew starts the coffee brewing process, then it is not possible either to execute this method again, or to execute the method cleanF (which initialises the task of cleaning the filter), until the initialised brewing process finishes.
The previous property can be interpreted as follows: initially being in state q, state which represents that the coffee machine is not active, whenever method brew is invoked and it is possible to brew a cup of coffee (i.e., the limit of coffee cups was not reached yet), then transition \(t_1\) shifts the ppDATE from state q to state \(q'\). While in \(q'\), state which represents that the coffee machine is active, if either method brew or method cleanF are invoked, then transitions \(t_3\) or transition \(t_4\) shift the ppDATE to state bad, respectively. This indicates that the property was violated. On the contrary, if method brew terminates its execution, then transition \(t_2\) shifts the ppDATE from state \(q'\) to state q. Note that the names used on the transitions, e.g. \(t_1\), \(t_2\), etc, are not part of the specification language. They are included to simplify the description of how the ppDATE works.
In addition to this, the Hoare triples in state q ensure the properties: (i) if the amount of brewed coffee cups has not reached its limit yet, then a coffee cup can be brewed; (ii) cleaning the filters sets the amount of brewed coffee cups to 0. Property (i) has to be verified if, while the ppDATE is on state q, the method brew is executed and its precondition holds. A similar situation stands for the property (ii) with respect to the method cleanF. Regarding state \(q'\), the Hoare triples in this state ensure the properties: (iii) no coffee cups are brewed; (iv) filters are not cleaned. Property (iii) and (iv) are verified if either method brew and method cleanF are executed, and their preconditions hold, respectively. Here, remember that this state represents that the coffee machine is active. Thus, if it occurs that either the method brew or the method cleanF are executed while the ppDATE is on this state, then, as this would move the ppDATE to state bad, one would expect the value of the variable cup to remain unchanged. This is precisely what is verified when either property (iii) or (iv) are analysed.
Note that none of the Hoare triples makes reference to the state of the coffee machine, i.e. there is no information about whether the machine is active or not. This is due to fact that the state of the machine is implicitly defined by the states of the ppDATE. If the ppDATE is in state q, the coffee machine is not active. However, if it is in state \(q'\), then the machine is active. Therefore, it is possible to assume that on each state the Hoare triples are context dependent and thus contain such information. This is the reason why, we can describe properties with the same precondition, but with different postconditions depending on the state of the ppDATE in which they are placed.\(\square \)
Example 2
In this example let us consider a file system where only 10 file transfers can be performed between a log in and log out of a user.
Figure 3 illustrates a ppDATE describing part of the behaviour of this system. This ppDATE ensures the property: no more than 10 file transfers take place in a single login session. In other words, once a user logs in the system (login), she can only perform 10 file transfers (transferFile) before logging out (logout). This fact is tracked using the ppDATE variable c. This variable keeps count of the number of files transferred in a single session. Whenever a user logs in, the ppDATE moves to state \(q'\) and c is set to 0 (zero). While in \(q'\), this variable is increased by one every time a file transfer is performed. If at some point the user transfers a file but the value of c is bigger than 10, then the ppDATE moves to state bad, i.e., the property was violated.
In addition to this, the Hoare triples in state \(q'\) ensure the properties: (i) the number of bytes transferred increases when a file transfer is done; (ii) renaming a file works as expected if the user has the sufficient rights. \(\square \)
4 The StaRVOOrS framework
The StaRVOOrS framework (Static and Runtime Verification of Object-Oriented Software), originally proposed in [5], combines the use of the deductive source code verifier KeY [2] with that of the runtime monitoring tool Larva [19], to analyse and monitor systems with respect to a ppDATE specification. Note that the definition of the specification language ppDATE, which enables the effective combination of the results from the two verification approaches, is a major contribution of StaRVOOrS. ppDATE allows our framework to naturally address the intrinsic differences between the verification tools—whereas one typically verifies data-centric properties in deductive verifiers like KeY, one typically focuses on control-flow properties using runtime verifiers like Larva.
The abstract workflow of the use of StaRVOOrS is given in Fig. 4. This workflow is applied fully automatically in four consecutive stages: Deductive Verification, Specification Refinement, Translation and Instrumentation, and Monitor Generation.
In the Deductive Verification stage, given a Java program P and a ppDATE specification S, the module Pre/post-Condition Generator transforms all the Hoare triples—assigned to the various states of S—into JML contracts , which are textually added to P as annotations of the respective methods. In this step, the association of pre/postcondition pairs to ppDATE states in S is lost, which is intentional and natural. Note that each ppDATE state represents the set of event histories leading to that state. The deductive verifier, however, offers analysis of the effect of methods in terms of system data, and has no notion of the history of events preceding a method call.Footnote 3 Once all JML contracts are generated, the Deductive Verifier module uses KeY in an attempt to statically verify each of them. The result is either a complete proof, or a partial proof where some branches are closed and others are not (see Sect. 2.1), or an entirely open proof, where no branches are closed. In our setting, partial proofs are the most common case. One reason is that we use KeY only fully automatically, not employing its interactive features. Also, we do not assume users to provide loop invariants, or similar annotations which support the prover. Finally, KeY has no knowledge of the context (ppDATE state) in which the Hoare triple at hand should hold. To illustrate this point, consider the Hoare triples (i) and (iii) from our (deliberately primitive) example in Fig. 2. The implementation of brew() is given by:

KeY will produce partial proofs for these Hoare triples because the specification does not provide any information on how q and \(q'\) relate to the field active. In general, the missing information can be an arbitrary condition on the system state, more than just a Boolean as is the case here.
In the Specification Refinement stage,Footnote 4 the Partial Specification Evaluation module evaluates the results produced by KeY in order to refine S. This refinement is performed in two steps. In the first step, all fully verified Hoare triples are deleted, resulting in a ppDATE
S’. Any Hoare triple related to a contract which is not fully verified by KeY is left in the states of S’ to be verified at runtime. In the second step, S’ is refined into a ppDATE
S” by strengthening the preconditions of those Hoare triples in S’ which were partially verified by KeY. For that, the partial KeY proofs are analysed, to extract branch conditions corresponding to the closed branches of the proof. In the example in Sect. 2.1, that ‘closed branch condition’ is \(\texttt {y\%2} = \texttt {0}\) in sequent (4). Note again that the branch condition is a condition on the prestate of the code being verified. Let us abbreviate the ‘closed branch(es) condition’ as cbc for now. A Hoare triple \(\{\pi \}{foo}\{\pi '\}\) that was partially verified by KeY is clearly equivalent to having two Hoare triples \(\{\pi \wedge {cbc}\}{foo}\{\pi '\}\) and \(\{\pi \wedge \lnot {cbc}\}{foo}\{\pi '\}\). However, as we know that the first one is valid (by the proof replay argument from Sect. 2.1), only the second one needs to be checked at runtime. For this reason, every Hoare triple \(\{\pi \}{foo}\{\pi '\}\) in S’ that was partially verified by KeY is replaced by \(\{\pi \wedge \lnot {cbc}\}{foo}\{\pi '\}\), resulting in S”. At runtime, checking such an optimised Hoare triple is trivial whenever \(\pi \) is false or cbc is true, as the postcondition does not need to be checked then. For instance, analysis of the partial proof of Hoare triple (i) in Fig. 2 will result in the closed branch condition \(\lnot \texttt {active}\). Therefore, (i) is replaced by  (we simplified away double negation). Note that, in cases where the history context, i.e., ppDATE state, is the only information that was missing to close a partial proof, cbc actually represents a refinement of the according ppDATE state to a condition on internal system data, which will always be true when foo is called in that state. We can remark already here that this is the phenomenon which made the monitoring speedup particularly dramatic in the Mondex case study, see Sect. 10.
(we simplified away double negation). Note that, in cases where the history context, i.e., ppDATE state, is the only information that was missing to close a partial proof, cbc actually represents a refinement of the according ppDATE state to a condition on internal system data, which will always be true when foo is called in that state. We can remark already here that this is the phenomenon which made the monitoring speedup particularly dramatic in the Mondex case study, see Sect. 10.
In the Translation and Instrumentation stage, the Specification Translation module translates S” into an equivalent specification in DATE format (D), which can be used by the runtime verifier Larva (see the next stage). The most significant change of this translation is that the Hoare triples are translated away, using notions native to DATE (see Sect. 7.2). This change also requires to instrument P, through the Code Instrumentation module, in order to (i) distinguish between different executions of the same code unit, and to (ii) evaluate Hoare triples in the states of S” at runtime. Regarding (i), method declarations get a new argument which is used as a counter for invocations of this method. Regarding (ii), not every condition in a pre/postcondition of a Hoare triple can be directly written as a Java Boolean Expression, e.g., quantified expressions. Thus, methods which operationalise the evaluation of those conditions are added to P.
Finally, in the Monitor Generation stage, the instrumented version of P (P’) and the DATE specification D are used by the Runtime Verifier module to generate a monitor M. For this, Larva generates M from D by using aspect-oriented programming techniques to capture relevant system events. Such events allow to link P’ with M. Later, once deployed, M and P’ are executed together. If M identifies any violation at runtime, it will report an error trace for further analysis.
5 Formal definition of ppDATEs
5.1 Notation
We will use the following notation to write quantified formulae, based on the notation used by Gries [27].
These formulae mean “for all x satisfying R, B is fulfilled” and “there exists x satisfying R for which B is fulfilled”, respectively. Both R and B are formulae potentially containing x as a free variable. We will refer to R and B as the range and body of the quantified formula, respectively. This notation relates to standard (un-ranged) quantified formulae in the following way:
5.2 ppDATE
In this section we formally define the notion of ppDATE previously introduced in Sect. 3. In order to do so, we first introduce formal definitions for triggers, conditions and actions.
Definition 1
Given a set of method names \(\varSigma \), the syntactic category of triggers is defined as follows:

where methodname \(\in \varSigma \). \(\square \)
In the previous definition, systemtrigger matches a visible system event, such as the point of entry into a method or the termination of a method execution. Given a method name \(\sigma \in \varSigma \),

represents entering method \(\sigma \) and

represents the termination of the execution of \(\sigma \).
In addition, actevent represents an event generated by the execution of an action in a transition of a ppDATE, which we will call action events. This kind of events can only be generated by bang (“!”) actions (see Definition 2). An action h! generates the action event h, which in the next step can activate the trigger h? This way, action events enable communication among ppDATEs, where h! and h? mean sending and receiving a message, respectively.
As we have mentioned before, whenever a transition is fired an action can be executed. The following shows the definition of actions.
Definition 2
Actions are syntactically defined as follows:

\(\square \)
skip is the effect-less action. The ‘\(=\)’ is an assignment operator, v is a ppDATE variable and e is a (side-effect free) expression that may depend on system variables and ppDATE variables; actevent! represents the generation of action event actevent; create represents the creation of a ppDATE, where template is a ppDATE template to be instantiated (see Definition 8), and \(\overline{{args}}\) are the values which the formal parameters of template are instantiated with; the ‘; ’ is the sequence operator for actions; if-then is a conditional whose branching condition depends on the valuations of system variables (\(\textit{Sys}\)) and ppDATE variables (\(V\)); and Program represents a side-effect free program (see Definition 3), i.e., it is restricted to not have any effect on the system which could in turn be observed by the (ppDATE generated) monitor. For instance, a Program could perform logging of system/monitor behaviour. More powerful Programs, which would for instance allow error recovery, are relevant, but left for future work.
Definition 3
A side-effect free program has the properties that
-
its execution always terminates,
-
the method calls on its body do not generate any observable system event,
-
it does not interfere with the system under scrutiny, i.e., it does not modify the values of system variables. \(\square \)
Boolean expressions are used in different contexts: (i) conditions (c) of transitions; (ii) conditions of if-then actions, and (iii) pre- and postconditions (\(\pi \), \(\pi '\)) in Hoare triples. As a syntactic category for such Boolean expressions, we chose Boolean JML expressions. They extend Boolean Java expressions, and thereby allow Java methods as sub-expressions (like in ‘m.get(k) == o’). Additional features of Boolean JML expressions include universal and existential quantification, which are frequently used in Hoare triples, the ability to refer in a postcondition to a) the return value (with ‘ ’), and b) the preexecution value of an expression (like in ‘
’), and b) the preexecution value of an expression (like in ‘ ’).
’).
Definition 4
Boolean JML expressions (BJMLE) are recursively defined as follows:
-
any side-effect free Boolean Java expression is a BJMLE,
-
if a and b are BJMLEs, and x is a variable of type t, the following expressions are BJMLEs:
-
!a, a&&b, and a||b
-
\(\texttt {a ==}> \texttt {b}\) (“a implies b”)
-
\(\texttt {a} <\texttt {==}> \texttt {b}\) (“a is equivalent to b”)
-
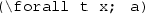
(“for all x of type t, a holds”)
-
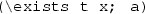
(“there exists x of type t such that a”)
-
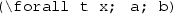
(“for all x of type t fulfilling a, b holds”)
-
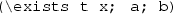
(“there exists an x of type t fulfilling a, such that b”)
-
-
replacing any sub-expression e in a BJMLE with
 gives a BJMLE,
gives a BJMLE, -
replacing any sub-expression in a BJMLE with
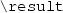 gives a BJMLE, (well-typedness is context dependent, see Definition 5) \(\square \)
gives a BJMLE, (well-typedness is context dependent, see Definition 5) \(\square \)
We do not give a formal definition of the semantics of BJMLE here, just the following comments. The meaning of negation, conjunction, disjunction, implication, and equivalence are standard. The same is true for the first two forms of quantification. Concerning the other two forms, “\(\ldots \)
a; b)”, they relate to standard quantification in exactly the same way as was explained in Sect. 5.1. (The only difference is that there we discussed meta-level notation, whereas BJMLE is part of ppDATE.) The constructs  and
and  are only allowed in postconditions of Hoare-triples (i.e., in \(\pi '\)).
are only allowed in postconditions of Hoare-triples (i.e., in \(\pi '\)).  refers to the return value of a (non-void) method.
refers to the return value of a (non-void) method.  allows to evaluate sub-expressions not in the post-state (which is the default), but in the prestate of a method’s execution. For instance, ‘
allows to evaluate sub-expressions not in the post-state (which is the default), but in the prestate of a method’s execution. For instance, ‘ ’ in a postcondition of method m says that the difference between the values of x before and after the execution of m is the value which y had before
m’s execution.
’ in a postcondition of method m says that the difference between the values of x before and after the execution of m is the value which y had before
m’s execution.
In order to allow or disallow  and
and  , in the following, we provide one syntactic category for postconditions, and one for all other conditions.
, in the following, we provide one syntactic category for postconditions, and one for all other conditions.
Definition 5
The syntactic category of postconditions over variables in Var, \({postcond}_{{Var}}\), is given by Boolean JML expressions over Var. (Well-typedness of postconditions is context dependent, assuming that  has the same type as the specified method.) The syntactic category \({cond}_{{Var}}\) is given by Boolean JML expressions over Var containing neither
has the same type as the specified method.) The syntactic category \({cond}_{{Var}}\) is given by Boolean JML expressions over Var containing neither  nor
nor  . \(\square \)
. \(\square \)
Now we can formally define ppDATE. As a ppDATE describes properties about a particular system, we assume that every time we make reference to the set of system variables, these variables belong to the system under scrutiny.
Definition 6
Given a set of system variables \(\textit{Sys}\) and a set of ppDATE variables \(V\), a \(\textit{ppDATE} \) m is a tuple \((Q,t,B,q_0,\varPi )\) such that:
-
Q is the finite set of states.
-
t is the transition relation among states in Q, where each transition is tagged with (i) a trigger; (ii) a condition; (iii) an action which may change the valuation of ppDATE variables: \(t \subseteq Q \times trigger \times cond_{\textit{Sys}\cup V} \times action \times Q\).
-
\(B \subseteq Q\) is the set of bad states.
-
\(q_0 \in Q\) is the initial state.
-
\(\varPi \) is a function which tags each state of m with Hoare triples for particular method names in \(\varSigma \): \(\varPi \in Q \longrightarrow {\mathcal P}(cond_{\textit{Sys}} \times \varSigma \times postcond_{\textit{Sys}})\).\(\square \)
We will write  to mean that, given a ppDATE
m whose transition relation is t, \((q,tr,c,a,q')\in t\). The subscript m is omitted if it is clear from the context. In addition, we will use the usual Hoare triple notation
to mean that, given a ppDATE
m whose transition relation is t, \((q,tr,c,a,q')\in t\). The subscript m is omitted if it is clear from the context. In addition, we will use the usual Hoare triple notation  \(\in \varPi (q)\) to denote \((\pi ,\sigma ,\pi ') \in \varPi (q)\).
\(\in \varPi (q)\) to denote \((\pi ,\sigma ,\pi ') \in \varPi (q)\).
Example 3
Consider once again, the ppDATE shown in Fig. 3. It can be formalised as follows: \(m=(Q,t,B,q_0,\varPi )\), where,
-
\(Q = \{ q, q', \texttt {bad } \}\),
-
\(V = \{ c \}\),
-
\( \varSigma = \{ \texttt {fileTransfer},\;\texttt {login},\;\texttt {logout} \}\),
-
\(B = \{ \texttt {bad } \}\),
-
\(q_0 = q.\)
Furthermore, the transition relation t consists of four elements, including:
 and
and  . In addition, relation \(\varPi \) is defined as follows:
. In addition, relation \(\varPi \) is defined as follows:

\(\square \)
In addition to ppDATEs which exist up-front, and ‘run’ from the beginning of a system’s execution, new ppDATEs can be created by existing ones. For instance, one may want to create a separate ‘observer’ for each new user logged into a system. For that, one needs to be able to define parameterised ppDATEs, which we call templates, and allow ppDATEs to create new instantiations of templates. Given a ppDATE m, the creation of a new ppDATE, which will run in parallel to m, can be achieved by using action create on a transition of m. This action receives as arguments a ppDATE template describing the ppDATE to be created and a list of arguments to instantiate the quantified variables on the template. Below, we formally define ppDATE templates.
Definition 7
ppDATE templates of order n are recursively defined as follows:
-
The set of ppDATE templates of order 0 is exactly the set of ppDATEs.
-
Assume C is a syntactic sub-category of ppDATE (Definition 6), i.e., a syntactic (sub-)category of \(Q,t,B,q_0,\) or \(\varPi \), respectively. If m is a ppDATE template of order n, then \(\lambda X\!\!:\!\!C.m'\) is a ppDATE template of order \(n+1\), where \(m'\) is the result of replacing, in m, some (sub-)term trm of category C by X. We call X the template variable of \(\lambda X\!\!:\!\!C.m'\). \(\square \)
In the above definition, a template of order \(n+1\) is defined by ‘abstracting’ over templates of order n, annotating the abstracted ‘hole’ X by the right category, such that template instantiation (see below) can be guaranteed to result in a well-typed ppDATE. When constructing a ppDATE template, the choice of trm in Definition 7 does not matter. Its only role is to carry well-typedness of ppDATEs over to ppDATE templates. Informally, the above definition says that, within \(\lambda X\!\!:\!\!C.m'\), the X can appear anywhere in \(m'\) where a term of category C is expected.
We will refer to ppDATE templates without referring to an order to mean templates that are of order greater than 0. Formally:
Definition 8
The set of ppDATE templates \(T_{ppd}\), is defined as the union of ppDATE templates of order \(n\ge 1\).
If \(\overline{X}\) is a vector of template variables \(X_1,\ldots ,X_n\) and \(\overline{C}\) is a vector of syntactic categories \(C_1,\ldots ,C_n\), then we can write \(\lambda \overline{X}\!\!:\!\!\overline{C}.m\) to mean \(\lambda X_1\!\!:\!\!C_1\ldots \lambda X_n\!\!:\!\!C_n.m\).
Finally, we define what it means to instantiate a ppDATE template:
Definition 9
Given a term trm of syntactic category C, the instantiation of a ppDATE template with term trm, denoted inst(m, trm), is defined by:
where m[X / trm] denotes the result of substituting all occurrences of X in m by trm.
We can expand template instantiation to multiple arguments in the following way. Given \(n\ge 2\), assume \(\overline{X} = X_1,\ldots ,X_n\), and \(\overline{C} = C_1,\ldots ,C_n\), and \(\overline{{trm}} = {trm}_1,\ldots ,{trm}_n\) (with \({trm}_i \in C_i\)). We extend the instantiation function inst to an arbitrary number of arguments in the following way:
ppDATE created using the template illustrated in Fig. 5
Example 4
Figure 5 illustrates a ppDATE template, based on the ppDATE depicted in Fig. 2. Let us call it one-at-a-time. This template has two parameters: C, which represents a condition, and S, which represents a method name. Then, by executing the action create(one-at-a-time,  ), it would instantiate the ppDATE depicted in Fig. 6, i.e., C is instantiated with
), it would instantiate the ppDATE depicted in Fig. 6, i.e., C is instantiated with  and S is instantiated with \(\texttt {brew}\). This ppDATE specifies the property: it is not possible to brew one more coffee cup until the brewing process is done.
and S is instantiated with \(\texttt {brew}\). This ppDATE specifies the property: it is not possible to brew one more coffee cup until the brewing process is done.
In the rest of this work we will only consider the use of deterministic ppDATEs. Formally:
Definition 10
We say that a ppDATE m is deterministic if, for any two transitions of m with same trigger tr which go from a state q to a different state, their conditions are mutually exclusive:

\(\square \)
Note that the previous property should hold for any possible instance of the (boolean) variables appearing in both c and \(c'\). In addition, although determinism on the Hoare triples’ preconditions is not problematic in itself, we choose to extend the determinism condition to ensure that for any two Hoare triples in a single state over the same function have disjoint precondition so as to have a more effective monitoring algorithm of these triples: for any  and
and  in \(\varPi (q)\), \(not (\pi _1\ and\ \pi _2)\).
in \(\varPi (q)\), \(not (\pi _1\ and\ \pi _2)\).
After having defined (individual) ppDATEs, we can now define a network of ppDATEs.
Definition 11
A ppDATE network \(pn\) is represented with a tuple \((M,V,\nu _0,T_{ppd})\):
-
M is a set of ppDATEs. If \(m \in M\), then we say that m = \((Q_m,t_m,B_m,q_{0m},\varPi _m)\).
-
\(V\) is a set of ppDATE variables.
-
\(\nu _0\) is the initial valuationFootnote 5 of variables in \(V\).
-
\(T_{ppd}\) is a set of ppDATE templates.\(\square \)
Note that on a network, whenever a trigger is activated, several ppDATEs can have an enabled transition ready to be fired, i.e., a transition whose trigger is active and whose condition holds. Whenever this happens all these enabled transitions are fired in parallel. Also note that the set of ppDATE variables \(V\) is global to the network of ppDATEs, rather than local to individual ppDATEs. Thereby, \(V\) is effectively the ‘shared memory’ of the network.
Finally, we extend the notion of deterministic ppDATE to a ppDATE network.
Definition 12
A ppDATE network \(pn= (M,V,\nu _0,\) \(T_{ppd})\) is deterministic whenever every ppDATE in M is deterministic and every ppDATE which can be created when executing action create is deterministic. \(\square \)
6 ppDATE semantics
In this section we present the semantics of a network of ppDATEs by introducing structural operational semantics (SOS) rules. These rules will show how a global configuration is shifted to a new one by considering events and system variables valuations in a system trace.
Informally, a global configuration  (of a ppDATE network) consists of a set
(of a ppDATE network) consists of a set  of local configurations (one for each ppDATE in the set of ppDATEs of the network and one for each generated instance of a ppDATE template), and a valuation \(\nu \) of the set of ppDATE variables \(V\) (associated to the ppDATE network). The local configurations store the current state, and record, for each ongoing method execution whose precondition was fulfilled at call time, the postcondition to be checked on exit.
of local configurations (one for each ppDATE in the set of ppDATEs of the network and one for each generated instance of a ppDATE template), and a valuation \(\nu \) of the set of ppDATE variables \(V\) (associated to the ppDATE network). The local configurations store the current state, and record, for each ongoing method execution whose precondition was fulfilled at call time, the postcondition to be checked on exit.
Every time the system under scrutiny generates an event, e.g., by entering or leaving a method, all local configurations in  with enabled transitions will replace their current state value by the state indicated in the fired transition, and execute the action of this transition, all simultaneously. For instance, given a ppDATE
m whose current state is q, and with a transition \(t_1\) of the form
with enabled transitions will replace their current state value by the state indicated in the fired transition, and execute the action of this transition, all simultaneously. For instance, given a ppDATE
m whose current state is q, and with a transition \(t_1\) of the form  , when a system event triggers tr (and condition c holds), then \(t_1\) is fired, state q is replaced by \(q'\) in the appropriate local configuration in
, when a system event triggers tr (and condition c holds), then \(t_1\) is fired, state q is replaced by \(q'\) in the appropriate local configuration in  , and a is executed. If the executed actions contain ppDATE variables assignments, the valuation \(\nu \) is updated. In addition, any action event generated by these executions will be stored in a buffer.
, and a is executed. If the executed actions contain ppDATE variables assignments, the valuation \(\nu \) is updated. In addition, any action event generated by these executions will be stored in a buffer.
Once all the previous enabled transitions are fired, every transition that become enabled by the events in the buffer will be fired as well. For instance, let us assume that action a in transition \(t_1\) (only) generates the action event h, i.e., \(a = h!\), and that a ppDATE
\(m'\) running in parallel to m is in state \(q''\), and has a transition \(t_2\) of the form  . Then, whenever \(t_1\) is fired, execution of h! will add to the buffer an event which will enable \(t_2\), due to the fact that trigger h? is activated by h and its condition (trivially) holds. Therefore, after firing \(t_1\), \(t_2\) will be also fired.
. Then, whenever \(t_1\) is fired, execution of h! will add to the buffer an event which will enable \(t_2\), due to the fact that trigger h? is activated by h and its condition (trivially) holds. Therefore, after firing \(t_1\), \(t_2\) will be also fired.
Note that the buffer will be emptied before firing the transitions enabled by the events consumed from the buffer. Therefore, the buffer only contains events generated by the recent action executions, and no events from previous ones. This procedure is repeated until no new action event is generated, i.e., the buffer is empty. In general, the process may not terminate, however if we want to guarantee termination, we can adopt an approach which ensures that there is no transitive mutual communication dependencies over the set of automata as explained in the original semantics of Larva [18].
6.1 Events, valuations, and traces
ppDATE networks describe which system behaviours are allowed, and which are not. Here, we consider as behaviour basically a series of system events, where each event also comes with a ‘snapshot’ of the values of (visible) system variables, taken at the time where the event occurs. Formally, these snapshots are valuations, i.e., mappings from variables to values (of adequate types). Apart from the observed system, the ppDATE networks themselves may create new events.
An event may therefore either be a system event (i.e., generated by the system under scrutiny due to entering or leaving a method) or an action event (i.e., generated by the execution of an action ! in a ppDATE transition). Formally:
Definition 13
Given a set of method names \(\varSigma \), the syntactic category of events is defined as follows:

\(\square \)
A systemevent consists of a systemtrigger which is indexed with a natural number representing the nth execution of the method associated to the trigger. Such an index will be considered an identifierFootnote 6 unique to each execution of the method.
We distinguish the set of system variables valuations \(\varTheta _{\textit{Sys}}\), with typical element \(\theta \), and the set of ppDATE variable valuations N, with typical element \(\nu \). We represent valuations both as functions and (functional) relationsFootnote 7, i.e., sets of pairs. This means that the notation \(\beta (v) = val\) is equivalent to the notation \((v, val) \in \beta \). The union of valuations is therefore a set union such that, for any two valuations \(\beta \) and \(\beta '\), \(\beta \cup \beta ' = \{ (v,val) \mid (v,val) \in \beta \ or\ (v,val) \in \beta ' \}\). In the presentation of examples, we limit the valuations to those variables which matter for the example at hand, for simplicity.
In our semantic rules, we will use union over valuations only when the domain of valuations do not overlap, as for instance in \(\theta \cup \nu \). Another operation on valuations is the modification of a valuation \(\beta \) at variable x by value val, written \(\beta [x\leftarrow val]\). It is defined as:

Given a set of variables S, a valuation \(\beta \) for S, and condition \(c \in cond_{S}\), we will write \(\beta \models c\) to denote that c is satisfied by \(\beta \). This is however not sufficient for postconditions as they can refer to two valuations, after and before (“ ”) a method’s execution. For that, \(\models \) will be overloaded. Given a set of system variables \(\textit{Sys}\), valuations \(\theta \) and \(\theta '\), and a postcondition \(c \in postcond_{\textit{Sys}}\), we will write \(\theta , \theta ' \models c\) to denote that c is satisfied by \(\theta \) and \(\theta '\). When this is used, \(\theta '\) will be the current valuation of \(\textit{Sys}\) when exiting a certain method execution, whereas \(\theta \) holds the valuation from before that method execution. We only sketch the definition of \(\models \) here as it follows the standard of first-order logic semantics. We use the two semantic truth values T and F. For \(c \in cond_{S}\), we define \(\beta \models c\)
iff
\({eval}_\beta (c) = T\), where \({eval}_\beta \) is recursively defined over the structure of c as standard in first-order logicFootnote 8, with the base case \({eval}_\beta (\texttt {x}) = \beta (\texttt {x})\) for variables x. For \(c \in postcond_{\textit{Sys}}\), we define \(\theta , \theta ' \models c\)
iff
\({eval}_{\theta , \theta '}(c) = T\). The definition of \({eval}_{\theta , \theta '}\) is almost identical to the definition \({eval}_\beta \), with the base case \({eval}_{\theta , \theta '}(\texttt {x}) = \theta '(\texttt {x})\) for program variables x. The only case in the definition where the pre-valuation \(\theta \) matters is the evaluation of
”) a method’s execution. For that, \(\models \) will be overloaded. Given a set of system variables \(\textit{Sys}\), valuations \(\theta \) and \(\theta '\), and a postcondition \(c \in postcond_{\textit{Sys}}\), we will write \(\theta , \theta ' \models c\) to denote that c is satisfied by \(\theta \) and \(\theta '\). When this is used, \(\theta '\) will be the current valuation of \(\textit{Sys}\) when exiting a certain method execution, whereas \(\theta \) holds the valuation from before that method execution. We only sketch the definition of \(\models \) here as it follows the standard of first-order logic semantics. We use the two semantic truth values T and F. For \(c \in cond_{S}\), we define \(\beta \models c\)
iff
\({eval}_\beta (c) = T\), where \({eval}_\beta \) is recursively defined over the structure of c as standard in first-order logicFootnote 8, with the base case \({eval}_\beta (\texttt {x}) = \beta (\texttt {x})\) for variables x. For \(c \in postcond_{\textit{Sys}}\), we define \(\theta , \theta ' \models c\)
iff
\({eval}_{\theta , \theta '}(c) = T\). The definition of \({eval}_{\theta , \theta '}\) is almost identical to the definition \({eval}_\beta \), with the base case \({eval}_{\theta , \theta '}(\texttt {x}) = \theta '(\texttt {x})\) for program variables x. The only case in the definition where the pre-valuation \(\theta \) matters is the evaluation of  -expressions:
-expressions:  . This means that, in postconditions, the post-valuation \(\theta '\) acts as the default, however not inside
. This means that, in postconditions, the post-valuation \(\theta '\) acts as the default, however not inside  -expressions, where instead the pre-valuation \(\theta \) counts. The other additional operator in postconditions is
-expressions, where instead the pre-valuation \(\theta \) counts. The other additional operator in postconditions is  . To handle its evaluation properly, we assume a special system variable named
. To handle its evaluation properly, we assume a special system variable named  . Whenever a non-void method returns, its return value, say val, is assigned to
. Whenever a non-void method returns, its return value, say val, is assigned to  , such that, in the post-valuation \(\theta '\), we have
, such that, in the post-valuation \(\theta '\), we have  .
.
A system trace is a sequence of tuples consisting of an event and a ‘system snapshot’, i.e., a valuation of the system variables taken at the time when that event occurs.
Definition 14
A system trace w is a sequence of tuples in \(systemevent \times \varTheta _{\textit{Sys}}\), i.e. \(w \in (systemevent \times \varTheta _{\textit{Sys}})^{*}\). \(\square \)
6.2 Configurations
Given a system trace w, each tuple in w will shift a global configuration of a ppDATE network to another. Global configurations are defined in terms of local configurations.
Definition 15
Given a set of method names \(\varSigma \), a local configuration is a tuple \((m,q,\rho )\) where m is a ppDATE, \(q\in Q_m\), and \(\rho \subseteq {\mathcal P}({systemevent} \times {postcond}_{Sys} \times \varTheta _{\textit{Sys}})\). \(\square \)
The tuple \((m,q,\rho )\) is a configuration of ppDATE m—where q represents the current state, and \(\rho \) allows to monitor potential violations of Hoare triples. For that, \(\rho \) stores which exit event (\(\in {systemevent}\)) should cause a checking of which postcondition (\(\in {postcond}\)). The semantic rules described below (Sect. 6.4) will guarantee that only method exit events (of the form

) will appear in \(\rho \). During the processing of a trace, the appearance of

at the same time as the current state has a Hoare-triple with a fulfilled precondition, \(\theta \models \pi \), the corresponding postcondition \(\pi '\) is associated with

in \(\rho \), together with \(\theta \). Later, the appearance of

will cause a look-up of

in \(\rho \), in order to check \(\theta , \theta ' \models \pi '\).
Example 5
Recall the ppDATE illustrated in Fig. 2, here called m. Its initial local configuration is \((m,q,\emptyset )\). Then, after firing transition \(t_1\) whenever the system event  (with \(id \in \mathbb {N}\)) occurs, assuming that the field cups is valuated to zero, the next local configuration is
(with \(id \in \mathbb {N}\)) occurs, assuming that the field cups is valuated to zero, the next local configuration is  . \(\square \)
. \(\square \)
Definition 16
Given a ppDATE network \(pn= (M,V,\nu _0,\)
\(T_{ppd})\), a global configuration for \(pn\) is a tuple  such that:
such that:
-
 is a set of local configurations. For each \(m \in M\), there is exactly one q and one \(\rho \), such that \((m,q,\rho ) \in L\). For each \((m,q,\rho ) \in L\), we have \(q \in Q_m\) and either \(m \in M\) or \(m = {inst}(t,\ \overline{{args}})\), for some \(t \in T_{ppd}\).
is a set of local configurations. For each \(m \in M\), there is exactly one q and one \(\rho \), such that \((m,q,\rho ) \in L\). For each \((m,q,\rho ) \in L\), we have \(q \in Q_m\) and either \(m \in M\) or \(m = {inst}(t,\ \overline{{args}})\), for some \(t \in T_{ppd}\). -
\(\nu \) is ppDATE variable valuation with domain \(V\).\(\square \)
Before giving an example, we define the notion of initial global configuration for a ppDATE network.
Definition 17
Given a ppDATE network \(pn= (M,V,\nu _0,\)
\(T_{ppd})\) where \(m \in M\) is the tuple \((Q_m,t_m,B_m,q_{0m},\varPi _m)\), the initial global configuration
\(C_{init}(pn)\) is defined as the tuple  , where \(L_0 = \{ (m,q_{0m},\emptyset ) \mid m \in M \}\) is the set of initial local configurations. \(\square \)
, where \(L_0 = \{ (m,q_{0m},\emptyset ) \mid m \in M \}\) is the set of initial local configurations. \(\square \)
Example 6
Let us assume a ppDATE network \(pn= (\{m,m'\},\{v\},\{(v,0)\},\emptyset )\), such that  . The initial global configuration for \(pn\) is \(C_{init}(pn) = (L_0,\{(v,0)\})\), where \(L_0 = \{ (m,q_{0m},\emptyset ),(m',q_{0m'},\emptyset )\}\). Then, if the given transition is fired, the new global configuration is \((L',\{(v,1)\})\), where \(L' = \{ (m,q_{0m},\emptyset ),(m',q_{1m'},\emptyset )\}\). \(\square \)
. The initial global configuration for \(pn\) is \(C_{init}(pn) = (L_0,\{(v,0)\})\), where \(L_0 = \{ (m,q_{0m},\emptyset ),(m',q_{0m'},\emptyset )\}\). Then, if the given transition is fired, the new global configuration is \((L',\{(v,1)\})\), where \(L' = \{ (m,q_{0m},\emptyset ),(m',q_{1m'},\emptyset )\}\). \(\square \)
In the above example, the action \(v=v+1\), does not generate any event. In general, however, actions may generate events. For storing action events (and process them in the next step), we introduce the concept of extended global configuration.
Definition 18
Given a ppDATE network \(pn= (M,V,\nu _0,\)
\(T_{ppd})\), and a set of system variables \(\textit{Sys}\), an extended global configuration for \(pn\) is a tuple  such that:
such that:
-
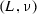 is a global configuration for \(pn\),
is a global configuration for \(pn\), -
\(E \subseteq {\mathcal P}(\xi )\) is a set of events,
-
\(\theta \in \varTheta _{\textit{Sys}}\) is a system variables valuation. \(\square \)
E contains the events to be processed in the next (small) step. In the operational semantics to be described below, E will either be a singleton set containing a system event, or a set of action events generated by the executions of actions in the latest transition.
Example 7
Let us assume a ppDATE network \(pn= (\{m,m'\},\{v\},\{(v,0)\},\emptyset )\), such that  ,
,  , \(\varPi _m(q_1) = \{ \{\pi \} \texttt {foo} \{\pi '\} \}\), with \(q_1\) and \(q_1'\) the initial states of m and \(m'\), respectively. In addition, let us assume that
, \(\varPi _m(q_1) = \{ \{\pi \} \texttt {foo} \{\pi '\} \}\), with \(q_1\) and \(q_1'\) the initial states of m and \(m'\), respectively. In addition, let us assume that  is an extended global configuration for \(pn\) (for some index \(id \in \mathbb {N}\)), where \(L_1 = \{ (m,q_1,\emptyset ),(m',q_1',\emptyset )\}\). Then, when the given transition of m is fired, given that \(\pi \) holds and the current system variables valuation is \(\theta \), the next extended global configuration for \(pn\) is \(C_2 = (L_2,\{(v,0)\},\{h\},\emptyset )\), where
is an extended global configuration for \(pn\) (for some index \(id \in \mathbb {N}\)), where \(L_1 = \{ (m,q_1,\emptyset ),(m',q_1',\emptyset )\}\). Then, when the given transition of m is fired, given that \(\pi \) holds and the current system variables valuation is \(\theta \), the next extended global configuration for \(pn\) is \(C_2 = (L_2,\{(v,0)\},\{h\},\emptyset )\), where  . After that, event h in \(C_1\) triggers the given transition of \(m'\), leading to the extended global configuration \(C_3 = (L_3,\{(v,1)\},\emptyset ,\emptyset )\), where
. After that, event h in \(C_1\) triggers the given transition of \(m'\), leading to the extended global configuration \(C_3 = (L_3,\{(v,1)\},\emptyset ,\emptyset )\), where  . \(\square \)
. \(\square \)
The structural operational semantics given in Sect. 6.4 formalises such behaviour.
6.3 Semantics of actions
When assigning meaning to actions, there are two levels to consider. One is the level of the local actions, executed when an individual ppDATE takes a transition. The semantics of those is sequential, as defined below. On top of the assignments changing the ppDATE variable valuation, the local actions may generate events, and create new instances of ppDATE templates.
The other level is parallel actions, where we compose simultaneous actions of transitions taken in parallel by different ppDATEs. Here, we need to devote special care to exclude conflicting writes to, as well as race conditions between reads and writes from/to, the same variable. Also, we need to make sure that if only one ppDATE writes to x, then the parallel composition propagates this effect. All this makes it necessary to keep track of all reads and writes at the local level, prior to execute the parallel composition. However, the treatment of the local effects and newly created ppDATEs is simpler: we just take the union of those when doing the parallel composition.
Definition 19
For each \(a\in {action}\), its meaning \([\![a]\!]_{\theta ,\nu }\) (relative to system/ppDATE variable valuations \(\theta \) and \(\nu \)) is given by a tuple \((\nu ', W, R, E, {New})\), where:
-
\(\nu ' \in N\) is a ppDATE variable valuation computed (locally) in a,
-
\(W \subseteq V\) is a set of ppDATE variables written to in a,
-
\(R \subseteq V\) is a set of ppDATE variables read from in a,
-
\(E \subseteq \textsf {actevent}\) is a set of action events generated in a,
-
\({New} \subseteq \textit{ppDATE} \) is a set of ppDATEs newly created in a.
Given that pvars returns the ppDATE variables appearing in its argument(s), \([\![a]\!]_{\theta ,\nu } = (\nu ', W, R, E, {New})\) is defined as follows

\(\square \)
Following the definition of actions (Definition 2), the prog in the last line above is a side-effect free program, i.e., it has no effect which could be noticed in the current formalism, which is why we can simulate it with skip. prog will have purposes orthogonal to our formalisation, like logging.
We are now in the position to define the parallel composition of actions. Imagine we have a configuration with 5 parallel ppDATEs, 3 of which have enabled transitions, with actions \(a_1\), \(a_2\), and \(a_3\), respectively. Assume moreover that the current ppDATE variable valuation is \(\nu \). The parallel composition of the meaning of \(a_1\), \(a_2\), and \(a_3\), is performed by \({mergeParalActs}_\nu (\{[\![a_1]\!], [\![a_2]\!], [\![a_3]\!]\}) = (\nu ', E', {New}')\). The function mergeParalActs takes a set of semantic actions as input, and computes a resulting valuation \(\nu '\), a resulting set of events \(E'\), and a resulting set of newly generated ppDATEs, \({New}'\). The sets \(E'\) and \({New}'\) will simply be the union of the corresponding sets from \([\![a_1]\!]\), \([\![a_2]\!]\), and \([\![a_3]\!]\). But the resulting valuation is slightly more involved. Actions may conflict (e.g., we write to the same variable in different actions), or have race conditions (i.e., we read from a variable and write to it in different actions). In those cases, we leave the result of mergeParalActs deliberately undefined. In all other cases, the different effects of the actions are merged. The index of the merging function, \(\nu \), serves as a fall back for those variables which have not been written to. In particular, \(\nu ' = \nu \) in case the set of actions to be merged is empty.
These explanations are formalised in the following function, merging a set of action meanings (Definition 19):
Definition 20
\({mergeParalActs}_\nu (\{(\nu _1, W_1, R_1, E_1, \textit{New}_1), \ldots , (\nu _n, W_n, R_n, E_n, \textit{New}_n) \})\) =

\(\square \)
Note that if there are no actions to merge, we have \({mergeParalActs}_\nu (\emptyset ) = (\nu ,\emptyset ,\emptyset )\).
6.4 Structural operational semantics
In this section we give structural operational semantics rules (SOS) for ppDATEs. These rules will have the following generic form:

where name is a label used to identify the rule, Goal is the property enforced by the rule and the premises \(H_1, \cdots , H_n\) are assumptions over the values of the Goal.
6.4.1 Auxiliary predicates
In the semantic definitions given below, we use the following predicates.
activatedBy Given a (transition) trigger tr and an event e, predicate \({activatedBy}(tr,e)\) holds if tr and e match, in the following way:

For instance, the trigger

is activated by the systemevent

and the trigger h? is activated by actevent h (generated before by the execution of action h!). \(\square \)
nextState Given a local configuration \((m,q,\rho )\), a state \(q'\), an event e, a system variables valuation \(\theta \) and a ppDATE variables valuation \(\nu \), predicate \({nextState}\) holds whenever there exists an enabled transition on m going from q to \(q'\). We formally write this as follows,

\(\square \)
checkOnExit Given a local configuration \((m,q,\rho )\), a system event

, a system variables valuation \(\theta \), and a postcondition \(\pi '\), predicate \({checkOnExit}\) holds if there exists a condition \(\pi \) such that the Hoare-triple  is associated to state q, and \(\pi \) holds. We formally write this as follows,
is associated to state q, and \(\pi \) holds. We formally write this as follows,

\(\square \)
enabled Given a local configuration l, an event e, a system variables valuation \(\theta \), and a ppDATE variables valuation \(\nu \), predicate \({enabled}\) holds if either l has an enabled transition or it has a Hoare triple associated to q which has to be memorised. Formally,
\(\square \)
toBeExecuted Given a local configuration \((m,q,\rho )\), an event e, a system variables valuation \(\theta \), a ppDATE variables valuation \(\nu \), and an action a, predicate \({toBeExecuted}\) holds if there exists an enabled transition such that a is its action. Formally,

\(\square \)
6.4.2 Small steps for local configurations
The first step to define SOS rules describing the behaviour of a ppDATE network is to introduce rules showing how a local configuration performs a small step.
Given an event e, a system variables valuation \(\theta \), and a ppDATE variables valuation \(\nu \), a small local configuration step (or simply small step local), written  , takes a local configuration \((m,q,\rho )\) to some other local configuration \((m,q',\rho ')\). This step relation is defined by the rules shown in Fig. 7. If e is an entry event of the form
, takes a local configuration \((m,q,\rho )\) to some other local configuration \((m,q',\rho ')\). This step relation is defined by the rules shown in Fig. 7. If e is an entry event of the form

, there are three different possibilities: (i) there is an enabled transition in m going from state q to state \(q'\), and there is a Hoare triple  associated to q such that \(\pi \) holds (\({entry}_1\)); (ii) there is an enabled transition in m going from state q to \(q'\), but no Hoare triple
associated to q such that \(\pi \) holds (\({entry}_1\)); (ii) there is an enabled transition in m going from state q to \(q'\), but no Hoare triple  associated to q such that \(\pi \) holds (\({entry}_2\)); or (iii) there are no enabled transitions in m, but there is a Hoare triple
associated to q such that \(\pi \) holds (\({entry}_2\)); or (iii) there are no enabled transitions in m, but there is a Hoare triple  associated to q such that \(\pi \) holds (\({entry}_3\)).
associated to q such that \(\pi \) holds (\({entry}_3\)).
In case of (\({entry}_1\)), the next state reached by the enabled transition is \(q'\), and \(\rho \) gets extended by the tuple

, in order to track the information about the postcondition which has to be checked upon the exit of method \(\sigma \). Entry event identifiers are assumed to be unique in traces, and thereby,

is unique in \(\rho \). In case of (\({entry}_2\)) and (\({entry}_3\)), only one of these two effects takes place. Then, apart from entry events, whenever e is either an exit event, i.e., it has the form

, or an action event, by the rules exit and act, respectively,  results in the local configuration \((m,q',\rho )\), where \(q'\) is the next state reached by the enabled transition.
results in the local configuration \((m,q',\rho )\), where \(q'\) is the next state reached by the enabled transition.
6.4.3 Small steps for extended global configurations
Given an extended global configuration  , the relation small step for extended global configurations (or simply small step global), written as \(\rightarrowtail \), takes EC to some extended global configuration
, the relation small step for extended global configurations (or simply small step global), written as \(\rightarrowtail \), takes EC to some extended global configuration  by following rule iter (depicted in Fig. 8). Note that in the rule’s premises we define the set
by following rule iter (depicted in Fig. 8). Note that in the rule’s premises we define the set  of all the local configurations
of all the local configurations  such that m has an enabled transition whose triggers are activated by the events in E.
such that m has an enabled transition whose triggers are activated by the events in E.  is used to define both the set
is used to define both the set  of local configurations in
of local configurations in  that will not change, and the set
that will not change, and the set  of the local configurations obtained after performing a small step on the local configurations in
of the local configurations obtained after performing a small step on the local configurations in  . These two sets are used to define
. These two sets are used to define  . Next, we define the set Acts of all the actions which label the ‘firing’ transitions, and merge the meaning of those actions, which results in the valuation \(\nu '\) and events \(E'\) of the new extended global configuration. We also initialise local configurations
. Next, we define the set Acts of all the actions which label the ‘firing’ transitions, and merge the meaning of those actions, which results in the valuation \(\nu '\) and events \(E'\) of the new extended global configuration. We also initialise local configurations  for the newly created ppDATEs from \({New}'\). Finally,
for the newly created ppDATEs from \({New}'\). Finally,  is the union of
is the union of  ,
,  and
and  .
.
Note that if mergeParalActs is undefined, due to conflicts in parallel variable assignments (see Definition 20), then no global small step is defined, i.e., the execution aborts.
6.4.4 Big steps for global configurations
Given a ppDATE network \(pn=(M,V,\nu _0,T_{ppd})\), a global configuration  such that for all \((m,q,\rho ) \in L\), \(m \in M\) and \(q \in Q_m\), and \(\nu \) a valuation of the ppDATE variables \(V\), a system event e and the system variables valuation \(\theta \), the relation big step rules for global configurations (or simply big step global), written
such that for all \((m,q,\rho ) \in L\), \(m \in M\) and \(q \in Q_m\), and \(\nu \) a valuation of the ppDATE variables \(V\), a system event e and the system variables valuation \(\theta \), the relation big step rules for global configurations (or simply big step global), written  , shifts
, shifts  to some global configuration
to some global configuration  , written
, written  , by rule shift given in Fig. 9. Note that here e and \(\theta \) are external to the global configuration of the ppDATE network: they come from the system acting as input to each step of the global configuration.
, by rule shift given in Fig. 9. Note that here e and \(\theta \) are external to the global configuration of the ppDATE network: they come from the system acting as input to each step of the global configuration.
This rule means that whenever e occurs while the current system variables valuation is \(\theta \),  shifts to
shifts to  if the transitive closure of the relation small step global (\(\rightarrowtail \), Fig. 8) takes the extended global configuration
if the transitive closure of the relation small step global (\(\rightarrowtail \), Fig. 8) takes the extended global configuration  to the extended global configuration
to the extended global configuration  . We need the transitive closure because the execution of actions may generate action events which also have to be consumed, meaning that we iterate using small step global until the set obtained by applying rule iter is the empty set. After having reached
. We need the transitive closure because the execution of actions may generate action events which also have to be consumed, meaning that we iterate using small step global until the set obtained by applying rule iter is the empty set. After having reached  , the small steps are saturated, because any configuration \((\textvisiblespace ,\textvisiblespace ,\emptyset ,\textvisiblespace )\) is a fixed-point of \(\rightarrowtail \).
, the small steps are saturated, because any configuration \((\textvisiblespace ,\textvisiblespace ,\emptyset ,\textvisiblespace )\) is a fixed-point of \(\rightarrowtail \).
Lemma 1
For each set of local configurations L, ppDATE variable valuation \(\nu \), and system variables valuation \(\theta \), the extended global configuration  is a fixed-point of the relation small step global, i.e.,
is a fixed-point of the relation small step global, i.e.,

Proof
In rule iter (Fig. 8), if \(E = \emptyset \), then  , and
, and  . From the note below Definition 20, we deduce that \((\nu ', E',{New}') = (\nu ,\emptyset ,\emptyset )\), such that
. From the note below Definition 20, we deduce that \((\nu ', E',{New}') = (\nu ,\emptyset ,\emptyset )\), such that  , and
, and  . Therefore,
. Therefore,  . \(\square \)
. \(\square \)
We can now define the semantics of ppDATEs by identifying how a system trace changes the global configuration associated to a network of ppDATEs.
Definition 21
We define how a system trace \(w \in (systemevent \times \varTheta _{\textit{Sys}})^{*}\) shifts a ppDATE from the global configuration  to the global configuration
to the global configuration  , written
, written  , by induction over w:
, by induction over w:

For this definition we will overload the operator we previously introduced to represent the relation big step global, i.e., \(\Rightarrow \) since it is straightforward to distinguish between the two from the context.
6.5 Valid traces and violating traces
Before defining violating system traces, we have to introduce the notion of counter-example.
Definition 22
Given a network of ppDATEs \(pn=(M,V,\nu _0,T_{ppd})\), a system trace \(w \in (systemevent \times \varTheta _{\textit{Sys}})^{*}\) is called a counter-example if  , and (i)
, and (i)  ; or (ii)
; or (ii)

,  and
and

\(\theta , \theta ' \not \models \pi '\). \(\square \)
(The symbol \(\mathbin {++}\) represents the concatenation of traces.) This means that a counter-example either (i) ends in a bad state (in one of the local configurations), or (ii) ends with the exiting of a method execution who’s postcondition (stored in \(\rho \)) is currently violated. Note that (i) and (ii) are not exclusive, so a counter-example may have both properties at once. Also note that violations of preconditions when entering methods is not mentioned here. In our semantics, the violation of preconditions does not as such result in a counter example. It only means that the postcondition of the corresponding Hoare triple does not need to be checked further on (see \({entry}_2\), Fig. 7).
Example 8
Recall the ppDATE
m shown in Fig. 2, and let us assume that it is in state q. Then, for any system variables valuation \(\theta \),  is a counter-example corresponding to the case (i) of Definition 22.
is a counter-example corresponding to the case (i) of Definition 22.
In addition, if the trigger  is activated and the postcondition of the Hoare triple \(\{\texttt {true}\}\ \texttt {cleanF()}\ \{\texttt {cups == 0}\}\) is violated when method cleanF terminates, then
is activated and the postcondition of the Hoare triple \(\{\texttt {true}\}\ \texttt {cleanF()}\ \{\texttt {cups == 0}\}\) is violated when method cleanF terminates, then  is a counter-example corresponding to the case (ii) of Definition 22. \(\square \)
is a counter-example corresponding to the case (ii) of Definition 22. \(\square \)
Definition 23
The set of violating system traces of a ppDATE network \(pn\), written \(\mathcal{VT}(pn)\), is defined to be system traces which have a counter-example of \(pn\) as a prefix. \(\square \)
Definition 24
The set of valid system traces of a ppDATE network \(pn\), written \(\mathcal{VAT}(pn)\), is defined to be the system traces which are not violating. \(\square \)
Example 9
The following system traces, for the coffee machine system of Fig. 2, are all valid:


 \(\square \)
\(\square \)
7 From ppDATE to DATE
In our framework, KeY first tries to prove all Hoare-triples of a ppDATE m, and then the partial proofs are used to get an optimised ppDATE \(m'\). To make the property \(m'\) runtime-checkable, we further translate away the (remaining/optimised) Hoare triples, to arrive at a set of parallel (pure) DATEs that can be processed by Larva.
In this section, we formally define DATEs, we present the algorithm used by StaRVOOrS to translate ppDATEs into DATEs, finally, after introducing the semantics of DATEs, we prove soundness of the translation.
7.1 DATE
DATE [18] is a formalism similar to ppDATE, except that the automata do not include Hoare triples in the states. DATEs also include support for timers, which are not in ppDATEs. However, since the work we present here does not use timers, we leave them out from the formalisation. Formally:Footnote 9
Definition 25
A DATE is a ppDATE of the form \((Q,t,B,q_0,\varPi _{\emptyset })\), where relation \(\varPi _{\emptyset }\) represents that there are no Hoare triples assigned to any of the states in Q, i.e., \(\varPi _{\emptyset }(q) = \emptyset \), \(\forall q \in Q\). \(\square \)
Note that since a DATE is effectively a ppDATE, the semantics for DATEs are already covered by the semantics of ppDATEs. We will also refer to a (deterministic) network of ppDATEs where each ppDATE in the network is a DATE, as a network of DATEs and similarly DATE templates.
7.2 Translation from ppDATEs to DATEs
Here we present how to translate a ppDATE (network) into a DATE (network). However, first, let us intuitively analyse how the ppDATE depicted in Fig. 2, which we will refer to as m, can be translated into a DATE \(m'\).
For simplicity, we assign the following names to the different Hoare triples in the states of m.
-
\(h_1\):
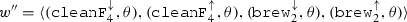
-
\(h_2\):

-
\(h_3\):
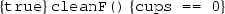
-
\(h_4\):
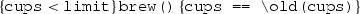
Then, we begin the translation by generating the DATE template illustrated in Fig. 10, which will be used to create DATEs in charge of controlling the postconditions of the previous Hoare triples.
Next, we start dealing with the translation of the transitions of m. \(m'\) will have exactly the same set of states as m, and it will have similar transitions to the ones of m. The only difference is that the transitions in \(m'\) will also have to address the verification of the Hoare triples. For instance, while being in state q, if the method brew() is executed and the precondition of \(h_1\) holds, then its postcondition will have to be verified whenever method brew() finishes its execution.
Therefore, for every transition of the form

such that a Hoare triple  is in q, \(m'\) will include a modified version of this transition in such a way that whenever this transition is fired, if \(\pi \) holds, then the execution of its action will have to create an instance of template \(exit\_cond\_checker\). Thus, transitions \(t_1\), \(t_3\) and \(t_4\) (recall Fig. 2) are modified as follows:
is in q, \(m'\) will include a modified version of this transition in such a way that whenever this transition is fired, if \(\pi \) holds, then the execution of its action will have to create an instance of template \(exit\_cond\_checker\). Thus, transitions \(t_1\), \(t_3\) and \(t_4\) (recall Fig. 2) are modified as follows:
where,
-
\(a_1\!:\)
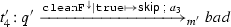
-
\(a_2\!:\)
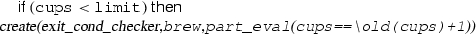 ;
; -
\(a_3\!:\)
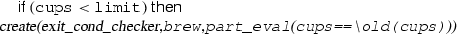 .
.
In the previous transitions we have used as the conditions of the if-expressions in actions \(a_1\), \(a_2\) and \(a_3\), the preconditions of the different Hoare triples to be verified in each case. Moreover, function part_eval partially evaluates its argument, replacing the expressions  operator the current value of e. If a postcondition does not include such operator, then part_eval is the identity. Note that even though the if-expression in the transitions \(t_1'\) and \(t_4'\) may seem unnecessary, we include it anyway in order to exactly reflect how the translation algorithm works.
operator the current value of e. If a postcondition does not include such operator, then part_eval is the identity. Note that even though the if-expression in the transitions \(t_1'\) and \(t_4'\) may seem unnecessary, we include it anyway in order to exactly reflect how the translation algorithm works.
In addition, if at a certain state, a Hoare triple has to be verified, but in that state there are no outgoing transitions with an event related to the method in the Hoare triple, then a new transition is added to \(m'\) in order to be able to control such Hoare triple. For instance, in state q the following self-transition has to be added in order to verify \(h_2\) and \(h_3\).
where,
-
\(a_4\!:\)
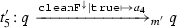
Again, we use the preconditions of the Hoare triples as conditions of the previous action.
Given a transition  such that (i) tr fires upon exiting a method, or (ii) tr fires upon entering a method but there is no Hoare triple associated to this method in q, these transitions remain untouched, i.e., it is translated as
such that (i) tr fires upon exiting a method, or (ii) tr fires upon entering a method but there is no Hoare triple associated to this method in q, these transitions remain untouched, i.e., it is translated as  . For instance, transition \(t_2\) is translated as follows.
. For instance, transition \(t_2\) is translated as follows.
-
\(t_2': \)
Figure 11 illustrates the DATE obtained when translating m following the previous steps. Note that whole translation would consist on the previous DATE and the generated template exit_cond_checker.
Translation to DATE of the ppDATE illustrated in Fig. 2
7.2.1 Translation algorithm
For clarity of presentation we give two algorithms, one for the case when no Hoare triples clashes arise, and one for the full case. Intuitively, we call it a clash if the behaviour of a method \(\sigma \), in a certain ppDATE state q, is defined by both, a Hoare triple in q, and an outgoing transition from q. Formally, we define a clashing Hoare triple as follows.
Definition 26
Given a ppDATE network \(pn=(M,V,\nu _0,T_{ppd})\) such that every ppDATE
\(m \in M\) is defined as the tuple \((Q_m,t_m,B_m,q_{0m},\varPi _m)\), a Hoare triple  \(\in \varPi _{m}(q)\), for some \(q \in Q_m\), is called clashing if an outgoing transition from q is guarded by trigger
\(\in \varPi _{m}(q)\), for some \(q \in Q_m\), is called clashing if an outgoing transition from q is guarded by trigger

(i.e.,

). A clash-free ppDATE is a ppDATE with no clashing Hoare triples. \(\square \)
We now present the algorithm to translate a clash-free ppDATE network into a DATE network. The translation works by replacing each Hoare triple  in a state q of a ppDATE by a new reflexive transition (from q to q) triggered by an entry into function \(\sigma \) such that the precondition \(\pi \) holds, and a parallel DATE is created, checking the postcondition.
in a state q of a ppDATE by a new reflexive transition (from q to q) triggered by an entry into function \(\sigma \) such that the precondition \(\pi \) holds, and a parallel DATE is created, checking the postcondition.
We assume a function part_eval
\(\in {postcond} \mapsto {cond}\), which removes  constructs in postconditions. The function performs partial evaluation—replacing each
constructs in postconditions. The function performs partial evaluation—replacing each  with the current value of e. Our algorithm syntactically places the part_eval function in an action that will be executed when the according method is entered, i.e., partial evaluation does not happen during the translation algorithm, but at runtime, when the method is entered.
with the current value of e. Our algorithm syntactically places the part_eval function in an action that will be executed when the according method is entered, i.e., partial evaluation does not happen during the translation algorithm, but at runtime, when the method is entered.
Algorithm 1
Given a clash-free ppDATE network \(pn=(M,V,\nu _0,T_{ppd})\), such that every ppDATE \(m \in M\) is defined as the tuple \((Q_m,t_m,B_m,q_{0m},\varPi _m)\), we can construct a DATE network equivalent to \(pn\) in the following manner:
-
1.
With each Hoare triple
 in a ppDATE state, replace in \(\pi '\) each instance of the
in a ppDATE state, replace in \(\pi '\) each instance of the  by the variable ret. This variable will represent the value returned by the method associated to the Hoare triple/ makes its own instance of this variable).
by the variable ret. This variable will represent the value returned by the method associated to the Hoare triple/ makes its own instance of this variable). -
2.
Generate the following DATE template: \({exit\_cond\_checker} = \lambda \ S,A:\varSigma ,cond.\)
This template will be used to create DATEs handling the verification of the postcondition of the method.
-
3.
Transform M, the set of ppDATEs of \(pn\), into the set of DATEs \(M' = \{ m' \mid m' = (Q_m,t'_m,B_m,q_{0m},\varPi _{\emptyset }), m \in M \}\) such that \(t'_m\) follows the rules below:
-
3a.
each Hoare triple
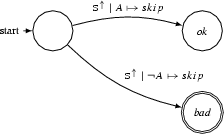 in \(\varPi _{m}(q)\) is replaced by
in \(\varPi _{m}(q)\) is replaced by 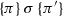
, where \(a = \textsf {create}(exit\_cond\_checker,\sigma ,\textit{part}\_\textit{eval}(\pi '))\);
-
3b.
each transition
 remains unchanged, i.e.
remains unchanged, i.e. 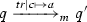
-
3a.
-
4.
Translate \(T_{ppd}\) (the set of ppDATE templates in pn) into a set of DATE templates \(T_{d}\) by repeatedly applying step 3a. and 3b. to the body of templates.
-
5.
Extend the set \(T_{d}\) by including the template generated in step 2. Let us call this extension \(T_{d}'\).
-
6.
Finally, the resulting DATE network is defined to be \((M',V,\nu _0,T_{d}')\).
This translation works well except that it would introduce non-determinism when the ppDATE includes clashes. To extend the translation to work in the presence of clashes, we transform Hoare triples clashing with a transition into a family of disjoint transitions, each of which performs the transition but also checks whether the postcondition checker should be created.
Algorithm 2
Given a (possibly clashing) ppDATE network \(pn\), we construct a network of DATEs equivalent to \(pn\) by using Algorithm 1 except that we replace steps 3.a and 3.b, by the following:
-
3\(a_1\). Each non-clashing Hoare triple:
 in \(\varPi _m(q)\) is turned into a transition
in \(\varPi _m(q)\) is turned into a transition 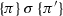
-
3\(a_2\). For each clashing Hoare triple:
 \(\in \varPi (q)\), clashing with n outgoing transitions,
\(\in \varPi (q)\), clashing with n outgoing transitions, 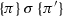
(\(0 \le k < n\)):
-
Replace
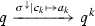
with:
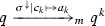
;
-
Add the following transition:
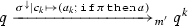
,
where, in both cases, \(a = \textsf {create}(exit\_cond\_checker,\sigma ,\textit{part}\_\textit{eval}(\pi '))\)
-
-
3b. each transition
 such that either \(\varPi _{m}(q) = \emptyset \), \(\varPi _{m}(q) \ne \emptyset \) but there is no Hoare triple associated to trigger tr, or trigger tr is activated by an exit event, remains unchanged, i.e.
such that either \(\varPi _{m}(q) = \emptyset \), \(\varPi _{m}(q) \ne \emptyset \) but there is no Hoare triple associated to trigger tr, or trigger tr is activated by an exit event, remains unchanged, i.e. 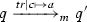 .
.
7.3 Proof of soundness of the translation algorithm
In this section we will show that the translation algorithms introduced in the previous section are sound.
7.4 Coupling invariant lemmas
Here, we formally introduce two lemmas which together form the coupling invariant that is used to prove soundness. The proofs of these lemmas can be found in “Appendix 1”.
Lemma 2 states that given a trace, both a ppDATE network \(pn\) and its translation to DATE will change their initial global configuration to global configurations  and
and  , respectively, such that \(\nu = \nu '\), and that for every
, respectively, such that \(\nu = \nu '\), and that for every  where m is in \(pn\), there is a local configuration \((m',q',\emptyset ) \in \tilde{L}\) such that \(m'\) is the translation of m and both m and \(m'\) are in the same state, and vice versa.
where m is in \(pn\), there is a local configuration \((m',q',\emptyset ) \in \tilde{L}\) such that \(m'\) is the translation of m and both m and \(m'\) are in the same state, and vice versa.
In this lemma we represent the translation of a single ppDATE to DATE with the function \(\kappa \in \textit{ppDATE} \mapsto \textit{DATE} \).
Lemma 2
Given a network of ppDATEs \(pn=(M,V,\nu _0,T_{ppd})\), its translation ppd2DATE
\((pn)\) = \((M',V,\nu _0,T_{d}')\), a trace \(w \in (systemevent \times \varTheta _{\textit{Sys}})^{*}\), and the global configurations  and
and  ,
,

Lemma 3 states that given a trace, if this trace shifts a ppDATE network \(pn\) and its DATE translation from their respective initial global configuration to some global configurations  and
and  , respectively, then for each entry
, respectively, then for each entry

in a \(\rho \) component of a local configuration in  there is one local configuration in
there is one local configuration in  whose DATE component is an instance of the template \(exit\_cond\_checker\) in charge of controlling \(\pi '\), and vice versa.
whose DATE component is an instance of the template \(exit\_cond\_checker\) in charge of controlling \(\pi '\), and vice versa.
Lemma 3
Given a network of ppDATEs \(pn=(M,V,\nu _0,T_{ppd})\), its translation ppd2DATE
\((pn)\) = \((M',V,\nu _0,T_{d}')\), a trace \(w \in (systemevent \times \varTheta _{\textit{Sys}})^{*}\), and the global configurations  and
and  ,
,

where,

\(\square \)
7.4.1 Proof of soundness
We can now prove the soundness of the translation algorithm. Below we provide the formalisation of this property and an intuitive explanation for it. However, a rigorous proof of this theorem can be found in “Appendix 2”.
Theorem 1
Given a ppDATE network \(pn=(M,V,\nu _0,T_{ppd})\), and its translation ppd2DATE \((pn)\) = \((M',V,\nu _0,T_{d}')\),
Proof
To prove the soundness of the translation algorithm we will show that both a ppDATE network \(pn\) and its translation to a DATE network have the same set of violating traces. Intuitively, we will prove that given a trace w which is violating for \(pn\), i.e., \(w \in \mathcal{VT}(pn)\), is also violating for \(pn\)’s translation, i.e., \(w \in \mathcal{VT}(\textit{ppd2DATE}(pn))\), and vice versa.
In the case when \(w \in \mathcal{VT}(pn)\), by definition of counter-examples of ppDATEs, w has a prefix \(w'\) such that either (i) \(w'\) takes the initial global configuration \(C_{init}(pn)\) to a global configuration \((L',\nu ')\) such that the state component of \(L'\) is a bad state; (ii) given a method \(\sigma \) and a system variables valuation \(\theta '\), \(w'\) can be written as

such that \(w_1\) takes \(C_{init}(pn)\) to a global configuration \((L',\nu ')\) where there exists a local configuration in \(L'\) whose \(\rho \) component contains a tuple

, such that \(\pi '\) fails to be satisfied in the ‘moment’ event

appears.
In the case of (i), we use the fact that (by Lemma 2), if \(w'\) takes the translation from the initial global configuration \(C_{init}(\textit{ppd2DATE}(pn))\) to a global configuration \((\tilde{L},\nu )\), for every local configuration in \(L'\), there is a local configuration in \(\tilde{L}\) such that its state component is the same. Thus, there is a local configuration in \(\tilde{L}\) whose state component is a bad state, which means that \(w'\) is a counter-example of the translation as well.
In the case of (ii), due to the fact that a Hoare triple  has to be verified, we know that some local configuration will have a \(\rho \) component such that
has to be verified, we know that some local configuration will have a \(\rho \) component such that

. We can now use the fact that by Lemma 3, tuple is handled by a DATE in the translation (which verifies the postcondition). Thus, there exists a DATE controlling \(\pi '\) which fails moving to a bad state, i.e., \(w'\) is a counter-example of the translation as well.
In order to prove the opposite direction, we assume \(w \in \mathcal{VT}(\textit{ppd2DATE}(pn))\). Again, since this is a counter-example and this is a DATE (and thus cannot fail due to a violated postcondition), it can be only the case that w has a prefix \(w'\) such that this prefix takes the initial global configuration \(C_{init}(\textit{ppd2DATE}(pn))\) to a global configuration \((\tilde{L},\nu )\) such that there is a local configuration in \(\tilde{L}\) whose state component is a bad state. Then, assuming that \(w'\) takes \(pn\) from the initial global configuration \(C_{init}(pn)\) to a global configuration \((L',\nu ')\), we proceed to do a case analyses depending whether the bad state belongs to a DATE which was controlling the postcondition of a Hoare triple or not. In the affirmative case, we will use this fact to show that, given certain method \(\sigma \) and a system variables valuation \(\theta '\), \(w'\) can be selected to be a prefix which can be written as

such that \(w_1\) takes \(C_{init}(pn)\) to a global configuration \((L',\nu ')\) where the verification of the postcondition fails whenever event

occurs. Therefore, \(w'\) is a counter-example of \(pn\). Finally, (by Lemma 2), there is a local configuration in  such that its state component is the same as the bad state in
such that its state component is the same as the bad state in  . Therefore, \(w'\) is a counter-example of \(pn\). \(\square \)
. Therefore, \(w'\) is a counter-example of \(pn\). \(\square \)
8 The StaRVOOrS tool implementation
In this section we present how the (fully automatic) verification tool StaRVOOrS [16] implements the framework presented in Sect. 4. To illustrate this, we use a running example of a bank system in which users log in to perform transactions.Footnote 10 The set of logged-in users is implemented as a Hashtable object, whose class represents an open addressing hashtable with linear probing as collision resolution. Method add, which is used to add objects into the hashtable, first attempts to put the corresponding object at the position of its computed hash code. However, if that index is occupied, then add searches for the nearest following index which is free. Figure 12 depicts a code snippet for this method. Within the hashtable object, users are stored into an array arr. This means that the set of logged-in users has its capacity limited by the length of arr. In order to check in a straightforward manner whether the capacity of arr is reached or not, a field size keeps track of the amount of stored objects and a field capacity represents the (total) number of objects that can be added into the hash table. In addition, this system has to fulfil the properties described with the ppDATE template depicted in Fig. 13. This template specifies the following properties:
-
(i)
A user has to be logged-in in order to perform a deposit, i.e. a deposit should happen between a login and a logout.
-
(ii)
Provided there is space in the hashtable, executing method add with object o and key k should add the object to the table.
Property (i) is verified with the transitions of the ppDATE template, whereas property (ii) is represented by the Hoare triple in state \(q_1\). If  , then there is room in the hashtable for one more element, and if method add places the object o in the hashtable, there exists an index in the array arr such that o is placed in that index, i.e.,
, then there is room in the hashtable for one more element, and if method add places the object o in the hashtable, there exists an index in the array arr such that o is placed in that index, i.e.,

. Note that the given Hoare triple is only included in state \(q_1\) since only a successful login leads to the execution of the method add, i.e., this Hoare triple is context dependent; and that  means that method login associated to the trigger is the one defined within object f. In addition, we assume that the specification of the system has a ppDATE with a single state q and single transition of the form
means that method login associated to the trigger is the one defined within object f. In addition, we assume that the specification of the system has a ppDATE with a single state q and single transition of the form  , such that the trigger
, such that the trigger  is activated by the declaration of an object o of the class UserInterface. Thus, this ppDATE creates an instance of the template in Fig. 13 every time an object of the class UserInterface is declared.
is activated by the declaration of an object o of the class UserInterface. Thus, this ppDATE creates an instance of the template in Fig. 13 every time an object of the class UserInterface is declared.
8.1 ppDATE specification as an input script for StaRVOOrS
Before describing how StaRVOOrS works, we need to introduce how a ppDATE specification is written as an input script for this tool. Below, we show the input script for the ppDATE template illustrated in Fig. 13, and the ppDATE which creates its instances. In addition, we give a brief description of each one of the sections this script. For a full description on how to write ppDATEs as an input script for our tool, one may refer to the StaRVOOrS User Manual.Footnote 11

The section IMPORTS lists the Java packages which may be used in any of the other sections of the script, in this case UserInterface and Hashtable. The section TEMPLATES contains the description of the ppDATE templates (tagged by TEMPLATE). Here, the section TRIGGERS is used to declare the different triggers which may be used in the transitions of the ppDATE, i.e, login_exit, logout_entry, deposit_entry, and the section PROPERTY describes the different states, i.e., q1, q2 and bad, and transitions of the ppDATE. Note that the syntax q1 (add_ok) associates the Hoare triple tagged as add_ok to state q1. This means that the Hoare triple add_ok has to be verified if the method associated to it, in this case method add, is executed whenever the ppDATE is in state q1. The section GLOBAL contains the description of the ppDATE. Here, ppDATEs are described in the same manner as in a TEMPLATE section. However, note that it is also possible, as it is the case in our example, to use the special section PINIT when describing the section PROPERTY. Section PINIT represents a ppDATE with single state, and a looping transition which is fired every time an object of the class listed within this section (UserInterface in our example) is declared, leading to the creation of an instance of the listed template for that object (prop-deposit-temp in our example). We have included this special case because it is quite common to have ppDATEs only focus on creating instances of a template upon declaration of a particular object. Regarding the section CINVARIANTS, class invariants are described by the syntax class_name {invariant}, meaning that invariant has to be fulfilled by all the methods in the class class_name. These invariants are only meant as a help for the deductive verification of the Hoare triples (see Sect. 8.2). If no invariants are needed, then this section can be omitted. Finally, the section HTRIPLES gives a list of named Hoare triples (tagged by HT). Here, PRE describes the precondition of the Hoare triple, POST describes the postcondition of the Hoare triple, METHOD indicates which one is the method associated to the Hoare triple, and ASSIGNABLE lists the (class) variables that might be modified when the method associated to the Hoare triple is executed. Note that the predicates in invariants, pre- and postconditions follows JML-like syntax and pragmatics. For instance, in the Hoare triple add_ok the second semicolon separates the range predicate (\(\texttt {i}>\texttt {=0}\)&& \(\texttt {i}<\texttt {capacity}\)) from the desired property over integers in that range, (arr[i]==o).
8.2 Running StaRVOOrS
StaRVOOrS is a fully automatic verification tool which takes the Java source code of the system under scrutiny and a file with the ppDATE specification for this system and produces (i) a runtime monitor, (ii) an instrumented version of the system given as input with event generation and additional code infrastructures required, (iii) a report summarising the results of the deductive verification of the Hoare triples, and (iv) a refined version (if any) of the provided ppDATE specification.
This tool implements the framework described in Sect. 4 with each stage of the framework, i.e., Deductive Verification, Specification Refinement, Translation and Instrumentation, and Monitor Generation, being performed automatically by the tool. Below, we describe the implementation of these stages through the use of the working example.
8.2.1 Deductive verification
The first step performed by StaRVOOrS is the deductive verification of the Hoare triples associated to the states of the ppDATE (template) using KeY. To accomplish this, StaRVOOrS extracts the Hoare triples specified in the ppDATE script, converts them into JML contracts, and then annotates these contracts in the Java sources, before the corresponding method declaration. For instance, the following JML contract associated to method add is extracted from the Hoare triple add_ok:

Note that the requires clause describes the precondition of add, the ensures clause describes the postcondition of add, and the assignable clause lists the (class) variables that might be modified when add is executed.
Once all the JML contracts are in place, i.e., they are annotated in the code, StaRVOOrS uses KeY to verify them. First, KeY generates proof obligations in Java Dynamic Logic for each JML contract. Next, it attempts to prove the contracts automatically. Finally, it stores the results of all the verification attempts in a XML file. Here, note that even though it could be possible to allow for user interaction (using KeY ’s elaborate support for interactive theorem proving), we chose to use KeY in automatic mode, since StaRVOOrS targets users untrained in theorem proving. StaRVOOrS generates a report summarising the results produced by KeY in an easy to understand format.
Using our running example, when KeY tries to verify the previous JML contract, it will result in a partial proof. This analysis is shown in the following fragment of the generated XML file:

This indicates that while KeY was symbolically executing method add, there was a branching in the condition arr[hash_function(key)] = null, leading to two possible execution paths (depending on its truth value). Recalling the code snippet in Fig. 12, this condition corresponds to the condition on the if-expression in line 4. Thus, the execution path for the condition arr[hash_function(key)] = null corresponds to the case where the array arr has a free slot at the hash code of key, whereas the execution path for the condition !arr[hash_function(key)] = null corresponds to the case where the program enters the while-loop in line 10, searching for the next free slot in arr. In addition, in the XML, the component verified represents whether KeY was able to prove the branch of the proof (verified=true), or not (verified=false). Therefore, from the previous fragment of the XML file we know that KeY was able to close the branch where the array arr has a free slot (= null) at the hash code of key, but it was not able to verify the other case (where the program enters a loop searching for the next free slot). The main reason why KeY was not able to prove the latter case is the lack of loop invariants to deal with the while-loop.
8.2.2 Specification refinement
The output of KeY is then used to refine the Hoare triples in the specification based on what was (partially) proved. The Hoare triples associated to JML contracts which were fully verified by KeY are entirely removed from the specification, while the precondition of the Hoare triples associated to partially proved JML contracts are refined based on what KeY managed to prove. The new precondition is the conjunction of the original precondition with the disjunction of new preconditions corresponding to open proof goals, i.e., the path condition on each different execution paths. Note that StaRVOOrS generates a new ppDATE specification script based on such refinements, instead of modifying the provided ppDATE script.
In the example, the precondition of the Hoare triple add_ok will be refined with the condition for the one goal not closed by KeY, i.e., !(arr[hash_function(key)] == null). The Hoare triple will thus be strengthened as follows:

8.2.3 Translation and instrumentation
Once the refined ppDATE specification is ready, StaRVOOrS translates it into (pure) DATE formalism using the algorithm from Sect.7.2. This enables the monitor generation by Larva (explained in the next stage). In addition, in order to properly address the refined ppDATE, our tool operationalise the conditions and instruments the code, as described below.
8.2.4 Pre/postcondition operationalisation
In this step, the tool syntactically analyses the specification for expressions in pre- and postconditions of the Hoare triples which may have to be operationalised, i.e., transformed into algorithmic procedures. For instance, transforming either existential or universal quantifications into loops.
During the operationalisation process, the tool creates Java code containing the implementation of all necessary methods for runtime verification, including those generated to algorithmically check the pre/postconditions.
In our example, as the postcondition of the Hoare triple add_ok has an existential quantifier, it has to be operationalised, producing the following method:

The for-loop declaration in line 3 is created from the conditions in the range of the existential quantification, i.e., \(\texttt {i}>\texttt {=0}\)&& \(\texttt {i}<\texttt {capacity}\), and the condition of the if-expression in line 4 is created from the condition in the body of the existential quantification, i.e., arr[i]==o. Thus, if any value on the range of the existential quantification fulfils its body, then this method returns true, i.e., exists a value that fulfils the existential quantification. Otherwise, it returns false, i.e., it does not exist a value fulfilling the existential quantification.
8.2.5 Code instrumentation
Next, StaRVOOrS instruments the Java source code of the system adding identifiers to each method associated to a Hoare triple in the refined ppDATE specification script, and additional code to get fresh identifiers. As mentioned in Sect. 4, these identifiers will be used to distinguish different executions of the same method. However, in order to avoid modifying all the calls to these methods in the entire system, we have opted to introduce this instrumentation in the form of auxiliary methods. For instance, in our working example the method add has to be instrumented, resulting in:

The method addAux implementation corresponds to the body of method add in Fig. 12. This method represents the instrumentation of method add with the extra argument Integer id, which is used as identifier. In addition, method add now simply calls addAux, but generating a fresh identifier for the call using function fid.getNewId.
Moreover, the previously generated DATE specification is modified accordingly, to refer to the instrumented version of the methods. In our example, the DATE specification would be modified to refer to method addAux instead of method add.
8.2.6 Monitor generation
Finally, StaRVOOrS uses Larva to automatically generate a monitor from the DATE specification obtained in the previous stage. Larva takes this DATE and generates the monitoring system and aspects instrumenting the communication between the system and the monitor [19].
9 Case study: SoftSlate Commerce
SoftSlate Commerce (or simply SoftSlate) [36] is an open-source Java shopping cart web application designed following a Model-View-Controller architecture. A user of SoftSlate sends a request to a server hosting the application via a web browser. Then, the server processes the received request and executes an action associated to it (Controller layer). Such action may require to interact with and/or modify the information in the database (Model layer), e.g., information about users, products, orders, etc. Finally, once the request is fully processed, the server sends back a response to the user. The information in this response will be reflected on a web page loaded on the browser (View layer). The administrator of the application interacts with it in a similar fashion.
SoftSlate offers a basic implementation of a shopping cart web application featuring outer space related pictures, whose server is set up by using Apache Tomcat [1]. This implementation is meant to be used by developers to start building their own web applications.
In this case study we analyse an extension of the SoftSlate basic implementation. This extension increases modularity of parts of the implementation, to better link it to the required properties. Basically, we have created a few helper methods in order to better observe the various steps performed by a user to checkout a purchase. In addition, we have modified a few methods to receive an entire object instead of some of its components, and to properly access the components.
As our main focus is to verify the source code offered by SoftSlate, in our extension we are not adding any new feature to the ones already provided in the basic implementation, i.e., the functionality of the basic implementation and our extension is the same.
Note that when we started developing this case study there was an open source version of SoftSlate available online. However, later, this version was not available anymore. Thus we cannot distribute the sources we have used. However, in [38] one may find the files for the ppDATE specifications described below.
9.1 ppDATE specification
Here we introduce two ppDATEs specifications, one describing a property related to the log in and log out of users in the web application, and one describing a property related to the checkout of the purchases performed by the users of the application. These properties address basic functionalities which we consider that a web cart application should offer.
Note that even though we could have either described more properties or specified more control- and data-oriented behaviour in the properties we are depicting in this section, the ppDATEs introduced here are sufficient to highlight the benefits of using StaRVOOrS in a real application. In addition, for readability reasons, Hoare triples are not going to be included on the figures depicting the ppDATEs. Moreover, as the application is placed in a server, the monitor generated by our tool is placed in the server as well.
9.1.1 Login–logout
Users can freely browse through the web site of the application. However, if they want to buy products (i.e., pictures), they have to be logged in the application, to be able to proceed to the checkout section.
Figures 14 and 15 illustrate the specification. The ppDATE in Fig. 14 creates instances of the ppDATE template login–logout whenever an object of class User is created, and the ppDATE template login–logout (Fig. 15) describes the following properties:
-
(i)
A user has to be logged in the application in order to perform a purchase, i.e., the checkout of a purchase can only happen between a login and a logout.
-
(ii)
If a user is logged in, then that user cannot successfully log in again in the application until she logs out from it.
-
(iii)
If a user is not logged-in, then that user cannot successfully log out from the application.
-
(iv)
A user can only proceed to the checkout section if her status is a valid one.
-
(v)
A user who is not a costumer cannot proceed to the checkout section.
The transitions of the ppDATE described by the template control properties (i)–(iii). Initially, this ppDATE is in state logout. Then, whenever there is a successful login, the ppDATE moves to state login. Later, once the user logs out, the ppDATE returns to state logout. Therefore, if a purchase is performed (i.e., an order is checkout) while the ppDATE is in state login, then the ppDATE remains in that state. However, if a purchase is performed while the ppDATE is in state logout, then it shifts to state bad.Footnote 12 In addition, while being at state logout, if an attempt to log in is not successful, then the ppDATE stays in that state; and if there is a successful logout, then the ppDATE shifts to state bad due to the fact the user is considered to be logged out while the ppDATE is in that particular state. Something similar happens when the ppDATE is in state login. (In Fig. 15, Fails and Ok are abbreviations, for presentation purpose, of real Java expression checking the failure or success of the respective operations.)
Regarding properties (iv) and (v), they are addressed using Hoare triples. For instance, property (iv) is represented as follows:

As the only non valid statuses are “Registered” and “Unapproved”, if the status of the user is not one of these values, then starting a purchase, i.e., using method prepareCheckout, should return “success”. Regarding property (v), a user is only considered to be a costumer if she has logged-in into the application. Even though this property seems to be similar to property (i), this similarity is only apparent. Property (i) only addresses the proper order in which the methods should be executed, whereas property (v) focuses on controlling how the data related to a user is modified during such executions. Finally, both properties (iv) and (v) are only placed in state login because that is the only state in which a successful purchase can occur, i.e., (iv) and (v) are context dependent data-oriented properties.
9.1.2 Purchases checkout
We consider that a purchase starts whenever an item (i.e., a product) is added to the cart. A user can continue either by adding other items to the cart or by removing some of the items from the cart. We refer to all the items in a cart as the order.
Once the user finishes the creation of her order, she may proceed to the checkout page. In SoftSlate, a checkout is realised in four steps. First, the user enters the contact information and delivery address. Then, the shipping method is selected (either ground transport or air transport), after which the user enters her credit card details. Finally, a confirmation for the order is requested. If accepted, the order is settled. Later, when the user receives the items, the order is considered to be completed.
Note that a user can modify her order as long as she has not yet confirmed it. If so, whenever she proceeds to the checkout section again, all its required steps have to be performed one more time. In addition, if the user removes all the items in an order, clears the cart or logs out,Footnote 13 then the order is considered to be removed.
Figures 16 and 17 illustrate a ppDATE specification where the ppDATE in Fig. 16 creates instances of the ppDATE template prop-checkout whenever an object of class User is created, and the ppDATE template prop-checkout (Fig. 17) describes the following properties:
-
(1)
The checkout of a purchase should be performed following the four required steps.
-
(2)
It should not be possible to buy zero or less items.
-
(3)
The expiration date of the credit card should not earlier than the current date.
-
(4)
The price of a product should be positive.
-
(5)
Before a purchase is completed, taxes should be processed.
-
(6)
The total cost of a purchase should be equal to the sum of the prices of all the products to be purchased.
-
(7)
If the price of an item changes, then its price in the order of the user should be updated.
Again, consider the transitions of the ppDATE described by the template. When the first item is added to the cart, the ppDATE shifts to state one. In this state, once the first step of the checkout is completed, the ppDATE shifts to state two, and so on until reaching state four. In state four, once the order is settled, the ppDATE shifts back to state start in order to wait for a possible new purchase. Moreover, while being at either state one, two, three or four, if there is any change in the order, then the ppDATE shifts to state one, meaning that all the steps of the checkout have to be performed again. This is enough to control property (1).
Note that for readability reasons, in states one, two, three and four we have not included transitions going to state start whenever the user logs out, the cart is cleared or all the items in the cart are removed. In addition, we have not included transitions going to state bad from either state one, two, three or four if a step of the checkout was performed in a wrong way. For instance, if while being at state one either a second step, a third step or a fourth step of a purchase occurs instead of the first step, then the ppDATE shifts to state bad.
Regarding property (7), since the method in charge of updating the orders whenever the price of an item changes in the database is fully implemented using different Java libraries, writing an appropriate Hoare triple for it would require introducing several work-arounds. Instead, we implemented a method which compares the prices of the items in the order with their prices in the database, and include it as part of the information validation process corresponding to the fourth step of the purchase. Thereby, in state four there are two transitions controlling the result of this method [Most real world applications of this kind would guarantee prices for some defined duration, and adjust it when that time has passed. For simplicity, we only model the latter in (7).].
Properties (2–6) are addressed with Hoare triples. Properties (2–4) are related to the integrity of the information introduced by either the users, in the case of (2) and (3), or the administrator, in the case of (4), on their requests to the server. Property (5) is related to the proper processing of taxes associated to the items in the current order. Property (6) enforces that the total amount that the user has to pay for her order should be equal to the sum of the totals of all the items included in the order.
As items could be added to the cart at any time during a purchase, property (2) is included in all the states of the ppDATE, with exception of the state bad.
On the other hand, property (3) is context dependent. This property should only be enforced on state three, which represents the step of a purchase where a user enters her credit card details. Note that, as it is in this case, a single property might be associated to several Hoare triples. For instance, below we introduce two of the four Hoare triples which describe property (3),


Regarding property (4), we assume that initially all the data in the database is properly set. Therefore, this property should only be enforced every time that the administrator modifies the price of an item. As this may happen at any time during a purchase, this property is included in all the states of the ppDATE, with exception of the state bad.
In relation to property (5), in SoftSlate whenever the taxes of items are processed, the status of the order changes to “Tax processed”. This change is done by using the following method,

This method might be simply specified as follows:

However, due to the fact that taxes are processed while the ppDATE is in state four, that we know which particular value should be written when updating the status of the order, i.e., “Tax processed”, and that ppDATE allows us to write context dependent properties, we include in four the following Hoare triple:

Regarding property (6), it is represented by the following Hoare triple:

In short, the new total amount is equal to the old total amount plus the amount of the newly added item.
9.2 Using StaRVOOrS
The previous specifications were analysed on a PC Pentium Core i7 using a sinlge core. A similar setup was used to perform the experiments in the following Sect. (9.3).
Since SoftSlate uses many Java libraries, to perform static analysis on its source code it was necessary to generate stub files for some of these libraries in order to allow KeY to find information about their method declarations.
9.2.1 Login–logout
When feeding StaRVOOrS with this property and the source code of SoftSlate, it automatically generates a runtime monitored version of the application and a report which summarises the results obtained from the static analysis.
Regarding the result of the translation, it consisted of a DATE specification which looks exactly like the original ppDATE specification. The static analysis and instrumentation process takes 11 seconds, where most time is used by KeY to statically analyse the Hoare triples (approximately 7 seconds). By inspecting the report we notice that KeY successfully verified all the Hoare triples in the ppDATE specification. Thus, the refined ppDATE specification to be translated was already a DATE, .i.e, the translation process did not have add any new transitions to the specification.
9.2.2 Purchases checkout
When feeding StaRVOOrS with this property and the source code of SoftSlate, it automatically generates a runtime monitored version of the application and a report which summarises the results obtained from the static analysis. The static analysis and instrumentation process takes 23 seconds, where most time is used by KeY to statically analyse the Hoare triples (approximately 20 seconds). By inspecting the report we can see that properties (2) and (3) are fully proved, properties (4) and (5) are not proved, and that property (6) and (7) are partially proved.
Regarding property (7), as KeY does not have any information about the state of purchases, and this property is context dependent, obviously, it is not able to prove it. However, thanks to the use of StaRVOOrS we can include this property in an appropriate state of the ppDATE, fact which guaranties that whenever a purchase reaches such state, this property is going to be verified at runtime by the generated monitor.
Regarding property (6), the report shows that this property postcondition is going to be checked upon entering method updateOrderAndDeliveryTotals only if the condition user.getOrder() != null holds. Thereby, this property is refined by StaRVOOrS as follows:

This refined version of property (6) is the one verified by the generated monitor at runtime.
Finally, the result of the translation consisted on one DATE to create instances of the obtained DATE template prop-checkout (the translation of its homonymous ppDATE template), and three generated DATE templates whose instances verify properties (4)–(6). Note that the instances of the generated DATE templates are created by actions on the transitions of the DATE template prop-checkout.
9.3 Experimentation
9.3.1 Properties analysis
9.3.2 Login–logout
Although this property may appear to be simple, by verifying it we discovered unexpected behaviour in SoftSlate when a user logs in, performs a purchase, and logs out. In spite of the fact that the user was logged in the application, the monitor flagged a violation of property (iii). It turned out that after performing the purchase, SoftSlate replaced the object representing the logged-in user by a new one.
More concretely, the log file generated by the monitor showed that a new monitor, corresponding to a new instance of the template login–logout, was generated for the ‘new’ user. So, we got two different user objects, the one who originally logged in into the system (let’s call it \(u_{{logged}}\)) and the new generated one (let’s call it \(u_{new}\)). The new monitor (corresponding to the user \(u_{new}\)) would then be in its initial state, that is in the state logout. Thus, when the (real) user tried to log out, the monitor corresponding to user \(u_{new}\) shifted to a bad state, while the monitor corresponding to user \(u_{logged}\) remained in state login. As a consequence, property (iii) was violated.
In order to understand whether this is an error in the implementation we inspected the source code to better understand how the login and purchase were implemented. We found that each instance of class User was associated to a session, whose information was unique for each different execution of the application. Though the relation between (real) users and the session is bijective (for each real user there is a unique session, and vice versa), there were (at least) two instances of the class User, \(u_{logged}\) and \(u_{new}\), associated with each session.
We were not sure what were the real reasons behind this design decision, but the implementation seemed correct, and our specification did not capture this situation. So, we decided to change our ppDATE template to capture this by including a Boolean variable reflecting whether the (real) user was connected or not, which we refer to as active. The updated ppDATE template is shown in Fig. 18. Further executions of the system (reproducing the previous executions and providing new ones) did not violate this property.
Extension on the ppDATE describing properties related to the log in and log out of users illustrated in Fig. 15
9.3.3 Purchases checkout
We also run the system many times in order to analyse whether the execution of SoftSlate fulfils the properties described by the provided ppDATE specification.
First, we performed several purchases to analyse if property (1) was fulfilled. We added some items to the cart, bought them, and added and removed items at any stage of the checkout of a purchase, and then completed the purchase. None of these operations violated this property. We re-run the system executing the same steps as above to check property (5), which was not violated.
Next, we continued performing purchases, but this time the administrator of the application introduced modifications in the price of some items during the purchases. By doing so we were able to analyse whether properties (4), (6) and (7) were violated.Footnote 14
In order to check whether property (4) held, we executed the system logged in as administrator and as a normal user (in parallel). The user performed a purchase (and thus the item was added to the cart), and as administrator we modified the price of the item introducing a negative value as its new price. At this moment the monitor reported that property (4) was violated. By inspecting the price of the modified item in the database, we could confirm that the negative value provided by the administrator was actually assigned to the item. This clearly was an error. We corrected this by not allowing to input negative numbers, and thus property (4) was finally satisfied.
On the other hand, when the administrator modified the price of an item introducing a positive value as its new price, then property (4) was fulfilled as expected. However, we noticed that property (7) was violated: some of the prices of the items in the order did not match with the prices in the database.Footnote 15 In particular, the mismatched values were those that were modified by the administrator: the new prices were propagated to the database but they were not updated in the visualisation of the cart (to the user). This was an error, and when inspecting the code we realised that there was a method implementing the propagation of the update, but it was not called when the change (done by the administrator) was performed. We have not yet corrected this error in the original code.
Property (6) was not violated by any of the previous executions.
9.3.4 Runtime verification overhead analysis
In this section we analyse the overhead added to SoftSlate by the monitor generated using StaRVOOrS. To perform this analysis, we considered three scenarios: several users performed one purchase, 10 purchases in a row, and 100 purchases in a row.
Table 1 shows the average execution time of: (a) an unmonitored execution of SoftSlate; (b) a monitored execution of SoftSlate using the original ppDATE specification S, and (c) a monitored execution of SoftSlate using specification S \(^\prime \), obtained from S via static (partial) proof analysis using StaRVOOrS. In all three scenarios, the users and the server hosting SoftSlate were ran in different computers, but with identical specifications. Note that as SoftSlate is an interactive application, in order to perform these experiments we have implemented a program which uses url connections to access the application and perform a purchase.Footnote 16 Therefore, our experiments consist on executing this program repeatedly and measuring its execution time.
As expected, adding a monitor to SoftSlate introduced overhead on its execution time. However, when we compared the overhead added by the monitor which uses the original ppDATE specification (without optimisations) (b), with the one added by the monitor which was generated using StaRVOOrS (c), one could notice a reduction in overheads gained by using our tool.
Through optimisations introduced by StaRVOOrS, we obtained a version of the monitor which, in relation to the times in (a), introduced in average a 25% of overhead to the execution time of the system. On the contrary, the monitor without the optimisations of StaRVOOrS introduced a 50% of overhead to the execution time.
Even though these results are not as impressive as the one we obtained on the case study analysed in [3] (Mondex, also reported here in Sect. 10), the monitor generated by our tool for SoftSlate still has a better performance than the one which uses the original ppDATE specification. The main difference lies in the amount of Hoare triples which have to be runtime verified in each case study. Every time an experiment is performed to analyse SoftSlate, the optimise monitor generated by StaRVOOrS verifies 3 Hoare triples, whereas the monitor using the original ppDATE specification (without optimisations) verifies 5. However, each experiment performed on Mondex requires the verification of 7 Hoare triples when using the unoptimised version of the monitor, whereas the optimised one does not have to verify any Hoare triples at all (cf. Sect. 10).
10 Case study: Mondex
Mondex is an electronic purse application which is used by smart cards products [32], and has been considered as a verification benchmark problem since 2006, originally appearing as case study as part of the Verified Software Grand Challenge [42]. Mondex’s original sanitised specification can be found in [37]. It consists of a Z specification [35], together with hand-written proofs of several properties.
Mondex essentially provides a financial transaction system supporting transferring of funds between accounts, or purses. Whenever a person has to make a transaction, electronic money is taken from their electronic purse and transferred to the target electronic purse. Such transactions are performed following a multi-step message exchange protocol: (1) the source and destination purses should (independently) register with the central fund transferring manager; (2) await a request to deduct funds from the source purse; (3) await a request to add the funds to the destination purse; and finally (4) an acknowledgement is sent to indicate that the transfer took place before the transaction ends.
In our version of this case study we consider a Java implementation running on a desktop computer instead of a Java Card implementation running on smart cards. The principal difference in the implementation is that in our version some methods return values to indicate whether their output is normal or erroneous, instead of raising Java Card exceptions. Our specification is strongly inspired by the JML formalisation presented in [40]. The full specification and source code of our case study can be found in [38]. The specification (see Fig. 19) consists of a ppDATE with 10 states, 25 transitions and a total of 26 different Hoare triples. The implementation of Mondex consists on 514 lines of code (without comments) which are distributed over 8 files.
Note that ppDATE allows us to represent the overall status of the observer using ppDATE states. In other pre/post-style specification approaches, one would instead introduce additional data, and corresponding additional constraints, as is indeed done in [40] when specifying Mondex with JML. Such additional data implies a certain complexity of the specification, which somehow lacks the structure of the problem. We believe that specifications of this kind are sometimes developed with an automaton in mind. In ppDATE, we can make that automaton explicit. This being said, we want to stress again that we took great advantage of the JML specification of Mondex in [40].
10.1 ppDATE property
Figure 19 illustrates a ppDATE describing the top-level specification of Mondex. To keep the ppDATE readable, the description of the different Hoare triples are not included in the figure. (We will show some of them below.)
At the automaton level, the ppDATE specifies the control-oriented property which indicates how the multi-step message exchange protocol is suppose to work. For instance, after the parties are initialised (encoded in state Parties Initialised), a message requesting to transfer more money than the one available in the source purse should fail. Otherwise, such a message should take the ppDATE to a state in which the protocol now allows for the money to be transferred to the destination purse (named Money deducted). Note that the ppDATE will not take any explicit action whenever the state BAD STATE is reached. It will stay in this state until the whole monitor is restarted.
In contrast, the pre/postconditions properties placed on the states of the ppDATE ensure the well-behaviour of the methods involved in the individual steps of the protocol, behaviour which obviously changes together with the status of the protocol. For instance, once two purses agree on participating in a money transfer and the destination purse has requested for certain amount of money, (encoded in state Money Deducted), method val_operation which transfers money from the source purse to the destination one should succeed and increase the money of the destination purse by the sent amount (provided the limit of its account has not been reached), as shown in the Hoare triple below:

On the other hand, if the same method is accessed after the funds have already been transferred (encoded in state Money deposit), then the destination purse content should remain unchanged, and the request should be ignored:

Note that both Hoare triples above have the same precondition, but depending on the state of the ppDATE (i.e., the state of the protocol) different behaviours (i.e., postconditions) are expected for method val_operation.
10.2 Using StaRVOOrS
For this case study, we have used a setup identical to the one described in Sect. 9.2. Running StaRVOOrS on the source code of Mondex and the ppDATE depicted in Fig. 19 automatically produces a runtime monitored version of the application and a report summarising the results obtained from the static analysis. The static analysis and instrumentation process takes 1 minute 20 seconds, where most time is used by KeY to statically analyse the Hoare triples (approximately 1 minute 15 seconds).
The monitor generated by our tool consists one DATE to control the main property, and 24 DATEs templates to control the postconditions which were only partially verified by KeY, with 106 states and 196 transitions in total. By inspecting the report we can see that the two Hoare triples associated to the initialisation and termination of a transaction were fully proved, and that all the other 24 triples about the methods involved in the transaction protocol were the partially verified ones. For instance, let us consider the property already discussed in the previous section about method val_operation, which we will refer here to as val_operation_ok:

The report shows that the postcondition will have to be checked at runtime only when the condition status != 2 holds upon entering val_operation (i.e., the destination purse is not waiting for the arrival of the requested money). Thus, the previous Hoare triple was refined by StaRVOOrS as follows:

This refined version of the property is the one which will be runtime verified by the generated monitor.
The size of the source code of the original implementation of Mondex was 23.5kB. After running the tool, the total size of all the generated files (i.e. instrumented version of the source code and the implementation of the monitor) grows to 277.4kB.
10.3 Experimentation
We now summarise the experimental results of applying our approach to the Mondex case study.
10.3.1 Normal behaviour
The Table 2 shows the execution time of: (a) an unmonitored implementation of Mondex; (b) a monitored implementation using the original ppDATE specification S, and (c) a monitored implementation using specification S’, obtained from S via static (partial) proof analysis using StaRVOOrS. In all three scenarios, the system is run over a numbers of transactions which do not violate the specification. Note that in case (c), statically analysing all the Hoare triples took KeY around 1 minute, which however is done once and for all prior to deployment.
As one would expect, the addition of a monitor to the system introduces execution time overhead (b). However, if we compare this overhead to the one added by the monitor which was generated by StaRVOOrS (c), one can see a substantial overhead reduction, gained through the use of our tool. Through our optimisations we obtain a version which is at least 10 times faster for a low number of transactions, and this factor rises up to 900 when the number of transactions is increased. This significant reduction in execution time overheads is mainly due to the fact that monitoring data-centric properties may be prohibitively expensive. In fact, using S, each method invocation involved in the transfer protocol creates an additional DATE that will check the postcondition on exit. However, the postcondition checker is only created if the precondition holds on method invocation. In this case study, this causes large overheads when monitoring the unoptimised specification. Using the results from static verification, however, strengthens the preconditions by additional constraints, which in the Mondex case state were always falsified at invocation time, meaning that no postcondition checker is ever created. Apparently, in Mondex, the algorithmic complexity of the individual method implementations is limited enough such that KeY could fully prove the methods correct (automatically) if only the internal constraints corresponding to the ppDATE states were provided to KeY. But as they are not, KeY generates those constraints (closed branch conditions, see Sect. 4), and adds their negation to the preconditions. With that, the preconditions are never true at runtime. This phenomenon cannot be fully generalised to cases where KeY really lacks (automated) proving power for the code at hand, or where the code is faulty of course.
10.3.2 Faulty behaviour
Usually, it is hard to get full proofs when using a static verifier like KeY without considering either user interaction with the prover or the use of special annotations, e.g., loop invariants, to help the prover on its task. However, it might be the case that the static verifier does not succeed in closing a branch in the proof due to the fact that the remaining open goal was generated by an erroneous execution path. KeY cannot per se determine which one of these situations is dealing with. Fortunately, Larva can detect the occurrence of the erroneous case whenever it appears at runtime.
We have intentionally injected errors into Mondex source to verify that the optimised monitor still detects them. Consider the case of a bug in the implementation of method val_operation—the value of variable balance is incremented with a different amount from the one given in the specification of the method. When analysing property val_operation_ok, KeY obviously does not manage to prove it. Therefore, the whole property will have to be runtime verified. The monitor spots this error reaching a bad state.
In addition, we have also considered incomplete and wrong specifications. In the case where the specification is too weak, the implementation may fulfil it for wrong reasons. As in all verification approaches, we may not catch this kind of problem. When using our verification approach there lies the possibility that the problem propagates to a state in which the specification is strong enough to identify it. For example, consider if the specification does not specify how the variables of a purse should be initialised by the ConPurse class constructor, and there is an implementation error where the variable balance is initialised to \(-1\) instead of being initialised to 0. In spite of the error in the specification, KeY would proceed normally with the proofs and the previous particular situation would not be directly controlled on runtime. However, this erroneous initialisation leads to an erroneous initial charge of money in the purses (performed using the method chargeMoney in class ConPurse). As balance is negative, the previous method fails to update it with the new amount of money. Hence, after applying chargeMoney the value of balance is still \(-1\). Thereby, whenever a purse tries to begin a transfer, either the method initialising the sender purse during a transaction or the method initialising the receiver purse during a transaction will fail its execution (the former due to insufficient funds and the latter due to a value overflow). This failure leads to an unsuccessful termination of the transfer, which is detected by the monitor controlling the transaction protocol and takes it to a bad state. This analysis can be easily conclude by inspecting the execution trace generated by the monitor. This trace allows one to backtrack through the execution of the different methods until reaching which was the problem which was the cause the failure. In this scenario, it is important to note that in spite of the fact that we have not enforced any Hoare triple on the constructor of class ConPurse, it was specified and proved correct using KeY.
On the other hand, if a Hoare triple has an overly weak precondition or overly strong postcondition, then KeY will fail to prove the Hoare triple. StaRVOOrS thus ensures that the Hoare triple is checked at runtime, which allows us to realise when expected results arise. Finally, another scenario is when the user uses erroneous data, not detected by the application. For instance, a user might request a transfer exceeding the amount of money in a purse. In this situation, the method initialising the sender purse during a transaction will fail its execution due to insufficient funds and this will lead to an unsuccessful termination of the transfer. This unsuccessful termination is detected by the runtime monitor controlling the transaction protocol.
11 Related work
The combination of different verification techniques is gaining more and more popularity. One active area of research is the combination of testing and static analysis, e.g. [8, 14, 17, 20, 25, 26, 39]. A direct comparison of our work with those would not be fully fair as we have different objectives. We are not aiming at generating test cases, but at monitoring the actual post-deployment runs of the system. What we have in common is that static analysis/verification is used to limit the dynamic efforts, there by filtering test cases, here by filtering checks at runtime.
Another line of research is the combination of testing and runtime verification. Decker et al. in [22] introduce an extension of the testing framework JUnit, which adds runtime verification artefacts to it. In this extension, during the execution of a test, a monitor is in charge of checking whether the actual executed test conforms with the property being monitored. In [7] Artho et al. present a framework where automated test case generation benefits from the use of runtime verification in a similar way to [22]. Falzon and Pace [24] study the combination of QuickCheck and Larva by presenting a technique which extracts monitors from a QuickCheck testing specifications. Even though this line of work have a different objective compare to ours, it is worth mentioning that the QuickCheck automata used in [24] are quite similar to ppDATEs. QuickCheck automata employ pre/postconditions as part of their transitions, as opposed to ppDATEs which include them in the states of the automata. This similarity may suggest that it might be possible to extend our approach by also including the possibility of perform testing.
Another area worth mentioning is the combination of runtime assertion checks with runtime verification. In [21] de Boer et al. present SAGA, a framework which combines runtime assertion checking with monitoring. In contrast to our approach which targets general data- and control-oriented properties, SAGA focuses on the verification of both data-flow and control-flow properties of Java classes and interfaces, e.g., interaction protocol among objects.
However, we are mainly interested in the combination of static verification and runtime verification such that static verification is used to reduce the overhead introduced to the system execution by monitoring properties. Wonisch et al. in [41] make use of program transformations in order to avoid unsafe program executions. In [12] the efficiency of runtime monitoring based on tracematches is improved by using a static analysis technique which reduces the runtime instrumentation needed. The technique consists on three stages: exclusion of some tracematches, elimination of inconsistent instrumentation points, and additionally refinement of this analysis considering the order of execution.
Other works use this kind of combination but with different goals. In [13] Bodden and Lam present CLARA, a framework which uses static techniques aiming to improve the monitors themselves, instead of verifying software. The work by Zee et al. in [43] investigates the combination of static and runtime verification, but aiming at a specification language whose specifications may be both statically and runtime checked. With this goal in mind, they extend the static verifier Jahob by adding techniques to verify specifications at runtime. In this approach, most of the properties which can be verified are data-oriented, as opposed to ours where control-oriented properties are covered as well. In [34] Sözer integrates static code analysis and runtime verification. On this approach, runtime verification statements are created from static code analysis alerts, in order to generate monitors which will allow to both check for possible faults in the system and eliminate false positives obtained in the static phase.
Many specification approaches, such as SPARK [9], JML [29] and SPEC# [10] are supported by both static and runtime verification tools. Nevertheless, to the best of our knowledge, static verification is not used to optimise the runtime verification of properties.
12 Conclusions
In this paper we have presented StaRVOOrS, a framework for verifying integrated data- and control-oriented properties for Java programs, using a combination of static and runtime verification. The StaRVOOrS tool-chain uses KeY [2] for static verification, and Larva [19] for the verification performed at runtime.
We have presented the language ppDATE which is based on automata and pre/post conditions to describe properties of both, the control flow and the data computations. The basic structuring principle of the language is the composition of parallel automata, whose transitions fire simultaneously in reaction to events of the observed system, but also in reaction to events generated by some automata in the previous step. A distinguishing feature of the language is the inclusion of functional properties of computation units into the above, thereby capturing the dependency of functional properties on the history of previous events, by assigning Hoare triples to (automata-theoretic) states. Finally, the template concept allows to parameterise components in a great variety of ways, and create concrete instantiations dynamically.
We also presented here a semantics of ppDATEs, precisely describing the interplay of transitions, event consumption and generation, Hoare triple monitoring, creation of template instances. We then use the semantics to prove soundness of the algorithm our tool uses to translate ppDATE into DATE, allowing us to employ the DATE tool Larva as a back-end for runtime verifying ppDATE specifications.
This article also reports on the application of StaRVOOrS to SoftSlate, an open-source shopping cart web application. In this case study, we analyse ppDATEs describing properties about the proper behaviour of the system while users perform purchases. We selected this case study because verifying a real application is always quite challenging, and dealing with it would gave us a better perspective regarding the benefits which can be obatined when using our tool. We also report on the application of StaRVOOrS to the verification benchmark Mondex, an electronic purse application. We demonstrate how properties can be verified using combined static and runtime verification. This case study was selected because it is a usual benchmark in the static verification community, and we thought that it would be interesting to analyse what the use of runtime verification could bring into play.
As with all case studies, the empirical observations are difficult to generalise. However, our experimental results give an indication of what gains are possible with our technique. For SoftSlate, the overhead of pure runtime verification (without employing static verification) is roughly 50%, a penalty which we get down to roughly 25% when using StaRVOOrS, by facilitating static verification (cf. Sect. 9.3.2). These differences are much smaller compared to when we applied StaRVOOrS to the Mondex case study, where pure runtime verification created a much higher overhead. Compared to that, the monitor created by StaRVOOrS was 10 times faster for a low number of transactions, and up to 900 times faster as the number of transactions increase. ‘ When using the monitor generated from the original specification provided for Mondex, the execution of each method involved in a transaction (7 in total) creates an additional DATE to be traversed in parallel, which is in charge of checking the postcondition. This would lead to the large overheads obtained in that case study. However, when using the monitor generated by StaRVOOrS, thanks to the optimisations introduced in the specification by this tool, no additional DATEs are created when a transaction is performed, because the additional checks in the preconditions are false at runtime.
As a final remark, note that the efficiency gain for monitoring will benefit from any improvements in the used static and runtime verifiers. For instance, if KeY is improved in such a way that more branches are closed during the static proof, then this will have an immediate effect in StaRVOOrS thus reducing the runtime overhead. Similarly, any optimisation performed in Larva will only bring benefits to our tool.
We are currently looking at ways of pushing our techniques further. On one hand, we are looking at techniques to add control-flow static analysis to StaRVOOrS, thus benefiting from further optimisation prior to deployment. We are also looking at extending the framework to deal with distributed systems [6], which brings in new challenges, and might require assume-guarantee reasoning to enable us to perform static analysis based optimisations.
Notes
The simplified rule ignores side effects or exceptions possibly caused by b.
Logical Automata for Runtime Verification and Analysis.
There exist approaches to deductive verification which are history-aware, including a KeY version for the compositional verification of distributed systems [4]. These approaches are however much more heavyweight, both in terms of specification as well as verification, than what we are aiming at in this work. The same holds for approaches based on refinement.
For readability, we use \(\wedge \) and \(\lnot \) in this paragraph, instead of the ppDATE syntax && and !.
A valuation is a mapping from variables to values of adequate types.
These identifiers can be created automatically using techniques as those presented in [24] or through stack frame references.
A (binary) relation R is functional if \(\{(x,y),(x,y')\} \subseteq R\) implies \(y = y'\).
To be precise, eval has one extra parameter, which is a logical variable assignment, needed to define the evaluation of quantified formulas. We omit that parameter since it is unimportant for our discussion here.
Note that the definition of DATE given here is different from the one given in [18] as \(\varPi _{\emptyset }\) was not defined in the original formulation. It is easy to see that the formulations are equivalent (modulo the differences mentioned above).
Both the source code and the ppDATE specification for this example are available from [38].
This document is available from [38], in the Downloads section.
Shifting to state bad means that a property was violated.
Logging out clears the cart.
Remember that properties (2) and (3) were fully proved statically.
This also happened when entering negative numbers, but we only found out this when focusing on checking property (7) after correcting the issue with negative inputs.
The package java.net is used here to handle the communication between our program and SoftSlate.
References
Apache Tomcat. http://tomcat.apache.org/
Ahrendt W, Beckert B, Bubel R, Hähnle R, Schmitt PH, Ulbrich M (eds) (2016) Deductive software verification—the KeY book (LNCS), vol 10001. Springer, Berlin
Ahrendt W, Chimento JM, Pace GJ, Schneider G (2015) A specification language for static and runtime verification of data and control properties. In: FM’15 (LNCS), vol 9109. Springer, Berlin
Ahrendt W, Dylla M (2012) A system for compositional verification of asynchronous objects. Sci Comput Program 77:1289–1309
Ahrendt W, Pace G, Schneider G (2012) A unified approach for static and runtime verification: framework and applications. In: ISoLA’12 (LNCS), vol 7609. Springer, Berlin
Ahrendt W, Pace GJ, Schneider G (2016) StaRVOOrS—episode II: strengthen and distribute the force. In: ISoLA’16 (1) (LNCS), vol 9952. Springer, Berlin
Artho C, Barringer H, Goldberg A, Havelund K, Khurshid S, Lowry M, Pasareanu C, Rosu G, Sen K, Visser W et al (2005) Combining test case generation and runtime verification. Theor Comput Sci 336(2–3):209–234
Artho C, Biere A (2015) Combined static and dynamic analysis. In: AIOOL’05 (ENTCS) vol 131, pp 3–14
Barnes J (2012) SPARK: the proven approach to high integrity software. Altran Praxis. http://www.altran.co.uk
Barnett M, Rustan K, Leino M, Schulte W (2005) The Spec# programming system: an overview. In: CASSIS’05 (LNCS) vol 3362. Springer, Berlin, pp 49–69
Barringer H, Goldberg A, Havelund K, Sen K (2004) Rule-based runtime verification. In: VMCAI’04, pp 44–57
Bodden E, Hendren LJ, Lhoták O (2007) A staged static program analysis to improve the performance of runtime monitoring. In: ECOOP’07 (LNCS), vol 4609
Bodden E, Lam P (2010) Clara: partially evaluating runtime monitors at compile time—tutorial supplement. In: RV’10 (LNCS) vol 6418, pp 74–88
Burdy L, Cheon Y, Cok DR, Ernst MD, Kiniry JR, Leavens GT, Rustan K, Leino M, Poll E (2005) An overview of JML tools and applications. Int J Softw Tools Technol Transf 7(3):212–232
Chen F, Roşu G (2005) Java-MOP: a monitoring oriented programming environment for Java. In: TACAS’05 (LNCS), vol 3440. Springer, Berlin, pp 546–550
Chimento JM, Ahrendt W, Pace GJ, Schneider G (2015) StaRVOOrS: a tool for combined static and runtime verification of Java. In: Bartocci E, Majumdar R (eds) Runtime verification (LNCS), vol 9333. Springer, Berlin, pp 297–305
Christakis M, Müller P, Wüstholz V (2012) Collaborative verification and testing with explicit assumptions. In: FM’12: formal methods - 18th international symposium, Paris, France, August 27-31, 2012. Proceedings, pp 132–146
Colombo C, Pace GJ, Schneider G (2009) Dynamic event-based runtime monitoring of real-time and contextual properties. In: FMICS’08 (LNCS), vol 5596. Springer, Berlin, pp 135–149
Colombo C, Pace GJ, Schneider G (2009) LARVA: a tool for runtime monitoring of Java programs. In: SEFM’09, IEEE Computer Society, pp 33–37
Csallner C, Smaragdakis Y(2005) Check ’n’ crash: combining static checking and testing. In: 27th International Conference on Software Engineering (ICSE 2005), 15-21 May 2005, St. Louis, Missouri, USA, pp 422–431
de Boer FS, de Gouw S, Johnsen EB, Wong PYH (2013) Run-time checking of data- and protocol-oriented properties of Java programs: an industrial case study. In: Shin Sung Y, Maldonado Jos C (eds) SAC. ACM, pp 1573–1578
Decker N, Leucker M, Thoma D (2013) jUnitRV—adding runtime verification to JUnit. In: NASA formal methods (LNCS), vol 7871. Springer, Berlin
Ernst G, Pfähler J, Schellhorn G, Haneberg D, Reif W (2015) KIV: overview and verifythis competition. Int J Softw Tools Technol Transf 17(6):677–694
Falzon K, Pace G (2012) Combining testing and runtime verification techniques. In Model-based methodologies for pervasive and embedded software, 8th international workshop, MOMPES 2012, Essen, Germany, September 4, 2012, pp 38–57
Flanagan Cormac, Leino K Rustan M, Lillibridge Mark, Nelson Greg, Saxe James B, Stata Raymie (2002) Extended Static Checking for Java. In Knoop Jens, Hendren Laurie J , editors, PLDI’02, pages 234–245. ACM
Ge X, Taneja K, Xie T, Tillmann N (2011) DyTa: dynamic symbolic execution guided with static verification results. In: Proceedings of the 33rd international conference on software engineering, ICSE 2011, Waikiki, Honolulu , HI, USA, May 21–28, 2011, pp 992–994
Gries D (1987) The science of programming, 1st edn. Springer, Berlin
Jacobs B, Smans J, Philippaerts P, Vogels F, Penninckx W, Piessens F (2011) Verifast: a powerful, sound, predictable, fast verifier for C and Java. In: NASA formal methods (LNCS), vol 6617. Springer, pp 41–55
Leavens GT, Poll E, Clifton C, Cheon Y, Ruby C, Cok D, Müller P, Kiniry J, Chalin P (2007) JML reference manual. Draft 1.200
Leino K Rustan M (2010) Dafny: an automatic program verifier for functional correctness. In: Clarke EM, Voronkov A (eds) Logic for programming, artificial intelligence, and reasoning (LPAR-16) (LNCS), vol 6355. Springer, Berlin
Maraninchi F, Rémond Y (2000) Running-modes of real-time systems: a case-study with mode-automata. In: Proceedings of 12th euromicro conference on real-time systems (ECRTS 2000), 19–21 June 2000, Stockholm, Sweden, pp 257–264
MasterCard International Inc. Mondex web page. http://www.mondexusa.com/
Reger G (2016) An overview of MarQ. In: Proceedings of runtime verification—16th international conference, RV 2016 (LNCS), vol 10012. Springer
Sözer H (2015) Integrated static code analysis and runtime verification. Softw Pract Exp 45(10):1359–1373
Spivey JM (1989) The Z notation: a reference manual. Prentice-Hall Inc, Upper Saddle River
SoftSlate Commerce. www.softslate.com/
Stepney S, Cooper D, Woodcock J (2000) An electronic purse: specification, refinement and proof. Technical monograph PRG-126, Oxford University Computing Laboratory
StaRVOOrS web page. http://cse-212294.cse.chalmers.se/starvoors/
Tillmann N, Halleux Jonathan de (2008) Pex-white box test generation for .nET. In: Beckert B, Hähnle R (eds) Tests and proofs (LNCS), vol 4966. Springer, Berlin, pp 134–153
Tonin I (2007) Verifying the mondex case study. The KeY approach. Technical Report 2007-4, Universität Karlsruhe
Wonisch D, Schremmer A, Wehrheim H (2013) Zero overhead runtime monitoring. In: SEFM’13 (LNCS), vol 8137. Springer, Berlin, pp 244–258
Woodcock J (2006) First steps in the verified software grand challenge. In: SEW’06. IEEE Computer Society, pp 203–206
Zee K, Kuncak V, Taylor M, Rinard MC (2007) Runtime checking for program verification. In: RV’07 (LNCS), vol 4839. Springer, Berlin, pp 202–213
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Proofs of coupling invariant lemmas
In order to prove both Lemmas 4 and 5, we introduce the following two propositions. Proposition 1 says that the translation algorithm only modifies the actions of the transitions in the translated ppDATE network. Proposition 2 says that for every transition in the translation either there is a similar transition in the original ppDATE network, or there is not such a transition, due to the fact that the transition is a new loop transition (added by the translation to control Hoare triples).
Remember that we represent the translation of a single ppDATE to DATE with the function \(\kappa \in \textit{ppDATE} \mapsto \textit{DATE} \).
Proposition 1
Given a ppDATE network \(pn=(M,V,\nu _0,T_{ppd})\) and its translation
ppd2DATE \((pn)\) = \((M',V,\nu _0,T_{d}')\),

Proof
Given a ppDATE \(m \in M\) and a state \(q \in Q_m\), whenever \(\varPi _m(q) = \emptyset \), \(\varPi _m(q) \ne \emptyset \) but there is no Hoare triple associated to the method related to trigger tr, or the trigger is associated to exiting a method, by Step 3b., transitions remain unchanged in the translation. Therefore, \(a' = a\) in these cases.
On the other hand, for each clashing Hoare triple  \(\in \varPi _m(q)\), by step 3\(a_2\)., the transition
\(\in \varPi _m(q)\), by step 3\(a_2\)., the transition  is replaced by one of the following transitions:
is replaced by one of the following transitions:

, or

.
Thereby, either

, or

.
Finally, as in step 3\(a_1\) non-clashing Hoare triples add new transitions but do not modified existing ones, this case trivially holds. \(\square \)
Proposition 2
Given a ppDATE network \(pn=(M,V,\nu _0,T_{ppd})\) and its translation
ppd2DATE \((pn)\) = \((M',V,\nu _0,T_{d}')\),

Proof
Each transition \(t' \in t_{m}'\) for any \(m' \in M'\) is obtained by applying either step 3\(a_1\), 3\(a_2\) or 4b.
If \(t'\) was obtained by applying step 3\(a_1\), then it is a new loop transition added by the translation, i.e., its origin and destination states are the same, and given a ppDATE \(m \in M\) such that \(\kappa (m) = m'\), there not exists a transition associated to \(t'\) in m. Therefore, the right side of the disjunction holds.
If \(t'\) was obtained by applying step 3\(a_2\), then, given a ppDATE \(m \in M\) such that \(\kappa (m) = m'\), either there exists one transition on m with the same trigger, same condition, and similar action (but without including the if-expression checking the precondition), or \(t'\) is a new loop transition added by the translation. In the first case the left side of the disjunction holds, whereas in the the second case the right side of the disjunction holds.
Finally, if \(t'\) was obtained by applying step 3b, then, given a ppDATE \(m \in M\) such that \(\kappa (m) = m'\), m has exactly the same transition. Therefore, the left-hand side of the disjunction holds in these cases. \(\square \)
Now, we proceed to prove the lemmas.
Lemma 4
Given a network of ppDATEs \(pn=(M,V,\nu _0,T_{ppd})\), its translation ppd2DATE
\((pn)\) = \((M',V,\nu _0,T_{d}')\), a trace \(w \in (systemevent \times \varTheta _{\textit{Sys}})^{*}\), and the global configurations  and
and  ,
,

Proof
We proceed to prove this lemma by induction on the length of the trace w.
-
Base case: \(w = \varepsilon \) (empty trace)

By Definitions 17 and 21, we know that

where  , and
, and  .
.
Next, by substitution with the antecedents we have to prove
As in  all the DATE components of the local configurations correspond to the translation of ppDATE in \(pn\), both (1) and (2) are trivially fulfilled, and the ranges of both (3) and (4) are never fulfilled, meaning that, as these ranges are empty (i.e., false), both expressions are trivially evaluated to true. In addition, (5) is trivially fulfilled. Thereby, the base case holds.
all the DATE components of the local configurations correspond to the translation of ppDATE in \(pn\), both (1) and (2) are trivially fulfilled, and the ranges of both (3) and (4) are never fulfilled, meaning that, as these ranges are empty (i.e., false), both expressions are trivially evaluated to true. In addition, (5) is trivially fulfilled. Thereby, the base case holds.
-
Inductive case: \(w = w':(e,\theta )\)
IH: 

Given the previous inductive hypothesis IH, we have to prove,

By Definition 21 we have,

Then, we proceed with the proof by assuming the antecedent of the implication. This assumption allows us to remove the existential quantifiers in the antecedents by introducing the fresh values \(L''\) and \(\nu ''\) in (i), and the fresh values  and \(\nu '''\) in (ii). Therefore, we have
and \(\nu '''\) in (ii). Therefore, we have

Next, by IH we know

In relation to L, by (i) we know it is obtained from \(L''\) after performing a big step with \((e,\theta )\). Thereby, the local configurations on L are either the same as in \(L''\), a modified version of the ones in \(L''\), or new local configurations added to control a DATE which is a new instance of a template.
Let us introduce the sets \(L_{nc}\), \(L_c\) and \(L_{new}\), to represent the local configurations in each one of the previous categories, respectively. Then, we know that
In addition, by using a similar approach with \(\tilde{L}\) and (ii), we introduce the following sets.
Let us come back now to the expression we want to prove.

By (iii) and (iv), as the values in both \(L_{nc}\) and \(\tilde{L}_{nc}\) are the same as in \(L''\) and \(\tilde{L}''\), respectively, we know that these values fulfil all the previous expressions. Thereby, we can reduce (viii) and (ix) to
Regarding the newly created local configurations in both \(L_{new}\) and \(\tilde{L}_{new}\), they do not fulfil the ranges of the universal quantifications in neither (x) nor (xi). In addition, by Propositions 1 and 2, we know that the only difference in the executed actions in the ppDATEs in \(pn\) and their translation is that the actions in the DATEs may include the creation of an instance of template \(exit\_cond\_checker\). Besides, by step 4 in the translation algorithm, we now that both the ppDATEs templates and their translations have similar transitions and are initialised in the same state. Thus, (xii) and (xii) are fulfilled for these values, and we can reduce (viii) and (ix) to
Therefore, we have to prove,

By (iii) and Proposition 1 we know that for every enabled transition of a ppDATE \(m \in M\), there is one enabled transition in \(\kappa (m) \in M'\) performing the same change of state and, if any, generating the same action events. Thereby, both \(pn\) and its translation will shift the local configurations in \(L_c\) and \(\tilde{L}_c\), respectively, in the same manner, i.e., \((x')\) holds.
In addition, by (iv) and Proposition 2 we know that for every enabled transition in a DATE \(m' \in M'\), there is either an enabled transition in a ppDATE \(m \in M\), where \(\kappa (m) = m'\), such that this transition performs the same change of state and, if any, generates the same action events, or the transition enabled in \(m'\) is a loop transition.
In the first case, both \(pn\) and its translation will shift the local configurations in \(L_c\) and \(\tilde{L}_c\), respectively, in the same manner. Thus, \((xi')\) holds.
In the second case, the local configuration obtained after the shift is in the same state as before the shift. Thus, by (iv), this \((xi')\) holds.
Moreover, by IH, Propositions 1 and 2 we know that whenever a ppDATE in \(pn\) creates an instance of a template, its translation will create an instance of the translation of such template, and vice versa. Besides, by the step 4 in the translation algorithm, as such instances have similar transitions, they will shift the local configuration associated to them in the same manner. Therefore, both \((xii')\) and \((xiii')\) are fulfilled.
Finally, in relation to (xiv), by Propositions 1 and 2 we know that only difference in the executed actions in \(pn\) and its translation is that the actions of the latter may include the creation of an instance of template \(exit\_cond\_checker\) (whose actions do not modify ppDATE variables valuations). In addition, by step 4 in the translation algorithm we know that both an instance of a ppDATE template and a similar instance of the translation of the template will fire similar transitions (with the same actions). Therefore, they perform the same modifications in the valuations \(\nu ''\) and \(\nu '''\). Thus, by (vii), (xiv) holds. \(\square \)
Lemma 5
Given a network of ppDATEs \(pn=(M,V,\nu _0,T_{ppd})\), its translation ppd2DATE
\((pn)\) = \((M',V,\nu _0,T_{d}')\), a trace \(w \in (systemevent \times \varTheta _{\textit{Sys}})^{*}\), and the global configurations  and
and  ,
,

where,

Proof
We proceed to prove this lemma by induction on the length of the trace w.
-
Base case: \(w = \varepsilon \) (empty trace)

By Definitions 17 and 21 we know that

where  , and
, and  .
.
Next, by substitution with the antecedents,

Thus, by the definition of \(\psi \) we have to prove that,

First, let us analyse the expression,

As \(\rho \) is always the empty set, the condition

will always evaluate to false. Therefore,

Then, as the range of the inner universal quantification is empty (i.e., false), it is trivially evaluated to true.
Finally, as the body of the previous universal quantification is simply the value true and its range is not empty, the whole expression is trivially evaluated to true.
Now, let us analyse the expression,

As in the initial configuration of the translation of \(pn\) there are no instances of DATE templates, the range of the universal quantification is always evaluated to false. Therefore,

Thus, as the range of the universal quantification is empty (i.e., false), the whole expression is trivially evaluated to true. Thereby, the base case holds.
-
Inductive case: \(w = w':(e,\theta )\)
IH: 

Given the previous inductive hypothesis IH, we have to prove,

By Definition 21 we have,

Then, we proceed with the proof by assuming the antecedent of the implication. This assumption allows us to remove the existential quantifiers in the antecedents by introducing the fresh values \(L''\) and \(\nu ''\) in (i), and the fresh values  and \(\nu '''\) in (ii). Therefore, we have
and \(\nu '''\) in (ii). Therefore, we have

Next, by IH we know that \(\psi (L'',\tilde{L}'')\). Thus, we have

In relation to L, by \((i')\) we know it is obtained from \(L''\) after performing a big step with \((e,\theta )\). Thereby, the local configurations on L are either the same as in \(L''\), a modified version of the ones in \(L''\), or new local configurations added to control a DATE which is a new instance of a template.
Let us introduce the sets \(L_{nc}\), \(L_c\) and \(L_{new}\), to represent the local configurations in each one of the previous categories, respectively. Then, we know that
In addition, by using a similar approach with \(\tilde{L}\) and \((ii')\), we introduce the following sets.
As in the translation the set \(\tilde{L}_{new}\) contains both the instances of ordinary templates and the instances of the templates about Hoare triples, we split \(\tilde{L}_{new}\) into the sets \(\tilde{L}_{new}'\) and \(\tilde{L}_{h}\), to represent each one of the previous categories, respectively. Thus,
Now, let us come back to the expression \(\psi (L,\tilde{L})\). By (iv) and \((v')\), we replace it by
By (iii), as the values in both \(L_{nc}\) and \(\tilde{L}_{nc}\) are the same as in \(L''\) and \(\tilde{L}''\), respectively, we know that the former fulfil \(\psi \). Thereby, we can reduce the previous expression to
In addition, newly created local configurations in both \(L_{new}\) and \(\tilde{L}_{new}'\) do not fulfil the ranges of the quantified expressions in \(\psi \). Then, we can discard them.
Next, by the definition of \(\psi \), we have

In relation to the configurations in \(\tilde{L}_c\), as they were obtained from configurations in \(\tilde{L}''\), by (iii) we know they fulfil (vii) (same DATE component). Thereby, we only need to prove that

Now, let us focus on (vi). If event e is either an exit event, or an entry event which does not require to verify any Hoare triple, then it does not introduce any new values in \(\rho \) components of the local configurations in \(L_c\). Thus, by (iii), (vi) is fulfilled in both cases.
If event e is an entry event which requires the check of Hoare triples, then by Lemma 4 and Proposition 1, we know that for every enabled transition which requires the verification of a Hoare triple in \(pn\), a similar transition will be fired in its translation whose action will create a DATE in charge of controlling such Hoare triple. Thus, for every new entry in a \(\rho \) component in \(L_c\), a new local configuration is added in \(\tilde{L}_h\). Thereby, (vi) holds.
Regarding \((vii')\), if event e is either an exit event, or an entry event which does not require to verify any Hoare triple, then \(\tilde{L}_h = \emptyset \). Thus, as the range of universal quantification is empty, \((vii')\) is trivially fulfilled in both cases.
If event e is an entry event which requires the check of Hoare triples, then by the rules \({entry}_1\) and \({entry}_3\) in the relation small step local, we know that a new tuple is going to be added to the \(\rho \) component of the local configuration in \(L_c\) which are associated to the ppDATEs whose current state possess a Hoare triple that has to be verified. In addition, a local configuration is going to be included in \(\tilde{L}_h\) for the DATE instantiated to control the corresponding Hoare triple. Thereby, \((vii')\) holds. \(\square \)
Appendix 2: Proof of soundness
Theorem 2
Given a ppDATE network \(pn=(M,V,\nu _0,T_{ppd})\), and its translation ppd2DATE \((pn)\) = \((M',V,\nu _0,T_{d}')\),
Proof
To prove this theorem we will show that,
In the following, we abbreviate \({ppd2DATE}(pn)\) by \(dn\).
-
\(w \in \mathcal{VT}(pn)\ implies \ w \in \mathcal{VT}(dn)\)
As \(w \in \mathcal{VT}(pn)\), by Definition 22 we know that it has a prefix \(w'\) such that either,
-
(i)
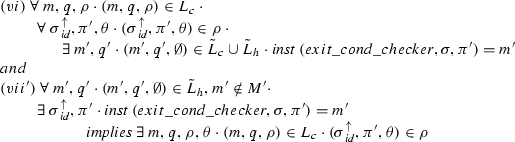 and
and 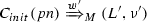 , or
, or -
(ii)
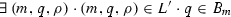
,
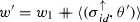 and
and 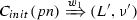
\(\theta , \theta ' \not \models \pi '\).
In relation to (i), let us assume that exists  such that
such that  . Then, by Lemma 2 we know that for every local configuration in
. Then, by Lemma 2 we know that for every local configuration in  , there is a local configuration in
, there is a local configuration in  such that its state component is the same. Therefore, as in
such that its state component is the same. Therefore, as in  there is a local configuration in a bad state, there is a local configuration in
there is a local configuration in a bad state, there is a local configuration in  in a bad state, i.e. \(w'\) is a counter-example of \(dn\). Thereby, \(w \in \mathcal{VT}(dn)\).
in a bad state, i.e. \(w'\) is a counter-example of \(dn\). Thereby, \(w \in \mathcal{VT}(dn)\).
Regarding (ii), it corresponds to the case where (at least) one Hoare triple is not fulfilled when event

occurs. Here, by Lemma 3 we have

Therefore, by (ii) and  we know that
we know that

Let us assume that the local configuration \((m',q',\emptyset )\) is the one satisfying the previous existential quantification. In addition, let us assume  to be given by
to be given by  . Then, once
. Then, once

occurs, as by (ii) we know that the \(\pi '\) is not fulfilled, \(m'\) will shift to a bad state. Thereby, \(w'\) is a counter-example of \(dn\), i.e. \(w \in \mathcal{VT}(dn)\).
-
\(w \in \mathcal{VT}(dn)\ implies \ w \in \mathcal{VT}(pn).\)
As \(w \in \mathcal{VT}(dn)\), by Definition 22 and the fact that every DATE in \(dn\) has no Hoare triples associated to its states, we know that it has a prefix \(w'\) such that,

Now let us assume that exists  such that
such that  . In addition, let us assume that the bad state in
. In addition, let us assume that the bad state in  belongs to a local configuration associated to a DATE
\(m'\), which is an instance of the template \(exit\_cond\_checker\), i.e., \(m'\) was created to control a Hoare triple. Let us represent this Hoare triple as
belongs to a local configuration associated to a DATE
\(m'\), which is an instance of the template \(exit\_cond\_checker\), i.e., \(m'\) was created to control a Hoare triple. Let us represent this Hoare triple as  . Then, by Lemma 3 we know that,
. Then, by Lemma 3 we know that,

We will assume that the ppDATE m and the valuation \(\theta \) are the ones fulfilling (1). Note that the index id is introduced by Lemma 3. Next, as \(m'\) is in a bad state we know that whenever

occurs, \(\pi '\) is not fulfilled. Thus, let us assume that the selected prefix is of the form

. Thereby, by Definition 22, \(w'\) is a counter-example of \(pn\), i.e. \(w \in \mathcal{VT}(pn)\).
On the other hand, if the bad state in  does not belongs to a local configuration associated to a DATE
\(m'\) which is an instance of the template \(exit\_cond\_checker\), then by Lemma 2 we know that there is a local configuration in
does not belongs to a local configuration associated to a DATE
\(m'\) which is an instance of the template \(exit\_cond\_checker\), then by Lemma 2 we know that there is a local configuration in  such that its state component is the same as the bad state in
such that its state component is the same as the bad state in  . Therefore, \(w'\) is a counter-example of \(pn\), i.e. \(w \in \mathcal{VT}(pn)\). \(\square \)
. Therefore, \(w'\) is a counter-example of \(pn\), i.e. \(w \in \mathcal{VT}(pn)\). \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ahrendt, W., Chimento, J.M., Pace, G.J. et al. Verifying data- and control-oriented properties combining static and runtime verification: theory and tools. Form Methods Syst Des 51, 200–265 (2017). https://doi.org/10.1007/s10703-017-0274-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10703-017-0274-y









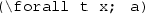
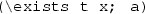
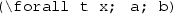
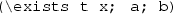
 gives a BJMLE,
gives a BJMLE, gives a BJMLE, (well-typedness is context dependent, see Definition
gives a BJMLE, (well-typedness is context dependent, see Definition 

 is a set of local configurations. For each
is a set of local configurations. For each 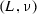 is a global configuration for
is a global configuration for 


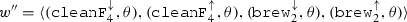

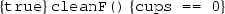
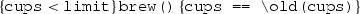




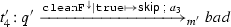
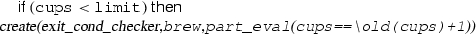 ;
;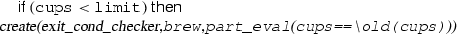 .
.
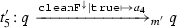

 in a ppDATE state, replace in
in a ppDATE state, replace in  by the variable
by the variable 
 in
in 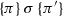
 remains unchanged, i.e.
remains unchanged, i.e. 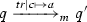
 in
in 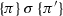

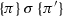
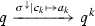
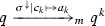
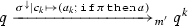
 such that either
such that either 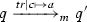 .
.







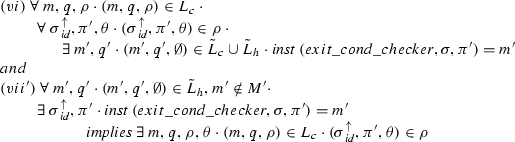 and
and 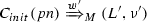 , or
, or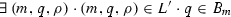
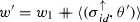 and
and