Abstract
Formal verification and validation play a crucial role in making cyber-physical systems (CPS) safe. Formal methods make strong guarantees about the system behavior if accurate models of the system can be obtained, including models of the controller and of the physical dynamics. In CPS, models are essential; but any model we could possibly build necessarily deviates from the real world. If the real system fits to the model, its behavior is guaranteed to satisfy the correctness properties verified with respect to the model. Otherwise, all bets are off. This article introduces ModelPlex, a method ensuring that verification results about models apply to CPS implementations. ModelPlex provides correctness guarantees for CPS executions at runtime: it combines offline verification of CPS models with runtime validation of system executions for compliance with the model. ModelPlex ensures in a provably correct way that the verification results obtained for the model apply to the actual system runs by monitoring the behavior of the world for compliance with the model. If, at some point, the observed behavior no longer complies with the model so that offline verification results no longer apply, ModelPlex initiates provably safe fallback actions, assuming the system dynamics deviation is bounded. This article, furthermore, develops a systematic technique to synthesize provably correct monitors automatically from CPS proofs in differential dynamic logic by a correct-by-construction approach, leading to verifiably correct runtime model validation. Overall, ModelPlex generates provably correct monitor conditions that, if checked to hold at runtime, are provably guaranteed to imply that the offline safety verification results about the CPS model apply to the present run of the actual CPS implementation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Cyber-physical systems (CPS) involve controllers and the relevant dynamics of the environment. Since safety is crucial for CPS, their models (e. g., hybrid system models [31]) need to be verified formally. Formal verification guarantees that a model is safe with respect to a safety property. The remaining task is to validate whether the model is adequate, so that the verification results for the model transfer to the actual system implementation [18, 42]. This article introduces ModelPlex [24], a method to synthesize correct-by-construction monitors for CPS by theorem proving automatically: it uses sound axioms and proof rules of differential dynamic logic [33] to formally verify that a model is safe and to synthesize provably correct monitors that validate compliance of system executions with that model. The difficult question answered by ModelPlex is what exact conditions need to be monitored at runtime to guarantee compliance with the models and thus safety.
System execution, however, provides many opportunities for surprising deviations from the model: faults may cause the system to function improperly [43], sensors may deliver uncertain values, actuators may suffer from disturbance, or the formal verification may have assumed simpler ideal-world dynamics for tractability reasons or made unrealistically strong assumptions about the behavior of other agents in the environment. Simpler models are often better for time-critical decisions and optimizations, because they make it possible to compute predictions at the rate required for real-time decisions. The same phenomenon of simplicity for predictability is often exploited for the models in formal verification and validation, where formal verification results are often easier to obtain for simpler models. It is more helpful to obtain a verification or prediction result about a simpler model than to fail on a more complex one. The flipside is that the verification results obtained about models of a CPS only apply to the actual CPS at runtime to the extent that the system fits to the model. ModelPlex enables tradeoffs between analytic power and accuracy of models while retaining strong safety guarantees.
Validation, i. e., checking whether a CPS implementation fits to a model, is an interesting but difficult problem. Even more so, since CPS models are more difficult to analyze than ordinary (discrete) programs because of the continuous physical plant, the environment, sensor inaccuracies, and actuator disturbance, making full model validation quite elusive.
In this article, we, thus, settle for the question of runtime model validation, i. e. validating whether the model assumed for verification purposes is adequate for a particular system execution to ensure that the offline safety verification results apply to the current execution.Footnote 1 But we focus on verifiably correct runtime validation to ensure that verified properties of models provably apply to the CPS implementation, which is important for safety and certification [5]. Only with such a way of validating model compliance is there an unbroken chain of evidence of safety claims that apply to the actual system, rather than merely to its model. ModelPlex provides a chain of formal proofs as a strong form of such evidence.
At runtime, ModelPlex monitors check for model compliance. If the observed system execution fits to the verified model, then this execution is safe according to the offline verification result about the model. If it does not fit, then the system is potentially unsafe because it evolves outside the verified model and no longer has an applicable safety proof, so that a verified fail-safe action from the model is initiated to avoid safety risks, cf. Fig. 1. System-level challenges w.r.t. monitor implementation and violation cause diagnosis are discussed elsewhere [8, 21, 45].
ModelPlex monitors in a Simplex [39] setting: a fallback action gets executed when sensor readings and control decisions do not comply with a monitor
Checking whether a system execution fits to a verified model includes checking that the actions chosen by the (unverified) controller implementation fit to one of the choices and requirements that the verified controller model allows. It also includes checking that the observed states can be explained by the plant model. The crucial questions are: What are the right conditions to monitor? Which monitor conditions guarantee safety without being overly restrictive? How can the correctness of such executable monitor conditions be proved formally? How can a compliance monitor be synthesized that provably represents all important aspects of complying with the verified model correctly? How much safety margin does a system need to ensure that fail-safe actions are always initiated early enough for the system to remain safe, even if its behavior ceases to comply with the model?
The last question is related to feedback control and can only be answered when assuming some constraints on the maximum deviation of the real system dynamics from the plant model [36]. Otherwise, i. e., if the real system might be infinitely far off from the model, safety guarantees are impossible. By the sampling theorem in signal processing [40], such constraints further enable compliance monitoring solely on the basis of sample points instead of the unobservable intermediate states about which no sensor data exists.Footnote 2
Extension In addition to providing proofs for the results, this article extends the short version [24] with support for a correct-by-construction approach to synthesize ModelPlex monitors by a systematic transformation in the differential dynamic logic axiomatization [33]. We leverage an implementation of this axiomatization in our entirely new theorem prover KeYmaera X [14] by performing the ModelPlex monitor proof construction in place, as opposed to splitting it over the branches of its classical sequent calculus [29]. Sequent calculi are usually preferred for proving properties, because they induce a sequent normal form that simplifies proof construction by narrowing proof search to proof rules for top-level operators and splitting the proof over independent branches as needed. Proofs cannot close during the ModelPlex monitor construction, however, because the proof represents the conditions on system executions that the verified model imposes. That is why proof branching in our previous ModelPlex implementation [24] led to sizeable monitors with nontrivial redundancy which were simplified with (unverified) external optimization tools and, thus, had to be reverified for correctness.
Our new ModelPlex monitor synthesis presented here exploits the flexibility of differential dynamic logic axioms [33] more liberally to significantly improve locality of the construction, which leads to reductions of the resulting monitors compared to our previous approach [24]. The axiomatic ModelPlex construction also preserves the structure in the model better. The ModelPlex construction now remains entirely under the auspices of the theorem prover without external simplification, thereby eliminating the need to reverify correctness of the resulting monitor. Efficiency during the ModelPlex monitor construction in the prover is retained using contextual rewriting in the uniform substitution calculus for differential dynamic logic [35]. We now also implemented optimizations of the ModelPlex monitor constructions as proof tactics that were previously performed manually. This leads to a fully automatic synthesis procedure for correct-by-construction ModelPlex monitors that produces proofs of correctness for the monitors it synthesizes.
2 Differential dynamic logic by example
This section recalls differential dynamic logic
 [29, 31, 33], which we use to syntactically characterize the semantic conditions required for correctness of the ModelPlex approach. Its proof calculus [29, 31, 33, 35] is also exploited to guarantee correctness of the specific ModelPlex monitors produced for concrete CPS models. A tactic for the proof calculus implements the correct-by-construction ModelPlex monitor synthesis algorithm.
[29, 31, 33], which we use to syntactically characterize the semantic conditions required for correctness of the ModelPlex approach. Its proof calculus [29, 31, 33, 35] is also exploited to guarantee correctness of the specific ModelPlex monitors produced for concrete CPS models. A tactic for the proof calculus implements the correct-by-construction ModelPlex monitor synthesis algorithm.
This section also introduces a simple water tank that will be used as a running example to illustrate the concepts throughout (Fig. 2).
The water level in the tank is controlled by a digital controller that can periodically adjust flow into and from the tank by adjusting two valves. Every time the controller decides on adjusting the flow, it measures the water level through a sensor (i. e., it samples the water level). As a safety condition, we want the water tank to never overflow: any control decision of the controller must be such that the water level stays within 0 and a maximum water level m at all times. We will use this example to introduce  and its syntax for modeling hybrid programs step by step. The final example is repeated in Appendix 1 for easy reference.
and its syntax for modeling hybrid programs step by step. The final example is repeated in Appendix 1 for easy reference.
2.1 Syntax and informal semantics
Differential dynamic logic has a notation for modeling hybrid systems as hybrid programs. Table 1 summarizes the relevant syntax fragment of hybrid programs together with an informal semantics. The formal semantics \(\rho (\alpha )\) of hybrid program \(\alpha \) is a relation on initial and final states of running \(\alpha \) (recalled in Sect. 2.2 below).
Syntax of hybrid programs by example Let us start by modeling the controller of the water tank example, which can adjust two valves by either opening them or closing them.

Here, we use (deterministic) assignment  to assign values to valves: setting a valve to 1, as in
to assign values to valves: setting a valve to 1, as in  means that the valve is open, while setting it to 0 means that the valve is closed. Now any valve can either be opened or closed, not both at the same time, which we indicate using the nondeterministic choice \(\alpha \cup \beta \), as in
means that the valve is open, while setting it to 0 means that the valve is closed. Now any valve can either be opened or closed, not both at the same time, which we indicate using the nondeterministic choice \(\alpha \cup \beta \), as in  . The controller first adjusts the incoming valve \(v_\text {in}\), before it adjusts the outgoing valve \(v_\text {out}\), as modeled using the sequential composition \(\alpha ;~\beta \).
. The controller first adjusts the incoming valve \(v_\text {in}\), before it adjusts the outgoing valve \(v_\text {out}\), as modeled using the sequential composition \(\alpha ;~\beta \).
For theorem proving, however, it often makes sense to describe the system at a more abstract level in order to keep the model simple. Let us, therefore, replace the two valves with their intended effect of adjusting water flow f.

Here, we use nondeterministic assignment  , which assigns an arbitrary real number to f, so we abstractly model that the controller will somehow choose water flow. Next, we need to restrict this arbitrary flow to those flows that make sense. Let us assume that the incoming and the outgoing pipe from our water tank can provide and drain at most 1 liter per second, respectively. For this, we use the test
, which assigns an arbitrary real number to f, so we abstractly model that the controller will somehow choose water flow. Next, we need to restrict this arbitrary flow to those flows that make sense. Let us assume that the incoming and the outgoing pipe from our water tank can provide and drain at most 1 liter per second, respectively. For this, we use the test  , which checks that \(-1\le f \le 1\) holds, and aborts the execution attempt if it does not. Together, the nondeterministic assignment and test mean that the controller can choose any flow in the interval \(f \in \left[ -1,1\right] \).
, which checks that \(-1\le f \le 1\) holds, and aborts the execution attempt if it does not. Together, the nondeterministic assignment and test mean that the controller can choose any flow in the interval \(f \in \left[ -1,1\right] \).
Now that we know the actions of the controller, let us add the physical response, often called plant, using differential equations. We use x to denote the current water level in the water tank.

The idealized differential equation  means that the water level evolves according to the chosen flow. This considerably simplifies water flow models (e. g., it neglects the influence of water level on flow, and flow disturbance in pipes). The evolution domain constraint \(x \ge 0\) models a physical constraint that the water level can never be less than empty. Otherwise, the differential equation would include negative water content in the tank below zero on negative flow, because differential equations evolve for an arbitrary amount of time (even for time 0), as long as their evolution domain constraint is satisfied. Note, that when the tank is empty (\(x=0\)) and the controller still chooses a negative flow \(f<0\) as permitted by the test
means that the water level evolves according to the chosen flow. This considerably simplifies water flow models (e. g., it neglects the influence of water level on flow, and flow disturbance in pipes). The evolution domain constraint \(x \ge 0\) models a physical constraint that the water level can never be less than empty. Otherwise, the differential equation would include negative water content in the tank below zero on negative flow, because differential equations evolve for an arbitrary amount of time (even for time 0), as long as their evolution domain constraint is satisfied. Note, that when the tank is empty (\(x=0\)) and the controller still chooses a negative flow \(f<0\) as permitted by the test  , the evolution domain constraint \(x \ge 0\) in the ODE will abort immediately. As a result, only non-negative values for f will make progress in case the tank is empty. This model means that the controller can choose flow exactly once, and then the water level evolves according to that flow for some time. Next, we include a loop, indicated by the Kleene star, so that the controller and the plant can run arbitrarily many times.
, the evolution domain constraint \(x \ge 0\) in the ODE will abort immediately. As a result, only non-negative values for f will make progress in case the tank is empty. This model means that the controller can choose flow exactly once, and then the water level evolves according to that flow for some time. Next, we include a loop, indicated by the Kleene star, so that the controller and the plant can run arbitrarily many times.

However, this model provides no guarantees whatsoever on the time that will pass between two controller executions, since differential equations are allowed to evolve for an arbitrary amount of time. In order to guarantee that the controller runs at least every \(\varepsilon \) time, we model controller periodicity and sampling period by adding the differential equation  to capture time, and a constraint \(t \le \varepsilon \) to indicate that at most \(\varepsilon \) time can pass until the plant must stop executing and hand over to the controller again. We reset the stopwatch t after each controller run using
to capture time, and a constraint \(t \le \varepsilon \) to indicate that at most \(\varepsilon \) time can pass until the plant must stop executing and hand over to the controller again. We reset the stopwatch t after each controller run using  .
.

Note, that through \(t \le \varepsilon \) the sampling period does not need to be the same on every control cycle, nor does it need to be exactly \(\varepsilon \) time.
Now that we know the sampling period, let us make one final adjustment to the controller: It actually cannot always be safe to choose positive inflow, as allowed by the test  (e. g., it would be unsafe if the current water level x is already at the maximum m). Since we know that the controller will run again at the latest in \(\varepsilon \) time, we can choose inflow such that it will not exceed the maximum level m until then, as summarized below.
(e. g., it would be unsafe if the current water level x is already at the maximum m). Since we know that the controller will run again at the latest in \(\varepsilon \) time, we can choose inflow such that it will not exceed the maximum level m until then, as summarized below.

Differential dynamic logic syntax by example Next, we want to prove that this program is correct. For this, we first need to find a formal safety condition that captures correctness. Since we want the tank to never overflow, all runs of the program must ensure \(0 \le x \le m\), which in  is expressed using the box modality
is expressed using the box modality
 . The formula
. The formula  is not true in all initial states, only in those that at least satisfy \(0\le x<\le m\) to begin with. The modeling idiom
is not true in all initial states, only in those that at least satisfy \(0\le x<\le m\) to begin with. The modeling idiom  expresses that, when started in an initial state that satisfies the initial condition \(\phi \), then all runs of the model \(\alpha \) result in states that satisfy \(\psi \), similar to a Hoare triple. Formula (1) below summarizes the water tank model and the safety condition using this idiom.
expresses that, when started in an initial state that satisfies the initial condition \(\phi \), then all runs of the model \(\alpha \) result in states that satisfy \(\psi \), similar to a Hoare triple. Formula (1) below summarizes the water tank model and the safety condition using this idiom.

This formula expresses that, when started with a safe water level between 0 and maximum (\(0\le x \le m\)) and with some positive sampling period (\(\varepsilon >0\)), our water tank model will keep the water level between 0 and maximum. It is provable in the  proof calculus.
proof calculus.
Syntax summary Sequential composition \(\alpha ;\beta \) says that \(\beta \) starts after \(\alpha \) finishes. The nondeterministic choice \(\alpha ~\cup ~\beta \) follows either \(\alpha \) or \(\beta \). The nondeterministic repetition operator  repeats \(\alpha \) zero or more times. Assignment
repeats \(\alpha \) zero or more times. Assignment  instantaneously assigns the value of term \(\theta \) to the variable x, while
instantaneously assigns the value of term \(\theta \) to the variable x, while  assigns an arbitrary value to x. The test ?F checks that a condition F holds, and aborts if it does not.
assigns an arbitrary value to x. The test ?F checks that a condition F holds, and aborts if it does not.  describes a continuous evolution of x within the evolution domain F.
describes a continuous evolution of x within the evolution domain F.
The set of  formulas is generated by the following grammar \(({\sim }\in \{<,\le ,=,\ge ,>\}\) and \(\theta _1,\theta _2\) are arithmetic expressions in \({+,-,\cdot ,/}\) over the reals):
formulas is generated by the following grammar \(({\sim }\in \{<,\le ,=,\ge ,>\}\) and \(\theta _1,\theta _2\) are arithmetic expressions in \({+,-,\cdot ,/}\) over the reals):

 allows us to make statements that we want to be true for all runs of a hybrid program (
allows us to make statements that we want to be true for all runs of a hybrid program ( ) or for at least one run (
) or for at least one run ( ). Both constructs are necessary to derive safe monitors: we need
). Both constructs are necessary to derive safe monitors: we need  proofs so that we can be sure all behavior of a model are safe; we need
proofs so that we can be sure all behavior of a model are safe; we need  proofs to find monitor specifications that detect whether or not a system execution fits to the verified model. Differential dynamic logic comes with a verification technique to prove correctness properties of hybrid programs (cf. [33] for an overview of
proofs to find monitor specifications that detect whether or not a system execution fits to the verified model. Differential dynamic logic comes with a verification technique to prove correctness properties of hybrid programs (cf. [33] for an overview of  and
and  , and [14] for an overview of KeYmaera X).
, and [14] for an overview of KeYmaera X).
2.2 Formal semantics of 
ModelPlex is based on a transition semantics instead of trace semantics [31], since it is easier to handle and fits to checking monitors at sample points.
The semantics of  , as defined in [29], is a Kripke semantics in which states of the Kripke model are states of the hybrid system. Let \(\mathbb {R} \) denote the set of real numbers, and \(V\) denote the set of variables. A state is a map
, as defined in [29], is a Kripke semantics in which states of the Kripke model are states of the hybrid system. Let \(\mathbb {R} \) denote the set of real numbers, and \(V\) denote the set of variables. A state is a map  ; the set of all states is denoted by
; the set of all states is denoted by  . We write
. We write  if formula \(\phi \) is true at
if formula \(\phi \) is true at 
 (Definition 2). Likewise,
(Definition 2). Likewise,  denotes the real value of term \(\theta \) at
denotes the real value of term \(\theta \) at 
 , while \(\nu (x)\) denotes the real value of variable x at state \(\nu \). The semantics of HP \(\alpha \) is captured by the state transitions that are possible by running \(\alpha \). For continuous evolutions, the transition relation holds for pairs of states that can be interconnected by a continuous flow respecting the differential equation and invariant region. That is, there is a continuous transition along
, while \(\nu (x)\) denotes the real value of variable x at state \(\nu \). The semantics of HP \(\alpha \) is captured by the state transitions that are possible by running \(\alpha \). For continuous evolutions, the transition relation holds for pairs of states that can be interconnected by a continuous flow respecting the differential equation and invariant region. That is, there is a continuous transition along  from state
from state  to state \(\omega \), if there is a solution of the differential equation
to state \(\omega \), if there is a solution of the differential equation  that starts in state
that starts in state  and ends in \(\omega \) and that always remains within the region \(H\) during its evolution.
and ends in \(\omega \) and that always remains within the region \(H\) during its evolution.
Definition 1
(Transition semantics of hybrid programs) The transition relation
\(\rho \) specifies which  is reachable from a
is reachable from a  by operations of \(\alpha \). It is defined as follows.
by operations of \(\alpha \). It is defined as follows.
-
1.
 iff
iff  and \(\nu (z) = \omega (z)\) for all state variables \(z \ne x\).
and \(\nu (z) = \omega (z)\) for all state variables \(z \ne x\). -
2.
 iff \(\nu (z) = \omega (z)\) for all state variables \(z \ne x\).
iff \(\nu (z) = \omega (z)\) for all state variables \(z \ne x\). -
3.
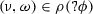 iff
iff  and
and  .
. -
4.
 iff for some \({r\ge 0}\), there is a (flow) function
iff for some \({r\ge 0}\), there is a (flow) function  with
with  , such that for each time \(\zeta \in [0,r]\) the differential equation holds and the evolution domain is respected
, such that for each time \(\zeta \in [0,r]\) the differential equation holds and the evolution domain is respected  , see [29, 34] for details
, see [29, 34] for details -
5.

-
6.

-
7.
 where \(\alpha ^{i+1} \,\hat{=}\, (\alpha ; \alpha ^i)\) and \(\alpha ^0 \,\hat{=}\, ?true\).
where \(\alpha ^{i+1} \,\hat{=}\, (\alpha ; \alpha ^i)\) and \(\alpha ^0 \,\hat{=}\, ?true\).
Definition 2
(Interpretation of  formulas) The interpretation \(\models \) of a
formulas) The interpretation \(\models \) of a  formula with respect to
formula with respect to  is defined as follows.
is defined as follows.
-
1.
 iff
iff  for \({\sim } \in \{=,\le ,<,\ge ,>\}\)
for \({\sim } \in \{=,\le ,<,\ge ,>\}\)
-
2.
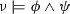 iff
iff  and
and  , accordingly for
, accordingly for 
-
3.
 iff
iff  for all
for all  that agree with
that agree with  except for the value of x
except for the value of x
-
4.
 iff
iff  for some
for some  that agrees with
that agrees with  except for the value of x
except for the value of x
-
5.
 iff
iff  for all
for all 
-
6.
 iff
iff  for some
for some 
We write \(\models \phi \) to denote that \(\phi \) is valid, i. e., that \(\nu \models \phi \) for all states \({\nu }\).
2.3 Notation and supporting lemmas
 denotes the bound variables [35] in \(\alpha \), i. e., those written to in \(\alpha \),
denotes the bound variables [35] in \(\alpha \), i. e., those written to in \(\alpha \),  are free variables [35] in \(\psi \), \(\varSigma \) is the set of all variables, and \(A \backslash B\) denotes the set of variables being in some set A but not in some other set B. Furthermore, \(\nu |_A\) denotes the state \(\nu \) projected to just the variables in A, whereas \(\nu _x^y\) denotes the state \(\nu \) in which x is interpreted as y.
are free variables [35] in \(\psi \), \(\varSigma \) is the set of all variables, and \(A \backslash B\) denotes the set of variables being in some set A but not in some other set B. Furthermore, \(\nu |_A\) denotes the state \(\nu \) projected to just the variables in A, whereas \(\nu _x^y\) denotes the state \(\nu \) in which x is interpreted as y.
In the proofs throughout this article, we will use the following lemmas specialized from [35, Lemmas 12, 14, and 15]. Hybrid programs only change their bound variables:
Lemma 1
(Bound effect lemma) If \((\nu ,\omega ) \in \rho (\alpha )\), then \(\nu =\omega \) on  .
.
The truth of formulas only depends on their free variables:
Lemma 2
(Coincidence lemma) If \(\nu =\tilde{\nu }\) on  then \(\nu \models \phi \) iff \(\tilde{\nu } \models \phi \).
then \(\nu \models \phi \) iff \(\tilde{\nu } \models \phi \).
Similar states (that agree on the free variables) have similar transitions:
Lemma 3
(Coincidence lemma) If \(\nu =\tilde{\nu }\) on  and \((\nu ,\omega ) \in \rho (\alpha )\), then there is an \(\tilde{\omega }\) such that \((\tilde{\nu },\tilde{\omega }) \in \rho (\alpha )\) and \(\omega =\tilde{\omega }\) on \(V\).
and \((\nu ,\omega ) \in \rho (\alpha )\), then there is an \(\tilde{\omega }\) such that \((\tilde{\nu },\tilde{\omega }) \in \rho (\alpha )\) and \(\omega =\tilde{\omega }\) on \(V\).
The notation \(\nu |_V=\tilde{\nu }|_V\) is used interchangeably with \(\nu =\tilde{\nu }\) agree on \(V\).
3 ModelPlex approach for verified runtime validation
CPS are almost impossible to get right without sufficient attention to prior analysis, for instance by formal verification and formal validation techniques. We assume to be given a verified model of a CPS, i. e. formula (2) is proved valid,Footnote 3 for example using the differential dynamic logic proof calculus [29, 33] implemented in  [37] and KeYmaera X [14]:
[37] and KeYmaera X [14]:

Formula (2) expresses that all runs of the hybrid system  , which start in states that satisfy the precondition \(\phi \) and repeat \(\alpha \) arbitrarily many times, only end in states that satisfy the postcondition \(\psi \). Note, that in this article we discuss models of the form
, which start in states that satisfy the precondition \(\phi \) and repeat \(\alpha \) arbitrarily many times, only end in states that satisfy the postcondition \(\psi \). Note, that in this article we discuss models of the form  for comprehensibility reasons. The approach is also applicable to more general forms of models (e. g., models without loops, or models where only parts are executed in loops).
for comprehensibility reasons. The approach is also applicable to more general forms of models (e. g., models without loops, or models where only parts are executed in loops).
The model  is a hybrid system model of a CPS, which means that it describes both the discrete control actions of the controllers in the system and the continuous physics of the plant and the system’s environment. For example, our running example of a water tank repeated below models a hybrid system, which consists of a controller that chooses flow and a plant that determines how the water level changes depending on the chosen flow.
is a hybrid system model of a CPS, which means that it describes both the discrete control actions of the controllers in the system and the continuous physics of the plant and the system’s environment. For example, our running example of a water tank repeated below models a hybrid system, which consists of a controller that chooses flow and a plant that determines how the water level changes depending on the chosen flow.

Formula (2) is proved using some form of induction with invariant \(\varphi \), i. e., a formula for which the following three formulas are provable:

which shows that a loop invariant \(\varphi \) holds after every run of \(\alpha \) if it was true before (i. e.,  ), that the loop invariant holds initially
), that the loop invariant holds initially  and implies the postcondition
and implies the postcondition  .
.
However, since we usually made approximations when modeling the controller and the physics, and since failures and other deviations may occur in reality (e. g., a valve could fail), we cannot simply transfer this safety proof to the real system. The safety guarantees that we obtain by proving formula (2) about the model  transfer to the real system, if the actual CPS execution fits to
transfer to the real system, if the actual CPS execution fits to  .
.
Example 1
(What to monitor) Let us recall the water tank example. First, since failures may occur we need to monitor actual evolution, such as that the actual water level corresponds to the level expected by the chosen valve positions and the actual time passed between controller executions does not exceed the modeled sampling period. The monitor needs to allow some slack around the expected water level to compensate for the neglected physical phenomena. Sections 3.2 and 3.5 describe how to synthesize such model monitors automatically. Second, the controller implementation differs from the model, e.g., it might follow different filling strategies, so we need to check that the implemented controller only chooses flows f that satisfy \(-1 \le f \le \tfrac{m-x}{\varepsilon }\). Section 3.4 describes how to synthesize such controller monitors automatically. Finally, we can monitor controller decisions for the expected real-world effect, since the hybrid system model contains a model of the physics of the water tank. Section 3.6 describes how to synthesize such prediction monitors automatically. The controller in the model, which is verified to be safe, gives us a fail-safe action that we can execute instead of the unverified controller implementation when one of the monitors is not satisfied.
Since we want to preserve safety properties, a CPS \(\gamma \) fits to a model  , if the CPS reaches at most those states that are reachable by the model, i. e.,
, if the CPS reaches at most those states that are reachable by the model, i. e.,  [27], because all states reachable by
[27], because all states reachable by  from states satisfying \(\phi \) are safe by (2). For example, a controller that chooses inflow more cautiously, such as only half the maximum inflow from the model, i. e., \(f\le \tfrac{m-x}{2\varepsilon }\), would also be safe. So would be running the controller more frequently than every \(\varepsilon \) time, but not less frequently.
from states satisfying \(\phi \) are safe by (2). For example, a controller that chooses inflow more cautiously, such as only half the maximum inflow from the model, i. e., \(f\le \tfrac{m-x}{2\varepsilon }\), would also be safe. So would be running the controller more frequently than every \(\varepsilon \) time, but not less frequently.
However, we do not know the true CPS \(\gamma \) precisely,Footnote 4 so we cannot use refinement-based techniques (e. g., [27]) to prove that the true CPS \(\gamma \) refines the model  . Therefore, we need to find a condition based on
. Therefore, we need to find a condition based on  that we can check at runtime to see if concrete runs of the true CPS \(\gamma \) behave like the model
that we can check at runtime to see if concrete runs of the true CPS \(\gamma \) behave like the model  .
.
Example 2
(Canonical monitor candidates) A monitor condition that would be easy to check is to monitor the postcondition \(\psi \) (e. g., monitor the safety condition of the water tank \(0 \le x \le m\)). But that monitor is unsafe, because if \(\psi \) is violated at runtime, the system is already unsafe and it is too late to do anything about it (e. g., the water tank did already overflow). Another monitor that would be easy to check is the invariant \(\varphi \) used to prove Formula (2). But that monitor is also unsafe, because once \(\varphi \) is violated at runtime, the controller is no longer guaranteed to be safe, since Formula (3) only proves it to be safe when maintaining invariant \(\varphi \) (e. g., in the water tank example, the invariant \(\varphi \equiv 0 \le x \le m\) is not even stronger than the safety condition). But if we detect when a CPS is about to deviate from \(\alpha \) before leaving \(\varphi \), we can still switch to a fail-safe controller to avoid \(\lnot \psi \) from ever happening (see Fig. 3). Yet even so, the invariant \(\varphi \) will not even contain all conditions that need to be monitored, since \(\varphi \) only reflects what will not change when running the particular model \(\alpha \), which says nothing about the behavior of the true CPS \(\gamma \).
The basic idea behind ModelPlex is based on online monitoring: we periodically sample \(\gamma \) to obtain actual system states \(\nu _i\). A state \(\nu _i\) includes values for each of the bound variables (i. e., those that are written) from the model  . For example, for our water tank we need to sample flow f (written to in
. For example, for our water tank we need to sample flow f (written to in  ), water level x (written to in
), water level x (written to in  ), and time t (written to in
), and time t (written to in  and
and  ). We then check pairs of such states for being included in the reachability relation of the model, which is expressed in
). We then check pairs of such states for being included in the reachability relation of the model, which is expressed in  semantics as
semantics as  . We will refer to the first state in such a pair by prior state and to the second one by posterior state. This is the right semantic condition to check, but not computationally represented. The important question answered by ModelPlex through automatic synthesis is how that check can be represented in a monitor condition in an easily and efficiently computable form.
. We will refer to the first state in such a pair by prior state and to the second one by posterior state. This is the right semantic condition to check, but not computationally represented. The important question answered by ModelPlex through automatic synthesis is how that check can be represented in a monitor condition in an easily and efficiently computable form.
Example 3
(Desired arithmetic monitor representation) For example, by manually analyzing the hybrid program of the water tank example, the result is expected to be the following real arithmetic formula. The annotations under the braces refer to the part of the hybrid program of the water tank that points us to the corresponding condition.

This formula describes that (i) the flow \(\nu _i(f)\) in the posterior state has to obey certain bounds, depending on the prior water level \(\nu _{i-1}(x)\), resulting from the nondeterministic assignment and the test; (ii) the posterior water level \(\nu _i(x)\) is given by the solution of the differential equation \(x + \int f dt = x+ft\), i. e., the posterior water level should be equal to the prior water level \(\nu _{i-1}(x)\) plus the amount resulting from flow \(\nu _i(f)\) in time \(\nu _i(t)\); finally, (iii) the evolution domain constraints must be true, meaning the posterior water level must be non-negative and the time \(\nu _i(t)\) must be between 0 and \(\varepsilon \). Note, that it is tempting to just read off a wrong condition \(\nu _i(t)=0\) from hybrid program  . Since t is not constant in the ODE following the assignment (
. Since t is not constant in the ODE following the assignment ( ), this condition must be phrased \(0 \le \nu _i(t)\). Also note, that it is very easy to get the evolution domain wrong: evolution domain constraints have to hold throughout the ODE, which includes the beginning and the end, so the check must include both \(\nu _{i-1}(x)\ge 0\) and \(\nu _i(x)\ge 0\). The sound proof calculus of
), this condition must be phrased \(0 \le \nu _i(t)\). Also note, that it is very easy to get the evolution domain wrong: evolution domain constraints have to hold throughout the ODE, which includes the beginning and the end, so the check must include both \(\nu _{i-1}(x)\ge 0\) and \(\nu _i(x)\ge 0\). The sound proof calculus of  prevents such mistakes when deriving monitor conditions.
prevents such mistakes when deriving monitor conditions.
The question is: How to find such an arithmetic representation automatically from just the formula (1)? And how to prove its correctness? ModelPlex derives three kinds of such formulas as monitors (model monitor, controller monitor, and prediction monitor, cf. Fig. 4) that check the behavior of the actual CPS at runtime for compliance with its model. These monitors have the following characteristics.
- Model monitor :
-
The model monitor checks the previous state \(\nu _{i-1}\) and current state \(\nu _{i}\) for compliance with the model, i. e.. whether the observed transition from \(\nu _{i-1}\) to \(\nu _{i}\) is compatible with the model. In each state \(\nu _{i}\) we test the sample point \(\nu _{i-1}\) from the previous execution \(\gamma _{i-1}\) for deviation from
 , i. e., test
, i. e., test 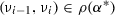 . If violated, other verified properties may no longer hold for the system so a failsafe action is initiated. The system itself, however, still satisfies safety condition \(\psi \) if the prediction monitor was satisfied at \(\nu _{i-1}\). Frequent violations indicate an inadequate model that should be revised to better reflect reality.
. If violated, other verified properties may no longer hold for the system so a failsafe action is initiated. The system itself, however, still satisfies safety condition \(\psi \) if the prediction monitor was satisfied at \(\nu _{i-1}\). Frequent violations indicate an inadequate model that should be revised to better reflect reality. - Controller monitor :
-
The controller monitor checks the output of a controller implementation against the correct controller model. If the controller implementation performs an action that the controller model allows in the present state, then it has been verified offline to be safe by Formula (2). Otherwise, the action is discarded and replaced by a default action that has been proved safe. In intermediate state \(\tilde{\nu }_{i}\) we test the current controller decisions of the controller implementation \(\gamma _{\text {ctrl}}\) for compliance with the model, i. e., test \((\nu _{i}, \tilde{\nu }_{i}) \in \rho (\alpha _{\text {ctrl}})\). The controller \(\alpha _\text {ctrl}\) will be obtained from the model
 through proof steps. Controller monitors have some similarities with Simplex [39], which is designed for switching between verified and unverified controllers. The controller monitor, instead, corresponds to the more general idea of testing contracts dynamically at runtime while defaulting to a specified default action choice if the contract fails. If a controller monitor is violated, commands from a fail-safe controller replace the current controller’s decisions to ensure that no unsafe commands are ever actuated.
through proof steps. Controller monitors have some similarities with Simplex [39], which is designed for switching between verified and unverified controllers. The controller monitor, instead, corresponds to the more general idea of testing contracts dynamically at runtime while defaulting to a specified default action choice if the contract fails. If a controller monitor is violated, commands from a fail-safe controller replace the current controller’s decisions to ensure that no unsafe commands are ever actuated. - Prediction monitor :
-
The model monitor detects deviations from the model as soon as possible on the measured data, but that may already have made the system unsafe. The role of the prediction monitor is to check the impact of bounded deviations from the model to predict whether the next state could possibly become unsafe upon deviation from the model so that a corrective action is advised. If the actual execution stays far enough away from unsafe states, the prediction monitor will not intervene because no disturbance within the bound could make it unsafe. In intermediate state \(\tilde{\nu }_{i}\) we test the safety impact of the current controller decision w.r.t. the predictions of a bounded deviation plant model \(\alpha _{\delta \text {plant}}\), which has a tolerance around the model plant \(\alpha _\text {plant}\), i. e., check \(\nu _{i+1} \models \varphi \) for all \(\nu _{i+1}\) such that \((\tilde{\nu }_{i},\nu _{i+1}) \in \rho (\alpha _{\delta \text {plant}})\). Note, that we simultaneously check all \(\nu _{i+1}\) by checking a characterizing condition of \(\alpha _{\delta \text {plant}}\) at \(\tilde{\nu }_{i}\). If violated, the current control choice is not guaranteed to keep the system safe under all disturbances until the next control cycle and, thus, a fail-safe controller takes over.
A simulation illustrating the effect of these monitors on the water tank running example will be discussed in Fig. 11, where an unsafe controller and small deviation from the idealistic model would result in violation of the safety property, if not corrected by the monitors synthesized in this article.
The assumption for the prediction monitor is that the real execution is not arbitrarily far off the plant models used for safety verification, because otherwise safety guarantees can be neither made on unobservable intermediate states nor on safety of the future system evolution [36]. We propose separation of disturbance causes in the models: ideal plant models \(\alpha _{\text {plant}}\) for correctness verification purposes, implementation deviation plant models \(\alpha _{\delta \text {plant}}\) for monitoring purposes. We support any deviation model (e. g., piecewise constant disturbance, differential inclusion models of disturbance), as long as the deviation is bounded and differential invariants can be found. We further assume that monitor evaluations are at most some \(\varepsilon \) time units apart (e. g., along with a recurring controller execution). Note that disturbance in \(\alpha _{\delta \text {plant}}\) is more manageable compared to a model of the form  , because we can focus on single runs \(\alpha \) instead of repetitions for guaranteed monitoring purposes.
, because we can focus on single runs \(\alpha \) instead of repetitions for guaranteed monitoring purposes.
3.1 Characterizing semantic relations between states in logic
All ModelPlex monitors relate states, albeit for different purposes to safeguard different parts of the CPS execution (Fig. 4). States are semantic objects and as such cannot be related, manipulated, or even just represented precisely in a program. This section develops a systematic logical characterization as syntactic expressions for such state relations, which will ultimately lead to computable programs for the corresponding monitor conditions. We systematically derive a check that inspects states of the actual CPS to detect deviation from the model \(\alpha \). We first establish a notion of state recall and show that compliance of an execution from state \(\nu \) to \(\omega \) with \(\alpha \) can be characterized syntactically in  .
.
The ModelPlex monitoring principle illustrated in Fig. 4 is intuitive, but its sequence of states \(\nu _i\) is inherently semantic and, thus, inaccessible in syntactic programs. Our first step is to introduce a vector of logical variables x and \(x^+\) for the symbolic prior and posterior state variables. The basic idea is that ModelPlex monitors identify conditions on the relationships between the values of prior and posterior state expressed as a logical formula involving the variables x and \(x^+\). Concrete states \(\nu _{i-1}\) and \(\nu _i\) can then be fed into the monitor formula as the real values for the variables x and \(x^+\) to check whether the monitor is satisfied along the actual system execution.
Definition 3 and Lemma 4 below describe central ingredients for online monitoring in this article and are true for models \(\beta \) of arbitrary form (not just for models  with a loop).
with a loop).
Definition 3
(State recall) Let \(V\) denote the set of variables whose state we want to recall. We use the formula  to express a characterization of the values of variables x in a state posterior to a run of \(\beta \), where we always assume the fresh variables \(x^+\) to occur solely in \(\varUpsilon ^+\). The variables in \(x^+\) can be used to recall this state. We define the satisfaction relation \((\nu , \omega ) \models \phi \) of
to express a characterization of the values of variables x in a state posterior to a run of \(\beta \), where we always assume the fresh variables \(x^+\) to occur solely in \(\varUpsilon ^+\). The variables in \(x^+\) can be used to recall this state. We define the satisfaction relation \((\nu , \omega ) \models \phi \) of  formula \(\phi \) for a pair of states \((\nu ,\omega )\) as \(\phi \) evaluated in the state resulting from \(\nu \) by interpreting \(x^+\) as \(\omega (x)\) for all \(x \in V\), i. e., \((\nu , \omega ) \models \phi \) iff \(\nu _{x^+}^{\omega (x)} \models \phi \).
formula \(\phi \) for a pair of states \((\nu ,\omega )\) as \(\phi \) evaluated in the state resulting from \(\nu \) by interpreting \(x^+\) as \(\omega (x)\) for all \(x \in V\), i. e., \((\nu , \omega ) \models \phi \) iff \(\nu _{x^+}^{\omega (x)} \models \phi \).
This enables a key ingredient for ModelPlex: establishing a direct correspondence of a semantic reachability of states with a syntactic logical formula internalizing that semantic relationship by exploiting the  modality of
modality of  .
.
Lemma 4
(Logical state relation) Let  . Two states \(\nu ,\omega \) that agree on \(\varSigma \setminus V\), i. e., \(\nu |_{\varSigma \setminus V} = \omega |_{\varSigma \setminus V}\), i. e., \(\nu (z)=\omega (z)\) for all \(z\in \varSigma \setminus V\), satisfy \((\nu ,\omega ) \in \rho (\beta )\) iff
. Two states \(\nu ,\omega \) that agree on \(\varSigma \setminus V\), i. e., \(\nu |_{\varSigma \setminus V} = \omega |_{\varSigma \setminus V}\), i. e., \(\nu (z)=\omega (z)\) for all \(z\in \varSigma \setminus V\), satisfy \((\nu ,\omega ) \in \rho (\beta )\) iff  .
.
Proof
- “
 ”:
”: -
Let \((\nu ,\omega ) \in \rho (\beta )\). Since \(\nu \) and \(\nu _{x^+}^{\omega (x)}\) agree except on \(x^+\), which are not free variables of \(\beta \), \((\nu ,\omega ) \in \rho (\beta )\) also implies by coincidence Lemma 3 that there is a \(\tilde{\omega }\) such that \((\nu _{x^+}^{\omega (x)},\tilde{\omega }) \in \rho (\beta )\) and \(\omega =\tilde{\omega }\) except on \(x^+\). Now \((\nu _{x^+}^{\omega (x)},\tilde{\omega }) \in \rho (\beta )\) implies that \(\nu _{x^+}^{\omega (x)}=\tilde{\omega }\) agree except on
 by bound effect Lemma 1. Hence, \(\nu _{x^+}^{\omega (x)}=\tilde{\omega }\) agree on \(x^+\) since
by bound effect Lemma 1. Hence, \(\nu _{x^+}^{\omega (x)}=\tilde{\omega }\) agree on \(x^+\) since  and, thus, also \(\omega _{x^+}^{\omega (x)}=\tilde{\omega }\) on \(x^+\). Since \(\omega =\tilde{\omega }\) agree except on \(x^+\) and \(\omega _{x^+}^{\omega (x)}=\tilde{\omega }\) agree on \(x^+\), also \(\omega _{x^+}^{\omega (x)}=\tilde{\omega }\) agree everywhere, which implies, \((\nu _{x^+}^{\omega (x)},\omega _{x^+}^{\omega (x)}) \in \rho (\beta )\), because \((\nu _{x^+}^{\omega (x)},\tilde{\omega }) \in \rho (\beta )\). As \(\omega _{x^+}^{\omega (x)} \models x=x^+\) for all x, so \(\omega _{x^+}^{\omega (x)} \models \varUpsilon ^+\). Consequently,
and, thus, also \(\omega _{x^+}^{\omega (x)}=\tilde{\omega }\) on \(x^+\). Since \(\omega =\tilde{\omega }\) agree except on \(x^+\) and \(\omega _{x^+}^{\omega (x)}=\tilde{\omega }\) agree on \(x^+\), also \(\omega _{x^+}^{\omega (x)}=\tilde{\omega }\) agree everywhere, which implies, \((\nu _{x^+}^{\omega (x)},\omega _{x^+}^{\omega (x)}) \in \rho (\beta )\), because \((\nu _{x^+}^{\omega (x)},\tilde{\omega }) \in \rho (\beta )\). As \(\omega _{x^+}^{\omega (x)} \models x=x^+\) for all x, so \(\omega _{x^+}^{\omega (x)} \models \varUpsilon ^+\). Consequently,  , which is
, which is  .
. - “
 ”:
”: -
Let
 , that is,
, that is,  . So there is a \(\tilde{\omega }\) such that \((\nu _{x^+}^{\omega (x)},\tilde{\omega }) \in \rho (\beta )\) and \(\tilde{\omega } \models \varUpsilon ^+\). Now \(\tilde{\omega } \models \varUpsilon ^+\) implies that \(\tilde{\omega }(x) = \tilde{\omega }(x^+)\). By the bound effect Lemma 1, \(\nu _{x^+}^{\omega (x)}=\tilde{\omega }\) agree except on
. So there is a \(\tilde{\omega }\) such that \((\nu _{x^+}^{\omega (x)},\tilde{\omega }) \in \rho (\beta )\) and \(\tilde{\omega } \models \varUpsilon ^+\). Now \(\tilde{\omega } \models \varUpsilon ^+\) implies that \(\tilde{\omega }(x) = \tilde{\omega }(x^+)\). By the bound effect Lemma 1, \(\nu _{x^+}^{\omega (x)}=\tilde{\omega }\) agree except on 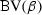 . Thus, \(\tilde{\omega }(x^+)=\nu _{x^+}^{\omega (x)}(x^+)=\omega (x)\) for all
. Thus, \(\tilde{\omega }(x^+)=\nu _{x^+}^{\omega (x)}(x^+)=\omega (x)\) for all 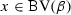 as
as  . Combining both yields that \(\tilde{\omega }=\omega \) agree on all
. Combining both yields that \(\tilde{\omega }=\omega \) agree on all  . Since \((\nu _{x^+}^{\omega (x)},\tilde{\omega }) \in \rho (\beta )\) and \(\nu _{x^+}^{\omega (x)}=\nu \) agree except on
. Since \((\nu _{x^+}^{\omega (x)},\tilde{\omega }) \in \rho (\beta )\) and \(\nu _{x^+}^{\omega (x)}=\nu \) agree except on  , coincidence Lemma 3 implies there is a \(\mu \) such that \((\nu ,\mu ) \in \rho (\beta )\) and \(\mu =\tilde{\omega }\) agree except on \(x^+\). So, \(\mu =\tilde{\omega }=\omega \) agree on
, coincidence Lemma 3 implies there is a \(\mu \) such that \((\nu ,\mu ) \in \rho (\beta )\) and \(\mu =\tilde{\omega }\) agree except on \(x^+\). So, \(\mu =\tilde{\omega }=\omega \) agree on  . And \(\mu =\nu \) agree except on
. And \(\mu =\nu \) agree except on  by bound effect Lemma 1. From the assumption that \(\nu =\omega \) agree except on
by bound effect Lemma 1. From the assumption that \(\nu =\omega \) agree except on  , it follows that \(\mu =\omega \) also on
, it follows that \(\mu =\omega \) also on  , so \(\mu =\omega \). Hence, \((\nu ,\mu ) \in \rho (\beta )\) implies \((\nu ,\omega ) \in \rho (\beta )\). \(\square \)
, so \(\mu =\omega \). Hence, \((\nu ,\mu ) \in \rho (\beta )\) implies \((\nu ,\omega ) \in \rho (\beta )\). \(\square \)
Suppose the CPS executed for some period of time and made it from state \(\nu \) to a state \(\omega \). That transition fits to the verified model  iff the semantic condition
iff the semantic condition  holds, i. e., the states \(\nu ,\omega \) are in the transition relation induced by the semantics of
holds, i. e., the states \(\nu ,\omega \) are in the transition relation induced by the semantics of  . The syntactic formula
. The syntactic formula  expresses something like that. Lemma 4 enables us to use formula (4) as a starting point to find compliance checks systematically.
expresses something like that. Lemma 4 enables us to use formula (4) as a starting point to find compliance checks systematically.

The logical formula (4) relates a prior state of a CPS to its posterior consecutive state through at least one path through the model  .Footnote 5 The formula (4) is satisfied in a state \(\nu \), if there is at least one run of the model
.Footnote 5 The formula (4) is satisfied in a state \(\nu \), if there is at least one run of the model  starting in the state \(\nu \) and resulting in a state \(\omega \) recalled using \(\varUpsilon ^+\). In other words, at least one path through
starting in the state \(\nu \) and resulting in a state \(\omega \) recalled using \(\varUpsilon ^+\). In other words, at least one path through  explains how the prior state \(\nu \) got transformed into the posterior state \(\omega \).
explains how the prior state \(\nu \) got transformed into the posterior state \(\omega \).
In principle, formula (4) would already be a perfect monitor for the question whether the state change to \(\varUpsilon ^+\) can be explained by model  . But formula (4) is hard if not impossible to evaluate at runtime efficiently, because it refers to a hybrid system
. But formula (4) is hard if not impossible to evaluate at runtime efficiently, because it refers to a hybrid system  , which includes loops, nondeterminism, and differential equations and is, thus, difficult to execute without nontrivial backtracking and differential equation solving. Yet, any formula that is equivalent to or implies (4) but is easier to evaluate in a state is a correct monitor as well.
, which includes loops, nondeterminism, and differential equations and is, thus, difficult to execute without nontrivial backtracking and differential equation solving. Yet, any formula that is equivalent to or implies (4) but is easier to evaluate in a state is a correct monitor as well.
To simplify formula (4), we use theorem proving to find a quantifier-free first-order real arithmetic form so that it can be evaluated efficiently at runtime. The resulting first-order real arithmetic formula can be easily implemented in a runtime monitor that is evaluated by plugging the concrete values in for x and \(x^+\). A monitor is executable code that only returns true if the transition from the prior system state to the posterior state is compliant with the model. Thus, deviations from the model can be detected at runtime, so that appropriate fallback and mitigation strategies can be initiated.
3.2 Model monitor synthesis
This section introduces the nature of ModelPlex monitor specifications, which form the basis of our correct-by-construction synthesis procedure for ModelPlex monitors. Here, we focus on the ModelPlex model monitor, but its principles continue to apply for the controller and prediction monitors, as elaborated subsequently.
Figure 5 gives an overview of the offline synthesis process for model monitors. Semantically, a monitor is a check that a pair of states \((\nu ,\omega )\) is contained in the transition relation  of the monitored hybrid systems model
of the monitored hybrid systems model  (Fig. 6). This corresponds to our intuitive understanding of a monitor: through sensors, we observe states of a system, and want to know if those observations fit to the model
(Fig. 6). This corresponds to our intuitive understanding of a monitor: through sensors, we observe states of a system, and want to know if those observations fit to the model  of the system. By Lemma 4, the syntactic counterpart in the logic
of the system. By Lemma 4, the syntactic counterpart in the logic  of this semantic condition
of this semantic condition  is the logical formula
is the logical formula  from (4). The
from (4). The  formula (4) syntactically characterizes the semantic statement that the hybrid system model
formula (4) syntactically characterizes the semantic statement that the hybrid system model  can reach a posterior stateFootnote 6 characterized by \(x^+\) from the prior state characterized by x. The
can reach a posterior stateFootnote 6 characterized by \(x^+\) from the prior state characterized by x. The  formula (4) is a perfect logical monitor but difficult to execute quickly, so we are looking for easier logical formulas \(F(x,x^+)\) that are equivalent to or imply formula (4). ModelPlex uses theorem proving to systematically synthesize a provably correct real arithmetic formula \(F(x,x^+)\) in a correct-by-construction approach.Footnote 7
formula (4) is a perfect logical monitor but difficult to execute quickly, so we are looking for easier logical formulas \(F(x,x^+)\) that are equivalent to or imply formula (4). ModelPlex uses theorem proving to systematically synthesize a provably correct real arithmetic formula \(F(x,x^+)\) in a correct-by-construction approach.Footnote 7
The intuition is that formula (4) holds because all conditions hold that are identified as implying formula (4) in its proof. Some of these conditions hold always (subgoals that can be proved to be valid always) while others will be checked at runtime whether they hold (subgoals that do not always hold but only during executions that fit to the particular hybrid system  ). If the ModelPlex monitor is satisfied at runtime, then the proof implying formula (4) holds in the current CPS execution.
). If the ModelPlex monitor is satisfied at runtime, then the proof implying formula (4) holds in the current CPS execution.
Note, that computationally expensive operations, such as quantifier elimination, are performed offline in this process and only arithmetic evaluation for concrete state values remains to be done online. If the ModelPlex specification (4) does not hold for the variable values from a prior and posterior state during the CPS execution (checked by evaluating \(F(x,x^+)\) on observations), then that behavior does not comply with the model (e. g., the wrong control action was taken under the wrong circumstances, unanticipated dynamics in the environment occurred, sensor uncertainty led to unexpected values, or the system was applied outside the specified operating environment).
Intuitively, a model monitor \(\chi _{\text {m}}\) is correct when the monitor entails safety if it is satisfied on consecutive observations, which is formalized in Theorem 1 below. Note, that Theorem 1 for models \(\beta \) without loops follows immediately from Lemma 4 and the safety proof. Thanks to Lemma 4, correctness of model monitors is also easy to prove:
Theorem 1
(Model monitor correctness) Let  be provably safe, so
be provably safe, so  and let
and let  . Let \(\nu _0, \nu _1, \nu _2, \nu _3 \ldots \in \mathbb {R}^n\) be a sequence of states that agree on
. Let \(\nu _0, \nu _1, \nu _2, \nu _3 \ldots \in \mathbb {R}^n\) be a sequence of states that agree on  , i. e.,
, i. e.,  for all k, and that start in \(\nu _0 \models \phi \). If \((\nu _i, \nu _{i+1}) \models \chi _{\text {m}}\) for all \(i < n\), then \(\nu _{n} \models \psi \) where
for all k, and that start in \(\nu _0 \models \phi \). If \((\nu _i, \nu _{i+1}) \models \chi _{\text {m}}\) for all \(i < n\), then \(\nu _{n} \models \psi \) where

Proof
Show  by induction over n, such that
by induction over n, such that  and \(\nu _0 \models \phi \) imply \(\nu _n \models \psi \). If \(n = 0\) then
and \(\nu _0 \models \phi \) imply \(\nu _n \models \psi \). If \(n = 0\) then  trivially by Definition 1. For \(n+1 > 0\) assume
trivially by Definition 1. For \(n+1 > 0\) assume  and
and  . By Lemma 4,
. By Lemma 4,  implies that
implies that  . Now
. Now  and
and  imply
imply  . Hence we conclude \(\nu _{n+1} \models \psi \) from \(\nu _0 \models \phi \) and
. Hence we conclude \(\nu _{n+1} \models \psi \) from \(\nu _0 \models \phi \) and  . \(\square \)
. \(\square \)
By Theorem 1, any formula implying \(\chi _{\text {m}}\) is also a correct model monitor, such as  , which more conservatively limits acceptable executions of the real \(\gamma \) to those that correspond to just one iteration of
, which more conservatively limits acceptable executions of the real \(\gamma \) to those that correspond to just one iteration of  as opposed to arbitrarily many.
as opposed to arbitrarily many.
Example 4
(Arithmetical model monitor condition) As illustrated in Fig. 5 and shown concretely below, we can simplify formula (5) into an arithmetical representation \(F(x,x^+)\) such that  , by applying the axioms of
, by applying the axioms of  . The synthesis algorithm to automatically generate the condition \(F(x,x^+)\) is presented in Section 3.3.
. The synthesis algorithm to automatically generate the condition \(F(x,x^+)\) is presented in Section 3.3.

The formula \(F(x,x^+)\) says that (i) only valid flows should be chosen for the posterior state, i. e., \(-1 \le f^+ \le \tfrac{m-x}{\varepsilon }\), (ii) that the posterior water level \(x^+\) must be determined by the prior level x and the flow over time \(x^+ = x+f^+t^+\), and (iii) that the evolution domain constraint must be satisfied in both prior and posterior state, i. e., \(x \ge 0 \wedge \varepsilon \ge t^+ \ge 0 \wedge \underbrace{f^+t^++x}_{x^+} \ge 0\).
This formula corresponds to the expected result from Example 3, since x corresponds to \(\nu _{i-1}(x)\) and \(x^+\) corresponds to \(\nu (x)\), and so forth.
The formula in Example 4 contains checks for water level x, flow f, and time t, because these are the variables changed by the model. If we want to additionally monitor that the model does not change anything except these variables, we can use Corollary 1 to include frame constraints for specific variables into a monitor (e. g., the value of variable \(\varepsilon \) is not changed by the water tank model, and therefore not supposed to change in reality).
Corollary 1
Theorem 1 continues to apply when replacing \(V\) by any superset  .
.
Proof
Any variable  can be added to Theorem 1 by considering
can be added to Theorem 1 by considering  instead of
instead of  , which has the same behavior but one more bound variable. \(\square \)
, which has the same behavior but one more bound variable. \(\square \)
So far, Theorem 1 assumed that everything stays constant, except for the water level x, the flow f, and the time t. This assumption is stronger than absolutely necessary, and, strictly speaking, prevents us from using the monitor in an environment where values that are irrelevant to the model and its safety condition change (e. g., the water temperature). Corollary 2 ensures monitor correctness in environments where irrelevant variables change arbitrarily. Theorem 2 and 3 can be extended with corollaries similar to Corollaries 1 and 2.
Corollary 2
When replacing \(V\) by any superset  , Theorem 1 continues to hold without the assumption that the \(\nu _k\) agree on \(\varSigma \backslash V\).
, Theorem 1 continues to hold without the assumption that the \(\nu _k\) agree on \(\varSigma \backslash V\).
Proof
Assume the conditions of Theorem 1 with any sequence of states \(\nu _0, \nu _1, \nu _2, \nu _3 \ldots \in \mathbb {R}^n\), with \(\nu _0 \models \phi \). Consider a modified sequence of states \(\bar{\nu }_0, \bar{\nu }_1, \bar{\nu }_2, \bar{\nu }_3 \ldots \) such that for all k: \(\nu _k\) agrees with \(\bar{\nu }_k\) on \(V\) and \(\bar{\nu }_k\) agrees with \(\nu _0\) on \(\varSigma \backslash V\), which, thus, satisfies the assumptions of Theorem 1. Hence, \((\nu _i, \nu _{i+1}) \models \chi _{\text {m}}\) implies \((\bar{\nu }_i, \bar{\nu }_{i+1}) \models \chi _{\text {m}}\) by Lemma 2 using  . Thus, \((\nu _i, \nu _{i+1}) \models \chi _{\text {m}}\) for all \(i<n\) implies \((\bar{\nu }_i, \bar{\nu }_{i+1}) \models \chi _{\text {m}}\) for all \(i<n\), so Theorem 1 implies \(\bar{\nu }_n \models \psi \). Since
. Thus, \((\nu _i, \nu _{i+1}) \models \chi _{\text {m}}\) for all \(i<n\) implies \((\bar{\nu }_i, \bar{\nu }_{i+1}) \models \chi _{\text {m}}\) for all \(i<n\), so Theorem 1 implies \(\bar{\nu }_n \models \psi \). Since  , Lemma 2 implies that \(\nu _n \models \psi \).
, Lemma 2 implies that \(\nu _n \models \psi \).
\(\square \)
Theorem 1 ensures that, when the monitor is satisfied, the monitored states are safe, i. e., \(\psi \) holds. We can get an even stronger result by Corollary 3, which says that a model monitor also ensures that inductive invariants \(\varphi \) of the model are preserved.
Corollary 3
Under the conditions of Theorem 1 it is also true that \(\nu _n \models \varphi \) for an invariant \(\varphi \) s.t.  ,
,  , and
, and  .
.
Proof
From  it follows that there exists a \(\varphi \) s.t.
it follows that there exists a \(\varphi \) s.t.  ,
,  , and
, and  . Hence
. Hence  and Theorem 1 applies with \(\varphi \) in place of \(\psi \). \(\square \)
and Theorem 1 applies with \(\varphi \) in place of \(\psi \). \(\square \)
Now that we know the correctness of the logical monitor representation, let us turn to synthesizing its arithmetical form.
3.3 Monitor synthesis algorithm
Our approach to generate monitors from hybrid system models is a correct-by-construction approach. This section explains how to turn monitor specifications into monitor code that can be executed at runtime along with the controller. We take a verified  formula (2) and a synthesis tactic choice (whether to synthesize a model, controller, or prediction monitor) as input and produce a monitor \(F(x,x^+)\) in quantifier-free first-order form as output. The algorithm, listed in Algorithm 1, involves the following steps:
formula (2) and a synthesis tactic choice (whether to synthesize a model, controller, or prediction monitor) as input and produce a monitor \(F(x,x^+)\) in quantifier-free first-order form as output. The algorithm, listed in Algorithm 1, involves the following steps:
-
1.
A
 formula (2) about a model
formula (2) about a model  of the form
of the form  is turned into a specification conjecture (5) of the form
is turned into a specification conjecture (5) of the form 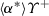 .
. -
2.
Theorem proving according to the tactic choice is applied on the specification conjecture (5) until no further
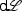 proof rules are applicable and only first-order real arithmetic formulas remain open.
proof rules are applicable and only first-order real arithmetic formulas remain open. -
3.
The monitor specification \(F(x,x^+)\) is the conjunction of the unprovable first-order real arithmetic formulas from open sub-goals. The intuition behind this is that goals, which remain open in the offline proof, are proved online through monitoring. Although this do not yield a proof for all imaginable runs, that way we obtain a proof for the current run of the real CPS.
The correctness of the monitoring conditions obtained through Algorithm 1 is guaranteed by the soundness of the  calculus. In the remainder of the section, we will exemplify Algorithm 1 by turning the model of the water tank example into a model monitor.
calculus. In the remainder of the section, we will exemplify Algorithm 1 by turning the model of the water tank example into a model monitor.

Generate the specification conjecture We map  formula (2) syntactically to a specification conjecture of the form (5), i. e.,
formula (2) syntactically to a specification conjecture of the form (5), i. e.,  . By design, this conjecture will not be provable. But the unprovable branches of a proof attempt will reveal information that, had it been in the premises, would make (5) provable. Through \(\varUpsilon ^+\), those unprovable conditions collect the relations of the posterior state of model
. By design, this conjecture will not be provable. But the unprovable branches of a proof attempt will reveal information that, had it been in the premises, would make (5) provable. Through \(\varUpsilon ^+\), those unprovable conditions collect the relations of the posterior state of model  characterized by \(x^+\) to the prior state x, i. e., the conditions are a representation of (4) in quantifier-free first-order real arithmetic.
characterized by \(x^+\) to the prior state x, i. e., the conditions are a representation of (4) in quantifier-free first-order real arithmetic.
Example 5
(Specification conjecture) The specification conjecture for the water tank model monitor is:

It is constructed by Algorithm 1 in steps “specification conjecture” and “set of proof goals” from the model by flipping the modality and formulating the specification requirement as a property, since we are interested in a relation between two consecutive states \(\nu \) and \(\omega \) (recalled by \(x^+\), \(f^+\) and \(t^+\)).
Use theorem proving to analyze the specification conjecture We use the axioms and proof rules of  [29, 33, 35] to analyze the specification conjecture
[29, 33, 35] to analyze the specification conjecture  . These proof rules syntactically decompose a hybrid model into easier-to-handle parts, which leads to sequents with first-order real arithmetic formulas towards the leaves of a proof. Using real arithmetic quantifier elimination we close sequents with logical tautologies, which do not need to be checked at runtime since they always evaluate to
. These proof rules syntactically decompose a hybrid model into easier-to-handle parts, which leads to sequents with first-order real arithmetic formulas towards the leaves of a proof. Using real arithmetic quantifier elimination we close sequents with logical tautologies, which do not need to be checked at runtime since they always evaluate to  for any input. The conjunction of the remaining open sequents is the monitor specification; it implies formula (4).
for any input. The conjunction of the remaining open sequents is the monitor specification; it implies formula (4).
In the remainder of this article, we follow a synthesis style based on the axiomatization of  . Axiomatization-style synthesis differs from the sequent-style synthesis of the short version [24] in the mechanics of the simplification step of Algorithm 1. The axiomatization of
. Axiomatization-style synthesis differs from the sequent-style synthesis of the short version [24] in the mechanics of the simplification step of Algorithm 1. The axiomatization of  allows working in place with fast contextual congruences. This leads to simpler monitors and simpler proofs since the synthesis proof does not branch and thus keeps working on the same goal (\(\tilde{g}=g\), so \(\left| G\right| =1\)), as opposed to the sequent-style synthesis, which may create new goals (\(\left| G\right| \ge 1\)). For comparison, the corresponding sequent-style synthesis techniques of the short version [24] of this article is elaborated in Appendix 3. The complete proof calculus is reported in the literature [29, 33, 35]. We explain the requisite proof rules on-the-fly while discussing their use in the running example.
allows working in place with fast contextual congruences. This leads to simpler monitors and simpler proofs since the synthesis proof does not branch and thus keeps working on the same goal (\(\tilde{g}=g\), so \(\left| G\right| =1\)), as opposed to the sequent-style synthesis, which may create new goals (\(\left| G\right| \ge 1\)). For comparison, the corresponding sequent-style synthesis techniques of the short version [24] of this article is elaborated in Appendix 3. The complete proof calculus is reported in the literature [29, 33, 35]. We explain the requisite proof rules on-the-fly while discussing their use in the running example.
Example 6
(Analyzing loops, assignments, and tests) The analysis of the water tank conjecture from Example 5 uses  to eliminate the loop,
to eliminate the loop,  to handle the sequential composition, followed by
to handle the sequential composition, followed by  to analyze the nondeterministic assignment
to analyze the nondeterministic assignment  . The hybrid program \(\textit{plant}\) is an abbreviation for
. The hybrid program \(\textit{plant}\) is an abbreviation for  , whereas \(\varUpsilon ^+\) is an abbreviation for \(x=x^+ \wedge f=f^+ \wedge t=t^+\). The nondeterministic assignment axiom
, whereas \(\varUpsilon ^+\) is an abbreviation for \(x=x^+ \wedge f=f^+ \wedge t=t^+\). The nondeterministic assignment axiom  introduces an existential quantifier. Note that rewriting can still continue in-place, as demonstrated by rewriting the sequential composition and test inside the quantifier.
introduces an existential quantifier. Note that rewriting can still continue in-place, as demonstrated by rewriting the sequential composition and test inside the quantifier.

Let us look more closely into the first step of Example 6, i. e.,  . Usually, proving properties of the form
. Usually, proving properties of the form  about loops requires an inductive variant in order to prove arbitrarily many repetitions of the loop body. With monitoring in mind, though, we can unwind the loop and execute the resulting conditions repeatedly instead, as elaborated in Lemma 5.
about loops requires an inductive variant in order to prove arbitrarily many repetitions of the loop body. With monitoring in mind, though, we can unwind the loop and execute the resulting conditions repeatedly instead, as elaborated in Lemma 5.
Lemma 5
(Loop elimination) Let \(\alpha \) be a hybrid program and  be the program that repeats \(\alpha \) arbitrarily many times. Then
be the program that repeats \(\alpha \) arbitrarily many times. Then  is valid.
is valid.
Proof
We prove in  using loop unwinding
using loop unwinding  , monotonicity
, monotonicity  and propositional reasoning as follows.
and propositional reasoning as follows.

\(\square \)
Lemma 5 allows us to check compliance with the model  by checking compliance on each execution of \(\alpha \) (i. e., online monitoring [18]), which is easier than for
by checking compliance on each execution of \(\alpha \) (i. e., online monitoring [18]), which is easier than for  because the loop was eliminated.
because the loop was eliminated.
We will continue Example 6 in subsequent examples. The complete sequence of proof rules applied to the specification conjecture of the water tank is described in Appendix 2. Most steps are simple when analyzing specification conjectures: sequential composition ( ), nondeterministic choice (
), nondeterministic choice ( ), deterministic assignment (
), deterministic assignment ( ) replace current facts with simpler ones (or branch the proof as propositional rules do). Challenges arise from handling nondeterministic assignment and differential equations in hybrid programs.
) replace current facts with simpler ones (or branch the proof as propositional rules do). Challenges arise from handling nondeterministic assignment and differential equations in hybrid programs.
Let us first consider nondeterministic assignment  . The proof rule for nondeterministic assignment (
. The proof rule for nondeterministic assignment ( ) results in a new existentially quantified variable. Using axiomatic-style synthesis, we can postpone instantiating the quantifier until enough information about what exact instance to use is discovered, see Example 7. The sequent-style synthesis, in contrast, must instantiate the quantifier right away, in order to continue synthesis on the existentially quantified formula. Appendix 3 discusses ways on how to instantiate such quantifiers ahead of time.
) results in a new existentially quantified variable. Using axiomatic-style synthesis, we can postpone instantiating the quantifier until enough information about what exact instance to use is discovered, see Example 7. The sequent-style synthesis, in contrast, must instantiate the quantifier right away, in order to continue synthesis on the existentially quantified formula. Appendix 3 discusses ways on how to instantiate such quantifiers ahead of time.
Next, we handle differential equations. Even when we can solve the differential equation, existentially and universally quantified variables remain. Let us inspect the corresponding proof rule from the  calculus [33] in its axiomatic form.
calculus [33] in its axiomatic form.

When solving differential equations, we first have to prove the correctness of the solution, as indicated by the left-hand side of the implication in axiom  . Then, we have to prove that there exists a duration T, such that the differential equation stays within the evolution domain H throughout all intermediate times \(\tilde{t}\) and the result satisfies \(\phi \) at the end. At this point we have four options:
. Then, we have to prove that there exists a duration T, such that the differential equation stays within the evolution domain H throughout all intermediate times \(\tilde{t}\) and the result satisfies \(\phi \) at the end. At this point we have four options:
-
we can postpone handling the quantifier until additional facts about a concrete instance are discovered, which is the preferred tactic in axiomatic-style synthesis;
-
we can instantiate the existential quantifier, if we know that the duration will be \(t^+\);
-
we can introduce a new logical variable, which is the generic case in sequent-style synthesis that always yields correct results, but may discover monitor specifications that are harder to evaluate;
-
we can use quantifier elimination (QE) to obtain an equivalent quantifier-free result (a possible optimization could inspect the size of the resulting formula).
Example 7
(Analyzing differential equations) Continuing Example 6, in the analysis of the water tank example, we solve the differential equation, see  . The condition
. The condition  , with the solution \(y(T)=f T+x\) of this example, is closed on a side branch. Next, we have an existential quantifier with an equality \(t=0\), so we can instantiate t with 0 by
, with the solution \(y(T)=f T+x\) of this example, is closed on a side branch. Next, we have an existential quantifier with an equality \(t=0\), so we can instantiate t with 0 by  . In the next step, we instantiate the existential quantifier
. In the next step, we instantiate the existential quantifier  with \(t^+\), as now revealed in the last conjunct \(t^+=T\); we do the same for
with \(t^+\), as now revealed in the last conjunct \(t^+=T\); we do the same for  by \(f=f^+\). Finally, we use quantifier elimination (
by \(f=f^+\). Finally, we use quantifier elimination ( ) to reveal an equivalent quantifier-free formula.
) to reveal an equivalent quantifier-free formula.

The analysis of the specification conjecture finishes with collecting the open sequents from the proof to create the monitor specification  . The axiomatic-style synthesis operates fully in-place, so there is only one open sequent to collect. In contrast, the sequent-style synthesis usually splits into multiple branches. Moreover, the collected open sequents may include new logical variables and new (Skolem) function symbols that were introduced for nondeterministic assignments and differential equations when handling existential or universal quantifiers. These can be handled in a final step by re-introducing and instantiating quantifiers, see Appendix 3.
. The axiomatic-style synthesis operates fully in-place, so there is only one open sequent to collect. In contrast, the sequent-style synthesis usually splits into multiple branches. Moreover, the collected open sequents may include new logical variables and new (Skolem) function symbols that were introduced for nondeterministic assignments and differential equations when handling existential or universal quantifiers. These can be handled in a final step by re-introducing and instantiating quantifiers, see Appendix 3.
Let us now recall our desired result from Example 3 and compare it to the formula synthesized in Examples 6 and 7. Also recall that \(\nu _{i-1}\) denotes the prior state and \(\nu _i\) denotes the posterior state of running the model, so we have the following correlations of symbols: \(\nu _{i-1}(f)\) corresponds to f, \(\nu _{i-1}(t)\) to t, \(\nu _{i-1}(x)\) to x, whereas \(\nu _i(f)\) corresponds to \(f^+\), \(\nu _i(t)\) to \(t^+\), and \(\nu _i(x)\) to \(x^+\).
The conjuncts from the synthesized formula cover all the desired conditions nicely, considering that \(x^+\) is expanded to its lengthier equal form \(x^+=x+f^+t^+\).
Remark 1
(Monitor evaluation at runtime) The complexity of evaluating an arithmetic formula over the reals for concrete numbers (such as a monitor for the concrete numbers corresponding to the current state) is linear in the formula size, as opposed to deciding the validity of such formulas, which is doubly exponential [10]. Evaluating the same formula on floating point numbers is inexpensive, but may yield incorrect results due to rounding errors; on exact rationals the bit-complexity can be non-negligible. We use interval arithmetic to obtain correct results while retaining the efficiency of floating-point computations. Interval arithmetic over-approximates a real value using an interval of two floating-point values that contains the real, which means the monitors become more conservative (e. g., to evaluate \(x \le m\) in interval arithmetic, consider \(x \in [x_l, x_u]\) and \(m \in [m_l,m_u]\), so \([x_l,x_u] \le [m_l, m_u]\) if \(x_u \le m_l\), which in turn implies \(x \le m\)). This leads to an interval-arithmetic formula \(\hat{F}(x,x^+)\) that implies \(F(x,x^+)\) and, thus, also implies the required monitor condition Formula (5).
3.4 Controller monitor synthesis
For a hybrid system  of the canonical form
of the canonical form  , a controller monitor
\(\chi _{\text {c}}\), cf. Fig. 8, checks that two consecutive states \(\nu \) and \(\tilde{\nu }\) are reachable with one controller execution \(\alpha _{\text {ctrl}}\), i. e., \((\nu ,\tilde{\nu }) \in \rho (\alpha _{\text {ctrl}})\) with
, a controller monitor
\(\chi _{\text {c}}\), cf. Fig. 8, checks that two consecutive states \(\nu \) and \(\tilde{\nu }\) are reachable with one controller execution \(\alpha _{\text {ctrl}}\), i. e., \((\nu ,\tilde{\nu }) \in \rho (\alpha _{\text {ctrl}})\) with  . This controller monitor is to be executed before a control choice by the controller is sent to the actuators. The program \(\alpha _\text {ctrl}\) is derived from \(\alpha \) by skipping differential equations according to Lemma 6 below. Recall that a differential equation
. This controller monitor is to be executed before a control choice by the controller is sent to the actuators. The program \(\alpha _\text {ctrl}\) is derived from \(\alpha \) by skipping differential equations according to Lemma 6 below. Recall that a differential equation  can be followed for a nondeterministic amount of time, including 0, which lets us skip it as long as its evolution domain constraint H is satisfied in the beginning, as captured by
can be followed for a nondeterministic amount of time, including 0, which lets us skip it as long as its evolution domain constraint H is satisfied in the beginning, as captured by  . That way, a controller monitor ensures that the states reachable by a controller enable subsequent runs of the plant, see Theorem 2. We systematically derive a controller monitor from the specification formula
. That way, a controller monitor ensures that the states reachable by a controller enable subsequent runs of the plant, see Theorem 2. We systematically derive a controller monitor from the specification formula  , see Fig. 7. A controller monitor can be used to initiate controller switching similar to Simplex [39], yet in provably correct-by-construction ways.
, see Fig. 7. A controller monitor can be used to initiate controller switching similar to Simplex [39], yet in provably correct-by-construction ways.
Lemma 6
(Differential skip) Let  denote a set of differential equations with evolution domain H. Then
denote a set of differential equations with evolution domain H. Then  is valid.
is valid.
Proof
We prove in  using [\(^{\prime }\)] skip derived from DW [35].
using [\(^{\prime }\)] skip derived from DW [35].

\(\square \)
Theorem 2
(Controller monitor correctness) Let \(\alpha \) be of the canonical form \(\alpha _{\text {ctrl}}; \alpha _{\text {plant}}\) with the continuous model  and let
and let  . Assume
. Assume  has been proven with invariant \(\varphi \) as in (3), i. e.,
has been proven with invariant \(\varphi \) as in (3), i. e.,  ,
,  , and
, and  . Let \(\nu \models \varphi \), as is checked by \(\chi _{\text {m}}\) (Corollary 3). Furthermore, let \(\tilde{\nu }\) be the state after running the actual CPS controller implementation and let \(\tilde{\nu }\) agree with \(\nu \) on \(\varSigma \backslash V\), i. e., \(\nu |_{\varSigma \backslash V} = \tilde{\nu }|_{\varSigma \backslash V}\). If \((\nu , \tilde{\nu }) \models \chi _{\text {c}}\) with
. Let \(\nu \models \varphi \), as is checked by \(\chi _{\text {m}}\) (Corollary 3). Furthermore, let \(\tilde{\nu }\) be the state after running the actual CPS controller implementation and let \(\tilde{\nu }\) agree with \(\nu \) on \(\varSigma \backslash V\), i. e., \(\nu |_{\varSigma \backslash V} = \tilde{\nu }|_{\varSigma \backslash V}\). If \((\nu , \tilde{\nu }) \models \chi _{\text {c}}\) with

then \((\nu , \tilde{\nu }) \in \rho (\alpha _{\text {ctrl}})\), \(\tilde{\nu } \models \varphi \), and there exists a state \(\omega \) such that \((\tilde{\nu }, \omega ) \in \rho (\alpha _\text {plant})\).
Proof
By Lemma 4,  implies \((\nu ,\tilde{\nu }) \in \rho (\alpha _\text {ctrl})\). The assumption
implies \((\nu ,\tilde{\nu }) \in \rho (\alpha _\text {ctrl})\). The assumption  furthermore implies \(\tilde{\nu } \models H\),
furthermore implies \(\tilde{\nu } \models H\),  by Lemma 6, hence
by Lemma 6, hence  and \((\nu ,\tilde{\nu }) \in \rho (\alpha )\) by Lemma 4. Since \(\nu \models \varphi \) by assumption, we get \(\tilde{\nu } \models \varphi \) from
and \((\nu ,\tilde{\nu }) \in \rho (\alpha )\) by Lemma 4. Since \(\nu \models \varphi \) by assumption, we get \(\tilde{\nu } \models \varphi \) from  . Now \(\tilde{\nu } \models \varphi \wedge H\), so there exists \(\omega \) s.t. \((\tilde{\nu },\omega ) \in \rho (\alpha _\text {plant})\). \(\square \)
. Now \(\tilde{\nu } \models \varphi \wedge H\), so there exists \(\omega \) s.t. \((\tilde{\nu },\omega ) \in \rho (\alpha _\text {plant})\). \(\square \)
The corollaries to Theorem 1 carry over to Theorem 2 accordingly.
3.5 Monitoring in the presence of expected uncertainty and disturbance
Up to now we considered exact ideal-world models. But real-world clocks drift, sensors measure with some uncertainty, and actuators are subject to disturbance. This makes the exact models safe but too conservative, which means that monitors for exact models are likely to fall back to a fail-safe controller rather often. In this section we discuss how we find ModelPlex specifications in the sequent-style synthesis techniques so that the safety property (2) and the monitor specification become more robust to expected uncertainty and disturbance. That way, only unexpected deviations beyond those captured in the normal operational uncertainty and disturbance of model  cause the monitor to initiate fail-safe actions.
cause the monitor to initiate fail-safe actions.
In  , we can, for example, use nondeterministic assignment from an interval to model sensor uncertainty and piece-wise constant actuator disturbance (e. g., as in [26]), or differential inequalities for actuator disturbance (e. g., as in [38]). Such models include nondeterminism about sensed values in the controller model and often need more complex physics models than differential equations with polynomial solutions.
, we can, for example, use nondeterministic assignment from an interval to model sensor uncertainty and piece-wise constant actuator disturbance (e. g., as in [26]), or differential inequalities for actuator disturbance (e. g., as in [38]). Such models include nondeterminism about sensed values in the controller model and often need more complex physics models than differential equations with polynomial solutions.
Example 8
(Modeling uncertainty and disturbance) We incorporate clock drift, sensor uncertainty and actuator disturbance into the water tank model to express expected deviation. The measured level \(x_s\) is within a known sensor uncertainty u of the real level x (i.e. \(x_s \in \left[ x-u,x+u\right] \)). We use differential inequalities to model clock drift and actuator disturbance. The clock, which wakes the controller, is slower than the real time by at most a time drift of c; it can be arbitrarily fast. The water flow disturbance is at most d, but the water tank is allowed to drain arbitrarily fast (may even leak when the outgoing valve is closed). To illustrate different modeling possibilities, we use additive clock drift and multiplicative actuator disturbance.

We analyze Example 8 in the same way as the previous examples, with the crucial exception of the differential inequalities. We cannot use the proof rule  to analyze this model, because differential inequalities do not have polynomial solutions. Instead, we use
to analyze this model, because differential inequalities do not have polynomial solutions. Instead, we use  (cf. Lemma 7) and the DE proof rule of
(cf. Lemma 7) and the DE proof rule of  [31] to turn differential inequalities into a differential-algebraic constraint form that lets us proceed with the proof. Rule DE turns a differential inequality
[31] to turn differential inequalities into a differential-algebraic constraint form that lets us proceed with the proof. Rule DE turns a differential inequality  into a quantified differential equation
into a quantified differential equation  with an equivalent differential-algebraic constraint. Rule
with an equivalent differential-algebraic constraint. Rule  turns a fluctuating disturbance
turns a fluctuating disturbance  into a mean disturbance
into a mean disturbance  , see Lemma 7.
, see Lemma 7.
Lemma 7
(Mean disturbance) Reachability with mean disturbance \(\bar{d}\) throughout approximates fluctuating disturbance  .
.
Proof
We prove in  using differential refinement
using differential refinement  [31].
[31].

Example 9
(Analyzing differential inequalities) Loops, assignments and tests are analyzed as in the previous examples. We continue with differential inequalities as follows. First, we eliminate the differential inequalities by rephrasing them as differential-algebraic constraints in step (DE). Then, we refine by extracting the existential quantifiers for flow disturbance \(\tilde{d}\) and time drift \(\tilde{t}\), so that they become mean disturbance and mean time drift in step ( ). Note, that the existential quantifier moved from inside the modality
). Note, that the existential quantifier moved from inside the modality  to the outside
to the outside  , which captures that the states reachable with fluctuating disturbance could also have been reached by following a mean disturbance throughout. The resulting differential equation has polynomial solutions and, thus, we can use
, which captures that the states reachable with fluctuating disturbance could also have been reached by following a mean disturbance throughout. The resulting differential equation has polynomial solutions and, thus, we can use  and proceed with the proof as before.
and proceed with the proof as before.

As expected, we get a more permissive monitor specification. Such a monitor specification says that there exists a mean disturbance \(\bar{d}\) and a mean clock drift \(\bar{c}\) within the allowed disturbance bounds, such that the measured flow \(f^+\), the clock \(t^+\), and the measured level \(x^+\) can be explained with the model. These existential quantifiers will be turned into equivalent quantifier-free form in subsequent steps by  .
.
So far, we discussed proof rule  to solve differential equations when synthesizing model monitors. Recent advances [41] on proving
to solve differential equations when synthesizing model monitors. Recent advances [41] on proving  properties (where \(\phi \) is phrased using equalities) point to an interesting direction for synthesizing model monitors without solving differential equations. In the next section, we will use
properties (where \(\phi \) is phrased using equalities) point to an interesting direction for synthesizing model monitors without solving differential equations. In the next section, we will use  techniques based on differential invariants, differential cuts [30], and differential auxiliaries [32] to handle differential equations and inequalities without requiring any closed-form solutions when synthesizing prediction monitors.
techniques based on differential invariants, differential cuts [30], and differential auxiliaries [32] to handle differential equations and inequalities without requiring any closed-form solutions when synthesizing prediction monitors.
3.6 Monitoring compliance guarantees for unobservable intermediate states
With controller monitors, non-compliance of a controller implementation w.r.t. the modeled controller can be detected right away. With model monitors, non-compliance of the actual system dynamics w.r.t. the modeled dynamics can be detected when they first occur. We switch to a fail-safe action, which is verified using standard techniques, in both non-compliance cases. The crucial question is: can such a method always guarantee safety? The answer is linked to the image computation problem in model checking (i. e., approximation of states reachable from a current state), which is known to be not semi-decidable by numerical evaluation at points; approximation with uniform error is only possible if a bound is known for the continuous derivatives [36]. This implies that we need additional assumptions about the deviation between the actual and the modeled continuous dynamics to guarantee compliance for unobservable intermediate states. Unbounded deviation from the model between sample points just is unsafe, no matter how hard a controller tries. Hence, worst-case bounds capture how well reality is reflected in the model.
We derive a prediction monitor, cf. Figs. 9 and 10, to check whether a current control decision will be able to keep the system safe for time \(\varepsilon \) even if the actual continuous dynamics deviate from the model. A prediction monitor checks the current state, because all previous states are ensured by a model monitor and subsequent states are then safe by (2).
In order to derive a prediction monitor, we use Lemma 8 to introduce a plant with disturbance as additional predicate into our logical representation.
Lemma 8
(Introduce predicate) Formula  is valid.
is valid.
Proof
Follows from  using the diamond variant of
using the diamond variant of  . \(\square \)
. \(\square \)
Definition 4
(\(\varepsilon \)-bounded plant with disturbance \(\delta \)) Let \(\alpha _{\text {plant}}\) be a model of the form  . An \(\varepsilon \)-bounded plant with disturbance
\(\delta \), written \(\alpha _{\delta \text {plant}}\), is a plant model of the form
. An \(\varepsilon \)-bounded plant with disturbance
\(\delta \), written \(\alpha _{\delta \text {plant}}\), is a plant model of the form  for some f, g with fresh variable \(\varepsilon > 0\) and with a clock
for some f, g with fresh variable \(\varepsilon > 0\) and with a clock  . We say that disturbance \(\delta \) is constant if
. We say that disturbance \(\delta \) is constant if  ; it is additive if \(f(\theta ,\delta ) = \theta - \delta \) and \(g(\theta , \delta ) = \theta + \delta \).
; it is additive if \(f(\theta ,\delta ) = \theta - \delta \) and \(g(\theta , \delta ) = \theta + \delta \).
Theorem 3
(Prediction monitor correctness) Let \(\alpha \) be of the canonical form \(\alpha _{\text {ctrl}}; \alpha _{\text {plant}}\) with the continuous model  and let
and let  . Let
. Let  be provably safe, i. e.,
be provably safe, i. e.,  has been proved using invariant \(\varphi \) as in (3). Let \(\nu \models \varphi \), as checked by \(\chi _{\text {m}}\) from Corollary 3. If \((\nu , \tilde{\nu }) \models \chi _{\text {p}}\) with
has been proved using invariant \(\varphi \) as in (3). Let \(\nu \models \varphi \), as checked by \(\chi _{\text {m}}\) from Corollary 3. If \((\nu , \tilde{\nu }) \models \chi _{\text {p}}\) with

then we have \(\omega \models \varphi \) for all \(\omega \) s.t. \((\nu , \omega ) \in \rho (\alpha _\text {ctrl};\alpha _{\delta \text {plant}})\).
Proof
Assume \((\nu , \tilde{\nu }) \models \chi _{\text {p}}\), i. e., \(\nu _{x^+}^{\tilde{\nu }(x)} \models \chi _{\text {p}}\). By Theorem 2,  implies \(\tilde{\nu } \models \varphi \), since \(\nu \models \varphi \). Furthermore, then there exists \(\mu \) such that
implies \(\tilde{\nu } \models \varphi \), since \(\nu \models \varphi \). Furthermore, then there exists \(\mu \) such that  with \((\nu _{x^+}^{\tilde{\nu }(x)}, \mu ) \in \rho (\alpha _{\text {ctrl}})\) and the two states \(\nu \) and \(\mu \) agree on all variables except the ones modified by \(\alpha _{\text {ctrl}}\), i. e.,
with \((\nu _{x^+}^{\tilde{\nu }(x)}, \mu ) \in \rho (\alpha _{\text {ctrl}})\) and the two states \(\nu \) and \(\mu \) agree on all variables except the ones modified by \(\alpha _{\text {ctrl}}\), i. e.,  . Now \(\mu \models \varUpsilon ^+\) implies \(\mu (x) = \mu (x^+) = \nu _{x^+}^{\tilde{\nu }(x)}(x^+) = \tilde{\nu }(x)\). (in other words, \(\mu |_{V} = \tilde{\nu }|_{V}\)). Also
. Now \(\mu \models \varUpsilon ^+\) implies \(\mu (x) = \mu (x^+) = \nu _{x^+}^{\tilde{\nu }(x)}(x^+) = \tilde{\nu }(x)\). (in other words, \(\mu |_{V} = \tilde{\nu }|_{V}\)). Also  . Thus, by Lemma 2,
. Thus, by Lemma 2,  since
since  and hence we have \(\omega \models \varphi \) for all \((\tilde{\nu }, \omega ) \in \rho (\alpha _{\delta \text {plant}})\). \(\square \)
and hence we have \(\omega \models \varphi \) for all \((\tilde{\nu }, \omega ) \in \rho (\alpha _{\delta \text {plant}})\). \(\square \)
Observe that this is also true for all intermediate times \(\zeta \in \left[ 0,\omega (t)\right] \) by the transition semantics of differential equations, where \(\omega (t) \le \varepsilon \) because \(\alpha _{\delta \text {plant}}\) is bounded by \(\varepsilon \).
Remark 2
By adding a controller execution  prior to the disturbed plant model, we synthesize prediction monitors that take the actual controller decisions into account. For safety purposes, we could just as well use a monitor definition without controller
prior to the disturbed plant model, we synthesize prediction monitors that take the actual controller decisions into account. For safety purposes, we could just as well use a monitor definition without controller  . But that would result in a rather conservative monitor, which has to keep the CPS safe without knowledge of the actual controller decision.
. But that would result in a rather conservative monitor, which has to keep the CPS safe without knowledge of the actual controller decision.
3.7 Decidability and computability
One useful characteristic of ModelPlex beyond soundness is that monitor synthesis is computable, which yields a synthesis algorithm, and that the correctness of those synthesized monitors w.r.t. their specification is decidable, cf. Theorems 4 and 5.
From Lemma 5 it follows that online monitoring [18] (i. e., monitoring the last two consecutive states) is permissible. So, ModelPlex turns questions  into
into  . For decidability, we first consider canonical hybrid programs \(\alpha \) of the form \(\alpha \equiv \alpha _\text {ctrl} ; \alpha _\text {plant}\) where \(\alpha _\text {ctrl}\) and \(\alpha _\text {plant}\) are free of further nested loops. To handle differential inequalities in
. For decidability, we first consider canonical hybrid programs \(\alpha \) of the form \(\alpha \equiv \alpha _\text {ctrl} ; \alpha _\text {plant}\) where \(\alpha _\text {ctrl}\) and \(\alpha _\text {plant}\) are free of further nested loops. To handle differential inequalities in  formulas of the form
formulas of the form  , the subsequent proofs additionally use the rules for handling differential-algebraic equations [31].
, the subsequent proofs additionally use the rules for handling differential-algebraic equations [31].
Theorem 4
(Monitor correctness is decidable) We assume canonical models of the form \(\alpha \equiv \alpha _{\text {ctrl}} ; \alpha _{\text {plant}}\) without nested loops, with solvable differential equations in \(\alpha _\text {plant}\) and disturbed plants \(\alpha _{\delta \text {plant}}\) with constant additive disturbance \(\delta \) (see Definition 4) and \(F(x,x^+),\varphi ,H\) to be first-order formulas. Then, monitor correctness is decidable, i. e., the formulas  ,
,  , and
, and  are decidable.
are decidable.
Proof
From relative decidability of  [33, Theorem 11] we know that sentences of
[33, Theorem 11] we know that sentences of  (i. e.,
(i. e.,  formulas without free variables) are decidable relative to an oracle for discrete loop invariants/variants and continuous differential invariants/variants. Since neither \(\alpha _\text {ctrl}\) nor \(\alpha _\text {plant}\) contain nested loops, we manage without an oracle for loop invariants/variants. Further, since the differential equation systems in \(\alpha _\text {plant}\) are solvable, we have an effective oracle for differential invariants/variants. Let \(\textit{Cl}_\forall (\phi )\) denote the universal closure of
formulas without free variables) are decidable relative to an oracle for discrete loop invariants/variants and continuous differential invariants/variants. Since neither \(\alpha _\text {ctrl}\) nor \(\alpha _\text {plant}\) contain nested loops, we manage without an oracle for loop invariants/variants. Further, since the differential equation systems in \(\alpha _\text {plant}\) are solvable, we have an effective oracle for differential invariants/variants. Let \(\textit{Cl}_\forall (\phi )\) denote the universal closure of  formula \(\phi \) (i. e., \(\textit{Cl}_\forall (\phi ) \equiv \forall _{z \in \text {FV}(\phi )} z . \phi \)). Note that when \(\models F\) then also \(\models \textit{Cl}_\forall (F)\) by a standard argument.
formula \(\phi \) (i. e., \(\textit{Cl}_\forall (\phi ) \equiv \forall _{z \in \text {FV}(\phi )} z . \phi \)). Note that when \(\models F\) then also \(\models \textit{Cl}_\forall (F)\) by a standard argument.
-
Model monitor
 : Follows from relative decidability of
: Follows from relative decidability of  [33, Theorem 11], because
[33, Theorem 11], because  contains no free variables.
contains no free variables. -
Controller monitor
 : Follows from relative decidability of
: Follows from relative decidability of  [33, Theorem 11], because
[33, Theorem 11], because  contains no free variables.
contains no free variables. -
Prediction monitor
 : First assume that
: First assume that  can be represented in a first-order formula B such that
can be represented in a first-order formula B such that 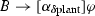 . Then, by
. Then, by 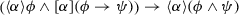
decidability splits into two cases:
-
Case
 : follows from case
: follows from case  (controller monitor) above.
(controller monitor) above. -
Case
 : Since the disturbance \(\delta \) in \(\alpha _{\delta \text {plant}}\) is constant additive and the differential equations in \(\alpha _\text {plant}\) are solvable, we have the disturbance functions \(f(\theta , \delta )\) and \(g(\theta ,\delta )\) applied to the solution as an oracleFootnote 8 for differential invariants (i. e., the differential invariant is a pipe around the solution without disturbance). Specifically, to show
: Since the disturbance \(\delta \) in \(\alpha _{\delta \text {plant}}\) is constant additive and the differential equations in \(\alpha _\text {plant}\) are solvable, we have the disturbance functions \(f(\theta , \delta )\) and \(g(\theta ,\delta )\) applied to the solution as an oracleFootnote 8 for differential invariants (i. e., the differential invariant is a pipe around the solution without disturbance). Specifically, to show  by Definition 4 we have to show
by Definition 4 we have to show  . We proceed with only
. We proceed with only  since the case
since the case  follows in a similar manner. By definition of \(\alpha _{\delta \text {plant}}\) we know \(0 \le x_0\), and hence continue with
follows in a similar manner. By definition of \(\alpha _{\delta \text {plant}}\) we know \(0 \le x_0\), and hence continue with  by differential cut \(0 \le x_0\). Using the differential cut rule [31], we further supply the oracle \(\text {sol}_x + \delta x_0\), where \(\text {sol}_x\) denotes the solution of
by differential cut \(0 \le x_0\). Using the differential cut rule [31], we further supply the oracle \(\text {sol}_x + \delta x_0\), where \(\text {sol}_x\) denotes the solution of  in \(\alpha _\text {plant}\) and \(\delta x_0\) the solution for the disturbance since \(\delta \) is constant additive. This leads to two proof obligations:
in \(\alpha _\text {plant}\) and \(\delta x_0\) the solution for the disturbance since \(\delta \) is constant additive. This leads to two proof obligations:-
Prove oracle
 , which by rule differential invariant [31] is valid if we can show
, which by rule differential invariant [31] is valid if we can show  where the primed variables are replaced with the respective right-hand side of the differential equation system. From Definition 4 we know that
where the primed variables are replaced with the respective right-hand side of the differential equation system. From Definition 4 we know that  and
and  and since \(\text {sol}_x\) is the solution of
and since \(\text {sol}_x\) is the solution of  in \(\alpha _\text {plant}\) we further know that
in \(\alpha _\text {plant}\) we further know that  ; hence we have to show
; hence we have to show  , which is trivially true.
, which is trivially true. -
Use oracle
 , which by rule differential weaken [31] is valid if we can show
, which by rule differential weaken [31] is valid if we can show 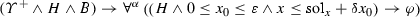
where \(\forall ^\alpha \) denotes the universal closure w.r.t. \(\alpha \), i. e., \(\forall x\). But since
 is valid, this is provable by quantifier elimination. Furthermore, we cannot get a better result than differential weaken, because the evolution domain constraint contains the oracle’s answer for the differential equation system, which characterizes exactly the reachable set of the differential equation system.
is valid, this is provable by quantifier elimination. Furthermore, we cannot get a better result than differential weaken, because the evolution domain constraint contains the oracle’s answer for the differential equation system, which characterizes exactly the reachable set of the differential equation system.
We conclude that the oracle is proven correct and its usage is decidable.
-
It remains to show that
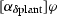 can be represented in a first-order formula B such that
can be represented in a first-order formula B such that  . We know from Lemma 7 that any fluctuating disturbance can be approximated by its mean disturbance throughout. So for all fluctuating disturbances in \(\left[ -\delta ,\delta \right] \) we have a corresponding constant additive mean disturbance from \(\left[ -\delta ,\delta \right] \), which yields solvable differential equations. Hence, there exists a first-order formula B such that
. We know from Lemma 7 that any fluctuating disturbance can be approximated by its mean disturbance throughout. So for all fluctuating disturbances in \(\left[ -\delta ,\delta \right] \) we have a corresponding constant additive mean disturbance from \(\left[ -\delta ,\delta \right] \), which yields solvable differential equations. Hence, there exists a first-order formula B such that  is valid. For the constant additive case, there even is a first-order formula B that is equivalent to
is valid. For the constant additive case, there even is a first-order formula B that is equivalent to  , because every constant additive disturbance can be replaced equivalently by a mean disturbance using the mean-value theorem for the disturbance as a (continuous!) function of time [30]. Consequently, the above cut to add B is possible if and only if the monitor \(\chi _{\text {p}}\) is correct, leading to a decision procedure. \(\square \)
, because every constant additive disturbance can be replaced equivalently by a mean disturbance using the mean-value theorem for the disturbance as a (continuous!) function of time [30]. Consequently, the above cut to add B is possible if and only if the monitor \(\chi _{\text {p}}\) is correct, leading to a decision procedure. \(\square \)
-
For computability, we start with a theoretical proof on the basis of decidability, before we give a constructive proof, which is more useful in practice.
Theorem 5
(Monitor synthesis is computable) We assume canonical models of the form \(\alpha \equiv \alpha _{\text {ctrl}} ; \alpha _{\text {plant}}\) without nested loops, with solvable differential equations in \(\alpha _\text {plant}\) and disturbed plants \(\alpha _{\delta \text {plant}}\) with constant additive disturbance \(\delta \) (see Definition 4). Then, monitor synthesis is computable, i. e., the functions  ,
,  , and
, and  are computable.
are computable.
Proof
Follows immediately from Theorem 4 with recursive enumeration of monitors. \(\square \)
We give a constructive proof of Theorem 5. The proof is based on the observation that, except for loop and differential invariants/variants, rule application in the  calculus is deterministic: from [31, Theorem 2.4] we know that, relative to an oracle for first-order invariants and variants, the
calculus is deterministic: from [31, Theorem 2.4] we know that, relative to an oracle for first-order invariants and variants, the  calculus gives a semidecision-procedure for
calculus gives a semidecision-procedure for  formulas with differential equations having first-order definable flows.
formulas with differential equations having first-order definable flows.
Proof
For the sake of a contradiction, suppose that monitor synthesis stopped with some open sequent not being a first-order quantifier-free formula. Then, by [31, Theorem 2.4] the open sequent either contains a hybrid program with nondeterministic repetition or a differential equation at top level, or it is not quantifier-free. But this contradicts our assumption that both \(\alpha _\text {ctrl}\) and \(\alpha _\text {plant}\) are free from loops and that the differential equations are solvable and disturbance is constant, in which case for
-
Model monitor synthesis \(\chi _{\text {m}}\): the solution rule
 would make progress, because the differential equations in \(\alpha _\text {plant}\) are solvable; and for
would make progress, because the differential equations in \(\alpha _\text {plant}\) are solvable; and for -
Prediction monitor synthesis \(\chi _{\text {p}}\): the disturbance functions \(f(\theta ,\delta )\) and \(g(\theta ,\delta )\) applied to the solution provide differential invariants (see proof of Theorem 4) so that the differential cut rule, the differential invariant rule, and the differential weakening rule [31] would make progress.
In the case of the open sequent not being quantifier-free, the quantifier elimination rule  would be applicable and turn the formula including quantifiers into an equivalent quantifier-free formula. Hence, the open sequent neither contains nondeterministic repetition, nor a differential equation, nor a quantifier. Thus we conclude that the open sequent is a first-order quantifier-free formula. \(\square \)
would be applicable and turn the formula including quantifiers into an equivalent quantifier-free formula. Hence, the open sequent neither contains nondeterministic repetition, nor a differential equation, nor a quantifier. Thus we conclude that the open sequent is a first-order quantifier-free formula. \(\square \)
3.8 A proof tactic for automatic monitor synthesis
Based on the decidability and computability results above, this section explains how to implement ModelPlex monitor synthesis (Algorithm 1) as an automatic proof tactic for correct-by-construction monitor synthesis. This proof tactic is formulated in the tactic language of our theorem prover  X [14].
X [14].  X features a small soundness-critical core for axiomatic reasoning. On top of that core, tactics steer the proof search: axiomatic tactics constitute the most basic constructs of a proof, while tactic combinators (e. g., sequential tactic execution) are a language to combine tactics into more powerful proof procedures. The tactic language of
X features a small soundness-critical core for axiomatic reasoning. On top of that core, tactics steer the proof search: axiomatic tactics constitute the most basic constructs of a proof, while tactic combinators (e. g., sequential tactic execution) are a language to combine tactics into more powerful proof procedures. The tactic language of  X provides operators for sequential tactic composition (; ), tactic repetition (\(^*\)), optional execution (?), and alternatives (
X provides operators for sequential tactic composition (; ), tactic repetition (\(^*\)), optional execution (?), and alternatives ( ) to combines basic
) to combines basic  tactics, see [14].
tactics, see [14].
For ModelPlex, we combine propositional axiomatic tactics with tactics for handling hybrid programs into a single tactic called synthesize, which performs the steps of Algorithm 1 in place such that the monitor is synthesized on a single proof branch by successively transforming the model. The synthesize tactic finds modalities with hybrid programs, and uses contextual equivalence rewriting to replace these modalities in place while retaining a proof of correctness of those transformations.



The synthesize tactic operates on a specification conjecture  . It combines tactic selection as in a regular expression with search, so that formulas are turned into axioms step-by-step (backwards search). Synthesize starts with \(\textit{prepare}\), which determines whether to synthesize a controller monitor (unwinds loops and skips differential equations) or a model monitor (unwinds loops). Then, it repeats rewriting hybrid programs until none of the hybrid program tactics is applicable anymore, indicated by \(\textit{locate}(\textit{rewriteHP})^*\). Note, that the synthesize tactic does not need to instantiate existential quantifiers at intermediate steps, since it can continue rewriting inside existential quantifiers. After rewriting hybrid programs is done, an optional local quantifier elimination step is made, cf. (6), in case that any universal quantifiers remained from the ODE in the innermost sub-formula, followed by instantiating the existential quantifiers using
. It combines tactic selection as in a regular expression with search, so that formulas are turned into axioms step-by-step (backwards search). Synthesize starts with \(\textit{prepare}\), which determines whether to synthesize a controller monitor (unwinds loops and skips differential equations) or a model monitor (unwinds loops). Then, it repeats rewriting hybrid programs until none of the hybrid program tactics is applicable anymore, indicated by \(\textit{locate}(\textit{rewriteHP})^*\). Note, that the synthesize tactic does not need to instantiate existential quantifiers at intermediate steps, since it can continue rewriting inside existential quantifiers. After rewriting hybrid programs is done, an optional local quantifier elimination step is made, cf. (6), in case that any universal quantifiers remained from the ODE in the innermost sub-formula, followed by instantiating the existential quantifiers using  .
.
At the heart of the synthesize tactic is locate, which searches for the topmost formula that includes a hybrid program (i. e., a diamond modality) and chooses the appropriate tactic to reduce that program. The proof search itself is backward in sequent-style, which starts from the monitor specification conjecture and searches for steps that transform the conjecture gradually into axioms. This tactic seems like a natural way of synthesizing monitors, since it starts from the conjecture and repeatedly applies proof steps until no more progress can be made (i. e., no more steps are applicable). However, repeated search for the topmost hybrid program operator incurs considerable computation time overhead, as we will see in Sect. 4.
To avoid repeated search, we provide another tactic using a forward chase. The forward chase uses proof-as-computation and is based on unification and recursive forward application of axioms, which allows us to construct a proof computationally from axioms until we reach the monitor specification conjecture. Each step of the recursive computation knows the position where to apply the subsequent step, so that no search is necessary.
4 Evaluation
4.1 Monitor synthesis
We developed two software prototypes: A sequent-style synthesis prototype uses  3 [37] and Mathematica. It uses Mathematica to simplify redundant monitor conditions after synthesizing the monitor in
3 [37] and Mathematica. It uses Mathematica to simplify redundant monitor conditions after synthesizing the monitor in  3, and therefore must recheck the final monitor for correctness. An axiomatic-style prototype is implemented as a tactic in
3, and therefore must recheck the final monitor for correctness. An axiomatic-style prototype is implemented as a tactic in  X [14], which generates controller and model monitors fully automatically and avoids branching by operating on sub-formulas in a single sequent. The axiomatic-style prototype synthesizes correct-by-construction monitors and produces a proof of correctness during the synthesis without the need to recheck.
X [14], which generates controller and model monitors fully automatically and avoids branching by operating on sub-formulas in a single sequent. The axiomatic-style prototype synthesizes correct-by-construction monitors and produces a proof of correctness during the synthesis without the need to recheck.
To evaluate our method, we synthesize monitors for prior case studies of nondeterministic hybrid models of autonomous cars, train control systems, and robots (adaptive cruise control [20], intelligent speed adaptation [25], the European train control system [38], and ground robot collision avoidance [26]), see Table 2. For the model, we list the dimension in terms of the number of function symbols and state variables, as well as the size of the safety proof for proving (2), i. e., number of proof steps and the number of proof branches. The safety proofs of Formula (2) transfer from  3 and were not repeated in
3 and were not repeated in  X.
X.
Table 3 summarizes the evaluation results. The main result is the completely automatic, correct-by-construction synthesis in  X with a single open branch on which the monitor is being synthesized. The monitor sizes in
X with a single open branch on which the monitor is being synthesized. The monitor sizes in  X are usually smaller than those of
X are usually smaller than those of  3, because the structure is preserved better so no external simplification is needed, cf. last column “unsimplified”. Without external simplification, very similar conditions with only small deviations are repeated on each open branch, For example, the controller monitor sizes listed the sequent-style synthesis need to be multiplied roughly by the number of open branches, in order to get the monitor size before external simplification.
3, because the structure is preserved better so no external simplification is needed, cf. last column “unsimplified”. Without external simplification, very similar conditions with only small deviations are repeated on each open branch, For example, the controller monitor sizes listed the sequent-style synthesis need to be multiplied roughly by the number of open branches, in order to get the monitor size before external simplification.
A detailed analysis follows in subsequent paragraphs below. For the monitor, we list the dimension of the monitor specification in terms of the number of variables, compare the number of manual steps among all steps and branches left open among all branches when deriving the monitor with or without Opt. 1, as well as the number of steps when rechecking monitor correctness. Finally, we list the monitor size in terms of the number of arithmetic, comparison, and logical operators in the monitor formula. The number of proof steps of  3 and
3 and  are not directly comparable, because both implement different calculi.
are not directly comparable, because both implement different calculi.  X leads to more but simpler proof steps.
X leads to more but simpler proof steps.
Performance Analysis We analyze the computation time for deriving controller monitors fully automatically in the axiomatic-style synthesis technique, comparing both the backward tactic and forward chase implementations introduced in Section 3.8 above. The computation time measurements were taken on a 2.4 GHz Intel Core i7 with 16GB of memory, averaged over 20 runs. Table 4 summarizes the performance measurements for the axiomatic-style synthesis in  X and the sequent-style synthesis in
X and the sequent-style synthesis in  3. Unsurprisingly, the repeated search for applicable positions in the backward tactic results in a considerable computation time overhead, when compared to the forward chase. Additional performance gains in the forward chase are rooted in (i) its ability to largely use derived axioms, which need only be proven once during synthesis (instead of repeatedly on each occurrence, as in the backward tactic); and (ii) its ability to postpone assignment processing and thus avoid intermediate stuttering assignments, which are necessary for successful uniform substitution [35], but result in additional proof steps if performed early.
3. Unsurprisingly, the repeated search for applicable positions in the backward tactic results in a considerable computation time overhead, when compared to the forward chase. Additional performance gains in the forward chase are rooted in (i) its ability to largely use derived axioms, which need only be proven once during synthesis (instead of repeatedly on each occurrence, as in the backward tactic); and (ii) its ability to postpone assignment processing and thus avoid intermediate stuttering assignments, which are necessary for successful uniform substitution [35], but result in additional proof steps if performed early.
For the sequent-style synthesis technique we list the time needed to perform the fully automated steps without Opt. 1 in  . The raw synthesis times are comparable to those in the chase-based axiomatic-style synthesis, because the sequent-style technique always operates on the top-level operator and does not need search. Recall, however, that in the sequent-style synthesis technique the monitors are simplified with an unverified external procedure and, therefore, need to be re-checked for correctness in
. The raw synthesis times are comparable to those in the chase-based axiomatic-style synthesis, because the sequent-style technique always operates on the top-level operator and does not need search. Recall, however, that in the sequent-style synthesis technique the monitors are simplified with an unverified external procedure and, therefore, need to be re-checked for correctness in  . This check needs considerable time, as listed in the last column of Table 4.
. This check needs considerable time, as listed in the last column of Table 4.
 X The axiomatic-style synthesis prototype supports proof search steering with fine-grained tactics, and applies tactics in-place on sub-formulas, without branching on top-level first. As a result, synthesis both with and without Opt. 1 is fully automatic and avoids redundancies in monitor conditions. The reasoning style of
X The axiomatic-style synthesis prototype supports proof search steering with fine-grained tactics, and applies tactics in-place on sub-formulas, without branching on top-level first. As a result, synthesis both with and without Opt. 1 is fully automatic and avoids redundancies in monitor conditions. The reasoning style of  X, as illustrated in Proof 3, uses frequent cuts to collect all monitoring conditions in a single open branch, which results in a larger overall number of branches than in sequent-style synthesis. The important characteristic is that these side branches all close, so that only a single branch remains open. This means that synthesis does not require untrusted procedures to simplify monitoring conditions that were duplicated over multiple branches, which also entails that the final rechecking of the monitor is not required, see column “proof steps (branches)”. Having only one branch and operating on sub-formulas also means that Opt. 1 does not need to be executed at intermediate stages in the synthesis process. Remaining existential quantifiers can be instantiated once at the end of the synthesis process, so that synthesis with and without Opt. 1 become identical.
X, as illustrated in Proof 3, uses frequent cuts to collect all monitoring conditions in a single open branch, which results in a larger overall number of branches than in sequent-style synthesis. The important characteristic is that these side branches all close, so that only a single branch remains open. This means that synthesis does not require untrusted procedures to simplify monitoring conditions that were duplicated over multiple branches, which also entails that the final rechecking of the monitor is not required, see column “proof steps (branches)”. Having only one branch and operating on sub-formulas also means that Opt. 1 does not need to be executed at intermediate stages in the synthesis process. Remaining existential quantifiers can be instantiated once at the end of the synthesis process, so that synthesis with and without Opt. 1 become identical.
KeYmaera X, however, is still in an early development stage and, so far, does not support differential inequalities and arbitrary differential equations in diamond modalities, so we cannot evaluate prediction monitor and model monitor synthesis fully. As development progress continues, these restrictions will diminish and we will analyze the model monitor and prediction monitor case studies with the axiomatic-style synthesis prototype once available.
KeYmaera 3 In the sequent-style synthesis prototype we support model monitor and prediction monitor synthesis for a wider range of systems, albeit at the cost of significantly increased manual interaction: for example, Opt. 1 has to be applied manually, since  3 does not provide sufficiently fine-grained steering of its automated proof search. Since optimization occurs after non-deterministic assignments and differential equations (i. e., in the middle of a proof), most of the synthesis process is user-guided as a consequence. For controller monitors, the sequent-style synthesis prototype without Opt. 1 is fully automatic (see number of manual steps in column “without Opt. 1” in lines 4-7, marked \(\chi _{\text {c}}\)). In full automation, however, the proof search of
3 does not provide sufficiently fine-grained steering of its automated proof search. Since optimization occurs after non-deterministic assignments and differential equations (i. e., in the middle of a proof), most of the synthesis process is user-guided as a consequence. For controller monitors, the sequent-style synthesis prototype without Opt. 1 is fully automatic (see number of manual steps in column “without Opt. 1” in lines 4-7, marked \(\chi _{\text {c}}\)). In full automation, however, the proof search of  3 results in increased branching, since propositional steps during proofs are usually cheap (see number of branches in column “without Opt. 1”). As a consequence, even though the relative number of manual proof steps is reduced, the massive branching of the automatic proof search implies that in absolute terms more manual steps might be necessary than in the completely manual process (see number of manual steps in line 3, Speed limit case study, where local quantifier elimination after solving ODEs is performed manually). This can be avoided with fine-grained tactic support, as is achieved in the axiomatic-style synthesis prototype.
3 results in increased branching, since propositional steps during proofs are usually cheap (see number of branches in column “without Opt. 1”). As a consequence, even though the relative number of manual proof steps is reduced, the massive branching of the automatic proof search implies that in absolute terms more manual steps might be necessary than in the completely manual process (see number of manual steps in line 3, Speed limit case study, where local quantifier elimination after solving ODEs is performed manually). This can be avoided with fine-grained tactic support, as is achieved in the axiomatic-style synthesis prototype.
Although the number of steps and open branches differ significantly between manual interaction for Opt. 1 and automated synthesis, the synthesized monitors are logically equivalent. But applying Opt. 1 usually results in structurally simpler monitors, because the conjunction over a smaller number of open branches (cf. Table 3) can still be simplified automatically. The model monitors for cruise control and speed limit control are significantly larger than the other monitors, because their size already prevents automated simplification by Mathematica. Here, the axiomatic-style synthesis approach is expected to provide significant advantage, since it does not duplicate conditions over many branches and, thus, computes small monitors even without further simplification.
4.2 Model simulation with monitoring
We tested the ModelPlex monitors with a simulation in MathematicaFootnote 9 on hybrid system models of the water tank example used throughout this article.
To illustrate the behavior of the water tank model with a fallback controller, we created two monitors: Monitor \(\chi _{\text {m}}\) validates the complete model (as in the examples throughout this article) and is executed at the beginning of each control cycle (before the controller runs). Monitor \(\chi _{\text {c}}\) validates only the controller of the model  (compares prior and posterior state of
(compares prior and posterior state of  ) and is executed after the controller but before control actions are issued. Thus, monitor \(\chi _{\text {c}}\) resembles conventional runtime verification approaches, which do not check CPS behavior for compliance with the complete hybrid model. This way, we detect unexpected deviations from the model at the beginning of each control cycle, while we detect unsafe control actions immediately before they are taken. With only monitor \(\chi _{\text {m}}\) in place we would require an additional control cycle to detect unsafe control actionsFootnote 10, whereas with only monitor \(\chi _{\text {c}}\) in place we would miss deviations from the model.
) and is executed after the controller but before control actions are issued. Thus, monitor \(\chi _{\text {c}}\) resembles conventional runtime verification approaches, which do not check CPS behavior for compliance with the complete hybrid model. This way, we detect unexpected deviations from the model at the beginning of each control cycle, while we detect unsafe control actions immediately before they are taken. With only monitor \(\chi _{\text {m}}\) in place we would require an additional control cycle to detect unsafe control actionsFootnote 10, whereas with only monitor \(\chi _{\text {c}}\) in place we would miss deviations from the model.
Figure 11 shows a plot of the variable traces of one simulation run. In the simulation, we ran the controller every 2 s (\(\varepsilon = \text {2\,s}\), indicated by the grid for the abscissa and the marks on sensor and actuator plots). The controller was set to adjust flow to \(\frac{5(m-x_0)}{2\varepsilon } = \frac{5}{2}\) for the first three controller cycles, which is unsafe on the third controller cycle. Monitor B immediately detects this violation at \(t=4\), because on the third controller cycle setting \(f=\frac{5}{2}\) violates \(f \le \frac{m-x_1}{\varepsilon }\). The fail-safe action at \(t=4\) drains the tank and, after that, normal operation continues until \(t=12\). Unexpected disturbance  occurs throughout \(t=\left[ 12,14\right] \), which is detected by monitor \(\chi _{\text {m}}\). Note, that such a deviation would remain undetected with conventional approaches (monitor \(\chi _{\text {c}}\) is completely unaware of the deviation). In this simulation run, the disturbance is small enough to let the fail-safe action at \(t=14\) keep the water tank in a safe state.
occurs throughout \(t=\left[ 12,14\right] \), which is detected by monitor \(\chi _{\text {m}}\). Note, that such a deviation would remain undetected with conventional approaches (monitor \(\chi _{\text {c}}\) is completely unaware of the deviation). In this simulation run, the disturbance is small enough to let the fail-safe action at \(t=14\) keep the water tank in a safe state.
5 Related work
Runtime verification and monitoring for finite state discrete systems has received significant attention (e. g., [9, 16, 23]). Other approaches monitor continuous-time signals (e. g., [11, 28]). We focus on hybrid systems models of CPS to combine both.
Several tools for formal verification of hybrid systems are actively developed (e. g., SpaceEx [13], dReal [15], extended NuSMV/MathSat [6]). For monitor synthesis, however, ModelPlex crucially needs the rewriting capabilities and flexibility of (nested)  and
and  modalities in
modalities in  [31] and
[31] and  [37]; it is thus an interesting question for future work if other tools could be adapted to ModelPlex.
[37]; it is thus an interesting question for future work if other tools could be adapted to ModelPlex.
Runtime verification is the problem of checking whether or not a trace produced by a program satisfies a particular formula (cf. [18]). In [44], a method for runtime verification of LTL formulas on abstractions of concrete traces of a flight data recorder is presented. The RV system for Java programs [22] predicts execution traces from actual traces to find concurrency errors offline (e. g., race conditions) even if the actual trace did not exhibit the error. We, instead, use prediction on the basis of disturbed plant models for hybrid systems at runtime to ensure safety for future behavior of the system and switch to a fail-safe fallback controller if necessary. Adaptive runtime verification [4] uses state estimation to reduce monitoring overhead by sampling while still maintaining accuracy with Hidden Markov Models, or more recently, particle filtering [17] to fill the sampling gaps. The authors present interesting ideas for managing the overhead of runtime monitoring, which could be beneficial to transfer into the hybrid systems world. The approach, however, focuses purely on the discrete part of CPS.
The Simplex architecture [39] (and related approaches, e. g., [1, 3, 19]) is a control system principle to switch between a highly reliable and an experimental controller at runtime. Highly reliable control modules are assumed to be verified with some other approach. Simplex focuses on switching when timing faults or violation of controller specification occur. Our method complements Simplex in that (i) it checks whether or not the current system execution fits the entire model, not just the controller; (ii) it systematically derives provably correct monitors for hybrid systems; (iii) it uses prediction to guarantee safety for future behavior of the system.
Further approaches with interesting insights on combined verification and monitor or controller synthesis for discrete systems include, for instance, [2, 12].
Although the related approaches based on offline verification derive monitors and switching conditions from models, none of them validates whether or not the model is adequate for the current execution. Thus, they are vulnerable to deviation between the real world and the model. In summary, this article addresses safety at runtime as follows:
-
Unlike [39], who focus on timing faults and specification violations, we propose a systematic principle to derive monitors that react to any deviation from the model.
-
Unlike [4, 17, 19, 22], who focus on the discrete aspects of CPS, we use hybrid system models with differential equations to address controller and plant.
-
Unlike [19, 39], who assume that fail-safe controllers have been verified with some other approach and do not synthesize code, we can use the same technical approach (
 ) for verifying controllers and synthesizing provably correct monitors.
) for verifying controllers and synthesizing provably correct monitors. -
ModelPlex combines the leight-weight monitors and runtime compliance of online runtime verification with the design time analysis of offline verification.
-
ModelPlex synthesizes provably correct monitors, certified by a theorem prover.
-
To the best of our knowledge, our approach is the first to guarantee that verification results about a hybrid systems model transfer to a particular execution of the system by verified runtime validation. We detect deviation from the verified model when it first occurs and, given bounds, can guarantee safety with fail-safe fallback. Other approaches (e. g., [3, 19, 39]) assume the system perfectly complies with the model.
6 Conclusion
ModelPlex is a principle to build and verify high-assurance controllers for safety-critical computerized systems that interact physically with their environment. It guarantees that verification results about CPS models transfer to the real system by safeguarding against deviations from the verified model. Monitors created by ModelPlex are provably correct and check at runtime whether or not the actual behavior of a CPS complies with the verified model and its assumptions. Upon noncompliance, ModelPlex initiates fail-safe fallback strategies. In order to initiate those strategies early enough, ModelPlex uses prediction on the basis of disturbed plant models to check safety for the next control cycle. This way, ModelPlex ensures that verification results about a model of a CPS transfer to the actual system behavior at runtime.
The new axiomatic-style monitor synthesis performs monitor construction in place, which enables correct-by-construction synthesis entirely within the theorem prover, constructing a proof as evidence of the correctness of the monitor. The axiomatic-style synthesis retains efficiency using contextual rewriting in a uniform substitution calculus for differential dynamic logic. It also preserves structure, leading to smaller monitor sizes.
Future research directions include extending ModelPlex with advanced  proof rules for differential equations [33, 41], so that we not only synthesize prediction monitors from differential equations without polynomial solutions, but also model monitors. An interesting question for certification purposes is end-to-end verification from the model to the final machine code, which this article reduces to the problem of a verified translation from the monitor formula to the monitor code. This last step is conceptually straightforward but technically nontrivial in languages like C.
proof rules for differential equations [33, 41], so that we not only synthesize prediction monitors from differential equations without polynomial solutions, but also model monitors. An interesting question for certification purposes is end-to-end verification from the model to the final machine code, which this article reduces to the problem of a verified translation from the monitor formula to the monitor code. This last step is conceptually straightforward but technically nontrivial in languages like C.
Notes
ModelPlex checks system execution w.r.t. a monitor specification, and thus, belongs to the field of runtime verification [18]. In this article we use the term runtime validation in order to clearly convey the purpose of monitoring (i. e., runtime verification monitors properties without offline verification; ModelPlex validates adequacy of models to transfer offline verification results to the online situation).
When such constraints are not available, our method still generates verifiably correct runtime tests, which detect deviation from the model at the sampling points, just not between them. A fail-safe action will then lead to earliest possible best-effort mitigation of safety risks (rather than guaranteed safety).
We use differential dynamic logic (
 ) and
) and  and KeYmaera X as a theorem prover to illustrate our concepts throughout this article. The concept of ModelPlex is not predicated on the use of
and KeYmaera X as a theorem prover to illustrate our concepts throughout this article. The concept of ModelPlex is not predicated on the use of  /KeYmaera X to prove (2). Other verification techniques could be used to establish validity of this formula. The flexibility of the underlying logic
/KeYmaera X to prove (2). Other verification techniques could be used to establish validity of this formula. The flexibility of the underlying logic  , its support for both
, its support for both  and
and  , and its proof calculus, however, are exploited for systematically constructing monitors from proofs in the rest of the article.
, and its proof calculus, however, are exploited for systematically constructing monitors from proofs in the rest of the article.It is an annoying fact of physics that there will never quite be a perfect model of \(\gamma \).
Consecutive states for
 mean before and after executions of \(\alpha \) (i. e., in \(\alpha \overset{\downarrow }{;} \alpha \overset{\downarrow }{;} \alpha \overset{\downarrow }{;}\) at the positions indicated with an arrow, not within \(\alpha \)).
mean before and after executions of \(\alpha \) (i. e., in \(\alpha \overset{\downarrow }{;} \alpha \overset{\downarrow }{;} \alpha \overset{\downarrow }{;}\) at the positions indicated with an arrow, not within \(\alpha \)).Recall that
 for variables \(V\).
for variables \(V\).The formula \(F(x,x^+)\) implies
 , because we will use non-equivalence proof steps to derive \(F(x,x^+)\) from
, because we will use non-equivalence proof steps to derive \(F(x,x^+)\) from  .
.By design, the disturbed plant \(\alpha _{\delta \text {plant}}\) also includes a clock \(x_0\), so the oracle additionally includes the trivial differential invariant \(x_0 \ge 0\).
We could run monitor \(\chi _{\text {m}}\) in place of \(\chi _{\text {c}}\) to achieve the same effect. But monitor \(\chi _{\text {m}}\) implements a more complicated formula, which is unnecessary when only the controller output should be validated.
In this example, this simplification is admittedly somewhat artificial but reminiscent of aspects of more general systems. In more complicated systems, such as adaptive cruise control, a controller needs to aim for passenger comfort, high fuel economy, and other secondary goals besides ensuring safety, so focusing on the safety-relevant features greatly fosters safety verification.
References
Aiello AM, Berryman JF, Grohs JR, Schierman JD (2010) Run-time assurance for advanced flight-critical control systems. In: AIAA guidance, navigation and control conference, AIAA, doi:10.2514/6.2010-8041
Alur R, Bodík R, Juniwal G, Martin MMK, Raghothaman M, Seshia SA, Singh R, Solar-Lezama A, Torlak E, Udupa A (2013) Syntax-guided synthesis. In: FMCAD, IEEE, pp 1–17
Bak S, Greer A, Mitra S (2010) Hybrid cyberphysical system verification with Simplex using discrete abstractions. In: Caccamo M (ed) IEEE Real-time and embedded technology and applications symposium, IEEE Computer Society, pp 143–152
Bartocci E, Grosu R, Karmarkar A, Smolka SA, Stoller SD, Zadok E, Seyster J (2012) Adaptive runtime verification. In: Qadeer S, Tasiran S (eds) Runtime verification. LNCS, vol 7687. Springer, Berlin, pp 168–182
Blech JO, Falcone Y, Becker K (2012) Towards certified runtime verification. In: Aoki T, Taguchi K (eds) International conference on formal engineering methods. LNCS, vol 7635. Springer, Berlin, pp 494–509
Cimatti A, Mover S, Tonetta S (2013) SMT-based scenario verification for hybrid systems. Form Methods Syst Des 42(1):46–66
Collins GE, Hong H (1991) Partial cylindrical algebraic decomposition for quantifier elimination. J Symb Comput 12(3):299–328
Daigle MJ, Roychoudhury I, Biswas G, Koutsoukos XD, Patterson-Hine A, Poll S (2010) A comprehensive diagnosis methodology for complex hybrid systems: a case study on spacecraft power distribution systems. IEEE Trans Syst Man Cybern Part A 40(5):917–931
D’Angelo B, Sankaranarayanan S, Sánchez C, Robinson W, Finkbeiner B, Sipma HB, Mehrotra S, Manna Z (2005) LOLA: Runtime monitoring of synchronous systems. In: TIME, IEEE Computer Society, pp 166–174
Davenport JH, Heintz J (1988) Real quantifier elimination is doubly exponential. J Symb Comput 5(1–2):29–35. doi:10.1016/S0747-7171(88)80004-X
Donzé A, Ferrère T, Maler O (2013) Efficient robust monitoring for STL. In: Sharygina N, Veith H (eds) Computer aided verification. LNCS, vol 8044. Springer, Berlin, pp 264–279
Ehlers R, Finkbeiner B (2011) Monitoring realizability. In: Khurshid S, Sen K (eds) Runtime verification. LNCS, vol 7186. Springer, Berlin, pp 427–441
Frehse G, Guernic CL, Donzé A, Cotton S, Ray R, Lebeltel O, Ripado R, Girard A, Dang T, Maler O (2011) SpaceEx: scalable verification of hybrid systems. In: Gopalakrishnan G, Qadeer S (eds) Computer aided verification. LNCS, vol 6806. Springer, Berlin, pp 379–395
Fulton N, Mitsch S, Quesel J, Völp M, Platzer A (2015) Keymaera X: an axiomatic tactical theorem prover for hybrid systems. In: Felty AP, Middeldorp A (eds) Automated deduction - CADE-25 - 25th international conference on automated deduction, Berlin, 1–7 Aug 2015, Proceedings, Springer, Lecture Notes in Computer Science, vol 9195, pp 527–538, doi:10.1007/978-3-319-21401-6_36
Gao S, Kong S, Clarke EM (2013) dReal: an SMT solver for nonlinear theories over the reals. In: Bonacina MP (ed) International conference on automated deduction. LNCS, vol 7898. Springer, Berlin, pp 208–214
Havelund K, Rosu G (2004) Efficient monitoring of safety properties. STTT 6(2):158–173
Kalajdzic K, Bartocci E, Smolka SA, Stoller SD, Grosu R (2013) Runtime verification with particle filtering. In: Legay A, Bensalem S (eds) Runtime verification. LNCS, vol 8174. Springer, Berlin
Leucker M, Schallhart C (2009) A brief account of runtime verification. J Log Algebr Program 78(5):293–303
Liu X, Wang Q, Gopalakrishnan S, He W, Sha L, Ding H, Lee K (2008) ORTEGA: An efficient and flexible online fault tolerance architecture for real-time control systems. IEEE Trans Ind Inform 4(4):213–224
Loos SM, Platzer A, Nistor L (2011) Adaptive cruise control: Hybrid, distributed, and now formally verified. In: Butler M, Schulte W (eds) Formal methods, Springer, LNCS, vol 6664, doi:10.1007/978-3-642-21437-0_6
McIlraith SA, Biswas G, Clancy D, Gupta V (2000) Hybrid systems diagnosis. In: Lynch NA, Krogh BH (eds) Hybrid systems: computation and cpmtrol. LNCS, vol 1790. Springer, Berlin, pp 282–295
Meredith PO, Rosu G (2010) Runtime verification with the RV system. In: Barringer H, Falcone Y, Finkbeiner B, Havelund K, Lee I, Pace GJ, Rosu G, Sokolsky O, Tillmann N (eds) Runtime verification. LNCS, vol 6418. Springer, Berlin, pp 136–152
Meredith PO, Jin D, Griffith D, Chen F, Rosu G (2012) An overview of the MOP runtime verification framework. STTT 14(3):249–289
Mitsch S, Platzer A (2014) ModelPlex: Verified runtime validation of verified cyber-physical system models. In: Bonakdarpour B, Smolka SA (eds) Runtime Verification - 5th International Conference, RV 2014, Toronto, ON, Canada, September 22–25, 2014. Proceedings, Springer, Lecture Notes in Computer Science, vol 8734, pp 199–214, doi:10.1007/978-3-319-11164-3_17
Mitsch S, Loos SM, Platzer A (2012) Towards formal verification of freeway traffic control. In: Lu C (ed) ICCPS, IEEE, pp 171–180, doi:10.1109/ICCPS.2012.25
Mitsch S, Ghorbal K, Platzer A (2013) On provably safe obstacle avoidance for autonomous robotic ground vehicles. In: Fox D, Hsu D (eds) Newman P. Robotics, Science and Systems. Technische Univ., Berlin
Mitsch S, Quesel JD, Platzer A (2014) Refactoring, refinement, and reasoning: A logical characterization for hybrid systems. In: Jones CB, Pihlajasaari P, Sun J (eds) Formal methods, vol 8442, Springer, pp 481–496, doi:10.1007/978-3-319-06410-9_33
Nickovic D, Maler O (2007) AMT: A property-based monitoring tool for analog systems. In: Raskin JF, Thiagarajan PS (eds) FORMATS. LNCSSpringer, Berlin, pp 304–319
Platzer A (2008) Differential dynamic logic for hybrid systems. J Autom Reason 41(2):143–189. doi:10.1007/s10817-008-9103-8
Platzer A (2010a) Differential-algebraic dynamic logic for differential-algebraic programs. J Log Comput 20(1):309–352, 2008, doi:10.1093/logcom/exn070, advance access published on 18 Nov
Platzer A (2010b) Logical analysis of hybrid systems. Springer, New York. doi:10.1007/978-3-642-14509-4
Platzer A (2011) The structure of differential invariants and differential cut elimination. Log Methods Comput Sci 8(4):1
Platzer A (2012a) The complete proof theory of hybrid systems. In: LICS, IEEE, doi:10.1109/LICS.2012.64
Platzer A (2012b) Logics of dynamical systems. In: LICS, IEEE, pp 13–24, doi:10.1109/LICS.2012.13
Platzer A (2015) A uniform substitution calculus for differential dynamic logic. In: Felty AP, Middeldorp A (eds) Conference on automated deduction. LNCS, vol 9195. Springer, pp 467–481, doi:10.1007/978-3-319-21401-6_32, 1503.01981
Platzer A, Clarke EM (2007) The image computation problem in hybrid systems model checking. In: Bemporad A, Bicchi A, Buttazzo G (eds) Hybrid systems: computation control. LNCS, Springer. doi:10.1007/978-3-540-71493-4_37
Platzer A, Quesel JD (2008) KeYmaera: A hybrid theorem prover for hybrid systems. In: Armando A, Baumgartner P, Dowek G (eds) International joint conference on automated reasoning. LNCS, vol 5195. Springer, Berlin. doi:10.1007/978-3-540-71070-7_15
Platzer A, Quesel JD (2009) European Train Control System: A case study in formal verification. In: Breitman K, Cavalcanti A (eds) International conference on formal engineering methods. LNCS, vol 5885. Springer, Berlin. doi:10.1007/978-3-642-10373-5_13
Seto D, Krogh B, Sha L, Chutinan A (1998) The Simplex architecture for safe online control system upgrades. In: American control conference, pp 3504–3508, doi:10.1109/ACC.1998.703255
Shannon C (1949) Communication in the presence of noise. Proc IRE 37(1):10–21. doi:10.1109/JRPROC.1949.232969
Sogokon A, Jackson PB (2015) Direct formal verification of liveness properties in continuous and hybrid dynamical systems. In: Bjørner N, de Boer FD (eds) FM 2015: formal methods– 20th international symposium, Oslo. 24–26 June 2015. Proceedings, Springer, Lecture Notes in Computer Science, vol 9109, pp 514–531, doi:10.1007/978-3-319-19249-9_32
Srivastava AN, Schumann J (2013) Software health management: a necessity for safety critical systems. ISSE 9(4):219–233
Wang D, Yu M, Low CB, Arogeti S (2013) Model-based health monitoring of hybrid systems. Springer, New York. doi:10.1007/978-1-4614-7369-5
Wang S, Ayoub A, Sokolsky O, Lee I (2011) Runtime verification of traces under recording uncertainty. In: Sen K, Khurshid S (eds) Runtime verification. LNCS, Springer, Berlin, pp 442–456
Zhao F, Koutsoukos XD, Haussecker HW, Reich J, Cheung P (2005) Monitoring and fault diagnosis of hybrid systems. IEEE Trans Syst Man Cybern Part B 35(6):1225–1240
Acknowledgments
Open access funding provided by Johannes Kepler University Linz. This material is based on research sponsored by DARPA under agreement number DARPA FA8750-12-2-0291. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright notation thereon. The research received funding from NSF, grant agreement CNS-1054246. The research leading to these results has received funding from the People Programme (Marie Curie Actions) of the European Union’s Seventh Framework Programme (FP7/2007-2013) under REA grant agreement no. PIOF-GA-2012-328378.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Running example: water tank
The running example for this article is a simple water tank that will be used to illustrate the concepts throughout. The water level in the tank is controlled by a digital controller that can periodically adjust flow into and from the tank by adjusting two valves. Every time the controller decides on adjusting the flow, it measures the water level through a sensor (i. e., it samples the water level). As a safety condition, we want the water tank to never overflow: any control decision of the controller must be such that the water level stays within 0 and a maximum water level m at all times.
For proving safety, we model this example as a hybrid system model in (9).

The water tank has a current water level x and a maximum water level m. The water tank controller, which runs at least every \(\varepsilon \) time units, nondeterministically chooses any flow f (written  ) between a maximum outflow \(-1\) and a maximum inflow \(\tfrac{m-x}{\varepsilon }\) (by the subsequent test
) between a maximum outflow \(-1\) and a maximum inflow \(\tfrac{m-x}{\varepsilon }\) (by the subsequent test  ). Note, that when the tank is empty (\(x=0\)) and the controller still chooses a negative flow \(f<0\) as permitted by the test
). Note, that when the tank is empty (\(x=0\)) and the controller still chooses a negative flow \(f<0\) as permitted by the test  , the evolution domain constraint \(x \ge 0\) in the ODE, which models a physical constraint that water level cannot be negative, will abort immediately. As a result, only non-negative values for f will make progress in case the tank is empty. Choosing flow directly simplifies the behavior of the actual water tank implementation (a single flow value models two valves).Footnote 11 The water level in the tank evolves according to the idealized differential equation
, the evolution domain constraint \(x \ge 0\) in the ODE, which models a physical constraint that water level cannot be negative, will abort immediately. As a result, only non-negative values for f will make progress in case the tank is empty. Choosing flow directly simplifies the behavior of the actual water tank implementation (a single flow value models two valves).Footnote 11 The water level in the tank evolves according to the idealized differential equation  . Besides the water level changing according to the flow
. Besides the water level changing according to the flow  , the differential equation system includes time
, the differential equation system includes time  to model controller periodicity (\(t \le \varepsilon \)). This considerably simplifies water flow models (e. g., it neglects the influence of water level on flow, and flow disturbance in pipes). The first conjunct \(x \ge 0\) in the evolution domain models a physical constraint that the water level can never be below zero (otherwise, the differential equation would include negative water content in the tank below zero on negative flow). The second conjunct \(t \le \varepsilon \) models the sampling period of our controller, that is it allows the ODE to be followed only for at most \(\varepsilon \) time before interrupting it for a control decision. Note, that through \(t \le \varepsilon \) the sampling period does not need to be the same on every control cycle, nor does it need to be exactly \(\varepsilon \) time. This water tank never overflows, as witnessed by a proof for the
to model controller periodicity (\(t \le \varepsilon \)). This considerably simplifies water flow models (e. g., it neglects the influence of water level on flow, and flow disturbance in pipes). The first conjunct \(x \ge 0\) in the evolution domain models a physical constraint that the water level can never be below zero (otherwise, the differential equation would include negative water content in the tank below zero on negative flow). The second conjunct \(t \le \varepsilon \) models the sampling period of our controller, that is it allows the ODE to be followed only for at most \(\varepsilon \) time before interrupting it for a control decision. Note, that through \(t \le \varepsilon \) the sampling period does not need to be the same on every control cycle, nor does it need to be exactly \(\varepsilon \) time. This water tank never overflows, as witnessed by a proof for the  formula (1).
formula (1).
However, since we made approximations when modeling the controller and the physics, and since failures and other deviations may occur in reality (e. g., a valve could fail), we cannot simply transfer this safety proof to the real system.
First, since failures may occur we need to monitor actual evolution, such as that the actual water level corresponds to the level expected by the chosen valve positions and the actual time passed between controller executions does not exceed the modeled sampling period. The monitor needs to allow some slack around the expected water level to compensate for the neglected physical phenomena. Sections 3.2 and 3.5 describe how to synthesize such model monitors automatically. Second, the controller implementation differs from the model, so we need to check that the implemented controller only chooses flows f that satisfy \(-1 \le f \le \tfrac{m-x}{\varepsilon }\). Section 3.4 describes how to synthesize such controller monitors automatically. Finally, we can additionally monitor controller decisions for the expected real-world effect, since the hybrid system model contains a model of the physics of the water tank. Section 3.6 describes how to synthesize such prediction monitors automatically. The controller in the model, which is verified to be safe, gives us a fail-safe action that we can execute in place of the unverified controller implementation when one of the monitors is not satisfied.
Appendix 2: Water tank monitor specification conjecture analysis

Appendix 3: Sequent-style monitor synthesis
This section lists the monitor synthesis approach in the sequent style of the short version [24]. Proof 2 shows a complete sequence of proof rules applied to the water tank specification conjecture of Example 5 on page 17, with \(\varUpsilon ^+ \equiv x=x^+ \wedge f=f^+ \wedge t = t^+\).

Instantiating existential quantifiers ahead of time. The sequent-style synthesis must instantiate existential quantifiers when they are met in the synthesis process, even though not all the information about the exact instance may be available at that time. Opt. 1 below introduces a heuristic to avoid duplicate work when instantiating existential quantifiers.
By axiom  , an existentially quantified variable can be instantiated with an arbitrary term \(\theta \), which is often a new logical variable that is implicitly existentially quantified [29].
, an existentially quantified variable can be instantiated with an arbitrary term \(\theta \), which is often a new logical variable that is implicitly existentially quantified [29].
Optimization 1
(Instantiation trigger) If the variable is not changed in the remaining \(\alpha \), \(x_i=x_i^+\) is in \(\varUpsilon ^+\) and x is not bound in \(\varUpsilon ^+\), then instantiate the existential quantifier by axiom  with the corresponding \(x_i^+\) that is part of the specification conjecture (i. e., \(\theta =x_i^+\)), since subsequent proof steps are going to reveal \(\theta =x_i^+\) anyway. This optimization is most effective in the sequent-style synthesis technique, which spreads F over many branches.
with the corresponding \(x_i^+\) that is part of the specification conjecture (i. e., \(\theta =x_i^+\)), since subsequent proof steps are going to reveal \(\theta =x_i^+\) anyway. This optimization is most effective in the sequent-style synthesis technique, which spreads F over many branches.
Otherwise, we introduce a new logical variable, which may result in an existential quantifier in the monitor specification if no further constraints can be found later in the proof.
Example 10
(Instantiating existential quantifiers) Continuing Example 6, we show the proof without and with application of Opt. 1. The corresponding steps in the water tank proof use  to instantiate the resulting existential quantifier \(\exists f\) (i) with a new logical variable F (without Opt. 1), and (ii) with posterior variable \(f^+\) (with Opt. 1). The hybrid program \(\textit{plant}\) is an abbreviation for
to instantiate the resulting existential quantifier \(\exists f\) (i) with a new logical variable F (without Opt. 1), and (ii) with posterior variable \(f^+\) (with Opt. 1). The hybrid program \(\textit{plant}\) is an abbreviation for  .
.

Re-introducing quantifiers In the sequent-style analysis, the fragments of the monitor are usually scattered over several branches, since many proof rules split into two or more branches, as  after
after  in Proof 2 above. At the same time, sequent-style reasoning has the main goal to make proving properties easy (as opposed to synthesis) and thus only works on the top-level operator of a formula, not inside as in the axiomatic-style synthesis. As a result, the sequent-style prototype cannot postpone instantiating existential quantifiers until later, so it either must use Opt. 1 or instantiate with a fresh variable (e. g., F in
in Proof 2 above. At the same time, sequent-style reasoning has the main goal to make proving properties easy (as opposed to synthesis) and thus only works on the top-level operator of a formula, not inside as in the axiomatic-style synthesis. As a result, the sequent-style prototype cannot postpone instantiating existential quantifiers until later, so it either must use Opt. 1 or instantiate with a fresh variable (e. g., F in  in Proof 2 above). In the latter case, in the final step of sequent-style synthesis we can re-introduce existential quantifiers and look for additional facts that let us instantiate the quantifier with a more useful variable, see Example 11.
in Proof 2 above). In the latter case, in the final step of sequent-style synthesis we can re-introduce existential quantifiers and look for additional facts that let us instantiate the quantifier with a more useful variable, see Example 11.
We use the invertible quantifier rule  to re-introduce existential quantifiers for the new logical variables (universal quantifiers for function symbols, see [29] for calculus details). Often, the now quantified logical variables are discovered to be equal to one of the post-state variables later in the proof, because those variables did not change in the model after the assignment. If this is the case, we can use proof rule
to re-introduce existential quantifiers for the new logical variables (universal quantifiers for function symbols, see [29] for calculus details). Often, the now quantified logical variables are discovered to be equal to one of the post-state variables later in the proof, because those variables did not change in the model after the assignment. If this is the case, we can use proof rule  to further simplify the monitor specification by substituting the corresponding logical variable x with its equal term \(\theta \).
to further simplify the monitor specification by substituting the corresponding logical variable x with its equal term \(\theta \).
Example 11
(Reintroducing existential quantifiers over multiple branches) Proof 2 uses a new logical variable F for the nondeterministic flow assignment  . After further steps in the proof, the assumptions reveal additional information \(F=f^+\). Thus, we re-introduce the existential quantifier over all the open branches (
. After further steps in the proof, the assumptions reveal additional information \(F=f^+\). Thus, we re-introduce the existential quantifier over all the open branches ( ) and substitute \(f^+\) for F (
) and substitute \(f^+\) for F ( ). The sole open sequent of this proof attempt is the monitor specification \(F(x,x^+)\) of the water tank model.
). The sole open sequent of this proof attempt is the monitor specification \(F(x,x^+)\) of the water tank model.

Appendix 4: Reasoning in KeYmaera X
In order to illustrate the underlying principle of the synthesize tactic, let us first consider a tactic  for nondeterministic assignment. The tactic rewrites a formula of the form
for nondeterministic assignment. The tactic rewrites a formula of the form  into
into  , and proves the correctness of this rewriting from the corresponding axiom
, and proves the correctness of this rewriting from the corresponding axiom  . Proof 3 illustrates this principle in more detail. First, the desired outcome is cut in as an equivalence to the current formula. This equivalence can be shown from the axioms, cf. right-most branch. Once proven correct, propositional tactics close one direction of the equivalence (left-most branch) and transform the equivalence into the desired outcome, cf. middle branch.
. Proof 3 illustrates this principle in more detail. First, the desired outcome is cut in as an equivalence to the current formula. This equivalence can be shown from the axioms, cf. right-most branch. Once proven correct, propositional tactics close one direction of the equivalence (left-most branch) and transform the equivalence into the desired outcome, cf. middle branch.

Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mitsch, S., Platzer, A. ModelPlex: verified runtime validation of verified cyber-physical system models. Form Methods Syst Des 49, 33–74 (2016). https://doi.org/10.1007/s10703-016-0241-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10703-016-0241-z








 iff
iff  and
and  iff
iff 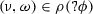 iff
iff  and
and  .
. iff for some
iff for some  with
with  , such that for each time
, such that for each time  , see [
, see [

 where
where  iff
iff  for
for 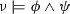 iff
iff  and
and  , accordingly for
, accordingly for 
 iff
iff  for all
for all  that agree with
that agree with  except for the value of x
except for the value of x
 iff
iff  for some
for some  that agrees with
that agrees with  except for the value of x
except for the value of x
 iff
iff  for all
for all 
 iff
iff  for some
for some 


 , i. e., test
, i. e., test 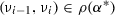 . If violated, other verified properties may no longer hold for the system so a failsafe action is initiated. The system itself, however, still satisfies safety condition
. If violated, other verified properties may no longer hold for the system so a failsafe action is initiated. The system itself, however, still satisfies safety condition  through proof steps. Controller monitors have some similarities with Simplex [
through proof steps. Controller monitors have some similarities with Simplex [ ”:
”: by bound effect Lemma
by bound effect Lemma  and, thus, also
and, thus, also  , which is
, which is  .
. ”:
”: , that is,
, that is,  . So there is a
. So there is a 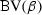 . Thus,
. Thus, 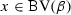 as
as  . Combining both yields that
. Combining both yields that  . Since
. Since  , coincidence Lemma
, coincidence Lemma  . And
. And  by bound effect Lemma
by bound effect Lemma  , it follows that
, it follows that  , so
, so 

 ; the posterior state
; the posterior state  formula (
formula ( of the form
of the form  is turned into a specification conjecture (
is turned into a specification conjecture (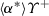 .
.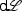 proof rules are applicable and only first-order real arithmetic formulas remain open.
proof rules are applicable and only first-order real arithmetic formulas remain open.



 : Follows from relative decidability of
: Follows from relative decidability of  [
[ contains no free variables.
contains no free variables. : Follows from relative decidability of
: Follows from relative decidability of  [
[ contains no free variables.
contains no free variables. : First assume that
: First assume that  can be represented in a first-order formula B such that
can be represented in a first-order formula B such that 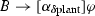 . Then, by
. Then, by 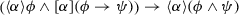
 : follows from case
: follows from case  (controller monitor) above.
(controller monitor) above. : Since the disturbance
: Since the disturbance  by Definition
by Definition  . We proceed with only
. We proceed with only  since the case
since the case  follows in a similar manner. By definition of
follows in a similar manner. By definition of  by differential cut
by differential cut  in
in  , which by rule differential invariant [
, which by rule differential invariant [ where the primed variables are replaced with the respective right-hand side of the differential equation system. From Definition
where the primed variables are replaced with the respective right-hand side of the differential equation system. From Definition  and
and  and since
and since  in
in  ; hence we have to show
; hence we have to show  , which is trivially true.
, which is trivially true. , which by rule differential weaken [
, which by rule differential weaken [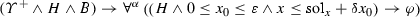
 is valid, this is provable by quantifier elimination. Furthermore, we cannot get a better result than differential weaken, because the evolution domain constraint contains the oracle’s answer for the differential equation system, which characterizes exactly the reachable set of the differential equation system.
is valid, this is provable by quantifier elimination. Furthermore, we cannot get a better result than differential weaken, because the evolution domain constraint contains the oracle’s answer for the differential equation system, which characterizes exactly the reachable set of the differential equation system.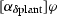 can be represented in a first-order formula B such that
can be represented in a first-order formula B such that  . We know from Lemma
. We know from Lemma  is valid. For the constant additive case, there even is a first-order formula B that is equivalent to
is valid. For the constant additive case, there even is a first-order formula B that is equivalent to  , because every constant additive disturbance can be replaced equivalently by a mean disturbance using the mean-value theorem for the disturbance as a (continuous!) function of time [
, because every constant additive disturbance can be replaced equivalently by a mean disturbance using the mean-value theorem for the disturbance as a (continuous!) function of time [ would make progress, because the differential equations in
would make progress, because the differential equations in 
 is maximum level (m),
is maximum level (m),  is current level (x),
is current level (x),  is commanded flow (f),
is commanded flow (f),  is the output of monitor
is the output of monitor  is the output of monitor
is the output of monitor  ) for verifying controllers and synthesizing provably correct monitors.
) for verifying controllers and synthesizing provably correct monitors. ) and
) and  and KeYmaera X as a theorem prover to illustrate our concepts throughout this article. The concept of ModelPlex is not predicated on the use of
and KeYmaera X as a theorem prover to illustrate our concepts throughout this article. The concept of ModelPlex is not predicated on the use of  /KeYmaera X to prove (
/KeYmaera X to prove ( , its support for both
, its support for both  and
and  , and its proof calculus, however, are exploited for systematically constructing monitors from proofs in the rest of the article.
, and its proof calculus, however, are exploited for systematically constructing monitors from proofs in the rest of the article. mean before and after executions of
mean before and after executions of  for variables
for variables  , because we will use non-equivalence proof steps to derive
, because we will use non-equivalence proof steps to derive  .
.