Abstract
The eliminative view of gauge degrees of freedom—the view that they arise solely from descriptive redundancy and are therefore eliminable from the theory—is a lively topic of debate in the philosophy of physics. Recent work attempts to leverage properties of the QCD \(\theta _{\text {YM}}\)-term to provide a novel argument against the eliminative view. The argument is based on the claim that the QCD \(\theta _{\text {YM}}\)-term changes under “large” gauge transformations. Here we review geometrical propositions about fiber bundles that unequivocally falsify these claims: the \(\theta _{\text {YM}}\)-term encodes topological features of the fiber bundle used to represent gauge degrees of freedom, but it is fully gauge-invariant. Nonetheless, within the essentially classical viewpoint pursued here, the physical role of the \(\theta _{\text {YM}}\)-term shows the physical importance of bundle topology (or superpositions thereof) and thus counts against (a naive) eliminativism.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Modern philosophers take seriously the ontological status of fields. But what they usually have in mind are relatively concrete entities, such as the electric and magnetic fields, and not elusive gauge fields, such as the electromagnetic potential. How then, to classify “gauge” degrees of freedom? Do these have an ontological significance similar to electric and magnetic fields, or are they only a notational convenience, born of a redundancy in our representations of the world? In the words of John Earman, are gauge degrees of freedom only “redundant descriptive fluff” [1]?
The eliminativist view of gauge degrees of freedom advocates not only that gauge degrees of freedom are redundant, but that they are also eliminable. The most developed form of eliminativism proposes a different, non-local gauge-invariant basis to describe our physical quantities. Non-local, yes, but controllably so: this is called the holonomy-basis.Footnote 1 Whether one can really write down a theory—an action functional or a Hamiltonian—in terms of holonomies (or Wilson loops) is challenging, to say the least, and so the status of holonomies as fundamental ontological buiding blocks is anything but secure. But we will not pursue this formidable challenge in this paper.
Likewise, the overall status of gauge degrees of freedom is too large a topic to be reviewed here. We plan only to analyze a recent argument against the eliminativist view, and show that it is founded on an incorrect mathematical treatment—and it is therefore not tenable in its current form. In the rest of this section, we introduce the argument and give a prospectus for the paper.
1.1 The \(\theta _{\text {YM}}\)-Term
In a recent paper, [3] engages with the details of the eliminativist program in the context of QCD. Dougherty’s first aim is to convince the reader that a \(\theta _{\text {\tiny YM}}\)-term in the QCD Lagrangian is mandatory.
In brief, the argument is as follows: the \(\theta _{\text {\tiny YM}}\)-term is necessary to account for certain experimental facts. To be more specific: the smallness of the masses of the up and down quarks gives rise to a chiral symmetry, whose effects (a parity doubling of the hadron spectrum, cf. [4, Sec. 19.10]) are not observed in experiments. This means that this chiral symmetry must be broken somehow. But the spontaneous breaking of this symmetry would generate Goldstone bosons, which are also not observed. Therefore, one must be able to break chiral symmetry without creating Goldstone bosons.
A solution is to have the breaking be effected through an anomaly.Footnote 2 Namely, under chiral transformations (also called a global U\((1)_A\) symmetry), it turns out that the path-integral measure for quark fields fails to be invariant: under that transformation the measure acquires a phase. Specifically, for a fermion field of flavor f, the chiral symmetry acts by a shift \(\psi _f\mapsto \exp (i\gamma _5\alpha _f)\psi _f\) (with \(\gamma _5\) the fifth Dirac gamma-matrix), whereas the fermion path-integral transforms asFootnote 3
where
Therefore, according to this argument, mathematical consistency and experimental evidence—the lack of both the relevant Goldstone bosons and of the parity doubling of the hadron spectrum—together would provide support for the physical significance of the \( \theta _{\text {YM}}\)-term as arising from a chiral anomaly. It is here important to stress the role fermions play in making the \(\theta _{\text {YM}}\)-term inescapable.
So far, so good. But agreed: this is not the end of the story: such a term would be CP-violating and thus gives rise to other questions of observability. However, the relation between CP-violation and the \(\theta _{\text {YM}}\text {-term}\) is not directly relevant to the central points of this paper, which is why we will avoid discussing it.Footnote 4
Having sketched the broader context for the discussion, we now very briefly embed within it Dougherty’s criticism of the holonomy formalism. Before we begin, it should be stated from the outset that our intention in this paper is only to set straight a specific misunderstanding of this criticism. The main target of our criticism is the mistaken belief that due to how \( \theta _{\text {YM}}\)-term transforms under gauge transformations, it cannot be accounted for within an eliminativist interpretation, such as the holonomy formalism. In his words: “This eliminative interpretation of gauge is at odds with the our current best theory of high-energy physics.” Or, a bit later, in more detail: “In this paper I defend the physical significance of the distinction between large and small gauge transformations against the eliminative interpretation of gauge.” [3, p.1]. We contend that: (1) Dougherty’s ‘large gauge transformations’ are not gauge transformations in the first place (a fact that, as we will prove, goes beyond a terminological dispute), and, more importantly, (2) the objective properties Dougherty (mis)attributes to ‘large gauge transformations’ are in fact captured in an eleminativist formalism such as the holonomy one, which only eliminates the bona-fide gauge transformations. So, first, it is apt to get clear on the distinction between ‘large’ and ‘small’ gauge transformations, and on how, if at all, such distinction could be serviced against the holonomy-based, eliminativist interpretation.
1.2 Dougherty’s Criticism
In his defense of eliminativism, [2] cites [8]’s use of the holonomy formalism in attempting to resolve the \(U(1)_A\) puzzle without the introduction of a \(\theta _{\text {YM}}\)-term (we will briefly describe this puzzle in Sect. 3.3).Footnote 5 According to [3] (cf. p.1, 7, 8, 16) the \(\theta _{\text {YM}}\)-term is only gauge-invariant under gauge transformations that have a particular behaviour at infinity (or at the relevant boundaries); the remaining transformations, called ‘large gauge transformations’, do not, according to Dougherty, leave the \(\theta _{\text {YM}}\)-term invariant. In his criticism of the eliminativist view, [3, p.1] writes passages such as (italic ours):
That is, a large gauge transformation relates representatives of different physical states. Mathematical differences between these representatives can reflect a physical difference, signaling the existence of some quantities and possibilities that cannot exist according to the received [eliminativist] philosophical position.
Or, later on [3, p.1]:
The Yang-Mills \([\theta \text {-}]\)vacuum term is not preserved by all gauge transformations. If the eliminative view of gauge transformations is right, this means that the Yang-Mills vacuum term is physically meaningless. If gauge transformations are redundancies then mathematical differences between gauge equivalent configurations can’t reflect physical differences. So the value of the Yang-Mills vacuum term can’t represent any physical fact.
Or, again [3, p.9]:
If we reject the size distinction [between small and large gauge transformations] and demand that gauge transformations on the boundary be treated just as gauge transformations elsewhere then this integral [that gives rise to the \(\theta \)-term] is ill-defined. The vacuum Yang-Mills term must therefore be excluded.
Dougherty’s claim then is that the non-eliminativist would be comfortable in separating the wheat from the chaff, for they could say: “some ‘gauge transformations’ relate distinct physical possibilities while others don’t. Thankfully, I, the non-eliminativist, haven’t eliminated any of them, so I can still tell the two kinds apart!” This strategy, it is claimed, is not available to Healey’s preferred holonomy formalism. The claim is that, since Healey’s eliminativism does not license a distinction between different types of gauge transformations, no restriction to one type of gauge transformation is allowed. In particular, one cannot keep just those transformations that would guarantee invariance of the \(\theta _{\text {YM}}\)-term. Therefore Healey would either have to equate what should be physically distinct states—those which, according to Dougherty, correspond to differences due to ‘large gauge transformations’—or be obliged to set \(\theta _{\text {YM}}\) to zero and thereby fall foul of the fact that at least allowing for a non-zero \(\theta _{\text {\tiny YM}}\)-term is a theoretical requirement.
As we hope to make clear, we disagree with Dougherty’s argument and conclusions. In particular, we disagree that “The Yang-Mills \([\theta \text {-}]\)vacuum term is not preserved by all gauge transformations.” It is preserved by all gauge transformations; as long as one is attentive to the strict meaning of these transformations. Our criticism could be chalked off to a terminological dispute, one of little substance to the debate about eliminativism. The reason the criticism matters is that, apart from trivial issues of terminology, holonomies only eliminate the more strict kind of ‘gauge transformations’ and are perfectly well able to register the effects of what Dougherty calls “large gauge transformations”. In particular, the \(\theta _{\text {\tiny YM}}\)-term contribution to the Yang-Mills action is gauge invariant and can be expressed in terms of holonomies. Indeed, lattice QCD, a formalism that employs holonomies (or rather, Wilson loops) as its basic variables, includes \(\theta \)-terms without any hangups (see e.g. [9] and references therein).
1.3 Our Criticism of Dougherty’s Criticism
Dougherty’s argument that the \(\theta _{\text {YM}}\)-term is only gauge-invariant under gauge transformations that have a particular behaviour at the boundaries is incorrect. For the \(\theta _{\text {YM}}\)-term is manifestly gauge-invariant under the action of all gauge transformations.
Nonetheless, behind Dougherty’s argument, there is a subtle and tempting reason to erroneously assume that the \(\theta _{\text {YM}}\)-term is gauge-variant. For, as Dougherty correctly states, the \(\theta _{\text {YM}}\)-term can also be expressed as a pure boundary contribution to the action functional over a topologically trivial domain M (i.e. one diffeomorphic to a 4-disk). And it is well-known that this boundary contribution (over the 3-sphere), which takes the form of a Chern-Simons boundary integral, can acquire different values even on configurations that have vanishing curvature, and are often thus called ‘pure-gauge’ (however, see the comment below Equation (3.1) for why this practice is misleading). The values of such boundary contributions can differ by an integer multiple of \(2\pi \). So, it would be natural to say that these values have some sort of gauge-dependence, i.e. that they change under “large gauge transformations”; this putative change is the one Dougherty wrongly appeals to in his argument.
The mistake, to be explicated below, is partly due to a terminological confusion: it lies in the construal of the term “large gauge transformation”, which is often mixed up with what are called “transition functions.” Although transition functions share some features with gauge transformations, they are fundamentally different objects which encode gauge invariant information. It is only under a particular type of change in the transition functions—changes which cannot be attributed to any gauge transformation—that the \(\theta _{\text {YM}}\)-term fails to be invariant. Thus, in order to clarify the mistake, it is helpful to first clarify the terminology. But to be clear: independent of the terminological dispute, the physical effects of transition functions can be captured by the holonomy formalism, and so are no obstacle to the eliminativist interpretation of gauge.
In practice, the term “large gauge transformation” has been used with two meanings:
(i) a smooth Lie-group-valued function on space or spacetimeFootnote 6 that is not connected to the group identity, i.e. not infinitesimally generated through exponentiation;
(ii) in the presence of asymptotic boundaries, it is a gauge transformation which does not asymptote to the identity.
In this article, we will exclusively use the term “large gauge transformation” in the sense attached to (i), i.e. not being connected to the identity.
To make his argument stick, Dougherty must use transformations that satisfy both (i) and (ii) i.e. transformations whose pullback to the boundary neither vanishes,Footnote 7 nor is connected to the identity. This is because only such transformations would change the value of the boundary Chern-Simons integral which re-expresses the \(\theta _\text {\tiny YM}\)-term.Footnote 8 However, the combination of (i) and (ii), required by Dougherty selects an empty set of functions. This is because there is no smoothFootnote 9 Lie-group valued function over \(\mathbb R^4\) that tends at infinity to a function over \({\partial }\mathbb R^4 \cong S^3\) that is not connected to the identity. This fact is strictly necessary to ensure the mathematical consistency of the equality between the bulk-integral defining the \(\theta _\text {\tiny YM}\)-term (which is manifestly gauge-invariant under all gauge transformations) and its expression in terms of Chern-Simons boundary integral (which is not invariant under large-gauge transformations over \(S^3\)). The goal of the following sections is to explain these facts, dissolve the apparent tension between them, and explore their consequences in sufficient detail.
Here, we briefly sketch with equations an abstract argument showing that the necessary transformations cannot be smoothly extended into the bulk (all notation will be explained later). For now we consider the simplest possible caseFootnote 10: that of a gauge potential A that is pure gauge on a 4-disk \(D^4\). Thus, \(A=g^{-1}{\textrm{d}}g\) for some \(g: D^4\rightarrow G\), and its associated curvature vanishes, i.e. \(F(A)=F(g^{-1}{\textrm{d}}g) =0\), so that the \(\theta _{\text {\tiny YM}}\)-term, defined as \( \frac{1}{8\pi ^2} \int _{ D^4 } \text {tr}( F\wedge F)\), manifestly vanishes—in all gauges. Thus,
where the second equality will be shown in the next section; and \(\textsf{CS}_{ S^3}\) is by definition the Chern-Simons functional (on \(S^3\)), with \( h:S^3 \rightarrow G\) here set to \(h=g_{|S^3}\).
The puzzle arises thus: it is a mathematical fact that certain \(\tilde{h}:S^3 \rightarrow G\) yield a non-vanishing \(\textsf{CS}_{S^3}(\tilde{h}^{-1}{\textrm{d}}\tilde{h})\). So how could the above equation (1.3) avoid mathematical inconsistency? In brief: such \(\tilde{h}\)’s are not of the form \(h=g_{|S^3}\) for a smooth \(g: D^4\rightarrow G\). That is, the \(\tilde{h}\)’s that yield these different values are “homotopically” different: they cannot be smoothly deformed into each other, and are thus said to differ by a “large” transformation. At a bit more length, the answer to our question then is that, crucially, large transformations of this kind cannot be extended into the \(D^4 \) bulk smoothly and therefore cannot define “gauge transformations" of the bulk configuration \(A=0\); there are no such transformations whose restriction to the boundary fits in (i) above. In other words, the large boundary transformations required to yield a non-zero value of the Chern-Simons functional are not of the form \(h=g_{|S^3}\) for a smooth \(g:D^4\rightarrow G\); and such transformations would not have the usual properties of gauge transformations. That is: such \(\tilde{h}\) are not restrictions to the boundary of gauge transformations of any kind—which, as we know, leave the value of the \(\theta _{\text {YM}}\)-term invariant. In this understanding, [3, p. 8 and 9] is mistaken when he says that: “we find that the Yang-Mills vacuum term varies under some gauge transformations,” and hence concludes: “if we [...] demand that gauge transformations on the boundary be treated just as gauge transformations elsewhere then [the integral \(\int \text {tr}(F\wedge F)\)] is ill-defined [and] the vacuum Yang-Mills term must therefore be excluded.”
Homotopically different h’s on the right hand side of (1.3) represent physically different configurations also in the bulk, and indeed must be accompanied by different curvatures in the bulk. In due course, we will prove all of these statements, thus avoiding a mathematical contradiction: the gauge-invariance properties of the \(\theta _{\text {YM}}\)-term cannot depend on the way we decide to write it, viz. as a bulk or as a boundary term.
1.4 Prospectus
This paper will proceed as follows. In section 2, we will give a brief introduction to the main mathematical concepts at play. We briefly review Chern classes in Sect. 2.1. There, we will recall what these classes have to do with the \(\theta _{\text {YM}}\) term in QCD, and discuss their gauge and topological invariance. In the following subsection 2.2, we finally bring in what Dougherty calls “large gauge transformations,” that underpin his argument and show in particular that they have nothing to do with gauge-transformations: they are quantities that encode the topological properties of the underlying bundle, and are not related to choices of gauge. Such topological properties are represented by the particular gluing, or relations, between topologically trivial charts; and the winding numbers encode this ‘gluing’ information.
These conclusions are valid for manifolds without boundary. In Sect. 3 we describe how these conclusions can be extended to the context of manifolds with boundaries. Here it is important to distinguish the Euclidean signature setting from the Lorentzian one. In the former case, in section 3.1, we can complete asymptotic boundaries and fall back on the results for the boundary-less manifolds. For the latter case, in section 3.2, we get two disconnected boundaries, and thus (assuming the fields behave nicely at space-like infinity), the \(\theta _{\text {YM}}\) topological invariant becomes a difference of two Chern-Simons terms, or of two winding numbers. Nonetheless, the conclusions about their invariance remains, but now it applies to the difference of winding numbers. In Sect. 4 we conclude: Sect. 4.1 summarizes the main points made in the paper. Finally, in Sect. 4.2, we briefly smoke a peace-pipe with Dougherty, by giving a criticism of our own of the eliminativism he targets. This criticism does take into account the role of the \(\theta _{\text {YM}}\)-term—but not its properties under gauge transformation, which, pace Dougherty, are compatible with eliminativism.
Since this article is an answer to [3], we follow him in accepting the same, intrinsically semiclassical, but standard, account of chiral symmetry breaking, cf. e.g. [4]. However, as we ackowledge in Appendix B, a fully non-perturbative account also exists [10, Ch. 3].
2 Topological Invariants and Fiber Bundles
In this Section, we will introduce aspects of the topology of fiber bundles, and proceed to assess gauge-invariance of the \(\theta _{\text {YM}}\)-term for closed manifolds in several different ways. In Sect. 2.1, we introduce the \(\theta _{\text {YM}}\)-term—also known as the Chern-number. Seen as a bulk, i.e. spacetime, integral, we show both gauge and topological invariance of the term. In Sect. 2.2 we relate this invariant to the appearance of ‘large’ transformations: they appear as Wess-Zumino integrals related to transition functions between charts. We also show that gauge transformations on a 4-dimensional disk-region cannot have non-trivial winding number at its boundary. This is entirely compatible with, and indeed required by, our considerations in this paper.
For completeness, in Appendix A we give a brief introduction to fibre bundles as the mathematical structure underpinning gauge theories. In this appendix we introduce the basic machinery: the connection-form (and its relational interpretation), and the relation between charts, gauge transformations and transition functions, crucial to our appraisal of the conclusions of [3].
Here is a summary of the concepts from Appendix A that we will require in what follows:
Summary of Appendix A. A gauge field configuration can be defined either:
-
(1)
“abstractly,” by providing a bundle \(\pi :P\rightarrow M\) and an Ehresmann connection \(\omega \in \Omega ^1(P,\mathfrak g)\); or
-
(2)
“in coordinates,” by providing an atlas of charts \(U_\alpha \subset M\), a set of sections \(\sigma _\alpha : U_\alpha \in P \), and compatibleFootnote 11 transition functions \(\mathfrak {t}_{\alpha \beta }:U_{\alpha \beta }\rightarrow G\) (these three ingredients define P), together with a choice of compatibleFootnote 12 gauge fields \(A_\alpha \in \Omega ^1(U_\alpha ,\mathfrak g)\) (this corresponds to the choice of \(\omega \)).
The coordinate description is redundant because it requires the introduction of auxiliary choices of sections, \(\sigma _\alpha \); different choices are related by “gauge transformations” of the \(A_\alpha \)’s and of the \(\mathfrak {t}_{\alpha \beta }\)’s. Therefore, gauge invariance requires all physical observables to depend on the choice of P and \(\omega \) only.Footnote 13
Crucially, transition functions and gauge transformations play entirely different roles. Gauge transformations act on the transition functions, but not vice-versa, and a gauge transformation’s domain of definition is the whole chart \(U_\alpha \), and not merely the overlaps \(U_{\alpha \beta }\) as is the case for the transition functions \(\mathfrak {t}_{\alpha \beta }\)’s. These technical differences reflect the fact that the \(g_{\alpha }\)’s and \(\mathfrak {t}_{\alpha \beta }\)’s play conceptually different roles. From the perspective of P, the gauge transformations \(g_\alpha \)’s encode the freedom of choosing a local section \(\sigma _\alpha \) (which is necessarily defined on the whole of \(U_\alpha \)). Conversely, the \(\mathfrak {t}_{\alpha \beta }\) encode—albeit somewhat redundantly—the way in which the charts are glued to one another, and thus the global structure of the bundle P.
2.1 The Chern-Number
For a closed 4-dimensional manifold M—that is, M compact and without boundary—the quantity (the notation will be explained in a moment, for now it is enough to notice that the integrand depends on A and is gauge-invariant)
is a topological invariant—not of M—but of the fibre bundle P over M. A connection-form \(\omega \) is defined over P and a collection of local gauge potentials \(A_\alpha \) is defined over an atlas of M, as above. Since \(\textsf{ch}_A\) is gauge-invariant, the integral can then be obtained through an appropriate partition of unity associated to the atlas. As a topological invariant of P, \(\textsf{Ch}[P]\) is not only completely gauge-invariant, but also independent of the choice of \(\omega \) over P. We call \(\textsf{Ch}[P]\) the (second) Chern-number of P.Footnote 14
If we write our physics in terms of gauge potentials, and allow them to live in different bundles, e.g. P and \(P'\), then the potentials A and \(A'\) might lead to different values of \(\textsf{Ch}[P]\). The question then is: how does A “know about” topological properties of P? And how can \(\textsf{Ch}[P]\) depend only on the topology of P and not on the detailed choices e.g. of A that go into its computation? This is the content of the Chern-Weil theorem (e.g. [11, Ch. 11.1]), that we briefly review below.
From now onwards, we will restrict to \(G = {\textrm{SU}}(N)\).
First, the Chern-number is computed as follows:
where
Of course, \(\textsf{Ch}(P)\) is nothing but the “\(\theta _{\text {\tiny YM}}\)-term,” (cf. (1.2)). Or, more specifically: the \(\theta _{\text {YM}}\)-term in the QCD Lagrangian can be written using (2.1) as:
where \(\theta \) is just a real-valued coefficient. The integrand \(\textsf{ch}_A\) defines the second Chern-class of the bundle P. The second Chern-class is manifestly gauge-invariant, given the gauge transformation properties of F (A.8) and the cyclicity of the trace.Footnote 15 This means that on the overlaps \(U_{\alpha \beta }\), \( \textsf{ch}_{A_\alpha } = \textsf{ch}_{A_\beta }\), which is why no chart index appears in the equations above, and why the integral can be performed with no further complications.
This also immediately tells us that \(\textsf{Ch}[P]\) can at most depend on the choice of \(\omega \), and not of gauge (i.e. of sections). We are now ready to review the Chern-Weil theorem, which shows that \(\textsf{Ch}[P]\) is not only gauge-invariant but also independent of the choice of \(\omega \) on P—that is it depends only on the topological properties of P.
A first hint of the ‘topological’ nature of \(\textsf{Ch}[P]\) comes from the observation that it does not change under a small arbitrary variation of A (i.e. the equations of motion of the action \(S[A] = \int \textsf{ch}_A\) are identically satisfied). This follows immediately from \(\delta F={\textrm{d}}_A\delta A\) and the Bianchi identity \({\textrm{d}}_A F=0\) where \({\textrm{d}}_A:={\textrm{d}}+[A, \cdot ]\) is the exterior gauge-covariant derivative (for the adjoint representation). But invariance can be proven also for finite, rather than infinitesimal, changes in connection. Consider two connections A and \(A'\), and now define \(\gamma := A' - A \in \Omega ^1(M)\) and a one-parameter family of connections \(A_s=A+s\gamma \), \(s\in (0,1)\), interpolating between A and \(A'\) (the space of connections is an affine space). Then, denoting the curvature of \(A_s\) as \(F_s\), one finds
Thus the difference \( \textsf{ch}_{A'}-\textsf{ch}_{A}\) is an exact differential form and thus vanishes when integrated over a closed manifold.Footnote 16 Since A and \(A'\) are arbitrary connections, it follows that \(\int _M \textsf{ch}_A\) over a closed manifold P does not depend on the choice of connection, i.e. that it is a topological invariant.
Summary The gauge invariance of \(\textsf{ch}_A\) tells us that \(\textsf{Ch}[P]\) depends at most on \(\omega \), and the Chern-Weil theorem tells us that \(\textsf{Ch}[P]\) does not depend on A (and therefore on \(\omega \)) at all. Therefore, \(\textsf{Ch}[P]\) can only reflect a (topological) property of the bundle P on which the connection is defined. A nontrivial, and extremely deep, fact is that the second Chern number of P is always an integer
We conclude this Section with a simple remark. The discussion above clearly shows that the Chern number (2.1) (and thus the \(\theta _{\text {YM}}\)-term) is gauge-invariant under all possible gauge transformations. And, just to be clear, this even holds at the level of the integrands:
This fact follows simply from the transformation properties of F (A.8) and the (graded) cyclicity of the trace (for \(\lambda , \eta \) as p and q-forms, respectively)
Therefore any non-gauge invariance of the \(\theta _{\text {\tiny YM}}\)-term is vetoed by this simple demonstration.
2.2 Transition Functions and Large Gauge Transformations
As we have just witnessed, the Chern-number and the so-called \(\theta _{\text {YM}}\)-term, (2.1), is completely gauge-invariant. Thus the inevitable question: whence Dougherty’s claims?
Here we will focus on his claim that “The Yang-Mills \([\theta \text {-}]\)vacuum term is not preserved by all gauge transformations.”, as discussed in Sect. 1.2 (where we include the full quote). We will now argue that one way Dougherty might have arrived at this conclusion, ignoring the previous simple argument for the gauge invariance of the \(\theta _{\text {YM}}\)-term, is through an uncatious invocation of boundaries.
Before we get to boundaries of the entire Universe, in Sect. 3, let us revisit the computation of the Chern-number under a new guise, by breaking up the manifold into charts and therefore introducing internal boundaries. Over each chart we can identify the gauge potential with a \({\mathfrak {g}}\)-valued differential 1-form A. However, this identification does not hold globally as emphasized in our discussion of transition functions (cf. equation (A.3)): one should be careful when drawing global conclusions from the following local statements.
First, we recall that the Chern density (2.2), i.e. \(\textsf{ch}_A:= \frac{1}{8\pi ^2}\text {tr}( F\wedge F)\), is a top-form on a 4-dimensional manifold and it is therefore closed.Footnote 17 Hence, the Poincaré lemma implies that the restriction of \(\textsf{ch}_A\) to a contractible space is exact, i.e. can be written as the differential of a 3-form. Indeed, on each chart \(U_\alpha \)—which is a contractible space where the connection A can be identified with a \({\mathfrak {g}}\)-valued 1-form \(A_\alpha \) (we will omit the chart-label \(\alpha \))—one has the following crucial identityFootnote 18 involving the Chern-Simons 3-form \(\textsf{cs}_A\)Footnote 19
There are two subtleties lurking behind this identity: one is the fact that it holds only chart-wise, and the second is that the Chern-Simons form is not gauge-invariant, since:
where the Wess-Zumino term \(\textsf{wz}_g\) is just the Chern-Simons form evaluated on the flat connection \(g^{-1}dg\):
In particle physics lingo, equations (2.6), (2.8), and (2.9) together say that “while the topological charge [\(\textsf{ch}_A\)] is gauge-invariant, the topological current [\(\textsf{cs}_A\)] is not.” [12, p. 31].
However, as demanded by mathematical consistency between the invariance of \(\textsf{ch}\) and its relation to \(\textsf{cs}\) in the first equation of (2.8), both sides of (2.9) must be closed 3-forms, and therefore \(\textsf{wz}_g\) is necessarily a closed 3-form, i.e.Footnote 20
Therefore, the gauge invariance of \(\textsf{ch}_A\) is not affected, even if we write it in terms of the gauge-variant functional \(\textsf{cs}\):
In particular, taking \(A=0\) and integrating this equation on a manifold with boundary, we see that the boundary integral of the Wess-Zumino term associated to a gauge transformation in the bulk necessarily vanishes. Equation (2.12) is a first important check, which we will now corroborate with a different calculation.
This different computation resolves possible confusion having to do with a particular way of expressing \(\textsf{Ch}[P]\). Namely, there is still one manner of computing \(\textsf{Ch}[P]\) chart by chart, using (2.8), which may confusingly appear gauge-variant. We will now set up the puzzle and then dissolve it. Instead of dealing with these issues on a very general basis, we will specialize our discussion to a more concrete example.
Consider the closed manifold \( M = S^4\) covered by two charts, isomorphic to 4-dimensional disks, \(U_{1}, U_2=D^4\), that overlap on a “transition belt” around the equator, \(U_{12}=S^3\times [-1,1]\).
We know that at the interface, by (A.3), \(A_1=A^{\mathfrak {t}}_2\), \(\mathfrak {t}\equiv \mathfrak {t}_{21}\). Denoting the subsets of the domain of the charts that lies above/below the equator, respectively, by \(\tilde{U}_1 = U_1 \setminus (S^3\times [-1,0])\) and \(\tilde{U}_2 = U_2 \setminus (S^3\times [0,1])\) (notice that \({\partial }\tilde{U}_1 = - {\partial }\tilde{U}_2 = S^3 \times \{0\} \simeq S^3\subset U_{12}\)), we have
where we used (2.9) and (2.10) (with \(\mathfrak {t}:U_{12}\rightarrow G\) replacing g in the latter equation).Footnote 21
Thus we see that, setting \({{\partial }\tilde{U}_1}\simeq S^3\) and denoting \(\textsf{WZ}_{S^3}(g) = \int _{S^3} \textsf{wz}_g\),
This equation is of crucial importance for us. We have not used gauge transformations, and yet, something that “looks like” a gauge-transformation, namely, a transition function, as in (A.3), has appeared in the computation. Now we will verify that the Wess-Zumino invariant related to \(\mathfrak {t}\) cannot change by applying a gauge transformation.
First of all, as discussed in Sect. A, \(\mathfrak {t}\) encodes a topological property of the bundle. It is therefore not to be interpreted as a gauge transformation, but as part of the definition of P. But things are subtle, because—as we summarized in the last paragraph of Sect. A—\(\mathfrak {t}\) participates in the definition of P in a way that depends on the choice of gauge, i.e. of sections \(\sigma _\alpha \). As a consequence, under a change in the choice of sections, the transition functions transform according to (A.7):
Thus, the question arises: why does the following equality,
hold?
From a strictly three-dimensional, or boundary, perspective there is no reason why this should be the case. In particular, we could always choose \(g_1 = e \) (the identity of G) and \(g_2\) such that \((g_2)_{|U_{12}}= \mathfrak {t}\), thus apparently trivializing the value of \(\textsf{WZ}_{S^3}\). However, once we take into account the whole domain of definition of the \(g_\alpha \)’s, which extends into the four-dimensional bulk of the two hemispheres, the above choice might simply be unavailable. That is, if \(\mathfrak {t}: S^3 \rightarrow G\) is large in the sense (i) of Sect. 1.3—not connected to the identity—there is no smooth extension of it that goes from the belt overlap \(U_{12}=S^3\) to the chart domain \(U_2 = D^4\). An extension would necessarily have to “break” somewhere inside \(U_2\). Only for \(\mathfrak {t}\)’s connected to the identity will there be a smooth \(g_2\) such that \((g_2)_{|U_{12}}= \mathfrak {t}\).
We can easily perform a proof by contradiction (reductio). For suppose it was possible to smoothly extend such \(g_\alpha \)’s into the interior of their charts. Then, following a radial evolution in the disk \(U_2=D_4\), we would find a g(x, r) such that \(g(x,r=1) = \mathfrak {t}(x)\) and \( \lim _{r\rightarrow 0} g(r, x)= g_o\) for all \(x\in S^3\), where \(g_o\) is some fixed element of G. But exploiting this radial parametrization we can define a 1-parameter family of gauge transformations \(\{ h_r(x):S^3 \rightarrow G \, | \, h_r(x) = g(r,x) \}_{r\in [0,1]}\), defined at the intersection \(S^3\), such that \(\textsf{WZ}(h_{r=0}=g_o)=0\) and \(\textsf{WZ}(h_{r=1}=\mathfrak {t})\ne 0\). But this cannot be right: \(\textsf{WZ}(h_r)\in \mathbb Z\), and since one cannot continuously jump between discrete values, \(\textsf{WZ}\) has to be constant on path-connected components of its domain. Let us prove this explicitly (by adding a differentiability assumption): denoting \(h_r(x) = g(r, x)\) and \(\xi _r = \frac{{\textrm{d}}h_r}{{\textrm{d}}r}h_r^{-1} \), we have, for an arbitrary \(r=r_o\),
where the second equality follows from (2.10).
The point is that any smooth map \(g_\alpha (x,r)\) from the 4-disk \(D^4\) into G—a gauge transformation according to (i)Footnote 22—automatically provides through “radial evolution” a homotopy of maps \(h_r(x) = g_{\alpha }(r,x):S^3\rightarrow G\) between a constant function \(h_{r=0}(x) = \lim _{r\rightarrow 0} g_{\alpha }(r,x) = g_o\) (at the central point) and its boundary value \(h_{r=1}(x) = g_{\alpha }(r=1,x)\). Or, in other words, the boundary value of any gauge transformation \(g_{\alpha }(x, r=1)\) on such charts must be connected to the identity.
And \(\textsf{WZ}_{S^3}(h)\) computes a “winding number” of the map \(h: S^3 \rightarrow G\); this is a topological quantity that cannot be undone by a smooth deformation of h. It follows from the above that a gauge transformation cannot change the winding number at the boundary. That is, the boundary value of a bulk gauge transformation \(g_\alpha \) must have trivial winding number as a map from \({\partial }U_\alpha \rightarrow G\), i.e. \(\textsf{WZ}_{S^3}(g_\alpha {}_{|{\partial }U_\alpha }) \equiv 0\). This of course means that \(\mathfrak {t}\) and \(g_2^{-1}\mathfrak {t}g_1\) are in the same homotopy class as maps from \(S^3\) into G, and therefore have the same winding number, as per equation (2.16).
Therefore, we conclude that in the simple case analyzed here, the second Chern number of the bundle \(\pi :P\rightarrow S^4\) is fully encoded into the winding number of the “equatorial” transition function \(\mathfrak {t}: S^3 \rightarrow G\). This winding number is an intrinsic property of \(\mathfrak {t}\) that cannot be changed by any gauge transformation.
So far we have discussed bundles on manifolds without boundaries. But to satisfactorily vanquish all doubts about gauge-invariance, we should also guarantee that it emerges when the \(\theta _{\text {\tiny YM}}\)-term is expressed not at intersections, but at boundaries. This is only possible when the curvature vanishes at the boundary; e.g. asymptotically. We now turn to this.
3 Manifolds with Boundaries
In the first Section, 3.1, we will examine Chern classes within a single bounded, Euclidean manifold and its relation to the Chern-Simons and Wess-Zumino functionals. In Sect. 3.2 we briefly examine the Lorentzian case, with two boundaries, one asymptotic past Cauchy surface and one asymptotic future one. (Like most of the literature (e.g. [4, p.454-455]), we neglect spatial boundary terms at infinity (on which A is supposed to vanish).) The Chern class then gives a difference of past and future Chern-Simons terms, (naively) representing a transition between different vacua of the theory. In Sect. 3.3, we briefly discern the meaning of non-trivial bundle topology viz. the meaning of individual winding numbers.
3.1 In Euclidean Signature
Setting aside an exhaustive treatment of fibre bundles over manifolds with boundaries, which goes beyond the scope of this article, we will content ourselves with discussing what happens first for \(M\cong D^4\) with a boundary \(S^3\), and then for \(M \cong \mathbb R^4\) complemented with its asymptotic boundary \(B^3_\infty \cong S^3\).
First, we recall that gauge transformations on \(D^4\) induces gauge transformations on \({\partial }D^4=S^3\) that are necessarily connected to the identity (as 3d objects). Armed with this fact, we can already see why our conclusions of gauge-invariance will hold in the bounded case: even if different enough A’s give different Chern-numbers (since they may yield different Chern-Simons terms at the boundary, according to (2.8)), such A’s would not be related by a gauge transformation, as guaranteed by equation (2.12). This proof was easy, but it doesn’t yet get to the bottom of the puzzle, which we can only articulate when expressing such integrals in terms of winding numbers, i.e. Wess-Zumino functionals. And for that, we need boundary conditions guaranteeing that the curvature vanishes,Footnote 23 which we can treat jointly with the asymptotic case.
Topologically, the space \(M \cong \mathbb R^4\) is justFootnote 24 a 4-disk, and we denote it \(\mathbb R^4_\infty \cong D^4\) to emphasize the addition of a sphere at infinity, \({\partial }\mathbb R^4_\infty = B^3_\infty \cong S^3\). The simple remark that \(D^4\) constituted one of two hemispheres in the previous discussion will become useful later.
The gain is that, now, a single chart covers the whole space; the loss is that this raises a puzzle: without any need for a transition function, what is left of the previous arguments we applied for the \(\textsf{WZ}\) term?
As standard, we start by requiring that the field strength vanishes sufficiently fast at infinity to render the Yang-Mills action, supplemented by the \(\theta _{\text {YM}}\) term, finite. This implies in particular that the gauge potential must approach a curvature-free configuration at infinity:
Note that this h need not be seen as a gauge transformation—vanishing curvature guarantees (3.1)—and thus a characterization as “pure gauge” can be misleading. For such an h may still ‘wind around’ the boundary, in which case A cannot be of the form \(A= g^{-1} {\textrm{d}}g \) throughout the region. That is, an A that has non-trivial winding number at the boundary must have curvature in the bulk.Footnote 25
For such an A, from (2.8) and (2.10) one has:
(we avoid the Chern-number notation, \(\textsf{Ch}\), because we do not have a closed base manifold, this preferrence will be maintained in what follows). Again, we know that no gauge transformation—which by definition must be extendible into \(\mathbb R^4_\infty \)—can be large at the boundary, nor can it change the local value of \(\textsf{ch}_A\), and therefore none can change the value of either of the integrals above. This quantity is therefore fully gauge-invariant, just as the left-hand side shows manifestly.
Intriguingly, even in this, single-boundary case, the Wess-Zumino invariant is still an integer! Of course, had we computed the quantity \(\int \textsf{ch}_A\) with arbitrary boundary conditions, we can get any (gauge-invariant) quantity, depending on the boundary conditions. \(\textsf{WZ}_{B^3_\infty }(h)\) is valued in the integers because of the asymptotic conditions required on the gauge potentials, which are necessary for the integral to converge. As before, this integer counts how many times the boundary map \(h:S^3 \rightarrow G\) winds around the group.
A deeper reason why this integral still yields an integer is that, due to the boundary conditions, it can be recast as an integral over a closed manifold, as before. That is, in the Euclidean case being studied here, we can connect the above computations with the previous ones performed for the closed manifold case, at the end of Sect. 2.2. It turns out that given the asymptotic boundary conditions (3.1), there is a “minimal” way to extend the bundle over \(M= \mathbb R^4_\infty \cong D^4\) to a bundle \(\overline{P}\) over a closed manifold \(\overline{M} \cong S^4\) (where we denote the closure by an overbar). Then, with this extension,
To understand \(\overline{P}\), it is enough to observe that the asymptotic boundary conditions (3.1) are just the minimalFootnote 26 requirements to be able to compactify \(\mathbb R^4\) to \(S^4\). If the field strength vanishes at infinity rapidly enough, we can compactify \(\mathbb R^4\) to \(S^4\) by simply adding oneFootnote 27 point at infinity—the North Pole in the stereographic projection of \(S^4\)—and declaring that at this point \(F=0\)—the only value it can assume by continuity. This compactification will take us back to our previously covered example.
3.2 In Lorentzian Signature
But there is still one remaining piece of the puzzle. Much of what we have done is based on an Euclidean-signature intuition for the manifold \(\mathbb R^4_\infty \): the \(\theta _{\text {YM}}\)-term measures the topology of a canonically defined bundle on \(\overline{P} \rightarrow S^4\) and \(\textsf{WZ}_{S^3_\infty }(h)\) measures the winding number of the asymptotic field configuration around the 3-sphere at infinity. Thinking about the Lorentzian case opens new perspectives.
To think about the manifold with Lorentzian signature, we can imagine squishing the boundary at infinity \(B^3_\infty \sim S^3\) from opposite sides, making it look more and more like a ‘thin lens’. This effectively separates the boundary into three components: a past and a future Cauchy surface, \(\Sigma _{\pm }\), and a “celestial sphere” \(S^2_\infty \) at spatial infinity.Footnote 28 Each Cauchy surface supports some (asymptotic) gauge-potential configuration that encodes a classical state of the theory. In our case, these states have half of their support on the northern (southern) hemisphere of \(S^3_\infty \) corresponding to the asymptotic past (future, respectively) Cauchy surfaces.
It is easy to find configurations that are curvature-free at asymptotic past and future infinities, \(\Sigma _{\pm \infty }\). For the same reason as in the previous case,Footnote 29 asymptotic conditions guarantee that the Chern-Simons terms are integer numbers, \(n_\pm \). And due to the fixed orientation of these surfaces, the Chern class gives a difference between these numbers, i.e. \(\int \textsf{ch}_A=n_+-n_-\).
Therefore, in a similar fashion to what we did throughout the paper, we can reconcile the fact that curvature-free boundary states h (3.1) can encode the physical, i.e. gauge-invariant, value of the \(\theta _{\text {\tiny YM}}\)-term—which only depends on the curvature.
To summarize some of these results from different contexts: while it is true that only the curvatures figure in the argument of \(\int \textsf{ch}_A\), this term is only related to Chern-Simons terms on the boundaries of the manifold (cf. (2.8)), and these latter terms do not depend on the curvature. For closed unbounded manifolds, winding numbers appear as differences of Chern-Simons terms at transition patches; for Euclidean bounded manifolds, the boundary is connected and we obtain a single winding-number (that cannot be changed by gauge transformations that properly extend into the bulk); but here, since the configurations are “pure gauge” at disconnected boundaries, we extract winding numbers from each connected boundary Chern-Simons term. The \(\theta _{\text {YM}}\)-term, \(\int \textsf{ch}_A\), will thus be related to a difference of winding numbers due to the inward/outward orientation of the two Cauchy slices with respect to the 4-dimensional bulk.
But, as emphasized after equation (3.1), curvature-free vacuum states with different nontrivial winding numbers,Footnote 30 although perfectly admissible, must include curvature in the bulk. This means that, although the individual boundary winding numbers associated to each boundary are not distinguishable by curvature invariants, transitions between them are. And this is because, crucially, the transition between different curvature-free boundary states with non-trivial winding numbers can never proceed through curvature-free histories.Footnote 31 Within the bulk of spacetime, one has to go through non-vanishing values of F that contribute to \( \textsf{ch}_A\), and values which are uncontroversially encoded in the holonomies.
3.3 Non-trivial Bundle Topology and the \(\theta \)-Vacuum
The quantity \(\int \textsf{ch}_A\) itself is computable even from an eliminativist perspective, since it is fully based on curvature observables encoded e.g. in infinitesimal holonomies. Therefore, even if the eliminativist view is incapable of describing the different, spatial and curvature-free A’s—the different winding numbers,—the integral \(\int \textsf{ch}_A\) could still have physical significance.
A simple comparison can be carried out with the observability of the energy levels of an atom. The energy of a given level—analogously: the winding number of a vacuum state associated to the past component of the boundary—is not a well defined concept, nor a physically meaningful one. Nonetheless the difference between the energies of two different levels are meaningful and physically measurable from the atomic spectra; and these differences are analogous non-vanishing values of the \(\theta _{\text {\tiny YM}}\)-term.
Maybe a more suggestive comparison is the phase of a quantum state in a Hilbert space. Although the phase of a single quantum state is not accessible by measurement (only the state’s ray in Hilbert space is), phase differences between states play a crucial role in quantum mechanics through interference phenomena. Perhaps the closest analogy here is to a Berry phase, where a system described by a certain ray is adiabatically altered and finally brought back to the initial ray. The interesting point is that the initial and final states of the system can have different phases even if they belong to the same ray. The phase difference in this system is encoded in the integral of a quantity over the evolution of the system. In the analogy, the initial flat configuration—corresponding to a ray on Hilbert space—is altered, with curvature being generated, and then it is brought back to the same ‘ray’ or flat configuration: the different winding numbers play the role of the different phases, which is encoded along the 4-manifold.
Indeed, [2, p. 179] makes a very similar analogy:
Models related by a “large” gauge transformation are characterized by different Chern-Simons numbers, and one might take these to exhibit a difference in the intrinsic properties of the situations they represent. But it is questionable whether the Chern-Simons number of a gauge-configuration represents an intrinsic property of that configuration, even if a difference in Chern-Simons numbers represents an intrinsic difference between gauge-configuration. Perhaps Chern-Simons numbers are like velocities in models of special relativity.
These observations then underpin the second role of the \( \theta _{\text {YM}}\)-term. That is, gauge theory allows the existence of distinct boundary states (e.g. initial and final states) that are all curvature-free but labelled by different winding numbers. These boundary states then represent different choices of initial and final vacua for the theory and the \( \theta _{\text {YM}}\)-term can represent, in a semiclassical (“instanton”) approximation, a transition from one such curvature-free boundary state to a different one [15, 16]. That is, as we saw, for asymptotically flat configurations, the Chern number gives a difference between winding numbers, \(\int \textsf{ch}_A=n_+-n_-=:\nu \). If one wants to include configurations with different winding numbers in the path integral, with weight factors \(f(\nu )\) for each sector, one can use the cluster decomposition of expectation values to argue that \(f(\nu )=\exp (i\theta \nu )\), where \(\theta \) is a free-parameter (cf. [4, p. 456]).Footnote 32 Thus the inclusion of the \( \theta _{\text {\tiny YM}}\)-term in the Lagrangian corresponds to allowing a superposition of all winding numbers, and the same parameter in the path integral will be included in the superposition of vacuum states.
Therefore, if the vacuum state can be computed through a path integral, and if this path integral is compatible with the cluster decomposition, one introduces the \(\theta \)-vacuum stateFootnote 33:
which transforms by a phase under shifts of the winding number. Then, each \(\theta \)-vacuum defines an independent sector of the quantum theory. The existence of the state (3.4) is compatible with both the impossibility of distinguishing vacuum states with different winding number (\(|n\rangle \)) from each other via local observables, as well as with the physical significance of the difference between winding numbers.Footnote 34\(\textsf{CS}(A)\).
One important point to observe from this argument, vis à vis eliminativism, is that it is at least a logical possibility to have a representation of \(\mathcal {L}_\theta \) in the physics and yet have no way of discerning the individual winding numbers entering the \(\theta \)-vacuum. That is, we can talk about transitions by appeal to the bulk properties of curvature, and not by appeal to the difference between boundary winding numbers. Indeed, this is what [2, p. 198] is referring to, when he writes: “there is no possibility of introducing a parameter \(\theta \)”. This quote is the sole evidence that [3] provides for Healey’s belief that the holonomy formalism cannot produce a \(\theta \)-term, but, again, it is mistaken. It takes Healey to be referring to the \(\theta \)-term, and not to the \(\theta \)-vacuum. But Healey is indeed referring to the impossibility of introducing individual winding numbers explicitly,Footnote 35 not to the impossibility of writing the \(\theta \)-term in the action in terms of holonomy variables. Furthermore, Healey’s quote goes on citing [8] to clarify that “from the [holonomy] perspective there is no need to introduce any [\(\theta \)] in the first place [even though in principle] one can introduce an arbitrary parameter \(\theta \) in the [holonomy] representation [...]". However, assessing whether the holonomy framework can offer a viable resolution of the \(U(1)_A\)-puzzle requires the introduction of the matter field and is beyond the scope of our discussion. And, moreover, there are other possibilities. Accounting for certain non-perturbative properties of the quantization of a gauge system [10, Ch. 3], one can provide an explanation of chiral symmetry breaking without either introducing Goldstone bosons nor invoking the topology of P as encoded in the \(\theta _{\text {YM}}\)-term. We discuss this in appendix B.
Here, we should again emphasize: in this paper, our intent was not to examine the full, non-perturbative quantum picture, nor [8]’s claims, nor their relation to [2]’s, and thus we have refrained from assessing the significance of the \(\theta _\text {\tiny YM}\)-term in these respective domains. Our intent was rather to correct a mistake in the treatment of gauge in the semiclassical picture—i.e. whether the \(\theta _{\text {YM}}\)-contribution to the Yang-Mills action is gauge invariant and can be accounted for in an eliminativist frameworkFootnote 36—irrespective of whether this picture, on its own, provides a completely satisfactory account of chiral symmetry breaking or not.
4 Conclusions
4.1 Summary of our discussion
About the eliminative view and the gauge-invariant properties of the \(\theta _{\text {YM}}\)-term, [3, p. 16] concludes:
[I] showed that if the eliminative view were true then the vacuum Yang-Mills \(\theta _{\text {YM}}\)-term [(2.1)] [...] would lead to inconsistency when integrated over any region [...] By Stokes’ theorem it is a matter of mathematical fact that this integral coincides with the integral of \(\textsf{cs}_A\). But this integral varies under large gauge transformations. So if I were to eliminate gauge from the theory then each configuration would be assigned contradictory values for the vacuum Yang-Mills term of the action: one for each class of representative gauge potentials that differ by a large gauge transformation.
Our discussion has explained, qualified, and rectified Dougherty’s statement.
The \(\theta _{\text {YM}}\)-term is manifestly gauge-invariant under all gauge transformations, as shown in Sect. 2. This is just a consequence of the cyclic trace identity and the transformation properties of the curvature—and Stokes’ theorem cannot change this fact.
Nonetheless, we felt it was important to explain some sources of confusion surrounding the \(\theta _{\text {YM}}\)-term. For instance, it may be expressed as Wess-Zumino integrals on gluing surfaces, and the arguments of these integrals look like gauge transformations. So doesn’t that indicate their gauge-variance, contrary to the brute fact mentioned above?
This puzzle is solved once we take into account that the arguments of these integrals on the gluing surfaces are transition functions, and not gauge transformations, and that in fact, non-trivial transition functions cannot be trivialized by gauge transformations. Gauge transformations are smooth, and they are associated to charts of the manifold. These two simple requirements mean gauge transformations cannot affect the value of the integral of \(\textsf{cs}_A\) on the boundary of the manifold: in accordance with the invariance of the Chern number.
Every difference that is attributed, in this loose manner of speaking, to ‘large gauge transformations’, has a gauge-invariant explanation solely in terms of curvature; and holonomies are sensitive to curvature
The same conclusion holds for asymptotic boundaries, for configurations that are asymptotically curvature-free. The only way to obtain a non-trivial winding number at the asymptotic boundary requires a non-vanishing curvature for A in the bulk—A is not a “pure-gauge” configuration. That is how the winding number can be represented by the \(\theta _{\text {YM}}\)-term—which depends only on the curvature. In Lorentzian signature (with appropriate boundary conditions at spacelike infinity) this means that transitions over time between winding numbers must be associated with curvature at some point in time.
[3] equivocates between the invariance of the \(\theta _{\text {YM}}\)-term and the variance of the Chern-Simons \(\textsf{cs}_A\). We have shown that there is no equivocation, since the equality of the two requires \(\textsf{cs}_A\) to be integrated over a boundary, and this quantity does not vary under bona-fide gauge transformations either.
Instead of this explanation for the discrepancy, Dougherty invokes a “size distinction”. The distinction in question is one between gauge transformations that may act solely on the boundary from those whose action on the boundary must be a smooth extension of those acting on the bulk. The relevance of this distinction assumes there is a choice to be made here, on whether to accept gauge transformations as acting solely on the boundary of the manifold or not. Moreover, [3] ties the eliminativist to the more permissive choice, where the action of any group-valued function supported on the boundary—whether a bona-fide gauge transformation or not—is interpreted as a viable gauge transformation. We have shown that this view is mathematically inconsistent. To be as clear as possible: no such choice exists. A size-distinction would lead to two different and incompatible notions of gauge. A boundary transformation that changes the (total) winding number cannot be extended to a bulk transformation that sends one solution of the equations of motion to another—as a gauge transformation would—and therefore this transformation cannot be called ‘a symmetry’, and is thus not an option the eliminativist can embrace.
Now we are equipped to answer [3, p. 16]’s two following rhetorical questions in the conclusions of his paper: “[It is] not enough to simply make an exception for large gauge transformations. Do we make an exception for any gauge transformation that’s nontrivial on the boundary of any region? Only those on the sphere at infinity that also spoil the gauge invariance of the vacuum Yang-Mills term?” We can say, respectively: “No, allow gauge transformations that are non-trivial at the boundary; and yes, we can exclude those that spoil gauge-invariance, but we would do so without making an exception, since the latter are not gauge transformations, and the effect that you attribute to these transformations are perfectly well encoded in the bulk curvature—which is explicitly contained in the holonomies.” Had this not been so, the \(\theta \)-term could never figure in lattice QCD—a formalism that employs holonomies as its basic variables. But of course, these terms frequently appear in this formalism (see [9] and references therein).Footnote 37
While it is true that on a manifold with asymptotic boundaries one can nonetheless use Stokes’ theorem to extract interesting and nontrivial features of the vacuum structure of Yang-Mills theory, none of these features provide a smoking gun against the eliminative view of gauge.
In sum, the eliminativist view, and the holonomy interpretation [2], is perfectly capable of encoding a non-zero \(\theta _{\text {YM}}\)-term in the action functional. Whether it needs to do this to resolve the \(U(1)_A\) puzzle, or whether it has an alternative route as claimed by [8], is a different story, that goes beyond the scope of this paper.
4.2 Against eliminativism nonetheless
Having arrived at the end of this paper, we can smoke a peace-pipe with Dougherty. As tobacco acceptable to both parties, we notice that the most developed understanding of the solution to the U\((1)_A\)-puzzle (i.e. the breaking of chiral symmetry without the introduction of Goldstone bosons), requires the physical significance of structures associated to the existence of the gauge symmetry: be it the role of the fibre bundle topology in the standard semi-classical account, or the role of different connected components of \(\mathcal {G}_3\) in the non-perturbative one. In both cases, the arguments militate against any naive implementation of eliminativism.
More broadly, eliminativism about gauge fields is unwarranted for many reasons, some of which we now briefly summarize. Gauge degrees of freedom simplify mathematical treatments of physical theories by allowing us to write our theories in terms of Lorentz-invariant action functionals (and path integrals): there is no available local Hamiltonian or Lagrangian, even in the Abelian case (i.e. electromagnetism) that employs only electric and magnetic fields.
Moreover, as a guide to theory-building, gauge degrees of freedom are introduced to mandate the local Gauss law: action functionals that employ them automatically ensure both the local Gauss law and charge conservation. At a pedestrian level, they guarantee that the details of the dynamics of the forces that interact with the charges will preserve the conservation of charge [17]. In this sense, gauge degrees of freedom fill an explanatory gap: they guarantee conservation laws and provide a framework by which to build theories that automatically respect these laws.
Fibre bundles provide a yet deeper, geometrical explanation of these degrees of freedom. Fibre bundles—and the connection and its curvature—allow us to formalize the notion that certain properties that are taken as, in a certain sense, “intrinsic”, such as “being a proton”, are in fact relational.
General relativity is relational in a similar way, and, similarly, has a good deal of structure that could be construed as eliminable. But, we would wager, most eliminativists are reluctant to limn that redundant structure (Healey certainly is, cf. [2, Ch. 4.2]). The parallel becomes blatant once we formulate general relativity in terms of connection forms (see footnote 14). As discussed at length by [18], applying the principal fiber bundle formalism to general relativity puts coordinate and gauge transformations on a par. Indeed, the Chern-number can also be calculated for a connection associated to parallel transport of tangent vectors on spacetime, where it bears many of the same properties as the more general Chern-number, associated to parallel transport of general vector bundles over spacetime.
More broadly, viz à viz eliminativism we see no relevant disanalogy between gauge fields and metrics, due to the simple fact that in the spacetime case there is certainly redundancy of mathematical representation (in that case, of geometry through the metric). But there most would agree this redundancy does not warrant a complete elimination of spacetime metrics from our theories. We see no reason to distinguish, in this aspect, gauge and gravitational theories.
We believe empirical signatures of the \(\theta \)-term are certainly compatible with, if not explained by, the reality of certain non-trivial topological, relational properties of the bundle.Footnote 38 Although this is not contrary to eliminativism—as already emphasized the \(\theta \)-term can be computed by means of holonomy variables—the holonomy formalism is certainly not the most perspicuous language in which to articulate these properties.
In sum, gauge degrees of freedom fill an explanatory gap, have a neat relationist interpretation, and are thoroughly warranted if we value consilience with other important theoretical structures of physics, such as Hamiltonians, actions, Lorentz invariance, etc. Demands for their complete elimination from our theoretical description of nature seems to ignore the criteria by which we interpret theories. However, a less sanguine deflation of their ontological status, that ascribes to them only relational status and relies on Leibniz equivalence to count/discern physical possibilities, is warranted. And such a position sits well with a via media position in the debate between spacetime substantivalism and relationism.
Notes
The most notorious proponent of eliminativism within the philosophy of physics community is Richard Healey, whose position is laid out in [2].
This solution, however, might not be appropriate in a non-perturbative treatment. See section B.
This is the standard argument first put forward by Fujikawa (cf. [5, Sec. 5.2] or [4, Sec. 22.2]). Now, the \(\theta _{\text {\tiny YM}}\text {-term}\) is a functional of the curvature, \(F_{\mu \nu }\), so why does it appear in a change in the measure of purely fermionic degrees of freedom? In Fujikawa’s implementation of a gauge covariant measure, one writes the fermion field in terms of a basis of eigenfunctions of the Dirac operator,
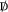 , which includes the gauge-covariant derivative \( {\textrm{D}}_\mu = {\partial }_\mu + A_\mu \), inside it (i.e.
, which includes the gauge-covariant derivative \( {\textrm{D}}_\mu = {\partial }_\mu + A_\mu \), inside it (i.e. 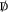 , where \(\gamma ^\mu \) are the Dirac gamma matrices). It then turns out that the determinant of the Jacobian under a chiral transformation in this orthonormal basis diverges and needs to be regularized. Fujikawa used a gauge-covariant Gaussian cut-off by insertion of the operator
, where \(\gamma ^\mu \) are the Dirac gamma matrices). It then turns out that the determinant of the Jacobian under a chiral transformation in this orthonormal basis diverges and needs to be regularized. Fujikawa used a gauge-covariant Gaussian cut-off by insertion of the operator 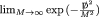 . Ultimately, the curvature appears through the decomposition:
. Ultimately, the curvature appears through the decomposition: 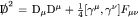 . One can choose instead a gauge-invariant measure, in which case the anomaly is shifted to renormalization counterterms (which then necessarily fail to satisfy the same invariances of the Lagrangian, [6, vol 2, ch.28]).
. One can choose instead a gauge-invariant measure, in which case the anomaly is shifted to renormalization counterterms (which then necessarily fail to satisfy the same invariances of the Lagrangian, [6, vol 2, ch.28]).Briefly, the field redefinitions above—modifying the definitions of the quarks by a chiral transformation—shift the coupling constant in front of the \(\theta _{\text {YM}}\)-term in the Yang-Mills Lagrangian: calling the coupling constant \(\theta \), they undergo a shift \(\theta \mapsto \theta + \sum _f \alpha _f\). But such field-redefinitions do more than that: they also change the mass terms in the Lagrangian density by \(m_f\mapsto \exp (i2\alpha _f)m_f\). Since physical quantities cannot be affected by a mere field-redefinition, this means that the only invariant quantity physical systems can depend on is the product \(e^{- i \theta } \prod _f m_f\) (cf. [4, Sec. 23.6]). This product defines an invariant version of the \(\theta \)-coupling, called \(\overline{\theta }\). Thus, if one flavor of quarks had zero mass, the puzzle would be resolved, since the product would, contingently, vanish. That doesn’t seem to be the case. Nonetheless, \(\overline{\theta }\) is observationally constrained to be close to zero: the current bound on \(\overline{\theta }\) is \(|\overline{\theta }|<2 \times 10^{-10}\) according to the particle data group (see [7]). The question of theoretical necessity of the \(\overline{\theta }\)-term hinges on important issues of naturalness and fine-tuning, and, since there is currently experimental reason to believe that it vanishes, one might feel compelled to explain its observational smallness. That is, what physicists refer to as the “Strong CP problem”—that Nature conspires to give the CP-violating \(\overline{\theta }\)-term a value close to zero—is a real problem that still lacks an agreed explanation (axions provide a possible mechanism, cf. [4, Sec. 23.6] and references therein). But Dougherty does not base his argument on the issue of explanation for the smallness of \(\overline{\theta }\).
We do not want to assess [8]’s claim; we mention it only for context.
See the previous quote from [3, p. 1] or, as well: “[a certain] gauge transformation is ‘large’ in the sense that it is nontrivial on the boundary of the region of integration. In particular, if we demand that the configuration be pure gauge at infinity then a large gauge transformation is one that is nontrivial at infinity, recovering the usual statement of the size distinction" [3, p. 9].
A proof of this mathematical fact is reviewed in Sect. 2.2, while a more concise argument is given below.
Twice-differentiable is sufficient for our purposes.
We will deal with the general case in the following sections.
Compatibility is here understood in the sense of equations (A.5).
Compatibility is here understood in the sense of equations (A.3).
Notice that it is possible to change \(\omega \) (resp \(A_\alpha \)) without changing P (resp \(\sigma _\alpha \) and \(\mathfrak {t}_{\alpha \beta }\)).
Topological invariants written in terms of local fields are well-known in the spacetime case, i.e. for M. Indeed, the Chern-number also applies to metric fields, from which we can obtain topological properties of M. In that context, the Chern theorem states that the Euler-Poincaré characteristic of a closed even-dimensional Riemannian manifold is equal to the integral of the Euler class. In practice, one replaces the gauge-curvature F in the definition of \(\textsf{Ch}[P]\) by a metric curvature (associated to a spin-connection: i.e. given an orthonormal basis of the tangent bundle, \(e_a\), the spin connection \(\textsf{w}^b_a\) is defined as \({\textrm{d}}e_a=\textsf{w}^b_a e_b\), and can again be identified with a \(\mathfrak {so}(n)\)-valued one-form obeying the usual properties. Curvature is defined analogously).
The proof is simple: \(\text {tr}(g^{-1}Fg\wedge g^{-1}F g)=\text {tr}(g^{-1}F\wedge F g) =\text {tr}( Fg \wedge g^{-1}F)=\text {tr}(F\wedge F)\).
For consistency, one should also check that the the 3-form \(\int _0^1\text {tr}(\gamma \wedge F_s){\textrm{d}}s\) is well defined, i.e. gauge-invariant. That this is the case follows from the fact that the difference \(\gamma \) between two connections transforms in the adjoint representation under gauge transformations, just like F, and therefore \(\text {tr}(\gamma \wedge F_s)\) is point-wise gauge-invariant for all values of s. (cf footnote 15).
In fact, the 4-form \(\text {tr}(F\wedge F)\) is closed in any dimensions as a consequence of the Bianchi identity, \({\textrm{d}}_AF=0\), where \({\textrm{d}}_A\) is the gauge-covariant exterior derivative.
This is easy to show:
$$\begin{aligned} 8\pi ^2 {\textrm{d}}\textsf{cs}_A= & {} {\textrm{d}}{\text {tr}}(A\wedge {\textrm{d}}A+\tfrac{2}{3}A\wedge A\wedge A)={\text {tr}}({\textrm{d}}A\wedge {\textrm{d}}A+2A\wedge A\wedge {\textrm{d}}A)\\= & {} {\text {tr}}(({\textrm{d}}A+A\wedge A)\wedge ({\textrm{d}}A+ A\wedge A))= 8\pi ^2 \textsf{ch}_A, \end{aligned}$$where in going from the first to the second line we used (2.7) to infer that \(\text {tr}(A\wedge A\wedge A \wedge A)\equiv 0\).
The Chern-Simons functional understood as the action for a 3d boundary theory, defines a classical theory of connections that is invariant only under gauge transformations that are not: large in the sense of (i) in Sect. 1.3. However, quantum mechanically, the situation can be improved, and the Chern-Simons functional can define a theory which is invariant under all gauge transformations, provided the coupling constant, i.e. the Chern-Simons “level”, is chosen to be an integer. This is because under large gauge transformations, the Chern-Simons action changes at most by a multiple of \(2\pi \)—hence allowing the Feynman’s path integral to still be invariant. This peculiarity lies at the root of the fascinating phenomenology of Chern-Simons theory and its quantum-deformed symmetry structure.
This is a corollary of the fact that \(\text {tr}(A\wedge A \wedge A \wedge A)\equiv 0\) (see footnote 18), since \({\textrm{d}}(g^{-1} {\textrm{d}}g) = - g^{-1} {\textrm{d}}g \wedge g^{-1} {\textrm{d}}g\).
From equation (2.11) and the the Poincaré lemma, \(\textsf{wz}_g \) is exact on a contractible manifold. However, since there are no compact manifolds without boundary—i.e. closed manifolds—which are contractible (cf. Exercise 2.4.6 in [13]), one can never use this observation to conclude that the integral of \(\textsf{wz}_g\) vanishes on the (closed) boundary of a four manifold—e.g. \(S^3=\partial D^4\).
It is clear that transformation which are not smooth to some degree are not allowed. Here we only need them to be at least \(C^2\).
Note that, for internal boundaries, i.e. for the intersection between charts, we can express the integrals in terms of Wess-Zumino integrals, as in (2.8), because it depends on the difference between two Chern-Simons functionals, and smoothness guarantees that this difference can be expressed purely in terms of the transition functions; i.e. Lie-group valued functions.
Following Penrose (cf. [14, Ch. 5]), the physically meaningful way to complement \(\mathbb R^4\) with a boundary depends on its metric (which so far has played no role whatsoever in our considerations). The choice followed here corresponds to the Euclidean 4-dimensional world, rather than a Minkowskian one (which requires the introduction of five different typologies of asymptotic boundaries: future and past time-like infinity, future and past null infinity, and spatial inifinity). However, ignoring this complication might be justified since the metric one picks on \(\mathbb R^4\) does not matter for the computation of the \(\theta _{\text {YM}}\)-term. Indeed, the computation in [4, Sec. 23.6] also disregards these subtleties. However, we personally find this argument not completely satisfactory. For now, we leave this subtle point aside.
The proof follows the one showing a gauge transformation can only have a trivial winding number, in the previous Section.
Here we are ignoring subtleties related to rapidity of the fall-offs at infinity and smoothness in the compactified manifold.
As opposed to a three-sphere.
See however footnote 24.
Together with assumptions about the field behaviour at spatial infinity, see e.g. [4, Ch. 23.5 p. 454-455].
Extra conditions at \(S_2^\infty \) may be needed to have well defined winding numbers on the past and future Cauchy surfaces independently. We will ignore this issue, since we can resolve the puzzle without it.
This follows from the same arguments exposed below equation (2.16).
Cluster decomposition is the assumption that far away processes do not influence expectations values of local observables. This holds only if the path integral appropriately factorizes over spacetime regions. The conclusion then follows from the additivity of the instanton number \(\nu \) over spacetime regions, since this yields the requirement \(f(\nu _1 + \nu _2) = f(\nu _1) \times f(\nu _2)\). Notice that the factorization of the instanton number requires some approximations (curvature-freeness at the interface between the regions). However, this heuristic argument is supported by more rigorous considerations of the path integral in the presence of chiral fermions—cf. footnotes 3 and 4 and references therein.
For an algebraic, non-perturbative, argument supporting this conclusion see Appendix B.
Indeed, a global observable that is capable of this type of distinction is.
For an explicit example consider G-valued transformations over \(S^3\), with \(G=\textrm{SU}(2)\). Then there exists a \(h:S^3\rightarrow G\) with nontrivial winding number. Nonetheless, since \(S^3\) is simply connected all holonomies built out of the connection \(A = h^{-1}dh\) are equal to the identity, regardless of whether h has a nontrivial winding number or not.
Once again, we refer to the QCD literature for a concrete construction [9].
Of course, these lattice computations should be understood as a Riemann-sum approximation of the \(\theta \)-term integral.
Although it may be significantly harder to constrain topological features of spacetime, there exist proposals to look for experimental signatures of non-trivial spacetime topologies. For instance, the ‘circles in the sky’ in the CMB would have constituted such a signature [19]. Another example of a global property of spacetime which can be seen as relational is its dimensionality. On the gauge bundle side, we have e.g. the charge group of the gauge theory. These examples make it clear that employing holonomies as the fundamental variable need not be either eliminativist or substantivalist. For more on how relations between subsystems are related to redundant degrees of freedom, see [20, 21].
Of course this example, which originally motivated Yang and Mills, is meant in the context of the (approximate) isospin symmetry. Otherwise, the electric charge tells protons and neutron apart in an intrinsic manner.
Given p, the inverse map is a bit more complicated because we must find \(g'\) such that \(g'\cdot p=\sigma (x)\), for some x. It will depend on the form of \(\sigma \).
Given an element of the Lie-algebra \(\mathfrak {g}\), we define the vertical space \(V_p\) at a point \(p\in P\), as the linear span of vectors of the form \(v_{\xi }(p):=\frac{d}{dt}{}_{|t=0}(\exp (t\xi )\cdot p)\) for \(\xi \in \mathfrak {g}\). And then the conditions on \(\omega \) are:
$$\begin{aligned} \omega (v_\xi )=\xi \qquad \text {and}\qquad g^*\omega =g^{-1}\omega g, \end{aligned}$$where \(g^*\omega _p(v)=\omega _{g\cdot p}(g_* v)\) where \(g_*\) is the push-forward of the tangent space for the map \(g:P\rightarrow P\). A choice of connection is equivalent to a choice of covariant ‘horizontal’ complements to the vertical spaces, i.e. \(H_p\oplus V_p=T_pP\), with H compatible with the group action.
The set of all \(g_\alpha \)’s on a given \(U_\alpha \) defines \({\mathcal {G}}_\alpha :=\{g_\alpha (x)\}\), which inherits from G the structure of an (infinite-dimensional) Lie-group, by pointwise extension of the group multiplication of G over \(U_\alpha \).
The instability mentioned in this quote is due to the fact that the chiral symmetry acts as what we could call a “meta-symmetry” between different \(\theta _{\text {YM}}\)-vacua, \(\theta \mapsto \theta +\lambda \). Key to the consistency of this formulation is the fact that the limit \(\lambda \rightarrow 0\) is not properly defined (i.e. the symmetry is not implemented in a weakly continuous way).
Cf. [24].
References
Earman, J.: Laws, symmetry, and symmetry breaking: Invariance, conservation principles, and objectivity. Philos. Sci. 71(5), 1227–1241 (2004)
Healey, R.: Gauging What’s Real: The Conceptual Foundations of Gauge Theories. Oxford University Press, Oxford (2007)
Dougherty, J.: Large gauge transformations and the strong cp problem. Stud. Hist. Philos. Mod. Phys. 37, 2020 (2019)
Weinberg, S.: The Quantum Theory of Fields. Volume 2 Modern Applications. Cambridge University Press, Cambridge (2005)
Bertlmann, R.: Anomalies in Quantum Field Theory. Springer, New York (1996)
DeWitt, B.S.: The Global Approach to Quantum Field Theory, Vol. 2 (Vol. 114). Clarendon Press, Oxford (2003)
Tanabashi, M., et al.: Review of particle physics. Phys. Rev. D 98(3), 030001 (2018). https://doi.org/10.1103/PhysRevD.98.030001
Fort, H., Gambini, R.: U(1) puzzle and the strong cp problem from a holonomy formulation perspective. Int. J. Theor. Phys. 39(2), 341–349 (2000)
Kan, A., Funcke, L., Kühn, S., Dellantonio, L., Zhang, J., Haase, J. F., . . . Jansen, K. (2021). 3+1D \(\theta \)-Term on the Lattice from the Hamiltonian Perspective
Strocchi, F.: Symmetry breaking in the standard model: a non-perturbative outlook. Springer lecture notes (2019)
Nakahara, M.: Geometry, Topology and Physics. CRC Press, Boca Raton (2003)
Schäfer, T., Shuryak, E.V.: Instantons in QCD. Rev. Mod. Phys. 70, 323–426 (1998). https://doi.org/10.1103/RevModPhys.70.323
Guillemin, V., Pollack, A.: Differential Topology. AMS Chelsea Pub. Retrieved from https://books.google.co.uk/books?id=FdRhAQAAQBAJ (2010)
Hawking, S. W., Ellis, G.F.R.: The Large Scale Structure of Space-Time (Cambridge Monographs on Mathemat- ical Physics). Cambridge University Press. Retrieved from http://www.amazon.com/Structure-Space-Time-Cambridge-Monographs-Mathematical/dp/052 (1975)
Belavin, A., Polyakov, A., Schwartz, A., Tyupkin, Y.: Pseudoparticle solutions of the yang-mills equations. Phys. Lett. B 59(1), 105–111 (1975)
Hooft, G.: Computation of the quantum effects due to a four-dimensional pseudoparticle. Phys. Rev. D 14, 3432–3450 (1976). https://doi.org/10.1103/PhysRevD.14.3432
Gomes, H., Roberts, B.W., Butterfield, J.: The Gauge Argument: A Noether Reason. In J. Read & N. J. Teh (Eds.), The philosophy and physics of noether’s theorems: A centenary volume (pp. 354–376). Cambridge University Press (2022). https://doi.org/10.1017/9781108665445.015
Weatherall, J.: Fiber bundles, Yang-Mills theory, and general relativity. Synthese 193(8), 2389–2425 (2016)
Cornish, N.J., Spergel, D.N., Starkman, G.D.: Circles in the sky: finding topology with the microwave background radiation. Class. Quant. Gravity 15(9), 2657–2670 (1998)
Gomes, H.: Gauging the boundary in field-space. Stud. Hist. Philos. Sci. Part B (2019). https://doi.org/10.1016/j.shpsb.2019.04.002
Rovelli, C.: Why Gauge? Found. Phys. 44(1), 91–104 (2014). https://doi.org/10.1007/s10701-013-9768-7
Kobayashi, S., Nomizu, K.: Foundations of Differential Geometry, Vol I. Interscience Publishers, a division of John Wiley & Sons, New York
Yang, C.N., Mills, R.L.: Conservation of isotopic spin and isotopic gauge invariance. Phys. Rev. 96, 191–195 (1954)
Strocchi, F.: Symmetries. Symmetry Breaking, Gauge Symmetries (2015)
Acknowledgements
HG would like to thank Jeremy Butterfield and Bryan Roberts, for patiently reading the manuscript and providing very valuable feedback. During the completion of this project AR has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 801505, as well as from Perimeter Institute for Theoretical Physics. Research at Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Research and Innovation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: A brief introduction to fibre bundles
The modern mathematical formalism of gauge theories relies on the theory of principal (and associated) fibre bundles. We will not give a comprehensive account here (cf. [22]), but only introduce the necessary ideas and objects. With fiber bundles, we can formalize the notion that certain properties that are taken as, in a certain sense, “intrinsic,” such as “being a proton,” are in fact relational. But these relations can have topological, i.e. global features.
The main idea underlying the physical significance of the fibre in a fibre bundle is perhaps best summarized in the original paper by [23]:
The conservation of isotopic spin is identical with the requirement of invariance of all interactions under isotopic spin rotation. This means that when electromagnetic interactions can be neglected, as we shall hereafter assume to be the case, the orientation of the isotopic spin is of no physical significance. The differentiation between a neutron and a proton is then a purely arbitrary process. As usually conceived, however, this arbitrariness is subject to the following limitation: once one chooses what to call a proton, what a neutron, at one space-time point, one is then not free to make any choices at other space-time points.
That is, what is a proton and what is a neutron at a given point is essentially a relational property.Footnote 39
The limitations on how to identify “a proton” at two different points of spacetime are imposed by a connection-form: another structure on the bundle. That is, a connection-form \(\omega \) allows us to define which points of neighbouring fibres can be taken as equivalent to an arbitrary starting-off point in an initial fibre. Curvature then acquires meaning as non-holonomicity, i.e. as a path-dependence intrinsic in this fibre-identification procedure. That is, the bundle carries relational properties which are captured by certain function(al)s of the connection, e.g. the curvature.
We are now going to formalize this intuitive description.
1.1 Principal fibre bundles
A principal fibre bundle is a smooth manifold P that admits a smooth action of a (path-connected, semisimple) Lie group, G, i.e. \(G\times P\rightarrow P\) with \((g,p)\mapsto g\cdot p\) for some action \(\cdot \) and such that for each \(p\in {P}\), the isotropy group is the identity (i.e. \(G_p:=\{g\in {G} ~|~ g\cdot p=p\}=\{e\}\)). Naturally, we construct a projection \(\pi :P\rightarrow {M}\), given \(p\sim {q}\Leftrightarrow {p=g\cdot {q}}\) for some \(g\in {G}\). So the base space M is the orbit space of P, \(M=P/G\), with the quotient topology, i.e.: characterized by an open and continuous \(\pi \). By definition, G acts transitively on each fibre.
Locally over M, it must be possible to choose a smooth embedding of the group identity into the fibres. That is, for \(U\subset M\), there is a map \(\sigma : U\rightarrow P\) such that P is locally of the form \(U\times G\), i.e. there is an isomorphism \(U\times G\rightarrow \pi ^{-1}(U)\) given by \((x, g)\mapsto g\cdot \sigma (x)\).Footnote 40 The maps \(\sigma \) are called local sections of P.
On P, we consider an Ehresmann connection \(\omega \), which is a 1-form on P valued in the Lie algebra \(\mathfrak {g}\) that satisfies appropriate compatibility properties with respect to the fibre structure and the group action of G on P.Footnote 41 This connection allows us to locally define “horizontal complements” to the fibres in P (see footnote 41). Through such complements one can horizontally lift paths \(\gamma \) in M to P. These horizontally lifted paths are commonly referred to as “parallel transports" in P along \(\gamma \) with respect to (horizontality as defined by) \(\omega \). As you go around a closed curve in M, parallel transport on P is called the holonomy of \(\omega \) along the closed path \(\gamma \). Its infinitesimal expression is the curvature of \(\omega \),
where \({\textrm{d}}_{{\tiny {P}}}\) is here the exterior derivative on the smooth manifold P, and \(\wedge _{{\tiny {P}}}\) is the exterior product on \( \Omega ^\bullet (P)\) (which is not to be confused with the notation for the curvature 2-form on P, used in (A.1)); it gives anti-symmetrized tensor products of differential forms.
1.2 Gauge transformations v. Transition functions
Given local sections \(\sigma _\alpha \) on each chart \(U_\alpha \), i.e. maps \(\sigma :U_\alpha \rightarrow P\) such that \(\pi \circ \sigma _\alpha = \textrm{id}\), we define A as the pullback of the connection, \(A_\alpha :=\sigma _\alpha ^*\omega \in \Omega ^1(U_\alpha , \mathfrak {g})\) (here \(\alpha \) is a chart index, not a spacetime one). Since the differential and the pullback operation “commute”, we also have:
where now \({\textrm{d}}\) and \(\wedge \) are the familiar exterior derivative and products in \(\Omega ^\bullet (M)\).
Notice that contrary to \(\omega \) and \(\Omega \), the \(A_\alpha \)’s and \(F_\alpha \) are defined over charts of the spacetime M, rather than the bundle P. The price to pay is the introduction of: (a) an (arbitrary) choice of section, and (b)—since global sections might not exist in general—an atlas of charts over M and a corresponding set of \(A_\alpha \)’s.
In other words, although \(\omega \) is globally defined on P, the \(A_\alpha \)’s are only defined on the respective charts \(U_\alpha \) of M through the choice of a local section \(\sigma _\alpha \). At fixed \(\omega \), and on a given chart \(U_\alpha \), different choices of section give \(A_\alpha \)’s related by a gauge transformation. The demand of gauge invariance reflects the arbitrary nature of the choice of section. We will come to this in a moment; first we need to worry about how to patch the charts together.
Given an atlas of charts \(U_\alpha \subset M\), this patching requires us to consider transition functions which relate the \(A_\alpha \)’s to each other on the overlaps \(U_{\alpha \beta }=U_\alpha \cap U_\beta \):
where
These transformation properties translate between choices of local sections across overlapping charts, and must satisfy the cocycle conditions (compatibility over threefold overlaps \(U_{\alpha \beta \gamma }=U_\alpha \cap U_\beta \cap U_\gamma \)):
Transition functions look similar to gauge transformations, and indeed act very similarly on the gauge potentials. These similarities reflect the fact that, on the overlap \(U_{\alpha \beta }\), both \(A_\alpha \) and \(A_\beta \) descend from the same \(\omega \) through different choice of sections—and, as we will now discuss, the role of gauge transformations is precisely to translate between different choices of sections, \(\sigma _\alpha \) and \(\sigma _\beta \).
Gauge transformations (i.e. changes of local sections) are encoded in mapsFootnote 42
that act on the respective \(A_\alpha \) and \(\mathfrak {t}_{\alpha \beta }\)’s as follows:
from which one derives using (A.2):
Notice that both the connection and the transition function transform under the action of a gauge transformation \(g_\alpha \). Thus, under a gauge transformation on \(U_\alpha \), equation (A.3) describing the relation between \(A_\beta \) and \(A_\alpha \), is left invariant. This is the basic reason why the transition functions collectively encode the global properties of the bundle P while the gauge transformations are simply redundancies.
Besides the fact that gauge transformations act on transition functions and not vice versa, another crucial distinction between gauge transformations and transition functions, that underlies their different roles, is that the domain of the gauge transformations \(g_\alpha \)’s is the whole of \(U_\alpha \), whereas that of \(\mathfrak {t}_{\alpha \beta }\) is a subset of \(U_\alpha \) (viz. its overlap with \(U_\beta \)).
We reiterate that the introduction of transition functions is generally necessary because, global sections do not exist unless the bundle is trivial, i.e. unless \(P= M \times G\) globally not just locally. In the trivial case, and only in the trivial case, all transition functions can be trivialized to be the identity, i.e. \(\mathfrak {t}_{\beta \alpha } = g_\beta g_\alpha ^{-1}\) for some choices of \(g_\alpha \)’s (and which thus can be themselves trivialized by gauge transformations in each domain). Only then, equation (A.3) is trivialized and the collection of \(A_\alpha \)’s yields a global gauge potential 1-form A.
Appendix 2: Non-perturbative approaches
A non-perturbative account of the chiral symmetry breaking mechanism which does not rely on topological features of the field configurations might be more satisfying (although perhaps not necessary). In this non-perturbative account, it is rather the topology of the gauge group that plays a crucial role.
Indeed, in the non-perturbative account of [10, Ch. 3], chiral symmetry is not “explicitly broken”, but rather gives rise to what one could roughly characterize as a “meta-symmetry” between non-communicating (\(\theta \)-)sectors of the theory. These sectors are labeled by their transformation properties under central elements of the algebra of observables which correspond to the equivalence classes \( T \in {\mathcal {G}}_3/{\mathcal {G}}_3^o\) of gauge transformations in \({\mathcal {G}}_3\) including those which are not connected to the identity modulo the ones that are connected to the identity, \( {\mathcal {G}}_3^o\subset {\mathcal {G}}_3\) (here \({\mathcal {G}}_3\) we refer to the residual time-independent gauge symmetries not fixed by the choice of temporal gauge, e.g. in a globally hyperbolic universe with a spatial slice \(S^3\), \({\mathcal {G}}_3 = C^\infty (S^3,G)\)). The technical, but crucial, ingredient entering this account is the non-weakly-continuous nature of the representation of the symmetries on the Hilbert space.
In more detail: the vacuum must be a representation of \( \mathcal {T} = {\mathcal {G}}_3/{\mathcal {G}}_3^o\) since the associated topological invariants define elements in the center of the Lie algebra of operators (see quote below). The idea is that the algebra of observables has a center given by operators that shift the winding number \(T_m|n\rangle = |n+m\rangle \), which forms an abelian group \(\mathcal {T}\) in the center of the algebra of observables. This means that the Hilbert space must provide an irreducible representation of \(\mathcal {T}\). Formally, the vacuum state is then a superposition \(|\theta \rangle \) of the \(|n\rangle \) “vacua”, with \(\theta \) as the label of the irreducible representation. The \(\theta =0\) vacuum then defines a sector in which all transformations in \({\mathcal {G}}_3\)—and not only the infinitesimally generated ones—act trivially.
Indeed, this entirely non-perturbative resolution of the U\((1)_A\)-puzzle avoids the topological properties of the bundle; rather, it resorts to topological properties of the group of (time-independent) gauge transformations \(\mathcal G_3\) that survive the imposition of temporal gauge.
As [24, p.12] explains:
The topological invariants [of the group of local gauge transformations \( \mathcal G_3\)] define elements of the center of the local algebra of observables; for Yang-Mills theories such elements [...] are labeled by the winding number [...] their spectrum labels the factorial representations of the local algebra of observables, the corresponding ground states being the \(\theta _{\text {YM}}\)-vacua. They are unstableFootnote 43 under the chiral transformations [...] and therefore chiral transformations are inevitably broken [within each factorial representation (sector) defined by a choice of \(\theta _{\text {YM}}\)-vacuum ...] Thus, the topology [of \({\mathcal {G}}_3\)] provides an explanation of chiral symmetry breaking in QCD, without recourse to the instanton semiclassical approximation.
Here we pursued neither a deeper analysis of philosophical underpinnings of the non-perturbative accountFootnote 44; nor its compatibility with eliminativism; nor a clarification of its relationship with the (semi)classical approach: all of these are interesting topics but lie well beyond the scope of this article (see the comments in Sects. 3.3 and 4.2).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gomes, H., Riello, A. Eliminativism and the QCD \(\theta _{\text {YM}}\)-Term: What Gauge Transformations Cannot Do. Found Phys 54, 24 (2024). https://doi.org/10.1007/s10701-024-00759-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10701-024-00759-5




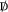 , which includes the gauge-covariant derivative
, which includes the gauge-covariant derivative 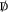 , where
, where 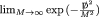 . Ultimately, the curvature appears through the decomposition:
. Ultimately, the curvature appears through the decomposition: 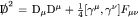 . One can choose instead a gauge-invariant measure, in which case the anomaly is shifted to renormalization counterterms (which then necessarily fail to satisfy the same invariances of the Lagrangian, [
. One can choose instead a gauge-invariant measure, in which case the anomaly is shifted to renormalization counterterms (which then necessarily fail to satisfy the same invariances of the Lagrangian, [