Abstract
We study the non-relativistic (NR) limit of relativistic spacetimes in relation with the topology of the Universe. We first show that the NR limit of the Einstein equation is only possible in Euclidean topologies, i.e., for which the covering space is \(\mathbb {E}^3\). We interpret this result as an inconsistency of general relativity in non-Euclidean topologies and propose a modification of that theory which allows for the limit to be performed in any topology. For this, a second reference non-dynamical connection is introduced in addition to the physical spacetime connection. The choice of reference connection is related to the covering space of the spacetime topology. Instead of featuring only the physical spacetime Ricci tensor, the modified Einstein equation features the difference between the physical and the reference Ricci tensors. This theory should be considered instead of general relativity if one wants to study a universe with a non-Euclidean topology and admitting a non-relativistic limit.






Similar content being viewed by others
Notes
It is possible to consider \(\varvec{\tau }\) not exact, and even \(\varvec{d} \varvec{\tau }\not =0\), but this requires torsion which we do not consider in this paper (see e.g. [10]).
[24] considers the more general case where odd powers of 1/c are present in the Taylor series. However, they are only physical, i.e., cannot be set to zero with a gauge transformation, from the order \(c^{-1}\) in \(g_{\mu \nu }\) and the order \(c^{-5/2}\) for \(g^{\mu \nu }\). Therefore, this does not change the main results of the present paper as it relies on the leading orders.
The only case when boundary conditions are not necessary is when exact homogeneity is assumed. This is however of little physical relevance, even for cosmology, as inhomogeneities (at least as perturbations) are always needed to make physical measurements and predictions. Therefore, boundary conditions are required.
Because the speed of light related to
 cannot be set to 1 for all \(\lambda \), then “unit” means that the norm of \(\varvec{u}\) is \(c_\lambda \).
cannot be set to 1 for all \(\lambda \), then “unit” means that the norm of \(\varvec{u}\) is \(c_\lambda \).See Stichel [29] for an example of
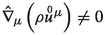 .
.There always exists a vector \(\varvec{G} \in \ker ({{\bar{R}}}_{\alpha \beta })\) such that \(G^\mu \tau _\mu = 1\). The reason is that \(\varvec{\tau }\) defines a foliation of \({\mathcal {M}}= \mathbb {R}\times \Sigma \) by \(\Sigma \) manifolds and that \(\bar{R}_{\alpha \beta }\) always has a zero eigenvalue in the ‘\(\mathbb {R}\)-direction’.
Note that while [20] defines one manifold
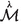 for each value of \(\lambda \) embedded in a 5-dimensional manifold \({\mathcal {N}}\) (with a diffeomorphism
for each value of \(\lambda \) embedded in a 5-dimensional manifold \({\mathcal {N}}\) (with a diffeomorphism 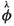 between
between 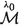 and
and 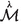 ), this is equivalent as considering a single manifold \({\mathcal {M}}\) with an auto-diffeomorphism, as is our case.
), this is equivalent as considering a single manifold \({\mathcal {M}}\) with an auto-diffeomorphism, as is our case.At first order, these coordinate systems differ by the transformation
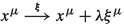 .
.
References
Bardeen, J.M.: Gauge-invariant cosmological perturbations. Phys. Rev. D 22, 1882–1905 (1980)
Barrow, J.D.: Non-Euclidean Newtonian cosmology. Class. & Quantum Gravity 37, 125007 (2020)
Buchert, T., Ehlers, J.: Averaging inhomogeneous Newtonian cosmologies. A &A 320, 1–7 (1997)
Dautcourt, G.: On the Newtonian limit of general relativity. Acta Phys. Pol. B 21, 755–765 (1990)
Di Valentino, E., Melchiorri, A., Silk, J.: Planck evidence for a closed Universe and a possible crisis for cosmology. Nat. Astron. 4, 196–203 (2020)
Dyer, E., Hinterbichler, K.: Boundary terms, variational principles, and higher derivative modified gravity. Phys. Rev. D 79, 024028 (2009)
Ehlers, J.: Republication of: On the Newtonian limit of Einstein’s theory of gravitation. Gen. Rel. Grav. 51, 163 (2019)
Galloway, G.J., Khuri, M.A., Woolgar, E.: The topology of general cosmological models. arXiv: arXiv:2010.06739 (2020)
Handley, W.: Curvature tension: Evidence for a closed universe. Phys. Rev. D 103, L041301 (2021)
Hansen, D., Hartong, J., Obers, N.A.: Non-relativistic gravity and its coupling to matter. J. High Energy Phys. 2020, 145 (2020)
Hartong, J., Obers, N.A., Oling, G.: Review on non-relativistic gravity. Front. Phys. 11 (2023)
Heckmann, O., Schücking, E.: Bemerkungen zur Newtonschen Kosmologie. I. Mit 3 Textabbildungen in 8 Einzeldarstellungen. Z. Astrophys. 38, 95 (1955)
Iwasaki, Y.: Quantum Theory of Gravitation vs. Classical Theory*): Fourth-Order Potential, Progress of Theoretical Physics 1587–1609 (1971)
Künzle, H.P.: Galilei and Lorentz structures on space-time : comparison of the corresponding geometry and physics. Annales de l’I.H.P. Physique théorique 17, 337–362 (1972)
Künzle, H.P.: Covariant Newtonian limit of Lorentz space-times. Gen. Rel. Grav. 7, 445–457 (1976)
Lachieze-Rey, M., Luminet, J.: Cosmic topology. Phys. Rep. 254, 135–214 (1995)
Lovelock, D.: The Four-Dimensionality of Space and the Einstein Tensor. J. Math. Phys. 13, 874–876 (1972)
Malament, D.B.: In: Colodny, R. (ed.) From Quarks to Quasars. University of Pittsburgh Press, USA (1986)
Malament, D. B.: In: Vol. 114, Studies in Logic and the Foundations of Mathematics. Elsevier, pp. 405–411 (1986)
Malik, K.A., Matravers, D.R.: TOPICAL REVIEW: A concise introduction to perturbation theory in cosmology. Class & Quant Gravity 25, 193001 (2008)
Misner, C.W., Thorne, K.S., Wheeler, J.A.: Gravitation. W.H. Freeman and Co, San Francisco (1973)
Morgan, J.W., Tian, G.: Ricci flow and the poincare conjecture. arXiv:math/0607607 (2006)
Peebles, P.J.E.: The large-scale structure of the universe. Princeton University Press, USA (1980)
Rendall, A.D.: On the definition of post-Newtonian approximations. Proceedings of the Royal Society of London Series A 438, 341–360 (1992)
Rosen, N.: General relativity with a background metric. Found. Phys. 10, 673–704 (1980)
Rosen, N.: Localization of gravitational energy. Found. Phys. 15, 997–1008 (1985)
Roukema, B.F., Bajtlik, S.: Homotopy symmetry in the multiply connected twin paradox of special relativity. MNRAS 390, 655–664 (2008)
Roukema, B.F., Różański, P.T.: The residual gravity acceleration effect in the Poincaré dodecahedral space. A &A 502, 27–35 (2009)
Stichel, P. C.: Cosmological model with dynamical curvature. arXiv:1601.07030 (2016)
Thurston, W.P.: Three dimensional manifolds, Kleinian groups and hyperbolic geometry. Bull. Amer. Math. Soc. 6, 357–381 (1982)
Tichy, W., Flanagan, É.É.: Covariant formulation of the post-1-Newtonian approximation to general relativity. Phys. Rev. D 84, 044038 (2011)
Uzan, J.-P., Luminet, J.-P., Lehoucq, R., Peter, P.: The twin paradox and space topology. Eur. J. Phys. 23, 277–284 (2002)
Vigneron, Q.: PhD thesis, Université Claude Bernard Lyon 1, (2021a). https://www.theses.fr/en/2021LYSE1117
Vigneron, Q.: 1+3 -Newton-Cartan system and Newton-Cartan cosmology. Phys. Rev. D 103, 064064 (2021)
Vigneron, Q.: Is backreaction in cosmology a relativistic effect? On the need for an extension of Newton’s theory to non-Euclidean topologies. Phys. Rev. D 105, 043524 (2022)
Vigneron, Q.: On non-Euclidean Newtonian theories and their cosmological backreaction. Class. & Quantum Gravity 39, 155006 (2022)
Vigneron, Q., Poulin, V.: Is expansion blind to the spatial curvature? Phys. Rev. D 108, 103518 (2023)
Vigneron, Q., Roukema, B.F.: Gravitational potential in spherical topologies. Phys. Rev. D 107, 063545 (2023)
York James, W.J.: Conformally invariant orthogonal decomposition of symmetric tensors on Riemannian manifolds and the initial-value problem of general relativity. J. Math. Phys. 14, 456–464 (1973)
Acknowledgements
This work was supported by the Centre of Excellence in Astrophysics and Astrochemistry of Nicolaus Copernicus University in Toruń, and by the Polish National Science Centre under Grant No. SONATINA 2022/44/C/ST9/00078. I am grateful to Pierre Mourier and Áron Szabó for constant discussions and commentaries on the manuscript. I thank Léo Brunswic and Fernando Pizaña for insightful discussions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A The NEN Theory
In this section, we present the properties of the non-relativistic theory in non-Euclidean topologies, i.e., the NEN theory, developed in [15] and [36, section 5.6 ].
1.1 A.1 Spacetime Equations
The theory is defined on a 4-manifold \({\mathcal {M}}= \mathbb {R}\times \Sigma \) where \(\Sigma \) is closed. \({\mathcal {M}}\) is equipped with a Galilean structure \(({\hat{h}}^{\alpha \beta }, \tau _\mu , {\hat{\nabla }}_\nu )\) as defined in Sect. 3.2. The spacetime equations of the NEN theory are

where \(\rho \) is the matter density; \(T^{\alpha \beta }\) is the energy-momentum tensor; \(\Lambda \) is the cosmological constant;  is the orthogonal projector (defined by relation (6)) to a vector \({{\tilde{G}}}^\alpha \) with \({{{\tilde{G}}}^\mu \tau _\mu {:}{=}1}\) called the Galilean vector (or Galilean observer) in \({\mathcal {M}}\). It is defined by two conditions: (i) in coordinates adapted to the \(\tau \)-foliation and such that \(\varvec{\partial }_t = \tilde{\varvec{G}}\), the time derivative of the spatial components of the space metric (which correspond to the expansion tensor of \(\tilde{\varvec{G}}\)) are
is the orthogonal projector (defined by relation (6)) to a vector \({{\tilde{G}}}^\alpha \) with \({{{\tilde{G}}}^\mu \tau _\mu {:}{=}1}\) called the Galilean vector (or Galilean observer) in \({\mathcal {M}}\). It is defined by two conditions: (i) in coordinates adapted to the \(\tau \)-foliation and such that \(\varvec{\partial }_t = \tilde{\varvec{G}}\), the time derivative of the spatial components of the space metric (which correspond to the expansion tensor of \(\tilde{\varvec{G}}\)) are
and (ii) \(\tilde{\varvec{G}}\) is vorticity free with respect to the Galilean structure, i.e.,
H(t) is the expansion rate of the finite volume of the spatial sections defined by \(\varvec{\tau }\), and \(\Xi ^{ij}\) is traceless-transverse and represents anisotropic expansion. Property (72) ensures that, without anisotropic expansion, there exists an adapted coordinate system (the one related to \(\tilde{{\varvec{G}}}\)) in the NEN theory such that the spatial metric can be separated in space and time dependence: \(h_{ij}(t,x^k) = a(t)^2 {{\tilde{h}}}_{ij}(x^k)\). This coordinate system defines what we call an inertial frame in classical Newton’s theory. Therefore, property (72) ensures its existence for the non-Euclidean version of the theory.Footnote 8
Equation (69) is the Trautmann condition, also present in Newton’s theory with the Newton-Cartan system. It ensures that no gravitomagnetism is present in the theory. In equation (70),  is an additional term with respect to the Newton-Cartan system. This term was added by [15, 36] for the theory to be defined on spherical or hyperbolic topologies, as it implies the spatial Ricci tensor (from equation (70)) to have the form \({\hat{{\mathcal {R}}}}^{ij} = \pm 2/a(t)^2\, {\hat{h}}^{ij}\), where a is the scale factor of expansion.
is an additional term with respect to the Newton-Cartan system. This term was added by [15, 36] for the theory to be defined on spherical or hyperbolic topologies, as it implies the spatial Ricci tensor (from equation (70)) to have the form \({\hat{{\mathcal {R}}}}^{ij} = \pm 2/a(t)^2\, {\hat{h}}^{ij}\), where a is the scale factor of expansion.
1.2 A.2 Spatial Equations
To allow for a more intuitive understanding of this theory, we present the spatial equations resulting from the above the spacetime equations. Assuming isotropic expansion (\(\Xi _{ij} = 0\)), and introducing the gravitational potential \(\Phi \) defined via the 4-acceleration of the Galilean vector (i.e., \({\hat{D}}^\mu \Phi {:}{=}{{\tilde{G}}}^\nu {\hat{\nabla }}_\nu {{\tilde{G}}}^\mu \)), we have (see [36] for a detailed derivation)
with the expansion law
where the dot derivative corresponds to \(\partial _t + v^c{\hat{D}}_c\) with \({\hat{D}}_i\) the covariant derivative with respect to the spatial metric; \(\varvec{v}\) is the spatial fluid velocity; \((a_{\not = \mathrm grav})^a\) is the non-gravitational spatial acceleration of the fluid; \(\left\langle \psi \right\rangle _{\Sigma }(t) {:}{=}\frac{1}{V_\Sigma }\int _\Sigma \psi \sqrt{\textrm{det}({\hat{h}}_{ij})}\textrm{d}^3 x\) is the average of a scalar field \(\psi \) over the volume \(V_\Sigma \) of \(\Sigma \). This system is valid in an inertial frame, i.e., in coordinates where the spatial metric is separated is space and time dependence.
We see that the spatial equations defining the NEN theory are algebraically equivalent to the cosmological Newton equations, but with the presence of a non-zero spatial Ricci tensor related to a spherical or hyperbolic topology. This shows that the NEN theory can be seen as an adaptation of Newton’s theory (by adding a curvature) such that it is defined on non-Euclidean topologies.
Appendix B Natural Metrics on Thurston’s Topological Class
We give the natural metrics for each Thurston’s topological class and some properties of their Ricci tensor (we denote \(N_{\ker {}} {:}{=}\dim [\ker ({\bar{{\mathcal {R}}}}_{ij})]\)):
-
For Euclidean topologies (the covering space \({\tilde{\Sigma }}\) of \(\Sigma \) is \(\mathbb {E}^3\)):
$$\begin{aligned} {{\bar{h}}}_{ij} = \delta _{ij}, \end{aligned}$$(79)with \({\bar{{\mathcal {R}}}}_{ij} = 0\) and \(N_{\ker {}} = 3\).
-
For \({\tilde{\Sigma }} = \mathbb {S}^3\) (spherical topologies):
$$\begin{aligned} {{\bar{h}}}_{ij}\textrm{d}x^i\textrm{d}x^j =\textrm{d}r^2 + \sin ^2r \left( \textrm{d}\theta ^2 + \sin ^2\theta \textrm{d}\varphi ^2\right) , \end{aligned}$$(80)with \({\bar{{\mathcal {R}}}}_{ij} = 2{{\bar{h}}}_{ij}\) and \(N_{\ker {}} = 0\).
-
For \({\tilde{\Sigma }} = \mathbb {H}^3\) (hyperbolic topologies):
$$\begin{aligned} {{\bar{h}}}_{ij}\textrm{d}x^i\textrm{d}x^j =\textrm{d}r^2 + \sinh ^2r \left( \textrm{d}\theta ^2 + \sin ^2\theta \textrm{d}\varphi ^2\right) , \end{aligned}$$(81)with \({\bar{{\mathcal {R}}}}_{ij} = - 2{{\bar{h}}}_{ij}\) and \(N_{\ker {}} = 0\).
-
For \({\tilde{\Sigma }} = \mathbb {R}\times \mathbb {S}^2\):
$$\begin{aligned} {{\bar{h}}}_{ij}\textrm{d}x^i\textrm{d}x^j = \textrm{d}r^2 + \sin ^2 r \, \textrm{d}\varphi ^2 + \textrm{d}z^2, \end{aligned}$$(82)with \({\bar{{\mathcal {R}}}} = 2\), \({\bar{{\mathcal {R}}}}_{\langle ij\rangle } \not =0\) and \(N_{\ker {}} = 1\).
-
For \({\tilde{\Sigma }} = \mathbb {R}\times \mathbb {H}^2\):
$$\begin{aligned} {{\bar{h}}}_{ij}\textrm{d}x^i\textrm{d}x^j = \textrm{d}r^2 + \sinh ^2 r \, \textrm{d}\varphi ^2 + \textrm{d}z^2, \end{aligned}$$(83)with \({\bar{{\mathcal {R}}}} = -2\), \({\bar{{\mathcal {R}}}}_{\langle ij\rangle } \not =0\) and \(N_{\ker {}} = 1\).
-
For \({\tilde{\Sigma }} = \tilde{SL2\mathbb {R}}\):
$$\begin{aligned} {{\bar{h}}}_{ij}\textrm{d}x^i\textrm{d}x^j = \textrm{d}x^2 + \cosh ^2 x \, \textrm{d}y^2 + \left( \textrm{d}z + \sinh ^2x \, \textrm{d}y\right) ^2, \end{aligned}$$(84)with \({\bar{{\mathcal {R}}}} = -5/2\), \({\bar{{\mathcal {R}}}}_{\langle ij\rangle } \not =0\) and \(N_{\ker {}} = 0\).
-
For Nil topologies:
$$\begin{aligned} {{\bar{h}}}_{ij}\textrm{d}x^i\textrm{d}x^j = \textrm{d}x^2 + \textrm{d}y^2 + \left( \textrm{d}z - x \textrm{d}y\right) ^2, \end{aligned}$$(85)with \({\bar{{\mathcal {R}}}} = -1/2\), \({\bar{{\mathcal {R}}}}_{\langle ij\rangle } \not =0\) and \(N_{\ker {}} = 0\).
-
For Sol topologies:
$$\begin{aligned} {{\bar{h}}}_{ij}\textrm{d}x^i\textrm{d}x^j = e^{-2z}\textrm{d}x^2 + e^{2z}\textrm{d}y^2 + \textrm{d}z^2, \end{aligned}$$(86)with \({\bar{{\mathcal {R}}}} = -2\), \({\bar{{\mathcal {R}}}}_{\langle ij\rangle } \not =0\) and \(N_{\ker {}} = 2\).
Appendix C Formulas for the NR Limit
In this section, the notion of spatial is related to the foliation defined by \(\varvec{\tau }\) and to the metric \(\hat{\varvec{h}}\) present in the Galilean structure.
1.1 C.1 Leading Order of the Fluid Orthogonal Projector
The projector orthogonal to a g-timelike vector  is defined as
is defined as

Its limit is



Equation (88) can also be written as

where  is the projector orthogonal to
is the projector orthogonal to  , with respect to the Galilean structure (defined by relations (6)).
, with respect to the Galilean structure (defined by relations (6)).
1.2 C.2 Expansion and Vorticity Tensors
The formalism of this section is presented in more details in [34].
For a Galilean structure, the expansion  and vorticity
and vorticity  tensors of a unit \(\tau \)-timelike vector \(\varvec{U}\) are defined as
tensors of a unit \(\tau \)-timelike vector \(\varvec{U}\) are defined as


These tensors are spatial. For two unit \(\tau \)-timelike vectors \(\varvec{U}\) and \(\varvec{T}\), such that \(\varvec{U} - \varvec{T} = \varvec{w}\), which is spatial, we have


where \({\hat{D}}_\alpha \) is the spatial derivative induced by \({\hat{h}}^{\alpha \beta }\) on the \(\tau \)-foliation, with \({\hat{D}}^\alpha {:}{=}{\hat{h}}^{\alpha \mu } {\hat{D}}_\mu \) (see section II.C.4. in [34]). From the general definition of a Galilean vector \(\tilde{\varvec{G}}\) given in Section 6.2.2, and using (95) and (96), for any unit \(\tau \)-timelike vector \(\varvec{U}\) we have


where  .
.
A symmetric tensor can be decomposed into a scalar part (i.e., proportional to the metric), a gradient part (i.e., the gradient of a vector) and a tensor part (a traceless-transverse tensor) [39], called SVT decomposition. In general, the scalar part has spatial dependence. The existence of a Galilean vector implies that the expansion tensors (in the framework of Galilean structures) of any \(\tau \)-timelike vector have a spatially constant scalar mode as shown by relation (97). Another consequence is the form of the vorticity (98) which is expressed as function of the vector present in the gradient part of the expansion tensor. These relations were already shown to hold in [34, 36] for Newton-Cartan and the NEN theory.
Finally, the definition (94) implies that the vector \(\varvec{B}\) present in the Galilean connection in the NR limit (see equation (20)) is irrotational ( ). Therefore formulas (97) and (98) applied for \(\varvec{B}\) give
). Therefore formulas (97) and (98) applied for \(\varvec{B}\) give

where \(\sigma \) is a scalar field and \(B^\mu - {{\tilde{G}}}^\mu = {\hat{D}}^\mu \sigma \).
1.3 C.3 First Order of the Lorentzian Connection
From the relation of the difference between two connections, we have

This leads to

This formula is in agreement with the “connection perturbation” introduced by [31] for the post-Newton-Cartan approximation (Table II in [31]).
Using  , which follows from (15), where \(k^{\alpha \beta }\) is defined with respect to the first order
, which follows from (15), where \(k^{\alpha \beta }\) is defined with respect to the first order  in equation (17), we have
in equation (17), we have


1.4 C.4 First Order of the Spacetime Curvature Tensor
Using the formula for the difference between two Riemann tensors

where  , we obtain:
, we obtain:


Then,

Using equations (102) and (103) along with  as
as  , we obtain
, we obtain


where we only keep spatial components as  is spatial, and
is spatial, and  .
.
Appendix D Spatial Metric at the Limit and Existence of the Galilean Vector
1.1 D.1 A Solution to Equation (56)
While we have not yet found the general solution for \({\hat{h}}_{ij}\) to the equation \({\hat{{\mathcal {R}}}}_{ij} = {\bar{{\mathcal {R}}}}_{ij}\), we give in this section a simple non-trivial solution. It can be found by writing the physical metric with a scalar-vector-tensor (SVT) decomposition with respect to the reference spatial metric \({{\bar{h}}}_{ij}\). In general, the contravariant and covariant components of the physical metric have a different decomposition:
where \(A_{ij}\) and \(B^{ij}\) are traceless-transverse tensors with respect to \({\bar{h}}_{ij}\), and \({{\bar{D}}}_i\) is the covariant derivative with respect to that same metric, with \({{\bar{D}}}^i {:}{=}{{\bar{h}}}^{ci}{{\bar{D}}}_c\). We recall that \({\hat{h}}_{ij}\) and \({\hat{h}}^{ij}\) are by definition inverse from each-other, and the same for \({{\bar{h}}}_{ij}\) and \({{\bar{h}}}^{ij}\).
We can rewrite equation (56) as
with \(C^a_{ij} {:}{=}{\hat{h}}^{ak}\left( {{\bar{D}}}_{(i}{\hat{h}}_{j)k} - \frac{1}{2}{{\bar{D}}}_k{\hat{h}}_{ij}\right) \). Then, a sufficient condition on \({\hat{h}}_{ij}\) to be solution of the above equation is
This condition implies that \({\hat{h}}_{ij} - {\hat{h}}_{kl}\bar{h}^{kl}\,{{\bar{h}}}_{ij}/3\) is a traceless-transverse tensor with respect to \(\bar{\varvec{h}}\). Then, from the uniqueness of the SVT decomposition, the gradient mode (i.e., \({\hat{D}}_{(i} A_{j)}\)) of \({\hat{h}}_{ij}\) is zero and we have
The condition (113) implies \(C^a_{ij} =0\), which is the difference between the physical \({\hat{D}}_i\) and the reference \({{\bar{D}}}_i\) connections. Therefore we have \({\hat{D}}_i = {{\bar{D}}}_i\), implying \({{\bar{D}}}_{k}{\hat{h}}^{ij} = 0\). Then, the contravariant gradient mode also vanishes and we have
As for the homogeneity of \({\hat{{\mathcal {R}}}}_{ij}\), we have
using \(\partial _i({{\bar{h}}}^{cd}{\bar{{\mathcal {R}}}}_{cd}) = 0\) and equation (56). Therefore, for spherical or hyperbolic topologies, where by definition \({\bar{{\mathcal {R}}}}_{ij} = \pm 2 \bar{h}_{ij}\), we obtain \(\partial _i{\hat{{\mathcal {R}}}} = 0\). In summary, from the guess (113), for \(\tilde{\Sigma } = \mathbb {S}^3\) or \(\mathbb {H}^3\), the spatial scalar curvature of the Galilean structure is homogeneous. However, it is not necessarily isotropic as we have the following relation:
with \({\hat{h}}_{ij} - \frac{1}{3} h^{cd}A_{cd} \, {\hat{h}}_{ij} \not = 0\).
1.2 D.2 Expansion Tensor of \(G^\mu \)
We consider a vector \(\varvec{G} \in \textrm{ker}({{\bar{R}}}_{\mu \nu })\). Then, from relation (48) and the definition of \(\bar{R}_{\mu \nu }\), in a coordinate system \(\{\varvec{\partial }_t, \varvec{\partial }x^i\}\) adapted to the \(\tau \)-foliation with \(\varvec{G} = \varvec{\partial }_t\), we can choose \({{\bar{h}}}_{ij}\) such that
From that equation and relation (115), the time derivative along \(\varvec{G}\) of the physical metric \({\hat{h}}_{ij}\) is
From the definition of the expansion tensor (92), this leads to  . Then from (121) and the fact that \({\hat{D}}_k A = 0\), \({\hat{D}}_k A_{ij} = 0\) and \({\hat{D}}_k \partial _{t|_G} A_{ij} = 0\) (using (120) along with the property \({\hat{D}}_i = {{\bar{D}}}_i\) for the last relation), we have
. Then from (121) and the fact that \({\hat{D}}_k A = 0\), \({\hat{D}}_k A_{ij} = 0\) and \({\hat{D}}_k \partial _{t|_G} A_{ij} = 0\) (using (120) along with the property \({\hat{D}}_i = {{\bar{D}}}_i\) for the last relation), we have

That property is equivalent as having (this follows from the unicity of the SVT decomposition)

with \({\hat{D}}_k H = 0\) and \(D_k\Xi _{ij} = 0\). From  and the definition of the volume of \(\Sigma \), i.e., \(V_\Sigma {:}{=}\int _\Sigma \sqrt{\textrm{det}\, {\hat{h}}_{ij}} \, \textrm{d}x^3\), we have \(H(t) = \dot{V}_\Sigma /(3V_\Sigma )\). Result (123) holds once condition (113) is fulfilled, or if we directly impose \({\hat{{\mathcal {R}}}}_{ij} = {\hat{{\mathcal {R}}}}(t)\, {\hat{h}}_{ij}/3\) in the case \({\tilde{\Sigma }} = \mathbb {S}^3\) or \(\mathbb {H}^3\). Equation 123 is the first of the two conditions (57) and (58) for \(\varvec{G}\) to be a Galilean vector.
and the definition of the volume of \(\Sigma \), i.e., \(V_\Sigma {:}{=}\int _\Sigma \sqrt{\textrm{det}\, {\hat{h}}_{ij}} \, \textrm{d}x^3\), we have \(H(t) = \dot{V}_\Sigma /(3V_\Sigma )\). Result (123) holds once condition (113) is fulfilled, or if we directly impose \({\hat{{\mathcal {R}}}}_{ij} = {\hat{{\mathcal {R}}}}(t)\, {\hat{h}}_{ij}/3\) in the case \({\tilde{\Sigma }} = \mathbb {S}^3\) or \(\mathbb {H}^3\). Equation 123 is the first of the two conditions (57) and (58) for \(\varvec{G}\) to be a Galilean vector.
From the general form of the physical spatial Ricci curvature (119) (depending on the guess (113)) and with (114), we see that imposing the physical spatial curvature to be only trace (i.e., \({\hat{{\mathcal {R}}}}_{ij} \propto {\hat{h}}_{ij}\)) leads to \(A_{ij} = 0\), and \(\partial _{t|_G} {\hat{h}}_{ij} \propto {{\bar{h}}}_{ij} \propto {\hat{h}}_{ij}\). Therefore, we have the following property:
That is: an isotropic spatial curvature implies an isotropic expansion. It is however not yet clear whether or not the reverse property is true.
Remark 8
We expect that the general solution of equation (56) would rather constrain \(\Xi _{ij}\) to be only harmonic, i.e., \({\hat{\Delta }} \Xi _{ij} = 0\), instead of gradient free. Indeed, being traceless-transverse and harmonic is the expected condition for a tensor representing global anisotropic expansion.
1.3 D.3 Vorticity of \(G^\mu \)
From the Galilean limit, the vector \(\varvec{B}\) present in the first order of  is irrotational with respect to the Galilean structure. Using relation (96) for the difference between two vorticity tensors, this implies that
is irrotational with respect to the Galilean structure. Using relation (96) for the difference between two vorticity tensors, this implies that  where \(\varvec{w} = \varvec{G} - \varvec{B}\) is a spatial vector. Then using \({\hat{R}}_{\mu \nu }{\hat{h}}^{\mu \alpha }G^\nu = 0\), which results from (50), we obtain
where \(\varvec{w} = \varvec{G} - \varvec{B}\) is a spatial vector. Then using \({\hat{R}}_{\mu \nu }{\hat{h}}^{\mu \alpha }G^\nu = 0\), which results from (50), we obtain
From the unicity of the Hodge decomposition, we have \({\hat{D}}_c{\hat{D}}^{[i}w^{c]} = 0\), which implies \({\hat{D}}^{[i}w^{j]} =0\). We just showed that  .
.
In conclusion, the vector \(\varvec{G}\) is a Galilean vector: \(\varvec{G} = \tilde{\varvec{G}}\).
1.4 D.4 Uniqueness of the Galilean Vector?
While \(\varvec{G}\) is a Galilean vector, it is not uniquely defined if \(\text {dim}[\ker ({{\bar{R}}}_{\alpha \beta })] > 1\) (see Sect. 5.2.3). For two independent Galilean vectors \(\tilde{\varvec{G}}_{(1)}\) and \(\tilde{\varvec{G}}_{(2)}\), we define the spatial vector \({\varvec{w} = \tilde{\varvec{G}}_{(2)} - \tilde{\varvec{G}}_{(1)}}\). Then from the difference between two expansion and vorticity tensors (equations (95) and (96)), the vector \(\varvec{v}\) is constrained by:
The second property is a direct consequence of the first one when calculating \(D_{[i}D_{j]} w^k\). In conclusion, if there is not a unique inertial frame at the NR limit, then this frame is define up to a global translation in the direction of zero spatial curvature.
Remark 9
Even if there is not a unique inertial frame, the closedness of \(\Sigma \) still implies the existence of a “preferred” one, due to topological properties [27, 32]. In other words, once we require the existence of a NR limit of either general relativity or the bi-connection theory, this implies the existence of a preferred observer in the Universe. Question: could the primordial power spectrum of the CMB be explained by the fondamental presence of such a preferred frame in the theory, and therefore be of topological origin?
Appendix E Derivation of the Dictionary
In this section, we consider isotropic expansion (\(\Xi _{ij} = 0\)). Using the Taylor series (11) and (12) of the spacetime metric, in a coordinate system \(\{\varvec{\partial }_t, \varvec{\partial }x^i\}\) adapted to the \(\tau \)-foliation and where \(\varvec{\partial }_t = \tilde{\varvec{G}}\), we have

and

where, as shown in Appendix C.2, \(B^\mu - {{\tilde{G}}}^\mu {=}{:}{\hat{D}}^\mu \sigma \) with \({\hat{D}}_i \sigma {:}{=}{\hat{h}}_{ki}{\hat{D}}^k \sigma \). We also defined \(k_{ij} {:}{=}k^{cd}{\hat{h}}_{ci} {\hat{h}}_{dj}\). We recall that \(B^\mu \) and \(\phi \) are defined in Sect. 3.4 where the NR limit is presented. For now, \(\phi \) is just a scalar field related to the 4-acceleration  of \(B^\mu \), i.e.,
of \(B^\mu \), i.e.,  .
.
The goal is to find if there is a relation between \(\phi \), \(\sigma \), \(k^{ij}\) and the gravitational field \(\Phi \). A powerful property is the fact that in both Newton’s theory and the NEN theory, \(\Phi \) is given by the 4-acceleration of the Galilean vector [34, 36], i.e., the 4-acceleration of inertial frames:

Using formula (60) in [34], we can express  as function of
as function of  and obtain (we keep only spatial indices as all the tensors involved are spatial):
and obtain (we keep only spatial indices as all the tensors involved are spatial):

Then using (99) and  , we obtain \({\hat{D}}^i \left( \phi -\frac{1}{2} {\hat{D}}^k \sigma {\hat{D}}_k \sigma - \partial _{t|_G}\sigma \right) = {\hat{D}}^i\Phi \), which leads to
, we obtain \({\hat{D}}^i \left( \phi -\frac{1}{2} {\hat{D}}^k \sigma {\hat{D}}_k \sigma - \partial _{t|_G}\sigma \right) = {\hat{D}}^i\Phi \), which leads to
up to an integration constant. We now have a link between \(\phi \), \(\sigma \) and \(\Phi \).
Let us consider the SVT decomposition of \(k^{ij} - {\hat{D}}^i \sigma {\hat{D}}^j \sigma \), as is usually done in the weak field limit:
with \({\hat{D}}_kF^k {:}{=}0\) and \(f^{ij}{\hat{h}}_{ij} {:}{=}0 {=}{:}{\hat{D}}_k f^{ki}\). The first order of the (modified) Einstein equation (42) is

This holds either in the Euclidean case (general relativity), or in the non-Euclidean case (bi-connection theory). Using formula (108) for  , with (132) and (131) we obtain
, with (132) and (131) we obtain
where K is the spatial Gaussian curvature: \({\hat{{\mathcal {R}}}}_{ij} = 2K/a^2\, {\hat{h}}_{ij}\). The unicity of the SVT decomposition applied on the above equation leads to
So for any K, we have \(f^{ij} = 0\) (more precisely, \(f^{ij}\) is harmonic), and using the Poisson equation (76) for \(\Phi \) with relation (135) we obtain
In the Euclidean case (i.e., \(K=0\)), which corresponds to the NR limit of Einstein’s equation and the usual Newton-to-GR dictionary, E and \(F^i\) are free. This is a usual gauge freedom in post-Newtonian theory. However, we see that in the non-Euclidean case, relations (136) and (137) imply \(E=0\) and \(F^i=0\).
Finally, the spacetime metric can be written as follows as function of the gravitational potential:

and

where \(E\not =0\) and \(F^i\not =0\) only if \(K = 0\).
It seems that in the non-Euclidean case, E and \(F^i\) are not anymore gauge variables and are necessarily zero, i.e., the metric needs to be written with the same form as in the standard post-Newtonian gauge with Newton’s theory. In the next Appendix, we show that this peculiarity in the non-Euclidean case comes from a gauge fixing we implicitly made in Sect. 6 by assuming that \({{\bar{R}}}_{\mu \nu }\) should not depend on \(\lambda \).
Appendix F Gauge Freedom in the NR limit
1.1 F.1 Gauge Freedom
Let us consider \(\mathbb {R}^4\) on which we define two Minkowski metrics \(\eta _{\mu \nu }\) and \({\tilde{\eta }}_{\mu \nu }\). The set of foliations which are flat with respect to \(\eta _{\mu \nu }\) are not necessarily flat with respect to \({\tilde{\eta }}_{\mu \nu }\). In other words, in a coordinate system where \(\eta _{\mu \nu } = \textrm{diag}(-1; 1; 1; 1)\), the relation \({\tilde{\eta }}_{\mu \nu } = \textrm{diag}(-1; 1; 1; 1)\) does not necessarily hold. This is because there are four degrees of freedom in defining \({\tilde{\eta }}_{\mu \nu }\) with respect to \(\eta _{\mu \nu }\), corresponding to a diffeomorphism \(\varphi \) of \(\mathbb {R}^4\) in itself. The freedom in changing \({\tilde{\eta }}_{\mu \nu }\) while preserving its properties of being a Minkowski metric is related to the differential \(\textrm{d}\varphi : T\mathbb {R}^4 \rightarrow T\mathbb {R}^4\) of \(\varphi \):
The same freedom applies for \(R_{\mu \nu }\) and \({{\bar{R}}}_{\mu \nu }\) in the bi-connection theory. Therefore, the role of the bi-connection condition (43) is to constrain the four degrees of freedom in the definition of the physical connection with respect to the reference one (or inversely).
This freedom arising when two tensors are defined on the same manifold is also present for the family of Lorentzian metrics  used in the NR limit: there is a diffeomorphism freedom in defining
used in the NR limit: there is a diffeomorphism freedom in defining  with respect to
with respect to  , with \(\lambda \not = \lambda _0\) for any \(\lambda _0 > 0\). However, while in the example related to the Minkowski metrics, this diffeomorphism is general, in the case of the family
, with \(\lambda \not = \lambda _0\) for any \(\lambda _0 > 0\). However, while in the example related to the Minkowski metrics, this diffeomorphism is general, in the case of the family  , because we impose
, because we impose  , that diffeomorphism freedom is constrained to be the identity in the limit \(\lambda \rightarrow \lambda _0\), and thus should also be parametrised by \(\lambda \):
, that diffeomorphism freedom is constrained to be the identity in the limit \(\lambda \rightarrow \lambda _0\), and thus should also be parametrised by \(\lambda \):  .
.
A consequence is that, at first order in \((\lambda - \lambda _0)\), the freedom in (re)defining  with respect to
with respect to  is a Lie derivative (see [20] for a detailed explanationFootnote 9):
is a Lie derivative (see [20] for a detailed explanationFootnote 9):

where \(\xi ^\mu \) is a vector field on \({\mathcal {M}}\). In perturbation theory, that freedom is called a gauge freedom as it does not change physics.
1.2 F.2 Gauge Invariant Variables in the NR Limit
Under the gauge transformation describe in the previous section,  and
and  transform as
transform as


The vector \(\xi ^\mu \) can be written as
where \({\mathcal {A}}^\mu \tau _\mu {:}{=}0 {=}{:}{\hat{D}}_\mu {\mathcal {A}}^\mu \), and N and \({\mathcal {A}}\) are scalar fields. We recall that \({{\tilde{G}}}^\mu \) is a Galilean vector. Then
where we used \({\hat{h}}^{\alpha \mu }{\hat{\nabla }}_\alpha {{\tilde{G}}}^\nu = -2\,H{\hat{h}}^{\mu \nu } -2\Xi ^{\mu \nu }\). Then using the SVT decomposition introduced in Appendix E we have

Using the definition (18) of  along with formula (88) (in which we replace
along with formula (88) (in which we replace  by \(B^\mu {=}{:}{{\tilde{G}}}^\mu + {\hat{D}}^\mu \sigma \); and we replace
by \(B^\mu {=}{:}{{\tilde{G}}}^\mu + {\hat{D}}^\mu \sigma \); and we replace  by
by  ), we get
), we get

Then, from (149) and (150), the gauge transformations (144) and (145) induce a transformation of the variables \(\sigma \), \(\psi \), E, \(F^\mu \), \(f^{\mu \nu }\) and \(\phi \) as follows:






Therefore, the following variables are gauge invariant:
\({\tilde{\Psi }}\) and \({\tilde{\Phi }}\) are the equivalent of the Bardeen potentials in the cosmological perturbation theory (weak field limit around a homogeneous and isotropic solution). We showed in Appendix E that \({\tilde{\Psi }} = {\tilde{\Phi }}\) either in the Euclidean case (i.e., with Newton’s theory from Einstein’s equation, as expected), or in the non-Euclidean case (from the bi-connection theory). Therefore, the gravitational slip (i.e., \({\tilde{\Psi }} - {\tilde{\Phi }}\)) is still zero in the bi-connection theory. Furthermore, we have \({\tilde{\Psi }} = {\tilde{\Phi }} = \Phi \), the gravitational potential, showing that this variable is gauge-invariant, again either in the Euclidean or non-Euclidean case. Equation (152)–(153) show that \(\sigma \), E and \(F^\mu \) can be set to zero by a gauge transformation.
1.3 F.3 Gauge Freedom in the Reference Curvature
As mentioned above, there is a diffeomorphism freedom in defining \({{\bar{R}}}_{\mu \nu }\) with respect to \(R_{\mu \nu }\). In the case of the NR limit, that freedom is present with respect to all the metrics  and their curvatures. This implies that, once we consider a NR limit, the diffeomorphism freedom on defining \(\bar{R}_{\mu \nu }\) with respect to the family of Lorentzian metrics is parametrised by \(\lambda \), leading, at first order, to
and their curvatures. This implies that, once we consider a NR limit, the diffeomorphism freedom on defining \(\bar{R}_{\mu \nu }\) with respect to the family of Lorentzian metrics is parametrised by \(\lambda \), leading, at first order, to

for any vector field \(X^\mu \). Under a gauge transformation we have  . As the difference between \({{\bar{R}}}_{\mu \nu }\) and
. As the difference between \({{\bar{R}}}_{\mu \nu }\) and  comes solely from diffeomorphism freedom, these two tensors have the same property, i.e., they take the form (46) in a certain (one for each) coordinate systemFootnote 10. In particular, as for \({{\bar{R}}}_{\mu \nu }\), there exists a vector
comes solely from diffeomorphism freedom, these two tensors have the same property, i.e., they take the form (46) in a certain (one for each) coordinate systemFootnote 10. In particular, as for \({{\bar{R}}}_{\mu \nu }\), there exists a vector  such that
such that  .
.
Because until now we supposed that \({{\bar{R}}}_{\mu \nu }\) was independent on \(\lambda \), this means that the calculation of Sect. 6 and Appendix E was performed in a specific gauge where \(X^\mu = 0\). This is why we found in Appendix E that E and \(F^i\) needed to vanish. In what follows we explain why, without the gauge choice \(X^\mu = 0\), E and \(F^i\) do not vanish anymore.
In a general gauge, equation (55) takes the form

with  , and the first order equation (133) (used to derive the dictionary) becomes
, and the first order equation (133) (used to derive the dictionary) becomes

Because  has the same properties as \({{{\bar{R}}}}_{\mu \nu }\), the resolution of equation (161) is equivalent as solving equation (55) in Sect. 6.2.1. In particular,
has the same properties as \({{{\bar{R}}}}_{\mu \nu }\), the resolution of equation (161) is equivalent as solving equation (55) in Sect. 6.2.1. In particular,  corresponds to a Galilean vector, and in Euclidean, spherical or hyperbolic topologies without anisotropic expansion we have
corresponds to a Galilean vector, and in Euclidean, spherical or hyperbolic topologies without anisotropic expansion we have

Then, writing \(X^\mu {=}{:}M{{\tilde{G}}}^\mu + {\hat{D}}^\mu {\mathcal {X}}+ {\mathcal {X}}^\mu \) with \({\mathcal {X}}^\mu \tau _\mu {:}{=}0 {=}{:}{\hat{D}}_\mu {\mathcal {X}}^\mu \), the additional term in equation (162), compared to equation (133), takes the form

A consequence is that reperforming the calculation of Section E, we obtain
Therefore, E and \(F^i\) are not anymore imposed to be zero, instead the gauge-invariant variables \({\mathcal {C}}{:}{=}E + {\mathcal {X}}\) and \({\mathcal {C}}^i {:}{=}F^i + {\mathcal {X}}^i\) are zero.
In conclusion, from either the Einstein equation (Euclidean case) or the bi-connection theory (non-Euclidean case), the spacetime metric  (respectively
(respectively  ) takes the form (64) [respectively (65)] as function of the gravitational potential, with \(\sigma \), E and \(F^i\) being free gauge fields in both cases.
) takes the form (64) [respectively (65)] as function of the gravitational potential, with \(\sigma \), E and \(F^i\) being free gauge fields in both cases.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Vigneron, Q. Non-Relativistic Regime and Topology: Topological Term in the Einstein Equation. Found Phys 54, 15 (2024). https://doi.org/10.1007/s10701-023-00749-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10701-023-00749-z





 cannot be set to 1 for all
cannot be set to 1 for all 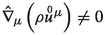 .
.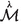 for each value of
for each value of 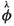 between
between 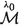 and
and 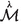 ), this is equivalent as considering a single manifold
), this is equivalent as considering a single manifold 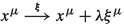 .
.