On the Reality of the Quantum State Once Again: A No-Go Theorem for $\psi$-Ontic Models

Abstract

In this paper we show that $\psi$-ontic models, as defined by Harrigan and Spekkens (HS), cannot reproduce quantum theory. Instead of focusing on probability, we use information theoretic considerations to show that all pure states of $\psi$-ontic models must be orthogonal to each other, in clear violation of quantum mechanics. Given that (i) Pusey, Barrett and Rudolph (PBR) previously showed that $\psi$-epistemic models, as defined by HS, also contradict quantum mechanics, and (ii) the HS categorization is exhausted by these two types of models, we conclude that the HS categorization itself is problematic as it leaves no space for models that can reproduce quantum theory.

Appendix: Calculation

The figure and the derivations in the Appendix are courtesy of the Assumptions of Physics project.

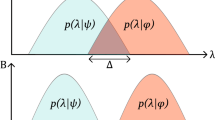
Entropy of mixed non-overlapping distributions. We want to show that, given two non-overlapping probability distributions $\rho _1$ and $\rho _2,$ the entropy of $\rho = \frac{1}{2} \rho _1 + \frac{1}{2} \rho _2$ is given by

$$\begin{aligned} H(\rho ) = 1 + \frac{1}{2} H(\rho _1) + \frac{1}{2} H(\rho _2). \end{aligned}$$

(14)

Let $U_1, U_2 \subset \Lambda$ be the respective supports of the distributions, which are non-overlapping i.e. $U_1 \cap U_2 = \emptyset$. We then have

$$\begin{aligned} H(\rho )&= - \int _\Lambda \rho \log \rho d\lambda \\&= -\int _{U_1} \rho \log \rho d\lambda -\int _{U_2} \rho \log \rho d\lambda \\&= -\int _{U_1} \frac{1}{2} \rho _1 \log \frac{1}{2} \rho _1 d\lambda -\int _{U_2} \frac{1}{2} \rho _2 \log \frac{1}{2} \rho _2 d\lambda \\&= - \frac{1}{2} \int _{U_1} \rho _1 \log \frac{1}{2} d\lambda - \frac{1}{2} \int _{U_1} \rho _1 \log \rho _1 d\lambda \\&\quad - \frac{1}{2} \int _{U_2} \rho _2 \log \frac{1}{2} d\lambda - \frac{1}{2} \int _{U_2} \rho _2 \log \rho _2 d\lambda \\&= - \frac{1}{2} \log \frac{1}{2} - \frac{1}{2} \log \frac{1}{2} + \frac{1}{2} H(\rho _1) + \frac{1}{2} H(\rho _2) \\&= 1 + \frac{1}{2} H(\rho _1) + \frac{1}{2} H(\rho _2). \\ \end{aligned}$$

Entropy of quantum mixed states. We want to show that, given two states $\psi$ and $\phi$, the entropy of the mixed state $\rho = \frac{1}{2}|\psi \rangle \langle \psi | + \frac{1}{2}|\phi \rangle \langle \phi |$ is

$$\begin{aligned} H(\rho ) = H\left( \frac{1+|\langle \psi |\phi \rangle |}{2}, \frac{1-|\langle \psi |\phi \rangle |}{2}\right) . \end{aligned}$$

(15)

Note that $\psi$ and $\phi$ will identify a two-dimensional subspace which can be thought, without loss of generality, as a qubit and therefore can be represented by a Bloch sphere. The picture represents the intersection of the Bloch sphere with the plane identified by $\psi$ and $\phi$. As $\rho$ is an equal mixture of the two states, it will be represented by the midpoint between the two. Taking the line that goes through $\rho$ and the center of the sphere, we can see that $\rho$ can also be seen as the mixture of the states $+$ and − which, since they represent equal and opposite directions, form a basis. To diagonalize $\rho$, then, means to express it in terms of + and −.

If $\theta _{\psi \phi }$ is the angle between $\psi$ and $\phi$, we have

$$\begin{aligned} |\langle \psi | \phi \rangle |^2 = \cos ^2 \frac{\theta _{\psi \phi }}{2}. \end{aligned}$$

(16)

The angle is divided by two because the angle on the Bloch sphere (i.e. in physical space) is double the angle in the Hilbert space. For example, for $z^+$ and $z^-$ the angle on the Bloch sphere would be $\pi$ and the inner product is zero (i.e. opposite directions in physical space correspond to orthogonal states).

Now we express $\psi$ and $\phi$ in terms of $+$ and −, remembering that they form a basis. Given that $\rho$ is at the midpoint, the figure is vertically symmetric. The angle between $\psi$ and +, then, is half of $\theta _{\psi \phi }$. The inner product between $\psi$ and + is

$$\begin{aligned}|\langle \psi | + \rangle |^2&= \cos ^2 \frac{\theta _{\psi +}}{2} \\&= \cos ^2 \frac{\theta _{\psi \phi }}{4}. \end{aligned}$$

(17)

Keeping in mind that we are composing vectors in the Hilbert space (and not in the geometry of the physical space) we have

$$\begin{aligned} \left| \psi \right\rangle&=\cos \frac{\theta _{\psi \phi }}{4}\left| + \right\rangle +\sin \frac{\theta _{\psi \phi }}{4}\left| -\right\rangle \\ \left| \phi \right\rangle&=\cos \frac{\theta _{\psi \phi }}{4}\left| + \right\rangle -\sin \frac{\theta _{\psi \phi }}{4}\left| -\right\rangle . \end{aligned}$$

The density matrices corresponding to the pure states are

$$\begin{aligned} \left| \psi \right\rangle \left\langle \psi \right|&=\cos ^2\frac{\theta _{\psi \phi }}{4}\left| +\right\rangle \left\langle +\right| \\&\quad +\cos \frac{\theta _{\psi \phi }}{4}\sin \frac{\theta _{\psi \phi }}{4} \left( \left| +\right\rangle \left\langle -\right| +\left| -\right\rangle \left\langle +\right| \right) \\&\quad +\sin ^2\frac{\theta _{\psi \phi }}{4}\left| -\right\rangle \left\langle -\right| \\ \left| \phi \right\rangle \left\langle \phi \right|&=\cos ^2\frac{\theta _{\psi \phi }}{4} \left| +\right\rangle \left\langle +\right| \\&\quad -\cos \frac{\theta _{\psi \phi }}{4}\sin \frac{\theta _{\psi \phi }}{4} \left( \left| +\right\rangle \left\langle -\right| +\left| -\right\rangle \left\langle +\right| \right) \\&\quad +\sin ^2\frac{\theta _{\psi \phi }}{4}\left| -\right\rangle \left\langle -\right| . \end{aligned}$$

We can now calculate the mixture

$$\begin{aligned}&\frac{1}{2}(|\psi \rangle \langle \psi | + |\phi \rangle \langle \phi |) \\&\qquad =\cos ^2\frac{\theta _{\psi \phi }}{4}\left| +\right\rangle \left\langle +\right| +\sin ^2\frac{\theta _{\psi \phi }}{4}\left| -\right\rangle \left\langle -\right| \\&\qquad =\frac{1+\cos \frac{\theta _{\psi \phi }}{2}}{2}\left| +\right\rangle \left\langle +\right| +\frac{1-\cos \frac{\theta _{\psi \phi }}{2}}{2}\left| -\right\rangle \left\langle -\right| \\&\qquad =\frac{1+|\langle \psi |\phi \rangle |}{2}\left| +\right\rangle \left\langle +\right| +\frac{1-|\langle \psi |\phi \rangle |}{2}\left| -\right\rangle \left\langle -\right| . \\ \end{aligned}$$

As $\rho$ is in a diagonal form, the entropy is given by (14).