Relaxation to Quantum Equilibrium and the Born Rule in Nelson’s Stochastic Dynamics

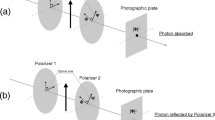
Abstract

Nelson’s stochastic quantum mechanics provides an ideal arena to test how the Born rule is established from an initial probability distribution that is not identical to the square modulus of the wavefunction. Here, we investigate numerically this problem for three relevant cases: a double-slit interference setup, a harmonic oscillator, and a quantum particle in a uniform gravitational field. For all cases, Nelson’s stochastic trajectories are initially localized at a definite position, thereby violating the Born rule. For the double slit and harmonic oscillator, typical quantum phenomena, such as interferences, always occur well after the establishment of the Born rule. In contrast, for the case of quantum particles free-falling in the gravity field of the Earth, an interference pattern is observed before the completion of the quantum relaxation. This finding may pave the way to experiments able to discriminate standard quantum mechanics, where the Born rule is always satisfied, from Nelson’s theory, for which an early subquantum dynamics may be present before full quantum relaxation has occurred. Although the mechanism through which a quantum particle might violate the Born rule remains unknown to date, we speculate that this may occur during fundamental processes, such as beta decay or particle-antiparticle pair production.

Appendix A Derivation of the \(c_n\) Coefficients

We sketch here the procedure used in Ref. [42] to decompose the wavefunction

$$\begin{aligned} \Psi (x,0) = \frac{1}{(2\pi \zeta ^2)^{1/4}} \, \exp \left[ -\frac{(x-h)^2}{4\zeta ^2} \right] \end{aligned}$$

on the basis of the eigenfunctions of the Hamiltonian (29):

$$\begin{aligned} \chi _n(x) = \Theta (x)\frac{\textrm{Ai}(x-E_n)}{\textrm{Ai}'(-E_n)}. \end{aligned}$$

Writing $\Psi (x,0) = \sum _n c_n \chi _n(x)$, the problem is reduced to finding an expression of the coefficients

$$\begin{aligned} c_n = \langle \chi _n\rangle {\psi } = \frac{1}{(2\pi \zeta ^2)^{\frac{1}{4}}}\int _0^{\infty }\textrm{d}x~\chi _n^*(x) \, \textrm{e}^{-\frac{(x-h)^2}{4\zeta ^2}}, \end{aligned}$$

where the asterisk denotes complex conjugation.

When the width $\zeta$ of the Gaussian is small enough with respect to h, the lower bound of the integral can be replaced by $-\infty$ and the $c_n$ have an analytical expression:

$$\begin{aligned} c_n&= \frac{1}{(2\pi \zeta ^2)^{\frac{1}{4}}\textrm{Ai}'(-E_n)}\int _{-\infty }^{+\infty }\textrm{d}x ~ \textrm{Ai}(x-E_n)\textrm{e}^{-\frac{(x-h)^2}{4\zeta ^2}}\\ \nonumber&= \frac{2\zeta }{(2\pi \zeta ^2)^{\frac{1}{4}}\textrm{Ai}'(-E_n)} \int _{-\infty }^{+\infty }\textrm{d}u ~ \textrm{Ai}(2\zeta u +h -E_n)\textrm{e}^{-u^2}\\&= \frac{(8\pi \zeta ^2)^{\frac{1}{4}}}{\textrm{Ai}'(-E_n)}\textrm{Ai}(h - E_n +\zeta ^4) \exp {\zeta ^2\left( h-E_n+\frac{2}{3}\zeta ^4\right) } , \end{aligned}$$

which is just the expression of Eq. (33). Note that we used the following identity:

$$\begin{aligned} \int _{-\infty }^{+\infty } \textrm{d}u~ \textrm{e}^{-u^2}\textrm{Ai}(2au+b) = \sqrt{\pi }\textrm{e}^{a^2b+\frac{2}{3}a^6}\textrm{Ai}(b+a^4). \end{aligned}$$