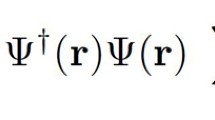A Model of Spontaneous Collapse with Energy Conservation

Abstract

A model of spontaneous collapse of fermionic degrees of freedom in a quantum field is presented which has the advantages that it explicitly maintains energy conservation and gives results in agreement with an existing numerical method for calculating quantum state evolution, namely the quantum trajectories model.

A Fermonic Eigenstates

The fact that there are only two allowed Fock states for fermionic fields, $| 0\rangle$ and $|1\rangle$, allows us to write the the fermion creation and destruction operators explicitly in terms of $2\times 2$ matrices. We define creation and destruction operators for fermions analogous to those we used for the bosonic field:

$$\begin{aligned} a= & {} \frac{1}{2}( \sigma _x -i\sigma _y) \nonumber \\ a^\dagger= & {} \frac{1}{2}( \sigma _x +i\sigma _y), \end{aligned}$$

(8)

where the $\sigma$ operators are Pauli spin operators acting on two states $|0\rangle$ and $|1\rangle$. Written explicitly, these operators are

$$\begin{aligned} a = \left( \begin{array}{cc} 0 &{} 0 \\ 1 &{} 0 \end{array} \right) , \quad a^\dagger = \left( \begin{array}{cc} 0 &{} 1 \\ 0 &{} 0 \end{array} \right) . \end{aligned}$$

(9)

It is easy to see that $a^\dagger$ has the action of taking the ground state of the system and converting it to the upper state, and vice versa:

$$\begin{aligned} a^\dagger \left( \begin{array}{c} 0 \\ 1 \end{array} \right) = \left( \begin{array}{c} 1 \\ 0 \end{array} \right) , \quad a \left( \begin{array}{c} 1 \\ 0 \end{array} \right) = \left( \begin{array}{c} 0 \\ 1 \end{array} \right) . \end{aligned}$$

(10)

As with bosonic operators, we can define the number operator

$$\begin{aligned} \hat{N} = a^\dagger a= & {} \frac{1}{4}(\sigma _x +i\sigma _y)(\sigma _x -i\sigma _y) \nonumber \\= & {} \frac{1}{4} (\sigma _x^2 + \sigma _y^2 - i[\sigma _x,\sigma _y])\nonumber \\= & {} \frac{1}{2} (1 + \sigma _z) \nonumber \\= & {} \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 0 \end{array} \right) , \end{aligned}$$

(11)

where we have used the properties of the Pauli matrices,

$$\begin{aligned}&\sigma _x^2 = \sigma _y^2 = \sigma _z^2 = 1&\nonumber \\&[\sigma _x ,\sigma _y] = 2i\sigma _z .&\end{aligned}$$

(12)

The diagonal elements of the matrix operator for $\hat{N}$ in the last line of (11) correspond to the allowed fermion occupation numbers, 0 and 1.

The creation and destruction operators also satisfy the fermion anticommutation relation:

$$\begin{aligned} \{a,a^\dagger \}= & {} \frac{1}{4} (\sigma _x +i\sigma _y)(\sigma _x -i\sigma _y) + (\sigma _x -i\sigma _y)(\sigma _x +i\sigma _y) \nonumber \\= & {} \frac{1}{4}(2 \sigma _x^2 +2\sigma _y^2 - i[\sigma _x,\sigma _y] + i[\sigma _x,\sigma _y])\nonumber \\= & {} 1, \end{aligned}$$

(13)

which is also easy to see by multiplying the explicit forms of the operators.

Note that the “spin” operators used here do not act on the spin degree of freedom which interacts with magnetic field. Instead, they act on a different degree of freedom with two states, which we have called $| 0\rangle$ and $|1\rangle$.

The Dirac fermion Hamiltonian can be written in terms of four relativistic spin-eigenstates as [21]

$$\begin{aligned} H = \sum _{\mathbf {k},s} ( \hbar \omega _{\mathbf {k},s} \hat{N}_{\mathbf {k},s,+} - \hbar \omega _{\mathbf {k},s} \hat{N}_{\mathbf {k},s,-}), \end{aligned}$$

(14)

where the index s refers to one of two spin states, and the final subscript ± refers to one of two “bands,” with either positive or negative energy. It is suggestive to rewrite this in terms of two zero point energies:

$$\begin{aligned} H= & {} \sum _{\mathbf {k},s} \left[ \hbar \omega _{\mathbf {k},s} \left( \frac{1}{2}\sigma _z^{(\mathbf {k},s,+)} +\frac{1}{2}\right) - \hbar \omega _{\mathbf {k},s} \left( \frac{1}{2} \sigma _z^{(\mathbf {k},s,-)} + \frac{1}{2} \right) \right] \nonumber \\= & {} \sum _{\mathbf {k},s} \frac{1}{2} \hbar \omega _{\mathbf {k},s} \left( \sigma _z^{(\mathbf {k},s,+)} - \sigma _z^{(\mathbf {k},s,-)} \right) , \end{aligned}$$

(15)

where $\sigma _z^{(\mathbf {k},s,\pm )}$ is the spin operator defined above, for an eigenstate with a particular choice of $\mathbf {k}$, spin s, and positive or negative energy band. This can be explicitly written as

$$\begin{aligned} \sigma _z^{(\mathbf {k},s,\pm )} = \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} -1 \end{array} \right) , \end{aligned}$$

(16)

acting on the two states $| 0\rangle$ and $|1\rangle$. This then leads to the natural interpretation that the state $|1\rangle$ corresponds to clockwise rotation in the complex plane with frequency $\omega _{\mathbf {k},s}/2$, and the state $|0\rangle$ corresponds to counterclockwise motion in the same complex plane with frequency $-\omega _{\mathbf {k},s}/2$, for the positive-energy band, as illustrated in Fig. 2, and the opposite for the negative-energy band.

Fig. 2

The number states of fermions seen as opposite rotations in the complex plane

We thus see that it is no accident that the wave function is complex, with two components given by the real and imaginary parts, and that there are two allowed occupation numbers 0 and 1. These can be seen as just two different expressions of having an intrinsic degree of freedom of the field with two allowed states. It also gives a natural way of thinking about the fact that the Schrödinger wave equation always gives clockwise rotation in the complex plane and never the opposite rotation.

The ground state of the system corresponds to all the states in the upper band rotating counterclockwise, and all the states in the negative-energy band rotating clockwise. This corresponds to an infinite negative total ground state energy, as also found in the analysis of the Dirac equation in terms of the negative-energy “Dirac sea.” As is the case with the infinite zero-point energy of photons, an infinite ground-state energy is not a fundamental problem, because it is a constant like any other constant, which can be subtracted from the total energy.

Another way to think about the fermion waves is that instead of having an oscillation corresponding to a springiness that stretches from zero to large amplitude, as in the case of bosons, the oscillation in a fermion wave corresponds to a twisting, that is, spiral wave with constant amplitude, and two choices of clockwise or counterclockwise rotation.