Absolute Distant Simultaneity in Special Relativity

There is no such thing as simultaneity of distant events.

(Einstein 1949, [5], p. 60).

Abstract

What is simultaneous with an event is what can interact with it; events have duration; therefore, any given event has distant events simultaneous with it, even according to Special Relativity. Consequently, the extension of our pre-relativistic judgments of distant simultaneity are largely preserved.

This observation of Einstein’s might be misunderstood. Indeed, I think that it has often been misunderstood, leading those who reflected on the nature of time to hold that our pre-relativistic view of simultaneity is a wholesale illusion. I shall try to explain why this is an exaggeration, resulting from a misunderstanding of the sense of ‘event’ as used by Einstein.

Science has time and again surprised us with its discoveries about the nature of the world. However, occasionally, some alleged discoveries have the air of paradox: the table can be used to explain what we mean by a solid thing, yet some scientists have claimed that it is not so; we stand up or sit down to explain what we mean by change, yet based on science, some have claimed that change is an illusion; and so on. And these claims are apparently supported by theories with strong empirical foundations. If we are to reject these paradoxical conclusions without rejecting the theories that seem to support them, we should show in what way that interpretation of the theories is wrong.

I shall try to show that the wholesale rejection of our pre-relativistic conception of the simultaneity of distant events, as well as its rendering as only frame-relative or conventional, belong to this family of merely apparent discoveries. With a proper understanding of event, simultaneity and other temporal concepts, distant simultaneity in Special Relativity can be shown to be observer- or frame-independent for a significant set of events, and to largely coincide with its ordinary pre-relativistic presumed extension, and this without introducing any privileged reference frame.

I argue for this conclusion by first considering the concept of simultaneity, then those of event and of the present, and lastly by tying all threads together in Special Relativity. As will be seen, my argument and conclusion are applicable also in General Relativity, in regions locally approximated by Special Relativity (with causal diamonds replacing Alexandroff intervals—see below).

Simultaneity

The concept of simultaneity, like other concepts of temporal order, is related to that of causation. The formulation of conceptual relations between the temporal and causal orders goes back to Hume [6],¹ Kant [7],² Poincaré [9],³ Reichenbach⁴ and others, and I shall follow their lead here. Their analyses are not identical, however, and mine is closer to Kant’s, in allowing the cause to be simultaneous with its effect (more on this below). I shall relate simultaneity to causality as follows:

What can influence and be influenced by an event, what can interact with an event, is simultaneous with that event.

Similar formulations can be found in more recent literature. Stein, for instance, while discussing the ‘specious present’ π of a perceiver, writes:

[L]et us call an event e “contemporaneous” with π if signals—interaction—influence—can occur mutually between e and π. ([13], p. 159).⁵

Other concepts of temporal order can be related to that of causality along similar lines. The past of an event consists of what is or could be a cause of that event but cannot be influenced by it (a cause which is no effect); and the future of an event consists of what can be or is affected by but cannot affect the event (an effect which is no cause).

Do these characterisations capture our concept of simultaneity? We characterise events as occurring at the same time without explaining the concept or having it explained to us in such an abstract, general way. So in virtue of which facts, if any, can such abstract characterisations claim to be analyses of the given concept?

The meaning of a concept is captured by its application and the criteria we adduce to correct misapplications or justify correct ones. The grandmother asks her grandchildren over the phone, ‘What are you doing now, children?’ and they respond, ‘We are watching a movie’: hearing them respond to her question justifies her when she reports, ‘Yesterday at 9:00 I talked with Alice and Bob; they were just watching a movie’. The conductor waves his baton and hears the attentive players respond: he can thus judge whether they are punctual, too early or too late. While I was sitting in my garden, reading a book, my neighbour was mowing the lawn: he saw me sitting there, waved to me, and I waved back. In all these cases the application is justified by interaction, or presupposes such possible interaction. This role of interaction in the application of the concept of simultaneity justifies the general characterisation above.

Such general characterisations are unlikely to coincide without any margins of error with a non-technical concept which is introduced and explained by means of examples. They are better interpreted as extracting from its use and explanations its dominant criteria of application, and giving them a definitional role in the implementation of the concept within a general theory. This is how the characterisation of simultaneity above should be seen and judged.

These conceptual characterisations are independent of any particular physical theory. When we apply them in Special Relativity (SR), they yield as the past of a point-event what is in its ‘past’, or affecting, apex-less full light cone; and as its future what is in its ‘future’, or affected, apex-less full light cone. (‘Past’ and ‘future’ are here in scare quotes in their occurrences before ‘light cone’ because otherwise they would involve a petitio.) However, according to this conception of simultaneity there is in SR no event simultaneous with a given point-event and different from it. Consequently, Stein, for instance, writes that ‘in Einstein–Minkowski space–time an event’s present is constituted by itself alone’ ([12], p. 15; cf. [13], p. 159). When something happens, nothing else happens with it.—But before accepting this radical conclusion, we should examine what ‘event’ means.

Events

When we apply the concept of event, we always apply it to something with a duration, to an interval. A standard dictionary definition of an event is a thing that happens or takes place, and this does not exclude events that take some, and even much time. Typical examples of the use of ‘event’ include ‘The party was a great event’ and ‘WWII was the most significant event of the twentieth century’: in both cases the event took some time, in the latter case 6 years. I shall call the events to which we actually apply our concept of event, actual events, to distinguish them from theoretical ones, namely from those that are idealisations within a theory (in a sense clarified below). As far as our concept of an event is applicable, we apply it only to intervals, not to durationless points. The temporal point has no empirical reality.

Of course, in our physical theories we do talk about temporal points. And I am not arguing here that temporal points, in some sense, are physically impossible. However, the temporal point events of our theories do not function as designators of such hypothetical physical point events: their contribution to the theory is independent of the existence of any such hypothetical points. If we discovered that no temporal point exists, this would not give us a reason to reject our theories as mistaken. Rather, the temporal point events of our theories function as the limit of a process of precisification. They are the limit of a process of considering the properties of shorter and shorter interval events. Physics’ temporal points are an idealisation—not in the sense of being better, but in the sense of taking a process of precisification to its mathematical, theoretical limit. This is their function within the theory.

The temporal point might only be an imaginary limit. Aristotle might have been right when he claimed that time is composed not of instants but of intervals (Physics 239b30, [1]). But whether or not this is so, the function of the temporal point in our physical theories is as the limit of a process and not as a designative term. Physics does not commit us to the existence of point events.

In addition, actual events are also always vague intervals, in the sense of not having a beginning or an end which can be defined with as high a degree of accuracy as we wish, namely, beginning and end which are point events. The party ended when the last group of people left our apartment, but this cannot be determined more accurately than an interval of a few seconds; WWII started with the German invasion to Poland and the ensuing declarations of war on Germany by Britain, France, and other countries—a process of days. Actual events are even necessarily vague: an actual event has actual events as its beginning and end, and therefore it begins and ends with events that have some duration.

Now

Similar considerations to those about the concept of event apply to other temporal concepts. I shall consider here our concept of the present, as designated by ‘now’. I consider this concept because it is widely discussed in the literature on Special Relativity and the philosophy of time. I also wish to contrast my approach with related ones found in the literature, and these focus mainly on the concept of the present.

‘Now’, like ‘event’, always designates an interval. The very utterance of ‘now’ takes time, and therefore it cannot normally designate anything shorter than a few milliseconds. But usually it stands for longer intervals. When the grandmother asked her grandchildren over the phone, ‘What are you doing now, children?’ a period of at least a few minutes was meant. An example of a use in which the word stands for a longer period is, ‘We are now living in the information age’. Such an extended and highly vague interval is also apparent in book titles: The Way We Live Now; Now We Are Six. But even when we try to capture a shorter moment, as in the orders ‘Now!’ or ‘Do it right now!’, an interval is always meant, as can be seen if we consider what would count as complying or failing to comply with such orders.

These observations on ‘now’ apply to other phrases designating the present as well (‘at present’, ‘at this very moment’, etc.): these also always stand for a vague interval, whose duration changes according to circumstances. Not to belabour the point, I’ll give only a few dictionary examples of the use of ‘present’: At present she’s working abroad; The play is set in the present; I am very busy at the present moment.

Notice that I am not talking about any specious or psychological present, the present as the subject allegedly experiences it (whatever this might mean⁶). I am discussing meaning, not experience, and I claim that when we apply ‘now’ and similar phrases they always designate an interval. On my account, there is nothing specious in what ‘now’ stands for, and my considerations involve no reference to any experienced present.

By contrast, earlier philosophical work that has tried to save something of the apparent simultaneity of distant events has done that by reference to the alleged specious present (Stein [13], Arthur [2], Savitt [11]). Consequently, unlike me, they are committed to the coherence of the idea of such a present. Arthur, for instance, after having noted that the concept of the specious present has been criticised, refers to defences of the idea, which shows that he relies on its being coherent. He also remarks, implying that this is problematic for him, that ‘the notion of the specious present is not without its difficulties’. These writers also try to give an estimation of the duration of this ‘psychological present’. All this is irrelevant to my considerations.

Although my paper is related in some respects to these earlier works, the approaches are thus fundamentally different. As will be apparent soon, I am trying to give an account of distant simultaneity by relating considerations on meaning to the theory of Special Relativity. I am not referring at any stage to an experiencing subject. The mentioned earlier works, however, try to show how SR reality is projected into our psychology or subjective experience, often contrasting the results of this projection with the strict physics of SR. Stein tries to explain what he takes to be our alleged intuitions about simultaneity, intuitions which he finds ‘illusory’, and he discusses ‘our ordinary experience, the time that we experience as a “moment”—a specious present’ (p. 162). Arthur looks for ‘an acceptable construal of becoming, and one that “saves the phenomenon” of our experience of the present too’. He similarly writes that ‘this discrepancy between theory and experience can be bridged by introducing the concept of the specious present’ (my italics). And Savitt defines his project by the slogan, ‘Philosophy of time should aim at an integrated picture of the experiencing subject with its felt time in an experienced universe with its spatiotemporal structure’; the specious present is then introduced. These writers also discuss the present, a focus which is a result of their interest in the experiencing conscious subject, while I primarily discuss distant simultaneity between events, be they past, present or future, and independently of whether they involve any conscious subject. I shall also try to show that neither illusion nor discrepancy is involved, and that recourse to a specious present is redundant.⁷

Distant Simultaneity in Special Relativity

Let us now tie together the different threads in SR. Any actual event in an observer’s history, or better, in the history of any physical entity (I am not allotting any special status to consciousness or mentality, namely, to an observer taken literally), is an interval. What is simultaneous with this event, according to our causal conception of simultaneity, is what can influence and be influenced by the physical entity during this interval, what can then interact with it. This is determined independently of frame of reference, and is therefore absolute.

The set of events that stand in this double causal relation to an event e is determined as follows. The past light cone that has as its apex the last moment of e consists of all events that can, as a whole, influence e or some part of e; the future light cone that has as its apex the first moment of e consists of all events that can, as a whole, be influenced by e or by some part of e; their intersection thus consists of all events that can, as a whole, both influence some parts of e and be influenced by some parts of e. (As a whole, in the sense that each part of such an event can both influence some parts of e and be influenced by some parts of e.) This intersection is a double cone, called the Alexandroff interval⁸ and illustrated as follows:

Any event inside the Alexandroff interval of an event can both be influenced by some earlier parts of the given event and influence some of its later parts. Any event outside the Alexandroff interval either cannot influence the event, or cannot be influenced by it, or both. Parts of an event outside the Alexandroff interval of a given event may be able to influence or be influenced by the given event, but not the event as a whole. The Alexandroff interval of a given event thus consists of the events simultaneous with that event

Although geometrically, the Alexandroff interval is a double cone, to describe it as such might be somewhat misleading: from an ordinary human perspective, it looks much more like a cylinder. If we measure distances in metres and time in seconds, then the opening angle of the Alexandroff double cone is 179.9999996 degrees; if we measure them in kilometres and hours, it is 179.99999990: a straight angle for all standard intents and purposes.

Accordingly, from this perspective, any actual event has a substantial set of distant events simultaneous with it. If we go back to the grandmother, say in Europe, talking with her grandchildren in distant Australia, then her present, designated by her use of ‘now’ in the question ‘What are you doing now, children?’ and standing for a vague interval of a few minutes, coincides with that of her distant grandchildren. Special Relativity doesn’t force us to change anything in this use of our concept of distant simultaneity. And this would be true for the great majority of standard ascriptions of simultaneous occurrence to distant actual events. Thus, frame-independent distant simultaneity between events exists in Special Relativity, and it applies to most common ascriptions of simultaneity.

Some distinctions from common ways of thinking of simultaneity should, however, be noted. My definition of simultaneity by means of causal concepts was intended to capture, or at least approximate, our concept of simultaneity, and not our judgments of simultaneity. It was not meant to yield a concept that coincides with all our pre-theoretical judgments of simultaneity. Before we learn about the finiteness of the speed of light, we take the night sky to show us the stars as they are at the moment we see them; but once we learn about that, as we had done long ago with Römer, before SR was developed, we judge what we see to belong to the past. Our concept of simultaneity was not affected by this discovery, although our applications of it were.—All the same, concept and judgments are not independent: we explain many of our concepts and learn them by means of particular applications, so the correctness of a substantial part of these applications is presupposed by the meaningfulness of the concept. Accordingly, ordinary applications of a concept must as a rule be preserved by its analysis, if it is to be meaningful or coherent. As can be seen, the causal definition above does that.

The Alexandroff interval conception of simultaneity, although it follows from our ordinary criteria of judging one event simultaneous with another, is in another respect an extension of our simultaneity concept to new circumstances. In pre-theoretical applications of our concept of simultaneity, we never considered, say, cases in which the event e₂ judged simultaneous with event e₁ is sufficiently remote from e₁ so that the temporal extension or ‘height’ of e₁′s Alexandroff double cone at e₂ has shrunk to a small fraction of its maximal height, at e₁. In this respect this conception is an optional, albeit natural way of extending our simultaneity concept to new circumstances. It does, however, incorporate our pre-relativistic criteria and ratify the application of this concept in ordinary circumstances.

Extension-wise, the concept of simultaneity as applied in SR is different from the one that applies in the world of Newtonian mechanics. Simultaneity in SR is limited in space: if an event lasts time t, then according to the Alexandroff interval conception, events simultaneous with it exist only up to a distance of ct/2 from its location. In the world of Newtonian mechanics, by contrast, since there is no upper limit on the speed of propagation of causal influence, any event has at any distance from it events simultaneous with it.

However, this aspect of the Newtonian concept of simultaneity is not part of our pre-theoretical one but is a result of its application within the world as described by Newtonian mechanics (which is not our world). We introduce, explain and apply our concepts of at the same time, earlier and later not by means of a description of the temporal relations between ourselves and distant galaxies but when talking about mundane events. Pace Stein, our ordinary concept of at the same time does not involve any ‘“intuitions” of something like “cosmic simultaneity”, or a “cosmic present”’ ([13], p. 162). The Newtonian theoretical extrapolation of our spatiotemporal concepts might be the simplest one, but it is still an extrapolation, and one that in fact proved to be wrong. Accordingly, although Special Relativity forces us to abandon some aspects of our concept of simultaneity as applied in the world of Newtonian mechanics, this does not mean that it modifies the concept or makes it inapplicable in our world.

Special Relativity did have some unforeseen consequences for the applicability of our concept of simultaneity. The fact that when we look beyond the moon, talk of simultaneity doesn’t always make sense wasn’t anticipated (the Alexandroff interval has finite dimensions, and therefore the simultaneous has spatial boundaries). Equally unanticipated was the fact that events lasting for a few nanoseconds can’t be said to be exactly simultaneous with similar events occurring just a few miles away (as we converge towards a point-event, the Alexandroff interval converges to zero in all dimensions). But these unexpected facts about inapplicability to the very distant or the extremely brief do not mean that there is anything problematic in the ordinary, pre-theoretical applications of the concept.

Another unexpected result, related to those just mentioned, is that if one event e₁ lasts less time than another event e, then it is possible that e₁ happens while e does, although no part of e is simultaneous with e₁. This happens if the Alexandroff interval of e contains e₁, while e is outside the Alexandroff interval of e₁. For instance, when we watch (= e) an almost instantaneous nuclear reaction in a bubble chamber (= e₁), the reaction occurs while we are watching it, although no interval in our history can be said to be simultaneous with it. In causal terms this means that although the scientists during the experiment can both influence and be influenced by the nuclear reaction, no stage in the scientists’ history could, as a whole, both influence and be influenced by the reaction. This result shows the limitations of the extrapolation of our concept of simultaneity to new kinds of circumstance, and therefore, although unanticipated, it does not reveal any problem with the ordinary applications of the concept of distant simultaneity. I also think that this result captures the actual way we came to describe the temporal relations between such events.

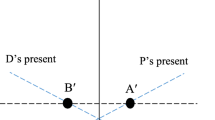
Relativistic space–time is usually divided into three or four regions relative to a given event: a time-like region, which can be further divided into a future region and a past region; a light-like surface, which I shall here count as belonging to the time-like regions; and a space-like region, containing all events which are neither in the future nor in the past of the given event. This trifold classification—past, future, and space-like—is justified relative to point-events. However, if we consider actual events, which always have a duration, then relative to each actual event space–time should be divided into four regions. To the three regions mentioned above we should add a present region, constituted by the Alexandroff interval. Moreover, given, first, that actual events always have vague boundaries, and secondly, that as mentioned above, a more realistic diagram of lines representing the propagation of light should have them roughly horizontal, the vague boundaries between the past and present regions, as well as those between the present and future ones, should merge in the vicinity of the event. The space-like region should start only some distance from the event, this distance depending on the degree of vagueness of the event’s beginning and end. The resulting diagram should therefore have only three regions near an event: past, present and future:

This diagram of space–time without idealisation to point-events clearly shows that from an ordinary perspective, Special Relativity affects the applicability of our concept of simultaneity when very large distances relative to the event duration are concerned, but that otherwise there is no problem in the classification of less distant events as simultaneous. Closer to home, we have only past, present and future