Comment on Healey’s “Quantum Theory and the Limits of Objectivity”

Abstract

In this comment we critically review an argument against the existence of objective physical outcomes, recently proposed by Healey [1]. We show that his gedankenexperiment, based on a combination of “Wigner’s friend” scenarios and Bell’s inequalities, suffers from the main criticism, that the computed correlation functions entering the Bell’s inequality are in principle experimentally inaccessible, and hence the author’s claim is in principle not testable. We discuss perspectives for fixing that by adapting the proposed protocol and show that this, however, makes Healey’s argument virtually equivalent to other previous, similar proposals that he explicitly criticises.

Introduction

In a recent paper [1], Healey proposes an argument to supposedly show that there exist situations in which quantum measurements cannot have “a unique, objective, physical outcome”. At the same time the author critically analyses two similar arguments put forward in [2] and [3], concluding that their “dependence on questionable implicit assumptions severely limits their significance”. Healey’s argument, however, contains a series of problems and attempting to resolve them leaves it prone to the same type of criticism raised about [2].

The argument is based on the computation of a set of correlation functions that violate a Bell-like inequality. This violation should signify the non-existence of objective physical outcomes in quantum mechanics. The argument involves a sequence of successive measurements that have been performed by different observers in every single run of a Bell’s inequality test. Two of these measurements are performed by observers Carol and Dan (who take the role of “Wigner’s friends” [5]), the others by “superobservers” Alice and Bob, who describe the “friends’ ”measurements unitarily and are capable of undoing them.

In deriving his no-go theorem, Healey uses the standard quantum formalism to compute expressions for correlation functions, but gives no prescription on how to relate these expressions to observable quantities. Moreover, if one assumes the standard prescriptions of quantum theory to relate all correlations entering the Bell-like inequality with recorded counts, these counts would not give rise to violation of the inequality in the proposed protocol. Hence, in the protocol it is not possible, even in principle, to test Healey’s claim against the existence of objective physical outcomes in quantum mechanics. In this respect, we would like to stress that a physical theory is composed of theoretical symbols provided with a consistent calculus to combine them (the formalism), together with a series of rules of correspondence. In the words of Jammer [4], “The formalism F, the logical skeleton of the theory, is a deductive, usually axiomatised calculus devoid of any empirical meaning; [...] To transform F into a hypothetic deductive system of empirical statements and to make it thus physically meaningful, some of the nonlogical terms, or some formulae in which they occur, have to be correlated with observable phenomena or empirical operations. [...] F without R is a meaningless game with symbols”.

The protocol proposed in Ref. [1] faces three main problems:

• 1. The violation of the proposed Bell’s inequality cannot, not even in principle, be tested, because in no region of space–time are the experimental data from which all the correlation functions can be extracted available. On the contrary, in standard Bell’s experiments the data is generated in space-like separation but eventually collected by somebody who lies in the future light-cone of the two measurement apparata which generated the data. In Healey’s proposal the data of Dan and Carol are necessarily “erased” (from the universe) according to the suggested unitary evolution before Alice’s and Bob’s measurements. So, although Carol and Dan could—after they generate their data—send the results out to somebody in the common future of their measurements who can then extract the correlations, any trace of that data must be erased before Alice’s and Bob’s measurement outcomes are obtained. Therefore, no observer dwelling in space time can ever test the inequality.

• 2. If one wants to make the argument testable, one needs to attribute an operational meaning to the computed expressions for the correlation functions. In standard quantum mechanics, the correlation functions correspond to the relative number of counts in respective measurements. However, in the protocol of Ref. [1] Alice and Bob could only evaluate all correlation functions, if they would register the counts from Carol’s and Dan’s measurements (i.e. if Alice and Bob actually perform measurements). In that case they need to use the standard “state-update rule” for the prediction of their subsequent measurements in contrast to the assumption of Ref. [1], wherein a measurement is assumed to proceed in accordance with a unitary interaction.¹ However, then, there would be no violation of the Bell’s inequality.

• 3. If Alice and Bob were to test their predictions and actually violate a Bell’s inequality with collected data, one would have to adapt the protocol in a way that renders the setup analogous to that proposed in Ref. [2]. In that case, however, one further has to require the standard assumptions for testing the violation of Bell’s inequalities namely “freedom of choice” and “locality”.

Description of the Protocol

Similarly to proposals [2] and [3], the gedankenexperiment introduced in [1] involves two “Wigners” (Alice and Bob) and their respective “friends” (Carol and Dan). The latter each receive one spin-1/2 particle (whose states are labeled by 1 and 2, respectively) of a maximally entangled pair. The protocol describes a series of operations applied by the four experimenters from the point of view of the two superobservers.

With respect to Alice’s lab, the protocol is defined by the following steps:

0: :

State preparation:

$|\psi (0) \rangle = \frac{1}{\sqrt{2}}\left( |\uparrow \rangle _1 | \downarrow \rangle _2 - | \downarrow \rangle _1 | \uparrow \rangle _2 \right) | r \rangle _C | r \rangle _D$. Where $| r \rangle _C$ and $| r \rangle _D$ are the initial (“ready”) states of Carol and Dan, respectively, that will record the outcome of their spin measurements (and therefore do not need to be initially further specified).

1: :

Dan measures: $|\psi (0) \rangle \rightarrow |\psi (1) \rangle = U_D | \psi (0) \rangle$; where $U_D |\downarrow _d \rangle _2 | r \rangle _D = | \text {``D sees 2} \downarrow _d \text {''}\rangle _{2D}$ := $|\downarrow _d \rangle _2 |\text {``sees }\downarrow _d\text {''}\rangle _D$(and equivalently for $|\uparrow _d \rangle _2$).

2: :

Carol measures: $|\psi (1) \rangle \rightarrow |\psi (2) \rangle = U_C | \psi (1) \rangle$; where $U_C |\downarrow _c \rangle _1 | r \rangle _C = | \text {``C sees 1} \downarrow _c \text {''}\rangle _{1C}$ (and equivalently for $|\uparrow _c \rangle _1$).

3: :

Alice undoes Carol’s measurement by applying $U_C^{\dagger }$:

$$\begin{aligned}&|\psi (2) \rangle \rightarrow |\psi (3) \rangle =\\&\quad =\frac{1}{\sqrt{2}}\left( |\uparrow _d \rangle _1 | ``\text {Dan sees 2} \downarrow _d\text {''} \rangle _{2D}\right. \\&\qquad \left. - | \downarrow _d \rangle _1 | ``\text {Dan sees 2} \uparrow _d\text {''} \rangle _{2D} \right) | r \rangle _C =| {\psi (1)} \rangle . \end{aligned}$$

4: :

Alice measures, corresponding to a unitary $U_A$. Analogous to $U_C$, the unitary $U_A |\downarrow _a \rangle _1 | r \rangle _A = | \text {``A sees 1} \downarrow _a\text {''}\rangle _{1A}$ (and equivalently for $|\uparrow _a \rangle _1$)

5: :

Bob undoes Dan’s measurement by applying $U_D^{\dagger }$.

6: :

Bob measures corresponding to a unitary $U_B$, which is defined as $U_B |\downarrow _d \rangle _2 | r \rangle _B = | \text {``B sees 2} \downarrow _b\text {''}\rangle _{2B}$ (and equivalently for $|\uparrow _b \rangle _2$) resulting in the state $|\psi (6)\rangle = U_A U_B |\psi (0) \rangle$.

Healey claims that this protocol allows to predict, in every run, the correlation functions between the outcomes of different observers.

After step $\mathbf {2}$, Alice predicts

$$\begin{aligned} E(c,d)=-\cos (c-d) \; , \end{aligned}$$

(1)

where $c-d$ is the relative angle between measurement directions $\mathbf {c}$ and $\mathbf {d}$.

After step $\mathbf {4}$, she predicts

$$\begin{aligned} E(a,d)=-\cos (a-d)\; . \end{aligned}$$

(2)

With respect to Bob’s laboratory, in relative motion with respect to Alice’s (see section “Analysis of the Protocol” for a discussion), the protocol looks as follows.

0*: :

State preparation:

$|\psi (0) \rangle = \frac{1}{\sqrt{2}}\left( |\uparrow \rangle _1 | \downarrow \rangle _2 - | \downarrow \rangle _1 | \uparrow \rangle _2 \right) | r \rangle _C | r \rangle _D$.

1*: :

Carol measures: $|\psi (0) \rangle \rightarrow |\psi (1^*) \rangle = U_C | \psi (0) \rangle$.

2*: :

Dan measures: $|\psi (1^*) \rangle \rightarrow |\psi (2^*) \rangle = U_D | \psi (1^*) \rangle$.

3*: :

Bob undoes Dan’s measurement by applying $U_D^{\dagger }$: $|\psi (2^*) \rangle \!\rightarrow \! |\psi (3^*) \rangle \!=\! | {\psi (1^*)} \rangle$.

4*: :

Bob measures, which is described by a unitary $U_B$.

5*: :

Alice undoes Carol’s measurement by applying $U_C^{\dagger }$.

6*: :

Alice measures corresponding to a unitary $U_A$, resulting in the final state $|\psi (6^*)\rangle = U_A U_B |\psi (0) \rangle$.

After step $\mathbf {4^*}$, Bob predicts

$$\begin{aligned} E(c,b)=-\cos (b-c)\; . \end{aligned}$$

(3)

Finally, after step $\mathbf {6}$, Alice (or alternatively Bob, after step $\mathbf {6^*}$) can compute the correlation

$$\begin{aligned} E(a,b)=-cos(a-b) \end{aligned}$$

(4)

for their observed outcomes a and b.

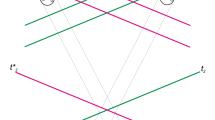
The main feature claimed by Healey—which supposedly improves the scheme in Ref.  [2]—is that in the setup of [1] there exist, for every run of the protocol, four regions of space–time where each of the observables $A_a$, $B_b$, $C_c$ and $D_d$ takes a unique, definite value (although admittedly they never co-exist, in so far as the measurement outcomes of the observers Carol and Dan are erased by the superobservers Alice and Bob). These regions are illustrated in Fig. 1. For the sake of clarity and convenience for our proposed modification of the protocol—and in accordance with Healey’s statement that the two laboratories are moving apart with constant velocities—we represent the space–time diagram in Fig. 1 with slight differences from the original in Ref. [1]. This leads to swapping points 1 (respectively 1*) with 2 (respectively 2*) interchanging the order of Carol’s and Dan’s measurements in both reference-frames, but does not affect the argument in any way.

Analysis of the Protocol

We present here what we consider the fundamental problems with the proposal in [1] and discuss perspectives for fixing them.

Unitary Measurements and Evaluating Probabilities

In order to test whether quantum mechanics violates the objectivity of physical outcomes in the sense of Healey, one would need to find an operational way that would enable, at least in principle, to collect statistics from which the correlation functions could be computed and inserted into the Bell’s expression. In the protocol there is no space–time region where the measurement counts for all four measurement settings—which would enable the computation of the four correlations functions—are accessible in principle, because the data of Carol’s or/and Dan’s measurements are erased before the data of Alice’s and Bob’s measurements get established.

Moreover, the computed correlation functions do not all correspond to correlations between measurement outcomes because the “measurements” of Carol and Dan are considered as unitary transformations. This gives rise to multiple problems in the argument. Firstly, the correlation functions E(a, d) and E(c, b) are computed from two different reference frames, namely the one of Alice and of Bob respectively (see Fig. 1). It is known that the notion of quantum state, and hence of entanglement as well as the computed correlation functions for a given state are reference-frame dependent. This is a consequence of the relativity of simultaneity in different reference frames [6]: observers in different reference frames assign different quantum states on their respective slices corresponding to t = const. It is thus not clear to us what combining expression (1)–(4), which are computed for different reference frames and thus for different quantum states, in a CHSH-like inequality is supposed to signify. We note that there would be no ambiguity, if the correlation functions would refer to measurement data, since those are of course reference frame independent.

Fig. 1

Space–time diagram of Healey’s protocol. Two laboratories (containing Alice-Carol-system 1 and Bob-Dan-system 2, respectively) are moving apart with constant velocity. Four agents perform a series of measurements (the order of $U_c$ and $U_d$ has been changed from the original protocol to avoid misunderstanding and to conform to the modified protocol of Fig. 2). In every run of the protocol there supposedly exist four space–time regions wherein correlations between the results could be established. The areas highlighted in yellow are those where, with respect to both reference frames, the measurements entering the expressions of the correlation functions have been performed and neither of them has been undone. Hence a correlation function can be agreed upon in both reference frames, whereas the blue (red) areas are those where correlations are relative to Alice’s (Bob’s) reference frame only

Secondly, one could equally assign different values to the reference frame dependent correlation functions E(b, c) and E(a, d) by an argument similar to that proposed in Ref. [7]. More concretely, with respect to Alice’s reference frame, the calculated correlation function $E(c,b) = 0$ for all times. For times between $t_1$ and $t_3$ the register b is in a fixed pre-measurement state $|r\rangle _b$ and the results $c=+1$ and $c=-1$ occur with equal probability, whereas for times between $t_3$ and $t_6$ the result of c is erased and the register is reset to it initial state $|r\rangle _c$ and the results $b=+1$ and $b=-1$ occur with equal probability. The mean value of the product of c and b (i.e. the correlation function) is zero independently of choice of the value assigned to the fixed states of the registers. Similarly, Bob would predict $E(a,d)=0$, since in his reference frame result d is erased before a is measured. Combining either of the two with (1), (4) and either (2) or (3) respectively still gives a violation of the CHSH-inequality, but with a different value of $3/\sqrt{2}$. However, combining the predictions of both reference frames, as done in [1], but using both $E(c,b)=0$ and $E(a,d)=0$ instead of (2) and (3) results in no violation of Bell’s inequality:

$$\begin{aligned} \begin{aligned}&|E(a,b)+E(b,c)+E(c,d)-E(a,d)|\\&\quad =|E(a,b)+0+E(c,d)-0|\le 2. \end{aligned} \end{aligned}$$

(5)

Note that we are not claiming that Eq. (5) as opposed to using Eqs. (1)–(4) is the correct way to evaluate correlation functions for the Bell test, but rather that there is an ambiguity in how to evaluate unobservable, reference-frame dependent quantities. Without specifying how the computed expressions are related to observable quantities, there seems to be no physical motivation to favour the one combination of values which leads to the alleged violation, over the one that predicts no violation of the inequality. Clearly, all these ambiguities appear because the computed expressions for correlation functions are not associated to observable quantities. If the four measurements would be identified with four space–time points in which counts are registered, then the correlations between these counts will be reference frame independent and there would be no problems. However, then no violation would be observed in the protocol.

Fig. 2

Space–time diagrams of the modified protocol. The modified protocol allows the observers to chose which operations to perform on their local system in each run. This allows to provide an operational meaning to the correlations between measured quantities. At the end of the protocol the highest-level observers, Alice and Bob, unambiguously agree on the correlation functions: i) E(a, b), ii) E(b, c), iii) E(a, d), iv) E(c, d). The colour legend is defined in Fig. 1

A Modified protocol that Gives the Expected Probabilities Suffers the Same Criticism that Healey Raises

The protocol proposed in Ref. [1] allows to observe in principle only the correlations between a and b (since at the end of the protocol the measurement results of Carol and Dan have been erased). For the “superobservers” Alice and Bob to evaluate all the correlation functions and test the proposed CHSH-like inequality in Ref. [1], one is forced to adapt the protocol to one wherein Alice can choose to measure either a or c and Bob either b or d by deciding whether or not to erase the measurement outcome of their “friends”. In the latter, each “superobserver” (Alice and Bob) performs the same measurement as their associated observer (Carol and Dan, respectively). Since in that case one allows for a “choice of setting” one has to ensure “locality” and “freedom of choice” as required in a standard Bell-inequality setup. In the original protocol of Healey, “locality” is not required, since all four measurements are fixed and performed in each round. Any assignment of four definite outcomes of course satisfies a Bell-like inequality by construction.

In the adapted protocol, Alice not erasing Carol’s measurement, but rather measuring Carol’s observable, allows for computing E(b, c), whereas Bob not erasing Dan’s measurement, but performing the same measurement instead will make E(a, d) experimentally accessible; whereas, both the “superobservers” not undoing their friends’ measurements allows for measuring E(c, d). This adapted protocol is illustrated in Fig. 2. Note that in the rounds where Alice, Bob or both decide to measure the observables of Carol or Dan or both respectively, and register counts in the respective measurements, they cannot erase these counts in a unitary fashion to continue with the subsequent measurements. Upon registering the counts in the first measurements, Alice and Bob will observe a statistics in the subsequent measurement, which is compatible with the state-update rule and not with a unitary transformation. The continuation of the protocol in its original form [1] but with the application of the state-update rule would not lead to a violation of Bell’s inequalities. It appears therefore that the only way to give an operational meaning to accessing the correlation functions and hence to the verification of Healey’s argument is to assume that in each run Alice and Bob chooses one of the two measurement settings—a step that was criticised by Healey.

It, therefore, seems to us that this setup is subject to the same criticism as [2] when one requires the actual computation of the terms violating the CHSH-inequality to correspond to measured values. Otherwise, we think Eqs. (1)–(4) need further justification.

In conclusion, the only possibility for the correlations to be in principle measured is to revise the scheme in a way that does not allow to be sure that the four values coexisted in each round, therefore suffering the very same criticism that was addressed towards proposal [2]. However, one can make a stronger assumption that these values are fixed even when they are not all co-measured, which then allows to derive the no-go theorem of Ref. [2].