What are the consequences that relativity theory has for the notion of the present, or more generally for our everyday notion of time? Famously, Minkowski said that given the experimental corroboration of relativity theory, “space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.”Footnote 1 A strong formal result appears to vindicate Minkowski’s view that before the background of the space-time physics of special relativity theory, time can only be a derivative, dependent notion: there is no sensible way to define a notion of simultaneity based solely on the resources of the spatio-temporal ordering of events in Minkowski space-time. What are the metaphysical consequences of this result?

Our commonsense metaphysics of time is, arguably, best expressed by presentism, which holds that “the present simply is the real considered in relation to two particular species of unreality, namely the past and the future” [32, p. 245]. Is presentism compatible with relativity theory, or does relativity theory refute presentism? The issue is complicated. Does relativity theory have an impact on metaphysics or on everyday notions at all? And if it does, what precisely is the notion of the present whose independent reality is threatened by relativity theory, and how can that threat be spelled out in a formally precise way?

In this paper, we will distinguish two different notions of the present, one based on simultaneity and one based on co-presentness. Simultaneity invokes a static role of the present in singling out something like a temporal location of an event (a time coordinate). Co-presentness, on the other hand, invokes a dynamic role of the present in separating a fixed past from an open future and in thereby anchoring a notion of coexistence. We hold that it is the latter role that is important for presentism as a doctrine in the metaphysics of time, and we will show that a relativity-proof notion of the present in its dynamical role can be defended by exploiting the idea that dynamic change must be based on the indeterministic realization of possibilities for the future.

Given the current state of the debate, the success or failure of such a defense must be assessed via formal results. We thus need to spell out which formal resources relativity theory offers, and how these can be used to ground a notion of the present. In this paper we will work within a formal framework that allows for making precise sense of spatio-temporal indeterminism and of the fixedness of the past vs. the openness of the future: branching space-times (BST; [4]). Our guiding idea will be that two events are dynamically co-present if they share exactly the same fixed past. In working out the formal details of this idea, we will make use of the fact that BST offers a rich notion of modal correlations, based on which we will be able to extend the notion of a fixed past.

Our paper is structured as follows. We introduce the basics of the debate about defining the present in special relativity in Sect. 1. We provide some motivation for our approach, which involves an extended present, in Sect. 2. In that section we stay within the Newtonian theory of branching time, which is a predecessor to BST. The main ideas of branching space-times and the necessary formal definitions are then introduced in Sect. 3. In Sect. 4 we prove our main formal result, Theorem 1, which states that a non-trivial relation of co-presentness can be defined in terms of the resources of BST. We discuss two possible definitions of co-presentness and prove their equivalence, and we indicate how space-like modal correlations can extend the dynamic present. We conclude in Sect. 5.

1 The Problem of Defining the Present in Special Relativity

In the Minkowski space-time of special relativity, each so-called event (element of the space-time) can be uniquely identified via its space-time coordinates, a set of four real numbers. There is, however, no unique way to divide up these coordinates into a three-dimensional spatial and a one-dimensional temporal part. Such a division is always relative to an inertial reference frame, and none of those frames is preferred—the principle of relativity states that all frames have to be treated on a par. One might therefore believe that only frame-invariant properties and relations have independent, objective reality, whereas other properties and relations cannot be taken metaphysically seriously.

Some important relations among events are frame-invariant. For example, whether one event can causally influence another one is independent of the choice of a reference frame: the causal order on Minkowski space-time is frame-invariant. Events that cannot causally influence one another are called “space-like related”; that relation, too, is frame-invariant. But whether two space-like related events have the same temporal coordinate—whether these events occur at the same time—depends on which frame one considers. The simultaneity of distant events is frame-relative.

These basic truths about the structure of Minkowski space-time can be translated into a formal claim about the definability of a notion of simultaneity. There is widespread agreement that such a notion of simultaneity has to be transitive, reflexive, and symmetric, i.e., it has to be an equivalence relation.Footnote 2 It follows that the simultaneity relation cannot be the relation of space-like relatedness, as that relation is not transitive. And there are no other sensible options either, as shown by Van Benthem’s theoremFootnote 3: If a relation R is definable on the basis of Minkowski space-time alone, it has to be invariant under that structure’s automorphisms, which include the Poincaré group and contractions. But once there are x, y for which \(x\ne y\) and xRy, one can employ suitable automorphisms to show that xRz for any event z. Thus, there are only two equivalence relations that can be defined on Minkowski space-time, identity and the universal relation. None of these provides a sensible notion of simultaneity: on the first option, as each event is identical only to itself, each event would be simultaneous only with itself, and on the second option, simultaneity would not discriminate among events at all. Therefore, no frame-invariant notion of simultaneity can be defined on the basis of the Minkowski space-time of special relativity.

It seems, therefore, that simultaneity cannot be an objective relation. This, in turn, might mean that the present is just a subjective notion, or even an illusion, which would completely undermine presentism. This challenge concerns the tenability of an objective notion of simultaneity as a necessary, not as a sufficient condition of the tenability of the doctrine of presentism as a whole. The challenge, therefore, arises prior to and independently of the additional question of how, assuming that such an objective notion is available, one should model the phenomenon of the passage of time. In this paper, we do not discuss the latter question. There is fairly widespread agreement in the literature that an indexical treatment of the passage of time is appropriate (see, e.g. [10]).

The metaphysical consequences of the mentioned formal result—no frame-invariant notion of objective simultaneity is definable in special relativity theory—are debatable. There appear to be four main ways of reacting:

  1. 1.

    Rejection of any metaphysical status of special relativity. It is not implausible to just shrug off any suggested metaphysical import of special relativity, pointing out that that theory is only valid within its range of applicability, which is far from universal. Many well established empirical facts, from details of the orbit of planet Mercury to gravitational effects on satellites or, recently, to gravitational waves cannot be modeled on the basis of special relativity theory alone. In this sense, special relativity is empirically refuted, and therefore it is implausible to expect to get any metaphysical mileage out of it. If we are looking for a space-time theory to provide metaphysical guidance, we need to look at the general theory of relativity, or even at a successor to that theory describing some form of quantum gravity. It may well be that such a theory will provide additional resources. For example, some cosmological models of general relativity allow for the definition of a class of fundamental observers that can anchor an absolute notion of cosmic time. Given these resources, one can then define two events to be absolutely simultaneous iff they happen at the same cosmic time.Footnote 4 So the whole discussion involving special relativity might be a non-starter.

  2. 2.

    Acceptance and revision of temporal notions. If one accepts the apparent indefinability of simultaneity as proof that the notion of the present makes no objective sense, one can try to live without it. While this attitude had already been recommended (for different reasons) by Spinoza,Footnote 5 it appears practically impossible: “now” is an essential indexical which has both theoretical and practical import for us.Footnote 6

  3. 3.

    Acceptance and relativization of temporal notions. Each concrete act of communication employing temporal determinations comes from the perspective of a corporeal being. Reflecting on this fact, one can relativize temporal determinations to the rest frame of that corporeal being,Footnote 7 and one can additionally point out that relativistic effects can be neglected for most practical purposes.Footnote 8 An absolute notion of simultaneity is not needed to account for our communication practices—even in hypothetical cases in which relativistic effects become important. If I say that events e and f are simultaneous, and you, speeding by in your space-ship, deny this, then we can understand that we are not in fact disagreeing, but saying different things: I say that e and f are simultaneous for me, and you say that they are not simultaneous for you. Such relativizations are in fact common: if I say, “It is raining”, and you say, at a different place, “It is not raining”, then we are not in fact disagreeing, and we can make the compatibility of our assertions explicit by mentioning our respective locations. We can also live with relativization when it comes to relativistic frames of reference. In fact, employing the Lorentz transformation between our frames, we will be able to make precise sense of the apparent disagreement and come to agree on the underlying objective facts about space-time.

  4. 4.

    Addition of structure. It is possible to add some structure to plain Minkowski space-time that will allow the objective anchoring of a non-trivial equivalence relation to be read, e.g., as absolute simultaneity. In fact, nothing about the results mentioned above rules out such additions, and Rakić [34] has shown precisely in which way an equivalence relation of simultaneity can be added as a conservative extension to the structure of a single Minkowski space-time.

Which of these options should a defender of presentism choose? While option (2) seems unavailable given the importance of the notion of simultaneity, option (1) can easily be invoked. Dialectically, however, that option is not fully satisfactory: the defense of the present either becomes hostage to specific empirical facts about the actual general-relativistic space-time we inhabit, or, going beyond general relativity, the issue is deferred to a future theory of quantum gravity about which there is no consensus yet. It would be better to provide a different response, and that is what we will try in this paper. In fact, we will provide two different responses, one based on option (3) and one based on option (4), which are geared towards two different questions about the present that are mostly run together, but which need to be kept apart.

As already stated in the introduction, the notion of the present plays a double role, one static and one dynamic. Terminologically, we will distinguish the two relations that characterize these two different roles as simultaneity vs. co-presentness. We hold that these relations both have to be equivalence relations,Footnote 9 but they need not be the same.

Simultaneity characterizes the present as the time of now, indicating a temporal location. Present events in this static sense are those that are simultaneous with now, having the same temporal coordinate. This static role of the present has no immediate metaphysical or ontological import, and it should therefore not be the target of our modeling efforts in defense of presentism. In our view, the present in the sense of the time coordinate of now can be fully accounted for by the relativizing strategy (3), making it a matter of perspective. The dependence on a concrete being’s rest frame is not problematic, as full agreement in communication can be ensured. As relativity theory poses no obstacle to defining an observer-relative notion of simultaneity anchoring the static present, we will not comment further on the notion of simultaneity here.Footnote 10

Co-presentness, on the other hand, characterizes the present as that which is currently (now) real, indicating an objective, dynamic boundary between the fixed past and the open future of possibilities. These modal notions have ontological import and must not be relativized to an observer or an agent.Footnote 11 Considering the above list of options, it is clear, therefore, that we need to invoke option (4): Additional formal structure over and above that provided by a single Minkowski space-time is needed to define a dynamic relation of co-presentness among events.

Rakić’s strategy of adding an equivalence relation to the basic structure of a single space-time is one route that might be used to anchor a dynamic relation of co-presentness. Following that recipe, one arrives at a relation that can in fact fulfill both the static and the dynamic requirements on a notion of the present: Rakić’s [34] result allows for a foliation of Minkowski space-time into space-like hypersurfaces to be added conservatively, and events on the same hypersurface can then be taken to be both simultaneous and co-present. While this may be an advantage, one might also be critical of the combination, as there is a price to be paid: first, there can be no empirical test of the chosen equivalence relation, and second, one undercuts the independently motivated strategy (3) of accounting for the static (coordinate) notion of simultaneity via relativization to a speaker’s rest frame.Footnote 12

In what follows we will work towards a different objective notion of dynamic co-presentness that is fully anchored in the modal notions of fixed past vs. open future. This relation will generally not work as a static relation of simultaneity, as the region of co-presentness will normally be extended both spatially and (coordinate-)temporally. The formal resources will be provided by the framework of branching space-times, which represents local indeterminism via sets of so-called transitions. Before we introduce that framework in Sect. 3, we first have to argue that the notion of an extended dynamic present makes good sense.

2 Making Room for an Extended Dynamic Present

The dynamic role of time is to account for the possibility of dynamic change, both with respect to which things exist and what their properties are. Change in that sense needs to be contrasted with so-called Cambridge change, which is just a thing’s having different properties at (or with respect to) different temporal locations. Dynamic change must be more than that if it really requires a dynamic notion of time, because the static notion of temporal location is sufficient to account for Cambridge change. It is, however, notoriously difficult to spell out what dynamic change amounts to.

As announced, in this paper we will explore a radical view of dynamic change: change as the indeterministic realization of one option from among a set of alternatives. Such indeterministic happenings clearly amount to change: if a radium atom decays, or if you choose to have tea rather than coffee for breakfast, or if a cat jumps to catch a bird, these are indeterministic events that did not have to happen, and their occurrence makes a difference to what the world is like, realizing one possibility for the future in contrast to all the others.

Given this indeterministic notion of dynamic change, we need a corresponding dynamic notion of time to anchor the indeterministic realization of possibilities. In a second radical move, we will explore the view that just as dynamic time is necessary for real change, so real change is necessary for real, dynamic time: No change without time, but also no time without change. In this way, we strongly dissociate the static notion of coordinate time (temporal location) from the dynamic notion of real time. This makes room for yet another move that may be perceived to be radical: we will allow a moment of real time to be extended not just spatially, but also coordinate-temporally.

Our view needs to be distinguished sharply from other theories of an “extended present” that are neither based on indeterminism, nor on a distinction between static (coordinate) and dynamic (indeterministic) time. Taking into account indeterministic change, we have at our disposal a richer background on which to define dynamic time. This allows us to hold on to (dynamic) co-presentness as an equivalence relation, in contradistinction to theories that posit overlapping present moments [2, 18]. Before we show how, we first comment on the consequences of the assumption that there is no dynamic time without indeterministic change.

2.1 Determinism: No Real Change, No Dynamic Time

If real time and real change presuppose indeterminism, it follows that there is no real change, and no real time, in a deterministic world. This may seem outrageous. Take a simple deterministic world, modeled via a single Newtonian space-time, in which a number of point particles move about on continuous trajectories. If initial conditions are properly chosen, so that there are no three-particle collisions or other problematic configurations, the motion of the particles in such a world may indeed be without physically possible alternatives, thus witnessing determinism. According to our approach, we have to say that in such a world, there is no real, indeterministic change. Never is there a non-trivial range of options from among which only one is realized; there is always and everywhere just one single option to begin with. But the particles in that world move around, changing their absolute as well as their relative locations. Surely that amounts to change in that world?

Given the distinctions we are making, we can agree that such a world harbours Cambridge change: the particles have different locations at different times. But from a dynamic perspective, nothing is really happening. The temporal coordinate is just like another spatial coordinate, along which there can of course be some variation of the configuration of the particles. But it is all just one four-dimensional block without any real dynamics. Everything is accounted for by four-dimensional geometry. From the point of view of dynamic time, every event in the whole deterministic four-dimensional space-time is co-present with every other event (and with itself, of course). The dynamic present of the deterministic world is maximally extended to the whole space-time block.Footnote 13

Matters are different once one introduces indeterminism. Are we warranted to do so? The matter is certainly controversial, and we cannot hope to provide a refutation of determinism in a few lines here. As so often in philosophy, the issue is one of which package deal one is willing to accept. Our dialectics runs as follows: If one is willing to accept a distinction of a static vs. a dynamic aspect of the present, and if one is willing to entertain the idea that dynamic time passes iff there is dynamic change iff there are indeterministic happenings, then the assumption of determinism amounts to a sceptical position: while we undoubtedly experience the world as dynamical in time, there is nothing in reality to back that experience. We believe that such scepticism is unwarranted, especially given the fundamental role of quantum indeterminism in current technological realizations of randomness. Our package deal is coherent, and it appears to us to be fruitful. One may start differently, of course. Following the Bohmian program of providing a deterministic version of quantum mechanics, one starts from a strong a priori assumption of determinism and tries to rework the existing physical theory of quantum mechanics in its light, tackling significant formal and conceptual obstacles along the way (see, e.g., [20]). In our view, that program still has to prove its fuitfulness, but the matter is certainly controversial (see, e.g., [14]). That said, we will stick with the assumption that indeterminism is available as a resource, and proceed to show what can be done with it.Footnote 14

Before we describe the indeterministic theory of branching space-times that provides all the resources we need for our definition of the dynamic, spatio-temporally extended present, we briefly discuss what an extended present looks like in a simpler theory of indeterministic branching histories that lacks a spatial dimension.

2.2 Branching Histories Without a Spatial Dimension

The theory of so-called branching time (BT) was formally developed by Prior [31], following an exchange about his earlier book, Time and modality [30], with Kripke (see [29]). Formally, the theory accounts for indeterminism as the tree-like branching of linear temporal histories (chronicles). Within a BT structure, branching occurs at so-called choice points, which are maximal in the intersection of histories. The elements of the structure are called moments. In BT, space is not formally represented. Each moment thus comprises all of space, as a momentary super-event. We provide the necessary definitions:

Definition 1

(BT structure) A BT structure\(\langle M,<\rangle \) is a partial order, i.e., a non-empty set M of moments with a relation < on M that is antisymmetric (\(\forall x,y\in M\,[x<y\rightarrow y\not < x]\)) and transitive (\(\forall x,y,z\in M\,[(x<y\wedge y<z)\rightarrow x<z]\)), that is also left-linear (\(\forall x,y,z\in M\,[(x<z\wedge y<z)\rightarrow (x\leqslant y \vee y<x)]\)) and jointed (any two elements have a greatest common lower bound).

Definition 2

(Histories) Given a BT structure \(\langle M,<\rangle \), the set \(\mathrm {Hist}\) of histories is the set of maximal linear subsets of M. Given \(m\in M\), we write \(H_m\) for the set of histories containing m.

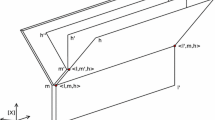
Figure 1 illustrates a BT structure with six histories. The partial ordering relation connects moments in the tree in the upward direction. Left-linearity of the ordering means that branching can happen only in the upward direction, like in a real tree. Histories are maximal linear paths through the branching tree, running from the root at the bottom to the tip of one of the branches on top.Footnote 15 Given left-linearity, histories are closed downward: if \(m\in h\) for some \(h\in \mathrm {Hist}\) and \(m' \leqslant m\), then \(m'\in h\) as well. The branching or splitting of histories allows for the representation of local indeterminism in a BT structure. Here is the formal definition:

Definition 3

(Undividedness, splitting, choice point) Two histories \(h_1,h_2\in H_m\) are undivided at m iff their intersection \(h_1\cap h_2\) contains a moment \(m' > m\) (strictly above m); we write \(h_1\equiv _m h_2\). Otherwise we say that \(h_1,h_2\in H_m\)split at m; we write \(h_1 \perp _m h_2\). Such a moment is a choice point, and is maximal in \(h_1\cap h_2\).

It is not difficult to prove that undividedness-at-m is an equivalence relation on the set \(H_m\) of histories containing m. Accordingly, there is a partition of \(H_m\) induced by \(\equiv _m\), the elementary possibilities open at m, for which we write \(\Pi _m\). The choice points in M are exactly those moments at which that partition is non-trivial, i.e., for which \(\Pi _m\ne \{H_m\}\). Belnap [5] has provided a useful dynamic reading of the realization of one of the possibilities open at a choice point, invoking the notion of a transition. Generally, a transition consists of an initial I followed by an outcome O, for which we write \(I\rightarrowtail O\). In the case of a choice point c as initial, the basic outcomes correspond exactly to the elements of the partition \(\Pi _c\): any moment in the partial ordering that comes after c belongs to one or more of the histories in the set \(H_c\), and that set is partitioned by \(\Pi _c\). Thus, the basic indeterministic event c gives rise to one of the possible outcomes represented by \(\Pi _c\). Accordingly, we can write a basic transition as

$$\begin{aligned} \tau = c\rightarrowtail H,\quad \quad H\in \Pi _c. \end{aligned}$$

One can define a natural ordering among the transitions, as follows:

Definition 4

(Transition ordering) Given two transitions \(\tau _1=m_1\rightarrowtail H_1\), \(\tau _2=m_2\rightarrowtail H_2\), we say that \(\tau _1\)precedes\(\tau _2\), written \(\tau _1\prec \tau _2\), iff (i) \(m_1<m_2\) and (ii) \(H_2\subseteq H_1\).

Transitions have recently been used by Rumberg [37] to provide a novel semantics for formal languages based on branching time; that paper contains a good overview of the theory of transitions in branching time.

In a branching time structure, each moment m has a unique past (by left-linearity of the ordering, there is no backward branching). The indeterministic structure of that past consists exactly of the transitions from choice points \(c<m\) to those basic outcomes that keep the possibility of m’s occurrence open. Given \(c<m\), there is, provably, always exactly one such transition, for which we write \(c\rightarrowtail \Pi _{c}{\langle m \rangle }\). We thus define the set of m-enabling transitions, \(\mathrm {TR}(m)\), as follows:

$$\begin{aligned} \mathrm {TR}(m) =_{df}\{ c\rightarrowtail \Pi _{c}{\langle m \rangle } \mid c<m, \ \text {{ c} a choice point}\}. \end{aligned}$$

It is easy to prove that these transitions form a chain (a linearly ordered set) with respect to the natural transition ordering \(\prec \). Along that chain, the bundle of histories becomes smaller at each indeterministic step: the occurrence of an indeterministic transition implies the exclusion of alternative histories.Footnote 16 See Fig. 1 for illustration.

Fig. 1
figure 1

A branching time structure and some of its transitions. The ordering is upwards

Full size image

2.3 The Extended Present in Branching Time

Given the formal background of branching time, we have at our hands a precise candidate definition of real time: time passes at exactly those moments that are choice points. At other moments, there is no indeterminism, no dropping off of histories, no realization of one possibility in contrast to others, no real change, and therefore no passing of dynamic time. Of course, as stressed above, static (coordinate) time also passes at other moments.Footnote 17 As dynamic time passes only at choice points, it follows that any stretch of moments between two choice points counts as co-present. Formally, we define co-presentness via the indeterministic past:

Definition 5

(Co-presentness in BT) Moments \(m_1,m_2\in M\) are co-present, written \(m_1\sim m_2\), iff \(\mathrm {TR}(m_1)=\mathrm {TR}(m_2)\).

As this definition is based on an identity, the relation \(\sim \) among the moments of M is clearly an equivalence relation.

We can show that co-present moments must be members of exactly the same histories.

Fact 1

Let \(m_1\sim m_2\), and let \(h\in H_{m_1}\). Then \(h\in H_{m_2}\) as well.

Proof

Assume for reductio that \(m_1\sim m_2\) and \(h\in H_{m_1}\), but \(m_2\not \in h\). We distinguish three cases.

  1. (1)

    \(m_2 \leqslant m_1\). This is impossible, as histories are closed downward.

  2. (2)

    \(m_1 < m_2\). In this case, \(m_2\in h'\) for some \(h'\ne h\), and as the ordering is jointed, there has to be a choice point \(c\in h\cap h'\) at which \(h\perp _c h'\). We have \(m_1 \leqslant c < m_2\) and \(h\not \in \Pi _{c}{\langle m_2 \rangle }\). It follows that \((c\rightarrowtail \Pi _{c}{\langle m_2 \rangle })\in \mathrm {TR}(m_2)\setminus \mathrm {TR}(m_1)\), i.e., \(m_1\not \sim m_2\).

  3. (3)

    \(m_1\) and \(m_2\) are incomparable. In this case, as the ordering \(\langle M,<\rangle \) is jointed, there is a greatest common lower bound c of \(m_1\) and \(m_2\), and it cannot be that \(c=m_1\) or \(c=m_2\) (this would lead to case (1) or (2)). It follows that \((c\rightarrowtail \Pi _{c}{\langle m_i \rangle })\in \mathrm {TR}(m_i)\) (\(i=1,2\)), but \(\Pi _{c}{\langle m_1 \rangle }\ne \Pi _{c}{\langle m_2 \rangle }\), so that again, \(m_1\not \sim m_2\).

\(\square \)

The other direction holds as well, so that we have at our hands an alternative definition of co-presentness in BT:

Fact 2

We have \(m_1\sim m_2\) iff \(H_{m_1} = H_{m_2}\).

Proof

The “\(\Rightarrow \)” direction has just been proved. For “\(\Leftarrow \)”, let \(m_1\not \sim m_2\). Note that for any \(m\in M\), we have \(H_m = \cap _{(c\rightarrowtail H)\in \mathrm {TR}(m)} H\). (We leave the proof of this step as an exercise.) This implies \(H_{m_1}\ne H_{m_2}\): we have \(\mathrm {TR}(m_1)\ne \mathrm {TR}(m_2)\) by assumption, and by the linear ordering of the \(\mathrm {TR}\), this implies that either \(\mathrm {TR}(m_1)\) and \(\mathrm {TR}(m_2)\) contain incompatible transitions from a choice point, so that \(H_{m_1}\cap H_{m_2}=\emptyset \), or one of the sets of transitions extends the other, which implies that \(H_{m_1}\subsetneq H_{m_2}\) (or the other way round). \(\square \)

Summing up, in BT, we can define an indeterminism-based notion of dynamic time via the indeterministic past of moments, or alternatively via the set of histories that the moments belong to. The non-overlapping regions of co-presentness are exactly those intervals on the tree of branching histories that lie between two consecutive choice points. Unless every moment is a choice point, some regions of dynamic co-presentness contain more than one moment. So, the dynamic present in BT is generally extended in static coordinate time, and thereby, the two notions of static and dynamic time come apart. See Fig. 2 for illustration.

Fig. 2
figure 2

A branching time structure, indicating some intervals of co-present moments according to Definition 5

Full size image

3 Branching Space-Times and Modal Correlations

Branching space-times (BST) makes the idea of branching histories compatible with relativistic space-time. BST combines two differently motivated partial orders: on the one hand, there is the causal partial ordering of space-time, e.g., the Minkowski ordering of special relativity. On the other hand, there is an indeterministic partial ordering, as in BT, which anchors local possibilities for the future. These two orderings are combined via Belnap’s ingenious definition of a BST history as a maximal directed setFootnote 18: in BST, two elements of the ordering, possible point events, belong to one history if and only if that history contains a common upper bound for them, which provides a perspective from which both of them have occurred. In this way, histories are generally not linear chains of moments as in BT, but can be full space-times. The BST partial ordering glues together several such possible histories at choice points.Footnote 19

An important feature of the spatio-temporal nature of the BST ordering is that two histories can split at different events. Such events then have to be space-like related: once two histories have split, they remain split; this is the BST equivalent of the BT notion of “no backward branching”. For illustration, consider Fig. 3, which depicts Alice (a) and Bob (b) each performing an indeterministic experiment in space-like separation. The individual histories each represent a two-dimensional space-time with V-shaped light cones above a and b, which are the sets of events in the respective history that are above a (or b, respectively) in the BST ordering. Each of the experiments (idealized coin tosses, or photons passing a beam splitter) conducted at a and at b has two immediate possible outcomes, \(+\) and −. Assuming that the two experiments are uncorrelated (an assumption that will be lifted below), there are four combined possibilities, which we can write mnemonically as \(a+b+\), \(a+b-\), \(a-b+\), and \(a-b-\).Footnote 20 These four combined possibilities correspond to four BST histories, \(h^{++},h^{+-},h^{-+}\), and \(h^{--}\), which are glued together at the point events a and b. These two point events occur in all the four histories, and they are the choice points at which the histories split. Histories \(h^{++}\) and \(h^{+-}\) split at the choice point b: it is the outcome \(b+\) vs. \(b-\) that separates the two histories. Histories \(h^{++}\) and \(h^{--}\), on the other hand, split at the two choice points a and b, as both these choice points have different outcomes.

Fig. 3
figure 3

BST structure with two uncorrelated choice points, a and b, and four histories, \(h^{++}\), \(h^{+-}\), \(h^{-+}\), and \(h^{--}\). The vertical straight lines are just visual guides to separate the histories, which represent 2-dimensional space-times for simplicity of illustration. The V-shaped regions indicate the light cones above a and b

Full size image
Fig. 4
figure 4

BST structure with two choice points, a and b, whose outcomes are modally (anti-)correlated. There are only two histories, \(h^{+-}\) and \(h^{-+}\)

Full size image

A consequence of multiple space-like choice points is that the respective choices might be coordinated: in BST, there is room for space-like modal correlations. That is, with respect to the set-up of Alice and Bob described above, there might be less than four resulting histories. For example, the outcomes at a and at b might be perfectly anticorrelated, leaving only two combined outcomes, \(a+b-\) and \(a-b+\) (see Fig. 4).

There is ample empirical evidence that coordinated indeterministic events exist.Footnote 21 Such coordination could be strict, as in Fig. 4, in which expected possibilities (combinatorially possible histories) are completely absent, or it could be probabilistic, preserving the underlying full space of possibilities but showing probabilistic correlations between space-like separated events. The gist of Einstein et al.’s complaint against the supposed completeness of orthodox quantum mechanics was to point out that quantum mechanics predicts the space-like coordination of experimental outcomes due to entanglement in multi-partite systems [13]. Their initial example had a modal flavor (concerning predictions that can be made with certainty), but many subsequent examples involve just probabilistic correlations. In this paper we stick to the modal case for simplicity’s sake.

The worry that quantum mechanics might be incomplete prompted the search for so-called hidden variables as completions of the quantum-mechanical description of reality, sometimes also with a view to providing a deterministic reading of the theory. Many classes of hidden variables would be detectable experimentally, as shown by research starting with Bell [3]. Experiments have vindicated the predictions of orthodox quantum mechanics to astonishing accuracy (see, e.g., [17]).

The formal apparatus of BST allows one to define a formally precise notion of space-like modal correlations.Footnote 22 We give a brief overview of the basic definitions of BST theory, referring to [4, 9] for more details and motivation.Footnote 23

A chain in a partial ordering is a linearly ordered subset (i.e., a subset in which any two elements are comparable). The notion of a history, which is invoked in the clauses of Definition 6, is provided by Definition 7.

Definition 6

(BST structure) A branching space-times structure is a non-empty partial ordering \(\langle W, <\rangle \) of possible point events that fulfills the following conditions:

  • The ordering is dense and without maxima or minima.

  • The ordering is continuous in the following sense: each lower bounded chain in W has an infimum in W, and each upper bounded chain in W has a supremum-in-h for each history h to which the chain belongs.

  • The prior choice principle: if a lower bounded chain O belongs fully to history \(h_1\) but not at all to history \(h_2\) (\(O\subseteq h_1\setminus h_2\)), then there is a choice point \(c<O\) that is maximal in the intersection of \(h_1\) and \(h_2\).

Definition 7

(BST histories) A directed set is a subset \(D\subseteq W\) such that for any \(e_1,e_2\in D\) there is some \(e_3\in D\) for which \(e_1\leqslant e_3\) and \(e_2\leqslant e_3\).

The set \(\mathrm {Hist}\) of histories is the set of maximal directed subsets of W. Given \(e\in W\), we write \(H_e\) for the set of all histories containing e.

Two histories \(h_1,h_2\in H_e\) are undivided at e iff their intersection \(h_1\cap h_2\) contains an event \(e' > e\); we write \(h_1\equiv _e h_2\). Otherwise, e is maximal in \(h_1\cap h_2\), and the two histories \(h_1,h_2\in H_e\)split at e; we write \(h_1\perp _e h_2\), and e is a choice point for \(h_1,h_2\).

As in the case of BT, undividedness-at-e is an equivalence relation on \(H_e\); the respective partition of the set of histories \(H_e\) is written \(\Pi _e\). The definition of a basic transition also carries over from BT; such a transition is of the form

$$\begin{aligned} \tau = e\rightarrowtail H,\quad \quad H\in \Pi _e. \end{aligned}$$

Basic indeterministic transitions, for which \(\Pi _e\ne \{H_e\}\), are the irreducible elements of indeterminism in a BST structure.

In our discussion of BT, we defined a notion of the indeterministic past of a moment m, via the set of transitions in that moment’s past, \(\mathrm {TR}(m)\). In BST, there are two corresponding notions. First, generally, given an event e, there is the set of cause-like loci for the occurrence of e. These are initials of transitions that make a difference as to the occurrence of e, i.e., at these events, all histories containing e split off from some history not containing e.

Definition 8

(Cause-like locus) Event c is a cause-like locus for e, \(c\in cll(e)\), iff there is some \(h\not \in H_e\) for which \(h\perp _c H_e\) (i.e., for which for all \(h'\in H_e\), we have \(h\perp _c h'\)) .

In BT, the cause-like loci of a moment necessarily have to lie in its past, allowing for an easy introduction of the set of enabling transitions of a moment, \(\mathrm {TR}(m)\), in Sect. 2.2. In BST however, due to the possibility of modal correlations, it may be that a cause-like locus for an event e is space-like related to e. Consider event e in \(h^{+-}\) of Fig. 4: by the above definition, using \(h=h^{-+}\) and noting that \(H_e = \{h^{+-}\}\), we have \(cll(e)=\{a,b\}\), but while \(a<e\), the other cause-like locus, b, is space-like related to e.

One can therefore consider a narrower class of events making a difference to the occurrence of e, namely, those cause-like loci that lie in the past of e.

Definition 9

(Past cause-like locus) Event c is a past cause-like locus for e, \(c\in pcl(e)\), iff \(c\in cll(e)\) and \(c<e\).

Barring certain infinite set-ups, which will not play a role in this paper, modal correlations are present in a BST structure iff for some event e, there is a cause-like locus that does not lie in e’s past, i.e., iff we have \(cll(e)\ne pcl(e)\) for some e.Footnote 24

For a cause-like locus \(c\in pcl(e)\) that lies in the past of an event e, its contribution to enabling the occurrence of e is easy to describe: one can prove that if \(c<e\), there is exactly one basic outcome \(H\in \Pi _c\) that is compatible with e, and indeed, we then have \(H_e\subseteq H\). In the presence of modal correlations, however, more than one basic outcome of a cause-like locus \(c\in cll(e)\) may be compatible with the event e, and so there will be no unique basic transition from c to one of c’s immediate basic outcomes that can be singled out via e. Still, there is a usefull general definition that covers both cases:

Definition 10

(Enabling outcome; enabling transition) Given some event e and some \(c\in cll(e)\), we define the e-enabling outcome of c, written \(\Pi _{c}{\langle e \rangle }\), to be

$$\begin{aligned} \Pi _{c}{\langle e \rangle } =_{df}\bigcup \{H\in \Pi _c\mid H\cap H_e\ne \emptyset \}. \end{aligned}$$

The e-enabling transition fromc is \(c\rightarrowtail \Pi _{c}{\langle e \rangle }\).

In case \(c<e\), as we have just remarked, \(\Pi _{c}{\langle e \rangle }\in \Pi _c\), so that the enabling transition \(c\rightarrowtail \Pi _{c}{\langle e \rangle }\) is a basic indeterministic transition. If \(c\not < e\), on the other hand, that transition may be non-basic. Still, it is generally the case that \(H_e\subseteq \Pi _{c}{\langle e \rangle }\) for any \(c\in cll(e)\). Therefore, even a non-basic transition \(c\rightarrowtail \Pi _{c}{\langle e \rangle }\) properly fulfills the role of enabling the occurrence of the event e.

Fact 3

Let \(c\in cll(e)\). Then \(H_e\subseteq \Pi _{c}{\langle e \rangle }\).

Proof

Let \(c\in cll(e)\), and let \(h\in H_e\). By the definition of cll, there is some \(h'\) for which \(h'\perp _c H_e\), so in particular, \(h'\perp _c h\). It follows that \(h\in H_c\), so there is some basic outcome \(H\in \Pi _c\) (which partitions \(H_c\)) for which \(h\in H\). So \(h\in H\cap H_e\), i.e., h is a witness for \(H\cap H_e\ne \emptyset \). By Def. 10, therefore, \(h\in \Pi _{c}{\langle e \rangle }\). \(\square \)

Generally, the cause-like loci of an event e allow us to define the set of those indeterministic (basic and perhaps also non-basic) transitions that together enable the occurrence of e, the event’s causae causantes (see [8]):

Definition 11

(Causae causantes) The causae causantes (originating indeterministic causes) of an event e are those transitions from cause-like loci of e that enable the occurrence of e in the sense of Definition 10:

$$\begin{aligned} CC(e) =_{df}\{ c\rightarrowtail \Pi _{c}{\langle e \rangle } \mid c\in cll(e)\}. \end{aligned}$$

The causae causantes are the BST generalization of the enabling transitions of a moment, \(\mathrm {TR}(m)\), that were defined in Sect. 2.2 in the context of BT.

4 Defining an Extended Dynamic Present in BST

In our discussion of BT we found that we could define a sensible notion of the extended dynamic present among the set of moments in two equivalent ways, either via sameness of the indeterministic past of the moments, or via sameness of the set of histories in which the moments occur.

Given the resources of BST, we can show that the same two approaches are available, and that they also characterize the same equivalence relation on the set of events, even in the presence of modal correlations. Based on modal correlations, we can provide BST structures in which the dynamic present extends arbitrarily far.

Our official definition of co-presentness is in terms of the indeterministic enabling conditions expressed via an event’s causae causantes.

Definition 12

(Co-presentness in BST) Events \(e_1,e_2\in W\) are co-present, written \(e_1\sim e_2\), iff \(CC(e_1) = CC(e_2)\).

Being based on an equality, the relation \(\sim \) is clearly an equivalence relation on W. It is well-defined no matter whether there are modal correlations or not, by the generality of Definition 11.

In BT we could show that there is an alternative way of characterizing \(\sim \) in terms of sameness of histories. An analogue of Fact 2 holds in BST as well:

Fact 4

We have \(e_1\sim e_2\) iff \(H_{e_1} = H_{e_2}\).

Proof

“\(\Leftarrow \)”: For this direction is suffices to check that the definition of cll(e), of \(\Pi _{c}{\langle e \rangle }\), and of CC(e) only make use of \(H_e\), not of e in isolation. Thus, sameness of set of histories implies sameness of causae causantes, and thereby, co-presentness according to Definition 12.

“\(\Rightarrow \)”: For this direction, we show that the set of histories \(H_e\) in which an event e occurs can be expressed via its causae causantesCC(e), which, to recall, are transitions of the form \(c\rightarrowtail \Pi _{c}{\langle e \rangle }\) for \(c\in cll(e)\). We show that for any \(e\in W\),

$$\begin{aligned} H_e = \bigcap _{c\in cll(e)} \Pi _{c}{\langle e \rangle }. \end{aligned}$$
(*)

Given (*), from \(e_1\sim e_2\), i.e., \(CC(e_1)=CC(e_2)\), we immediately have \(H_{e_1}=H_{e_2}\).

To establish (*), note first that the “\(\subseteq \)” direction follows directly from Fact 3. For “\(\supseteq \)”, take some \(h\not \in H_e\) and some \(h'\in H_e\). As \(e\in h'\setminus h\), by the prior choice principle there is some \(c^* < e\) for which \(h\perp _{c^*} h'\), and as \(c^* < e\), in fact \(h\perp _{c^*} H_e\), so that \(c^*\in cll(e)\), and \(\Pi _{c^*}{\langle e \rangle }\in \Pi _{c^*}\) is a basic outcome of \(c^*\). As \(e\in h'\), we have \(\Pi _{c^*}{\langle e \rangle } = \Pi _{c^*}{\langle h' \rangle }\), and as \(h\perp _{c^*} h'\), we have \(h\not \in \Pi _{c^*}{\langle e \rangle }\). Thus, a fortiori, \(h\not \in \bigcap _{c\in cll(e)} \Pi _{c}{\langle e \rangle }\). \(\square \)

This is a welcome result: even though BST allows for modal correlations, there are still two differently motivated definitions of co-presentness that characterize the same relation.Footnote 25

A typical shape of a region of co-presentness in the absence of modal correlations is shown in Fig. 5.

Modal correlations allow for more extended regions of co-presentness. A pertinent example is shown in Fig. 6. The generalization to larger sets of correlated choice points is suggestive: if many space-like related, modally correlated choice points exist, a region of co-present events can extend arbitrarily far.

Fig. 5
figure 5

The region of events co-present with event e in one history of a BST structure. There are four binary (\(+/-\)) choice points a, b, c, and d, and no modal correlations. Thus there are 16 possible histories, of which \(h^{++++}\) is shown. Event e and all events in the shaded region have just a single causa causans, \(b\rightarrowtail +\). They occur in exactly those eight histories in which choice point b has outcome \(+\)

Full size image
Fig. 6
figure 6

The region of events co-present with event e in one history of a BST structure. There are four binary (\(+/-\)) choice points a, b, c, and d, and outcomes of b and of c are modally correlated. Thus there are eight possible histories, of which \(h^{++++}\) is shown. Event e and all events in the shaded region have a set of two causae causantes, \(\{b\rightarrowtail +,c\rightarrowtail +\}\). They occur in exactly those four histories in which choice point b (and thus, by modal correlation, also choice point c) has outcome \(+\)

Full size image

In BST, any history \(h\in \mathrm {Hist}\) is a space-time. The restriction of \(\sim \) to h is also an equivalence relation. That equivalence relation is (barring the deterministic one-history case) neither the identity nor the universal relation.Footnote 26 We can sum up this result as a Theorem that shows that we have indeed reached our goal: we have defined a non-frame-dependent, non-trivial equivalence relation of co-presentness on relativistic space-times, based on spatio-temporal indeterminism.

For full precision, let us call a BST structure featureless if either (i) it contains just a single history (i.e., no indeterminism), or (ii) it has at least one history consisting wholly of choice points and in which there are no modal correlations. Our Theorem then reads as follows:

Theorem 1

Let \(\langle W, <\rangle \) be a BST structure that is not featureless. Then for any history \(h\in \mathrm {Hist}(W)\), the relation of co-presentness \(\sim \) restricted to h, \(\sim _{|h}\), is a non-trivial equivalence relation on h, i.e., neither the identity nor the universal relation on h, defined wholly in terms of the relativistically sound basic notions of BST.

5 Conclusion

In this paper we have tried a novel approach to defining an ontologically fundamental notion of co-presentness that does not go against the tenets of relativity theory. Such a notion could be used by presentists to strengthen their case that the doctrine of the present as the real (and the past and the possible future as unreal) does not go against modern physics. We have not worked out a full theory of presentism here. Rather, our investigation has focused on providing relativistically tenable formal foundations for presentism, culminating in Theorem 1, which states that given the resources of branching space-times, it is possible to define a non-trivial equivalence relation of co-presentness on relativistic space-time structures.

After a survey of possible reactions to the problem of the present in relativity theory, we made a terminological distinction between a static role of the present, which is served by the relation of simultaneity, and a dynamic role of the present, with the corresponding relation of co-presentness. Both of these relations need to be equivalence relations, but they need not coincide. We argued that simultaneity, the sharing of a temporal coordinate, does not by itself have any fundamental ontological import, so that a relativizing strategy with respect to simultaneity seems promising. Such a strategy is well served by remarking that each observer provides their own reference frame, which is enough to guarantee successful communication in a relativistic world, even if the observers talk about the simultaneity of distant events. The notion of co-presentness, on the other hand, does have ontological import, and can therefore not be relativized to an observer or to any other arbitrarily chosen frame. Formal results about the definability of equivalence relations on Minkowski space-time imply that additional structure is needed to anchor a non-trivial relation of co-presentness.

We argued that a formal representation of indeterminism can provide the needed additional structure, and that this addition is in fact congenial to the notion of dynamic time as requiring real (indeterministic) change. The resulting picture is one of an extended dynamic present, implying a formal distinction between static (coordinate) simultaneity and dynamic co-presentness. After working out the basics of our approach in the simpler framework of branching time, we provided our full analysis in the framework of branching space-times (BST).

Given that BST allows for modal correlations, the spatial extension of the dynamic present can reach as far as the modal correlations do. In the limit, the dynamic present could extend across a maximal space-like hypersurface.

Our analysis makes no predictions about the actual spatio-temporal extension of the dynamic present, but it characterizes an interface at which empirical results about space-like correlations could be used to provide a verdict about the size of the Now. In our view, such a division of labor is a welcome result of the clarification of the formal basis of an extended dynamic present.