Virtual Black Holes and Space–Time Structure

Abstract

In the standard formalism of quantum gravity, black holes appear to form statistical distributions of quantum states. Now, however, we can present a theory that yields pure quantum states. It shows how particles entering a black hole can generate firewalls, which however can be removed, replacing them by the ‘footprints’ they produce in the out-going particles. This procedure can preserve the quantum information stored inside and around the black hole. We then focus on a subtle but unavoidable modification of the topology of the Schwarzschild metric: antipodal identification of points on the horizon. If it is true that vacuum fluctuations include virtual black holes, then the structure of space-time is radically different from what is usually thought.

Introduction

A theory is needed that blends black holes with other, ordinary forms of matter. Among other things, this requires a treatment that explains what happens to the quantum information that appears to be absorbed by black holes [1,2,3]. To do this well, we need a description of black holes in terms of pure quantum states  [4,5,6,7,8]—as opposed to thermodynamical objects. Thermodynamical objects are described as density matrix states, and in particular in the black hole case  [9, 10], they lack time reversal symmetry.

Here we show how quantum pureness, as well as time reversal symmetry, are to be naturally restored. Neither General Relativity, nor quantum mechanics, need any essential modifications; all that is needed is an analysis that is slightly more accurate than usual. The fact that a modification is needed in the topology of the spacetime structure of the Schwarzschild solution¹, may be seen as an almost inevitable consequence of the unitarity requirement; it was simply overlooked in the earlier treatments of black holes, while, curious as this topology may seem to be at first sight, it is just totally natural.

Thus we insist that we are not talking of a “new model”, not even a new “theory”, but rather a novel way to compute things, applying known laws of physics as precisely as we can. One discovers this way why previous approaches hit upon “firewalls”  [11], and what has to be done to handle them. Firewalls do not go away all by themselves, but they can be avoided by applying sufficiently careful approaches  [12]. This account is based on work that was published recently  [13, 14]

Fig. 1

Local light cone coordinates $u^\pm$ near the horizon. The local time coordinate points upward everywhere, but the time coordinate for distant observers goes up in region $I$ and down in region $II$. Also shown is a local Cauchy surface. As the distant time variable proceeds, particles on this Cauchy surface move upwards in $I$ and downwards in $II$ (arrows)

Figure 1 shows the horizon region of a black hole, magnified. One sees that the time coordinates for distant observers converge at the origin, so that a time boost for a distant observer corresponds to a Lorentz boost for an observer located near the origin. Because of this difference between the local time coordinates, creation and annihilation operators for distant observers do not coincide with those of a local observer, but are related via a Bogolyubov transformation [15,16,17]. Hence also the vacuum states (defined as the states where all annihilation operators vanish) do not coincide for these different observers. One finds that the vacuum state $|\Omega \rangle$ for the local observer near the horizon, turns into the Hartle-Hawking state $|HH\rangle$ for the distant observer:

$$\begin{aligned} |HH\rangle = C\sum _{E,n}e^{\textstyle -{\textstyle \frac{1}{2}}\beta E}|E,n\rangle _I\,|E,n\rangle _{II}\ ;\qquad \beta =\frac{1}{k_BT_H}=\frac{8\pi G M}{\hbar \, c^3}\ , \end{aligned}$$

(1.1)

where $M$ is the black hole mass, $T_H$ the Hawking temperature, and $k_B$ is Boltzmann’s constant. $C$ is a normalisation constant. $E$ stands for the energies of the states in region $I$ and region $II$, and $n$ stands short for possible other quantum numbers.

The particles are assumed to reside in regions $I$ and $II$, but of course are expected to travel on to either region $III$ or region $IV$. Now, in a black hole just formed by a collapse, the particles originally in region $II$ are seen in region $III$ instead, which is thought to describe the inside of the black hole. Since such particles are invisible for observers in region $I$, thought to be the outside universe, it seemed appropriate to average over their energies $E$ and quantum numbers $n$. The probability of an observation of a particle with energy $E$ and quantum numbers $n$ in region $I$ was therefore expected to be a mixture of the states $|E,n\rangle$ with Boltzmann factors $e^{-\beta E}$. This is a thermal, mixed, state. As one also sees in statistical systems, the entire state is a pure, but entangled state.

For the distant observer, the energies $E$ are conserved, and hence they stay small. For a local observer, however, the quantities $E$ are Lorentz boost eigen values; the energies of the particles are not invariant under Lorentz boosts, but they are sent to ± infinity very rapidly, as time proceeds for the distant observer.

Since we define energy with the positive sign both in regions $I$ and $II$, while time runs backwards in region $II$, we see that the total eigenvalues for these Lorentz boosts are always $E-E=0$, which was to be expected: the vacuum for the local observer is invariant under Lorentz boosts there.

Hard and Soft Particles

As soon as the local observer considers states other than the Hartle-Hawking state of Eq. (1.1), he will have particles there whose energies rapidly go to infinity as distant time proceeds. It is inevitable, therefore, that particles in the eyes of local observers become hard particles. A hard particle is here defined to be a particle whose mass and/or kinetic energy has become larger that $M_{\mathrm {Planck}}$, so that it acts as a non negligible source of a gravitational field. Indeed, since these energies go to infinity so rapidly, one certainly cannot allow to neglect these gravitational forces.

The hard particles in question will always line up with either the future or the past event horizon (see Fig. 1), and if, after a few moments, we get very many hard particles there, they will form an impenetrable curtain, or firewall. These firewalls appear to partly invalidate Hawking’s original argument for the emergence of the Hartle-Hawking state (1.1), as was noted by Almheiri et al.  [11]

Particles whose energies, in a given Lorentz frame, are small compared to $M_{\mathrm {Planck}}$, will have weak gravitational fields, and thus will be called soft particles. There is no need to neglect their gravitational fields entirely; it suffices to state that, here, a perturbative treatment of the gravitational forces suffices.

During its entire history, a black hole has in-going matter (including the original implosion event out of which it is borne), as well as out-going matter, consisting of Hawking radiation as well as the residues of its final explosion. All of these we wish to represent in terms of pure quantum states. As they deviate from the Hartle-Hawking state, we must expect them to form firewalls both on the future and the past event horizon. Note that we keep our discussion as much as possible symmetric under time inversion. Indeed, the quantum theory is expected to be entirely $CPT$ symmetric.

There appear to be three problems with these firewalls:

(i):

They would invalidate Hawking’s original derivation of the Hartle-Hawking state, Eq. (1.1), since it assumes that the local observer sees a vacuum, not a firewall. The past firewall might be overcome, since it merely represents the imploding matter, which could be taken into account, but the firewall along the future event horizon, representing the vary late Hawking particles, selected to be in a quantum state different from the late $HH$ state by the late detections, deviates too much from the vacuum state that was assumed.

(ii):

The firewalls represent a strictly infinite number of quantum states, adding particles from Lorentz boosts to the distant past and/or distant future; these are much more states, it seems, than the ones needed to accommodate for the expected Hawking entropy. Indeed, the firewalls would represent a black hole information problem that must be addressed.

(iii):

It will be hard to treat the firewalls in a $CPT$ invariant formalism.

Thus, we conclude that the firewalls cannot be taken into account at all in a comprehensive treatment of the black hole quantum states. The only way to proceed is, to temporarily assume their complete absence. Whenever a firewall threatens to be formed, we must have to our disposal a possibility to remove the firewall. We do not see this yet, but we note two things:

(a):

It is perhaps reasonable to suspect that the entire set of pure quantum states of a black hole may be represented by allowing only soft particles in its environment, and

(b):

in the real physical world, we never encounter hard particles at all. The most energetic cosmic rays observed ever are still significantly less energetic than the Planck energy.

Thus, at this point, the absence of hard particles is a mere conjecture, but we shall see that the conjecture will be totally justified by our findings below. So let us start from here.

The Gravitational Back Reaction

The calculation of the gravitational field of a hard particle is not hard, but not entirely trivial either. What one does is first start from the standard Schwarzschild expression of the gravitational field of a static particle. The effects of electric charge or spin can be totally ignored. Next, one performs a strong Lorentz boost. The boost has the effect that the points that were originally close to the static particle, such that the Schwarzschild metric deviates significantly from the vacuum form there, are rapidly contracted by the Lorentz contraction, becoming a flat pancake. This pancake is the only place where gravitational curvature could be suspected to be significant. Thus, one finds that space and time at points either in front of, or behind the fast moving particle, must be flat. We have two flat half-spaces, glued together at all spacetime points in the transverse direction as seen by the speeding particle. It is this seam where all gravitational curvature will be concentrated.

Fig. 2

The gravitational field of a fast moving particle. Going practically with the speed of light, the particle (1) with momentum $\delta p^-$ in the light cone minus direction, causes two flat pieces of space-time to be seamed together along a seam with a mismatch, causing curvature. The extent $\delta u^-$ by which a spectator particle (2) is dragged along, is linear in $\delta p^-$, and depends non-trivially on the transverse separation $\delta \tilde{x}$ of the two particles, see Eq. (3.1)

The effect of this seam is that, when replacing spacetime again by a flat space-time, we see that a spectator particle is dragged along by a distance $\delta u^-$ in the minus light-cone direction $u^-$, whose value depends on the transverse separation $\delta \tilde{x}=\tilde{x}_2-\tilde{x}_1$ of the two particles, see Fig. 2. The amount of the dragging is given by  [18,19,20]

$$\begin{aligned} \delta u^-=-\,4G\,\delta p^-\log |\tilde{x}_2-\tilde{x}_1|\ . \end{aligned}$$

(3.1)

Here, the logarithm would be easy to guess, since, because of the linearity in $\delta p^-$, Einstein’s equation must reduce here to a Laplace equation in two dimensions. The only non trivial term in the equation is the factor 4 in front.

Particles and Footprints: The Firewall Transformation

Since we now only admit soft particles on the black hole metric, we limit ourselves to local vacuum solutions only. Thus we get the eternal black hole metric, and worry about its initial and final states later (the metric of these states can only be made visible anyhow at time epochs vastly separated from what is relevant to understand the evolution along relatively short time intervals). See Fig. 3.

Fig. 3

The black hole Penrose diagram [21] with only soft particles added. Since this means that all gravitating matter is absent, the diagram is that of the eternal black hole. Soft particles are indicated by small wavy lines. This is our starting point for all black hole quantum states. Light cones are oriented the same way everywhere, as indicated. Solid sine-curved line shows a typical Cauchy surface relevant for a distant observer

Since the gravitational forces acting between soft particles are weak, one may apply standard quantum field theory and perturbative gravity to follow the behaviour of fields and particles throughout this Penrose diagram. As long as our time intervals $\tau =t/4M$ are of order 1, we can still follow the evolution quite precisely. However, the particles are effectively Lorentz boosted, so we cannot follow the evolution much longer. Sooner or later, some of the particles will cross the borderline between soft and hard. As soon as we have a hard particle, we have to calculate its effect on the other (soft) particles by applying Eq. (3.1), adapted to the fact that we are not seaming flat space-times together, but parts of Schwarzschild space-time.

The effect of a hard particle on the surrounding soft ones is most easily described by comparing a Penrose space-time with hard particle in it, with an empty Penrose space-time. Let our hard particle have momentum $\delta p^-$ in the angular direction $\Omega =(\theta ,\,\varphi )$. Soft particles at the angular spot $\Omega '=(\theta ',\,\varphi ')$ will be dragged into the $u^-$ direction by an amount

$$\begin{aligned} \delta u^-=8\pi G f(\Omega ',\,\Omega )\delta p^-\ ,\quad (1-\Delta _\Omega )f(\Omega ',\,\Omega )=\delta ^2(\Omega ',\,\Omega )\ . \end{aligned}$$

(4.1)

Here, $\Delta _\Omega$ is the angular Laplacian, and this equation only differs from Eq. (3.1) by the term 1 in the equation for $f$. It comes about from the fact that we are on a sphere instead of a locally flat space-time.

Considering now many particles entering at different angles, we can describe their momentum as a distribution over the angles,

$$\begin{aligned} \begin{aligned} \delta p^-(\Omega )\&= \sum _i\delta p_i^-\delta ^2(\Omega ,\,\Omega _i)\ ,\\ \delta u^-(\Omega ')\&= 8\pi G\int \mathrm{d}^2\Omega f(\Omega ',\,\Omega )\delta p^-(\Omega )\ . \end{aligned} \end{aligned}$$

(4.2)

Now here, we considered a small change $\delta p^-$ in the in-going momentum $p^-(\Omega )$ and the change $\delta u^-$ it brings about in the positions $u^-(\Omega ')$ of the out-going Hawking particles. From here, it is only a small step to postulate that our system started with both $u^-(\Omega ')$ and $p^-(\Omega )$ being zero. We then get:

$$\begin{aligned} u^-(\Omega ')\ =\ 8\pi G\int \mathrm{d}^2\Omega \, f(\Omega ',\,\Omega )\, p^-(\Omega )\ . \end{aligned}$$

(4.3)

The tiny step from Eqs. (4.2)–(4.3) is actually the first instance where we deviate from textbook physics. This is the only “new physics” so-far in our approach, and actually it is almost unavoidable. We could say that, when the black hole was just about to form, no particles yet had entered, so $p^-(\Omega )$ was zero. The variable $u^-(\Omega ')$ then represents the “starting positions” for all particles emerging from the black hole, and all later particles are considered by listing how far they went from that position.

Now, according to standard quantum mechanics, this displacement is also represented by exponentiating the momentum operator $p^\pm (\Omega ')$, which therefore may be regarded as the functional Fourier transform of the position operators $u^\mp (\Omega ')$:

$$\begin{aligned}{}[u^\pm (\Omega ),\,p^\mp (\Omega ')]=i\delta ^2(\Omega ,\,\Omega ')\ ,\qquad [u^\pm (\Omega ),\,p^\pm (\Omega ')]=0\ . \end{aligned}$$

(4.4)

This observation allows us to invert Eq. (4.3) as follows:

$$\begin{aligned} u^+(\Omega ')\ =\ -8\pi G\int \mathrm{d}^2\Omega \, f(\Omega ',\,\Omega )\, p^+(\Omega )\ . \end{aligned}$$

(4.5)

Thus, we obtain perfect time reversal symmetry.

In what follows, we consider the positions $u^-(\Omega ')$ of the particles going out (the out-particles) as being the footprints of the particles going in (the in-particles). Note that, as soon as $p^-(\Omega )$ exceeds the Planck energy, the positions $u^-(\Omega ')$ will become large; hence their momenta become small: The footprints left by the hard particles are themselves soft particles, and vice versa. Thus, what we really have to do is disentangle the hard components of the in- and out-particles from the soft components. This way, we end up with a space-time that contains soft particles only. We have cis-Planckian and trans-Planckian duality!

Note that the “footprints” were identified as actually being the out-particles. If we would have kept the in-particles as well as their footprints, the out-particles, we would have made a mistake by counting every particle twice. Thus, in-particles that became too hard while entering the horizon, are simply being removed and replaced by the soft ones. This way we verified a posteriori that our initial assumption is verified: all hard particles can be removed, a procedure one could characterise as the firewall transformation.

We arrived at our first amendment on Nature’s Constitution:

A particle may be replaced by its footprint: particles entering through the future event horizon, leave their footprints on the past event horizon. With the Green function $f$, the momentum of the in-particle is transformed to the position operators of the out particles.

This is a Fourier transformation on the wave functions.

Expansion in Spherical Harmonics

Since we are dealing here with spherically symmetric, linear equations, it is advised to expand our variables in terms of  [22] the spherical harmonics $Y_{\ell \,m}(\Omega )$, with $|m|\le \ell$:

$$\begin{aligned} u^\pm (\Omega )=\sum _{\ell ,m}u^\pm _{\ell m}Y_{\ell m}(\Omega )\ ,\qquad p^\pm (\Omega )=\sum _{\ell ,m}p^\pm _{\ell m}Y_{\ell m}(\Omega )\ . \end{aligned}$$

(5.1)

Eqs. (4.3)–(4.5) now read as follows:

$$\begin{aligned}&[u^\pm _{\ell m},\,p^\mp _{\ell ' m'}]\ =\ i\delta _{\ell \ell '}\delta _{mm'},\quad [u^\pm _{\ell m},\,p^\pm _{\ell ' m'}]\ =\ 0\ ; \end{aligned}$$

(5.2)

$$\begin{aligned}&u^-_{\ell m}\ =\ \frac{8\pi G}{\ell ^2+\ell +1}\,p^-_{\ell m}, \quad u^+_{\ell m}\ =\ -\frac{8\pi G}{\ell ^2+\ell +1}\,p^+_{\ell m}\ ; \end{aligned}$$

(5.3)

$$\begin{aligned}&[u^+_{\ell m},\,u^-_{\ell ' m'}]=\frac{8\pi G\,i}{\ell ^2+\ell +1}\delta _{\ell \ell '}\delta _{mm'}, \quad [p^-_{\ell m},\,p^+_{\ell ' m'}]= \frac{i(\ell ^2+\ell +1)}{8\pi G}\delta _{\ell \ell '}\delta _{mm'}\ .\nonumber \\ \end{aligned}$$

(5.4)

Observe that Eq. (5.4) explain the minus signs in (5.3) and (4.5).

Most importantly, the equations decouple entirely; at every value for $\ell$ and $m$, we have separate equations for just two operators $u^\pm$ and two operators $p^\pm$.

Our next problem is: how exactly should we physically interpret the existence of two regions, $I$ and $II$ ?

Regions $I$ and $II$

The commutation rules (5.2) simply imply that, at every $\ell ,\,m$, we have one dynamical variable $u^+$ and one variable $p^-$, obeying

$$\begin{aligned} p^-=-i\partial /\partial u^+\ ,\end{aligned}$$

(6.1)

while $u^-$ and $p^+$ are related to these by Eq. (5.3). The in- and out-particles in regions I and II are indicated in Fig. 4. If $u^+>0$, the particle is in region $I$, if $u^+<0$, it is in region $II$.

Fig. 4

a Wave functions $\psi (u^{+})$, at $u^{+}>0$ , describe particles entering in region $I$ ; b The out-particles in region $I$ have wave function $\psi (u^{-})$ with $u^{-}>0$ ; c and d In region $II$, the in-particles have $u^{+}<0$ and the out-particles have $u^{-}<0$ 

It is now very important to realise that, if the in-particle were entirely in region $I$, so that $\psi (u^+)=0$ when $u^+<0$ , then the Fourier variable $p^-$ must be non-vanishing both when $p^->0$ and $p^-<0$. Therefore, the footprint of a particle in region $I$ necessarily lives both in region $I$ and in region $II$. We cannot keep regions $I$ and $II$ separate; the wave functions in $I$ and $II$ are necessarily connected.

Our equations are to be interpreted as a boundary condition at the origin, where in-particles are replaced by out-particles, their footprints. Now the Fourier transformation is unitary; it preserves the norm of the states, but only if we combine the wave functions in regions $I$ and $II$. Therefore, region $II$ will be absolutely essential for obtaining a unitary evolution law for the black hole.

If region $II$ were to represent a different black hole, then the unitary evolution would directly connect these two black holes. When one black hole would be considered separated from the other, unitarity would fail  [14].

The Basic, Explicit, Calculation

As explained above, we have a simple, unitary evolution law; however, it only works if all in- and out-particles can be identified exclusively by their momentum distributions, $p_{\ell m}^\mp$. This will be assumed to be the case, for the time being. Thanks to the spherical harmonics expansion, all calculations can be done explicitly. From here on, we omit the subscripts $\ell ,\,m$, since the different $\ell$ and $m$ values do not mix.²

Thus, writing $u=u^+,\ p=p^-$ for the in-particles, we have a single wave function $\psi (u)$, where

$$\begin{aligned} \langle u|p\rangle ={\textstyle \frac{1}{\sqrt{2\pi }}}e^{\textstyle ipu}\ .\end{aligned}$$

(7.1)

The dependence on the scaled time parameter $\tau =t/4GM$ is:

$$\begin{aligned} p(\tau )=p(0)e^\tau \ ,\qquad u(\tau )=u(0)e^{-\tau }\ , \end{aligned}$$

(7.2)

which is opposite for the out-particles. It is then convenient to write both $u$ and $p$ in terms of exponentials, since these exponents will grow or shrink linearly in time, while the positions will also vary linearly in time far from the black hole. We are invited to use the tortoise coordinates.

Close to the origin, therefore, we write

$$\begin{aligned} u=\sigma _u\,e^{\textstyle \varrho _u}\ ,\quad p=\sigma _p\,e^{\textstyle \varrho _p}\ , \end{aligned}$$

(7.3)

where we were forced to add explicit variables $\sigma _u=\pm \,1$ and $\sigma _p=\pm \,1$, since the exponents themselves would only be positive. Thus, $\sigma _u=\pm \,1$, depending on whether we are in region $I$ or region $II$.

Expressing the wave function in terms of $\sigma _u$ and $\varrho _u$, we multiply with a Jacobian factor $e^{\textstyle {\textstyle \frac{1}{2}}\varrho _u}$ in order to preserve unitarity, so,

$$\begin{aligned} \tilde{\psi }_{\sigma _u}(\varrho _u)\equiv e^{\textstyle {\textstyle \frac{1}{2}}\varrho _u} \psi (\sigma _u\,e^{\textstyle \varrho _u})\ ,\qquad \tilde{\hat{\psi }}_{\sigma _p}(\varrho _p)\equiv e^{\textstyle {\textstyle \frac{1}{2}}\varrho _p}\hat{\psi }(\sigma _p e^{\textstyle \varrho _p})\ ; \end{aligned}$$

(7.4)

Indeed, the norm is preserved:

$$\begin{aligned} |\psi |^2=\sum _{\sigma _u=\pm }\int _{-\infty }^\infty \mathrm{d}\varrho _u|\tilde{\psi }_{\sigma _u}(\varrho _u)|^2=\sum _{\sigma _p=\pm }\int _{-\infty }^\infty \mathrm{d}\varrho _p|\tilde{\hat{\psi }}_{\sigma _p}(\varrho _p)|^2\ . \end{aligned}$$

(7.5)

We write the Fourier transform in terms of a kernel $K_{\sigma }(\varrho )$, as follows:

$$\begin{aligned} \tilde{\hat{\psi }}_{\sigma _p}(\varrho _p)= & {} \sum _{\sigma _u=\pm 1}\int _{-\infty }^\infty \mathrm{d}\varrho \,K_{\sigma _u\sigma _p}(\varrho )\,\tilde{\psi }_{\sigma _u}(\varrho -\varrho _p)\ , \end{aligned}$$

(7.6)

$$\begin{aligned} \hbox {with }\quad K_\sigma (\varrho )\equiv & {} {\textstyle \frac{1}{\sqrt{2\pi }}}e^{\textstyle {\textstyle \frac{1}{2}}\varrho }\,e^{\textstyle -i\sigma \,e^\varrho }\ . \end{aligned}$$

(7.7)

The integral converges since the kernel becomes rapidly oscillating when $\varrho$ is large.

We have a symmetry under the transformation

$$\begin{aligned} \varrho _p\rightarrow \varrho _p+\lambda \ ,\quad \varrho _u\rightarrow \varrho _u-\lambda \ , \end{aligned}$$

(7.8)

which is a consequence for the symmetry

$$\begin{aligned} p\rightarrow p\,e^{\textstyle \lambda }\ ,\quad u\rightarrow u\,e^{\textstyle -\lambda }\ \end{aligned}$$

(7.9)

in the Fourier transformations. We can make use of this symmetry by Fourier transforming the wave functions with respect to the variables $\varrho _u$ and $\varrho _p$. Write

$$\begin{aligned} \tilde{\psi }_{\sigma _{\! u}}(\varrho _u)\equiv \breve{\psi }_{\sigma _{\! u}}(\kappa )\, e^{\textstyle -i\kappa \varrho _u} \ ;\qquad \tilde{\hat{\psi }}_{\sigma _{\!p}}(\varrho _p)\equiv \breve{{\hat{\psi }}}_{\sigma _{\!p}}(\kappa )\,e^{\textstyle i\kappa \varrho _p}\ . \end{aligned}$$

(7.10)

Thus, $\kappa$ is the eigen value of the Lorentz transformation at the origin, which is the time boost for the external observer. In short, $\kappa$ is the energy. It is conserved in the process where an in-particle leaves its footprint in the out-particles. Consequently, the Fourier transform now reduces to the multiplication of the wave function by a factor:

$$\begin{aligned} \breve{\hat{\psi }}_{\sigma _{\! p}}(\kappa )=\sum _{\sigma _p=\pm 1}F_{\sigma _{\!u}\sigma _{\! p}}(\kappa )\breve{\psi }_{\sigma _{\!u}}(\kappa )\ ;\qquad F_\sigma (\kappa )\equiv \int _{-\infty }^\infty K_\sigma (\varrho ) e^{\textstyle -i\kappa \varrho }\mathrm{d}\varrho \ . \end{aligned}$$

(7.11)

The integral can be worked out:

$$\begin{aligned} F_\sigma (\kappa )=\int _0^\infty \frac{\mathrm{d}y}{y} y^{{\scriptstyle \frac{1}{2}}-i\kappa }\,e^{-i\sigma y}\ =\ \Gamma ({\textstyle \frac{1}{2}}-i\kappa )\,e^{\textstyle -{\textstyle \frac{i\sigma \pi }{4}}-{\textstyle \frac{\pi }{2}}\kappa \sigma }\ . \end{aligned}$$

(7.12)

In Eq.  (7.11), the matrix $\left( \begin{array}{ll} F_{+} &{} F_{-}\\ F_{-} &{} F_{+}\\ \end{array}\right)$ is unitary: $F_+F_-^*=-F_-F_+^*$ and $|F_+|^2+|F_-|^2=1$ . After adding the factor $\log (8\pi G/(\ell ^2+\ell +1))$ (see Eq. 5.3), we see that Eq.  (7.11) acts as a boundary condition, bouncing the in-going wave back as an out-going wave. During the entire evolution, the Hamiltonian is just the dilation operator  [23]:

$$\begin{aligned} H= & {} -{\textstyle \frac{1}{2}}(u^+p^-+p^-u^+)={\textstyle \frac{1}{2}}(u^-p^++p^+u^-)\ \end{aligned}$$

(7.13)

$$\begin{aligned}= & {} i\frac{\partial }{\partial \varrho _{u^+}}\ =\ -i\frac{\partial }{\partial \varrho _{u^-}}= -i\frac{\partial }{\partial \varrho _{p^-}}\ =\ i\frac{\partial }{\partial \varrho _{p^+}}\ =\ \kappa \ . \end{aligned}$$

(7.14)

Again we emphasise the simplicity of these equations, they are merely one-dimensional ordinary differential equations, hiding nothing.

The bounce guarantees that soft particles never become hard, both in the far future and in the far past. Thus, we obtain the complete set of (pure) quantum states of the black hole.

As for the range of allowed $\ell$ values, there are still some things to be sorted out. In practice, it seems, that the total number of $(\ell ,\,m)$ partial waves that is to be included tends to coincide with the total number of Hawking particles emitted during the black hole lifetime.

An other remark is that, after leaving their footprints in the set of out-particles, an in-particle may be seen to continue its ways in regions $III$ and/or $IV$. One might be worried that this would violate the no-quantum-cloning principle. Our best answer to that is that regions $III$ and $IV$, in all respects, appear to represent ‘time beyond $\pm \,$infinity’. Thus, these particles do not over count the quantum states, but merely extend the time line to beyond infinity, without causing any harm to any of the known physical principles.

The Antipodal Identification

In the above calculations, we have not yet explained the physical interpretation of the quantum states in region $II$. Up to this point, we treated region $II$ as a universe that is exactly as real as the one described in region $I$. Since we projected all pure quantum states of the black hole as soft excitations of the vacuum in the metric described by the Penrose diagram of the eternal black hole, we cannot afford to discard region $II$. Indeed, the matrix $F$ in Eq. (7.11) is unitary only if we keep the components that map states from region $I$ into those of region $II$ and vice versa (the off-diagonal components of the matrix $F$).

The option that region $II$ would describe a different black hole in some other universe, or at least far from the original black hole, is ruled out  [14]. The only option we have is to postulate that region $II$ refers to the same black hole as region $I$. This, however, would lead to cusp singularities if in-particles would generate out-particles at the same spot of the horizon. A local observer would spot this as a singularity, which is against the philosophy of Einstein’s theory of General Relativity.

We can, however, postulate that region $II$ represents a different spot on the horizon:

$$\begin{aligned} (\theta ,\,\varphi )_I\equiv (\theta ',\,\varphi ')_{II}\ . \end{aligned}$$

(8.1)

This mapping must respect the space-time metric, which must be equal at both sides. Therefore, the mapping must be an isometry, which in this case implies that it must be an element $A$ of the symmetry group $O(3)$.

Applying the transformation twice must give us the identity: $A^2={\mathbb {I}}$ . Therefore, all its eigenvalues are $\pm \, 1$. If there were an eigenvalue $+\,1$, there would be a point $x$ on the horizon with $Ax=x$, which would lead to a cusp singularity of the type we just excluded. Therefore, all eigenvalues are $-\,1$, so that $A=-\,{\mathbb {I}}$, which is the mapping sending all points of the horizon to their antipodes. [24, 25]

Fig. 5

Time slice of the Schwarzschild metric with antipodal identification. Opposite points on the seam are glued together

Fig. 6

Space-time topology of a black hole in 4 dimensions. The white region is a ‘vacuole’, where space and time are totally absent. Again, opposite points on the seam are to be identified

Figure 5 illustrates the effects of this antipodal identification. Space-time is divided in half, the two sides are identified. Thus, if we follow a trajectory in space-time (not necessarily a geodesic), we can travel from region $I$ to region $II$, which leads us to the opposite side of the same black hole. The effect of this is that, while the original space-time had every point $(r,\,t,\,\Omega )$ mapped into two spacetime points in the regular coordinate system, $(\pm \,x,\,\pm \,y,\,\Omega )$, this is now again reduced to one space-time point.

We regard this as a new amendment for Nature’s constitution:

All space-time metrics describing objects such as black holes, must have a single Minkowski space-time in their asymptotic region, such that all points of space-time can be connected to this asymptotic space-time by time-like geodesics.

Most importantly, there should be no points that have other asymptotic regions than the regular ones; presumably one can also demand that all true space-time singularities are to be screened off by some cosmic censorship condition. This is certainly the case in our description of the Schwarzschild metric.

While entering a black hole, a particle might continue its way in region $III$ or $IV$, but its footprint lives on outside the horizon. There is no moment in time that the particle, or its footprint, are at two places at the same time, which is forbidden by the no-cloning condition of quantum mechanics. The particles spend a brief time in regions $III$ or $IV$ as enjoying their “after life”, beyond time $= \pm \,$infinity.

It is also important to note that, with the antipodal identification, particles emerging at opposite sides of the black hole, will be strongly entangled  [14] which also implies a strong deviation from purely thermal behaviour  [26].

A remarkable consequence of the antipodal identification is the fact that the variables $u^\pm$ and $p^\pm$ all switch signs when followed from region $I$ to region $II$, just as what happens in the spherical harmonics with odd $\ell$. Therefore, in our spherical harmonic expansion, only odd values of $\ell$ are allowed. As usual, $m$ can have any integer values between $-\,\ell$ and $\ell$.

Also, as we have seen, time switches its sign when passing from region $I$ to region $II$. In fact, the entire topology of space-time can be described by excising a 3-sphere out of Minkowski space-time and gluing the 4-dimensional antipodes together, see Fig. 6.

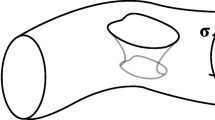
We can also consider this topology in Euclidean space-time, where it can be regarded as an instanton. This instanton will control the spontaneous generation of a black hole out of vacuum fluctuations, after which it immediately evaporates. Thus we see fluctuating black holes populating vacuum space-time. One might imagine space-time to be saturated with such fluctuating virtual black holes, see Fig. 7.

Fig. 7

Space-time foam originating from multitudes of virtual black holes

Fig. 8

A time-like Möbius strip. The grey cross marks a spot on the black hole horizon

A Time–Like Möbius Strip

The fact that the black hole space-time topology really is non-trivial can be seen by embedding a 2 dimensional sub manifold in space-time; imagine a strip ranging from the horizon in region $I$ back to the horizon at its antipode in region $II$. Begin at a point $r_0=2GM\ , \ t_0=0\ , \ (\theta _0,\varphi _0)=\Omega _0$ on the horizon. Move to larger $r$ values, then travel to the antipode: $\ r_0=2GM\ ,\ t_0\ , \tilde{\Omega }_0= (\pi -\theta _0,\,\varphi _0+\pi )$ . One arrives at the same point, so the (space-like) curve is closed. Now look at the environment $\{\mathrm{d}x\}$ of this curve. Continuously transport $\mathrm{d}x$ around the curve. The identification at the horizon demands

$$\begin{aligned} \mathrm{d}x\leftrightarrow -\mathrm{d}x\ , \end{aligned}$$

(9.1)

both for the space coordinates and for time. If we keep $\mathrm{d}t=0$ we have a three dimensional curve, but the identification at the horizon then has negative parity. If we would keep $\mathrm{d}x$ time-like, then we see that time changes sign at the horizon, and we cannot undo this using small deformations, as in the inhomogeneous part of the Lorentz group. So this is a Möbius strip, in particular in the time direction (see Fig. 8). The mapping obtained by making a trip around this Möbius strip is a $CPT$ inversion. Quantum field theories are invariant under such inversions, as opposed to any of the transformations $C,\ P,$ or $T$ separately, or any other combination of these three.