Abstract
“What data will show the truth?” is a fundamental question emerging early in any empirical investigation. From a statistical perspective, experimental design is the appropriate tool to address this question by ensuring control of the error rates of planned data analyses and of the ensuing decisions. From an epistemological standpoint, planned data analyses describe in mathematical and algorithmic terms a pre-specified mapping of observations into decisions. The value of exploratory data analyses is often less clear, resulting in confusion about what characteristics of design and analysis are necessary for decision making and what may be useful to inspire new questions. This point is addressed here by illustrating the Popper-Miller theorem in plain terms and using a graphical support. Popper and Miller proved that probability estimates cannot generate hypotheses on behalf of investigators. Consistently with Popper-Miller, we show that probability estimation can only reduce uncertainty about the truth of a merely possible hypothesis. This fact clearly identifies exploratory analysis as one of the tools supporting a dynamic process of hypothesis generation and refinement which cannot be purely analytic. A clear understanding of these facts will enable stakeholders, mathematical modellers and data analysts to better engage on a level playing field when designing experiments and when interpreting the results of planned and exploratory data analyses.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The interplay of induction and deduction in science has been intensely discussed along the last four centuries (Magnani et al. 1999). Bacon (1620) prominently stated the value of methodical observation against the cognitive biases of medieval scholasticism. Hume (1739) saw that no induction from any amount of past cases can logically ensure the conformity of future cases, while recognising that induction is a main driver of hypothesis generation. Peirce (1878) introduced the concept of abduction and the related case of inference to the best explanation (IBE), describing processes by which new hypotheses are generated by relating empirical observations to domain knowledge (Magnani 2017; Magnani 2001).
Learnings from this extensive debate have only partially percolated into current experimental science, resulting in a persistent lack of clarity about the specific roles of pre-planned and exploratory data analyses. Of note, data analyses investigating causal relationships (Pearl 2009) are not considered exploratory here due to the substantial theoretical assumptions that are typically involved. Exploratory analyses are routinely used for data dimensionality reduction and visualisation (Tukey 1977; Gelman 2004; Jebb et al. 2017) especially when many measurements are collected from relatively few samples, such as in clinical research (Biesecker 2013), forensics (Aitken and Taroni 2004) and environmental sciences (Reimann et al. 2008) among others. One motivating context here is the identification of predictors of sensitivity to cancer therapies. Development of cancer drugs over the last fifty years delivered radiotherapy, chemotherapy and cancer immunotherapies which improved survival and quality of life for many, albeit not yet for all cancer patients (Chabner and Roberts 2005; Rosenberg 2014). To date, most molecular predictors of cancer response have been established by clinical confirmation of hypotheses based on preclinical experiments and on exploratory analysis of clinical data (Perez-Gracia 2017; Wilson and Altman 2018; Barker et al. 2009; Berry 2012; Yarchoan et al. 2017; Goldberg et al. 2017). Predictive, personalized, preventive, participatory (P4) cancer medicine (Hood and Friend 2011) is an emerging paradigm underpinning the development of potentially more effective cancer treatments and prevention strategies. P4 calls for a robust epistemological support to guide the interpretation of massive data pipelines currently enabling integrative analysis of DNA, RNA, protein expression and epigenetic features at single cell resolution (Stuart and Satija 2019). Specifically, it is well known that these analyses can generate false positive results even under harsh probabilistic constraints, fueling the debate on reproducibility in experimental sciences (Baker 2016; Johnson 2013; Wasserstein and Lazar 2016). This debate also harbours questions about whether probability is the best language to quantify evidence from data for decision making, as other algorithmic approaches seem to provide attractive alternatives (Breiman 2001; Langley 1995; Langley 2000).
Lack of clarity about the specific value of pre-planned and of exploratory data analyses may arise from a lack of awareness of the limitations of "large p, small N” studies (West 2003), or from broader misunderstandings of statistical inference. This issue is addressed here by illustrating the Popper-Miller theorem (Popper and Miller 1983; Rochefort-Maranda and Miller 2018) using plain language and a graphical support. Popper and Miller proved that the estimation of probabilities per se cannot generate new hypotheses, thus clearly identifying pre-planned data analyses as the mathematical and algorithmic description of a hypotetico-deductive mapping of data into decisions. Popper also clearly identified exploratory data analysis as the analytic component of a process of hypothesis generation and refinement which cannot be entirely analytic as it entails human ingenuity and creativity. Consistently with Popper-Miller, we show that statistical inference can only reduce an investigator’s uncertainty about the truth of a merely possible hypothesis. A critical understanding of these facts based on one simple graph will enable a more effective engagement between statisticians and other stakeholders when planning experiments and when assessing how to act on the basis of exploratory or confirmatory data analysis results.
2 Popper-Miller in a Nutshell
Popper-Miller relies on distinguishing possibility from probability (Hýek 2001; O’Neill and Summers 2015). A possible hypothesis is any statement which truth can be accepted or rejected based on objective measurements. A possible hypothesis becomes also probable when its likelihood of being true is quantified either as a sampling frequency or as a subjective degree of belief (Lindley 1971). Popper-Miller states that probability estimation alone cannot be hypothesis-generating because the possibility of a hypothesis is implied by the decision to estimate its truth probability, and not vice versa. Equivalently, measurements become data when related to a specific and pre-existing hypothesis. It follows that numerical representations of observations or experimental results cannot ”speak by themselves” because their status as data is defined by their relation to a necessary context, established through an open-ended abductive process characteristic of human creativity (Magnani 2019).
Remarkably, Popper-Miller applies also to statistical inferences determining structural features of data analysis models, such as smoothing of time series (Murphy 2002), modelling mixture distributions (McLachlan and Peel 2000) or the identification of prognostic or predictive factors (Lee 2019). Popper-Miller applies here because estimation of specific dynamics, data clusters or associations implies the possibility of and interest for these estimates and not vice versa.
A corollary to Popper-Miller is that probability estimation is not a mechanism that by itself can inform an investigator on how to refine her current hypotheses because this step entails a statement of new possibilities (Popper and Miller 1987). Popper synthesized this argument against “probability magic” stating that “whatever we may think of induction, it certainly is not analytic” (Popper 1957). This argument reflects common practice, where probability estimates are motivated by and supplemented with dynamic and contextual factors including subject-matter expertise, assessments of the potential consequences of decisions for individuals and organisations, preferences and risk attitudes of end-users, stakeholders, regulators and decision-makers (French and Rios-Insua 2010). Although these arguments have been extensively explored (Kuhn 1962; Maio 1998; Fuller 2003), the current debate on the role of algorithms as mechanisms for unbiased discovery (Anderson 2008; Calude and Longo 2017; Langley 2019; Coveney et al. 2016) calls for further clarificationFootnote 1.
3 Popper-Miller in a Picture
Let \(t_0\) mark the time when a statement H becomes a possible hypothesis for an investigator. Prior to \(t_0\) no evidence about H is quantifiable by this investigator because she is unable to interrogate any measurement about what she has not yet conceived as possible. Here we do not describe the process of hypothesis generation occurring at time \(t_0\), as any such attempt would rely on context-specific arguments and on an understanding of cognitive psychology well beyond the scope of this work. After \(t_0\), Duhem and Quine showed that evidence about H is quantifiable relative to the auxiliary assumptions adopted as a basis for collecting and analysing data (Ariew 1984). Evidence may be sought about population frequencies, unobservable quantities or future data values (Rubin 1981). Typically, p-values are used to measure evidence against a single hypothesis, Neyman-Pearson testing is used to choose between two hypotheses (Lehmann and Romano 2005) and methods fulfilling the likelihood principle are used to quantify the truth probability of a hypothesis relative to a set of alternatives (Berger and Wolpert 1984; Royall 1997).
At \(t_0\) a probability \(p_0\) of H being true may or may not be included among the investigator’s auxiliary assumptions, depending on whether H is thought of as merely possible or also probable prior to data collection. In practice, mere possibility of H is typical at early stages of investigation and estimates of its truth probability may be quantified at later stages. To reflect this practical distinction, Popper-Miller is illustrated here for merely possible and for probable hypotheses.
3.1 Popper-Miller for Merely Possible Hypotheses
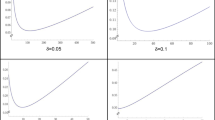
Prior to data collection, the truth of a merely possible hypothesis H is a random variable taking the values ”H is true” or ”H is false” with unknown probabilities \(p_0\) and \(1-p_0\) respectively. Figure 1 shows the variance \(V_0\) and entropy \(e_0\) (Shannon 1948) (see Appendix) of this binary random variable, which quantify the investigator’s uncertainty about the statement ”H is true”. Variance and entropy are concave functions symmetric about \(p_0=0.5\) where their maxima \(V^{max}_0=0.25\) and \(e^{max}_0=1\) are attained. In Duhem and Quine’s terminology, \(p_0=0.5\) is the weakest auxiliary assumption available to the investigator at \(t_0\) because her uncertainty about the truth of her merely possible hypothesis H is maximised. Figure 1 shows that any estimate \(p_{t}\) about the truth of H calculated from data observed at \(t>t_0\) can only reduce the investigator’s uncertainty relative to \(p_0=0.5\), because \(V_{t} \le V^{max}_0\) and \(e_{t} \le e^{max}_0\) for any \(p_{t} \in [0,1]\). Equivalently, no estimate \(p_{t}\) can increase the investigator’s uncertainty about the truth of a hypothesis above her maximum uncertainty after deeming this hypothesis merely possible. For probability estimation to be hypothesis-generating, there ought to be at least one estimate \(p_{t}\) increasing \(V_{t}\) or \(e_t\) beyond their respective maxima \(V^{max}_0\) and \(e^{max}_0\). However, no such estimate exists or, equivalently, ”probabilistic support is not inductive” (Popper and Miller 1987).
variance and entropy of the binary random variable "H is true” for a possible hypothesis H plotted against the unknown probability that the hypothesis is true prior to data collection, \(p_0\). Maximum uncertainty is attained at \(p_0=0.5\). Any departure from \(p_0=0.5\) at \(t>t_0\) can only decrease the investigator’s uncertainty about the truth of H, showing that probabilistic support cannot be per se hypothesis generating
3.2 Popper-Miller for Probable Hypotheses
When the investigator is willing to quantify \(p_0\), elicitation is used to map her beliefs into coherent probability statements (Garthwaite et al. 2005; O’Hagan et al. 2006). If elicitation is successful, a possible hypothesis becomes probable and the elicited value of \(p_0\) quantifies the investigator’s expectation about \(p_{t}\) prior to collecting data. Here \(p_0\) can be thought of as the proportion of exchangeable experiments within the design space expected to show that the possible hypothesis H is true. Given \(p_0\), the investigator may conduct her study and estimate \(p_{t}\) using Bayes’theorem (see Appendix) (Robert 2007; Bernardo and Smith 2000; O’Hagan and Forster 2004; Gelman et al. 2013). When elicitation yields \(p_0=0.5\), Figure 1 shows that the investigator’s uncertainty about the truth of H cannot be increased by any Bayesian estimate \(p_{t}\). When \(p_0\ne 0.5\) it is possible that \(V_0 \le V_{t} \le V^{max}_0\) and \(e_0 \le e_{t} \le e^{max}_0\) due to \(p_{t}\) being closer to 0.5 than \(p_0\), manifesting prior-data conflict (Evans and Moshnov 2006). Also in this case, no Bayesian estimate can increase the investigator’s uncertainty about the truth of H above its maximum attained at \(p_t=0.5\) and representing her belief in the mere possibility of H. Since no Bayesian estimate can have any bearing on the possibility of H no matter how different \(p_0\) and \(p_t\) might be, Figure 1 shows that Bayesian probability estimation cannot be a stand-alone algorithm for hypothesis generation (Gelman and Shalizi 2013).
4 Discussion
A simple graphical tool is provided to show why probability estimation cannot be hypothesis generating per se, which is the essence of the Popper-Miller theorem. A critical understanding of this fact can further motivate scientists to “experimenting with experiments”, taking full advantage of long-standing and recent results in experimental design (Fisher 1935; Cox and Reid 2000; Steinberg 2014). Even more importantly, decision-makers can use this graphical tool to show that elements beyond retrospective analysis of any complexity are necessarily involved in hypothesis generation and to require that these elements are transparently described when evaluating any validation or extrapolation strategy. A waning awareness of Popper-Miller, especially when exploring high-dimensional data using innovative algorithms, may result in weak decision making and in misperception of the role of probability estimation and data analysis in empirical research. Specifically, shared ownership of hypothesis generation between data scientists and subject matter experts cannot confer confirmatory value to exploratory analysis.
A common avenue to maintain and promote awareness about the specific values of exploratory and confirmatory analyses is to engage investigators and decision makers in the determination of the error rates of decisions to be informed by the analysis results. For instance, elicitation of loss function components from decision makers naturally leads to a prospective definition of what a data analysis ought to deliver (e.g. March and Shapira 1987; Smith 2010). However, this engagement requires a commitment to decision rules seldom specified in sufficient detail. Many investigators will then seek for clarity about what probabilistic support can be afforded in more common conditions. These can be broadly classified between instances where data sampling and analysis strategies are dynamically updated along a study while its main objectives remain unchanged, and studies which objectives are changed during their conduct. In the first scenario, methods for sample size re-estimation and for sequential analysis can be used to protect decisions from foreseeable errors (Bothwell et al. 2018; Chuang-Stein et al. 2006; Esserman et al. 2018; Le Tourneau et al. 2009). In the second scenario, the original data sampling design may be inappropriate to inform the new objectives. Exploratory analysis of data generated thus far may show what data source may inform the new hypotheses to be investigated in the reminder of the study. In both scenarios, Popper-Miller shows that hypotheses are first generated in the mind of investigators and then tested through the mechanics of data analysis algorithms or that, equivalently, “we need both exploratory and confirmatory” analysis (Tukey 1980).
Availability of data and material
NA.
Change history
10 October 2021
Reference citations and publication year in reference Magnani, L was corrected.
Notes
Algorithms optimised for discovery of relations among sets of commonly measured variables using large repositories of observations do not necessarily embed a mechanistic model enabling interpretation nor considerations about sampling bias.
References
Aitken, C. G. G., & Taroni, F. (2004). Statistics and the Evaluation of Evidence for Forensic Scientists. Hoboken: Wiley.
Anderson, C. (2008). The end of theory: The data deluge makes the scientific method obsolete. Wired Magazine, 2008.
Ariew, R. (1984). The Duhem Thesis. The British Journal for the Philosophy of Science, 35, 313–325.
Bacon, F. (1620). The New Organon. Cambridge University Press, 2012, edited by Lisa Jardin and Michael Silverthorne.
Baker, M. (2016). Is there a reproducibility crisis? A Nature survey lifts the lid on how researchers view the “crisis rocking science” and what they think will help Nature, 533, 452–454.
Barker, A. D., Sigman, C. C., Kelloff, G. J., Hylton, N. M., Berry, D. A., & Esserman, L. J. (2009). I-SPY 2: An adaptive breast cancer trial design in the setting of neoadjuvant chemotherapy. Clinical Pharmacology and Therapeutics, 86, 97–100.
Berger, J., & Wolpert, R. (1984). The Likelihood Principle. IMS Lecture Notes Monograph Series 6.
Bernardo, J. M., & Smith, A. F. M. (2000). Bayesian Theory. Hoboken: Wiley.
Berry, D. A. (2012). Adaptive clinical trials in oncology. Nature Reviews Clinical Oncology, 9, 199–207.
Biesecker, L. G. (2013). Hypothesis-generating research and predictive medicine. Genome Research, 23, 1051–1053.
Bothwell, L. E., Avorn, J., Khan, N. F., & Kesselheim, A. S. (2018). Adaptive designs clinical trials: A review of the literature and ClinicalTrials.gov. BMJ Open, 8, e018320.
Breiman, L. (2001). Statistical modeling: The two cultures. Statistical Science, 16, 199–215.
Calude, C. S., & Longo, G. (2017). The deluge of spurious correlations in big data. Foundations of Science, 22, 595–612.
Chabner, B. A., & Roberts, T. G., Jr. (2005). Chemotherapy and the war on cancer. Nature Reviews Cancer, 5, 65–72.
Chuang-Stein, C., Anderson, K., Gallo, P., & Collins, S. (2006). Sample size reestimation: A review and recommendations. Therapeutic Innovation and Regulatory Science, 40, 475–484.
Coveney, P. V., Dougherty, E. R., & Highfield, R. R. (2016). Big data need big theory too. Philosophical Transations of the Royal Society - Series A. https://doi.org/10.1098/rsta.2016.0153.
Cox, D. R., & Reid, N. (2000). The theory of the design of experiments. London: Chapman & Hall.
Esserman, L. et al (2018). Unblocking the Potential of the Platform Trial In: Platform Trial Design in Drug Develoment: Umbrella Trials and Baket Trials, Antonijevic Z. and Beckman R.A. Eds Champan & Hall.
Evans, M., & Moshnov, H. (2006). Checking for prior-data conflict. Bayesian Analysis, 1, 893–914.
Fisher, R. (1935). The Design of Experiments Oliver and Boys. London: Edinburgh.
French, S., & Rios-Insua, D. (2010). Kendall’s library of statistics, statistical decision theory. Hoboken: Wiley.
Fuller, S. (2003). Kuhn vs Popper Icon Books. Cambridge, UK: Duxford.
Garthwaite, P. H., Kadane, J. B., & O’Hagan, A. (2005). Statistical methods for eliciting probability distributions. Journal of the American Statistical Association, 100, 680–701.
Gelman, A. (2004). Exploratory data analysis for complex models. Journal of Computational and Graphical Statistics, 13, 755–779.
Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. (2013). Bayesian data analysis. London: Chapman & Hall.
Gelman, A., & Shalizi, C. R. (2013). Philosophy and the practice of Bayesian statistics. British Journal of Mathematical and Statistical Psychology, 66, 8–38.
Goldberg, K. B., Blumenthal, G. M., McKee, A. E., & Pazdur, R. (2017). The FDA oncology center of excellence and precision medicine-minireview. Experimental Biology and Medicine, 243, 308–312.
Hood, L., & Friend, S. H. (2011). Predictive, personalized, preventive, participatory (P4) cancer medicine. Nature Reviews Clinical Oncology, 8, 184–187.
Hume, D. (1739). A Treatise of Human Nature. Cambridge University Press, 2012, edited by John P. Wright.
Hýek, A. (2001). Probability, logic, and probability logic. The Blackwell Guide to Philosophical Logic - Chapter 16.
Jebb, A. T., Parrigon, S., & Woo, S. E. (2017). Exploratory data analysis as a foundation of inductive research. Human Resource Management Review, 27, 265–276.
Johnson, V. E. (2013). Revised standards for statistical evidence. PNAS, 110, 19313–19317.
Kuhn, T. (1962). The Structure of Scientific Revolutions. Chicago: University of Chicago Press.
Langley, P. (1995). Applications of machine learning and rule of induction. Communication of the ACM, 38, 54–64.
Langley, P. (2000). The computational support of scientific discovery. International Journal of Human-Computer Studies, 53, 393–410.
Langley, P. (2019). Scientific discovery, causal explanation, and process model induction. Mind and Society, 53, 1–14.
Le Tourneau, C., Lee, J. J., & Siu, L. L. (2009). Dose Escalation Methods in Phase I Cancer Clinical Trials. Journal of the National Cancer Insistute, 101, 708–720.
Lee, E. R. (2019). A systematic review on model selection in high-dimensional regression. Journal of the Korean Statistical Society, 48, 1–12.
Lehmann, E.L., & Romano, J.P. (2005). Testing Statistical Hypotheses. Springer Texts in Statistics.
Lindley, D. V. (1971). Making decisions. Hoboken: Wiley.
Magnani, L. (2001). Abduction, reason and science. Processes of discovery and explanation. New York: Springer.
Magnani, L. (2017). The abductive structure of scientific creativity. An essay on the ecology of cognition. Switzerland: Springer International Publishing.
Magnani, L. (2019). AlphaGo, locked strategies, and eco-cognitive openness. Philosophies, 4, 1–16.
Magnani, L., Nersessian, N. J., & Thagard, P. (Eds.). (1999). Model-Based Reasoning in Scientific Discovery. New York: Springer Science and Business Media.
Maio, D. G. (1998). Error and the growth of experimental knowledge. Chicago: Chicago University Press.
March, James G., & Shapira, Zur. (1987). Managerial perspectives on risk and risk taking. Management Science, 33, 1404–1418.
McLachlan, G., & Peel, D. (2000). Finite Mixture Models. Wiley Series in Probability and Statistics.
Murphy, K.P. (2002). Dynamic bayesian networks: representation, inference and learning. University of California, Berkeley, PhD Thesis.
O’Hagan, A., & Forster, J. (2004). Kendall’s Advanced Theory of Statistics. Volume 2B: Bayesian Inference. Wiley Classics Library.
O’Hagan, A., Bick, C. E., Daneshkah, A., Eiser, R., Garthwaite, P. H., Jenkinson, D. J., et al. (2006). Uncertain judgements: Eliciting experts’ probabilities. Hoboken: Wiley.
O’Neill, M. & Summers, E. (2015). Collins English Dictionary Collins, https://www.collinsdictionary.com.
Pearl, J. (2009). Causal inference in statistics: An overview. Statistical surveys, 3, 96–146.
Peirce, C. S. S. (1878). The probability of induction. The Popular Science Monthly, 12, 705–718.
Perez-Gracia, Jose Luiz, et al. (2017). Strategies to design clinical studies to identify predictive biomarkers in cancer research. Cancer Treatment Reviews, 53, 79–97.
Popper, Karl R. (1957). Probability magic or knowledge out of ignorance. Dialectica, 11, 354–374.
Popper, K., & Miller, D. (1983). A Proof of the Impossibility of Inductive Probability. Nature, 302, 687–688.
Popper, K., & Miller, D. (1987). Why probabilistic support is not inductive. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 321, 569–591.
Reimann, C., Filzmoser, P., Garrett, R. G., & Dutter, R. (2008). Statistical data analysis explained: Applied environmental statistics with R. Hoboken: Wiley.
Robert, C. P. (2007). The Bayesian Choice. New York: Springer Verlag.
Rochefort-Maranda, G., & Miller, D. (2018). Bibliography of the Popper-Miller Theoremhttps://warwick.ac.uk/fac/soc/philosophy/people/miller/Popper-Miller-bibliography.pdf.
Rosenberg, S. A. (2014). Decade in review-cancer immunotherapy-entering the mainstream of cancer treatment. Nature Review Clinical Oncology, 11, 630–632.
Royall, R. (1997). Statistical evidence - a likelihood paradigm. Boca Raton: Chapman & Hall, CRC.
Rubin, D. B. (1981). The Bayesian Bootstrap. The Annals of Statistics, 9, 130–134.
Shannon, C. E. (1948). A mathematical theory of communication. Bell System Technical Journal, 27, 379–423.
Smith, J. Q. (2010). Bayesian decision analysis - principles and practice. Cambridge: Cambridge University Press.
Steinberg, D. M. (2014). George Box and the design of experiments: Statistics and discovery. Applied Stochastic Models in Business and Industry, 30, 36–45.
Stuart, T., & Satija, R. (2019). Integrative single-cell analysis. Nature Reviews Genetics, 20, 257–272.
Tukey, J. W. (1977). Exploratory Data Analysis. Boston: Addison-Wesley.
Tukey, J. W. (1980). We need both exploratory and confirmatory. The American Statistician, 34, 23–25.
Wasserstein, R. L., & Lazar, N. A. (2016). The ASA’s statement on p-values: Context, process, and purpose. The American Statistician, 70, 129–133.
West, M. (2003). Bayesian factor regression models in the “Large p, Small n” Paradigm Bayesian Statistics 7, J. M. Bernardo, M. J. Bayarri, J. O. Berger, A. P. Dawid, D. Heckerman, A. F. M. Smith and M. West (Eds.), Oxford University Press.
Wilson, J. L., & Altman, R. B. (2018). Biomarkers: Delivering on the expectation of molecularly driven, quantitative health. Experimental Biology and Medicine, 243, 313–322.
Yarchoan, M., Hopkins, A., & Jaffee, E. M. (2017). Tumor mutational burden and response rate to PD-1 inhibition. New England Journal of Medicine Correspondence, 377, 2500–2501.
Acknowledgements
Many thanks to David Miller, David Spiegelhalter, Andrew Gelman, D.R.Cox, Pietro Muliere and Lorenzo Magnani for their insightful feedback on earlier versions of this work.
Funding
This work was carried out while the Author was employee of Janssen-Cilag, Ltd.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares no conflicts of interest.
Code availability
Figure 1 was generated using R (https://cran.r-project.org/). The code is available upon request to the Author.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendix
Appendix
The variance \(V_0\) and entropy \(e_0\) of the Bernoulli random variable taking value 1 when "H is true” with probability \(p_0\) and 0 otherwise are respectively:
The standard form of Bayes’theorem is:
The odds form of Bayes’theorem is:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rigat, F. Why Probability isn’t Magic. Found Sci 28, 977–985 (2023). https://doi.org/10.1007/s10699-021-09815-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10699-021-09815-z