Abstract
I present a systematic interpretation of the foundational purpose of constructions in ancient Greek geometry. I argue that Greek geometers were committed to an operationalist foundational program, according to which all of mathematics—including its entire ontology and epistemology—is based entirely on concrete physical constructions. On this reading, key foundational aspects of Greek geometry are analogous to core tenets of 20th-century operationalist/positivist/constructivist/intuitionist philosophy of science and mathematics. Operationalism provides coherent answers to a range of traditional philosophical problems regarding classical mathematics, such as the epistemic warrant and generality of diagrammatic reasoning, superposition, and the relation between constructivism and proof by contradiction. Alleged logical flaws in Euclid (implicit diagrammatic reasoning, superposition) can be interpreted as sound operationalist reasoning. Operationalism also provides a compelling philosophical motivation for the otherwise inexplicable Greek obsession with cube duplication, angle trisection, and circle quadrature. Operationalism makes coherent sense of numerous specific choices made in this tradition, and suggests new interpretations of several solutions to these problems. In particular, I argue that: Archytas’s cube duplication was originally a single-motion machine; Diocles’s cissoid was originally traced by a linkage device; Greek conic section theory was thoroughly constructive, based on the conic compass; in a few cases, string-based constructions of conic sections were used instead; pointwise constructions of curves were rejected in foundational contexts by Greek mathematicians, with good reason. Operationalism enables us to view the classical geometrical tradition as a more unified and philosophically aware enterprise than has hitherto been recognised.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 The Question
Ancient Greek geometers were obsessed with constructing things. Why? That is the question I propose to answer.
Euclid’s Elements spends almost as much time showing how to draw geometrical figures as it does proving theorems about them. In fact, it seems Euclid thought drawing was a prerequisite for proving. For instance, the first theorem involving squares is the Pythagorean Theorem (Elements I.47). In the proposition right before it, Euclid explains in detail how to construct a square by ruler and compass. The same goes for every other geometrical entity ever used in the Elements: first you construct it, and only then can you say anything about it. Without constructions there can be no geometry, Euclid seems to be saying.
And not only Euclid. All the best Greek geometers had their own signature constructions. Three famous construction problems dominated higher geometry for centuries: doubling the cube, trisecting the angle, squaring the circle. The long list of mathematicians who contributed their own distinctive solutions to these problems is a who’s who of everybody who was anybody in ancient geometry.
What fundamental motivations—what philosophy—drove ancient Greek geometers to this fixation with constructions? Why did Greek mathematicians think it was a good idea to spend hundreds of years trying to make an angle the third of another, or a cube twice the volume of another, in dozens of different ways? Why did they so stubbornly bang their heads against the same wall for century upon century? What sin could be so grave that they imposed on themselves such a Sisyphean task?
Why indeed make things at all? And furthermore, why do so only sometimes, with Janus-faced inconsistency? Why meticulously articulate recipes for transferring line segments by ruler and compass, only to then suddenly move entire triangles like it’s nobody’s business in the very next proposition, as Euclid seemingly does? (Sect. 3.4) The higher problem tradition appears no less schizophrenic: it often “constructs” things only by assuming much more intricate entities as “given,” seemingly by magic. A cube twice the volume of another evidently has to be made, yet cones can apparently be sliced at will to produce conic sections with precise properties. Archytas evidently thinks the cube with twice the volume is an exotic entity that must be produced rather than assumed, yet in his solution he seems to treat the very complicated intersection of a torus and a cylinder as self-evidently given simply by decree (Sect. 4.2.1).
“Anyone who has not defined a thing through terms that are prior and more intelligible has not defined it at all,” says Aristotle (Topics VI.4). Surely one should be able to say the same about constructions: anyone who has not constructed a thing through means that are constructively simpler and more immediately given than the thing itself has not constructed it at all. Yet this simple principle is seemingly in conflict with much of the Greek geometrical tradition. To cut an angle into three equal parts was regarded by Greek mathematicians as a difficult research challenge. Yet in their solutions they assume, seemingly as primitive, operations that seem considerably more convoluted than the problem they are used to solve. In what sense are those peculiar assumptions more basic or given than the entities they are used to construct? How can a constructivist research program be maintained and make any sense if the starting assumptions used for constructions is a Wild West where anything goes? How could Greek geometers be so consistent for centuries on end in their agreement that constructing basic entities such as the third of an angle is of the utmost importance, yet at the same time so dramatically at odds with one another as to what kind of assumptions are the best or most legitimate basis for such constructions?
Is there any coherent logic to all of this? I say there is. My answer shall be that the Greeks had a philosophically sophisticated conception of mathematics—operationalism, as I shall call it—which explains these things perfectly. The Greeks knew exactly what they were doing. They had very well-reasoned replies to the questions posed above, and these kinds of methodological considerations were a prominent part of mathematical thought in Greek antiquity.
1.2 General Aspects of My Thesis
I claim that ancient Greek mathematicians deliberately pursued a philosophically sophisticated foundational program based on constructions by ruler, compass, and other instruments. It is evident that constructions played a prominent role in Greek geometry, and that construction problems were a significant niche of research. But most leading scholars have rejected the notion that this is an indication of an overall constructivist philosophy of mathematics. Many have supposed that Greek mathematicians were probably not concerned with such philosophical questions, such as Mueller, who raises questions similar to those in our introductory section only to assert that “it seems unlikely that there are philosophically satisfactory answers to such questions” (Mueller, 1981, 29).
But it is perfectly possible that Greek mathematicians were ardent philosophers of mathematics. That would make sense contextually. We know that Greek mathematics and philosophy were born in a fiercely critical and combative intellectual climate (Lloyd, 1996, 1979; Szabó, 1978). Rival schools of thought attacked each other with penetrating critiques, often challenging the epistemological foundations of entire philosophical systems. My operationalist interpretation of Greek geometry fits this picture. Operationalism is a reply to philosophical critics who are trying to cast doubt on the certainty of mathematical reasoning. These critics, I hypothesise, would have tried to discredit mathematics by showing that it was subject to fallacies, paradoxes, and self-contradictions. We know from the philosophical tradition that such modes of criticism were common weapons in Greek thought, so it is easy to imagine that they would have been mobilised against mathematics as well.
So, in my view, Greek mathematicians were highly philosophical in the sense that they were sensitive to philosophical critiques and actively concerned with mounting a philosophically sophisticated defence against them. On the other hand, I propose that the relation between mathematicians and philosophers was antagonistic. It is likely, I believe, that Greek mathematicians—like so many mathematicians of later eras—were proudly autonomous and felt that they had little to learn from philosophers. So I suggest that Greek mathematicians were heavily influenced by philosophical context in the sense that they were prodded to address the epistemological foundations of mathematics in a philosophically advanced way, yet they were not at all influenced by philosophers in the sense of accepting any philosophical teachings or deferring to philosophers on any issues.
This is why I propose that the right way to understand the philosophy of Greek mathematics is to study the foundational assumptions implicit in advanced technical works. The main evidence for my operationalist hypothesis shall be of this form. I shall argue that only an underlying operationalist foundational program can make sense of otherwise inexplicable choices made in technical works. This will lead to a very different picture of the philosophy of geometry than anything one can find explicitly in surviving philosophical prose sources, such as Aristotle, Plato, or Proclus. But absence from such sources does not necessarily mean much, just as one won’t learn the views of 17th or 20th century mathematicians by reading Spinoza or Wittgenstein.
The origin of operationalism in philosophical critique that I have hypothesised has another important consequence, namely that operationalism is conceived for subtle theoretical purposes. Operationalism was conceived, I suggest, purely to address fundamental epistemological questions. It is not meant to be useful in applied mathematics or as a research tool in creative mathematics.Footnote 1 On the contrary, in applied or exploratory research settings, mathematicians would often put aside operationalist principles. Operationalism is used for putting a mathematical theory into a fully rigorous form.
Yet operationalism celebrates concrete constructions and embraces their physicality and real-worldness. This is a point that invites confusion, and indeed I shall argue that previous literature has fallen into misinterpretations for this reason. From a modern point of view, it is natural to take for granted that the foundations of mathematics is a matter of pure theory, while constructions with physical tools can only be of practical relevance. This is completely wrong, according to the operationalist perspective. To understand the philosophy of Greek geometry, we must abandon the dogma that to make mathematics rigorous it “should” be separated from any links to physical reality and turned into purely formal and abstract theory. Operationalism, in contrast to this modern dogma, anchors mathematical rigour in the physical realm. Technical mathematical sources detailing constructions with various curve-tracing devices have often been misinterpreted as quasi-practical, whereas the operationalist perspective suggests that they should instead be read as epistemologically motivated foundational investigations.
The possibility of a coherent reading of classical geometry along such lines has been clouded not only by modern dogmas about what rigorous pure mathematics “should” look like, but also by conflation with applied works. Operationalism places strict constraints on what kinds of curves and constructions are permissible in geometry. In applied mathematics it is often useful to abandon these constraints. For instance, according to my interpretation, Greek geometers carefully articulated operationally stringent ways of constructing conic sections, which they saw as forming the epistemological foundations of that theory. But when they needed to actually draw conics in practice, such as when producing sundials or burning mirrors, they chose completely different methods of generating the curves. Likewise, what makes a curve suitable for trisecting an angle is very different from what makes a curve suitable describing planetary motions, because the former is a matter directly concerned with the operationalist foundations of geometry while the latter is not. Since the operationalist foundational program is a reply to philosophical challenges to the epistemological foundations of mathematics reasoning, it is perfectly natural that its principles are useful only for that purpose and not in applications.
Similarly, and again in contrast with some modern associations, the role of empirical considerations in operationalist mathematics does not in any way conflict with or diminish the importance of deductive proofs. Operationalism does not appeal to empirical considerations to replace deductive proofs, but solely to provide epistemological justification for deductive proofs—that is to say, to ensure that deductive mathematics is not subject to contradictions, inconsistencies, paradoxes, fallacies, and meaninglessness. Operationalism appeals to the practical for purely theoretical reasons. It cares little about actually realising constructions for any pragmatic end, but much about realisability-by-construction-in-principle as a crucial mark of rigorous and reliable thought.
The operationalist reading of Greek geometry suggests the following timeline. Axiomatic-deductive mathematics was born in the Classical period: the -5th and -4th centuries. From the outset, it was forged in the furnace of philosophical critique. For this reason, operationalist foundational considerations were part of sophisticated theoretical mathematics from the very beginning.
In the Hellenistic period, the -3rd and -2nd centuries, mathematics was perhaps no longer such an active target of philosophers trying to discredit its claims to epistemological authority. Yet those original challenges were still thoroughly well understood, and the operationalist defence against them was still regarded as essential to properly rigorous mathematics.
Later eras are of secondary interest. The goal of my operationalist thesis is to reconstruct the philosophy of geometry of the golden age of Greek mathematics. At the end of the Hellenistic period the Greek geometrical tradition seems to have been disrupted and never truly recovered, as is well known. For our purposes, sources beyond, say, \(-100\) are primarily of interest for their traces and remnants of lost earlier work.
Compared to most standard accounts of the evolutionary timeline of Greek geometry, the timeline of my operationalist reading differ most notably in two respects. First, I place refined foundational work somewhat earlier than many scholars would. This goes naturally with my emphasis on the philosophical context in those early days, and my reinterpretation of what some have seen as quasi-practical meddling with constructions as in fact systematic foundational-theoretical work. Secondly, I argue that the operationalist foundational program remained essentially unchanged throughout the golden age of Greek geometry, say \(-450\) through \(-150\), and was more or less universally accepted among mathematicians in those centuries. Most historians are disinclined to see so much uniformity. Yet I shall argue that much apparent diversity and even conflict in the geometrical tradition can be better understood as varied manifestations of the same fundamental ideals than as disjoint convictions altogether.
Attributing particular philosophical convictions to the entire Greek geometrical tradition is a bold and debatable proposition. However, even if I am historically wrong about this claim in its full generality, my detailed articulation of this particular perspective is very likely to be a fruitful lens for at least some purposes. Even if the philosophical perspective I outline was not as dominant as I hypothesise, the germs of it were almost certainly felt in antiquity and was without a doubt read into the ancient tradition by early modern interpreters. The operationalist vision of the Greek geometrical tradition—which has never before been articulated systematically—was very likely perceived, at least in germinal form and at least as a possibility with some attractive arguments in its favour, by many ancient and early modern mathematicians. Most likely, this perspective often informed their thought, even if they did not accept it as their definitive philosophy of mathematics. This paper can be a lens for understanding these tendencies in the history of mathematical thought, whether they were as prominent as I claim or not. I believe that my thesis is viable as a historical hypothesis, but if more cautious minds wish to reserve judgement on that point, I hope they can still find value in my work in these secondary respects.
1.3 Operationalism in 17th-Century Mathematics
My reading of the Greeks is influenced by the way 17th-century mathematicians viewed constructions. Descartes, Huygens, Leibniz and other leading early modern mathematicians were arguably outright operationalists in their geometrical practice. At any rate, they clearly embraced many key tenets of the operationalism that I attribute to the Greeks. This has been extensively documented in Bos (2001) in the case of Descartes and Blåsjö (2017) in the case of the subsequent generation. Here we confine ourselves to a brief summary of the main points of these studies relevant to the present purpose.
Descartes gave a programmatic vision for geometry and its foundations in his Géométrie of 1637. Its cornerstone is a curve-tracing method intended as a generalisation of the ruler and compass and other construction tools of the Greek tradition. Descartes’s method is based on linked rulers whose motions are constrained by pegs and mutual contact. Descartes’s own figures clearly depict these things as physical objects (Descartes, 1637, 318, 321). This shows very clearly and unequivocally the key elements of the operationalist conception of geometry: geometry takes place in physical space; physical pegs and rulers are identified with mathematical points and lines; curves are defined in terms of physical motions, and curves that cannot be generated in this way are deemed inadmissible in geometry; these constructions are unquestionably introduced for foundational reasons (they are in fact useless for almost all practical purposes).
All of these points are equally prominent and undeniable in the late 17th century. Huygens, Leibniz, and Jacob and Johann Bernoulli devoted major efforts to extending the construction arsenal of the geometer, while remaining unequivocally faithful to these principles. Notable examples include their extensive use of curve-tracing recipes based on tractional motion, and other physically given curves such as the catenary and the elastica (Bos, 1988; Blåsjö, 2017, Chapters 5, 6, 8).
Besides embodying these operationalist principles in mathematical practice, this 17th-century tradition also makes many of its core philosophical principles perfectly explicit. This includes clear expressions of the following core theses of the operationalist view that I attribute to ancient Greek geometers. Constructions are necessary for a curve to be admitted into geometry (Blåsjö, 2017, 16, 44, 134, 209). Constructions are grounded in motion (Blåsjö, 2017, 16, 44–45, 114, 121, 124, 134, 209). Constructions should be effected by an instrument (Blåsjö, 2017, 39, 104, 121, 134). Construction by motion should be determined by one single motion, not assume the coordination of multiple motions (Blåsjö, 2017, 41, 45, 74, 112, 134). Pointwise constructions are unacceptable (Blåsjö, 2017, 16–17; Bos, 2001, 177, 189). Constructions that are not physically effectible are unacceptable (Blåsjö, 2017, 40, 43, 74). But practical feasibility or accuracy, although desirable, is not essential (Blåsjö, 2017, 116–118, 121). Constructions ensure the existence of objects (Blåsjö, 2017, 46; Hobbes, 1845, VII.205). Constructions ensure the logical consistency of definitions (De Risi, 2016, 35; Heath, 1949, 71).
These very close parallels between ancient and 17th-century geometry can, I believe, help us understand aspects of Greek mathematics for which we have little documentation by looking at analogous developments in the 17th century, where we have much better sources. Indeed, the project of the present work was conceived in precisely this way, by approaching Greek mathematics with a mindset soaked in 17th-century ideas.
Let us look at some conclusions suggested by this perspective. Consider for instance the relation between practical applications and the kinds of foundational-geometrical constructions studied by leading mathematicians. Leibniz discovered that the catenary is very closely related to the exponential or logarithm function. This relationship means that one can find the logarithm of any number by performing simple measurements on a hanging chain. Leibniz alleges that “this may be helpful since during long journeys one may lose one’s table of logarithms \(\ldots\) In case of need the catenary can then serve in its place” (Blåsjö, 2016, 2017, 137). It is quite clear that this was not really a viable proposal of any practical utility to speak of. I have done this construction many times with students and with an ordinary necklace and ruler one normally does not get any better accuracy than a single decimal point. Leibniz most likely knew this full well. His remark about practical applicability should probably be taken more as a quaint illustration that brings home an interesting mathematical point in a striking way. It may also have been not unreasonable at the time to hope that future developments might bridge the gap between theory and practice on this point. The same is true of several other constructions at the time [such as those described in Blåsjö (2017, Chapter 5)]: mathematical investigations that fit into a foundational research program are dressed up with a veneer of pseudo-practicality and come with some remarks about allegedly useful applications. The latter have illustrative and pedagogical value, and perhaps even some far-fetched potential for practice, but they were in all likelihood very much secondary to a theoretically driven research agenda. I suspect that one can say the same about the alleged practical applicability of the three classical construction problems mentioned in Sect. 4.1.1.
Another such parallel may illuminate how and why the three classical construction problems became canonised in the first place. In the context of the early calculus, it was natural to seek the integral of all possible algebraic expressions. For instance, integrating \(1/\sqrt{1-x^{4}}\) was soon recognised as the natural next frontier beyond integrals that could be done by existing standard functions. However, it was not found very suitable to pose the question in this technical insider language. Instead, the challenge was given greater force and elegance, and more compelling packaging, in the form of a concrete physical problem that readily reduced to it. The paracentric isochrone problem was conceived by Leibniz for this very purpose, it seems (Blåsjö, 2017, 32, 156–157, 183–184). Neither Leibniz nor anyone else at the time were interested in actually finding the path along which a particle under the influence of gravity travels with constant radial velocity as seen from a fixed origin. In the same way, the Greeks did not have any burning need to trisect a bunch of angles and double a bunch of cubes. In ancient and early modern geometry alike, these questions were conceived as illustrative encapsulations of broader theoretical questions. They were not selected because they were interesting in their own right, but because they pinpointed issues that were key to a systematic enlargement of geometrical problem solving practice. They were the kinds of problems for which, when you solved them, other mathematicians would have no interest in actually using your solution for its ostensible purpose, but a very high interest in extracting the method of your solution and use it a myriad other contexts. To solve these problems means being able to solve many others. That is how they were selected, and that is what made them interesting.
That, at any rate, seems to have been how Leibniz interpreted the Greek tradition. And Leibniz’s interpretation carries considerable weight, in my opinion. The interpretations of historical mathematics by people such as Leibniz are not just any interpretations. They are historical interpretations made by people who not only were trained in a tradition still dominated by ancient masterpieces to a considerable extent, but who also spent decades of active research effort in extending mathematics by purposefully following in their footsteps. It is not far-fetched to think, therefore, that the 17th century is a quite good window into the more ancient past in these respects.
2 Why Construct?
This section sets out the philosophy of operationalism. This is the theoretical lens that I shall use to interpret Greek geometry in later sections.
We begin by looking at the most fundamental threats to the reliability and rigour of geometry. If our house is built on rotten pillars it is only a matter of time before it comes crashing down. Critics have indeed identified some ominous cracks in the bedrock of geometry. Any serious attempt at establishing firm foundations of geometry must give a coherent and systematic account of why such problems could never occur on its watch.
Operationalism does this emphatically. But not only that. Operationalism accomplishes this proactively rather than reactively. It doesn’t solve problems as they arise. Instead it focusses on positive virtues, and derives the solutions to the problems as effortless corollaries. The operationalist program of grounding geometry in concrete constructions is eminently justifiable on positive grounds, and furthermore negates a range of severe threats to the certainty of mathematical knowledge.
2.1 Problems with Non-constructive Mathematics
2.1.1 False Diagrams
Figure 1 show a famous example of how an incorrectly drawn, yet plausible-looking diagram can quickly lead to absurd results. The Greeks were evidently well aware of this type of problem, as witnessed by a remark in Plato: “geometrical diagrams \(\ldots\) have often a slight and invisible flaw in the first part of the process, and are consistently mistaken in the long deductions which follow.” (Cratylus, 436d, Jowett transl.) We even know for a fact that Euclid himself wrote a (now lost) treatise on fallacies in geometry which is likely to have dealt with these kinds of issues (Acerbi, 2008).
a “Proof” that all triangles are isosceles. The point in the middle is defined as the intersection of the bisector of the top angle and the perpendicular bisector of the base. By construction, the top two triangles are congruent (AAS), and the two base triangles are congruent (SAS). It follows that the remaining two triangles are congruent (SSRA). Hence the left and right sides of the original triangle are equal. Since we started with an arbitrary triangle, we have thus proved that any triangle is isosceles. b Correctly drawn version of the diagram. The “proof” does not work, since it relied on aspects of the false diagram that do not hold on the correctly drawn diagram
The fallacy of Fig. 1 is often used to justify the modern view of geometry in the vein of Hilbert. On this account, the erroneous proof shows the danger of relying on visual and intuitive assumptions (Maxwell, 1963, 23; Mumma, 2010, 261; Kline, 1972, 1006–1007; Wagner, 2018, 315). The solution is to purge geometry of any kind of reasoning based on diagrams,Footnote 2 and instead formalise the subtle issues of betweenness and relative position involved here as precise axioms so that geometry can proceed through purely logical deduction.
But this is not the only possible diagnosis and treatment of the problem with this erroneous proof. Another point of view is to say: the problem is not that the proof relied too much on diagrammatic reasoning, but that it did so too little. The problem is not that the proof is insufficiently divorced from visual considerations, but that it is too divorced from them. The example doesn’t show that diagrams are dangerous even if they are just schematic accompaniments to otherwise logically solid proofs, but rather that diagrams are dangerous when they are merely treated as such. The solution is not to place less emphasis on diagrams, but more. That is, to demand diagrams to be not merely schematically sketched but in fact precisely constructed according to the most exacting standards and rigorous proofs that these constructions accomplish the configurations in question. This would indeed prevent errors of this type from occurring. No one adhering to this mode of doing geometry would ever find themselves reasoning about false diagrams like the one in the above example.
This diagnosis of the source of error in the false proof above leads immediately to the conclusion that precise constructions of angle bisectors, bisectors of segments, and perpendicular lines are foundationally very important, and that no proof must ever be formulated without all entities occurring in it having been introduced through rigorously verified and precise procedures. This is exactly what we find in Euclid’s Elements. Without fail, Euclid always meticulously shows how to construct all entities involved in all of his propositions. And all the constructions needed to ensure that we end up with the correct Fig. 1b rather than the deceptive Fig. 1a are carefully spelled out as core propositions right at the heart of the Elements: how to bisect an angle (I.9), bisect a line segment (I.10), erect a perpendicular from a point on a line (I.11), and drop a perpendicular from a point to a line (I.12). It is surely not a coincidence that Euclid hastened to explicate precisely the tools needed to solve the diagram problem mentioned by Plato.
2.1.2 Existence and Hidden Assumptions
It is impossible to conduct a serious axiomatic study of geometry without paying attention to existence issues. For example, the assumption that squares exist may seem innocent enough, but in fact it implies the parallel postulate.Footnote 3 Hence any investigation that aims to elucidate the fundamental assumptions of geometry cannot treat any object whose existence has not first been either proved or explicitly postulated. To do otherwise would be to render the entire enterprise of axiomatic geometry useless and moot, since it would open a back door through which any number of hidden assumptions can creep in. The point of an existence proof for squares, then, would not so much be to establish that there is such a thing as squares, but to ensure that any foundational assumptions involved in supposing the existence of squares have been systematically accounted for.
Another example showing how seemingly innocuous existence assumptions can be tantamount to fundamental assumptions about the structure of space occurs in Legendre’s attempt to prove by contradiction, using only the first four postulates of Euclid, that the angle sum of a triangle cannot be less than \(180^{\circ }\). His proof implicitly assumes that given two intersecting lines, and a point not on those lines, it is possible to draw a line through that point that intersects the two given lines (Heath, 1956, I.214; Rosenfeld, 1988, 105). This assumption does not hold in hyperbolic geometry. Hence Legendre’s attempted proof is invalid, since the contradiction did not come from the assumption he intended to refute, but from an innocent-seeming existence assumption introduced along the way in his argument. This shows once again the danger of letting even the most harmless-looking existence or construction assumptions proliferate without explicit control. Inconsistencies can arise from even the most inconspicuous of assumptions. The moral of the story is that the mathematician must stick to a minimalistic set of stringently controlled construction principles, whose consistency should be as unquestionable as possible.
Issues of this nature were recognised in antiquity. Quite possibly, even the specific issue of Legendre’s assumption may have been investigated in works that are no longer extant, such as the lost treatise On parallel lines by Archimedes. At any rate, closely related issues emerge explicitly in the treatments of parallels by Simplicius and Al Jawhari (Rosenfeld, 1988, 45, 48). On a more conceptual level, Aristotle pinpoints the same type of fallacy in the work of some “who suppose that they are constructing parallel straight lines: for they fail to see that they are assuming facts which it is impossible to demonstrate unless parallels exist. So it turns out that those who reason thus merely say that a particular thing is, if it is.”Footnote 4
Aristotle draws the obvious conclusion that existence issues must be controlled by either explicit postulates or existence proofs. “What is denoted by the first [terms] ...is assumed; but, as regards their existence, this must be assumed for the principles but proved for the rest.”Footnote 5 Thus “What a triangle is, the geometer assumes, but that it exists he proves.”Footnote 6 In Greek geometry, constructions are the means by which existence is assured. The link between constructions and existence is stressed by Proclus in his commentary on the Elements (Proclus, 1970, 183).
2.1.3 Existence and Consistency
Reasoning about objects merely defined verbally, as opposed to constructed, can be very dangerous. For example, suppose I add to Euclid’s Elements the definition: “A superright triangle is a triangle each of whose angles is a right angle.” Then I may reason that I know from I.32 that the external angle of a superright triangle is two right angles. Then it follows from I.13 that two right angles are equal to three right angles—an obvious contradiction.
The definition of a superright triangle is disturbingly similar to that of an equilateral or isosceles triangle, and the reasoning sounds just like the kind of thing we do in geometry all the time. So it casts doubt on the entire enterprise of geometry. How do we know that the propositions of the Elements are not one or two steps away from leading to contradictions? The geometers must reply with some definitive criterion that explains why none of their theorems are susceptible to this kind of error.
In a way it is clear what the problem is. There are no superright triangles. Hence one can consider the problem solved by ensuring the existence of the objects one speaks of. One way of accomplishing this would be to say: Only constructive definitions, that imply a recipe for making the object defined, are permitted in mathematics. This is clearly not the path taken by Euclid, however. For instance, Euclid defines a square at the outset but only shows how to produce one much later, in I.46, based on substantial previous results. This corresponds to the strategy of avoiding the superright triangle fallacy by demanding that we cannot make a propositional statement about a particular class of objects unless we have first shown beforehand that the class in question is nonempty. Thus the types of inferences made in the false argument are only warranted if supported by suitable existence proofs, and that is why theorems about triangles cannot be applied to superright triangles, but can be applied to equilateral and isosceles triangles, which Euclid indeed proves exist by means of constructions.
The momentous discovery of the incommensurability of the diagonal of a square and its side—that is to say, that this ratio, \(\sqrt{2}\), “does not exist” in the realm of “numbers” (meaning rational numbers)—could be taken as further proof that existence questions can be very subtle and far from intuitively obvious.
But existence is not the only aspect that should be emphasised here. Another important lesson from the superright triangle example is the danger of defining objects through multiple conditions. A superright triangle is defined as: having three sides; having one right angle; another right angle; ant yet another right angle. The first two conditions were fine. It was taking all of them together that was impossible. The more conditions you add, the greater the risk of ending up with an inconsistency.
Another example of this is to say: Let ABC be a triangle such that: one angle is a right angle; the sides next to the right angle have lengths 4 and 7; the third side has length 9.Footnote 7 Again, some of these conditions would have been fine on their own, but all of them taken together are inconsistent. Hence defining or introducing an object through a list of specifications of its properties is unacceptable. Doing so would leave the door wide open for possible inconsistency to enter mathematics, and hence ruin the claim to certainty of mathematical reasoning.
A rigorous mathematical theory needs a systematic guarantee that such errors cannot be committed. Constructions are a way to provide such a guarantee. Instead of introducing objects by a list of properties, construction builds it up step by step. Thus properties can no longer be ascribed to an object merely by decree. Rather they must be introduced by a rigorously controlled stepwise process. Each step in this process involves the application of a construction postulate or a demonstrated construction proposition or theorem, which means that assumptions and conditions of validity are carefully monitored and reduced to a few axiomatic principles.
This has an important implication for what types of constructions can be assumed as axiomatic. If the goal of constructions is to eliminate the danger of imposing multiple (potentially inconsistent) conditions at once, it follows that the primitive construction principles themselves must as far as possible be defined in terms of a single simple characteristic, rather than a combination of multiple elements.
2.1.4 Verbal Logic Fallacies
One could argue that the challenge posed by the superright triangle fallacy is not convincingly solved by the insistence on existence proofs. As far as syllogistic or propositional logic is concerned, it seems perfectly in order to say that if t is by definition a kind of triangle, and the claim P(x) is true for any triangle x, then we may infer that P(t) holds. The qualifications regarding existence necessary to safeguard against the superright triangle fallacy feel quite external to this logical mechanics. Perhaps careful attention to existence proofs can “save” verbal logic. But one may well ask whether a paradigm that invites such problems in the first place is worth saving.
The mathematician might well say: Geometry is the most reliable branch of knowledge. More reliable than verbal logic, which derives its credibility, insofar as it has any, from mathematics more than than conversely. The superright triangle fallacy relies on abstract verbal logic. But abstract verbal logic has no foundational status in mathematics. All mathematical statements are about concrete constructions and operations. Any uses of abstract verbal logic in mathematical texts is merely a psychological or pedagogical shorthand for actual constructive operations. (It is suggestive in this connection that Euclid’s proofs are all “purely quantifier free”—that is, they never make assertions of the form “there exists \(\ldots\)” or “for all \(\ldots\)”. This is “remarkable” (Avigad et al., 2009, 707) from the point of view of modern mathematics, and could perhaps be an indication that Greek mathematicians distanced themselves from syllogistic or propositional logic where such phraseology is commonplace.)
Indeed, we know for a fact that logical paradoxes and fallacies figured prominently in Greek thought in the classical era. Some of these are clearly relevant to mathematics. Zeno’s paradoxes of motion are the most famous examples, and clearly pose a foundational challenge to geometry. But, arguably, already the liar paradox shows that natural-language propositional logic is incoherent. Namely, it shows that verbal logic allows propositional statements P to be formulated that are inherently contradictory. “This statement is false” or “I am lying” are examples of such statements P, because, arguably, P implies \(\lnot P\) and \(\lnot P\) implies P, whence there is no way of assigning a truth value to P without ending up with a contradiction. This kind of thing clearly poses an issue for a logic-based conception of mathematics, not least in connection with proofs by contradiction.
Another example of a paradox discussed in ancient times was that of the horn: What you have not lost, you have; but you have not lost horns; therefore, you have horns. Here again the blind, mechanical application of logical inferences in a quasi-algebraic manner leads to an absurd conclusion. As with the superright triangle fallacy, it is possible to attribute the problem to some specific cause: in this case not so much an existence issue as a certain misleading ambiguity in the first premiss. Furthermore, the fallacy may be regarded as “obvious.” But trying to defuse the paradox in these ways does not solve the core issue exposed by the paradox, namely that “blind” logic, in and of itself, seems to lead to erroneous conclusions.
This multitude of logical paradoxes arguably validates the suspicion mentioned above that when we supplemented verbal logic with existence proofs we had perhaps not gotten to the bottom of all its problems yet. It would not have been out of character for the Greeks to have been sensitive to such challenges and to have taken radical steps to protect themselves from logical fallacies and paradoxes.
2.2 Operationalism
2.2.1 Operationalism Defined
Above we have seen a number of specific considerations that point toward the foundational importance of constructions. I shall now articulate a philosophy of geometry—operationalism—that synthesises these isolated indications into a systematic foundational program. Operationalism is a term most closely associated with a 20th-century movement in philosophy of science that grew out of relativity theory and quantum mechanics. Several of its key tenets, however, are much older and more universal. I propose that this rich tradition in philosophy of science was largely foreshadowed in Greek philosophy of geometry. I shall argue that the key commitments and motivations of modern operationalism and related traditions could very plausibly have been precisely mirrored in Greek geometrical thought.
The core principle of operationalism is that “we mean by any concept nothing more than a set of operations; the concept is synonymous with the corresponding set of operations” (Bridgman, 1927, 5). Thus “triangle,” for example, means: the figure obtained when drawing three intersecting lines with a ruler. This diagram is not a drawing of a triangle, or a physical instantiation of the formal concept of a triangle, or in some other way subordinated to or derived from some purer concept of triangle. No, a diagram resulting from these operations simply is what a triangle is. This is the root meaning of “triangle” and the foundational bedrock on which any claim about triangles ultimately rests. When Euclid says “let ABC be a triangle,” he strictly speaking simply means: draw one line, then another, then another (making three points of intersection).Footnote 8
Geometry is readily interpreted in operationalist terms, in a manner consistent with Euclid’s Elements and Greek geometry generally. What is a line? Take a piece of string and pull the ends; that’s a straight line. What is a circle? Take a piece of string and hold one end fixed and move the other end while keeping the string taut; that’s a circle.Footnote 9 What does it mean for two things to be equal? Put one on top of the other; if they align, and neither sticks out beyond the other, then they are equal.Footnote 10 What is a right angle? Cut the space on one side of a line into two equal pieces; that’s a right angle.Footnote 11
In effect, every statement Euclid makes in his geometry can be read as a statement about operations or the outcome of operations. It could easily have been otherwise. Most geometry treatises of later eras do not allow themselves to be interpreted in operationalist terms. Consider for example the parallel postulate (Fig. 2), whose convoluted phrasing in Euclid has caused much consternation. It transpires already from the Elements itself that Euclid could have used a simpler, equivalent statement in place of it, such as: given any line and any point not on this line, there is no more than one parallel to the line through that point. Why did Euclid opt for his much more convoluted formulation of the postulate? From the point of view of modern mathematics, his choice is strange, as witnessed by the majority of more modern treatments that much prefer the formulation in terms of existence of parallels. But from an operationalist point of view Euclid’s choice makes perfect sense. Euclid’s version of the postulate is purely about operations: if you draw two lines, and perform an operation that shows that they stand in such-and-such a relation, then if you extend them such-and-such a thing will happen. Everything is formulated in terms of actions that the geometer performs. The existence formulation, on the other hand, is incompatible with operationalist principles. It only makes sense in some kind of Platonist or preformationist framework that assumes that all the objects of geometry are already “out there,” independently of any geometer.
Euclid’s parallel postulate (Elements, Postulate 5): “If a straight line falling on two other straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.” (Heath, 1956, I.202)
Similarly, Euclid doesn’t say “there are infinitely many prime numbers” but rather: if you have a list of prime numbers, you can make a larger list of prime numbers.Footnote 12 This achieves the same thing but without needlessly entangling itself with the quasi-metaphysical assumption that “the set of all prime numbers” is a preexisting entity whose properties we are proving theorems about. There is no need for mathematics to make assumptions of that type. Doing so would only invite attacks from philosophical sceptics.
Operationalism avoids the dubious ontological assumption that the totality of all objects of geometry are somehow already at our disposal. The modern formulation of the parallel postulate assumes that mathematics can, so to speak, survey the totality of all lines through a particular point and make proclamations about this infinite set. Operationalism doesn’t make such an assumption. When it says “all right angles are equal to one another” (Elements, Postulate 4), it does not assume that the set of all right angles is a meaningful entity about which we can make statements. Rather, the postulate means: if you make one right angle, the another right angle, then those two right angles are equal to one another.Footnote 13
Or consider a prototype geometrical proposition: the Pythagorean Theorem (Elements I.47). Again, this theorem does not say that every element of the infinite set of all right-angle triangles has a particular property. Rather, operationally speaking, it says: if you have drawn a right-angled triangle, and if you then draw the square on each of the sides, then the areas of those particular squares are related in such-and-such a way. Until you have drawn a right-angled triangle, the theorem can be said to have no content.
Operationalist geometry is automatically protected from the fallacies discussed above in straightforward ways. The existence and false diagram issues are resolved because they could never arise in strict operationalist practice (insofar as the construction procedures admitted have high practical accuracy, as for example ruler and compass does). And the verbal logic problems do not arise since verbal logic is not accorded any foundational role in operationalist mathematics. Thus operationalism very conveniently cuts off in one fell swoop numerous lines of attack of philosophical scepticism directed at mathematics, without the need for any sacrifices in mathematical content.
2.2.2 Modern Philosophical Motivation
The big-picture philosophical considerations that made operationalism and related programs attractive in modern times could very well have been influential in antiquity as well.
In modern physics, operationalism was at the heart of a philosophical critique of the fundamental assumptions of Newtonian mechanics, which eventually led to relativity theory. Many of the ideas in those writings can be applied virtually verbatim to ancient geometry as I interpret it. Here for example is a typical passage from Ernst Mach’s famous critique of Newton:
Absolute space and absolute motion ...are pure things of thought, pure mental constructs, that cannot be produced in experience. ...[They have] therefore neither a practical nor a scientific value; and no one is justified in saying that he knows aught about it. It is an idle metaphysical conception. ...All our principles of mechanics are ...experimental knowledge concerning the relative positions and motions of bodies. ...No one is warranted in extending these principles beyond the boundaries of experience. In fact, such an extension is meaningless, as no one possesses the requisite knowledge to make use of it. (Mach, 1883, II.VI)
Ancient mathematicians might have justified their emphasis on constructions in much the same terms. The domain of constructions is the domain in which geometrical statements are meaningful and have testable truth-value. Imagining the claims of geometry to extend beyond this domain is hubristic as well as pointless. It would accomplish nothing but needlessly saddling geometry with metaphysical baggage. Thus operationalism exposed a certain naiveté in previous, more philosophically unreflective scientific practice.
But in addition to this critical element, operationalism was also positive and forward-looking: it offered a powerful heuristic for reforming conceptions of fundamental scientific concepts. This heuristic proved very fruitful and was pivotal in Einstein’s formulation of special relativity.Footnote 14 Physicists drew the conclusion that “we do not know the meaning of a concept unless we can specify the operations which were used ...in applying the concept in any concrete situation” (Bridgman, 1952, 7). Thus physicists realised that they had operated with naive concepts of time and space. This worked fine for most purposes, but critical foundational investigations revealed that these naive assumptions were ultimately untenable. Relativity theory showed that traditional assumptions about time and space were ultimately inconsistent and incoherent, and that the way to fix these problems is to reduce the concepts of space and time down to concrete operations with measuring rods and clocks.
Greek mathematicians could very well have had similar experiences. That is, they could very plausibly have found that attempts at clarifying mathematical concepts—both in the context of critical philosophical analysis and in technical research—ultimately forced them to abandon naive conceptions of mathematical objects in favour of strictly operational explications. The examples discussed in Sect. 2.1 can be read in such a way.
The empirical character of operationalism also makes it naturally aligned with a scientific worldview, and has often gone hand in hand with an “us versus them”—scientists versus philosophers—attitude that is as much about rejecting other perspectives as it is about affirming its own principles (Bridgman, 1927, 28, 1952, 10). Positivism, which is closely related to operationalism, also has such a history [from Comte (1830) to the Vienna Circle and beyond], of using a strict empirical theory of meaning to reject much grandiose philosophising as wrongheaded and even strictly meaningless.
It is possible that this dynamic was paralleled in antiquity. Ancient mathematicians would have felt that their geometry was a lot more grounded in reality than even quasi-science such as the four elements theory, not to mention more abstract philosophy such as, say, Aristotle’s doctrine of causes. Ancient mathematicians would have felt that their results were qualitatively different from philosophy in terms of reliability, objectivity, and many other dimensions. They may even have felt, as members of the Vienna Circle later did, that much philosophy was empty gibberish. As Ptolemy said: “only mathematics can provide sure and unshakeable knowledge”; other “divisions of theoretical philosophy should rather be called guesswork than knowledge.” (Almagest, I.1, Toomer, 1998, 36)
Perhaps this would have led them to articulate general methodological principles that would “explain” why their form of reasoning and knowledge was superior to that of the philosophers, as many scientists have been inclined to do ever since.
What methodological dicta might Greek mathematicians have seized upon to set their field apart from philosophy? Certainly not anything like the modern identification of mathematics with logic and axiomatic-deductive reasoning. Logic and deduction were already highly prized among Greek philosophers. If anything, they were too obsessed with deductive logic: Zeno’s argument that there can be no such thing as motion is one example among many of extreme faith in abstract deductive reasoning even when it is in blatant conflict with the most basic common sense. Axiomatics too was far from the exclusive purview of mathematicians; indeed it is obvious that basing one’s theories on a list of allegedly evident but ultimately unjustified axioms is very convenient for mathematicians and sophists alike. It may even be reasonable to say that the abundance of deductive philosophical systems that were clearly in conflict with one another would rather have been an incentive for the mathematics to insist that, unlike the philosophers, they did not rely on abstract logic.
Operationalism would have been an alternative readily at hand. Constructions had always been a central part of geometry, from the time of the Egyptian “rope-stretchers” whom the Greeks identified as the originators of the field. Later theoretical developments, such as the irrationality of \(\sqrt{2}\), had spoken in favour of taking geometry as the foundational bedrock of all mathematics. It would have been a short and natural step for the mathematicians to tie the foundations of their subject to their already ubiquitous ruler and compass. To the mathematicians it would have cost little to embrace all-out radical operationalism. Virtually all of mathematics was readily susceptible to being reframed in such a paradigm. It would have been a way of legitimating existing practice that would have necessitated little or no deviation from what they were already doing. Meanwhile, other branches of philosophy stood no chance of founding their teachings on an operationalist basis. So if the mathematicians were looking for a way to set themselves apart from the philosophers—to explain why their field had cumulative progress, universal agreement, and inviolable truths while philosophy had paradoxes and schools in constant disagreement with one another without any prospect of reconciliation—then operationalism would have been a natural option readily at hand.
Unlike most of philosophy, any statement of geometry is readily equated with a claim regarding certain empirical circumstances. Ancient mathematicians had a golden opportunity to highlight this natural attribute of their field as an epistemic virtue. They could pose to head-in-the-clouds philosophers the very difficult challenge of explaining what good a theory is if it has no “cash value” in the real world, in the form of empirically testable claims. And they could stress that geometry, by contrast, has no need to engage in that kind of theorising.
Related to this is the ideal of falsifiability. When the geometers claim that any triangle has an angle sum of two right angles, they are sticking their necks out. If their claim was false, it should be simple enough to find a counterexample. The operationalist formulation of geometry makes it possible to press this point very strongly. The theorem simply means: if you put a ruler down on a piece of paper and draw three intersecting lines, then cut out the three corners and put them point-to-point, then the three pieces fill precisely the angle on one side of a straight line. The very meaning of the theorem directly contains a concrete recipe for testing and potentially falsifying it.
Also remarkable is that this operational meaning of a geometrical theorem is theory-independent. You do not need to accept the definitions and postulates of the mathematicians in order to perform this empirical test. Sceptics who try to criticise mathematics in general terms can thus be confronted with a concrete challenge: regardless of whether you accept any of our assumptions or modes of reasoning, we offer you hundreds upon hundreds of claims of the form: if you perform such-and-such concrete operations, then the outcome will always be one particular way rather than another. Feel free to prove us wrong, the mathematician can say. It would be impossible to meet the challenge and very difficult to try to dismiss it as illegitimate. The operationalist formulation of mathematical statements is reducible to straightforward recipes whose neutrality and objectivity is very difficult to deny. This is in stark contrast with many philosophical claims, which must often be bought into or rejected wholesale along with an entire theory because of their interdependent nature—not merely in the innocent sense that they derive mutual support and plausibility from one another, but in the more fundamental sense that even their very meaning is inherently bound up with the system as a whole. Operationalism ensures that geometry is not like that. Operationalist geometry is not an entangled holism. And for this reason the avenues of attack available to a would-be sceptic are severely limited.
Thus operationalism ensures that geometrical claims are meaningful to outsiders. This is put to good use in Plato’s Meno, 84d–85, where an uneducated slave boy is led to discover what is in effect a special case (the isosceles case) of the Pythagorean Theorem. A modern formulation in terms of algebraic symbolism and terminology is opaque and meaningless to the uninitiated. But the Greek operationalist formulation of the theorem makes it immediately meaningful and accessible without any prerequisite knowledge or higher-order technical concepts. Thus this way of doing geometry makes its content universally available and communicable to anyone.
2.2.3 Modern Mathematical Motivation
The operationalist reading of Greek mathematics that I have proposed has much in common with considerations that led to renewed interest in constructive mathematics in the 20th century, and even with more radical foundational critiques such as the intuitionism of Brouwer.
In this context I would draw a distinction between operationalism and constructivism. Both prohibit mathematical theorems from speaking about non-constructed objects. Hence both solve a number of the problems noted above in the same way. Nevertheless I would characterise operationalism as the more radical of the two. Constructivism is closer to ordinary abstract-logic mathematics: it restricts the kinds of objects mathematics can speak about, but otherwise it leaves the nature of mathematical reasoning the same. Operationalism goes further. It sees constructions not only as a means of ensuring that objects are safe to treat, but as constituting the very meaning of all mathematical concepts and the fundamental nature of all mathematical reasoning.
While both operationalism and constructivism eliminate problems such as that of the superright triangle, operationalism arguably does so in a more proactive rather than reactive manner. Constructivism can be seen as the result of a defensive retreat: a crutch the abstract logic paradigm invented to solve specific problems that it encountered. As with any such ad hoc response to criticism, a concern may linger whether the whole rot was truly eliminated by this quick fix. Operationalism does more to get back on the front foot. It not only solves the particular issue at hand, but it also emphatically disavows the entire way of thinking that gave rise to it in the first place.
Consider first the issue of what objects can legitimately be studied in mathematics. Operationalism solves existence-related issues since “if experience is always described in terms of experience, \(\ldots\) we need never be embarrassed” to find that we were talking about imagined concepts with no connection to reality (Bridgman, 1927, 6–7). “The language of Euclidean geometry ...is reliable only because the mathematical systems and relations, which are symbolized by the words of that language as conventional signs, have been constructed beforehand independently of that language” (Brouwer, 1975, 98). That is one major advantage of operationalism.
But, more fundamentally, the operationalist grounding in concrete experience or practice means not only that the objects we speak of exist and are meaningful but, more than that, that the entire practice itself is consistent.
In mathematics much the same situation arises that arises in physics; in foundation studies, in which one wants to secure the maximum awareness of what one is doing and the maximum security that he is not involving himself in contradiction, one would do well to use only concepts whose meaning is found in \(\ldots\) unambiguously performable operations. For in this way, \(\ldots\) the description of a situation in mathematics reduces to the description of an actual experience, \(\ldots\) and actual experience is not self-contradictory. (Bridgman, 1955, 17)
This was no empty threat, as shown by Russell’s Paradox, which proved that naive attempts at using logic to ground mathematics were not a way to ensure rigour and unequivocal clarity, as intended, but rather that this way of thinking readily permits incoherent statements. Unlike “let S be the set of all superright triangles,” which is deceptive since the set is empty, the statement “let R be the set of all sets that are not elements of themselves” is not only misleading in this benign way but in fact, far worse, is altogether incoherent, since the definition implies that R must be an element of itself and also that it must not be. This shows that definitions of the form “the set of all objects having a particular property” can be problematic.
Brouwer diagnoses the problem with Russell’s Paradox in a manner very much aligned with operationalism.
By a propositional function ...the logicians ...mean a statement about x ...; they reckon that by that statement a class is defined, consisting of all things ...which by substitution make the statement true. [Thus they speak of] all things for which the statement \(\varphi x\) is true. ...As the fundamental domain of operations, within which the relations meant by the words or symbols must exist, they choose not some [already constructed] mathematical system, but the chimerical ‘everything’. ...[They thus] give a linguistic system of statements and propositional functions priority over mathematics. ...They postulate that these sentences define classes and that it is allowed to reason about these classes according to the laws of classical logic. ...It is not surprising that they ...came up against contradictions [such as Russell’s Paradox]. ...Exactly because Russell’s logic is no more than a linguistic system, deprived of a presupposed mathematical system to which it would be related, there is no reason why no contradictions would appear. (Brouwer, 1975, 88–89)
Note well that this is not merely about a constructivist restriction on what objects are permissible in mathematics. Rather, what is at stake here is something much deeper: a rejection of the logic-centered mathematical paradigm altogether, in favour of a radical operationalist conception of the nature of mathematical reasoning and the basis for its epistemological credibility.
Superright triangles (Sect. 2.1.3) are an example of a class defined verbally by its properties, just like the \(\varphi x\) classes criticised by Brouwer. This type of issue occurs naturally in geometry, as do other reasons to treat logic with suspicion more generally, as we saw above (Sect. 2.1.4). Russell’s Paradox shows that such suspicions were well founded and that the issues are by no means confined to “non-mathematical” examples, or examples whose fallacy is obvious. Though they would in all likelihood not have been familiar with Russell’s Paradox per se, it is not unrealistic to imagine that Greek mathematicians may have arrived at conclusions similar to that of Brouwer regarding the dubiousness of pure logic, and the status of operationalism as the only reliable warrant not only of meaning but also of consistency.
3 Operationalism and Euclidean Geometry
3.1 The Role of Diagrams in Geometry
3.1.1 Diagrams as the Ontology of Geometry
The following interpretation is half right and half wrong, according to the operationalist reading of Greek geometry:
Undoubtedly, many mathematicians would simply assume that geometry is about spatial, physical objects, the sort of thing a diagram is. \(\ldots\) The centrality of the diagram \(\ldots\) meant that the Greek mathematician would not have to speak up for his ontology. \(\ldots\) The diagram \(\ldots\) acted, effectively, as a substitute for ontology. \(\ldots\) One went directly to diagrams, did the dirty work, and, when asked what the ontology behind it was, one mumbled something about the weather and went back to work. (Netz, 2003, 56–57)
I agree that, indeed, diagrams—physicality and all—were accepted as the de facto ontology of mathematics. And I also agree that mathematicians were adverse toward and disinterested in philosophical accounts of geometry that did not square well with this practice.
However, I do not believe that Greek mathematicians “simply assumed” these things, and could only “mumble something about the weather” if pressed on the issue. I claim that, on the contrary, Greek mathematicians had a philosophically sophisticated defence of their ontological stance. In this section I am going to attempt to articulate how they might have replied, instead of merely “mumbling something about the weather,” if they had been pressed on a range of key philosophical issues.
3.1.2 Diagrammatic Reasoning
From a modern point of view, the right way to do geometry is as a formal axiomatic-deductive system. The Greek tradition has often be interpreted as aspiring toward, but falling short of, this ideal. This view has it that Euclid’s Elements was a valiant attempt at a formal treatment of geometry, especially for its time, but that it contains some fundamental flaws stemming from Euclid’s inability to fully avoid implicit reliance on intuitive and visual assumptions.
Operationalism, by contrast, embraces visual reasoning and keeps abstract logic at arm’s length. This arguably fits the Greek geometrical tradition better than modern formalistic conceptions of geometry. Indeed it is well known that Greek geometry sometimes bases inferences on diagrammatic considerations that are not explicitly formalised. The most famous example is Elements I.1, where the existence of a point of intersection of two circles is tacitly assumed but can arguably not be formally justified from Euclid’s definitions and postulates. It is fashionable nowadays to characterise visual reasoning and intuition as a source of perpetual error and naiveté, while formalism is iron-clad rigour par excellence. But this view is neither a priori plausible nor historically sustainable. Manders (2008a, 66) puts is well: “I detect ignorance and empty (arrogant, even panicked) dismissiveness on the part of the critics of diagram-based demonstration. \(\ldots\) It is hard to escape the impression that philosophers of mathematics have had something at stake in dismissing properly geometrical reasoning methods out of hand.” Basing geometry on visual reasoning about figures is natural in that it grounds knowledge in immediate experience and the clearest possible intuition. This is a commonsensical epistemological stance. Any attempt to discredit operationalism needs to be argued from first principles other than the axiomatic assumption that logical formalism and rigour are the same thing.
Modern scholarship has shown that Euclid’s use of diagrammatic reasoning is by no means a haphazard reliance on intuition, but rather that it can readily be interpreted as a careful use of systematic principles. Two separate modern studies have fully formalised Euclidean diagrammatic reasoning, spelling out in considerable technical detail sets of axioms that rigorously and systematically delineate between permissible and impermissible diagrammatic inferences. Hence they have concluded that: “The use of diagrams in a Euclidean proof is not soft and fuzzy, but controlled and systematic, and governed by a discernible logic” (Avigad et al., 2009, 701). “There is, in fact, an underlying logic to Euclid’s methods that can be made every bit as rigorous as other methods of presenting geometry. The idea that his methods are inherently informal should therefore be banished forever” (Miller, 2007, 85). This suggests that the Elements should not be seen as a failed attempt at a full axiomatic formalisation of geometry, but rather as a coherent and well-considered attempt at doing another kind of geometry altogether. Operationalism provides precisely such an interpretation.
The modern mathematician rejects anything not obtained through logical deduction from formal axioms. The operationalist classical geometer rejects anything not obtained through concretely defined operational procedures. We can formulate the difference between the two points of view in terms of what kind of audience the geometer is trying to convince. If we adopt the modernistic point of view, we can picture the audience of a mathematical proof as a veritable logic-parsing machine. The mathematician feeds in statements, in the form of symbolic strings in a suitable formal language, one by one, and the machine tests whether each statement follow from the one before it based on basic logical inference rules or previously established theorems. This point of view fits very uneasily with classical geometry for a range of reasons, including the use of diagram-based reasoning.
The operationalist point of view, on the other hand, envisions the audience of a mathematical proof differently. A Euclidean proof is addressed at a person with a ruler and compass. This person is every bit as critical as the logic machine of the modernists. He is hell-bent on trying to argue against us at every stage. But our strategy for convincing him to nevertheless concede the truth of our theorems is not by appeals to formal logical inferences. Instead we make him draw things. We build our results up from simple operations with ruler and compasses. In this way we put our critic in a difficult position. He is forced to either agree with us, or to deny a very specific, concrete claim about a very specific, concrete figure that he himself has drawn. For instance, what is the person with the ruler and compass supposed to say regarding the intersection of the circles in Elements I.1? He just drew the two circles himself on a piece of paper. It would be ridiculous for him to claim that there is no justification for the assumption that they intersect. They clearly intersect right there in front of his eyes, and it was he himself who drew it using tools whose validity he had admitted.
Since operationalism gives absolute primacy to the concretely constructed diagram, the sceptic has no other foothold from which to reject the proof. The logic machine of the modernist paradigm would catch the gap in I.1 at once, and shoot down our proof. But operationalist mathematics is not susceptible to that kind of critique. Geometrical proofs are claims about what happens when you carry out concrete constructions. Constructed diagrams is all there is, so the only way to question a geometrical proof is to question what it says about a concretely constructed diagram. The sceptic cannot hide behind sophistical logic and vague generalities, but is forced to either concede the validity of the proof or deny something so obvious that he will look ridiculous.
I propose that the diagrammatic inferences Euclid permits are precisely those that such a sceptic, who has drawn the diagram himself, could not reasonably doubt. This fits well with Manders’ observation that Euclid permits diagrammatic inferences only of properties of the diagram that are invariant under minor variations or imperfections in the drawing process (Manders, 2008a, 69, 2008b, 91–94). Thus, for example, in Elements I.1, the equality of the legs of the triangle can of course not be established merely by visual inspection of the diagram; rather, these equalities have to be derived from postulates and definitions, as do all exact properties of diagrams in Euclid’s geometry. Indeed, a sceptic could very well question whether such properties hold, despite having just constructed the diagram himself. The equality of the legs is not immediate from the diagram in and of itself, but only follows when we remind ourselves that we used the same radius for both circles and so on. You could draw the diagram without keeping such things in mind. You could not, however, draw the diagram without directly experiencing one circle cutting unequivocally right through the other one.
Operationalism relies on diagrammatic reasoning only in this restricted sense. It attributes foundational status to diagrams in certain respects, but of course it does not go so far as to say that the truth of propositions or veracity of solutions to problems can be verified merely by measurements in a diagram. Of course such things have to be established by rigorous demonstration, which is obviously the main preoccupation of Greek mathematical sources. What Plato says about inferring geometric truths from diagrams remains true also for operationalists: “If someone experienced in geometry were to come upon [diagrams] very carefully drawn and worked out \(\ldots\), he’d consider them to be very finely executed, but he’d think it ridiculous to examine them seriously in order to find the truth in them about the equal, the double, or any other ratio.” (Republic, VII, 529, Plato, 1997, 1146) Indeed, exact properties such as ratios cannot be inferred from diagrams, no matter how carefully drawn, just as Plato says. But the operationalist enterprise of avoiding false diagrams based on constructions does not rely on such epistemic overreach. Instead, its use of diagrammatic reasoning is much more restrictive and limited to essentially qualitative or topological (or “inexact” in Manders’s terminology) inferences from diagrams.
In sum, operationalism makes sense of Euclidean practice with regard to diagrammatic reasoning. It eliminates the need to attribute to Euclid a big logical blunder in his very first proof, or the need to denigrate the more visual aspects of Euclid’s reasoning as lowly intuition and an imperfect form of mathematics. Instead it articulates a philosophy of mathematics that incorporates this aspect of Euclidean mathematical practice into a coherent and purposeful whole.
3.1.3 Generality
Basing geometrical reasoning on diagrams gives rise to the so-called generality problem. Geometrical theorems are about entire classes of objects—infinite sets of them. For instance, the angle sum of all triangles. Yet all geometrical proofs in the classical tradition are always illustrated with, and reason based on, one particular diagram. The generality problem, then, is the challenge of reconciling the idea that the diagrams of geometry are concrete, specific objects with the notion that can nevertheless ground universal truths.
A standard way to defend geometrical reasoning against this challenge is to say that geometrical proofs concern only properties that hold generally and do not rely on incidental properties that hold only for the particular diagram. This view was expressed already by Proclus [Proclus (1970, 162); see Mumma (2010, 257) for similar remarks among early modern authors]. Such a view is compatible with operationalism.
But operationalism also suggests an alternative way of dealing with the generality problem, namely by denying the premiss that there is such a thing as “all triangles” in the first place. Before you have put your pen on the paper, there is no geometry. There are no lines, no circles, no triangles. We do not make the metaphysical assumption, as the modernists do, that there is some preexisting universe of these things “out there” about which geometry looks for universal truths. One consequence of this is that the “problem” of generality ceases to exist. The theorem is not: there is an infinitude of triangles and all of those have angle sum \(180^{\circ }\). Instead it is: any triangle has angle sum \(180^{\circ }\). Which really means: if you put your ruler down and draw a line segment, then another one, then another one, then the angles of that one triangle has angle sum 180 degrees.Footnote 15 The theorem has no other meaning than that. And the proof is not a logical schema talking about an infinite class of objects. Rather, it is a set of instructions for the sceptic to carry out that will convince him, regardless of which triangle he started with, that the theorem is true for that triangle.Footnote 16 It is precisely the strength of the insistence on constructions to reduce everything from the abstract to the concrete in this way. We only talk about what we can see and draw and put on the table right in front of us. To do otherwise would be to engage in empty metaphysics.
Greek geometry is remarkably consistent with such a reading. Indeed, as Netz has observed, Greek mathematical texts never explicitly claim generality beyond the concrete proof based on a particular diagram (Netz, 2003, 242).
Operationalism rejects certain deep-seated assumptions that are often taken for granted in modern mathematics. From a modern point of view, any reliance on diagrams in mathematics is inherently problematic, since mathematics is in essence independent of diagrams. On this view, diagrams are merely a secondary representation of mathematics, and furthermore one contaminated by intuition and other limitations. How, then, can diagrammatically based reasoning be a legitimate way of doing mathematics? That is, how could we ever be sure that what is true of diagrams is true of the “actual” content of mathematics? Operationalism does not answer the question but rejects it. There is nothing more “actual” than the diagram.
Likewise, the generality problem is dissolved since operationalism rejects the Platonist ontology of mathematics (Bridgman, 1955, 100) on which it is based. Nothing exists except what the geometer has constructed. “Wheresoever in logic the word all or every is used, this word, in order to make sense, tacitly involves the restriction: insofar as belonging to a mathematical structure which is supposed to be constructed beforehand” (Brouwer, 1975, 76),
To be sure, many who are concerned about the generality problem will feel that operationalism “solves” the problem only by introducing further problems of equal or greater magnitude. For one thing, operationalism implies that “the very nature of meaning itself makes it impossible to get away from the human reference point” (Bridgman, 1955, 112), since nothing exists or has meaning in geometry except through human agency. But operationalism denies that this is a problem, as Platonists would have it.
Regarding the generality problem more specifically, a modern mind may feel that the operationalist solution merely shifts the problem one step over. Even the operationalist is committed to a form of generality, in the sense that the proof of, say, the angle sum theorem must always work for any given triangle. Isn’t the operationalist mathematician still obligated to somehow justify that the proof has this form of generality, which is essentially the original generality problem in slightly different guise? It is of course true that the proof is intended to be general in this sense, but officially the operationalist mathematician does not need to be committed to having proved that it is. The operationalist mathematician can simply say: I assert that such-and-such a construction will always have such-and-such an outcome; if you want to prove me wrong, feel free to try to come up with a counterexample.
Of course, psychologically the mathematician presenting a proof must be convinced that it will always work, for if a counterexample would be forthcoming he would be exposed as a fool. But this can be left to the discretion of the mathematician’s intuition. Internally, operationalist mathematicians are of course concerned with this kind of generality. But externally, as a reply to sceptical and philosophical challenges to the epistemological status of mathematics, there is no need for them to saddle themselves with the burden of claiming that their proofs themselves have inherent characteristics that strictly ensure such generality. Instead they can restrict themselves to presenting the proof as a challenge to any sceptic: apply these construction and inference steps to any one figure that fulfils the conditions stated, and you will find that you cannot credibly doubt the validity of any step, and hence you will become convinced that the proposition holds for that figure. It is possible, for the operationalist, to maintain that this is what a proof is.Footnote 17
One may well feel that this restrictive view of what a proof is sells mathematics short and fails to account for the nature and status of mathematical knowledge. However that may be, the fact remains that operationalism makes it possible to take such a stance. The restrictive view of the nature of proofs fits naturally with the operationalist conception of mathematical content and meaning, while it is incompatible with a Platonist conception of the nature of a mathematical theorem. The restrictive view is a scorched-earth defensive position that can be useful when under philosophical attack. Saying that this is the only sense of mathematics one is willing to defend is a powerful way of cutting off lines of philosophical attack without changing the practice of mathematics substantially. Operationalism makes taking such a stance possible, but it does not demand it. Operationalism does not preclude one from holding more expansive beliefs and defending them for instance along the lines indicated by Proclus.
3.1.4 Diagram Cases
An issue for diagrammatic reasoning connected to the generality problem is that proofs in Euclid’s Elements are sometimes dependent on non-universal properties the diagram. For example, I.35 should obviously hold if AD and EF overlap, yet the wording of the proof is adapted to the case illustrated in the figure, where the line segments do not overlap. It is trivial to adapt the proof to the overlapping case. Other times the adaptation needed is less trivial. For instance, the proof of I.7 needs to be somewhat substantially adapted if point D falls within the triangle ABC. This issue of cases was addressed in tedious detail by later Greek commentators and was surely known to Euclid himself (Heath, 1956, I.19, I.246). Euclid evidently omits such details for purely practical reasons: including full proofs for each case would be too tedious. A reader who can follow the proofs that Euclid does give can also be expected to be able to supply the minor variations of these proofs needed to address the cases not directly covered by them.
For the philosophical interpretation of Euclid’s method, the issue of cases is neither here nor there. On any interpretation, whether standard or operationalist, dealing with the other cases is strictly speaking necessary. While this issue is somewhat problematises the account we gave above regarding generality, this is not a problem for operationalism specifically.
3.1.5 Manuscript Diagrams
Operationalism implies that drawing accurate diagrams is important for some purposes.Footnote 18 However, diagrams in Greek mathematical treatises, as they have come down to us, are very often curiously oversimplified and crudely schematic. This could be regarded as at odds with the operationalist interpretation of Greek geometry.
I counter this objection by denying that the manuscript diagrams are representative of ancient geometrical practice. As Carman (2018) has argued, a degeneration of diagrams converging to such simplistic versions is the predictable outcome of repeated copying by generations of scribes largely ignorant of mathematical content, for the simple reason that an ignorant copyist can easily misinterpret a subtle diagram in a simplistic way while a converse transition toward a more subtle and exact diagram can only be introduced by someone with a solid understanding of the mathematical content.
For example, the figure for the Pythagorean Theorem (Elements I.47) is often drawn in manuscripts with the two legs of the triangle being equal, even though the theorem holds for any right-angle triangle. The diagram thereby gives the misleading impression that the theorem is less general than it really is. But it is indeed plausible that repeated copying converges to this kind of specificity, assuming copyists largely ignorant of mathematical content. A scribe might get a version of the figure where the legs look similar and mistakenly assume that exact equality was intended. He then copies it this way, and specificity is introduced, and thereafter passed on to subsequent copies. No one was likely to restore more generality in the diagram, because that would require revising the figures based on mathematical understanding, which was not the task of copying scribes.
Hence this aspect of the manuscript sources is likely an artefact of transmission that says nothing about ancient geometry. There are a number of indications that “ancient mathematicians were indeed interested in making drawings that were accurate” (Saito & Sidoli, 2015, 158), and that “Greek geometers were interested in working with instruments so as to produce metrically accurate diagrams” (Sidoli & Saito, 2009, 606), unlike later copyists.
Furthermore, the extent to which the operationalist reading of ancient geometry demands exactness of diagrams should not be overstated. Several of the core tenets of operationalism do not depend on great exactness of diagrams in the first place (Sect. 4.6.5). Also, insofar as exactness of diagrams is important in geometry generally, that is not the same thing as the diagrams in written works needing to be exact. Indeed, the relation of written works to geometrical practice was likely different in antiquity than today: written ancient works should perhaps be regarded as a mere secondary and incomplete representation of geometrical practice rather than as constitutive of geometrical practice itself. Moreover, the philosophical importance of basing geometry on constructions that can in principle yield accurate diagrams does not imply that every single diagram must be drawn according to such standards (just as, for example, a mathematician may use infinitesimal methods casually and informally despite being officially committed to a more formal account of their foundations that could be invoked when needed but is not part of everyday practice).
For all these reasons, I do not consider the manuscript diagram tradition to pose a problem for operationalism.
3.1.6 Physicality of Geometry
Operationalism implies that mathematics is in its very essence anchored in physical reality and instrumental practice. This notion was vehemently resisted in the Platonic tradition. Plato’s opinion was reportedly that mathematicians who “descended to the things of sense” were “corrupters and destroyers of the pure excellence of geometry” (Plutarch, 1917, 471–473). Proclus’ view is typical of this tradition:
The unchangeable, stable, and incontrovertible character of the propositions [of mathematics] shows that it is superior to the kinds of things that move about in matter. ...And how can we get the exactness of our precise and irrefutable concepts from things that are not precise? \(\ldots\) We must therefore posit the soul as the generatrix of mathematical forms and ideas. Proclus (1970, 3, 11)
However, in ancient sources, these kinds of claims come exclusively from philosophers. There is no evidence that mathematicians shared these sentiments. On the contrary, the combative way in which these claims are presented in the sources clearly show that they were far from a consensus opinion. The passage from Proclus above is his answer to the question: “Should we admit that [the objects of mathematics] are derived from sense objects ...as is commonly said ...?” Proclus (1970, 10; emphasis added) Likewise, Plato himself openly puts his view in diametrical contrast with that of the geometers:Footnote 19
No one with even a little experience of geometry will dispute that this science is entirely the opposite of what is said about it in the accounts of its practitioners. \(\ldots\) They give ridiculous accounts of it, \(\ldots\) for they speak like practical men, and all their accounts refer to doing things. They talk of ‘squaring,’ ‘applying,’ ‘adding,’ and the like, whereas the entire subject is pursued for the sake of knowledge \(\ldots\) [and] for the sake of knowing what always is, not what comes into being and passes away. (Plato, Republic, VII, 527, 1997, 1143)
Again, Plutarch reports on the same conflict and makes it crystal clear that Plato’s views on geometrical method was diametrically opposed to that of the leading mathematicians of his day: “Plato himself censured Eudoxus and Archytas and Menaechmus for endeavouring to solve the doubling of the cube by instruments and mechanical constructions” (Thomas, 1939, 389). So not only is there no evidence that any notable Greek mathematician was a Platonist, but the Platonic sources themselves clearly and openly admit that their view is an ideological extreme that was not widely shared, especially not among mathematicians.
Non-platonic sources often take a more balanced view of the relation between mathematics and physical matter. According to Aristotle, “obviously physical bodies contain surfaces and volumes, lines and points, and these are the subject-matter of mathematics” (Physics, 193b, Aristotle, 2001, 238). And mathematical authors do not seem to mind mingling physical notions into the foundations of geometry, as, for example, when Heron defines a straight line as a line “completely stretched between its endpoints” (Heron, 1912, 17), or a circle as the line traced by the end of a segment which rotates around its other end (Heron, 1912, 27). Of course mathematics is in some sense abstracted or idealised. “When we think of mathematical objects we conceive them, though not in fact separate from matter, as though they were separate.” (Aristotle, On the Soul, 431b, Heath, 1949, 11) “Geometry investigates physical lines but not qua physical.” (Aristotle, Physics, 194a, Aristotle, 2001, 239) This kind of ambivalence is perfectly compatible with operationalism. The point of view expressed in these passages does not deny that geometry is ultimately physical, although it recognises the obvious fact that mathematics idealises away from irrelevant physical particulars.
Modern scholarship has tended to exaggerate the alleged division between geometry and physical reality, in my opinion. This is not surprising since such a view aligns with modern conceptions of mathematics. Typical of this mainstream view are interpretations such as the following.
Traditionally, geometry was taken to be an abstract inquiry into the properties of magnitudes that are not to be found in nature. Dimensionless points, breadthless lines, and depthless surfaces of Euclidean geometry were not traditionally taken to be the sort of thing one might encounter while walking down the street. Whether such items were characterized as Platonic objects inhabiting a separate realm of geometric forms, or as abstractions arising from experience, it was generally agreed that the objects of geometry and the space in which they are located could not be identified with material objects or the space of everyday experience. (Jesseph, 2015, 205)
This interpretation is based on philosophical sources. There is virtually no evidence that such a view was accepted among ancient mathematicians. For one thing, geometry was in antiquity extensively applied in optics, mechanics, geography, hydrostatics, etc., and all of this is obviously based on precisely the assumption that geometry can be identified with “the space of everyday experience” and “the sort of thing one might encounter while walking down the street.” This is clearly taken for granted without hesitation in all of these applied works. Aristotle calls optics, harmonics, and astronomy “branches of mathematics” (Physics, II, 194a8, Aristotle, 2001, 239). Pappus even reports the view that “the science of mechanics \(\ldots\) includes geometry” (Collection, VIII.1, Cohen & Drabkin, 1966, 183–184).
Indeed, we may ask ourselves: Why would Greek geometers want to emphasise that geometry was divorced from physical reality? Doing so would obviously cause them a massive headache in terms of trying to explain how geometry could nevertheless be so successfully employed across numerous branches of applied mathematics in which these same mathematicians were themselves very often engaged. What would they have stood to gain from nevertheless taking such a view that could have outweighed this enormous cost? It is hard to see any reason intrinsic to mathematics itself. To anyone who is a Platonist for independent reasons, however, the motivation for taking such a stance is abundantly clear.
Operationalism embraces the physicality of geometry. It therefore makes the applicability of geometry seem perfectly natural. Admittedly, the operationalist restriction that geometry can only speak of objects we ourselves have constructed may appear to be in conflict with some applications of geometry. Greek mathematicians applied geometrical theorems to, for example, astronomical triangles determined by heavenly bodies or the center of the earth. Clearly such triangles are not practically constructible. Does this mean that the applicability of mathematics is just as mysterious in operationalism as in Platonism? No. Operationalism suggests that the geometry of such triangles is epistemologically less secure than the geometry of constructed triangles in our midsts. It involves a leap of faith, or the assumption that our experience with ruler and compass—or stretched strings, if you like—generalises to astronomical distances. This assumption is indeed a crucial point that makes the geometry of astronomical triangles potentially very different from terrestrial ones: and it is indeed correct, according to our modern understanding of the nature of space, to make such a distinction. So operationalism is not incompatible with applying geometry in such cases, but rather prudently and accurately clarifies the fundamental assumptions involved when doing so.
3.1.7 Platonic Definitions
Some of Euclid’s definitions and idealisations are often taken to prove that the objects of geometry cannot be physical. According to Euclid, “a point is that which has no part” and “a line is breadthless length,” whereas, the argument goes, in physical reality anything we consider a point really has some extension, however small, and any line, such as that drawn by a pen, has some breadth, however negligible. This point is made in various ancient sources. For example:
The mathematicians talk idly when they say that they will bisect a given straight line. For the straight line shown to us on the board has length and breadth, whereas the straight line conceived by them is ‘length without breadth’. And the line shown on the board will not be a line, and those who attempt to cut it are cutting not the real line but the unreal. (Sextus Empiricus, 1936, 139)
Perceptible lines [are not] such lines as the geometer speaks of ...for no perceptible thing is straight or round in the way in which he defines ‘straight’ and ‘round’; for a hoop touches a straight edge not at a point, but [in an entire segment or multitude of points] as Protagoras used to say it did, in his refutation of the geometers. (Aristotle, Metaphysics, 998a, Aristotle, 2001, 721)
However, there is no inconsistency between these definitions and a physicalist view of geometry. On the contrary, these kinds of idealisations are an essential part of any theory relating to physical reality. Thus Ptolemy treats the moon as a point when determining its position in its orbit, for instance (Toomer, 1998, 188–189). Obviously no one would infer that Ptolemy is therefore committed to some peculiar ontology in which the moon is a mathematical point with no extension. The convention of treating it as such is simply a common-sense idealisation that is the only sensible thing to do for many mathematical purposes, regardless of what one’s estimation of the actual body of the moon may be. It is the same for instance in Archimedes’s work on levers, where the lever arm is a weightless mathematical line and the weights are applied at mathematical points. Since such idealisations are unequivocally used without further ado in applied mathematics, it makes no sense to take them to be inconsistent with a physicalist view of geometry. The argument that Euclid’s definitions prove that his geometry is divorced from reality would, if valid, prove that the Greeks did not intend their astronomy or their statics to apply to the real world either, which is obviously absurd.
It is more plausible to read these definitions as specifications of idealisations made in geometry, rather than as ontological claims about the ultimate nature of geometrical objects. Heron clearly takes such a view, for example:
Already in ordinary language use we have the notion of a line as something which has only length, but not at the same time width and thickness. For we say: \(\ldots\) a road of 50 stades, as we concern ourselves with the length only, but not at the same time its width. (Heron, 1912, 17)
Proclus makes the same point—also using the example of a road—and attributes this view to “the followers of Apollonius” (Proclus, 1970, 82).Footnote 20 That is, Proclus puts this view right at the mainstream of Greek geometry at its peak. In these passages, the identification of geometry with everyday physical objects is evident, and the allegedly Platonic or ontological aspects of the definitions is merely a common-sense matter of simplifying assumptions and directing attention only to the relevant aspects of the situation.
There is a further argument for why one must not make too much of the alleged ontological import of Euclid’s definitions of point and line. Namely, that they are the most extraneous part of the Elements. Almost every statement of the Elements is carefully formulated to correspond precisely to the justification of specific inferences in deductive proofs. Many definitions are of this type, such as the definition of a circle which is used already in I.1 to infer that since two line segments are radii of the same circle, they must be equal. The definitions of point and line, however, are not of this type: they serve no direct role in the deductive structure of the theory. There are even grounds for suspecting that they are later additions that were not in the original text of Euclid at all (Russo, 1998, 2004, 320–326). Yet despite being arguably the most unreliable and inconsequential parts of the entire Elements, these are the very passages always cited as virtually the only textual evidence in mathematical sources of alleged anti-physicalist tendencies in Greek geometry.
3.2 Interpreting Euclid
3.2.1 Impracticality of Euclid’s Constructions
Operationalism makes actual, physical constructions with ruler and compass the foundation of all geometry. However, it does so for theoretical reasons. Operationalism does not mean that the Greeks in fact obsessively constructed every diagram for their every proof according to the most exacting standards and elaborate ruler-and-compass procedures. They surely did not do this any more than Hilbert refused to use diagrams in any context despite his avowal to base nothing on them in formal geometry. The operationalist interpretation says that the Greeks considered such constructions to be the rigorous foundation for geometry in principle, just like Hilbert and other modernists would insist that in principle a geometrical proof can be reduced to a formal argument independent of any diagram. Neither ideology requires absolute adherence to their foundational stringency in every context; indeed, they both obviously violate it all the time. The purpose of the official stance is to serve as the ultimate arbiter of mathematical rigour whenever foundational issues are at stake.
Hence observations such as the following do not stand in any conflict with the operationalist interpretation of geometry.
Euclid’s problem-constructions are not practical instructions for the use of a compass and straightedge—despite the fact that this is the most common way of explaining Euclid’s approach. ...Although the problem-constructions of Elements I–VI emulate the possible actions of a human geometer, they quickly become rather far removed from any series of actions that a human geometer would actually perform. ...As we progress farther into the problems, it becomes less and less tenable that Euclid would have believed a human geometer would actually follow all of the constructive steps in exactly the way that he sets them out. ...The algorithms detailed by the Elements are almost prohibitively laborious to carry out with real instruments. \(\ldots\) Obviously simpler constructions are overlooked in favor of constructions that call on previously established problems. (Sidoli, 2018b, 432, 436, 428, 433)
This is a standard feature of any mathematical theory that derives complex results from simple principles. In the same way, modern analysis officially defines limits in terms of \(\epsilon\)–\(\delta\) arithmetic, but only the most basic results are established directly from this root definition. In most situations, the analyst does not specify concretely how to find the \(\delta\) needed for any given \(\epsilon\), but rather relies on lemmas that have proved once and for all certain useful higher-order results that follow from the definition. It it evident in such situations that the proof of the final theorem could be expanded into a proof from first principles by incorporating the proof of the lemma into it. It is also evident that this would not generally be the easiest way of proving the final theorem directly from first principles. The path via the lemma is useful not because it is a stepping stone in the most direct way of proving that one theorem, but because it reduces cognitive complexity of the theory overall. None of this undermines the foundational status of the \(\epsilon\)–\(\delta\) definition in any way. Similarly, the foundational status of constructions in Euclid is not affected by the above observations.
The following observations should be interpreted in an analogous manner, I propose.
A characteristic of Euclid’s practice in setting out problem-constructions is that a subroutine acts as a black box in the sense that the internal constructive operations that lead to its output are not directly recoverable. \(\ldots\) In fact, there is no problem-construction in Elements I–VI or the Data in which an object that would have been involved in a subroutine is not later introduced by its own problem-construction step, if it is required. ...
[For example,] it is difficult for us to imagine how a circle could have been constructively introduced without first introducing its center, but \(\ldots\) Euclid’s practice in his problem-constructions is consistent in introducing objects whose production is described by a problem as fully formed, without any auxiliary constructions that may have been used in the original problem-construction. Hence, if in the course of a problem-construction a circle is introduced as passing through three given points \(\ldots\)—as, for example, in Elem. IV.4 or IV.5 \(\ldots\)—then the circle’s center will not have been introduced at the same time. Now, of course, the problem-construction of such a circle will first involve finding its center, but since this operates as a subroutine, its center is not immediately available when the circle is called in. Hence, if its center is required, it must be introduced by its own introduction rule. ...
This discussion makes it clear how remote Euclid’s procedures are from the actions of any human geometer—any person actually producing one of these diagrams would see that the objects produced in the subroutines are already there in the figure and do not need to be introduced again. (Sidoli, 2018b, 435, 411, 436)
In my view, this does not point to the non-actuality of Euclid’s constructions. Rather, it is merely a consequence of using intermediary lemmas to reduce cognitive complexity. It is precisely because it can be treated as a “black box” that the previous construction results are useful in reducing cognitive complexity. The human mind can only process so much information at any given time, which is why, to prove complex results, we must use earlier results as stepping-stones without calling all of their constructions and proofs actively to mind. This is an artefact of human cognitive abilities that has nothing to do with the foundational status of constructions in geometry.
3.2.2 The “Collapsible” Compass
Elements I.2 shows how to transfer a length to another position by ruler and compass. However, with an actual physical compass, one can do this much more straightforwardly, by simply opening the compass to the given length and then lifting it and putting it down with one leg at the given point where the length needs to be placed. Euclid acts as if this is not possible. As is often observed, Euclid behaves as if his compass is “collapsible”: it stays at a fixed opening while drawing a particular circle but as soon as it is lifted from the paper it “collapses,” so that the opening to which it was set is lost and cannot be transferred elsewhere.
Many have pointed to this as evidence that Euclid’s constructions do not correspond to actual ruler and compasses, since no actual compasses are collapsible (Sidoli, 2018b, 422, Acerbi, 2010b, 229). This conclusion clashes with the operationalist reading of geometry. And indeed I believe there are good grounds to reject it.
The Elements masterfully reveals the minimum assumptions necessary for geometry. The fact that one can do away with the assumption that a compass can transfer length is an interesting foundational insight. Since Euclid can prove this, he does. This does not imply that he is opposed to the idea of a non-collapsible compass. One could simply delete Proposition I.2 from the Elements and all the rest would still stand verbatim as a treatise about constructions with non-collapsible compasses. Hence Proposition I.2 can be viewed as an optional exercise in foundational minimalism within a paradigm fully based on physical compasses, rather than as evidence of conceptions fundamentally at odds with such a paradigm. An argument in favour of this interpretation of I.2 as optional is the fact that, in solid and spherical geometry, where no equivalent of I.2 is forthcoming, Greek mathematicians seem to have been perfectly content to assume that lengths could be unproblematically transferred by the compass (Sects. 5.2.1 and 5.3).
Analogous situations are commonplace in modern mathematics. For example, open any textbook on abstract algebra and turn to the definition of a group. The definition of a group says that in any group there is an (“identity”) element e such that \(g*e=e*g=g\) for any element g in the group. As far as this definition is concerned, there could potentially be several such identity elements. However, all textbooks immediately proceed to show that the identity element is in fact unique. These textbook authors could have made life easier for themselves by simply making the uniqueness of the identity element part of the definition. Then there would have been no need to prove it a separate theorem. But it is better to keep definitions and axioms as simple and minimalistic as possible, for instance in order to minimise the risk of inconsistency and because proving properties instead of gratuitously including them in the definition illuminates fundamental relationships. Note well, however, that one cannot infer from this that the uniqueness of the identity is somehow a secondary or less embraced aspect of the group concept. It is proven as a theorem rather than included in the definition solely because of the technical possibility of doing so, not because it was seen as less essential than the definitional group properties. This does not show that the fundamental conception of a group that mathematicians have in mind is ambivalent regarding the uniqueness of the identity. On the contrary, it is arguably a core aspect of the intuitive notion of a group that has, prima facie, no less of a claim to being fundamental than the definitional properties. But if one tries to find the smallest set of key properties of a group to take as definitional, then one finds that uniqueness of the identity is a property that can most efficiently be made into a theorem.
In the same way, I claim, Proposition I.2 does not show that Euclid’s fundamental notion of the circle-drawing constructions and postulates were divorced from a physical compass. It does not prove this any more than a modern textbook proves that the uniqueness of the identity is fundamentally divorced from the group concept. Just as a modern algebra textbook would have nothing a priori against including uniqueness of the identity in the definition of a group, so Euclid may very well have had nothing a priori against assuming a non-collapsible ruler. Just as the modern algebra textbooks nevertheless arrives at the conclusion that it is better to make the uniqueness of the identity into a theorem because that enables the minimisation of definitional properties overall, so Euclid may very well have decided to assume only a non-collapsible ruler purely for reasons of axiomatic minimalism. This is not in any way in conflict with operationalism.
3.2.3 How Can You Know a Circle and Not Its Midpoint?
In Elements III.1, Euclid constructs the midpoint of a given circle. This may seem to suggest that, according to Euclid, we can know that something is a circle without knowing its midpoint. Or in other words, we can evidently know that something is a circle without having constructed it ourselves. This is in apparent conflict with operationalism, which holds that a circle simply means the figure produced by a compass, which cannot be done without knowing the midpoint. According to operationalism, the only circles we ever talk about in geometry are ones we have concretely constructed ourselves. It is anathema to operationalism to do geometry to objects introduced by fiat, such as a circle pre-drawn on a piece of paper without its midpoint indicated. Yet this seems to be basically what Euclid is doing in this proposition.
But there is no need to view this as a fundamental conflict. Even though operationalism implies that you must have drawn the circle yourself, and hence must have known the midpoint already, nothing stops you from investigating whether you can reconstruct the midpoint if you pretend for the sake of argument that you do not know it. In this way, Elements III.1 is interesting in its own right and can be useful for various purposes,Footnote 21 but it does not have the foundational implication that circles can be known without their midpoint. Just as Elements I.2 does not imply that Euclid is opposed to moving lengths with a non-collapsible compass (Sect. 3.2.2), so also Elements III.1 does not imply that Euclid thinks it makes sense to speak of circles given in some way other than by a compass. Just as Euclid proves I.2 because he can, he proves III.1 because he can—not because he thinks they are epistemologically essential. From an operationalist point of view, these constructions can be viewed as optional. They could be deleted from the Elements and the whole work would still make coherent epistemological sense, because moving lengths could be considered a primitive capacity of the compass, and the midpoint of a circle can be considered known by virtue of the circle having been constructed by a compass in the first place. The fact that Euclid shows that it is possible to work around these assumptions does not imply that he rejects them.
In other words, an author concerned with nothing but operationalist foundations should not have included III.1 in the Elements, but an author fully committed to operationalist foundations could still very well choose to include this theorem because he found it interesting from some other point of view. Operationalism doesn’t tell you what theorems to prove. Interest in particular geometrical investigations should come from elsewhere. Operationalism says only that wherever such motivations may take you, you should carefully ensure that the investigations you pursue are consistent with operationalist foundational principles. As indeed III.1 is.
3.2.4 The Parallel Postulate as Construction
While Euclid’s Postulates 1–3 have often been identified with ruler and compass constructions, such an interpretation is often resisted for the parallel postulate. However, even Euclid’s Postulate 5, the parallel postulate (Fig. 2), “is clearly constructive in the sense in which is it articulated. It acts as an introduction rule for a point as the intersection of two given lines” (Sidoli, 2018b, 423). In other words, the parallel postulate “can be viewed as a construction method for producing certain triangles. In view of ...remarks of Geminus and Proclus, it seems likely that Euclid viewed his postulate in this way, or he would have called it an axiom.” (Beeson, 2016, 8–9)
In this way the parallel postulate is directly analogous to the ruler-and-compass postulates, which likewise licenses the introduction of geometrical objects by postulating that a certain construction can be carried out. Just as it is possible to draw a straight line from a given point to a given point (Postulate 1), so it is possible to extend converging straight lines until they meet (Postulate 5). It is remarkable indeed that among the many possible equivalents of the parallel postulate—several of which have often been considered preferable by later authors—Euclid uses what is perhaps the most directly constructive formulation possible. This fits very well with the operationalist reading of the Elements.
It is notable also that Euclid formulates the parallel postulate (as his geometry generally) in terms of finite line segments rather than lines in the modern sense. In a modern setting, one takes the full lines as preexisting and assumes that it makes sense to speak of them either intersecting or not. But that is not operationally sound. Operationally, we can only speak of what we have constructed, which restricts us to finite configurations. This agrees with Euclid’s formulation of the parallel postulate, which says that the lines will cross “if produced.” That is to say, the crossing of the lines is not a preexisting relationship with a predetermined truth-value in some Platonic realm that assumes omniscient access to infinite lines.Footnote 22 On the contrary, saying that the lines intersect only becomes meaningful after we ourselves have extended them so as to concretely produce this intersection.
3.2.5 Non-verifiability in the Theory of Parallels
It is often felt that the theory of parallels “involves infinity” in some way that the ruler-and-compass postulates and constructions do not. But there is no such distinction as far as the parallel postulate is concerned. It is true that the parallel postulate says that under certain conditions two lines will meet if they are extended far enough, so to speak. But how far is far enough? No bound is given. A geometer who has extended the lines for miles and still not found an intersection might come to doubt the postulate. But this is not qualitatively different from the other postulates. A geometer trying to draw an enormous circle by fixing one end of stretched string and moving the other end may likewise feel pessimistic that the curve will ever close back up on itself as the postulate and definition demand. So the parallel postulate is not any less constructive than the earlier postulates in this regard.
Non-Euclidean geometry suggests another sense in which the parallel postulate is special. In hyperbolic geometry, Euclid’s postulates effectively hold in small neighbourhoods, whereas on a larger scale the parallel postulate fails while the other postulates remain true. This may seem to suggest that the parallel postulate is a more “global” assumption than the other postulates, and hence an assumption that extrapolates recklessly beyond experience in a way the other postulates do not. But I do not think it is possible to make such a qualitative distinction. The earlier postulates already make far-reaching idealisations and assumptions about the space of geometry that by necessity go beyond past experience no less than the parallel postulate does. For one thing, if the universe is finite—as was the standard cosmological conception in antiquity—the ruler-and-compass postulates fail as well. Obviously the identification of geometry with physical experience—which is central to operationalism—is contingent on the assumption that the postulates correspond to physical reality. This assumption is subject to verification in any given case. The parallel postulate is not different from the other postulates in this regard.
Another way of trying to get at the “infinity” aspect of the theory of parallels is in terms of decidability.
The notion of constructivity can be applied to relations as well as operations. The simplest account of a constructive relation is as one which is decidable, i.e., as one for which there is a uniform way of deciding whether or not it holds of a given object or objects. ...[Euclid] makes no attempt to show that one can decide whether or not two straight lines are parallel before he treats parallels. ...He introduces the relation with a nonconstructive sense (never meeting, even if extended ad infinitum). The sensible conclusion seems to be that, whatever tendency Euclid has toward using constructibility as a proof of meaningfulness for operations, he has none toward using decidability as a proof of meaningfulness for relations. (Mueller, 1981, 40–41)
This critique is indeed very much applicable to the operationalist interpretation of geometry, which holds that concepts have meaning only in terms of concrete operations. How can Euclid, by that standard, prove results about parallels, if the concept of parallelism is not reducible to concrete, finitistic operations? Just as we argued above that operationalist geometry does not have the “omniscience” to speak of such things as all right triangles or all lines through a given point, so also an operationalist geometer does not have the omniscience to survey the full extent of two given lines (extended arbitrarily far) to know whether they intersect or not.
But again one can question whether the situation regarding parallels is really qualitatively different from that regarding for example circles. Consider Euclid’s definition of a circle:
A circle is a plane figure contained by a single line [which is called a circumference], (such that) all of the straight lines radiating towards [the circumference] from one point amongst those lying inside the figure are equal to one another (Elements, Definition I.15)
Is it “decidable” whether a given figure is a circle or not? Arguably, no. You could never check all the straight lines for equality. And if you per chance found two such straight lines that were not equal, this would not show that the figure was not a circle, but only that the point of origin of those two lines is not the “one point” (the midpoint) that the definition speaks of. To conclusively show that something is not a circle, you would have to go through all points in the interior of the figure and, for each one of them, find two unequal segments from there to the circumference. This is arguably as impossible as verifying that two straight lines never meet. Hence I question whether there is any special decidability or meaningfulness problem with respect to parallel lines that does not apply equally to other geometrical concepts such as that of a circle.
The ability to decide whether or not a figure is a circle is not needed in the Elements. All Euclid needs to know is that the figures he constructs with his compass are in fact circles, which arguably follows directly by construction. By contrast, Euclid needs the concept of parallelism to be meaningfully applicable to geometrical objects that are not specifically constructed in a way that guarantee that they have this property. Thus, if someone challenged Euclid during the proof of Proposition I.1 to explain what he means by something being a circle, he does not need to rely on the definition of a circle being directly constructively meaningful in itself. Instead, it is enough that the particular circles involved in the proof are constructively knowable to be circles, which follows not from the definition per se but rather from their generation by a compass or rotating line segment.
Now imagine that someone challenges Euclid during the proof of I.27 to explain what he means by two lines being parallel. Just as in the circle case, he does not need to rely on his definition on this concept to be inherently constructively meaningful. Rather, it is enough that he can constructively show that this definition applies to the particular lines involved in the proof. This time this is known from an argument by contradiction rather than directly by construction, but why should this make a difference as far as meaningfulness is concerned?
Altogether, it therefore seems to me that decidability issues, while they do point to limitations of strict verificationism generally, do not provide grounds to conclude that Euclid was unconcerned with verificationist thinking on the basis of his theory of parallels particularly. It is true that the definition of parallel lines is not immediately translatable into finite operationalist terms. But neither is the definition of a circle. Nor does Euclid need his definitions to be operational in the abstract and in isolation. Rather, he only needs it to be operationally knowable that they apply to the particular objects that occur in his proofs. This indeed fits with the operationalist view that there is no geometry except the geometry of concretely constructed figures. Definitions in the abstract are indeed meaningless. It is not a problem for operationalism that some definitions do not have a direct operational meaning in general; rather, it is a necessary consequence of operationalism that definitions by themselves cannot have any meaning and that there is nothing general. The content of geometry is particular constructed figures. Terms can only have meaning as instantiated in such figures.
3.2.6 Linguistic Arguments
The language of Greek mathematics “makes the author and temporality disappear from a proof” (Acerbi et al., 2018, 270). At first sight, this may be perceived as suggesting a Platonic conception of the transcendent and eternal character of mathematics. Indeed, some have seized on the passive, impersonal formulations in construction proofs (e.g., “let the circle ABC have been described”) as evidence that the constructions are merely imagined to have taken place rather than being something the geometer is actively engaged in (e.g. Lachterman, 1989, 67). Furthermore, the Greek verb form (third person imperative) of Euclid’s constructions is the same as the Biblical “let there be light,” suggesting that geometrical entities are commanded into existence at will rather than manually produced by a geometer-craftsman. However, this inference has been compellingly countered by Netz, who argues that this grammatical construction is merely a reflection of a tradition in which, due to technical limitations of the visual media available, presentations of proofs would take place after the diagram had been drawn.
Of the media available to the Greeks \(\ldots\) none had ease of writing and rewriting. ...[Standard media were papyri and wax tablets, and, for larger audiences, such as Aristotle’s lectures,] the only practical option was wood \(\ldots\) painted white. ...None of these [ways of representing figures] is essentially different from a diagram as it appears in a book. \(\ldots\) The limitations of the media available suggest \(\ldots\) the preparation of the diagram prior to the communicative act—a consequence of the inability to erase. ...This, in fact, is the simple explanation for the use of perfect imperatives in the references to the setting out—‘let the point A have been taken’. It reflects nothing more than the fact that, by the time one comes to discuss the diagram, it has already been drawn. (Netz, 2003, 14, 16, 25)
If this interpretation is correct, Euclid’s grammatical choice reflects only incidental cultural circumstances and says nothing about philosophical commitments.
Other linguistic aspects of Greek mathematical terminology line up well with the operationalist conception of concrete constructions as the foundations of geometry. The association between construction and proof in the minds of Greek geometers is so close that one word,  , is used for both concepts (Lloyd, 1979, 106). Similarly, a theorem is a
, is used for both concepts (Lloyd, 1979, 106). Similarly, a theorem is a  —a figure (Netz, 2003, 35–36; Hintikka & Remes, 1974, 73). It has even been argued that, etymologically speaking, to prove,
—a figure (Netz, 2003, 35–36; Hintikka & Remes, 1974, 73). It has even been argued that, etymologically speaking, to prove,  , originally meant to “show” or “point out” in a visual sense (Szabó, 1978, 188). It has also been argued that Euclid’s use of
, originally meant to “show” or “point out” in a visual sense (Szabó, 1978, 188). It has also been argued that Euclid’s use of  rather than
rather than  as his term for a “point” may suggest a deliberate association with a physical and visual mark as opposed to the abstract notion of point expounded in philosophical literature (Russo, 1998, 208, 2004, 181).
as his term for a “point” may suggest a deliberate association with a physical and visual mark as opposed to the abstract notion of point expounded in philosophical literature (Russo, 1998, 208, 2004, 181).
3.2.7 Constructions are Not Merely Existence Proofs
The idea of constructions as existence proofs has for many been a convenient way to shoehorn the constructive aspect of Greek geometry into modern conceptual categories (Zeuthen, 1896). Existence is no doubt part of the story, as I have argued and as Proclus indicates (see esp. Sect. 2.1.2; Proclus, 1970, 157, 183). But in truth it is very difficult to imagine how qualms about the possible nonexistence of basic geometric entities could possibly be so great as to motivate the extremely thorough attention to constructions throughout Greek geometry. Are we really to believe that the Greeks seriously doubted the existence of such a thing as the third of an angle, and that this was the reason why they spent hundreds of years constructing it over and over again by a variety of methods? Surely this makes no sense. Clearly there was something more than existence at stake here, as the Greeks saw it.
Another way of proving this is by examples such as Elements III.1, in which Euclid shows how to construct the midpoint of a given circle. It is impossible to doubt the existence of the midpoint of a circle, because a circle is defined in terms of its midpoint (Definition I.15). So knowing that something is a circle means knowing that its midpoint exists, yet constructing it is apparently still of interest. There are various examples of this type in the Elements (Sidoli, 2018b, 410).
3.2.8 Does “Given” Imply Constructible?
“Given” is a technical term in Greek geometry. It is used in problem enunciations, such as: “In a given pentagon, which is equilateral and equiangular, to inscribe a circle” (Elements, IV.13). From an operationalist point of view, it is essential that any object assumed as given in the enunciation of a problem is constructible, and also that any theorem only speaks of constructible objects. Hence operationalism suggests that we think of “given” as meaning constructively available to us. Thus construction problems are in effect about enlarging the universe of givens.
This interpretation has strong textual support. Indeed, the theorems of the Elements only speak of objects that have first been shown to be in this universe of constructibles, which suggests that Euclid meant his theorems to apply only to “given” (that is to say, constructively produceable) objects. Table 1 gives one illustration of this unfailing consistency.Footnote 23
Furthermore, the very first definition of Euclid’s Data—the authoritative work on givens—reads: “Given in magnitude is said of figures and lines and angles for which we can provide equals.” This is an operationalist definition if there ever was one. Givenness amounts to constructibility. Givenness has to do with what we can do. Indeed, “the use of the first person plural [in this definition] is somewhat unusual in Greek mathematical prose and should be taken as deliberate. That is, the issue involved in the notion of given is not primarily about the existence of the object, but rather about what we, as mathematicians, are able to do” (Sidoli, 2018a, 367). Similarly, when Pappus defines “what mathematicians call given,” he characterises it as things that are “obtainable” (Jones, 1986, 84) or “can be provided” (Acerbi, 2011, 129).
So the operationalist conception of the notion of “given” fits very well with Euclidean practice in both word and deed. Nevertheless, some resist the identification of givenness with constructibility: “Every constructed object is given, but not every given object is constructed \(\ldots\) because we ...apply the term given to objects that we assume and set out, as well as to objects that we construct” (Sidoli, 2018a, 368). A philosophical consequence of this is that “since the notion of given also applies to objects that are simply assumed at the beginning of the discourse, Euclid seems to be unconcerned with the ultimate origin of such objects ” (Sidoli, 2018b, 411). This interpretation conflicts with the operationalist point of view, according to which the ultimate origin of geometrical objects is a matter of paramount importance to Euclid and other Greek mathematicians.
I believe we should reject this notion of a dichotomy between given as in specified in the problem enunciation and given as in constructed. Essentially, the objects assumed as given in the enunciations of problems are previously constructed. Within the framework of the Elements, Euclid never assumes a regular heptagon, for example, as “given,” even though as far as the above interpretation is concerned that would be perfectly permissible. Similarly, he does not assume a square as given before he has constructed squares in I.46. From the operationalist point of view, it is evident why. It is of the utmost importance to restrict mathematics to objects that are proven constructible. It is also evident that, whatever “given” means, “any object that can be constructed from given objects is fully given” (Sidoli, 2018a, 375)—indeed the whole point of problems is to show that certain objects are given in this sense. If the only givens permitted are previously constructed objects, this fits together into a coherent program for keeping track of the established scope of constructibility.
If, on the other hand, the givens of a problem can be anything and do not need to answer to any constructive standard, then their role and purpose become much more puzzling. The very rigid restriction to a constructive standard in the solution to problems is evident: “all of the objects introduced in the constructions of problems can be unproblematically produced by applications of the postulates and previously established problems” (Sidoli, 2018b, 407). Why would the Greeks insist on this if the starting points are arbitrary anyway? Why insist that the one and only way to prove that givenness transfers from one object to another is by strict construction, if the initial givenness was not itself constructive? It makes a lot more sense to see problems as the investigation of the propagation of givenness, meaning constructibility, from primitively constructible objects to more complex ones.Footnote 24
I therefore resist the interpretation that “given means little more than assumed or produced by the permitted operations” (Sidoli, 2018a, 359, emphasis added), and that “there does not appear to have been any restriction on the objects that can be assigned in setting out a problem [i.e., assumed]” (Sidoli, 2018a, 398–399). Instead I claim that, effectively, given means only produced by the permitted operations, not assumed, and that constructibility is a fundamental restriction on what is allowed to be assumed in setting out a problem. Or perhaps better put: I do not need to claim that this is the meaning of “given” per se, but only that the purpose of having the concept of given in Greek mathematics is to use it to this end. Rephrased in this way, my view is not in conflict with the more literalist interpretation cited above. It is even possible to reconcile my interpretation with the theoretical possibility of a problem whose enunciation assumes as given a non-constructible object. The solution to such a problem would have a hypothetical status, just as a theorem of the form “if the Riemann Hypothesis is true, then ...” does in modern mathematics: it could be illuminating for certain purposes, but it would be self-evidently different in status from any normal problem solution and would in a strict sense not add to the body of mathematical knowledge.
If indeed the objects given in the enunciations of theorems and problems were not required to be constructed beforehand, this leaves open the possibility that they are self-contradictory, such as a superright triangle. This calls all of mathematics into question. In particular, any proof by contradiction would become vacuous sophistry, since the contradiction obtained could then very well not derive from the counterfactual assumption made for the sake of argument, but from the impossible objects assumed to be “given” at the outset.
Altogether, the hypothesis that only constructed or constructible objects are permissible as givens is well justified and makes coherent sense of the Greek corpus. The hypothesis that there is no such requirement—and that hence that the enunciations of theorems and problems are a free-zone of anarchy where anything goes—can perhaps not be directly disproven from the sources, but would be peculiar and unmotivated.
3.3 Proofs by Contradiction
Proofs by contradiction are often used in Greek geometry.Footnote 25 This may seem incompatible with operationalism. Proofs by contradiction involves reasoning about figures that are not only not constructed but even altogether impossible, whereas operationalism tells us that mathematics is solely about what we ourselves have constructed.Footnote 26 If it is perfectly fine to do mathematics to fictional, non-constructed objects in proofs by contradiction, why should it not be fine to do so in mathematics as a whole, contrary to the decrees of operationalism?
I say that there is no such incongruity. The use of non-constructed entities in proofs by contradiction do not show that mathematicians have carte blanc to disregard core principles of operationalism if they feel like it. On the contrary, the form of argument used by Euclid in these cases is very well tailored to be compatible with operationalism. For what these proofs show is that a diagram with particular properties could not be the outcome of a construction. This is shown by proving that, if it were the outcome of a construction, then constructive practice leads to inconsistent results, which is assumed impossible. In other words: “The widely held belief that ‘proofs by contradiction’ are ‘not constructive’ is mistaken. One can constructively prove that a certain construction is impossible by proving that if it were possible, then another construction that is clearly impossible would also be possible” (Edwards, 2005, 186).
This is why Euclid, after having made the counterfactual assumption, always proceeds according to his usual standards of construction for the rest of the proof, when drawing consequences from the counterfactual assumption. Therefore, when a contradiction is reached, this proves that either the hypothesised figure is impossible, or, if it is possible to construct it, that constructive practice leads to self-contradictions. So Euclidean proofs by contradiction are not about things outside the scope of operationalism; rather, their point is precisely to investigate whether the counterfactual assumption is consistent with operationalist practice.
In a proof by contradiction, it is important to admit only one counterfactual assumption and for the rest to be very strict, in order to be sure that the counterfactual assumption, and that alone, was the source of any contradiction obtained. Aristotle points this out (Prior Analytics, 65b). He uses the following example. In order to show that the diagonal of a square is incommensurable with its side, one must derive the contradiction strictly from the negation of this statement. One must not smuggle in unrelated issues and derive the contradiction from them, such as replicating within an ostensible proof of the incommensurability of the diagonal the arguments Zeno used to derive a contradiction in his paradox against motion. For the same reason, it is crucial for Euclid to make only isolated and controlled counterfactual assumptions, and for the rest stick to the same strict principles of proof and construction as elsewhere.
A proof by contradiction is only convincing if one’s entire system of reasoning is consistent. Otherwise the source of the contradiction could have been something other than the counterfactual assumption one is trying to refute. If geometry is inconsistent, all geometrical theorems—not only those proved by contradiction—would become worthless, since a theorem only has meaning if it says that something is thus and not otherwise, which can no longer be maintained if the system is inconsistent. History shows that inconsistencies can very easily creep into formal axiomatic systems, against the best efforts of even top mathematicians devoted specifically to building rigorous foundations. “Great logicians (Frege, Curry, Church, Quine, Rosser) have managed to propose quite serious systems of logic which later turned out to be inconsistent” (MacKenzie, 2004, 93). In the case of Euclidean geometry specifically, one high-profile attempt at formalising it proved to be inconsistent (Miller, 2012).
Hence Greek geometry can credibly be challenged on such grounds: How do we know that Euclidean geometry is consistent at all? Operationalism avoids or minimises this challenge by reducing as far as possible any contradiction among principles and assumptions to a contradiction in physical experience itself. A Euclidean proof by contradiction does not merely show that one statement in an axiomatic-deductive theory contradicts another. Of course Euclid does indeed derive his contradictions from statements within his theory—that is to say, ultimately from the postulates. But since the postulates are construction postulates, the force of a proof by contradiction can be expressed purely in terms of constructions, without relying on the assumption that the postulates constitute a consistent axiomatic system. Instead, a Euclidean proof by contradiction translates into a concrete recipe for how, if the counterfactual figure assumed for the sake of demonstration could really be constructed by ruler and compass, concrete physical experience produces inconsistent results. So we do not need to place inordinate trust in mathematicians as to whether they formulated a consistent axiom system in the first place. Instead we only need to trust that actual physical experience is not self-contradictory (that is to say, in physical experience, a particular object cannot be both larger than and also smaller than another object, a stick cannot be both one meters long and two meters long, and so on).
It is also interesting to note that even according to modern notions of constructive mathematics, the geometry of “Euclid[’s Elements] is essentially constructive as it stands” (Beeson, 2016, 12). My operationalist interpretation is not equivalent to this modern constructivist one. Nevertheless, this modern analysis supports my point that Euclid’s use of proof by contradiction is limited and certainly more restrictive than the classical logic inference rule \(\lnot \lnot P \rightarrow P\) for any proposition P.
Altogether, I have tried to turn an apparent weakness into a strength. Proofs by contradiction are not a problem for operationalism because the counterfactual assumption involves non-constructed entities. Rather, proofs by contradiction are a problem for formalistic conceptions of geometry because of the challenge to establish the consistency of all geometry but the counterfactual assumption. Operationalism meets this challenge. Formalism does not, by itself.
3.4 Superposition
3.4.1 The Problem with Superposition
In the Elements, Euclid appeals to superposition to establish two triangle congruence theorems (I.4, I.8). His proofs are based on placing one triangle on top of the other, seemingly treating them as moveable physical objects. This is often regarded as one of the major flaws of the Elements. Euclid’s use of superposition is seen as a naive appeal to empirical or intuitive considerations that should have no place in a formal treatment of geometry (Heath, 1956, I.249; Mueller, 1981, 21; Klein, 2004, 200; Russell, 1902, 165). It is furthermore often said that Euclid himself realised as much, and therefore avoided the use of superposition whenever he could, and only used it with regret in a few instances because he could think of no alternative (Heath, 1956, I.249, I.225; Knorr, 1978, 161; Mancosu, 1996, 29).
Yet there are obvious problems with this reading. How could such a sophisticated geometer make such an elementary blunder? And in an early key theorem that is hugely important to his entire edifice, no less. And if Euclid disapproved of his own use of superposition to prove the triangle congruence theorems, then why did he not opt for the obvious alternative, namely to take these theorems as axioms? This is generally regarded as the “right answer” to the problem from the point of view of modern mathematics (Heath, 1956, I.249). Euclid could surely not have failed to see this possibility.Footnote 27
Another puzzling aspect of Euclid’s use of superposition is the baffling contrast between the obsessive focus on precise ruler-and-compass constructions in I.1–3 and the sudden use of the apparently very different and incompatible principle of superposition in I.4. One way to address this has been to regard superposition as theoretical or hypothetical in character.Footnote 28 This view is based on emphasising the distinction between problems and theorems. The two play by different rules: problems are strictly constructive, while theorems are more theoretical, whence merely supposing a triangle to have been moved is permissible in proofs of theorems (such as I.4) but not in solutions of problems (such as I.1–3). But then why did Euclid go to such lengths to show how to move a line segment in I.2? If theorems do not depend on such constructive procedures, then why does Euclid so consistently insert them in just the right places throughout the Elements?
3.4.2 Euclid’s Use of Superposition
Euclid first uses superposition to prove the side–angle–side triangle congruence theorem (I.4; Fig. 3). I propose that, in the strict operationalist framework adopted by Euclid, we must read this theorem as follows. It is “given” that two triangles have the same side–angle–side. Whenever something is “given” in a Euclidean proposition, we must understand this to mean “has been produced by a construction recipe such that the resulting objects are known to satisfy the stated conditions.” The meaning of the theorem is therefore: if you have constructed two triangles, ABC and DEF, in such a way that the construction recipe implies that \(DE=AB\), \(DF=AC\), and \(\angle BAC = \angle EDF\), then those two triangles are congruent—that is to say, all remaining sides and angles are pairwise equal as well.
The initial steps of Euclid’s proofs of the SAS (I.4), SSS (I.8), and ASA (I.26) triangle congruence theorems. In each case, Euclid supposes that the given triangles are not congruent and derives a contradiction from this assumption. The counterfactual, non-aligning configurations are obtained by superposition in I.4 and I.8, but not in I.26
This operationalist reading of the theorem enables us to give a different interpretation of the proof as well: superposition does not involve lifting one triangle, like a cardboard cutout, and putting it on top of the other. Rather, it means constructing a copy of one triangle in the same place and orientation as another. This is done in order to be able to conclude that the third side EF coincides with BC using the fact that two points uniquely determine a line. The theorem therefore proves that if we want to make a copy of a given triangle ABC, we do not necessarily need to follow the same steps we did when constructing ABC. Instead, it is enough to know that our DEF construction is equivalent to our ABC construction in terms of the side–angle–side.
Superposition, therefore, really means “reconstruction in a different place.” This interpretation is not at all far-fetched. After all, I.2 reads: “to place at a given point a straight line equal to a given straight line,” and it transpires from the proof that this obviously means: to construct at the given point a copy of the given straight line. Everything in Euclid must be understood to be shorthand code for a ruler-and-compass construction, including the notion of “placing” a figure at a given location. Since this is undeniable in the case of I.2, it is natural also in the case of I.4.Footnote 29
Euclid’s subsequent uses of superposition are readily interpreted in an analogous manner to my reading of I.4. Euclid uses superposition again in I.8, the side–side–side triangle congruence theorem. As I read it, the theorem says that if you have constructed a triangle is such a way that you know that the lengths of its sides correspond to the lengths of the sides of another triangle, then you may infer that the triangles are congruent. Euclid uses superposition for a third and final time in III.24, a theorem stating that similar segments of circles on equal line segments are congruent. Similar segments of circles means segments subtending the same central angle (Definition III.11), so similar segments are closely associated with the side–angle–side (in this context, radius-central angle-radius) triangles of I.4. Superpositioning circle segments is therefore in effect equivalent to superpositioning side–angle–side triangles. Because of this close correspondence it is not surprising that superposition is used here in an analogous way to I.4. It hence poses no new interpretative issues.
My interpretation of superposition is in large part not new. To a significant extent it agrees with the mature view of Zeuthen. In a widely cited paper, Zeuthen (1896) argued that Euclidean constructions should be considered existence proofs, which, as discussed above, I see as an overly restricted and modernistic view of the role of constructions in Greek geometry. However, decades later, in one of his last works, available only in Danish, Zeuthen developed a more sensitive appreciation of the role of constructions as it relates to superposition (Zeuthen, 1917, Chapter VIII, pp. 66–86, entitled “Figurflytning hos Euklid” [“Movement of figures in Euclid”]). Here he explicitly rejects his earlier view that Euclid’s principle of superposition is based on motion, and instead argues, as I do, that when Euclid speaks of placing one figure on top of another he really means reconstructing it in that position by means of ruler and compass (Zeuthen, 1917, 68).Footnote 30
Zeuthen admits that there is a major problem with his interpretation, namely that Euclid proves how to constructively move an angle in I.23 and how to construct a triangle from three given line segments in I.22. If the proofs of I.4 and I.8 are meant to involve not moving the triangles but rather reconstructing them using ruler and compass, then it would seem that these constructions are needed before these theorems can be established. But Euclid uses I.4 and I.8 to prove I.22 and I.23, so the theorems are the foundations for the corresponding constructions rather than conversely, which is contrary to Zeuthen’s constructivist interpretation of the superposition principle. Indeed, Zeuthen accepts the conclusion that Euclid’s reasoning is ultimately circular [Zeuthen (1917, 72, 176) and Vitrac (1990, 297) raises the same problem in his discussion of the similar view of Wagner (1983)].
I avoid the problems with Zeuthen’s interpretation by adopting a more radical operationalist interpretation. On my reading, Euclid’s reasoning is perfectly sound and involves no circularity. I.22 and I.23 are not assumed in I.4 and I.8. This interpretation is made possible by my rejection of the Platonic interpretation of these theorems as being abstract inferences that hold for all triangles with the given conditions. On the Platonic view, the equalities of certain sides or angles in the hypotheses of the theorems are simply given absolute truths. But in operationalist geometry, properties of figures cannot be simply given in such an abstract manner. Instead, we can only ever make inferences about triangles we have made ourselves. Any equalities of sides or angles cannot be merely “given” but must be consequences of the constructions of the triangles in question.
It follows that we are only allowed to apply these triangle congruence theorems in cases where we know how to constructively reproduce one triangle in the position of the other. But, from an operationalist point of view, this in not actually a restriction at all. The only way we could know that the angles of the two triangles are equal is by construction. Any time we are in a position to apply I.4, we must have constructed the two triangles using some definitive recipe that guarantees that the given angle is equal in the two triangles. This knowledge must come from one of two sources. Either the two angles are directly identical (not only in magnitude but also in position), which makes them equal by Common Notion 4 (“things coinciding with one another are equal to one another”). In such a case, the proof does not need to do any moving of angles, so it poses no problems for the interpretation of superposition as reconstruction. The second way in which we can know that two angles are equal is by virtue of their constructions being equivalent. In such a case, the reconstruction of one triangle in the place of the other is possible by repeating in the position of the second triangle whatever construction recipe produced the first triangle to begin with.
So instead of asking how we could reproduce one triangle on top of the other in I.4, I ask: how could we not? That is to say, how could we know that the angle–side–angle of two triangles are equal unless we know how those triangles were made? It is impossible, from an operationalist point of view, to have the knowledge that the second triangle has side–angle–side in common with the first, without also having the knowledge of how the triangles were made, and hence how to (re)produce them constructively. This reading squares well with Definition 1 of Euclid’s Data: “Given in magnitude is said of figures and lines and angles for which we can provide equals.” It makes no sense, from an operationalist point of view, to speak of a given angle being equal to another given angle unless we can constructively (re)produce that angle.
There is nothing strange about able to reproduce specific angles without being able to reproduce any angle. I.23 shows how to copy any angle, including an angle drawn at will (by simply laying down any two lines with your ruler). I.4 does not depend on the ability to do this, but only on the ability to copy a particular angle involved in the particular triangles we are applying the theorem to. For the latter we do not need a general theorem like I.23, but only specific knowledge of the specific configuration we have constructed. For example, I can define the angle in question as the angle of an equilateral triangle, or the angle I obtain by placing some number of equilateral triangles side by side and connecting certain points in this configuration. If my angle at A was given by such a construction recipe, then I can repeat the same construction recipe (or one proven to be equivalent to it) when producing the angle at D. In this way I can know that the angle at D equals the angle at A, and be able to reproduce it, without relying on any general ability to copy any angle.
3.4.3 Euclid’s Non-use of Superposition
As noted above, a standard view is that Euclid studiously avoided the use of superposition whenever he could. In my view, this is a misconception stemming from a misunderstanding of the sense in which Euclid uses superposition in the triangle congruence proofs. Many of the examples usually given to prove that Euclid could have simplified his proofs with superposition are based on the traditional interpretation of superposition as motion of a rigid figure. If one adopts my much more restrictive interpretation of superposition as reconstruction, there is no longer such an array of missed opportunities in the Elements.
For example, one common claim is that if superposition is allowed then there is no need for elaborate ruler-and-compass constructions for such things as transferring a line segment to a different place, which Euclid gives in I.2.Footnote 31 On my reading of Euclid, this kind of objection is a non-starter, since I have argued that Euclid’s so-called superposition proofs are based on much more limited and refined principles than at-will physical motion of any geometrical object.
Postulate 4, which states that all right angles are equal, is often said to be trivially demonstrable if superposition is allowed.Footnote 32 I disagree. Euclid’s definition of a right angle (Definition I.10) is readily interpreted operationally, namely as the cutting-in-half of the neighbourhood on one side of a line. The statement that all right angles are equal then amounts to the claim that this construction recipe gives equal or congruent results no matter at which point it starts. Assuming position-invariance of constructions arguably amounts to assuming the homogeneity of space. Indeed, Euclid’s Postulate 4 can quite plausibly be interpreted as being intended to capture the homogeneity of space, since it is false on the surface of a cone (Clifford, 1886, 222; Henderson & Taimina, 2004, 58). This shows that Postulate 4 is by no means a trivial consequence of superposition, since on the surface of a cone a right angle at the cone point will be smaller than a right angle elsewhere, and hence does not coincide with it when brought to lie on top of it. It is possible that Euclid may have thought of cone points as the only possible obstacle to homogeneity of space in the kind of “flat piece of paper” (or zero curvature) geometry he is talking about, and hence included Postulate 4 to rule out such points.
If we assume that a given construction recipe always gives equal or congruent results no matter at which point it starts, then indeed Postulate 4 is a consequence of this principle. As we saw, my reading of Proposition I.4 is indeed based on attributing this assumption of position-invariance of constructions to Euclid. My reading would arguably fit better if this principle was the postulate, and Euclid’s Postulate 4 a corollary of it. But if the intent of Postulate 4 is to rule out cone points, and cone points are seen as the only possible deviation from homogeneity in the presence of the other axioms, then Postulate 4 can be read as effectively tantamount to postulating position-invariance of constructions generally. Interpreted this way, Euclid’s Postulate 4 fits perfectly with my reading of superposition: Postulate 4 cannot be proved by superposition; rather, it provides the foundations for superposition by guaranteeing the position-invariance of constructions on which superposition is based. We do not know what Euclid meant with Postulate 4, but since in any case the interpretation of it is inevitably intertwined with subtleties of this sort, I do not think Postulate 4 should be given too much weight when trying to interpret Euclid’s intention in his superposition proofs in the body of the Elements.
Arguably the most important case of Euclid’s non-use of superposition is in his third triangle congruence theorem, I.26 (Fig. 3) (Heath, 1956, I.225; Dijksterhuis, 1929, 147; Morrow in Proclus, 1970, 273). A standard view is that “Euclid’s failure to use superposition in I,26 is somewhat surprising; it constitutes one piece of evidence for a widely held thesis that Euclid found something unsatisfactory in this method of proof” [Mueller (1981, 22), who spells out the proof by superposition that he has in mind]. However, Euclid’s preference for reduction to I.4 in place of direct superposition can be explained as a sound and reasonable strategy that has nothing to do with distrust in superposition but rather merely the desire to minimise the need to consider separate diagrammatic cases.Footnote 33 Indeed, the proof of I.26 has no case-division complications, since it constructs one definitive triangle (BCG) for comparison purposes. If, on the other hand, one had tried to compare ABC directly to a superpositioned version of DEF, there is a lot more ambiguity in how exactly the counterfactual diagram should be drawn. We need to argue by contradiction that DEF does not fit on top of ABC, but in what way does it not fit? Where exactly should D be positioned in relation to A in this counterfactual diagram? This is a messy question. Euclid’s proof bypasses such issues. Hence Euclid’s avoidance of superposition is perfectly reasonable without any need to suppose that he found superposition inherently dubious.
4 Operationalism and the Classical Construction Problems
4.1 Introduction
4.1.1 Why Trisect an Angle? Double a Cube? Square a Circle?
Higher Greek geometry is as obsessed with constructions as Euclid was. Greek geometers devoted great efforts, across several centuries, to three fundamental problems in particular:
-
Doubling the cube: given a cube, make a cube with twice the volume.
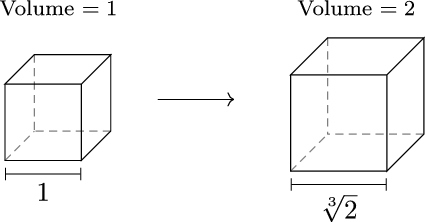
-
Trisecting the angle: given an angle, cut it into three equal parts.
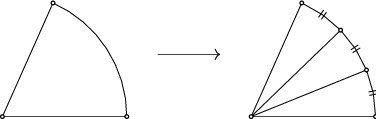
-
Squaring the circle: given a circle, construct a square with the same area.
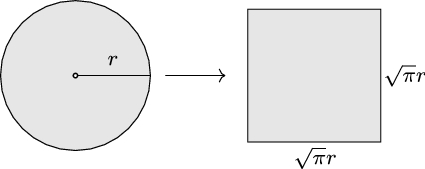
In other words, the great prizes of Greek geometry was not proving things, but making things. These problems “were rallying-points for mathematicians ..., and the whole course of Greek geometry was profoundly influenced by the character of the specialized investigations which had their origin in the attempts to solve these problems.”Footnote 34
From a modern point of view, the Greek obsession with these problems is a peculiar oddity if not altogether inexplicable. What core conviction in the Greek mathematical psyche was so strong and deeply rooted that they remained doggedly determined to cut an angle into three equal pieces or die trying, while modern mathematicians can hardly wrap their heads around how this could even be considered a research problem at all.
But the operationalist outlook puts the matter in a different light. We have seen how dangerous it can be to assume that mathematical entities are given by abstract properties or logical sentences of the form “let x be an angle such that \(x=\theta /3\)” (Sects. 2.1.2–2.1.4). We have also seen a second, independent reason for making constructions foundational. Namely, that talking about geometrical configurations without constructing them can easily make us march right into paradoxical errors even with arguments that at first sight looked just like any from the Elements (Sect. 2.1.1). We saw that Euclid’s construction of an angle bisector was key to avoiding that error. Naturally, cutting an angle into three equal pieces is the problem next in line in this enterprise to secure the foundations of mathematics.
The Greeks did not say that this is what they were doing. The record is virtually silent on why they wanted to solve those three problems. But I believe the operationalist background is the only way to make sense of this research program.
One alternative is to not attempt to explain it at all. Many modern commentators seem to view the Greek obsession with constructions as an idiosyncratic quirk. According to this view, just as one geometer may be particularly focussed on proving theorems about triangles and another about conic sections, so many of the Greeks happened to be especially interested in proving what can be constructed using certain tools, and how. As far as the philosophy of geometry is concerned, this peculiarity of the Greek taste is of no more consequence than any other technical details of this or that line of inquiry that the Greeks happened to pursue. I do not find this interpretation of the role of the construction problems at all convincing: it is a non-explanation that attributes a large part of the historical record to sheer whim.
Another way to try to account for the importance of the classical problems is in terms of their alleged usefulness. It is possible to construe the three classical construction problems as useful for certain applied purposes.Footnote 35 But it is more likely that these alleged applications were used to boost the status of an already existing research program than that they were the actual motivation for these mathematical developments.Footnote 36 This is quite evident, unless one is willing to believe that mathematicians spent 600 years trying to double the cube because an oracle supposedly once told someone to double the size of an altar, or because there was a burning practical need to determine the optimal dimensions of stone-throwing machines in a dozen different ways (those are the main applications the sources repeatedly mention). The overall nature of the sustained research program on the classical construction problems in Greek times cannot be well explained in terms of such aims. If practical results were the goal, one would expect to see much more focus on numerical and approximative methods (Sect. 4.6.8). Instead we find many solutions based on ingeniously conceived motions that are out of touch with practice and quite clearly selected for the sake of some sort of theoretical purity.
Similarly, the research program on the classical problems makes little sense as an effort whose primary goal is to supply existence proofs, as noted in Sect. 3.2.7. For one thing, this perspective does not explain why the Greeks were so interested in going back over the same material and re-solve the same problem over and over again with particular variations in fundamental assumptions. All the more so when the existence of the solution is seemingly more obvious than the existence of the curves or other auxiliary means assumed to construct it, as frequently happens.
Another attempt at explaining the purpose of constructions is given by Proclus. He needs to explain away the obvious prominence of constructions in mathematics, since it clashes with the Platonic belief that the objects of mathematics are eternal and independent of human actions situated in space and time. He accomplishes this by alleging that constructions play a role in geometry not because they have anything to do with the essential nature of geometrical objects but because of limitations of the human mind. The mind needs this crutch of concretely exhibiting figures in the imagination as a stepping stone, even though the end goal is a pure understanding that is higher and independent of such operations.Footnote 37 This account is defensible in the case of Euclidean geometry. It makes sense that step-by-step constructions can assist the mind in forming the concept of a parallelogram or a dodecahedron. But this picture makes no sense for the higher problem tradition. In order for, say, an angle trisection to make any sense from this point of view, it would have to construct the third of an angle using only things that are more immediately accessible to the imagination than the idea of the third of an angle itself. It is obvious that the classical problem tradition comes nowhere near to accomplishing anything of the sort. In the solutions to the classical problems, the means assumed to construct the objects sought are much less readily imagined than the objects themselves. Therefore it makes no sense to maintain that the constructions are meant to assist the imagination in conceiving the sought objects by building them up stepwise from simpler starting points.
Operationalism, by contrast, makes sense of the tradition of the classical construction problems. On this view, constructions are the foundations of all geometry. The three construction problems cannot be solved by ruler and compass. The Greeks effectively knew this, though they could not strictly prove it. So any solution is based on introducing some additional construction tool or method beyond the Euclidean ones. The classical construction problems were selected, I believe, to be representative of a whole body of geometry representing the next step beyond ruler and compass. Solving the classical construction problems meant devising the definitive foundations of higher geometry, just as Euclid provided the definitive foundations of elementary geometry. The classical construction problems were not interesting in isolation but as showcases for rethinking the foundations of geometry as a whole. As such, it makes perfect sense that generation upon generation of the very best mathematicians would devote major efforts to this particular research program, and to rework the same problems over and over again based on different fundamental assumptions.
If this reading is correct, it follows that the solutions to the classical construction problems would have been devised with a conscious emphasis on foundations. Solutions would have to be accompanied by (perhaps implicit) reasons for why that new construction method should be granted foundational status and not some other one. Clearly this must be based on some convincing rationale. Minimalism and stringency in this regard is clearly essential. If you can just introduce whatever constructions you like at any time, then the whole project of operationalist mathematics becomes meaningless.
Solving the classical construction problems would thus have been perhaps the “most philosophical” part of geometry. Hence I believe it is essential, when studying the ancient solutions to these problems, to try to understand what vision for the foundations of geometry they are meant to encapsulate. Unfortunately we have next to no source material on such questions. The sources we have for Greek mathematics are almost exclusively formal mathematical texts: definition-theorem-proof, with no informal commentary, contextualisation, or motivation of any kind. Therefore, we must study the technical works in the Greek geometrical tradition and extract the implicit foundational assumptions on which they are based. What does a technical analysis of these proofs say about the assumptions these mathematicians made regarding mathematical method and the purpose and rules for constructing geometrical objects? Answering this question shall be our goal in this section.
4.1.2 Algebraic Aspects of the Classical Problems
In modern terms, the classical construction problems can be interpreted as follows. Doubling a cube is equivalent to constructing a line segment of length \(\root 3 \of {2}\), the side length of a cube with twice the volume of a unit cube. Trisecting an angle is equivalent to solving a particular cubic equation. This can be seen by trigonometry, since constructing the required points on the arc is equivalent to constructing the point perpendicularly below it on the axis, whence the trisection of an angle amounts to constructing \(\cos (\theta /3)\) from \(\cos (\theta )\), and by trigonometric addition formulas we know that \(\cos (\theta )=4\cos ^{3}(\theta /3)-3\cos (\theta /3)\). Squaring the circle is equivalent to constructing a line segment of length \(\pi\). This follows from the theorem shown in Fig. 34. Since \(\pi\) is a transcendental number, this is in a definite sense “more complicated” than the n-section of an angle, which is an algebraic problem. Thus the complexity of these problems form a clear hierarchy:
The scope of ruler and compass, meanwhile, corresponds algebraically to the ability to solve quadratic equations, or, what comes to the same thing, to the ability to perform the four arithmetical operations as well as square root extraction.
Although these are modern terms, it is likely that Greek mathematicians had a sense of such a hierarchy. For instance, for squaring the circle they resorted to methods that they likely found more questionable than those used for the simpler problems. I shall argue below that they relaxed operationalist ideals precisely and only insofar as the complexity of the problem at hand necessitated doing so.
The insolubility of these problems by ruler and compass was quite clearly taken for granted by the ancient mathematicians who worked on them. The actual proofs of this insolubility is a staple topic of abstract algebra courses to this day (Hartshorne, 2005, 243–245), but the importance of such proofs should not be overestimated. It would be a mistake to think that these modern results somehow undermine the Greek problem tradition. The Greek tradition is not hampered by ignorance of these results, but rather founded upon an awareness of them. Nothing about the Greek problem tradition would change if they had been able to prove these results.
It should also be noted that the Greek mathematical tradition saw the doubling of the cube as a special case of the more general problem of finding two mean proportionals. That is to say, given a and b, find x and y such that \(a:x=x:y=y:b\). The duplication of the unit cube is the special case of finding x when \(a=1\) and \(b=2\). The Greek methods for doubling the cube are really ways of finding two mean proportionals, but I shall ignore this distinction and restrict my discussions to cube duplication for simplicity and clarity, since everything generalises straightforwardly to the general setting of two mean proportionals without anything of interest from the point of view of operationalism being added.
4.1.3 Overview Chronology of the Three Classical Problems
Table 2 gives a chronological overview of all solutions of the classical construction problems in Greek mathematics that have been recorded. The chronological order as well as a number of the attributions to specific mathematicians are tentative. Almost all of these solutions are known to us only through much later sources; specifically, the vast majority only through Pappus’s Collection and Eutocius’s commentary on Archimedes. These authors lived many centuries after the golden age of Greek geometry had ended, and their brief accounts are no doubt far from a complete and faithful picture of the lost original works. The approximate chronology and attributions in the table are my attempt at roughly summarising the secondary literature;Footnote 38 I am not contributing anything new in these regards. My contribution shall consist in the operationalist interpretation of these solutions.
As the table shows, these problems formed the basis for a sustained, continuous research program for more than two centuries, from Hippias around \(-420\) to Diocles around \(-190\),Footnote 39 attracting the attention of many of the best mathematicians in between. The sheer multitude of solutions speaks to the centrality of the problems, and also suggest that no solution was viewed as fully satisfactory.
The surviving record of solutions is surely incomplete. For example, Simplicius lists the circle quadratures mentioned in the table and then says that, in addition, “many others constructed a solution of this problem in diverse ways” (Thomas, 1939, 335).
4.1.4 Origins of the Classical Problem Tradition
There are some earlier signs of theoretical interest in constructions that suggest that the solutions to the three classical problems were, at the time of Hippias, already embedded in a coherent program that took constructions as a foundational paradigm of geometry.
Proclus attributes to Oenopides (ca. –450) the discovery of Elements I.12 (to draw a perpendicular to a given line through a given point not on that line) and I.23 (to move an angle to another location). This can only mean that Oenopides worked within a theoretical framework specifically restricted to ruler and compass, for in a pre-theoretical context these results are trivial (Heath, 1981a, 175).
Anaxagoras (ca. –470) supposedly worked on squaring the circle (Heath, 1981a, 173). This problem was surely also the motivation for Hippocrates (ca. –440) to square circular lunes (Heath, 1981a, 183–200). Hippocrates also proved that cube duplication is equivalent to finding two mean proportionals (Heath, 1981a, 200–201). The sophistication of Hippocrates’s work suggests that at this time the construction paradigm and at least two of the great construction problems were well established.
The squaring of the circle was evidently such a famous problem already in –414 that it was referenced in popular culture (Aristophanes, The Birds, 1005).
These indications suggest that the solutions in Table 2 should be considered part of a well-established tradition that had already been the subject of much attention well before the record available to us even begins. The hypothesis that an operationalist paradigm dominated Greek geometry from an early stage onwards fits well with this picture.
Knorr has challenged this view and argued that geometry remained more pre-theoretical for much longer than suggested here. According to Knorr,
Oenopides would surely not have been occupied in a consciously formal geometric effort, for the astronomical context indicates that he was showing how to arrange the construction of astronomical devices, like sundials, via appropriate instruments of construction. The latter surely included compasses and rulers, but we have no reason to suppose that he rejected the use of others \(\ldots\) [such as] set squares. (Knorr, 1975, 16)
This is a peculiar argument since it makes no sense for someone using a set square to prove Elements I.12, or even to conceive of it as a proposition at all. Similarly, it is easy to see why an operationalist would be interested in the highly theoretical and impractical copying of angles by ruler and compass in Elements I.23, while it is difficult to imagine why anyone else would even conceive of this as a proposition. The mere fact that Oenopides used these things in astronomy is not in conflict with an interest in the foundations of geometry any more than Plato and Aristotle should be considered non-theoretical philosophers because they discuss applied topics. If anything, one could argue that it is precisely because they think philosophy is so important in so many areas that they are all the more interested in its theoretical foundations. In the same way, theoretical and applied interests could very well have gone hand in hand for mathematicians.
Knorr continues in the same vein:
The conscious restriction to a specific set of constructing techniques, like the compass and straightedge in sharp separation from others, would be premature at Hippocrates’ time. \(\ldots\) The trisection of the angle became a problem only after a tightening of the restrictions on construction techniques, and hence only within a formally more sophisticated geometric field. By contrast, the problems of the cube and the circle present difficulties at the much earlier level of development. (Knorr, 1975, 41)
I disagree. I don’t see how the problem of the quadrature of the circle, as a construction problem, makes much sense in a pre-theoretical framework. The basic area result of Fig. 34 is evident by polygonal approximation (Fig. 4)—an idea that is bound to suggest itself readily to any mathematician devoting effort to circle quadrature. From there it follows that a piece of string or tape measure is sufficient to square any circle in an obvious way, by measuring its circumference. How, then, could a research program on circle quadrature be meaningful without deliberate foundational restrictions on construction techniques? That could only make sense if we believe that these simple ideas were unknown even informally, until rigorously proven by Archimedes (Knorr, 1975, 83 indeed argues for this). But it is all but impossible to imagine how the very basic idea of Fig. 4 could have eluded people like Hippocrates, whose work on lunes shows that he worked extensively in this area and proved much more intricate results than this.Footnote 40 Meanwhile, the angle trisection problem, which Knorr believes only becomes relevant as a byproduct of later theoretical developments, is natural from an operationalist point of view. It is a short step beyond angle bisection, whose importance as a construction problem we justified in simple terms in Sect. 2.1.1. Angle division also arises immediately from the natural problem of constructing regular polygons. Therefore it makes sense, from an operationalist point of view, that the trisection problem would have been part of the tradition from the outset.
4.1.5 Operationalist Demands on Curve Construction
Higher geometry necessitates that new construction means be introduced beyond ruler and compass. On what grounds can one judge which new means are better than others? In accordance with Sect. 2, operationalist philosophy of mathematics suggests the following criteria.
-
Realisability Constructions must be generative and realisable in concrete experience.
This ensures that all mathematical claims have an unequivocal meaning that is statable in theory-independent terms accessible to outsiders and potentially falsifiable. It also means that mathematics need not assume the reliability or consistency of abstract verbal logic, only the consistency of physical experience itself.
-
Unicity Constructions should be defined in terms of one single property, not multiple simultaneous conditions. In other words, the outcome of a construction should be defined in the form “the result of doing X,” not in the form “the result of doing X until or while conditions Z and Y are met.”
Defining something in terms of multiple properties inhibits primitive generation and increases the risk of inconsistency.
-
Single degree of freedom Curves can favourably be traced by some mechanical contraption moving a pen, but in such cases the configuration moving the pen should be driven by one single “input” motion (which may very well produce multiple other motions as side-effects by pushing various mechanical parts etc.).
This is a consequence of the previous points. Just as an axiom system runs less risk of being inconsistent if it derives statements instead of assuming them as additional postulates, so also a curve tracing scheme runs less risk of being incoherent or impossible if it defines secondary motions in terms of a primary one rather than stipulate multiple simultaneous conditions.
-
Definitive termination Constructions should produce entities definitively and finitely, not in terms of gradual approximations or convergent infinite processes.
This ensures that entities have unequivocal meaning and that, once constructed, they are unequivocally available to serve as subcomponents of subsequent constructions.
-
Practical accuracy Constructions should be accurate in practice.
This protects against the danger of reasoning based on false diagrams.
-
Primitiveness The assumptions on which constructions are premised should be more basic and immediate than the entities constructed with their aid.
Otherwise they cannot serve to give meaning to the entities they construct in a credible way.
We shall now turn to the specific constructions proposed in the Greek tradition and investigate to what extent they can be viewed as consistent with these priorities.
4.2 Cube Duplication
4.2.1 Archytas
Archytas’s method for doubling a cube amounts to taking the intersection of three surfaces (Fig. 5): a cone (\(x^2 + y^2 + z^2 = 2^2 x^2\)), a cylinder (\(x^2 + y^2 = 2 x\)), and a torus (\(x^2 + y^2 + z^2 = 2 \sqrt{x^2 + y^2}\)). If one of the four intersection points is projected onto the xy plane (the plane that contains the axis of the cone and is perpendicular to the axis of the cylinder), the distance from there to the origin (the vertex of the cone) is \(\root 3 \of {2}\). Hence, assuming that the intersection of these surfaces can be found, the problem has been solved.
This is a perplexing solution to the cube duplication problem, since it appears to be based on taking for granted things that are more complicated than the problem itself. How could someone be perfectly happy to take very complicated intersections of various surfaces at will, yet still feel that that finding \(\root 3 \of {2}\) is a challenging puzzle? The source is of no help in explaining how this is supposed to make sense. It simply says that when a circle rotates so as to generate the torus, “it will cut the cylindrical surface in its rotation, and will draw in it a certain line”; and then the “conical surface ...will meet [that] cylindrical line at a certain point” (Netz, 2004, 291). In other words, the intersections shown in Fig. 5 are assumed to become immediately available to us merely by being defined. If one can call into being by simple decree such a complicated object as the curve of intersection of a cylinder and a torus, then why can one not do the same with a segment of length \(\root 3 \of {2}\) or a cube of a certain volume?
This seems baffling, but, in fact, one can make perfect operationalist sense of all of this in a rather straightforward way, namely as follows (Figs. 6 and 7). Consider a door. That is to say, a plane, one edge of which is attached to an axis (the z-axis) around which the plane is moveable. In this plane we draw a semicircle, corresponding to the generating circle of the torus. This circle touches the axis of the door in one point, has unit radius, and has a diameter along the bottom edge of the door. As we move the door, this semicircle traces out the top half of a torus in space, so to speak, although there are no actual physical solids involved in this construction.
On the floor under the door we draw a circle, corresponding to the base of the cylinder. This circle touches the axis in one point and has unit radius. Its diameter starting at the axis of the door corresponds to the x-axis; we may take it to be the threshold of the door. The door intersects this circle in two points: one point is always the same, at the axis itself, and the other point changes as we move the door. Standing on the floor we have a metal rod with a foot that ensures that it is always perpendicular to the floor. As we move the door, we also move this rod, and we always place it right where the door intersects the circle on the floor. In terms of Archytas’s setup, this means that, for any given position of the door, the metal rod represents the intersection of that plane with the cylinder. And hence the intersection of the rod with the semicircle drawn on the door is on the surface of both the cylinder and the torus.
Now for the cone. Again, there is no actual cone involved. Instead all we need is a compass. One leg of the compass is fixed in position along the threshold of the door. The other leg is free to rotate. The opening of the compass is fixed at \(60^{\circ }\). When we move the door, we also move the compass leg until it touches the door. It will lay flat against the door and hence the compass leg is a line on the surface of the door.
We keep moving these three objects until the metal rod, the circle on the door, and the compass leg all intersect in the same point. This is the sought point of intersection of the three surfaces that solves the problem. The reconstruction up to this point is essentially that proposed by Knorr.Footnote 41
But we can do even better than Knorr’s reconstruction. We can eliminate the need for adjusting the various parts by hand. We could make the circle on the floor a rail or groove in which the rod stands, so that it is automatically constrained to move along this curve only. Then when we start with the door in the threshold position we only need to move the door, whereupon the rod and the compass will be forced to move as required without any additional manual involvement from us. Furthermore, instead of drawing the semicircle on the door, we can replace it with a radial stick that is nailed to the door at the midpoint of the semicircle, around which it can rotate. At its other end, this radial stick has a nail sticking out of it. With the door it its stating position, we place the radial stick so that the nail is touching the rod (on the inside, toward the axis). Then as the door moves, and hence forces the rod to move, this in turn forces the nail on the radial stick to move. Meanwhile the leg of the compass is being forced to move toward the nail from above. At a certain point the configuration locks, because the rod needs to go inward and the compass leg needs to go downward but the nail is stuck between them and prevents them from moving any further.
Thus we have built a machine that produces the required solution in a deterministic way and according to demonstrable mathematical principles. This is a good solution to the problem that fits perfectly in the operationalist tradition.
This solves all the apparent mysteries of Archytas’s method. It makes perfect sense that Archytas had in mind a construction such as the one I have outlined. I consider it more plausible that this is what Archytas did than that he relied on the perplexing notion of accepting the intersection of a cylinder and a torus as primitively given. Admittedly, the source we have does not directly support this, but that is of little consequence, for it is a third-hand account at best, written many hundreds of years after the original, that could plausibly have missed Archytas’s operationalist point altogether. There is even some textual support, namely that Archytas’s solution was at one point criticised from a Platonic point of view as being instrumental rather than purely geometrical (Thomas, 1939, 389), which makes little sense as a critique of the solution as transmitted in surviving sources, but makes perfect sense as a critique of the solution as I have reconstructed it.
4.2.2 Pseudo-Plato
The pseudo-Platonic machine for doubling the cube is shown in Fig. 8. As we push the point M along the x-axis, the conditions imposed and welded into the machine mean that there is only one way the machine can move. In particular, the pen point P is forced to move along one particular curve, \(2(1+x)^{2}=y(x^{2}+y^{2}+x)\). When the point P hits the y-axis, its y-value is \(\root 3 \of {2}\), so we have doubled the cube. The source is explicit about the physicality of the contraption: it consists of several “rulers” whose “motion” is constrained by various “grooves” and “knobs” (Netz, 2004, 273–275).
The pseudo-Platonic cube duplication by moving rulers. The pen point P traces a curve as M is pushed. The rulers \(l_{1}\), \(l_{2}\), \(l_{3}\) constrain the motion of the entire configuration as follows: \(l_{1}\) and \(l_{2}\) are rigidly attached to one another at right angles; \(l_{1}\) is forced to pass through \((0,-2)\), and \(l_{3}\) through \((-1,0)\), due to the pegs fastened at those points; \(l_{3}\) is at right angles to \(l_{2}\); M can move only along the x-axis
The least convincing aspect of this solution from the point of view of actual execution is how to ensure that \(l_{3}\) is perpendicular to \(l_{2}\). If we are merely trying out one position of the machine after another we can adjust it manually for each individual case. But it is much more satisfying to have the machine trace a continuous curve, rather than trying to find the configuration where P falls on the y-axis by trial and error. I do not see an easy way implementing this, although it could be done in principle and the source does address it.Footnote 42 Therefore, I think we must count the pseudo-Platonic machine as problematic—though certainly not altogether a failure—as far as the requirement of continuous, single-motion curve tracing is concerned.
4.2.3 Philon, Apollonius, Heron
Philon’s cube duplication is shown in Fig. 9. The ruler must be fitted into position by trial and error until the condition is fulfilled. For this reason the solution cannot be considered exact, but only approximative. On the other hand, the practical realisation is simple and uses only basic tools. In this respect it has clear advantages over previous solutions in addition to its clear disadvantage.
Heron’s solution (Fig. 10) is a rather trivial variation on that of Philon. It appears to have no theoretical or practical advantages to speak of.Footnote 43
Heron’s variant of Philon’s cube duplication of Fig. 9. The same configuration is achieved by an equivalent condition
Unlike almost all other solutions in Table 2, we do not need to rely only on secondary accounts by Eutocius and Pappus in these cases. Full treatises by Philon and Heron containing these constructions have survived.Footnote 44 The hands-on nature of the constructions is explicit. Thus for instance Philon writes: “Taking a ruler, ...I juggle it about, always keeping one part of it touching the corner [of the rectangle], until” the two lengths indicated are equal as required (Marsden, 1971, 111).
There is some unclarity as to Apollonius’s solution. What Eutocius calls Apollonius’s solution is trivially identical to that of Heron, only with pointless cosmetic changes.Footnote 45 It makes little sense for Eutocius to include it as a separate solution in his catalogue. And, more importantly, it makes little sense that Apollonius would have contributed something so trivial and useless (assuming that he knew Philon’s solution). More plausible, and in accord with other sources (Heath, 1896, cxxv–cxxvii; Knorr, 1975, 305–308), is that Apollonius’s work was about the connection between Philon’s solution and conic sections. The circle in Fig. 9 is \((x - 2) x + (y - 1) y = 0\) and the point where the ruler cuts it in the sought configuration can be obtained by intersecting this circle with the hyperbola \(xy=2\) . So we can replace the trial-and-error ruler-fitting procedure with the drawing of a simple hyperbola. If we accept the hypothesis that this was Apollonius’s point, then his contribution was clearly mathematically interesting. Showing that conic sections subsume previous work speaks to the centrality of the theory of conics. On the other hand, doubling the cube by conics was already old news, so this solution does not constitute progress in terms of doubling the cube based on simpler construction assumptions (except that this solution uses only one conic section, rather than the intersection of two as the previously recorded solutions had done).
4.2.4 Eratosthenes
Eratosthenes’s cube duplication is shown in Fig. 11. The main drawback of the construction is that it requires the coordination of multiple conditions instead of producing the solution by a single motion. For the rest it is a simple construction using nothing but basic tools. As Eratosthenes noted, it can also be adapted to yield any number of mean proportionals (such as \(\root 4 \of {2}\), \(\root 5 \of {2}\), \(\root 6 \of {2}\), etc.) by increasing the number of triangles.
The account of this solution transmitted by Eutocius is supposedly a verbatim letter by Eratosthenes himself. The text explicitly speaks about the realisation of the construction “by a machine,” that is to say triangles sliding along “grooves” inside “a box ...made of wood, or ivory, or bronze” (Netz, 2004, 296).
4.2.5 Nicomedes
Nicomedes’s cube duplication is shown in Fig. 12. It uses the conchoid compass that arises more naturally in the context of angle trisection (see Sect. 4.3.1). Nicomedes reportedly criticised Eratosthenes’s cube duplication when he offered his own (Netz, 2004, 298), and indeed an obvious advantage is that it is a single-motion construction rather than a trial-and-error process.
4.2.6 Diocles
Diocles doubled the cube by means of a particular curve, the cissoid, \(y^2 (r + x) = (r - x)^3\), as shown in Fig. 13b.Footnote 46 This curve can readily be traced by a single-motion linkage device, as shown in Fig. 13a. This manner of generation is not in the sources. However, it suggests itself naturally from the way the cissoid is defined in the sources. Any mathematician in Greek times who would have spent even the slightest effort thinking about how the cissoid could be mechanically realised would have come up with this idea. I believe they did. Indeed, the ease with which the abstract geometrical definition of the cissoid lets itself be interpreted in mechanical terms suggestively hints that such an interpretation was intended. If so, this cube duplication fits well in the operationalist tradition.
a A linkage machine for drawing the cissoid. The linkage is operated by pushing the motion point M. The vertical grey ruler and the two marked points on the horizontal diameter are fixed in position. As the bottom point is pushed, it causes the other components of the linkage to move as indicated by arrows. The two points on the circumference of the circle are constrained so that they can only move along the circle, and furthermore the grey rulers ensure that they are always symmetrically placed with respect to the vertical axis. The motion of the left circumference point causes the diagonal black ruler to rotate about its fixed point. The right circumference point moves the vertical black ruler along with it, while this ruler is also locked at right angles to the diameter. The intersection of the two hollowed black rulers traces the cissoid. b Diocles’s cube duplication by the cissoid
Disturbingly, however, the sources clash with this interpretation. Instead the cissoid is “constructed” by marking a bunch of points belonging to it (which can be done by ruler and compass, just as they can on a conic section for instance) and then fitting a curve along these points by naive interpolation. This is profoundly unsatisfactory from an operationalist point of view. Indeed, it is arguably conceptually incoherent altogether regardless of whether one is an operationalist or not. For the entire use of the cissoid for a problem such as cube duplication consists in producing one particular point of intersection. It is useless to produce a bunch of points elsewhere on the curve. Obviously only the points nearest the intersection will help interpolate that point, and since that is the goal we are better off targeting that area by trial and error already in the point-production phase. Producing points elsewhere, and fitting a curve to this entire set of points, serves no purpose.Footnote 47
A version of Diocles’s own text survives in Arabic, making this one of the few cube duplications for which we have a full source rather than merely a paraphrased extract in Eutocius or Pappus. Diocles’s text is explicit on precisely the pointwise aspect of the construction that I just criticised. Eutocius’s account is a bit more ambiguous in this respect, but basically seems to back the Arabic version of the Diocles text.Footnote 48 On the other hand the text has obviously been corrupted in transmission in intrusive ways, so the authenticity of specific details cannot be assumed. This was pointed out by (Toomer, 1976, 31) on grounds completely independent of my operationalist reconstruction. Eutocius’s account appears to be based on more or less the same corrupt version of the original that was the basis for the Arabic text (Knorr, 1989, 87).
In fact, the internal logic of Diocles’s text contains traces that the linkage construction was originally intended, and readily suggests how a corruption from there to a pointwise construction could have occurred.
In the surviving text of Diocles’s On burning mirrors, Diocles begins his discussion of cube duplication by the cissoid with the following result (Toomer, 1976, 96–98). In Fig. 14, let H be defined as the intersection of KB and \(\Theta Z\), where arc DK = arc DZ. Diocles says: “The reason that \(A\Theta : \Theta Z = \Theta Z : \Theta B\) is clear.” (Elements VI.13) “But I say that \(Z\Theta : \Theta B = \Theta B : \Theta H\) also.” Indeed Diocles proves that this follows from the definition of H. Now H is a point on the cissoid, and by repeating this construction for various other choices of \(\Theta\) one can construct more and more points on the cissoid and then proceed with the cube duplication from there in the manner corresponding to Fig. 13b.
But, strikingly, this argument can be simplified and reformulated by omitting all the parts related to K. Taking \(\Theta\) arbitrarily on the diameter, and constructing the perpendicular \(\Theta Z\), one immediately has \(A\Theta : \Theta Z = \Theta Z : \Theta B\) by Elements VI.13. From there, constructing \(\Theta H\) such that \(Z\Theta : \Theta B = \Theta B : \Theta H\) simply means constructing the third proportional of two given segments: a well-known standard construction (Elements VI.11). Hence the point H and its key property could easily have been introduced without any reference to the point K, the line KB, or the condition arc DK = arc DZ. Nor are these entities related to K ever needed for any other reason in the remainder of the text. All of the rest of Diocles’s text uses only the ability to construct points H on the cissoid, and the relation between \(A\Theta\), \(\Theta B\), \(Z\Theta\), and \(\Theta H\), so it works equally well if H is defined and constructed in the simplified manner as a third proportional.
It is surely impossible that Diocles could not have seen this. So why did he include all the matters related to K, which are superfluous as far as the logic of the text as transmitted is concerned? My reconstruction of the linkage device suggests an obvious explanation: The entities related to K in Fig. 14 are there because they correspond exactly to the linkage device of Fig. 13a. If Diocles wanted to construct the cissoid pointwise—as his text ostensibly does—then he could easily have omitted everything related to K and used the simpler, obvious alternative construction of H as a third proportional instead. But if Diocles wanted to demonstrate that the points H generated by his linkage device stands in this particular relation to \(A\Theta\), \(\Theta B\), \(Z\Theta\), then everything about his Proposition 11 makes perfect sense. The point of this proposition is not to give a pointwise construction of the cissoid but to derive properties of points generated by the cissoid linkage.Footnote 49
This suggests that Diocles’s original text contained a discussion of the linkage generation of the cissoid. One can easily imagine that some later editor or compiler lacking an understanding of the fundamental importance of this might have chosen to copy only the “mathematical” part of Diocles’s text. This would give us exactly Diocles’s Proposition 11 as transmitted. Subsequently, somebody working from this purely “mathematical” version might realise that the text in this form only amounts to a pointwise construction of the cissoid, even though for the purposes of forming the intersection in Fig. 13b a continuous version of the cissoid is needed. Hence that person may have felt the need to address this “gap” by adding the remark that the full curve be interpolated from the many individual points generated. This would explain how the in my opinion foundationally nonsensical notion of pointwise construction could have found its way into the text. On this hypothesis, the availability of the cissoid as a continuous curve would have been assured in the original treatise by the linkage discussion and hence assumed implicitly in the “mathematical” part of the treatise. So only when the linkage discussion was separated from the demonstrations did the perceived “gap” occur and the need for pointwise construction and curve-interpolation arise.
Diocles’s text treats conics by pointwise construction as well. I shall discuss this in Sect. 4.4.3. That context will make the plausibility of corruption along the above lines even more plausible, because it is likely that Diocles’s original did indeed use pointwise constructions of conics for applied purposes (constructing burning mirrors), while keeping this strictly separated from theoretical problems such as doubling a cube—a distinction that later compilers could very well have failed to appreciate, and hence corrupted the text accordingly.
4.2.7 Sporus and Pappus
The cube duplications by Sporus and Pappus are identical in construction. They reproduce the same final outcome as Dicoles’s in Fig. 13b, but they replace the use of the cissoid by an equivalent characterisation of the intersection point in terms of an equality of line segments (Fig. 15). This is to be found by trial and error, by varying the inclination of a ruler until the two segments are equal. Pappus, at least, is explicit about this being a trial-and-error process with an actual ruler.
4.3 Trisection
4.3.1 Neusis Angle Trisections
Angles can be trisected if we allow neusis (Fig. 16)—that is, the ability to place a marked ruler in such a way that the marked segment fits precisely between two given curves, while the ruler is also passing through a given point.Footnote 50 Angle trisection by neusis is shown in Fig. 17.
From an operationalist point of view, neusis is in many respects attractive. It is concrete and simple, uses only the most basic tools, and can be carried out with considerable precision.
But neusis has one major flaw, namely that the placement of the ruler is a trial-and-error process that is not exact and deterministic. We can put a nail at the given point and place the ruler against it, and then arrange that the first marked point hits the first curve. But whether the end of the marked segment then hits the second curve or not cannot be guaranteed at the same time. Realistically, we must repeat the procedure over and over again until this outcome is reached, as far as we can judge by eye. There is no guarantee that we will ever hit upon the right position with this trial and error process, although we can keep making improved guesses. Neusis is therefore approximative.
Figure 18 shows a variant neusis angle trisection associated (possibly spuriously) with Archimedes. In terms of operationalist foundational status, it comes to much the same thing as the previous neusis construction.
The weaknesses of the neusis angle trisection could be removed if it could be translated into a method that produced the sought point in one definitive position as the intersection of two curves, just as Euclid always finds points in his constructions as intersections of circles and lines. Nicomedes did precisely this. He devised an angle trisection of this type, assuming that, in addition to circles and lines, we also add to our construction arsenal the ability to draw conchoids. As shown in Fig. 19, a conchoid can be defined in a manner analogous to how Euclid defines a circle: it is the set of all points that stand in a certain distance relation to lines drawn from a particular point. But Nicomedes did not stop with that definition. Instead he proposed a physical tool (shown in Fig. 20) for tracing the curve. Figure 21 shows how to reproduce the angle trisection of Fig. 17 using Nicomedes’s tool.
Nicomedes’s angle trisection makes perfect sense from an operationalist point of view. He was clearly concerned with practical realisation with a physical instrument, as the sources explicitly say. He would also have been aware of the simple neusis construction, so evidently he considered his method to be an improvement upon it in some respect. I do not believe it makes any sense to take Nicomedes’s solution to be an improvement in terms of practical accuracy or utility. But from a more theoretical point of view, Nicomedes’s solution addresses exactly the foundational issues with simple neusis, namely the coordination of multiple conditions and the trial-and-error or approximative nature of the construction. Instead Nicomedes’s method produces the solution with a deterministic, single-motion process, which, as we have seen, is operationally crucial.
One theoretical advantage of Nicomedes’s solution over the neusis ones is that it makes the existence of a solution more unquestionable. With neusis, the existence of a solution must be taken as intuitively obvious, even though, as we know, existence is a dangerous assumption when multiple simultaneous conditions are imposed, as in the case of the superright triangle of Sect. 2.1.3. By reducing the construction to a single, unequivocal generative process, Nicomedes’s solution effectively reduces the existence issue to a fundamental continuity assumption regarding the intersections of curves.
4.3.2 Angle Multisection by the Quadratrix
The earliest specifically attested solution in Table 2 is Hippias’s trisection of an angle by the quadratrix. Actually the quadratrix enables any multisection of an angle just as easily as a trisection, as Hippias surely knew. None of the other angle trisections can do this. The other angle trisections are obviously favourable if we do not mind limiting ourselves to trisection only. The quadratrix is clearly overkill for this problem. But Hippias probably knew this and introduced the quadratrix with the more general multisection problem in mind. For this purpose, it is most likely as good of a curve as one could hope for. One may even speculate that it was precisely because the quadratrix is so good for multisection that so many later Greek mathematicians focussed on trisection rather than multisection, having concluded that the quadratrix had effectively closed the field as far as general multisection is concerned, while there was still work to do on trisection since simpler methods are possible there.
The quadratrix (Fig. 22) solves the multisection problem in the simplest possible way (Fig. 23): to cut the angle associated with the ray QC into n equal pieces, simply drop the perpendicular from Q to the horizontal axis, then cut this segment into n equal pieces (which is readily done by ruler and compass; Elements VI.10), and find the points on the quadratrix with those y-values. The rays from the origin through these points define equal parts of the angle.
It seems quite evident, thus, that the quadratrix must have been conceived as an angle-multisection curve; it can virtually be defined as the curve that translates n-section of a segment into n-section of an angle. Or for that matter, any time we can cut a segment into a given proportion, then with the help of the quadratrix we can also cut an angle into that same proportion, by precisely the same logic as above.
This perfect fit between the quadratrix and multisection suggests that Hippias arrived at this curve by “reasoning backwards,” asking himself what kind of curve would have the property that if you multisect its ordinate then you multisect the corresponding angle. Only then, I imagine, would he have tried to make the curve so defined more concrete by characterising it in terms of some kind of construction. We should keep this in mind when we evaluate the constructive status of the curve. According to my thesis, the Greeks were already at this point committed operationalists obsessed with constructions as the only legitimate way to introduce geometrical entities. The quadratrix may at first sight appear to weigh against this thesis, since its definition is quite abstract and does not readily correspond to constructive generation in the real world. Indeed, the quadratrix is not the kind of thing one would arrive at by trying to come up with constructions that go a bit beyond ruler and compass but are still as acceptable as possible from an operationalist point of view. There are clearly better options for that.
But this does not prove that Hippias had no interest in operationalism. If anything, Hippias must have had an interest in operationalism, because the quadratrix is not interesting otherwise. The quadratrix only makes sense as a solution to a theoretical interest in angle multisection as a well-defined and crystalised foundational research problem. For the purposes of any kind of applied or intuitive geometry, or any non-constructive (Platonic) theoretical geometry, the quadratrix serves no purpose. Someone not interested in operationalism would have no incentive to spend so much effort studying this complicated curve.
The quadratrix was not conceived by starting from the question of what would be the most acceptable form of construction, but from starting from a curve defined as the curve that would accomplish the geometer’s dream of directly converting cutting a line segment into any ratio into cutting an angle in that same ratio. Keeping this in mind, the classical definition of the quadratrix is as operational as it can be under the circumstances. It would have been easy, for someone not concerned with operationalism, to define the curve as the set of all points with a certain property (viz., the set of all points \((\theta ,y)\) such that y is proportional to \(\theta\), which is readily stated in Greek mathematical language in terms of arc lengths etc.). Instead we find a preference for the much more operationalist characterisation in terms of motions.
The motion definition of the quadratrix is well conceived for the purposes of analysing its possible constructive generation. It immediately suggests an instrumental construction like that shown in Fig. 24. This is a perfectly good operationalist constructions, provided that we accept the cogwheel principle that arc length can be translated into rectilinear displacement. This assumption is a fairly big ask, whose accuracy and practical viability can be questioned. But it is an assumption that fits naturally in an operationalist framework. Whether it should be operationally accepted is debatable, but that it is operationally meaningful is clear.
Generating the quadratrix mechanically. a If hollowed rulers could be made to move at the right speeds, they could force a pen to trace the curve. But how can we ensure that the motions of the rulers are suitably coordinated? b Coordinating the motions using a cogwheel mechanism. The length of arc turned by the wheel attached to the radial ruler is translated into an equal vertical displacement of the horizontal ruler
An equivalent way of generating the quadratrix, which uses strings instead of cogwheels, is shown in Fig. 25. Foundationally, it comes to the same thing as the cogwheel method: the fundamental principle in both cases is the intertranslatability of circular arc and straight line, or rotation and rectilinear displacement. In both cases, this is achieved by a circle being in one-to-one contact with a straight line as it rotates. I shall frame my analysis below in terms of the cogwheel construction, but because of this essential equivalence the same conclusions apply in the string generation case.
String-based generation of the quadratrix. (Suardi, 1752, Plate II, Figure 5)
The cogwheel way of generating the quadratrix does not fully solve the issue of the coordination of the motions. It shows how rotational motion can be translated into proportional rectilinear motion, but we still have to address the issue of how to achieve a particular ratio of the speeds of the two motions. If the cogwheel has radius r, the vertical displacement for a rotation arc of \(\gamma\) is \(\gamma r\). To obtain the quadratrix as defined above, we need a displacement of 1 to go with a rotation of \(\tfrac{\pi }{2}\), so we need to make \(r=\tfrac{2}{\pi }\). So the machine cannot be constructed without first knowing \(\pi\), or in other words the rectification of a circle.
Whether such a prior knowledge of \(\pi\) is inherently necessary for the setup of the quadratrix is debatable. In the semi-polar coordinate system \((\theta ,y)\), the quadratrix (inscribed in a unit circle) has the equation \((\theta ,\tfrac{2\theta }{\pi })\), since it starts at \((\theta ,y)=(\tfrac{\pi }{2},1)\) and goes to \((\theta ,y)=(0,0)\) with proportional speeds in the \(\theta\) and y directions. But it is not this occurrence of \(\pi\) that causes the issue. We could just as well have considered the curve \((\theta ,y)=(\theta ,a\theta )\) for any a. Any such curve achieves the same goal in terms of multisection in just the same way as above.Footnote 51
For instance, if we take \(a=1\) we can use a unit-circle cogwheel, so we no longer need to know \(\pi\) for that part of the setup. It is true that now instead the point on the vertical axis is \((\theta ,y)=(\frac{\pi }{2},\frac{\pi }{2})\), so if we wanted to trace the curve from above to below we would have to first mark off the length \(\frac{\pi }{2}\) on the y-axis before we can set up the machine, and hence need to know \(\pi\) after all. So this does not actually simplify the setup and we might as well stick with the traditional form of the quadratrix.
If the quadratrix is conceived more abstractly in terms of lines rather than physical rulers, one could argue that the dependence on \(\pi\) can be avoided. For instead of tracing the curve from its top position downwards, we could start with the two rulers in their horizontal position and trace the curve from the bottom up. We could then get the intersection with the vertical axis for free, so that no part of the setup depended on prior knowledge of \(\pi\) (Bos, 2001, 43). As long as we can assume that the two motions are uniform, this produces a curve of the form \((\theta ,y)=(\theta ,a\theta )\). It is not necessary to ensure that the two speeds are in a particular ratio, only that they are both uniform. Only after the motion is completed can we draw the circle whose arc the quadratrix can multisect. So we cannot custom-make a quadratrix so defined to a particular arc of a given radius. But this is not a problem. If I can multisect any arc of a reference circle, I can multisect any arc of some other circle. For instance, I can use Elements I.23 to move any angle into the reference circle drawn about the quadratrix, then multisect it there, and then move it back again.
But this scheme is a bit more problematic than the original, \(\pi\)-dependent one in terms of realisation by rulers and a moving pen. For if the pen is in the wrong position when the two rulers are in their horizontal position, this will prevent the machine from turning at all. Hence for the sake of this instrumental generation we are dependent on specifically determining a starting point after all, which must involve \(\pi\) as above.
In a sense the dependence on \(\pi\) is not a problem, because it can be resolved without any additional assumptions. As Fig. 26 shows, the cogwheel assumptions we needed to generate the quadratrix can just as easily be used to generate \(\pi\) in an obvious way. So the setup of the quadratrix machine can be done by the same tools that are required for its operation once set up.
This further limits the appeal of the more abstract, supposedly \(\pi\)-independent generation of the quadratrix. For what it accomplished was the avoidance on \(\pi\) in setting up the line segments needed to produce the configuration, while retaining the assumption that the two motions can somehow be ensured to be uniform. But as Fig. 26 shows, the line segment issue is arguably no issue for the instrumental generation either; rather, the coordination of the motions is the core issue, and the principle used to solve it (the cog wheel) eliminates the line segment issue as a separate point. Thus the more abstract generation has only succeeded in eliminating a minor issue, while doing nothing to solve the real crux of the matter, which it simply avoids by making the uniformity of the motions a mere stipulation without any indication of how such a thing can be realised. For these reasons I do not regard this abstract generation of the quadratrix as altering the fundamental \(\pi\)-dependence of the curve.
4.4 Conic Sections
4.4.1 Uses of Conic Sections to Solve Construction Problems
Cube duplication and angle trisection can be reduced to conic sections in a variety of ways, as seen in Table 2 and summarised in modern form in Figs. 27, 28 and 29. The construction in Fig. 27a, using a parabola and a hyperbola, seems to be Menaechmus’s original solution, which quite possibly occasioned the introduction of conics sections in Greek geometry altogether. Unfortunately there are many question marks regarding the attribution and dating of the remaining conic section solutions to the classical problems. For example, the cube duplication by two parabolas (Fig. 27b) has often been attributed to Menaechmus, since Eutocius presents it right after the one he explicitly credits to Menaechmus, without any indication that it is from another author. On the other hand, this solution by two parabolas occurs in Diocles, in a way that could be seen as suggesting originality (Toomer, 1976, 170). Both possibilities are perfectly plausible, even though these authors are a century and a half apart. Similar uncertainty attaches to the other conic section solutions.
Angle trisection by conics. Unattributed solution that recreates the neusis configuration of Fig. 17 by means of the intersection of a hyperbola and a circle
I shall offer an operationalist interpretation of the conic section tradition that is in my opinion satisfying from an internalist mathematical point of view. I shall reconstruct two distinct tracks, each of which is squarely operationalist and prominently concerned with the instrumental generation of conic sections. I consider it plausible that these ideas were indeed prominent in the minds of Greek mathematicians. This is perfectly consistent with the historical record, but admittedly so are many other hypotheses since the record is so incomplete.
4.4.2 Generation by Conic Compass
Conic sections can be operationalised by means of the generalised compass shown in Fig. 30. This “conic” (or “perfect”) compass is discussed in a number of medieval Arabic sources.Footnote 52 Eutocius’s text also makes a vague allusion to a “compass” for drawing parabolas,Footnote 53 which could plausibly be a reference to this instrument. In fact, this method of generating a conic section can be considered virtually implicit in the definition of a cone as the rotation of a line about an axis. This is effectively the definition used by Euclid Elements XI, Definition 18: “When a right triangle with one side of those about the right angle remains fixed is carried round and restored again to the same position from which it began to be moved, the figure so comprehended is a cone.” Note that the conic compass interpretation of this definition is completely analogous to how we interpreted surfaces as moving curves in Sect. 4.2.1.
Eratosthenes says that Menaechmus not only “wrote demonstratively” on the duplication of a cube by conics, but also showed “how to practically do this by hand” (Netz, 2004, 294–295). We do not know what this method of Menaechmus’s was, but I think the conic compass is the likeliest candidate (cf. Sect. 4.6.7).
All conics used to solve the classical problems are readily produced by the conic compass. Table 3 shows how the conic compass can be set up to produce each of them.Footnote 54 As we see, the parameters needed to calibrate the conic compass in all of these cases are constructible by ruler and compass (since they involve only the four arithmetical operations and square roots), so there is no circular reasoning or other non-performable demands involved.
As this reconstruction suggests, an easy and natural way to set up the conic compass is to specify its parameters in terms of an initial position where the pen arm is perpendicular to the plane. Strikingly, this corresponds exactly to an otherwise peculiar oddity of the early history of conic sections, namely that conic sections were defined as the intersection of a cone with a plane perpendicular to its side.Footnote 55 This is reflected in the very names for conic sections used before Apollonius, for instance in the works of Archimedes. There, ellipse, parabola, and hyperbola are called, respectively, “section of an acute-angled cone,” “section of a right-angled cone,” and “section of an obtuse-angled cone.” This restriction to always assume the cutting plane to be perpendicular to the side at first appears artificial and strange. Why not any plane, since they all yield conic sections? This mystery can be explained by the hypothesis that it is due to thinking in terms of the conic compass. All conic sections generated by the conic compass in the manner I have indicated, with the pen arm initially in perpendicular position, are indeed of the type assumed in the old theory of conics. If one thinks of conics as cones sliced by a plane, then the natural way to characterise parabolas are as those intersections obtained when the cutting plane is parallel to the side of the cone. But if one thinks of conics in terms of the conic compass, it is natural to instead characterise parabolas as precisely those curves one obtains when \(\theta =45^{\circ }\), that it to say when the total cone angle \(2\theta\) is right, so that we are cutting a right-angled cone. The curve drawn by a conic compass with perpendicular initial position of the pen arm is a parabola if and only if \(2\theta\) is right (in this case the pen arm is in a horizontal position precisely once in the course of a full rotation, pointing toward the “point at infinity” of the parabola). It is suggestive at the very least that the early terminology of conics, which is otherwise mysterious, fits so naturally with the conic compass point of view.
Apollonius’s Conics marked a departure from tradition. Right away in his Definition 1, Apollonius uses a more general definition of a cone; in effect: the figure generated when one point on a line remains fixed, while another point on the line moves along a circle. This includes “skew” or “oblique” cones (Definition 3) that are not cones by Euclid’s definition and hence do not correspond to the surface generated by the pen arm of the conic compass of Fig. 30. Nevertheless, as Apollonius showed, the sections of skew cones are not more general; they can all be obtained as sections of Euclidean cones and by the conic compass. From an operationalist point of view, it is problematic to specify a conic as a section of an oblique cone, because how could such a section be actualised or constructed?
It is striking, therefore, that when Apollonius sets out to actually construct conics with given properties (I.52–60), he expressly uses only non-oblique cones. “The cone will be a right cone,” i.e. non-oblique, he explicitly proves in each construction. That is to say, Apollonius solves the problem of constructing a conic with certain given properties, by showing how to—constructively from those givens—determine a right cone that has the desired conic as a section. These are the constructions that are the basis for introducing conic sections with given properties into mathematical arguments, analogously to how Euclid’s postulates allow the introduction of lines and circles, or Elements I.46 allows the introduction of a square with a given side. Because Apollonius specifically uses only right cones in these constructions, they are effectively recipes for how to draw these conic sections using the conic compass. The way in which Apollonius derives the specifications of the cone needed from the givens effectively corresponds to adding more entries to our Table 3.Footnote 56
In summary, the hypothesis that the early Greek theory of conics was based on the conic compass is supported by: its continuity with other constructions in the problem tradition; its striking fit with the early terminology of conics; its suitability for generating all the conics actually used in solutions of the classical problems in a convenient way; the fact that Apollonius’s construction propositions—which were the basis for how conics were introduced into mathematical arguments not only in his own works but e.g. in Pappus and elsewhere (Bos, 2001, 51)—effectively amount to concrete recipes for how to calibrate and position the conic compass in order to actually draw the desired conic.
4.4.3 Generation by Strings
The conic compass way of generating conics is, I claim, a natural way to operationalise the mainstream Greek theory of conics. But the Greek corpus also contains traces of a second approach. When Pappus introduces the hyperbola of Fig. 29, he does so in the kinds of standard terms that I propose should be operationalised by the conic compass. Interestingly, however, Pappus then goes on to say that “some” do it “another way,” and gives a second construction in which the same hyperbola is introduced in terms of its focus, directrix, and eccentricity. This points to a fundamentally distinct approach to conic sections, of which only scattered bits survive from Greek times. The other traces are a passage elsewhere in Pappus that suggests that the basic focus-directrix characterisation of conics was involved in some way in a lost work by Euclid (Jones, 1986, 593–595), and a clear discussion of the focus-directrix property of parabolas by Diocles (On burning mirrors, Props. 4, 10; Toomer, 1976, 16–17).
Characterising conic sections in terms of their focal points leads naturally to an alternative way of generating them, namely by means of rulers and strings, in the manner indicated in Figs. 31 and 32. These constructions are not found in Greek sources. But Pappus’s and Diocles’s use of conics defined in focus-directrix terms to solve the cube duplication problem only makes sense if conics with prescribed focus-directrix properties can be constructed. Seeing as so many other solutions of this problem in Greek sources are explicitly concerned with instrumental generation, it makes little sense that these solutions would disregard the same issue in the case of these conics. The string constructions of Fig. 32 are so natural that it is hard to imagine how they could fail to suggest themselves to mathematicians concerned with such matters. They fit well in the Greek context.
String-based generation of parabolas, such as those of Fig. 27. The vertical ruler moves with its foot along the directrix. The thick line \(FP+PR\) is a string of constant length with its endpoints fixed at F and R. The string is kept taut by a pen at P. The pen point P traces the parabola with the focus-directrix property \(DP=FP\)
String-based generation of conics with given focal points. From Frans van Schooten De Organica Conicarum Sectionum in Plano Descriptione Tractatus (1646). a Ellipse with focal points H, I, and defining property \(HE+EI=\) constant. Middle: Parabola with focus B, directix GE, and defining property \(BD+DG=\) constant (where G is the point perpendicularly below D). The ruler GI is moveable but always perpendicular to GE. The string IDB has constant length. b Hyperbola with focal points C, F, and defining property \(Fc-Cc=\) constant. The string NcC has constant length
From an operationalist point of view, the following hypothesis makes a lot of sense: whoever first made substantial use of the focus-directrix characterisation of the parabola also realised that this translates into an alternative way of tracing the curve (as in Fig. 31), and used this to solve the cube duplication problem in a new way (as in Fig. 27b). This could explain why there are two solutions in Fig. 27. Why solve the problem by conics in two very similar ways? Why this seemingly pointless redundancy? If one’s means of generating conics work just as well for hyperbolas as parabolas, there seems to be little reason to seek a solution in terms of parabolas only. Indeed, if one uses the conic compass to produce the curves of Fig. 27, there is little reason to favour one over the other, especially since the parabolas have different steepness and hence require the compass to be recalibrated anyway (as detailed in Table 3). But if the curves are to be generated by the string methods of Fig. 32, then it becomes more attractive to work with parabolas only, as this leads to a simpler and more unified construction procedure.
Let us see this in more detail by spelling out how to reproduce the two solutions of Fig. 27 using string procedures. It is clear from Fig. 31 that it is straightforward to produce the parabolas of Fig. 27b in this manner. If we instead want to produce Fig. 27a some more work is needed. The parabola is the same as one of the above, but the other curve needed, the hyperbola, is no longer a trivial variation of the same construction procedure. Not only is a somewhat different instrument needed, but the string calibration is more involved as well. The focal points of the hyperbola are (2, 2) and \((-\,2,-\,2)\), and the string length needs to be calibrated so that \(CE=2(\sqrt{2}-1)\). Clearly this is rather more elaborate than the parabola–parabola setup of Fig. 27b. Hence it makes sense that a mathematician who favours a focus-directrix approach to conic sections, and therefore their generation by strings, will also favour the second of the two solutions in Fig. 27. This would explain why Menaechmus (who I hypothesise used the conic compass) gave the solution of Fig. 27a, while Diocles (who uses a focus-directrix approach) gives the parabola–parabola solution of Fig. 27b.
The fact that the focus-directrix theory and the parabola–parabola solution go together in Diocles’s treatise gives some support to this hypothesis. But, unfortunately, beyond this the source evidence does not directly support this reconstruction, but rather directly contradicts it. Diocles’s treatise—or what is supposedly his treatise, which is only preserved in a corrupted Arabic version—is clear on how parabolas are to be generated, namely by producing lots of points on it by ruler and compass, and then fitting a curve through these points. Thus “we mark numerous points ...and bend along the resultant points a ruler made of horn” (Toomer, 1976, 66), or we “mark many points close to each other” and “draw with the curved ruler a line passing through ...points marked in this way” (Toomer, 1976, 92). It is not known what kind of instrument exactly this mysterious curved or flexible ruler is supposed to be (Toomer, 1976, 159–160). Diocles uses it also for the cissoid (Toomer, 1976, 100), so it cannot be specific to conic sections. Obviously there is no such general-purpose curve-fitting instrument that has any mathematical substance. The curve is simply interpolated in a naive way, evidently.
In my opinion, it makes no sense to claim (as Diocles’s text explicitly does) to “solve” the cube duplication problem by assuming “curves” that are defined as interpolated from a set of points. Such a “solution” obviously comes down to pure trial and error and eyeballing: construct a point on each curve, see which way you need to adjust it to get closer to an intersection, repeat. As we know, the point of intersection itself cannot be constructed by ruler and compass, so the process can only close in on the point with arbitrarily good precision but never reach it. So eventually one must estimate the point of intersection. Counting this as a “solution” is obviously inconsistent with the core assumptions in the Greek construction problem tradition. It is evident that virtually any problem one can think of, including for example the quadrature of the circle, can be “solved” in this sense of gradual approximation. It is obvious that this was clearly dismissed out of hand as completely unacceptable by the vast majority of Greek mathematicians, or else the tradition of solutions to the three classical construction problems would have looked unrecognisably different.
So the approximate, pointwise construction is worth nothing. The naive interpolation by some mysterious bendable “ruler” also lacks value and purpose. The one and only purpose of the parabolas, as far as duplicating the cube is concerned, is to find the point of intersection. This is done by constructing points as close to the intersection as possible, perhaps on both sides of the intersection. The location of the intersection can then be estimated from these points, either by connecting the two points nearest the intersection, or, more realistically if precision is desired, by constructing gradually better points until they are so close that there is no significant gap left between them. Tracing the entire parabolas is useless for these purposes, as is constructing any points on the parabolas other than those that approximate the intersection. These things serve no mathematical or practical purpose whatsoever.Footnote 57 It is therefore conceptually nonsensical to express this so-called “solution” to the problem in terms of tracing parabolas. In fact, it follows that if Diocles’s solution is a solution to the cube duplication problem at all, it is a solution by ruler and compass, since everything of any mathematical substance in the solution is done entirely by ruler and compass, and the allusion to parabolas is purely cosmetic and gratuitous.
I therefore feel that this aspect of the solutions in “Diocles’s” text must be due to an author who did not understand and did not fit into the ancient Greek geometrical tradition. Presumably this was not Diocles himself but some later editor. We know for a fact on independent grounds that the text is obviously corrupt in numerous respects, including several entire passages of trivial and erroneous reasoning that could not possibly be due to a mathematician of any competence and sophistication (Toomer, 1976, 31). It is even easy to imagine how such a corruption might have occurred. For the pointwise construction of parabolas does make sense for the sake of practically constructing parabola cutouts for practical uses such as constructing burning mirrors, which is exactly how Diocles first uses such constructions in his treatise (Toomer, 1976, 66). Possibly Diocles included this method for such purposes only, and some later compiler figured he could shortcut later proofs by allowing this method in the geometrical arguments as well, even though that is conceptually incoherent.
Another argument for the implausibility of “Diocles’s” method being part of the Greek tradition proper is the following. The pointwise, ruler-and-compass construction of any number of points on the parabolas in Fig. 27b is immediately obvious from the core algebraic property \(py=x^{2}\) of the parabola. This property was by all indications recognised as central, or in fact more likely taken as the very essence of parabolas, from the inception of conic section theory, as the solution in Fig. 27a suggests. It was in any case well entrenched by the time of Apollonius. So why does Diocles construct points on the parabola by the focus-directrix property? This accomplishes nothing that could not easily be done without focus-directrix theory. So this would make it seem as if Diocles is merely reworking in a different language a type of solution that had been readily available (and evidently not accepted) for a long time. If the focus-directrix property is associated with string generation, on the other hand, then Diocles is offering a fundamentally new construction and solution of the problem.
For these reasons I think it is not implausible to hypothesise that Diocles (or whoever it was who first proposed to duplicate the cube by two parabolas defined in terms of focus and directrix) meant the parabolas to be constructed by the string-and-ruler method, which is a continuous, single-motion mechanism that fits well in the Greek tradition as I have construed it. This makes perfect sense of his method, and entails that he made a meaningful contribution to the problem-solving tradition rather than offered a solution that is conceptually naive and fundamentally inconsistent with the tradition in several key respects.
Let us consider now the other attested solution to a classical construction problems by conics that involves focal language. As mentioned above, this is the hyperbola of Fig. 29, which Pappus says “some” characterise in a way that amounts to specifying its focus, directrix, and eccentricity. Interestingly, this does not correspond to the nowadays most well-known approach to hyperbolas via their focal properties, namely that shown in Fig. 32. Instead, the natural way of reconstructing an implied construction seems to be that of Fig. 33. As we see, this particular setup is well suited for generation by strings. Thus, in this case as well as in the parabola case, the uses of focus-directrix conics in solutions to the classical problems lend themselves well to concrete physical realisation by strings.
String-based generation of hyperbolas with eccentricity 2, such as that of Fig. 29. The horizontal ruler moves with its foot along the directrix. The thick line \(FP+PR+RP\) is a string of constant length with its endpoints fixed at F and P. The string is wrapped double around PR, so that, as PR decreases, FP increases by twice that length. The pen point P traces the hyperbola with the focus-directrix property \(FP=2DP\)
4.5 Circle Quadratures
4.5.1 Quadratrix
The quadratrix of Fig. 22 can be used to square the circle because it intersects the horizontal axis at x-coordinate \(2/\pi\). However, this is a deeply unsatisfactory way of accomplishing the quadrature of a circle for obvious reasons. One issue is that the point of intersection with the x-axis is only a limit point, and not actually part of the definition of the curve, regardless of whether we consider it defined as a point set or in terms of moving rulers. But more importantly, the quadratrix can only be produced, as we have seen, by tools that already imply the ability to produce \(\pi\) in much more straightforward ways. It makes little sense to consider the quadratrix to be somehow given yet \(\pi\) not be; rather, constructing \(\pi\) is a prerequisite for producing the quadratrix.
Pappus reports precisely this critique: the quadratrix quadrature of the circle “takes into the assumption the very thing for which it seems to be useful. ...For how is it possible [that the two motions] come to a halt at the same time, unless the ratio of the straight line ...to the arc ...is known beforehand? For the velocities of the motions must be in this ratio, also” (Sefrin-Weis, 2010, 132). Pappus cites Sporus as his source for this critique. However, it is difficult to imagine that this obvious objection was not recognised much earlier; indeed from the very outset of serious work on the quadratrix.
Since the drawbacks of the quadratrix in this regard are so blatant, I find it difficult to believe that it would ever have been considered a viable solution to circle quadrature. An alternative interpretation would be as follows. When the quadratrix was shown to imply circle quadrature (whether this was done by Dinostratus or Hippias himself or whoever it may have been), the point was not to propose this as a solution to circle quadrature but to illuminate the foundational assumptions involved in admitting the quadratrix, somewhat as follows.
We saw above that the quadratrix can be constructively generated if we assume the cogwheel principle. It may reasonably be felt that this is asking quite a lot. It would be reasonable to inquire whether one could avoid this big assumption and instead produce the curve by some simpler means. Proving that the quadratrix implies circle quadrature shows, in a sense, that there is no simpler way: not only is \(\pi\) necessary to produce the quadratrix in the particular manner shown above using cogwheels, but in fact any way of generating the quadratrix enables us to construct \(\pi\). This justifies the cogwheel construction and suggests that no simpler construction is possible, since any other solution must have “\(\pi\)-ness” in it somewhere as well. This is an interesting result that makes perfect sense in an operationalist context.
It is possible that this is all the classical mathematicians claimed with their investigations regarding the link between the quadratrix and circle quadrature, and that no one actually proposed that the quadratrix should be considered a viable way of squaring a circle. The supposed use of the quadratrix to the latter end is only mentioned by late commentators who could very well have been confused on this point and in any case give no historical detail that would enable us to say anything definitive one way or the other (Heath, 1981a, 225–226). The most puzzling thing, if we accept my interpretation, is how the name “quadratrix” got stuck to the curve. The curve is very well suited to angle multisection and poorly suited to circle quadrature, so it is quite evident that the former must be considered its real purpose.Footnote 58 Perhaps it was only because the quadratrix is so excellent for multisection, and hence widely accepted and celebrated, that the on other grounds questionable idea of applying it to circle quadrature was even considered.
Hence my interpretation suggests that the name “quadratrix” must be due to some sort of confusion or mixup among later commentators, even though several of them use this name consistently. According to my interpretation, it would not have made sense for the classical mathematicians to use “quadratrix” as the primary name for the curve. It would, however, have made sense for them to say that the curve of Hippias is “a quadratrix”—that is, a curve that implies circle quadrature. Perhaps this later gave rise to some terminological confusion. It is surely more plausible that later commentators misunderstood the point of the terminology than that the elementary and obvious objections to the quadratrix raised by Sporus were somehow missed by generations of first-rate mathematicians who worked on this curve many centuries earlier. Regarding the plausibility of the later tradition getting names and labels wrong, one may note that the attribution of the cube duplication of Sect. 4.2.2 to Plato—which occurs in Eutocius, one of the best sources—is obviously extremely implausible and almost certainly a mistake.
4.5.2 Archimedean Spiral
Archimedes proved the basic area result for a circle shown in Fig. 34, which implies that circle quadrature reduces to finding the circumference of a circle, or, in more modern algebraic terms, a line segment of length \(\pi\). Archimedes also showed that the subtangent of an Archimedean spiral is such a line segment (Fig. 35). The Archimedean spiral is defined in terms of a combination of rectilinear and circular motions: a ray is rotating uniformly about its endpoint, while a point is moving outward along it at uniform radial speed. In other words, the Archimedean spiral has the equation \(r=a\theta\) in polar coordinates. It is interesting that Archimedes defines his spiral in terms of motions and derives the locus property (essentially \(r=a\theta\)) as a theorem,Footnote 59 even though it is the latter rather than the former that is doing all the work in the subsequent proofs. Since Archimedes’s choice to nevertheless insist on a motion definition of the curve is not explicable on grounds internal to the technical arguments of the treatise, it must have been motivated by broader considerations—perhaps operationalist ones, which would indeed explain a preference for motion, as noted in Sect. 4.6.3.
“The area of any circle is equal to a right-angled triangle in which one of the sides about the right angle is equal to the radius, and the other to the circumference of the circle.” (Archimedes, 2002, 91)
The operational status of the Archimedean spiral is comparable to that of the the quadratrix. Like the quadratrix, it involves a coordination of circular and linear motion that can be accomplished by means of cogwheels (Fig. 36). But unlike the quadratrix, it does not have calibration issues that require the initial and final states of the machine to be coordinated. As in the case of the quadratrix, cogwheel generation of the spiral is quite useless for circle quadrature purposes, since cogwheels alone can be used to square the circle in much simpler ways.
Generation of the Archimedean spiral by a cog mechanism. The cogwheel is rigidly attached (by an axis through its midpoint) to the plane underneath it. As the cogwheel rotates, it rotates the entire plane along with it, including the part of the spiral drawn so far. At the same time it pushes the cogged ruler (which is above the plane and does not move with it) and its attached pen by a horizontal displacement proportional to the angle turned. The cogwheel and ruler can be kept in an elevated plane so as to not interfere with the pen’s motion in the plane. The pen point tracing the curve is aligned with the midpoint of the circular wheel. The rest of the pen should be regarded as above the plane in which the tracing takes place
As in the case of the quadratrix, a string wrapping around a circle can be used in place of a cogwheel. Figure 37 shows how the Archimedean spiral can be generated in this way.Footnote 60 Again, the ability to wrap strings around a given circle, which is assumed here, is in itself sufficient to square the circle without the detour of drawing the spiral.
String-based generation of the Archimedean spiral. \(CC'\) is a fixed circle with midpoint O. The ruler OR rotates around the fixed point O. The string \(CC'RP\) is fastened at the fixed point C and the moving pen point P, and it is wrapped around the moving ruler. The portion \(CC'\) of the string wrapped around the circle equals OP. As the ruler turns, more and more of the string becomes wrapped around the circle, thereby pulling the pen P outwards in proportion to the angle turned
It is unclear how Archimedes intended tangents to be drawn.Footnote 61 The fact that Archimedes does not address this may seem to indicate a willingness on his part to reason geometrically about entities simply supposed or imagined as opposed to actually constructed. However, there is reason to believe that Archimedes would not have accepted such a stance, expect perhaps with great regret and as a last resort. Indeed, when Greek geometers can construct tangents, rather than merely assume them, they do so, as Euclid does for the tangent of a circle in Elements III.16–17. In the Conics, Apollonius finds the tangent to a parabola by first constructing its point of intercept with the axis and then connecting that point to the given point of tangency (Fig. 38). To construct the spiral tangent in Fig. 35 in an analogous way clearly requires the circle quadrature problem to have been solved already. This does not appear to be what Archimedes intended, because if he meant this he ought to have stated the result as a construction problem for the tangent, rather than, as he in fact does, as a theorem establishing a property of the tangent.
Archimedes’s angle trisection by neusis (Sect. 4.3.1) also suggests an interest in actual construction, as opposed to reasoning abstractly about entities merely postulated. Surely Archimedes would not have been interested in angle trisection by neusis if it were not for the fact that neusis is an actualisable construction. For if one can just imagine things, then one can just imagine the third of an angle right away, making it pointless to imagine a neusis construction for it. This suggests that Archimedes had an interest in actual construction in this context, thereby making it less likely that he was completely unconcerned with the issue in his work on spirals.
In any case, if the tangent to the spiral is to be used to square the circle, the tangent obviously needs to be constructed in some way that does not presupposes circle quadrature or rectification. How? I can see no good option. One can of course simply try to eyeball it with a ruler.Footnote 62 Another possibility is to construct the secant line of the spiral through the point of tangency and a nearby point. By taking the nearby point sufficiently close to the point of tangency, the secant can be made to approximate the tangent with any desired degree of accuracy. This is obviously less satisfying than an exact construction.
Like the quadratrix, the Archimedean spiral is well suited for angle multisection. This is immediate from its equation \(r=a\theta\): n-secting \(\theta\) is equivalent to n-secting r, which is easily done. Namely, given \(\theta\), we have the associated r as a line segment. On this segment we can mark off r/n, and draw a circle through this point with midpoint (0, 0). This circle will cut the spiral in the point \((r/n,\theta /n)\), so the angle has been n-sected. Archimedes was surely well aware of this, although that is not made explicit in surviving sources.
4.5.3 The Cylindrical Helix
The cylindrical helix is connected to circle quadrature by the result shown in Fig. 39. A cylindrical helix can be constructed in a number of ways. In terms of motion, it is the path of a point whose x and y coordinates trace an ordinary circle, while its z coordinate is increasing uniformly. So the helices on a unit cylinder are parametrised by \(x=\cos t\), \(y=\sin t\), \(z=at\). Equivalently, a cylindrical helix is the path of a stretched string on the surface of the cylinder. Or again equivalently, if we cut a right triangle out of paper, and wrap it around the cylinder while keeping one leg along the base of the cylinder, then the hypothenuse traces a cylindrical helix.Footnote 63
Circle quadrature by tangent to a cylindrical helix. Drawn is the tangent of a cylindrical helix at the point on the helix one full revolution away from its starting point. The distance between the starting point of the helix and the point where this tangent line hits the ground plane is equal to the circumference of the base circle of the cylinder. The result is independent of the steepness of the helix
The definition in terms of motion makes the cylindrical helix closely related to the quadratrix and the Archimedean spiral, so it is not surprising that it can be used to square the circle. But, interestingly, the other two constructions of the cylindrical helix circumvent the need for the difficult coordination of two motions. So a cylindrical helix can be physically realised in simple and concrete ways without assuming cogwheels. According to our analysis, it was precisely the cogwheel assumption—or the coordination of the two motions—that was the core issue making the quadratrix and the Archimedean spiral unsatisfactory as circle quadratures. So it seems a dream scenario that the cylindrical helix can accomplish the same goals as these curves while avoiding their biggest drawbacks.
Unfortunately, the issue of how to construct the tangent to the cylindrical helix remains. It is highly questionable whether this can be done in a satisfying way. In the case of the Archimedean spiral we mentioned the possibility of approximating the tangent by secants. This method is far from satisfying even in that case, and trying to use it on a three-dimensional cylindrical helix is surely quite a nightmare, not least since we would have to pass lines through the interior of the cylinder.Footnote 64 The construction of the cylindrical helix by wrapping a triangle suggests an alternative way: while keeping the vertical leg in place along the cylinder, unwrap the rest of the triangle again, until it is a flat triangle in the tangent plane that contains the vertical leg. Then the hypothenuse in the unwrapped position is the tangent line of the cylindrical helix traced by the hypothenuse in the wrapped position. But then the subtangent used for circle quadrature is simply the straightened-out version of the horizontal leg of the triangle. This comes to the same thing as assuming the ability to wrap a piece of string around the cylinder and then straightening it out to produce the circumference as a line segment. Of course this assumption would immediately solve the quadrature problem by itself. So the whole business with the cylindrical helix is useless for quadrature purposes unless some other way of producing the tangent can be found.
The cylindrical helix has another interesting property, as the Greeks knew: it is the only “homeomeric” curve other than the line and circle (Acerbi, 2010a); that is, a curve, any part of which can be superimposed and fit perfectly anywhere else on the curve. In this way the helix can be construed as a natural next curve beyond the Euclidean ones, and one may be tempted to argue, as for example Galileo later did, that “the cylindrical helix, of which all parts are similar[,] ...therefore seems to belong among the simple lines” in addition to straight lines and circles (Galileo, 1953, 16). It is not known whether ancient mathematicians shared this sentiment. From an operationalist point of view, the homeomeric property of the helix is not foundationally relevant.
4.5.4 Cycloid
It is likely, though not documented, that Greek mathematicians considered the cycloid (Fig. 40). The idea of the curve is simple and suggests itself naturally in the Greek context, where many combinations of circular and rectilinear motions were investigated at length. It is also easy to see that the cycloid solves the quadrature of the circle,Footnote 65 because the base segment b of the cycloid arch equals the circumference c of the generating circle. The area of the circle, cr/2, is readily constructed from there. Nevertheless, this solution does not seem to have been taken seriously by the great Greek geometers.
The reason for there being no surviving evidence that the Greeks studied the cycloid in connection with circle quadrature is most likely not that the failed to conceive of it, but that they dismissed it out of hand as obviously unsatisfactory. It is useful to understand what their reasons might have been for this.
First of all, rolling is a problematic notion. From an operationalist point of view, a mechanical or physical definition of a curve is of course not a problem at all, but rather a strength. So there is no problem with the cycloid in that regard. However, there is reason to believe that the particular mechanical generation involved here is especially unreliable. An indication of this is given by the wheel paradox, which was well known in antiquity (Drabkinl, 1950): while the circumference of the rolling circle is exactly equal to the base of the cycloid, a smaller concentric circle moving along with it covers the same horizontal distance with the same angular revolution, which means that it covers a base longer than its circumference. So a point on this inner circle does not trace a cycloid even though a point on the outer circle does. This is because the inner circle is not purely rolling, but is rather “slipping,” that it, it is being yanked ahead by the motion of the larger circle. This shows how easily there can be a miscoordination between the rectilinear and rotational motions in any attempt to draw a cycloid. If the motion of a point on this inner circle can be so easily distorted away from a cycloidal path, then how can we trust that a point on the outer circle itself is not suffering from similar issues? How can we know that the motion of the big circle is pure rolling and that there is no slipping involved?
Another line of critique is that the cycloid “solution” of the circle quadrature problem comes dangerously close to merely assuming the problem solved. What makes the cycloid solution work is not really the cycloid itself but only the base segment of it. So the solution is arguably more based on postulating that we can find a line segment equal to the circumference of the circle (which obviously solves the problem), rather than any substantive use of the cycloid curve per se. Another way of putting it is that, by “unrolling” the circumference of a circle, the cycloid solution basically amounts to assuming that we have a “measuring tape” or that we can wrap strings around figures and straighten them out again. This is already achieved by the cogwheel principle of Fig. 26. Since the real work is done by this principle, smuggling it in indirectly via the cycloid serves little purpose.
4.5.5 Conclusion on Circle Quadratures
We have seen that the constructions involved in the recorded circle quadratures can be operationalised (at least except the drawing of tangents). Hence this work is in accord with operationalist principles such as only speaking of constructed objects. However, as quadratures of the circle, none of these solutions are at all convincing, operationally speaking. This is because they can only be operationalised by effectively relying on some principle—such as the wrapping and straightening of strings or measuring tapes, or cogwheels—that by itself leads to a much more direct and simple squaring of the circle in an obvious way. It is quite possible that the mathematicians of the golden age agreed with this, including Archimedes and Apollonius themselves. Archimedes says that “earlier geometers tried to [square the circle, but resorted to] assuming lemmas not easily conceded.”Footnote 66 It is perfectly plausible that this assessment can be generalised to the entire Greek tradition of attempts at circle squaring, and that no serious geometer ever claimed to have solved the problem without “assuming lemmas not easily conceded.”
The constructions we have discussed above may not have been intended as actual solutions of the circle quadrature problem but as stepping-stones in a research program exploring this problem. The results shed light on foundational interrelations between various construction assumptions. It is interesting to know that the ability to draw and take tangents of spirals or cylindrical helices implies the ability to square a circle. Such results fit into a broader program of classifying curves and problems according to their complexity and interrelations. Such results also suggest paths toward actual solutions of the circle quadrature problem, since it is conceivable that some hitherto unforeseen instrument or mechanical device could produce these curves in an operationally convincing way that avoided the dependence on circle-quadrature-equivalent assumptions. It is possible that the works in question by Archimedes, Apollonius, et al. did not claim more than this. It seems to me that, from an operationalist point of view, this is the interpretation that would make most sense.
According to this interpretation, circle quadrature would have had to have been considered provisionally “solved”—say by strings or cogwheels—in some sense, because that would be the only way in which speaking of a circle with area equal to a rectilinear figure could have any meaning from an operationalist point of view. However, there could very well have been widespread dissatisfaction with these provisional solutions, such as a sense that they assumed too much and trivialised the problem rather than solved it. For this reason it would still have made sense to keep looking for more operationally sound and restrictive ways of squaring the circle.
Nevertheless, it is possible to construe the sequence of proposed circle quadratures as progressing toward operational improvement. The spiral is operationally preferable to the quadratrix in that it removes the issues concerning initial state calibration and the use of a limit point of the constructed curve. But it still seems to need something like cogwheels for its construction, which is not ideal. The cylindrical helix constitutes progress in the sense that it is a curve that can be physically realised in simple ways that do not need such an assumption. Thus, although neither solution is fully satisfactory, they nevertheless make some sense within a research program attentive to operationalist concerns.
4.6 Conclusions
Table 4 schematically summarises our discussion of how solutions to the three classical problems fare with respect to operationally important desiderata. The table covers all solution methods for which a source has survived. It evaluates these methods according to the criteria defined in Sect. 4.1.5. Naturally, my attempts at quantifying the extent to which these criteria are met are to be considered very rough indications. They are for crude overview purposes only. Nevertheless I think a global, comparative analysis of this entire corpus taken together is essential. In this section I shall consider what conclusions can be drawn from such an analysis.
4.6.1 Cohesion of the Classical Tradition
Operationalism enables us to view the classical problem tradition as a coherent enterprise based on a universally agreed and consistent foundational program. I have offered such a reading. No other hypothesis, to my knowledge, comes close to offering a unified explanation of the classical problem tradition. Clearly there was considerable disagreement on whose solution was the best one, but this can plausibly be read as disagreements about whose solution better embodies the foundational ideals envisioned than as disagreements about those foundational ideals themselves. My operationalist reconstructions of the theory of conics and the solutions by Archytas and Diocles show that these can be readily and plausibly reconciled with the commitment to physical generation by moving instruments that is unequivocally prominent in the rest of the tradition. If these reconstructions are rejected, the classical problem tradition is much less conceptually coherent.
4.6.2 Physicality of Geometry
The operationalist thesis that geometry takes place in the physical, as opposed to the mental, world is well supported by the classical problem tradition. Half of the attested solution methods are explicitly and unequivocally physical in nature. In this way they are inconsistent with Platonic or modern formalist conceptions of mathematics. It is plausible that the remaining solutions were intended as physical as well. This could have been evident to any reader without the need for formulations that make this completely explicit, just as physical realisability by ruler and compass is never explicit in the Elements but is nevertheless obvious. Chances are that the construction tradition would have been even more explicitly physical than Table 4 indicates if we had the original sources. Plutarch claims that Archytas, Eudoxus, and Menaechmus doubled the cube “by instruments and mechanical constructions” (Thomas, 1939, 389; cf. Sect. 3.1.6). Yet none of these three solutions survive in a form that is explicitly physical.
4.6.3 Generation of Curves by Motion
The explicit use of motion to define curves in a large proportion of the solutions (Table 4) also makes a lot more sense from a physicalist or operationalist point of view, as opposed to a Platonic or formalistic one. Defining a curve by motions means defining it in terms of its generation, as opposed to in terms of its properties: an obvious operationalist advantage, as we have seen. The reference to motion in these constructions is easily avoidable: instead of speaking of the figure generated by such-and-such a motion, one can readily translate the same relation into a motion-free formulation—essentially “the set of all points such that \(\ldots\)”. Euclid’s definition of a circle is an example of the latter type of definition, so the option of using such definitions instead of motion would have been perfectly evident and established. The operationalist thesis, if accepted, explains why so many leading mathematicians nevertheless deliberately opted for motion definitions.
4.6.4 Determinate Realisability
The classical problem tradition shows frequent adherence to core operationalist principles, as seen in Table 4. It is unlikely that the record would be so consistent on realisability, single degree of freedom, definitive termination, and primitiveness if Greek geometers had not been deliberately and prominently concerned with these issues. For instance, the conchoid was quite clearly conceived for the exact purpose of solving the degree of freedom and termination issues of simple neusis. We also see that deviations from operationalist desiderata are greater the harder the problem in question is,Footnote 67 which indicates that such deviations were committed reluctantly.
4.6.5 Practical Accuracy
The column regarding practical accuracy in Table 4 is a very rough indication only and should not be relied upon in any strict sense. I have marked construction schemes as having questionable realisability and primitiveness when their setup involves tools or objects that can only be built in something like a carpenter’s workshop and not by simple everyday means. Typically, I have marked their practical accuracy as questionable as well in such cases, since it would typically require skilled craftsmanship to realise these construction schemes with any kind of accuracy. It is of course debatable to what extent something like a precision carpentry workshop should be considered at the disposal of the geometer.
Despite this caveat, it seems safe to conclude that practical accuracy of the solutions do not seem to have been a high priority in the classical problem tradition. Practical accuracy was surely valued but seems to have been clearly subordinated to more core concerns. The corpus of solutions seems consistent with the assumption that Greek geometers deliberately sought the greatest possible practical accuracy only insofar as that did not interfere with the constraints imposed by the other foundational principles we have highlighted. Meanwhile, it is extremely difficult to imagine how this corpus of solutions could be the outcome of a quest for practically accurate solutions as a primary goal.
Realistically, my guess would be that tools such as the conchoid compass, conic compass, or the cissoid, quadratrix, and Archytas machines (as I have reconstructed them) were never used to produce solutions of any practical accuracy to speak of. I and others have recreated these machines in a rough-and-ready way with common tools one can find in a hardware store. With such methods it is not generally realistic to get a trisection accuracy of more than, say, two degrees, or an approximation to \(\root 3 \of {2}\) accurate to more than one or possibly two decimals at most. My guess would be that Greek mathematicians did this too.Footnote 68 The accuracy could certainly be improved if one mobilised dedicated precision engineering. However, my guess would be that the Greeks probably did not do this, nor was it their intention that it ever be done. However, they may very well have found it appealing and perhaps essential that it could be done in principle.
Indeed, the actual realisability of proposed constructions in principle is the essential thing from an operationalist point of view. Great practical accuracy can be seen as separate from most of the core tenets of operationalism.Footnote 69 A construction can have the property of being eminently actualisable in a concrete way quite independently of accuracy questions. Of the core foundational motivations for operationalism in Sect. 2, only the false diagram issue is essentially dependent on accuracy. The other core tenets of operationalism remain in effect as long as practical execution of the construction is indeed possible, even if relatively crude. Furthermore, one could argue that the theoretical exactness and practical perfectability-in-principle of the classical construction machines make them in some sense more “exact” than methods (such as numerical and algebraic approximation algorithms) that more readily produce better approximations in practice but do not even in theory exhibit the perfect solution itself.
4.6.6 Implications for Interpreting Euclid
Euclid’s Elements is ambiguous as to whether he has in mind ruler and compass, or if he is simply reasoning abstractly about lines and circles. But the classical problem tradition again and again favours concrete physical instruments even though more abstract accounts would have been perfectly possible. For instance, Nicomedes could have stopped at neusis, or he could have stopped at the point-set definition of the conchoid (which is so similar to Euclid’s definition of a circle), but evidently he thought his mechanical tracing device was the best way to go. Furthermore it is surely undeniable that the classical problem tradition was meant as a generalisation of the Euclidean program—an extension of the same foundational ideals. Therefore, when so many of the best Greek geometers opt for solutions to the classical problems based on physical tools, this all but proves that they considered physical tools to have been the basis of Euclid’s geometrical program as well.
This argument assumes that Nicomedes and others favoured the physical tools for foundational reasons. It is true that the sources do not explicitly say that this is what the physical tools were for. But what else could their purpose have been? The questionable practical value of these tools suggest that they could hardly be used for anything but a theoretical, foundational purpose.
4.6.7 Pointwise Constructions
I believe that mathematicians of the classical and Hellenistic eras rightly and universally rejected the notion of solving the classical construction problems by means of curves constructed pointwise. By a pointwise construction I mean an ostensible construction of a curve that is actually a construction of many individual points on the curve, one by one. I have argued above in Sects. 4.2.6 and 4.4.3 that such “constructions” make little sense conceptually. In modern terms, if the curve in question is \(y=f(x)\), such constructions effectively amount to plugging in x-values into a formula f(x) and checking whether the resulting output solves the problem or not. By trial-and-error and improved guessing, one can come as close as one wishes to the desired solution this way. It serves no substantive purpose to pretend otherwise, and phrase such constructions in terms of the curve \(y=f(x)\). All the actual work is done by the trial-and-error procedure and there is no sense in which interpolating a curve from a set of constructed points contributes anything of actual value toward the solution.
This is a profoundly different state of affairs from constructions in which the curve generation is primary, such as the conchoid, conics, quadratrix, etc. In these canonical constructions, the curve is generated by a process that is independent of x and y coordinates, and the curve so produced is then used to read off the x or y coordinates of certain intersection points. In the case of pointwise constructions, however, the curve is generated precisely by employing a relationship between x and y coordinates, yet the curve is still in these cases used to read off the x or y coordinates of certain intersection points. In this latter case, the reasoning is circular. It is nonsensical to use the curve to read off x-values since the curve was obtained by plugging in x-values in the first place. Any knowledge about x or y values in such a case comes solely from the trial-and-error pointwise process. It is therefore foundationally nonsensical to consider a curve given by a pointwise “construction” to be in any way comparable to curves given by instruments.
Indeed, pointwise constructions occur in the classical tradition only once, in the solutions associated with Diocles, and that can plausibly be due to corruption. I showed above that these solutions can readily be reinterpreted in a way that avoids reliance on pointwise constructions. These reconstructions are simple and would suggest themselves naturally to anyone with basic familiarity with the way curves are generated in the earlier Greek tradition. In Table 4, the pointwise Diocles constructions correspond to the conics focus-directrix and cissoid entries. These rows would lose their single degree of freedom and definitive termination attributes if pointwise constructions are used instead of my reconstructions. The strong adherence to these two attributes in other solutions makes it implausible that they would have been gratuitously abandoned in the manner the corrupt Diocles manuscript would have it, when obvious ways of avoiding this clash with tradition were readily at hand.
Furthermore, if pointwise constructions were generally considered acceptable, it makes no sense that they would occur only in one source. Numerous other opportunities to use pointwise constructions would have readily suggested themselves to Greek geometers. For instance, the quadratrix admits of a pointwise construction.Footnote 70 The absence of any evidence that Greek mathematicians pursued those possibilities suggests that they did not consider this method of construction acceptable. Indeed, if pointwise constructions are accepted, then the division between Euclidean means and conic sections collapses, since conic sections can be constructed pointwise by ruler and compass. It is quite evident that the Greek tradition did not accept this conflation. Hence it cannot have accepted pointwise constructions either.
I disagree with Knorr’s unconvincing speculation that pointwise constructions were in fact the primary conception of conic sections even to their originator Menaechmus himself (Knorr, 1975, 63, 1989, 117). Eratosthenes says that Menaechmus’s practical construction can only be done “with difficulty” (Netz, 2004, 295). This makes perfect sense as a description of the conic compass method, which is a challenge to build and operate as a physical instrument. It makes little sense, however, as a description of pointwise construction, which is not difficult at all, albeit potentially time-consuming.Footnote 71
Indeed, the only precedence for pointwise constructions of conics that Knorr is able to cite are from Diocles (in the source discussed above) and passages in Eutocius and Anthemius that are explicitly concerned with the practical generation of the curves for mechanical purposes such as building burning mirrors. As discussed in Sect. 4.4.3, it makes perfect sense to use pointwise constructions for such practical purposes, as indeed Diocles also does. However, it would be foundationally naive and nonsensical, in my opinion, to take this to be a legitimate way of solving the classical construction problems. The historical record fits precisely this distinction that I have argued for on conceptual grounds. It is precisely and expressly for practical purposes only that we find the use of pointwise constructions, not as solutions to the classical problems, except in the sole case of Diocles. And since this very work by Diocles discusses the practical generation of burning mirrors by a pointwise construction, one can readily imagine how later corruption could have let that methodology creep into the text of Diocles’s solutions of the classical problems as well, through the intervention of later editors with imperfect understanding of the classical problem tradition. This would have been a superficial corruption, since these solutions are so easily restored to a form that avoids this foundational naiveté.
4.6.8 Numerical Methods
Numerical methods for approximating cube roots were known in antiquity (Thomas, 1939, 60–63; Becker, 1957, 69–70; Heath, 1981b, 323–326). This immediately implies the ability to double the cube (or find two mean proportionals) numerically. But evidently Greek mathematicians considered this type of solution irrelevant to the classical problem tradition. Similarly, Archimedes’s Measurement of a Circle amounts to a numerical-approximative solution (whose precision can be made arbitrarily high) to the circle quadrature problem, yet, as far as we can judge, Archimedes evidently did not consider this a solution, but rather regarded his construction by means of the spiral as his contribution to the circle quadrature problem. At any rate, that is how the matter was interpreted by several late ancient commentators (Thomas, 1939, 335; Heath, 1897, xxxv).
This speaks to the foundational role of the construction problem tradition. If practical purposes were the goal, numerical methods would be very good and useful. But if, as I have claimed, the problem tradition is part of a philosophical program to ground the foundations of all mathematical reasoning in constructions, then it is evident why the Greek did not embrace numerical methods. It is ultimately geometry that provides the foundations for arithmetical and algebraic reasoning in Greek mathematics, as has often been argued. This fits well with the operationalist reading. For one thing, it follows from the operationalist thesis that the consistency of mathematics is inherited from the consistency of metrical physical experience itself (Sect. 3.3). From an operationalist point of view, numerical or algebraic methods cannot be the basis for solving construction problems, because only geometric constructions could give legitimacy to those methods in the first place.
One could argue that for instance Archimedes’s circle area approximation is grounded in constructions, and hence operationally legitimate. Indeed, Archimedes uses only constructible polygons (namely \(2^{n}\)-gons) to approximate the circle. But the trifling idea that a circle can be approximated by a constructible polygon had always been obvious and is of no use in solving the circle quadrature problem in a foundationally satisfactory manner. Numerical approximations fail the operationalist requirement of definitive termination. There are indeed other proposed solutions that also fail to meet this requirement, as seen in Table 4, but it is quite evident that this was recognised as a major drawback. It seems likely that Nicomedes’s conchoid was conceived precisely with the express goal of avoiding this major problem with neusis. And other methods that do well on definitive termination in Table 4 have clearly sacrificed quite a lot to achieve this, as seen by the much greater simplicity of the methods that allow themselves to neglect this goal. The record thus suggests that definitive termination was prized highly, even though it was recognised that dropping it would simplify everything immensely. For this reason, approximative methods could never be satisfactory solutions to the classical problems.
4.6.9 My View Contrasted with Others
My view clashes with traditional interpretations. Concerns related to concrete execution of constructions have often been seen as secondary or external to geometrical theory itself. Operationalism says otherwise. Actual realisability is far from a mere side issue relevant only to applications. Rather, it is the very core of the foundations of mathematics also at its most pure level of theory and philosophy. Thus I disagree with for example Knorr, who summarises the late problem tradition as follows:
The efforts on the cube duplication among the later writers are ...instigated ...by the interest in providing practical forms of the solution. Hero affirms his neusis to be “the most convenient for practical use,” and Pappus repeats this judgement; Eutocius notes the practical advantages of the Philonian form; both Sporus and Pappus devise neuses of their own; Eutocius describes pointwise constructions of conics to accommodate the difficulties that mechanical writers experience in this regard;Footnote 72 Isidore invents a compass for tracing parabolas. In related contexts, Anthemius uses pointwise constructions for ellipses and parabolas; Sporus criticizes the use of the quadratrix for circle quadrature on the grounds that one cannot synchronize the linear and rotatory motions needed to draw the curve—and objection that may touch on a real difficulty in the mechanical realization of the constructions, but is pointless in a theoretical context. In sum, the practical element overshadows any concern over theoretical questions throughout the later discussions of these constructions. (Knorr, 1989, 118)
I disagree in two respects. Firstly, it is not true that concern for practical execution is associated only with the later part of the problem tradition, as Knorr seems to suggest. The solutions by Eratosthenes and Nicomedes are clear proof of the contrary. They were active at the peak of Greek geometry, and their prominent concern with practical realisation of their solutions is explicit and unequivocal. It is plausible that they are representative of the tradition up to that point, and that only lack of sources prevents us from proving this explicitly. For instance, we know that neusis, which Knorr associates with a practical turn, was a mainstream feature of the tradition from an early stage. Are we really to believe that earlier generations thought of neusis merely “theoretically,” and that its close and obvious correspondence with a concrete operation with a ruler is a more or less unintended coincidence? Surely that is extremely implausible. Instead of postulating a rift in attitudes between early and late geometers, a more natural interpretation is that assessments of the advantages and disadvantages of for example neusis remained basically constant throughout the Greek tradition. From this point of view, the comments about practical execution in later sources do not reflect a change in attitudes; rather, such remarks occur in later eras only, because only then do we have discursive sources that go into such issues at all, whereas for the early eras all that has survived is the purely formal proposition-proof core of what those mathematicians wrote. The operationalist reading enables us to view the practice-oriented remarks in later sources as a natural continuation of existing tradition rather than a divergent oddity.
More fundamentally, I reject the anachronistic assumption that “theoretical” and “practical” concerns can be dichotomised in the way Knorr suggests. On the contrary, according to operationalism, practical realisability is the theoretical foundations of geometry. Attention to actual realisability is not “pointless in a theoretical context.” On the contrary, a “theoretical” geometry in which for instance the quadratrix is considered given by its abstract definition yet in which the third of an angle needs to be constructed makes no sense. There can never have been such a stage of Greek geometry, because it is conceptually incoherent and void of any rationale. The very idea of constructing the third of an angle becomes nonsensical if one is allowed to conceive purely “theoretical” construction means without any attention to realisability. Such a “theoretical” “construction” is not a construction at all: it merely shows that one imagined entity (such as a quadratrix) is related to another imagined entity (such as the third of an angle). If Greek geometers cared only about such “theory,” then why did they want to construct the third of an angle at all? To allow such “constructions” is to void the concept of construction of any credible meaning and any restriction in scope. It would be trivial to imagine any number of geometric entities that can be used to “construct” the third of an angle in this sense. A research program on the classical problems would therefore immediately collapse unless the concept of construction is much more restricted and controlled. Restricting constructions to what is concretely actualisable in physical reality is the obvious and natural way to impose such a restriction. Thus the fact that Greek geometers were always heavily focussed on construction problems proves that they must have been sensitive to issues of practical realisability, or else the enterprise they were engaged in would have been nonsensical.
Cuomo makes a point similar to that of Knorr:
The duplication of the cube, far from being the epitome of pure mathematics, was quite generally associated with applied mathematics. \(\ldots\) Its practical applications were emphasized (Eratosthenes, Hero); authors criticized their predecessors because of the cumbersomeness of their procedures (Eratosthenes, Nicomedes). \(\ldots\) Whatever its historical origin, then, the problem over the years acquired various and contrasting meanings which overrode its mathematical significance. (Cuomo, 2000, 135)
Again, operationalism suggests another reading. Attention to practice is not a “contrasting” concern that “overrode” pure mathematics; rather, it is an inherently essential part of mathematics itself, even—or in fact especially—at the level of its ultimate theoretical foundations. Operationalism, again, saves us from having to posit rampant disunity of the classical problem tradition.
Fowler, too, perceives heterogeneity in the classical tradition:
In broad terms, we see three phases of development [with respect to foundational attitudes regarding neusis]. The early geometers, from Hippocrates to Archimedes, seem to have used the neusis-construction freely, as a basic construction of mathematics. This was followed by a period, represented by Apollonius and Nicomedes, in which the scope and implications of the construction were investigated, and its relation with other constructs was explored. Finally, in late antiquity, we find Pappus laying down formal criteria that the use of constructions must satisfy. (Fowler, 1999, 285)
I disagree. An obvious counterargument against the alleged, carefree acceptance of neusis is of course that Euclid does not use it in the Elements. Surely this proves that Greek geometry at its peak was deeply interested in the minimalistic reduction of construction assumptions to ruler and compass only. Fowler tries to explain this away unconvincingly, by trying to construe “the apparent [!] concern for ruler-and-compass constructions in the Elements” as a side-effect of the mathematical nature of the problems it treats (effectively, their corresponding to quadratic relations algebraically) rather than any primary interest in constructive-foundational issues. Only later, according to this reading, “would [the] underlying constructions move into prominence and be of interest in their own right” (Fowler, 1999, 288). This radical view is at odds with a face-value reading of Book I of the Elements, which puts constructions front and center.
But there are even deeper problems with Fowler’s periodisation. It is evident that the three classical problems were already well entrenched in what Fowler calls the first period. Therefore it makes no sense to ascribe construction-foundational obliviousness to the geometers of these generations, as Fowler does. There is no coherent way in which a mathematician can take the three classical problems to be central, yet at the same time not have a carefully thought out position on issues such as whether neusis should be accepted as a fundamental construction. It is impossible to conceive of circle quadrature and angle trisection as problems at all, unless one prohibits the use of construction means that solve these problems in a trivial way, such as the possibility of wrapping a piece of string along a curve and then stretching it into a straight line segment of equal length. And it is impossible to judge which among several proposed constructions to the same problem (a state of affairs that occurred already in pre-Euclidean times) is better, unless one has precise prescriptive criteria that constructions should satisfy. These criteria must surely be foundational in nature; indeed, all evaluative statements of constructions in the ancient record assess the method in and of itself in terms of its inherent properties, not in terms of its broader position in a mathematical theory or research program (which would have been more akin to the internalistic explanation that Fowler proposes in the Euclidean case).
Meanwhile, it is implausible that much later commentators like Pappus would have invented foundational-prescriptive rules out of thin air, when everything else they say is subservient to the sources they are copying with little or no original contribution of their own. And if such foundational concerns are a late invention, what are the odds that the entire centuries-long tradition can be plausibly reconstructed as having aimed at such concerns all along, as the operationalist reading shows?
The characteristics Fowler associates with his three phases have more to do with the availability of sources than with any actual historical transitions, I believe. Of the solutions to the classical problems before Archimedes, we know virtually nothing about the full works and contexts in which they were embedded. Perhaps indeed “the scope and implications of the construction were investigated” in these works, for all we know. Fowler associates such investigations with the second phase, but it is perhaps not coincidental that this is the first period for which we have information about how such constructions were embedded in entire treatises and what their overall goals were. We have such information for Apollonius’ work on neusis, which is what Fowler is referring to, but we have no such information for the work on the classical construction problems by Hippias, Archytas, Eudoxus, Menaechmus, etc. So the apparent emergence of such concerns in the generation of Apollonius could very well be an artefact of the source scarcity of the earlier period rather than an indication of any actual change in the attitudes of Greek mathematicians over time concerning constructions. The same goes for the unprecedented methodological remarks by Pappus in Fowler’s phase three: this is surely not because earlier mathematicians lacked methodological opinions, but because their thought on such issues—which must have been extensive and sophisticated for the classical tradition to make any sense—has not come down to us.
Knorr makes another case for disunity based on the testimony of Eratosthenes, who says:
It is said that Archytas of Tarentum solved this [cube duplication or mean proportionals problem] with the aid of semicylinders, while Eudoxus did so with the so-called curved lines; as it happens, all of them wrote demonstratively, and it was impossible practically to do this by hand (except Menaechmus, \(\ldots\) and this with difficulty). But we have conceived of a certain easy mechanical way of taking proportionals. (Netz, 2004, 294–295)
From this (Knorr, 1975, 63) concludes that, “evidently, views on the importance of mechanical approaches varied over the course of antiquity and might sometimes be a matter merely of personal preference.” I disagree. I believe a commitment to mechanical realisation always remained a prominent concern throughout the classical tradition. The physicality and realisability columns of Table 4 testify to this.
The statement by Eratosthenes can readily be interpreted in a manner consistent with the operationalist reconstruction of the classical tradition. I have argued that the solutions by Archytas and Menaechmus were, in the original, explicitly based on instrumental generation. However, these instruments are conceived for theoretical reasons and would be difficult to build in actual practice. I believe Archytas and Menaechmus would very much have liked to come up with even more practicable constructions. The record does not show, in my opinion, that they disregarded mechanical generation, but that they prioritised it as much as they could while remaining true to the other operationalist ideals such as unicity, single degree of freedom, and definitive termination. Eratosthenes is able to give a mechanically simpler construction only by sacrificing these other desiderata. Of course, when introducing his method, Eratosthenes is going to highlight the particular criteria on which his method shines, and downplay the others. So it makes perfect sense that he contrasts the mechanical simplicity of his method compared to the impracticality of the earlier ones. But this does not show that values had changed. The record is perfectly consistent with the operationalist desiderata being constant over time, and that all these mathematicians tried to meet all of them. Trying to come up with a method that meets all of these conditions is very difficult or impossible. But mathematicians will keep trying, and when they have a candidate of their own they will naturally try to highlight what advantages it has relative to the others. Insofar as they do not emphasise or meet other conditions, this could very well be due to the impossibility of doing so due to mathematical limitations inherent in the construction they were able to come up with. That is to say, such differences can very well be due to unintended and unavoidable mathematical contingencies rather than to preexisting personal preferences.
5 Operationalism Elsewhere
5.1 Hierarchy of Methods
The Greeks were concerned, when giving constructions, to proceed by means that are the “simplest” possible in some sense. The methodological dictum that it is “not a small error for geometers” to solve a problem “from a non-kindred kind”—that is, using more advanced assumptions or methods than necessary—is found in Pappus and seems to have been a prominent concern for Apollonius as well (Knorr, 1975, 346, 1982, 272; Sefrin-Weis, 2010, 145, 271–275; Jones, 1986, 530; Acerbi et al., 2018, 273, 276). Something like it must surely have been a concern even earlier, because the preoccupation with the three classical construction problems necessitates it. It is indeed essential to have some “rules of the game” of this sort as a mathematical community when research is focussed on solving construction problems. Obviously, if anything goes it is trivial to solve any construction problem. Hence a meaningful research program of this type can only be sustained given considerable attention to, and restrictions on, what constitutes a legitimate construction method. So the very nature of the problem solving enterprise demands that mathematicians keep to minimalistic, carefully justified methods in some sense.
Such a concern for methodological purity and minimalism in construction assumptions goes perfectly with operationalism. Simplicity of constructions is the very bedrock on which the reliability of mathematical reasoning is based. Constructions need to be simple to avoid any risk of involving inconsistent or hidden assumptions, to achieve accuracy with intuitive means, and to serve as sources of operational meaning for basic entities by having greater immediacy than any theorem about them.
But many have questioned the alleged role of a hierarchy of methods in ancient geometry as testified by Pappus. First of all it is evident that the Greek geometrical corpus does not obey the particular dicta articulated by Pappus. Pappus’s hierarchy of methods has three levels: ruler and compass; conic sections; and higher curves. But Pappus explicitly criticises Archimedes and Apollonius for not following his rule of always sticking to the lowest possible level in this hierarchy for any given problem (Sefrin-Weis, 2010, 145; Bos, 2001, 49), and himself extensively reports many solutions that do not do so either.Footnote 73 This indeed proves that the rather simplistic hierarchy proposed by Pappus was far from a universal guiding principle among Greek geometers. But it does not follow by any means that they therefore had no concern for hierarchies of method more broadly. If anything, it seems strange that Pappus would have invented his rule completely out of the blue, especially since it is at odds with many things he himself brings up.
There are a few exceptional places in the Greek corpus where ruler and compass would have sufficed for a certain problem, yet other methods, such as neusis or conics, are used. If this practice was widespread, this would seem to suggest a disregard for the foundational issues connected with operationalism. It would indeed be problematic for the operationalist reading of Greek mathematics if people like Archimedes did not take the distinction between neusis and Euclidean constructions very seriously. But the isolated instances of such practice usually adduced do not prove anything of the sort. For example, Pappus’s objection of this type against Apollonius concerns the Conics, but it is hardly compelling to insist that conics be avoided in favour of ruler and compass in a few isolated instances in a treatise that is entirely devoted to conics from start to finish. Obviously, gratuitous uses of conics in such a work is in no way an indication of a disregard for the foundational distinction between conics and ruler and compass generally.Footnote 74 Similarly, Archimedes could perhaps have avoided some particular neusis, but that in a work that uses other neuses that are not reducible to ruler and compass, which would make carrying out the reduction in the simplest case rather pointless (Dijksterhuis, 1987, 138–139; Heath, 1897, c–ciii). Furthermore, this is in a work whose primary aim is arguably the quadrature of the circle—the hardest of the classical construction problems that certainly puts us way beyond the scope of ruler and compass and even neusis. The fact that Archimedes used neusis freely in such a work, whose main purpose is perhaps precisely to expand on previous construction methods, does not mean that he did not have any regard for the distinction between neusis and ruler and compass altogether. The same can be said for Hippocrates’s avoidable use of neusis, which also occurs in the context of circle quadrature.Footnote 75 In sum, all examples used to argue that classical mathematicians were unconcerned with whether certain higher constructions could be reduced to ruler and compass are from works where the overall purpose of the treatise means that a reduction to ruler and compass in those isolated cases would arguably have been pointless, since the treatise as a whole is concerned precisely with what cannot be reduced to ruler and compass.
More fundamentally, there is the possibility in such cases that these mathematicians may have known perfectly well what particular instances of, say, neusis could be accomplished by ruler and compass, and used them without hesitation for that very reason. This would be analogous to how basic Euclidean constructions are used. For example, Elements I.46 shows how to construct a square. Once this is proved one can (and everybody does) treat the introduction of a square on a given segment as if it were a primitive operation, without giving its construction details. This of course does not imply that any mathematician who introduces a square is unaware of the foundational ramifications of doing so, or has no regard for the constructive justification of this step. Rather they merely leave the subconstructions needed to make a square implicit since they are common knowledge. The same could be the case for certain cases of neusis and perhaps other constructions.
Another basis on which the hierarchy-of-methods picture has been questioned is that, allegedly, Pappus’s decree would have been “unworkable” in ancient times since the Greeks had no way of proving impossibility results of the type that a certain problem is unsolvable by certain means (Knorr, 1975, 347; Sefrin-Weis, 2010, 274 holds a similar view). It is true that the Greeks lacked systematic proofs to settle such questions definitively. Nevertheless, a research program paying prominent attention to hierarchies of methods was by no means “unworkable.” Experience, intuition, and informal arguments would easily have been more than sufficient to guide such research in a convincing and sound way. It is plausible that considerations of that nature led Greek mathematicians to use “last resort” methods that they would have otherwise avoided for circle quadrature, use the quadratrix for multisection but prefer simpler means for trisection, and so on.
5.2 Spatial Euclidean Geometry
5.2.1 Lines and Planes
Euclid treats three-dimensional geometry from Elements Book XI onwards. We must now investigate the question: How does Euclid introduce objects in a three-dimensional setting? What are the construction rules by which geometrical entities can be introduced into a geometrical argument in this setting? Unfortunately Euclid does not address these questions with anything like that clarity of the explicit postulates of Book I. But his basic rules seem to be:
- 3Dpoint:
-
Points can be taken at will in space, just as in the plane.
- 3Dline:
-
Any two points can be joined with a line. This does not seem to require an ambient plane. We may think of it as stretching a string between the two points.
- 3Dplane:
-
Given a line and a point,Footnote 76 the plane containing them is available to us. We can imagine taking a stiff sheet of paper, laying it against the line, and rotating it until it hits the point.
- 3D2D:
-
In any such plane, we can do all our usual plane geometry.
- 3Dlentr:
-
Lengths of line segments can be transferred from anywhere onto any plane. We can imagine this as being done with a compass.
It has been objected that 3Dlentr is an unwarranted use of I.2, which was proved only for the plane but is now used indiscriminately in space to transfer lengths from one plane to another (Mueller, 1981, 208). But as I argued in Sect. 3.2.2, it is perfectly possible to read Euclid as considering the transferring of lengths by the compass as a valid, axiomatically given operation.
Euclid also assumes in his solid geometry that he can apply the triangle congruence theorems of Book I to triangles in different planes, which again can be considered objectionable since he proved them by planar means (Mueller, 1981, 208). But with our interpretation of superposition as reconstruction (Sect. 3.4), no planarity assumption is needed in these proofs; 3Dlentr is enough to be able to apply the proofs to triangles in different planes.
Elements XI.1–3 try to justify that a plane that contains a segment of a line contains the whole line, that three points or two intersecting lines determine a plane, and that planes intersect in lines. But the proofs are very poor in several ways, one of which is that they do not unequivocally reduce to clearly articulated fundamental principles.Footnote 77 In particular, Euclid does not give a mathematically useful definition of a plane,Footnote 78 which makes it impossible to prove fundamental propositions about them in a meaningful way. For our purposes, we might as well consider XI.1–3 and the 3D principles as axiomatic.
The next propositions are:
XI.4. If a straight line is set up at right angles to two straight lines which cut one another at their common point of section, then it is also at right angles to the plane passing through them.
XI.5. If a straight line is set up at right angles to three straight lines which meet one another at their common point of section, then the three straight lines lie in one plane.
These propositions are puzzling, because it is not immediately evident how to construct the configuration in question. We have emphasised at length that, in operationalist geometry, it is essential to only speak of constructible geometrical entities and configurations, and indeed Euclid’s plane geometry follows this requirement meticulously. But how are we supposed to “set up” a straight line at right angles to two or three other lines? Constructing the perpendicular of one line in a given plane is handled in I.11, but it is a world of difference to require a line to satisfy several perpendicularity conditions simultaneously. It is anathema to operationalism to introduce objects defined only implicitly by a set of conditions they satisfy.
This is all the more striking since XI.5 is proved by contradiction (assuming that the three lines do not lie in a plane and deriving a contradiction). It is obviously essential for the logic of this argument that the initial configuration assumed was not self-contradictory already, like the superright triangle of Sect. 2.1.3. Euclid simply says “Let a straight line AB be set up at right angles to the three straight lines BC, BD, and BE at their intersection B.” This seems like exactly the kind of thing the superright triangle example warns against, namely uncontrolled introduction of a complex object defined not constructively but by a set of properties it is assumed to have. This is unacceptable in an operationalist, not to say in any rigorous, mode of doing geometry, because configurations introduced in such an uncontrolled manner can easily be self-contradictory. For instance, I could add to Euclid’s sentence: and let BS be a straight line set up at right angles to AB, BC, BD, and BE at their intersection B. There is no such BS line. We must have some way of knowing that the configuration assumed in XI.5 is not of this type. Otherwise, for one thing, the contradiction derived from the assumption that BC, BD, and BE do not lie in the same plane could not be taken to disprove this assumption, for another possibility would be that the configuration was self-contradictory to begin with and that it was this that was the actual source of the contradiction derived, and not the assumption about the lines being non-coplanar. One could choose to argue that it is intuitively clear which configurations are coherent and which are contradictory, but a much better way of managing such issues is by building everything up from a few constructive principles, which isolates the need to invoke intuition to the core principles only.
But I believe in these cases Euclid can be saved. To make operationalist sense of XI.4, it seems to me that we must read it as follows (Fig. 41). I take a line, FE, and a point A not on that line, and I consider their plane. In that plane, I apply I.11 to make a perpendicular AB to FE. I then take another point, \(C'\), at will and make another perpendicular, \(C'D'\), to FE in the same way. Now, \(C'D'\) may not cut FE in the same point (E) as AB did. But this is required by the theorem. To fix this, consider the plane of FE and \(C'D'\) and use plane geometry (Elements I.31) to produce the parallel CD to \(C'D'\) through E. Now I have the “straight line is set up at right angles to two straight lines which cut one another at their common point of section” that the theorem is talking about. So we do not need to make the operationally unacceptable concession that the configuration of XI.4 is merely imagined or otherwise introduced without construction. Rather, there is a straightforward way of constructing it that could be considered implicit in the Elements, by the 3D rules outlined above. XI.5 can be treated in the same way.
Note that my reading makes it essential to start with the “vertical” line and then construct the “base” lines to which it is to be perpendicular from it. We could not draw the set of intersecting lines first and then raise perpendicular upon them, which would seem like the most natural thing to do given Euclid’s wording. Indeed, doing so would essentially mean that we could solve XI.11–12 (which are the first construction problems in Book XI):
XI.11. To draw a straight line perpendicular to a given plane from a given elevated point.
XI.12. To set up a straight line at right angles to a give plane from a given point in it.
But the proof of these propositions depend on XI.4, so XI.4 must be done using more primitive and basic constructions than XI.11–12 for the text to make sense. My reading satisfies this requirement.
The reasoning involved in my reading can be summed up for reference in a lemmatic construction problem:
- 3D\(\bot\)plane:
-
Given a line, make a plane perpendicular to that line.
We do this by making two perpendiculars to the line in the same point, as above, and then use 3Dplane to get the plane. XI.4 proves that the line is indeed perpendicular to the plane (and not only to the two lines used in the construction).
Most of the remaining material in Book XI can be straightforwardly operationalised using the 3D principles and the constructions Euclid provides as propositions. That is to say, no entities are assumed in the course of proof other than such as can be produced by those constructions. For instance, XI.7, XI.9, XI.10 need only the simple 3D principles described above, while XI.14 can be achieved by 3D\(\bot\)plane.
In XI.16, Euclid implicitly assumes:
- 3Dplane-int:
-
Given two (non-parallel) planes, their intersection is available to us.
This is not a new construction principle but reducible to the ones we have already mentioned. For operationalist purposes, we must resist the notion that one can simply “let” a curve be the intersection of two surfaces and assume that the curve so defined is concretely at hand just like any that we have made using ruler and compass. This is a very abstract, point-set-condition way of defining a curve, and one that could be very difficult to realise physically. But for planes we can produce the intersection much more concretely. Since we know that planes intersect along straight lines,Footnote 79 we only need to extend two lines from one plane that hit the other plane wherever, and then connect this two points of intersection. This is very much physically realisable with strings or rulers on physical planes, and needs nothing but the previously outlined 3D construction principles.
The one disturbing exception to the operationalist reading I have offered is:
XI.6. If two straight lines are at right angles to the same plane, then the straight lines are parallel.
I do not see any way of interpreting this proposition that makes it operationally acceptable at this point in the Elements. Operationalism demands that we only state theorems about entities that we know how to construct. But how are we supposed to construct “two straight lines at right angles to the same plane”? 3D\(\bot\)plane does not help us. With that strategy, we could make two lines that are each perpendicular to a particular plane, but we could not ensure that this would be the same plane for both lines. We could raise perpendiculars from lines in one of those planes, but we could not ensure that they would be perpendicular to the plane as opposed to merely the reference line used for the construction.
What we need for XI.6 to make operational sense is precisely XI.11–12. If we had those constructions already, the configuration of XI.6 would be readily realisable and hence not pose any problems for an operationalist reading. But doing XI.6 first does not make operationalist sense. In fact, the construction problems XI.11–12 are not logically dependent on XI.6 (which is not used at all in the rest of Book XI). It is tempting, therefore, to suppose that the order of the propositions has been corrupted. An independent argument for this is that the proof of XI.6 implicitly assumes that the two parallels cannot meet the plane in the same point, and XI.13 (“From the same point two straight lines cannot be set up at right angles to the same plane on the same side”) is devoted specifically to ruling out this very possibility (as noted by Joyce, 1998). So the placement of XI.6 is not only operationally unacceptable but foolish also for independent logical reasons.
In sum, Book XI is not as clearly operationalist as the earlier books of the Elements, but it does allow an operationalist reading. Book XI is also of lower mathematical quality by anyone’s standards, for many reasons that are independent of operationalism. It makes some sense to suppose that a better version of this theory once existed and that that theory was more operationalist in character. For why else would the text contain construction problems such as XI.11–12? These are clearly theoretical propositions; it is surely safe to assume that they were not included for practical applications in, say, architecture or carpentry. But what theoretical purpose could they serve, if non-operationalist ways of introducing objects have already been used numerous times before they are proved? If one can simply “let a straight line be set up at right angles to three straight lines,” as Euclid does in XI.5, then why does the perpendicular to a plane need to be constructed, as Euclid does in XI.11–12? Why can one not simply “let” such perpendiculars be introduced at will? The operationalist reading makes coherent sense of these enigmas. With some simple adjustments (such as moving XI.6 and being a bit more explicit about the foundational construction assumptions), the operationalist reading allows us to view the theorems and problems of Book XI as foundationally coherent.
5.2.2 Solids
Euclid’s definitions of solids are operationally sound. They may be interpreted as follows.
Definition XI.12. A pyramid is a solid figure contained by planes which is constructed from one plane to one point.
It is implied that the base figure is some polygon drawn in a plane. The vertex of the pyramid can be taken at will outside of this plane, and then the edges and walls of the pyramid are constructively available by 3Dline and 3Dplane.
Definition XI.13. A prism is a solid figure contained by planes two of which, namely those which are opposite, are equal, similar, and parallel, while the rest are parallelograms.
We can use 3D\(\bot\)plane to make the parallel planes, and 3Dlentr to make sure the opposite end polygons are equal. The other walls are available by 3Dline and 3Dplane, and can be proved to be parallelograms.
Definition XI.14. When a semicircle with fixed diameter is carried round and restored again to the same position from which it began to be moved, the figure so comprehended is a sphere.
Definition XI.18. When a right triangle with one side of those about the right angle remains fixed is carried round and restored again to the same position from which it began to be moved, the figure so comprehended is a cone.
Definition XI.21. When a rectangular parallelogram with one side of those about the right angle remains fixed is carried round and restored again to the same position from which it began to be moved, the figure so comprehended is a cylinder.
Rotating a figure around an axis must be admitted as an additional construction principle. It is indeed striking how these solids are defined through operational generation rather than by their properties (“what you get when you \(\ldots\)” rather than “a figure such that \(\ldots\)”).
As we emphasised above in the case of planes, Euclid does not need the assumption that taking the intersection of one surface and another, or the intersection of a solid and a plane, makes the intersection available to us. Instead, the kinds of intersections of figures by planes that Euclid considers are such that the intersection can be constructed by ruler and compass and the basic 3D principles. Thus a parallelepiped sliced with a plane parallel to a face makes a parallelogram (assumed in XI.25), and a cylinder sliced perpendicularly to the axis makes a circle (assumed in XII.13). Furthermore, a sphere cut by a plane through the midpoint makes a circle, as Euclid assumes in XII.17. This follows immediately from Euclid’s definition of a sphere, insofar as the plane contains the diameter used at the axis of rotation. Euclid also needs the assumption that other planes through the midpoint likewise produces equal circular intersections (Heath, 1956, III.431); this does not follow from the rotational definition per se but can be derived via its consequence that all points of the sphere are equidistant from the midpoint.
The five regular polyhedra—the subject of Elements XIII—are another showcase for Euclid’s strong emphasis on constructions, as is well known. Euclid spells out in detail how to produce these solids with ruler and compass and the basic 3D principles.(Footnote 80 The regular polyhedra are good examples of geometrical objects whose existence is not evident, which makes their construction all the more essential.
In sum, Euclid’s treatment of solid figures is readily susceptible to an operationalist reading. Parts of Euclid’s stereometry books are demonstrably poor by any standard—that is, completely independently of operationalist considerations—presumably due to corruption. Once this is corrected, deviation from operationalism is minimal.
5.3 Spherical Geometry
Spherical geometry provides another test case for the operationalist reading of Greek geometry. Theodosius’s Spherics (ca. \(-100\)) develops the geometry of the surface of a sphere in a manner that is in many ways analogous to Euclid’s Elements. I shall argue that this treatise too is consistent with operationalism.
First of all it is abundantly clear that the Spherics is very much concerned with performing actual constructions on a physical sphere.Footnote 81 To this end, an ordinary compass is also useful on a globe: it can be used to draw circles on the surface of a globe, and it can be used to transfer lengths (meaning the spatial, and not the geodesic, distance between two points) not only on the globe itself but also from the globe onto a flat sheet of paper. Like the Elements, the Spherics is not explicit about how the constructions it describes can be realised by physical instruments, but it is quite evident that this is what the author had in mind.Footnote 82
This alone is yet more evidence of the centrality of constructions in Greek mathematics. However, operationalism maintains not only that constructions are important but also that they are the proper foundational bedrock of mathematical theory. It is not evident whether constructions in the Spherics serve such a purpose, or whether they are merely practical and geared toward applications, such as in astronomy, which clearly provided the main impetus to study spherics.
Recent scholarship indeed makes a sharp distinction between constructions intended to be actually performed for applied purposes, and ostensible constructions that are merely imagined for theoretical purposes while being in reality unrealisable.
In the Spherics, the use of constructions in writing proofs was distinct from the use of constructions in showing how to solve a given problem. ...The techniques used in solving a problem are constrained by the possible operations of some assumed set of geometric tools, while constructions employed in proofs—indeed, even the constructions employed in the proof of a problem—are not subject to this constraint. (Sidoli & Saito, 2009, 583–584)
This interpretation is diametrically opposed to operationalism. Operationalism demands that all constructions be physically realisable. If this requirement is not met, the entire operationalist foundational program collapses. Fictive “constructions” that can only be imagined and not concretely carried out are as useless as no constructions at all. Hence we must investigate whether the theoretical constructions too can be operationalised.
The core construction said to be theoretical as opposed to actual is that of taking the intersection of the sphere with a plane.
From the outset, [the Spherics] contains a distinction between constructions that can be carried out with the postulates, and thus tools, of elementary geometry, and those that are more conceptual, or abstract, but are nevertheless required by the need to write proofs about solid objects ...[namely,] the operation of cutting a sphere with a plane. (Sidoli & Saito, 2009, 586)
We have no instrument for slicing spheres. ...The slicing of a sphere with a plane to produce a circle requires a chef in Plato’s heaven to wield a planar cleaver. (Thomas, 2014, 229)
I agree that merely defining a curve as the intersection of a surface with a certain plane does not make that curve constructively available to us. But the Spherics does not need such an assumption, for the same reason I argued above that the Elements does not either. Just as the intersections of solids Euclid considers in the Elements are all constructible and determined by the generation of those solids, so also in the Spherics a concrete construction of the intersection of a sphere with a plane can be read off the definition. The Spherics, in its Definition 1, defines a sphere as a figure such that all straight lines from a particular point (the center or midpoint) to the surface are of equal length. This can be physically conceived as the set of all points reachable by a pen attached to one end of a string whose other end is fixed (just as a circle in plane can be generated in the same way). This conception implies a concrete way of drawing the intersection with a plane: hold up a physical plane, such as a stiff sheet of paper, and trace on it the curve that the pen can reach while holding the string stretched.
The first proposition in the Spherics proves that this curve is a circle. Its method of proof works well with the operationalist conception of the curve I have outlined. The proof considers the perpendicular from the plane through the midpoint of the circle, which is operationally sound by Elements XI.11, as discussed in Sect. 5.2.1. It then notes that all points on the curve are associated with a right triangle having as one of its legs this fixed perpendicular, and as its hypothenuse a radius of the sphere. Since the latter is constant by definition, it follows that so is the distance from the foot of the perpendicular to the curve traced, which proves that this curve is a circle.
The Spherics assumes that whenever we consider the intersection of a sphere by a plane, not only do we get a circle as just proved, but also the plane of that circle is available for us to do Euclidean geometry in (e.g., Spherics I.2–4). This is unproblematic given the above operationalisation. Furthermore, whenever we are “given” a circle on our sphere, the Spherics likewise assumes that the plane of that circle is available to us (e.g., Spherics I.7). We can view being given a circle as nothing but a shorthand for being given the corresponding plane. This explains why the plane is immediately available, as the Spherics assumes. Another way of producing circles on the sphere is by drawing it with a compass on the surface of a globe, just as one would in a plane. But, foundationally speaking, the definition in terms of the intersecting plane is better viewed as the primitive one, and its equivalence with drawing with a compass to be a derivative result to be proved. Indeed, while “given” circles always come with a plane, they do not come with a pole, i.e., the point where the fixed leg of the compass needs to be placed, as they would have if they had been drawn with the compass. The pole of a given circle is instead constructed in Spherics I.21.
I propose that this conception of spherical geometry—in terms of a pen on a string and sheets of stiff paper that can be fixed in various positions—is the right way to view the foundations of the subject. Hence I reject the following interpretation:
What look like constructions in the proofs of Propositions 1 and 2, since there are no instruments to perform them, are better thought of as thought experiments. \(\ldots\) There is no way to do these things. (Thomas, 2018, 6)
My point with the pen on a string is that there is in fact a way to do these things. The important thing is that this physical realisation can in principle be invoked as the foundations of the subject. But of course this does not mean that a working geometer will actually go through constructions of this type when they are doing spherical geometry. They will not do so any more than they will construct the squares on the sides of the triangle according to Euclid’s construction recipes every time they apply the Pythagorean Theorem. Yet those actual constructions are foundationally essential.
Just as Euclid had to construct the regular polyhedra, and could not simply introduce them as a “thought experiment,” so also spherical geometry as I have conceived it is very much restricted in terms of what geometrical entities can be introduced and in what order, so that everything can be articulated and given meaning in terms of actual operations without circularity. But I believe the Spherics does nothing to violate this condition.
Just as my operationalist interpretation of conic sections does not involve any physical cone (Sect. 4.4), so my operationalist interpretation of spherical geometry involves no physical sphere. Foundationally, these theories are analogous. There is, however, a great practical difference. In the case of spherical geometry one really does want to work with a physical globe, for instance for astronomical purposes. So there is to a certain extent a mismatch, in the case of spherical geometry, between the official foundations of the subject as I have interpreted them, and the practical needs of a working geometer. We cannot practically pass a sheet of paper through the surface of an actual globe, of course, so when we solve problems in spherical geometry we are interested in giving constructions not only in the official foundational context but also in a form that is practicable in a physical globe.
This is indeed what the Spherics does. Spherics I.18 is the problem: “To set out the diameter of a given circle in a sphere.” The construction gives a recipe for producing this diameter that consists entirely of operations that can be performed on the outside of the sphere, namely by picking three arbitrary points on the circle, then setting out the triangle they define on a flat sheet of paper (presumably by holding a compass against the sphere and setting the opening to the distance between two of points and then marking this distance on the paper), and then performing certain Euclidean constructions there to produce the diameter of the sphere as a line segment on this sheet of paper (Sidoli & Saito, 2009, 590). However, for the purposes of proving that this construction is valid, it is necessary to consider the corresponding configuration inside the sphere, in the plane of the circle. This internal configuration too is built up with constructions. Insofar as the internal plane of the circle can be considered constructively available, this internal construction in itself already solves the problem. It explicitly produces the diameter of the circle. Yet the text goes through the extra trouble of making a replica of this entire configuration on a plane outside the sphere. I all but agree with the following conclusion from this state of affairs:
Although [the] internal diameter is constructed using standard techniques, it does not, in fact, solve the problem. The internal diameter is, clearly, only constructed for the sake of the proof. It is constructed in order to introduce a new set of starting points from which Theodosius will argue that the external line is equal to the internal diameter. In this problem, it becomes clear that Theodosius intends a functional difference between the use of construction for the sake of proof and its use as a practical technique for drawing figures. The internal diameter, which is constructed for the sake of the argument, does not solve the problem. The problem is only solved when another line has been drawn outside the sphere, which is equal to this internal diameter. The difference must, in some sense, be practical. If the geometer is working with a real spherical body, [the outer configuration] can be drawn on a flat surface [using ruler and compass]. The internal diameter, on the other hand, is not immediately accessible to the practical tools of the geometer. (Sidoli & Saito, 2009, 591)
However, I would say that, strictly speaking, the internal diameter does in fact solve the problem. From a foundational point of view, the internal construction alone is a perfectly good solution. As I interpret it, the need for the external solution does not come from any kind of principle inherent to geometrical method per se, but is due solely to a voluntarily imposed restriction geared toward a particular type of application. This view is essentially compatible with the above passage, while also being consistent with operationalist philosophy. From this point of view, the constructions inside the sphere are not imaginary or hypothetical. On the contrary, it is precisely the fact that they can be physically realised that ensures the certainty and soundness of the reasoning.
Similarly, I essentially agree that:
[Some] constructions ...provided in the course of demonstrations ...have a purely theoretical function. For example, in Spher. I 8, the poles of a circle are constructed for the sake of the demonstration, and in Spher. I 19, a great circle is produced in a sphere by passing a plane through its center. When the related problems are later established [in I.20–21], however, they show how to produce these same objects in such a way that they may actually be produced on a real globe. (Sidoli & Saito, 2009, 601)
But note well that these “purely theoretical” constructions are eminently realisable in the foundational sense I have outlined. They indeed serve a theoretical purpose, and the Spherics is indeed interested in achieving the same thing by working outside the globe only. Nevertheless, they can be translated into physical operations just as readily as anything in Greek geometry.
Spherics I.2 finds the midpoint of a given sphere. It does so by taking its intersection by an arbitrary plane, then raising the perpendicular through the midpoint of the resulting circle, and then bisecting the part of this perpendicular contained in the sphere. This corresponds directly to Elements III.1, where Euclid finds the midpoint of a circle in an analogous way. My interpretation in Sect. 3.2.3 was that it is not really foundationally coherent to consider a circle known but not its midpoint, although it is of course nevertheless possible to pose for oneself the challenge of reconstructing the midpoint if one pretends that it is not known. My interpretation of spherical geometry requires me to view Spherics I.2 similarly. It is interesting that the midpoint of a sphere can be reconstructed, and in a pleasing and elegant way, but in principle the very meaning of the concept of a sphere implies that its midpoint is known, so foundationally speaking the problem must be regarded as gratuitous.
Nevertheless, just like Elements III.1, Spherics I.2 can be useful for practical purposes. One can use it to find the midpoint of a physical globe. The emphasis on the theoretical or thought-experiment nature of the foundational constructions in the Spherics has led some to deny this. Spherics I.2, on this view, is an example of a “construction ...that can be carried out ...only by an ideal agent but that we are unable even to approximate,” because “getting the plane is a real difficulty” (Thomas, 2014, 231). I do not think we need to be so pessimistic. Spherics I.1 proved that the intersection of a sphere with a plane is a circle. Therefore, we can henceforth consider a second manner of physically realising the intersection of a sphere with a plane, namely by cutting a circular disc out of stiff paper and pressing it against the inner walls of the globe. This can be done readily and accurately. On this disc I can do all the plane geometry constructions I want. I can also drill a hole in the middle of it a run a stick through it perpendicularly. This stick I can extend to a diameter of the sphere and bisect it to find the midpoint. This seems to me a workable and useful way of finding the midpoint of a given sphere. Far from being something we cannot do, it is in fact something we can easily do with useful results.
The idea of putting physical plane figures together until they fit arguably has venerable precedent in Greek geometry in the form of the regular polyhedra and even solid angles generally. For the purposes of the Elements such an assumption is not strictly needed, because the 3D construction principles outlined in Sect. 5.2.1 suffice in theory. However, the practical realisation of the regular polyhedra by fitting together polygons immediately suggests itself. The realisation of an intersection of a sphere with a plane by means of a physical disc is arguably no stranger or more foreign to geometry than this most obvious construction of these polyhedra that had a prominent status in Greek geometry. Of course you have to prove that the shapes fit together to form the polyhedra, as Euclid does in the Elements, but Spherics I.1 accomplishes the analogous goal for the intersection discs.
The disc method makes sense for Spherics I.2, but it is not possible to consider it the primary operationalisation of intersecting a sphere with a plane. First of all Spherics I.1 is needed to justify the disc method, but to prove it one needs some operationalisation of the intersection already. Then Spherics I.6, which proves that the circles of intersection are smaller the further the plane is from the midpoint of the sphere, makes perfect sense, and is a natural continuation of Spherics I.1, if we conceptualise the intersections using the pen-on-a-string method, but would have a strange interpretation if we took the cutout discs as the fundamental meaning of intersections. But most importantly, Spherics I.18, which finds the diameter of a given intersection circle, cannot be made operationally coherent using the disc operationalisation as far as I can see, since the proof depends on the intersection being operationally available to us, which presupposes our ability to produce it and hence that we could already produce the diameter, which is the goal of the problem. With the pen-on-a-string operationalisation instead, this makes perfect sense. This example goes to show that it is no trivial matter for a particular operationalisation of fundamental concepts of geometry to be consistent with the manner in which the theory is developed.
5.4 Sections of Solids
There are some indications that Greek geometers saw conic sections as part of a broader class of sections of various kinds of solids. Thus Eutocius says that “solid loci have obtained their name from the fact that the lines used in the solution of problems regarding them have their origin in the section of solids, for example the sections of the cone and several others.”Footnote 83 Above I have given an operational reconstruction of how Greek geometers could have viewed sections of cylinders and tori (Sect. 4.2.1), cones (Sect. 4.4.2), and spheres (Sect. 5.3). I have interpreted all of these cases in a unified manner. In all cases, there is no actual solid present. Rather, the solid is a way of speaking about the set of all positions of a line or point moving subject to a particular restriction. From this point of view, the policy (alluded to by Eutocius) of seeking solutions to problems in terms of sections of solids makes perfect sense. Without this interpretation, it is baffling why sections of solids should be accepted as primitive construction operations. But the operationalist interpretation, in which a solid is merely a shorthand for a moving instrument, makes this a natural and unified class of constructions, just as Eutocius suggests.
A lost work by Perseus on sections of a torus fits into this tradition (Heath, 1981b, 203–206; Proclus, 1970, 91). Perseus evidently considered all sections of a torus obtained by intersecting it with a plane parallel to its symmetry axis (that is to say, a vertical plane if the torus is lying flat on the ground). Such sections are indeed readily operationalised in the manner of Sect. 4.2.1. (Let l be the torus axis, and let R be the radius of the torus hole, and r the radius of the torus ring. Attach a stick \(\rho\) to l that can rotate around l while always remaining perpendicular to l. On \(\rho\), at a distance \(R+r\) from l, attach another stick of length r, whose other endpoint can move in the plane of l and \(\rho\). Let P be the non-attached end of this second stick. As \(\rho\) rotates around l, and P is kept in contact with a vertical plane, P will trace a toric section on that plane.) Thus Perseus’s work fits naturally into the operationalist tradition as I have reconstructed it.
5.5 Theories of Numbers and Magnitudes
“Euclid’s arithmetic is hardly less ‘active’ than his geometry” (Mueller, 1981, 60). “One will not find in Euclidean arithmetic any essentially nonconstructive arguments or assertions” (Mueller, 1981, 77). Euclid’s more general and abstract theory of magnitudes, however, is more problematic. Some have argued that aspects of it betray “evidence of Euclid’s adherence to a constructive point of view” (Mueller, 1981, 127, who rejects this view), while others have identified non-constructive assumptions in these parts of the Elements (Mueller, 1981, 122–128, 232). I shall not go into these issues. It may indeed be that the theory of magnitudes should be seen as a somewhat separate research track in Greek mathematics that did not concern itself as much with operationalist considerations. Even if that were so, I do not believe that undermines the fundamental significance of the operationalist point of view in geometry. Indeed, the theory of magnitudes was most likely the most recent theoretical development Euclid included in the Elements, and it makes sense that mathematicians would have focussed on achieving the main goals of the theory first, and provisionally postponed some foundational issues. Therefore, in my view, it is impossible to argue convincingly against the importance of operationalism in Greek geometry overall based on certain possibly non-constructive particulars in these parts of the Elements.
It is well known that Greek mathematicians studiously avoided speaking of infinities, and instead used cautious finitistic circumlocutions, surely for reasons of foundational rigour. The method of exhaustion is exemplary in this regard. So is Elements IX.20, which is often paraphrased as proving the infinitude of primes, while strictly speaking proving rather that any finite list of relatively prime numbers can be expanded into a larger list of relatively prime numbers.
A comparable form of argument occurs in Zenodorus’s proof that the circle has greater area than any polygon of the same perimeter (Heath, 1981b, 207–212; Thomas, 1941, 386–395; Blåsjö 2005). Acerbi maintains that this work exhibits non-constructive tendencies:
Nonconstructive assumptions are frequently made in Greek geometry. An interesting example comes from the tract On Isoperimetric Figures. The main theorem, namely, that a regular polygon in greater than a nonregular polygon isoperimetric to it and having the same number of sides, is proved by a sort of “local symmetrization.” One assumes that the maximal polygon is neither equilateral nor equiangular and drives this assumption to contradiction by showing how to construct, by making two adjacent sides or two angles equal, a greater isoperimetric polygon. The problem lies in the fact that the existence of a maximal polygon is posited without proof.Footnote 84
I disagree. Nothing in the logic of Zenodorus’s arguments rests in any essential way on anything non-constructive. The proofs do not depend on the existence of a maximal polygon. Instead they prove that any given non-regular polygon can be improved by symmetrisation, and hence cannot be maximal (just as Elements IX.20 proves that a finite list of primes cannot be complete). This is a perfectly constructive result. There is no need to formulate this as a proof by contradiction that “the” maximal polygon cannot be irregular. Doing so adds no new insight to the constructive formulation to the problem, and only needless inserts an existence assumption. The surviving paraphrase of Zenodorus’s lost original does explicitly refer to the maximal polygon, and hence makes precisely this avoidable assumption. But we do not know what Zenodorus’s own formulations were. Just as Elements IX.20 is often paraphrased as “there are infinitely many primes,” so also Zenodorus’s theorems may have been stated in a similarly sloppy form by writers (whether Zenodorus himself or someone later reporting on his work) who were focussed on other things than systematic foundations on these occasions. But that is a cosmetic matter. The fact remains that all of Zenodorus’s results and proofs are readily formulated in impeccably constructivist terms, following obvious and well-known precedent in Euclid. Therefore they cannot, in my opinion, be used to infer non-constructivist commitments. In any case it is interesting that Acerbi, when trying to argue that Greek mathematics was non-constructivist, repeatedly relies on this one example whose non-constructivist element is superficial and readily removed.
Perhaps I may be permitted to add a further speculation on the subject of number theory. To produce a list of primes, one may start with a list of the integers and systematically cross out all numbers divisible by 2, then all divisible by 3, and so on. This elementary idea is known as “the sieve of Eratosthenes.” But surely it is much too basic to have been unnoticed before Eratosthenes, who lived after Euclid, meaning after Greek number theory had reached a refined state. We know of Eratosthenes’s work on this only indirectly, through the much later and much less sophisticated Nicomachus. Indeed Nicomachus does not say that Eratosthenes discovered the algorithm but only that he was the one who likened it to a sieve (Nicomachus, 1926, 204), which fits our assumption that Eratosthenes surely was not the first to notice this way of generating primes. Nevertheless one would think Eratosthenes’s name became attached to this idea for a reason. Presumably he did more with this algorithm than merely point out that it was reminiscent of a sieve.
Could it be that Eratosthenes proposed the sieve as an operationalist definition of prime numbers, and organised the foundations of number theory on this basis (just as his cube duplication is operational, as we saw in Sect. 4.2.4)? Euclid’s definition of a prime number—“a prime number is that which is measured by a unit alone” (Elements, Definition VII.11)—is not immediately operational, but the sieve of Eratosthenes can be seen as an explication of an operationalisation implicit in it. Hence the sieve of Eratosthenes can be linked to the broader operationalist foundational program. This could potentially explain why an excellent mathematician such as Eratosthenes would have concerned himself with such a seemingly trivial idea.
This hypothesis about the sieve of Eratosthenes is of course sheer speculation. The historical record is much too thin on this point to do anything but speculate wildly. Nevertheless it is an occasion to reiterate the operationalist principle that mathematics should deal with objects specified as “the thing you get when you \(\ldots\)” rather than “the thing with the property that \(\ldots\)”—the sieve of Eratosthenes is indeed a way of bringing prime numbers from the latter realm to the former.
5.6 Astronomy
In astronomy, Greek mathematicians worked extensively with epicyclic curves to model planetary orbits. Such curves can readily be used to trisect an angle.Footnote 85 In my view it is unlikely that Greek mathematicians failed to realise this. Much more likely is that we do not find any epicyclic solutions in the surviving record of angle trisections because such a solution would have been regarded as clearly less satisfactory than the other available options. Epicyclic curves are indeed operationally highly dubious, just like the plain cycloid (cf. Sect. 4.5.4). So, from an operational point of view, it makes perfect sense that the Greeks would think of epicyclic curves as excellent for astronomy but unacceptable for foundational geometrical questions. On other accounts of the classical problem tradition, however, this fact becomes more of a mystery.
Epicyclic curves clearly had many advantages. Their definition is clear and definite. They are composed of nothing but circular motions, and hence can be construed as closely related to the Euclidean compass. They were also regarded as particularly natural and appropriate for fundamental natural processes.Footnote 86 Furthermore, epicyclic curves were eminently susceptible to calculation (namely trigonometry), as the astronomical tradition demonstrates.
It is telling that epicyclic curves were still not used to trisect angles, despite these clear and clearly recognised advantages. Evidently, the Greeks strived for something else with the angle trisection enterprise. The standards they used to assess solutions to the classical construction problems evidently included essential desiderata beyond the palpable advantages of the epicyclic curves that they were so happy to embrace in astronomy. The operationalist interpretation makes sense of this, by taking the construction tradition to be entirely focussed on the foundational legitimation of the certainty of theorem-proof geometrical reasoning. It is natural that the criteria of construction in this context will be different from those in applied subjects.Footnote 87 Others have tried to explain the purpose of the classical construction problems by appeal to their applicability, to the need for explicit and workable curve descriptions, or the need to represent geometric entities in the imagination (Sect. 4.1.1). But none of these interpretations explain why different curves should be accepted in astronomy than in attempts to solve the classical construction problems.
5.7 Pythagorean Mathematics
According to many accounts—both ancient and modern—“the Pythagoreans” played a significant part in the early history of Greek geometry. But little is known for certain about this early period. Burkert gave an authoritative and widely accepted argument that “the apparently ancient reports of the importance of Pythagoras and his pupils in laying the foundations of mathematics crumble on touch” (Burkert, 1972, 415). However, the operationalist interpretation of the Greek geometrical tradition suggests a somewhat different perspective. When Burkert speaks of “the foundations of mathematics,” he takes for granted the traditional view that a core pillar of Greek geometry was its Platonist detachment from the physical world. According to this view, “Greek geometry assumed its final form in the context of [Plato’s] Academy \(\ldots\) after Plato had \(\ldots\) fixed its position as a discipline of pure thought” (Burkert, 1972, 422). Operationalism of course denies this. According to the operationalist reading, a Platonic emphasis on “pure thought” and detachment from physicality is not the “final form” of Greek geometry, but rather a philosophical aberration that is in some ways out of touch with the point of view of the ancient mathematicians themselves.
Indeed, it is striking that Burkert’s key arguments against Pythagoras’s mathematical significance are really arguments that he did not advocate a proto-Platonist philosophy of mathematics. Burkert’s overall thesis is that “that which was later regarded as the philosophy of Pythagoras had its roots in the school of Plato” (Burkert, 1972, preface). And indeed he proves convincingly that there was a clear tendency to distort history in this way in Platonic sources that is not consistent with more reliable sources outside this tradition. For example, Burkert shows that when Proclus mentions Pythagoras in his “catalogue of geometers,” and attributes to him “a nonmaterialistic procedure” in mathematics, this, unlike the rest of the catalogue of geometers, is not based on the highly credible Eudemus. Instead it is copied from Iamblichus, i.e., from the biased Platonic tradition (Burkert, 1972, 409–411). (From this it does not follow, as Burkert tries to argue, that Eudemus did not mention Pythagoras as a geometer. It follows only that Eudemus in this place likely did not associate Pythagoras with proto-Platonic views. This is enough to give Proclus the motivation to supplement his account with phrases from Iamblichus, even if Eudemus had mentioned Pythagoras in the original.) Burkert also observes that “Aristotle [says] expressly of the Pythagoreans [that] ‘they apply their propositions to bodies’—bringing out the distinction, in this regard, between them and all genuine Platonists” (Burkert, 1972, 409). Eudemus and Aristotle are clearly much more credible than the much later, more biased, and less intellectually accomplished Iamblichus and Proclus.
Thus Burkert’s arguments that Pythagoras’s alleged proto-Platonist philosophy of geometry is a fabrication of biased sources are quite convincing. However, it does not follow from this that the Pythagoreans did not take a profound theoretical and foundational interest in geometry altogether. Burkert tends to conflate these two conclusions, because he sees no alternative path to theoretical mathematics than through Platonic-style abstraction and detachment from physical considerations. Burkert believes that early work on geometrical constructions “is still not doing mathematics for its own sake”; rather, the “discovery of pure theory” was a later “accomplishment” (Burkert, 1972, 424). But operationalism rejects such a dichotomy between constructions and “pure theory.” Instead, operationalism articulates a sense in which earlier mathematicians, such as the Pythagoreans, could have made profound and foundationally sophisticated contributions while vehemently rejecting Platonising tendencies in the philosophy of geometry.
Indeed, when going beyond his convincing case against Pythagoras the Platonist, to the more general case of trying to minimise the significance of Pythagoras and his followers in the history of geometry, Burkert find himself on the back foot. He is forced to try to explain away Aristotle’s compelling statement that “the so-called Pythagoreans were the first to take up mathematics; they advanced this study, and having been brought up in it they thought its principles were the principles of all things” (Burkert, 1972, 412). Burkert’s thesis leaves him little choice but to dismiss the centrality of mathematics implied by this statement as “a psychological conjecture of Aristotle, which the historian is not obliged to accept” (Burkert, 1972, 414). That Proclus was wrong is plausible enough, but having to postulate that Aristotle was wrong comes at a considerably higher cost. And while Burkert was able to discredit Proclus’s mention of Pythagoras in the catalogue of geometers, he cannot deny that numerous attributions of mathematical discoveries to Pythagoreans made by Proclus are indeed based on Eudemus and hence credible (Burkert, 1972, 449–450). Thus even Burkert must admit that “Pythagoreans made significant contributions to the development of Greek geometry.” Yet he hastens to add: “but the thesis of the Pythagorean foundation of Greek geometry cannot stand” (Burkert, 1972, 465).
I do not make any claims of my own regarding the Pythagorean mathematical tradition.Footnote 88 My point is only to observe that Burkert’s argument is based on tacitly assuming a monolithic conception of what “the foundations of Greek geometry” consisted in. The operationalist reading of Greek geometry problematises this assumption. It shows that one cannot simply take for granted that “the foundations of geometry” means what modern authors think it should mean. Operationalism offers an alternative vision, according to which much early Greek geometry may very well have been eminently foundational, but in a sense different from that commonly assumed by modern observers. This at least raises the possibility that early traditions such as that of the Pythagoreans may have been more foundationally significant than Burkert’s argument admits.
6 Conclusion
Making is the idée fixe of Greek geometry. In Euclid’s Elements, the first postulates and the first propositions are about making; in his Data, even the first definition is about what can be made. The three most persistent research problems in Greek geometry are about making something.
I have argued that Greek geometers had a grand plan behind this—a coherent, deliberate philosophy that makes perfect sense of this entire program of research. Rigour, to the Greeks, meant operationalism, and for good reason. Operationalism safeguards mathematics against a multitude of plagues. It prevents us from reasoning about entities and concepts that are inconsistent, incoherent, non-existent, or imaginary. It grounds mathematics in reality and gives a straightforward account of what geometry is and what geometrical statements mean.
Mathematicians would have had every reason to articulate such a philosophy. Greek antiquity was an age of sceptical philosophical attacks. Mathematics would have found itself under fire, and its enemies were no fools. The logic and rigour of mathematical proofs were by and large hugely impressive. Yet it had a conspicuous Achilles heel: a veritable self-destruct button that could bring the entire edifice crashing down at the slightest trigger. For if there was any way an inconsistency could slip into mathematical reasoning undetected, then everything that followed would immediately be rendered logically worthless. What guarantee do we have that this will never happen, or indeed that it has not already happened?
This vulnerability pertains especially to the way objects are introduced into mathematical discourse. It is safe to say “let ABC be a right-angled triangle,” but if you say “let ABC be a triangle with two right angles” or “let ABC be a right-angle triangle with side lengths 4, 7, and 9” then you have introduced an inconsistency and all is lost. Geometry needs to systematically guarantee that it could never commit an error of this type. In other words, it needs a meticulous gatekeeping policy that only allows the most carefully vetted entities to enter mathematical discourse.
Constructions are the answer to this problem. By insisting that geometry only speaks of entities that are constructed, the mathematician immediately knocks the legs out under boogeymen examples of inconsistent objects such as the superright triangle. In fact, more generally, constructions guarantee the consistency of geometrical entities by subsuming geometry in physical experience. In the 19th century, hyperbolic geometry was proved consistent—or rather equiconsistent with Euclidean geometry—when it was shown that models of it could be constructed in Euclidean space. Hyperbolic geometry thereby inherited the credibility of the ambient Euclidean geometry, whose consistency was, if not proven, at least testified by extensive experience. In the same way, when ancient mathematicians founded geometry on physical constructions, they made geometry equiconsistent with metrical physical experience. Geometry thereby inherited the consistency credibility of physical experience: that is to say, believing that there is an inconsistency in geometry is tantamount to believing that there are inconsistencies in physical experience itself, such as a ruler being both twice as long and also equally long as another.
It is clearly essential for this argument that construction really means actual, physically realisable construction. It is not very essential to this argument, however, that these constructions can be practically executed with significant precision. Attention to concrete realisability in principle is still a severe form of intellectual hygiene that rules out a great many possible sources of inconsistency and hidden assumptions that could easily creep into a system with less exacting standards.
Constructions are essential not only for consistency but also for the careful monitoring of potential hidden assumptions. It may seem innocent enough to assume that a square exists, or that, given any two lines and a point somewhere between them, one can draw a line through that point cutting both lines. In fact, however, both of these assumptions depend on the parallel postulate. This hidden dependency is not obvious if one introduces these objects merely by decree or “thought construction.” Explicating concrete steps and postulates corresponding to physical operations, on the other hand, forces rigorous attention to the underlying assumptions.
Constructions can support these foundational purposes only if they are explicable in terms of concrete, practical execution. If we loosen this requirement, and allow “constructions” that are merely mentally imagined, then the strength of all of these arguments is immediately null and void. The nebulous notion of constructions as merely some form of thought experiment does not have anything like the rigour to answer the foundational challenges of consistency and assumption control. Insisting on physical realisability is a way of taking the vagueness and imprecision of our imagination and intuition out of the equation, and instead grounding the concept of constructions in what is concretely knowable and testable in actual experience.
Salient aspects of the Greek geometrical tradition are best understood in these terms, I claim. To Euclid, constructions always come before theorems. Mathematics about what is not constructed is not properly mathematics at all, according to operationalism, for it is wide open to sceptical attacks and can readily succumb to paradox or self-contradiction at any moment. Greek geometers were determined to carry this program through for higher geometry that goes beyond the scope of Euclid’s ruler and compass. The three classical construction problems are little but a thinly veiled research program to do exactly this: that is to say, to find specific, concrete constructions that enlarge the scope of geometry while remaining as true as possible to the philosophical principles of operationalism.
Those are the main theses I have argued for in this work. On many points this is a radical departure from established interpretations of Greek geometry. The strength of my case is in the big picture. The most convincing support for my interpretations comes not from detailed source evidence but how each part fits into a coherent whole. While no one part of my revisionist take is beyond question on its own, the fact that I can sustain my perspective across a wide range of case studies lends indirect support to specific claims as well.
I may well have too much faith in this form of evidence, but then again other scholars may have too little. It is true that next to nothing of the operationalist philosophy that I attribute to Greek geometers is actually explicitly documented in any surviving ancient source. But then again there is virtually no direct documentation of the philosophical views of the great mathematicians of antiquity altogether, whether operationalist or otherwise. As for sources that do speak of the philosophy of mathematics, my interpretation largely goes against them, if anything. But those sources are almost exclusively written by philosophical authors. People like Plato, Aristotle, and Proclus should not be taken to speak for the mathematicians any more than Hegel and Wittgenstein are good guides to the philosophy of mathematics of Hilbert.
And if philosophically explicit sources asserting the key principles of operationalism is what you want, then you have it in abundance in the 17th century. There it is stated by mathematicians, and not any mathematicians. Viète, Descartes, Huygens, Leibniz, etc.: these were the closest peers of the Greek mathematicians the world has ever seen before or since. Unlike Plato, Aristotle, and Proclus, they lived and breathed geometry and were technically excellent mathematicians. Unlike, arguably, Pappus, Eutocius, and medieval Arabic and Renaissance European geometers, they perceptively and creatively built on the ancient problem tradition in their own work. These are the people who did not hesitate to ascribe operationalist principles to the ancients. The word of interpreters of such credentials should not be dismissed lightly, in my opinion.
As for the ancient Greek mathematicians themselves, they are silent on philosophical issues as far as surviving sources are concerned. But it is impossible to deny, in my opinion, that they must have had a sophisticated appreciation of the kinds of foundational issues that I have discussed. How could their studious constructive-foundational pedantry have stemmed from any other source? What else could have driven them to fixate manically on two or three construction problems for centuries?
If my hypothetical reconstruction is not accepted, the Greek tradition is full of paradoxes. How can Euclid obsessively reduce everything to ruler and compass in Elements I.1–3 only to immediately turn to a completely antithetical method in I.4? How can the Greeks give pride of place to the three classical construction problems, only to then propose solutions to these problems by means of entities that are not themselves constructed such as conics or the intersecting surfaces of Archytas? If I can simply “let” surfaces and their intersections come into being by decree, then why can I not just “let” an angle be the third of another? How can constructions by physical instruments and motions be considered an unequivocally essential aspect of a solution by half of the first-rate mathematicians who worked on the three classical problems, only for it to be entirely disregarded by the other half? None of this makes any sense. My operationalist reconstruction of the Greek geometrical tradition solves these glaring interpretative problems. My reconstruction is speculative, yes. But it is also the only hypothesis that does not force us to attribute rampant incoherence to the philosophy of Greek geometry.
Notes
Interestingly, operationalism can have advantages in such areas as well, as we shall see some examples of below. But I propose that this should be regarded as a bonus side effect rather than a primary intent.
The existence of a square implies the existence of similar triangles of arbitrary magnitude, which Wallis showed implies the parallel postulate (Fauvel & Gray, 1987, §16.A1). “Square” here means a square in the sense of Euclid’s Definition 22: an equilateral quadrilateral with four right angles.
Aristotle, Posterior Analytics, 76a, (Heath, 1949, 50).
Aristotle, Posterior Analytics, 92b, (Heath, 1949, 70).
This example occurs in a 16th-century geometry textbook (Heitholt & Sauer, 2019, 183).
Cf. Euclid’s definition of a triangle, Elements, Definition I.19. On this idea more generally cf. also Knorr (1975, 139): constructions are fundamentally “what the ancients mean by mathematical knowledge.”
Cf. Elements, Definition I.15.
Cf. Elements, Common Notion 4. This is arguably what equality means, in its most fundamental sense. It is of course not a way to prove that two things are equal, because a proof must establish the result by exact means from first principles. Euclid later develops a more general notion of equality, which allows for example two triangles of different shapes to be “equal” (in area). But this extended notion of equality is derived from the earlier, primitive one.
Cf. Elements, Definition I.10.
Cf. Elements, IX.20.
One may feel that, if Euclid had wanted to emphasise this way of interpreting the right-angle postulate, he could have made this more explicit for instance by saying any two right angles in place of all right angles. But he may have taken this kind of synonymity for granted. For example, in Elements XI.18, he speaks of “all” the planes containing a given line, but then, for the purposes of the proof, immediately operationalises this as any one (arbitrarily drawn) plane containing that line.
Einstein repeatedly stated in many places that he was influenced by Mach. For a clear and explicit example of operationalist principles in action in his work, see for instance the operational definition of simultaneity—the linchpin of the entire theory—given in Einstein (1916, Section VIII).
This way of reading Euclidean propositions is similar to that of Panza (2011, 57–58).
The conception of a proof as a refutation of a sceptic fits the Greek context well. Extracting concessions from a determined opponent in incremental steps is the main mode of philosophical discourse in many Socratic dialogues, which are in this respect representative of the broader philosophical culture.
A more reconciliatory reading of this passage would be that Plato is not putting himself in opposition to the geometers but merely lamenting the necessity, due to human limitations, of speaking in practical language to represent abstract ideas. Such a reading is advanced by Panza (2012, 67).
The same idea, but with a wall in place of a road, is also mentioned by Sextus Empiricus, who attributes it to Aristotle (Bett and Empiricus, 2018, 168–169).
Which can be construed as comparable to the assumption that the Russel set R (Sect. 2.2.3) exists and that \(R\in R\) must be either true or false.
Based on text searches in Fitzpatrick (2008).
My view on this is similar to that of Panza (2011, §2.1).
E.g., Elements I: 4, 6, 7, 8, 14, 26, 27, 29.
The dichotomy between constructions and proofs by contradiction is emphasised by e.g. Sidoli (2018b, 407–415). For an interpretation of diagrams in proofs by contradiction that instead deemphasises their exceptional status, see the argument in Manders (2008b, 111) that “there is \(\ldots\) no special reason to doubt the cogency of diagram-based reasoning in reductio proof.”
Nor does it appear that he was overly stingy in trying to keep axioms to a minimum, judging by the fact that various later commentators argued that his fourth and fifth postulates were avoidable.
For this reason, Heath’s claim that “the phraseology \(\ldots\) Euclid employs [in I.4] \(\ldots\) leaves no room for doubt that he regarded one figure as actually moved and placed upon the other” (Heath, 1956, I.225) should be rejected. Heath’s interpretation is criticised on linguistic and other grounds in Sidoli (2018b, 446).
Zeuthen’s thesis has been reinvented a number of times. Evidently without being aware of Zeuthen’s work, Wagner (1983) proposed the same interpretation. On this point Wagner is exactly right, in my view. But his short notes leaves much to be desired in terms of follow-through, for he says nothing about I.22 and I.23, which, as we shall see, are of considerable and obvious interpretative importance. Thus Wagner is puzzled as to why Euclid “chose to omit the proof” of the “triangle reproduction theorem” Wagner feels is implicitly assumed in I.4 and I.8 (69), when in fact Euclid did not omit this but rather proved it at length in I.22 and I.23.
Again apparently independently, Shabel (2003, 33) likewise proposed that Euclid’s superposition proofs are not based on motion but on reconstruction. Unlike Wagner, but like Zeuthen (and on the same grounds), Shabel also concludes that Euclid’s reasoning is circular.
It is unfortunate that Zeuthen’s account has been forgotten, especially since it is more sophisticated than the more often cited article by Wagner. Vitrac (1990, 297), Saito (2009, 809, 2018b, §5.3) all discuss what is in fact Zeuthen’s thesis without being aware that he proposed it.
Heath (1981a, 218). This great prominence of the classical construction problems in Greek geometry is generally accepted; a case in point being Knorr (1975). A minority dissenting view is Acerbi et al. (2018, 277), who suggests that this impression may be amplified by “the compilatory attitude of the late commentators”: “compiling many solutions to the same problem creates a false impression of a mass effort.” In my view, the apparent centrality of the classical construction problems cannot be explained away in this manner. It is one of my key overall points in this work to argue that the classical construction problems form a natural whole with the constructivist tendencies that are inextricably embedded in all aspects of Greek geometry.
Knorr (1975, 22) argues for such an interpretation of the story that the Delian oracle implored the doubling of a cubical altar.
Proclus (1970, 64), building on the Platonic idea he outlines earlier (37, 44) that learning is recollection, or the bringing out of what was already latently there but which our minds needed some stimulus bring into consciousness.
Sefrin-Weis (2010) in particular is a useful starting point for this literature. Naturally, the solutions in the table without author attribution are especially difficult to place chronologically.
Assuming that the standard chronology is more or less accurate. Knorr (1975, 81) argues that the quadratrix solutions have been dated mistakenly early, and hence that the entire tradition got going later than this. At the other end, it is possible that Diocles was active a few decades earlier (Knorr, 1975, 234), thereby shrinking the period of prime activity from that side as well.
Van der Waerden (1975, 135–136) gives a high estimate of the level and sophistication of Hippocrates’s mathematics.
Knorr (1989, 109–110). See also Masià (2016) for a recent study of Archytas’s solution and a survey of other interpretations, which, however, is not interested in our core concern, the issue of mechanical generation, as it explicitly states (197). Another recent study claims that “Archytas’ \(\ldots\) heavy reliance on motion” was an “anomaly” “alien to the later development of Greek geometry” (Menn, 2015, 408). This is not true, as Table 4 shows.
The source does not say unequivocally one way or the other whether the operation should be continuous, but it does propose a way of ensuring that \(l_{1}\) and \(l_{3}\) “remain throughout parallel” (Netz, 2004, 273), namely by a fourth ruler, \(l_{4}\), that cuts across \(l_{1}\) and \(l_{3}\) to complete a rectangle. But this cannot be done in a very straightforward way since side lengths of the rectangle should remain variable. We could do it with something like moveable square pegs through the holes where \(l_{4}\) intersect \(l_{1}\) and \(l_{3}\), but this seems awkward for continuous operation. One may also try to achieve perpendicularity by an L-shaped constraint, one leg of which is attached to \(l_{3}\) and the other lying against \(l_{2}\). But it is problematic to assume that that entire leg will remain in contact with \(l_{2}\) throughout the motion.
Eutocius (Netz, 2004, 278) rightly points out that Philon’s original version is easier to implement in practice. One conceivable sense in which Heron’s variant could serve a purpose might be if the construction is not taking place on a sheet of paper, so that the circle cannot be drawn. This could perhaps be relevant in the engineering contexts that Heron is interested in.
See Marsden (1971, 41, 111) for their accounts and translations of the full treatises.
The final configuration is the same as that of Fig. 10. Eutocius formulates the solution in terms of a circle centered at the midpoint of the rectangle such that the chord between its axis intercepts cuts through the corner of the rectangle. This is obviously equivalent to Fig. 10, only it would seem to suggest that the solution should be found by trying different radii of the circle instead of different inclinations of the ruler through the corner point—a pointless distinction. But Eutocius then says that the circle in question should be found by trying different positions of a ruler through the corner point, which obviously erases any difference with Heron’s construction, if one could even speak of there having been any to begin with.
As we see, the construction does not directly solve the problem, i.e. it does not produce \(\root 3 \of {2}\) directly, but rather produces a scaled version of the actual solution. So the construction must be followed by an extra scaling step. This is an unaesthetic aspect of Diocles’s solution. However, it is not theoretically problematic since the scaling can be done by Euclidean means.
Conceivably, one could argue that it would make a bit more sense if we need to extract two mean proportionals between various different givens all the time, not just \(\root 3 \of {2}\) once. Then one could produce a large number of points on the cissoid once and for all, and use it as a nomographic tool many times after that. But there is no indication that such a usage was intended, and the practical value of this would be very questionable. One might imagine that the use of a single fixed curve saves time and effort compared to many of the previous proposals we have seen which require separate constructions for each case. But the cost of using a single curve is quite high. Each such application of the cissoid would require pre- and post-processing, so to speak, in the form of two scalings. First one must scale “into” the figure, since the ratio 2 : 1 in our figure needs to be a : b generally to find the two mean proportionals of given segments a and b, and the radius is fixed if we are using a fixed cissoid for all cases. Then one must scale the answer “out of” the figure, because of the issue with the scaling factor k. Since these auxiliary constructions are needed anyway, it would be hard to argue that the use of a fixed cissoid is qualitatively preferable to for instance the solution by Philon that, although unlike the fixed cissoid it requires the approximate construction itself to be carried out in each case, is more directly adapted to the givens (in Philon’s case, working directly with an a : b rectangle).
One brief phrase in Eutocius’s text hints at the interpolation of the curve from points, saying that the defining property of the cissoid determines points on it, “to which we join lines (by the application of a ruler [from one point to its neighbor]) – and then we shall have a certain line [i.e., the cissoid] figured in the circle” (Netz, 2004, 280). Or in an alternative translation: “If we place our ruler against these points and join them by straight lines, we will have a certain line drawn in the circle” (Toomer, 1976, 199). Eutocius does call the pointwise process “continuous” (Netz, 2004, 280, 283; Toomer, 1976, 201) though this seems to mean merely sequential.
In other words, it is effectively a derivation of the “equation” for the curve traced by the linkage. Indeed, by rewriting \(A\Theta : \Theta Z = \Theta Z : \Theta B = \Theta B : \Theta H\) as \((r+x) : \Theta Z = \Theta Z : (r-x) = (r-x) : y\) we get the equation for the cissoid \(y^2 (r + x) = (r - x)^3\).
Neusis is sometimes described as a “marked ruler” construction in contrast with the unmarked straightedge of Euclid. But this is a misleading way of putting it. The difficulty with neusis lies entirely in the trial-and-error placement procedure discussed below, not in the marking of the ruler. Arguably, Elements I.2–3 effectively show that we might as well consider even the Euclidean straightedge to be marked or markable, so marking is a non-issue.
This was surely well understood in antiquity. One may even speculate that it could be why Proclus speaks of “the quadratrices of Hippias” in the plural (Heath, 1981a, 225–226).
Hogendijk (1985, 36), Martines (2014, 297) and Rashed (2003). At least one of these authors, al-Sijzi, attached foundational importance to its single-motion character, contrasting this with “non-measurable” curves such as the cylindrical helix which is generated by double motion (Rashed, 2003, 31–34).
“The parabola is drawn by the compass invented by our teacher, Isidore the Milesian mechanician” (Netz, 2004, 290). This particular attribution would place the invention of the conic compass centuries later than my hypothesis would have it, but the author of this remark (which appears to be not Eutocius himself but a later editor Netz (2004, 290) and Knorr (1989, 99)] could likely have had imperfect knowledge of the earlier tradition; or been motivated more by loyalty to their teacher than an objective commitment to historical accuracy; or knowledge of the conic compass was lost and then independently rediscovered by Isidore (such independent discovery would speak to the naturalness of the idea of the conic compass). When al-Sijzi introduces the conic compass, he mentions Eutocius’s allusion as a source of inspiration (Rashed, 2004, 284).
All of these results can be verified using the method explained in Blåsjö (2016, 287).
This connection was first suggested, very briefly, in Blåsjö (2016, 287).
Apollonius’s choice of cones is not the same as those I used above, since he does not place the vertex of the cone perpendicularly above the starting points of the conics he is tracing. It is possible that the early theory of conics used the simplest case of a perpendicular starting point, while Apollonius desired to abstract away from this for the sake of generality. Indeed, Apollonius’s constructions produce not only one cone but an infinite family of cones that solve each construction problem.
This is similar to the point I made above in Sect. 4.2.6 with respect to the use of the cissoid in the same treatise.
Knorr (1975, 84–85) also argues that the quadratrix was first devised for angle division.
On spirals, Definition 1 and Proposition 14 respectively (Archimedes, 2002, 165, 167).
This construction was described by Huygens (Oeuvres, XI, 216).
As Crippa (2014, 95) notes, a number of later commentators tried to address this step, without reaching a satisfactory solution.
Leibniz, for one, seems to have considered this the method implied by Archimedes (Crippa, 2014, 416).
This way of producing a cylindrical helix is discussed by Heron (Mancosu & Arana, 2010, 414–415).
Regarding the operationalism of three-dimensional geometry in general, see Sect. 5.2.1.
This was observed for instance by Leonardo da Vinci (Magazu et al., 2019, 765).
Heath (1897, 233). Archimedes contrasts this with his quadrature of the parabola. In no surviving source does he (or any other of the great Greek geometers) claim to have solved the circle quadrature problem.
As indicated in the column for the degree of problem solves. Cf. Sect. 4.1.2. The circle quadrature solutions (indicated as “degree \(\infty\)” since the problem is transcendental) are operationally even worse than the table conveys, for reasons discussed above.
In favour of the plausibility that Greek geometers really did build their machines, one may mention not only the explicit physicality of several sources, but also the rich and longstanding connection between mathematics and engineering in antiquity. Archimedes famously engaged in a range of engineering projects (Dijksterhuis, 1987, 21–29) and Archytas reportedly constructed “a wooden dove that flew” [Berryman (2009, 96) that is, some kind of automaton contraption that used pneumatic or other mechanical principles to imitate a living bird], for example.
This conclusion has also been reached independently by modern operationalist philosophers of science, on grounds that have nothing to do with ancient geometry: “Concepts which are to be of value to the factual sciences must be definable by operations which are (1) logically consistent; (2) sufficiently definite (if possible, quantitatively precise); (3) empirically rooted, i.e., by procedural and, finally, ostensive links with the observable; (4) naturally and, preferably, technically possible; (5) intersubjective and repeatable.” (Feigl, 1945, 258, emphasis added).
Clavius at one point enthusiastically accepted the quadratrix as a solution to the quadrature of the circle and other problems, on the grounds that it could be produced by a pointwise construction—a poorly conceived idea that would not have occurred to anyone with a proper familiarity with the Greek tradition (Mancosu, 1992, 93–96; Bos, 2001, Chapter 9). As Bos shows, Clavius was corrected by Lansbergen and later added qualifications to his claim. Clavius’s error is of the same kind as the unsustainable reasoning attributed to Diocles that I criticised in Sects. 4.2.6 and 4.4.3.
Given p, take x at will, and erect a perpendicular of length y such that \(py=x^{2}\), or in other words \(p:x=x:y\), which is readily done by Elements VI.11. Repeat for many x.
Importantly, in his catalogue of cube duplications (cited in Table 2), Eutocius does not give pointwise constructions of the conics. When he does mention pointwise constructions of conics elsewhere, in his commentary on Apollonius’s Conics, he explicitly frames this as a practice-oriented matter set apart from theory (Knorr, 1989, 83).
Thus in Table 2, T and D should be done by conic sections according to Pappus’s dictum, yet he gives many other kinds of solutions without any further qualms.
Heath (1896, cxxix) agrees with this, and spells out plausible reasons for why Apollonius may have made such a choice in the Conics despite keen awareness and respect for the issue in other contexts.
Heath (1981a, 183, 196). Assuming that this was the intended goal of Hippocrates’s work on the quadrature of lunes.
Or equivalently: three points (join two of them), or two intersecting lines (consider one line and an endpoint of the other).
Definition I.7 says “a plane surface is a surface which lies evenly with the straight lines on itself,” which is as useless as the analogous definition of a straight line as a line “which lies evenly with points on itself” (Definition I.4). This exceedingly vague and useless definition is plausibly a later corruption of the text that was not in Euclid’s original text. Russo (1998, 2004, 320–326) argues convincingly that it is a truncated version of a description given by Heron. According to this hypothesis, Euclid would probably not have defined a straight line at all in the original Elements. Indeed, it is obvious that any theory must involve some undefined terms.
This is XI.3, or if that proof is found too questionable it can be taken as an axiomatic assumption.
See, e.g., Heath 1981a, 416–418) for an overview of Euclid’s constructions of the regular polyhedra.
“The problems in the Spherics were written in such a way that they could be carried out on an actual globe and, hence, must have derived from an interest in producing accurate diagrams” (Sidoli & Saito, 2009, 606). “Although the text is structured as a purely deductive treatise, it was written by and for individuals who used material objects ...[and were interested in] solving problems in spherical geometry by drawing diagrams on a real globe” (Sidoli & Saito, 2009, 607).
“[Solutions to problems in the Spherics generally correspond to] practical operations that would be used in the process of carrying out these constructions on real globes using the basic tools of Greek geometry, a straight edge and compass. ...Many features of Theodosius’s approach ...are best understood by an appeal to such practical considerations” (Sidoli & Saito, 2009, 587). Specifically, the use of a compass to transfer lengths clearly appears implied (Sidoli & Saito, 2009, 589).
Acerbi et al. (2018, 277). The same argument is made in Acerbi (2010b, 96–97). Acerbi continues: “Moreover, the process of ‘local symmetrization’ is not effective: it cannot produce, starting from a given polygon, the maximal (regular) one in a finite number of steps. The approach, then, is eminently non-constructive.” The fact that the symmetrisation process does not terminate in a finite number of steps is irrelevant, just as it is irrelevant that the algorithm used in Elements IX.20 will never produce a complete list of primes. So this is a non-starter of an argument.
For example, in the early 17th century, Etienne Pascal showed how to trisect an angle by the cardioid, a special case of an epicyclic curve (Dudley 1987, 10).
The metaphysical naturalness of uniform circular motion had long been emphasised, e.g. in Plato, Timaeus 34a, and Aristotle, De caelo II.6. Ptolemy, Almagest, IX.2, justifies epicyclic motion by appeal to such arguments.
Another example of this is pointwise construction of parabolas, as discussed in Sect. 4.4.3.
As noted in Sect. 4.1.3, the operationalist reading of Greek mathematics suggests that sophisticated foundational work and articulate philosophy of geometry must have been present in roughly Pythagorean times, i.e., at a somewhat earlier stage than most historians would be inclined to say. But how much of that should be attributed to Pythagoreans is a question I leave open.
References
Acerbi, F. (2008). Euclid’s pseudaria. Archive for History of Exact Sciences, 62(5), 511–551.
Acerbi, F. (2010a). Homeomeric lines in Greek mathematics. Science in Context, 23, 1–37.
Acerbi, F. (2010b). Il silenzio delle sirene: La matematica greca antica. Rome: Carocci.
Acerbi, F. (2011). The language of the Givens: Its forms and its use as a deductive tool in Greek mathematics. Archive for History of Exact Sciences, 65(2), 119–153.
Acerbi, F. (2018). Hellenistic mathematics. In P. T. Keyser & J. Scarborough (Eds.), The Oxford handbook of science and medicine in the classical world. Oxford: Oxford University Press.
Archimedes. (2002). The works of archimedes (T. L. Heath Trans.). Cambridge University Press, 1897; Dover Publications reprint.
Aristotle. (2001). The basic works of aristotle. R. McKeon (Ed.) Random House, 1941; Modern Library paperback edition.
Avigad, J., Dean, E., & Mumma, J. (2009). A formal system for Euclid’s elements. The Review of Symbolic Logic, 2(4), 700–768.
Axworthy, A. (2018). The debate between Peletier and Clavius on superposition. Historia Mathematica, 45(1), 1–38.
Becker, O. (1957). Das Mathematische Denken der Antike. Göttingen: Vandenhoeck & Ruprecht.
Beeson, M. (2016). Constructive geometry and the parallel postulate. The Bulletin of Symbolic Logic, 22(1), 1–104.
Berryman, S. (2009). The mechanical hypothesis in ancient Greek natural philosophy. Cambridge: Cambridge University Press.
Bett, R., & Empiricus, S. (2018). Against those in the disciplines. Oxford: Oxford University Press.
Blåsjö, V. (2005). The isoperimetric problem. American Mathematical Monthly, 112(6), 526–566.
Blåsjö, V. (2016a). How to find the logarithm of any number using nothing but a piece of string. The College Mathematics Journal, 47(2), 95–100.
Blåsjö, V. (2016b). The how and why of constructions in classical geometry. Nieuw Archief voor Wiskunde, Ser. 5, 17(4), 283–291.
Blåsjö, V. (2017). Transcendental curves in the Leibnizian calculus. Amsterdam: Elsevier.
Bos, H. J. M. (1988). Tractional motion and the legitimation of transcendental curves. Centaurus, 31(1), 9–62.
Bos, H. J. M. (2001). Redefining geometrical exactness: Descartes’ transformation of the early modern concept of construction. Berlin: Springer.
Bridgman, P. W. (1927). The logic of modern physics. New York: Macmillan.
Bridgman, P. W. (1952). The nature of some of our physical concepts. New York: Philosophical Library.
Bridgman, P. W. (1955). Reflections of a physicist (2nd ed.). New York: Philosophical Library.
Brouwer, L. E. J. (1975). Over de Grondslagen der Wiskunde, Ph.D. thesis, University of Amsterdam, 1907. Quoted from the translation in L. E. J. Brouwer, Collected Works, I, North-Holland.
Burkert, W. (1972). Lore and science in ancient pythagoreanism. Cambridge: Harvard University Press.
Carman, C. C. (2018). Accounting for overspecification and indifference to visual accuracy in manuscript diagrams: A tentative explanation based on transmission. Historia Mathematica, 45(3), 217–236.
Clifford, W. K. (1886). Lectures and essays. London: Macmillan.
Cohen, M. R., & Drabkin, I. E. (Eds.). (1966). A source book in Greek science. Cambridge: Harvard University Press.
Comte, A. (1830) Cours de philosophie positive (vol. 6, pp. 1830–1842). Paris: Rouen, Bachelier.
Crippa, D. (2014). Impossibility results from geometry to analysis: A study in early modern conceptions of impossibility. Ph.D. thesis, Univeristé Paris Diderot Paris 7.
Cuomo, S. (2000). Pappus of Alexandria and the mathematics of late antiquity. Cambridge: Cambridge University Press.
De Risi, V. (2016). Leibniz on the parallel postulate and the foundations of geometry. Basel: Birkhäuser.
Descartes, R. (1637). La Géométrie. Leiden.
Dijksterhuis, E. J. (1929). De Elementen van Euclides: Deel 1. Groningen: Noordhoff.
Dijksterhuis, E. J. (1987). Archimedes. Princeton: Princeton University Press.
Drabkin, I. E. (1950). Aristotle’s wheel: Notes on the history of a paradox. Osiris, 9, 162–198.
Dudley, U. (1987). A budget of trisections. Berlin: Springer.
Edwards, H. (2005). Essays in constructive mathematics. Berlin: Springer.
Einstein, A. (1916). Relativity: The special and general theory (3rd ed.) (R. W. Lawson, Trans.). Methuen & Co.
Fauvel, J., & Gray, J. (Eds.). (1987). The history of mathematics: A reader. London: Macmillan Education and Open University.
Feigl, H. (1945). Operationism and scientific method. Psychological Review, 52(5), 250–259.
Fitzpatrick, R. (2008). Euclid’s elements of geometry. Morrisville, NC: Lulu. Available at: http://farside.ph.utexas.edu/books/Euclid.
Fowler, D. (1999). The mathematics of Plato’s academy (2nd ed.). Oxford: Oxford University Press.
Galileo, G. (1953). Dialogue concerning the two chief world systems (S. Drake, Trans.). University of California Press.
Hartshorne, R. (2005). Geometry: Euclid and beyond. Berlin: Springer.
Heath, T. L. (1949). Mathematics in Aristotle. Oxford: Oxford University Press.
Heath, T. L. (1956). Euclid: The thirteen books of the elements. Cambridge University Press, 1925. Reprinted by Dover Publications.
Heath, T. L. (1981a). A history of Greek mathematics, Volume I: From thales to Euclid. Oxford: Clarendon Press, 1921. Dover Publications reprint.
Heath, T. L. (1981b). A history of Greek mathematics, volume II: From aristarchus to diophantus. Oxford: Clarendon Press, 1921. Dover Publications reprint.
Heath, T. L. (1896). Apollonius of Perga: Treatise on conic sections. Cambridge: Cambridge University Press.
Heath, T. L. (1897). The works of archimedes (1st ed.)., Dover Publications, 2002 Cambridge: Cambridge University Press.
Heitholt, J., & Sauer, T. (2019). Jakob Köbels Feldmessung: Elementare Fehler oder strategische Vereinfachungen? Mathematische Semesterberichte, 66, 179–202.
Henderson, D. W., & Taimina, D. (2004). Experiencing geometry (3rd ed.). Pearson: Prentice Hall.
Heron, A. (1912). Opera Quae Supersunt Omnia, vol. IV: Heronis Definitiones cum variis collectionibus Heronis quae feruntur Geometrica, Bibliotheca scriptorum Graecorum et Romanorum Teubneriana.
Hilbert, D. (1894). Grundlagen der Geometrie. Lecture notes. Niedersäch- sische Staats- und Universitätsbibliothek, Cod. Ms. Hilbert, 594.
Hintikka, J., & Remes, U. (1974). The method of analysis: Its geometrical origins and its general significance (Vol. XXV)., Studies in the philosophy of science Boston: Reidel.
Hobbes, T. (1845). The English works of Thomas Hobbes of Malmesbury. W. Molesworth (Ed.), (vol. 11). London, 1839–1845.
Hogendijk, J. (1985). Ibn Al-Haytham’s completion of the conics. Berlin: Springer.
Jesseph, D. (2015). Hobbes’s theory of space. In V. De Risi (Ed.), Mathematizing space. Berlin: Springer.
Jones, A. (1986). Pappus of Alexandria: Book 7 of the collection. Berlin: Springer.
Joyce, D. E. (1998). Euclid’s elements. https://mathcs.clarku.edu/~djoyce/elements/elements.html.
Klein, F. (2004). Elementary mathematics from an advanced standpoint: Geometry. Mineola: Dover Publications.
Kline, M. (1972). Mathematical thought from ancient to modern times. Oxford: Oxford University Press.
Knorr, W. R. (1975). The ancient tradition of geometric problems. Basel: Birkhäuser.
Knorr, W. R. (1978). On the early history of axiomatics: The interaction of mathematics and philosophy in Greek antiquity. In J. Hintikka, D. Gruender, & E. Agazzi (Eds.), Theory change, ancient axiomatics, and Galileo’s methodology: : Proceedings of the Pisa conference on the history and philosophy of science (Vol. I, pp. 145–186). Dordrecht-Boston: Reidel.
Knorr, W. R. (1982). The hyperbola-construction in the conics, Book II: Ancient variations on a theorem of apollonius. Centaurus, 25(4), 253–291.
Knorr, W. R. (1989). Textual studies in ancient and medieval geometry. Basel: Birkhäuser.
Lachterman, D. R. (1989). The ethics of geometry: A genealogy of modernity. London: Routledge.
Lloyd, G. E. R. (1979). Magic, reason and experience: Studies in the origins and development of Greek science. Cambridge: Cambridge University Press.
Lloyd, G. E. R. (1996). Adversaries and authorities: Investigations into ancient Greek and Chinese science. Cambridge: Cambridge University Press.
Mach, E. (1883). The science of mechanics: A critical and historical account of its development. Open Court Publishing, 1919 (first edition 1883).
MacKenzie, D. A. (2004). Mechanizing proof: Computing, risk, and trust. Cambridge: MIT Press.
Magazu, S., Coletta, N., & Migliardo, F. (2019). The Vitruvian Man of Leonardo da Vinci as a representation of an operational approach to knowledge. Foundations of Science, 24, 751–773.
Mancosu, P. (1992). Descartes’s Géométrie and revolutions in mathematics. In D. Gillies (Ed.), Revolutions in mathematics (pp. 83–116). Oxford: Oxford University Press.
Mancosu, P. (1996). Philosophy of mathematics and mathematical practice in the seventeenth century. Oxford: Oxford University Press.
Mancosu, P. (2004). Visualization in logic and mathematics. In P. Mancosu, et al. (Eds.), Visualization, explanation and reasoning styles in mathematics (pp. 13–30). Berlin: Springer.
Mancosu, P., & Arana, A. (2010). Descartes and the cylindrical helix. Historia Mathematica, 37(3), 403–427.
Manders, K. (2008a). Diagram-based geometric practice. In P. Mancosu (Ed.), The philosophy of mathematical practice (pp. 65–79). Oxford: Oxford University Press.
Manders, K. (2008b). The Euclidean diagram. In P. Mancosu (Ed.), The philosophy of mathematical practice (pp. 80–133). Oxford: Oxford University Press.
Marsden, E. W. (1971). Greek and Roman artillery: Technical treatises. Oxford: Oxford University Press.
Martines, G. (2014). Isidore’s compass. Nuncius, 29(2), 279–311.
Masià, R. (2016). A new reading of Archytas’ doubling of the cube and its implications. Archive for History of Exact Sciences, 70(2), 175–204.
Maxwell, E. A. (1963). Fallacies in mathematics. Cambridge: Cambridge University Press.
Menn, S. (2015). How Archytas doubled the cube. In B. Holmes & K.-D. Fischer (Eds.), The frontiers of ancient science: Essays in honor of Heinrich von Staden (pp. 407–436)., Beiträge zur Altertumskunde 338. Berlin: De Gruyter.
Miller, N. (2007). Euclid and his twentieth century rivals: Diagrams in the logic of Euclidean geometry. Stanford, CA: CSLI Publications.
Miller, N. (2012). On the inconsistency of Mumma’s Eu. Notre Dame Journal Formal Logic, 53(1), 27–52.
Mueller, I. (1981). Philosophy of mathematics and deductive structure in Euclid’s elements. Cambridge: MIT Press.
Mumma, J. (2010). Proofs, pictures, and Euclid. Synthese, 175, 255–287.
Netz, R. (2003). The shaping of deduction in Greek mathematics: A study in cognitive history. Cambridge: Cambridge University Press.
Netz, R. (2004). The works of archimedes (Vol. 1). Cambridge: Cambridge University Press.
Nicomachus of Gerasa. (1926). Introduction to arithmetic (M. L. D’ooge Trans.). London: Macmillan.
Panza, M. (2011). Rethinking geometrical exactness. Historia Mathematica, 38(1), 42–95.
Panza, M. (2012). The twofold role of diagrams in Euclid’s plane geometry. Synthese, 186(1), 55–102.
Pasch, M. (1976). Vorlesungen über neuere Geometrie. Reprint of the 1926 edition with M. Dehn by Springer.
Plato. (1997). Complete works, J. M. Cooper (Ed.), Hackett.
Plutarch. (1917). Lives, Volume V: Agesilaus and pompey. Pelopidas and Marcellus (B. Perrin Trans.). Loeb Classical Library 87, Cambridge, MA: Harvard University Press.
Proclus. (1970). A commentary of the first book of Euclid’s elements (G. R. Morrow Trans.). Princeton University Press.
Rashed, R. (2003). Al-Quhi et al-Sijzi: Aur le compas parfait et le tracé continu des sections coniques. Arabic Sciences and Philosophy, 13(1), 9–43.
Rashed, R. (2004). Oeuvre mathématique d’al-Sijzi, Volume 1: Géométrie des coniques et théorie des nombres au Xe siècle, Éditions Peeters.
Rosenfeld, B. A. (1988). A history of non-Euclidean geometry: Evolution of the concept of a geometric space. Berlin: Springer.
Russell, B. (1902). The teaching of Euclid. The Mathematical Gazette, 2(33), 165–167.
Russo, L. (1998). The definitions of fundamental geometric entities contained in book I of Euclid’s elements. Archive for History of Exact Science, 52, 195–219.
Russo, L. (2004). The forgotten revolution: How science was born in 300 BC and why it had to be reborn. Berlin: Springer.
Saito, K. (2009). Reading ancient Greek mathematics. In E. Robson & J. Stedall (Eds.), The Oxford handbook of the history of mathematics (pp. 801–826). Oxford: Oxford University Press.
Saito, K., & Sidoli, N. (2015). Diagrams and arguments in ancient Greek mathematics: Lessons drawn from comparisons of the manuscript diagrams with those in modern critical editions. In K. Chemla (Ed.), The history of mathematical proof in ancient traditions (pp. 135–162). Cambridge: Cambridge University Press.
Sefrin-Weis, H. (2010). Pappus of Alexandria: Book 4 of the collection, edited with translation and commentary by Heike Sefrin-Weis. Berlin: Springer.
Sextus Empiricus. (1936). Against physicists, against ethicists (R. G. Bury Trans.). Loeb Classical Library 311, Cambridge, MA: Harvard University Press.
Shabel, L. (2003). Mathematics in Kant’s critical philosophy. London: Routledge.
Sidoli, N. (2018a). The concept of given in Greek mathematics. Archive for History of Exact Sciences, 72(4), 353–402.
Sidoli, N. (2018b). Uses of construction in problems and theorems in Euclid’s elements I–VI. Archive for History of Exact Sciences, 72(4), 403–452.
Sidoli, N., & Saito, K. (2009). The role of geometrical construction in Theodosius’s spherics. Archive for History of Exact Sciences, 63, 581–609.
Suardi, G. (1752). Nuovi Istromenti Per La Descrizione Di Diverse Curve Antiche E Moderne E di molte altre, che servir possono alla speculazione de’ Geometri, ed all’ uso de’ Pratici, Brescia: Rizzardi.
Szabó, A. (1978). The beginnings of Greek mathematics, synthese historical library. Berlin: Springer.
Thomas, I. (1939). Greek mathematical works I: Thales to Euclid., Loeb Classical Library 335 Cambridge: Harvard University Press.
Thomas, I. (1941). Greek mathematical works II: From aristarchus to Pappus., Loeb classical library 362 Cambridge: Harvard University Press.
Thomas, R. (2014). Acts of geometrical construction in the spherics of theodosius. In N. Sidoli & G. Van Brummelen (Eds.), From Alexandria, through baghdad: Surveys and studies in the ancient Greek and medieval islamic mathematical sciences in Honor of J. L. Berggren (pp. 227–238). Berlin: Springer.
Thomas, R. S. D. (2018). An appreciation of the first book of spherics. Mathematics Magazine, 91, 3–15.
Toomer, G. J. (1976). Diocles on burning mirrors. Berlin: Springer.
Toomer, G. J. (1998). Ptolemy’s almagest. Princeton: Princeton University Press.
Tóth, I. (1966). Das parallelenproblem im corpus aristotelicum. Archive for History of Exact Sciences, 3, 249–422.
Van der Waerden, B. L. (1950). Science awakening I (4th ed.) Dordrecht: Kluwer, 1975. Originally published as Ontwakende wetenschap, Groningen: Noordhoff.
Vitrac, B. (1990). commentary in Euclid d’Alexandrie, Les éléments (Vol. 1). Paris: Presses Universitaires de France.
Wagner, R. (2018). Cognitive stories and the image of mathematics. Theoria: An International Journal for Theory, History and Foundations of Science, 33(2), 305–323.
Wagner, R. J. (1983). Euclid’s intended interpretation of superposition. Historia Mathematica, 10(1), 63–70.
Zeuthen, H. G. (1896). Die geometrische Construction als Existenzbeweis in der antike Geometrie. Mathematische Annalen, 47(2–3), 222–228.
Zeuthen, H. G. (1917). Hvorledes Mathematiken i tiden fra Platon till Euklid blev rationel videnskab, Det Kongelige Danske videnskabernes selskabs skrifter, Naturvidenskab og Mathematik, Afd. 8, Raekke I.5, Copenhagen.
Acknowledgements
This research was funded by the Dutch Research Council (NWO): OCENW.KLEIN.222.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Blåsjö, V. Operationalism: An Interpretation of the Philosophy of Ancient Greek Geometry. Found Sci 27, 587–708 (2022). https://doi.org/10.1007/s10699-021-09791-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10699-021-09791-4
















































