Data-driven aggregate modeling of a semiconductor wafer fab to predict WIP levels and cycle time distributions

Abstract

In complex manufacturing systems, such as a semiconductor wafer fabrication facility (wafer fab), it is important to accurately predict cycle times and work-in-progress (WIP) levels. These key performance indicators are commonly predicted using detailed simulation models; however, the detailed simulation models are computationally expensive and have high development and maintenance costs. In this paper, we propose an aggregate modeling approach, where each work area, i.e., a group of functionally similar workstations, in the wafer fab is aggregated into a single-server queueing system. The parameters of the queueing system can be derived directly from arrival and departure data of that work area. To obtain fab-level predictions, our proposed methodology builds a network of aggregate models, where the network represents the entire fab consisting of different work areas. The viability of this method in practice is demonstrated by applying it to a real-world wafer fab. Experiments show that the proposed model can make accurate predictions, but also provide insights into the limitations of aggregate modeling.

1 Introduction

The electronics industry is a large, competitive industry in which semiconductors are the essential components of electronic devices. Equipment in semiconductor manufacturing systems is capital intensive and thus must be optimally utilized to reduce the costs and maximize the throughput. However, high equipment utilization can lead to longer cycle times (i.e., the total time a product spends in the factory), negatively impacting on-time delivery. A model that predicts cycle times and other performance metrics can help assess this trade-off.

Semiconductor manufacturing can be divided into two main parts: the front-end and back-end process. In a front-end wafer fabrication facility (i.e., wafer fab), integrated circuits (ICs) are fabricated on a blank disk of semiconducting material (e.g., silicon) using photolithography techniques. A wafer fab is considered a complex job shop, with many different product types and re-entrant process flows (Gupta and Sivakumar 2006; Chen et al. 2013). During production, wafers move through the wafer fab in batches of multiple wafers, so-called lots, and are manufactured layer by layer. From a functional point of view, work areas are the main building blocks of a wafer fab. Examples of work areas in a wafer fab are photolithography, etching, and oxidation. Each work area consists of several workstations, and each workstation consists of one or multiple machines that provide similar processing capabilities. As the layers are built, a lot visits each work area numerous times; the precise number depends on the specific product. After ICs are manufactured on the wafer in the front-end, the back-end assembly and test facilities assemble the ICs into a package, and these final goods receive a full functional test. A product spends the majority of its production time in a wafer fab—up to several months in the front-end compared to several weeks in the back-end.

In this work, we develop an efficient simulation model to predict cycle time distributions and (the mean and variance of) WIP levels in an entire front-end wafer fab. We propose a network of aggregate models, where each aggregate model abstracts all the machines in a work area into a single-server queueing system. Unlike other model abstraction methods, this model does not require a detailed simulation model, and the parameters of the model can be derived directly from arrival and departure data, thus reducing development and maintenance costs. These parameters consist of a WIP-dependent aggregate process time distribution and a WIP- and layer-type-dependent overtaking distribution. The former represents the inter-departure time of lots in a given work area and the latter dictates the sequence of lots in the queue of the aggregated model. We will demonstrate the viability of this method in practice by applying it to one of the real-world wafer fabs of Nexperia, a global semiconductor manufacturer. First, we will show how such an aggregate model performs when it is used to model a single work area. In this analysis, we predict the (mean and variance of) WIP levels and cycle time distributions in the corresponding work areas. Then, we connect the individual aggregate models to create a network of aggregate models to model the entire factory. We will use this network to predict the residual expected cycle times of lots already in the system, the cycle time distributions of lots that are yet to start, and (the mean and variance of) the total WIP levels in the fab.

While our experiments are based on real-world data from Nexperia, the potential applications of the proposed methodology extend to the wafer fabs from other semiconductor manufacturers and even to other job shop production systems. In practice, it is common to divide a wafer fab or other job shops into distinct work areas and to produce multiple types of products simultaneously. Accordingly, the aggregate models proposed in this paper are derived directly from arrival and departure data of work areas, and products are routed through the network of work areas based on their product type. In many manufacturing systems, this data can be obtained by a manufacturing execution system (MES) or other data collection systems, facilitating the application of our methodology.

The main contributions of this paper can be summarized as follows. (1) We propose a novel modeling methodology for building a network of aggregate models to abstract complex job shops. The main advantage of the model is that it is based on the aggregation of a complete work area into one simple model, the parameters of which are directly derived from arrival and departure data in that work area. Hence, the aggregate model does not require a detailed simulation model that may require a lot of cost and effort to be built and maintained. Previous literature showed how to build a single aggregate model (Veeger et al. 2011), but our paper is the first to consider a network of aggregate models. (2) We validate the proposed modeling approach by applying it to a wafer fab of Nexperia using real-world production data. This leads to a data-driven simulation model that can accurately predict future cycle times and WIP levels in the wafer fab. We also identify situations where the predictions by the model are inaccurate and explore possible improvements. Furthermore, we use the insights from the real-world case study to provide future research directions on this topic. (3) We propose a method to realistically initialize the order of lots in the queue of the aggregate model. This way, we can take a snapshot of the current situation in the real-world fab and use this as the starting state of the simulation. This enables the model to make accurate predictions for the lots in the system at the beginning of the simulation without the need for a warm-up period.

The remainder of the paper is organized as follows. Section 2 provides an overview of the relevant literature. Section 3 describes the aggregate modeling approach, how it can be used to represent a work area, and how multiple aggregate models are connected in a network. Section 4 shows the performance of the proposed methodology for single work areas and the entire wafer fab. Finally, we discuss the results in Sect. 5 with concluding remarks and future work.

2 Literature review

There is wide literature on quantitative methods for assessing the performance of semiconductor manufacturing systems. The first approach uses classical queueing models (e.g., Connors et al. 1996; Shin et al. 2019). In this approach, production dynamics are approximated by a set of balance equations that can efficiently estimate the mean cycle times. However, this approach is limited in dealing with complex production dynamics, such as machine downtime, rework, and dispatching rules (Seok et al. 2020). Therefore, queueing models are found to be less satisfactory to modeling real-life semiconductor manufacturing systems, where complicated tool specifications and process flows are typical (Shanthikumar et al. 2007).

The second approach is to apply machine-learning methods to predict future cycle times by directly using historical data. Backus et al. (2006) compare the clustering, K-nearest neighbor, and regression tree methods to predict the remaining cycle-time of lots based on the observed cycle times of the previous lots with similar characteristics. However, the authors only estimate the mean cycle times and do not predict the probability distribution of the cycle time. These distributions are estimated by Tirkel and Parmet (2017), where the authors use workstation-level data to fit various statistical distributions to the cycle time of a wafer lot in a specific production step. Lingitz et al. (2018) use a variety of regression techniques, and Schneckenreither et al. (2021) use artificial neural networks to forecast cycle times. Furthermore, Seidel et al. (2020) propose a data-driven approach to predict the cycle time distribution. Here, the remaining cycle time at each production step is modeled with an empirical distribution, which is used to make wafer-out predictions (i.e. the prediction of the moment a wafer leaves the fab) at each step. These methods can quickly predict cycle times, but cannot be used to assess other key aspects of manufacturing systems, such as WIP levels, or to evaluate planning and control policies.

The third approach uses discrete-event simulation to assess the key performance indicators of manufacturing systems and to evaluate what-if scenarios (Negahban and Smith 2014). A discrete-event simulation model may include many details of the factory to accurately approximate factory dynamics. For example, Sivakumar and Chong (2001) analyze the cycle time of a back-end semiconductor facility by varying different input variables, and Lin and Chen (2015) use a detailed simulation model to find optimal dispatching schedules. However, detailed simulation models are computationally expensive, which is an issue, especially in real-time applications (Kim et al. 2003). Therefore, Dangelmaier et al. (2007) state that model simplification is needed to achieve efficient simulation experiments.

Based on our review of simulation models for semiconductor manufacturing systems, we identify three main research streams for this purpose: (1) using simulation metamodels, (2) aggregating non-bottleneck stations within a detailed simulation model, and (3) using the concept of effective process time (EPT) to obtain an aggregate representation of a work area. In this paper, we also use the concept of EPT; thus, our paper comes closest to the research stream (3). In the remainder of this section, we first provide a brief review of the research streams (1) and (2). Then, we explain the concept of EPT in detail and focus on the literature related to the research stream (3).

(1) Using simulation meta-models. In the presence of a detailed simulation model, one approach to efficiently evaluate the performance of a semiconductor manufacturing system is to use a metamodel that represents the outputs of simulation experiments. Specifically, a metamodel uses a detailed simulation to approximate the response surface to represent the relationship between simulation inputs and output. Simulation runs are performed according to a design of experiments to determine this surface. The metamodel predicts an output value based on the input variables without actually running the simulation. Yang (2010) use neural-network-based metamodeling to estimate the cycle-time and throughput relationship, and Bekki et al. (2014) and Batur et al. (2018) show that a metamodel can be used to efficiently obtain cycle-time distributions. Yang et al. (2011) uses nonlinear regression models to map the mean of steady-state cycle time as a function of throughput and product mix. Similarly, Gopalswamy and Uzsoy (2019) investigate the estimation of clearing functions (i.e., a function that describes the relationship between the throughput of a production resource and the workload available to it in a planning period). While simulation metamodels and clearing functions reduce the burden in simulation-based performance assessment, the identification and estimation of the functional forms of such models remain to be a difficult task in practice. Furthermore, an additional challenge arises when they are used for decision making. For example, the fitting of a clearing function is based on training data, and when it is thereafter used within a multi-period optimization model to make sequential decisions (e.g., Haeussler and Missbauer 2014), not updating it again may influence the accuracy of the performance assessment, raising a question on how these aggregation models can or should be used (i.e., offline or online).

(2) Aggregating non-bottleneck stations within a detailed simulation. Another way to simplify a detailed simulation model is by aggregating the non-bottleneck workstations. These workstations can be handled in different ways. Zhou et al. (2016) reduce the size of the simulation model by deleting non-critical workstations and ensure model robustness by using a closed-loop correction method. Brooks and Tobias (2000) and Johnson et al. (2005) simplify the model by replacing the non-bottleneck workstations with a constant delay, but these models are not used to predict cycle-time distributions or WIP levels. Sprenger and Rose (2010) use the so-called delay distributions to aggregate workstations before and after the bottleneck workstation. Another delay-based approach is proposed by Seok et al. (2020). In their approach, when a machine group (i.e. a workstation) reaches the steady-state, it is abstracted by a so-called mean delay model (MDM). The MDM is monitored, and when dynamic changes are registered (e.g. lot-arrival changes), the aggregated workstation is switched back to a corresponding low-level workstation. Seok et al. (2021) introduce multi-group MDMs, which aggregate several single MDMs to efficiently estimate cycle-time distributions. Lidberg et al. (2020) use aggregation within the context of discrete-event simulation.

The disadvantage of the model simplification methods described above as part of research streams (1) and (2) is that they require a detailed simulation to determine the response surfaces or identify bottleneck workstations. Developing and maintaining a detailed simulation to obtain the abstracted model requires considerable resources in practice (Shanthikumar et al. 2007). However, the approaches based on the EPT concept do not require building a detailed simulation model in the first place.

(3) EPT modeling. The aggregate model proposed in this paper uses the concept of EPT, a term first introduced by Hopp and Spearman (2011) and is defined as “the time seen by a lot from a logistical point of view”. The EPT represents the aggregated value of various components, such as the raw process time, setup time, handling time, and preemptive and non-preemptive outages. That is, the EPT associated with a work area includes not only the process times but also the time losses due to other sources in that work area. It is possible to compute the realizations of EPT from merely the arrival and departure times of lots in that work area. Such track-in and track-out data are often available in the highly automated semiconductor industry (Jacobs et al. 2003; Kock et al. 2011). Based on the concept of EPT, Kock et al. (2008) propose a model with a WIP-dependent EPT distribution to aggregate G/G/m queueing systems and use this model to predict the mean cycle time, where the WIP of a workstation is defined as the total number of lots at this workstation, including the input buffer. This model is WIP-dependent to better imitate the real-life behavior of a workstation at different WIP levels. For example, when the WIP level is higher, machine utilization may be higher, and thus, throughput will also be higher at these workstations. Veeger et al. (2009) apply this model to predict the mean cycle time as a function of throughput and product mix of a semiconductor cluster tool workstation. A summary of the development and theory behind the EPT-based aggregate modeling concept is given by Veeger (2010).

The aggregate model can accurately predict the mean cycle time (Veeger et al. 2010); however, it cannot predict cycle time distributions. This limitation is primarily caused by First-Come-First-Serve (FCFS) dispatching rules in the aggregate model. A semiconductor workstation typically contains multiple machines, in parallel and sequence, with different processing speeds and tool eligibility. Additionally, sequence-dependent setup times cause some products to be prioritized over others to minimize setups. These factors cause some lots to be processed before lots already in the system, thus overtaking them. A simple FCFS rule cannot capture this dynamic. To deal with this issue, Veeger et al. (2010b, 2011) considers the order in which lots are processed by introducing a so-called WIP-dependent overtaking distribution. Similar to the EPT distribution, this distribution is determined from arrival and departure events and is used to sample the number of lots an arriving lot overtakes in the queue of the aggregate workstation. Veeger et al. (2011) demonstrate that the aggregate model with overtaking can accurately predict cycle time distributions in a single semiconductor workstation with multiple product types.

As mentioned in Sect. 1, wafers are built up layer-by-layer, and a wafer undergoes different operations for each layer type. These operations depend on the characteristics and level of complexity of the respective layer type. Thus, lots in a specific layer type may see different processing speeds than the lots in other layer types, requiring that the number of overtaken lots is also dependent on the layer type. To address this issue, Deenen et al. (2021) propose an overtaking distribution that is WIP- and layer-type-dependent. In our paper, we also use an aggregate model with a WIP-dependent EPT distribution and a WIP- and layer-type-dependent overtaking distribution. However, different from Deenen et al. (2021), we build a network of these aggregate models that can be used to model an entire wafer fab. This way, our proposed methodology can predict the cycle time distribution and the (mean and variance of) WIP levels for the entire wafer fab, not just one specific work area.

3 Method

This section describes the method used to predict the cycle times and WIP levels in a wafer fab. The concept of aggregate modeling for a single work area and the corresponding model parameters will be explained in Sect. 3.1 and Sect. 3.2, respectively. It should be noted that the aggregate model and its parameters outlined in these sections have been previously published within the context of a single work area, and they are presented here for completeness. The novelty of this work lies in the application of the aggregate model to all work areas in a real-world wafer fab (as depicted in Sect. 1), and the integration of the models into a network, which is explained in Sect. 3.3. Finally, the novel heuristic to initialize the entire model is explained in Sect. 3.4.

3.1 Aggregate model for a single work area

We model each work area as a single-server with an infinite buffer. This aggregate queueing model has a WIP-dependent process time distribution (Veeger et al. 2010, 2010b, 2011) and a WIP- and layer-type-dependent overtaking distribution (Deenen et al. 2021). Figure 1 illustrates this aggregation procedure for the implant work area. Other work areas are aggregated similarly. Figure 1a shows the flow line of implant, consisting of three workstations: implanters, strippers, and inspection, each having its buffers and parallel machines. This entire work area is modeled with the aggregate model depicted in Fig. 1b. The aggregate model consists of two parts: (1) a queue that handles arrivals according to an overtaking distribution, and (2) a server that handles departures according to an EPT distribution. The queue and server are different from common queue-server models (such as the G/G/1 model) in the sense that the queue contains all the lots in the system, including the lots that are in process, and the server does not hold any lot. This server is not a physical server that processes lots, but rather a timer that determines when the next lot leaves the queue. When the timer elapses, the first lot in the queue leaves the system.

Fig. 1

a Example of a work area: implant. b The proposed aggregate model

In the first part of the model, an overtaking distribution determines how many lots a new arrival overtakes in the queue. In the real world, multiple machines operate in parallel, and priority dispatching rules may be used. This may cause lots to go faster through the work area and depart before lots that arrived earlier, thus overtaking them. When a new lot arrives at the queue, the number of lots to overtake $K \in \{0,1, \dots ,w\}$ is sampled from the cumulative distribution $F_K(k;w,l_i)$, which specifies the probabilities $P(K \le k;w,l_i)$ that at most k lots are overtaken with w the WIP level upon arrival of the lot and $l_i$ the layer type of the arriving lot i. The WIP level w is counted excluding the new lot arrival. The new lot is placed at position $w - K$, where w is the back, and position 0 is the front of the queue. For example, in Fig. 1b, there are $w = 3$ lots in the queue. If $K = 2$ lots are overtaken, the new lot is placed at position $w-K=3-2=1$ in the queue, which is behind the first lot. If the new lot overtakes no other lots, it is placed at the back of the queue (position $3-0=3$).

The overtaking distribution depends on both the WIP level w and the layer type $l_i$ of the arriving lot i. The WIP-dependency accounts for the fact that when there are more lots in a work area, it is more likely that a new arrival overtakes more lots. The layer-type dependency handles the different characteristics of each re-entrance flow in a wafer fab. For each wafer layer, a lot undergoes several operations in the same set of work areas. There is a strong correlation between the duration of these operations and the layer type being processed (Deenen et al. 2021). For example, a more complex layer type may need more precise processing, which is more time-consuming. This speed difference between layer types causes lots to be processed quicker in some layer types than others, thus overtaking more lots. Another reason is that only a small portion of the available machines are eligible to produce certain critical layer types, causing a lot to have more queueing time in these layer types than in non-critical layer types.

In the second part of the model, a WIP-dependent EPT distribution $F_E(t;w)$ handles the departures from the work area. In Fig. 1b, this distribution is represented by a timer. The duration of the timer, which is represented with the random variable E, is sampled from the WIP-dependent EPT distribution $F_E(t;w)$, which specifies the probability $P(E \le t;w)$ that the duration E is less or equal to t at WIP level w (to be specific, w is the number of lots in the system just after the timer started). Whenever this duration elapses, the lot at the front of the queue departs, and a new timer starts when either a new lot arrives in an empty system or a lot departs in a non-empty system. This distribution is WIP-dependent because when more lots are available in the unaggregated system, more machines can operate simultaneously, i.e. machines have a higher utilization, resulting in higher throughput and lower inter-departure times. As will be explained in Sect. 3.2, the EPTs in the aggregated system generally correspond to the inter-departure times of lots in the unaggregated system. Thus, a higher WIP will result in lower EPTs.

3.2 Model parameters for a single work area

Both the EPT distribution $F_E(t;w)$ and the overtaking distribution $F_K(k;w,l_i)$ are based on real-world arrival and departure events at each work area, indicated by a and d in Fig. 1a. For each lot i, the arrival time $a_i$ and departure time $d_i$ are collected. We will first illustrate how EPTs are determined with an example. Then, we will elaborate on the algorithm used to calculate the EPT and overtaking realizations from the arrival and departure data.

An example of five EPT realizations is shown in Fig. 2. In this figure, each row represents the activities each lot undergoes expressed in time. In the real world, a lot goes through multiple operations in a work area. Before it can be processed, a lot may be idle as it needs to wait in the queue for an operator or because of a machine breakdown. These downtime states and other non-processing activities, such as setup time, contribute to the cycle time of a lot. In an empty system, the EPT equals the time between the first arrival and the next departure. In a non-empty system, the EPT of the aggregate model equals the time between two departures, i.e. inter-departure time. For example, the first lot (lot 1) in Fig. 2 arrives at the work area at time $t=0$. This lot undergoes three processing steps indicated by the yellow boxes and departs the systems at $t=12$. During this time, a second lot (lot 2) arrived at $t=1$ and departed at $t=6$ before lot 1 was completed. The first EPT realization (EPT 1) at this work area equals the time between the first arrival (of lot 1) and the next departure (of lot 2), which is 6 time units. The next EPT (EPT 2) is equal to the next inter-departure time, which is the time between the departure of lot 2 and the departure of lot 1 and equals 6 time units. Therefore, the EPT is an aggregate measure that describes the time between two lot departures from the aggregated perspective, while accounting for all possible lower-level dynamics (i.e., all of the five duration types shown in Fig. 2).

Fig. 2

EPT realizations of five lots

For the algorithm used to calculate the EPT and overtaking realizations, the reader is referred to Appendix A. For each lot i, the algorithm constructs (1) the EPT of lot i with the corresponding WIP level at the start of lot i’s EPT and (2) the number of overtaken lots by lot i with the corresponding WIP level upon arrival of lot i. The EPT realizations are grouped per WIP level. For each WIP level w, the mean and coefficient of variation of the EPT are calculated, $t_e(w)$ and $c_e(w)$, respectively. Due to data limitations and noise in practice, a curve fitting procedure is used to estimate $F_E(t;w)$ for all WIP levels, as will be demonstrated in Sect. 4.2. Similarly as in previous literature (Veeger et al. 2011), we assume that the EPT distributions, $F_E(t;w)$, are gamma distributed, with mean $t_e(w)$ and coefficient of variation $c_e(w)$. In our experiments with real-world data, the gamma distribution fits the data well. We advise practitioners to validate which distribution fits their data. As long as the chosen distribution can be characterized with the two parameters (i.e., the mean $t_e(w)$ and the coefficient of variation $c_e(w)$), our proposed methodology continues to be applicable.

The overtaking realizations are grouped per WIP level and layer type, and are used to obtain the overtaking distributions $F_K(k;w,l_i)$. There are very few distribution fitting procedures available for a discrete distribution where the sampled value K is always less or equal to a finite value (i.e., the WIP level w) (Veeger et al. 2011). Therefore, we use empirical distributions for $F_K(k;w,l_i)$.

We assume that all the samples from the EPT and overtaking distributions are independent and identically distributed (i.i.d.) random variables within the same WIP level (and layer type, in the case of the overtaking distribution). Although the individual EPT and overtaking realizations may not be truly i.i.d., we consider this a reasonable assumption because our model often leads to accurate predictions of the WIP and cycle time, see Sect. 4.3 for details.

3.3 Network of aggregate models for the entire wafer fab

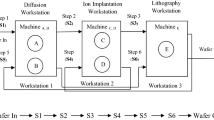
To model the entire wafer fab, we propose to model each work area as a separate aggregate model. An overview of the main work areas of a typical wafer fab is shown in Fig. 3. All work areas are connected to indicate the re-entrant flows and different routing of product types. Each lot that is released in the fab (on the left-hand side in Fig. 3) has a predetermined routing. This routing, which states the sequence of work areas the lot has to visit, depends on the lot’s product type. Due to the cyclic behavior of the process flow, this routing includes multiple visits to the same work areas. The aggregate model of that specific area handles each visit to a work area. Once the processing of the lot is finished in that area, the lot is sent to the subsequent work area based on the routing. This process is repeated until the lot is completed and leaves the fab.

Fig. 3

Main work areas in a wafer fab

An example of the routing of two product types is given in Table 1. The routing of each product type contains a subset of all the existing layer types. In this example, product types 1 and 2 both start with layer type A. This layer consists of two steps: visiting the photolithography work area and visiting the dry etching work area. During these visits, both product types are in layer type A. Therefore, the same overtaking distribution will be used to determine their position in the queue of the aggregate model. In step 3, both product types visit the dry etching work area; however, they are in different layer types. Thus, their position in the queue of the aggregate model will be determined by sampling from different overtaking distributions. After oxidation, both product types will be sent to a different subsequent work area: product type 1 to photolithography and product type 2 to implant. This way, the flow of lots of different product types is emulated in the network of aggregate models. This illustrates that the model can handle a high product mix, even if this product mix changes, as the proposed network is robust to different product routings. Additionally, the network can handle newly introduced product types since they generally exist of known layer types .

Table 1 An illustrative example of the first part of the routing of two product types

3.4 Initialization

To predict the WIP levels over time in work areas and the cycle times of the lots that are already present in the system, the start state of the aggregate simulation model is crucial. Unlike in previous work on EPT models, where a warm-up period is used to account for the start-up phenomenon, we initialize each aggregate model with a specific start state and use no warm-up in the simulation. This way, we initialize the system in a state similar to the real-world system at a specific point in time and simulate from that point onward. In this case, the start state refers to (1) how many and which lots are present, and (2) in what order these lots are queued in each aggregate model (as illustrated in Fig. 1b). Recall that the queue of each aggregate model does not represent an actual physical queue. Instead, it is a fictitious queue that contains all the lots of the complete aggregated area. To approximate the queue’s ordering, we propose an initialization heuristic that uses the aggregate model’s WIP-dependent and layer-type-dependent overtaking distribution. This heuristic is applied to every single work area in the entire wafer fab. The general idea of the heuristic is that it uses the arrivals of all the lots currently in the corresponding real-world work area and mimics what overtaking behavior they would have had in the aggregate model. Since the overtaking distribution is WIP-dependent, we use dummy lots to fill the queue during the initialization process. These dummy lots represent the lots present in the queue upon arrival of a specific lot but already departed at the time of initialization.

The initialization heuristic is shown in Algorithm 1 and works as follows. First, it constructs list $L = \{1,2,..., {|L |} \}$ containing all the lots in the real-world aggregated area and sorts the list by ascending arrival time. The queue length (or WIP level) of the aggregate model, w, is initially zero. Each lot $i \in L$ will then sequentially arrive at this queue. For each arriving lot i, the difference in WIP, $\Delta w$, is calculated between the WIP level observed by lot i upon arrival in the real world, $aw_i$, and the current WIP level in the aggregate model, w. If $\Delta w$ is negative, $|\Delta w |$ number of dummy lots are added to the end of the queue, if positive, the first $\Delta w$ dummy lots are removed from the queue. Then, an overtaking realization K is sampled from $F_K(\cdot ;;w_{c},l_{i})$, where $l_i$ is the layer type of lot i. Finally, lot i is inserted in the queue such that it overtakes K lots. This process is repeated until all the lots in L are inserted in the queue.

4 Real-world case study

In this section, we will analyze how the proposed method performs in the real world by applying it to one of Nexperia’s front-end wafer fabs. In Sect. 4.1, we discuss what data is collected and how we split this data into three datasets. Next, we will explain in Sect. 4.2, using an example, how we calculate the model parameters for a single work area. The considered wafer fab consists of 21 work areas, of which the main work areas are depicted in Fig. 3. For each work area, an aggregate model is built, and the performance is analyzed. In Sect. 4.3, we evaluate the performance of these aggregate models in isolation. We will show that the aggregate model can give accurate predictions for the majority of the work areas and time periods. However, we also identify situations where the predictions are not accurate and discuss possible improvements for these situations. Then, we will connect the aggregate models into a network to simulate the entire wafer fab and analyze its performance in Sect. 4.4. For the cycle time predictions, we distinguish between the area cycle time and fab cycle time. The former refers to the time a lot spends in one specific work area during a single visit, and the latter refers to the time a lot spends in the complete wafer fab.

4.1 Data collection and experimental setup

The data is collected from the MES over an eight-month period. Pre-processing steps are applied to the raw data to extract correct timestamps and label them as arrivals or departures at a work area. The dataset contains approximately 12,000 unique lots from 340 product types, with an average of 53 work area visits per lot.

In a real-world implementation, the aggregate model can be used in a rolling horizon manner, where the model is updated regularly to make new predictions. However, the goal of this work is to analyze the performance of individual predictions of future cycle time distributions and WIP levels. Therefore, we use three datasets as shown in Fig. 4a, where the time of prediction is the beginning of months 8, 9, and 10, for datasets 1, 2, and 3, respectively. This emulates a rolling horizon in which the model is updated every month; however, in reality, a different updating frequency can be chosen. The procedure to make predictions is as follows. First, the aggregate model parameters, the EPT, and overtaking distributions for all the work areas are determined based on two months of historical data (i.e., training data). However, the amount of historical data is a trade-off between having enough data to fit the model parameters and maintaining data validity due to potential changes in the system over time. Then, the aggregate model is initialized with the state of the real-world system at the time of prediction, as explained Sect. 3.4. The aggregate model is subsequently employed to forecast future cycle times and WIP levels for the next two months (i.e., test data), which are then compared against the actual cycle times and WIP levels. A future prediction horizon of two months is chosen because the total cycle time of lots is one to two months, and our goal is to predict when the lots present in the fab will finish production.

Using historical data, the aggregate model can also be used to predict cycle times and WIP levels of the training period, i.e., predicting over the same period as the model parameters are determined. While this is not feasible in practice, it gives insight into the model behavior. Therefore, we distinguish between analyses on the time period train and test. The predicted values we obtain with the aggregate model are compared to actual real-world values, referred to as predicted and actual, respectively. Figure 4b shows the four resulting scenarios which are used in the remainder of the results: predicted train, actual train, predicted test and actual test.

Fig. 4

Experimental setup. a Three datasets and their corresponding time periods. b Four different scenarios used during the experiments

For each dataset, we perform 30 simulation replications. The simulations are run on an Intel^® Core^™ i7-8650U CPU running at 1.90 GHz and with 24GB of RAM. The simulation model is built using the C-Sharp (C#) Simulation Library (CSSL) developed by Adan and Deenen (2021). CSSL is an open-source class library for C# and comprises classes as building blocks to build and execute discrete-event simulations easily. In our experiments, the computational time to train the model, i.e. determining the model parameters, never exceeds 35 s. Testing the trained model with a simulation of 30 replications, where each replication simulates two months of production, takes approximately 110 s.

4.2 Calculating the model parameters for single work areas

This section demonstrates how the EPT model works by applying it to one of the work areas in the wafer fab and shows the potential implementation challenges. As an example, we apply the EPT model to the implant work area, as shown in Fig. 1. The implant area contains three sequential processing steps, and each step can be performed on multiple machines. For each lot, we collect the arrival event a at the first buffer and the departure event d after the last processing step. These events are used to compute the measured $t_e(w)$ and $c_e(w)$, shown in the left and middle plots of Fig. 5a.

As mentioned earlier, the EPT behavior is WIP-dependent. When the WIP in the work area is higher, the machine utilization will likely be higher, resulting in higher throughput. This means inter-departure times in the work area will be shorter; thus, a lower EPT will be measured. Two noteworthy issues are capturing this WIP dependency from actual production data. First, the number of realizations for high and low WIP levels is usually limited or nonexistent. For instance, the implant work area never had a WIP level of less than 90. This lack of data is caused by aggregating the complete work area consisting of multiple workstations. Even though specific tools might have run dry occasionally, the WIP in the complete area was always high. Another reason for a constant high WIP is that certain areas are the bottlenecks of the wafer fab, and the fab has been running at high utilization to maximize the overall throughput. This also explains the fact that $t_e(w)$ does not decrease for the majority of the observed WIP range. The second issue is that the data is often quite noisy. For the WIP-dependent EPT distributions, these issues are overcome by using a curve fitting procedure that approximates the measured mean EPT $t_e(w)$ for WIP level w, denoted by ${\hat{t}}_e(w)$. In particular, the following exponential function is fitted similarly to Veeger et al. (2010):

$$\begin{aligned} {\hat{t}}_e(w) = \theta + (\eta - \theta )e^{-\lambda (w-1)} \end{aligned}$$

(1)

where $\theta$ represents the extreme value of ${\hat{t}}_e(w)$ at $w = \infty$, $\eta$ represents the value of ${\hat{t}}_e(w)$ when $w=1$ and $\lambda$ is the so-called decay constant. Similarly, an exponential function of the same form as Equation (1) is used to approximate the coefficient of variation $c_e(w)$ as a function of the WIP level w by ${\hat{c}}_e(w)$. In this work, we use the Python library SciPy’s nonlinear least-squares fitting procedure with default settings (Virtanen et al. 2020) to estimate the variables in Equation (1). Due to the aforementioned limited amount of data in low WIP ranges, this procedure does not always yield the parameters that could be used to predict cycle times accurately (Deenen et al. 2021). To improve this, an educated guess is made to estimate $\eta$, which is the EPT realization of a lot in the case that $w=1$. In this case, there is no other lot present, and the EPT realization is equal to its cycle time in this area. The cycle time of such a lot does not contain any queueing and consists solely of the sum of all processing times and setup times on the machines and the transport times between the machines. The estimate for the mean and variance of the processing and setup times is based on data from the manufacturing execution system (MES), and the transport times are estimated with the help of an experienced operator. Using the educated guess for $\eta$, the parameters $\theta$ and $\lambda$ are estimated with the nonlinear least-squares fitting procedure.

The right plot in Fig. 5a shows the cumulative distribution function of the observed overtaking for $230 \le w < 244$. Similar to the EPT distribution, there are no overtaking realizations for specific WIP levels. We group the data into buckets that contain a range of WIP levels. The chosen ranges of these WIP levels depend on how much data is available. We constructed the ranges such that each range contained at least ten empirical overtaking realizations, and the total number of buckets did not exceed 100 for each layer type. For very high or low WIP levels with no observations, samples are taken from the closest group in terms of WIP. Practitioners are advised to validate what ranges for the WIP buckets are the most suitable for the available data.

This method is applied similarly to all the other work areas in the wafer fab. Figures 6a and 7a show the results of the fitting procedure in the wet etch and sputtering work area, respectively. In practice, we advise validating this procedure for each area carefully to ensure that the desired behavior is obtained from real-world data.

Fig. 5

Implant work area for dataset 3; an example of a work area where the aggregate model yields accurate predictions. a Measured and fitted mean EPT t_e (left) and coefficient of variability c_e (middle) for all layer types combined and cumulative overtaking probabilities per layer type (right) for $230 \le w < 244$. b Measured and predicted normalized WIP levels of the training period (left) and test period (middle), and kernel density estimates of the area cycle time distributions of both the train and test period (right)

Fig. 6

Wet etch work area dataset 3; an example of a work area where the aggregate model yields accurate predictions. a Measured and fitted mean EPT t_e (left) and coefficient of variability c_e (middle) for all layer types combined and cumulative overtaking probabilities per layer type (right) for $139 \le w < 152$. b Measured and predicted normalized WIP levels of the training period (left) and test period (middle), and kernel density estimates of the area cycle time distributions of both the train and test period (right)

Fig. 7

Sputtering work area dataset 3; the aggregate model predicts well for the train period, but cannot capture the behavior well in the test period. a Measured and fitted mean EPT t_e (left) and coefficient of variability c_e (middle) for all layer types combined and cumulative overtaking probabilities per layer type (right) for $63 \le w < 75$. b Measured and predicted normalized WIP levels of the training period (left) and test period (middle), and kernel density estimates of the area cycle distributions of both the train and test period (right)

4.3 Analyzing the performance of single work areas

In this section, we will analyze the performance of the aggregate models on single work areas in isolation. This means that, for each aggregate model, we use the same lot arrivals as we measured at the corresponding work area in the real world. Then, we compare the predicted area cycle time distributions and WIP levels of the aggregate models to their actual counterparts in the real world. The main goal of this exercise is to identify situations where the proposed EPT model yields accurate predictions and where it does not, given that the information on the arriving lots in the area is known.

If there is a deviation in the prediction, two different sources can cause this: (1) an error caused by limitations of the aggregate model to capture the real-world system’s behavior, the aggregation error, and (2) an error due to outdated model parameters because real-world conditions (such as capacity) radically changed. To distinguish between the two error types, the performance of the aggregate model will be analyzed for both the train and test period, as explained in Sect. 4.1. Deviations in the training period are likely due to the aggregation error since this is the same period used to calculate the parameters of the aggregate model. If the aggregate model performs well in the training period but not in the test period, outdated model parameters are likely the source of error.

For the majority of the work areas—examples are the implant and wet etch work area—the aggregate model can accurately predict the area cycle time distribution and WIP levels (see Figs. 5b and  6b). The predicted WIP levels are obtained through 30 replications of the simulation, computing the mean ($\mu$) and standard deviation ($\sigma$) at each hour. In the plots, this is shown as a line through $\mu$ surrounded by a shaded area of $\mu \pm 2 \sigma$. For both areas, we observe that the model can accurately predict the WIP and the area cycle time distributions for the test period. However, we notice that the WIP predictions become slightly less reliable for longer prediction horizons in both the training and test periods, suggesting an aggregation error. This is shown by (1) an increasing standard deviation of the prediction and (2) larger mismatches between the measured and predicted WIP value as the prediction horizon grows. Still, the WIP predictions seem to be reasonably accurate for a prediction horizon of up to approximately 30 days.

Fig. 8

Mean EPT, number of arrivals, and number of departures measured at the sputtering work area for the train and test period

We also observe situations where the aggregate model performs poorly due to an error caused by outdated model parameters. This happens when conditions in a work area radically change between the train and test period. For instance, changes in the capacity of highly utilized equipment or changes in operational decision-making, such as different dispatching rules or priorities. This can be observed for the sputtering work area in Fig.7. The WIP and area cycle time predictions are accurate for the training period but are clearly inaccurate for the test period. Figure 8 depicts the mean EPT, arrivals, and departures measured at the real-world work area for both the train and test period. The measured mean EPT significantly differs between the training and test periods. Since the EPT is WIP-dependent, this might be caused by a higher WIP. However, the WIP in both the train and test period is primarily in the range where the maximum capacity, i.e., minimum EPT, is reached. Therefore, it seems that the capacity of the sputtering work area has been changed. This is likely caused by the installation of a new machine or the qualification of an existing machine enabling it to run more product types.

A possible solution for this problem is to retrain the EPT model on a time period that only includes the new behavior of the work area. Instead of using a training period of 60 days, we experimented with shorter periods prior to the test period. This is a trade-off between the amount of training data and the validity of that training data. Shortening the training period leads to fewer data in narrower WIP ranges, but the data is more recent and less likely to be collected in a time period where the work area had significantly different behavior. Figure 9 illustrates the result of shortening the training period on both the EPT parameters (left) and the resulting WIP predictions (middle and right). Recall that the parameter $\theta$ of the fitted function on the mean EPT in Equation (1) determines the maximum capacity of the aggregate model. Interestingly, we found—with trial-and-error—that a training period of 18 days or shorter yielded a $\theta$, which could accurately predict the WIP. Decreasing the training period further to significantly shorter periods would also yield deviating behavior due to less data. Unfortunately, we did not have access to other historical data to evaluate what exactly changed in that time period. The data on which machines were running, their capacities, and for what recipes they were qualified would be valuable for this analysis. For example, as an alternative to the trial-and-error approach we used, automatic retraining triggers could be developed based on the shop-floor production data, e.g., retraining the EPT models when new machines are installed or new recipes are qualified.

Fig. 9

A comparison of the performance of the aggregate model with train periods of 60, 20, and 18 days prior to the test period. The fitted mean EPT $t_e$ for all the train periods (left), and the normalized WIP predictions with the training period of 20 days (middle) and 18 days (right) are shown. The WIP levels are normalized similarly to the predictions with the training period of 60 days, which can be seen in Fig. 7b

4.4 Analyzing the performance for the complete wafer fab

In this section, we will analyze the performance of the complete wafer fab, which is modeled with a network of aggregate models, as explained in Sect. 3.3. In this analysis, we take a snapshot of the state of the wafer fab at a certain point in time and simulate from that point onward. This snapshot contains information about which lot is in what work area and is used to initialize the aggregate models. Then, we use the real-world wafer starts, i.e., wafers released into the fab at their first production step, as new arrivals in the system during simulation. This is also practically feasible since these wafer starts are known and planned for several months ahead. In contrast to the previous section, the real-world measured arrivals at individual work areas are not used in the simulation. Instead, all work areas are connected in a network, and each departure at one work area triggers an arrival at the subsequent work area.

4.4.1 Predicting WIP and cycle time distributions

The left and middle plots of Fig. 10 show the WIP predictions of the implant and wet etch work area, respectively. These are the same work areas and time periods which were used for the analysis on isolated work areas, shown in the middle plots of Figs. 5b and 6b. We observe that the resulting WIP predictions are not sufficiently accurate, especially compared to the results for the isolated work areas. The right plot of Fig. 10 shows the fab cycle time distribution of the most common product type. Note that the fab cycle time is different from the area cycle time analyzed before. The mean fab cycle time is predicted accurately, however, the prediction of the distribution is very poor.

In the network of aggregate models, the arrivals at each work area depend on the departures of other work areas. We identify that the main problem of the poor predictions originates from the fact that the aggregate model does not preserve the sequence of departures at a work area accurately enough, which has not been recognized in the literature before. This is problematic for the following reasons. First of all, this introduces more stochastic behavior in a work area. Instead of having deterministic arrivals, as was the case in the isolated work area analysis of Sect. 4.3, we now have stochastic arrivals. This explains the increased standard deviations on the predicted WIP. Besides, the overtaking distribution does not capture the dispatching strategy of the fab well enough. Although the proposed model can predict the cycle time distributions (of all lots combined) well for the isolated work areas, it does not accurately predict which individual lots are leaving the area at which time. This is important because lots can be in different stages of their production process and have different subsequent work areas to visit. We already use overtaking distributions with layer-type dependency, but more information on lots should be used to characterize the overtaking behavior, depending on the dispatching strategy used in the real world. In wafer fabs, lots are often steered towards their final due date, using intermediate operation due dates per production step. This means that if a lot had long cycle times in previous steps, it will be behind schedule and late on its current operation due date. This accumulated lateness will give the lot higher priority at its current step and is likely to overtake more lots compared to lots ahead of schedule. This lack of steering lots towards its due date in the aggregate model explains the much wider distribution of the predicted fab cycle compared to the measured fab cycle time.

Fig. 10

Poor predictions based on the complete wafer fab simulation. Measured and predicted WIP levels of the test period for the implant (left) and wet etch (middle) work area for dataset 1. The right plot shows the kernel density estimations of the measured and predicted fab cycle time distribution of the most common product type

The network of aggregate models can, however, predict three things well: (1) total WIP in the wafer fab, (2) mean fab cycle times, and (3) expected residual fab cycle times. The first prediction of the total WIP is shown in Fig. 11. Again, we observe that the WIP predictions for the first 30 days are fairly accurate for all datasets. After that, the WIP predictions might deviate, particularly in dataset 1 and, to a smaller extent in dataset 3. As was seen before, this can be solved by retraining the aggregate models to account for the changing conditions in the wafer fab. The second prediction, the mean fab cycle times, is shown for the most common product type in the right plot of Fig. 10. Even if the predicted distribution is not accurate (possibly due to a lack of information on the overtaking behavior), the EPT model can still accurately predict the mean fab cycle times. This property is very useful in the third prediction, the expected residual cycle times, which will be discussed in the next section.

Fig. 11

Measured and predicted WIP of the complete wafer fab for the test period of dataset 1 (left), 2 (middle), and 3 (right). Note that the y-axis does not start at the origin to give a clearer view of the performance of the model

4.4.2 Predicting expected residual fab cycle times

This section will focus on predicting the expected residual fab cycle time of lots that are already in the system, so-called wafer outs. The residual fab cycle time represents the time it takes a lot—which is already in the system—to go from the current production step until the end of production. In practice, wafer out predictions are compared to the due dates to determine the priority when dispatching lots. For example, if the wafer out prediction is later than the due date, a lot gets high priority and vice versa. Hence, an accurate wafer out prediction is crucial in maximizing on-time delivery performance. We make a point estimate of the expected residual cycle time for all initial lots and compare this to the actual measured residual cycle time. In the simulation of the proposed aggregate model, the point estimate is the mean of 30 replications. We also benchmark with two other methods using historical data: the current way of working at Nexperia and the historical data approach. In the remainder of this section, we will first explain both benchmark methods. After that, we will compare the performance of the proposed model to the benchmarks.

4.4.3 Benchmark methods

The current way of working at Nexperia to predict the expected cycle time of a lot works as follows. For each product type, an estimated total cycle time is given. This cycle time is based on historically realized cycle times and expert knowledge. This total cycle is translated to residual cycle time per production step in a linear manner. It is assumed that each production step takes an equal amount of time. Thus, the total cycle time is divided by the total number of production steps—taken from the predefined production routing of its product type—to determine the time per production step. Although it is known that this prediction method has limited accuracy, it is chosen as the current way of working due to its straightforward implementation and ease of maintainability.

Another approach to predict residual cycle times is using a historical data prediction inspired by Seidel et al. (2020). This big data approach collects the time stamps of all the processing steps from all the lots in a specific time period. With these time stamps, the realized residual cycle time from each production step per lot can be reconstructed. Per product type, the data points are grouped per production step, and the median is taken. Then, a polynomial is fitted through these medians with a nonlinear least squares fitting procedure, resulting in a prediction for each product type.

Fig. 12

The linear and historical data prediction for the residual cycle time per production step of an example product type

An example of both methods is shown in Fig. 12 for an example product type. Generally, the steps at the beginning of the production process take more time than the last steps. This is caused by the characteristics of the manufacturing process; many steps have longer processing times at the beginning of the process, such as an oxidation step where the wafers have to go in a furnace for many hours. Another reason for this is that the waiting time is much longer in the first part of the process because lots at the start of the process go through bottleneck equipment, where the WIP is often high. The historical data prediction captures the different cycle times per production step, and therefore, is a better benchmark than the linear method of the current way of working.

4.4.4 Performance of the proposed model versus benchmarks

The prediction error for one lot is the difference between the measured residual cycle time and the predicted residual cycle time. For all lots present in the system at the beginning of an analyzed time period, this prediction error is determined. For each method, a kernel density estimation of the distribution of the prediction errors is shown in Fig. 13. As a reference, the distribution of the residual cycle times overall lots is depicted in Fig. 14. For all datasets, the simulation of the proposed aggregate model outperforms the current way of working in predicting the residual cycle time. Thus, it can be argued that the weaknesses of the aggregate modeling have only minor effects on the residual cycle time predictions. This is because the predicted mean cycle time can be very accurate, although the total cycle time distribution is not necessarily that accurate (as shown in Fig. 10). For dataset 1, the performance of the proposed aggregate modeling approach and the historical data approach is closely matched—with the latter slightly better—but for datasets 2 and 3, the simulation model is certainly dominant. The difference between these datasets can be explained by the loading of the fab, which consists of (1) the volume and (2) the type of the lots which are released into production. The loading volume is reflected in the total WIP in the fab, shown in Fig. 15. Recall that the corresponding months of the datasets were shown in Fig. 4a. The WIP in the test part of datasets 2 and 3 is higher, causing cycle times to be longer than observed before. As was explained in Sect. 3.3, the network of aggregate models emulates the flow of lots during production. Therefore, if more lots or a different combination of product types are loaded into the proposed model, the WIP and cycle times will change accordingly. We can conclude that the proposed aggregate model is robust to changing loading conditions when predicting wafer outs, unlike the other two prediction methods.

Fig. 13

Kernel density estimation of the error distributions of the residual cycle time predictions for dataset 1 (left), 2 (middle), and 3 (right). Three prediction methods are used: the proposed simulation model, the historical data approach, and the current way of working

Fig. 14

Kernel density estimations of the residual cycle time of all lots present in the fab

Fig. 15

Total WIP in the real-world fab for the analyzed time period

5 Conclusions and future work

This paper presents a simple and efficient modeling method to abstract multi-product complex job shops, such as a front-end semiconductor wafer fabrication facility. We propose a network of aggregate models, where each aggregate model abstracts all the machines in one work area into a single-server queueing system. Unlike other model abstraction methods, this model does not require a detailed simulation model, because the parameters of the model are derived directly from arrival and departure data, thus reducing development and maintenance costs. These parameters consist of a WIP-dependent effective processing time (EPT) distribution and a WIP- and layer-type-dependent overtaking distribution. We demonstrate the viability of this modeling method in practice by applying it to one of the real-world wafer fabs of Nexperia. This results in a data-driven simulation model which can be used to predict future cycle times and WIP levels. To initialize the model such that it realistically resembles the state of the real-world fab, we propose a queue initialization algorithm that determines the starting order of lots in the aggregate model.

We have analyzed (1) the performance of the aggregate model for single work areas and (2) the performance of the network of aggregate models for the complete wafer fab. In the first analysis, the results show that the aggregate model can accurately predict the (mean and variance of) WIP levels, and cycle time distributions for the majority of the work areas and considered time periods. However, if conditions radically change (such as changes in the capacity of highly utilized equipment) between the training period and test period, then the model cannot make accurate predictions for the test period and should be re-trained with new data. This is illustrated in one case study and significantly improved the performance. In the second analysis, the performance of the model varies for different predictions. On the one hand, the predictions for the WIP levels in work areas and total cycle time distribution are not sufficiently accurate. One of the problems is that the overtaking behavior does not capture the behavior well enough to manage the flow of lots in a network. On the other hand, the network of aggregate models does yield accurate predictions for the total WIP level in the fab, the mean total cycle times, and the expected residual cycle times. For expected residual cycle times, the results show that the proposed model clearly outperforms the two benchmark methods—current practice and a historical data approach—and is much more robust against changing loading conditions.

In future research, the proposed methodology can be improved in two main areas. The first one is that the aggregate model can be extended by addressing non-stationary behavior. If conditions radically change, such as long-term changes in capacity or a change in dispatching strategies, the model has to be retrained. It would be useful to develop retraining triggers based on, for instance, changes in the trend of the measured EPT and overtaking data. In our approach, we simulate the system without considering events that may change the wafer fab’s capacity, such as preventive maintenance, holidays, or new machines. This information may also be used to preemptively change the aggregate model parameters to handle upcoming changes in capacity. I.e., adjusting the aggregate model parameters in advance of anticipated changes in a system’s capacity, in order to ensure that the model remains accurate. At the same time, if the aggregate model is used to make decisions that influence the estimated probability distributions of cycle times, the link between such decisions and the statistical inference obtained from the aggregate model has to be considered. The second area to improve the proposed model is to extend the overtaking distribution such that the flow of lots in a network is captured better. For the wafer fab in this work, adding an operational due date dependency would be interesting. For other wafer fabs or other job shop systems in general, this addition might also be beneficial, but it is advised to consider any property which characterizes dispatching priorities of the lots since this influences the overtaking behavior.

Appendix A: Algorithm to determine EPT and overtaking realizations

We present the algorithm to determine EPT and overtaking realizations as two separate algorithms. Specifically, Algorithm 2 and 3 describe how the EPT- and overtaking realizations are calculated, respectively, for each lot. We adjusted the EPT algorithm of Veeger et al. (2011) such that it also records the layer type of each lot. An overview of the notations is given in Table 2.

In Algorithm 2, the algorithm distinguishes between an arrival (line 3) and a departure event (line 8). For an arrival event, a new EPT is started if the lot arrives in an empty system by setting s equal to $\tau$, and the WIP level sw is set to 1 (line 5). For every lot, its arrival number i, number of lots just before arrival len(xs) and layer type l is appended (indicated by $\mathbin {++}$) to the end of list xs (line 7). For a departure event, the EPT is calculated by taking the difference between the current time $\tau$ and the EPT start time s, and is written to output together with the WIP level sw (line 9). The function detOvert calculates the number of overtaken lots k (line 10), which is written to output with corresponding WIP level aw and layer type l (line 11). If the system is not empty, the EPT timer is restarted and the corresponding WIP level is recorded (line 13). If the system is empty, the timer will be started when a new lot arrives.

The function detOvert described in Algorithm 3 calculates the number of lots the current lot has overtaken. The function iteratively removes each lot from xs and assigns its arrival number to i, the number of lots before arrival to aw, and its layer type to l. If the arrival number j is lower than the i (line 5), then lot j is overtaken by lot i. The overtaken lots are added to list ys and the length of this list is equal to the number of overtaken lots k. If lot j is equal to lot i, the function returns the list $ys \mathbin {++}xs$ (which does not include lot i), the number of overtaken lots len(ys), and the WIP level when lot i entered the system aw (line 8).

Table 2 Summary of notation for the algorithms