Capacity planning in a decentralized autologous cell therapy manufacturing network for low-cost resilience

Abstract

The goals for increased patient access and fast fulfillment have motivated considerable interest in autologous cell therapy manufacturing networks having multiple and geographically distributed manufacturing facilities. However, the cost of safety manufacturing capacity to mitigate supplier disruption risk—a significant risk in the emerging cell manufacturing industry—would be lower if manufacturing is centralized. In this paper, we analyze a decentralized network that has as its objective to minimize the cost of network resilience for mitigating supplier disruption by making use of the fact that bioreactors for autologous therapy manufacturing are small enough to be relocatable. We model this problem as a Markov decision process and develop efficient algorithms that are based on real-time demand data to minimize safety manufacturing capacity and determine how relocatable capacity should be distributed while satisfying resilience constraints. In case studies, based in part on data collected from a Chimeric antigen receptor T cell therapy manufacturing facility at the University of Pennsylvania, we compare decentralized network models with different heuristic algorithms. Results indicate that transshipment in a decentralized network can result in a significant reduction of required safety capacity, reducing the cost of network resilience.

1 Introduction

Autologous cell therapy is an emerging personalized therapeutic method that uses a patient’s cellular material in the development of therapies for several cancers and shows promise for treating blood disorders and autoimmune diseases (Wang et al. 2019). Improving patient benefit is a major objective of this industry. The transition from clinical trials to commercial products for autologous cell therapy is evolving rapidly because of these potential patient benefits and this transition is presenting many challenges, particularly risks associated with an emerging supplier base.

In this paper, we address a key firm-level commercialization challenge for the autologous cell therapy manufacturing industry: determining manufacturing capacity and a reagent replenishment policy in a distributed manufacturing facility network, given supplier disruption risk. We take advantage of the fact that bioreactors for autologous cell therapy manufacturing can be relocatable, allowing us to introduce the concept of dynamic resilience, which we show can reduce manufacturing capacity safety stock and hence the cost of network resilience without compromising network resilience, thereby enhancing firm competitiveness.

Our interest in decentralized multi-facility manufacturing networks, relative to centralized single facility networks is motivated by the objective to improve patient service quality. A centralized manufacturing network has less demanding regulatory requirements, greater potential for economies of scale, greater consistency in operations, but less patient access and longer fulfillment time. However, a decentralized manufacturing network can fulfill cell therapy requests closer to the demand locations, resulting in higher patient access, shorter fulfillment time, and reduce distribution costs.

Supplier disruptions in the cell manufacturing industry are of concern for two reasons. First, patients who qualify for cell therapy often have short term dire prognoses, a supplier disruption can cause a delay in the completion of a cell therapy, and therefore significantly increase patient mortality risk. Second, supplier disruptions in this industry are not uncommon. The cell manufacturing industry is an emerging industry with a limited supplier base for certain key reagents, and hence there may be only a single supplier for a key reagent. Further, the industry is heavily regulated in the U.S. by the Federal Drug Administration (FDA), and FDA requirements for reagent uniformity and quality are a challenge to satisfy for even a single supplier. Satisfying these requirements for multiple suppliers would be much more of a challenge. Thus, a typical strategy for mitigating supplier disruption risk common in many other industries—sourcing from multiple suppliers for the same raw material or work in progress—is not considered applicable in the cell manufacturing industry. Further, the cell manufacturing industry has witnessed several major supplier disruptions. In 2017 alone, the cell manufacturing industry witnessed reagent supply disruptions due to Hurricane Maria, a severe flu season (Jarvis 2017; Wendelbo and Blackburn 2018), and a shutdown of a major cell therapy supplier due to sterility issues (Palmer 2017). More recently, significant reagent supplier disruption has been caused by the COVID-19 pandemic (Bachanova1 et al. 2020) as demand for several key reagents (Bell 2020) needed for COVID-19 antigen testing kits surged, leading to shortages of those same key reagents for autologous cell therapy manufacturing, shortages that are forecasted to persist into mid-2021 (Fitzpatrick et al. 2020).

Faced with the challenge germane to supplier disruption risks, a natural solution is to increase the inventory levels of raw material, work-in-progress (WIP), and the final product and/or adding manufacturing capacity. However, such procedures for strengthening supply chain resilience and agility also can be expensive; and some of which could be inappropriate in autologous cell manufacturing, e.g. increasing buffer WIP and final product. Competitive advantage is enhanced if a firm’s supply chain resilience and agility are at least as good as the competition’s but at lower cost. Different from handling reagent supplier disruption in a centralized facility, a decentralized network can re-balance specimen and reagent inventories among facilities. Another standard technology that enables reconfigurability of a supply chain is the development of the relocatable manufacturing module (REMO) (Malladi et al. 2020; Faugere et al. 2020), e.g. bioreactors in personalized medicine manufacturing, 3D printers, smart lockers in relocatable storage network, mobile intensive care units (ICU) and ventilators in epidemic/pandemic control (Li 2021). We remark that a bioreactor in autologous cell therapy production is used to manufacture a therapy for a specific, individual patient, and is typically small enough to be portable, hence it can be considered as a REMO (Wang et al. 2019). Supply chain resilience can be further enhanced by also relocating manufacturing modules (e.g. bioreactors) based on real-time data-driven demand analysis. The current FDA regulatory structure does not allow cell therapy bioreactors to be relocated without recertification. However, we hope our research will influence future regulatory reform for cell therapy industry.

The reconfigurability of a decentralized manufacturing network can blend the advantages of a distributed supply chain system of easy patient access and fast fulfillment, and a centralized supply chain system to enable economies of scale, resource risk “pooling” and cost reduction. Therefore, we propose a dynamic resilient decentralized manufacturing network for autologous cell therapy which allows the supply chain system to respond to and recover from supplier disruptions by sharing demand, transshipping inventory and relocating manufacturing capacities where needed in the network. Such a reconfigurable supply chain will be dynamically resilient and either lean or agile, depending on need.

1.1 Contributions

The objective of this paper is to investigate ways to reduce the cost of supply chain resilience in a decentralized autologous cell therapy manufacturing network under supplier disruption risks. We propose analytical and numerical methods for determining (i) the bioreactor quantities and reagent replenishment policies for the reagent at each manufacturing facility and (ii) specimen and reagent transshipment and bioreactor relocation policies. The solution of the models will help address questions such as:

• How many bioreactors should be invested at each facility?

• How many units of reagent should each facility order?

• When and where to transship specimen or reagent and relocate bioreactors to ensure a desired level of resilience with lower cost?

We present the problem model in Sect. 3. Analysis of the proposed model are presented in Sect. 4. Solution algorithms are presented in Sect. 5. In Sect. 6, we compare different decentralized models and different heuristic algorithms based in part on data collected from a CAR-T cell therapy manufacturing facility at the University of Pennsylvania. We show that compared to the case where no transshipment can occur, transshipment in a decentralized network can result in a significant reduction of required safety capacity reducing the cost of the network resilience.

2 Related literature

We now present a review of the resource sharing and supplier disruption literature and how this literature is related to our research. Resource sharing operations that we consider include demand sharing (transshipping specimens), inventory transshipping (transshipping units of reagent) and equipment relocation (relocating bioreactors). A comprehensive review of the literature on capacity planning and resource management under supplier disruption risks in a centralized manufacturing network can be found in Li (2021).

Resource sharing There is ample research in resource sharing, e.g. demand allocation (Tiemessen et al. 2013), lateral transshipment (Wong et al. 2005; Paterson et al. 2011) and multi-echelon inventory assignment (de Kok et al. 2018). Multi-period inventory replenishing and transshipping in a supply chain network are modeled and analyzed in Karmarka (1981) and Karmarka (1987). Rudi et al. (2001) demonstrated the potential of transshipping strategies outperforming a centralized system using a two-facility example. Herer et al. (2002) and Herer et al. (2006) investigated how inventory transshipping can increase supply chain agility corresponding to the number of fulfillment nodes in a supply chain. Zhao et al. (2008) examined inventory sharing in a two-location network for a make-to-stock product. Different supply chain structures that allow inventory transshipping are compared in Lien et al. (2011). A two-echelon single-warehouse multiple-retail supply chain with transshipping is considered in Axsater et al. (2002) and Wee and Dada (2005). An equipment (usable resource) relocation problem is shown to be similar to a dynamic facility location problem. A single facility (batched capacity) relocation problem is studied in Halper and Raghavan (2011) and Qiu and Sharkey (2013), and a multiple facility relocation problem is analyzed in Ghiani et al. (2002), Melo et al. (2005) and Jena et al. (2015). A production capacity relocation and inventory control problem is studied in Malladi et al. (2020), and a storage capacity relocation problem is modeled and analyzed in Faugere et al. (2020).

Mitigating supplier disruption risks in a decentralized network Due to regulatory requirements for cell therapy manufacturing, multi-sourcing (Dada et al. 2007; Wang et al. 2010) is not used as a strategy to mitigate supplier disruption risks. For instance, in the U.S., FDA regulations for cell therapy manufacturing are such that a cell therapy manufacturer only has a single reagent source or dealing with the regulatory hurdle to have more than a single source is particularly onerous. Schmitt et al. (2015) show that a decentralized network structure, even without transshipping inventory, reduces cost variance through what is termed the risk diversification effect. Given inventory replenishment plans, inventory transshipping in a two-retailer network with supplier disruptions is studied in Zhao et al. (2005). Sosic (2006) and Yan and Zhao (2015) extend the two-location problem to n-retailer (n $\ge$ 2) cases. Hu et al. (2008) extends research in Zhao et al. (2005) to the case where joint inventory replenishment and transshipment decisions are allowed. Ozen et al. (2012) studied inventory transshipping with demand distribution updates. Our research contributions include the determination of a policy and structural results for manufacturing capacity relocation that provides network resiliency at low cost in a decentralized cell therapy manufacturing supply chain network, tractable gap analysis (i.e., upper and lower bounds on the cost function), analysis of several heuristics for autologous cell therapy manufacturing problem, and two case studies that illustrate the potential for resource sharing and the impact of supplier correlations.

3 Problem and model

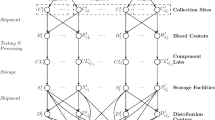
Consider an autologous cell therapy manufacturing network with multiple and geographically distributed manufacturing facilities. Each facility has its own reagent inventory, idle bioreactors, working bioreactors (manufacturing-in-process), and local demand in the form of patient specimens waiting in the facility’s arrival queue for therapy manufacturing to begin. The decision-making chronology between epochs at each facility is as follows,

• 1. The production quantities are selected.

• 2. Reagent replenishment decisions are made.

• 3. Bioreactor relocation and specimen and reagent transshipment decisions are determined.

• 4. Reagent inventory is replenished and some bioreactors are reset to idle.

• 5. Bioreactor relocation and specimen and reagent transshipment are executed.

• 6. New patient specimens arrive just before the next epoch and are added to the facility’s arrival queue.

Ideally, these decisions would be made by a global controller, based on local demand reagent availability data for all facilities and the following local information for all facilities: the set of patients waiting for their therapy manufacturing to begin, the current reagent inventory level, the current number of idle bioreactors, and the current number of bioreactors that have been manufacturing therapies for $\tau$ epochs, for all possible $\tau$. We assume T epochs are required for therapy manufacturing.

The capacity planning problem includes the operational problem of determining reagent replenishment, bioreactor relocation, and specimen and reagent transshipment policies for all manufacturing facilities in addition to the following interrelated design problem: determine a priori the total number of bioreactors for the network – a number held constant over the planning horizon – and how these bioreactors initially should be distributed across the facilities. We refer to this capacity planning problem as the Co-Net case, given it involves the Coordination between and Cooperation of all the facilities in the Network. A useful and tractable special case of Co-Net is Iso-Net, which does not permit bioreactor relocation or specimen and reagent transshipment, resulting in a Network of facilities acting in Isolation.

We now model both the Iso-Net and Co-Net cases as finite horizon MDPs. Assume there are L facilities, and the problem planning horizon has ${\mathcal {T}}$ decision epochs, where T is considerably smaller than ${\mathcal {T}}$. For example, assume epochs occur weekly, three weeks are required to manufacture a therapy ($T =3$), and the problem horizon contains 52 epochs (${\mathcal {T}}=52$). Let $[\cdot ]$ be the set operator such that $[z] = \{1,\ldots , z\}$ for any integer $z \ge 1$. At epoch t, we define a system state ${\mathbf {x}}_t=({\mathbf {s}}_t,{\mathbf {b}}_t,{\mathbf {r}}_t,{\mathcal {A}}_t)$,

• $\mathbf {s_t}=\{s^l_t,l\in [L] \}$, where $s^l_t\ge 0$ is the number of specimens waiting for therapy manufacturing to begin at facility l at epoch t

• ${\mathbf {b}}_t=\{{\mathbf {b}}^l_t,l\in [L] \}$, where ${\mathbf {b}}^l_t=(b^{l,0}_t,\ldots ,b^{l,T-1}_t)$, $b^{l,\tau }_t\ge 0$ is the number of bioreactors at facility l at epoch t that are $\tau$ epochs from completing therapy manufacturing, and where $b^{l,0}_t$ is the number of idle bioreactors at facility l at epoch t

• $\mathbf {r_t}=\{r^l_t,l\in [L] \}$, where $r^l_t\ge 0$ is the number of units of reagent at facility l at epoch t

• ${\mathbf {A}}_t=\{A^l_t,l\in [L] \}$, where $A^l_t$ is the maximum number of units of reagent that can be supplied to facility l at epoch t. The dynamics of the process $\{{\mathcal {A}}_t,t\ge 0\}$ is described by the epoch and action invariant Markov chain $Pr({\mathbf {A}}_{t+1}|{\mathcal {A}}_t)$, where ${\mathcal {A}}_t=\{A_t,\ldots ,A_{t-\tau } \}$ for some given constant $\tau \ge 0$.

Let $\mathbf {m_t}=\{m^l_t,l\in [L] \}$, where $0\le m^l_t\le \min \{s^l_t,b^{l,0}_t,r^l_t\}$ is the number of therapies start manufacturing at facility l at epoch t. Once therapy manufacturing has begun, the decision-maker can select the following decision variables for $t\in [{\mathcal {T}}]$:

• $\mathbf {w_t}=\{w^l_t,l\in [L] \}$, where $w^l_t\ge -(s^l_t-m^l_t)$ is the number of specimens transshipped into facility l if $w^l_t$ is non-negative and from location l if $w^l_t$ is non-positive. We assume the total number of specimens in the network is identical before and after transshipment, i.e. $\sum _l w^l_t=0$.

• $\mathbf {a_t}=\{a^l_t,l\in [L] \}$, where $0\le a^l_t\le A^l_t$ is the reagent replenishment at facility l.

• $\mathbf {e_t}=\{e^l_t,l\in [L] \}$, where $e^l_t\ge -(r^l_t - m^l_t + a^l_t)$ is the units of reagent transshipped into facility l if $e^l_t$ is non-negative and from facility l if $e^l_t$ is non-positive. We assume the total number of units of reagent in the network is identical before and after transshipment, i.e. $\sum _l e^l_t=0$.

• $\mathbf {q_t}=\{q^l_t,l\in [L] \}$, where $q^l_t\ge -(b_t^{l,0} - m^l_t + b_t^{l,1})$ is the number of bioreactors relocated into facility l if $q^l_t$ is non-negative and from location l if $q^l_t$ is non-positive. We assume the total number of idle bioreactors in the network is identical before and after relocation, i.e. $\sum _l q^l_t=0$.

We are assuming that all transshipments can occur within one period, which we believe is a reasonable assumption for the domain of interest (assuming all FDA restrictions are waived). We remark that allogeneic bioreactors, larger pharmaceutical manufacturing modules, or metal 3D printers, each of which may require a 20-foot/TEU container for relocation, would likely require more than a week to move and would remove manufacturing capacity during the move, which would require a more complicated model. We note that under current regulations, relocation requires recertification and hence serves as a barrier to a more flexible supply chain design. However, our analysis can be used to understand the implications of changing the regulatory structure without affecting patient safety.

Let ${\mathbf {d}}_t=\{d^1_t,\ldots ,d^L_t\}$ be stochastic demands occurred during period t, where we assume $d^l_t$’s are independent. The system dynamics are

$$\begin{aligned}&s^l_{t+1} = s^l_t - m^l_t + d^l_t+w^l_t,\quad r^l_{t+1} = r^l_t - m^l_t + a^l_t+e^l_t,\quad Pr({\mathbf {A}}_{t+1}|{\mathcal {A}}_t),\\&b_{t+1}^{l,\tau } = {\left\{ \begin{array}{ll} b_t^{l,0} - m^l_t + b_t^{l,1}+q^l_t &{} \tau = 0,\\ b_t^{l,\tau +1} &{} 1\le \tau \le T-2,\\ m_t^l &{} \tau = T-1. \end{array}\right. } \end{aligned}$$

We remark that the Markovian process $\{{\mathcal {A}}_t, t\in [{\mathcal {T}}]\}$ is capable of modeling a variety of supply processes including but not limited to uncertain, restricted and correlated suppliers. We assume that transshipment/relocation decisions are made at the beginning of each decision epoch just after therapy manufacturing begin but before the realization of patient demands. Therefore, the maximum quantities of specimen/reagent/bioreactor that can be removed from facility l are $s^l_t-m^l_t$, $r^l_t - m^l_t + a^l_t$ and $b_t^{l,0} - m^l_t + b_t^{l,1}$, respectively. The action spaces of ${\mathbf {w}}_t$, ${\mathbf {e}}_t$ and ${\mathbf {q}}_t$ are

$$\begin{aligned}&\{{\mathbf {w}}_t: w^l_t\ge -(s^l_t-m^l_t), \sum _l w^l_t=0 \}, \qquad \{{\mathbf {e}}_t:{e}_t\ge -(r^l_t - m^l_t + a^l_t),\sum _l e^l_t=0\},\\&\{{\mathbf {q}}_t:{q}^l_t\ge -(b_t^{l,0} - m^l_t + b_t^{l,1}),\sum _l q^l_t=0\}. \end{aligned}$$

We assume that the single period cost accrued in period t is additive over facilities, i.e.

$$\begin{aligned}C({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t,{\mathbf {d}}_t|{\mathbf {x}}_t)=\sum _l C^l(w^l_t,a^l_t,e^l_t,q^l_t,m^l_t,d^l_t|x^l_t).\end{aligned}$$

The cost of facility l consists of multiple components:

• $c_R a^l_t$ is the reagent replenishment cost for the reagent, where $c_R$ is the cost per unit of regent.

• $h_R(r^l_{t+1} - s^l_{t+1})^+$ is the reagent overstock holding cost, charged if there are more units of reagent than specimens at epoch $t+1$, where $h_R$ is the holding cost per excess unit of reagent.

• $h_B(b^{l,0}_{t+1}-s^l_{t+1})^+$ is the bioreactor overstock holding cost, charged if there are more idle bioreactors than specimens at epoch $t+1$, where $h_B$ is the bioreactor holding cost per excess idle bioreactor.

• $p_R(s^l_{t+1} - r^l_{t+1})^+$ is the reagent understock penalty, charged if there are less units of reagent than specimens at epoch $t+1$, where $p_R$ is the penalty cost per insufficient unit of reagent.

• $p_B(s^l_{t+1} - b^{l,0}_{t+1})^+$ is the bioreactor understock penalty, charged if there are less idle bioreactors than specimens at epoch $t+1$, where $p_B$ is the penalty cost per insufficient idle bioreactor.

• $K_S\frac{|w^l_t|}{2}$ is the cost of transshipping $w^l_t$ specimens from/to facility l that is charged on facility l.

• $K_R\frac{|e^l_t|}{2}$ is the cost of transshipping $e^l_t$ units of reagent from/to facility l that is charged on facility l.

• $K_B\frac{|q^l_t|}{2}$ is the cost of relocating $q^l_t$ bioreactors from/to facility l that is charged on facility l.

Therefore,

$$\begin{aligned} C^l(w^l_t,a^l_t,e^l_t,q^l_t,m^l_t,d^l_t|x^l_t) =\,&c_R a^l_t + K_R\frac{|e^l_t|}{2} + h_R\left( r^l_{t+1} - s^l_{t+1}\right) ^+ + p_R\left( s^l_{t+1} - r^l_{t+1}\right) ^+\\&\quad + K_B\frac{|q^l_t|}{2} + h_B\left( b^{l,0}_{t+1}-s^l_{t+1}\right) ^+ + p_B\left( s^l_{t+1} - b^{l,0}_{t+1}\right) ^+\\&\quad + K_S\frac{|w^l_t|}{2}. \end{aligned}$$

We model the Co-Net first and then model the Iso-Net as a special case of Co-Net. For the Co-Net problem, we seek a $b^0_1=\left( b^{1,0}_1,\ldots ,b^{L,0}_1\right)$ (the capacity planning phase) and a policy that determines ${\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t$ and ${\mathbf {m}}_t$ as functions of ${\mathbf {x}}_t=({\mathbf {s}}_t,{\mathbf {b}}_t,{\mathbf {r}}_t,{\mathbf {A}}_t)$ for all $t\ge 1$ (the operational phase) to find an minimum of the criterion

$$\begin{aligned} c_B \sum _l b^{l,0}_1 + v^\pi \left( {\mathbf {x}}_{1}\left( b^0_1\right) \right) , \end{aligned}$$

(1)

where $c_B$ is the expense of purchasing a bioreactor. $v^\pi ({\mathbf {x}}_{1}(b^0_1))$ is the expected total discounted cost over the infinite horizon, assuming policy $\pi$ and ${\mathbf {x}}_{1}$ (which is depending on the selection of $b^0_1$), and discount factor $\beta \in [0,1)$, assuming ${\mathbf {s}}_1={\mathbf {r}}_1={\mathbf {0}}$, and $b^{l,\tau }_1=0$ for $\tau =1,\ldots ,T-1$. Let

$$\begin{aligned} \varPi ({\mathbf {x}}_t) =&\{({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t):0\le {\mathbf {a}}_t\le {\mathbf {A}}_t, \sum _l w^l_t = 0,\sum _{l} e^l_t = 0,\sum _l q^l_t=0,\\&w^l_t\ge -\left( s^l_t-m^l_t+d^l_t\right) , e^l_t\ge -\left( r^l_t - m^l_t + a^l_t\right) ,q^l_t \ge -\left( b_t^{l,0} - m^l_t + b_t^{l,1}\right) ,\forall l,\\&0\le m^l_t\le \min \{s^l_t,b^{l,0}_t,r^l_t\} \}, \end{aligned}$$

and assume

$$\begin{aligned} \varPi ^U({\mathbf {x}}_t) =&\{({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t)\in \varPi ({\mathbf {x}}_t) :{\mathbf {w}}_t={\mathbf {e}}_t={\mathbf {q}}_t={\mathbf {0}}\}. \end{aligned}$$

We proceed as follows to solve a Co-Net problem:

• (i) Let $b^0_1$ be given.

• (ii) Determine $\pi ^*$ such that $v^{\pi ^*}({\mathbf {x}}_{1}(b^0_1))\le v^\pi ({\mathbf {x}}_{1}(b^0_1))$ for all $\pi$.

• (iii) Determine $b^{0'}_1$ such that

  $$\begin{aligned}c_B \sum _l b^{l,0'}_1 + v^{\pi ^*}({\mathbf {x}}_{1}(b^0_1))\le c_B \sum _l b^{l,0}_1 + v^{\pi ^*}({\mathbf {x}}_{1}(b^0_1))\end{aligned}$$

  .

• (iv) If $\Vert b^{0'}_1-b^{0}_1\Vert \le \epsilon$, then stop. Otherwise, $b^{0'}_1\rightarrow b^{0}_1$, and go to Step (ii).

Proposition 1

Criterion (1) is convex in $b^0_1$.

Proof

$c_B\sum _{l}b^{l,0}_1$ is linear in $b^{l,0}_1$’s, therefore, it remains to show that $v^*_1$ is convex in $b^{l,0}_1$’s. Let

$$\begin{aligned}g_t({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t|{\mathbf {x}}_t) = {\mathbb {E}}[C({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t,{\mathbf {d}}_t|{\mathbf {x}}_t)+\beta v_{t+1}^*({\mathbf {x}}_{t+1})],\end{aligned}$$

if we can show that $g_t$ is convex in ${\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t$ and $b^{l,0}_t$’s, then we can show $v^*_t$ is convex in $b^{l,0}_t$’s (so that $v^*_1$ is convex in $b^{l,0}_1$’s) by the following lemma in Bertsekas et al. (2003) (Proposition 2.3.6).

Lemma 1

If $f(x,y): {\mathbb {R}}^n\times {\mathbb {R}}^m\rightarrow {\mathbb {R}}$ is convex in x and y, and $Y\in {\mathbb {R}}^m$ is a convex set, then $g(x)=\min _{y\in Y} f(x,y)$ is convex in x.

Therefore, it remains to show that $g_t$ is convex in ${\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t$ and $b^{l,0}_t$’s. By induction, it is trivial to show the single period cost, i.e. C is convex in $b_\cdot ^0$. Suppose $g_{t+1}$ is convex in ${\mathbf {w}}_{t+1},{\mathbf {a}}_{t+1},{\mathbf {e}}_{t+1},{\mathbf {q}}_{t+1}, {\mathbf {s}}_{t+1}, {\mathbf {r}}_{t+1}$ and $b^{l,0}_{t+1}$’s, then by Lemma 1, and hence, $v^*_{t+1}$ is convex in ${\mathbf {s}}_{t+1}, {\mathbf {r}}_{t+1}$ and $b^{l,0}_{t+1}$’s. We introduce another lemma from Bertsekas et al. (2003) (Proposition 1.2.4).

Lemma 2

If $f:{\mathbb {R}}^m$ is convex, then $g(x)=f(Ax+b)$ is convex in $x\in {\mathbb {R}}^n$ for any $A\in {\mathbb {R}}^{m\times n}$ and $b\in {\mathbb {R}}^m$.

Since ${\mathbf {s}}_{t+1}, {\mathbf {r}}_{t+1}$ and $b^{l,0}_{t+1}$’s are linear functions of ${\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t$ and $b^{l,0}_t$’s, then by Lemma 2, $g_t$ is convex in ${\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t$ and $b^{l,0}_t$’s. $\square$

Proposition 1 suggests that, assuming $v^{\pi ^*}({\mathbf {x}}_{1},b^0_1)$ is bounded, a coordinate descent search, for example (Wright 2015), will find a global minimum of Criterion (1).

Since the state and action spaces of $v^{\pi }({\mathbf {x}}_{1}(b^0_1))$ are countable, we now show the existence of a $b^0_1$ and $\pi$ such that $v^{\pi }({\mathbf {x}}_{1}(b^0_1))$ is finite. It is sufficient to assume $L=1$. Let $a_t=s_t-r_t+K$, and $0\le K\le \infty$. Assume also that $b^0_t\ge m_t=\min \{s_t,r_t\}$ for all $t\ge 1$. Then,

$$\begin{aligned}s_{t+1}=s_t-m_t+d_t,\quad r_{t+1}=s_t-m_t+K. \end{aligned}$$

A standard induction argument shows that for all $t\ge 2$,

$$\begin{aligned}&s_{t+1}=d_{t-1}-\min \{d_{t-1},K\}+d_t,\quad r_{t+1}=d_{t-1}-\min \{d_{t-1},K\}+K,\\&m_{t+1}=d_{t-1}-\min \{d_{t-1},K\}+\min \{d_t,K\}. \end{aligned}$$

Assume $0\le {{\bar{d}}}_m\le d_t\le {{\bar{d}}}^M$ for all $t\ge 1$, and note $d_t-\min \{d_t,K\}=(d_t-K)^+$. Then,

$$\begin{aligned} m_t\le ({{\bar{d}}}^M-K)^++\min \{{{\bar{d}}}^M,K\}={{\bar{d}}}^K. \end{aligned}$$

Let $b^0_1=T{{\bar{d}}}^M$, and note that for all $t\ge 1$ $\sum _{\tau =0}^{T-1}b^\tau _t=T{{\bar{d}}}^M$, $b^\tau _t\le {{\bar{d}}}^M$ for all $\tau \le 1$, and ${{\bar{d}}}^M\le b^0_t\le T{{\bar{d}}}^M$. Thus for all $t\ge 1$,

$$\begin{aligned}&s_{t}\le ({{\bar{d}}}^M-K)^++{{\bar{d}}}^M,\quad r_t\le ({{\bar{d}}}^M-K)^++K,\\&{{\bar{d}}}_m\le a_t = d_{t-1}\le {{\bar{d}}}^M, \end{aligned}$$

and state and action space for an MDP seeking a K that minimizes (1) with respect to $\pi$ for $b^0_1=T{{\bar{d}}}^M$ are finite and the single period cost is bounded. Results in Li (2021) (Sect. A.1.1) guarantee it is always optimal to choose $m^l_t=\min \{s^l_t,b^{l,0}_t,r^l_t \}$. Results in Puterman (1994) (Theorem 6.2.10) guarantees there exists a fixed point to

$$\begin{aligned} Hv({\mathbf {x}}_t) =&\min _{{\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t}{\mathbb {E}}[C({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t,{\mathbf {d}}_t|{\mathbf {x}}_t)+\beta v({\mathbf {x}}_{t+1})]\\ s.t.&({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t)\in \varPi ({\mathbf {x}}_t)\nonumber . \end{aligned}$$

(2)

which leads to identifying $\pi ^*$ and $v^{\pi ^*}(b^0_1,{\mathbf {x}}_1)$. We note that by replacing action space $\varPi ({\mathbf {x}}_t)$ by $\varPi ^U({\mathbf {x}}_t)$, we obtain an Iso-Net problem.

4 Bounds

We have identified value of $b^0_1$ that guarantee the existence of a bounded solution to the Co-Net problem since its state and action space are finite. However, although finite, these state and action space can be quite large, challenging problem tractability. We now seek more computationally tractable bounds on the solution to the Co-Net problem.

We note that the Iso-Net problem is L independent facility Co-Net problems with $\varPi ({\mathbf {x}}_t)$ replaced by $\varPi ^U({\mathbf {x}}_t)\subseteq \varPi ({\mathbf {x}}_t)$, which can be decomposed into multiple single facility problems with much smaller state and action spaces than the Co-Net problem. For each single facility problem, we minimize a criterion $c_Bb^{l,0}_1+v^{\pi ^l}(x^l_1,b^{l,0})$ for each l, where $v^{\pi ^l}(x^l_1,b^{l,0})$ is the expected cost function for location l. The sum of these criterion is an upper bound on the solution of the Co-Net problem. We note that if the transshipping/relocation costs are significantly large (i.e. All K’s approaching infinity),, any resource sharing would incur an unacceptable cost, and thus the Iso-Net heuristic can produce an exact optimal solution.

We then present a lower bound of Co-Net. Let

$$\begin{aligned}C^L({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t,{\mathbf {d}}_t|{\mathbf {x}}_t)=C({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t,{\mathbf {d}}_t|{\mathbf {x}}_t) \end{aligned}$$

such that $K_S=K_R=K_B=0$; hence $C^L\le C$. We further assume ${\mathbf {s}}_t$, $b^\tau _t$ (for $\tau =0,\ldots ,T-1$) and ${\mathbf {r}}_t$ can be immediately relocated before the determination of ${\mathbf {m}}_t$ for all t. It is straightforward to show that this problem is equivalent to an $L=1$ with state vector $(\sum _{l} s^l_t,\sum _{l} b^{l,\tau }_t,\tau =0,\ldots ,T-1,\sum _{l} r^l_t,{\mathbf {A}}_t)$, and demand $\sum _{l} d^l_t$ for all t.

Let $a_t = \sum _{l} a^l_t$, $s_t = \sum _{l} s^l_t$, $b^\tau _t = \sum _{l} b^{l,\tau }_t$, $r_t = \sum _{l} r^l_t$, $m_t = \sum _{l} m^l_t$, and $d_t = \sum _{l} d^l_t$, an optimal equation of the operational problem of the lower bound problem is

$$\begin{aligned} H^L v({x}_t) =&\min _{{a}_t,{m}_t\in {\mathbb {Z}}}{\mathbb {E}}[ C^L({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t,{\mathbf {d}}_t|{\mathbf {x}}_t)+\beta v({x}_{t+1})]\\ s.t. \quad&0\le {a}_t\le \sum _{l}{A}^l_t,\nonumber \\&0\le m_t\le \min \{s_t, b^{0}_t, r_t\}\nonumber . \end{aligned}$$

(3)

This problem produces a lower bound of Co-Net since $C^L\le C$ and its feasible region is a relaxation of (2).

In summary, upper and lower bounds on the computationally challenging Co-Net problem can be determined by solving L single facility problem and one single facility problem, respectively.

5 Solution algorithms

5.1 Solving a capacity planning phase problem

We have shown earlier that there exist $b^{1,0}_1,\ldots , b^{L,0}_1$, such that there is an optimal expected total discounted operation cost and that a global minimum can be iteratively searched using a coordinate descent algorithm. We introduce the implementation details to solve a capacity planning phase problem for Co-Net.

In iteration k, the coordinate descent algorithm sample an improving coordinate, choose a searching step size $\delta _k$, and evaluate

$$\begin{aligned}v^{\pi ^*}\left( {\mathbf {x}}_1\left( b^{1,0}_1,\ldots ,b^{i_k,0}_1-\delta _k,\ldots ,b^{L,0}_1\right) \right) \quad \text {and}\quad v^{\pi ^*}\left( {\mathbf {x}}_1\left( b^{1,0}_1,\ldots ,b^{i_k,0}_1+\delta _k,\ldots ,b^{L,0}_1\right) \right) . \end{aligned}$$

We remark that the learning step size $\delta _k$ is a non-increasing integer such that $\lim _{k\rightarrow \infty }\delta _k=1$. Update $b^{i_k,0}_1$ to the design candidate from $\{b^{i_k,0}_t-\delta _k, b^{i_k,0}_1, b^{i_k,0}_t+\delta _k\}$ that produces the smallest total cost. Keep iterating until a stopping criterion. Details of the coordinate descent search are summarized in Algorithm 1.

5.2 Solving an operational phase problem

Given a bioreactor system design, $\left( b^{1,0}_1,\ldots ,b^{L,0}_1\right)$, it is often a challenge to solve an exact operational phase problem to obtain an optimal expected total operational cost $v^{\pi ^*}\left( {\mathbf {x}}_1,b^{1,0}_1,\ldots ,b^{L,0}_1\right)$. The computational challenge motivates our research in design of heuristics. We present three Approximate Dynamic Programming (ADP) heuristic, each of which solves a surrogate model with an approximated cost-to-go function. Let $\pi$ be a policy obtained from an ADP heuristics, and $v^\pi$ be an evaluation of policy $\pi$. We then replace $v^{\pi ^*}$ by $v^\pi$ in Algorithm 1, and hence approximately solve the capacity planning phase problem.

5.2.1 Myopic heuristic (MYO)

The MYO heuristic minimizes a single period cost at epoch t

$$\begin{aligned} \min _{({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t)\in \varPi ({\mathbf {x}}_t)}&{\mathbb {E}}[C({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t,{\mathbf {d}}_t|{\mathbf {x}}_t)] \end{aligned}$$

(MYO)

This heuristic is myopic as the cost-to-go function is ignored. MYO can be reformulated as a mixed integer programming (MIP) problem.

5.2.2 Extended myopic heuristic (E-MYO)

Due to the fact that a myopic policy would potentially understock reagent if a supplier disruption occurs, we extend the myopic heuristic by hybridizing

• (i) Reagent inventory replenishment decision by solving an computational efficient Iso-Net model, denoted as ${{\hat{\mathbf {a}}}}_t$

• (ii) Resource sharing decision by solving a single period cost minimization problem, given reagent inventory replenishment policy ${\mathbf {a}}_t={{\hat{\mathbf {a}}}}_t$.

Let $\varPi ({\mathbf {x}}_t|{{\hat{\mathbf {a}}}}_t)$ be a hybrid action space at epoch t, i.e.

$$\begin{aligned} \varPi ({\mathbf {x}}_t|{{\hat{\mathbf {a}}}}_t) =&\{({\mathbf {w}}_t,{{\hat{\mathbf {a}}}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t): \sum _l w^l_t = 0,\sum _{l} e^l_t = 0,\sum _l q^l_t=0,\\&w^l_t\ge -(s^l_t-m^l_t+d^l_t), e^l_t\ge -(r^l_t - m^l_t + {{\hat{a}}}^l_t),q^l_t \ge -(b_t^{l,0} - m^l_t + b_t^{l,1}),\forall l\\&0\le m^l_t\le \min \{s^l_t,b^{l,0}_t,r^l_t\} \}. \end{aligned}$$

The E-MYO heuristic minimizes a single period cost over the hybrid action space at epoch t

$$\begin{aligned} \min _{({\mathbf {w}}_t,{{\hat{\mathbf {a}}}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t)\in \varPi ({\mathbf {x}}_t|{{\hat{\mathbf {a}}}}_t)}&{\mathbb {E}}[C({\mathbf {w}}_t,{{\hat{\mathbf {a}}}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t,{\mathbf {d}}_t|{\mathbf {x}}_t)]. \end{aligned}$$

(E-MYO)

E-MYO can also be reformulated as a MIP. We note that if the disruption probability and the bioreactor purchase cost are both zero. The number of idle bioreactors could be always at least as large as the minimum of the number of patients in the arrival queue and the number of units of reagent. In this setting, the problem reduces to a repeated newsvendor problem, and for this special case, both the MYO and EMYO heuristics produce an exact optimal solution.

5.2.3 Mean demand lookahead heuristic (MDL)

An MDL heuristic extends a MYO heuristic by approximating the cost-to-go function as the total cost over a lookahead horizon. We calculate the lookahead period cost based on deterministic state transitions assuming that the realized demands in each lookahead period equals to the mean demand. For example, given ${\mathbf {s}}_t$, we cast deterministic state transition ${\mathbf {s}}_{t+1}={\mathbf {s}}_t-{\mathbf {m}}_t+ {{\bar{\mathbf {d}}}}$, where ${{\bar{\mathbf {d}}}}$ is the mean demands per period. However, we use distributional demand to calculate the expect cost in each lookahead period.

Let ${\mathcal {A}}({\mathcal {L}})=\{{\mathbf {A}}_{t+1},\ldots ,{\mathbf {A}}_{t+{\mathcal {L}}}\}$ be a realization of supplier capacities in an ${\mathcal {L}}$-period lookahead horizon, and ${{\bar{x}}}_{t+j}({\mathcal {A}}(j))$ be a hypothesis state at epoch $t+j$ assuming ${{\bar{\mathbf {d}}}}$ and $\{{\mathbf {A}}_{t+1},\ldots ,{\mathbf {A}}_{t+j}\}$ are realized in the first j lookahead periods. An ${\mathcal {L}}$-lookahead MDL (MDL-${\mathcal {L}}$) heuristic solves a multi-period problem

(MDL-${\mathcal {L}}$) can be reformulated as a MIP, however, if the cardinality of ${\mathbf {A}}$ is huge, the number of decision variables in (MDL-${\mathcal {L}}$) grows exponentially. Therefore, we would rely on cut generation methods (i.e. Benders decomposition) (Benders 1962; Bertsimas and Tsitsiklis 1997; Lasdon 2002) to accelerate the computational process of proper decisions $({\mathbf {w}}_t,{\mathbf {a}}_t,{\mathbf {e}}_t,{\mathbf {q}}_t,{\mathbf {m}}_t)$. MDL policies achieve its best decision quality if the disruption period is bounded by ${\mathcal {L}}$, since in this setting, the MDL covers the entire lookahead horizons without disruption uncertainties.

6 Case studies

6.1 Case study 1: the potential of resource sharing

We investigate the cost efficiency of a Co-Net, comparing to an Iso-Net, under the same resiliency assumption, i.e. $p_B$’s in a Co-Net and an Iso-Net are the same; and $p_R$’s in both problems are also identical. We consider a two facility network ($L=2$). The specifications of the facilities are based on the Clinical Cell and Vaccine Production Facility (CVPF) at the University of Pennsylvania (see Table 1). We adopt system specifications (e.g. demand distribution, production duration, etc.) from Wang et al. (2019), and adopt cost assessments from Harrison et al. (2019).

Table 1 System specs and cost parameters

Resource sharing costs are estimated based on surveys with researchers at the NSF Engineering Research Center for Cell Manufacturing Technology (CMaT). Penalty costs are derived based on service levels provided by clinicians, see (Li 2021). We consider a simple supplier disruption profile described by two independent Bernoulli processes, $Ber(p_1)$ and $Ber(p_2)$: at each decision epoch, the supplier of facility 1 has a probability of $p_1$ to be disrupted and be not able to supply any reagent; and the supplier of facility 1 has a probability $1-p_1$ to be undisrupted and be capable to supply as much reagent as required; and similar for the supplier disruption process $Ber(p_2)$. Using Iso-Net as a baseline model, we compare performances of four heuristics: MYO, E-MYO, MDL-1 and MDL-2. MDL-1 is an MDL heuristic with one lookahead periods, and MDL-2 is an MDL heuristic with two lookahead periods. We consider four supplier disruption profiles, let $p=[p_1,p_2]$:

• (i) Mild: $p_1=p_2=0.1$

• (ii) Moderate: $p_1=p_2=0.3$

• (iii) Severe: $p_1=p_2=0.6$

• (iv) Asymmetric: $p_1=0.3$ and $p_2 = 0.6$.

Testing results in this section are based on 400 simulation scenarios. Several performance measures reported include: average expected total cost, number of bioreactors, average specimen transshipment, average bioreactor relocation and average reagent transshipment.¹ As the penalty costs are selected based on a given service level (probability of production delay), the waiting time of Iso-Net, E-MYO and MDL are similar (as resources are optimized to achieve such delay probabilities while being cost efficient), while the waiting time of MYO is large due to shortness of inventory buffer. Hence, we do not include waiting time as a metric for our case study. Figure 1 depicts the average expected total costs of the baseline Iso-Net and Co-Net heuristics under each supplier disruption profiles.

Fig. 1

Case study 1: average expected total cost comparison

The MYO heuristic has degraded performance comparing to the Iso-Net baseline. MYO heuristic fails to build sufficient reagent safety stock and hence results in a higher total cost. The E-MYO heuristic utilizes reagent decision provided by the Iso-Net baseline to build safety stock which results in significant cost reductions comparing to MYO. On the other hand, the flexibility of resource sharing also results in significant cost reduction comparing to the Iso-Net baseline. In the cases of mild and moderate supplier disruption risk, MDL-1 produces the lowest cost; and in the cases of severe and asymmetric supplier disruption risk, MDL-2 outperforms the rest of the methods. This is because of the fact that an MDL heuristic is able to (i) build up sufficient safety stock, and (ii) utilize the flexibility of resource sharing during the lookahead periods.

Figure 2 compares bioreactor quantities suggested by different heuristics. All Co-Net heuristics suggest less total bioreactors, see Fig. 2a. While producing much lower expected total cost, E-MYO, MDL-1 and MDL-2 reports 9.5% less bioreactor investment when supplier disruption risk is mild, and E-MYO reports 25% less bioreactor investment when supplier disruption risk is severe.

Fig. 2

Case study 1: bioreactor quantity comparison

Allowing bioreactor relocation results in better bioreactor utilization. In the first three cases, where supplier disruption profiles are symmetric, all methods suggest larger bioreactor quantity as the suppliers suffer worse disruption risks. When the supplier disruption profile is asymmetric, the Co-Net methods intend to keep buffer bioreactors at the location with more severe supplier risk while keep the other facility lean, see red dotted lines in Fig. 2b, c.

Next, we present the comparison results on resource sharing. Figure 3 presents the comparison of average specimen transshipment quantity when different methods are applied. We note that E-MYO suggests negligible specimen transshipment quantity, since E-MYO keeps higher redundant reagent stock at both facilities and transshipping reagent is much cheaper than transshipping patient specimen in our problem setting. This can be verified by the fact that E-MYO transships more reagent than other methods (see Fig. 5). MYO transships the largest number of reagent among all investigated methods.

Fig. 3

Case study 1: average specimen transshipment quantity comparison

Fig. 4

Case study 1: average bioreactor relocation quantity comparison

Figure 4 presents the comparison of average bioreactor transshipment quantities when different methods are applied. We observe the largest bioreactor transshipment quantities for MYO among all methods. The comparison of average reagent transshipment is presented in Fig. 5. The E-MYO method has the largest reagent transshipment quantities in all testing scenarios.

Fig. 5

Case study 1: average reagent transshipment quantity comparison

Lastly, we present cost saving results with and without bioreactor relocation, see Fig. 6. We note that transshipping specimen/reagent could potentially have less regulatory restrictions comparing to relocating bioreactors. In Fig. 6, we compare Iso-Net (none of the resource sharing is allowed), Co-Net (solved by MDL, and all resource sharing is allowed) and Co-Net without bioreactor relocation (MDL with bioreactor relocation forced as zero values). Resource sharing (even without bioreactor relocation) yields significant cost saving, we would like to also emphasize the cost reduction by allowing bioreactor relocation (8% to 12% savings in the total cost). In addition, the cost saving is more significant in the cases that supplier disruption probabilities are higher.

Fig. 6

Case study 1: cost savings with and without bioreactor relocation

6.2 Case study 2: the supplier correlations

We investigate how a decentralized network could benefit from a dynamic resilient design (i.e. Co-Net) if the suppliers of facilities are independent, positively correlated or negatively correlated. We compare performances of four heuristics, MYO, E-MYO, MDL-1 and MDL-2, and use Iso-Net as a baseline model. We consider three supplier correlation scenarios:

• (i) Independent: $p_1=p_2=0.3$, and for all t, $Pr(A^1_t=0|A^2_t)=0.3$ for any $A^2_t$, and $Pr(A^2_t=0|A^1_t)=0.3$ for any $A^1_t$

• (ii) Positively correlated (identical): $p_1=0.3$, and for all t, $Pr(A^2_t=0|A^1_t=0)=1$ and $Pr(A^2_t=\infty |A^1_t=\infty )=1$

• (iii) Negatively correlated (flipped): $p_1=0.3$, and for all t, $Pr(A^2_t=\infty |A^1_t=0)=1$ and $Pr(A^2_t=0|A^1_t=\infty )=1$.

Testing results in this section are based on 400 simulation scenarios. We compare performances of different methods based on average expected total cost, number of bioreactors, average specimen transshipment, average bioreactor relocation and average reagent transshipment.

Figure 7 depicts average expected total cost of the baseline Iso-Net and Co-Net heuristics in each supplier correlation scenario

Fig. 7

Case study 2: average expected total cost comparison

When the suppliers are independent, the MYO heuristic has degraded performance comparing to the baseline Iso-Net, while the other three Co-Net heuristic outperform the baseline with cost reduction as large as 14.3% (MDL-1). In the case of identical (strong positively correlated) suppliers case, MYO and MDL-1 both failed to reduce the total cost comparing to the baseline Iso-Net. E-MYO and MDL-2 have negligible cost reduction comparing to the baseline. When suppliers are strong negatively correlated, flipped supplier states in our case, resource sharing produce the largest cost reduction. All Co-Net methods outperform the baseline Iso-Net with the largest cost reduction of 38.2% (MDL-1).

Figure 12 compares bioreactor quantities in different supplier correlation scenarios. The largest bioreactor investment saving occurs when the suppliers are negatively correlated, i.e. the E-MYO achieves 33.3% less bioreactors comparing to the baseline Iso-Net while reducing the expected total cost at the same time (Fig. 8).

Fig. 8

Case study 2: bioreactor quantity comparison

We observe less resource sharing when the suppliers are positively correlated, and more resource sharing when suppliers are negatively correlated (see Figs. 9, 10 and 11 for comparison of average specimen transshipping, bioreactor relocation and reagent transshipping quantities).

Fig. 9

Case study 2: average specimen transshipment quantity comparison

Fig. 10

Case study 2: average bioreactor relocation quantity comparison

Fig. 11

Case study 2: average reagent transshipment quantity comparison

7 Conclusions

We have modeled and analyzed the capacity planning problem in a decentralized network under supplier disruption risk to determine the best number of bioreactors in each facility, the best reagent replenishment policy, and the best resource sharing plans. For the case where facilities are operated independently (Iso-Net), we show it is equivalent to solve multiple centralized regional networks. For the case where facilities are coordinating by resources sharing (Co-Net), we analyze structural properties of Co-Net, discuss computational challenges and develop heuristic algorithm to solve the Co-Net models. In the case studies, we compare different decentralized models and different heuristic polices based in part on data collected from a CAR-T cell therapy manufacturing facility at the University of Pennsylvania. Testing results suggest that instead of increasing resource redundancy at all facilities, the Co-Net model only provide limited level of redundancy and adaptively reconfigure the network with lower investment and operational costs. For future research following this work, it is worthy to explore modeling and analyzing various type of disruptions in the setting of decentralized cell therapy manufacturing. Another research path worth exploring is on improving the quality of bounds and heuristic solutions, for instance using reinforcement learning or neural approximate dynamic programming.

Appendix

1.1 Statistical significance results

We present boxplots of total discounted costs at each setting - x-axis indicates the methods, and y-axis is the total discounted cost from 400 simulation runs. As you can see from the boxplots, the cost reduction is significant.

Fig. 12

Case study 2: bioreactor quantity comparison