Optimizing production levels in maritime inventory routing with load-dependent speed optimization

Abstract

Maritime inventory routing problems with load-dependent speed optimization involves determining optimal routes, as well as vessel speeds and loads at these routes, so that inventory limits are satisfied at both production and consumption ports. This paper considers a variant where production rates can be selected from several available alternative production levels, as opposed to the normal situation where production rates are chosen a priori. In both cases, production rates remain constant for the duration of the planning horizon. The effect on transportation costs when considering production levels as decision variables is evaluated. The resulting solutions are compared with solutions obtained when production rates are considered as fixed parameters. Computational experiments on a set of benchmark instances from the literature confirm that the process of determining the optimal production levels plays a crucial role in improving the solutions to maritime inventory routing problems with load-dependent speed optimization. Optimizing the production levels can reduce transportation costs by up to 35%.

1 Introduction

Maritime transportation, which bears the responsibility of moving approximately 80% of the total global trade volume (UNCTAD 2018), is truly the worldwide economy’s lifeblood. The world would often be unable to complete commercial transactions between the various continents without maritime transport, whether it relates to raw materials such as oil and gas, manufactured products, or food. Because of the continuous growth in global trade, the need for vessels capable of sailing at a higher speed increased. At the same time, due to an increasing fuel consumption and imposing environmental fees when cruising at high speeds, there has been an increased interest in determining optimal speeds to reduce transportation costs.

In the last few years, research has been conducted to better understand the relationships between speed, load, and fuel consumption of vessels in maritime inventory routing. However, production rates have been considered as constants. In this article, we consider a case where fixed production rates at production facilities can be chosen from several available options. That is, we study the maritime inventory routing problem (MIRP) with load-dependent speed optimization and optimized production levels. Mathematical models are presented to find optimal production levels in each production facility, as well as optimal vessel routes, speeds, and loads. Mathematically, the problem is formulated over a fixed planning horizon, and it is assumed that the production rates remain constant at their selected levels for the duration of the planning horizon. Restrictions on inventory levels and vessel loads at the end of the planning horizon are also modelled. The objective of the models is to minimize the transportation costs, which involve sailing costs between the ports and operational costs in each port.

This article, continues with Sect. 2 where the most relevant related literature is discussed. In Sect. 3 a detailed problem definition is given. Two mathematical models are provided in Sect. 4: one for the case with a priori production levels, and one for the case with optimized production levels. Sect. 5 presents the computational experiments conducted to evaluate the importance of choosing production levels when planning transportation, and Sect. 6 contains our concluding remarks.

2 Literature review

In the following, we present pertinent contributions related to the MIRP and then to the production routing problem (PRP). This is followed by a discussion of literature on speed optimization in maritime transportation in general and then literature specifically on the modeling of fuel consumption as a function of speed and load. For further literature on the inventory routing problem (IRP), we refer to the works by Andersson et al. (2010), Coelho et al. (2014), and most recently Soysal et al. (2019).

2.1 Maritime inventory routing problem

A MIRP is an inventory routing problem where the transportation is performed by one or more seagoing vessels (Song and Furman 2013). Christiansen and Fagerholt (2009) provided an introduction to the area and discussed various applications of MIRPs. In over a decade, ExxonMobil research, Georgia Tech, and Carnegie Mellon University have worked on several variants of maritime inventory routing (see for example Engineer et al. (2012); Goel et al. (2012)). This collaboration included the generation of the MIRPLib website Papageorgiou et al. (2014) whose instances feature regularly in the literature and prominently in competitions. Recently, Friske et al. (2022) reviewed MIRP solutions methods, focusing on matheuristics.

Agra et al. (2015) identified a stochastic short-sea shipping problem where the sailing times and the time spent in ports are uncertain. Then, Agra et al. (2016) studied a MIRP with a heterogeneous fleet of vessels and a single commodity transported between production and consumption ports. Each port had a fixed production or consumption rate over the planning horizon and a limited storage capacity. Due to uncertain weather conditions a log-logistic distribution was assumed for the travel times between ports. Maulana et al. (2019) and Teitsma (2021) studied MIRPs with heterogeneous fleets of vessels and multiple products being transported between ports. Teitsma (2021) also provided heuristics to shorten the computational time for solving large instances. Siswanto et al. (2019) studied a problem where each port has multiple time windows. They provided a mathematical formulation for the problem and a heuristic to deal with large instances.

Vågen and Nikolaisen (2019) provided a mathematical model considering uncertainty in the travel times and the arrival times at loading ports. Rodrigues et al. (2019) compared several techniques used to solve a MIRP with uncertain travel times. Diz et al. (2019) considered robust optimization when the time spent by vessels to perform loading and unloading operations at the ports is uncertain. Later, Liu et al. (2021) presented a distributionally robust optimization approach that can be used with uncertain sailing times and uncertain waiting times at ports. Agra et al. (2018) introduced a decomposition algorithm to deal with uncertainty in sailing times.

De et al. (2017) considered a slow steaming strategy when optimizing vessel routes. The authors formulated a non-linear mixed-integer model, where the sustainability aspects of the equilibrium between fuel consumption and vessels’ speed were captured using a non-linear equation. Ghiami et al. (2019) introduced an approach to improve the transportation of liquefied natural gas by vessels traveling between offshore production platforms and onshore facilities, taking into account that a portion of the gas evaporates during transportation and storage. Goel et al. (2012) presents an LNG-inventory routing problem (a MIRP variant) in which the consumption rate is considered as a decision variable. Gocmen and Yilmaz (2018) reviewed existing literature on the MIRP and suggested several directions for future research.

Eide et al. (2020) examined the importance of considering the load on board vessels when calculating the sailing costs. They aimed to reduce the sum of sailing and operating costs by simultaneously optimizing vessels’ routes, speeds, and loads. However, the authors considered the production levels as constants and did not consider any restrictions regarding inventory levels at ports or loads onboard vessels at the end of the planning horizon.

2.2 Production routing problem

The PRP combines the IRP and the lot-sizing problem in one model to jointly optimize production, inventory, and distribution decisions. Adulyasak et al. (2015) presented a review of several mathematical formulations for the problem. A PRP aims to reduce the total costs, including the cost of production, inventory, and transportation. The problem studied in this paper, unlike the PRP, takes production costs as sunk, so that the total costs only include transportation and port visit costs.

Russell (2017) developed two heuristics approaches to determine an initial solution for PRP. The final solution is found by a multi-iteration enhancement process. Qiu et al. (2018) presented a new heuristic to solve the PRP. Computational results showed that the proposed method was competitive in terms of the solution quality obtained. Li et al. (2019) investigated a multi-product PRP and developed a three-level heuristic for solving the problem. Neves-Moreira et al. (2019) studied a PRP with delivery time windows. The authors developed a three-phase method. In the first phase, the size of the problem is reduced by simplifying certain dimensions such as the number of locations, products, and possible routes. In the second phase, an initial PRP solution is found, and in the third phase, different mixed-integer programming models are used to improve the initial solution. Wang et al. (2021) focused on the PRP under uncertain conditions. The authors considered that the cost and demand uncertainty is simultaneous, and formulated three mathematical programming models.

2.3 Speed optimization

Norstad et al. (2011) noted that the maritime routing problems typically studied in the scientific literature considered the speed and fuel consumption of the vessels to be fixed. However, in practice, the speed of vessels can be changed within a specific range during sailing, and the fuel consumption per unit of time can be represented as a cubic function of the speed. The authors illustrated the positive effects of optimizing the speed of vessels by using a multi-start local search heuristic that considers the vessels’ speed as a decision variable. The technique used to determine vessel speeds in a situation with time windows for port visits was later proven to provide optimal speed levels by Hvattum et al. (2013). Andersson et al. (2015) suggested a new technique to incorporate speed optimization into ship routing using mathematical programming and a linearization technique.

Wen et al. (2016) investigated speed optimization in full-shipload tramp transportation. The problem consists of various cargoes that must be shipped directly between ports using a heterogeneous fleet of vessels. The vessels differ in their speed ranges and load-dependent fuel consumption rates, considering that the vessels are always either empty or full. The authors proposed a three-index formulation that was solved using a branch-and-price algorithm. Norlund and Gribkovskaia (2017) highlighted how well speed optimization techniques work when weather conditions are considered. They developed an approach for estimating the fuel consumption for supply vessels serving offshore oil and gas installations using simulation and optimization.

Psaraftis and Kontovas (2013) presented a survey of maritime transportation models where speed is considered as a decision variable. They addressed the benefits and weaknesses of lowering vessels’ speed, related to costs and pollution. The authors classified the models based on whether or not they can decide the optimal speed as a function of payload. Psaraftis and Kontovas (2014) discussed some of the practical problems arising when optimizing speeds at an operational level. The authors presented several models that dealt with a single vessel’s speed optimization for several routing scenarios. The models integrated many fundamental aspects, such as freight rate, fuel price, cargo’s inventory cost, and the payload-dependent fuel consumption. The article clarified the gap between economic performance-optimization solutions and environmental efficiency optimization solutions.

An approach for constructing an accurate speed curve and fuel consumption was proposed by Bialystocki and Konovessis (2016). The authors discussed many factors that may have an impact on fuel consumption. A simple algorithm for estimating fuel consumption was developed.

2.4 Fuel consumption models

Bialystocki and Konovessis (2016) estimated the non-linear relationship between the speed and fuel consumption of a vessel by the formula $F(\mu )= 0.1727\mu ^2-0.217\mu$, where F is the fuel consumption and $\mu$ is the vessel speed. The formula assumes that the fuel consumption is independent of the load; hence the load is implicitly considered as a constant to calculate the fuel consumption of a vessel. Andersson et al. (2015) combined three speed alternatives to calculate an approximated linear overestimation of fuel consumption. They used a cubic function to approximate the fuel consumption per time unit. This corresponds to a rate of consumption per unit of distance that is quadratic in the speed. In their work, a vessel has a minimum speed, that can be used for sailing at a minimum cost, and a maximum speed that results in the highest fuel consumption. Figure1 illustrates the convexity of the fuel consumption curve. As a result, the curve’s linearization results in an overestimation of the fuel consumption.

Fig. 1

The non-linear relationship between the fuel consumption and the speed of a vessel (Andersson et al. 2015; Bialystocki and Konovessis 2016). The approximation is expressed by the dashed red line

The relationship between a vessel’s speed and the time used to travel a fixed distance is also non-linear. Hence, in the mathematical models there is also an overestimation of travel times when a fuel consumption function is linearized (Andersson et al. 2015). This overestimation is illustrated in Fig. 2.

Fig. 2

The relationship between travel time and speed of a vessel (Andersson et al. 2015; Bialystocki and Konovessis 2016). The approximation is expressed by the dashed red line

Psaraftis and Kontovas (2014) suggested that the fuel consumption of a vessel depends both on its speed and load. They introduced a formula to calculate the daily fuel consumption, which is $f(v,w)=kv^3 (w+A)^{2/3}$ with k being a given constant, v being the vessel’s speed, w being the vessel’s payload, and A being the vessel’s weight when the vessel is empty except its fuel. The function is convex when considering a fixed load, which leads to an overestimation in the cost function when it is linearized. However, if the speed is fixed the function is concave with respect to the load, which leads to an underestimation in the cost function when it is linearized. Fig. 3 illustrates the daily sailing cost for a single vessel with five different load levels.

Fig. 3

The non-linear relationship between load, speed, and the sailing cost of a vessel (Psaraftis and Kontovas 2014)

3 Problem description

This work examines how optimizing production levels influences the transportation costs in MIRPs where the fuel consumption depends on both the load and speed of vessels. We consider a geographical area where a single commodity is transported between different ports by a heterogeneous fleet of vessels which are different in terms of sizes, capacities, and operating costs. Traveling distances between each pair of ports are given. The ports are divided into production and consumption ports. Each consumption port has a fixed consumption rate, and each production port has several production levels from which one should be chosen.

Both consumption and production ports have storage facilities with given lower and upper inventory limits. The maximum inventory levels cannot be exceeded, and shortages at the consumption ports are not allowed. The initial inventories of ports and the initial loads of vessels are known. Depending on the size of demands, inventories, and the quantities loaded or unloaded, each port can be visited several times during a given planning horizon. The number of visits to each port is, however, limited by a maximum number of visits that cannot be exceeded and a minimum number of visits that must be carried out. In addition, there is a minimum required time between two consecutive visits for each port. Additional maximum and minimum levels of inventory at each port are imposed at the end of the planning horizon, to reduce end-of-horizon effects.

The starting location is known for each vessel, as well as the distances between that location and the ports. Each vessel can sail at different speeds. The vessels come in a variety of sizes to suit a variety of needs. The vessels’ scale is classified in this study by how much load the vessel can carry, which is called the deadweight tonnage (DWT). The vessels differ in their operational speed depending on their sizes, where the larger vessels typically can operate at a higher speed. The vessels’ loading and unloading rates also vary depending on the vessel size.

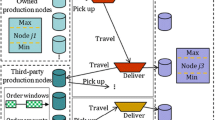
Figure 4 shows an example of routes for two vessels, starting from their respective initial locations, passing through several ports, before reaching their respective final positions. The green filled circles correspond to a production port (P1), while the red filled circles are consumption ports (D1, D2, D3, and D4). For each port, several visits can be made, and the visit number is indicated in parentheses.

Fig. 4

Example of a solution to a MIRP

As shown in Fig. 4, vessel 1, following the solid arrows, starts from its origin (Origin 1) and goes to production port P1 for the first visit, then sails to consumption port D1 for the first visit, continues to consumption port D3 for the first visit, and ends up at Destination 1, as the route is completed. Vessel 2, following the dashed arrows, starts from its origin (Origin 2) and goes to production port P1 for the second visit, then sails to consumption port D2 for the first visit, continues to consumption port D1 for the second visit, goes to consumption port D3 for second visits, then sails to consumption port D4 for the first visit, ending at Destinations 2, as the trip is completed.

4 Mathematical models

We provide two mathematical models; both are linear and formulated based on a model without production level optimization as provided by Eide et al. (2020). Both models aim to minimize transportation and operating costs in a continuous-time problem allowing for split pickups and deliveries . The first model deals with production levels as parameters, in contrast to the second model, which consider the production levels as decision variables. In both models, production levels are considered constant over the planning horizon, and in contrast to Eide et al. (2020), there are restrictions to control inventory levels and vessel loads at the end of the planning horizon.

In the following, V indicates a set of vessels and N a set of ports. The starting point for each vessel $v \in V$ is a known point at sea or near a port. A pair (i, m) represents a node in the network, where i is a port and m is a visit number. The direct movement from node (i, m) to node (j, n) is represented by the tuple (i, m, j, n).

4.1 Model with production rates as preset decision

The following model deals with vessels’ routes, load, and speed as decision variables, while production levels are considered as parameters. First, we describe the sets, variables, and parameters of the model.

4.1.1 set

• V : set of vessels

• N : set of production and consumption ports

• $S^A$ : set of possible nodes (i, m)

• $S_v^A$ : set of nodes that can be visited by vessel v

• $S_v^X$ : set of all possible moves (i, m, j, n) of vessel v

• $S_v^S$ : set of breakpoints for the speed of vessel v, with $S_v^S = \{ 1, 2, \ldots , U \}$

• $S_v^L$ : set of breakpoints for the load level of vessel v, with $S_v^L = \{ 1, 2, \ldots , R \}$

Thus, a maximum number of visits for each port is determined through the set $S^A$. The sets $S_v^A$ allows the model to express that some vessels may be unable to visit certain ports. The sets $S_v^X$ enable the model to disallow certain trips to be carried out by a given vessel.

4.1.2 Variables

• $x_{imjnv}$ : 1 if vessel $v \in V$ moves directly between nodes

• (i, m) and (j, n), 0 otherwise, $v \in V$, $(i,m,j,n) \in S_v^X$

• $x_{imv}^O$ : 1 if vessel v departs from its initial position to node (i, m), 0 otherwise, $v \in V$, $(i,m) \in S_v^A$

• $z_{imv}$ : 1 if vessel v finishes its route at node (i, m), 0 otherwise, $v \in V$, $(i,m) \in S_v^A$

• $z_{v}^O$ : 1 if vessel v is not used in the planning horizon, 0 otherwise, $v\in V$

• $o_{imv}$ : 1 if vessel v operates at node (i, m), 0 otherwise, $v\in V$, $(i,m) \in S_v^A$

• $y_{im}$ : 1 if there is a visit (i, m) to port i, 0 otherwise, $i \in N$, $(i,m) \in S^A$

• $q_{imv}$ : the amount loaded or unloaded by vessel v at node (i, m), $v \in V$, $(i,m) \in S_v^A$

• $f_{imjnv}$ : the amount of product that vessel v transports from node (i, m) to node (j, n), $v \in V$, $(i,m,j,n) \in S_v^X$

• $f_{imv}^O$ : the amount of product that vessel v transports from the origin to node (i, m), $v\in V$, $(i,m) \in S_v^A$

• $f_{imv}^D$ : the amount of product that vessel v has left onboard when ending its route after visiting node (i, m) , $v \in V$, $(i,m) \in S_v^A$

• $g_{imjnvls}$ : auxiliary variable to determine the speed and load of vessel v when going from (i, m) to (j, n), with s corresponding to a given choice of speed and l of a level of load, $v\in V$, $s\in S_v^S$, $l\in S_v^L$, $(i,m,j,n) \in S_v^X$

• $g_{imvls}^O$ : auxiliary variable to determine the speed and load of vessel v when going from its origin to (i, m), with s corresponding to a given choice of speed and l of a level of load, $v \in V$, $s \in S_v^S$, $l \in S_v^L$, $(i,m) \in S_v^A$

• $p_{imjnvl}$ : 1 if a level of load in the interval between the two adjacent breakpoints l and $l+1$ is chosen on route (i, m, j, n) of vessel v, 0 otherwise, $v \in V$, $l\in S_v^L \setminus \{R\}$, $(i,m,j,n) \in S_v^X$

• $p_{imvl}^O$ : 1 if a level of load in the interval between the two adjacent breakpoints l and $l+1$ is chosen on route from origin to node (i, m) 0 otherwise, $v \in V$, $l \in S_v^L \setminus \{R\}$, $(i,m) \in S_v^A$

• $t_{im}$ : start time of visit number m to port i, $(i,m) \in S^A$

• $s_{im}$ : inventory level in port i at the start of visit m, $(i,m) \in S^A$

4.1.3 Parameters

• T : number of time units in the planning horizon

• $H_i$ : minimum number of visits to port $i \in N$

• $M_i$ : maximum number of visits to port $i \in N$

• $D_i$ : production or consumption per time unit at port $i \in N$

• $J_i$ : 1 if $i \in N$ is a production port and $-1$ if $i \in N$ is a consumption port

• $P_{iv}$ : port cost at port $i \in N$ for vessel $v \in V$

• $C_v$ : capacity of vessel $v \in V$

• $L_v$ : initial load onboard vessel $v \in V$

• ${\overline{L}}^T$ : maximum aggregated load for the vessels at the end of the planning horizon

• ${\underline{L}}^T$ : minimum aggregated load for the vessels at the end of the planning horizon

• ${\overline{S}}_i$ : upper bound on the inventory level at port $i \in N$

• ${\underline{S}}_i$ : lower bound on the inventory level at port $i \in N$

• $S_i^0$ : the initial inventory level in port $i \in N$ at the beginning of the planning horizon

• ${\overline{S}}_i^T$ : maximum inventory at port $i \in N$ at the end of the planning horizon

• ${\underline{S}}_i^T$ : minimum inventory at port $i \in N$ at the end of the planning horizon

• $A_{im}$ : earliest time for starting visit m to port i, $(i,m) \in S^A$

• $B_{im}$ : latest time for starting visit m to port i, $(i,m) \in S^A$

• $K_i$ : minimum time between two consecutive visits to port $i \in N$

• ${\underline{Q}}_i$ : minimum quantity to load or unload in each visit to port $i \in N$

• $U_{im}$ : latest time for finishing visit m to port i, $(i,m) \in S^A$

• $T_v^Q$ : time needed for loading or unloading each unit by vessel $v \in V$

• $T_{ijvs}^{PP}$ : time required by vessel $v \in V$ to sail from port $i \in N$ to port $j \in N$ with speed $s \in S_v^S$

• $T_{ivs}^{OP}$ : time required by vessel $v \in V$ to sail from its origin to port $i \in N$ with speed $s \in S_v^S$

• $L_{vl}$ : possible levels of load $l \in S_v^L$ that can be transported on vessel $v \in V$

• $C_{ijvls}^{PP}$ : sailing cost from port $i \in N$ to port $j \in N$ with vessel $v \in V$ with load $l \in S_v^L$ and with speed $s \in S_v^S$

• $C_{ivls}^{OP}$ : sailing cost from origin to port $i \in N$ by vessel $v \in V$ with load $l \in S_v^L$ and with speed $s \in S_v^S$

4.1.4 Objective function

$$\begin{aligned} \min ~&\sum _{v \in V} \sum _{(i,m,j,n) \in S_v^X} \sum _{l \in S_v^L} \sum _{s \in S_v^S} C^{PP}_{ijvls} g_{imjnvls} + \sum _{v \in V} \sum _{(i,m) \in S_v^A} \sum _{l \in S_v^L} \sum _{s \in S_v^S} C^{OP}_{ivls} g^O_{imvls} \nonumber \\&+ \sum _{v \in V} \sum _{(i,m) \in S_v^A} P_{iv}o_{imv} \end{aligned}$$

(1)

The objective function (1) expresses the minimization of the sum of sailing costs between ports, depending on the chosen load and speed, and the operational cost in each port. This objective function is optimized over a set of constraints, which are split into groups as follows:

4.1.5 Routing constraints

$$\begin{aligned}&\sum _{(j,n) \in S_v^A} x^O_{jnv} + z^O_v = 1&v \in V \end{aligned}$$

(2)

$$\begin{aligned}&o_{imv} - \sum _{(j,n,i,m) \in S_v^X} x_{jnimv} - x^O_{imv} = 0&v \in V, (i,m) \in S_v^A \end{aligned}$$

(3)

$$\begin{aligned}&o_{imv} - \sum _{(i,m,j,n) \in S_v^X} x_{imjnv} - z_{imv} = 0&v \in V, (i,m) \in S_v^A \end{aligned}$$

(4)

$$\begin{aligned}&\sum _{v \in V} o_{imv} = y_{im}&(i,m) \in S^A \end{aligned}$$

(5)

$$\begin{aligned}&y_{i(m-1)} - y_{im} \ge 0&(i,m) \in S^A : H_i + 1 \le m \le M_i \end{aligned}$$

(6)

$$\begin{aligned}&y_{im} = 1&(i,m) \in S^A : m \in \{1, \ldots , H_i\} \end{aligned}$$

(7)

Constraints (2) state that each vessel should either depart from its origin to a port or not be used at all. Constraints (3) enforce that when a node is visited by a vessel, that vessel either comes to the node from its origin or from another node. Constraints (4) make sure that when a vessel arrives at a node, that vessel must either leave the node and go to another node or finish its trip there. Constraints (5) ensure that a node is visited if and only if a vessel is loading or unloading during the visit. Constraints (6) guarantee that visits to each port are counted sequentially. Constraints (7) define the number of mandatory visits for port i.

4.1.6 Loading and unloading constraints

$$\begin{aligned}&q_{imv} \le \min \{C_v, {\overline{S}}_i - {\underline{S}}_i\}o_{imv}&v \in V, (i,m) \in S_v^A \end{aligned}$$

(8)

$$\begin{aligned}&{\underline{Q}}_i o_{imv} \le q_{imv}&v \in V, (i,m) \in S_v^A \end{aligned}$$

(9)

Constraints (8) ensure that the quantity loaded or unloaded cannot exceed the port capacity nor the vessel capacity. Constraints (9) ensure that the quantity loaded or unloaded in each visit to a port is at least equal to a minimum required quantity.

4.1.7 Product flow constraints

$$\begin{aligned}&f^O_{imv} = L_v x^O_{imv}&v \in V, (i,m) \in S_v^A \end{aligned}$$

(10)

$$\begin{aligned}&f^O_{jnv} + \sum _{(i,m,j,n) \in S_v^X} f_{imjnv} + J_i q_{jnv} = \sum _{(j,n,i,m) \in S_v^X} f_{jnimv} + f^D_{jnv}&v \in V, (j,n) \in S_v^A \end{aligned}$$

(11)

$$\begin{aligned}&f_{imjnv} \le C_v x_{imjnv}&v \in V, (i,m), (j,n) \in S_v^A \end{aligned}$$

(12)

$$\begin{aligned}&f^D_{jnv} \le C_v z_{jnv}&v \in V, (j,n) \in S_v^A \end{aligned}$$

(13)

Constraints (10) state that the load of the vessel when sailing from its origin equals its initial load. Constraints (11) guarantee that the incoming product flow must be equal to the outgoing product flow for each node, modified only by the quantity loaded or unloaded at the node. Constraints (12) ensure that when a vessel sails from a node to another node, its load must at most be equal to its capacity. Constraints (13) are equivalent to constraints (12), but considering a movement from a port visit to the vessel’s destination.

4.1.8 Time constraints

$$\begin{aligned}&t_{im} - t_{i(m-1)} - \sum _{v \in V} T^Q_v q_{i(m-1)v} - K_i y_{im} \ge 0&(i,m) \in S^A : m > 1 \end{aligned}$$

(14)

$$\begin{aligned}&t_{im} + \sum _{v \in V} T^Q_v q_{imv} - t_{jn} \nonumber \\&+ \sum _{v \in V} \sum _{l \in S^L_v} \sum _{s \in S_v^S} \max \{ U_{im} + T^{PP}_{ijvs} - A_{jn}, 0 \} g_{imjnvls} \le U_{im} - A_{jn}&(i,m), (j,n) \in S^A \end{aligned}$$

(15)

$$\begin{aligned}&\sum _{v \in V} \sum _{l \in S^L_v} \sum _{s \in S_v^S} T^{OP}_{ivs} g^O_{imvls} \le t_{im}&(i,m) \in S^A \end{aligned}$$

(16)

$$\begin{aligned}&t_{im} \ge A_{im}&(i,m) \in S^A \end{aligned}$$

(17)

$$\begin{aligned}&t_{im} \le B_{im}&(i,m) \in S^A \end{aligned}$$

(18)

Constraints (14) enforce the minimum time between consecutive visits of port i. Constraints (15) connect the start time of visit m to port i with the start of visit n to port j when a vessel sails from node (i, m) to node (j, n). Constraints (16) guarantee that when a vessel travel from its origin to carry out visit m at port i, the start time of that visit should at least be equal to the minimum time required by the vessel for traveling. Constraints (17) and (18) define a time window for each visit.

4.1.9 Vessel speed and load constraints

$$\begin{aligned}&\sum _{l \in S^L_v} \sum _{s \in S_v^S} g_{imjnvls} = x_{imjnv}&v \in V, (i,m,j,n) \in S_v^X \end{aligned}$$

(19)

$$\begin{aligned}&\sum _{l \in S^L_v} \sum _{s \in S_v^S} g^O_{imvls} = x^O_{imv}&v \in V, (i,m) \in S_v^A \end{aligned}$$

(20)

$$\begin{aligned}&f^O_{imv} = \sum _{l \in S^L_v} \sum _{s \in S_v^S} L_{vl} g^O_{imvls}&v \in V, (i,m) \in S_v^A \end{aligned}$$

(21)

$$\begin{aligned}&f_{imjnv} = \sum _{l \in S^L_v} \sum _{s \in S_v^S} L_{vl} g_{imjnvls}&v \in V, (i,m,j,n) \in S_v^X \end{aligned}$$

(22)

$$\begin{aligned}&\sum _{v \in V} \sum _{(i,m) \in S^A_v} f^D_{imv} \ge {\underline{L}}^T&\end{aligned}$$

(23)

$$\begin{aligned}&\sum _{v \in V} \sum _{(i,m) \in S^A_v} f^D_{imv} \le {\overline{L}}^T&\end{aligned}$$

(24)

$$\begin{aligned}&0 \le g_{imjnvls} \le 1&v \in V, (i,m,j,n) \in S_v^X, s \in S^S_v, l \in S^L_v \end{aligned}$$

(25)

$$\begin{aligned}&0 \le g^O_{imvls} \le 1&v \in V, (i,m) \in S_v^A, s \in S^S_v, l \in S^L_v \end{aligned}$$

(26)

Constraints (19) enforce that the speed and load of a vessel must be determined if the vessel travels between two nodes. Constraints (20) correspond to constraints (19), in the case of travel from the origin to a node. Constraints (21) and (22) compute the load of an arc in terms of the load of the vessel. Constraints (23) and (24) ensure that the total load on-board vessels the end of the planning horizon are within given bounds, so as to limit any end-of-horizon effects. Constraints (25) and (26) define the upper and lower bounds of the g-variables, which are used to express the speed and the load of a vessel. The g-variables are connected to the p-variables in the following constraints, to ensure that the effect of loads on fuel consumption is linearized appropriately:

$$\begin{aligned}&\sum _{l \in S^L_v \setminus \{R\}} p_{imjnvl} = x_{imjnv}&v \in V, (i,m,j,n) \in S_v^X \end{aligned}$$

(27)

$$\begin{aligned}&\sum _{s \in S^S_v} g_{imjnv1s} \le p_{imjnv1}&v \in V, (i,m,j,n) \in S_v^X \end{aligned}$$

(28)

$$\begin{aligned}&\sum _{s \in S^S_v} g^O_{imv1s} \le p^O_{imv1}&v \in V, (i,m) \in S_v^A \end{aligned}$$

(29)

$$\begin{aligned}&\sum _{s \in S^S_v} g_{imjnvls} \le p_{imjnv(l-1)} + p_{imjnvl}&v \in V, (i,m,j,n) \in S_v^X, l \in S^L_v \setminus \{1, R\} \end{aligned}$$

(30)

$$\begin{aligned}&\sum _{s \in S^S_v} g^O_{imvls} \le p^O_{imv(l-1)} + p^O_{imvl}&v \in V, (i,m) \in S_v^A, l \in S^L_v \setminus \{1, R\} \end{aligned}$$

(31)

$$\begin{aligned}&\sum _{s \in S^S_v} g_{imjnvRs} \le p_{imjnv(R-1)}&v \in V, (i,m,j,n) \in S_v^X \end{aligned}$$

(32)

$$\begin{aligned}&\sum _{s \in S^S_v} g^O_{imvRs} \le p^O_{imv(R-1)}&v \in V, (i,m) \in S_v^A \end{aligned}$$

(33)

Constraints (27) guarantee that if an arc is used by vessel v, a breakpoint defining a load level of the vessel must be chosen. Constraints (28) ensure that if a vessel travels between two nodes and its load is between the minimum load and the first level breakpoints, then the value of the speed and load can be larger than zero if and only if the first interval is chosen. Constraints (29) are equivalent to constraints (28), but the travel is from an origin to a node. Constraints (30) show that if a vessel travels on an arc, its load and speed value can be larger than zero if and only if one of the intervals connected to the selected breakpoint is chosen. Constraints (31) show the same as constraints (30), but the travel is from an origin to a node. Constraints (32) ensure that if a vessel travels between two nodes and its load is between the last breakpoint and the maximum load, then the value of the speed and load can be larger than zero if and only if the last interval is chosen. Constraints (33) are equivalent to constraints (32), but the travel is from an origin to a node.

4.1.10 Inventory constraints for consumption ports

$$\begin{aligned}&s_{im} \ge {\underline{S}}_i&(i,m) \in S^A : J_i = -1 \end{aligned}$$

(34)

$$\begin{aligned}&s_{i1} = S^O_i - D_i t_{i1}&i \in N : J_i = -1 \end{aligned}$$

(35)

$$\begin{aligned}&s_{im} = s_{i(m-1)} + \sum _{v \in V} q_{i(m-1)v} - D_i (t_{im} - t_{i(m-1)})&(i,m) \in S^A : J_i = -1, m > 1 \end{aligned}$$

(36)

$$\begin{aligned}&s_{im} + \sum _{v \in V} q_{imv} - D_i \sum _{v \in V} T^Q_v q_{imv} \le {\overline{S}}_i&(i,m) \in S^A : J_i = -1 \end{aligned}$$

(37)

$$\begin{aligned}&s^O_{i} + \sum _{m=1}^{M_i} \sum _{v \in V} q_{imv} - D_i T \ge \max \{{\underline{S}}_i, {\underline{S}}^T_i\}&i \in N : J_i = -1 \end{aligned}$$

(38)

$$\begin{aligned}&s^O_{i} + \sum _{m=1}^{M_i} \sum _{v \in V} q_{imv} - D_i T \le {\overline{S}}^T_i&i \in N : J_i = -1 \end{aligned}$$

(39)

Constraints (34) ensure that there is no shortage at the start of each visit to a consumption port. Constraints (35) set the inventory level at the start of the first visit to each consumption port. Constraints (36) set the inventory level at the start of each subsequent visit to a consumption port. Constraints (37) ensure that the storage capacity is not exceeded at the end of each visit to a consumption port. Constraints (38) and (39) guarantee that the level of inventory at the end of the planning horizon is within acceptable bounds.

4.1.11 Inventory constraints for production ports

$$\begin{aligned}&s_{im} \le {\overline{S}}_i&(i,m) \in S^A : J_i = 1 \end{aligned}$$

(40)

$$\begin{aligned}&s_{i1} = S^O_i + D_i t_{i1}&i \in N : J_i = 1 \end{aligned}$$

(41)

$$\begin{aligned}&s_{im} = s_{i(m-1)} - \sum _{v \in V} q_{i(m-1)v} + D_i (t_{im} - t_{i(m-1)})&(i,m) \in S^A : J_i = 1, m > 1 \end{aligned}$$

(42)

$$\begin{aligned}&s_{im} - \sum _{v \in V} q_{imv} + D_i \sum _{v \in V} T^Q_v q_{imv} \ge {\underline{S}}_i&(i,m) \in S^A : J_i = 1 \end{aligned}$$

(43)

$$\begin{aligned}&s^O_{i} - \sum _{m=1}^{M_i} \sum _{v \in V} q_{imv} + D_i T \le \min \{ {\overline{S}}_i, {\overline{S}}^T_i \}&i \in N : J_i = 1 \end{aligned}$$

(44)

$$\begin{aligned}&s^O_{i} - \sum _{m=1}^{M_i} \sum _{v \in V} q_{imv} + D_i T \ge {\underline{S}}^T_i&i \in N : J_i = 1 \end{aligned}$$

(45)

Constraints (40) ensure that the storage capacity is not exceeded at the start of each visit to a production port. Constraints (41) and (42) are equivalent to constraints (35) and (36), but for the production ports. Constraints (43) ensure that there is no shortage at the end of each visit to a production port. Constraints (44) guarantee that the inventory level at each production port is below a given limit at the end of the planning horizon. Constraints (45) ensure that there is a minimum inventory level at each production port when reaching the end of the planning horizon, to facilitate the possibility to load the product also when replanning at a later point in time.

4.1.12 Variable domains

$$\begin{aligned}&x_{imjnv} \in \{0, 1\}&v \in V, (i,m,j,n) \in S_v^X \end{aligned}$$

(46)

$$\begin{aligned}&x^O_{imv} \in \{0, 1\}&v \in V, (i,m) \in S_v^A \end{aligned}$$

(47)

$$\begin{aligned}&o_{imv} \in \{0, 1\}&v \in V, (i,m) \in S_v^A \end{aligned}$$

(48)

$$\begin{aligned}&z_{imv} \in \{0, 1\}&v \in V, (i,m) \in S_v^A \end{aligned}$$

(49)

$$\begin{aligned}&z^O_{v} \in \{0, 1\}&v \in V \end{aligned}$$

(50)

$$\begin{aligned}&y_{im} \in \{0, 1\}&(i,m) \in S^A \end{aligned}$$

(51)

$$\begin{aligned}&p_{imjnvl} \in \{0, 1\}&v \in V, (i,m,j,n) \in S_v^X, l \in S^L_v \setminus \{R\} \end{aligned}$$

(52)

$$\begin{aligned}&p^O_{imvl} \in \{0, 1\}&v \in V, (i,m) \in S_v^A, l \in S^L_v \setminus \{R\} \end{aligned}$$

(53)

$$\begin{aligned}&q_{imv} \ge 0&v \in V, (i,m) \in S_v^A \end{aligned}$$

(54)

$$\begin{aligned}&f_{imjnv} \ge 0&v \in V, (i,m,j,n) \in S_v^X \end{aligned}$$

(55)

$$\begin{aligned}&f^O_{imv} \ge 0&v \in V, (i,m) \in S_v^A \end{aligned}$$

(56)

$$\begin{aligned}&f^D_{imv} \ge 0&v \in V, (i,m) \in S_v^A \end{aligned}$$

(57)

$$\begin{aligned}&s_{im} \ge 0&(i,m) \in S^A \end{aligned}$$

(58)

$$\begin{aligned}&t_{im} \ge 0&(i,m) \in S^A \end{aligned}$$

(59)

4.2 Model with production rates as decision variables

To study the effect of production levels on fuel consumption, and thereby the total transportation and operating costs, production levels are now included as decisions variables rather than as parameters. Hence, fixed production levels that achieve highest transportation cost savings will be chosen. The resulting model has the same structure as the model with preset production rates, but with a number of modifications, which are explained in the following.

4.2.1 Additional or modified notation

• $S^{PROD}$ : set of all possible production levels

• $D_i$ : consumption rate at port i per unit of time, $i \in N : J_i = -1$

• $P^{RATE}_{ie}$ : production rate at level $e \in S^{PROD}$ at port i per unit of time, $i \in N: J_i = 1$

• $p^{LVL}_{ie}$ : 1 if production level $e \in S^{PROD}$ is selected at port i and 0 otherwise, $i\in N: J_i = 1$

The following two new groups of constraints are then considered:

$$\begin{aligned}&\sum _{e \in S^{PROD}} p^{LVL}_{ie} = 1&i \in N : J_i = 1 \end{aligned}$$

(60)

$$\begin{aligned}&p^{LVL}_{ie} \in \{0, 1\}&e \in S^{PROD}, i \in N : J_i = 1 \end{aligned}$$

(61)

Constraints (60) and (61) ensure that each production port has a fixed production level during the planning horizon. The inventory constraints for production ports, specifically constraints (41)–(45), are then replaced by the following constraints:

$$\begin{aligned}&s_{i1} = S^O_i + \sum _{e \in S^{PROD}} P^{RATE}_{ie} p^{LVL}_{ie} t_{i1}&i \in N : J_i = 1 \end{aligned}$$

(62)

$$\begin{aligned}&s_{im} = s_{i(m-1)} - \sum _{v \in V} q_{i(m-1)v} + \sum _{e \in S^{PROD}} P^{RATE}_{ie} p^{LVL}_{ie} (t_{im} - t_{i(m-1)})&(i,m) \in S^A : J_i = 1, m > 1 \end{aligned}$$

(63)

$$\begin{aligned}&s_{im} - \sum _{v \in V} q_{imv} + \sum _{e \in S^{PROD}} P^{RATE}_{ie} p^{LVL}_{ie} \sum _{v \in V} T^Q_v q_{imv} \ge {\underline{S}}_i&(i,m) \in S^A : J_i = 1 \end{aligned}$$

(64)

$$\begin{aligned}&s^0_{i} - \sum _{m=1}^{M_i} \sum _{v \in V} q_{imv} + T \sum _{e \in S^{PROD}} P^{RATE}_{ie} p^{LVL}_{ie} \le \min \{ {\overline{S}}_i, {\overline{S}}^T_i \}&i \in N : J_i = 1 \end{aligned}$$

(65)

$$\begin{aligned}&s^0_{i} - \sum _{m=1}^{M_i} \sum _{v \in V} q_{imv} + T \sum _{e \in S^{PROD}} P^{RATE}_{ie} p^{LVL}_{ie} \ge {\underline{S}}^T_i&i \in N : J_i = 1 \end{aligned}$$

(66)

Some of these constraints (62, 63, 64) are non-linear due to including a product of two variables, the first of which is binary and the second of which is continuous. One new variable can replace the product of a binary and a continuous variable by imposing new constraints (Bisschop 2021). Hence, we add the following variables:

$w_{iem}$:

: auxiliary continuous variable used to replace the product $p^{LVL}_{ie} t_{im}$, $e \in S^{PROD}$, $(i,m) \in S^A$

$w^{OP}_{iem}$:

: auxiliary continuous variable used to replace the product $p^{LVL}_{ie} \sum _{v \in V} T_v^Q q_{imv}$, $e \in S^{PROD}$, $(i,m) \in S^A$

Now, constraints (62) can be replaced by:

$$\begin{aligned}&s_{i1} = S^O_i + \sum _{e \in S^{PROD}} P^{RATE}_{ie} w_{ie1}&i \in N : J_i = 1 \end{aligned}$$

(67)

$$\begin{aligned}&w_{ie1} \le T p_{ie}^{LVL}&e \in S^{PROD}, i \in N : J_i = 1 \end{aligned}$$

(68)

$$\begin{aligned}&w_{ie1} \le t_{i1}&e \in S^{PROD}, i \in N : J_i = 1 \end{aligned}$$

(69)

$$\begin{aligned}&w_{ie1} \ge t_{i1} - T(1-p^{LVL}_{ie})&e \in S^{PROD}, i \in N : J_i = 1 \end{aligned}$$

(70)

$$\begin{aligned}&w_{ie1} \ge 0&e \in S^{PROD}, i \in N : J_i = 1 \end{aligned}$$

(71)

Constraints (63) can be replaced by:

$$\begin{aligned}&s_{im} = s_{i(m-1)} - \sum _{v \in V} q_{i(m-1)v} + \sum _{e \in S^{PROD}} P^{RATE}_{ie} (w_{iem} - w_{ie(m-1)})&(i,m) \in S^A : J_i = 1, m > 1 \end{aligned}$$

(72)

$$\begin{aligned}&w_{iem} \le T p^{LVL}_{ie}&e \in S^{PROD}, (i,m) \in S^A : J_i = 1, m > 1 \end{aligned}$$

(73)

$$\begin{aligned}&w_{iem} \le t_{im}&e \in S^{PROD}, (i,m) \in S^A : J_i = 1, m > 1 \end{aligned}$$

(74)

$$\begin{aligned}&w_{iem} \ge t_{im} - T(1-p^{LVL}_{ie})&e \in S^{PROD}, (i,m) \in S^A : J_i = 1, m > 1 \end{aligned}$$

(75)

$$\begin{aligned}&w_{iem} \ge 0&e \in S^{PROD}, (i,m) \in S^A : J_i = 1, m > 1 \end{aligned}$$

(76)

To linearize constraints (64), we replace them with the following constraints:

$$\begin{aligned}&s_{im} - \sum _{v \in V} q_{imv} + \sum _{e \in S^{PROD}} P^{RATE}_{ie} w^{OP}_{iem} \ge {\underline{S}}_i&(i,m) \in S^A : J_i = 1 \end{aligned}$$

(77)

$$\begin{aligned}&w^{OP}_{iem} \le T p^{LVL}_{ie}&e \in S^{PROD}, (i,m) \in S^A : J_i = 1 \end{aligned}$$

(78)

$$\begin{aligned}&w^{OP}_{iem} \le \sum _{v \in V} T^Q_v q_{imv}&e \in S^{PROD}, (i,m) \in S^A : J_i = 1 \end{aligned}$$

(79)

$$\begin{aligned}&w^{OP}_{iem} \ge \sum _{v \in V} T^Q_v q_{imv} - T(1-p^{LVL}_{ie})&e \in S^{PROD}, (i,m) \in S^A : J_i = 1 \end{aligned}$$

(80)

$$\begin{aligned}&w^{OP}_{iem} \ge 0&e \in S^{PROD}, (i,m) \in S^A : J_i = 1 \end{aligned}$$

(81)

5 Computational study

This section describes the test instances and presents the computational results and their interpretation. The computational tests were run on a computer with a 1.90 GHz Intel i5-8350U CPU, 32 GB of RAM, using Microsoft Windows 10 Enterprise 64-bit version. AMPL is used to code the models, which are then solved using CPLEX 12.9.

5.1 Test instances description

The test instances used in this study are made using data from six scenarios, labeled from A to F. The data for these instances were first used by Agra et al. (2013), then later by Agra et al. (2016), before Eide et al. (2020) added information relevant when considering the fuel consumption as a function of speed and load. The six scenarios differ in the number of production ports (1 or 2), the number of consumption ports (2 or 3), and the number of vessels (from 1 to 3). The instances obtained from the scenarios also vary in terms of the initial inventory levels and demand rates at the consumption ports. Furthermore, the instances differ in the length of the planning horizon (30 or 60 days).

Based on their characteristics, a unique name is associated to each instance. The name starts with the scenario letter, then the number of ports, the number of vessels, the length of the planning horizon, and an index. The names of the 12 instances used are shown in Fig. 5.

Each vessel’s operational characteristics include the capacity, initial load, potential speeds, and the daily cost of sailing for different speeds and loads. Three types of vessels are considered with speeds in the ranges [13.5, 19], [14.4, 20], and [16.2, 21] knots. To linearize the fuel consumption for the three vessel types, three breakpoints are used. These are taken as the minimum and maximum speeds, as well as an intermediate value taken as 15, 16, or 18, for the different vessel types, respectively. A heterogeneous fleet of vessels is considered in the instances. In other words, instances from B to F have several vessels with different speed ranges and capacities. In addition, a similar approach is applied for the vessel loads, where each vessel has three load options as a set of load level breakpoints. The lowest load option is 0, which represents an empty vessel, the largest load option is equal to the vessel capacity, which represents a full ship, and the middle breakpoint is when the vessel sails at exactly half of its capacity.

When using the model that considers the production rates as parameters, the rates are taken as given in the instances used by Eide et al. (2020). For the model that deals with the production rates as decision variables, a set of possible production rates must be specified. In all our test instances, 20 potential production levels are considered for each production port, and their corresponding production rates are the integers from 0 to 19. These values are close to the fixed production rates in the original instances. The second modification of the instances from Eide et al. (2020) is the introduction of constraints regarding port inventory levels and vessel loads at the end of the planning horizon. To reduce end-of-horizon effects, the minimum inventory levels for ports were set to 25% of the average initial inventory levels, calculated separately for production and consumption ports. Similarly, the lower bound on the total load on-board vessels at the end of the planning horizon was set to 25% of the total load on-board the vessels at the beginning of the planning horizon. The upper bounds were set to equal the capacities of vessels and inventories, respectively.

5.2 Computational time

The time limit for solving each instance was set at 30 hours. The time required to solve the proposed instances varied widely depending on the size of each instance. Table 1 shows the minimum, average, and maximum time in seconds when solving each of the two mathematical models. As shown in the table, optimizing the production rates decreased the average time needed to find an optimal solution. Oftentimes, the computational time increases when introducing more variables and constraints. However, in this case the computational time is reduced: the new variables may enable finding good solutions more quickly and this allows the branch-and-cut algorithm to cut larger parts of the solution space, which helps to find an optimal solution and its proof of optimality faster.

However, these result only hold for the instances used in the reported experiments. Additional runs were made for larger instances, namely variants of D-5-2-30-1, E-5-2-30-1, and F-4-3-30-1, where the planning horizon was set to 60 days instead of 30 days. For these cases, the model that optimize the production rates could not solve the instances within the time limit, whereas the other model was successful.

Table 1 A comparison of the computational time required to solve the mathematical models

5.3 Sailing costs and savings

Next, a comparison of sailing costs and savings is presented. The sailing costs are expressed in units of 1,000 US dollars. Fig. 5 shows the results for each of the 12 instances as solved by both models.

Fig. 5

Cost comparison for the different instances when production rates are preset and when they are optimized

As shown in the Fig. 5, considering the production levels as decision variables led to an decrease in the fuel consumption in all but one instance. Table  2 shows the cost saving in each instance. The minimum saving is 0.0% (instance A-4-1-30-1), the maximum saving is 34.71% (instance C-4-2-30-1), while the average saving is 11.4%.

5.4 Production levels

The emphasis of this study is on the production levels when they are considered as decision variables rather than as fixed parameters. Table 2 presents the final production rates for the different instances, and shows the cost saving in each instance when moving from preset rates to optimized rates.

Table 2 The production rates in the different instances for the two models

The results show that considering the production levels as decision variables led to increased rates for some ports and decreased rates for others.

Since shortages in the consumption ports are not allowed, the vessels are forced to leave the production ports at specific times to meet the demand of the consumption ports. If the production rates are low, the vessels can be forced to load less than the preferred amount when leaving the production ports, which in turn may lead to more port visits being required, thus increasing the fuel consumption. Another alternative to avoid increasing the legs is to wait at the production ports until the preferred quantity is produced and uploaded, then sailing at higher speeds towards the consumption ports. Thus, the vessels face two challenges, the first is an increase in the fuel consumption as a result of sailing at high speeds, and the second is the upper speed limits of vessels, which may prevent reaching to the consumption ports at the required time. In such cases, increasing production rates may decrease the total costs (see instances A-4-1-60-1, A-4-1-60-2, B-3-2-60-1, B-3-2-60-2, C-4-2-60-1, and C-4-2-60-2).

In contrast, any quantity transported from production ports to consumption ports exceeding the amount required to meet the demand could lead to an increase in transportation costs. This is due to the impact of load in the cost function. The storage capacity of the production ports is limited. Thus, when the production rate is too high, the vessels are forced to either load more than the preferred amount when leaving the production ports (instances A-4-1-30-1 and B-3-2-30-1) or to conduct more visits to the production ports, hence increasing the route lengths (instances C-4-2-30-1, D-5-2-30-1, and E-5-2-30-1). Both actions aim to avoid violating the storage capacity of the production ports. Therefore, in this case, a decrease of the production rates can lead to a decrease in the total costs.

Besides, when there are more than one production port in the problem, there may be an increase in the production rates of some ports and a decrease in others (instance F-4-3-30-1). This may be due to a mixture of the reasons mentioned above, or due to one port having a more suitable geographical location and thus being the preferred port for production.

5.5 Vessel loads

The vessel’s load between one port and another is represented by the flow on the leg connecting the two ports. This flow should satisfy the ports’ demands and final inventory requirements. Since sailing with a larger tonnage increases fuel consumption, hence total transportation costs, it is interesting to study the effect of optimizing the production levels on the loads of the vessels. To this end, a comparison is made between the solutions of the two mathematical models in terms of the average vessel load. This average is found by taking the average over each leg in the vessel routes, thus ignoring the distance travelled with each load.

The average load of the vessels when the production rates are considered as parameters is 44.23, whereas the average load of the vessels is 42.61 when production rates are optimized. Hence, optimizing the production levels decreased the average loads of the vessels. This decrease is due to that the average load in instances (C-4-2-30-1, D-5-2-30-1, E-5-2-30-1, and F-4-3-30-2) significantly more when production rates are considered constants than when they are considered variables, while in these instances production rates are much higher than rates after optimization. Thus, the vessels are forced to sail with a higher load to avoid violating the production ports’ storage capacities, and this is one of the reasons that led to a high decrease in transportation costs compared to other instances.

5.6 Vessel speeds

In this section, the average vessel speed (in knots) is evaluated. Each vessel sails at a single speed on each leg of its route, but the chosen speed can be different between the legs. The average speed in each instance is taken as the average of the speeds of all the traversed legs, thus again ignoring the distance travelled for at each speed. Table 3 presents the minimum, average, and maximum speed recorded over the 12 test instances. As seen in the table, the change in the average speed is small. This means that optimizing the production levels does not clearly affect the average speed.

Table 3 Comparison of average vessels’ speed , in knots, between the models

5.7 Analysis of solution structure

The solution structure can be analyzed by looking at the decisions regarding the vessels’ routes, speeds, and loads. These differ depending on whether the fixed production rates are considered as parameters or decision variables. By examining the solutions, we find that optimizing the production rates leads to different routing decisions for all but one of the instances. This means that the production rates have a clear impact on the structure of the routes.

Since shortages in consumption ports are not allowed, when the production rate is preset, vessels are forced to leave the production ports at specific times in order to catch up with the demand in consumption ports. Increasing the production rates allows vessels to load more cargo before leaving the production ports. This allows to unload more in each consumption port, leading to a decrease in the number of visits to some consumption ports.

In other cases, the increase in production rates, while not allowing the reduction of the number of visits of consumption ports, leads to improved delivery routes. Unloading more goods in a consumption port gives more flexibility on the time for revisiting the port and as consequence better routes may be found.

Moreover, even if the vessel leaves the production port with the same load, that departure may happen earlier when the port has an increased production rate because the vessel spends less time waiting for the production port to produce enough to load the specific amount of cargo. This may allow to reverse the order of visits to the consumption ports from one sequence of visits to the next one. While the distance traveled is the same, the cost decreases due to the impact of load in the sailing costs. This can be illustrated with an example, as shown in Fig. 6. Two consumption ports consume at a rate of 1 unit of product per time unit. Each leg of the route takes 1 time unit and, for demonstration proposes, we assume that loading and unloading takes no time. If the vessel visits each port every 3 time units, repeating the sequence P1-D1-D2 (see left hand side of Fig. 6) the vessel’s load is 6 during the leg P1-D1, 3 during the leg D1-D2 and 0 during the leg D2-P1. The total effort in terms of units of product transported during the sequence, having visited each consumption port twice and returning to the production port, is $2 \times 6 + 2 \times 3 + 2 \times 0 = 18$.

However, if the second repetition of the visiting sequence is reversed, we obtain the route shown in the right hand side of Fig. 6. In this case, since D1 is visited again 4 time units after the first visit, 4 units of product have to be unloaded at D1 during the first visit. On the other hand, only 2 units must to be unloaded at D2, since it is revisited after 2 time units. After completing two visits to each consumption port and returning to the production port, the total effort in terms of units of product transported is $2 \times 6 + 2 \times 2 + 2 \times 0 = 16 < 18$.

The reduction of production rates in ports may lead to (at least) two different types of improvements. In the model with preset rates, a visit to a production port close to the end of the time horizon might be needed to avoid the overflow of its inventory capacity. This may be avoided by reducing the production rate. Also, with a slower production, vessels tend to travel with less cargo, which decreases the cost of the routes.

Fig. 6

Example of how alternating visiting sequences may allow saving fuel due to reducing the average load on vessels, with the numbers on the arcs representing vessel loads

Instance C-4-2-30-1, which recorded the highest cost saving, is an example of the benefit of lowering production rates in some cases. As shown in the left-hand side of Fig. 7, both vessels visit production ports before ending their voyage for the purpose of not exceeding the storage capacity of these ports. By reducing the production rate at ports P1 and P2 by 1.6 and 1.37 units, respectively, (see the right side of Fig. 7), we could avoid visiting production ports at the end of the voyages, and thus reducing the fuel consumption.

Fig. 7

Instance C-4-2-40-1 shows how reducing the production rates could avoid visiting production ports at the end of the voyages, and thus reducing fuel consumption

5.8 Iterative refinement of production levels

Rather than having a discrete set $S^{PROD}$ of production levels to choose from, the allowed levels may be formed by a continuous interval, ranging from a minimum allowed production level to a maximum allowed level. In this case, the production rate at each production port could be expressed as a continuous variable in the mathematical model. However, instead of linearizing such a model having a product of two continuous variables, we propose an iterative refinement strategy.

First, an initial discrete set $S^{PROD}$ of values is formed by including the minimum production rate, the maximum production rate, and a set of equidistant intermediate values. The model with flexible production rates is then solved to obtain an initial solution. In the next step, for each production port, a new set of possible production rates is considered, consisting of the rates that are just below and just above the rate selected in the initial solution, in combination with a more refined set of intermediate production level values. The process can be repeated more times, but in the following computational testing, we consider only two steps.

In the first step, we consider 20 production levels, with rates from 0 to 19. Table 4 illustrates the production rates from the solutions in the first and second step of running the model with flexible production rates, as well as the cost saving (in %) obtained in the second step. For example, in the instance A-4-1-60-1, the optimal production rate in the first run is 8. New production rates within the range [7, 9] are then considered in the second step. The result shows that the best production rate is now 8.79, which leads to an extra, but quite small, cost saving.

Table 4 Comparison of total costs in a multi-stage approach

As shown in Table 4, the maximum additional saving is 0.46% (instance B-3-2-60-2), and the average saving is 0.06%. The saving occurred in the second run due to giving the model an ability to quantify production rates as fractional numbers. However, it is possible that no saving occurs if the change in the production rates does not affect other decision variables. Regarding the computational time for the second run of the model, 10 out of 12 instances needed less time compared to the time required in the first run. Anyway, the time required for the first and second run is close in most instances.

5.9 Cost of changing production rates vs. saving in the fuel consumption

To study the pure effect of production rates on transportation fuel consumption, costs related to changing production rates were ignored in our proposed model. In practice, changing production rates may require changing the number of knobs, operators, staff, and many other things. Hence, costs of changing production rates may be far greater than the savings one would get from reduced transportation costs. Therefore, it is interesting to examine the effect of considering the costs of changing production rates on the results. To this end, some modifications in the model that handles production rates as variables are needed as follows:

Additional parameters:

$P^{PREV}_{i}$:

: production rate at port i in the period preceding the beginning of the planning horizon, $i \in N: J_i = 1$

$C^{U}$:

: cost of changing the production rate per unit

Now, the objective function (1) can be replaced by the non-linear function:

$$\begin{aligned} \min ~&\sum _{v \in V} \sum _{(i,m,j,n) \in S_v^X} \sum _{l \in S_v^L} \sum _{s \in S_v^S} C^{PP}_{ijvls} g_{imjnvls} + \sum _{v \in V} \sum _{(i,m) \in S_v^A} \sum _{l \in S_v^L} \sum _{s \in S_v^S} C^{OP}_{ivls} g^O_{imvls} \nonumber \\&+ \sum _{v \in V} \sum _{(i,m) \in S_v^A} P_{iv}o_{imv} + \sum _{i \in N : J_i = 1} \mid P^{PREV}_{i} - \sum _{e \in S^{PROD}} P^{RATE}_{ie} p^{LVL}_{ie} \mid C^{U} \end{aligned}$$

(82)

The modified objective function is nonlinear due to the absolute value in its last term. We can linearize it as follows:

Additional variables:

$p^{change}_{i}$:

: auxiliary continuous variable used to replace the absolute value $\mid P^{PREV}_{i} - \sum _{e \in S^{PROD}} P^{RATE}_{ie} p^{LVL}_{ie} \mid$

Now, the modified objective function (82) can be replaced by the following linear expression:

$$\begin{aligned} \min ~&\sum _{v \in V} \sum _{(i,m,j,n) \in S_v^X} \sum _{l \in S_v^L} \sum _{s \in S_v^S} C^{PP}_{ijvls} g_{imjnvls} + \sum _{v \in V} \sum _{(i,m) \in S_v^A} \sum _{l \in S_v^L} \sum _{s \in S_v^S} C^{OP}_{ivls} g^O_{imvls} \nonumber \\&+ \sum _{v \in V} \sum _{(i,m) \in S_v^A} P_{iv}o_{imv} + \sum _{i \in N : J_i = 1} p^{change}_{i} C^{U} \end{aligned}$$

(83)

The following 2 new groups of constraints are then included:

$$\begin{aligned}&p^{change}_{i} \ge P^{PREV}_{i} - \sum _{e \in S^{PROD}} P^{RATE}_{ie} p^{LVL}_{ie}&i \in N : J_i = 1 \end{aligned}$$

(84)

$$\begin{aligned}&p^{change}_{i} \ge - P^{PREV}_{i} + \sum _{e \in S^{PROD}} P^{RATE}_{ie} p^{LVL}_{ie}&i \in N : J_i = 1 \end{aligned}$$

(85)

In the computational study, assuming that, the production rates before the beginning of the planning horizon are equal to the production rates when they are considered as parameters and the cost of changing the production rates per unit at any port equals to a very small number close to zero, gives the same savings in the fuel consumption when the cost of changing production is not considered at all, but with changes in the production rates in several instances. These changes are due to the model avoiding any change in the production rates as long as this change will not lead to a decrease in the fuel consumption. Table 5 shows the change in the production rates in each instance when adding the cost of changing production rates as a small number close to zero.

Table 5 The production rates in the different instances when adding a cost when changing the production rates as a small number close to zero

As an example, in instance A-4-1-60-2 which contains one production port, increasing the production rates by 3 units decreases the fuel consumption by 40.75 (8.41%). Thus, changing the production rates is certainly profitable as long as the cost of the change is not greater than $40.75 \div$3 = 13.58 per unit. Over this value, changing the production rate might be still profitable if the model is able to find a solution with a smaller change in the rate and enough saving in fuel consumption. Fig. 8 illustrates the effectiveness of optimizing the production levels in this instance. In this case, solving the model with larger values of CU, we are not able to find a different solution, thus the cost increase in a linear way until we reach the point where it is beneficial not to change the production rate at all.

Fig. 8

Example of the usefulness of optimizing the production levels when considering the cost of the change

On the other hand, Fig. 9 shows that, for instance C-4-2-30-1 which contains two production ports, when the cost of changing the production rate increases, it is possible to find new solutions that, changing the production rate less, get a better cost than the one obtained when the cost of changing the production rate was considered almost 0. Observe that, since in this case the original production rates are not integer we had to create new production levels equal to the original rates to enable the model to find a solution without change in production rate.

Fig. 9

The relationship between the cost of changing the production rates and the cost saving in instance C-4-2-30-1

Regarding the computational time needed to run the model, adding production change costs increased the required time in 9 out of 12 instances. The minimum time is 2.63 (instance A-4-1-30-1), the maximum is 15240 (instance E-5-2-30-1), while the average is 2342.42.

6 Conclusions

Maritime transportation has a significant role in global trade. Reducing transportation costs not only has positive consequences for transportation companies, but also on the global economy and on the carbon footprint. This paper introduced a mathematical model for maritime inventory routing problems with optimized production levels. When simultaneously optimizing the load and speed of vessels and the production rates, overall transportation costs can be lowered significantly. The mathematical models used also take into account requirements for the inventory levels and vessel loads at the end of the planning horizon, to reduce any end-of-horizon effects that may otherwise distort the evaluation of the optimization of production rates.

However, there are still some limitations to this work. The biggest challenge is the computational time needed to run larger instances. In particular, the mathematical model with optimized production levels could not be solved for a planning horizon of 60 days for the largest instances tested. Furthermore, only a small number of breakpoints are used for linearizing the fuel consumption curves, both with respect to load levels and speed levels. Thus, it is possible that the linearization leads to some small errors in the calculation of the objective function value, compared to the true fuel costs.

There are several considerations that could influence our conclusions regarding the usefulness of optimizing production rates. The first is that when the cost of changing production rates was considered in the model, the same cost was associated to the process of increasing and decreasing production rates. Also, It was considered that all production facilities have the same change cost. In reality, the cost of changing production may differ from one production facility to another, as well as the cost of increasing production may be different from the cost of reducing production. In addition, the cost of changing production rates was taken as a constant value per unit. In practice, the cost of changing production within certain limits may be less than the cost outside them. Therefore, more research is needed regarding the cost of changing production rates. Second, with more than one production facility, a company may wish to keep some balance in the production levels between different facilities. This was not included in the presented models, and the solutions could therefore allow moving all production from several facilities to only one. Finally, the cost of storage is ignored in the models. Considering that cost may significantly affect the results obtained in this article.