A performance model for mobile robot-based part feeding systems to supermarkets

Abstract

In a context where companies are striving to produce highly customised goods in small batches and within short lead times, increasing attention is being put on the design and management of part feeding systems. This research is the first to model automated part feeding to supermarkets in a factory environment, considering an innovative technology called vertical robotic storage and retrieval systems. This technology allows automating the storage, picking, and internal transportation activities in an integrated process, thanks to rack-climbing robots roaming in both the shop floor and the storage racks. We develop an analytical model based on the queuing network approach to analyse the system performance, and we use it to perform numerical experiments and to evaluate the design trade-offs with reference to a real case in the automotive industry. Results show that an increase in the number of robots leads to better performance since the positive impact on the response time is stronger than the negative impact on the waiting times of robots at the supermarkets due to congestion. Furthermore, a configuration with multiple small supermarkets improves the efficiency of the replenishment process, compared to a setting with few big supermarkets.

1 Introduction

The evolution of markets is requiring companies to reshape their production systems. Lifecycles are shortening and customers are demanding increasingly customised products and short lead times (e.g. Zhang et al. 2007; Dörmer et al. 2015). This entails manufacturing and transporting goods in small batches and leads to a sharp increase in the number of part variants handled in the factory (Fathi et al. 2016). In this context, modern factories call for responsive and efficient part feeding systems, synchronised with production systems and thus able to deliver to the production line the right part variants in small totes in time for the products’ assembly (Limère et al. 2012; Chankov et al. 2016).

Part feeding is recognised as one of the main issues faced in the design and management of assembly systems (Boysen et al. 2015; Caputo et al. 2018), and an extensive body of literature is available on this topic, mostly dealing with the preparation, storage, and transportation of unit loads to assembly stations. Nonetheless, some gaps remain to be addressed. In particular, despite the widespread adoption of supermarket warehouses (Boysen et al. 2009; Lolli et al. 2016; Emde 2017), the replenishment process from the CW to the supermarkets is still understudied. Moreover, recently introduced automated material handling technologies have not been investigated in the context of part feeding systems, although they could be able to support tote replenishment activities in a flexible and responsive way. Among such technologies, the vertical robotic storage and retrieval system (VRSRS) is an emerging solution for tote handling based on mobile robots which can both navigate the shop floor and enter the storage racks (Fig. 1). Unlike other systems, that support the automation of either storage, picking, or transportation of unit loads inside the factory, VRSRS may allow seamlessly integrating these activities, while keeping layout flexibility. Only one paper has studied this technology so far (Azadeh et al. 2019), considering the deployment of VRSRS in a distribution centre and developing closed queueing network models of an end-of-aisle picking system composed of a single storage aisle and a dedicated picking station, thus neglecting the possibility for robots to navigate outside the storage racks.

Fig. 1

(Source: exotec.com/en/solutions)

Mobile robots in VRSRS inside (a) and outside (b) the storage racks

Based on these premises, this paper studies the design of a supermarkets replenishment system based on the VRSRS technology, addressing the following research questions (RQs):

• RQ1 What is the relationship between the number of robots and the supermarkets replenishment lead-time?

When designing automated part feeding systems, a key issue is the right sizing of the equipment given the required performance. In the system under analysis, a critical performance is the replenishment lead-time to supermarkets, including both travel times of the mobile robots and waiting times. An increase in the equipment size (i.e., in the number of robots) may have a beneficial impact on the lead-time but may also increase congestion and waiting times of robots inside the system. Hence, we investigate the relationship between the number of robots, that represent the main component of the investment cost of this system, and the supermarkets replenishment lead-time.

• RQ2 What is the relationship between the design of supermarkets and their replenishment lead-time?

Supermarkets are decentralised storage areas located on the shop floor, close to the assembly lines, where space is a critical resource: overly increasing the amount of stock in these areas affects the efficiency of production operations (Hanson and Brolin 2013; Faccio et al. 2018). On the other hand, reducing the number of supermarkets and their storage capacity puts a strain on the part feeding system, since it leads to an increase in the average distance between storage areas and assembly stations and to the need of a more responsive replenishment. Literature has already addressed this trade-off considering the transportation of unit loads from supermarkets to assembly lines. However, the results might change when shifting the focus to supermarkets replenishment and considering an automated system based on VRSRS. For instance, while a bigger number of supermarkets may reduce the average travel time to reach assembly stations, it may also increase the average travel time between the CW and the supermarkets; moreover, the waiting times of robots before the supermarkets must be taken into account. Therefore, with this RQ we aim at studying the relationship between the replenishment system performance and the design variables related to supermarkets, i.e. their number and size, when considering VRSRS. In other words, we look for the best option, in terms of replenishment lead-time, between a system configuration with several, small supermarkets and a configuration with few, big supermarkets.

To answer the RQs, we develop an analytical model that allows to estimate the system performance. The model extends the one by Azadeh et al. (2019) to include supermarket replenishment activities in a factory environment. Differently from Azadeh et al. (2019), the developed model considers a multi-aisle central warehouse (CW) and a number of supermarkets, with robots performing storage and retrieval cycles both in the CW and in the supermarkets. In addition, the model is a semi-open queuing network (SOQN), allowing to capture the impact of the robot fleet size on the system performance, including the waiting time of replenishment requests before being processed. We solve the model through the matrix–geometric method (MGM), we validate it through discrete-event simulation, and we perform numerical experiments using real-world data.

The contributions of this paper are as follows. We are the first to study and discuss the adoption of automated material handling systems for supermarket replenishment, focusing on the VRSRS technology which is still understudied in the extant literature. We present an analytical model that represents a further example of the application of the queuing network theory to industrial problems. Through such model, we provide new and useful insights for the design of automated part feeding systems to supermarkets and for starting to understand the value of the VRSRS technology.

The remainder of this paper is organised as follows. Section 2 gives an overview of the scientific literature on part feeding to assembly lines, highlighting the contributions that deal with automated systems. Sections 3–6 describe the model, analysis, and design insights, and Sect. 7 reports conclusions and directions for future research.

2 Related literature

The majority of studies on part feeding to assembly lines focus on the selection of feeding policies, through descriptive models (e.g. Bozer and McGinnis 1992; Caputo and Pelagagge 2011), case studies (e.g. Hua and Johnson 2010; Hanson and Brolin 2013), and analytical models (e.g. Faccio 2014; Limère et al. 2015; Caputo et al. 2018). The other contributions deal with the design and performance improvement of part feeding systems, considering, for instance, inventory centralisation level (e.g. Battini et al. 2009; Emde and Boysen 2012b) and kitting system selection and optimisation (Hanson and Medbo 2019).

According to the very recent study by Schmid and Limère (2019), five main processes may be identified within the scope of assembly line feeding: preparation of unit loads required by assembly stations, transportation of unit loads from the storage areas to the assembly stations, usage of parts for assembly activities, intermediate storing of parts in supermarkets, and replenishment of supermarkets. In Table 1, we organise the reviewed literature according to this process classification, highlighting the contributions that deal with the introduction of automated systems.

Table 1 Summary of the main contributions on part feeding systems

As shown in Table 1, most of the reviewed papers consider in their study the preparation and transportation of unit loads. Preparation refers to the so-called kit assembly operation (e.g. Bozer and McGinnis 1992; Limère et al. 2012) or to the breakdown of big unit loads, such as pallets, into boxes or totes before moving them to assembly stations (e.g. Hanson and Brolin 2013; Schmid and Limère 2019). The papers dealing with transportation, instead, often consider the choice between the movement of big unit loads, performed through forklift trucks, as opposed to the transport of small boxes or totes, by means of tugger trains (e.g. Limère et al. 2012; Caputo et al. 2018). Moreover, a few contributions focus on the routing (Emde and Boysen 2012a), scheduling (e.g. Emde and Gendreau 2017), and loading (Diefenbach et al. 2019) of tugger trains in just-in-time contexts.

There is relatively less research on the usage and intermediate storing of parts. The usage process includes the search and picking of parts performed by assembly operators: most contributions deal with the trade-off between time spent to search and pick parts at the assembly stations and time spent to prepare unit loads in the previous processes (e.g. Hanson and Brolin 2013; Faccio et al. 2018). Some studies also take into account ergonomics issues (Neumann and Medbo 2010; Battini et al. 2017). As regards intermediate storing, some contributions only include in their total cost functions the inventory carrying costs at the supermarkets (e.g. Lolli et al. 2016; Caputo et al. 2018). Other ones present models and procedures to choose the number, size, and location of supermarkets (e.g. Battini et al. 2010; Emde and Boysen 2012b; Nourmohammadi et al. 2019a, b), that are decision variables of the so-called assembly line feeding problem (Schmid and Limère 2019). For instance, Battini et al. (2010) investigate the suitability of using supermarkets through a linear programming-based procedure considering inventory and transportation costs. Their results suggest that the adoption of supermarkets depends on several features of both assembly shop floor and parts; for instance, supermarkets are not suggested for big parts such as engines, while a high number of supermarkets is required in the case of parts with high value and small size. Emde and Boysen (2012b) introduce the so-called supermarket location problem. They develop a mathematical model to find the optimal number and placement of supermarkets and perform a computational study to evaluate the trade-off between the investment costs for supermarkets and the cost of transportation from supermarkets to assembly stations. They show that introducing supermarkets is beneficial when their number is relatively low (i.e., lower than five in their setting). Recently, the design of part feeding systems with supermarkets has been considered together with the assembly line balancing problem by Nourmohammadi et al. (2019a, b), that develop a hierarchical programming model considering the costs for installation, transportation, and inventory at supermarkets.

The papers dealing with supermarkets often neglect their replenishment from the CW or, in few cases, add the replenishment costs to their total cost functions, without any further modelling or optimisation of this process (e.g. Caputo et al. 2015a; Limère et al. 2015). The only exception is Emde (2017), that introduces a programming model to minimise the total stock in the supermarkets and the total number of replenishments in the time window, by varying the replenishment lot size and schedule.

Table 1 also shows that the number of papers on the automation of assembly line feeding processes is scarce, and no contributions regarding automated systems supporting replenishment and intermediate storing are available. Two types of automated systems supporting the preparation process can be found in literature: robotic kitting systems, where robots are placed in a kitting station or on-board automated storage/retrieval systems (Sellers and Nof 1989); hybrid robot-operator systems, where robots support operators in the picking (Boudella et al. 2018) or sorting (Fager et al. 2020) of parts. For the usage process, the reviewed literature describes vibratory bowl feeders (Lim et al. 1994) and flexible feeders (e.g. Loy and Reinhart 2010; Finetto et al. 2014) for the automated orientation of parts before they are picked by the operators, as well as dual head placement machines for the picking of parts at circuit card assembly lines (Wilhelm and Zhu 2009). As concerns the transportation process, literature deals with automated unloading of tugger trains through shooter-racks (Emde et al. 2012) and automated transportation of kits through conveyors and elevators (Zijm et al. 2000), AGVs (Hwang et al. 2002), and, more recently, mobile robots (Kousi et al. 2019).

Mobile robots can also be employed in the replenishment and intermediate storing of parts through VRSRS, a new technology characterised by robots that can move both vertically (when climbing the storage racks) and horizontally (when travelling within a storage level or outside the racks). To the best of our knowledge, only one paper focused on VRSRS exists, provided by Azadeh et al. (2019): they consider a system made of a single storage aisle with a dedicated picking station, located at the aisle input/output point, and they develop closed queueing network models to estimate the system performance, provide design insights, and make a comparison with autonomous vehicle storage and retrieval systems. Therefore, their models do not take into account the navigation of robots outside the storage racks and are not suitable to study the behaviour of VRSRS in a factory environment.

3 System description

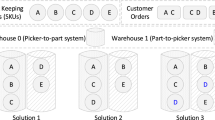
Figure 2 shows the layout of the part feeding system to supermarkets considered in this paper. It consists of a CW that replenishes a number of supermarkets feeding, in turn, the assembly stations. This layout is widely adopted by companies in industries like the automotive and the mechanical one. Table 2 reports the notation used in this paper.

Fig. 2

Layout of the VRSRS-based part feeding system

Table 2 Main notation

All warehouses are VRSRS with two single-deep storage racks per aisle. Each aisle is divided into several storage columns denoted as rack sections (Fig. 3). In each aisle, the first and last columns (i.e., columns 0 and $N_{C} ~ + ~1$), as well as the first and last tiers (i.e., tiers 0 and $N_{T} + {\text{~}}1$), are not used for storing, in order to let robots move across the rack sections. While the CW is usually made of multiple aisles, a supermarket always consists of a single aisle.

Fig. 3

(Adapted from Azadeh et al. 2019)

Side view of an aisle of the VRSRS

The aisles can be entered only by the robots, which handle mono-item totes denoted as ‘full totes’. The robots are able to visit each rack section by moving vertically and horizontally in sequence along the outer unidirectional path, and each storage location of a rack by moving vertically in both the up and down directions. Each aisle has one input/output (i/o) point located at the coordinates $x_{{i/o}} = - 2$ and $y_{{i/o}} = 1$. As illustrated in Fig. 2, robots can also travel outside the warehouses to replenish the supermarkets passing through the CW exit point located in the middle of the cross-aisle (point A) and reaching the supermarket area passing through point B. Considering the side view of the system (Fig. 3), the CW exit point coordinates are $x_{A}$ ($x_{A}$ < $x_{{i/o}}$) and $y_{A} = y_{{i/o}}$.

The supermarket feeding works according to the kanban system: whenever a tote is taken from the supermarket, its replenishment is triggered (Emde 2017). To fulfil the supermarket demand, robots (1) store an empty tote in the CW, (2) retrieve the required full tote from the CW, (3) reach the CW exit point and then the supermarket, (4) store the full tote in the supermarket, (5) retrieve an empty tote from the supermarket, and (6) come back to the CW exit point. The retrieval of full totes from supermarkets to feed assembly stations is out of scope and it could be managed in different ways. For instance, if the supermarkets have a limited height, operators could manually retrieve full totes and store empty totes by accessing the supermarkets from their external sides.

As we consider that robots also handle returning empty totes from the supermarkets to the CW, they perform dual command cycles in the CW and supermarkets. We assume that the dual command cycle is always performed within a specific rack section, i.e. there is always at least one empty location available in the same rack section to store the empty tote. This assumption is always true for supermarkets as we assume to have $N_{T}^{{S,~F}}$ storage tiers dedicated to full and $N_{T}^{{S,~E}}$ storage tiers dedicated to empty totes. As regards the CW aisles, this assumption is reasonable given the high number of storage columns and storage tiers, which makes it very likely to always find at least one empty storage location in each column (Azadeh et al. 2019).

The other modelling assumptions are listed below:

• Totes are stored randomly within the CW, i.e. the probability of choosing any rack section as well as any location in a rack section is based on the uniform distribution. We make the same assumption for the storage tiers dedicated to full totes within the supermarkets.

• The empty storage location to perform dual command cycles in the CW is randomly selected, as well as the empty tote position to perform dual command cycles in the supermarkets.

• The replenishment of the CW is carried out after the regular shift, when the assembly stations are not working, and is therefore out of the scope of this paper. This assumption is in line with most of the previous studies on the modelling and analysis of automated warehouses through both queuing and simulation models (e.g., Bozer and Aldarondo 2018; Zou et al. 2018; Tappia et al. 2019) and it is valid in several real cases, in which the assembly activity is not organised in three shifts.

• Stock-out never happens at the CW. We assume that full totes required by the supermarkets are always available in the CW.

4 Semi-open queuing network model

Coherently with the RQs, we model the part feeding system to supermarkets as a SOQN. This type of queuing network allows including the waiting time of replenishment requests before being processed by a robot in the estimation of the total replenishment lead-time, which therefore represents the time interval between the tote consumption at the supermarket and the storage of a new tote of the same product (e.g. Jia and Heragu 2009; Roy 2016). Moreover, using SOQNs makes possible to evaluate the relation between the inter-arrival time of tote replenishment requests and the system performance, and therefore to evaluate the trade-off between the throughput time in the inner network, which is determined by the number of robots, and the waiting time at the external queue. Section 4.1 provides the model description, whereas Sect. 4.2 describes the solution approach.

4.1 Modelling approach

The single-class SOQN model is reported in Fig. 4. The model is open with respect to the requests for tote replenishment and closed with respect to the number of robots, that corresponds to the fixed robot fleet size.

Fig. 4

SOQN model of the VRSRS-based part feeding system

In this model, one type of customer (i.e. requests for tote replenishment) and N_R robots circulate in the network. We assume the arrival process for tote replenishment requests to be Poisson with parameter λ. At the synchronisation station (node J), the first request waiting at the external queue B₁ and the first available robot at the buffer B₂ are matched together.

Once in the system, the robot performs a dual command cycle in a randomly selected storage aisle of the CW starting (and returning) from (and to) the i/o point (nodes 1 to $N_{A}^{{CW}}$). Each storage aisle is modelled as a single-server station with general service time distribution. Through such modelisation we prevent blocking, as only one robot is allowed to enter an aisle at a certain time. If another robot wants to enter an occupied aisle, it needs to wait until the previous robot in the queue has exited that aisle. The expected travel distance, $d_{{CW}}$, is estimated based on an equal probability of accessing any storage location according to the random storage policy and can be calculated using Eq. 1.

$$d_{{CW}} = 2*\left| {x_{{i/o}} - x_{0} } \right| + \left( {N_{T}^{{CW}} + 1} \right)*h~ + 2*\frac{{N_{C}^{{CW}} *w}}{2} + \left| {\left( {N_{T}^{{CW}} + 1} \right)*h - y_{s} } \right| + \left| {y_{s} - y_{r} } \right| + y_{r} + 2*~\left| {y_{{i/o}} - y_{0} } \right|~$$

(1)

Upon entering the storage aisle from the i/o point, the robot covers a horizontal distance equal to $\left| {x_{{i/o}} - x_{0} } \right|$. The travel pattern followed by robots within the storage racks is modelled as in Azadeh et al. (2019). First, the robot moves vertically to reach the last tier and horizontally to reach the selected column. Then, it moves vertically to reach an empty position with coordinate $y_{s}$, unloads the empty tote, reaches the retrieval position ($y_{r}$) in the same column, picks up the full tote and comes back to the tier 0. At last, it moves to the point ($x_{0} ,~y_{0}$) by moving horizontally and it comes back to the i/o point covering a horizontal and a vertical distance equal to $\left| {x_{{i/o}} - x_{0} } \right|$ and $\left| {y_{{i/o}} - y_{0} } \right|$, respectively.

The time required for a robot to reach the supermarket is modelled through infinite-servers (node $N_{A}^{{CW}} + 1$ and nodes from $N_{A}^{{CW}} + 2$ to $N_{A}^{{CW}} + N_{S} + 1$) as we assume that the aisles linking the CW and the supermarkets are large enough not to have interference among robots and that robots can skip obstacles with a short delay. Node $N_{A}^{{CW}} + 1$ models the travel from the i/o point of the CW storage aisle to, first, point A and, then, the supermarket area (point B). Based on the random storage policy assumption within the CW, the mean travel distance at this node, $d_{{CW \to B}}$, ${\text{is~}}$ as follows:

$$d_{{CW \to B}} = \frac{{L^{{CW}} }}{4} + d^{{A \to B}}$$

(2)

Nodes from $N_{A}^{{CW}} + 2$ to $N_{A}^{{CW}} + N_{S} + 1$ refer to the travel required to move from point B to the selected supermarket S_i. The mean travel distance, $d_{{B \to S_{i} }}$, ${\text{is~}}$ as follows:

$$d_{{B \to S_{i} }} = \left\{ {\begin{array}{*{20}l} {\left| {\frac{{N_{S} }}{2} - S_{i} } \right|*d^{S} } \hfill & {\quad N_{S} \;is\;odd} \hfill \\ {\left( {\left| {\frac{{N_{S} }}{2}~ - S_{i} + 0.5} \right|} \right)*d^{S} } \hfill & {\quad N_{S} ~\;is\;even} \hfill \\ \end{array} } \right.$$

(3)

In order to avoid blocking among robots, each supermarket is modelled like a single aisle of the CW through a single-server station (nodes from $N_{A}^{{CW}} + N_{S} + 2$ to $N_{A}^{{CW}} + 2*N_{S} + 1$). The expected travel distance inside the supermarket, $d_{S}$, can be obtained through Eq. 4:

$$d_{S} = 2*\left| {x_{{i/o}} - x_{0} } \right| + ~2*\left| {y_{{i/o}} - y_{0} } \right| + \left( {N_{T}^{S} + 1} \right)*h + ~2*\frac{{N_{C}^{S} *w}}{2} + \left| {\left( {N_{T}^{S} + 1} \right)*h - y_{s} } \right| + \left| {y_{s} - y_{r} } \right| + y_{r}$$

(4)

Then the robot comes back to the CW (nodes from $N_{A}^{{CW}} + 2*N_{S} + 2$ to $N_{A}^{{CW}} + 3*N_{S} + 2$). The expected travel distances, $d_{{S_{i} \to B}}$ and $d_{{B \to CW}}$, can be calculated by using Eqs. 3 and 2, respectively, as they correspond to the distance from a CW storage aisle to the selected supermarket.

Based on the travel distances, we calculate the travel time, $~t_{k}$, for each node k (k = $CW,~CW \to B,~B \to S_{i} ,~S,S_{i} \to B,B \to CW$) assuming a trapezoidal velocity–time relationship (Eq. 5). Such assumption allows considering the robot acceleration and deceleration delays (a) as well as the robot velocity, as in previous contributions on storage and retrieval systems using robots or shuttles (e.g. Lerher et al. 2015; Zou et al. 2016; Tappia et al. 2017). Based on the information provided by material handling systems manufacturers, we consider different values for the velocity inside and outside the storage racks ($v_{{IN}}$ and $v_{{OUT}}$, respectively). Therefore, in Eq. 5, $v_{k} = v_{{IN}}$ for k = $CW,~S$ while $v_{k} = v_{{OUT}}$ for the remaining nodes.

$$t_{k} = \left\{ {\begin{array}{*{20}l} {2*v_{k} /a + \left( {d_{k} - 2*v_{k}^{2} /\left( {2*a} \right)} \right)/v_{k} } \hfill & {\quad t_{k} > 2*v_{k} /a} \hfill \\ {2*\sqrt {d_{k} /a} } \hfill & {\quad t_{k} < 2*v_{k} /a} \hfill \\ \end{array} } \right.$$

(5)

Then, we compute the service time for each node, $~st_{k}$. For k = $CW$. and $S$, the service time is given by the sum the travel time, $t_{k}$, and of the fixed times required for the robot to load and unload the totes ($2\tau$). For the remaining nodes, the service time is equal to the travel time. Table 3 reports the expected value of the service times.

Table 3 Expected value of the service times

The service rate of each node, $\mu _{k}$, is equal to the inverse of the expected value of the service time (Eq. 6).

$$\mu _{k} = E\left[ {st_{k} } \right]^{{ - 1}}$$

(6)

Finally, we compute the squared coefficients of variation of the service times inside the CW, $c_{{CW}}$, and the supermarkets, $c_{S}$, through Eq. 7.

$$c_{k} = \left( {E\left[ {st_{k}^{2} } \right] - E\left[ {st_{k} } \right]^{2} } \right)/E\left[ {st_{k} } \right]^{2}$$

(7)

4.2 Solution approach

The queuing network in Fig. 4 is a single-class SOQN composed of infinite-servers and multiple single-server stations which have generally distributed service time. Since this type of networks do not have product-form exact solutions, we obtain the system performance measures through a solution approach combining the MGM with the decomposition–aggregation method, which is the most accurate approach to solve SOQNs (Roy 2016).

According to this solution approach, the original network is reduced to a two single-servers network (Fig. 5). The procedure for reducing the original network into a two single-servers network is an application of Norton’s theorem for Gordon–Newell networks (Chandy et al. 1975). The first $N_{A}^{{CW}} + N_{S} + 1$ nodes are modelled as a single server with load-dependent service time (Station A), as well as the complement network (Station B). Then, the load-dependent service-rates for station A and B ($\mu _{A}^{{ - 1}} \left( k \right)$ and $\mu _{B}^{{ - 1}} \left( k \right)$, respectively) are obtained by modelling the stations as closed networks and solving them by using the approximate mean value analysis (AMVA, Buitenhek et al. 2000).

Fig. 5

Reduced semi-open queuing network

At this point, the MGM is applied to solve the two single-servers network. The MGM was developed by Neuts (1981) to solve Markov processes having a repetitive property called the matrix–geometric property, according to which the generator matrix can be described in a block-tridiagonal form with repetitive elements and the solution of the steady-state probability vector can be given in matrix–geometric form. The first step is the development of the generator matrix, which contains the transition rate from all the combinations of the states of the system. Each state of the system is defined by the vector $\left( {l,~m,~n} \right)$ where $l \ge 0$ is the number of requests in the external queue, $0 \le m \le K$ is the number of requests at Station A, and $0 \le n \le K$ is the number of requests at Station B. Since a request can enter the network only if it is matched with a robot, and considering that the number of robots circulating in the network is fixed (thus, $m + n \le ~K$), the first two dimensions can be aggregated without losing information. Therefore, the state of the system can be represented by the vector $\left( {p,n} \right)$, where $p$ is equal to the sum of the number of requests in the external queue and the number of totes at Station A. The generator matrix of the reduced network, $\user2{Q}$, is given by Eq. 8, while “Appendix 1” reports its submatrices.

$$\user2{Q} = \left[ {\begin{array}{*{20}c} {\user2{B}_{0} } & \user2{C} & {} & {} & {} & {} & {} & {} & {} \\ {\user2{A}_{1} } & {\user2{B}_{1} } & \user2{C} & {} & {} & {} & {} & {} & {} \\ {} & {\user2{A}_{2} } & {\user2{B}_{2} } & \user2{C} & {} & {} & {} & {} & {} \\ {} & {} & \ddots & \ddots & \ddots & {} & {} & {} & {} \\ {} & {} & {} & {\user2{A}_{{K - 1}} } & {\user2{B}_{{K - 1}} } & \user2{C} & {} & {} & {} \\ {} & {} & {} & {} & {\user2{A}_{K} = \user2{A}} & {\user2{B}_{K} = \user2{B}} & \user2{C} & {} & {} \\ {} & {} & {} & {} & {} & \user2{A} & \user2{B} & \user2{C} & \ldots \\ {} & {} & {} & {} & {} & {} & {} & \vdots & \ddots \\ \end{array} } \right]$$

(8)

After identifying $\user2{Q}$, the rate matrix $\user2{R}$ is calculated iteratively through Eq. 9, involving the repetitive part of the generator matrix (Neuts 1981).

$$\user2{C} + \user2{RA}_{1} + \user2{R}^{2} \user2{A}_{2} = 0$$

(9)

By using the rate matrix $\user2{R}$, all the stationary probability vectors are obtained. The boundary stationary probabilities ${\varvec \pi }_{0}$ and ${\varvec \pi }_{1}$ are calculated by solving the system of linear equations (Eq. 10), where $\user2{F} = \left( {\user2{I} - \user2{R}} \right)^{{ - 1}}$.

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {{\varvec \pi }_{0} } & {{\varvec \pi }_{1} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\user2{B}_{0} } & {\user2{C}_{0} } \\ {\user2{A}_{1} } & {\user2{B}_{1} + \user2{RA}_{2} } \\ \end{array} } \right] = \left[ {0,0} \right] \\ & \left[ {\begin{array}{*{20}c} {{\varvec \pi }_{0} } & {{\varvec \pi }_{1} } \\ \end{array} } \right]\left[ {{{\user2 e}^{\prime}~~Fe}} \right]^{'} = 1 \\ \end{aligned}$$

(10)

The other stationary probability vectors, corresponding to the repeating states, can be obtained by using the matrix geometric property, e.g. ${\varvec \pi }_{2} = {~{\varvec\pi} }_{1} \user2{R}$.

Knowing the stationary probability vectors, the performance measures of interest are calculated. The expected external queue length at buffer $B_{1}$, $Q_{{B_{1} }}$, the expected queue length at buffer $B_{2}$, $Q_{{B_{2} }}$, and the expected number of requests at Stations A and B, $Q_{{l_{A} }}$ and $Q_{{l_{B} }}$, are given by Eqs. 11 to 14.

$$Q_{{B_{1} }} = {\varvec \pi }_{1} \left[ {\begin{array}{*{20}c} 0 \\ \vdots \\ 0 \\ 1 \\ \end{array} } \right] + {\varvec \pi }_{2} \left[ {\begin{array}{*{20}c} 0 \\ \vdots \\ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ 2 \\ \end{array} } \right] + \cdots + {\varvec \pi }_{{K - 1}} \left[ {\begin{array}{*{20}c} 0 \\ \vdots \\ {K - 2} \\ {K - 1} \\ \end{array} } \right] + {\varvec \pi }_{K} \user2{F}\left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \vdots \\ K \\ \end{array} } \right] + {\varvec \pi }_{{K + 1}} \user2{F}^{2} \user2{e}$$

(11)

$$Q_{{B_{2} }} = {\varvec \pi }_{0} \left[ {\begin{array}{*{20}c} K \\ {K - 1} \\ \vdots \\ 0 \\ \end{array} } \right] + {\varvec \pi }_{1} \left[ {\begin{array}{*{20}c} {K - 1} \\ {K - 2} \\ \vdots \\ 0 \\ \end{array} } \right] + \cdots + {\varvec \pi }_{{K - 1}} \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right]$$

(12)

$$Q_{{l_{A} }} = ~{\varvec \pi }_{1} \left[ {\begin{array}{*{20}c} 1 \\ \vdots \\ 1 \\ 0 \\ \end{array} } \right] + {\varvec \pi }_{2} \left[ {\begin{array}{*{20}c} 2 \\ \vdots \\ 2 \\ 1 \\ 0 \\ \end{array} } \right] + \cdots + {\varvec \pi }_{{K - 1}} \left[ {\begin{array}{*{20}c} {K - 1} \\ {K - 1} \\ {K - 2} \\ \vdots \\ 1 \\ 0 \\ \end{array} } \right] + {\varvec \pi }_{K} \user2{F}\left[ {\begin{array}{*{20}c} K \\ {K - 1} \\ \vdots \\ 1 \\ 0 \\ \end{array} } \right]$$

(13)

$$Q_{{l_{B} }} = \mathop \sum \limits_{{k = 0}}^{{K - 1}} {\varvec \pi }_{k} \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \vdots \\ K \\ \end{array} } \right] + {\varvec \pi }_{K} \user2{F}\left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \vdots \\ K \\ \end{array} } \right]$$

(14)

In Eqs. 11, 13, and 14, $\user2{e}$ is the column vector of ones and $\user2{F} = \left( {\user2{I} - \user2{R}} \right)^{{ - 1}}$, where $\user2{I}$ is the identity matrix.

Knowing $Q_{{B_{2} }}$, the robot utilisation, $U_{R}$, is given by Eq. 15.

$$U_{R} = \frac{{K - Q_{{B_{2} }} }}{K}$$

(15)

Finally, based on Little’s Law, the throughput time for the first network, $E\left[ {LT_{A} } \right]$, and for the second network,$~E\left[ {LT_{B} } \right]$, and the expected replenishment lead-time, $E\left[ {LT} \right]$, are obtained by using Eqs. 16, 17, and 18, respectively.

$$E\left[ {LT_{A} } \right] = {\text{~}}\frac{{Q_{{l_{A} }} }}{\lambda }$$

(16)

$$E\left[ {LT_{B} } \right] = {\text{~}}\frac{{Q_{{l_{B} }} }}{\lambda }$$

(17)

$$E\left[ {LT} \right] = {\text{~}}E\left[ {LT_{A} } \right] + E\left[ {LT_{B} } \right] + \frac{{Q_{{B1}} }}{\lambda }$$

(18)

5 Model validation

The solution procedure presented in Sect. 4 is implemented using Matlab software and validated through discrete-event simulation. The simulation model is built using Arena software. Similarly to the analytical model, also in the simulation model we consider exponential interarrival times between replenishment requests, and we assume that a random storage policy is adopted. The other assumptions reported in Sect. 3 for the analytical models (e.g. queues of infinite capacity for storage aisle and supermarket, FCFS service rule for managing all the queues) are also implemented in the simulation model. Unlike the analytical model, the simulation model assumes discrete space and considers the real travel distances. Travel times are computed based on the trapezoidal velocity–time relationship. The simulation flowchart is reported in “Appendix 2”.

We set the CW storage capacity to 8832 totes and $\left( {N_{T}^{{CW}} *h} \right)/\left( {N_{C}^{{CW}} *w} \right) = 1,$. as it is the optimal ratio obtained in Azadeh et al. (2019). The data used are reported in Table 4. Data about the VRSRS (e.g. robot horizontal and vertical speed) were provided by the supplier Exotec Solutions, while the other data (e.g. distance between CW and supermarkets) refer to a real case. The case concerns the assembly plant of a European tier-1 supplier in the automotive dustry producing braking systems for cars.

Table 4 Data used in the model validation

To compare the results of the analytical model and simulation, we consider 36 scenarios differing among each other in the request arrival rate, λ, namely 100, 110, and 120 requests/hour, the number of robots circulating in the system, N_R, namely 6, 7, and 8, the number of supermarkets, N_S, namely 5 and 7, and the supermarkets size, S^S, corresponding to the number of full totes that meet a 0.5- and 1-shift demand of the assembly stations (therefore, the storage capacity of each supermarket ranges between 58 and 192 totes). The resulting robot utilisation, U_R, varies between about 45% and 75%. For each scenario, we run 15 replications to estimate the following statistics: expected robot utilisation, U_R, expected replenishment lead-time, $E\left[ {LT} \right]$, expected queue length at the external buffer, $Q_{{B_{1} }}$, and expected queue length at the idle robot buffer, $Q_{{B_{2} }}$. The number of replications is set to obtain a ratio between the half-width of the 90% confidence interval and the mean value lower than 5% for all the scenarios.

Table 5 shows the results about the model accuracy. The average absolute error is calculated as $\left| {A - S} \right|/S \times 100\%$, where A and S denote the estimates obtained through the analytical and simulation model, respectively. Across the 36 scenarios, the average absolute error for the robot utilisation is about 3%. The average absolute percentage error for the expected total throughput time is about 2%. For the expected queue length at buffers, the average absolute percentage error is 13.5% for B₁ and 4.9% for B₂. The maximum error is related to the expected queue length at the external buffer. As illustrated by Jia and Heragu (2009), errors in the external queue length can be up to 50% using the proposed solution approach, which is, to the best of our knowledge, the most effective method for solving semi-open queuing networks. These errors are in line with those obtained in other applications of the MGM found in previous literature (e.g. Buitenhek et al. 2000; Jia and Heragu 2009; Tappia et al. 2019), and can be considered acceptable for the initial design phase.

Table 5 Summary of average absolute and range percentage errors

6 Design insights

This section presents a computational study to develop insights on the design of a VRSRS-based part feeding system to supermarkets, thus answering the RQs using the model proposed in Sect. 4 to estimate the system performance. We consider the same data and real case-based setting used for the validation. The scenarios we investigate were selected in close collaboration with the tier-1 automotive supplier already mentioned in Sect. 5, which is evaluating the adoption of the VRSRS technology. Such scenarios differ in the request arrival rate (λ = 100, 110, 120 requests/hour), the number of supermarkets (N_S = 3, 5, 7), and the supermarket size (S^S = 0.5-, 1-, 2-shift demand of the assembly stations; therefore, the supermarket storage capacity ranges between 58 and 640 totes). With refer to λ and N_S, the intermediate values (i.e., 110 requests/hour and 5 supermarkets) are the real values taken from the automotive company, while the other values are set in order to study how system performance varies following both a positive and negative deviation from the real values. Moreover, the number of robots circulating in the system (N_R = 5, 6, 7, 8, 9, 10) is varied in order to cover a wide range of values of the robots utilization, from 35 to 95%. As system performance measures, we consider: expected queue length at the external buffer, $Q_{{B_{1} }}$, expected queue length at the idle robot buffer, $Q_{{B_{2} }}$, expected robot utilisation, U_R, throughput time for the first network (i.e. waiting time and service time at the CW and travel time from the CW to the assigned supermarket), $E\left[ {LT_{A} } \right]$, throughput time for the second network (i.e. waiting time and service time at the supermarket and travel time from the supermarket to the CW), $E\left[ {LT_{B} } \right]$, and expected supermarkets replenishment lead-time, $E\left[ {LT} \right]$. All the results are reported in “Appendix 3”.

6.1 Relationship between number of robots and replenishment lead-time

In this section, we investigate the relationship between the number of robots and the expected replenishment lead-time to supermarkets. In all scenarios, the replenishment lead-time decreases with the number of robots N_R. This happens because the positive impact on the waiting time at the external queue is stronger than the negative impact on the waiting time at the supermarkets due to congestion.

The marginal benefits of adding more robots decrease with the number of robots and increase with the arrival rate. Figure 6 shows this trend considering a setting with few big supermarkets (i.e. N_S = 3 and S^S = 2-shift demand). The reduction in the replenishment lead-time is up to 16% in the case of λ = 120 requests/hour by using 7 robots instead of 6, while it becomes lower and lower when adding more robots. Indeed, when the system capacity, function of the number of robots, is too aligned with the arrival rate, adding robots leads to a reduction in the response time. Conversely, when there are enough robots to meet the arrival rate without long waiting time outside the system, there is no reason to invest more in robots.

Fig. 6

Expected replenishment lead-time varying N_R and λ with N_S = 3 and S^S = 2-shift demand

We observe the same behaviour considering all the other settings defined by the combination of the number and size of supermarkets. However, as shown in Fig. 7, the maximum reduction in the replenishment lead-time decreases from 16% in the configuration with few big supermarkets to 10% in the configuration with multiple small supermarkets (i.e. N_S = 7 and S^S = 0.5-shift demand). We can conclude that adding robots is less beneficial in the case of multiple small supermarkets, which require a lower number of robots, fixing the required replenishment lead-time, compared to few big supermarkets.

Fig. 7

Expected replenishment lead-time varying N_R, N_S, and S^S with λ = 120 requests/hour

6.2 Impact of supermarket design on replenishment lead-time

In this section, we deepen the relationship between the replenishment lead-time to supermarkets and the supermarket-related design variables (i.e. size and number). First, we discuss the effect of each variable keeping the other one fixed, then we draw conclusions on their combined effect.

Keeping fixed the number of supermarkets, the expected replenishment lead-time improves by decreasing the supermarkets size in all the settings. For instance, Fig. 8 shows this behaviour in the case of $N_{R}$ = 6 and $\lambda$ = 120 requests/hour. The reason lies in the reduction of the throughput time for the second network: the smaller the supermarket size, the shorter the travel distances inside it, and, in turn, the shorter the time to perform the retrieval and storage operations and the waiting time for the supermarket availability. Moreover, the waiting time at the external queue decreases consequently.

Fig. 8

Expected replenishment lead-time varying S^S and N_S with λ = 120 requests/hour and N_R = 6

Looking at the effect of the number of supermarkets, we observe that the replenishment lead-time decreases with it, keeping fixed the supermarket size (Fig. 8). This is valid for any number of robots and arrival rate. To understand this effect, we need to consider the different behaviour of the throughput time for the first ($E\left[ {LT_{A} } \right]$) and second ($E\left[ {LT_{B} } \right]$) networks when varying the number of supermarkets. The higher the number of supermarkets, the lower the throughput time for the second network and the higher the throughput time for the first network. The effect on the throughput time for the second network is explained by the shorter travel distances inside the supermarkets and by the lower arrival rate at each supermarket (since the total demand is split among a higher number of delivery points), that further reduces the waiting time for the supermarket availability. This implies an increase in the service rate of the second network, resulting in a higher number of robots at the CW and therefore in a higher waiting time to access the CW storage aisles.

The benefit in the replenishment lead-time with the number of supermarkets decreases with a low arrival rate. The lower the arrival rate, the lower the reduction in the waiting time for the supermarket availability, until the decrease in the throughput time of the second network does not balance the increase in the throughput time of the first network anymore. The benefit in the replenishment lead-time with the number of supermarkets also decreases with a small supermarkets size as the waiting time at the supermarkets is already low.

In summary, a configuration with multiple small supermarkets improves the efficiency (i.e. lower number of robots and shorter lead-time) of the replenishment process. This result enriches the findings of previous literature, that, considering the transportation of unit loads from supermarkets to assembly lines, suggests to increase the number of supermarkets until an optimal value beyond which the additional costs of installation and inventory overcome the cost savings in transportation (Battini et al. 2010; Emde and Boysen 2012b). In light of our results, we can conclude that the optimisation of the entire part feeding system (including both replenishment to supermarkets and transportation to assembly stations) could lead to a higher optimal number of supermarkets, compared to previous findings, when VRSRS technology is adopted. Moreover, our results show that, once fixed the number of supermarkets, their replenishment lead time improves if supermarkets are smaller. Therefore, the adoption of VRSRS may allow saving space on the shop floor while, at the same time, improving the performance of the replenishment system.

7 Conclusions

This paper studies a part feeding system based on the VRSRS technology, focusing on the replenishment process to supermarkets in assembly plants. It addresses a twofold literature gap, namely the design of the supermarkets replenishment system and the analysis of new material handling technologies in a factory environment.

We develop an accurate analytical model, based on the queuing network approach, to analyse the system performance, and we validate it through simulation. Then, we carry out numerical experiments to evaluate the design trade-offs of the analysed system and we study the impact of the system design variables (i.e. number of robots, supermarkets number and size) on the replenishment lead-time. Results show that an increase in the number of robots always leads to better performance since the reduction of the replenishment lead-time is stronger than the negative impact on the waiting times. Moreover, a configuration with multiple small supermarkets improves the efficiency (i.e. lower number of robots and shorter lead-time) of the replenishment process, allowing to conclude that, when the VRSRS technology is adopted, the optimisation of the entire part feeding system could result in a higher optimal number of supermarkets compared to previous literature findings. The developed model, as well as the design insights stemming from its application, are valid for any factory in which the logistics system consists of a number of warehouses located on the shop floor and replenished with totes from a CW. Therefore, the possible application domains may include both assembly and manufacturing systems, with stations organised either in a line, in a job shop, or in fixed-position assembly islands.

As this is a first attempt to address the adoption of automation for supermarket replenishment, we see several potential areas for further research. The model can easily incorporate changing layout (e.g., dimensions, distances, and supermarket design) and could be extended by considering also the replenishment of the CW and the transportation of unit loads to assembly stations, so as to develop insights on the design of the entire part feeding process. Future works could also address the design trade-offs from a cost perspective, considering for instance the supermarket location problem, already tackled by Emde and Boysen (2012b) with reference to a manual part feeding system.

Appendices

Appendix 1

Appendix 1 reports the sub-matrices that compose the generator matrix Q (Eq. 8). All the matrices are square matrices of size $\left( {K + 1} \right)~{\text{x~}}\left( {K + 1} \right)$.

$$\user2{B}_{0} = \left[ {\begin{array}{*{20}c} { - \lambda } & 0 & 0 & \ldots & 0 \\ {\mu _{B} \left( 1 \right)} & { - \left( {\mu _{B} \left( 1 \right) + \lambda } \right)} & 0 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & {\mu _{B} \left( {K - 1} \right)} & { - \left( {\mu _{B} \left( {K - 1} \right) + \lambda } \right)} & 0 \\ 0 & 0 & 0 & {\mu _{B} \left( K \right)} & { - \left( {\mu _{B} \left( K \right) + \lambda } \right)} \\ \end{array} } \right]~$$

(19)

$$\user2{C} = ~\lambda \user2{I}$$

(20)

$$\user2{A}_{1} = \left[ {\begin{array}{*{20}c} 0 & {\mu _{A} \left( 1 \right)} & \ldots & 0 & 0 \\ \vdots & \ddots & \ddots & \ldots & \vdots \\ 0 & 0 & \ldots & {\mu _{A} \left( 1 \right)} & 0 \\ 0 & 0 & \ldots & 0 & {\mu _{A} \left( 1 \right)} \\ 0 & 0 & \ldots & 0 & 0 \\ \end{array} } \right]$$

(21)

$$\user2{B}_{1} = \left[ {\begin{array}{*{20}c} { - \mu _{A} \left( 1 \right)} & 0 & \ldots & 0 & 0 \\ 0 & { - \mu _{A} \left( 1 \right)} & \ldots & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \ldots & { - \mu _{A} \left( 1 \right)} & 0 \\ 0 & 0 & \ldots & 0 & 0 \\ \end{array} } \right] + \user2{B}_{0}$$

(22)

$$\user2{A}_{2} = \left[ {\begin{array}{*{20}c} 0 & {\mu _{A} \left( 2 \right)} & \ldots & 0 & 0 \\ \vdots & \ddots & \ddots & \vdots & \vdots \\ 0 & 0 & \ldots & {\mu _{A} \left( 2 \right)} & 0 \\ 0 & 0 & \ldots & 0 & {\mu _{A} \left( 1 \right)} \\ 0 & 0 & \ldots & 0 & 0 \\ \end{array} } \right]$$

(23)

$$\user2{B}_{2} = \left[ {\begin{array}{*{20}c} { - \mu _{A} \left( 2 \right)} & \ldots & 0 & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & \ldots & { - \mu _{A} \left( 2 \right)} & 0 & 0 \\ 0 & \ldots & 0 & { - \mu _{A} \left( 1 \right)} & 0 \\ 0 & \ldots & 0 & 0 & 0 \\ \end{array} } \right] + \user2{B}_{0}$$

(24)

$$\user2{A}_{K} = \left[ {\begin{array}{*{20}c} 0 & {\mu _{A} \left( K \right)} & \ldots & 0 & 0 \\ \vdots & \ddots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & {\mu _{A} \left( 2 \right)} & 0 \\ 0 & 0 & 0 & 0 & {\mu _{A} \left( 1 \right)} \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]$$

(25)

$$\user2{B}_{K} = \left[ {\begin{array}{*{20}c} { - \mu _{A} \left( K \right)} & \ldots & 0 & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & \ldots & { - \mu _{A} \left( 2 \right)} & 0 & 0 \\ 0 & \ldots & 0 & { - \mu _{A} \left( 1 \right)} & 0 \\ 0 & \ldots & 0 & 0 & 0 \\ \end{array} } \right] + \user2{B}_{0}$$

(26)

Appendix 2

The simulation model of the VRSRS-based part feeding system to supermarkets is described in Fig. 9.

Fig. 9

Detailed simulation flowchart for the first (a) and second (b) sub-system of the VRSRS-based part feeding system

Appendix 3

Appendix 3 reports the detailed results of the numerical experiments for $\lambda$ = 100 requests/h (Table 6), $\lambda$ = 110 requests/h (Table 7), and $\lambda$ = 120 requests/h (Table 8).

Table 6 Results varying N_S, S^S, and N_R with λ = 100 requests/hour

Table 7 Results varying N_S, S^S, and N_R with λ = 110 requests/hour

Table 8 Results varying N_S, S^S, and N_R with λ = 120 requests/hour