Optimal pricing with free gift cards in a two-product supply chain

Abstract

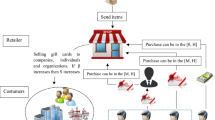
We develop a model of free gift card promotions in a two-product supply chain. We analyze three cases with different gift card strategies based on whether the wholesale and retail prices are changed or unchanged. The results indicate that, in the strategy of unchanged wholesale and retail prices, the retailer and two manufacturers are better off. The gift card promotions can effectively stimulate the demands of two products. We find that the two manufacturers benefit more from the gift card promotion than the retailer does. In the strategy of unchanged wholesale prices and changed retail prices, if the gift card value is not very large, the retailer’s profit margins and average consumer surplus from the gift card promotion are increasing in the gift card value. In the strategy of changed wholesale and retail prices, the retailer and two manufacturers have an incentive to raise the retail and wholesale prices under certain conditions. Furthermore, we show that, keeping the prices at the level of no gift cards is the dominant strategy for the supply chain and consumers, and the difference between retail prices and wholesale prices of two products is the key factor in determining the gift card value.

Appendix

Proof

Proposition 1

Substituting Eqs. (1) and (2) into Eq. (4), we have

$$\begin{aligned} \pi _r^{NG}(p_1,p_2)=\frac{n(a_1-p_1)(p_1-w_1)}{a_1}+\frac{n(a-2-p_2)(p_2-w_2)}{a_2}. \end{aligned}$$

Taking the first and second derivations of $\pi _r^{NG}(p_1,p_2)$, we have

$$\begin{aligned} \frac{\partial \pi _r^{NG}(p_1,p_2)}{\partial p_1}=\frac{n(a_1+w_1-2p_1)}{a_1}, \, \frac{\partial ^2 \pi _r^{NG}(p_1,p_2)}{\partial p_1^2}= & {} -\frac{2n}{a_1},\\ \frac{\partial \pi _r^{NG}(p_1,p_2)}{\partial p_2}=\frac{n(a_2+w_2-2p_2)}{a_2},\, and \; \frac{\partial ^2 \pi _r^{NG}(p_1,p_2)}{\partial p_2^2}= & {} -\frac{2n}{a_2}. \end{aligned}$$

Then, the Hessian matrix is

$$\begin{aligned} H=\left[ \begin{array}{cc} \frac{\partial ^2 \pi _r^{NG}(p_1,p_2)}{\partial p_1^2} &{} \frac{\partial ^2 \pi _r^{NG}(p_1,p_2)}{\partial p_1 \partial p_2} \\ \frac{\partial ^2 \pi _r^{NG}(p_1,p_2)}{\partial p_1 \partial p_2} &{} \frac{\partial ^2 \pi _r^{NG}(p_1,p_2)}{\partial p_2^2} \\ \end{array}\right] =\left[ \begin{array}{cc} -\frac{2n}{a_1} &{} 0 \\ 0 &{} -\frac{2n}{a_2} \\ \end{array}\right] . \end{aligned}$$

Since $|H_1|=-\frac{2n}{a_1}<0$ and $|H_2|=\frac{4n^2}{a_1a_2}>0$, then $\pi _r^{NG}$ is jointly concave in $p_1$ and $p_2$. From the first-order-condition, the optimal retailer prices are given by $p_1^*(w_1)=\frac{a_1+w_1}{2}$ and $p_2^*(w_2)=\frac{a_2+w_2}{2}$.

Substituting Eq. (1) and $p_1^*(w_1)$ into Eq. (5), we have

$$\begin{aligned} \pi _{m1}^{NG}(w_1)=\frac{n}{2a_1}(a_1-w_1)w_1. \end{aligned}$$

Taking the first and second derivations of $\pi _{m1}^{NG}(w_1)$ , we have $\frac{\partial \pi _{m1}^{NG}(w_1)}{\partial w_1}=\frac{n(a_1-2w_1)}{2a_1}$ and $\frac{\partial ^2 \pi _{m1}^{NG}(w_1)}{\partial w_1^2}=-\frac{n}{a_1}$. Since $\frac{\partial ^2 \pi _{m1}^{NG}(w_1)}{\partial w_1^2}<0$, then $\pi _{m1}^{NG}(w_1)$ is concave in $w_1$. From $\frac{\partial \pi _{m1}^{NG}(w_1)}{\partial w_1}=0$, we get the optimal wholesale price of product 1 $w_1^{NG*}=a_1/2$. Then, we get the optimal retail price of product 1 $p_1^{NG*}=3a_1/4$.

Substituting Eq. (2) and $p_2^*(w_2)$ into Eq. (6), we have

$$\begin{aligned} \pi _{m2}^{NG}(w_2)=\frac{n}{2a_2}(a_2-w_2)w_2. \end{aligned}$$

Taking the first and second derivations of $\pi _{m2}^{NG}(w_2)$ , we have $\frac{\partial \pi _{m2}^{NG}(w_2)}{\partial w_2}=\frac{n(a_2-2w_2)}{2a_2}$ and $\frac{\partial ^2 \pi _{m2}^{NG}(w_2)}{\partial w_2^2}=-\frac{n}{a_2}$. Since $\frac{\partial ^2 \pi _{m2}^{NG}(w_2)}{\partial w_2^2}<0$, then $\pi _{m2}^{NG}(w_2)$ is concave in $w_2$. From $\frac{\partial \pi _{m2}^{NG}(w_2)}{\partial w_2}=0$, we get the optimal wholesale price of product 2 $w_2^{NG*}=a_2/2$. Then, we get the optimal retail price of product 2 $p_2^{NG*}=3a_2/4$. $\square$

Proof

Proposition 2

Substituting $w_1=a_1/2$, $w_2=a_2/2$, $p_1=3a_1/4$ and $p_2=3a_3/4$ into Eq. (10), we have

$$\begin{aligned} \pi _r^{GUWP}=\frac{n[a_1a_2(a_1+a_2)+a_1a_2rg-2(a_1+a_2)r^2g^2-8r^3g^3]}{16a_1a_2}. \end{aligned}$$

Taking the first and second derivations of $\pi _r^{GUWP}$, we have $\frac{\partial \pi _r^{GUWP}}{\partial g}=\frac{n[a_1a_2-4(a_1+a_2)rg-24r^2g^2]}{16a_1a_2}$ and $\frac{\partial ^2 \pi _r^{GUWP}}{\partial g^2}=-\frac{n(a_1+a_2+12rg)}{4a_1a_2}$. Since $\frac{\partial ^2 \pi _r^{GUWP}}{\partial g^2}<0$, then $\pi _r^{GUWP}$ is concave in $g$. From $\frac{\partial \pi _r^{GUWP}}{\partial g}=0$, we get the optimal gift card value $g^{GUWP^*}=\frac{\sqrt{a_1^2+8a_1a_2+a_2^2}-(a_1+a_2)}{12r}$. $\square$

Proof

Corollary 1

According to Proposition 2, we have

$$\begin{aligned} \frac{\partial G^{GUWP^*}}{\partial r}= & {} \frac{a_1+a_2-\sqrt{a_1^2+8a_1a_2+a_2^2}}{12r^2}<0,\\ \frac{\partial G^{GUWP^*}}{\partial a_1}= & {} \frac{1}{12r}(\frac{a_1+4a_2}{\sqrt{a_1^2+8a_1a_2+a_2^2}} -1)>0,\\ and \; \frac{\partial G^{GUWP^*}}{\partial a_2}= & {} \frac{1}{12r}(\frac{4a_1+a_2}{\sqrt{a_1^2+8a_1a_2+a_2^2}} -1)>0. \end{aligned}$$

$\square$

Proof

Proposition 3

From Tables  1 and 4, we can get the results of this Proposition. $\square$

Proof

Proposition 4

Substituting $w_1=a_1/2$ and $w_2=a_2/2$ into Eq. (10), we have

$$\begin{aligned} \pi _r^{GUW}= & {} \frac{n}{4a_1a_2}[(6a_1a_2+10a_2rg+6r^2g^2)p_1+(6a_1a_2+10a_1rg+6r^2g^2)p_2\\&-12rgp_1p_2 -4(a_2p_1^2+a_1p_2^2)-(2a_1a_2+5r^2g^2)(a_1+a_2)\\&-8a_1a_2rg-2r^3g^3]. \end{aligned}$$

Taking the first and second derivations of $\pi _r^{GUW}$ , we have

$$\begin{aligned} \frac{\partial \pi _r^{GUW}}{\partial p_1}= & {} \frac{n(3a_1a_2+5a_2rg+3r^2g^2-4a_2p_1-6rgp_2)}{2a_1a_2},\\ \frac{\partial \pi _r^{GUW}}{\partial p_2}= & {} \frac{n(3a_1a_2+5a_1rg+3r^2g^2-4a_1p_2-6rgp_1)}{2a_1a_2},\\ \frac{\partial ^2 \pi _r^{GUW}}{\partial p_1^2}= & {} -\frac{2n}{a_1}, \, and \; \frac{\partial ^2 \pi _r^{GUW}}{\partial p_2^2}=-\frac{2n}{a_2}. \end{aligned}$$

Then the Hessian matrix is

$$\begin{aligned} H=\left[ \begin{array}{cc} \frac{\partial ^2 \pi _r^{GUW}}{\partial p_1^2} &{} \frac{\partial ^2 \pi _r^{GUW}}{\partial p_1 \partial p_2} \\ \frac{\partial ^2 \pi _r^{GUW}}{\partial p_1 \partial p_2} &{} \frac{\partial ^2 \pi _r^{GUW}}{\partial p_2^2} \\ \end{array}\right] =\left[ \begin{array}{cc} -\frac{2n}{a_1} &{} -\frac{3nrg}{a_1a_2} \\ -\frac{3nrg}{a_1a_2} &{} -\frac{2n}{a_2} \\ \end{array}\right] . \end{aligned}$$

We have $|H_1|=-2n/a_1<0$ and $|H_2|=\frac{n^2(4a_1a_2-9r^2g^2)}{a_1^2a_2^2}$. Since $0<g<a_i/2(i=1,2)$, then $|H_2|>0$. So $\pi _r^{GUW}$ is jointly concave in $p_1$ and $p_2$. From the first-order-condition, we get the optimal retailer prices. $\square$

Proof

Corollary 2

According to Proposition 4, we have

$$\begin{aligned} \frac{\partial (p_1^{GUW^*}-a_1/2)}{\partial g}= & {} \frac{r[81r^4g^4+9a_1a_2rg(4a_1-11rg)+4 a_1^2a_2^2]}{2(4a_1a_2-9r^2g^2)^2}>0,\\ \frac{\partial (p_1^{GUW^*}-a_1/2)}{\partial r}= & {} \frac{g[81r^4g^4+9a_1a_2rg(4a_1-11rg)+4 a_1^2a_2^2]}{2(4a_1a_2-9r^2g^2)^2}>0,\\ \frac{\partial (p_2^{GUW^*}-a_2/2)}{\partial g}= & {} \frac{r[81r^4g^4+9a_1a_2rg(4a_2-11rg)+4 a_1^2a_2^2]}{2(4a_1a_2-9r^2g^2)^2}>0,\\ \frac{\partial (p_2^{GUW^*}-a_2/2)}{\partial r}= & {} \frac{g[81r^4g^4+9a_1a_2rg(4a_2-11rg)+4 a_1^2a_2^2]}{2(4a_1a_2-9r^2g^2)^2}>0,\\ \frac{\partial (p_1^{GUW^*}+p_2^{GUW^*}-rg)}{\partial g}= & {} -\frac{3a_1a_2r(2a_1-3rg)(2a_2-3rg)}{(4a_1a_2-9r^2g^2)^2}<0,\\ \frac{\partial (p_1^{GUW^*}+p_2^{GUW^*}-rg)}{\partial r}= & {} -\frac{3a_1a_2g(2a_1-3rg)(2a_2-3rg)}{(4a_1a_2-9r^2g^2)^2}<0. \end{aligned}$$

$\square$

Proof

Proposition 5 and Corollary 3

According to the proof of Proposition 4, we know that given a gift card value $g$, when $a_1=a_2=a$, the optimal solutions of $p_1^*$ and $p_2^*$ are determined by the two first-order conditions

$$\begin{aligned}&\frac{n}{2 a^2}[3 a^2+a (5 rg-4p_1)+3rg (rg-2 p_2)]=0, \end{aligned}$$

(17)

$$\begin{aligned}&\frac{n}{2 a^2}[3 a^2+a (5 rg-4p_2)+3 rg (rg-2 p_1)]=0. \end{aligned}$$

(18)

From Eqs. (17) and (18), we get $p_1^*=p_2^*=\frac{3 a^2+5 a G+3 r^2g^2}{2 (2 a+3 rg)}$. Substituting them into Eq. (17), we have

$$\begin{aligned} \pi _r^{GUW}(p_1^*,p_2^*)=\frac{n(a^4+2 a^3rg-a^2r^2g^2-4 a r^3g^3+3 r^4g^4)}{4 a^2 (2 a+3 rg)}. \end{aligned}$$

Taking the first and second derivations of $\pi _r^{GUW}(p_1^*,p_2^*)$, we have

$$\begin{aligned} \frac{\partial \pi _r^{GUW}(p_1^*,p_2^*)}{\partial g}=\frac{ n(a^4-4 a^3 rg-27 a^2 r^2g^2+27 r^4g^4)}{4 a^2 (2 a+3 rg)^2} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \pi _r^{GUW}(p_1^*,p_2^*)}{\partial g^2}=\frac{n (81 r^4g^4+108 a r^3g^3-48 a^3 rg-7 a^4) }{2 a^2 (2 a+3 rg)^3}. \end{aligned}$$

Since $0<g\le a/2$, then $0<rg\le a/2$. If $a/7\le rg\le a/2$, then $\frac{\partial \pi _r^{GUW}(p_1^*,p_2^*)}{\partial g}<0$. So, $\pi _r^{GUW}(p_1^*,p_2^*)$ is decreasing in $g$ and the optimal gift card value $G^*=\frac{a}{7r}$. if $0<rg\le a/7$, then $\frac{\partial ^2 \pi _r^{GUW}(p_1^*,p_2^*)}{\partial g^2}<0$. So, $\pi _r^{GUW}(p_1^*,p_2^*)$ is concave in $g$ and the optimal gift card value $g^*$ is determined by the first-order condition $\frac{\partial \pi _r^{GUW}(p_1^*,p_2^*)}{\partial g}=0$. Thus, when $0<g\le a/2$, the optimal gift card value satisfies $g^*<\frac{a}{7r}$. $\square$

Proof

Proposition 6

Substituting Eqs. (7), (8) and (9) into Eq. (10), we have

$$\begin{aligned} \pi _r^{DG}= & {} \frac{n}{a_1a_2}\{[a_2(a_1-p_1)+rg (a_2-p_2)] (p_1-w_1)\\&+[rg (a_1-p_1)+a_1 (a_2-p_2)](p_2-w_2) \\&-rg[(a_1+rg-p_1) (a_2+rg-p_2)]\\&+\frac{r^2g^2}{2}(p_1-w_1+p_2-w_2+rg)\}. \end{aligned}$$

Taking the first and second derivations of $\pi _r^{DG}$ , we have

$$\begin{aligned} \frac{\partial \pi _r^{DG}}{\partial p_1}= & {} \frac{n[2a_2(a_1+2rg-2p_1+w_1)+rg(3rg-6p_2+2w_2)]}{2a_1a_2},\\ \frac{\partial \pi _r^{DG}}{\partial p_2}= & {} \frac{n[2a_1(a_2+2rg-2p_2+w_2)+rg(3rg-6p_1+2w_1)]}{2a_1a_2},\\ \frac{\partial ^2 \pi _r^{DG}}{\partial p_1^2}= & {} -\frac{2n}{a_1},\, and\; \frac{\partial ^2 \pi _r^{DG}}{\partial p_2^2}=-\frac{2n}{a_2}. \end{aligned}$$

Then the Hessian matrix is

$$\begin{aligned} H=\left[ \begin{array}{cc} \frac{\partial ^2 \pi _r^{DG}}{\partial p_1^2} &{} \frac{\partial ^2 \pi _r^{DG}}{\partial p_1 \partial p_2} \\ \frac{\partial ^2 \pi _r^{DG}}{\partial p_1 \partial p_2} &{} \frac{\partial ^2 \pi _r^{DG}}{\partial p_2^2} \\ \end{array}\right] =\left[ \begin{array}{cc} -\frac{2n}{a_1} &{} -\frac{3nrg}{a_1a_2} \\ -\frac{3nrg}{a_1a_2} &{} -\frac{2n}{a_2} \\ \end{array}\right] . \end{aligned}$$

We have $|H_1|=-\frac{2n}{a_1}<0$ and $|H_2|=\frac{n^2(4a_1a_2-9r^2g^2)}{a_1^2a_2^2}$. Since $0<g\le \frac{a_i}{2}(i=1,2)$, then $|H_2|>0$. So $\pi _r^{DG}$ is jointly concave in $p_1$ and $p_2$. From $\frac{\partial \pi _r^{DG}}{\partial p_1}=0$ and $\frac{\partial \pi _r^{DG}}{\partial p_2}=0$, the optimal retailer prices are given by

$$\begin{aligned} p_1^{*}(w_1,w_2)=\frac{2a_1a_2(2a_1+2w_1+rg)-rg(6a_1 rg+9 r^2g^2+2a_1w_2+6rgw_1)}{2(4a_1a_2-9r^2g^2)} \end{aligned}$$

and

$$\begin{aligned} p_2^{*}(w_1,w_2)=\frac{2a_1a_2(2a_2+2w_2+rg)-G(6a_2 rg+9 r^2g^2+2a_2w_1+6rgw_2)}{2(4a_1a_2-9r^2g^2)}. \end{aligned}$$

Substituting $p_1^*(w_1,w_2)$ and $p_2^*(w_1,w_2)$ into Eq. (11), we have

$$\begin{aligned} \pi _{m1}^{DG}= & {} \frac{n w_1 }{2 a_1a_2 (4 a_1 a_2-9 r^2g^2)}[4 a_1^2 a_2^2+2a_1a_2^2rg-10a_1a_2r^2g^2 \\&-3a_2r^3g^3+4a_2(2r^2g^2-a_1a_2)w_1+2rg(3r^2g^2-a_1a_2)w_2]. \end{aligned}$$

Taking the first and second derivations of $\pi _{m1}^{DG}$ , we have

$$\begin{aligned} \frac{\partial \pi _{m1}^{DG}}{\partial w_1}= & {} \frac{n}{2 a_1a_2 (4 a_1 a_2-9 r^2g^2)}[4 a_1^2 a_2^2+2a_1a_2^2rg-10a_1a_2r^2g^2 \\&-3a_2r^3g^3+8a_2(2r^2g^2-a_1a_2)w_1+2rg(3r^2g^2-a_1a_2)w_2] \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \pi _{m1}^{DG}}{\partial w_1^2}=-\frac{4n(a_1a_2-2r^2g^2)}{a_1(4 a_1 a_2 -9 r^2g^2)}. \end{aligned}$$

Since $\frac{\partial ^2 \pi _{m1}^{DG}}{\partial w_1^2}<0$, then $\pi _{m1}^{DG}$ is concave in $w_1$ and the optimal wholesale price of product 1 is determined by the first-order-condition.

Substituting $p_1^*(w_1,w_2)$ and $p_2^*(w_1,w_2)$ into Eq. (12), we have

$$\begin{aligned} \pi _{m2}^{DG}= & {} \frac{n w_2 }{2 a_1a_2 (4 a_1 a_2-9 r^2g^2)}[4 a_1^2 a_2^2+2a_1^2a_2rg-10a_1a_2r^2g^2\\&-3a_1r^3g^3+4a_1(2r^2g^2-a_1a_2)w_2+2rg(3r^2g^2-a_1a_2)w_1]. \end{aligned}$$

Taking the first and second derivations of $\pi _{m2}^{DG}$ , we have

$$\begin{aligned} \frac{\partial \pi _{m2}^{DG}}{\partial w_2}= & {} \frac{n}{2 a_1a_2 (4 a_1 a_2-9 r^2g^2)}[4 a_1^2a_2^2+2a_1^2a_2rg-10a_1a_2r^2g^2\\&-3a_1r^3g^3+8a_1(2r^2g^2-a_1a_2)w_2+2rg(3r^2g^2-a_1a_2)w_1] \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \pi _{m2}^{DG}}{\partial w_2^2}=-\frac{4n(a_1a_2-2r^2g^2)}{a_2(4 a_1 a_2 -9 r^2g^2)}. \end{aligned}$$

Since $\frac{\partial ^2 \pi _{m2}^{DG}}{\partial w_2^2}<0$, then $\pi _{m2}^{DG}$ is concave in $w_2$ and the optimal wholesale price of product 2 is determined by the first-order-condition. Solving $\frac{\partial \pi _{m1}^{DG}}{\partial w_1}=0$ and $\frac{\partial \pi _{m2}^{DG}}{\partial w_2}=0$, we can get the optimal wholesale prices of two products $w_1^{DG^*}$ and $w_2^{DG^*}$. Substituting $w_1^{DG^*}$ and $w_2^{DG^*}$ into$p_1^*(w_1,w_2)$ and $p_2^*(w_1,w_2)$, we get the optimal retail prices of two products $p_1^{DG^*}$ and $p_2^{DG^*}$. $\square$

Proof

Corollary 4

The proof of this Corollary is similar to that of Corollary 2. $\square$

Proof

Corollary 5

The proof of this Corollary is similar to that of Corollary 2. $\square$

Proof

Corollary 6

Let $G=rg$. According to Proposition 6 and Proposition 1, we have

$$\begin{aligned} w_1^{DG^*}-w_1^{NG^*} =\frac{a_1a_2G(4 a_1^2 a_2^2-9 a_1^2 a_2 G-6a_1 a_2 G^2+19a_1 G^3-6 G^4)}{2(16 a_1^3 a_2^3-65 a_1^2 a_2^2 G^2+70 a_1a_2 G^4-9 G^6)} \end{aligned}$$

and

$$\begin{aligned} w_2^{DG^*}-w_2^{DG^*}=\frac{a_1 a_2 G (4 a_1^2 a_2^2-9 a_1a_2^2 G-6 a_1a_2 G^2+19 a_2 G^3-6 G^4)}{2(16 a_1^3 a_2^3-65 a_1^2 a_2^2 G^2+70 a_1a_2 G^4-9 G^6)}. \end{aligned}$$

When $a_1 \le a_2$, then $w_1^{DG^*}-w_1^{NG^*}>0$. Let $G_1^{DG}$ be the smallest positive real root of $6 G^4-19 a_1 G^3+6 a_1a_2 G^2+9 a_1^2 a_2 G-4 a_1^2 a_2^2=0$. When $a_1 > a_2$ and $0<G<G_1^{DG}$, then $w_1^{DG^*}-w_1^{NG^*}>0$; when $a_1 > a_2$ and $G_1^{DG}\le G<a_2/2$, then $w_1^{DG^*}-w_1^{NG^*}<0$.

When $a_1\ge a_2$, then $w_2^{DG^*}-w_2^{NG^*}>0$. Let $G_2^{DG}$ be the smallest positive real root of $6 G^4-19 a_2 G^3+6 a_1a_2 G^2+9 a_1 a_2^2 G-4 a_1^2 a_2^2=0$. When $a_1< a_2$ and $0<G<G_2^{DG}$, then $w_2^{DG^*}-w_2^{NG^*}>0$; when $a_1<a_2$ and $G_2^{DG} \le G<a_1/2$, then $w_2^{DG^*}-w_2^{NG^*}<0$. $\square$