Batch scheduling in the histopathology laboratory

Abstract

Histopathology laboratories aim to deliver high quality diagnoses based on patient tissue samples. Timely and high quality care are essential for delivering high quality diagnoses, for example in cancer diagnostics. However, challenges exist regarding employee workload and tardiness of results, which both impact the diagnostic quality. In this paper the histopathology operations are studied, where tissue processors are modeled as batch processing machines. We develop a new 2-phased decomposition approach to solve this NP-hard problem, aiming to improve the spread of workload and to reduce the tardiness. The approach embeds ingredients from various planning and scheduling problems. First, the batching problem is considered, in which batch completion times are equally divided over the day using a Mixed Integer Linear Program. This reduces the peaks of physical work available in the laboratory. Second, the remaining processes are scheduled to minimize the tardiness of orders using a list scheduling algorithm. Both theoretical as well as historical data were used to assess the performance of the method. Results show that using this decomposition method, the peaks in histopathology workload in UMC Utrecht, a large university medical center in The Netherlands, may be reduced with up to 50 % by better spreading the workload over the day. Furthermore, turnaround times are reduced with up to 20 % compared to current practices. This approach is currently being implemented in the aforementioned hospital.

1 Introduction

Histopathology and anatomic pathology laboratories aim to deliver timely diagnoses to patients. Amongst others, the laboratories deliver rapid diagnoses during surgeries and fast diagnostics for patients suspecting to have cancer. In this context, high quality care within the shortest possible time is expected from the laboratories. Consequently, employees experience a high work pressure. Therefore, challenges exist regarding both employee workload and turnaround times all over the world (Muirhead et al. 2010; Buesa 2009). This paper considers the scheduling of tissue samples over the various histopathology activities, from which one activity is executed by multiple batching processors. The aim is to deliver fast reports for the patients and to create a leveled workload for the employees. Or, in other words, increased speed of diagnostics and reduced work pressure.

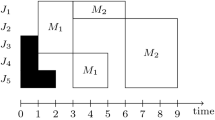
The motivation of this research can be found in the histopathology laboratory of UMC Utrecht, a Dutch university hospital, where tissue processors (batching machines) are in the middle of a labor intensive multiple stage process chain. Histopathology processes are complex processes (Brown 2004). The processes can be divided into five main activities: grossing, tissue processing, embedding, sectioning and staining, and examination (Leeftink et al. 2016). In the grossing stage, tissues are trimmed in representative parts by a technician, and put into cassettes. In the automated tissue processing stage, the tissue in these cassettes is fixated and dehydrated using various chemicals. This process takes up to 12 h depending on the tissue size, and multiple cassettes are batched during this process. After tissue processing, the tissues are embedded in paraffin wax by a technician, to be sectioned in very thin sections by another technician. When these sections are put on slides, the slides receive a staining using an automated stainer which can be continuously loaded. Hereafter, the residents and pathologists can examine the slides under the microscope or using digital examination. All stages consist of single-unit parallel processors (employees), except for the tissue processing stage. Here, parallel batch processors are to be scheduled with large processing times compared to the other stages. All jobs have equal routing through all stages, and all jobs have a due date reflecting their priority.

The spread of workload is an important performance indicator for jobs with manual tasks. Workload is one of the main factors influencing job satisfaction. Furthermore, it also influences the quality of the executed work, and therefore the quality of care: When employees have a large pile of jobs in front of them, they not only feel rushed, but also process the jobs with less accuracy (Fournier et al. 2011; Meijman et al. 1998; Schaufeli and Bakker 2004). This research aims to level the workload perceived by staff. We do so by minimizing the inventory peaks, which are seen by staff as the amount of work that needs to be done. Also, the exact amount of workload cannot (rapidly) be assessed by staff, as jobs look very similar but may require very different processing times. When striving for a leveled workload, the maximum inventory should be minimized.

In addition to employee workload, the turnaround time (TAT) is of concern in histopathology laboratories (Muirhead et al. 2010). Patients awaiting their diagnosis experience high anxiety and uncertainty levels, especially in cancer care (Paul et al. 2012; Liao et al. 2008). Therefore, timely diagnoses are needed and activities need to be scheduled in such a way that the tardiness of jobs is minimized.

The TAT and workload optimization of a series of processes requires a system-wide approach. In this research we aim to integrally optimize processes by considering all resources involved, and addressing the tactical level of control in addition to the operational (Hans et al. 2012). To address both levels, we decompose the problem at hand in the batching problem and the scheduling problem. More specifically, on a tactical level we determine optimal batch completion times in order to spread the workload. To solve this batching problem, we use an (M)ILP approach. Furthermore, on an operational level the jobs are scheduled such that the tardiness of jobs is minimized using adaptions of existing scheduling approaches. In Sect. 3 we show that both these sub-problems are NP-hard.

Although this paper is motivated by the histopathology laboratory, scheduling of multi-stage process chains with batch processors is also relevant in other systems in healthcare, and in manufacturing environments. A healthcare example can be found in the sterilization plant, where centrifuges are an essential part of the processes. In manufacturing, an example is a ceramic plant, where pottery has to be baked in an oven.

The contribution of this paper is threefold. First, we optimize a new 3-stage system, where batching is included in the second stage. This NP-hard problem is not only relevant for health care, but also applicable in other industries. Furthermore, by considering this system, this paper contributes to the scarce literature on hybrid flow shops with parallel batching (HFPB). Second, we develop a new, novel solution method which addresses both the tactical level as well as the operational level. Third, the practical applicability of this method is demonstrated with a real-life case study of a large academic hospital in The Netherlands.

This paper is organized as follows. Section 2 describes the literature, followed by the formal problem description in Sect. 3, and the batching and scheduling models in Sects. 4 and 5. Section 6 gives some numerical results, and Sect. 7 describes a case study in the histopathology laboratory. Section 8 gives conclusions and opportunities for further research.

2 Literature

In the histopathology laboratory, parallel batch processors are part of the process chain. In this research, we consider a 3-stage HFPB with identical parallel batching machines in the second stage. In a HFPB, at least one stage has multiple machines, and some of the machines considered can process multiple jobs simultaneously (Amin-Naseri and Beheshti-Nia 2009). This system is known from the process industry (Gupta and Karimi 2003; Harjunkoski et al. 2014; Mendez et al. 2006). In Sect. 2.1 we first describe the hybrid flow shop (HFS) scheduling literature, since this is the core problem under consideration, followed by the literature on the HFPB in Sect. 2.2, where parallel batching constraints are added to the HFS.

2.1 Hybrid Flow Shop

The HFS is well studied in the literature. The HFS is a flow shop in which in at least one stage multiple machines are available. We refer to Ruiz and Vazquez-Rodriguez (2010) and Ribas et al. (2010) for extensive reviews of the HFS literature. The HFS literature can be divided in three categories, based on the number of stages: two-stage, three-stage, and k-stage (Allaoui and Artiba 2004). Only some specific configurations of the two-stage HFS [i.e. $F2||C_{max}$, see Johnson (1954)] are solvable within polynomial time. The two-stage HFS with parallel machines is NP-complete, even in its simplest form with one machine in one stage, and two in the other stage (Gupta 1988; Hoogeveen et al. 1996).

Frequently used solution methods for HFS problems are exact methods, heuristics, and metaheuristics (Ruiz and Vazquez-Rodriguez 2010). Exact methods are often based on branch and bound techniques and can only be applied to problem instances of small sizes for complexity reasons (Liu et al. 2010). Therefore, many authors use heuristics, metaheuristics, or a combination of these techniques to solve HFS and HFPB scheduling problems. Dispatching rules, such as Earliest Due Date (EDD), Shortest Processing Time (SPT), and Longest Processing Time (LPT) have shown to result in good performing solutions for specific optimization criteria in HFS scheduling and batch scheduling and are easily applicable in complex environments (Liu et al. 2010; Mendez et al. 2006; Ruiz and Vazquez-Rodriguez 2010). Metaheuristics, such as simulated annealing and genetic algorithms, are able to improve upon these solutions (Ruiz and Vazquez-Rodriguez 2010).

Besides variations in the number of stages and solution methods, HFS configurations are distinguished based on different objective functions [i.e. flow time or due date based (Amin-Naseri and Beheshti-Nia 2009)] and constraints. These constraints are added to the general HFS to come closer to real-life problems. Allaoui and Artiba (2014) studied the HFS with availability constraints, to ensure preventive maintenance activities to be executed. Mirsanei et al. (2011) proposed a simulated annealing approach for the HFS problem with sequence-dependent setup times. Multiprocessor task scheduling in a hybrid flow shop environment was studied by Engin et al. (2011). They developed a genetic algorithm to solve the HFS with multiprocessor tasks. The HFS with recirculation was studied by Bertel and Billaut (2004). They proposed an ILP formulation, and developed a genetic algorithm for solving industrial size instances. Precedence constraints in a 2-stage HFS with parallel machines in the second stage was considered by Carpov et al. (2012). A randomized list scheduling heuristic was proposed, together with the examination of global lower bounds. Gupta et al. (1997) studied a similar system, but with parallel machines in the first stage, and a single machine in the second stage. They proved both problems are equivalent and NP-hard, and proposed a branch and bound algorithm using several lower bounds and heuristic methods. A combination of these two systems, together with the aforementioned batching requirements, reflects the 3-stage system under review in this study.

2.2 Hybrid Flow Shop with Parallel Batching

The extension to the HFS of interest in this study is the HFS with parallel batching. There are two types of batching known; serial batching and parallel batching. In serial batching, jobs in a batch are processed sequentially. For a recent example of HFS with serial batching, we refer to Ghafari and Sahraeian (2014), who proposed a genetic algorithm. In parallel batching, all jobs in a batch are processed in parallel. Only a limited number of studies considered a HFS with parallel batching in one or multiple stages, where batch compositions can differ throughout the stages. Bellanger and Oulamara (2009) were the first to study the two-stage HFPB with parallel batching in the second stage with task compatibilities, which they motivated by the tire manufacturing industry. They proposed three heuristics together with their worst-case analyses. Luo et al. (2011) considered a two stage HFPB with parallel batching in the first stage, motivated by the processes of a metalworking company. Since the problem is NP-hard, they determined the batches upfront using a clustering algorithm, to reduce the problem complexity. More recently, Rossi et al. (2013) studied a two-stage HFPB reflecting a hospital sterilization department. They recommend closing batches before completion, for example as a function of the elapsed time or by fixing the capacity threshold. The work of Amin-Naseri and Beheshti-Nia (2009) is the closest to our problem, since they studied the 3-stage HFPB where batching was allowed in any stage aiming to minimize the maximum completion time. They proposed three two-phased heuristics based on a combination of Johnson’s rule, scheduling algorithms for parallel machines, and theory of constraints. Furthermore, they developed a three dimensional genetic algorithm which outperformed their heuristics. However, besides the different objective function, they allowed for jobs to start processing on batching machines after the first job of that same batch already started processing, since only completion times were aligned, which is not applicable to our case.

2.3 Conclusions

Concluding, it is known that the HFS problem in which the tardiness is minimized in itself is a complex problem, since it is NP-hard. Furthermore, there is only scarce literature available on the HFS extension with parallel batching, since the complexity of the HFS increases even more by adding these constraints. In addition to the HFPB with a tardiness objective, we encounter a workload leveling objective. To the best of our knowledge, this system, the 3-stage HFPB with parallel batching in the second stage where the intermediate storage has to be kept to a minimum, has not been considered before in the literature and has never been applied in a hospital or manufacturing setting.

3 Formal problem description, complexity, and decomposition

We consider a set of G stages, with each stage g having $M_g$ identical parallel resources. All jobs need processing in all stages and can be processed by all resources. Each job j is of a certain job family f, with a corresponding release time $r_j$. The processing times $p_{j,g}$ are known for each job in each stage, and deterministic, based on the job family. Preemption of jobs is not allowed, and jobs cannot be split over multiple machines in a stage. Transportation times are not included in the model. If they would be included, the only effect is seen in the timing of jobs in the next stages, which would increase with the transportation times. Operator workload is not affected, since transportation is an automated process. There is unlimited intermediate storage available between stages, which should be kept to a minimum. In order to schedule all jobs over all resources, regular working hours are considered. Thus, for all resources, the start time s and end time e for each day are known. Resource breakdowns are not included. In the second stage, parallel batch machines are available. The capacity of each batch b is unlimited. Furthermore, the processing time of a batch $p^b$ equals the largest processing time of all jobs that are assigned to that batch (1).

$$p^b = \max _{j \in J_b}{p_j} \quad \forall b \in B,$$

(1)

where $J^b$ is the subset of jobs that are assigned to batch b.

The jobs in this system should be scheduled in such a way that the tardiness of jobs and the maximum inventory between stages are minimized. Following the notation of Graham et al. (1979), the problem can be described as:

$$FH3B(m_1,m_2,m_3)|p-batch(2),r_j|I_{max}, \sum {}{T_j}.$$

(2)

Here, a three-stage HFPB with $m_1$ resources in the first stage, $m_2$ resources in the second stage, and $m_3$ resources in the third stage is defined. $p{-}batch(2)$ shows that stage 2 consists of parallel batching machines, and $r_j$ shows that all jobs have a release time. The two performance indicators considered are the peak inventory levels and the tardiness. Therefore, $I_{max}$ is the first objective function, since the maximum inventory should be minimized. The second objective, $\sum {T_j}$, corresponds with the minimization of the total tardiness of all jobs. The mathematical problem formulation can be found in “Appendix”.

The problem is unary NP-hard, since the two stage HFS as well as the flow shop with batching are known to be NP-hard (Gupta 1988; Potts and Kovalyov 2000). There remain two options for solving the problem: Complete enumeration over all possible solutions, or heuristics (Graham et al. 1979). Due to the large solution space, complete enumeration will be prohibitively time consuming, thus we will focus on heuristics for solving this problem.

A few approaches exist that combine batch size, batch assignment, and batch sequencing decisions (Prasad and Maravelias 2008). However, these approaches only allow for very small instances, with limited number of resources and jobs (Harjunkoski and Grossmann 2002). Therefore, in accordance with this research, we propose to decompose the batching and scheduling decisions in the remainder of this research. Since in practice the batch timing is often determined at a tactical level a few times a year, and the job scheduling is an operational level task, we developed a new decomposition approach in which the batch timing is determined first (‘Batching problem’, see Sect. 4), and the scheduling of jobs second (‘Scheduling problem’, see Sect. 5). Herein, the batching problem aims to minimize the inventory peaks, whilst the scheduling problem aims to minimize the total tardiness. Both these individual problems remain NP-hard, as shown in Sects. 4.1 and 5.1 respectively.

4 Phase 1: Batching problem

The batching problem focuses on scheduling batches while aiming to minimize the inventory peak between the batching and its subsequent stage. This section gives the formal problem description, including the definitions, problem goal, and approach.

4.1 Introduction

Consider a three-stage HFPB with multiple parallel batching machines in the second stage. When a parallel batch processor is followed by labor-intensive processes, the highest inventory peaks, and therefore peaks in workload, occur at the moment a batch processor is finished and all jobs become available for the next stage. Since the batch processing time depends on the size of the jobs in the batch, the batching moments in relation to their output should be controlled in order to equally spread the inventory. Therefore, the batching problem determines the timing of the batches, while the minimum interval between two subsequent batches is maximized.

The work of Van Essen et al. (2012) is the closest to our approach. They developed several solution methods to minimize the interval between completion times of scheduled surgeries by optimizing their sequence. Here, this is done to reduce the expected waiting time of emergency surgeries, which may start at the aforementioned completion times. They proved this problem is strongly NP-hard for two or more operating rooms (Van Essen et al. 2012). However, their aim is to minimize the maximum interval, whilst we want to maximize the minimum interval. Furthermore, they assumed the surgeries were already assigned to fixed operating rooms. We consider the more advanced case, where the batches have to be scheduled over multiple machines. However, this is against a cost of an increased solution space and additional decision making, which makes the problem even harder to solve.

The moment that a batch is finished is referred to as batch completion moment (BCM). The interval between two subsequent BCMs is defined as the batch completion interval (BCI), see Fig. 1. The length of the BCIs depends on the assignment, sequence, and timing of the batches. Since the batching problem is considered at a tactical level, we assume no information on future job arrivals is available.

Fig. 1

Batch Completion Moments (BCMs) and Batch Completion Intervals (BCIs) for a 2-machine problem

4.2 Definitions and goal

Our aim is to find a cyclic batching schedule, at a daily level. For a day, we consider the set of B batches each of a given batch type t, where each batch of a certain type has a corresponding batch type processing time $p_t$. All jobs with a processing time lower than the batch type processing time (i.e. $p_{j,2} \le p_t$) are eligible for a batch of this batch type.

To spread the output of batches during the day, we aim to equally spread the BCMs over the day, such that peaks in workload in the subsequent stage are minimized. Taking into account the expected load of one batch, we want to maximize the interval between two subsequent batches, and between subsequent batches with the same load. The smallest interval accounts for the highest peak in workload, and is therefore our main objective: the maximization of the smallest BCI.

If multiple batches of the same batch type are scheduled, the minimum batch completion interval is maximized per batch type as well. This ensures that jobs of a certain job family are processed more equally spread over the day, which is especially important when weights are added to having certain job families in inventory, as in the histopathology laboratory.

4.3 Approach

To determine the optimal batching schedule, we formulated a Mixed Integer Linear Program (MILP). Despite the NP-hardness of the optimization problem, we can solve real-life instances using this mathematical program. In the MILP, batch sequencing, batch timing, and batch-machine assignment constraints are included. This way, the BCIs can be determined, using the sequence in which all batches are finished by taking the interval in between subsequent batches. We first introduce some additional notation. Hereafter, the objective and constraints are given.

Notation OBJ1 and ${ OBJ2}_t$ are the two objective variables, where the first one is the minimum overall batch completion interval, and the second the minimum batch completion interval per batch type t. Let $X_{b,m}$ be 1 iff batch b is assigned to machine m, and 0 otherwise. Let $Y_{b,b^{\prime}}$ be 1 iff batch b ends before batch $b^{\prime}$. The sequence in which all batches finish is stored by the position of each batch. Let $P_b$ be the position of batch b in this sequence. $S_b$ and $C_b$ refer to the starting time and end time of batch b respectively. Finally, let ${\mathscr{M}}$ be a sufficiently large number.

Objective

$$\max {\alpha OBJ1 + \beta \sum _{t \in T}{OBJ2_t}}$$

(3)

Constraints

$$\sum _m{X_{b,m}}=1\quad \forall b \in B$$

(4)

$$\sum _{b^{\prime}}{Y_{b^{\prime},b}}+1= P_b\quad \forall b \in B$$

(5)

$$Y_{b,b^{\prime}} + Y_{b^{\prime},b}= 1\quad \forall b, b^{\prime} \in B, b < b^{\prime}$$

(6)

$$P_{b^{\prime}} - 1 + {\mathscr{M}}^1 \cdot Y_{b^{\prime},b}\ge P_b\quad \forall b, b^{\prime}\in B$$

(7)

$$S_b + p^b= C_b\quad \forall b \in B$$

(8)

$$S_b\ge s\quad \forall b \in B$$

(9)

$$e\ge C_b\quad \forall b \in B$$

(10)

$$S_{b^{\prime}} + {\mathscr{M}}^2 \cdot (2 - X_{b,m} - X_{b^{\prime},m})\ge C_b - {\mathscr{M}}^2 \cdot (1-Y_{b,b^{\prime}})\quad \forall b,b^{\prime} \in B, \forall m \in M$$

(11)

$$C_{b^{\prime}} - C_b + {\mathscr{M}}^3 \cdot (1-Y_{b,b^{\prime}})\ge OBJ1\quad \forall b,b^{\prime} \in B$$

(12)

$$C_{b^{\prime}} - C_b + {\mathscr{M}}^3 \cdot (1-Y_{b,b^{\prime}})\ge OBJ2_t\quad \forall t \in T, \forall b,b^{\prime} \in B_t$$

(13)

$${\text{all variables}}\ge 0$$

(14)

The objective of the ILP is a weighted sum of the two objectives mentioned, i.e. maximize the minimum batch completion interval and maximize the minimum interval between the completions of two batches of the same type (3). Each batch should be assigned to exactly one machine (4). The position of a batch in the sequence equals the number of batches finished before this batch added with one (5). For example, if a batch is the third one to finish, there were already two batches that finished before him, thus the position in the sequence $P_b = 2+1 = 3$. A batch b is either scheduled before a specific other batch $b^{\prime}$, or after that same batch $b^{\prime}$ (6). Cycles in the positioning are not allowed, thus the position of batch b should be strictly less than the position of batch $b^{\prime}$, if batch b is scheduled before batch $b^{\prime}$ (7). The completion time equals the starting time of a batch plus its processing time (8). A batch starts processing after the machine starting time (9), and finishes before the machine end time (10). The completion time of a batch should be smaller than the starting time of a successive batch scheduled on the same machine (11). We want to find the minimum batch completion interval between all batches (12) and between the batches from each batch type (13).

Let B be the number of batches, T the number of batch types, and M the number of machines. Then, the MILP consists of $5B + (M+T+2,5)B^2$ constraints and $1 + T + (3+B+M)B$ variables, from which $(1+B+M)B$ integer and $1 + T+ 2B$ continuous. Thus, for real life instances, with a maximum of 4 machines, 12 batches, and 3 batch types, the batching problem consists of 1428 constraints and 232 variables.

5 Phase 2: Scheduling problem

The scheduling problem focuses on scheduling all jobs in all stages, while aiming to minimize the tardiness of jobs. This section gives the formal problem description, including definitions, the problem goal, and approach.

5.1 Introduction

The optimization problem in which jobs are scheduled on a single-machine in order to minimize the total tardiness, is proven NP-hard (Du and Leung 1990). The multi-machine case with multiple stages increases the computational complexity of this single-machine problem, and therefore is NP-hard as well. Therefore, exact scheduling approaches, for example based on Gupta and Karimi (2003), can be developed to solve small instances of the resource assignment and scheduling problem. This exact approach is formulated as an ILP, by fixing the batch times in the ILP formulation from “Appendix”. However, due to the complexity of the problem, solving this adapted ILP still takes more than a week for real life instances, while in the histopathology practice a solution should be generated in less than 10 min.

As an approximation alternative, we consider a list scheduling algorithm. A list scheduling algorithm is a well known method to multi-machine job shop scheduling (Kim 1993). It generates fast solutions, and can easily be implemented in the histopathology practice. Therefore, we propose a list scheduling heuristic to solve the scheduling problem.

5.2 Definitions and goal

Our aim is to find a job-machine assignment for a given problem instance. Herein, the batch timing is known, but jobs still need to be assigned to batches. We propose a list scheduling algorithm, in which multiple sequencing rules can be taken into account (Tsubone et al. 1996). We consider the following sequencing rules:

• EDD rule Arrange jobs on based on their due date $d_{i}$, and select the earliest due job first.

• SPT rule Arrange jobs on their processing time $p_{i,j}$, and select the job with shortest processing time first.

• LPT rule Arrange jobs on their processing time $p_{i,j}$, and select the job with longest processing time first.

Furthermore, we consider some modifications to these rules, since the due dates and processing times of jobs may be equal for similar jobs:

• EDD–SPT rule Arrange jobs first on their due date $d_i$, if due dates are equal, arrange jobs on their processing time $p_{i,j}$. Select earliest due jobs first, and, if due dates are equal, jobs with shortest processing time first.

• SPT–EDD rule Arrange jobs first on their processing time $p_{i,j}$, if due dates are equal, arrange jobs on their due date $d_i$. Select jobs with shortest processing time first, and, if processing times are equal, earliest due jobs first.

The objective of the scheduling problem is to minimize the tardiness of jobs. However, the maximum inventory level is evaluated as well, being the output of the decomposition approach.

5.3 Approach

We designed a multi-phase list scheduling algorithm. In each phase s, it selects a machine m, chooses an unscheduled job j, assigns this job to the earliest available time at this machine, and updates the machine availability and job status. The choice of the machine depends on the availability of the machine. The choice of the job depends on the chosen sequencing rule and the job availability.

In the first phase, the algorithm assigns jobs to batches of the second stage of the HFPB. In the second phase, the jobs are scheduled in the first stages, and the third phase schedules the jobs in the third stage. It might be needed to reschedule the batch assignment in the second phase, since after assignment in the second phase, the jobs might not be finished processing in the first stage before the original batch timing. However, by first scheduling the batches, and thereafter the first stage, jobs that have an earlier due date, but later batch timing, might be assigned to a stage one machine after a job with a later due date but earlier batch timing. This way, the later due job might not unnecessarily be delayed by one batch, and the earlier due job is still processed on time for its own batch.

6 Numerical analysis

This section describes the experiments that are conducted to analyze the performance of the proposed methods. The impact of the problem size and sequencing rules are evaluated in terms of tardiness and maximum inventory level. We test the batching and scheduling approach on 342 scenarios, as described in Sect. 6.1, and evaluate the performance in Sect. 6.2. Furthermore, a case study is presented in Sect. 7.

6.1 Experiment conditions

Each experiment spans a one day period of eight working hours. The batching and scheduling problem repeats itself every day. The number of batching machines is set at 1, 2, and 4, with 2, 3, 5, or 8 batches depending on the number of machines. The number of job families is set at 1, 2, and 3, with uniform distributed target throughput times in minutes on the intervals [320, 500], [540, 950], and [1080, 1800] respectively, which corresponds with the histopathology practice. The corresponding discrete batch processing times of each job family are set at 120, 190, and 230 min, which reflect the different batch configurations of the histopathology laboratory. The number of non-batching machines is varied between 1 and 2 identical machines in the pre-batching stage, and between 3, 5, and 7 identical machines in the post-batching stage. The number of jobs is set at 10, 80, and 130. The job processing times in minutes in non-batching stages were derived from a uniform distribution on the interval [5, 15], and [1, 5] respectively. All jobs are available at the start of the planning horizon. A summary of all input variables and parameter is given in Tables 1 and 2. Note that not all combinations of parameter values are valid, which leaves us with 342 scenarios.

Table 1 Variations in experiment variables

Table 2 Uniform distributed intervals of experiment parameters

For the batching problem, we derive one optimal solution per problem instance. For each of these instances, 50 scheduling instances are generated using the distributions of Table 2. With these instances the effect of the five sequencing rules are analyzed. Preliminary research indicated that 50 replications are needed to obtain relevant results. All experiments are based on random numbers.

All experiments are solved on a HP laptop personal computer with 2GB RAM, using CPLEX 12.6 in AIMMS 4.0 (CPLEX 2011; Bisschop and Entriken 1993) .

6.2 Performance

We first illustrate the results of the algorithms by discussing the details of one specific experiment instance. Thereafter, overall results on all experiments are presented. The tardiness performance is given in minutes, whereas the inventory performance is given in number of jobs.

6.2.1 Sequencing rules

All scenarios were tested against the five sequencing rules. Table 3 shows the results in terms of tardiness and inventory peak for all sequencing rules. The SPT and SPT–EDD sequencing rules both significantly outperform all other rules with respect to the tardiness criterion ($p < 0.01$). For the inventory level, the LPT sequencing rule is significantly outperformed by all other rules ($p < 0.01$), and the SPT rule is significantly worse than the SPT–EDD sequencing rule ($p < 0.01$). The EDD rule performs best on the inventory criterion. Therefore, depending on the performance indicator of interest, a different sequencing rule results in the best performance. However, since both the performance indicators are of our interest, we decided to continue the experiments with the SPT–EDD sequencing rule. The remainder of the experiment results in this section are based on this sequencing rule.

Table 3 Sequencing rule experiment results

6.2.2 Performance of one experiment

Consider a specific experiment, which represents the situation with one grossing employee, five sectioning employees, four batching machines, five batches during the day, one batch during the night, and 80 jobs divided over three job families. The scheduling model uses the SPT–EDD sequencing rule, since it is the best performing sequencing rule.

In Fig. 2, the inventory level of the plant during working hours is shown for an example instance. The effects of the SPT–EDD sequencing rule can be observed, since the workload decline is steeper when peaks are higher. Furthermore, one can see that the maximum inventory level equals 22 jobs.

Fig. 2

Inventory levels for replication 48 of the selected experiment

This results in a tardiness of 2133 min, which are incurred by 8 jobs, from which 6 jobs are processed during the night. This gives an average tardiness of about 267 min per tardy job.

6.2.3 Overall performance

The results of all 342 experiments are shown in Tables 4, 5, 6, and 7 in these tables, data from multiple experiments are combined to obtain the displayed aggregated results.

Table 4 Aggregated performance in tardiness in minutes and peak inventory in number of jobs for SPT–EDD sequencing rule

Table 5 Average tardiness in minutes per number of jobs scheduled for SPT–EDD sequencing rule

Table 6 Average inventory peak per number of family types in minutes for all machine-batch combinations for SPT–EDD sequencing rule

Table 7 Average tardiness per number of family types in minutes for all machine-batch combinations for SPT–EDD sequencing rule

Effect of number of non-batching machines An increase in non-batching machines ($M_1$ and $M_3$) corresponds with a decrease in tardiness, but not necessarily in improved inventory performance, as shown in Table 4. When adding an extra grosser, the peak inventory increases. Since the output of the grossing stage increases, more tissue is processed in the first batches, which causes this inventory peak increase. However, for the third stage, adding extra machines positively impacts the peak inventory, since more jobs can be processed simultaneously, which reduces the inventory at a faster pace.

Effect of number of jobs Table 4 shows the effects of increasing the number of jobs. When more jobs are to be processed, higher inventory levels are present and a higher utilization of resources is derived. Therefore, the tardiness increases, as shown in Table 4. Furthermore, a relation between the number of batches and number of jobs can be observed, as shown in Table 5. When jobs are processed more spread over the day in multiple batches, the tardiness decreases.

Effect of number of job families Recall that the job families determine the distribution of the due dates and processing times of jobs. Thus, a job of a certain job family has a batch processing time corresponding to that family. Therefore, the complexity of the scheduling problem is expected to increase when including more job families. Where Table 6 shows that more job families relate to lower inventory, Table 7 does not show a clear relation between tardiness performance and the number of job families. A possible explanation can be found in the characteristics of the job families, which may increase or decrease the possibility to derive a good solution. For example, if a certain job family with a more strict due date is added to an instance, the tardiness will increase compared to the situation where this job family is excluded from the instance.

Effect of number of batching machines and batches Increasing the number of batches run on the different machines has the expected effect of decreasing the peak inventory level, as shown in Table 6 and tardiness, as shown in Table 7. However, the number of machines, which impacts the timing of the batches, does not show a significant relation with the peak inventory level and tardiness. As shown in Table 7, some combinations perform better than others. This indicates that the timing of batches is important to derive a solution with low tardiness and inventory.

Furthermore, Tables 6 and 7 show that a tradeoff has to be made between the tardiness criterion and the peak inventory criterion. For example comparing including 5 or 8 batches on 4 machines, one can see that different configurations lead to either a solution with better inventory performance, or a solution with better tardiness.

Conclusions Based on the experiments, multiple effects are observed. First, the SPT–EDD sequencing rule performs best according to the tardiness performance indicator. Second, the number of batches, the number of jobs, and therefore the load of the system, has a large effect on the maximum inventory level and on the tardiness of jobs. Third, the number of machines and the number of job families do not show a clear relation with the inventory level and tardiness.

7 Case study

As a case study we consider the histopathology laboratory of the Department of Pathology of University Medical Center Utrecht (UMC Utrecht). This case study also inspired this research. UMC Utrecht is a 1,042 bed academic hospital which is committed to patient care, research, and education. In the pathology department of UMC Utrecht there are several units, such as the histopathology laboratory, the immunochemistry laboratory, the DNA-laboratory, and the unit cytology. The histopathology laboratory evaluates tissue of close to 30,000 patients each year, resulting in the examination of some 140,000 slides each year. The histopathology laboratory of UMC Utrecht has provided real life data to evaluate the applicability and performance of the solution method. We consider 200 different problem instances based on historical data of 22,379 patients derived from January to December 2013. A summary of all input variables and parameter is given in Table 8. Each instance includes four job types, depending on the batch processing time: large sized specimens, average sized specimens, small sized specimens (including biopsies), and priority specimens. All jobs consist of a number of slides, which vary according to their job type. This is included as a weight factor to the inventory levels. Furthermore, the moment of arrival in the laboratory is included as the release time of a job. The due date of a job is derived from the target turnaround time, as shown in Table 9. Furthermore, this table shows the corresponding batch processing time of the job families. The turnaround time (TAT) targets per job type, and therefore the corresponding due dates, are set by hospital management, the Dutch government, and external parties, to ensure a timely diagnosis for all patients. The batch processing times are set by the tissue processor manufacturer, academic standards, and laboratory management, as shown in Table 9 as well.

Table 8 Variations in case study variables

Table 9 TAT targets and processing times per job family

We consider two scenarios. First we consider the initial situation, for which only the scheduling problem is solved using the EDD sequencing rule, which was used in the histopathology laboratory. The batching problem is not solved since the batching moments are fixed in the initial situation. Second the batching policy as derived from the batching model is considered, where the effect of processing 3, 4, and 5 batches during the day is evaluated. We apply the SPT–EDD dispatching rule in the scheduling stage, since it showed the best performance in Sect. 6. We restricted the large jobs to be processed during the night, since their batch processing time equals 8 to 12 h.

7.1 Initial situation

In the initial situation, all jobs are processed in batches during the night, except for small jobs, which are processed on fixed moments during the morning, but only consist of a very small amount of jobs (1–3 slides per batch). This results in a high workload during the morning, as shown in Fig. 3 for one representative instance (95 jobs, replication 43). All 95 jobs become available, which together account for 193 slides. Overall weighted inventory performance is shown in the first column of Table 10.

Fig. 3

Workload performance in the initial situation

Table 10 Inventory performance of the case study in number of slides

The tardiness performance for the initial situation, in which 0 batches are allowed during the day, is shown in the first columns of Table 11. One can see that only a small percentage of average and small jobs are finished before their due date. This is a direct result of tissue processing during the night, which leads to a one-day delay for all jobs.

Table 11 Tardiness performance of the case study in minutes

7.2 Batching policy

We consider three case study experiments, based on the number of batches. More extensive experiments with their results are available with the authors. The batches were divided over the job types according to the distribution of job families as follows: (1-1-1), (1-2-1), (1-2-2) which represent the number of priority, small, and average job type batches respectively for the 3, 4, and 5 batch situation. Since large jobs are restricted to be processed during the night, they are excluded from the batching model. Furthermore, recall that jobs with lower batch processing times than a batch processing time are allowed to be processed in these batches. For example, a priority job can be processed in a batch of small sized jobs, but with the processing time of a small sized job.

Figure 4 shows the spread in workload for the same selected instance (95 jobs, replication 43), but now considering the batching policy including 5 batches. Figure 5 shows the corresponding batch timing derived from the batching model. There is a maximum of 33 jobs in inventory and a maximum of 104 slides. All experiments show the expected large decreases of peak inventory compared to the initial situation, as shown in Table 10. The initial peak can be reduced with up to 50 %. The tardiness results are shown in Table 11. These results confirm that including multiple batches is significantly better than the initial situation, as expected from the numerical results, with 5 batches deriving the best overall performance. The reduction in tardiness is correlated with a 20 % reduction in turnaround time. Since many jobs do not have to wait anymore for an entire night, this has a major impact on the turnaround time. All experiments show improved average results regarding their norms, but specific patient types experience reduced performance compared to the initial situation, such as priority patients. This shows a more fair division of resources over jobs is derived.

Fig. 4

Workload performance with the batching policy

Fig. 5

Batch timing derived from the batching model

In conclusion, our approach finds a good schedule for a real-life sized histopathology problem within reasonable time. Furthermore, a 20 % reduction in turnaround time and 50 % reduction in peak inventory can be derived when implementing this schedule. Based on this analysis, UMC Utrecht is currently implementing planning and control approaches in the histopathology laboratory regarding the planning and scheduling of tissue processing batches (Leeftink et al. 2016).

8 Conclusions and discussion

This is the first paper to consider the 3-stage HFPB with batching processors in the second stage. We have introduced a decomposition solution method to optimize and prospectively assess the planning and scheduling of batches and jobs, and applied this approach to the processes in the histopathology laboratory. The Phase-1 model includes a novel workload spreading approach, which was based on a surgery sequencing approach as recently introduced in the literature (Van Essen et al. 2012). Despite its NP-hardness, we could solve real-life instances of this optimization problem to optimality. The Phase-2 model includes a list scheduling algorithm, to ensure practical applicability without compromising the performance.

The results show that through a reduction in the tardiness the turnaround time in our case study can be reduced by 20 % through eliminating unnecessary waiting, for example during the night hours. Furthermore, peaks in workload can be reduced by more than 50 % by shifting a part of the pile from the morning towards the afternoon, and all tardiness norms can be met. Numerical analyses showed that in the scheduling model the SPT–EDD sequencing rule performs best in terms of tardiness and peak inventory. Furthermore, it was shown that increasing the number of batches has the expected effect of decreasing the peak inventory level and the tardiness.

In the model, a few assumptions were made. One important assumption is that batches consist of the same amount of jobs. In practice, if two batches of the same batch type are scheduled within a small time frame, only a few new arrivals have occurred, and thus the workload resulting from the second batch will be small compared to the workload resulting from the first batch. However, Fig. 2 shows approximately equally sized peaks, which corresponds with the assumption that all batches will induce the same load when supply and demand in the surrounding stages are wisely set.

When release times are taken into account, as in the case study, this assumption might get violated, since not enough jobs are available for the first batches. In relation to this, the effects of arrival patterns of jobs is of interest. Therefore, further research could be done to include a weighted batch completion interval according to the job arrivals. This might result in even more leveled batch loads, and therefore in a more leveled inventory distribution.

We assumed deterministic processing times for both manual and non-manual tasks. The machines are pre-programmed, and therefore deterministic processing times reflect reality. On the opposite, manual labor work always includes variation, and therefore stochastic processing times seem a more realistic representation of reality. However, there is a large difference in service time of the batch processor (multiple hours) compared to the technicians (a few minutes). Therefore, the effects of service time variation are neglected in our model. Furthermore, since decisions are to be made at a tactical level, we expect including stochastic service times of technicians does not have a large influence on the outcomes.

In relation to this, we assumed the use of identical machines with stable processing rates. In practice, employees work at different paces, which would favor non-identical machines in some stages to better reflect reality. Furthermore, employees tend to work harder in the end of the afternoon to finish the last pile of work, when needed, and are mostly willing to work a few minutes in overtime, if that guarantees finishing the last jobs. We did not include these soft deadlines in our model, which might have led to an overestimate of the tardiness and inventory peaks.

This research assumes the workload to be reflected by the maximum inventory level. This relation is especially important for systems with manual activities, such as the histopathology laboratory. However, this objective can be important in manufacturing environments as well, since work-in-process levels should be kept to a minimum (Tsubone et al. 1996). Further research is needed to evaluate the actual impact on job satisfaction and the quality of the executed work, since this is hard to prospectively assess using mathematical modeling.

The perceived workload used throughout this research includes the number of jobs, but not the expected processing time, as usual in industry environments. The expected processing times can easily be incorporated in the methods proposed, by introducing a weighted inventory. However, we choose to use the perceived workload in number of jobs, since we concluded, together with the technicians and other laboratory staff, that the perceived workload was mainly influenced by the number of jobs that still had to be done, and not by the minutes of work spent on those jobs. Since jobs look very similar, a technician cannot see upfront whether a job has a high or low processing time, thus the number of jobs is the only practically relevant indication of the perceived workload.

Concluding, this research proposed a decomposition planning and scheduling method in order to reduce the turnaround time and the maximum inventory levels in a three stage HFPB. The results are applicable in many practical situations. For a concrete case in the histopathology laboratory of a large university medical center in The Netherlands, turnaround times could be reduced with up to 20 %, while the workload was halved. Therefore, the pathology staff has decided to implement these results in their laboratory.

Appendix: Model formulation

This appendix presents the model developed for scheduling the 3-stage HFPB. For notation, refer to Table 12. The objective and constraints are as follows:

Table 12 Notation

1.1 Objective

$${\text{minimize}}\,\alpha \cdot \sum _{i \in I}{D_i} + \beta \cdot V^{{\text{max}}}$$

(15)

1.2 Constraints

$$\sum _{j \in J_{i,g}}{Z_{i,j}} = 1 \quad \forall i \in I,g \in G$$

(16)

$$\sum _{i \in I_j}{ZF_{i,j}} \le 1 \quad \forall j \in J$$

(17)

$$Z_{i,j} \ge ZF_{i,j} \quad \forall i \in I_j$$

(18)

$$\sum _{i^{\prime} \notin NC_{i,g}}{X_{i^{\prime},i,g}} + \sum _{j \in J_{i,g}}{ZF_{i,j}} = 1 \quad \forall i \in I, g \in G$$

(19)

$$\sum _{i^{\prime} \notin NC_{i,g}}{X_{i^{\prime},i,g}} \le 1 \quad \forall i \in I, g \in G$$

(20)

$$X_{i,i^{\prime},g} + X_{i^{\prime},i,g} + \sum _{j \notin J_{i,g} \cap J{i^{\prime},g}}{Z_{i^{\prime},j}} \le 1 \quad \forall i,i^{\prime} \in I_g, i^{\prime}>i, g \in G$$

(21)

$$Z_{i,j} + 1 - X_{i,i^{\prime},g} - X_{i^{\prime},i,g} \ge Z_{i^{\prime},j} \quad \forall i,i^{\prime} \in I_g, i^{\prime}>i, j \in J_{i,g} \cap J_{i^{\prime},g}, g \in G$$

(22)

$${\mathscr{M}}^1 \cdot (1-X_{i,i^{\prime},g}) + T_{i^{\prime},g} \ge T_{i,g} + \sum _{j \in J_{i,g}}{Z_{i,j} \cdot w_{i,g} \cdot p_{i,j}} \quad \forall g \notin G^{batch}, i \in I, i^{\prime} \notin NC_{i,g}$$

(23)

$$\sum _{j \in J_{i,g}}{ZF_{i,j} \cdot r^j} \le T_{i,g} \quad \forall g \in G, i \in I$$

(24)

$$r_i \le T_{i,1} \quad \forall i \in I$$

(25)

$$\sum _{j \in J}{\sum _{b \in B}{Q_{i,j,b}}} = 1 \quad \forall i \in I$$

(26)

$$\sum _{j \in J}{\sum _{b \in B}{Q_{i,j,b} \cdot S_{j,b}}} = T_{i,g} \quad \forall i \in I, g \in G^{batch}$$

(27)

$$T_{i,g-1} + \sum _{j \in J_{i,g-1}}{(Z_{i,j} \cdot (w_{i,g} * p_{i,j})} \le \sum _{j}{\sum _{b}{Q_{i,j,b}}} \cdot S_{j,b} \quad \forall i \in I, g \in G^{batch}$$

(28)

$$T_{i,g} + \sum _{j \in J_{i,g}}{(Z_{i,j} \cdot pb_j)} \le T_{i,g^{\prime}} \quad \forall i \in I, g \in G^{batch}, g^{\prime} \in NS_{i,g}$$

(29)

$$T_{i,g} + \sum _{j \in J_{i,g}}{Z_{i,j} \cdot w_{i,g} \cdot p_{i,j}} - d_i \le D_i \quad \forall i \in I, g \in G^{final}$$

(30)

$$V_t = \sum _{i}{W_{i,t}} \quad \forall t \in \{1, \ldots , H\}$$

(31)

$$W_{i,t} \ge W^1_{i,t} + W^2_{i,t} - 1$$

(32)

$${\mathscr{M}}^2 \cdot W^1_{i,t} \ge t - (T_{i,g} + \sum _{j \in J_{i,g}}{(Z_{i,j} \cdot pb_j)} \quad \forall t \in \{1, \ldots , H\}, g\in G^{batch}$$

(33)

$${\mathscr{M}}^2 \cdot W^2_{i,t} \ge T_{i,g} - (t+1) \quad \forall t \in \{1, \ldots , H\}, g\in G^{final}$$

(34)

Each job is processed in each stage exactly once (16). There is one job that is the first to be processed on a certain operational machine j (17), and a job i can only be processed first on a machine j if the job is assigned to that machine (18). Since the successors and predecessors of all orders are tracked, a job i can be processed first on the machine j to which it is assigned, or succeeds another job $i^{\prime}$ on that same machine (19). Furthermore, jobs can only have one direct successor (20). Successive jobs i and $i^{\prime}$ cannot be processed by machines that cannot process them both, but should be processed by the same machine j (21) (22). These equations were included, since they performed best in the review of (Gupta and Karimi 2003). In non-batching stages, all machines are only able to process one job at a time. Therefore, job $i^{\prime}$ can only start processing on machine j after its predecessor i is finished (23). Furthermore, the release time of the machines (24) and job (25) should be taken into account. Each job i should be assigned to exactly one batch b (26), and the batch starting time should be equal to the job timing of each job i in that batch b (27). A batch b can start processing after the completion time in the previous stage of the jobs that are in that batch (28). The start time of jobs in the post-batching stage, should be later than the batch completion time (29). We considered two objectives, the tardiness and the inventory. The tardiness of orders is determined by the completion time of a job i minus the due date of that job (30). To determine the inventory at time t, the sum of all jobs that are in inventory at time t is determined (31). Using two auxiliary variables, a job is in inventory at time t (32) if its completion time in the batching stage is lower than t (33), and the start time in the post-batching stage is higher than t (34). Note that all variables should be non-negative.

In practice, more constraints have to be added to this model. For example working hours of machines and staff may differ (machines can run during the night, while staff is not available). Furthermore, requirements on employee education might be needed for specific job types. These constraints can easily be added to the model, for example using auxiliary variables.

The problem is a Quadratic Problem, due to constraints (28) and (27). When batch timing decisions are fixed, for example by solving the batching problem, the decision variable $S_{j,b}$ is replaced by a parameter $s_{j,b}$, with fixed start times as derived from the batching model for batch b on machine j. Furthermore, equations (28) and (27) can be replaced by equations (35) and (36). This way, the model becomes linear, and thus a Mixed Integer Linear Program (MILP).

$$T_{i,g-1} + \sum _{j \in J_{i,g-1}}{(Z_{i,j} \cdot (w_{i,g} * p_{i,j})} \le \sum _{j}{\sum _{b}{Q_{i,j,b}}} \cdot s_{j,b} \quad \forall i \in I, g \in G^{batch}$$

(35)

$$\sum _{j \in J}{\sum _{b \in B}{Q_{i,j,b} \cdot s_{j,b}}} = T_{i,g} \quad \forall i \in I, g \in G^{batch}$$

(36)