1 Introduction

Concrete filled hollow section (CFHS) columns are conventional type of composite columns with high fire resistance without additional fire protection materials. Concrete with low thermal conductivity work as fire protection, and the steel tubular element keeps concrete confinement during the fire exposure. Utilizing additional steel core is a method proposed recently by different researchers for increasing load bearing capacity of these composite columns and designing more slender structural elements which are more favorable for architectural purposes. The research presented in this paper introduces an innovative approach to enhance the structural performance of columns by substituting the solid steel core with high-strength bundles of bars. These bar bundles, configured in various ways, exhibit equivalent performance to solid elements but with smaller individual steel components. It is well-understood that the production process and chemical composition of steel can induce residual stresses in the final products, and these stresses tend to increase with size, resulting in imperfections that can be mitigated by using smaller elements. The specific arrangement of the bar bundles and the presence of ribs on the surface of the reinforcing bars enhance the overall composite performance and strengthen interaction between the steel and the infill concrete or grout, particularly at elevated temperatures. Furthermore, the point contacts between the rebars minimize the transfer of heat through conduction between them, thereby improving the thermal efficiency of these columns. Ultimately, the utilization of high-strength steel augments the load-bearing capacity of these composite columns, enabling the design of more slender columns while reducing material consumption.

The CFHS columns have been extensively investigated experimentally and numerically in both ambient conditions and fire. The joint European research on the fire performance of CFHS [1] and the large-scale tests conducted by the National Research Council of Canada [2] are the wide studies on this topic. Effects of different parameters have been investigated on CFHS columns: (a) geometrical parameters: such as elliptical sections [3], circular and square shape [4, 5]; (b) boundary conditions: application of fire load with non-uniform exposure on the sections [6]; effect of support condition [7] or large eccentricity [4]; and finally (c) Post-fire mechanical performance of these sections under constant axial loads [8] or with considering cyclic thermal and mechanical loads [9]. Various methods have been proposed by researchers in recent times to enhance the thermo-mechanical performance of composite columns. Utilizing double skin sections is one of the famous methods studied from different points of view. Geometry is again the first parameter for both circular and square hollow sections [10] and then the type of concrete used for filling, which can be normal self-consolidating concrete [11] or Ultra-high performance concrete [12].

The single fire test conducted by Klingsch in 1984 [13] was one of the first studies on CFHS columns with a steel core. The most recent studies from Kleibömer [14] and Neuenschwander [15] were on CFHS columns with a solid steel core in the middle. Their focus was on the behavior of these columns in the event of a fire, and the strength of contact between core and concrete was studied at different temperatures. Besides experimental investigations, numerical methods were developed for predicting the thermal or thermo-mechanical behavior of different types of CFHS columns. One-dimensional models were mainly used for global structural models, in which the performance of the whole structure made by CFHS elements under fire was a matter of control [5, 16]. The three-dimensional models developed by the finite element method focused on one specific element or the connection between the beam and column. Most of the researchers used sequential method for investigating the thermo-mechanical behavior of the composite sections with different software, such as: DYNA3D as a strong software for predicting the behavior of concrete under extreme loading [17], Programming in Visual Fortran [18], Ansys [19], ABAQUS [20] and computer code BoFIRE [21] which researchers used for simulating thermal or thermo-mechanical behavior of CFHSs.

The most recent study includes the outcomes of extensive experimental fire tests conducted on the proposed bar-bundle columns, with the aim of examining their thermo-mechanical performance. In addition, the study involved the creation of a numerical model that has been calibrated and validated to account for the composite behavior observed during the fire [22]. The objective of the entire experimental and numerical study is to develop a simplified approach, utilizing parametric study, for the design of bar-bundle columns.

2 Columns Fabrication

The columns for this fire tests were manufactured under the supervision of industrial partners, started with setting the bars in their location utilizing some stencils (Figure 1a), and then the bars were bundled together with straps (Figure 1b) and fixed by several tack welds throughout their length (Figure 1c). Both ends of the bar bundles flattened to provide full contact between the bar bundle and the head plates, and thus the force introduction via the head plate into the entire bar bundle could be ensured. For centralizing the bar-bundle inside the cladding tube, spacers made of fiber-reinforced concrete were fixed around the bar-bundles (Figure 1b), besides two alignment plates welded at both ends of the cladding tube (Figure 1d) to keep bar-bundles in the center.

Figure 1
figure 1

Fabrication process of bar-bundle columns

Full size image

Thermocouples were positioned at various points across the section and at five different heights along the length of the column. These thermocouples were firmly affixed to the rebars through spot-welding to ensure that the connections remained intact during the grouting process. After all adjustments, the rebars were located in the center of the tube and the tube was fixed to the end plates by circumferential fillet welds. Then the columns were placed vertically, and the grout was pumped by high pressure into the columns from the inlet located at the bottom of the cladding tube. The swelling grout without aggregate was used to assure that all spaces between the bars were filled completely. Columns were stored for 100 days to reach their highest strength. According to DIN 4102-4, four vapor outlets [27], two on top and two on bottom considered on the tube to avoid explosive failure of the tube caused by the high vapor pressure building up by the heated grout (spalling due to evaporated moisture content of grout during fire exposure).

3 Experimental Tests

3.1 General

The experimental tests in this project were carried out to examine the thermo-mechanical performance of bar-bundle columns. These tests involved full-scale fire testing, as well as material testing, which helped to determine the temperature-dependent properties of the materials utilized in the manufacturing process of the columns. The material properties were necessary for calibrating and validating the numerical simulation.

3.2 Full-Scale Fire Tests

3.2.1 Test Details and Set-Up

This article presents the results of a collaborative research project that extensively examined the suggested columns under both ambient conditions and fire case. The project involved conducting many tests in cold case, exploring various column sections and heights [23]. As a result, the sizes were selected to allow for meaningful comparisons with the investigations conducted in both cases. In the investigations at cold case, the impact of residual stress in the steel bars on the imperfections of the columns was thoroughly investigated. Hence, it was essential to employ reinforcing bars of different sizes in accordance with market availability. Nevertheless, when conducting tests in fire conditions, the height of the columns remained constant to minimize the number of variables, although different heights and slenderness ratios were explored under ambient conditions.

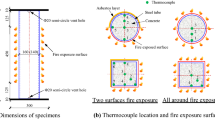
Fire tests were conducted on three columns with different configurations of bars (3, 7, and 19 bars) in the core with a similar length of 4.09 m. The geometrical and structural details of the columns are defined in Table 1. All columns were manufactured by a cladding tube made of cold-formed structural hollow sections of steel grade S355 and high-strength rebars with grade S670. The columns were filled with grout with strength equivalent to C80/95. All fire tests were conducted with nominally pinned-fixed support conditions. The pinned end was realized by rocker bearing set-up using a half cylinder installed on the hydraulic jack. The mechanical load was applied by a hydraulic press with a capacity of 6 MN from the bottom of the furnace with 10 mm eccentricity, and columns were fixed by a reaction beam from the top. To minimize heat loss and avoid any thermal damage to the equipment, columns were insulated with 20 cm mineral wool from the top and bottom. The amount of axial force and the vertical deformation were continuously recorded by sensors inside the hydraulic press, and the horizontal deformation was measured by a LVDT (Linear Variable Differential Transformer) sensor installed from the side to the middle of the columns’ height.

Table 1 Geometrical and Structural Details of the Columns
Full size table

The tests started with applying an axial pre-load (P0) with an eccentricity of 10 mm and held constant for 30 min prior to the fire exposure, and after starting the fire, mechanical load kept constant for 90 min. After 90 min, without stoping ISO-fire, the load was increased with a speed of 8 kN/s till the nonlinear geometrical failure (buckling) occurred, and once the columns buckled, the load was defined as the load-bearing capacity of the columns under 90 min of standard fire. The fire exposure followed the standard ISO-834 curve using 6 oil burners located at the bottom of the furnace, and the fire temperature was measured by 6 plate thermocouples installed near the column on both sides and at 3 different levels. The temperature-time history of a different part of the sections in 5 levels was recorded by K-type thermocouples installed on the rebars during the construction of the column.

3.2.2 Thermal Results

The temperature distribution within the column section was monitored using thermocouples placed on rebars at five different levels. The recorded temperatures of the rebars are shown in Table 2, with each bar labeled by number and level (A to E from top to bottom). It is observed that the temperature measurements taken by the thermocouples placed at levels A and E are relatively low, which can be attributed to the fact that these thermocouples were situated near the top and bottom of the columns, in close proximity to the insulation components.

Table 2 The Recorded Temperature Development of the Bar-Bundles in Columns C1, C2, and C3
Full size table

The maximum temperature of the rebars in columns C1, C2, and C3 reached to respectively 250°C, 110°C, and 200°C after 90 min of exposure to ISO fire (Table 2). The variation observed in the results can be attributed primarily to the differences in the thickness of the grout cover present in the columns. Specifically, the columns had grout covers with thicknesses of 23.5 mm, 44.2 mm, and 28.4 mm, respectively. A correlation can be observed between the thickness of the grout cover and the core temperature, with thicker grout covers generally resulting in lower core temperatures. However, the range of the core temperature is much lower than the temperatures were reported for the CFHS columns with solid steel core [15] with identical section sizes, the core temperature reached to approximately 600°C under 90 min standard fire. There are two major effective parameters on the low temperature recorded in the proposed columns. First the thermal resistance of grout is higher than normal concrete conventionally used as filler of CFHS columns. And second, effect of the air layer build-up between steel tube and concrete by increasing the temperature. It is known that by starting the fire and increasing the temperature of the steel tube, the tube starts to expand radially, which builds up an air layer between the tube and grout, performing as an extra insulating layer. By increasing the temperature of grout and its radial expansion, the thickness of the air layer reduces over time. Because of the ribs on the rebars and their configuration, the connection between the grout and bar-bundle is strong and the grout cannot expand freely, which means the reduction of the air layer’s thickness will be slow over time, besides the low thermal conductivity of grout which reduces the temperature transfer into the section. In contrast, the connection between concrete and solid steel core in CFHS columns with the solid core is comparatively weak, because of the shape and the smooth surface of the core which generate weak interlocking with concrete. By increasing the temperature, both tube and concrete expand freely, which reduces the air layer thickness faster and affects speed of the core temperature raise. The temperature data obtained from the bars in columns C2 and C3 show notable peaks during the time frame of approximately 20 to 40 min after exposure to fire. On the other hand, column C1 did not exhibit any sudden rise in temperature during the same time period. The peaks are linked to the number of bars, their size, and their configuration. The grout between the bars has a moisture content that evaporates over time and needs to find a way between the bars to release. In C1, there is only one space between the bars with big size, which lets the vapor distribute in a large space till finding a way to release. When the size of the bar is small, and the number of them is high, it means there are small spaces between them, and with the assumption that the spaces are filled completely by grout, the evaporated moisture of this grout would trap between the bars until finding a way to release. This phenomena causes a partially high pressure inside the column that is more significant in C3 with more numbers small bars and peaks. High moisture and vapor pressure cause errors in recorded temperature by thermocouples [28]. However, after all, vapor was released from the vapor outlets and the peaks were eliminated from the recorded temperature and increased semi-linearly till the end of fire tests.

3.2.3 Thermo-mechanical Results

The thermo-mechanical behavior of all columns follows a similar principle, as presented in Figure 2. The diagram shows the vertical deformation of the columns during the fire tests. By starting the ISO fire, the tube heats up very fast and expands longitudinally and causes a positive deformation of the columns. In the first minutes of the test (app. 20 min) the tube takes the whole mechanical load, and expands linearly till it reaches to the critical temperature, after that, the material goes to the plastic phase, and in a short time tube fails, which leads to a negative deformation and re-distribution of loads to the core elements. The amplitude and range of the peak depend on the amount of the load and thickness of the tube. For similar columns size, The lower the load and the thicker the tube, the higher the amplitude and range of the peak. In other words when subjected to a lower mechanical load, the tube can endure the load for an extended duration and undergo greater expansion.

Figure 2
figure 2

Vertical deformation of the columns C1, C2 and C3 throughout the 90 min standard fire tests

Full size image

Following the tube’s failure, it primarily serves to confine the grout and does not contribute remarkably to load-bearing. During this time the temperature of core raise slowly, and the grout and bars elongate longitudinally and radially for 90 min; in the first minutes after tube failure, both grout and rebars has contribution in the load bearing however by increasing the temperature in the bar-bundle they expand faster and the positive deformation is semi-linear. The expansion continues for 90 min and then by increasing the loads to the critical load (\(P_{cr}\)) columns fails under first mode of buckle (loads defined in Table 1).

3.3 Material Properties

3.3.1 General

In the presented research, the temperature-dependent mechanical properties of the applied S670 rebars and the thermal properties of the grout were also investigated. The cladding tubes were made of steel grade S355, which is a standard material and its thermo-mechanical properties were considered according to Eurocode 3-1-2 [24] in numerical simualtions. In this type of composite columns the grout has thermal protection role and does not have significant influence on load-bearing of the columns in fire, so only thermal properties of the grout were determined through the test and the temperature dependent mechanical properties were considered according to Eurocode 2-1-2 [25]; the compressive strength of grout cylinders were between 80 MPa to 95 MPa, which is equivalent to C80/95.

3.3.2 Temperature-Dependent Material Properties of Steel Rebars S670

The steady-state tensile tests were conducted on non-standard specimens to evaluate applicability of Eurocode 3-1-2 [24] stress–strain characterization and definition of reduction factors. The specimens were rebars with 18, 28, and 35 mm sizes and 1.1 m lengths. The middle of the rebars for measurement by extensometer was milled to a round rod with respectively 14, 20, and 20 mm diameter with an original gauge length of L0=100 mm. The temperature of the specimen in the top, middle, and bottom of the L0 part were measured throughout the tests by K-type thermocouples. Before the tensile tests at elevated temperatures, the material properties at room temperature were measured on standard specimen cut from the rebars of the same size and same production batch, and the tests were repeated twice for each bar size; the rounded average Young’s modulus was 210,000 N/mm2 and the effective yield strength was 850 N/mm2.

Figure 3
figure 3

Comparison of steady-state test on bars with 18, 28, and 35 mm size under 400, 500, 600, and 700°C with Eurocode 3-1-2

Full size image

The specimens were subjected to the temperatures 400°C, 500°C, 600°C, 700°C with heating rate of 3 K/min and the temperature kept constant for 30 min till the whole section reached the target temperature; then the specimen was loaded (displacement-controlled setup) with 0.3%/min strain rate to failure. Results of stationary tests on the high-strength rebars show that the stiffness reduction doesn’t have remarkable difference from normal steel, however, yield and ultimate tensile strength reduced significantly in comparison with the proposed reduction factors by Eurocode 3-1-2 [24] for normal steel (Figure 3). Figure 3 shows the comparison between the test results of the steady-state test without thermal creep and the Eurocode stress–strain-lines (derived of transient tests).

The average reduction factors for the effective yield strength (\(k_{y,\theta } = f_{y,\theta }/f_{y}\)) and for the proportional limit (\(k_{p,\theta } = f_{p,\theta }/f_{y}\)) as well as the slope in the elastic range (\(k_{E,\theta } = E_{a,\theta }/E_{a}\)) were calculated and compared with the factors suggested by the Eurocode 3-1-2 [24] for normal steels in Table 3.

Table 3 Comparison of Measured Reduction Factors for Steel Grade S670 with Eurocode 3-1-2
Full size table

3.3.3 Thermal Properties of Grout

The thermal properties of the grout significantly influence the thermal performance of the bar-bundle under fire exposure. In order to conduct accurate numerical simulations, it is necessary to determine the bulk density, thermal conductivity, and specific heat capacity of a material at various temperatures. Since the details of the conducted tests are not the focus of the current paper, a summarized description is reported here.

For the production of the columns, a grout cement of the grade CEM I 42.5R - Rheoment from the company Thomas Zement GmbH & Co. KG was chosen. This cement is characterized by its high flow-ability at low water-cement ratios (0.3 was chosen here). Since the voids between the bars to be filled are very small, no aggregate was added. The specimens for each test were prepared and stored for at least 100 days under normal climatic conditions (23°C, 50% relative humidity) until they were tested.

The thermo-gravimetric analysis (TGA) was used to determine the temperature-dependent bulk density of the grout, by examining physical and chemical properties at elevated temperature. The weight change of the sample caused by the reactions such as dehydration, oxidation, decomposition, and phase changes were recorded with heating rate of 10 K/min. Air was chosen as the gas in the chamber to simulate a realistic fire scenario. Three measurements of raw density were recorded for the climate-stored (23°C, 50% RH) samples at temperatures ranging from 25°C to approximately 1000°C. Figure 4 shows the averaged density curve as a function of sample temperature and were compared to those determined by Eurocode 2-1-2 [25]. Mass of the samples dropped sharply from 20°C to 120°C, due to moisture evaporation, and then reduces almost linearly till temperature reaches about 600°C and another mass drop and after that the curves remained almost constant at a value of approximately 1680 kg/m3. The mass loss was also greater than predicted by Eurocode 2-1-2 [25], with a quick mass loss at the beginning of the temperature exposure due to moisture evaporation.

Figure 4
figure 4

Thermal properties of the grout-density

Full size image

For determination of the specific heat capacity of material Differential Scanning Calorimetry (DSC) were used. The samples and reference probes (here Saphir Al2O3) are heated at a constant rate, and the temperature difference between the two is measured to determine the specific heat capacity of the sample. Three measurements were taken, and the resulting curves were smoothed and averaged to produce a final curve which was used in numerical simulation (Figure 5).

Figure 5
figure 5

Thermal properties of the grout-specific heat

Full size image

The Slug Calorimeter test was designed based on the ASTM E119 standard to determine the thermal conductivity of the grout. The test involves exposing a square steel cross-section, protected on both sides by non-flammable material, to a controlled temperature-time environment in an oven. The heat flow through the material should only be one-dimensional, and the temperatures on the surfaces of the material and within the steel cross-section are recorded. Due to the low temperature difference the measured results under ca. 150°C have to be approximated. After conducting three tests and obtaining temperature profiles from the Slug Calorimeter test, a numerical model was developed. The results of this model showed a high level of agreement between the simulations and measurements. The result of the test and its comparison with Eurocode 2-1-2 [25] and the simplified curved used for numerical simulation are presented in Figure 6.

Figure 6
figure 6

Thermal properties of the grout-thermal conductivity

Full size image

4 Numerical Simulations

4.1 General

A numerical model was developed by ABAQUS standard software for simulating the fire behavior of bar-bundle columns. Two-dimensional models were developed for heat transfer analysis of the columns and performing parametric study for the definition of effective parameters on the thermal behavior of the columns. Three-dimensional advanced models were developed for coupled temperature-displacement analysis of the columns subjected to standard ISO fire. The models incorporate the experimentally established temperature-dependent material properties and the boundary conditions in the fire tests, in order to develop a calibrated model which can adequately predict the thermo-mechanical behavior of the bar-bundle columns. Furthermore, parametric studies were performed for proposing a simplified method can be used to design the bar-bundle columns.

4.2 Model Details and Boundary Conditions

The steel material is defined as isotrop-plastic material in ABAQUS standard and all material properties defined temperature-dependent. The Concrete Damage Plasticity (CDP) model in ABAQUS utilized to model the tensile and compressive behavior of a quasi-brittle material such as grout or concrete. For the definition of the temperature-dependent mechanical and damage-relevant properties of concrete, Eurocode 4-1-2 [26] was considered. In the implicit analysis, definition of complex thermo-mechanical models with considering CDP increases the convergence problems. Therefore, a linear approach is considered for the damage evaluation in tension and the viscous regularization (viscosity parameter) is used to accelerate the computational time and to suppress numerical instabilities due to convergence problems. Wahid et. al [29] calibrated these parameters at high temperatures and propose 35°C for the dilatation angle and (0.001t) for the viscosity, where t is the time span in which the fire acts on the concrete element.

The boundary conditions were applied on a reference node defined on the surface of the end plates. The initial axial load (\(P_0\)) applied with 10 mm eccentricity on the head plate whilst the node is only allowed to move in the Z-direction and rotate around Y-direction (Identical to fire test-Table 1) which represents the pinned boundary condition. The nominally fixed support is defined in the middle of foot plate which is not allowed to move and rotate in all directions. However since realization of a perfect fixed support in fire tests is difficult, the support has a small rotation possibility, therefore, the rotational stiffness of the support around Y-direction is modeled by a spring with stiffness of 1000 Nm/mrad.

As mentioned the columns were insulated in both ends to avoid thermal damage to equipment. In the model also 20 cm from top and bottom of the columns is not subjected to fire. Considering above mentioned boundary conditions allows the model to predict the thermo-mechanical behavior of bar-bundle columns realistically and achieving valid results.

4.3 Heat Transfer Analysis

Thermal analysis was done first on the two-dimensional model to investigate effect of different parameters and calibrate the model with fire test results. The effect of air layer build-up between the tube and grout by their radial expansion under heating, can be defined by gap conductance in ABAQUS software. However, the correct definition of the parameters has a direct effect on the results. For this purpose, some initial simulations were performed, which show the thickness of the air layer reaches maximum to 2 mm after 90 min of ISO-fire exposure, considering different column and bar sizes. It is known that the gap conductance depends on many parameters besides the thickness of the air layer, like temperature of air layer by time and its partial pressure or moisture content of it. For a conventional concrete-filled hollow section, Espinos [30] considered 200 W/(m\(^{2}\)K), and for a concrete filled hollow section with a solid steel core, Neuenschwander [20] proposed 100 W/(m\(^{2}\)K). In this study, effective heat transfer coefficient of 50 W/(m\(^{2}\)K) is considered, which shows good agreement with test results (Figure 7) with the exception of the peaks caused by the vapor pressure (Sect. 3.2.2).***

Figure 7
figure 7

Comparison of bar temperature in fire tests and numerical simulation (red dashed lines) in columns C1, C2, C3

Full size image

The sensitivity analyses were performed on section diameter, tube thickness, grout/concrete cover thickness, and the number and size of the bars. The results show that the tube thickness has the lowest effect on temperature distribution in the section. The effect of sections’ diameter as the next parameter was evaluated under constant cladding tube thickness of 5 mm and concrete cover of 20 mm, and then the temperature of bars with column sizes 100, 200, and 300 mm and for 1, 3, 7, and 19 bar were calculated. Results show by increasing the column size, the temperature of the bars decreases. Increasing column size means increasing material volume, which needs more energy to increase its temperature. Therefore, under standard fire load, the temperature of the section with a smaller size increases faster, although the concrete cover is equal in all of them.

The next parameter was the effect of concrete cover thickness in sections with constant size. Obviously, by increasing the concrete cover, the temperature of the bars decreases. This effect is shown in Figure 8 for a constant column size of 300 mm, tube thickness of 5 mm, and different configurations of bars. The changes in maximum temperature of bars with changing concrete cover from 10 mm to 50 mm are approximately 100 degrees.

Figure 8
figure 8

Effect of concrete cover changes (10, 20, 30, 40, 50 mm) on bar temperature—with constant column size (300 mm) and different bar configuration

Full size image

The results show that size of columns, concrete cover and size of the core are the most effective parameters on temperature behavior of the columns. Size of the core individually depends on the number of the bars, their configuration and size which can be defined by one parameter known as profile factor and can be calculated with formula in Figure 9.

Figure 9
figure 9

Profile factor (the ratio of the area \(A_m\) to the volume V)

Full size image

These results indicate the realization of one of the goals of this project. Using a bar-bundle as a core instead of a solid core by decreasing the volume of steel in the core, reduces the temperature of the core, which leads to lower stiffness reduction of material and reaching higher fire resistance columns.

4.4 Thermo-mechanical Analysis

A three-dimensional advanced nonlinear model was developed in this project to simulate the thermo-mechanical performance of the bar-bundle columns. For avoiding time-consuming and highly nonlinear coupled temperature-displacement analysis with complex convergence problems, the sequential method is used. Firstly, buckling analysis was carried out, and the nodal deformation of the first mode was transferred by a very small factor (L/1000) to the final model as imperfection. Secondly, a pure heat transfer analysis was performed on the columns, and the nodal temperature history was transferred to the final model. And eventually, the mechanical analysis was done on a model considering initial imperfection and nodal temperature-time changes. All geometrical properties and boundary conditions were defined according to the fire tests. The mechanical load applied in two steps, first initial load (\(P_0\)) applied on the model with ambient temperature, and in step two while the model reads the temperature-time of each node from heat-transfer analysis, the mechanical load kept constant.

Hard contact is considered between all contacted surfaces. Upper and lower load introduction plate are tied to the upper and lower surface of the cladding tube. The friction between concrete and cladding tube is considered with the friction coefficient of 0.3. The contact strength between bars and mortar was measured at room temperature with the push-out test at Technical Univerity of Munich. The contact was defined on the basis of the temperature-dependent cohesion behavior and the bond strength decreased with increasing temperature according to the reduction factors proposed by [31].

Figure 10
figure 10

Compare the vertical deformation of columns in fire tests with two series of simulation results

Full size image

Two series of simulations were performed with two accuracy levels (Figure 10). The initial series of models was carried out with considering material properties according to Eurocode 2-1-2 [25] and 3-1-2 [24] (steel: elasto-plastic and grout: elastic), nominal support condition, and big mesh size with a maximum 30 mm dimension. The second series were calculated with more accurate definitions for all boundary conditions. Material properties defined based on experimental tests and temperature-dependent concrete damage plasticity were considered for grout. The support condition is simulated by spring with pre-calculated deformation and rotation stiffness. And finally, the mesh size was reduced to a optimum size of 20 mm which resulted in more comparable results with fire tests. The maximum difference between the measured and calculated load-bearing capacity of the columns under 90 min of ISO fire was 1.5%. Parametric analyses were also performed on the thermo-mechanical performance of the columns. For this purpose, the fire resistance of the columns was calculated under 60, 90, and 120 min of standard fire with similar sections and different column lengths (Table 4).

Table 4 Simulation Results of Columns Load Bearing Capacity for Different Length and Fire Resistance Duration with Similar Boundary Condition as Fire Tests
Full size table

In comparison with the load-bearing capacity of columns with a 2 m length under ISO fire, by increasing the length to 4 m, the load-bearing capacity reduces an average of 67%. For a length of 6 m, this reduction reaches 71%, and for columns with 8 m and 10 m length, the load-bearing reduces 80% and 88% respectively.

With a similar simulation method, parametric analyses were performed and the buckling coefficient was calculated, which is the ratio of buckling resistance calculated from simulation to the cross-sectional plastic resistance. The results shown in Figure 11, have been superimposed on buckling curve "c" proposed by Eurocode 3-1-2 [24].

Figure 11
figure 11

Evaluation of the buckling coefficient with the relative slenderness at elevated temperature with Eurocode 3-1-2

Full size image

Following diagrams (Figure 12) represent the buckling coefficient calculated by parametric analysis on the bar-bundle columns with different slenderness. Tube size and thickness and the bar sizes are employed according to commercially available dimensions. The results separated to fire resistance of 30, 60, 90 and 120 min for bar-bundles with 1, 3, 7 and 19 bars. Results are plotted over relative slenderness of the columns at high temperature.

Figure 12
figure 12

Comparison of load bearing capacity in case of fire for different fire resistance time (R30 to R120) and different bar configuration

Full size image

The results show that the load-bearing capacity in columns with 1 and 3 bars reduces much more than the columns with 7 and 19 bars by increasing the slenderness in the event of a fire. Especially, the columns with 1 and 3 bars have a significant reduction of load bearing after 60 min of fire, which is mainly related to the configuration and size of the bars. Columns with 7 and 19 bars, with a more efficient load distribution, have shown higher resistance with increasing temperature.

5 Simplified Model

The current regulations do not provide a design method for calculating CFHS columns with steel core. However, it has been discovered that the design method suggested in Annex H of Eurocode 4-1-2 [26] for CFHS columns leads to un-conservative predictions of slender column performance. In the new version of Eurocode going to be published in 2023, a new method is proposed according to the Espinos [30] studies. The similar process is considered in this research for developing a simplified design method for the bar-bundle columns which follows the bellow steps:

  • Calculation of the equivalent temperature of each component of the composite columns by following formulas at the desired time of the standard fire, which is depending on the profile factor of the bars and the thickness of the concrete cover. The formulas are defined according to results of the parametric study and third degree polynomial functions were generated using Matlab coding. The formulas are applicable in the specified limits and the indexes a, c and s are corresponding to tube, concrete and bars respectively. Duration of fire exposure: \(30 min< t_{fi} < 120 min\) Profile factor: \(15< \frac{A_m}{V} < 75\) Concrete cover: \(20 m< c < 50 mm\) Ratio of profile factor to concrete cover: \(0.5< r = \frac{A_m/V}{c} < 4\) Temperature of Tube:

    $$\begin{aligned} \theta _{a,eq}&= 373+2.17\left( \frac{A_m}{V}\right) +15.56t_{fi}-0.07\left( \frac{A_m}{V}\right) ^2+0.039t_{fi}\left( \frac{A_m}{V}\right) -0.16t_{fi}^2 \nonumber \\&\quad +0.0006\left( \frac{A_m}{V}\right) ^3-0.00017t_{fi}^2\left( \frac{A_m}{V}\right) -0.00017t_{fi}^2\left( \frac{A_m}{V}\right) +0.0006t_{fi}^2 \nonumber \\ \end{aligned}$$
    (1)

    Temperature of Concrete:

    $$\begin{aligned} \theta _(c,eq)&=-132.3+19.27(\frac{A_m}{V})+9.28t_{fi}-0.56(\frac{A_m}{V})^2+0.15t_{fi}(\frac{A_m}{V})-0.08t_{fi}^2 \nonumber \\&\quad +0.0045(\frac{A_m}{V})^3-0.0007t_{fi}(\frac{A_m}{V})^2-0.00047t_{fi}^2(\frac{A_m}{V}) +0.00035t_{fi}^3 \nonumber \\ \end{aligned}$$
    (2)

    Temperature of bars:

    $$\begin{aligned} \theta _(s,eq)&=2.4-58.7r +0.81t_{fi}+1.5r^2+4.6rt_{fi}+0.007t_{fi}^2 \nonumber \\&\quad +1.8r^3-0.36r^2t_{fi}-0.014r t_{fi}^2 \end{aligned}$$
    (3)

    It should be mentioned that the formulas are defined with considering thermal properties of conventional concrete (Eurocode 2-1-2 [25] ) as filler and for calculation of bar’s temperature with the grout used in this project, ca. 150°C should be subtracted from the temperature calculated by the formulas. Furthermore, they are generated based on maximum temperature at each element and results are with small difference overestimated to be in the safe side.

  • The plastic resistance under axial compression: The strength of each component may be determined according to Eurocode 4-1-2 [26] and the properties presented in part 3.2.

    $$\begin{aligned} N_{fi,pl,R}=\frac{A_a f_{y,\theta }(\theta _{a,eq})}{\gamma _{M,fi,a}}+A_c f_{c,\theta } (\theta _{c,eq})+A_s f_{s,\theta } (\theta _{s,eq}) \end{aligned}$$
    (4)

    Where, \(A_{i}\) is the area of the cross section of part i \(f_{i,\theta }\) is the design strength of part i at the temperature of \(\theta _{eq}\) \(\gamma _{M,fi,i}\) is the partial factor for the materials in the fire situation which can be considered equal to 1.0

  • The effective flexural stiffness:

    $$\begin{aligned} EI_{fi,eff}= \phi _{a,\theta } (EI)_{a,\theta }+\phi _{c,\theta }(EI)_{c,\theta }+\phi _{s,\theta } E_{s,\theta } (I_{s,\theta }+\alpha _i A_sz^2) \end{aligned}$$
    (5)

    where, \(I_{i,\theta }\) is second moment of area of each component of the cross section \(\gamma _{i,\theta }\) is the reduction factor depending on the thermal stresses Since the temperatures calculation method proposed here are based on maximum possible temperatures in each element, actually we considered safety factor by using higher temperatures than the real values. Therefore it is recommended to consider 1.0 for all of reduction factors in calculation of effective flexural stiffness. For calculating concrete effective flexural stiffness \(EI_{c,\theta }\), concrete should be defined as a cracked element with a reduction factor of 0.6 (Eurocode 2-1-2 [25]). With regard to the temperature gradient in concrete, the cross-section of the concrete elements is reduced by the edge zone proposed in the new version of Eurocode 2-1-2 (2012) [25]. The thickness of the edge zone \(a_z\) [m] may be determined according to the following equation.

    $$\begin{aligned} a_z= {\left\{ \begin{array}{ll} 0.011\sqrt{1+\frac{R_{fi}-27}{27}\sqrt{\frac{w}{0.0125}}} &{} \text {for } 0.075< w < 0.20 \\ 0.011\sqrt{1+4\frac{R_{fi}-27}{27}} &{} \text {for } w>0.20 \end{array}\right. } \end{aligned}$$
    (6)

    where, \(R_{fi}\) the design value of the resistance for the criterion of load-bearing capacity in case of fire (min) w a cross-sectional dimension, used to determine the reduced cross-section (half the component dimension for circular cross-sections) At high temperatures, there is a possibility of slip between the bars, which is less for columns with 3 bars and becomes greater for columns with 19 bars. In addition, as the temperature increases, the slip between the bars becomes greater. This effect should be taken into account in calculation of the sectional moment of inertia using the parallel axis theorem by including a reduction factor (\(\alpha _s\)): \(0.4< \alpha _s < 0.6\)

  • Calculation of the Euler buckling load or elastic critical load:

    $$\begin{aligned} N_{fi,cr}=\frac{\pi ^2EI_{fi,eff}}{l^2_\theta } \end{aligned}$$
    (7)

  • Defenition of the relative slenderness at elevated temperature:

    $$\begin{aligned} \lambda _{\theta }=\sqrt{\frac{N_{fi,pl,cr}}{N_{fi,cr}}} \end{aligned}$$
    (8)

  • Finally, it is possible to calculate design value in fire condition based on reduction factor \(\chi\) which should be defined based on the corresponding buckling curve which according to the results shown in parametric analysis the curve “c” shall be employed.

Figure 13
figure 13

Comparison of the load-bearing capacity of bar-bundle columns with different configuration and slenderness, between the results of the simulation and the simplified design method

Full size image

The load-bearing capacity of the bar-bundle columns calculated with the proposed simplified calculation method of the columns was also compared with the results of the simulations. The results show minor differences in the range of 10%. The few results outside this range refer to columns with a 1 bar core, which was not investigated experimentally (Figure 13).

6 Conclusion

In summary, the paper proposes a novel approach for developing the thermo-mechanical performance of CFHS columns with solid steel cores by replacing the solid core with high-strength bar bundles with pressed grout as filler. The results of experimental tests, numerical simulation and parametric studies show that the new approach fulfills the initial purposes of the project:

  • Injection of swelling grout without aggregate with high pressure into the tube filled the space between the bars bundles completely and made strong contact with the bar bundles. The strong contact doesn’t let grout expand freely, which results in a thicker air layer between the tube and grout and delays the temperature transfer to the core for a longer time.

  • The high thermal resistance of the utilized grout has a significant effect on the reduction of core temperature-time development and also temperature distribution in the grout, which slows down the radial expansion of the grout.

  • Using bar-bundles with different configurations and the ribs on their surface strengthens the contact between grout and bar-bundle, which lets grout have more contribution to load bearing capacity of the columns: And, the point contact between them reduces the thermal conduction in the steel core.

  • Utilizing high-strength steel for bar-bundle allows the design of slender columns with high load-bearing capacity and low induced imperfection by the distributed residual stress inside steel elements.

  • The tube could keep the confinement of the grout throughout the fire tests and avoid any explosion failure or local buckling because of internal vapor pressure.

  • The developed numerical models can reasonably estimate the fire performance of the proposed columns, which can be a reliable replacement for costly large-scale fire tests.