1 Introduction

Sandwich panels are frequently used for buildings, for they are lightweight and durable, and allow for fast (so efficient) construction. Their fire resistance must be known to ensure a fire cannot easily spread between compartments or buildings. Also, panel failures influence the fire itself, due to changing oxygen supply, a phenomenon that increasingly receives attention, see e.g. [1]. Standards exist to verify panel fire resistance. For example, ISO 13784-1:2014 [2] specifies the tests that are needed to evaluate the fire performance of sandwich panels. And the European EN 13501-1:2019 [3] and EN 13823:2020 [4] are used to determine the fire performance of building components. However, these design standards do not cover all relevant aspects: An intermediate scale test was conducted for sandwich panels based on EN 13823, and data showed an unacceptably low level of repeatability [5]. And  two types of fire tests for sandwich panels were conducted, an ISO 13784-1 standard test and a modified test [6]. Results showed that slight modifications to the standard test could lead to significantly different outcomes. As such, it can be questioned whether standard tests are good enough to assess all design scenarios safely. This is partly solved by the application of non-standard tests, however, these are expensive, especially when full-scale. Besides, a different test is needed for each variation of parameters. Therefore, simulations are increasingly used, since they are economical and allow for a wide variety of parameters to be studied. They may also provide insights not accessible by tests (e.g. related to internal stresses and strains).

Besides the general setup of a sandwich panel system, with its panels and frame, details in a sandwich panel system may influence the structural behaviour under fire. This is particularly true for connections, their behaviour even leading to progressive collapse, as shown by [7]. Other researchers, [8], tested the shear resistance of sandwich panel screw connections at elevated temperatures. Self-tapping screws were tested, which failed by the bearing of the sandwich panel faces. Paper [9] investigated single-shear experiments of screw connections at ambient and elevated temperatures. The failure modes differed as a function of temperature and screw type.

As mentioned above, simulations may help in better understanding thermal and structural panel behaviour. Not being exhaustive, commercial software seen often in research includes [10], frequently used for non-linear problems in the field of applied mechanics. In addition, Opensees is shown to be useful for simulating structures in fire [11, 12], while Comsol is recognised for handling multidisciplinary models [13]. A typical fire-structure coupled simulation first starts with a Heat Transfer (HT) analysis, which predicts the temperature distribution within the structure in time. Related thermal boundary conditions are obtained by using a standard fire curve or a fire dynamics simulation. In the latter case, the Adiabatic Surface Temperature (AST) concept [14] can be used to transfer the temperatures from the fire simulation to the HT analysis. Subsequently, the temperature distribution in time is transferred to a Structural Response (SR) analysis to predict mechanical behaviour. Following these procedures and using a fire dynamics simulation, a so-called One-Way Coupled (OWC) fire-structure simulation is carried out. Additionally, structural behaviour (e.g., a panel failure causing an opening) may influence the development of the fire. The structural behaviour can be coupled back to the fire dynamics simulation, which is defined as a Two-Way Coupled (TWC) simulation, demonstrated by [1, 15], for sandwich panels at one side of a compartment. In both OWC and TWC simulations, (screw and bolted) connections are often simplified as (non-linear) spring elements or rigid connections, since it is computationally expensive to model a global-scale structural system including small-scale connections.

The simplification by using spring elements means that certain non-linearities, temperature dependencies, path dependency in the case of plasticity, and various other phenomena are not considered, which in turn can result in unrealistic system modelling and incorrect failure predictions. For instance, the behaviour and failure modes of screw connections may change when temperatures increase, such as from bearing to shear, see [16, 17]. Similar findings affect sandwich panel systems, as can be read in [8]. To solve these issues, an improvement is the use of “submodelling”, which was originally developed to model a region of a finite element model by a refined mesh for detailed analysis, e.g. as demonstrated by [18]. However, submodelling is a one-directional method, meaning that the behaviour from the (small-scale) refined model cannot be fed back to the (global-scale) original model. In the context of this paper, recently a two-scale model has been developed by [19, 20], which allows for a two-directional transfer of information between the small-scale and global-scale models. An application to schematically illustrate the two-scale model is shown in Figure 1. At (a), it shows the global-scale structure, as a set of sandwich panels that are connected to a supporting horizontal L-section by screws, i.e. small-scale components, as shown in Figure 1b. As mentioned earlier, such screw connections may be simplified as spring elements in a finite element model, see Figure 1c. Differently, the two-scale model consists of (i) a global-scale model, with a spring element for each connection, Figure 1c, which accounts for the overall behaviour of the structure. Secondly, it has (ii) for each connection a small-scale model, which accounts for the local and detailed behaviour of the screw connection (Figure 1d). This definition of the two-scale model is used throughout this paper. The simulation is divided into several load steps. In each load step, first the global-scale model is used, and afterwards provides thermal and mechanical boundary conditions to the small-scale model, which subsequently is used to predict the connection stiffness in each direction to be used for the spring element. In the two-scale model [19, 20] Abaqus specific submodelling [10] is used to provide the boundary conditions for the small-scale models, but similar functionality is available in most other finite element programs.

Figure 1
figure 1

Sandwich panel system, test and simulation models at different scales

Full size image

Simulations have been demonstrated to work for specific applications, either on the global scale (a fire on a simple panel) or on the small scale (a temperature load on a single screw connection), often loaded by a standard fire curve. In this paper, the quality of simulations for combined situations is investigated, i.e. a furnace fire on a set of panels including details and connections. First, two full-scale sandwich panel fire resistance tests are introduced, including data on the temperature distribution for both tests, and the panel deflection for the first test, all in Sect. 2.1. Then the finite element models as used for the fire-structure simulations are presented in Sect. 2.2, including the two-scale model in Sect. 2.3. Initial results from basic simulations are presented in Sect. 3. Predictions for the mechanical behaviour of the first test show to be not satisfactory, and further investigations are carried out by means of a parameter study in Sect. 4. Similarly, the second test is further studied in Sect. 5. Finally, Sect. 6 presents conclusions and future work.

2 Fire Resistance Tests, Finite Element Models, Two-Scale Model

2.1 Fire Resistance Tests

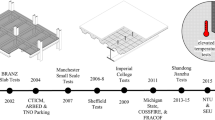
Two sandwich panel fire resistance tests are presented here, carried out in the past. They have been selected based on (a) the availability of test reports, and involved laboratory and research staff for discussions; (b) the availability of furnace and test setup details, and measurement data for both thermal and mechanical aspects; (c) their relevance for sandwich panels and connections; (d) their applicability for simulation models, and specifically the two-scale model; (e) their variety and increasing complexity of failure modes, in this case panel deformations (only) for Test 1 and connection failures for Test 2. Both tests use the same type of sandwich panel: The panel consists of a 0.6 mm thick steel face all around a 100 mm core of mineral wool. An overview of the tests is shown in Figure 2.

Figure 2
figure 2

Top row: test 1, sandwich panel façade test, bottom row: test 2, stud bolts test

Full size image

Test 1 was a full-scale sandwich panel façade test, shown in the top row of Figure 2, and reported in detail in [21]. Four sandwich panels were used, each having dimensions of 5000 × 1000 × 100 mm. These panels were fixed to a Rectangular Hollow Section (RHS) frame by 16 screws to each horizontal section and 11 screws to each vertical section, see Figure 2. Self-drilling screws of type “JT3-D-6 H-5.5/6.3 × 147” were used, with a major diameter of 6.3 mm and 147 mm in length. The thickness of the RHS webs and flanges was 5 mm. The complete frame with four panels was positioned in the furnace opening. The internal side of the sandwich panels was exposed to the furnace heat following a standard ISO-834 fire curve, and temperatures and displacements on the external (fire unexposed) side were measured by thermocouples and displacement sensors, shown as orange and green crosses in Figure 2. No failure was observed during and after the 90 min of the test.

Test 2 is shown in the bottom row of Figure 2, and full details are found in [22]. A single 600 × 600 × 100 mm sandwich panel was used in this test. For its positioning, a steel L-section was clamped to the furnace ceiling via three M10 stud bolts, and the sandwich panel was fixed to the L-section by three self-tapping screws of type “JZ3-6.3 × 115-E16”, having a major diameter equal to 6.3 mm. The thickness of the L-section web and flange was 8 mm. A steel C-section was fixed at the bottom of the sandwich panel with numerous screws, carrying stacked steel weights to provide a downwards-directed load of 1 kN. The sandwich panel was heated in the furnace following an ISO-834 fire curve. Three thermocouples were embedded inside the insulation layer along the top (the orange crosses in Figure 2), and no displacement sensors were used. Test 2 was meant to verify the resistance of the stub bolts, however, following the report, it failed after 50 min for other reasons. Namely, at that moment, the loading weights fell (they were loosely stacked within the C-section), due to failure of the panel. Photos in the report show the panel after the test, being completely detached from the L-section, and another photo, not part of the report but shown as an inset in Figure 7, shows strong vertical bearing (even rupture towards the face edge) of the screw holes in the panel face.

2.2 Finite Element Models

The fire-structure simulations in this paper utilise finite element models developed in the commercial finite element program Abaqus [10]. For the HT analyses, a standard ISO-834 fire curve is applied as temperatures on the fire-exposed surfaces of the sandwich panels. To verify this standard fire curve approach, in Sect. 4 also a Computational Fluid Dynamics (CFD) simulation of the furnace is tested, making use of the program Fire Dynamics Simulator (FDS) [23]. Further details will be given there.

The setup of the finite element models follows the setup of the tests in Sect. 2.1, where less relevant components (e.g. the furnace and frame fixations around the RHS frame in Test 1; steel weights, C-section, and the insulation between L-section and sandwich panel in Test 2) are not modelled (the C-section and weights are modelled as a load, this will be shown later). Sandwich panel faces and (frame) sections are modelled by shell elements, and the sandwich panel insulation core is made by volume elements, as detailed in Table 1.

Table 1 Finite Element Models: Parts, Elements, Materials, and Solver
Full size table

Figure 3 (on the left and in the middle) shows the finite element models, where orange lines are locations where boundary conditions act in the HT model to impose the ISO 834 fire curve, and the green lines indicate the positions where boundary conditions are positioned in the SR model (constraints or loads). Note that for Test 2 the L-section is clamped to the furnace ceiling, but not the panel itself. Conductivity and mechanical contact between parts are handled by Abaqus proprietary “interaction properties”, indicated by the bold red lines in Figure 3. Material properties are given on the right of the figure. Steel temperature-dependent thermal and mechanical properties are taken from [24], where engineering stress–strain relations (\(\sigma _{eng},\varepsilon _{eng}\)) in the design standard need to be converted into true stress–strain (\(\sigma _{true},\varepsilon _{true}\)) values. The resulting stress–strain curves are shown in Figure 3 at the bottom right. For the mineral wool insulation, [25] proposed a temperature-dependent conductivity curve for densities between 120 to 140 kg/m\(^3\), and [26] found that the conductivity of mineral wool (theirs having a density of 30 kg/m\(^3\)) changes rapidly when the temperature exceeds 600°C. The density of the mineral wool in the tests was 120 kg/m\(^3\) and based on the previous information, a relation is developed as indicated by the dotted curve in Figure 3 (top right). The mechanical behaviour of the mineral wool is assumed to be linear elastic with Young’s modulus equal to 30 N/mm\(^2\). For the screw connections, initially spring finite elements are used, their (bi-linear) spring stiffness based on table 3 in [27] and Figure 10 in [15].

Figure 3
figure 3

Finite element models (left, middle) and material properties (right)

Full size image

2.3 Two-Scale Model

The two-scale model as used later in this paper, for indicated simulations, is presented in Figure 4. A typical example of the controlling script is provided in Appendix A, and all code and scripts of all simulations in this paper are available open-source at [28]. In this paper, in general the input of temperature loads to the two-scale model is arranged by a (standard) fire curve. Optionally, also a fire simulation can be used, as shown in Figure 4, on the complete left. In this latter case, the thermal data from FDS (per CSV file) is converted into a Python script (py-file) that can be read by Abaqus. This is accomplished through the use of the in-house developed ReWriteAST2py script, which is similar to the one used in [1] and [15].

Figure 4
figure 4

Overview of the two-scale model (in the large box right), optionally linked to an FDS fire simulation (complete left)

Full size image

In the next step, the Two-scale model controlling script initiates the finite element models and calls Abaqus to execute the models, in a loop in a clockwise direction. The first step in the loop is carried out by the Update global-scale HT model script, to initiate or update the HT model. This involves loading a basic HT script, appending thermal load data, and providing user-defined step and restart information. Hereafter, the completed HT model is submitted to Abaqus for analysis.

Once HT results are available, the Two-scale model controlling script calls the Update global-scale SR model script, which loads a basic global-scale SR script, appends step and restart information, updates the stiffness of all spring elements that model the connections, and reads in the HT results. Abaqus is called to solve the model, and hereafter, the TempCalculationpy script is used to distil for each spring element the temperature vs. time data, to be used for the small-scale models.

For each connection, a small-scale model exists, which is only simulated by an SR analysis (no HT), since a connection is only a very small part of the global-scale structure. As such, the averaged temperature at the spring element ends is used for the complete geometry of the small-scale model. The Update small-scale SR model script updates the small-scale model by loading a basic small-scale SR script, appending step and restart information, and updating the boundary conditions in time (from the global-scale SR model, using submodelling).

Once the analyses of all small-scale models are complete, the Two-scale model controlling script activates another script, OutputRequestpy. This script analyses the contact forces and nodal displacements for the last two increments in the load step, and by this predicts the spring stiffness to be used in the global-scale model for the next load step.

Using the two-scale model as explained above, its setup for Test 2 is shown in Figure 5. On the left, the global-scale model is given, with for one screw connection on the left an overlaid plot of the small-scale model. On the right, further details are shown for the small-scale model at the top, and for the global-scale model at the bottom.

Figure 5
figure 5

Setup of the two-scale model for Test 2

Full size image

In the small-scale (screw connection) model, the panel face and L-section are modelled by volume elements C3D8R, with a refined mesh near the drilling hole to accommodate larger stress gradients. The edges of the small-scale parts of the panel face and L-section, shown in green, have boundary conditions following the submodelling approach. The strength properties of the screws at ambient temperature are taken from table 3.1 in EN 1993-1-8 [29], and temperature-dependent reduction factors of the material properties follow EN 1993-1-2 [24]. Further note that the proprietary Abaqus ductile damage model is used, with settings as shown in the figure, to indicate the failure of plates and screws. The contact between the L-section drilling holes and the screw circumferences is modelled by Abaqus’ “threaded connection interaction”, which has been shown to simulate reasonably well the behaviour of the normally threaded contact surfaces, see [20]. Other potential contact pairs, e.g. screw head to panel face and panel face to L-section, are modelled using frictionless contact.

3 Simulation Results

In this section, results are presented for basic fire-structure simulations, which involve a fire curve (no FDS, so also no OWC or TWC), and a global-scale model (no two-scale model). As the results are not immediately satisfactory, parameter studies for Test 1 and two-scale model simulations for Test 2 are presented in Sect. 4 and 5 respectively.

3.1 HT Analyses

Figure 6 shows a comparison of the results of the HT analyses and the tests. Temperatures on the fire unexposed side (for Test 1) and the insulation core (for Test 2) are predicted most of the time within the temperature envelopes of the tests. Envelopes are used, since temperatures were measured at several locations, see Figure 2, whereas the simulations did not show significant temperature differences over these locations, because a uniform distributed standard fire curve was applied. The small differences for Test 1 may be due to approximated material properties for the insulation.

Figure 6
figure 6

HT analyses vs. tests

Full size image

For Test 2, temperature measurements were taken at the top, as shown in Figure 2. The small difference at the end of the test can be attributed first to the opening of the gap between the panel and the L-section, then to the sandwich panel that fell off and as such exposed the temperature gauges.

In conclusion, the HT analyses show good agreement with both tests for the structure temperatures measured. However, as a temperature curve is used for the simulations, instead of a fire simulation of the furnace, temperatures in the simulations are relatively equally distributed over the area of the panels, whereas in the test these temperatures fluctuated due to the fire dynamics.

3.2 SR Analyses

Using the setup of the SR analyses as given in Sect. 2.2, Figure 7a on the complete left shows the deflections of Test 1 and its simulation after 5500 s, both showing the panel bent towards the fire due to thermal expansion. In the graph in the middle, the centre out-of-plane deflection of the sandwich panel versus time is plotted black, whereas the simulation prediction is in red. The displacement in the simulation agrees well with the test for the first 100 s (not visible due to the scale of the horizontal axis), but hereafter the test first shows irregular behaviour (possibly transient), followed by limited out-of-plane deflections as compared to the simulation. Only in the final stage, after about 3000 s, displacements of the test and the simulation agree again. Note that the test did not fail, and also the simulation does not indicate any failure. The significant differences in displacements between the simulation and the test will be studied further in Sect. 4.

Figure 7
figure 7

SR analyses vs. tests

Full size image

Test 2 was not designed to include measurements concerning mechanical behaviour. Therefore, Figure 7b presents a graph for the simulation only, showing the vertical displacement at the load application point versus time. At the beginning (non-linear) vertical displacements are caused by thermal expansion and changing material properties due to increasing temperatures. Once the temperatures stabilise, so do the vertical displacements of the panel. Whereas the test fails, the simulation does not show any failure due to its basic level of modelling. Therefore it is stopped at 3600 s, after failure in the test (note that it has no use to continue the simulation, as temperatures do not rise further). For this reason, more advanced simulations, including a two-scale model, are studied in Sect. 5.

4 Test 1: Parameter Study

Whereas for Test 1 the basic HT simulation results agree reasonably well with the tests, the basic SR simulation needs improvements. To investigate this further, here several parameters are studied, and individually reported in the dedicated Sects. 4.1 to 4.5.

4.1 FDS Furnace Model instead of Fire Curve

All simulations in this paper see the temperature load of the tests modelled by the ISO-834 fire curve. As a result, for Test 1 the temperatures as shown by the simulation are evenly distributed over the panel’s fire-exposed side, which is different for the test in the furnace. Contrarily, in this subsection, an OWC fire-structure simulation of the furnace is carried out, so using FDS [23] to obtain the fire load, Figure 8a. Results are shown in Figure 8b. The measured temperatures in the furnace of the test are shown by the orange envelope in Figure 8a, and these temperatures meet the requirements of the ISO 834 standard (black curves). The FDS simulation of the furnace yields the temperatures indicated by the green envelope, which fit nicely within the experimental one. However, FDS shows less variation in temperatures (a smaller envelope) compared to the test, probably due to its more smoothly controlled burners. Figure 8b shows the panel out-of-plane deflection versus time for the test (dotted line), the HT analysis using the standard fire curve (orange), and the HT analysis after FDS (green curve). It is positive that the test furnace is modelled well with FDS, and a standard fire curve can be used with confidence in the simulations. However, it is unlikely that the use of a fire curve, instead of a complete FDS model of the furnace, causes the significant differences in out-of-plane displacement between the basic fire-structure simulation and Test 1.

Figure 8
figure 8

Comparison of simulations with FDS or fire curve

Full size image

4.2 Thermal Expansion Coefficient

The thermal expansion of the panel steel faces, which may be partly or fully restricted during the test, influences the panel’s out-of-plane behaviour. It is therefore relevant that standards EN 1993-1-2 and BS 5950–8 [24, 30], and ASCE Manual and Report No. 78 [31] advise differently on values for the steel’s thermal expansion coefficient as a function of temperature, as shown in Figure 9a.

Figure 9
figure 9

(a) Steel’s thermal expansion coefficient by several standards, (b) Simulations using the different advised thermal expansion coefficients

Full size image

In Test 1, the out-of-plane displacements of the fire unexposed face were measured at different locations, and here the upper bound (centre point) is shown as the black curve in Figure 9b. The basic simulation in Sect. 3 (using EN 1993-1-2 steel properties) is repeated with the thermal expansion coefficient as advised by the other standards. Figure 9b shows that both the ASCE Manual and Report No. 78 and BS 5950-8 show similar behaviour as EN 1993-1-2, all correctly predicting the maximum out-of-plane deflection (in the centre of the plate, at 5500 s). Similar to the previous section, assumptions on the steel’s thermal expansion coefficient values cannot be responsible for the out-of-plane displacement differences between the simulation and the test.

4.3 Tongue and Groove Connection Modelling

The four sandwich panels in Test 1 are longitudinally connected by tongue and groove connections, see an opened connection in Figure 10 on the left. During the test, the (thermally induced) deformations of the panels may lead to these connections being stressed, coming loose, or even a vertical gap may occur, which in turn changes the mechanical boundary conditions and thus the structural behaviour. In the basic simulations of Sect. 3, the longitudinal connections are modelled with a “C” shape for the groove, see Figure 10, for mesh simplicity and conformity. The connection at both the left and right side has a steel face around the full connection geometry, and penetration is prevented by contact definitions, as explained in Sect. 2.2. In this section, a more realistic “E” shape of the groove is studied.

Figure 10
figure 10

Comparison of simulations with different shapes of the tongue and groove connection

Full size image

In the middle of Figure 10, the temperatures predicted by the HT analyses, at the centre of the panel, are plotted, using the left vertical axis. No significant differences exist for the “C” and “E” shaped connections, however, locally, some temperature differences can be seen near the tongue and groove, as shown in the figure on the complete right. Concerning the SR analyses (black curves, using the right vertical axis), the “E” connection panel shows gradually smaller out-of-plane displacements from 1200s onwards, compared to the “C” shape used in Sect. 3. Though the “E” shape of the groove is somewhat more realistic than “C”, it shows less resemblance with the test (dotted line). This should likely be attributed to the fact that certain details in the connection are not modelled, like the exact lip geometry, the air seal, the intumescent strip, etc. This lack of modelling may offset the “C” model to seemingly correct predictions, and the “E” to too low predictions. In any case, this section makes clear that the modelling of the tongue and groove connection is important, however, it does not explain the large differences between the simulation and the test for out-of-plane displacements.

4.4 Screw Connection Stiffness

In the basic simulations of Sect. 3, spring finite elements are used for the screw connections, their bi-linear stiffness based on the “component method”, table 3 in [27] and Figure 10 in [15]. However, realistic spring stiffness may differ, and therefore here a parameter study is carried out, see Figure 11.

Figure 11
figure 11

SR analyses for different types of stiffness for the spring finite elements

Full size image

Besides the original bi-linear setup, this comprises two values for linear stiffness, and a rigid constraint, i.e. fixation. For the first 200 s in the test, temperatures increase quickly, and the resulting thermal expansion of the fire-exposed face causes rapid out-of-plane deformations of the panel. Some differences exist for the out-of-plane deflections (plotted against the left vertical axis) for the different stiffness definitions, however, these differences are obscured in the graph due to the scale used. Starting from “Stage 1”, temperatures no longer rise significantly, but Young’s modulus of the steel fire exposed face reduces strongly as indicated by the black line, plotted against the right vertical axis. This reducing stiffness overrules thermal expansion and so the panels bend back a little, between “Stage 1” and “Stage 2”. Finally, after “Stage 2”, Young’s modulus only decreases marginally, thermal expansion takes prevalence, and again increases the out-of-plane displacement. Although the stiffness of the connection influences the overall structural behaviour, clearly it is not the cause of the large differences in out-of-plane displacements between the simulation and the test.

4.5 Adhesive Layer Modelling

The final aspect investigated here is the behaviour of the adhesive layer between the panel faces and the insulation core. Namely, initially the out-of-plane deflection of the panel must be caused by the larger expansion of the fire-exposed face (compared to the unexposed face), but only if this expansion can be transferred to the panel via the adhesive layer (later out-of-plane deflection is believed to be also a function of temperature gradients in the panels’ thickness direction of the sides, i.e. the tongue and groove connections). As such, adhesive failure may affect structural behaviour, as found by [32]. Therefore, in this section an adhesive layer is modelled in addition to the simulation of Sect. 3.2, as shown in Figure 12 on the left.

Figure 12
figure 12

Modelling an adhesive layer, and related static and dynamic SR simulations

Full size image

The layer thickness is 5 mm for modelling reasons, e.g. to maintain proper element aspect ratios. Material properties of polyurethane as found in [33] are used: The adhesive is assumed to behave as linear elastic with Young’s modulus as given in Figure 12. As Young’s modulus of the adhesive is larger than that of the modulus of the mineral wool, the simulation with the adhesive layer (green curve) shows stiffer behaviour compared to the basic simulation (orange curve) during the complete test. However, the melting point (not modelled) of the adhesive layer is relatively low at approximately 60°C, and so its properties diminish soon after the start of the test. As a consequence, the fire-exposed side of the face may (partly) detach from the insulation core, which could explain the subsequent dynamic phenomena, indicated in Figure 7a. A third simulation is therefore carried out, without a connection between the thin-walled face and the insulation at the fire-exposed side. This effectively means a face exposed to the fire concerning thermal behaviour, but without structural effects. Since a static solver may have issues with the (partly) loose face (i.e. due to singularities) or the thin face structural instability modes (transient phenomena due to the lack of elastic support by the adhesive and insulation), an (implicit) dynamic solver is used. Figure 12 shows by the red curve that of all previous varied parameters, this last simulation is the only one that clearly reduces the out-of-plane displacements, at the location in the graph that matters most, and by leaving the final out-of-plane displacements unchanged. Therefore, it is believed that the adhesive behaviour and the subsequent fire-exposed face behaviour, with structural instabilities and related interactions with the adhesive, are at least contributing factors in the difference in out-of-plane deformations between the simulation and the test.

5 Test 2: Two-Scale Model Application

For Test 2 in Sect. 3, in the basic simulation the screw connections are simplified by spring elements. This may be a cause for the differences between the test and simulation, since the test failed by the vertical bearing of the face at the screw connections. Therefore, in preparation for using a two-scale model, first the original HT analysis is studied in more detail concerning the screw connections, in Sect. 5.1. Then the connections are studied for their mechanical behaviour in 5.2 by using submodelling. Finally, following the setup explained in Sect. 2.3, SR analyses are carried out using a two-scale model, as presented in Sect. 5.3.

5.1 HT Analysis of Connections

Figure 6b shows that for the test measurements on the panel, HT analysis predictions are accurate up to 2300 s, at which point possibly a gap occurred between the panel and L-section, and up to 3000 s, when failure was observed. In the test no measurements were taken at the connections, however, with some confidence the HT analysis can provide this information, see Figure 13. The temperature contour plot shows the x − y-plane cross-section of the sandwich panel at the end of the simulation. The lower part is heated uniformly, while the top remains at a lower temperature due to its connection to the ceiling, which is assumed to remain at ambient temperature. The start and end nodes of the springs are indicated with red dots. For the middle spring element they can be seen both, whereas for the right spring only the end node is visible. Related to these locations, the panel face close to the L-section is somewhat isolated against the heat by the L-section, as seen by its lower temperatures compared to the face on the opposite side. Possibly this is due to less radiation and conduction thanks to the relatively cool L-section, as connected to the ceiling. Section 2.3 explains that the thermal boundary conditions for the small-scale model are taken from the average temperature of the spring start and end nodes, here given by the green curve. As can be seen, this average temperature and the temperatures of the panel face and L-section are all very close, so this approach seems to be valid. The HT analysis predicts the average temperature of the screw to be 730°C when the gap occurs (at 2300 s) and for failure at 3000 s, a temperature of the screw connection equal to 780°C is predicted. This information is further used in Sect. 5.3.

Figure 13
figure 13

HT analysis, results near the connections

Full size image

5.2 SR Analysis of Connections, including Submodelling

The basic SR simulation uses three linear elastic spring elements, based on Linear stiffness-1 as presented in Figure 11 and recommended by table 3 in [27]. The shear force vs. shear deformation behaviour of spring elements 1 and 2 (located left and in the middle) is illustrated in Figure 14. Spring element 3 (right) behaves the same as element 1 thanks to symmetry, and absolute shear deformations are plotted for comparison purposes. The figure on the left shows that the horizontal shear deformation (in z-direction) rapidly increases at the beginning of the fire due to thermal expansion of the panel (faces) and less expansion of the L-section, since the latter has more mass and is connected to the ceiling. Then horizontal shear deformation reduces. This is likely because the temperature difference between the panel face and the L-section reduces, and also thermal-induced plasticity and related relaxation may play a role. Concerning vertical shear deformations (in y-direction), Figure 14b shows that shear deformations of all spring elements are small and remain relatively constant during the simulation. Naturally, thermal expansion cannot cause vertical shear deformations, as the panel is only mounted at the top. Initially, all three springs show elastic downwards shear deformations due to the load, then the left and right springs (spring element 1, orange) see their shear deformations reduced, probably due to panel relaxation in the vertical direction, which is possible because due to horizontal expansion the panel left and right corners are not restrained by the L-section anymore, see the contour plot. As temperatures continue to increase, Young’s modulus reduces, which helps to reduce the differences between the springs further.

Figure 14
figure 14

SR analysis, vertical (a) and horizontal (b) shear force vs. shear deflection behaviour of spring elements 1 and 2 in the basic global-scale simulation

Full size image

Most importantly, a comparison between Figure 14a and b indicates that the maximal vertical shear deformation, related to the 1 kN load, is considerably smaller than the horizontal shear deformation, due to thermal expansion. However, all evidence for test 2 points to a failure by the vertical bearing of the screw connections, and so large shear deformations in the y-direction are expected. To enforce failure a load of 2 kN instead of 1 kN is tried, as shown by the dotted lines in Figure 14b. As a result, vertical shear deformations are about twice as high, which makes sense, however, these shear deformations are still far lower than the horizontal shear deformations. This does not correspond with the photographic evidence, see Sect. 2.1, which suggests horizontal bearing, without any vertical bearing visible.

To improve the understanding of the behaviour of the screw connections, now “classic” submodelling is tried. Practically, this involves the application of the two-scale model as presented in section 2.3, but differently, first the global-scale model is used for the full simulation time, then the small-scale model is run for the same period, and so no interaction between the two scales takes place. Results for the (small-scale) submodel of screw connection 1 (which is located left, similar to right) for shear are shown in Figure 15. The shear deformation of the screw connection in z-direction is taken as the difference between the displacements of the two drilling holes, in the panel face and L-section respectively. For the shear force (displayed along the right vertical axis), the contact forces between the screw shank and L-section are used (their surfaces shown by red lines in Figure 5). Tangent stiffness, presented in the figure on the right, is calculated by finite differences between each two increments. The shear force and deformation vs. time curves differ significantly from those of the original (global-scale) model as shown in Figure 14, due to multiple non-linearities. Specifically, temperature-dependent material properties, plasticity, and changes in boundary conditions are all simultaneously involved. As indicated in Figure 15, four distinct stages can be observed during the test. During stages (a) and (b), shear related z-directional deformation of the connection increases due to the thermal expansion of the panel face, more than the expansion of the L-section. However, the contact force increases in stage (a), while it decreases due to steel weakening in stage (b), resulting in a negative tangent stiffness, see Figure 15b. Stage (c) relates to the reduction of deformations, wherein the contact force of the small-scale model decreases and eventually shows negative values. Finally, screw connection behaviour stabilises in stage (d), probably because the linear spring element in the global-scale model remains stiff (whereas in the small-scale model this stiffness is certainly predicted lower due to the non-linearities incorporated).

Figure 15
figure 15

Shear displacement and force vs. time for screw connection 1 by submodelling

Full size image

The behaviour of the screw connection as found by submodelling is quite different from a linear spring (as used in the original global-scale model), demonstrated clearly in Figure 15. This necessitates the use of the two-scale model, elaborated in the next two subsections. First, it is tried to predict and understand the failure of the panel by a simulation with an increasing prescribed displacement (Sect. 5.3), then the test is simulated as realistically as possible, with the original load and the two-scale model, in Sect. 5.4.

5.3 Two-Scale Model: Predicting the Failure Load of the Test

For predicting the failure load of Test 2, here the two-scale model is used as presented in Sect. 2.3. However, to be able to study the ultimate load of the panel, displacement control is used to load the panel and screw connections, and therefore thermal expansion of the steel is switched off. To avoid arbitrary combinations between the prescribed displacement values and temperature curve values, the simulation is carried out for several fixed temperatures.

The total simulation time of 3600 s is divided into 12 load steps, which implies that the spring stiffness in the global-scale model is updated every 300 s. Automated time stepping is used for the increments, both for the global- and small-scale models. However, to avoid the case where only 1 or 2 increments are needed for a load step, and consequently, the spring stiffness cannot be predicted by finite differences well enough at the end of the load step, the small-scale model is set to ensure that at least five increments end at equally distributed intervals along the load step. Then connection stiffness is calculated based on the finite differences over the last (fifth) interval.

Results of the simulations are shown in Figure 16, for fixed temperatures of 400°C, 600°C, 700°C, and 900°C, respectively. On the left of Figure 16, the vertical reaction force is shown as a function of the vertical prescribed displacement. In the test, a vertical load of 1 kN was applied, and the information in Figure 16a indicates that large vertical displacements for this load are expected at temperatures between 700°C and 900°C. In Figure 13, the simulation shows that at the time the test fails, the temperature of the screws equals 780°C, which corresponds with the temperature range predicted here for large vertical displacements of the panel.

Figure 16
figure 16

(a) Reaction force vs. prescribed displacement of the panel; (b) Vertical shear force vs. shear deformation for small-scale model and global-scale springs

Full size image

Figure 16b shows the vertical shear load vs. shear deformation of the screw connections. Dotted lines are used for the global-scale model’s spring representing screw connection 1 (left spring, equals right spring thanks to symmetry). Continuous lines are used for the small-scale model. For the global-scale model, the irregular behaviour comes from the update of the spring stiffness (by the small-scale model) after each load step. As such, this is not the case for the small-scale model, which shows smooth behaviour. As the screw shear deformation values almost equal the panel’s prescribed displacement, it is clear that the vertical displacements of the panel (Figure 16a) are caused by the shear deformation of the screws. On the complete right of figure 16, the plastic strain in the face is shown for the small-scale model, the screw is not visualised for clarity: Vertical bearing is more severe for higher temperatures. In conclusion, the two-scale model predicts large vertical displacements of the panel and vertical bearing of the screw holes in the panel face, all somewhere between 700°C and 900°C. This corresponds with the temperature of the screws in the test at the time of failure, being predicted as 780°C.

5.4 Two-Scale Model: Application for Test 2

The displacement-controlled simulation above shows that the two-scale model can give usable failure predictions for the screw connection, and so in this section, the two-scale model is implemented for the load-controlled Test 2 (stud bolts test). The fire-structure model setup is the same as used at the end of Sect. 5.2, using submodelling, however, now the three springs in the global-scale model are updated every 300 s by information from three small-scale models. Regarded differently, here the same simulation is carried as in the previous section, except that now the 1 kN load is applied, instead of a prescribed displacement, and thermal expansion is switched on. The resulting vertical displacement vs. time graph (not shown) is very similar to the original model (with three springs only), see Figure 7. Note that the vertical displacements in Figure 7 (max. 6 mm) are to a large extent due to thermal expansion, as indicated by the far smaller displacements (max. about 2 mm) in Figure 16a. Different from the basic simulation, the two-scale model indicates failure at 1820s, due to failure of the small-scale model of screw connection 1, by too high plastic strains, their character shown in Figure 17.

Figure 17
figure 17

Small-scale model for screw connection 1, Test 2. On the left contour plot of plastic strains; on the right plastic strains along the circumference of the drilling hole in the face

Full size image

The plastic strains for screw connections 1 (left, equals right due to symmetry) and 2 (middle) are shown in the centre and right of the figure. This by plotting the plastic strain along the circumference of the drilling hole in the face, at the element layer closest to the L-section. The negative z-direction is at 0°C, and the positive y-direction sits at 90°C, so the contour plot and circular strain plot look mirrored. For the left/right screw connections, plastics strains (orange, at 1820s) are the highest at around 30°C, which can be attributed to the combination of thermal expansion in the (horizontal) z-direction and the external load in the (vertical) y-direction. For the middle screw connection, at the symmetry plane, plasticity is only due to the vertical load, in y-direction, and indicates the start of vertical bearing. Comparing the results with submodelling (Sect. 5.2, indicated by the green curves, at 3600 s), plastic strains are predicted much higher for the two-scale model, stressing the importance of mutual feedback of global- and small-scale models.

In Sect. 5.3, the spring stiffness changed rather smoothly in the global-scale model, see Figure 16 in the middle. However, the spring stiffness in the current simulation (two-scale, Test 2) fluctuates strongly, as shown in [34]. This may be caused by two issues. First of all, the screw connections are not only loaded, but also unloaded due to the steel becoming weaker for higher temperatures. This could imply fluctuations if the small-scale model would not handle unloading properly. However, Appendix B proves that the small-scale model handles loading and unloading rather well. Secondly, the spring stiffness in the global-scale model is determined by the finite differences between load and displacement for the small-scale model for the last increment. If these finite differences are extremely small for directions where no action takes place (e.g. the horizontal z-direction for the middle screw connection) then numerical noise and alternating load steps with and without action may cause strong fluctuations. Although this is not an ideal situation, it is reassuring to realise that as soon as displacements resurface above the noise floor, naturally relevant stiffness values are predicted again.

In summary, the two-scale model indicates the vertical bearing of the screw connections, following the reported failure of the test. However, this vertical bearing is related to even more severe yielding in horizontal direction, due to thermal expansion, which was not visible (but present) in the test. To determine the panel failure due to the vertical load, a prescribed displacement was needed at the load application.

6 Conclusions and Future Work

Two full-scale fire resistance tests have been presented. The first test was a sandwich panel façade test, in which four sandwich panels, coupled with longitudinal tongue and groove connections, and screw connected to a frame, were subject to a furnace fire on a single side of the panels. Out-of-plane deflections were recorded, but the structure did not fail in the test. The second test involved a stud bolts test, where one panel was loaded vertically, fixed with screws to an L-section, and this section bolted to the furnace ceiling. After heating the complete panel from all sides, this second test very likely failed by the vertical bearing of the screw holes in the panel faces.

To investigate the quality of fire-structure simulations for these tests, first basic simulations have been carried out. In general, the heat transfer analyses agree well with the tests: For Test 1 the simulation is most of the time within, and only 20% of the time at most 20% outside the envelope, whereas Test 2 simulations are always within the measured range. The structural response analyses need investigation: For the first test, out-of-plane deflections were overestimated (100 mm predicted, 40 mm measured) at the beginning of the test. Therefore a parameter study was carried out, studying (a) the type of fire load (standard fire curve or CFD-FDS); (b) the (steel) thermal expansion coefficient; (c) the tongue and groove modelling; (d) the connection stiffness; and (e) the adhesive between face and insulation core. The study indicated that adhesive decomposition, resulting in face delamination and possibly related instabilities brought back the out-of-plane deflection to 70 mm. As such, this is at least partly the cause of the simulation flaws, and needs to be modelled more accurately. In addition, the study proved that for standard furnace tests, it is acceptable to use a standard fire curve instead of a fire dynamics simulation, both concerning thermal and mechanical predictions, as differences in out-of-plane displacement were within 10%.

For the second test, the basic simulation did not show failure, only horizontal bearing due to thermal expansion, whereas the test failed by vertical bearing. This was further investigated by first studying the temperatures of the screw connections, which showed to be at most 7% different from the surrounding components. Hereafter, the springs, representing the screw connections in the global-scale model, were replaced by small-scale models via submodelling. This showed significant connection non-linearities, and horizontal bearing due to thermal expansion, up to 0.7 mm. Therefore, the failure load of the panel was investigated by a prescribed displacement instead of a fixed load, which indicated the failure load of the test, between 0.8 kN and 2.0 kN, for 700 and 900 degrees Celcius respectively. Finally, a two-scale model was used, which indicated vertical bearing, besides still more significant horizontal bearing.

Future tests should include more simulation-relevant measurements, e.g. information on (local) buckling, adhesive delamination, and connection behaviour. Also, global-scale models need to include features specific to the structure to be simulated (i.e. adhesive layers, a dynamic solver), only known after tests and basic simulations, and connections may be decisive for global-scale behaviour, which can be incorporated by a two-scale model. Finally, the tests exhibited complex behaviour across different scales, and modifications and improvements of the simulations increased their fidelity. Therefore fire-structure simulations should always be verified with tests and compared with basic simulations, and modifications in the simulation models should be anticipated.