Thermal and Structural Response of Beam-end Shear Connections During a Large Compartment Fire Experiment

Abstract

The role of steel connections is essential in structural fire design and analysis for steel-framed composite structures. The current structural design provisions provide strength reduction factors of load-carrying members and their end-connection elements at elevated temperatures, based on small-scale experiments under uniform heating conditions. The realistic thermal and structural evolution in member connections, especially as part of full-scale floor assemblies exposed to a large compartment fire, has not been well characterized. A large compartment fire experiment was recently conducted on a 9.1 m by 6.1 m composite floor assembly as part of a two-story steel-framed building. The test assembly had a total of ten shear-tab (fin-plate) connections subjected to combined fire and mechanical loading. This paper presents the measured thermal response of these connections to fire and comparison with the corresponding Eurocode 3 predictions with two methods (1) incorporating the beam bottom flange temperature at midspan and (2) the section factor method. The results show that the Eurocode 3 methods conservatively predict the maximum temperature during heating and the cooling rate but overestimate the high-temperature strength of connections when estimated using the section factor method, showing that the Eurocode 3 simplified approaches are not meant to provide the details of the failure mode for connections. This study suggests that estimating the strength of connections using strength reduction factors may not guarantee a safe structural fire design. In addition, this paper estimated the total axial force (from slab and beam) at the composite connection via using the strain gauge measurements close to the column bases which were not exposed to fire. It suggests realistic axial load and rotational demand on the shear connection due to restraints to thermal elongation or contraction of supported members should be considered in future design guidance as should designing and detailing the connections for ductility to withstand the inelastic deformation demands during the heating and the cooling phases.

1 Introduction

Fire safety design of buildings consists of designing structural components and fire protection to meet the specified performance objectives. At a minimum, these performance objectives include maintaining structural integrity such that compartmentalization is not compromised [1]. However, quantifying the fire-induced effects on structures have been challenging due to lack of design tools validated against experimental data. Particularly, the thermal response of steel beam connections in a large compartment fire is one of these significant uncertainties [2,3,4]. A comprehensive review on previous research on steel connections is presented in Fischer et al. [3], and some of the literatures are briefly summarized as follows.

Component-level testing aims to examine one beam end connection as a single component, isolated from the rest of the frame within a small furnace at a steady-state heating. Examples of the research carried out for steel connections at the component level were Yu et al. [5], Hu and Engelhardt [6], Spyrou et al. [7, 8]. However, as pointed out by Fischer et al. [3], these tests were limited to constant temperatures (i.e., between 400°C to 700°C), ignoring the nuances of the time–temperature curve of varying fire scenarios, thermal gradient across the connection, and connection rotations during a realistic fire scenario.

An alternative of component tests is experimental investigations at a cruciform beam-to-column subassembly level. For instance, Lawson [9] tested eight connections used in a cruciform beam-to-column subassembly at elevated temperatures using the ISO 834 standard fire curve [10]. The test assembly, placed within the furnace, consisted of two stub beams (UB305×165×40, 1.28 m in length) connected to a column using end-plate or double-angle connections. This study concluded that the bolt temperatures were relatively lower than the beam lower flange temperatures. Similarly, Al-Jabri et al. [11] investigated twenty end-plate connections to three different beams (UB254×102×22, UB356×171×51, and UB610×229×101, all 1.9 m in length). These specimens were heated to failure while the applied load was maintained constant. The results showed that the concrete slab on top of the steel beam acted as a “heat sink” which reduced the beam top flange temperature by 20% to 30%. Those cruciform beam-to-column subassemblies tests with furnaces used steel beams shorter than 2.0 m, which underestimated the effect on the connections of thermal expansion and centenary action of moderate to long span beams used in a real building.

Structural performance of connections in fire can be also studied using a single beam test setup, i.e., one beam supported by two columns at the beam ends. Liu et al. [12] investigated the behavior of axially restrained steel beams with end-plate and double-angle connections. The beam specimens were UB178×102×19 shapes with the length of 2.0 m, placed in a 2.0 m by 3.4 m furnace. The ISO 834 fire curve was used to heat the specimens. This study addressed the importance of avoiding failure of the connections to maintain the development of the catenary action, which might prevent the beams from run-away deformation and failure at very high temperatures. Wang et al. [13] carried out another ten fire tests, with a similar test setup as Liu et al. [12], to study the behavior and robustness of various steel connections. The study showed that no connections failed when the beam specimen was in catenary action, and the web cleat connection provided the best performance compared with end-plate connections and fin plate connections. The research on the robustness of the steel connections by Liu et al. [12] and Wang et al. [13], was limited to a single steel beam without including a concrete slab which might provide additional stiffness as a composite beam, unlike more recent investigations by Pakala et al. [14], Fischer et al. [15], and Choe et al. [16, 17].

Pakala et al. [14] investigated two W12×30 beams (3.5 m in length) with double-angle connections. The furnace temperature was increased following the ASTM E119 [18] temperature–time curve. Superior ductility of the double angle connections was demonstrated in the tests. The beam-end rotations reached approximately 0.1 rad, and it was found the composite action between the slab and beam improves the connections performance by reducing the fire induced forces in the beam. Fischer et al. [15] tested 3.8 m long composite beams (including W10×17, W10×22, and W12×22 shapes) with various simple connections (shear tab, single angle, and double angle). Radiant heaters were used to heat the specimens at a constant rate of heating (7°C/min) and cooling (12°C/min). The study showed that the maximum compressive axial force in the connection can reach 3.7 times of the connection shear demand, and the maximum tensile axial force can be 1.8 times greater than the shear demand. Choe et al. [16, 17] tested full-scale composite floor steel beam assemblies with the beam span of 12.8 m. Four fire tests were carried out, varying the simple connection types (shear tab and double-angle connections) as well as the inclusion or exclusion of the slab continuity over girders. Natural gas burners were used to heat the structural assembly in a longitudinal compartment, at a heat release rate of 4 MW. The result showed that large compressive forces (i.e., 700 kN to 1000 kN) were developed at the connection region when the beam temperatures reached around 400°C to 500°C. All four tested specimens developed local buckling at the beam ends due to this large compressive force, which was developed from rotation induced bearing of the beam flange against the supports during the heating phase. Despite important observations as discussed above, single beam frame tests cannot capture the structural interactions with the neighboring bays in a real building as well as the actual influence of the reinforced concrete slab on the connections, especially once the tensile membrane action becomes the predominant element driving the structural capacity [19].

Performing multi-bay or system level tests to investigate the behavior of beam-end shear connections under fire is a solution to overcome the limitations of the single beam frame test setup. However, these tests require significant laboratory space and research budget to perform, which limits the number of such experiments being carried out. The Cardington tests [20] were performed on an eight-story full-scale steel composite floor building. The building was 33 m in height with a 5 × 3 bays in floor plan and each bay has a 9 m in length and 6 m or 9 m in width. An imposed load of 2.4 kPa was applied on the floor using sandbags. The connections investigated were end-plate for the girder-to-column connections, and shear tab for the girder-to-beam connections. In the seventh test, 40 kg/m² of wood cribs were used to meet the office building fuel load density within a 10.9 m × 6.95 m compartment. The columns and the girder-to-exterior-column connections were protected with vermiculite-cement spray, but the beam-to-girder connections were left unprotected. Note that only parts of the primary beams were protected, i.e., approximately 1.0 m from the connections. No structural collapse was found in the test, although the axial forces in the girder-to-column connections reached 460 kN in compression and 345 kN in tension analyzed from the strain gauge data [21]. The Ostrava Fire test [4, 21] was conducted on a three-story steel frame with end-plate connections. The fire compartment was 3.80 m × 5.95 m × 2.78 m in size. The total mechanical load was 5.7 kPa, and wood cribs with a fire load density of 1039 MJ/m² was used to generate a natural fire heating regime. The columns were protected with the fiber-silicate boards, the beams and connections were left unprotected. No structural collapse occurred, and the axial forces of the beams reached 300 kN. The Ostrava Fire test further confirmed the Eurocode 3 [22] prediction accuracy on the unprotected steel connection temperatures under a natural fire scenario [4].

In addition, the Veselí Fire Tests investigated the shear tab connections and reverse channel connections in a two-story steel–concrete composite structure, with dimensions of 10.4 m × 13.4 m in plan and 9.0 m in total height under different natural fire tests [23, 24]. The first test was carried out at the upper floor with a self-weight of 2.35 kPa, under a travelling fire scenario (pre-flashover) with a fuel load density of 173.5 MJ/m² [25]. A maximum of 350 kN horizontal axial force was identified at the connection of a central 9.0 m beam [24]. The second test was conducted at the lower floor with a total mechanical load of 6.35 kPa, under a compartment fire scenario (flashover) with a higher fuel load density of 520 MJ/m². Most of the strain gauges at the columns were damaged during the second test, hence horizontal forces in the connections were not analyzed. The reverse channel connections presented high ductility in both fire tests, and no structural collapse was identified. For shear tab connections, it was suggested that the mechanical behavior on the connection was principally affected by the elevated temperatures distribution via material properties reduction [24].

It is important to note that the temperature histories and thermal gradients at the connections obtained from these multi-bay fire tests [4, 20, 21] may not be fully representative for all steel buildings. One reason is that the inconsistency of the fire protection schemes among those tests and also along with the actual fire protection design practice: in the Cardington seventh test the primary beam at mid-span was left unprotected whereas the girder-to-column connections were protected while in the Ostrava Fire Test, all the beams and connections were left unprotected. However, following the prescriptive design practice, typically most of the structural steel members are protected, unless some secondary beams are left unprotected as part of a two way design of the floor slab panel for tensile membrane action. In addition, currently in Eurocode 3 and other similar provisions used in many other countries including the United States, the thermal gradient of the beam end connections is estimated using the empirical equations based upon the bottom flange temperature of composite floor beams. The bottom flange beam temperature utilized in these methods are assumed to be remote from the connection. The thermal gradient across the beam-end connections is then used to calculate the connection capacity incorporating strength reduction factors for bolts and welds. The reliability of those Eurocode 3 predictions is unknown especially for the fire-protected connections and full-scale typical beam sizes and spans within a large compartment fire [26, 27] due to lack of such experimental temperature data. Furthermore, even if the thermal response of the steel connection components was within the range predicted by Eurocode 3 methods, to what extent this will ensure a robust structural fire design is also uncertain, based on the lack of supporting experimental data and analysis. Finally, based upon the literatures above, for the structural test setup with cruciform beam-to-column subassembly or single beam frame, standard fire curves ISO 834 [10] and ASTM E119 [18] have often been used as the fire environment for the steel connections, but once the structural scale is increased to a multi-bay level with large compartments, natural fires have been adopted using wood cribs or actual furniture as the fuel load. The predictive accuracy of the Eurocode on the steel connections thermal response under a standard fire curve within a large compartment at a multi-bay compartment level is still unknown.

The work presented in this paper aims to: (1) compare the Eurocode 3 connection design (temperature and strength) provisions for shear connections with experimental data [28] from a large-scale compartment fire test recently conducted at the National institute of Standards and Technology (NIST) and (2) identify gaps in knowledge or data for structural design of shear connections under fire conditions to inform future research need. The large-scale compartment fire test described hereafter investigated the fire-structure interaction of the 6.1 m by 9.1 m composite floor assembly in a two-story steel gravity frame designed following the United State practice. The details of experimental design, measurement systems, and test results are presented in Choe et al. [28, 29]. The connection temperature data and other relevant information useful to describe the fire testing conditions are reproduced in Sect. 2. This paper will enrich the experimental data library for thermal and structural response of the shear-tab (fin-plate) connections with fire protection subjected to a full-scale large compartment fire similar to standard fire exposure predominantly accepted in current design practice.

2 Fire Test

2.1 Test Building and Fire Compartment

The NIST fire test program utilized a two-story steel gravity frame with composite floors at the first story level (Figure 1). The two-story test frame had two by three bays in plan, and the fire test bay (9.1 m × 6.1 m × 3.8 m) was located at the south-central bay on the ground floor. The steel columns were continuous over two stories with the total height of 7.2 m. The composite floors consisting of a concrete slab with steel decking were designed to resist an ambient design gravity load of 8.6 kPa. The slab was reinforced with cold drawn welded wire mesh, comprising 3.4 mm diameter bars at 150 mm centers, giving a reinforcement cross-sectional area of 60 mm²/m width. All W-shapes were rolled with ASTM A992 [30] steel, with the minimum specified yield strength of 345 MPa and modulus of elasticity of 200 GPa. The floor specimen in the test bay was hydraulically loaded to 5.3 kPa according to the ASCE 7 [31] load combination for extraordinary events (1.2 × dead load + 0.5 × live load).

Figure 1

(Source: NIST); (b) Plan view of the test building and test bay location; and (c) Locations of composite connection temperature measurements in the fire test bay (C1 through C10)

NIST large compartment fire experiment [28, 29] on a steel-composite building. (a) Photo taken during the experiment

For passive fire protection of exposed steel beams in the test bay, a medium density (ranging from 240 kg/m³ to 350 kg/m³) sprayed fire-resistive material (SFRM) was applied as prescribed in the relevant Underwriter Laboratory (UL) listings for the 2-h fire-resistance rating. The beam-end connections and exposed surfaces of the columns within the test bay were applied with a thicker SFRM coating to match with a 3-h rating of the columns.

2.2 Connections and Temperature Instrumentation

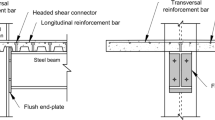
Two types of simple shear connections were used in the tested composite floor specimen, including standard shear tabs for the beam-to-column flange and beam-to-beam web connections and extended shear tabs for the beam-to-column web connections according to the AISC 360 specification [1]. All shear tabs were 9.5 mm in thickness and made of ASTM A36 [32] steel (the minimum yield stress of 245 MPa). The size of fillet welds was 6.3 mm. All structural bolts (Gr. A325 specified in the ASTM F3125 [33]) had a diameter of 19 mm. The dimensions of the short-slot holes (21 mm in width and 25 mm in length) drilled on the shear tabs conform to the AISC 360 specification [1].

Type K thermocouples were used to measure the temperature distribution through the connection. The bare beads of ceramic fiber sheathed thermocouples (Model: XT-K-20-SLE) were peened [32] to the steel beam web, shear tab, and the bolt heads prior to being covered with the Omega high temperature cement (Model: CC HIGH TEMP) and applying the SFRM on the exposed structural steel. Examples of the connections and mounted thermocouples are demonstrated in Figure 2a and b.

Figure 2

(a) Thermocouple locations at connection C1, tagged as C1_1 to C1_6; and (b) Thermocouple locations at connection C4 (standard shear tab) and connection C5 (extended shear tab), prior to SFRM installation

2.3 Strain Gauges Instrumentation

Strains of load-bearing steel elements were measured using linear strain gauges (with a nominal resistance of 120 Ω) manufactured by Tokyo Measuring Instruments Laboratory Co, Ltd. (www.tml.jp). The QF series strain gauges (Model: QFLA-6-11) with an operating temperature up to 200°C were attached to structural members not directly exposed to the test fire: (1) the base of steel columns 51 mm above the end plates anchored to the strong floor, see Figs. 3 and 4; (2) center of the column splices above the test floor assembly; and (3) midspan of the W14×22 beams in the south-west bay. Note that the strain gauges on column splices were to monitor the yielding of splice plates, whereas the rest were used to estimate thermally induced forces from the restraint to thermal expansion or contraction of the test floor assembly exposed to fire. This analysis and strain gauge measurements are presented in Sect. 5.

Figure 3

Locations of the strain gauge instrumentation close to the column base, structural assembly plan-view

Figure 4

Locations of the strain gauge instrumentation close to the column base, (a) Column base with four strain gauges (note that strain gauges of SSWB and SSEB sections are lettered in green); (b) Strain gauge SSWB_1 (51 mm above the end plates); and (c) Column base with two strain gauges

2.4 Mechanical and Fire Loading

The vertical shear load imposed on the connections during the fire experiment was in the range of 20% to 40% of the ambient design capacities (see Choe et al. [28] for each connection applied load ratio). The fire load (or exposure) was applied using natural gas burners [35,36,37] following the ASTM E119 temperature–time curve [18] with the duration of 107 min. The applied fire load density was estimated at 921 MJ/m² with ± 1.5 MJ/m² uncertainty (95% confidence interval). At 107 min the heat release rate reached its maximum value of 10.8 MW. As demonstrated in Figure 5, the test revealed that the measured time–temperature curve matched better with the ISO Standard Fire curve [10] (which includes slightly higher temperature than the ASTM E119 curve) after 45 min. The maximum standard deviation of the upper layer gas temperature was around 70°C throughout the heating regime. This standard fire environment created the condition in which the floor test assembly including the beam-end connections was exposed to a structurally significant fire. Throughout the heating phase of the test fire, large compressive forces could be initially induced in the beam-end connection regions due to restraint to thermal expansion along with significant beam end negative rotation, with these compressive forces decreasing and becoming tensile as the connected beams underwent catenary action at large vertical displacements. During the cooling phase, the tensile forces on the connections might increase and the rotational demand might slightly decrease as the connected (restrained) beams cooled down and tried to recover thermal strains from the heating phase.

Figure 5

A comparison between measured upper layer gas temperature within the test compartment, and the ASTM E119 and ISO-834 fire curves

2.5 Measured Temperatures

The gas-phase and steel temperatures measured from the experiment are presented in Figure 6, including upper layer gas temperature below the floor specimen soffit and temperatures of the west primary beam bottom flange (average of thermocouple TBi_5 and TBi_6) and connection C5 during 7 h of testing period (including a cooling phase after the burner was switched off at 107 min). As shown in Figure 6, the upper layer gas temperature decreased sharply from 1040°C to 490°C during the first 10 min into cooling. This sharp decrease in temperatures might create large tensile forces in the connection regions due to restrained thermal contraction of the connected beam.

Figure 6

(a) Comparison of the time–temperature responses of the upper layer gas, west primary beam bottom flange, and steel connection C5; (b) Thermocouple locations at connection C5, tagged as C5_1 to C5_7; and (c) Thermocouple instrumentation locations at west primary beam midspan, tagged as TBi_1 to TBi_6

The bottom flange temperature of the west primary beam reached its measured maximum value of 760°C during heating, then the temperature decreased more gradually during cooling. The increase in the connection temperatures was slower than the beam temperature because the connection had a thicker SFRM layer than the beams. The maximum value of the connection temperature was recorded 540°C at C5_3. Temperatures of the bottom and middle bolts (C5_3 and C5_4, respectively) indicated higher component temperatures compared to those measured at bottom and top edges of welds (C5_6 and C5_7, respectively). This might be because the weld temperatures were affected by the thermal shadow effect due to column flanges, the heat conduction loss to the connected column web at this region, or both. Those relative relationships of temperatures were further evaluated using Eurocode 3 methods in the subsequent section.

3 Connection Temperatures

3.1 Eurocode 3 Method

As described in Eurocode 3, temperatures of the beam-end connections with a composite slab atop can be estimated using the bottom flange temperature of the connected steel beam at midspan. Since the depths of the steel beam shapes (i.e., W16×31 and W18×35) used in the NIST experiment were greater than 400 mm, two equations are used as follows:if h is less or equal than D/2:

$$\theta_{h} = 0.88\theta_{o}$$

(1)

otherwise:

$$\theta_{h} = 0.88\theta_{o} \left[ {1 + 0.2\left( {{{1 - 2h} \mathord{\left/ {\vphantom {{1 - 2h} D}} \right. \kern-0pt} D}} \right)} \right]$$

(2)

where $\theta_{h }$ is the temperature at height h (mm) of the steel beam, see Figure 7; $\theta_{o }$ is the bottom flange temperature of the steel beam remote from the connection; h is the height of the component being considered above the bottom of the beam in (mm); D is the depth of the beam in (mm).

Figure 7

Thermal gradient within the depth of a composite connection (figure from Eurocode 3)

If the gas temperature is known, the Eurocode 3 step-by-step section factor method can be used to estimate the steel beam bottom flange temperature θ_o as follows:

$$\Delta \theta_{a,t} = \frac{{{{\lambda_{p} A_{p} } \mathord{\left/ {\vphantom {{\lambda_{p} A_{p} } V}} \right. \kern-0pt} V}\left( {\theta_{g,t} - \theta_{a,t} } \right)}}{{d_{p} c_{a} \rho_{a} \left( {1 + {\emptyset \mathord{\left/ {\vphantom {\emptyset 3}} \right. \kern-0pt} 3}} \right)}}\Delta_{t} - \left( {e^{{{\emptyset \mathord{\left/ {\vphantom {\emptyset {10}}} \right. \kern-0pt} {10}}}} - 1} \right)\Delta \theta_{g,t}$$

(3)

$$\emptyset = \frac{{c_{p} \rho_{p} }}{{c_{a} \rho_{a} }}{{d_{p} A_{p} } \mathord{\left/ {\vphantom {{d_{p} A_{p} } V}} \right. \kern-0pt} V}$$

(4)

where $A_{p} /V$ is the section factor for steel members insulated by fire protection material in (m⁻¹); c_a is the temperature dependent specific heat of steel in (J/kgK); c_p is the temperature independent specific heat of the fire protection material in (J/kgK); d_p is the thickness of the fire protection material in (m); $\lambda_{p}$ is the thermal conductivity of the fire protection in (W/mK); $\rho_{a}$ is the unit mass of steel in (kg/m³); $\rho_{p}$ is the unit mass of the fire protection in (kg/m³); $\theta_{a,t}$ is the steel temperature at time t in (°C); $\theta_{g,t}$ is the ambient gas temperature at time t in (°C); $\Delta_{t}$ is the time interval in (seconds).

As detailed above, theoretically two analytical methods can be used to estimate temperatures of connection components: if the steel beam bottom flange temperature at midspan is known, then empirical Eqs. (1) and (2) can be employed directly; if the gas temperature within the compartment is known, then Eq. (3) can be used to estimate the steel beam temperature which is a main variable of Eqs. (1) and (2). The following section will examine those two methods, utilizing the experimental data to evaluate the applicability of the Eurocode 3 provisions.

3.2 Comparison Between the Measurements and Eurocode 3 Predictions—Method 1

Following the Eurocode 3 convention as illustrated in Figure 7, dimensionless thermal gradients of all ten connections (C1 through C10) are summarized, see Figure 8. These gradients represent the measured temperature distribution in the connections at 107 min as the connected structural beam members reached their maximum deflections, compared with the thermal gradient estimated using the Eurocode 3 method. Table 1 summarizes the maximum component temperatures of the ten different connections measured at 107 min. Measured temperatures of the end connections of the secondary and primary W16×31 beams were in excess of 500°C, whereas the end connection temperature of the primary W18×35 beams was below 400°C. The temperature discrepancy among the tested beam-end connections is mainly due to the variation in thickness of applied SFRM protection as summarized in Table 1. As shown in Figure 8, for components of the standard shear tabs connecting W16×31 beams, the dimensionless experimental temperatures vary from 0.35 to 0.7, less than the values calculated using the Eurocode 3 (0.7 to 0.88). For the extended shear tabs at the ends of W18×35 beams, the measured dimensionless temperatures range from 0.5 to 0.86, which remain below 0.88 calculated using Eqs. (1) and (2). This comparison demonstrates that the Eurocode 3 provisions, estimating temperatures of the standard shear tabs as a function of the beam bottom flange temperatures at midspan, are conservative. It is noteworthy that under a natural fire (rather than in a standard fire), the temperature difference between the connections and the beam flange at midspan might be even greater. Under natural fire fueled by wood cribs, e.g. [4, 23,24,25], the spatial variation in the upper layer gas temperature might be greater due to other influencing factors (e.g., distribution of fuel, ventilation, wood properties), as opposed to these test conditions in which near uniform heating was created in this NIST experiment. In addition, the temperature profiles of the connections (e.g., C1, C4) in Figure 8 were slightly different with the profile suggested by Figure 7. Note that there was no protection fail during the experiment. This profile difference might be due to instrumentation locations of the thermocouples on the connections, see Figure 9b as an example: C1_4 measured the bolt, whereas C1_3 and C1_5 were on the shear tab closer to the welded location which had a more “shadowed” view compared with the C1_4, hence likely yielding lower temperatures.

Figure 8

Thermal gradient within the depth of the steel connections, test versus Eurocode 3

Table 1 Summary of the Connections: Connected Members, Types, SFRM Thickness (± Represented as Standard Deviation), and Measured Maximum Component Temperatures of the Connections

Figure 9

(a) Comparison between predicted temperatures with the measured temperatures: north and south primary beams at midspan, and steel bolt temperatures at same height C1_4 & C4_4; (b) Thermocouple locations at connection C1, tagged as C1_1 to C1_6; and (c) Thermocouple locations at connection C4, tagged as C4_1 to C4_6

3.3 Comparison Between the Measurements and Eurocode 3 Predictions—Method 2

An example of comparison between the measured and predicted temperatures based upon the step-by-step section factor method (method 2) is presented in Figure 9. In this example, the connection components C1_4 and C4_4 were situated at the diagonal locations within the test bay plan.

The measured upper layer gas temperature, $\theta_{g,t}$, is used as the input variable of Eq. (3) with a 5 s time interval for calculation. Note that the measured gas temperature during the heating phase of the experiment, closely matching with the ISO-834 standard fire curve, provides a good benchmark to examine the applicability of Eurocode 3 since standard fire curves (e.g. the ISO-834 fire curve) are a common fire situation considered for design. Note that the heating phase of the experiment was designed to follow the ASTM E119 fire curve, since the research was carried out in the United States. ISO-834 standard fire curve was mentioned due to the application of the Eurocode 3 method in this section.

In addition, this study utilized the steel member density $\rho_{a}$ of 7850 kg/m³, and the temperature-dependent specific heat of the steel $c_{a}$ according to Eurocode 3. The section factor of the W16×31 shape, $A_{p} /V$, was taken to be equal to 203 m⁻¹ with a three-sided fire exposure. The SFRM thermal conductivity $\lambda_{p}$ is 0.086 W/mK [38], and its specific heat $c_{p}$ is assumed to be 1200 J/kgK [39]. There are also two SFRM-related parameters used for calculation, including the unit mass, $\rho_{p}$, ranging from 240 kg/m³ to 350 kg/m³; and the applied thickness $d_{p}$. The measured value of $d_{p}$ was 18 mm on average for the north primary beam, with 3 mm standard deviation and was 19 mm for the south primary beam with 2 mm standard deviation. The average temperatures of the north and south primary beams reached a maximum value of 780°C and 670°C, respectively, approximately 2 min after the fire was extinguished (i.e., at 109 min). The Eurocode 3 prediction, incorporating the step-by-step method, on these primary beams suggests a maximum value ranging from 580°C to 690°C at 115 min. The steel beam temperature predicted using the same method (Eq. (3)) was lower than the corresponding values of measured temperatures, and yet the connection temperatures of the components C1_4 and C4_4 are conservative when calculated using Eqs. (1) and (2). The predicted maximum temperature of those two connection components is approximately 540°C, i.e. higher than their measured value of 400°C on average.

The step-by-step section factor method using Eq. (3) is a preliminary step for calculating the steel connection component temperatures using Eq. (1) and (2). The accuracy of the section factor method was further investigated; See Figure 10 and Table 2. Except for the east primary beam, the predicted maximum temperatures of steel members used in the experiment are approximately 6% lower than the measured values on average. Furthermore, the average cooling rate of all beams in the experiment is 110°C/h, about 9% greater than the predicted rate. The discrepancy between the predicted and the measured cooling rate might be due to the fire conditions created during the experiment where natural gas was used as fuel. This test fire, which seldom generated smoke, applied continuous radiation to the surface of the passive fire protection; however, in a real building fire, this situation is highly unlikely. The sooty smoke within the compartment upper layer from burning combustibles might partly obscure radiation from the flames to the fire protection.

Figure 10

Comparison of the predicted with measured temperatures: (a) Secondary beam (thermocouples at the bottom flange of beam midspan, TB6_5 and TB6_6 failed at 167 min); and (b) East primary beam

Table 2 Comparison Between the Test and the Eurocode 3 Prediction on Steel Beam Temperatures (for Maximum Temperature, Eurocode 3 Method Considers the Upper Bound Prediction for Comparison Except for East Primary Beam; for Cooling Rate, Eurocode 3 Method Considers the Mean Value)

Figure 11a and b present the predicted and measured values of maximum temperatures as well as cooling rates respectively, for all the measured connection components on the ten connections considered in this study. In Figure 11a, the error bar of the test measured maximum temperature represents the standard deviation of two connection components on the same beam at two different ends; and the error bar of the Eurocode 3 predicted maximum temperature refers to the temperature variation due to the range of SFRM input variables, i.e. unit mass and thickness. Figure 11a suggests that Eurocode 3 tends to overpredict maximum temperatures of the connection components when actually heated to 400°C or lower. However, the predicted temperatures (using Eurocode 3) become comparable to the measured temperatures of the connection components when actually heated in excess of 400°C. It is important to repeat herein that this comparison is made under the situation where the SFRM thickness on the connection region was at least 43% thicker than the SFRM on the beams. To further examine the impact of SFRM thickness varying between the beam midspan and the connection region, Figure 11a also includes the comparison with another data from the long-span composite beam fire test carried out at NIST [40]. In this test, the SFRM thickness on the connection region was at least 68% greater than that on the steel beam. For this case, Eurocode 3 method overestimates the connection temperatures of which measured values were actually lower than 300°C. Figure 11b presents the comparison between the measured and predicted cooling rates. This plot comparison shows that, in most cases (approx. 95%), Eurocode 3 predicts much rapid cooling rates, from 70°C/h to 120°C/h for the connections used in this study, whereas the measured cooling rates significantly vary from 10°C/h to 110°C/h. This difference would be influenced by several factors, including the Eurocode 3 overestimation on maximum temperatures leading to a higher slope, the thicker SFRM applied on the connection region resulting in slow cool-down, or both.

Figure 11

Comparison of the measured against Eurocode 3 predicted temperatures for shear connections used in the NIST fire tests [28, 40] including eight connection components from composite beam test CB-SP-SC [40]: (a) Maximum temperature; and (b) Cooling rate within 5 h

4 Capacity of the Connections

The connection C2 was selected as an example to demonstrate the limitation of the Eurocode method on capacity, against the experimental observations. The reasons for selecting C2 are as follows: (1) the shear tab connections of the secondary beam in the test bay, C2 and C3, are supposed to carry the largest floor area for vertical loadings (see Figure 1), in comparison to the shear tab connections of the north and south primary beams; as well as the extended shear tab connections of the west and east primary beams. (2) as summarized in Table 1, connection C2 had higher maximum measured component temperatures of 660°C, in comparison to 570°C for connection C3.

The shear capacity of welds and bolts used in the connection C2 was estimated using the Eurocode 3 reduction factors and experimentally measured temperatures. Figure 12a demonstrates that the bolts of connection C2 would have failed in shear at 575°C (around 100 min after the gas burner ignition), as the demand started exceeding the capacity estimated using the Eurocode 3 reduction factors of bolts. However, this behavior was not witnessed during the experiment [28], see Figure 12b and c. Note that the “measured applied load” was estimated according to the total mechanical load applied on the corresponding floor area, according to the ASCE 7 [31] load combination for extraordinary events (1.2 × dead load + 0.5 × live load).

Figure 12

(a) Reduction of connection capacity with experimental increasing temperature at connection C2, against the corresponding measured applied load; (b) connection C2 covered with SFRM after cooling; and (c) bolts used in connection C2 after fire test

Figure 13 illustrates the overestimation of connection temperature C2 predicted using the Eurocode 3 bolt strength reduction factor. As shown, at 90 min, the bolt reduction factor decreases to as low as 0.11 when calculated using the measured bottom flange temperature of the steel beam at midspan or ranges from 0.20 to 0.31 when the Eurocode 3 step-by-step section factor method is used. Those two predictions are conservative, as compared to the actual 0.46 estimated via the temperature measurement at bolt C2_4.

Figure 13

(a) Reduction factor of the bolt based on different methods and measured temperature at the C2 middle row, C2_4 (beam thermocouples at bottom flange failed at 167 min); and (b) Thermocouple locations at connection C2, tagged as C2_1 to C2_5

However, in the case of C6 connection, the Eurocode 3 prediction of bolt strength reduction factor is less conservative, see Figure 14 at 90 min. This bolt reduction factor (based on the thermocouple measurement at this bolt) decreases to 0.53. This result is within the predictive range of 0.48 to 0.74 based upon the Eurocode 3 step-by-step section factor method but higher than the reduction factor 0.35 predicted using the measured beam bottom flange temperature at midspan. Although these predictions still imply no bolt failures, the post-fire inspection of the experiment discovered that three of five bolts from the connection C6 middle row to lower row experienced partial shear rupture failure, Figure 15b. This was due to the combined large axial force and bending moment, induced by the thermal restraint and thermal bowing effects during the heating phase. It suggests the current Eurocode 3 simplified approaches are not suitable for providing the details of the failure mode for connections.

Figure 14

(a) Reduction factor of the bolt based on Eurocode 3 methods and measured temperature at the C6 lower row, C6_5 (bolt thermocouple failed at 106 min); and (b) Thermocouple locations at connection C6, tagged as C6_1 to C6_7

Figure 15

Post-test photographs of extended shear tab (primary-beam-to-column) connections [28]: (a) north end of the east primary beam, C10; (b) south end of the east primary beam, C6; (c) north end of the west primary beam, C5; (d) south end of the west primary beam, C9

Some photographs of the extended shear tab connections after fire testing are shown in Figure 15. The deformed shape of the connecting plate was highly affected by the lateral support conditions of W12×106 columns. The extended shear tabs welded to the webs of the interior columns displayed out-of-plane deformations, whereas the bolts used in these connections barely deformed. Conversely, the extended shear tabs attached to the webs of the exterior columns maintained their original shapes after fire exposure, however, the bottom three bolts in the connection displayed partial shear ruptures. The welded joint appeared to be structurally sound regardless of locations of the columns.

Post-test photographs of the standard shear tabs of the secondary beam (W16×31) are shown in Figure 16. Although local buckling was present at the beam ends, damage in the connecting shear tabs and bolts appeared to be minor. There was no apparent indication of weld joint failures. Similar observations were made in the standard shear tab connections of the north and south primary beams. Additional photographs and details of post-test inspections on all beam-end connections can be found in the full test report [26].

Figure 16

Post-test photographs of the end connections of the secondary beam [28]: (a) east beam web; (b) west beam web; (c) east shear tab connection, C3; (d) west shear tab connection, C2

It is important to note that the heated slab had a reinforcement cross-sectional area of 60 mm²/m width. This very light, low ductility reinforcement resulted in extensive slab cracking around the edge of the test panel early in the heating phase [29], increasing the rotation demand on the connection in the heating phase, and shear demand in the connection zone due to excessive tensile force induced by restraint to thermal contraction as the connected beam cooled down.

5 Axial Forces at Composite Connections

5.1 Assumptions of the Analysis

To characterize the nature and magnitude of the axial forces at composite connections, strain gauge measurements close to the column base were utilized. The interpreted axial forces using the column strains were resultant axial forces from steel beam and concrete slab due to their composite action during thermal expansion and contraction. Note that a possible solution for differentiating the two sources of the forces, i.e., particularly the steel beam forces at the shear tab connections, might be solved via extracting the beam element end forces at the connections from a well-validated model using finite element method (FEM). However, considering the current paper length, developing a validated FEM model with analyzing the connection forces and relevant parametric sensitivity studies will be presented in a separate publication. This section focuses on utilizing the experimental measurements only (i.e., strain gauges data).

The analysis was carried out under those assumptions: (1) composite action between the steel beam and concrete slab is intact (no shear stud failure was identified in the test); (2) column base is idealized as being “fixed” to the strong floor; (3) no yielding or plastic hinges developed at the column, i.e., linear elasticity is assumed along the column full height. An example of the analysis is presented in Appendix A.1.

5.2 The Use of the Axial Forces

It is important to note the calculated axial forces presented in Sect. 5, are not measured values. The readers should be advised to use measured data (strains and displacements) for model validation purpose. The validity and limitation of the calculated axial forces are summarized in Appendix A.2.

5.3 Corrections of the Strain Gauge Data

Although the strain gauges close to the column base were not directly exposed to fire (see Figs. 3 and 4), the surrounding bays were still subjected to minimal temperature increase due to the heat loss from the test compartment to the “ambient environment”. To eliminate those thermal effects on the strain measurements, the measured raw strain gauges data were post-processed using Eq. (5) below, provided by the manufacturer’s data sheet. The total expanded uncertainty (k = 2) of reported strain data measured using QF strain gauges was approximately 1%.

$$\varepsilon_{corrected} = \varepsilon_{raw} - \left( { - 52.4 + 3.82 \times T - 6.43 \times 10^{ - 2} \times T^{2} + 2.36 \times 10^{ - 4} \times T^{3} - 1.06 \times 10^{ - 7} \times T^{4} } \right)$$

(5)

where ε_corrected is the corrected strain (µm/m), ε_raw is the measured raw strain (µm/m), and T is the temperature of a strain gauge (°C). The corrected strains were used to estimate thermally induced forces from the restraint to thermal expansion or contraction of the test floor assembly exposed to fire, although it was found the temperature effects on the strain gauges using Eq. (5) were nearly negligible.

5.4 Strains and the Axial Forces at Composite Connections (Surrounding Bays)

The calculation procedure for the axial force at the composite connection using the strains close to the column base were detailed in Appendix A.1. In response to the thermal expansion and contraction of the test bay floor assembly, as demonstrated in Figs. 17 and 18, the composite connections at the SSWB and SSEB instrumented columns were subjected to compressive axial forces reaching their maximum of 320 kN and 250 kN respectively at around 90 min, although the upper layer gas temperatures continued increasing until the burners were shut off at 107 min. This is likely due to steel softening of the south primary beam when its average temperature reached above 600°C at 90 min (see Figure 9), i.e., more than half of its strength was not sustained. In addition, the vertical displacement, observed local buckling and lateral distortion of this beam would also contribute such compressive force reduction. Note that the maximum force at SSEB instrumented column was lower than the force at the SSWB instrumented column, since the restrained force was “suddenly” released at around 41 min, see Figure 18b, probably due to the significant concrete fracture development observed at this moment (Figure 19).

Figure 17

(a) Strains for SSWB series, and (b) Total axial force at the composite connection on SSWB instrumented column (error bar was the standard deviation of four strain gauges’ measurements)

Figure 18

(a) Strains for SSEB series, and (b) Total axial force at the composite connection on SSEB instrumented column (error bar was the standard deviation of four strain gauges’ measurements)

Figure 19

(a) Strains for NWB series, and (b) Strains for NEB series, see Figure 3 for strain gauge locations

In contrast, as shown in Figs. 20 and 21, the composite connections at the SNWB and SNEB instrumented columns were subjected to lower compressive axial forces, compared to the values at SSWB and SSEB instrumented columns. This is because the interior columns connected to the north primary beam in the test bay were framing into more steel members in the surrounding bays and restrained by the concrete all around, enabling more effective force distribution to the surrounding structures.

Figure 20

(a) Strains for SNWB series, (b) Total axial force at the composite connection on SNWB instrumented column (error bar was the standard deviation of two strain gauges’ measurements)

Figure 21

(a) Strains for SNEB series, (b) Total axial force at the composite connection on SNEB instrumented column (error bar was the standard deviation of two strain gauges’ measurements)

The compressive axial forces at composite connections of the SNWB and SNEB instrumented columns reached their maximum of 155 kN and 185 kN respectively at around 70 min, which were 165 kN and 65 kN lower than the forces at the composite connections of the SSWB and SSEB instrumented columns respectively. Apart from the reason that the average temperature of the north primary beam reached above 600°C at 70 min (see Figure 9), i.e., more than half of its strength was not sustained, the other reason is likely because the higher restrained condition also caused local buckling of the connected north beam in the test bay, which appeared to happen around 60 min, at peak strains of NWB and NEB (see Figure 19). In addition, slab integrity failure with center cracks appeared at south of the secondary beam was also identified at around 70 min.

5.5 Strains and the Axial Forces at Composite Connections (Test Bay)

Figures 22 and 23 demonstrate that the composite connections at the SWB and SEB instrumented columns were subjected to compressive axial forces in the south primary beam longitudinal direction. Those two columns were under the bi-directional bending for its strong and weak axes on the cross-section, due to the thermal expansion of the south primary beam and the west and east primary beam. Linear elastic stress superposition was assumed for isolating the effects of the force from the west and east primary beam.

Figure 22

(a) Strains for SWB series, (b) Total axial force at the composite connection on SWB instrumented column in the south primary beam longitudinal direction (error bar was the standard deviation of four strain gauges’ measurements)

Figure 23

(a) Strains for SEB series, (b) Total axial force at the composite connection on SEB instrumented column in the south primary beam longitudinal direction (error bar was the standard deviation of four strain gauges’ measurements)

Hence, once measured strains are higher than the yield point of 1725 micro-strain (i.e., $f_{y} /E = 345 MPa/200GPa$), the interpreted axial forces may have become less valid. Note that both yield strength of 345 MPa and modulus of elasticity of 200 GPa for ASTM A992 [28] steel are minimum specified values rather than the measured values. The axial forces at the composite connections of the SWB and SEB instrumented columns in the south primary beam longitudinal direction, were 625 kN and 515 kN at 74 min and 53 min respectively, when the measured strains reached yielding. Both values were significantly higher than the axial forces at the composite connections at the surrounding bays presented in Sect. 5.4, because higher constraints for the south primary beam due to thermal expansion compared with the east or west surrounding bays having limited constraints for force distribution.

In contrast, as presented in Figure 24, the compressive axial forces in the west and east primary beams on the SWB and SEB instrumented columns, were much lower than the values at the connections of the south primary beam (see Figs. 22 and 23), due to very limited restraints to prevent the thermal elongations of the west and east primary beams towards south. The magnitudes were 140 kN and 120 kN when the measured strain reached yielding at 74 min and 53 min respectively. Note that there was no apparent local buckling identified in the west and east primary beams.

Figure 24

Total axial forces at the composite connection on: (a) SWB strain gauges instrumented column in the west primary beam longitudinal direction, (b) SEB strain gauges instrumented column in the east primary beam longitudinal direction (error bar was the standard deviation of four strain gauges’ measurements)

Nevertheless, three bolts in the extended shear tab connection to the southeast column of the test bay, connection C6, see Figure 15b, partially ruptured under such low total compressive axial forces, see Figure 24b. However, there was no bolts partial rupture failure in the connection C1, which apparently was subjected to much higher total compressive axial forces on the standard shear tab, see Figure 23b. This may be due to the detailing difference of the composite connections, that the connection C6 had a much larger gap between the connected steel beam bottom flange and the column web, whereas the gap of the connection C1 was much smaller, see Figure 25. The smaller gap could successfully mitigate the axial compressive force on the bolts of the shear tab, to redistribute load demand to the beam bottom flange which starts contacting the column under large composite beam deflections. Again, such detailing is not included in the current simplified Eurocode 3 approach.

Figure 25

The detailing of the composite connections C6 and C1 prior to SFRM installation, note the beam bottom flange to the column gap difference for C6 and C1

6 Conclusions

This paper compared the Eurocode 3 connection design (temperature and strength) provisions for shear tab connections with the data from a recent large-scale compartment fire test on a composite floor assembly. It was found Eurocode 3 tends to overpredict maximum temperatures of the connection components when actually heated to 400°C or lower. In contrast, the predicted temperatures become comparable to the measured temperatures when actually heated in excess of 400°C. Further, it was also found in most cases (approx. 95%), Eurocode 3 predicts much rapid cooling rates of the temperatures of the connection components, from 70°C/h to 120°C/h for the connections used in this study, whereas the measured cooling rates significantly vary from 10°C/h to 110°C/h. Although the Eurocode 3 simplified approaches are not meant to provide the details of the failure mode for connections, this study demonstrates that the Eurocode 3 method might lead to the conservative prediction on temperatures of connection components, if the connection region is applied with thicker SFRM than the connected beam.

However, designing shear connections using the Eurocode 3 temperature provisions may not guarantee a safe structural fire design, since experimental evidence showed that the connections could reach design limit states (e.g., partial shear ruptures of bolts) at lower temperatures (e.g., connection C6 in this study). This is because the Eurocode 3 method does not account for (1) additional sources constituting the capacity of a connection, such as the presence of slab, slab continuity to adjacent bays and extent of slab cracking in the fire, and (2) additional sources for the demand, such as thermally induced axial forces due to the restraint to thermal expansion or contraction as well as catenary action. All these factors are needed to be incorporated for reliable estimation of the connection integrity.

To characterize the nature and magnitude of the axial forces (from steel beam and concrete slab) at composite connections, strain gauge measurements close to the column base were utilized. It was found the axial force of the composite connections in the surrounding bays could reach 320 kN in compression (i.e., at the southwest edge beam based on SSWB strain series). In contrast, the axial force of the composite connections in the test bay could be significantly higher, e.g., 625 kN for the south primary beam west end prior the SWB strain series reached yielding.

It is therefore strongly recommended that the influence of the axial load demands (i.e., compressive/tensile load demands) and rotational demands on the connection must be considered in future design guidance, through a combination of direct design and detailing to ensure that the connections have dependable deformation capacity for both the heating and the cooling phases, and that bolt or weld failure is prevented. The extent of cracking of the concrete slab over the connection region is important in determining the axial and rotational demands on these connections and also needs to be considered.

7 Disclaimer

Certain commercial entities, equipment, software, or materials may be identified in this paper in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose.

Appendices

Appendix

A.1: Calculation of the Axial Force at the Composite Connection (Surrounding Bays)—An Example

Taking the axial force calculation at the composite connection above SSWB strain gauges instrumented column as an example, the axial force $W$ can be estimated as follows:

• (1) The bending moment, $M_{SSWB}$, at the corresponding strain gauges instrumented cross-section was calculated via:

  $$\frac{{M_{SSWB} {{h_{column} } \mathord{\left/ {\vphantom {{h_{column} } 2}} \right. \kern-0pt} 2}}}{{E_{steel} I_{column} }} = \varepsilon_{strain}$$

  (A.1)

where $h_{column}$ is the W12×106 column section height, 0.327 m, $I_{column}$ is the section area moment of inertia, 0.00038834 m⁴, $E_{steel}$ is the minimum specified Young’s modulus of elasticity 200 GPa for ASTM A992 steel [30], and $\varepsilon_{strain}$ is the post-processed measured strains with temperature correction due to the strong axis bending, see Figure 4a for strain gauge locations.

• (2) The relationship between the axial force $W$ and the bending moment $M_{SSWB}$, are (see Figure 

  Figure 26

  

  Calculation schematic for axial force $W$ at composite connection above SSWB instrumented column (see Figure 3 for SSWB locations from structural assembly plan-view)

  26):

  $$R_{B} = \frac{W}{{2L^{3} }}a^{2} \left( {3L - a} \right)$$

  (A.2)
  $$M_{SSWB} = W\left( {a - c} \right) - R_{B} \left( {L - c} \right)$$

  (A.3)

  where $R_{B}$ is the reaction force due to the restraint from the upper frame, and $a, L, c$ are all constant geometrical dimensions shown in Figure 26. Hence, the axial force $W$ can be solved with equations A.1, A.2, and A.3.

A.2: Benchmarking the Method Presented in Sect. 5 (Test Bay)

The validity and limitations of the analytical method presented in Sect. 5, were benchmarked against the test measured HD8 and HD9 displacements. Those test measurements were horizontal displacements towards South at the vicinity of composite connections of the SWB and SEB strain gauges instrumented columns above test floor. As demonstrated in Figure 

Figure 27

Calculation schematic for axial force W at composite connection above SSWB instrumented column (see Figure 3 for SSWB locations from structural assembly plan-view)

27, the interpreted analytical displacements were around 29% and 24% lower than the corresponding measured HD8 and HD9 at 73 min and 54 min respectively when the measured strains reached yielding point. This underestimate was due to the simplified assumption that the column base was “fixed” to the strong floor, whereas in reality there was certain level of rotational flexibility hence less rigid. It further implies that the interpreted total axial forces presented in Sect. 5, were likely overestimated due to this assumption. Note that once the measured strains surpassed the yielding point, the interpreted analytical HD9 was even higher than the measured value, see Figure 27b. This is unlikely (due to the “fixed” boundary assumption), hence further suggesting the limitation of the analytical method after the strains reached yielding.