Abstract
This paper presents a novel algorithm, called Visual Fire Power, for measuring the heat release rate of a turbulent flame using video footage taken from two cameras, located at an approximate right angle to each other and at a known distance from the fire. By measuring the time-averaged volume of the fire, Visual Fire Power can measure heat release rate in situations where traditional calorimetry may be impractical (such as experiments outdoors), as well as uniquely providing a method for comparing the heat release rates of different flames in the same experiment, e.g. externally venting flames from different windows of the same compartment. The algorithm was benchmarked against synthetic data and calculated the volume of common solids with approximately 30% uncertainty. The relationship between volume and heat release rate was then calibrated from videos of burners at known heat release rates. These experiments were used to calculate the Orloff-DeRis constant \(\gamma\), which linearly relates flame volume and heat release rate. The value for \(\gamma\) was found to be \(1505\pm 183\) kW/m3. The algorithm was demonstrated on recordings of a standard Polish facade fire test. Improving the range of data measured in both fire testing and fire experiments could help to increase our knowledge of fire dynamics and provide better data for researchers and engineers in the future.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The heat release rate of a fire captures its growth rate. It helps to determine the size of a fire, the burning rate, or the severity of damage to nearby structures. The heat release rate is, therefore, a key variable in fire [1] but measuring it can be challenging. Thanks to the invention of oxygen consumption calorimetry, it is possible to measure the heat release rate of fires at many different scales to an impressive degree of accuracy, knowing that the net heat of combustion per unit mass of oxygen consumed is approximately constant for most materials, usually around 13.1 MJ/kgO2. This approach involves collecting the emissions from a fire for analysis and therefore requires special equipment and is limited to laboratory conditions. There are also other methods for measuring the heat release rate, such as measuring the mass loss rate of the fuel source, measuring the plume temperatures, or solving the energy balance for experiments in compartments. However, these methods are not always available either. It would therefore be advantageous to have an inexpensive and simple method for measuring the heat release rate of fires in situations where collecting the fire plume is impractical.
In 1984, Orloff and De Ris [2] identified that the heat release rate of a turbulent flame was linearly proportional to its volume following the equation:
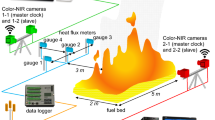
for some constant \(\gamma\), which we will refer to as the Orloff-DeRis constant, where \(\dot{Q}(t)\) is the time-dependent heat release rate and \(V(t)\) is the time-dependent flame volume. For circular pool fires in quiescent conditions, they found that \(\gamma =1200\) kW/m3 across a variety of common fuels. Their method for measuring the volume relied on the fire having a simple geometry that could be inferred from its height, but this is not always the case for real fires, therefore their approach could not be applied to flames with a complex shape. This paper, therefore, presents a novel algorithm, named Visual Fire Power, for measuring the heat release rate of a turbulent fire using ordinary video footage from two cameras placed at a right angle to each other and at known distances from the fire, by using the recorded footage to measure the time-averaged flame volume. This setup is shown in Figure 1.
A diagram of the basic setup required to use the Visual Fire Power method. Two cameras are located at a right angle to each other and at known distances from the fire. The grey shaded area represents occluded regions that would cause an overestimate of the volume using previous reconstruction methods.
Visual Fire Power could be a particularly valuable contribution to standardised fire tests, such as those used to test facades. For regulatory purposes, many countries will allow a facade to be used on a building if it has passed a standardised fire test, for example the BS 8414 standard in the UK [3]. These tests subject a mock-up of a facade to a particular fire scenario, and then compare the performance against certain failure criteria, most commonly the maximum vertical flame spread on the facade. The results from these standard tests are used to give a pass or fail for regulatory purposes, but the data measured during the tests could be a valuable source of scientific knowledge as well [4]. Unfortunately, the information measured during these tests is usually restricted to coarse temperature measurements and qualitative observations which is not the most valuable data to quantify fire behaviour. The heat release rate is a key variable in quantifying the flammability of a system, and this is also true for facades. Given that most standard facade fire tests are already filmed, the Visual Fire Power method would provide an inexpensive and easy way to add a measurement of the heat release rate to these tests and improve the quality of the data recorded in them.
The method could also be used more generally to add heat release rate measurements in situations where other methods of measuring heat release rate would be impractical, such as experiments taking place outdoors [5], or other kinds of fire experiments. Visual Fire Power can also provide additional fidelity for experiments through measuring heat release rate from separate flames (e.g., different window plumes in a compartment fire), whereas oxygen calorimetry and mass loss rate measurements provide the total heat release rate for the whole experiment.
This paper presents an explanation of the Visual Fire Power method and a discussion of the previous research that it builds on, before verifying the accuracy of the method against synthetic data. Finally, the method was calibrated against experiments of known heat release rates to find a value for the Orloff-DeRis constant \(\gamma\) (see Equation 1).
2 Methodology
2.1 Background
In 1984 Orloff and De Ris identified that the volume of a turbulent, buoyant flame was approximately linearly proportional to the heat release rate [2] i.e., \(\dot{Q}(t)=\gamma V(t)\) for some constant \(\gamma\), which we will refer to as the Orloff-DeRis constant. They arrived at this conclusion after they combined correlations of flame height and heat release rate from the Froude modelling of pool fires and found that the volumetric heat release rate of the fires should be approximately constant. They then supported the theory with evidence from experiments. In their paper, the volume \(V(t)\) was calculated by measuring the flame height of a pool fire, based on a threshold value of radiative heat flux measured from probes at different heights, and then assuming the flame was cylindrical. Additionally, only the volume of the steady burning flame was considered, and therefore they did not calculate a time-dependent heat release rate, but an average volume over a 60 s period. Their experimental data showed a clear linear trend between flame volume and heat release rate with a slope of \(\gamma =1200\) kW/m3.
Their initial work has since been followed by further studies that support a constant volumetric heat release rate for buoyant diffusion flames [6,7,8,9,10]. However, [11] found that for turbulent jet flames the volumetric heat release rate was also approximately constant, with the relation:
suggesting that the result may hold for turbulent fires in general.
Providing a theoretical explanation for a constant volumetric heat release rate is difficult [7, 8]. In a diffusion flame, fuel and air meet through diffusion, entrainment, and turbulence. In a flame, the total heat release rate can be defined over a single flame surface \(S\) with an approximate flame thickness \(\delta\). The average volumetric heat release rate is relatively constant as the flame thickness and the average reaction rate over the flame surface are approximately constant, and the volume can be approximated by the surface area multiplied by the flame thickness.
It is not possible to measure \(S\) directly as the flame surface will have a fractal geometry, with the flame being made up of many flamelets of different sizes. Therefore, proxies are used instead to estimate the volume \(V\). In the research by Orloff and De Ris [2] the flame volume was estimated by taking the flame height as the first moment of the flame radiation intensity taken via scanning radiometry, and assuming a cylindrical geometry for the flame. In [6,7,8,9,10] the flame volume was also estimated by assuming simple geometries (such as cylinders, cones, or trapeziums) and calculating the flame height based on visual measurements, using a region of 50% flame intermittency over some fixed period of time. Calculating \(V\) from the flame height requires knowledge of the shape of the fire in advance and would not work for cases where the geometry was not known or changes over time. An alternative approach is to calculate \(V\) using multiple cameras from different angles, as was developed in [12, 13] for measuring the radiative heat flux emitted from a fire. This method relied on knowing the location of the fire ahead of time, and allocating a grid of 3D pixels, known as voxels, to the region where the fire might appear. These voxels were then attributed to light rays projecting from each pixel in the videos of each camera viewing the fire. By identifying which pixels contained fire in each video, and then matching these to their attributed voxels, it was possible to reduce the voxel grid to only the region that contained fire. This approach from [12, 13] was then used by Stratton in [14] to measure the volume of various furniture fires, which were then compared to the heat release rate of those fires calculated via oxygen consumption calorimetry. These experiments obtained an Orloff-DeRis constant of \(\gamma =1878\) kW/m3 for the 50% intermittency region.
Unfortunately, the methodology used in [12,13,14] is computationally expensive. A single frame of a video contains upwards of 106 pixels, and a grid of voxels of 1 cm3 in size would require upwards of 106 voxels to cover a 1 m3 fire. A matrix relating the voxels and pixels for a single camera could therefore contain up to 1012 values (at least 1 TB of data). There are many methods to reduce these computational costs, such as removing irrelevant pixels [15] or reducing the resolution of each image, but even with reductions, the method is still computationally intense when producing more fine grained results. The methodology also requires many cameras to provide accurate results, as rays that pass through a region containing fire and into a region that does not contain fire but cannot be seen by another camera are still assumed to contain fire, overestimating the volume. Examples of these regions are shaded in gray in Figure 1.
The Visual Fire Power method, presented here, improves on this approach by requiring only two cameras, located approximately at a right angle to each other and at a known distance from the fire. The distance from the fire can also be estimated using objects in the scene with known dimensions. The method only uses information from the pixels making up the outline of the region containing fire in each image. As it only uses a small number of pixels and does not extrapolate data into voxels, this approach is very fast; at most, the outline of a fire in an image would contain on the order of 103 pixels, meaning the information being processed is in the order of KB of data. This allows each frame of a video to be processed in under a second, allowing for almost real time measurement of the heat release rate. This method will be explained in the next section.
2.2 Visual Fire Power
The Visual Fire Power method can be broken down into 5 steps, which are illustrated in Figure 2:
-
1.
Calibrate Cameras: Calculate the camera matrix and pose for each camera.
-
2.
Threshold Images: Define which pixels in each image contain the flame.
-
3.
Identify Flame Surfaces: Define a contour around the flame in each image and break these into an upper and lower flame surface.
-
4.
Combine Surfaces into 3D: Orthographically project the upper and lower flame surfaces from each camera into 3D space and combine to define a 3D flame region.
-
5.
Convert Volume to Heat Release Rate: Calculate the volume of the combined flame region and convert to a heat release rate using Equation 1.
Step 1 is a common task in computer vision, called camera calibration, and methods already exist for accurately estimating the camera matrix and pose. The work in this paper was implemented in OpenCV [16], and details on the algorithms used can be found in [17].
Step 2 is also a common task in computer vision, known as image segmentation, where each pixel in the image is labelled as being in a specific region. In this case, a pixel either contains the flame or it does not. This process will therefore output a binary image, where each pixel is labelled as either 1 or 0 depending on whether it does or does not contain the flame, respectively.
Step 3 involves identifying the outline of the image region that contains the flame. If step 2 went perfectly, then this would be a simple process. However, there will often be some noise in the binary image, and so it may be necessary to first process the binary image using morphological transforms, such as filling holes in a connected region [17]. The OpenCV library has built-in functions for both morphological transforms and for finding contours in binary images. A contour is given as a list of coordinates \((u, v)\), where \(u\) is the horizontal distance from the top-left corner of the image in pixel units, and \(v\) is the vertical distance. After locating the flame contour, this can then be broken into an upper and lower flame surface by finding the \(v\) coordinate as a function of the \(u\) coordinate in the flame contour \(C\). These surfaces are shown explicitly in Figure 2.
Step 4 then projects the lists of coordinates in \({C}_{\mathrm{u}}\) and \({C}_{\mathrm{l}}\) back into 3D, using the method of orthographic projection, which is described in more detail in Appendix 1. This gives two sets of coordinates \(\left({X}_{o}^{i},{Y}_{o}^{i},{Z}_{o}^{i}\right)\) from each camera, \(i \in \{1, 2\}\), for the upper and lower surface of the object. To manage potential discontinuities in \({C}_{u}\) and \({C}_{l}\), a smooth curve is fitted to these surfaces before projecting them back into 3D. Let us assume that the \({Z}_{o}\) coordinate is in the vertical direction. Because the cameras are at a right angle to each other, we can define \({X}_{o}\) and \({Y}_{o}\) such that one camera will be located in the \(XZ\) plane, the other in the \(YZ\) plane. This means that for both the upper and lower surfaces, each camera will have \(Z\) as a function of \(X\) or \(Y\) depending on the coordinates. The surfaces can then be combined over all \(X\) and \(Y\) coordinates by taking:
This method of combining the orthographic projections means that the top surface of the object will be convex, and the bottom surface will be concave. While such a shape may not be appropriate for all instantaneous structures of a flame, the flame volume we are measuring is based on the 50% intermittency region of a time-averaged turbulent fire. In a quiescent buoyant fire or vertical jet fire, splitting the fire into a concave lower surface and a convex upper surface is appropriate, as these fires are approximately cylindrical or conic. However, there may be some deviation from this when horizontal winds are applied to a fire, so this assumption would need further investigation.
Finally, step 5 calculates the volume of this combined surface by numerically integrating between the upper and lower surfaces of the combined 3D shape. This effectively draws columns between discrete areas of the upper and lower surfaces, then sums their volumes to give the total volume of the fire region. The volume is then converted to a time-dependent heat release rate using the Orloff-DeRis constant, which we will calibrate in Sect. 3.2.
3 Results
3.1 Verification on Synthetic Data
To verify this 3D reconstruction method, we tested it on objects with known volume and cameras with known parameters using an idealised, virtual environment in the 3D graphics software Blender [18]. In this scenario, the camera matrix and pose of each camera was known exactly (Step 1), and the object was coloured so that the boundary could be identified perfectly in each image (Step 2). Therefore, the only sources of error in measuring the volume were from imperfect image resolution and from the assumptions of the Visual Fire Power method. These assumptions are that every ray that hits the camera's image plane is orthogonal to that plane (or parallel to each other, this is the definition of an orthographic projection) and that the object can be well represented by a convex and a concave surface connected by vertical lines. The method of combining the contours from two rectangular images also means that the base of the reconstructed object will be rectangular.
The assumption that every ray striking the image plane is parallel to each other becomes more valid for rays travelling from further away from the camera, and also for rays closer to the centre of the image (the axis of projection). However, at greater distances the image resolution also becomes more of an issue, as each pixel represents the average intensity from a larger region of space. Therefore, it was necessary to test the Visual Fire Power method on a variety of different shapes, and with the cameras located at a range of distances and offsets from the true \({X}_{o}\) and \({Y}_{o}\) axes.
To compare both the overall range of errors, and the importance of each of these parameters on the error, we performed a one-at-a-time (OAT) sensitivity analysis, where the value of each sensitivity parameter is varied alone, with the other parameters remaining constant. Figure 3 shows a picture of the experimental setup in Blender used to perform the sensitivity analysis. We performed the analysis on five different 3D shapes with known volumes: a cube (2 m across), a sphere (2 m diameter), a cylinder (2 m diameter and height), a cone (2 m diameter and height), and a torus (outer diameter 2 m, inner diameter 0.5 m). Although real fires will deviate from these shapes, it is expected that they would most closely resemble either a cuboidal shape [6], a cylinder [2], or a cone [8], as these have all been used to approximate fire geometries in the past. The sphere was also included to test the algorithm on curved surfaces, and the toroid was included to demonstrate the inability of the method to detect holes within a shape. The distance from the cameras to each shape was varied between 5 to 15 times the height of the shape. The default distance of 10 times the shape height was similar to the distance to fire size ratio of the front facing camera in the calibration experiments (see Sect. 3.2). When increasing the distance from the camera, the resolution of the image was fixed such as the mm per pixel of the shape in each image was constant. This was to help separate the error due to orthographic projection from the error due to imperfect resolution. The virtual cameras had a focal length of 50 mm, and a sensor width of 36 mm, the default values in Blender and within the range of ordinary cameras. This meant that the mm/pixel for the default distance of 20 m from the object with a resolution of 3840 × 2160 was \(\frac{36}{3840}\times \frac{\mathrm{20,000}}{50}=3.75\) mm/pixel. The angular offset of the cameras was varied between − 10 to + 10 degrees, and translational offset was varied between − 0.05 to + 0.05 times the height of the shape; these ranges were chosen based on the expected human error when setting up cameras in a real laboratory setting. Figure 4 shows how the percentage error in measuring the volume of each shape varies with a percentage change in each sensitivity parameter, alongside plots of what the top and bottom surfaces estimated for each shape look like. The most sensitive parameters for all shapes were the distance from the object and the rotational offset, with the translational offset having a much smaller effect on the calculated volume. This makes sense, as the rotational offset moves the shapes away from the centre of the image (the optical axis) which increases the error from orthographic projection in the same way as moving the camera closer to the object. From Figure13 it can be seen that the size of the error in measuring the height of the shape will depend on the slope formed between the height of the shape and the optical axis, and the width of the object. This means that the error in measuring a single point should decrease at a rate of \(1/{Z}_{c}\) where \({Z}_{c}\) is the distance from the camera to the shape. The error in the volume will also decrease on the order of \(1/{Z}_{c}\) as \({Z}_{c}\) increases, as higher order terms in the linearized expression of error will tend to zero faster.
Screenshot of the setup in Blender used to perform the sensitivity analysis on the Visual Fire Power method. The three sensitivity parameters are labelled. The positions of the cameras match with the setup described in Figure 1.
This can be seen in Figure 5, which plots the volume error against \(1/{Z}_{c}\). The y-intercept of a linear fit represents the residual error in measuring the volume of that shape when the assumption of perfect orthographic projection has been met (the camera being an infinite distance away). For the cube, this is expected to be approximately 0, as the assumptions of upper and lower, convex and concave rectangular surfaces match perfectly with the real shape; but for other shapes this residual error will depend on how much these assumptions deviate from reality. For the cylinder and the cone, the size of this residual error can be estimated by comparing the true volume to the volume of an equivalent square-based shape, i.e., comparing the volume of a cylinder to the volume of a cuboid and the volume of a cone to the volume of a square based pyramid. Table 1 shows the predicted residual error and the y-intercept of the fits for each shape. The estimated residual errors and the intercepts match closely, suggesting the algorithm works as intended, and would work best on fires with a rectangular fuel source. For fires with a non-rectangular fuel source, an overhead camera could be added to the method, located along the Z axis, away from the smoke plume. A camera on the \(Z\) axis is not currently implemented in this algorithm, though including additional cameras requires a different reconstruction method.
Error in calculating the volume of known simple solids for cameras at different distances \({Z}_{c}\). As \(1/{Z}_{c}\) approaches \(0\), the assumption of orthographic projection becomes more valid. The intercept of each line is given in Table 1.
We also tested how sensitive the algorithm was to changes in the resolution of the image. Reducing the resolution of each image significantly accelerates the algorithm, as fewer pixels need to be considered. To change the resolution, we introduced a scale factor, with a value between 0 and 1, that is multiplied with the original resolution of the image. Figure 6 shows how the volume error changes (with respect to the baseline error for that shape at a resolution of 3840 × 2190) as the inverse of the scale factor \(SF\) (i.e., \(1/SF\)) varies between 1 and 10 (\(SF\) varying between 0.1 and 1).
3.2 Calibration with Experimental Fire Data
After verifying that the Visual Fire Power method worked as intended for calculating volume, and quantifying its inherent uncertainty, we then performed a series of experiments involving fires with known heat release rates, in order to assess whether the assumption of constant volumetric heat release rate was appropriate, and to estimate what this value might be. An application of the Visual Fire Power method would be to measure the heat release rates from fire tests that cannot include measurements from calorimetry. Therefore, the calibration experiments were chosen to represent a fire located against a wall: a similar scenario to intermediate-scale facade test methods such as PN-B-02867 [19] and ISO 13785–1 [20].
Pictures of the experimental setup are shown in Figure 7. It consisted of sand burners 800 × 160 × 550 mm that were located 250 mm from a 2000 × 150 × 2500 mm masonry wall. The experiments were performed with both a single burner and two burners side by side and with and without the inclusion of a 2 m/s wind, directed perpendicular-to and towards the masonry wall. The flow rates used for the different burner configurations are given in Table 2. The fuel was a mixture of 95% propane and 5% butane. The gas flow rates were converted to heat release rates by approximating the molar rate of the fuel to be that of an ideal gas with the same molecular weight, and using values for the chemical heat release rate of the two fuels burned in air given in [21]. This gave a value of 80.21 MJ/m3 for the fuel. Comparing this to calculations using the lower heating value of the two fuels burned in oxygen using a bomb calorimeter, the value of 80.21 MJ/m3 represents a combustion efficiency of 94%. We assumed a \(\pm\) 5% uncertainty due to combustion efficiency and flow rate. The experiments were filmed using two Vmotal GSV 8580 action cameras located at a right angle to each other, placed approximately 10 m from the fire in the XZ plane, which was the closest distance that could capture the entire experimental setup, and 5 m from the fire in the YZ plane, which was the furthest distance the camera could be set up in this direction due to space constraints. These cameras were chosen due to their low cost and simplicity, which meant that the precise parameters of the camera (ISO, focal length) were not available, however it was possible to choose a fixed exposure (the one for brightest conditions was chosen) and to calculate the focal length through camera calibration (see [17]). The resolution of the images was 3840 × 2160 pixels. These two cameras took footage at a rate of 2 FPS (frames per second). This was a decision taken to reduce the memory cost and ensure that the data could be collected and transferred easily. This could be important for long experiments, or series of field experiments, where limited memory can be an important factor. A third camera also recorded the experiments at a rate of 30 FPS, to assess the impact of the frame rate on the size of the flame region detected in the images. It was placed next to the camera facing the \(XZ\) plane.
Pictures of the calibration experiments using sand burners against a masonry wall with known heat release rates. The flow rates are given in Table 2.
Unlike the cases using synthetic data, here the boundary of the flame is uncertain. Step 2 of the Visual Fire Power method involves identifying which pixels in each frame do or do not contain flame. Each pixel in a digital colour image contains three channels for red, green, and blue light that usually store a value between 0 and 255. Image segmentation can be implemented by combining rules based on the varying intensities of these channels and the relationships between them (such as hue, saturation, and lightness). Such rules have been used before to identify the flame region, either by using the overall brightness of the pixels [22] or by using multiple rules for each channel [23,24,25]. Image segmentation can also be achieved using clustering algorithms, such as k-means clustering [26], or by using supervised machine learning methods, such as neural networks [27]. In this work, we used the simplest technique of taking a minimum pixel brightness as our threshold. Any pixels above this brightness were labelled as containing flame.
The volume of a flame is not an instantaneous quantity. In the work of [6] the flame volume was calculated using the flame height, defined by an area of 50% intermittency over a period of 30 s. The choice of these values is arbitrary, and the flame height and volume will change depending on the size of the time-window (the period over which intermittency is calculated) and the intermittency value (the percentage of time that a pixel needs to contain flame to be considered as part of the time-averaged flame). In the work of [12,13,14], different time-windows and intermittency thresholds were experimented with before selecting a 6 s time-window and an intermittency of 100%. In other words, the volume of the flame was calculated using every pixel that had contained flame for any length of time over a period of 6 s, this led to an average volumetric heat release rate of 800 kW/m3. In this work, we selected an intermittency region of 50%, to be consistent with the common definition of flame height. This meant that, for example, over a 10 s time-window, any pixel that contained flame for more than 5 s would be considered part of the flame. In the work of [12,13,14], this 50% intermittency region gave an average volumetric heat release rate of 1878 kW/m3, which is what we compared our results to.
The size of the time-window will affect the calculated flame volume. Figure 8 shows the mean flame volume and the variation (standard deviation) in flame volume over the same 75 s period, when using different time-windows to calculate the flame region. As the flow rate was constant, it would be expected that the variation in the flame volume (as indicated by the standard deviation of a sample of 30 frames from the same period) would decrease with larger time windows. Figure 8 confirms that this is indeed the case, with the variation decreasing and the volume measured at the end of the period tending to a similar value as the time window increases. These plots suggest that a time window of more than 20 s would be appropriate to capture the time symmetry of the flame. For these calibration experiments, a time-window of 30 s was used, in keeping with the size of the window used in [6].
Mean flame volume (top) and variation in flame volume (bottom) calculated, using Steps 1–4 of the Visual Fire Power method, over the same period of burning using a fixed intermittency of 50% but varying the size of the time-window. As the flow rate is constant, the variation is expected to decrease with window size.
As well as the size of the time-window and the choice of intermittency, the frame rate of the camera could also have an impact on the size of the flame region. Figure 9 shows how the size of the flame region varies with frame rate given a fixed time-window of 30 s and an intermittency of 50%. This figure suggests that, over a 30 s time-window, the framerate does not have a large impact on the size of the flame region, varying in area only by \(\pm\) 5 mm2. This implies that a framerate of 2 Hz was sufficient. The impact of framerate would likely be larger though if a very short time window was used, as only a small number of frames would be used for averaging, meaning the variance would be larger. An analysis of the eddy frequency of the flame following the method by Pagni [28], considering that the characteristic diameter of the rectangular burner can be only roughly approximated, resulted in a flame shedding frequency between 0.60 – 0.83 Hz. This means that an accidental synchronization between the camera and frequency of the flame is possible, however, in our case highly unlikely.
Mean flame area (top) and variation in flame area (bottom) calculated by orthographically projecting images from the camera facing the \(XZ\) plane, over the same period of burning using a fixed intermittency of 50%, a fixed time-window of 30 s, but using different framerates (given in frames per second)
The calibration experiments were run for at least 120 s for each flow rate in Table 2. For each experiment, the volume of the 50% intermittency region over a 30 s time-window was calculated over a 60 s duration, giving sufficient time for the flow rate to stabilise between the changes in flow rate and wind conditions. An example of the volume calculated over this period is shown in Figure 10. The mean volume over this 60 s period is shown for each experiment in Figure 11. The error bars represent the 95% confidence interval of the individual experiments (1.96 standard deviations), calculated from the variation over the 60 s period (as shown in Figure 10). In Figure 11, the lines representing the constant volumetric heat release rates calculated by Orloff and De Ris [2] and Stratton [14] are shown for comparison alongside a volumetric heat release rate that was found by performing a least squares linear regression on the experimental data. The grey shaded area shows the 95% confidence interval of the fit. This is narrower than the 95% confidence regions from the individual experiments (see Figure 10), as using data from all of the experiments together increases the confidence in the central data. This shaded region in Figure 11 represents the expected out-of-sample variation of \(\gamma\) for cases similar to these experiments. To validate the method to more general conditions, further research would be needed to perform experiments across a wide range of fires.
Example of volume measurements with time for a single calibration experiment with two sand burners at a heat release rate of 40 kW each (a total of 80 kW). Each scatter point on Figure 10 represents the mean of one of these experiments with the error bars giving the 95% confidence interval of the data (the region containing 95% of the data, assuming it is normally distributed).
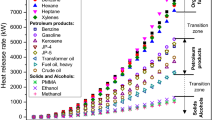
Results from the calibration experiments, using the Visual Fire Power method to predict the volume of fire from sand burners at constant heat release rates, located against a wall, with and without a 2 m/s incoming wind. Outlines of the flames are shown for different datapoints for context. The least-squares fit from these experiments falls between the values of \(\gamma\) from the work of Orloff & De Ris [2, 6] and Stratton [14], which lends confidence to the results of these experiments. The grey shaded area gives the 95% confidence interval of the linear fit.
The calibration experiments give a final value of \(1505\pm 183\) kW/m3 for the Orloff-DeRis constant converting volume to heat release rate in the Visual Fire Power method. This falls between the values of 1100 and 1200 kW/m3 derived by Orloff and De Ris [2, 6] and the value of 1878 kW/m3 derived by Stratton [14] (taking the value for the 50% intermittency volume), which lends some confidence to the calibrated value. Future work should investigate whether these values hold for fires of different scales and fuel types, as well as different ventilation conditions.
3.3 Application to Facade Testing
In the introduction, we mentioned that Visual Fire Power could provide an easy way to include heat release rate measurements into fire testing, such as those performed on facades. Different national facade fire test standards are often quite different and record different criteria to determine whether a facade passes or fails. However, nearly all of these failure criteria across different standards relate to a facade’s flammability [29]. The heat release rate is a key variable in identifying the flammability of a material or facade system, and so the inclusion of this measurement into standard tests could be of great benefit.
To demonstrate the application of Visual Fire Power, we applied the algorithm to a test performed according to the PN-B-02867 test standard [19]. The standard involves igniting a 600 × 300 mm, 20 kg wood crib 50 mm from the facade at its centreline, and then removing the crib after 15 min. The facade is then observed for an additional 15 min for continued fire behaviour. Throughout the test, a fan applies an average 2 m/s air flow towards the facade; this is in contrast to other similar test standards, where no wind is included.
Figure 12 demonstrates the heat release rate curve measured during one of these tests using the Visual Fire Power algorithm. This was a test where the facade did not ignite or contribute to the fire. The curve follows the expected qualitative behaviour of the wood crib: a period of rapid growth, followed by a period of steady burning, followed by a sharp drop when the crib was removed at 15 min. This gives us confidence that Visual Fire Power could be used in commercial facade testing.
4 Conclusions
This paper has demonstrated an efficient method to measure the heat release rate of a turbulent fire using regular video footage from two cameras, located at a right angle to each other and at a known distance from the fire. The Visual Fire Power method relies on the fact that, for a turbulent fire, the time-averaged volume of the fire is linearly proportional to its heat release rate according to the Orloff-DeRis constant \(\gamma\).
The method was evaluated on synthetic data in the 3D graphics software Blender, where it was used to predict the volume of basic 3D shapes with fixed volume. The accuracy of the method was most sensitive to the distance that the cameras were located from the object being analysed, and the uncertainty in the method was found to be around 30% on average. The method was then calibrated on experiments using sand burners at fixed heat release rates. The value of the Orloff-DeRis constant in these experiments was found to be \(1531\pm 187\) kW/m3 with an R2 coefficient of 0.61. This value falls between the values found in previous work [2, 6, 14].
The Visual Fire Power method is an inexpensive and easy way to measure the heat release rate of turbulent fires in situations where a more complex method might be infeasible; for instance, it could be used to measure the heat release rate of fire experiments that took place outside, to measure the heat release rate of separate regions of fire in the same experiment, or to improve the measurements of facade flammability taken during standardised facade fire tests such as BS 8414. These tests are often already filmed, so the addition of a second camera would be simple to achieve. Improving the range of data measured in both these standard tests and in fire experiments in general could help to increase our knowledge of fire dynamics and provide better information for researchers and engineers in the future.
References
Babrauskas V, Peacock RD (1991) Heat release rate: the simple most important variable in fire hazard. Fire Saf J 18:255–272
Orloff L, de Ris J (1982) Froude modeling of pool fires. Symp Combust 19:885–895. https://doi.org/10.1016/S0082-0784(82)80264-6
BSI (2015) BS 8414–1:2015 Fire performance of external cladding systems. Test method for non-loadbearing external cladding systems applied to the masonry facade of a building
Bonner M, Wegrzynski W, Papis BK, Rein G (2020) KRESNIK: a top-down, statistical approach to understand the fire performance of building facades using standard test data. Build Environ 169:106540. https://doi.org/10.1016/j.buildenv.2019.106540
Čolić A, Pečur IB (2020) Influence of horizontal and vertical barriers on fire development for ventilated façades. Fire Technol 56:1725–1754. https://doi.org/10.1007/s10694-020-00950-w
De Ris JL, Orloff L (2005) Flame heat transfer between parallel panels. Fire Saf Sci. https://doi.org/10.3801/IAFSS.FSS.8-999
De Ris JL (2013) Mechanism of buoyant turbulent diffusion flames. Procedia Eng 62:13–27. https://doi.org/10.1016/j.proeng.2013.08.040
Xin Y (2014) Estimation of chemical heat release rate in rack storage fires based on flame volume. Fire Saf J 63:29–36. https://doi.org/10.1016/j.firesaf.2013.11.004
Shen G, Zhou K, Wu F et al (2019) A Model considering the flame volume for prediction of thermal radiation from pool fire. Fire Technol 55:129–148. https://doi.org/10.1007/s10694-018-0779-y
Li K, Mao S, Feng R (2019) Estimation of heat release rate and fuel type of circular pool fires using inverse modelling based on image recognition technique. Fire Technol 55:667–687. https://doi.org/10.1007/s10694-018-0795-y
Hu L, Zhang X, Wang Q, Palacios A (2015) Flame size and volumetric heat release rate of turbulent buoyant jet diffusion flames in normal- and a sub-atmospheric pressure. Fuel 150:278–287. https://doi.org/10.1016/j.fuel.2015.01.081
Mason P (2003) Estimating thermal radiation fields from 3D flame reconstruction. Lincoln University, Lincoln
Mason PS, Fleischmann CM, Rogers CB et al (2009) Estimating thermal radiation fields from 3D flame reconstruction. Fire Technol 45:1–22. https://doi.org/10.1007/s10694-008-0041-0
Stratton BJ, Spearpoint M, Fleischmann C (2005) Determining flame height and flame pulsation frequency and estimating heat release rate from 3D flame reconstruction. University of Canterbury, Christchurch
Graham D (2016) Tomographic reconstruction of a swirling flame. Imperial College London, London
Bradski G (2000) The openCV library. Dr Dobb’s J Softw Tools 120:122–125
Bradski G, Kaehler A (2008) Learning openCV: computer vision with the openCV library. O’Reilly Media Inc, Sebastopol
Blender Online Community (2018) Blender - a 3D modelling and rendering package. Stichting Blender Foundation, Amsterdam
PKN (2013) PN-B-02867:2013–06 Fire protection of buildings. Method for testing the degree of fire propagation through external walls from the outside and classification rules
ISO (2002) ISO 13785–1:2002 Reaction-to-fire tests for façades. Part 1: Intermediate-scale test
Khan MM, Tewarson A, Chaos M (2016) Combustion characteristics of materials and generation of fire products. In: Hurley MJ, Gottuk D et al (eds) SFPE handbook of fire protection engineering, 5th edn. Springer, New York, pp 1143–1233
Audouin L, Kolb G, Torero JL, Most JM (1995) Average centreline temperatures of a buoyant pool fire obtained by image processing of video recordings. Fire Saf J 24:167–187. https://doi.org/10.1016/0379-7112(95)00021-K
Çelik T, Demirel H (2009) Fire detection in video sequences using a generic color model. Fire Saf J 44:147–158. https://doi.org/10.1016/j.firesaf.2008.05.005
Çelik T, Demirel H, Ozkaramanli H, Uyguroglu M (2006) Fire Detection in Video Sequences Using Statistical Color Model. IEEE International Conference on Acoustics Speech and Signal Processing, Volume 2 https://doi.org/10.1109/ICASSP.2006.1660317
Chen J, Bao Q (2012) Digital image processing based fire flame color and oscillation frequency analysis. Procedia Eng 45:595–601. https://doi.org/10.1016/j.proeng.2012.08.209
MacQueen J (1967) Some methods for classification and analysis of multivariate observations. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics
Ronneberger O, Fischer P, Brox T (2015) U-Net: Convolutional Networks for Biomedical Image Segmentation
Pagni P (1990) Pool fire vortex shedding frequencies. Appl Mech Rev 43:166
Bonner M (2021) A top-down approach to understand the fire performance of building facades using standard test data. Imperial College London, London
Acknowledgements
This research has been funded by the Engineering and Physical Sciences Research Council (EPSRC, UK) and Arup (UK), and ITB statutory grant NZP-130/2019. Thank you to Egle Rackauskaite, Eirik Christensen, Benjamin Khoo, Francesca Lugaresi, and Nikolaos Kalogeropoulos for their support and suggestions. Figure 1 used some graphics produced by Arthur Scammel. The 3D icons in Figure 4 are by Yu Luck from The Noun Project.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix 1: An Explanation of Orthographic Projection
Appendix 1: An Explanation of Orthographic Projection
This section explains the concept behind orthographic projection, where the position of an object in a 3D space is estimated using 2D projections of that object. The concepts and notation are taken from [17], but are summarised here to help explain the Visual Fire Power method.
In computer vision, cameras are typically represented using the pinhole camera model, shown in Figure 13. Light rays from an object located a distance \(Z\) away from the camera all pass through a single point: the camera’s centre of projection or pinhole. The light rays will then strike the image plane at a distance \(f\) away from this centre of projection. This distance \(f\) is the focal length and is an intrinsic property of the camera. The axis that passes through the centre of the image plane, through the centre of projection, is referred to as the optical axis of the camera. It is clear from Figure 13, using the premise of similar triangles, that an object with its base located along the optical axis at a distance \(Z\) from the centre of projection with a height of \(X\) will appear on the image plane as having height \(x= \frac{-Xf}{Z}\).
A 2D illustration of the basic pinhole camera model. Light rays from an object a distance \(Z\) away from the camera’s centre of projection (or pinhole) must pass through this point and land on the image plane a distance \(f\) away. This model can easily be generalised into 3D. It is also possible to take into account the distortions caused by including a lens rather than a perfect pinhole. Details on this can be found in [17]
This model can be extended into 3D by defining a coordinate system \(({X}_{c}, {Y}_{c}, {Z}_{c})\) relative to the camera’s pinhole or centre of projection \(C\), with \({X}_{c}\) and \({Y}_{c}\) located along the horizontal and vertical lines of the image plane, and \({Z}_{c}\) pointing along the axis of projection, away from the image plane. The projection of any coordinate in 3D space onto the image plane can be performed through matrix multiplication with a camera matrix:
where \(f\) is the focal length of the camera and \({c}_{x}\) and \({c}_{y}\) are the distance in pixels from the top-left corner of the image plane to the centre of the image plane (which is also the centre of projection). This matrix will transform a 3D coordinate as follows:
Dividing the first two coordinates by the third coordinate \({Z}_{c}\) will give you a coordinate in the image plane \(\left(\begin{array}{cc}\frac{f{X}_{c}}{{Z}_{c}}+{c}_{x}& \frac{f{Y}_{c}}{{Z}_{c}}+{c}_{y}\end{array}\right)\). This is the projection shown in Figure 13 but with an additional translation by \(\left(\begin{array}{cc}{c}_{x}& {c}_{y}\end{array}\right)\). This allows us to define a new coordinate system in the image plane, with its origin at the top left corner of the image. These are referred to as pixel coordinates \((u,v)\), with \(u\) representing the horizontal distance from the top left corner in pixel units and \(v\) representing the vertical distance. This will also depend on the resolution of the image, but this is captured in the value of \(f\), which is in pixel units.
If we are considering more than one camera, we are usually more interested in a set of global coordinates defined in relation to some object in the world. To map between these object centred coordinates \(\left(\begin{array}{ccc}{X}_{o}& {Y}_{o}& {Z}_{o}\end{array}\right)\) and the camera centred coordinates \(\left(\begin{array}{ccc}{X}_{c}& {Y}_{c}& {Z}_{c}\end{array}\right)\), we need to know the position and rotation (called the pose) of the camera with relation to the reference object. This rotation and translation can be represented by a rotation matrix \(R\) and a translation vector \(T\), where:
where \({r}_{ij}\) are the components of a standard 3D rotation matrix, and \({T}_{x}, {T}_{y}, {T}_{z}\) are the distances from the camera to the reference world origin \(O= \left(\begin{array}{c}{X}_{o}\\ {Y}_{o}\\ {Z}_{o}\end{array}\right)\). This allows for the following mapping between coordinates in the 3D world and coordinates in the image plane:
Each of these transformations can be inverted in the following way:
Which means the image plane can be inversely projected back into 3D coordinates. However, objects that were at different distances will now be collapsed onto the same plane. This method of projection is known as orthographic projection and is the basis of the Visual Fire Power algorithm.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bonner, M., Węgrzyński, W. & Rein, G. Visual Fire Power: An Algorithm for Measuring Heat Release Rate of Visible Flames in Camera Footage, with Applications in Facade Fire Experiments. Fire Technol 59, 191–215 (2023). https://doi.org/10.1007/s10694-022-01341-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10694-022-01341-z