Abstract
Flame spread experiments upon a BROOF(t4) compliant flat roof mock-up located below a vertical barrier were carried out for variations in gap height, inclination, subjacent insulation material, and the barrier type (stainless-steel board or photovoltaic (PV) module). A binary flame spread scenario was identified, where re-radiation from the flame facilitated self-sustained flame spread if the gap height to the horizontal panel was below 10 cm for the stainless-steel board and 11 cm for PV modules. These were defined as the critical gap heights. Inclination of the PV modules increased the critical gap height and caused a 25% faster flame spread rate (FSR) than the FSR below horizontal modules with the same gap height at the location of ignition. The faster FSR for inclined modules caused a 40% reduction of the maximum temperature measured at a depth of 70 mm in the insulation materials (242°C). Based on temperatures measured in the insulation materials, the 60 mm polyisocyanurate (PIR) insulation performed slightly better than the 50 mm mineral wool insulation. However, it is expected that the mineral wool would outperform the PIR insulation if tested with the same thickness, as it insulates significantly better at high temperatures. Finally, no sustained flame spread was observed on the back side polymer sheet of the PV modules, but one of the three PV module brands produced burning droplets. Based on the experiments, it can be concluded that the current standards are inadequate as the introduction of a PV system on a compliant roof construction enables flame spread.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During the initial two decades of the current millennium, there has been an exponential growth in the global energy capacity produced by photovoltaic (PV) installations, from a capacity of 0.54 GW in 2000 to 760 GW at the end of 2020 [1]. PV systems are available in all sizes, from the single PV cell on the side of a power bank, through domestic and commercial installations on building property, to terrestrial installations of almost 1 GW, such as the Longyangxia Dam Solar Park in China [2]. The increased amount of PV systems is linked to a continuous cost reduction of the PV modules [3, 4], and thus, energy cost, which also makes it attractive for commercial and domestic property owners to utilise their otherwise unused roof constructions for building attached PV installations (BAPV).
However, PV installations cause an increased probability of ignition [5,6,7,8,9,10], and the physical presence of the PV modules modify the fire dynamics of the existing roof construction [11,12,13,14]. The potential risk is exemplified by the recent legal dispute between Walmart and Tesla, where Walmart requested Tesla to remove BAPVs from 244 of their warehouses, because of the seven fires that occurred between 2012 and 2019 [15, 16].
Generally, statistical data for PV-related fires is sparse and there is no knowledge about any recent data from any fire brigades, but a recent analysis estimated that the annual fire incident frequency is 28.9 fires per GW capacity [17]. In Italy, around 460 PV related fires occurred annually between 2011 and 2015 according to Bonomo et al. [18], whereas a German survey from 2013 identified a total of 430 PV related fires [5]. No comprehensive data exist for the US [19], but according to the PV Magazine, the number of PV-related fires in Arizona alone has gradually increased from 25 in 2015 to 56 in 2018 [20]. Mohd Nizam Ong et al. wrote an overview of the best practice for the design and installation phases of roof top installed PV systems. They found that fire safety was often included in the installation guidelines covering the electrotechnical part of the technology, whereas fire safety related to the interaction with the hosting building was rarely mentioned in the design [21]. With an expected service life of 25 to 40 years for PV systems [22], it is deemed that understanding of the long term fire-related risk of PV systems is essential to ensure sustainable growth of the technology.
The presence of PV arrays on a roof establishes a gap between the backside of the PV module and the top of the roof construction that can be considered a semi-enclosure, which introduces a significant change of the fire dynamics in the case of a fire. To prevent flame spread along flat roof constructions without a BAPV system, the roofing membrane or roofing system should be compliant with standards, such as the North American UL 790 [23] or European EN 13501-5 [24]. The PV modules are designed to be compliant with UL 61730 [25] (previously UL 1703 [26]) or IEC 61730 [27, 28], which are almost similar and mainly focused on the electrical system and thus, reduction of ignition probability. UL 61730 does, but IEC 61730 does not, acknowledge that the PV module, as a physical object, modifies the fire dynamics, which is why a series of standard tests based on UL 790 [23] have been introduced. However, the standards are pass/fail tests where the specifications to the test setup are vague and thus permit interpretations. As a result, the outcomes of the tests are not necessarily independent of the test facility and the test personnel.
The European Committee of Electrotechnical Standardization, CENELEC, has published the test report CLC/TR 50670 ‘External fire exposure to roofs in combination with photovoltaic (PV) arrays — Test method(s)’ [29]. In this test method, a gas burner designed as a substitute to the wood wool basket from test method 1 in CEN/TS 1187 [30] by Currenta GmbH und Co. OHG [31] is installed in between the tested PV module and a non-combustible surface. The PV module should be inclined \(30^\circ\) with the lowest edge elevated 15 cm above the subjacent surface. The suggested method is deemed to be a test of the PV module when exposed to a flame, rather than the combination of a roof and a PV module. As such, it can be concluded that no test method considers the system behaviour between components, as the current methods are tests of individual components.
However, Cancelliere et al. [32] fitted a modified version of the CLC/TR 50670 test set-up in combination with 0.375 m2 roofing membrane within the single burning item extraction hood in an attempt to classify the PV modules as a construction product (EN 13813 [33]). Since their modified tests were a combination of two products interacting with each other, the test method is not deemed to test a single construction product, but rather the test of a system in a specific pre-defined geometry which does not represent a likely geometry. As such, the tested method aligns with UL 61730 and is deemed to be a pass/fail-test.
Overall, research associated with the reduction of fires related to BAPV systems can be separated into two sub-fields, namely (i) a reduction of the ignition probability related to electrotechnical engineering [34,35,36,37,38], and (ii) a mitigation of the consequences in case of ignition, which is often related to fire safety engineering. From a fire safety engineering perspective, the current research can be categorised into additional subfields, from examination of individual components, through analysis of specific fire dynamic scenarios, to large scale experiments.
In terms of large scale experiments, Backstrom et al. summarised the result from experiments conducted with modified versions of the US standard test method for roofing materials UL 790 [39], whereas Kristensen and Jomaas conducted a series of large-scale experiments to understand flame spread on flat roof constructions with BAPV systems [40]. Common for all of these experiments was the fact that they can be considered as pass/fail-experiments, where it is tested whether a given experimental set-up results in sustained flame spread. As such, large scale experiments are ideal if the objective is to understand the behaviour of a specific set-up reused on multiple similar roof constructions, but the consequence of parametric nuances are not understood, although it can have significant impact on the consequences.
Examination of individual variables such as material parameters or geometry is the direct opposite of large-scale experiments. The advantage of using a smaller scale is an increased understanding of individual parameters in a highly complex fire dynamic system, as several complex factors are simplified. But the focus on one parameter does not enable comparison across various parameters, whereupon a one parameter study does not identify how essential the studied parameter is in the complex system. As an example, the one-directional flame spread study in a horizontal semi-enclosure by Kristensen et al. examined the influence of gap height, but substituted the complex thermal properties of the roofing membrane with the well-known simple behaviour of polymethyl methacrylate (PMMA) [14]. Despite the fact that both materials are polymers, the presence of flame retardants in the roofing membrane is expected to render the outcome significantly different. Cancelliere and Licilotti tested the reaction to fire of four types of PV modules, whereupon they concluded that the highest rated type of module could reduce the spread of fire [41]. Their examinations in the cone calorimeter revealed that the critical heat flux of the PV module back sheet was 26 kW/m2 [42]. Despinasse and Krueger developed a novel test procedure, wherein they applied a gas burner to either the front or back side of PV modules and defined burn-through within 15 min as a failure criteria [43]. In general, those studies are an examination of relevant test methods, with the aim of categorise a PV module as compliant or non-compliant based on the reaction to different test regimes. Other research teams have focused on how the PV module caused deflection of the flames from a fire in between the BAPV module and the hosting roof construction, causing an increased heat flux towards the subjacent surface, which they conclude can enhance the probability of flame spread [11,12,13,14]. However, those experiments are either performed as steady state or as strictly geometric studies with the simplest possible material properties, whereupon it is anticipated, but can be questioned, if the results can be extended to more complex scenarios.
In the light of both the single parameter and large-scale experiments having their limitations, thus making it difficult to grasp the crucial parameters of the highly complex fire dynamics system, the aim of the current experiments was to examine how multiple parameters affect one-dimensional flame spread. The fire dynamic system was defined as the interaction between the initial fire and the semi-enclosure created by the PV module and the roof construction. By reusing the design concept from the flame spread studies on PMMA below a horizontal panel by Kristensen et al. [14], all parameters not related to the size of the roof could be studied by examining the phenomena below a single module, rather than below multiple panels on a large scale roof construction. As both genuine PV-related fire incidents and large-scale studies [40] conclude that ongoing fires are restricted by the edge of the PV arrays, the transition from the initial ignition to a fire is found to be more relevant. Also, the re-use of the experimental design concept enables a stepwise increase of complexity, where one parameter can be added and analysed, whereupon another parameter can be modified in a slightly more complex system and so on. Thus, a full understanding of each parameter might not be obtained, but it is possible to compare the significance of each parameter against each other, which is deemed to be the ideal compromise between the single parameter and large-scale experiments.
Roof inclination, wind load and the increased fire load caused by the PV infrastructure (i.e. cables, connectors, mounting system, combiner boxes and inverters) are some of the variables that might influence the fire dynamic scenario. The wind load and roof inclination are deemed to be stochastic parameters that might be difficult to modify. A wind load could be introduced from any side of the experimental set-up and depending on the intended flame spread direction, some extent of concurrent or opposed flame spread should be expected. Such scenario is interesting within the initial phase of the fire, as the wind direction could influence which nearby materials that are going to be ignited. For high wind velocities the concentration of combustible pyrolysis gases might be diluted to an extent where ignition is impossible. However, when the fire is established, it is assumed that the deflection of the flames below the modules reassembles concurrent flame spread, no matter the direction of the wind. It is also accepted that an inclination is an essential part of all roof constructions to ensure drainage of water from the surface. On flat roof constructions, a fall of minimum 1:40 (1:80 for the finished roof) is the minimum accepted. Similar to the wind direction, the roof inclination might affect the initial flame spread, but post ignition it is deemed that the influence is neglectable compared to the consequences of the deflected flame. It is recognised that cables, connectors, and mounting system represents an increased fire load to the roof. However, these components are relatively localised and does not cover the whole roof. That does not correspond well with the consequences of large PV-related fires reported by the insurance company Allianz [44], as well as the outcome of the large-scale experiments by Kristensen and Jomaas [40].
Based on the above, the current study focuses on the importance of the following four parameters: (i) The type of panel acting as a vertical barrier above the initial fire; (ii) The gap height between the roof surface and the vertical barrier; (iii) The inclination of the vertical barrier; (iv) The material subjacent to the roofing membrane. It is assumed that one roofing membrane is representative for all roofing membranes used on the European marked, as they have passed the same test regime to comply with a given classification (herein the European EN 13501-5, ‘Fire classification of construction products and building elements—Part 5: Classification using data from external fire exposure to roofs tests’, [24], BROOF(t4)).
The first three parameters are all related to the property or geometry of the panel above the roof construction. As current research seems divided into two schools distinguished by considering PV modules as a fire load [41,42,43] or not [11, 12, 14], it is essential to understand whether the polymer back sheet affect the flame spread scenario. The importance of the gap height and inclination were indicated in the steady-state experiments by Ju et al. and Tang et al. [12, 13], whereas the one-dimensional studies in horizontal gaps by Kristensen et al. [14] verified that the gap height had a significant effect on the flame spread scenario. Finally, the materials below the roofing membrane are of interest for three reasons. (i) The thermal properties of insulation materials vary as a function of product and temperature. Although the roofing membrane is assumed to thermally thin, heat transfer between the lower surface of the roofing membrane and the upper surface of the subjacent material might affect the heating of the roofing membrane. (ii) Many BAPV systems are retro-fitted on existing buildings where the roof might be unfit for a large DC system due to the existing insulation material. The worst-case scenario is a roof insulated only with expanded polystyrene. Such a construction will require a mitigation layer to prevent severe consequences. (iii) To isolate the behaviour of the roofing membrane from the subjacent material and enable a direct comparison with the one-dimensional flame spread studies on PMMA in horizontal semi-enclosures by Kristensen et al. [14], a part of the experiments were conducted on calcium silicate board. As such, the influence of flame retardants in the PVC-based membrane can be observed without the influence from commercial insulation products.
2 Re-Radiation in Semi-Enclosures with PV Modules
Two of the four parameters are related to the geometry of the array of the PV modules, rather than the material properties of the components in the semi-enclosure. The introduction of a vertical barrier (here: a PV module) above a heat source results in an additional heat flux towards the surface below the barrier. In fact, it has been shown that introducing a PV module enabled flame spread upon a commercially available roofing membrane that did not have flame spread without the PV module [40]. This can be explained by the fact that the added heat flux resulted in a combined heat flux, \(q^{\prime\prime}_{f}\), that exceeded the critical heat flux for the membrane [11]. By using a similar experimental set-up (Figure 1), Ju et al. [12] and Tang et al. [13] verified the presence of an additional heat flux when a flame is deflected below a vertical barrier. In addition to the verification, they suggested expressions to predict the flame extension [12] or heat flux towards the subjacent surface [13] (see Equation 1) as a function of inclination \((\theta ),\) gap height \((H)\), and distance to the heat source \((\pm r)\) [13].
where: \(a=0.074, b= -1.232\)
Two of the experimental campaigns were directly linked to PV systems on flat roofs [11, 12], whereas Tang et al. used the setup to examine re-radiation from flames deflected below an inclined ceiling towards a floor. However, the gap height in the experiments by Tang et al. was no larger than 0.4 m, so they were more similar in dimension to a PV-roof system than the distance between a ceiling and a roof.
All of these experiments reported a significant heat flux increase caused by the introduction of a vertical barrier represented by a PV module [11, 12] or a non-combustible surface [13]. When the panel was inclined, the buoyancy driven mass flow caused the highest amount of fuel upstream, leading to a longer flame extension, and thus, heat flux towards the subjacent surface. The results from Kristensen et al. and Ju et al. align very well, especially when compared via the non-dimensional parameters defined by the left and right side of Equation 1, as shown in Figure 2. However, none of the two datasets correspond well with the model by Tang, as the right-hand side of Equation 1 assumes significantly larger values than the left-hand side, which is elaborated in the following section.
The significantly smaller values on the x-axis for the plots based on data by Ju et al. are caused by a lower ratio between the gap distance \((H)\) and the distance between the heat source and the nearest heat flux gauge (r). By comparing the left-hand side of the model by Tang et al. (Equation 1) with the data by Kristensen and Ju, it is noticed that the experimental data are significantly lower than the model predictions (Figure 2). It is not possible to make any exact comparison between similar measurements by Tang and Kristensen or Ju, but for \(H=0.194\, m,\, \theta =10^\circ ,\, r=0.2 \,m\), the heat flux is estimated to \({\dot{q}}_{f}^{\prime\prime}\approx 5.3 \,kW/{m}^{2}\) for \(\dot{Q}=7 \,kW\) in the experiments by Ju et al. [12], whereas the heat flux is measured to \({\dot{q}}_{f}^{\prime\prime}\approx 10\, kW/{m}^{2}\) for \(\dot{Q}=6.73\, kW,\, H=0.25\, m,\, \theta =0^\circ\) at the same distance to the heat source in the experiments by Tang et al. [13]. This does not correspond with the overall trend in the three papers, where the upstream heat flux, at a similar distance, should increase as a function of a gap height reduction as well as an inclination increase from \(0^\circ\) to \(10^\circ\). Additionally, the reduction of the heat release rate (HRR) should also lead to a reduced heat flux, whereupon all three parameters (\(\theta , H, r\)) in the experiment by Tang et al. should result in a heat flux smaller than the one measured by Ju et al.
However, the different heat fluxes may be explained by the dimensions of the gas burners, which affected two relevant parameters: (i) The view factor towards the heat flux gauge, and (ii) The Froude number. A circular burner with an internal diameter of 10 mm was used by Ju et al., whereas Tang et al. used a squared burner with a side length of 120 mm. Thus, the view factor from the vertical part of the flame was higher in the experiments by Tang, which caused a higher radiative heat transfer towards the point of the heat flux gauge. Looking at the Froude numbers [45], the buoyancy driven turbulent diffusion flame in the experiments by Tang et al. (\(Fr= 3.54\times {10}^{-10}\)) will result in a lower convective heat transfer compared to the laminar diffusion flow in the experiments by Ju et al. (\(Fr=1.55\times {10}^{-4}\)), which will cause a higher heat transfer rate.
Although there is a limited coherence between the two data sets and Equation 1, with the suggested scaling factor, a, and exponent, b, the theory behind the model seems relevant and a with more experimental data, combined with taking the burner dimensions and flow characteristics into account, an increased understanding of the geometric issue could probably be obtained. Of course, it has been of great interest to develop a unified theory incorporating the geometric variables as well as some of the material parameters.
But with the current exponential growth of global PV capacity and with the limited level of understanding, it is necessary to find a balance between need to know and nice to know. It is a practical problem, which needs to be solved with a practical approach and thus, an experimental campaign where it is accepted that known theory can be applied to explain the results, whereas theory cannot necessarily be used to predict the exact outcome of a specific set-up.
As such, the aim of the current experiential study is not to develop new or elaborate on existing theory. It is a fundamental study where the significance of the four selected parameters presented in the introduction are examined.
3 Experimental Setup
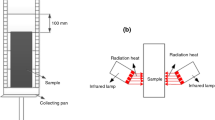
An experimental set-up was designed so that the four relevant parameters (panel type, gap height, panel inclination, and material subjacent to the roofing membrane) could be adjusted. The set-up consisted of a roof a mock-up frame (see Figure 3a), and a simple frame on which the stainless-steel board or PV module could be installed at various heights and inclinations (see Figure 3b).
To prevent significant preheating of the insulation materials from the source of ignition, the mock-up frame was partitioned into three sections with lengths of respectively 265 mm, 700 mm and 265 mm (Figure 3a). The roof mock-up itself was installed as a box in the centre, which could host the three different roof constructions (RCs) presented in Table 1. All walls of the box as well as the top surface of the two flanges were made of 22 mm thick calcium silicate board [46].
All the RCs had an upper layer of the roofing membrane (L1), with the dimensions of 118 cm by 37 cm. The subsequent layers L2–L5 (see Table 1) were fitted inside the centre-box and were limited to 70 cm by 30 cm, and had a total depth of 15 cm. It was assumed that no conductive heat was transferred from the source of ignition to the roof construction mock-up. Thus, all energy gained by the insulation was gained from the burning roofing membrane. To enable an easy adjustment of the gap distance, two lab-jacks were installed below the mock-up.
An experimental matrix (Table 2) was designed to obtain a gradual increase of material complexity. As such, the initial nine experiments (#1–#9) were designed to examine the existence of a critical gap height for the given set-up below a stainless-steel plate. In the next nine experiments (#10–#18), the subjacent calcium silicate board was replaced with mineral wool to understand the influence of the conductive heat transfer. Afterwards, in experiments #19–#31, the stainless-steel board was replaced with PV modules to determine its influence on the flame spread rate (FSR) and the heat transfer through the subjacent insulation materials. The final examined parameter was the inclination of the modules, to examine the importance of the findings by Tang et al., who reported that a gradual increase of the inclination (up to \(20^\circ\)) cause an enhanced heat flux towards the upstream (see Figure 1) subjacent surface.
The gap distances, all between 8 cm and 12 cm, were measured between the upper surface of the roofing membrane and the lower side of the stainless-steel board (#1–#18). For the experiments conducted with PV modules, the distances were measured to the back of the module and not to the back of the frame. For the experiments with an inclined PV module (#32–#42), the gap distances were measured at the centre location of the ignition source.
3.1 Materials and Experimental Roof Mock-Up
A PVC-based roofing membrane, classified as BROOF(t4) in accordance with EN 13501-5 (ENV 1187) when tested upon mineral wool or PIR insulation [24, 47, 48], was used for all the experiments. To mimic a larger roof construction and thus prevent shrinkage of the heated roofing membrane, the membrane was mechanically fastened on all four sides by 25 mm wide, thin, metal sheets and bolts connected to the aluminium profile system. The width of the upper layer of the membrane, L1, was 37 cm, whereas the width of all subjacent layers was limited by the 30 cm width of the mock-up box.
In general, two types of materials were used below the roofing membrane: (i) a 22 mm thick calcium silicate board (RC-A), and (ii) a mock-up roof construction (which had two variants, RC-B & RC-C). Due to the assumption of an original worst-case scenario roof construction insulated with expanded polystyrene (EPS), none of the mock-up roof constructions resembled a classic roof construction build-up. To mitigate the consequences in case of fire, it was tested if an additional layer of insulation, installed on top of the original roof, could prevent vertical flame spread, and thus ignition of the EPS insulation. The two layers tested as vertical mitigation solutions were: (A) 50 mm mineral wool [49], and (B) 60 mm polyisocyanurate (PIR) insulation protected by a layer of alufoil on both horizontal surfaces [50]. The thermal properties of the subjacent materials can be found in Table 3.
3.2 Panels
Two types of panels were used in the experiments: (i) A 3 mm thick stainless-steel board, and (ii) PV modules (three different types). In the flame spread studies with PMMA [14], the stainless-steel board was used as a substitute for the PV modules, thus making it possible to increase the number of experiments. In this experimental campaign, the same stainless-steel board was used as a bridge, to understand the influence of the PV module and a non-combustible surface. Based on the findings in earlier re-radiation studies [11, 12, 40], it was not expected that the use of a stainless-steel board instead of a PV module would have a significant influence on the FSR. Those conclusions align well with the back sheet only representing 2.8% to 3.5% of the module weight, whereas the encapsulate represents 6.3% to 8% [55]. The two highly thermally stable fluoropolymers Tedlar® and Kynar® are among the most used products for back sheets [55, 56] and with a heat of combustion between 4.1 kJ/g and 5.4 kJ/g [57], a very limited additional heat flux was expected. In contrast, the heat of combustion of the commonly used encapsulate ethyl vinyl acetate (EVA) [55] is 41.6 kJ/g [58] and despite previous research indicating that the contribution is limited, it does, theoretically, increase the fire load on the roof.
As such, it is decided to examine the potential influence of the PV module back sheet. To avoid the possible increased heat flux caused by combustion of the PV module, a stainless-steel board (1.7 m by 1.0 m) was used in the initial 16 experiments. As the same panel were used to study flame spread on PMMA in horizontal semi-enclosures [14], the reuse enabled understanding of the difference between flame spread on PMMA and a PVC-based roofing membrane with flame retardants.
A total of 23 pre-used, or faulty, though non-damaged, PV modules were obtained for use in the experiments. Because limited information was available regarding the construction of the three PV modules (Table 4), the experimental matrix was designed so each type of module was used for autonomous sub-studies within the overall experimental campaign. However, comparison of the PV modules was possible across the sub-studies, as experiments 32, 33, 36 and 39 share both geometry and type of roof construction (Table 2).
3.3 Source of Ignition
The use of a wood crib was preferred as ignition source over an electric DC arc for two reasons: (i) To ensure a reproducible and well-tested source of ignition [59], and (ii) To prevent the risk related to high voltage direct current.
The four-layer wood cribs, with five pine sticks (81 mm by 9 mm by 9 mm) in each layer, was elevated by a single stick along two edges parallel to the direction of flame spread. Ceramic paper (80 mm by 50 mm by 2 mm) was soaked in 10 g of methanol and placed below the wood crib, whereupon it was ignited. Using the cone calorimeter without external heat from the cone heater, the peak mass loss and heat release rate of the wood crib were measured to respectively 0.36 g/s and 5.4 kW [60], which was slightly lower than the calculated mass loss rate of 0.47 g/s for the four upper layers (using the method introduced by McAllister [61]).
In each experiment, the wood crib was built at the centreline with the left side of the crib located 8 cm from the left edge of the roofing membrane. Thus, it was assumed that no conductive heat transfer from the wood crib towards the roof mock-up took place as the distance between the right side of the wood crib and the left side of the roof mock-up was 10 cm (see Figure 3).
With re-radiation from the initial fire plume being the focal point of the flame spread scenario, it was assumed that the domain of the ignition source, being the area gaining heat from the wood crib, can be determined by the length of the deflected flame. Flame spread outside the domain was defined as self-sustained flame spread upon the roofing membrane.
Based on the empirical formulas by Hasemi et al. [62, 63], which require the assumption of a turbulent diffusion flame, a deflected flame length of 24 cm was calculated for a 5.4 kW fire at gap heights between 8 cm and 12 cm. As such, limited radiative heat transfer from the ignition source was expected towards the first 10 cm of the roof mock-up during the ignition phase of the experiments (see Figure 3). The expectation was verified in the experiment as the initial section of the mitigation layer, and to some extent the subjacent EPS insulation, was affected by the deflected flame.
3.4 Measurements
Because of the heat transfer from the burning wood crib towards the initial part of the roof mock-up, no instrumentation was installed within the first 20 cm from the left edge. In the following 50 cm, 20 shielded thermocouples (14-gauge type-k) were installed from the side of the insulation at a depth of 15 cm (see Figure 3).
Propagation of the flame front and burn-out edge was recorded with a camcorder (Panasonic HC-V770 HD, 25 fps). Subsequently, the locations of the flame front and burn-out edge were found in MATLAB by analysing a binary conversion of a single pixel-line as a function of time from ignition.
The radiative heat flux was measured by a Schmidt-Boelter heat flux gauge (Hukseflux SBG01-020) installed in the centre of the right flange, at a distance of 9 cm from the right edge of the roof mock-up. To protect the heat flux gauge a ø60 mm hole was cut in the roofing membrane and a ø50 mm quartz disc, elevated by 1 mm, was installed above the sensor. As such, the heat flux gauge was protected from melting membrane, flame impingement and condensation of the hot pyrolysis gases upon the water-cooled sensor.
4 Results
Overall, the experiments had two main outcomes. Either no flame spread was observed outside the domain of the wood crib (see Figure 4), or self-sustained ignition of the roofing membrane occurred, whereupon the fire propagated along a significant length of the roof surface (see Figure 5). In general, the outcome of the experiments was linked to the gap height, verifying the existence of a critical gap height as defined in the flame spread studies in horizontal semi-enclosures on PMMA [14]. It can be seen from Figure 5 that the experimental outcomes for ‘no spread’ were almost identical when using the stainless-steel board (a) and a PV module (b). It is worth to note that both areas are asymmetrical and shifted towards the right, thus indicating a convective heat loss caused by an edge effect. A similar effect is expected at the right side of the experimental setup. For the experiments with a gap height above the critical distance, the maximum flame spread length (FSL) was around 15 cm.
For the experiments conducted with PV modules (Experiments #19–#42), the PV cells delaminated from the PV module when the backside was heated. As all tested PV modules were poly- or monocrystalline silicon modules, the PV cells were not visibly affected by the heat exposure. In all of the experiments, except #26, the glass panel of the PV modules remained intact and there were no indications of self-sustained flame spread along the back sheet, as only the area of the location with direct flame impingement burned away (see Figure 6a). As the dimensions of the burned away PV back sheets material were similar to the areas of the roofing membrane (see Figure 6), the similarity imply that substantial heating over a longer duration of time is necessary to degrade the back sheet thermally.
In the four experiments conducted with PV3 (#39–#42), flaming droplets were observed from the lower end of the inclined module to a sheet of mineral wool protecting the floor. Due to continuous dripping, self-sustained burning continued for more than a minute. The dripping was observed at the edge of the area where the PV back sheet was burned away and did not occur at the end of the PV module. Based on that observation, some PV modules might be considered a fuel load as well as an ignition source as the drops might ignite other components. The design of the experimental set-up (see Figure 3a) was the only reason that the drops were able to drip onto the mineral wool, as the subjacent area normally would be part of the hosting roof construction were roofing membrane would be ignited no matter the burning droplets. For horizontal roofs it was deemed that the importance of the dripping was insignificant as it did not extend the area affected by the initial fire, which are expected to extinguish at the end the PV array [40]. However, it might be an important observation with respect to building integrated PV (BIPV) systems installed at steep inclinations, where the dripping can enhance the downward flame spread rate and thus ignite a larger area.
In all the experiments with PV modules, burned parts of the back sheet membrane and PV cells fell from the glass panel and obstructed the camera view (see Figure 5d–h). In some cases (see Figure 6b), the PV cells might have reduced radiative heat transfer from the flame towards the roof mock-up, reducing the time where combustible pyrolysis gases were found in a high enough concentration to obtain sustained burning. Finally, it was concluded that the quality of heat flux measurements made them inadequate for further analysis as they were deemed unreliable for two reasons. In some experiments did the flame front not reach the location of the heat flux gauge, and if the flame front reached the location of the heat flux gauge, the PV cells delaminated from the module and obstructed the view.
4.1 Analysis of Video Recordings
The videos from the experiments were used to extract relevant data, such as the one-dimensional location of the flame front and burn out zone. The flame front location was used to determine the maximum flame spread length (FSL) and flame spread rate (FSR), whereas the burn out zone was used to determine the width of the pyrolysis zone. It was defined that the flame front could only be tracked in one direction, from left to right, whereas the burn out zone was defined as the location(s) between a previously ignited part of the roofing membrane and the pyrolysis zone.
The developed method, named single pixel line analysis, is a way to convert a two-dimensional video of one-dimensional flame spread into a single plot. From Figure 5 it can be seen that there is no significant difference between the flame front locations along the vertical part of the flame at each interval. As such, a single vertical pixel line (1 pixel × 1280 pixels) represents the flame location as well as the full two-dimensional image. That is evident when the 300 s intervals from Figure 5(a, b, d, f–h) are plotted on top of each other in Figure 7a. By refining the intervals from 300 s to 1 s, the flame location can be known during the full experiment as seen in Figure 7b, where the two white lines mark the edges of the roofing membrane, and the red line mark the right side of the wood crib. By converting of the two-dimensional RGB image into a two-dimensional binary plot through the use of MATLAB’s Color Thresholder, the flame front location, marked with yellow in Figure 7c, can be tracked via an automatic algorithm analysing the binary matrix. A similar algorithm was developed to track the burn out zone, but in some cases the debris from the PV modules (see Figure 5d–h) obstructed the view, generating vertical black columns (see Figure 7b–c). Thus, the current burn out zone algorithm required assistance to differentiate actual burn out from an obstructed view. By generating a smooth curve fit for the two data sets, as well as transforming pixels into mm, the flame front and burn out zone could be plotted as a function of time (see Figure 7d), whereupon the width of the pyrolysis zone could be calculated as a function of time.
Visual overview of relevant steps in the single pixel line analysis process of experiment #25. Notice that time in represented on the y-axis in subplots a, b, and c. (a) Image of single pixel line for 300 s intervals equivalent to Figure 5a, b, d, f–h. (b) Intervals reduced to 1 s. Vertical white lines mark the ends of the roofing membrane, and the red line mark the right side of the wood crib. (c) Binary conversion of flame. Flame front and burn out zones identified. Notice that the distance is reduced to the width of the roofing membrane. (d) Plot of flame front and burn out location, as well as width of pyrolysis zone, as a function of time. The grey rectangle defines the location of the subjacent roof mock-up (see Figure 3). Note two things: (i) The black line defining the pyrolysis zone is covered by the red flame front line until the burn out zone detach from the wood crib after 700 s. (ii) The axes are switched compared to subplots a, b, and c
Due to the material properties of the roofing membrane, the behaviour of the flame front and burn out zone are significantly different. In all experiments with sustained flame spread, the flame front moved from the left towards the right. When the maximum flame spread length (FSL) was reached, being the full length, or a part of the full length, the ignited area burned out and became part of the burn out zone. As such, the flame front can only exist at one location as a function of time, whereas the burn out zone can exist at multiple locations, being at the left and right side of the pyrolysis zone, as well as in between separated pyrolysis zones at the end of the experiments.
The terms flame spread length (FSL) and flame spread rate (FSR) were defined as respectively the maximum value of the flame front, and the gradient for a flame front location of 600 mm.
4.2 Flame Spread Length (FSL)
For the experiments conducted below the stainless-steel board (Experiments #1–#18), the critical gap height was identified to be around 11 cm, as no flame spread occurred for a gap height of 12 cm, and consistent results were obtained when the gap was 10 cm (see Figure 8a). The critical gap height interval reduced slightly when the stainless-steel board was replaced with a PV module, as there was a significant difference in the flame spread length (FSL) when the gap height was reduced from 12 cm to 11 cm (see Figure 8a). As expected, the experiments with the stainless-steel board with a gap height of 11 cm have some scatter, as they are in the transition region for the critical height. Taking that into account, the repeatability of the experiments was deemed acceptable.
The experiments conducted with a horizontal stainless-steel board (#1–#18) and a PV module (#19–#31) yielded different FSL when the gap was below the critical gap height. For the experiments with a stainless-steel board, the FSL gradually increased as a function of a gap height reduction, whereas flame spread occurred along the full length of the experimental setup in the experiments with PV modules (see Figure 8a). Due to the lack of self-sustained burning along the back sheet of the PV modules (see Figure 6a), the increased spread is not expected to be due to the additional heat flux from the ignited back sheet membrane. A more likely explanation is that the increased FSL in the experiments with PV modules was caused by a change of geometry that will be discussed in the following paragraph.
The PV modules were supported by an aluminium frame with a depth of 4 cm (PV1 in Table 4), whereas the stainless-steel board had no frame. When the PV modules were installed horizontally, a smoke layer formed. As the burning of the PVC-based and flame retarded roofing membrane did not result in a clean combustion process, the smoke layer was black (indicated by the soot residue in Figure 6a), which entailed a high emissivity, and thus additional radiative heat transfer towards the subjacent roof mock-up. It was assumed that the enclosed smoke layer acted as an additional heat flux towards the full length of the roofing membrane, whereupon the different behaviour can be explained with Quintiere’s expanded version of Williams’ fundamental equation for flame spread in Equation 2 [64, 65]. In line with Quintiere, the re-radiation from the roofing membrane is presumed to be insignificant, whereupon the flame spread rate, \({v}_{p}\), solely depends on the overall gained heat flux, \({\dot{q}}_{f}^{\prime\prime}\left(x\right)\), which Quintiere define as the radiation and convection from the flame in a simple flame spread scenario on a thin fuel. As such, the smoke layer formed below the PV module cause an additional heat flux to the overall heat flux which in this scenario can be defined as \({\dot{q}}_{f}^{\prime\prime}\left(x\right)= {\dot{q}}_{flame, rad}^{\prime\prime}\left(x\right)+ {\dot{q}}_{flame, conv}^{\prime\prime}\left(x\right)+ {\dot{q}}_{smoke, rad}^{\prime\prime}\left(x\right)\). Despite the unlimited upper boundary of the definite integral in Equation 2, the contributions from flame radiation and convection are more distinct in the near proximity of the flame front, whereas it is assumed that the contribution from the smoke layer, \({\dot{q}}_{smoke, rad}^{\prime\prime}\left(x\right)\), is constant along the full length of the PV module. As such, the frame, by acting as a physical barrier, caused longer length with a significant heat flux, \({\dot{q}}_{f}^{\prime\prime}(x)\), towards the subjacent roof construction compared to the experiments conducted with the flat stainless-steel board [64].
At a gap height of 8 cm, a significant difference related to the subjacent insulation material can be noticed in the experiments below a stainless-steel board. The experiments conducted with a calcium silicate board propagated around 10 cm longer than the experiments conducted with a layer of mineral wool (see Figure 8a). A similar trend was evident when the PV modules were inclined \(10^\circ\), as the FSL was significantly longer for the experiments conducted with PIR insulation compared to similar experiments with mineral wool (see Figure 8b).
Based on the experiments conducted with inclined modules (Figure 8b), it was concluded that the critical gap height determined for horizontal modules did not represent the critical gap height for all inclinations, as the FSL for an inclination of \(10^\circ\) and a gap height of 12 cm exceeded the defined domain of the wood crib, \({x}_{dom}\), significantly. This corresponds well with the concept of the model developed by Tang et al. (see Equation 1), where it can be seen that the upstream heat flux, \({\dot{q}}_{f}^{\prime\prime}\), to a certain extent, will increase for positive inclinations, \(\theta\), if the heat release rate (HRR), \(\dot{Q}\), gap height, H, and distance to the heat source, r, are kept constant. As the HRR from the wood crib is assumed similar for all experiments, it can be concluded that the critical gap height is above 12 cm for PV modules at an inclination of \(10^\circ\). The theory by Tang et al. [13] corresponds well with the visual observations from the experiments, as seen from the frames displayed in Figure 9. The photos show that the initial flame spread on the right side of the wood crib is significantly larger than flame spread to the left (at 300 s after ignition) (see Figure 9b). In comparison to the flame spread rate below a horizontal module (see Figure 5), the flame spread rate below an inclined PV module is significantly faster, as the FSL of around 80 cm is reached 570 s after ignition as opposed to 750 s below the horizontal PV module (Figure 5e).
However, none of the experiments with inclined modules reach the maximum obtained FSL as seen in the experiments conducted with horizontal PV modules (see Figure 8). For the given experimental set-up, an increased inclination, as well as increased gap height, cause a reduction of the FSL, as seen in Figure 9, where the flame front is stagnant between subfigures e and f. The results do not correlate well with the binary scenario below the horizontal modules, where the FSL was near the maximum length measured in the experiments with PV modules for a gap height of 11 cm or lower. From Figure 9e it is seen that the fire has detached from the source of ignition, but is unable to progress despite a wide pyrolysis zone that is assumed to entail a high heat release rate, as it is almost extinguished after 630 s (see Figure 9f). Based on Figure 8b, it can be concluded that it was a general trend that is linked to the experimental set-up rather than to the gap height and inclination.
Two additional observations related to the FSL of the inclined modules are: (i) The FSL was similar (79 cm to 84 cm) for the experiments conducted with similar roof construction and geometry, even with different PV modules (Experiments #32, #33, #36, and #39), and (ii) The FSL was enhanced for reduced gap heights at similar inclinations of \(10^\circ\).
The similar FSL for four almost identical experiments indicates that the semi-enclosure geometry is more important than the material parameters of the PV modules. Naturally, a full validation of this relatively bold postulate will require a more extensive comparison across a significantly higher number of modules.
The relationship between the gap height and the FSL can be explained by the limited sample width of the roofing membrane, which only allowed one-dimensional flame spread, rather than two-dimensional flame spread, as would be the case on a roof construction.
If it is assumed, that the flame front reassembles a 37 cm wide gas burner moving across the sample, with a constant HRR, the different FSL can be linked to the similar gap height, at the location of the FSL, \({H}_{FSL }=H+tan\left(\theta \right) FSL\), which are all between 22.8 cm and 23.7 cm. As such, the expected heat flux at the maximum FSL will be within the same magnitude in accordance with Equation 1. The assumption of a similar heat release rate could be validated through oxygen calorimetry [60], but also fall well in line with the examination of sample width importance by Jiang et al. [66], as they found that increased sample width caused enhanced radiative heat transfer towards the pre-heating zone. As such, the fixed width does not represent the infinite scenario.
Despite the limitations related to the sample width of the roofing membrane, the comparisons of FSL are deemed very relevant. Although the restricted sample width does not affect the ignition phase as the actual domain of the wood crib is significantly smaller than the width of the roofing membrane (see Figure 4). Thus, the definition of a critical gap height should not be based on the FSL, but solely on whether a specific set-up caused flame spread outside the domain of the ignition source. If that was the case, it should be assumed, that flame spread will occur below the full PV array, as seen in the large scale experiments [40]. Based on these findings, it can be concluded that the test set-up in the test method CLC/TR 50670 [67] is not strict enough as self-sustained flame spread will occur for gap heights below 15 cm and inclinations below \(30^\circ\).
4.3 Flame Spread Rate (FSR)
When the fire propagated outside the domain of the ignition source, the flame spread rate (FSR) remained almost constant as a function of time and location of the flame front (see Figure 7d). For the experiments conducted with a horizontal panel (#1–#31), the results for a gap height below 11 cm indicate a dependency of both the panel and insulation type, as seen Figure 10a. Similarly as for the flame spread length, it is assumed that the frame of the PV module might be the main reason for the significant difference in the FSR obtained for the experiments conducted with a stainless-steel board and a PV module, respectively.
The constant height of the smoke layer enclosed by the horizontal PV module efficiently induced an additional reduction of the actual gap height, which caused a restriction of the gap wherein the entrained air could enter the fire plume, and the combustion products could leave the semi-enclosure. It is assumed that the reduced gap could have caused one or two of the following physical phenomena, which could both entail a reduction of the FSR: (i) The reduced gap enhanced the velocity of the entrained air and, thus, increased the convective heat loss at the flame front. (ii) The reduced gap height could limit the overall entrainment of air into the fire plume, causing a less efficient combustion process and, thus, a lower heat release rate.
Focusing on the experiments with a gap height below 11 cm, the flame spread rate for experiments conducted with the calcium silicate board (CSB) is consequently higher than the experiments conducted with mineral wool.
That corresponds well with the thermal properties of these materials. Although the roofing membrane is assumed to be a thermally thin fuel, the specific heat, \({c}_{p}\) (Table 3), of the two materials will affect the FSR. The material with the lowest \({c}_{p}\) will heat up faster and, thus, have a quicker establishment of a temperature equilibrium between the roofing membrane and the upper layer of the subjacent material. As such, the conductive heat transfer is reduced in the initial flame spread phase. Subsequently, the flame spread phase turn into a burning phase, where it is assumed that the temperature equilibrium exists no matter the subjacent material, whereupon the specific heat becomes irrelevant, as the conductivity of the subjacent material defines the amount of energy necessary to maintain the temperature equilibrium at the upper layer of the material.
It is assumed that the presence of the aluminium foil on the PIR insulation affects the flame spread rate. However, due to the inconsequent FSR values in the experiments, it cannot be concluded whether the aluminium foil leads to enhanced or reduced FSR. If no air gap existed between the roofing membrane and the upper surface of the PIR insulation, the layer of alufoil would have no effect on the flame spread rate, whereupon a low FSR would be achieved. Contrary, an air gap between the roofing membrane and the alufoil would cause a reflection of the radiation towards the underside of the membrane. As a result, the roofing membrane heats up faster, thus causing a higher FSR.
For the experiments conducted with inclined PV modules (Figure 10b), the correlation between gap height and FSR seems less evident as the FSR is more constant across the experiments. Compared to the experiments conducted with horizontal panels, the FSR is significantly higher, which could be consequence of two physical phenomena related to the inclination of the modules; (i) As concluded in the three re-radiation studies [11,12,13] the inclination cause an increased heat flux towards the fuel in front of the flame front and thus, an increased flame spread rate, (ii) the inclination of the modules permits the buoyancy driven flow of combustion products to follow the back sheet of the PV modules, whereupon it does not obstruct the air entrained into the plume. Thus, the increased convective heat loss suggested to confine the FSR in the experiments with the horizontal modules was eliminated.
For two repeated sets of experiments with inclined PV modules (#32–#33 and #34–#35), similar results are obtained for when mineral wool is used as mitigation layer, whereas a difference of 0.6 mm/s is noticed in the two experiments with PIR insulation (Figure 10b). The variation indicate that the designed fire dynamic system is highly sensitive, as small uncontrollable or unintended difference might have a huge impact on the experimental outcome. In general, it should be noticed that the difference in all repeated experiments conducted with PIR-insulation, is significantly higher than for the repeated experiments with mineral wool or the calcium silicate board. The difference is assumed to be caused by the fact that the PIR insulation swell when heated, contrary to the other materials which keeps their initial physical properties. As such, the PIR insulation might not swell in the same manner for each experiment, whereupon the outcome of the experiments varies.
In the experiments conducted with same geometry and roof construction but with different PV modules (experiments #32, #33, #36, and #39) a significant FSR variation was observed with values of respectively 2.63 mm/s and 2.73 mm/s for PV1, 3.17 mm/s for PV2, and 2.30 mm/s for PV3 (Figure 10b). With the overall repeatability of the FSR in the experiments with horizontal PV modules and Mineral wool, as well as experiment #32 and #33 with a inclined module and mineral wool (Figure 10), it is assumed that difference was related to the PV module, where the properties of the back sheet membrane or the dimensions of the PV modules might have affected the FSR. No conclusion can be based on single experiments, but the finding emphasises the importance of understanding how the physical dimensions of PV modules might affect the consequences of an ignition below a PV system.
4.4 Exposure
Whereas the initial experiments (#1–#9) were conducted with the non-combustible calcium silicate board to enable a gradual increase of complexity from the flame spread studies with PMMA in horizontal gaps [14], the remaining 34 experiments were conducted with the roof construction types RC-B or RC-C (Table 1). A mitigation layer of either 60 mm PIR insulation or 50 mm mineral wool was installed on top of a layer of EPS insulation. The membrane directly above EPS represents a worst-case roof construction from a fire safety point of view.
To make a link between the fire in the semi-enclosure and the temperatures measured in the subjacent insulation materials, it was necessary to quantify the magnitude of the heat transferred from the fire towards the surface of the roof.
An often-used parameter to quantify the energy released from a forest fire is the fireline intensity [68, 69], I [kW/m], defined by Byram in 1959 [70]. Using the nomenclature of Byram, Fireline intensity is defined as the product of the flame spread rate, R, the density of the fuel per area, W [kg/m2], and the heat of combustion, H [kJ/kg]. Similar to a forest fire, the instrumentation of the conducted experiments was limited, which was why the fireline intensity (Equation 3) was deemed as the best well-known parameter to quantify the amount of energy released within the semi-enclosure and thus the magnitude of heat transferred to the material below the roofing membrane [70].
As the roofing membrane was assumed to have a homogeneous density and heat of combustion, the fireline intensity was proportional to the FSR. As such, experiments with similar FSRs, such as #22 and #40 (see Figure 11), yielded similar fireline intensities and thus an assumption of equal magnitudes of heat transferred towards the subjacent insulation material. That assumption did not correlate with the outcome of the experimental campaign where the flame spread behaviour in the experiments with horizontal panels were significantly different than the experiments below inclined modules. Comparing two experiments with similar FSRs, the duration and width of the pyrolysis zone below the horizontal PV module in experiment #22 (Figure 11a) is significantly larger than the equivalent values when the PV module was inclined in experiment #40 (Figure 11b).
Comparison of the flame front and burn out location, as well as width of pyrolysis zone, as a function of time for experiments #22 and #40. The grey rectangle defines the location of the subjacent roof mock-up (see Figure 3)
By replacing the FSR with the area of the pyrolysis zone as a function of time, Apyro(t) [m2/s], it was considered to implement the importance of the one-dimensional pyrolysis zone length, lpyro(t) [m], as the area was assumed to be rectangular with a width, w [m], similar to the width of the roofing membrane: Apyro(t) = wlpyro(t). With the change of geometric the parameter in Equation 3, the unit of the fireline intensity, I, was changed to energy per second, [J/s], and thus renamed intensity. As the length of the pyrolysis zone varied as a function of time, cross-experimental comparison could only be enabled by summing the intensity at similar time internals for each experiment. The most exact cross-experimental comparison would be achieved by summing the intensity for each second as seen in Equation 4, which will yield the combined fire load, qf [J].
A gross experimental comparison of the fire load assumed a constant heat of combustion and thus a similar combustion efficiency. That was most likely not the case due to the restricted air entrainment in the experiments with low gap heights, whereupon it is deemed that the value of the actual fire load was not well-represented by qf.
When assuming a constant heat of combustion, the calculated fire load was proportional with the Exposure, E, defined as the integral of the pyrolysis zone length during the duration of experiment as seen in Equation 5. As such, it was decided to use the term Exposure [m s] for cross experimental comparison quantification of the heat transfer magnitude.
Overall, there is a correlation between the FSR (Figure 10) and Exposure (Figure 12), where a slower FSR cause a higher Exposure. For the experiments with a horizontal gap height of 11 cm or below, as well as most of the experiments conducted with inclined modules, the limited FSL affects the Exposure value. It is relevant to note that the experiments with a horizontal PV module caused a significantly higher exposure compared to the similar experiments conducted below the stainless-steel board (see Figure 12a). Again, that might be linked to the frame of the PV modules restricting the natural flow of the combustion products to form a smoke layer.
The influence of the restricted smoke layer below the horizontal modules was confirmed when the PV modules were inclined, as the Exposure dropped significantly (Figure 12b), although it is necessary to take the slightly limited FSL values into account for those experiments (Figure 12b). However, the reduction of the exposure tends to be more than 50%, whereas the average reduction of FSL was around 20% for gap heights of 11 cm and below (Figure 12b). Naturally, the 12 cm gap height with an inclined module caused a higher Exposure than the horizontal module, as the FSL exceeded the domain of the ignition source due to the increased re-radiation. A final, and more essential reason for the reduced Exposure, was the higher flame spread rate (FSR). The higher FSR indicated a faster heating of the roofing membrane ahead of the flame front, which was linked to a higher HRR and thus higher mass loss rate. As the thickness of the fuel was limited to the 1.5 mm thickness of the roofing membrane, a higher mass loss rate resulted in a shorter duration of the fire and, consequently, a smaller Exposure.
From a practical point of view, the Exposure is relevant as the roof construction below the PV array is a part of the building envelope and thus the only barrier that prevents the fire from entering the property and transform the roof fire into a building fire which might result in more severe consequences. As such, the term Exposure was developed as neither the FSL nor the FSR incorporated the duration of the fire, whereupon they were not suited as a parameter for comparison of temperatures within the subjacent insulation materials which is a product of a time-dependent, transient, scenario.
4.5 Temperature
For the experiments conducted with horizontal modules, there was a reasonable correlation between the Exposure and the temperature in the insulation materials below the roofing membrane, where a larger Exposure caused higher temperatures (see Figure 13). For lower Exposure values, such as for the experiments conducted with mineral wool below the stainless-steel board (#10–#18), it should be noted that the maximum temperatures measured in each layer was dependent of the FSL (see Figure 13). As the shortest horizontal distance between the right side of the wood crib and the nearest column of thermocouples (TCs) was 30 cm, the duration of the vertical heat transfer towards those TCs was short, compared to the experiments where the flame front travelled further. Consequently, the measured maximum temperatures were lower.
For the experiments conducted with the horizontal PV modules (#10–#31), there was a significant temperature difference measured at depths of 10 mm and 20 mm (Figure 13a–b), as the experiments conducted with mineral wool consequently caused higher values. It is assumed that the upper layer of the alufoil at the top of the PIR insulation caused a significant reduction of radiative heat transfer from the fire plume due to the low absorbance of the alufoil [52]. These observations correspond well with a series of large scale experiments [40], where it was concluded that a layer of alufoil caused significantly lower temperatures within the subjacent mineral wool.
Purely based on the 0.014 \(Wm^{-1}K^{-1}\) conductivity difference between the mineral wool and PIR insulation (Table 3), the temperature difference should increase with an enhanced depth. However, the trend seems to be different through a depth of 5 cm (see Figure 13c–e), which might be related to the conductivity being temperature dependent, and the physical changes of the PIR insulation. Although the conductivities at high temperatures is not tested for construction products, it is known that mineral wool products used in industry have a conductivity of around 0.12 \(Wm^{-1}K^{-1}\) when heated to \(500\,{^{\circ}\rm{C}}\) [71]. On the other hand, the behaviour of the PIR insulation was complex. The conductivity at high temperatures is unknown, but the thickness increased when the material was heated, and mass loss was observed due to thermal degradation. Based on those findings, the relevance of the conductivities, reported in the product data sheets (Table 3), can be questioned in case of fire as they are not representative for high temperature cases.
The influence of the insulation thickness was evident when looking at the maximum temperatures recorded in the EPS insulation at a depth of 70 mm (Figure 13f). With the mineral wool having a thickness of 50 mm, the upper surface of the subjacent EPS was exposed to temperatures of minimum \(250\,{^{\circ}\rm{C}}\) (Figure 13e), which exceeded the melting temperature of EPS (\(100\,{^{\circ}\rm{C}}\)) [72]. Thus, the subjacent EPS melted or evaporated, leaving a heated airgap, which expanded due to the supplied heat. As the thickness of the PIR insulation was 10 mm larger, the temperature was reduced significantly before reaching the EPS insulation, which caused a lower temperature measured at 70 mm.
Combined with the previous findings, it can be concluded that the significant temperature differences measured at a depth of 70 mm below the mitigation layers of mineral wool and the PIR insulation were most likely related to the thickness of the insulation material, rather than the thermal properties of the insulation products at ambient temperature.
For the experiments with inclined modules, the temperature findings were less consistent (Figure 14). First of all, the faster flame spread rate (see Figure 10b) and lower Exposure (see Figure 12b) caused a shorter period of time, where the upper surface of the roof mock-up gained heat from the fire. Although the upper surface probably reached the same temperatures as in the experiments with the horizontal panels, the shorter duration caused a significantly lower temperature at the depths of 10 mm and 20 mm (Figure 14a and b). At the same time, only few of the experiments caused a FSL above 80 cm (see Figure 8) whereupon no fire occurred just above the nine thermocouples furthest to the right of the roof mock-up (see Figure 3a). In general, the temperature was reduced as function of depth within the area of the installed thermocouples.
In summary, the maximum temperatures measured within the PIR insulation, mineral wool, and the subjacent layer of EPS insulation revealed that the high temperatures caused by the fire rendered the conductivity from the datasheets redundant. Compared to the mineral wool, the layer of aluminium foil on top of the PIR insulation caused significantly lower temperatures within a depth of 10 mm and 20 mm. However, the magnitudes of the maximum temperatures were similar through a depth of 50 mm, whereupon the higher thickness of the PIR insulation resulted in significantly lower temperatures within the EPS insulation. As such, it is assumed that a mitigation layer of 60 mm mineral wool would have protected the EPS insulation better than the PIR insulation. If flame spread on the roof is rendered unavoidable for commercial roof constructions with PV modules, it suggested to design a test method for insulation products exposed high temperatures as the conductivity from the product datasheets are insufficient when the physical characteristics of the insulation changes as a consequence of the high temperatures.
5 Conclusion
One-dimensional flame spread within a semi-enclosure in between a roof mock-up and a vertical barrier was studied and analysed based on 42 experiments with a focus on four parameters. Three of the four parameters were related to the vertical barrier: (i) the type of barrier being a stainless-steel board or a PV module, (ii) The inclination of the barrier from horizontal to 15\(^\circ\), and (iii) the gap height between the barrier and the roof mock-up. The final parameter was the influence of the material below the roofing membrane (BROOF(t4)). The material below was either a calcium silicate board, or an insulation product acting as a mitigation layer on top of a worst-case scenario roof construction insulated with EPS insulation. Two insulation products were used, namely 50 mm mineral wool or 60 mm PIR insulation. The lowest temperatures in the EPS insulation were measured in the experiments conducted with PIR insulation, but based on the temperature development through the two insulation products, the overall performances of the mineral wool were deemed better. If compared at the same thickness, it is expected that the lowest temperatures will be measured below the mineral wool.
A binary flame spread scenario was observed for the given experimental set-up with horizontal panels. No flame spread was observed if the gap height was 12 cm, whereas sustainable flame spread occurred if the gap height was below a critical gap, determined to be 10 cm for the stainless-steel board, and 11 cm for the PV modules. For PV modules inclined between 10\(^\circ\) and 15\(^\circ\), it was concluded that the critical gaps height are above 12 cm, as the inclination increased the heat flux below the most elevated part of the modules, which were in accordance with previous steady state experiments [11,12,13].
For experiments conducted with horizontal panels, it was found that the geometry alone caused a significant difference in the flame spread behaviour, as the aluminium frame of the PV module blocked the flow of buoyant combustion gases whereupon a layer of hot smoke was formed. The hot smoke layer had multiple effects on the flame spread scenario: (i) It increased the flame spread length, as the enclosed smoke enhanced the pre-heating ahead of the flame front. (ii) It reduced the flame spread rate, as the smoke layer reduced effective gap height and thus, increased the velocity of the ambient air entrained into the fire plume.
The effect of the trapped smoke layer was eliminated when the PV modules were inclined, as it allowed an upwards buoyancy driven flow of the combustion products upstream the PV modules. The deflection of the modules caused an increased heat flux upstream which resulted in a significantly faster flame spread rate compared to the experiments conducted with horizontal modules.
In all experiments conducted with PV modules, it was noticed that the polymer based back sheet membrane were only burned away at the location with direct flame impingement, whereas the remaining part of the back sheet were sooty, but intact. With no self-sustained flame spread on the PV module it can be discussed if the PV module itself should be considered as a fire load or rather as a facilitator of flame spread.
Dripping was observed in the experiments with one of the three tested types of PV modules. The importance of the dripping was deemed insignificant for flat roofs, but it is acknowledged that it might be relevant for constructions with difference geometries.
For the roofing membrane, it can be concluded that compliance with the standards does not prevent flame spread upon the mock-up, which indicate a potential breach of a fundamental fire safety strategy, namely the one requiring no flame spread along the façade of a building. As such, it can be concluded that the introduction of a building applied PV system might result in more severe consequences in case of an initial fire on the roof. Based on that, it is suggested to develop a new test method that takes the re-radiation from the deflected flame into account. Until then, stakeholders, including property owners, as well as the fire and rescue service, should re-consider their response in case of ignition as flame spread on the building envelope is very likely.
It should be emphasized that the critical gap heights determined for the experimental set-ups cannot be implemented directly into industry, as they are not universal, and the limited width of the roof mock-up does not represent an infinite flat roof. However, the findings are very relevant to all stakeholders dealing with BAPV installations, as the analysis of the examined parameters highlights key mechanisms of the flame spread and thus, potential methods to reduce the consequences of a PV related fire.
Change history
02 June 2022
A Correction to this paper has been published: https://doi.org/10.1007/s10694-022-01267-6
References
Masson G, Detollenaere G (2021) Snapshot of Global PV Markets 2021, 1–16. https://iea-pvps.org/wp-content/uploads/2021/04/IEA_PVPS_Snapshot_2021-V3.pdf. Accessed 16 July 2021
Voiland A (2017) Longyangxia Dam Solar Park, NASA Earth Obs. https://earthobservatory.nasa.gov/images/89668/longyangxia-dam-solar-park. Accessed 1 May 2020
Haegel NM, Margolis R, Buonassisi T, Feldman D, Froitzheim A, Garabedian R, Green M, Glunz S, Henning HM, Holder B, Kaizuka I, Kroposki B, Matsubara K, Niki S, Sakurai K, Schindler RA, Tumas W, Weber ER, Wilson G, Woodhouse M, Kurtz S (2017) Terawatt-scale photovoltaics: trajectories and challenges. Science 356:141–143. https://doi.org/10.1126/science.aal1288
Haegel NM, Atwater H Jr, Barnes T, Breyer C, Chiang Y, De Wolf S, Dimmler B, Feldman D, Goldschmidt JC, Hochschild D, Inzunza R, Kaizuka I, Kroposki B, Kurtz S, Leu S, Margolis R, Matsubara K, Metz A, Metzger WK, Morjaria M, Niki S, Nowak S, Peters IM, Philipps S, Reindl T, Richter A, Rose D, Sakurai K, Shikano M, Sinke W, Sinton R, Stanbery BJ, Topic M, Tumas W, Ueda Y, Van De Lagemaat J, Verlinden P, Vetter M, Warren E, Werner M, Yamaguchi M, Bett AW (2019) Terawatt-scale photovoltaics: transform global energy. Science 364:836–838. https://doi.org/10.1126/science.aaw1845
Sepanski A, Reil F, Vaassen W, Janknecht E, Hupach U, Bogdanski N, van Heeckeren B, Schmidt H, Bopp G, Laukamp H, Grab R, Philipp S, Thiem H, Huber J, Haselhun R, Häberlin H, Krutzke A, Neu B, Richter A, Bansemer B, Halfmann M, (2015) Leitfaden: Bewertung des Brandrisikos in Photovoltaik-Anlagen und Erstellung von Sicherheitskonzepten zur Risikominimierung. http://www.pv-brandsicherheit.de/fileadmin/downloads_fe/Leitfaden_Brandrisiko_in_PV-Anlagen_V01.pdf.
Sepanski A, Reil F, Vaaßen W, Janknecht E, Hupach U, Bogdanski N, van Heeckeren B, Schmidt H, Bopp G, Laukamp H, Grab R, Philipp S, Thiem H, Huber J, Haselhuhn R (2018) Assessing Fire Risks in Photovoltaic Systems and Developing Safety Concepts for Risk Minimization, 2018. https://www.energy.gov/sites/default/files/2018/10/f56/PVFireSafetyFireGuideline_Translation_V0420180614_FINAL.pdf.
Brooks B (2012) The ground-fault protection blind spot: A safety concern for larger photovoltaic systems in the United States, Sol. Am. Board Codes Stand. 18.
Zhao Y, de Palma J, Mosesian J, Lyons R, Lehman B (2013) Line–line fault analysis and protection challenges in solar photovoltaic arrays. Ind Electron IEEE Trans 60:3784–3795. https://doi.org/10.1109/TIE.2012.2205355
Reil F, Sepanski A, Herrmann W, Althaus J, Vaaßen W, Schmidt H (2011) Qualification of arcing risks in PV modules, in: 38th IEEE Photovolt. Spec. Conf., Austin, TX, pp 727–730. https://doi.org/10.1109/PVSC.2012.6317709.
Herz M, Friesen G, Jahn U, Köntgens M, Lindig S, Moser D (2021) Quantification of techniocal risks in PV power systems 2021, IEA-PVPS T13–23:2021, International Energy Agency - Photovoltaic Power Systems Programme | IEA-PVPS. https://iea-pvps.org/wp-content/uploads/2021/11/Report-IEA–PVPS-T13-23_2021-Quantification-of-Technical-Risks-in-PV-Power-Systems_final.pdf.
Kristensen JS, Merci B, Jomaas G (2018) Fire-induced reradiation underneath photovoltaic arrays on flat roofs. Fire Mater 42:316–323. https://doi.org/10.1002/fam.2494
Ju X, Zhou X, Gong J, Zhao K, Peng Y, Zhang C, Ren X, Yang L (2019) Impact of flat roof – integrated solar photovoltaic installation mode on building fire safety. Fire Mater 42:936–948. https://doi.org/10.1002/fam.2755
Tang F, Zhu Y, Chen L, Sun X, McNamee M, Van Hees P, Hu L (2021) Experimental study and analysis of radiation heat fluxes received by a floor beneath an inclined ceiling. Fire Mater 45:205–214. https://doi.org/10.1002/fam.2925
Kristensen JS, Faudzi FBM, Jomaas G (2021) Experimental study of flame spread underneath photovoltaic (PV) modules. Fire Saf J 120:103027. https://doi.org/10.1016/j.firesaf.2020.103027
Bera A, Sarkar A, Factbox (2019) Walmart and Tesla fought in private long before solar lawsuit, REUTER. https://www.reuters.com/article/us-walmart-tesla-solar-lawsuit-factbox-idUSKCN1VC1EH?utm_campaign=trueAnthem%3A+Trending+Content&utm_content=5d5ea25d57819f000168f76d&utm_medium=trueAnthem&utm_source=twitter
Groom N, Balu N (2019) Walmart sues Tesla for negligence after repeated solar system fires, REUTERS. https://www.reuters.com/article/us-walmart-tesla-solar-lawsuit/walmart-sues-tesla-for-negligence-after-repeated-solar-system-fires-idUSKCN1VA26B
Mohd Nizam Ong NAF, Sadiq MA, Md Said MS, Jomaas G, Mohd Tohir MZ, Kristensen JS (2021) Fault tree analysis of fires on rooftops with photovoltaic systems. J. Build. Eng. 46:103752. https://doi.org/10.1016/j.jobe.2021.103752
Bonomo P, Saretta E, Frontini F, Caccivio M, Bellenda G, Mazinine G, Cancelliere P (2017) Fire safety of PV modules and buildings: overview, bottlenecks and hints. In: Smets A, Taylor N, Helm P (Eds), 33rd Eur. Photovolt. Sol. Energy Conf. Exhib. WIP - Renewable Energies, Amsterdam, NL, pp 2299–2303
Weaver J (2019) There are – data missing – solar power fires per year, PV-Magazine. https://www.pv-magazine.com/2019/08/23/there-are-data-missing-solar-power-fires-per-year/. Accessed 15 June 2021
Sylvia T (2020) Solar system fires are on the rise in the U. S., PV Mag. https://www.pv-magazine.com/2020/04/23/solar-system-fires-are-on-the-rise-in-the-u-s/. Accessed 5 May 2020
Mohd Nizam Ong NAF, Mohd Tohir MZ, Said MSM, Nasif MS, Alias AH, Ramali MR (2021) Development of fire safety best practices for rooftops grid-connected photovoltaic (PV) systems installation using systematic review methodology. Sustain Cities Soc 78:103637. https://doi.org/10.1016/j.scs.2021.103637
National Renewable Energy Laboratory | NREL, Energy analusis - Useful life, NREL - Natl. Renew. Energy Lab. (n.d.). https://www.nrel.gov/analysis/tech-footprint.html.
Underwriters Laboratories, ANSI/UL 790 Standard for Standard Test Methods for Fire Tests of Roof Coverings, (2018). https://standardscatalog.ul.com/standards/en/standard_790_8.
European Committee for Standardization, EN 13501–5:2016 Fire classification of construction products and building elements - Part 5: Classification using data from external fire exposure to roofs tests, CEN (2016)
Underwriters Laboratories, UL 61730 (2018)
Underwiters Laboratories, UL/ANSI 1703 Flat-Plate Photovoltaic Modules and Panels, (2018). https://standardscatalog.ul.com/standards/en/standard_1703_3.
European Committee for Electrotechnical Standardization, EN IEC 61730–1:2018 Photovoltaic (PV) module safety qualification - Part 1: Requirements for construction, CENELEC (2018)
European Committee for Electrotechnical Standardization, EN IEC 61730–2:2018 Photovoltaic (PV) module safety qualification - Part 2: Requirements for testeng, CENELEC. (2018)
BSi British Standards, PD CLC/TR 50670:2016 - External fire exposure to roofs in combination with photovoltaic (PV) arrays — Test method(s) (2016)
European Committee for Standardization, CEN/TS 1187: 2012 Test methods for external fire exposure to roofs, CEN (2012)
Gmbh C, Reil F, Halfmann M, Bulk J, Trettin C (2014) Untersuchungen zum Verhalten von Photovoltaik-Modulen bei externen Brandeinwirkungen, sowohl bei additiven als auch integrierten Systemen, mit der Zielsetzung einer harmonisierten europäischen normativen Prüf- und Beurteilungsmethode. https://doi.org/10.2314/GBV:848482131.
Cancelliere P, Manzini G, Traina G, Cavriani MG (2021) PV modules on buildings: outlines of PV roof samples fire rating assessment. Fire Saf J 120:103–139. https://doi.org/10.1016/j.firesaf.2020.103139
European Committee for Standardization, EN ISO 13823:2020 Reaction to fire tests for building products – Building products excluding floorings exposed to the thermal attack by a single burning item, CEN (2020)
Alam MK, Khan F, Johnson J, Flicker J (2015) A comprehensive review of catastrophic faults in PV arrays: types, detection, and mitigation techniques. IEEE J Photovolt 5:982–997. https://doi.org/10.1109/JPHOTOV.2015.2397599
Falvo MC, Capparella S (2015) Safety issues in PV systems: design choices for a secure fault detection and for preventing fire risk. Case Stud Fire Saf 3:1–16. https://doi.org/10.1016/j.csfs.2014.11.002
Chen S, Yang G, Gao W, Guo M (2021) Ladder network with string voltage and current measures 11:219–231
Dhere NG, Shiradkar NS (2012) Fire hazard and other safety concerns of photovoltaic systems. J Photonics Energy 2:22006. https://doi.org/10.1117/1.JPE.2.022006
Khoshnami A, Sadeghkhani I (2018) Fault detection for PV systems using Teager-Kaiser energy operator. Electron Lett 54:1342–1344. https://doi.org/10.1049/el.2018.6510
Backstrom B (2013) Validation of roof configuration 2 experiments project 9. http://www.solarabcs.org/current-issues/docs/Validation_of_Roof_Configuration_2_Experiments.pdf. Accessed 22 Nov 2021
Kristensen JS, Jomaas G (2018) Experimental study of the fire behaviour on flat roof constructions with multiple photovoltaic (PV) panels. Fire Technol 54:1807–1828. https://doi.org/10.1007/s10694-018-0772-5
Cancelliere P, Liciotti C (2016) Fire behaviour and performance of photovoltaic module backsheets. Fire Technol 52:333–348. https://doi.org/10.1007/s10694-014-0449-7
Yang HY, Zhou XD, Yang LZ, Zhang TL (2015) Experimental studies on the flammability and fire hazards of photovoltaic modules. Materials 8:4210–4225. https://doi.org/10.3390/ma8074210
Despinasse M-C, Krueger S (2015) First developments of a new test to evaluate the fire behavior of photovoltaic modules on roofs. Fire Saf J 71:49–57. https://doi.org/10.1016/j.firesaf.2014.11.011
Allianz Risk Consulting, Fire Hazards of Photovoltaic ( PV ) Systems, Tech Talk. 8 (2019). https://www.agcs.allianz.com/content/dam/onemarketing/agcs/agcs/pdfs-risk-advisory/tech-talks/ARC-Tech-Talk-Vol-8-Fire-Hazards-PV-Systems-EN.pdf. Accessed 1 June 2021
Drysdale D (2011) Chapter 4: diffusion flames and fire plumes. In: An Introd. to Fire Dyn. 3rd Ed., pp 121–179. https://doi.org/10.1002/9781119975465.ch4.
Scandi Supply, FireFree ScandiBoard 850 - Datasheet, (2011). http://www.scandisupply.com/Files/Filer/EU/Data85020111007(GB.pdf.
Kristensen JS, Blacklock N, Lee C, Raftery T (2021) Personal correspondance with Bauder UK, pp 1–4
Bauder Limited, Product Data Sheet: Bauder Thermofol U15 FR Membrane, 353 (2021). https://www.bauder.co.uk/getmedia/5f449e55-e498-4949-b9ac-b5866b46971d/Bauder-Thermofol-U15-Membrane-Product-Data-Sheet_1.pdf. Accessed 29 Nov 2021
ROCKWOOL A/S, ROCKWOOL Stålunderlag Data sheet, (2020). https://cdn01.rockwool.dk/siteassets/o2-rockwool/dokumentation-og-certifikater/dokumentation/andet/datablade/staalunderlag.pdf?f=20200225035353. Accessed 16 April 2020
Kingspan Insulation Ltd, Kingspan Thermaroof TR26 LPC / FM, (2020). https://www.kingspan.com/gb/en-gb/products/insulation/insulation-boards/therma/thermaroof-tr26-lpc-fm. Accessed 16 April 2020
Plastform Ltd, Plastopor EPS 70, (n.d.). http://plastform.hr/eng/fasadni-stiropor-eps-70.php. Accessed 18 Oct 2021
Incropera FP, DeWitt DP (2002) Fundamentals of Heat and Mass Transfer, 5th editio, John Wiley & Sons
ScandiBoard, ScandiBoard 850 Material safety data sheet Material safety data sheet, (2012) 1–8. http://www.scandisupply.com/Files/Filer/EU/MSDS.
Bentz DP, Prasad KR (2007) NISTIR 7401 Thermal Performance of Fire Resistive Materials I. Characterization with Respect to Thermal Performance Models, Gaithersburg. https://concrete.nist.gov/~bentz/nistir7401.pdf.
Peeters JR, Altamirano D, Dewulf W, Duflou JR (2017) Forecasting the composition of emerging waste streams with sensitivity analysis: a case study for photovoltaic (PV) panels in Flanders. Resour Conserv Recycl 120:14–26. https://doi.org/10.1016/j.resconrec.2017.01.001
Danz P, Aryan V, Möhle E, Nowara N (2019) Experimental study on fluorine release from photovoltaic backsheet materials containing PVF and PVDF during pyrolysis and incineration in a technical lab-scale reactor at various temperatures. Toxics. https://doi.org/10.3390/toxics7030047
Tewarson A, Chu F, Jiang F (1994) Combustion of halogenated polymers, fire. Saf Sci 4:563–574. https://doi.org/10.3801/iafss.fss.4-563
Riga A, Collins R, Mlachak G (1998) Oxidative behavior of polymers by thermogravimetric analysis, differential thermal analysis and pressure differential scanning calorimetry. Thermochim Acta 324:135–149. https://doi.org/10.1016/S0040-6031(98)00530-9
Drysdale D (2011) Steady Burning of Liquids and Solids, in: An Introd. to Fire Dyn., John Wiley & Sons, Ltd, Chichester, UK, pp 181–223. https://doi.org/10.1002/9781119975465.ch5.
Janssens ML (1991) Measuring rate of heat release by oxygen consumption. Fire Technol 27:234–249. https://doi.org/10.1007/bf01038449
S. McAllister, M. Finney (2013) Effect of crib dimensions on burning rate, Seven Int. Semin. Fire Explos. Hazards ISFEH7. 7:1–10. https://doi.org/10.3850/978-981-07-5936-0_08-02.
Hasemi Y, Yokobayashi S, Wakamatsu T, Ptchelintsev AV (1995) Firesafety of building components exposed to a localized fire - scope and experiments on ceiling/beam system exposed to a localized fire. In: ASIAFLAM, InterScience Communications, Hong Kong, pp 351–361
Lattimer BY (2016) Heat transfer from fires to surfaces. In: Hurley MJ, Gottuk D, Hall JR, Harada K, Kuligowski E, Puchovsky M, Torero J, Watts JJM, Wieczorek C (Eds), SFPE Handb. Fire Prot. Eng. Fifth Ed., pp 745–798. https://doi.org/10.1007/978-1-4939-2565-0.
Williams FA (1977) Mechanisms of fire spread, Symp. (Internatio Nal) Combust. 16:1281–1294
Quintiere JG (2006) Fire spread on surfaces and through solid media. In: Fundamentals of fire phenomena, ch. 8. John Wiley & Sons, Ltd
Jiang L, Xiao H, Zhou Y, An W, Yan W, He J, Sun J (2014) Theoretical and experimental study of width effects on horizontal flame spread over extruded and expanded polystyrene foam surfaces. J Fire Sci 32:193–209. https://doi.org/10.1177/0734904113505677
European Committee for Electrotechnical Standardization, TR 50670:2016 External fire exposure to roofs in combination with photovoltaic (PV) arrays - Test method(s), CENELEC (2016)
Bradstock RA, Auld TD (1995) Soil temperatures during experimental bushfires in relation to fire intensity: consequences for legume germination and fire management in South-Eastern Australia. J Appl Ecol 32:76. https://doi.org/10.2307/2404417
Keeley JE (2009) Fire intensity, fire severity and burn severity: a brief review and suggested usage. Int J Wildl Fire 18:116–126. https://doi.org/10.1071/WF07049
Byram GM (1959) Combustion of forest fuels. In: Davis KP (Ed) For. Fire control use, pp 61–89. https://doi.org/10.2307/1932261.
ROCKWOOL A/S, ProRox SL 960 | Data Sheet, Data Sheet (2019) https://p-cdn.rockwool-rti.com/siteassets/tools--documentation/products-industrial/product-data-sheets/english/rw-ti-pds-prorox-sl-586-en.pdf?f=20200924084410.
EPS Industry Alliance, Fire Resistance | EPS Industry Alliance (2012). http://www.epsindustry.org/building-construction/fire-resistance. Accessed 16 Nov 2021
Acknowledgements
The authors would like to thank Ingka Services AB (formerly IKEA Services AB), ROCKWOOL International A/S and Kingspan Holdings (Irl) Limited for the financial support of the PhD project of Jens Steemann Kristensen.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kristensen, J.S., Jacobs, B. & Jomaas, G. Experimental Study of the Fire Dynamics in a Semi-enclosure Formed by Photovoltaic (PV) Installations on Flat Roof Constructions. Fire Technol 58, 2017–2054 (2022). https://doi.org/10.1007/s10694-022-01228-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10694-022-01228-z