Fire Behaviour of a Prestressed Thin-Walled Concrete V-Beam

Abstract

The present work investigates the fire behaviour of a prestressed thin-walled concrete V-beam with variable cross section along its longitudinal axis. In particular, the results obtained from different modelling strategies implemented through analytical computations and Finite Element (FE) thermo-mechanical analyses conducted both with Euler–Bernoulli beam elements and with shell elements were compared. The models were able to properly allow for the prestressing force and its variation with temperature. The mode of failure was analysed both at ambient temperature and at elevated temperature by employing the ISO 834 standard heating curve as well as parametric fire curves so as to investigate the behaviour in the cooling phase. The outcomes showed that the beam model was not capable of accurately predicting the failure mode by largely overestimating the time of collapse. Indeed, the FE analysis with shell elements highlighted that beam behaviour assumptions with sections that remain plane were not satisfied as fire progressed. Furthermore, it also showed that the failure mode was not flexural in the longitudinal direction but due to the failure of the webs in transverse bending that interacted with longitudinal stresses. Finally, the analyses conducted by applying parametric fire curves highlighted possible failure in the cooling phase, which emphasises the need of careful analysis for these types of structural members.

1 Introduction

Industrial buildings are often made of precast concrete elements because of ease and speed of erection. One of the advantages of precast concrete members is the possibility to produce many different shapes that can be easily built at the production site by satisfying both structural and aesthetic objectives. In this respect, I-sections, V-sections, inverted V-sections and TT-sections, to name a few types, can be commonly found in roof structures. These beams can be highly complex with cross sections that may vary along the longitudinal axis as well as characterised by thin-walled slender parts. Moreover, in order to cover significant spans, they are typically prestressed. Industrial halls may store large quantities of combustible material and fire can be consequently a significant threat. Thus, the assessment of the structural fire performance becomes paramount. However, fire behaviour of such members is not straightforward to foresee. Thin elements composing the cross sections are typical, because prestressed concrete members are often made of higher concrete strength than ordinary reinforced concrete elements. This may lead to reduced protection to the steel reinforcement. Moreover, cold worked prestressing steel strands are more sensitive than hot rolled steel reinforcement to elevated temperature by exhibiting higher degradation of the mechanical properties [1]; hence, temperature increase in the prestressing strands may cause significant loss of load-bearing capacity. In early works, Troxell [2] reported researches on the response of prestressed concrete members in fire; Gustaferro and Selvaggio [3] and Gustaferro [4] performed experimental tests on the fire behaviour of prestressed concrete slabs and beams. More recently, Kodur and Hatinger [5] proposed a performance-based methodology to evaluate the fire resistance of prestressed concrete double T-beams under realistic fire, loading, and restraint scenarios. Bamonte et al. [6] showed that the analysis of the flexural behaviour of prestressed concrete members with massive sections exposed to natural fire curves cannot be limited to the heating phase, being the cooling phase fundamental to capture the failure mode. Kodur and Shakya [7, 8] investigated the flexural and shear response of prestressed concrete hollow core slabs under fire conditions. Indeed, a finite element model that exploited solid elements was necessary to assess the fire behaviour. Fellinger [9] and Venanzi et al. [10] also investigated the fire behaviour of hollow-core concrete slabs. In spite of not being the core of this work, extensive interest in the behaviour of post-tensioned concrete elements can be also found in literature [11,12,13,14].

With regard to the modelling of concrete thin-walled open sections, the classical assumption of plane sections may not be strictly true, in particular as fire progresses; thus, a beam model may not be sufficient to capture the structural behaviour in an accurate way. Moreover, sections with vertical or inclined deep webs may be shear critical [15,16,17]. In fact, Bamonte et al. [15] found that by analysing the load-bearing capacity in fire of an inverted V-section, shear is more dangerous than flexure. They studied the mechanical response analytically based on the thermal field obtained through finite element analysis. These findings were also shown in [16] where the assessment of a V-section to cracking and corrosion was carried out. Also, TT-sections may experience shear failure as highlighted by Franssen and Brüls [17], in which the shear capacity was computed according to ENV 1992–1-2 [18]. Thus, careful investigation on the structural fire behaviour is required and from the state of the art it emerges that, despite the extensive use of such structural members in the design practice, there is a lack of research works on the topic. In this respect, the present work aims at examining the performance of a prestressed thin-walled concrete V-beam with variable cross section along its longitudinal axis subjected to the ISO 834 heating curve and parametric fire curves by carrying out a comprehensive comparative numerical thermo-mechanical analysis with different modelling strategies. The paper is organised as follows: in Sect. 2 the case study and the numerical modelling along with preliminary analyses at ambient temperature are presented; in Sect. 3 the thermal analysis is described; in Sect. 4 the results of the mechanical analyses are comprehensively reported and discussed; finally, in Sect. 5 conclusions are drawn.

2 Description of the Case Study and Numerical Modelling

The case study is represented by a prestressed thin-walled concrete V-beam with variable cross section along its longitudinal axis, that could be found on the market. The beam is simply supported, the span measures 16.84 m and it is intended as a roof beam. Figure 1a shows the longitudinal axis as well as representative cross sections. The height of the section is 380 mm at the support and 840 mm at midspan, whereas the total width remains unchanged and it is equal to 2.40 m.

Figure 1

(a) Actual longitudinal view of the beam and the line in red is the adopted beam modelling approximation; (b) beam cross-sections at different locations used in the beam modelling; (c) schematic view of the roof structure. Dimensions in m

Concrete is of class C40/50. The reinforcement meshes and reinforcement bars have characteristic yield strength fyk = 450 MPa. The number of rectilinear prestressing strands varies along the beam axis: 4 at the support and 10 at midspan (see Fig. 1b). The area of each strand is 93 mm². The distance between the bottom edge of the beam and the centroid of the strands is 40 mm; thus, the concrete cover is about 34.5 mm. The prestressing strands have characteristic ultimate strength fpk = 1860 MPa and characteristic strength value at 1% elongation fp1k = 1670 MPa. The prestressing stress after long-term losses was estimated to be equal to 1140 MPa. The reinforcement in the webs is characterised by a mesh of bars whose diameter φ is equal to 6 mm and the spacing is equal to 100 mm in both longitudinal and transverse directions. Then, between the core of the cross section and the webs additional reinforcement was placed by doubling up to steel area in both directions. The concrete cover of the reinforcement mesh was determined by means of tests in situ on an identical beam and it was estimated between 10 mm and 20 mm without noticeable variation along the length of the beam and it is defined as the distance between the exposed side of the cross section and the edge of reinforcement bar. The uniform distributed applied load in the fire load combination is 7.95 kN/m. The roof structure is made of an insulated steel sheeting that spans between the V-beams, as schematically shown in Fig. 1c.

2.1 Numerical Modelling

The comparative numerical analysis of the case study was carried out with the thermo-mechanical software SAFIR [19] that is capable of including the prestressing force and of taking into account its variation with temperature. Two types of numerical modelling were considered: (1) beam model; (2) shell model.

2.1.1 Beam Modelling

A beam model was developed with Euler–Bernoulli fibre-based beam elements [19]. Thus, only failure caused by normal stresses in the longitudinal direction could be detected. The beam was divided into six cross sections as highlighted in Fig. 1b. For instance, the part of the beam 2.1 m long from the support was modelled with one geometry, which conservatively corresponds to the cross section at the support. However, the number of strands was changed according to the actual distribution in the beam. The additional longitudinal reinforcement mainly consisting of the reinforcement mesh in the webs was neglected. The mechanical model consisted of 58 Bernoulli beam elements with two Gauss points, as shown in Fig. 2. Since the cross-section variation, the change of self-weight was accurately taken into account. No longitudinal slip between concrete and the strands was considered. The concrete uniaxial material model, as defined in EN 1992–1-2 [1] with explicit creep [20, 21] and tension strength equal to 1 MPa, was employed. The prestressing steel model of cold worked class B type from EN 1992–1-2 [1] was considered with elastic modulus E_s = 195 GPa. The prestressing force was applied by imposing equivalent residual stresses to the strands.

Figure 2

Beam model

2.1.2 Shell Modelling

The shell model was also developed in SAFIR [19] and the shell element was used for modelling reinforced concrete slabs in the fire condition by Moss et al. [22] and Lim et al. [23], where in the latter validation against experimental data was performed. In order to model the beam in the more accurate way, shell elements with different thickness and reinforcement were used based on their location. This led to 11 types of shell elements. The distance of the reinforcement mesh in the webs to the exposed edge was varied in order to investigate its effect, because it was found that the concrete cover thickness could be between 10 mm and 20 mm. The mechanical model consisted of 7848 quadrangular elements characterised by 4 Gauss points on the shell area and 10 Gauss points in the thickness, as illustrated in Fig. 3a. A bi-axial plane stress element that included the explicit transient creep strain model developed by Gernay et al. [24] was employed. The concrete model is calibrated on the EN 1992–1-2 model and it is able to take into account the non-reversibility of transient creep strain when the stress and/or the temperature decrease. As in this case study, even though the temperature in the case of the ISO 834 heating curve was always increasing and the external applied load remained constant, some fibres underwent stress reduction owing to differential thermal expansion. Thus, the use of an explicit transient creep model allowed a more accurate analysis and even more so for the parametric fire curve analyses that include the cooling phase. Plasticity is based on a Drucker-Prager yield function in compression and a Rankine cut off in tension. Damage is formulated using a fourth-order tensor to capture the different damage processes in tension and compression including the effect of stress reversal on the concrete stiffness (crack closure) [25]. Compressive strength equal to 40 MPa was considered. The fracture energy to approximate the tension-stiffening effect was taken as 6000 N/m². This value was chosen based on the considerations made by Nia and Gernay [26] to have a more robust numerical simulation. In this respect, the characteristic concrete tensile strength was lowered from 2.5 MPa, typical of a C40/50 concrete strength class, to 1 MPa. The other material parameters were considered as default values [19]. Concrete degradation followed the EN 1992–1-2 provisions for siliceous aggregates. The reinforcement bars and the prestressing strands were included and accurately oriented with respect to the beam axes. They were modelled according to the appropriate steel uniaxial material law by EN 1992–1-2 for bars and strands. For the latter, as for the beam analysis, the prestressing steel model of cold worked class B type from EN 1992–1-2 was considered with elastic modulus E_s = 195 GPa and the prestressing stresses were introduced as residual stresses. In Fig. 3b, the principal membrane forces are shown. As expected, at the strand location, tension (red lines) was present, whereas the other parts of the beam were in compression (blue lines). Boundary conditions representative of a simply supported scheme were applied. Indeed, the whole edge of the actual beam is conceived to be vertically supported. The loads coming from the roof were applied as uniformly distributed linear loads on the top of the webs, whilst the self-weight was assigned to each shell as a load per unit area.

Figure 3

Shell mode: (a) mesh definition and supports; (b) membrane principal stresses after gravity load application

2.1.3 Preliminary Numerical Analyses at Ambient Temperature

A series of preliminary analyses was carried out in order to identify the failure mode at ambient temperature for each modelling strategy. In this way, it was already possible to detect if any difference in the failure mode occurred. Moreover, it will also serve to investigate whether any discrepancy might exist between the failure mode at ambient and at elevated temperature. Analytical computation of the ultimate bending moment is also included and it provides another means of comparison. Thus, both analytical and numerical analyses of the collapse load multiplier were performed, as reported in Table 1. In particular, in the numerical analyses the load was incrementally augmented up to failure of the beam and the load multiplier was obtained as the ratio between the failure load and the applied load in the fire combination. It has to be noted that in the shell model, the load was incrementally increased on the top of the webs since the load carried from roof is applied at that position.

Table 1 Comparison of the Load Multiplier and Failure Mode at Ambient Temperature

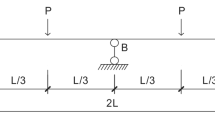
The shell model analysis was also run for three different concrete cover thicknesses, i.e. 10 mm, 15 mm and 20 mm, for the reinforcement mesh in the webs. As expected, for each model the critical cross section was not located at midspan because of the variable geometry of the beam along the longitudinal axis. Moreover, the failure mode was not the same for all the modelling strategies. First, the analytical analysis exhibited the highest load multiplier, i.e. 3.42, in terms of ratio between the ultimate and the applied bending moment and the critical cross section was located at about 5 m from the support, i.e. ≈ L/3, as depicted in Fig. 4a. Mainly due to the modelling approximation, the FE beam model collapsed by sustaining less load than the analytical model, i.e. −12%. In fact, failure was observed at about L/4, as illustrated in Fig. 4b, which corresponds to the change of the cross section from Cross-section 4 to Cross-section 5, as illustrated in Fig. 1a. For the shell model, failure was mainly caused by collapse of the webs that opened up under increasing applied load at cross sections towards the supports (approximately L/8) where the webs are more inclined, as shown in Fig. 4c. This is also confirmed by the fact that, when the concrete cover increased and the reinforcement mesh moved towards the upper part of the web, the load multiplier increased too. In fact, since the large inclination of the webs towards the supports, i.e. about 15° with respect to the horizontal plane, the structural behaviour of the webs in the transverse direction can be approximated as a cantilever that is prestressed in the orthogonal direction. Therefore, the position of the reinforcement mesh closer to the tension side, i.e. for c = 20 mm, is beneficial in terms of load-bearing capacity. Indeed, the failure mode was due to an interaction between transverse and longitudinal flexural stresses with concrete failure identified at the joint between the web and the core and at the web tip. In sum, the different modelling strategies provided load multipliers with maximum difference of 24% and different failure modes for which the shell model gave a more comprehensive understanding of the beam behaviour by also considering the behaviour in the transverse direction.

Figure 4

Ambient temperature analysis: (a) bending moment diagram at failure determined through analytical analysis; (b) deformed shape of the beam model at failure; (c) deformed shape amplified by a factor of 5 and vertical displacements of the shell model at failure for c = 15 mm

3 Thermal Analysis

First, the thermal analysis of the beam was carried out according to different methods based on the modelling strategy and under the nominal fire curve ISO 834. In this respect, for the FE beam model a 2D thermal analysis was employed, whereas for the FE shell model a 1D thermal analysis was exploited. Second, only for the FE shell model, parametric fire curves were used in order to investigate the behaviour in the cooling phase too and for convenience the results are shown in Sect. 4.3.2 along with the mechanical analyses. In all models the thermal exposure, either represented by the ISO 834 heating curve or by a parametric fire curve, was applied to the bottom of the beam. Conversely, at the top of the beam, an adiabatic boundary condition was imposed.

3.1 2D Thermal Analysis for the Beam Model

The beam element developed in SAFIR is based on a fibre formulation for which a cross-sectional two-dimensional thermal analysis is performed at each Gauss point. Based on the beam subdivision illustrated in Fig. 1, six thermal analyses were performed. Therefore, the heat flux along the longitudinal axis of the beam element was neglected and 2D transient thermal analysis was performed on the cross sections by means of linear triangular finite elements. Numerical integration in the plane of the elements was performed on 3 Gauss points.

Due to the thermal properties of concrete, a fine mesh was used to accurately capture nonlinear thermal gradients. In this respect, depending on the cross section, from 4500 to 5500 fibres were used, as shown in Fig. 5. The thermal properties of concrete were taken from EN 1992–1-2 [1] with material emissivity equal to 0.7 and convection coefficient for exposed and unexposed surfaces 25 W/m²K and 4 W/m²K, respectively. The density value was 2400 kg/m³ with moisture content of 2%. Only the prestressing strands were modelled, whereas the presence of additional reinforcement was not considered. The prestressing steel thermal properties were those provided in EN 1992–1-2.

Figure 5

2D thermal analysis for beam modelling according to the ISO 834 heating curve: mesh and temperature distribution after 60 min in Cross-section 6

Figure 6c shows the temperature evolution within the core part of the cross section at Cross-section 6. As expected, it is possible to observe that a significant thermal gradient established in the cross section. The strand temperature increased up to about 300°C after 60 min and 400°C after 90 min, which means that the effective yield strength f_py,θ became, respectively, about 70% and 50% of the value at ambient temperature according to EN 1992–1-2. Moreover, the webs were the most heated parts of the cross section owing to their thin thickness and the results are given in Fig. 6d. Indeed, it is interesting to note that there is not much difference between the bottom (exposed sides) of the core and the webs of the cross section, whereas a clear difference is observable looking at the temperature at the top (unexposed edge) with the top edge of the webs being hotter than the core one because of thinner thickness.

Figure 6

(a) Shell finite element model subdivided into different shell types; (b) temperature distribution in the webs after 30 min of exposure to the ISO 834 heating curve; (c) comparison between 2D and the 1D thermal analyses of the core due to the ISO 834 heating curve (d) comparison between 2D and the 1D thermal analyses of the webs due to the ISO 834 heating curve

The results of the 2D thermal analysis will be also used later on to analytically estimate the fire performance of the beam by means of the 500°C isotherm method.

3.2 1D Thermal Analysis for the Shell Model

As shown in Fig. 6a, the shell model was divided into 11 parts that are representative of different properties of the structural member in terms of thickness and reinforcement. As for the beam analysis, the thermal properties of concrete were taken from EN 1992–1-2 [1] with material emissivity equal to 0.7 and convection coefficient for exposed and unexposed surfaces 25 W/m²K and 4 W/m²K, respectively. When in Sect. 4.3.2 the thermo-mechanical behaviour under parametric fire curves is described, only the convection coefficient on the exposed side was changed and it was taken equal to 35 W/m²K. Thus, the same thermal material properties as those used for the beam thermal analysis in Sect. 3.1 were employed. As previously mentioned, the thermal analysis of shell elements implies a one-dimensional heat flux analysis through the thickness, as shown in Fig. 6b. This is justified by the small thickness of the parts composing the beam cross-section. In this respect, Fig. 6c and Fig. 6d show the comparison between the 2D and 1D thermal analyses of the core and the webs of the cross section under the ISO 834 heating curve applied to the bottom edge. It is possible to observe good agreement between the two thermal analyses.

4 Mechanical Analysis

Three mechanical analyses were carried out in order to investigate the thermo-mechanical behaviour of the beam exposed to the ISO 834 heating curve: (1) analytical analysis based on the simplified 500°C isotherm method; (2) FE beam-based element analysis; (3) FE shell-based element analysis. Moreover, the FE shell-based thermo-mechanical analysis was performed under the exposure of different parametric fire curves in order to investigate the behaviour in the cooling phase.

For all relevant analyses, concrete constitutive laws with explicit creep as described in Sect. 2.1.1 and Sect. 2.1.2, were considered, whereas the other material characteristics of concrete made of siliceous aggregates were assumed in accordance with EN 1992–1-2 [1], such as the reduction factors of the mechanical properties at elevated temperature. Moreover, also for the strands and the reinforcement steel, relevant material properties as for EN 1992–1-2 [1] were taken. Possible spalling was not considered in this work.

4.1 The Simplified 500°C Isotherm Method

The EN 1992–1-2 provisions [1] include the 500°C isotherm method for the verification of the cross-section capacity of a reinforced concrete element subjected to the ISO 834 heating curve or to a parametric fire curve. Briefly, the method identifies a reduced concrete cross-section, which is unaffected by the temperature in terms of compressive strength, and which corresponds to all fibres characterised by temperature below 500°C at a given time after the fire start. For the reinforcement, based on the temperature in each bar/strand, the retention factor of the yield strength at elevated temperature is computed and the reduced strength is then evaluated. Finally, once the reduced effective concrete cross section and the reduced strength of the steel reinforcement are identified, the bending capacity of the cross section is evaluated as for the ambient temperature calculation. As an example, in Fig. 7, the 500°C isotherm of a beam cross section after 60 min of exposure to the ISO 834 is shown.

Figure 7

500°C isotherm position after 60 min of exposure to the ISO 834 of Cross-section 4

By applying the 500°C isotherm method, the evolution in time of the resisting bending moment in the fire situation, M_Rd.fi, was compared with the applied bending moment in the fire situation, M_Ed.fi, as shown in Fig. 8. It is possible to observe that the ultimate condition, i.e. when M_Rd.fi = M_Ed.fi, at the critical cross-section occurred after 100 min of exposure to the ISO 834 heating curve, which means that the temperature in the strands is about 435°C, i.e. the strength is approximately 38% of that at ambient temperature.

Figure 8

Evolution in time of the resisting bending moment of the critical section according to the 500°C isotherm method

Moreover, a simplified evaluation of the shear resistance was performed by exploiting the 500°C isotherm method and by considering the reinforcement mesh capable of carrying shear in the webs. Thus, the shear capacity of webs in their plane was computed at the supports. By following the procedure described in Bamonte et al. [15], the shear force in the web V_Ed* and the effective depth of the cross section d* in the web plane read

$$\begin{gathered} V_{{Ed}}^{*} = \frac{{V_{{Ed}} }}{{2\sin \beta }} \hfill \\ d^{*} = \frac{d}{{\sin \beta }} \hfill \\ \end{gathered}$$

(1)

where V_Ed is the shear force at the supports in the fire combination, d is the effective depth of the cross section in the vertical plane at the supports and β is the inclination of the web with respect to the horizontal plane, as shown in Fig. 9.

Figure 9

Section properties at the support

Neglecting transverse bending effects, the contribution to the shear capacity is given by the steel reinforcement $V_{{Rd.s}}^{*}$ and by the inclined concrete struts $V_{{Rd.c}}^{*}$, respectively.

$$\begin{gathered} V_{{Rd.s}}^{*} = 0.9A_{{sw}} \frac{{d^{*} }}{s}f_{{ywd}} \cot \theta \hfill \\ V_{{Rd.c}}^{*} = 0.9d^{*} b_{w} \alpha _{{cw}} \nu f_{{cd}} \frac{{\cot \theta }}{{1 + \cot ^{2} \theta }} \hfill \\ \end{gathered}$$

(2)

where A_sw is the area of the steel reinforcement that resists to shear, s is the spacing of the steel reinforcement, f_ywd is the design yield strength of the steel reinforcement, θ is the angle of the inclined strut, b_w is the width of the web, α_cw is the coefficient that allows for the effect of prestressing, ν is the effectiveness factor equal to 0.6, f_cd is the design cylindrical compressive strength of concrete. Thus, it is possible to determine the evolution of the shear capacity in time knowing the position of the 500°C isotherm and the temperature in the steel mesh at a number of time intervals, as illustrated in Fig. 10, in which the effect of prestressing is neglected in the fire situation, i.e. α_cw is taken equal to 1.0. In particular, Fig. 10 shows three cases characterised by concrete cover thickness of the steel reinforcement in the webs equal to 10 mm, 15 mm and 20 mm, respectively. As expected, with c = 10 mm the shear capacity V_Rd.s* decreases more rapidly than for c = 15 mm and c = 20 mm and the ultimate condition regarding the shear capacity of the beam, i.e. when V_Ed* = min{V_Rd.s*;V_Rd.c*}, occurred at 50 min after being exposed to the ISO 834 heating curve, whereas for c = 15 and c = 20 mm it corresponded to about 70 min and 75 min, respectively. Hence, this hints that shear can be critical in these types of section, as observed in [15]. However, it is worth pointing out that the inclination of the webs close to the supports with respect to the horizontal plane is such (β = 13.2°) that the webs are more likely to resist in transverse bending once the material properties have degraded due to elevated temperature. In fact, this way to compute the shear capacity would be more appropriate for higher inclinations of the webs with respect to the horizontal plane (β > 45°). Nonetheless, this analysis confirms that for this type of sections, the fire behaviour is not obvious and a careful in-depth investigation is recommended.

Figure 10

Evolution in time of the resisting shear force at the support for different cover thicknesses according to the 500°C isotherm method

4.2 FE Beam-Based Analysis

The finite element beam-based analysis showed that loss of load-bearing capacity of the beam occurred after 103 min of exposure to the ISO 834 heating curve, as illustrated in Fig. 11a. Due to the inherent nature of the beam finite element formulation, failure owing to normal stresses, mainly caused by bending, was observed (see Fig. 11c). It is interesting to note that the stress in the strands increased in the first 12 min of the analysis, as reported in Fig. 11b. This is mainly caused by the differential thermal expansion. As fire progressed and the temperature in the strands increased, the prestressing stress reduced because of degradation of the mechanical properties at elevated temperature. Eventually, failure was determined by loss of strength in the prestressing strands. The temperature in the strands was again about 435°C, i.e. the strength was approximately 38% of that at ambient temperature. By comparing the results with the 500°C isotherm method, it is possible to observe that the time of failure is remarkably similar. This highlights that, despite being a simplified analysis, the 500°C isotherm method provides, for this case study, accurate results if the structural element experiences failure caused by normal stresses in the longitudinal direction. However, due to the cross-section shape, the assumption that implies the sections to remain plane will not be likely satisfied as the fire progresses. Moreover, the webs are particularly inclined and the effect of transverse bending moment of the webs may reveal significant, as already observed in the preliminary ambient temperature analysis described in Sect. 2.1.3. In this respect, the beam model is not adequate to capture such mechanisms and FE shell-based analysis is needed to investigate these issues.

Figure 11

FE beam-based analysis: (a) evolution in time of the vertical displacement at midspan; (b) evolution in time of the stress in the strands; (c) deformed shape at failure

4.3 FE Shell-Based Analysis

4.3.1 Exposure to the ISO 834 Heating Curve

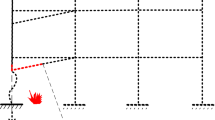
The fire behaviour under the ISO 834 heating curve was analysed. In particular, the analysis with the minimum concrete cover thickness equal to 10 mm of the reinforcement mesh in the webs is first in-depth presented. It will be shown in the following that the concrete cover thickness has great significance on the structural fire performance of the beam. The foremost outcome of the mechanical analysis was the behaviour at failure of the beam that was mainly caused by transverse flexural collapse of the webs that interacted with longitudinal bending, as previously highlighted in Sect. 2.1.3 and shown here in Fig. 12a and b. Moreover, not only the failure mode was different from the beam model analysis results at elevated temperature, it occurred at a significantly shorter time, i.e. at about 38 min with c = 10 mm. A lower fire resistance of the shell-based model was somehow expected by looking at the collapse load multipliers of Table 1 that are characterised by smaller values than the beam model. The cross section located at 3 m from the support was critical and its position, i.e. about L/5, depended on the applied load and the geometry of the beam, such as the web inclination, as reported in Fig. 13a and c. Due to the small inclination angle, i.e. about 18°, with respect to the horizontal plane of the webs at the critical section, shear in the web planes was not critical. Furthermore, Fig. 13b also shows that the sections did not remain plane as the fire progressed. Indeed, an open thin-walled cross section with variable geometry such the one under study is more sensitive to sectional distortions than a compact cross-section, e.g. a rectangular shape. Moreover, highly nonlinear thermal gradients that established in the cross section and large deformations in the transverse direction coupled with the longitudinal direction that occurred as the fire progresses also contributed. In this respect, the tips of the webs underwent vertical displacement towards the end of the analysis that was between 1/10 and 1/6 of the web length. Thus, a beam analysis under classical assumptions of plane sections introduces a degree of approximation that may not be accurate enough to describe the fire behaviour of such members. Figure 14a and b indicate that flexural collapse in the longitudinal direction was not relevant. In fact, by the time failure occurred, the average prestressing stress in the strands did not reduce from its initial value with relatively low vertical displacements at the beam midspan. Conversely, the point at the top edge of the webs at the critical section exhibited larger vertical displacements as shown in Fig. 14c, that suggests a different nature of the collapse mode.

Figure 12

Cover thickness equal to 10 mm: (a) deformed profile at failure; (b) deformed shape and vertical displacement in m at failure amplified by a factor of 2

Figure 13

Cover thickness equal to 10 mm: (a) beam transverse deformed shape at failure; (b) critical section total strains at failure; (c) beam longitudinal deformed shape at failure

Figure 14

Cover thickness equal to 10 mm: (a) evolution in time of the vertical displacement at midspan; (b) evolution in time of the average prestressing stress in the strands; (c) evolution in time of the vertical displacement of the top of the webs at the critical section

A low value of the concrete cover entailed quicker increase in temperature and quicker degradation of the steel reinforcement. Moreover, since in the transverse direction the web at the critical section with large inclination can be roughly approximated with a cantilever loaded at the tip, the reinforcement should be placed towards the unexposed edge of the web to better withstand the hogging transverse flexural stresses. At the same time, a larger concrete cover thickness is beneficial because the temperature rise in the reinforcement is slowed down. To analyse the effect of the concrete cover thickness, other two analyses were carried out with values of 15 mm and 20 mm, that were in the range of what found from tests in situ. In particular, the results of the analysis performed with c = 15 mm are thoroughly reported. As a result, Fig. 15 shows the deformed profile and shape at failure of the beam. It is possible to observe that deformations are smaller but the failure mode remained the same, i.e. collapse owing to loss of the transverse flexural strength of the webs, but at different cross sections along the beam, that interacted with longitudinal stresses. In particular, concrete failure at the joint between the core and the web was observed. Moreover, as the concrete cover thickness increases the cross section exhibiting failure tended to get closer to the support. In fact, with a thicker concrete cover the position of the rebars is more favourable to withstand the hogging moment and the inclination of the webs has to be larger. In addition, given the fact that with a thicker concrete cover the reinforcement bars are more protected the time at which failure occurred increased sensitively with respect to the analysis with c = 10 mm: 56 min (+ 47%). In Fig. 16a, it is possible to observe the evolution in time of the vertical displacement of the top of the webs at the critical section and at midspan. It is interesting to note that at the beginning of the fire the webs tended to close because of the thermal bow typical of cantilevers; then, as the fire progressed and loss of stiffness and strength occurred they opened up to failure. Figure 16b shows the evolution in time of the average prestressing stress in the strands, which increased for the first 20 min owing to differential thermal expansion within the cross section; then it started to decrease because of thermal degradation. In Table 2 the comparison between the outcomes of the analyses, that also includes the one with c = 20 mm, is reported. It is evident that a shell-based modelling provides more insight into the fire behaviour of such a beam, for which a careful analysis is recommended.

Figure 15

Cover thickness equal to 15 mm: (a) deformed profile at failure; (b) deformed shape and vertical displacement in m at failure amplified by a factor of 2

Figure 16

Cover thickness equal to 15 mm: (a) evolution in time of the vertical displacement of the top of the webs at the critical section and at midspan; (b) evolution in time of the average prestressing stress in the strands

Table 2 Comparison of the Time of Failure and Failure Mode at Elevated Temperature under the ISO 834 Heating Curve

4.3.2 Exposure to Parametric Fire Curves

In order to investigate the fire behaviour in the cooling phase, the beam modelled with shell elements and with cover thickness equal to 15 mm was subjected to parametric fire curves in accordance with Annex A of EN 1991–1-2 [27]. Indeed, failure after the time of maximum gas temperature is possible; in particular in reinforced concrete elements because of delayed temperature increase in the cross sections, of material degradation and of load redistribution [6, 28]. In this respect, this situation can be dangerous when tackling an emergency and certainly the knowledge of the fire behaviour in the cooling phase can provide useful information that can be exploited by first responders and fire brigades. Thus, three parametric fire curves were selected with values of compartmentation factor b, opening factor O, design value of the fire load density related to the total surface area of the enclosure q_td, compartment time factor Г and parameter t_lim that are reported in Table 3.

Table 3 Parametric Fire Curve Parameters

Fire 01 and Fire 02 are characterised by medium fire growth rate, i.e. t_lim = 20 min, whereas Fire 03 by fast fire growth rate, i.e. t_lim = 15 min. All three parametric fire curves, depicted in Fig. 17, are representative of fully-developed and ventilation-controlled fires and are characterised by different properties in order to analyse different scenarios, as shown in Table 4. In fact, two of them (Fire 01 and Fire 03) exhibit a higher increase rate of temperature than the ISO 834 heating curve up to the peak gas temperature that occurs at 25 min for Fire 01 (983°C) and at 16 min for Fire 03 (914°C), respectively. The cooling rate of these two fire curves is: 21°C/min for Fire 01 and 28°C/min for Fire 03. Differently, Fire 02 closely follows the ISO 834 heating curve (Г ≈ 1) up to 36 min, time at which the peak gas temperature (857°C) is attained, before decreasing to 20°C with cooling rate of about 10°C/min. Indeed, these characteristics may significantly influence the heating of the structural element and consequently the thermal damage. The results in terms of the temperature development in the web reinforcement, in the strands and in the concrete at the exposed and unexposed web surfaces are reported in Fig. 18, respectively. The charts were interrupted at the time of failure, which mainly occurred owing to transverse bending of the webs that interacted with longitudinal stresses, as highlighted in Fig. 19. Thus, the failure mode did not change from the analyses at ambient temperature and under the ISO 834 heating curve. Collapse occurred only for Fire 01 and Fire 02 because the beam survived complete burnout of Fire 03. In both analyses that exhibited collapse, i.e. Fire 01 and Fire 02, failure of concrete material was observed at the joint between the web and the core of the cross section as well as at the tip of the web. Moreover, failure occurred beyond the peak gas temperature, i.e. in the cooling phase, and delayed heating due to low thermal conductivity and high thermal capacity of concrete was the main factor. Indeed, for Fire 01 failure occurred at about 43 min and 18 min after the beginning of the cooling phase, as reported in Table 4. For Fire 02 collapse was detected at 80 min and 44 min after the attainment of the peak gas temperature; hence, well into the cooling phase (more than half of the total analysis time). This also confirms that attention should be paid when analysing such beams.

Figure 17

Parametric fire curves

Table 4 Parametric Fire Curve Analysis

Figue 18

(a) Temperature evolution in the web rebars; (b) temperature evolution in the strands; (c) temperature evolution in the concrete on the exposed web surface; (d) temperature evolution in the concrete on the unexposed web surface

Figure 19

Deformed shape amplified by a factor of 5 at the end of the mechanical analysis: (a) Fire 01; (b) Fire 02; (c) Fire 03

Regarding Fire 01, the beam experienced failure of concrete and at the time at which the reinforcement bars in the web attained about their maximum temperature, i.e. approximately 500°C (see Fig. 18a), that was recorded at 40 min; therefore, 15 min after the time of the peak gas temperature. It is interesting to note in Fig. 18a that the maximum temperature in the web reinforcement attained during Fire 02, i.e. 510°C, is very close to the one reached during Fire 01 even though the peak gas temperature and the heating rate differ quite markedly. This is essentially due to the combination of a longer heating phase and of a smaller cooling rate of Fire 02 that allows the cross section to reach comparable temperatures in the rebars. Furthermore, the maximum temperature in the web reinforcement was recorded at 61 min, i.e. 25 min after the peak gas temperature. This indicates that failing to account for the cooling phase may lead to an underestimation of the maximum temperature that, for instance, in the web reinforcement was about -17% for both Fire 01 and Fire 02. Fire 02 analysis went on slightly longer and failure occurred in the cooling phase when the temperature in the webs was approximately uniform (450–480°C), as shown in Fig. 18c and Fig. 18d. Moreover, it is noteworthy to observe that, despite the fact Fire 02 was characterised by less than half of the fire load density q_td than Fire 01, a low value of the opening factor, i.e. three times smaller than Fire 01, entailed a longer duration of the fire with slow cooling rate that contributed to significant delayed heating and to eventual failure of the structural member. The temperature in the strands was always equal or below 300°C meaning that the strength was higher than 70% of the value at ambient temperature and the average prestressing stress at failure was equal to 974 MPa and to 883 MPa for Fire 01 and Fire 02, respectively. Figure 20 shows the comparison of the vertical displacements of the tip of the webs at the critical cross section, which denotes their “runaway” at failure. Despite the heating rate and peak gas temperature of Fire 03 were higher than the ISO 834, the fire was too short and the cooling rate not slow enough to heat up the section in such a way to induce failure and at the end of the analysis the average prestressing stress was 1072 MPa. However, residual displacements were observed, that for the vertical displacement of the webs were more than 10 cm. The magnitude of the residual displacements is certainly of interest because it is related to the damage of the beam caused by the thermal action. Finally, the fire analysis under natural fire curves revealed that the behaviour of such beam is not straightforward. Indeed, despite the failure mode is identical to the one observed by applying the ISO 834 heating curve, the beam can experience failure in the cooling phase.

Figure 20

Vertical displacement of the tip of the webs at the critical cross section

5 Conclusions

The paper showed the results of a numerical comparative analysis on the structural fire behaviour of a prestressed thin-walled concrete V-beam by implementing different modelling strategies. A preliminary numerical analysis aimed at investigating the failure mode at ambient temperature revealed that the failure mode of the shell-based model was different from the one obtained from the numerical and the analytical beam modelling. In particular, failure of the webs owing to transverse bending that interacted with longitudinal stresses was identified. This was also confirmed by computing the load multiplier as a function of the concrete cover thickness of the steel reinforcement in the webs. In fact, by increasing the concrete cover, the beam exhibited higher load multiplier that hinted the beneficial effect of having the rebars towards the tension side by approximating the largely inclined webs as cantilevers loaded on their tips. With regards to the beam fire behaviour, the FE beam model showed longitudinal flexural failure after 103 min of exposure to the ISO 834 heating curve. In this respect, the 500°C isotherm method included in EN 1992–1-2 provided good agreement with the FE beam analysis by highlighting collapse after 100 min. The more detailed shell model analysis showed that failure occurred owing to transverse flexural mode of the webs accompanied by interaction with longitudinal stresses. The concrete cover thickness of the steel reinforcement in the webs had significant influence on the load-bearing capacity of the beam. Indeed, failure under the ISO 834 heating curve occurred at 38 min, 56 min and 69 min for concrete cover thickness equal to 10 mm, 15 mm and 20 mm, respectively. These outcomes showed that the beam modelling is not adequate to accurately capture the fire behaviour of the analysed beam and, in this case, it significantly overestimated the load-bearing capacity. In addition, an analysis under natural fire curves in the form of parametric fire curves was performed. It showed the same failure mode as for the analysis under the ISO 834 heating curve and highlighted the possibility of failure in the cooling phase due to delayed heating owing to concrete low thermal conductivity and high thermal capacity. Finally, careful modelling should be considered when the fire performance of prestressed thin-walled concrete V-beams has to be assessed.