Abstract
A novel multi-wavelength densitometer was built for the purpose of continuous and simultaneous measurements of light obscuration in smoke layers, concurrently in five bands (λ = 450 nm, 520 nm, 658 nm, 830 nm and 980 nm). This device was used for determining transmittance and visibility in smoke parameters of a smoke layer from the fire of 1.00 dm3 of n-Heptane in a 0.33 × 0.33 m tray located in a test chamber (9.60 × 9.80 × 4.00 m3). The performance of the device was compared with a commercial Lorenz densitometer at 880 nm. Significant differences in measured value of transmittance were observed between the different sensors – from 65% at 450 nm (blue light), 80% at 658 nm (red light) to 95% at 980 nm (IR). The visibility in smoke, estimated following the theory of Jin for light reflecting signs (K = 3), ranged from 7.5 m (blue light) to 12 m (red light) and for the light-emitting (K = 8) signs from 18 to 32 m, respectively. The performed experiment has confirmed the applicability and added value of multi-wavelength measurements of light-extinction in fire experiments. The device was sensitive to temperature variations and requires active cooling and careful warm-up prior to experiments, to reach the expected sensitivity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Optical properties of fire smoke are in the focal point of the fire science, highly relevant to both physical experiments and computer modelling of fires. The obscuration of light by smoke is usually presented in the form of a ‘visibility in smoke’ parameter. In performance-based analyses for fire safety engineering of buildings, the visibility in smoke is often the first tenability criterion that exceeds its threshold value [1], in consequence shaping the fire safety solutions in the building. The smoke obscuration also influences the visibility of evacuation signs, the response to the information on the signs, behaviour and the movement speed of people who are evacuating [2]. Finally, low visibility in smoke will be one of the critical challenges that firefighters face when performing rescue operations.
Despite the profound relevance of visibility in smoke to the fire safety engineering, the existing theory of visibility in smoke was criticized as oversimplified, based on a limited range of experimental results and highly sensitive to user-dependent properties [3]. Even though multiple studies were performed to improve the existing theory to include for more diverse visibility of various evacuation signs (e.g. [4, 5]), the conventional approach is still the simplest model introduced by Jin [6]. This model is based on a limited number of experiments (primarily from the 1960s and 1970s) on the obscuration of monochromatic light by homogenous cold smoke [7, 8]. The development of this model was summarized in [2, 9].
To better understand how light is obscured by the fire smoke and its implications on the performance of evacuation lighting and signage, it is essential to recognize the effects of polydisperse smoke (non-homogenous) on polychromatic light. This assumption is a significant improvement in the precision as compared to the traditional approach, but also resulting in higher complexity of the problem. To enable future research under these conditions, we have developed a novel construction of a smoke densitometer, that may be installed directly within a smoke reservoir and measure smoke extinction concurrently in five wavelengths. In this paper, we discuss similar developments in the past, the construction of the device with particular technical challenges that were faced in the development phase, calibration and exemplar use in an n-Heptane compartment fire experiment.
1.1 Obscuration of Light in Smoke Layers
The obscuration of light passing through a medium is often described with Bougher-Lamber-Beer law (Eq. 1). The ratio of light intensity measured at a target in obscured conditions (I), to the light intensity measured with a clean optical path (I0) is the transmittance (τ). The light obscuration depends on three elements: specific light extinction coefficient (σs), the mass density of smoke (m) and the length of the optical path (l). Another common way to present the light extinction of the smoke is the natural logarithm of τ, which is called the obscuration density (OD) and is presented in [dB/m].
It was recognised that this application of the Bougher-Lambert–Beer law has many limitations emerging from the preliminary assumptions of the law [3], among which: (a) it should be used for monochromatic light, (b) it should be used for single or parallel light sources, (c) the light absorption is considered dominant over light scattering effects. Despite above mentioned profound limitations, this relation is still commonly used to determine the light extinction in fire smoke. Significant simplification in the practical use of this method was introduced by unifying the value of the specific light extinction coefficient (σs) for flaming combustion, with a value of
σs = 8.7 m2/g (± 1.1 m2/g) [10]. This value was determined based on seven studies involving 29 fuels, for light wavelength λ = 633 nm. A major implication of determination of a nearly universal value of σs was enabling to determine the mass concentration of smoke based on light extinction coefficients. This universal value was widely adopted in engineering tools of fire science, among them the most popular CFD code FDS [11]. Other values of σs can be found in literature and engineering guidance – e.g. the value of 4.7 m2/g used in the design of visibility conditions in road tunnels [12] or other values of σs reviewed by [9].
In [13], the value of σs was discussed as a function of light wavelength. This was done by investigating a large batch of measurements of specific light extinction coefficient in wavelengths ranging from UV (385 nm) to far-IR (10 600 nm), with corresponding values of σs from 12 m2/g to 1 m2/g respectively. The value of σs decreased with increasing wavelength. A least-square fit to the experimental data was found (Eq. 2), with R = 0.98675. However, it must be emphasized that this fit applies to stoichiometric and overventilated combustion [13].
As the σs asymptotically grows with the decreasing wavelength, the differences in σs in the lower end of the visible spectrum are profound, which was confirmed in qualitative result analysis of some experiments on the visibility of evacuation signs, e.g. [9, 14, 15] or research on the applicability of free space outdoor optic connectors in foggy weather [16]. As the value of σs can differ significantly within the visible spectrum, it is obvious that the light obscuration through the smoke at different wavelengths will take different values. In fact, past research was focused on exploiting this optical characteristic of smoke for remote analysis of characteristic smoke diameter, as summarized in Sect. 1.3.
1.2 Multi-Wavelength Smoke Densitometers in the Literature
Differences in the obscuration of light at different wavelengths were often connected to the distribution of particle sizes of the smoke [15, 17, 18]. As the particle size distribution depends on the properties of burning material and the conditions in which the combustion occurs, this approach was considered for remote identification of burning fuel.
Jin [15] has considered the impact of light obscuration at a different wavelength on the visibility of evacuation signs. He has recognized that the extinction coefficient in short wavelengths is larger than for long wavelengths and that the difference between them is also a function of time. The difference diminishes as an effect of coagulation of smoke particles. The particle size of 1 µm was proposed as the boundary above which the wavelengths stops being an important factor for visibility. He has calculated the ratios of the visibility in red light to the one of blue light, for smouldering and flaming polystyrene, flaming wood and flaming kerosene.
Dobbins and Jizmagian [18] proposed two methods to determine the mean size of polydispersed dielectric spheres, first of which was the determination of a single spectral transmittance together with knowledge of particle concentrations. This approach is similar to how smoke obscuration effects are determined with Bougher’s law. The size of polystyrene particles used in the experiment (0.126–1.305 µm) was close to the size distribution of soot particles commonly found in fire smoke [19]. For a polydispersion of known concentrations, they were able to compute the particle sizes with one transmittance measurement, following a revised version of Lambert–Beer law from their previous work [20].
Cashdollar et al. [17] proposed to use a white light source and a compact three-wavelength detector assembly to determine the average particle size and mass concentration of smoke. They have used the Mie theory and Dobbins revised Bougher’s transmission law [18] to calculate sizes and concentrations. The beam separation was obtained with two cube beamsplitter filters, centred at wavelengths 450 nm, 630 nm and 1000 nm (nominal bandwidth 10 nm). The light intensity was measured with silicon photodiodes and the entire assembly was mounted in one small casing (8 cm × 10 cm × 5 cm). The smoke obscuration was measured at an optical path of 0.1 m, within a gas sampling test section connected to a fire-tunnel. For wood fire smoke log-transmission ratios were: ln τ(1000 nm)/ln τ(450 nm) = 0.25; ln τ(1000 nm)/ ln τ(630 nm) = 0.47 and ln τ(630 nm)/ln τ(450 nm) = 0.54. These ratios allow for determination for mean particle sizes. A reasonably good agreement was found between these measurements and two other sizing methods (transmission electron microscopy and ionization-type particulate detectors). Authors emphasized that this device may be used in field experiments.
Uthe [21] did investigate the applicability of multi-wavelength LIDAR method to remotely determine extinction coefficient measurements and mean particle sizes of aerosols. The experimental study was performed with 14-wavelength transmissometer. Ten different wavelengths between 390 and 1640 nm, as well as 3900 nm, were produced with Zirconium arc-lamp; wavelength 3390 nm with a He–Ne laser and 10,600 nm with a CO2 laser. The light intensity was measured by photodiodes (Silicone, Germanium, PbSe or HgCdTe) behind narrow-band optical filters. The facility consisted of a long (10 m) aerosol chamber with a cross-section of 0.50 × 0.50 m, to which compressed air with different dusts was supplied. Ratios of extinction between the transmittance measured at 1 045 nm and 514 nm were presented as a function of Saurer mean diameter for submicron particles, allowing for identification of the aerosol type. They have concluded that a single laser system (Nd:YAG 1060 nm) and its first harmonic (530 nm) would be useful to evaluate particles of sizes < 1 µm. For particles with sizes greater than 1 µm, the ratio of extinction coefficients at 1045 and 514 nm converges to value of 1.2 and is no longer sensitive to particle size. A similar conclusion was drawn in [9] where it was stated that as the particle sizes increases, the integral optical property of the soot cloud approaches that of monodisperse particles and particle sizes are no longer important. This is somewhat similar to the observations of Jin [15].
Limitations of optical transmission to the determination of the particle sizes were investigated by Swanson et al. [22]. They have discussed the underlying theory and presented the derivation of the Bougher-Lambert–Beer law, as well as the theory of Mie and the radiative transport equation (RTE). The application of Bougher-Lambert–Beer law was verified in a scattering environment and the Hodkinson's findings related to the restriction of aperture related to scattered light were emphasized. A method of determination of the particle sizes with two measurements of transmittance was validated for monodisperse polystyrene particles with a size of 0–1 µm. Aspey et al. [23] have further improved this method using High-Level Synthesis (HLS) approach and polychromatic LED. They have investigated the spectral change in transmitted polychromatic light, which was used to determine Mie scattering parameters in a wood smoke in the function of time. It was observed that for the wood smoke forward scattering of blue wavelength is approximately three times that for the green detector and the red detector measured negligible forward scattering.
The use of multi-wavelength light transmission was also proposed by Wilkens and van Hees [24] to improve the research capabilities of a cone-calorimeter [25]. This implementation would allow for determination of the mean particle diameter of the smoke produced in the calorimeter, through non-intrusive light transmission measurement. They have reviewed the methods of smoke identification used in the conventional standardized fire testing apparatus and performed theoretical considerations on the limitations of the proposed tool and also in-depth discussion of previous developments. An apparatus similar in the concept was built by Chaudhry and Moinuddin [26]. A sealed box was used as a combustion chamber to burn different materials and the smoke was further transported into five separate light chambers. These chambers were equipped with transmittance measurements with specific wavelengths 275 nm, 365 nm, 405 nm, 620 nm and 960 nm. Both absorbed (measured at angle 0°) and scattered (at angle 90°) light were recorded. A Random Forest machine learning algorithm was trained based on the experimental results, in order to predict the burning material based on the measurements at these five wavelengths. The overall success rate of the algorithm was 96.6%–97.5% showing the high applicability of this method. For some materials such as cardboard and polystyrene, the success rate was lower, respectively 60.3% and 59%. The difficulties with the use of this approach were associated with obtaining meaningful results for both scattering (at a certain angle) and absorption.
Another recently developed approach was done with tomographic reconstruction of an image of LED, captured with a digital camera through a smoke layer. By comparing the predicted and observed shape and light intensity of the LED, the smoke layer opacity could be reverse engineered. This approach could be used for multi-wavelength observations, as typical LEDs consist of red, green and blue diodes [27].
Summarizing previous efforts it was found, that the past use of multi-wavelength optical transmittance meters was limited to the determination of the mean diameter of smoke particle size and consequently, the type and source of the smoke. Most of the devices constructed were connected to bench-scale apparatus (boxes, tube burners, smoke tunnels). The Cashdollar’s apparatus [17] was meant to be used in field experiments, although such use was not reported in the literature. The limitation of the proposed solutions was (1) requirement to know the mass density of smoke or (2) need for high accuracy of the transmittance measurements, which excludes the use of this type of apparatus in field experiments. The direct measurements in compartment scale fire experiments are needed as the optical properties of smoke generated in small and large scale may not necessarily be the same [28]. It is possible to samples the gas from smoke layers, although as Wilkens [24] stated, this would be considered an intrusive approach. Furthermore, following findings of Jin [15] an Aspey [23], the properties of smoke will change with time and that could distort the size of smoke particles and the light extinction measurements in consequence.
For our future research on the visibility in smoke in compartment fires, validation studies for computer models and smoke obscuration effects on evacuation lighting and signage we are interested in the differences of light transmittance through smoke-layers in full-scale experiments, rather than properties of smoke generated in bench-scale apparatus. To fit our purpose, the tool used to measure the light transmittance would have to (a) be mounted directly within the smoke layer, (b) be able to measure the transient change of the transmittance in real-time and (c) allow for result comparison with the existing body of measurements from EN 54–7 test chamber [29], such as one used in [30]. For this purpose, the most promising solution was to construct an optical densitometer based on laser diodes and photo-diodes, that could be mounted within a single casing and share the same optical path. The sources cannot interfere with each other and the interference from the fire source and other light sources (such as emergency lighting) should be limited by aperture, narrow-band filters and internal structure of the receiver. Following these limitations, we have constructed a densitometer that consists of five separate sets of laser—photo-diode couples within one casing, with their light extinction recorded simultaneously over an identical optical path. The sets differ by their specific wavelength and in our case these were: 450 nm (blue), 520 nm (green), 658 nm (red), 830 nm (IR) and 980 nm (IR).
2 Development of the Multi-Wavelength Densitometer
2.1 The Prototype Design
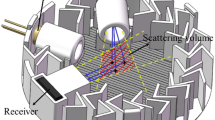
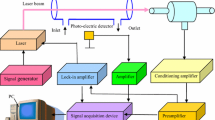
Two prototype multi-wavelength densitometers were constructed based on commercially available 50–100 mW lasers. The list of system components is given in Appendix A. As in [31], the device was built to be installed in a hot smoke layer; thus, the construction of the device was designed to allow for easy replacement if an element is damaged. Five different lasers were installed within one casing, each connected optically with a photodiode behind a matching optical cut-off narrow band filter on the opposite side of the device. A micro alignment system was used to target the laser beam directly on the photodiode. The device was built on a rigid aluminium structure. The laser and photo-diode casings were connected to an external cooling apparatus (cold air), which was controlled with a thermostatic controller to maintain a constant temperature within the box. Photodiodes were connected to five signal amplifiers, built within the receiver casing, which were further connected to the data acquisition system. The measurements at all five wavelengths are performed simultaneously and share the same timeline. The prototype device and general scheme of operation are shown in Fig. 1. The internal build and details of the device are shown in Fig. 2. The calibration data obtained at a thermal equilibrium (26 °C) is shown in Appendix B. With the exception of two data points (520 nm and 658 nm at τ ~ 0.5) in range of τ from 0.2 to 0.8 the device had a calibration error of less than 10%, which for a prototype device we consider as sufficient to evaluate the concept of multi-wavelength densitometry.
The first prototype device had a length of 0.92 m and was built to match the size of the accredited Lorenz densitometer used in the laboratory, allowing direct comparison between the prototype and existing densitometer. An alternate variant of the densitometer was constructed with a longer optical path (2 m) and additional mounting mechanism. This mechanism allows for automated lowering and rising of the densitometer within a test chamber. This capability will be used in future to capture the obscuration density gradient within a small box (2 × 2 × 1 m).
2.2 Thermal Stabilisation of the Device
A possible practical problem with measuring the optical properties of smoke with laser-based densitometer is the thermal drift of lasers. The intensity of light emitted by the laser changes with its temperature. In consequence, the ratio of measured and initial light intensity stops being dependant only on the optical properties of smoke. In order to minimize influence of this factor we have fit the densitometers with an air based cooling system, that was steered by a thermostatic controller, set for an operating temperature of 26 °C. The laser and photo-diode casings were insulated from the hot smoke layer with a layer of mineral wool (5 cm, 120 g/m3). If the temperature inside the box exceeded 26 °C, a low-velocity air supply pumping cold air (8–13 °C) was enabled, to cool the interior and maintain the temperature at 26 °C. Multiple variants of air supply velocity and temperatures were tested. Supply of air at too high velocity has caused vibrations of the laser unit, which interfered with the light intensity measurements. Supply of colder air has caused higher temperature gradients, which resulted in unpredictable changes in the light intensity.
The device must have been pre-heated for approx. 90–150 min before each experiment, for the laser temperature to stabilize. Once the thermal stability of the lasers was reached, the values of light intensity (further considered as our I0) were saved. The illustration of measurements performed in the pre-heating period is shown in Fig. 3. In the first 45 min of the warm-up period, the lasers heat up with different speed. Thermostatic device is first triggered at approx. 10th minute and since approx. 40th minute it works continuously. After 45 min the thermal stabilization is obtained and further changes of light intensity are insignificant.
3 Experimental Setup
To confirm the applicability of the device for research on compartment fires we have performed an experiment involving an n-Heptane pool fire, known as the TF-5 fire, in a standardized EN 54–7 [29] test chamber with dimensions of 9.60 × 9.80 × 4.00 m3 (Fig. 4). This experiment was in principle a recreation of an experiment published previously in [3]. The test rig is built from a steel structure, with gypsum plasterboards. The compartment is closed from the exterior, but is not airtight. During the experiments we have observed no smoke in the hall where the compartment is placed. This lead to an assumption that the compartment is sufficiently sealed from exterior and no significant exchange of gasses occurred between the compartment and exterior during the experiment.
Before the experiments the densitometer was calibrated following the procedure described in [31]. The details of the calibration are given in Appendix B.
A fuel tray with dimensions of 0.33 × 0.33 m2 was filled with 1000 ml of n-Heptane and placed on top of a scale. The mass-loss rate measurements were used to determine the Heat Release Rate, following the assumption that the Heat of Combustion value is Hc = 44,400 kJ/kg. No ventilation was used in the experiment (the compartment was sealed). The obscuration density was measured with the prototype densitometer and an accredited optical densitometer (Lorenz, λ = 880 nm) of the chamber, located next to each other, Fig. 5. Temperature measurements were performed with thermocouples (type K 1 mm Ni–Cr, extended uncertainty 0.3%) directly above the source of the fire and next to the optical densitometers. The thermocouple readings were not corrected for radiation. Additional measurements included light intensity of evacuation lighting as well as the spectrogram of the light of one of the lighting points. These measurements were performed for a parallel experiment and are out of the scope of this investigation.
4 Results
4.1 HRR and Smoke Temperature
Three n-Heptane TF5-type fires were performed in the experimental chamber. The burnout time varied between 320 and 350 s. As the fuel was burning out at slightly different times, some significant differences between experiments were observed in measured mass loss rate towards the end of the experiments. As those differences may skew the optical measurements, only the first 300 s of the experiment were taken into account in quantitative result analysis. The average Heat Release Rate (HRR) of the fire was approx. 87 kW, with a peak value of approx. 117 kW in the 200th second of the experiment. The individual HRR curves for each experiment and a mean curve are shown in Fig. 6.
The measurements of the temperatures are shown in Fig. 7. The temperature evolution followed the growth and decay of the fire, with a peak value at approx. 200th second of the experiment. After 300 s the temperature of the smoke layer was decaying. The peak temperature measured was 101 °C and 63 °C directly above the fire and near the densitometers, respectively. The variability of the temperature measured at the densitometers was smaller than for the central point directly above the fire.
The view of the course of a single experiment is shown in Fig. 8. At the moment of ignition the chamber is free of any smoke, with visible two rows of evacuation lighting lamps and a small reflecting sign in the top-left corner. As the fire develops, a smoke layer forms under the ceiling, which can be identified by a “cone” of light under the lamps. After approx. 3 min, the smoke is so dense, that the reflective sign is no longer visible by the camera. A the end of the experiment, the depth of the smoke layer is approximately half of the height of the compartment.
4.2 Smoke Obscuration
The measurements of the smoke obscuration at different wavelengths are shown in Fig. 9. As expected, the lowest transmittance was observed for shortest wavelength (λ = 450 nm, blue light), while the highest transmittance was observed for the IR lasers (λ = 880 nm and 980 nm). All lasers of the multi-wavelength densitometer show similar trends (in terms of peaks and lows) of the transmittance measured, while the Lorenz densitometer shows a more flat-out curve, which may be a result of internal averaging within the densitometer controller. It also must be noted that the measurement of the light obscuration with the red (λ = 658 nm) laser was fully successful only in the first experiment. In further experiments, this laser failed after approx. 180 s into experiment and further measurements from this laser were discarded.
The scatter of results obtained with multi-wavelength densitometer is larger than for the Lorenz device, however that may be as well attributed to the higher sensitivity for smoke obscuration measurements at lower wavelengths (450–658 nm) than at the IR band. In fact, the prototype densitometer at λ = 980 nm has shown similar scatter as the Lorenz densitometer. In the visible spectrum, the value of the transmittance measured by the red (λ = 658 nm) laser at the end of the experiment is approx. 80%, while for green (λ = 520 nm) and blue (λ = 450 nm) it is 70% and 65% respectively.
The value of transmittance may be used to calculate the light extinction coefficient, which following the theory of Jin [7] (Eq. 3) can be expressed as the visibility in smoke.
A plot of visibility for the K = 3 (light-reflecting signs) is shown in Fig. 10 and for K = 8 (light-emitting signs) on Fig. 11. As observed, the difference between visibility estimation is significant in the visible band. In the case of light reflecting signs, the visibility for blue light at the end of the experiment is approx. 7 m, while for red it is 12.5 m and for IR at λ = 880 nm, it is 25 m. The difference expressed in visibility in smoke [m] is even larger for light-emitting signs (K = 8), with measured values of respectively 18 m, 32 m and 65 m. As the tenability criterion is usually a single sharp value (e.g. 10 m [2]), the wavelength sensitivity may be an important factor to consider.
4.3 The Role of Particle Size Distribution
As identified in the literature review (Sect. 1.3), the ratio of light extinction coefficients for different wavelengths is related to the particle size distribution. As shown in [21] this may be used to identify the type of material being burnt. A theoretical considerations of relation between particle size and light scattering and extinction are given in [9] and a practical application idea in [26].
The smoke in our experiment was from an n-Heptane pool fire. The n-Heptane fire smoke characteristics are known from similar tests in a chamber of the same type, as discussed by Keller et al. [32]. They have used a scanning mobility particle sizer (SMPS) that can classify the particles according to their electrical mobility by means of an electrostatic classifier and counts them optically. A single scan takes approx. 55 s, which for a transient phenomenon (n-Heptane combustion) introduces some unavoidable bias. To limit this bias, the measurement was repeated five times within each experiment. The particle size distribution obtained for n-Heptane fire is shown in Fig. 12a. Particle generation in flaming combustion of n-Heptane in a similar setup was also measured by Li et al. [33]. They have used Fast Particulate Spectrometer (DMS500) to record particle number concentration and distribution. A particle distribution curve was determined for many tray sizes, including a 33 cm tray similar to the tray used in our research. For easier comparison with the results of [32], the results of this study were redrawn on Fig. 12b following the same scale.
Particle distribution (number concentration of particles dw/d Log dp, [#/cm3]) in function of particle diameter (dp) in an n-Heptane fire of a similar size, in a compartment with similar dimensions to the one in the current study. a is reproduced from [32] and b is redrawn from [33]. On a the time refers to the start of measurement and one full measurement takes approx. 1 min
The multi-wavelength densitometer shown in this paper could be possibly used to identify the ratio of extinction coefficients between different wavelengths of the device, as shown in Fig. 13. Such a comparison was performed in the past, as reported in literature, eg. by Uthe [21], who received ratio between light extinction at wavelength of 1045 and 514 nm of 0.25 for rosin smoke (mean particle diameter below 100 nm). In our case, the value obtained by comparing the extinction at 980 and 450 nm for n-heptane smoke (with assumed particle distribution as on Fig. 12) converged at 0.19. Another comparison may be made with the data of Jin, who measured ratios between blue and red of approx. 1.2–1.4 for polystyrene, which is close to the value measured in the initial phase of our experiment. Despite the shortcomings in the precision of the developed apparatus, these approximations indicate that there is potential in remote sensing the particle distribution size with our apparatus. This could be improved, if instead of simple ratio of transmittance more advances algorithms are used to investigate the light transmission at different wavelengths, as suggested in [26]. Furthermore, more data on particle size distribution is required, in order to calibrate such a measurement.
5 Conclusions
Visibility in smoke is among the key tenability criteria used by modern Fire Safety Engineering. It is paramount to the design of evacuation signage and lighting and is one of the most critical factors that need to be addressed during firefighting operations. Despite the profound meaning of this parameter for fire safety, the dependence of the light extinction in smoke on the wavelength of light is rarely taken into account in research or engineering. Most of the modern research is referring to the visibility in the red light band, while light commonly used in buildings is polychromatic and usually covers the whole visible spectrum.
To allow for the future research on the light extinction in smoke layers, we have constructed a multi-wavelength densitometer, capable of measurements in five bands: blue (λ = 450 nm), green (λ = 520 nm), red (λ = 658 nm) and IR (λ = 830 nm and λ = 980 nm). We have performed three experiments with flaming combustion of n-Heptane (also known as the TF-5 fire) based on EN 54–7 [29]. We have measured significant differences in light transmittance and visibility in smoke layers for different wavelengths. In the visible light band, the transmittance measured in same conditions was from 65% (blue light) to 79% (red light). The smoke obscuration expressed as visibility in smoke for light reflecting signs was 7 m (blue light) to 12.5 m (red light). The transmittance and visibility in smoke for the IR band were significantly higher.
Furthermore, as indicated in the literature the ratios between the light extinction coefficient are related to mean particle diameter of the smoke, which means device as shown in here could be used to remotely identify the smoke properties. However, more precise extinction measurements, a method to account for scattering and possibly a database with reference values may be required to make this approach robust. Alternatively, as shown in [26], machine learning approach could be used to identify the smoke based on transmittance values at different wavelengths, rather than specific ratios between the measurements.
The multi-wavelength densitometer may be a useful tool in research focused on the visibility in smoke, validation of numerical models of smoke obscuration and research on evacuation signage and lighting. Our future research will include measuring the light extinction in smoke layers from different materials and types of combustion (flaming, smouldering, pyrolysis) and estimation of the light extinction of emergency lighting sources.
Notes
The trade names used in this study are given to allow for reproduction of the results presented in the paper, and are not an endorsement by the Authors or recommendation of the particular type or make of the devices.
References
Levy C, Martin D, Meacham BJ (2015) Assessing variability in engineer selection of tenability criteria. In: SFPE Europe Conference on Fire Safety Engineering. SFPE
Yamada T, Akizuki Y (2016) Visibility and Human Behavior in Fire Smoke. SFPE Handbook of Fire Protection Engineering. Springer, New York, NY, pp 2181–2206
Węgrzyński W, Vigne G (2017) Experimental and numerical evaluation of the influence of the soot yield on the visibility in smoke in CFD analysis. Fire Saf J. 91:389–398. https://doi.org/10.1016/j.firesaf.2017.03.053
Collins BL, Dahir MS, Madrzykowski D (1993) Visibility of exit signs in clear and smoky conditions. Fire Technol. 29:154–182. https://doi.org/10.1007/BF01038537
Yamada T, Kubota K, Abe N, Iida A (2004) Visibility of emergency exit signs and emergency lights through smoke. 560–569
Jin T (1978) Visibility through fire smoke. J Fire Flammabl 9:135–155
Jin T (1970) Visibility through Fire Smoke (I). Bull Fire Prev Soc Japan 19
Jin T (1971) Visibility through Fire Smoke (II). Bull Fire Prev Soc Japan 21
Zhang Q, Rubini PA (2011) Modelling of light extinction by soot particles. Fire Saf J 46:96–103
Mulholland GW, Croarkin C (2000) Specific extinction coefficient of flame generated smoke. Fire Mater. 24:227–230: https://doi.org/https://doi.org/10.1002/1099-1018(200009/10)24:5<227::AID-FAM742>3.0.CO;2-9
McGrattan K, Hostikka S, McDermott R, Floyd J, Weinschenk C, Overholt K (2017) Sixth edition fire dynamics simulator technical reference guide volume 1. Mathematical Model. 1:1–147
PIARC Technical Committee 3.3 Road Tunnel Operation (2008) Road tunnels: a guide to optimising the air quality impact upon the environment
Widmann JF (2003) Evaluation of the planck mean absorption coefficients for radiation transport through smoke. Combust Sci Technol. 175:2299–2308. https://doi.org/10.1080/714923279
Zhang Q (2010) Image based analysis of visibility in smoke laden environments, Department of Engineering, The University of Hull, PhD Thesis
Jin T (1974) Visibility through Fire Smoke (IV). Bull Fire Prev Soc Japan 22:1–8
Nebuloni R (2005) Empirical relationships between extinction coefficient and visibility in fog. Appl Opt. 44:3795–3804. https://doi.org/10.1364/AO.44.003795
Cashdollar KL, Lee CK, Singer JM (1979) Three-wavelength light transmission technique to measure smoke particle size and cocnentration. Appl Opt. 18
Dobbins RA, Jizmagian SG (1966) Particle Size Measurements Based on Use of Mean Scattering Cross Sections*. J Opt Soc Am 1345:1351–1354
Mulholland GW (2008) Smoke Production and Properties. In: SFPE Handbook of Fire Protection Engineering, Fourth Edi. NFPA & SFPE. Quincy. MA
Dobbins RA, Jizmagian GS (1966) Optical Scattering Cross Sections for Polydispersions of Dielectric Spheres. J Opt Soc Am. 56:1345. https://doi.org/10.1364/JOSA.56.001345
Uthe EE (1982) Particle size evaluations using multiwavelength extinction measurements 21:6–11
Swanson NL, Billard BD, Gennaro TL (1999) Limits of optical transmission measurments with application to particle sizing techniques. Appl Opt 38:5887–5893
Aspey RA, Brazier KJ, Spencer JW (2005) Multiwavelength sensing of smoke using a polychromatic led : mie extinction characterization using HLS analysis. IEEE Sens J 5:1050–1056
Wilkens K, Van Hees P (2015) Obtaining additional smoke characteristics using multi-wavelength. In: Fire and Materials. San Francisco. USA
Lindholm J, Brink A, Hupa M (2009) Cone calorimeter – a tool for measuring heat release rate. Finnish-Swedish Flame Days 2009. 4B. https://doi.org/https://doi.org/10.1002/fam
Chaudhry T, Moinuddin K (2017) Method of identifying burning material from its smoke using attenuation of light. Fire Saf J. 93:84–97. https://doi.org/10.1016/j.firesaf.2017.08.001
Arnold L, Belt A, Schultze T, Sichma L (2020) Spatiotemporal measurement of light extinction coefficients in compartment fires. Fire Mater fam. 2841:59–65. https://doi.org/10.1002/fam.2841
Evans D, Walton WD, Baum HR, Notarianni KA, Lawson JR, Tang HC, Keydel KR, Rehm RG, Madrzykowski D, Zile RH (1992) In-situ burning of oil spills: mesoscale experiments. Fifteenth Arct Mar Oil Spill Progr Tech Semin. 12:593–657
EN 54–7:2018 (2018) Fire detection and fire alarm systems. Smoke detectors. Point smoke detectors that operate using scattered light, transmitted light or ionization. CEN
Vigne G, Węgrzyński W (2016) Influence of variability of soot yield parameter in assessing the safe evacuation conditions in advanced modeling analysis. Results of physical and numerical modeling comparison. In: 11th Conference on Performance-Based Codes and Fire Safety Design Methods. SFPE
Węgrzyński W, Antosiewicz P, Burdzy T, Zimny M, Krasuski A (2019) Smoke obscuration measurements in reduced-scale fire modelling based on froude number similarity. Sensors. 19:3628. https://doi.org/10.3390/s19163628
Keller A, Loepfe M, Nebiker P, Pleisch R, Burtscher H (2006) On-line determination of the optical properties of particles produced by test fires. Fire Saf J. 41:266–273. https://doi.org/10.1016/j.firesaf.2005.10.001
Li Y, Chen D, Wang F, Yuan W, Zhang Q, Zhang Y (2013) An experimental study on the particle concentration and size distribution of smoke generated by flaming N-heptane. Appl Mech Mater. 391:61–65
Funding
This research was funded by the Building Research Institute statutory grant financed by the Ministry of Science and Higher Education, Grant number NZP-122/2018.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: List of System Components
The components of the system were:
-
20 channel data logger type Graphtec GL840 Midi Logger;Footnote 1
-
Lasers with the following characteristic:
-
450 nm, 50 mW;
-
520 nm, 50 mW;
-
658 nm, 80 mW;
-
830 nm, 100 mW;
-
980 nm, 50 mW
-
Five photodiodes OSRAM type IR PIN; TO5; 850 nm; 400 – 1100 nm; 55°; THT; 2nA, type BPX61;
-
25 mm circular bandpass optical filters, with peak transmittance at 450 nm, 520 nm, 656,3 nm, 830 nm and 1000 nm.
Additionally, five photodiode amplifier systems were built using the following elements:
Modular switches;
-
Modular symmetric power supply unit (± 15 V) and a power supply unit 15 W, 12 V, 1.25 A (shared);
-
Symmetric transformer 2 × 15 V;
-
Microcircuit LM 725;
-
Potentiometer;
-
Resistors (100Ω—100kΩ);
-
Ceramic capacitors (100, 220, 500 pF);
-
An electrolytic capacitor (4,7 µF).
Appendix B: System Calibration
The densitometer calibration was performed following the procedure previously described in [31]. The calibration was performed on a thermally stabilized unit, at 26 °C. A calibration filter holder was built on the bench of the densitometer, as shown in Fig. 14. The structure allowed for secure fixing of the different filters and blocking of a particular beam of light. The filters used in this process were a set of four SCHOTT® optical filters:
-
NG11, d = 1.12 mm;
-
NG11, d = 2.45 mm;
-
NG4, d = 1.08 mm;
-
NG4, d = 1.86 mm.
The transmittance of the filter at a given wavelength is known and shown in Fig. 15.
Internal transmittance of the calibration filters, calculated with a tool provided by the manufacturer (https://www.schott.com/advanced_optics/)
For each measurement point, we have compared the measured value of transmittance (I/I0) with the expected value based on the filter characteristic (Fig. 16). For most of the calibration points, the measured error was less than 10%. For some points, the measured error exceeded 10%. Notable outlier points are for 520 nm and 658 nm wavelength at the transmittance between 0.5 and 0.6, which had 13.88% and 14.40% error. These values of transmittance are at the expected lower end of the range of the transmittance in smoke layers measured in the test chamber. This observation was taken into account in the investigation of the results of experiments.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Węgrzyński, W., Antosiewicz, P. & Fangrat, J. Multi-Wavelength Densitometer for Experimental Research on the Optical Characteristics of Smoke Layers. Fire Technol 57, 2683–2706 (2021). https://doi.org/10.1007/s10694-021-01139-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10694-021-01139-5