Abstract
Characterising the risk of the fire spread in informal settlements relies on the ability to understand compartment fires with boundary conditions that are significantly different to normal residential compartments. Informal settlement dwellings frequently have thermally thin and leaky boundaries. Due to the unique design of these compartments, detailed experimental studies were conducted to understand their fire dynamics. This paper presents the ability of FDS to model these under-ventilated steel sheeted fire tests. Four compartment fire tests were modelled with different wall boundary conditions, namely sealed walls (no leakage), non-sealed walls (leaky), leaky walls with cardboard lining, and highly insulated walls; with wood cribs as fuel and ISO-9705 room dimensions. FDS managed to capture the main fire dynamics and trends both qualitatively and quantitatively. However, using a cell size of 6 cm, the ability of FDS to accurately model the combustion at locations with high turbulent flows (using the infinitely fast chemistry mixing controlled combustion model), and the effect of leakage, was relatively poor and both factors should be further studied with finer LES filter width. Using the validated FDS models, new flashover criteria for thermally thin compartments were defined as a combination of critical hot gas layer and wall temperatures. Additionally, a parametric study was conducted to propose an empirical correlation to estimate the onset Heat Release Rate required for flashover, as current knowledge fails to account properly for large scale compartments with thermally thin boundaries. The empirical correlation is demonstrated to have an accuracy of ≈ ± 10% compared with the FDS models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Urbanization is considered as one of the current global challenges. As population increases, affordable and accessible housing is becoming a key problem. Consequently, people in Low and Middle Income Countries (LMICs) are forced to build their own low quality Informal Settlements (ISs) resulting in an estimated one billion people, increasing, living within ISs. IS growth is mostly concentrated in the Global South (GS) and more specifically in Africa, South East Asia and South America. In 2050, it is estimated that IS populations will rise to 1.2 billion, which will increase the dwellings density in these settlements and, as a direct result, will increase the fire risks [1].
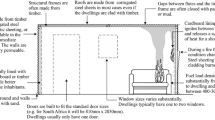
Fire risks in ISs arise from the poor infrastructure (such as lack of water or lack of consistent and affordable safe energy), dwellings proximity and the flammable construction materials as presented in Fig. 1a. Informal Settlements Dwellings (ISDs) are often built using locally sourced cheap materials, which then highly depends on the settlement location. For example, in Cape Town, South Africa, ISDs are commonly made out of timber or steel walls and lined with cardboard for thermal insulation. Currently, as shown in Fig. 1b, the fire safety community is focused on understanding the fire dynamics within the ISDs and the fire spread mechanisms between the dwellings. Around the globe and specifically within the GS, many destructive IS fires have occurred in the past few years, leaving many dead and thousands homeless. A selected few of these fires are presented in Table 1.
(a) Proximity in an informal settlement in Western Cape South Africa, (b) fire spread in informal settlements tests [7]
Experimentally: de Koker et al. [7] studied the fire spread in informal settlements by conducting a full scale experiment involving 20 dwellings, where six dwellings were cladded with timber and 14 cladded with steel. This experiment showed how the fire behaviour in ISs could be similar to that found in wildland fires with a continuous fire front. This conclusion, however, is based only on one test and the observation of the authors, therefore, it is recommended that further investigation via CFD models will be needed. Cicione et al. [8, 9] studied experimentally the fire dynamics and spread via single and multiple outdoors IS dwellings at full scale with different claddings (timber and steel), and it was concluded that the timber clad dwelling contributes more to fire spread. Wang et al. [10] conducted 300 + bench scale material testing on various materials collected from IS in Western Cape, SA. The study created a database for the flammability [11], Heat Release Rate (HRR), and Critical Heat Flux (CHF) for these materials using a cone calorimeter.
Numerically: Computational Fluid Dynamics (CFD) model validation is currently considered as a key tool in future urban fire spread studies and risk mapping, however, the accuracy and efficiency of these models are usually considered to be a barrier to using it instead of experiments. The validation guide [12] of the Fire Dynamics Simulator (FDS), a commonly used CFD code for fire, presents a wide range of validation cases, however, there is a limited number of under-ventilated compartment fire tests for which validation has been performed and can adequately match the conditions of an IS compartment fire. ISD fires are unique, due to the usage of thermally thin boundary walls, high fuel loads, the presence of substantial leakage, and flammable wall lining materials [13]. Cicione et al. [8] did a demonstration study using two single dwelling tests where one was constructed via steel sheet cladding and the other was timber cladding and conducted a sensitivity analysis for the different input parameters used in these models. The tests were then modelled via FDS and the inputs were varied in attempt to match the main measurements (e.g. gas layer temperatures and the heat fluxes from the openings). Cicione et al. then created a simplified FDS model [14] to predict the fire spread between three dwellings using a pool fire instead of the wood cribs used in the tests. Beshir et al. [15] numerically studied the effect of adding horizontal openings (collapsible ceilings) to the design of the ISDs, and found that having partially collapsible ceilings will significantly decrease the size of the external fire plumes from the ISDs. This will decrease the fire spread risk from a post-flashover dwelling fire to the surroundings. Beshir et al. [16] also numerically studied the effect of the ventilation location within an ISD by changing the location of the window in respect to the door and it was found that the heat flux from the vertical openings (both door and window) could decrease by as much as 60%, or increase up to 30% (compared to a default case).
Using risk mapping and Geographic Information System (GIS) techniques, Stevens et al. [17] presented initial methods to assess and quantify the fire risks in ISs due to different spatial factors. Stevens et al. (2020) also identified a few knowledge gaps that could potentially be filled with the help of modelling e.g. effects of wind, slope and fuel load on the fire dynamics and spread between ISDs. Cicione et al. [18] used risk mapping software, namely B-risk, to try to understand the fire spread between dwellings in ISs, with large simplifications in how the dwelling is modelled. In addition to the previously mentioned publications, there are some other studies on the fire spread in ISs looking at other different aspects, e.g. detecting the fire history via Geographic Information System (GIS) [19], understanding -theoretically- critical separation distance between the ISDs in a couple of SA ISs [20], creating ISDs blocks within each settlement based on the critical separation distances [21], and studying the effect of the wind on the fire dynamics within the ISDs [22]. Therefore, there is a need to link between the detailed experimental and numerical studies for the ISs dwellings and the large scale risk mapping and GIS research. To do so, the knowledge from the detailed small and lab based studies should be used to create empirical equations/models to feed into the large scale risk mapping models and also to accurately define the occurrence criteria of different fire dynamics phenomenon (e.g. the conditions needed for flashover).
Based on the previous studies, the gap of knowledge related to the compartment fires in a typical ISD was identified and more in-depth studies were conducted. Beshir et al. [23] studied experimentally the HRR required for flashover (\({\dot{\mathrm{q}}}_{\mathrm{fo}}\)) within a quarter scale ISO-9705 ISD. One of the main conclusions in this work was that the current well known empirical correlations used to estimate the \({\dot{\mathrm{q}}}_{\mathrm{fo}}\) do not predict those found in thermally thin bounded compartments as found in ISDs. The thermally thin boundary conditions (walls) led to walls being heated up rapidly due to their high conductivity and low thermal mass, then re-radiating more energy to the fuel package compared to thermally thick walls [19]. This raised the importance of the boundary wall’s emissivity. Wall emissivity is not considered in the well-known \({\dot{\mathrm{q}}}_{\mathrm{fo}}\) empirical correlation developed by McCaffrey, Quintiere and Harkleroad (MQH) [24] where the effective heat transfer coefficient (\({h}_{k}\)) is mainly based on the conductivity of the walls and relies on the assumption that the walls are all thermally thick, and act as black bodies. The MQH equation is:
where \({h}_{k}\) is the effective heat transfer coefficient, (for thermally thin bounded compartments \({h}_{k}=\frac{k}{\delta }\), where k is the thermal conductivity of the wall material and δ is the thickness of the wall), \({A}_{T}\) is the total wall area, \({A}_{o}\) is the opening area and \(H\) is the opening height and \({A}_{o}{H}^\frac{1}{2}\) is defined as the ventilation factor (\({V}_{f})\). Another limitation of the MQH equation is that it takes no account to the growth history of the HRR, which makes it irrelevant in the case of thermally thin bounded compartment fires. Peatross and Beyler[25], therefore, updated the heat transfer coefficient to account for the heat transfer through highly conductive (thermally-thin walls), where the new \({h}_{k}\) correlation was defined as:
where ρ is the density of the wall material, c is the specific heat of the wall and t is the time. For walls with the thickness of 0.5 mm (e.g. informal settlements’ dwellings), \({h}_{k}\) will always be 0.012 kW/m2K, which ignores any differences in wall emissivity (or any other thermal properties) and assumes that the \({\dot{\mathrm{q}}}_{\mathrm{fo}}\) changes with the ventilation factor only. The \({h}_{k}\) calculated with this method must also be multiplied by a factor of 2.5 to be used in the MQH equation; the limitations of this method are presented in Sect. 5 for the informal settlements’ case.
These findings highlighted the importance of conducting a new heat transfer parameter and empirical correlation study to estimate the \({\dot{\mathrm{q}}}_{\mathrm{fo}}\) for the thermally thin ISDs compartments. Through a validated FDS model, Beshir et al. [23] developed the following empirical correlation for the small scale thermally thin compartments with ultra-fast fires:
where \(\theta_{rad}\) is defined as \(({T}_{B}^{2}+{T}_{S}^{2})({T}_{B}+{T}_{S}\)), where TB is the boundary/wall temperature and TS is the temperature of the surrounding internal gases. Equations 3 and 4 are used together to predict the \({\dot{q}}_{fo}\) using as inputs only the wall emissivity (ε), the total area (AT), and the ventilation factor (\(Vf)\).
To further understand the effect of the walls/boundaries on the fire dynamics in these ISDs, Wang et al. [26] studied experimentally the effect of different wall boundaries via four lab based full-scale ISO-9705 single ISDs with steel sheet cladding. The four experiments considered ISDs with normal construction gaps (leakage), a sealed dwelling (no leakage), a highly insulated and sealed dwelling and a dwelling with flammable linings (Cardboard).
In this study, the experimental work done by Wang et al. [26] will be used to assess the capability of the FDS software to model under-ventilated full-scale ISD compartment fires. The validated models will then be used to attempt to further understand the fire dynamics and the effect of the boundary conditions on these compartments. The paper therefore focuses on:
-
Validating FDS using the large scale experiments and different modelling methods to increase the efficiency of the simulations (decrease the cost).
-
Understanding the effect of the re-radiation from the walls on the time and HRR required for flashover, therefore, the classic definition for flashover criteria e.g. the hot gas layer temperature to reach 525°C will be discussed in this study.
-
Updating the empirical correlation for \({\dot{q}}_{fo}\) as conducted previously [23], for thermally thin large scale compartments with more realistic fuel load (wood cribs).
2 Methodology
2.1 Experimental Design and Measurements
The experimental campaign consisted of four single ISO-9705 sized rooms with similar dimensions of (3.6 × 2.4 × 2.4 m). The floor of each compartment was insulated with 8 mm thick cement board and the compartment was built on the top of it. The boundary walls were constructed using 0.51 mm corrugated galvanized steel sheets attached to a timber frame with the dimensions of 0.038 × 0.089 m in cross-section and attached using gang nails and self-tapping screws. The sheeting was attached through pre-drilled holes using wide flanged screws. Each dwelling was designed with two openings, i.e. a door and a window, with internal dimensions of 2.0 m (height) × 0.8 m (width) and 0.6 m × 0.6 m respectively and both located in the front long wall, 0.7 m and 2.0 m away from the right front corner, respectively as presented in Fig. 2.
(a) The plan (b) and the front views of the instrumentation location from [26]
The dwelling design and the fuel load were chosen based on surveys conducted in ISs in the Western Cape, SA, where the average load was found to be 410 MJ/m2 [13]. Therefore, two wood cribs (112 kg each) were placed at the centre of the compartment with a separation distance of 0.18 m. Each crib was of 7 layers and 10 sticks in each layer. Each stick was of 0.038 m × 0.064 m × 1.219 m and density of 540 kg/m3, which gives a fuel load of approximately 438 MJ/m2, assuming a heat of combustion of 17.5 MJ/m2 [33] The ignition source during the four tests was 8 packages of mop head strips soaked in Gasoline-87, in plastic bags, placed in the four corners of each crib.
The main scope of this study is to understand the effect of the different boundary conditions on the internal and external fire dynamics. The standard design of the dwelling is presented in Fig. 2a and the tests were heavily equipped with measurement points as presented in Fig. 2a: 1.0 m × 1.0 m scales were placed in the middle of the dwelling to measure the mass loss rate of the cribs, six thermocouple (TCs) trees were suspended from the ceiling to the floor. Each thermocouple tree consisted of 10 Inconel sheathed Type-K thermocouples with a 1.0 mm diameter, the wall temperature was measured using three thermocouples attached to the external boundary of each wall at heights of 0.4 m, 1.2 and 2.0 m. To measure the flow velocity through the openings six bi-directional flow probes were placed at the door and three were placed at the window, as shown in Fig. 2b.
The gas concentrations (O2 and CO2) within the compartment were measured using three in-house constructed gas analysers with sampling points located 10 cm from the top left front and back corners and at the same location as the top window flow probe (NB: the left side is the window side).
The incident radiant heat fluxes outside of the compartment were measured using Thin Skin Calorimeters (TSCs) [27], where two TSCs were placed at a height of 1.6 m from the floor at distances 2.0 and 3.0 m from the window and four TSCs were placed in front of the door at two heights 1.6 m and 2.5 m at distances 2.0 and 3.0 m from the door. To measure the radiative heat fluxes from the side walls, three TSCs were placed at a height of 1.2 m and distances 0.05 m, 0.5 m and 1.0 m from the compartment (see Fig. 2a).
The four boundary conditions tested in this study were as follows, Case_1 was the typical dwelling with all the gaps between the steel sheets/walls filled with ceramic blanket pieces to avoid any leakage during the tests and will be titled “No Leakage” (NL), Case_2 was the same case without the gaps filled to study the effect of the leakage and titled as “Leakage” (LK), Case_3 was the same as the LK case with the internal walls lined with cardboard and titled as “Cardboard” (CB), and Case_4 was the same as the NL case but with a high level of insulation (Rockwool R23), of thickness 14 cm, placed between two steel sheets for the walls and titled “High Insulation” (HI).
The main differences between the four cases in terms of fire dynamics have been presented previously [26] and will not be discussed further in this paper. As a summary of the main conclusions from the experiments, Wang et al. [26]concluded that the walls boundary conditions significantly changed the flashover time, where the NL case had earlier flashover (at 311 s), the combustible lining materials caused double flashovers (at 300 and 395 s) and the wall insulation delayed the flashover time (at 417 s) by around 31% compared to the NL case.
2.2 Numerical Model and Modelling Methods
2.2.1 Fire Dynamics Simulator (FDS) and the Adapted Modelling Techniques
Fire applications accompanied with buoyancy and low-Mach number can be solved by FDS through appropriate representations of the Navier–Stokes equations via a second order finite difference numerical scheme. In this research, FDS (version.6.7) is used to model the four different previously mentioned tests, where the boundary conditions of these tests are unique and FDS has not yet been used to validate these unique experimental combinations.
Modelling the fire spread over the cribs (e.g. [28]) is a highly complex problem due to the nature of combustion phenomena (e.g. pyrolysis, radiation, ignition). Moreover, as previous literature has indicated, the walls are a critical radiator to both the surroundings and fuel package. Thus the assumption of using the grey gas model in compartment fires, as adopted in FDS, will be examined for its appropriateness. Where, the fraction of thermal radiation based on energy released from the fire is a function of both the flame temperature and chemical composition and both are not known for large scale fires. In simulations where the cell sizes are of the order of cm or larger, the temperature near the surface of the flame will not rely on when calculating the source term in the Radiation Transport Equation (RTE). Therefore, if the FDS user prescribes a non-zero radiative fraction, a grid cell cut by the flame radiates that fraction of the chemical energy that is released within this cell. If it is desired to use the RTE, then the radiative fraction needs to be set to zero and therefore the source term in the RTE will be based only on the gas temperature and the chemical composition. In this work the default radiative fraction by FDS was used (Default = 0.35).
FDS uses the Large Eddy Simulation (LES) modelling technique, where the turbulence model represents the closure of the Sub Grid Scale (SGS) flux terms. In FDS, the gradient diffusion is the turbulence model used for the SGS momentum and scalar flux terms closure. Therefore, a model is needed for the turbulent transport coefficient (the eddy viscosity and the eddy diffusivity), where the eddy diffusivity is calculated using a constant Schmidt and Prandtl number for the mass and thermal diffusivity, respectively. Given that, the most important variable therefore is the eddy viscosity term (\({\mu }_{t})\). FDS gives several options of turbulent viscosity models namely, constant coefficient Smagorinsky, dynamic Smagorinsky, Deardorff’s, Verman’s, Renormalization Group (RNG) and the Wall Adapting Local Eddy viscosity (WALE) models. By default FDS uses a variation of Deardorff’s turbulent viscosity model[29]. The WALE model of Nicoud & Ducros [30] was generated as a method to properly scale the eddy viscosity in the vicinity of a wall, while by default FDS uses constant coefficient Smagorinsky [31] with Van Driest damping [32] for the eddy viscosity in the first off-wall grid cell. This is due to the fact that Deardorff model was found to be less accurate near the wall and this damping factor is added to the eddy viscosity model to accurately damp the viscosity towards zero with the correct rate. This default approach will be used near the wall in all of the simulations in this paper, however, the damping function proposed by the WALE model will also be tested to understand which near wall approach works better for modelling these conditions in ISDs (thermally thin) compartment fires.
Additionally, to model the convection heat transfer to solids, FDS adopts two different approaches that will be compared in this work. The first and default approach is implemented by finding the maximum value of the convective heat transfer coefficient among three different functions as follows:
where for the first function, C is an empirical coefficient for natural convection (1.52 for a horizontal plate and 1.31 for a vertical plane or cylinder), \({T}_{w}\) is the wall surface temperature, \({T}_{g}\) is the gas temperature in the center of the first gas phase cell, \({k}_{g}\) is the thermal conductivity of the gas, L is a characteristic length related to the size of the physical obstruction, \(Nu\) is the Nusselt number, and \(\delta n\) is the normal grid spacing. The Nusselt number,\(Nu\), depends on the geometric and flow characteristics, thus, for many flow patterns, it is given by:
For planar surfaces, the default values are C1 = 0, C2 = 0:037, n = 0:8, m = 0:33, and L = 1 m. For cylindrical surfaces, the default values are C1 = 0, C2 = 0:683, n = 0:466, m = 0:33, and L = D, the diameter of the cylinder. Various correlations for planes, cylinders, and spheres can be found in the literature [33][34]. The second approach exploits the so called wall models to predict the transition from the viscous region to the fully turbulent region that takes place in the inner wall layer. Generally speaking, wall models aim to mimic the sudden change from molecular to turbulent transport close to the walls using algebraic formulations, without resolving the smallest length scales.
It is important to note that FDS may uses two alternative methods to represent the leakage through a compartment boundary, the first is by using pressure zones, while the second uses HVAC vents. Leakage here refers to any air that escapes through small gaps (e.g. the gaps between the walls in this study). In the case when the leakage area is smaller than the cell size, the gaps won’t be modelled directly, and the HVAC model needs to be used to connect the leaking compartment to the surroundings, which is used in this study. Modelling leakage for the case (LK) will be discussed later.
In order to reduce the computational effort, Kallada Janardhan & Hostikka [35] proposed a predictive CFD simulation for the fire spread on wood cribs by conducting a correction for the mesh dependency of the fuel surface area for the case where the CFD grid cells are larger than the sticks that makes use of the ignition temperature for pyrolysis. In this work, this method is implemented to model the fire spread over the wood cribs with a coarser mesh, which is expected to increase the efficiency of the simulations. The study by Kallada Janardhan & Hostikka [35] validated the use of the ignition temperature model and the proposed area adjust method for coarse mesh fire spread simulations and performed room scale fire spread simulations. Compared to the fine mesh simulations, the proposed method reduced the CPU time by approximately 80%. In this study the area adjust method was adopted and tested with smaller compartments (e.g. ISO 9705 size) compared to the large scale compartments used in Kallada Janardhan & Hostikka [35] (e.g. tunnel fire experiments of SP Sweden [36]). The area correction factor is simply the ratio between the total wood surface area of with the coarse mesh and the real crib total surface area. To capture the total surface area for the wood crib with coarser mesh (e.g. 0.06 m) a one wood crib simulation was done with a prescribed Heat Release Rate Per Unit Area (HRRPUA) and the total HRR was used to calculate the total surface area of the wood crib with this specific cell size. This ratio was then multiplied by the bulk density to compensate for the usage of the coarser mesh. Additionally, the FDS “Time Shrink Factor” command is used to decrease the computational power. The Time Shrink Factor was set to be 5, with the output results ensured to be independent of the presence of the shrink factor. Wills [37] discussed the effect of the Time Shrink Factor on different aspects in compartment fires (e.g. wall temperature, smoke temperature, soot concentration and incident heat flux) which are essentially the same parameters that are of the interest of this work.. Generally, the FDS command “Time Shrink Factor” is used to decrease the required computational power in applications at which only the steady-state solution (in a time-averaged sense) is desired. In these situations, the specific heat of the various materials is reduced by a specified factor, speeding up the heating of these materials, roughly by the same factor. Simply, the use of this factor accelerates the initial growth phase in order to “reach” the steady-state condition of interest in a shorter time.
The factor is applicable for situations that tend towards a steady-state condition, which is exactly the case of the work here. Wills had emphasized that simulations of compartment fire scenarios with growth phase and using “Time Shrink Factor”, the results still captured the qualitative behaviour compared to the case without the factor. Wills presented a study that investigates the FDS command “Time Shrink Factor” and how it affects both the model results and running time of the simulations with regard to applications stated by the FDS User’s Guide [38] to be relevant to steady-state condition. The study performed simulations with a “Time Shrink Factor” of 2, 5, and 10, then, compared the results of these cases against a case without the factor in order to show the effect on results. In general, different aspects in compartment fires such as wall temperature, air/smoke temperature, smoke movement, soot concentration, and incident heat flux, were all evaluated which are essentially the same parameters that are of the interest in the current work.
The results of the measured temperature at a lower portion of the wall, which is near the fire and below the smoke layer, showed that the results are consistent between the simulations which demonstrates that the “Time Shrink Factor” does not have a noticeable effect on these results. Furthermore, the results of the calculated heat release rate for each of the scenarios, showed that for the scenarios with the “Time Shrink Factor”, the heat release rate is much less steady than the regular simulation, where heat release rate of the highest “Time Shrink Factor” of value 10 varies between 550 and 450 kW, while the regular simulation varies between 510 and 490 kW. Eventually, it was concluded that the results with and without the “Time Shrink Factor” have produced similar results for the heat transfer in areas close to the fire. Other results within the simulation such as smoke production and temperature within the room have been shown to be affected by the “Time Shrink Factor”. The simulations that utilized the “Time Shrink Factor” resulted in lower upper layer temperatures and less dense smoke, where the larger the “Time Shrink Factor” and the less the fire is steady, the more it affected the results. Therefore, this factor could be considered for use when the smoke production is not of interest and does not affect the concerned areas, and to be considered for use when the area of interest (wall heat transfer) is mostly near the fire, and not from the smoke interacting with the wall.
2.2.2 Modelling Main Inputs
2.2.2.1 Domain and Cell Size
The domain of each model was of 5.0 m × 6.0 m × 4.0 m (X, Y, Z) accompanied with a cell size of 0.06 m for the whole domain. Given the size of the domain and the limitations of the computational power available to the authors (noting that the simulations were using 8 meshes on the University of Edinburgh’s supercomputer “Eddie”, which consists of 7000 Intel Xeon cores), it was decided that a classic cell size sensitivity analysis for these simulations was not merited. A smaller cell size of 3 cm will increase the number of cells within the computational domain from 600,000 cells to around 5,000,000 cells which will dramatically increase the computational cost and makes much greater computational demands. The current cost of the 600,000 cells full simulation is around 72 h, using 8 cores on Eddie. Therefore, it was decided to choose the cell size based on the wood crib design and according to the method proposed by Kallada Janardhan & Hostikka [35]. A cell size check was however conducted using the method proposed by Ma and Quintiere [39]namely the D* method where D* is calculated via Eq. 7:
where D* is the characteristic length scale of the fire plume, \(\dot{Q}\) is the HRR, \({\rho }_{\infty }\) is the ambient air density, \({T}_{\infty }\) is the ambient air temperature, \({C}_{p}\) is the specific heat of air and \(g\) is the gravitational acceleration. Based on the D* the cell size to be used in the simulations, should be less than 0.1 D*. Assuming a HRR of around 3000 kW, the recommended cell size will be around 26 cm where the cell size used in these simulations (e.g. 6 cm) is around four times smaller. The D* also showed good performance with wood cribs modelling as reported by other researchers [40, 41]. This approach is similar to that by Cicione et al. [8] when modelled large scale ISDs, also Cicione et al. [14] conducted a cell sensitivity study to model the fire spread between multiple dwellings with very close conditions to the ones in this study and it was found that a 0.1 m cell size was fine enough to capture the gas layer temperature, heat fluxes to the surroundings and the lining materials burning behaviour.
2.2.2.2 Simple Pyrolysis Model
The HRRPUA of the wood (Pine wood) and cardboard were taken from the previous cone calorimeter study [10] under the heat flux of 75 kW/m2 for both materials. The ignition temperature of the wood and the cardboard, was set to be 250°C [42] and 260°C [43] respectively. The heat of combustion was taken as 20 MJ/kg [44] for the dominating fuel (Pine wood). The chemical composition of the wood was set as input for the FDS as C3.4H6.2O2.5 [45] with a soot yield of 0.015 [46]. The accelerant/igniters (gasoline)’s HRRPUA curve used in the tests, was based on the early stage HRR curve of the tests in Wang et al. [26].Where a sensitivity analysis for these inputs has been discussed by Cicione [14].
2.2.2.3 Materials Thermal and Physical Properties
The wood’s bulk density was chosen as 535 kg/m3 [44], which was adapted to 455 kg/m3 based on the cell size according to the method proposed by Kallada Janardhan & Hostikka [35], while the specific heat was assumed to be 1.3 J/Kg, and the conductivity to be 0.2 W/m.K. The steel was assumed to have a specific heat of 0.6 J/Kg, conductivity of 45 W/m.K, density of 7850 kg/m3, and emissivity of 0.23 (new shiny galvanized steel sheets) [47].
2.2.2.4 1-D Conduction Heat Transfer
The steel sheets were of thickness of 0.5 mm which is also the thickness of the 1-D heat transfer model. Since the steel walls thickness (0.5 mm) was much less than the cell size, therefore, the walls back side condition was set as EXPOSED–FDS command—for the 1-D heat transfer interaction between the two sides of the wall.
2.2.2.5 The Instrumentation
The thermocouple trees within the compartment were simulated using thermocouples of the same size (1.0 mm). The flow velocities were measured using a device with the quantity v-velocity, the TSCs were simulated using the device with the quantity radiative heat flux gas and the wall temperatures were measured using the wall and back wall temperature devices. The gas concentrations were measured with gas analysers for the O2 and CO2 at the same locations for the experiments.
2.2.3 Boundary Conditions Modelling
In this paper the main difference between the four cases is how the boundary/walls were modelled. In this section the boundaries of the three cases LK, CB and HI modelling will be explained.
2.2.3.1 Leakage Case (LK)
The steel sheets corrugations are defined based on the width and the depth as presented in Fig. 3 at which they are considered the main leakage area in the ISDs. In the experimental work, the corrugation dimensions used were around 0.07 m width and 0.025 m depth therefore the total area of each corrugation was approximated to 0.000625 m2. The effective corrugations for the leakage were assumed to be only the top ones between the ceiling and the walls because during the developed period, the hot gas escapes only through these corrugations due to the buoyancy effect. Additionally, it was observed that any external flaming (apart from that bursting from the window and the door) were through the top corrugations, as presented in Fig. 3. Therefore, a total of 51 and 34 corrugations were assumed for the long (0.031875 m2) and short walls (0.02125 m2), respectively.
2.2.3.2 Cardboard Case (CB)
The cardboard was modelled in the same way as for the wood with an adapted bulk density of 15 kg/m3. FDS usually holds one heat of combustion in the pyrolysis model, therefore, the burning rate of the cardboard was then multiplied by a factor equal to the ratio of the heat of combustion cardboard to that for the wood to compensate for the relatively low heat of combustion required to be used in the simulations (the heat of combustion of the cardboard is around 33 MJ/kg [48]).
2.2.3.3 High Insulation Case (HI)
To model the insulation the 1-D heat transfer of the wall was increased to 0.14 m thick and the conductivity was increased to 0.035 W/m.K [49].
3 Sensitivity Analysis
In this section, the effect of the time-reduction parameter used in the model (Time Shrink Factor), in addition to the near-wall modelling methods, will be checked in a sensitivity analysis to ensure that the outputs of the modelling methodology to be used will be independent on both techniques.
3.1 Time Shrink Factor
A few trials were conducted on the NL case with different time shrink factors (0.0, 5.0 and 7.0), consequently, an acceptable of 5.0 was found to be used in all the simulations which accordingly reduced the overall computational time by the same factor. As shown in Fig. 4a, the total HRR curve is almost identical in the steady state for all the numerical cases while the time to flashover was accelerated by around 100 s with the 7.0 factor. In terms of the measurements, the hot gas layer temperature was the most affected value. As presented in Fig. 4b, FDS matched with the experimental results at the steady state when using the factor of 5.0, with is deemed to be an acceptable value of variation of around + 5 and 10%.
3.2 Logarithmic Law (Log-Law) of the Wall and Near-Wall Turbulence Model
Three different methods were used to study the near wall heat transfer and turbulence behaviour, namely the default method of constant coefficient Smagorinsky with Van Driest damping for the eddy viscosity in the first off-wall grid cell, the near wall heat transfer treatment (Log-Law) and the near wall turbulence model (the damping function proposed by the WALE model). As presented in Fig. 5, both the Log-Law and the near wall WALE model did not affect the wall temperature in the NL case. The computational time was not affected, and might be effective when extra boundary conditions are added to the simulation (e.g. wind effect), therefore, it is still recommended to check the effect of these two models in future studies.
4 Validation
The validation process focuses on six different aspects for each case as follows: combustion efficiency, internal gas temperature, wall temperatures, flow through the openings, heat fluxes to the surroundings and the total HRR. The total HRR was measured using oxygen depletion calorimetry and the experimental apparatus was positioned under the hood.
4.1 Gas Concentration (Gas Analysers)
Gas analysers were placed in three different locations in each test (top left back corner, top left front corner and at 10 cm from the top of the window), however, only one location will be presented for each case and more results are available per request to the authors.
The back gas analyser for the NL case is shown in Fig. 6a. FDS captured the O2 concentration accurately in terms of values and time and correctly estimating the rise in the CO2 values, however underestimated the concentration by around − 33% (where % (under/over prediction) = [(Numerical value-Experimental value)/ Experimental value] *100). That was also found at the window LK case in Fig. 6b, where FDS accurately predicted the time for the drop and rise in O2 and CO2 concentrations, respectively, however, it underestimated the CO2 peak by around − 27% and accurately captured the drop in the O2. The time and values of the cardboard and wood burning peaks in the CB peak in Fig. 6c at both ≈ 300 and ≈ 400 s respectively, were estimated well. O2 and CO2 values in the HI case front location Fig. 6d were underestimated by around − 27% but the time was accurately captured. Therefore, in general, FDS captured both the drop and rise time for the O2 and CO2 concentrations respectively in all cases and all locations, and managed to capture the O2 concentration values at the back of the compartment in all cases, but underestimated it for the front and window location. This is believed to be due to the complexity of solving the mixing and turbulence occurring at these two locations.
To further understand these slight variations, it is important to explain how FDS models turbulent combustion. Modelling chemical reactions in any turbulent flow is usually mathematically challenging due to the fact that the length and time scales associated with the reactions could be of orders of magnitude below what can be spatially and temporally resolved by this specific simulation. In complex reactions (where CO and soot occurs) FDS uses a simple mixing environment method to close the mean chemical source term and each computational cell will be considered as a turbulent batch reactor and the rate of mixing is dominated by turbulence. The basic idea behind the model in FDS is to consider the three physical processes of diffusion, SGS advection and buoyant acceleration and to take the fastest of these processes (locally) as the controlling flow time scale. One of the main parameters in this model is the LES filter width (Cell size) which directly affects the SGS model and eventually the mixing modelling. The mixing then determines the combustion rate, based on infinitely fast chemistry, that occurs in each cell. Therefore, using a cell size of 0.06 m3 affects the accuracy of the SGS model, the mixing and the combustion efficiency, and this could be the reason behind these variations between the numerical simulations and experimental results for the gas concentrations. All in all, FDS managed to, within tolerable accuracy, estimate the gas concentrations trends in the four experiments.
4.2 Internal Gas Temperature (TC Trees)
To cover all locations, only the top and bottom thermocouples in the four cases in four different corners (LB, RB, LF, RF), were compared with the results from the simulations to understand to what extent FDS managed to replicate the gas layer development. Figure 7 shows that the current model did not accurately replicate the growth phase (up to 200 s) in all the cases and that was expected, as there was not sufficiently accurate information/data about the igniters and the HRRPUA for the gasoline was estimated to the best fit. FDS, however, managed to capture the peak time for all of the thermocouples and in all cases and locations, quantitatively, it estimated accurately the top gas layer temperature, with underestimation of ≈ − 15% at the left front location which is just behind the window—this could again be because of the limitations of the turbulence modelling and combustion accuracy, as observed in the same location for the gas analysers. The lower thermocouple results were less accurate with under/overestimation ≈ ± 20%, where these TCs were located just next to the wood cribs where all the cold air flow, the pyrolyzed gas release and the buoyancy effect occurs. This is expected to increase the turbulence/mixing challenges, however, the variation between the numerical and experimental results did not exceed an acceptable value (± 20%) given the low importance of the gas temperature at these locations.
4.3 Wall Temperatures (TC Walls)
In the experimental work, wall temperatures were measured using thermocouples (gas phase measurement) attached to the steel sheets (externally) via high temperature cement, while in FDS this was calculated using the wall temperature device which is a solid phase measurement.
As expected and presented in Fig. 8, FDS overestimated wall temperatures compared to that in the experimental work. This does not necessarily undermine the general capabilities of FDS as in the experiments a gas phase measurement device was used to give a solid phase measurement (wall temperature). On the other hand, FDS qualitatively captured the difference between the NL case, the CB case (with the peak due to the cardboard captured at ≈ 300°C) and the HI case (with external wall temperature of ≈ ambient temperature).
4.4 Flow Through the Openings (Flow Probes)
Modelling the velocity flow field through the compartment openings is quite challenging and this usually requires high resolution grids even for simple pool fire simulations. Due to the high turbulence at the openings, in this study capturing the exact velocity at each point along the height of the door or the window was challenging for the model under these conditions and using this cell size (e.g. 0.06 m), the main emphasis will be on capturing the neutral plane of the door post flashover, which could give a rough indication for the ability of FDS to mimic the size of the external plume; additionally, the velocity of the flow at the top and bottom flow probes at the door in each case was compared to the experimental results. FDS managed to capture the neutral plane to be between FP-2 and FP-3 in all cases and that was the case in the experimental work as presented in Wang et al. [26]. FDS managed to capture the flow velocity at the top FPs in the NL and HI cases with an accuracy of − 20%. For the LK and CB cases, due to the leakage, the top FPs velocity is less than the NL cases by around 3–35 m/s, FDS, however, did not manage to capture the effect of the leakage on the top FPs velocity as presented in Fig. 9b, c.
4.5 Heat Fluxes to the Surroundings (TSCs)
The heat fluxes from the compartment to the surroundings were measured at nine different locations, however, in this paper, only two locations (at 2.0 m away and 1.6 m height from the door and the window) in each test will be presented, the rest is available upon request. As presented in Fig. 10, FDS estimated the heat fluxes from the window and the door for the cases with no leakage (NL and HI) and for the cases with the leakage (LK and CB) with an underestimation of ≈ 10% and ≈ 30%, respectively. Again, that raises the importance of modelling the leakage accurately and shows another affected end result in addition to the flow field through the openings. Furthermore, FDS apparently failed to capture the high heat flux peak for the cardboard burning at 200 s in the CB case, but this case is not of great importance given the rapid decrease in the value and that the fire spread between dwellings doesn’t depend only on an instantaneous heat flux, however, the heating time is more important.
4.6 Total HRR (Hood Oxygen Calorimetry)
As per Fig. 11 the total heat release rate was mostly overestimated by FDS and that was rather expected given the uncertainties associated with the oxygen calorimetry method in addition to the gases not being efficiently sucked into the large hood. That gave an overestimation of FDS by + 5 to 25%, however, FDS managed to adequately predict both the time to flashover and the \({\dot{q}}_{fo}\) for each case as presented in Table 2.
Conventionally, the flashover time is defined as the time when the gas layer temperature reaches 525°C, which was believed to be enough for the gas layer to radiate around 20 kW/m2 to the floor, however, as it was found by Beshir et al. [23] that the re-radiation to the fuel package in compartments with thermally thin boundaries is not just derived by the interaction between the fuel package and the gas layer, but also by the hot boundaries (walls). Therefore, in this computational study, four heat flux measurement devices were placed in the four corners of the compartment and the time to flashover was defined as the time when these four devices reached 20 kW/m2. Temperature-wise the wall temperature (at the middle of each wall) at the same time (flashover-time) was captured numerically in order to define the critical wall temperature needed to achieve flashover. As presented in Table 2, the wall gas layer temperature needed to reach flashover in all cases ranged between 360 and 460°C, which means that flashover could occur with hot layer temperature around − 32% or − 40% less compared to the well-known 525°C and 600°C flashover criteria. As an overall observation and as presented in Table 2, numerically there is around + 28% increase in the time to flashover when comparing the NL (thermally thin bounded) dwelling to the NL (thermally thick bounded) dwelling (e.g. experimentally there is 31% difference). This is considered a significant increase in time and would highly affect the fire spread rate between dwellings when looking at the fire spread in a large scale full informal settlement with hundreds of dwellings Fig. 12.
The higher temperatures of the walls in the HI case is believed to be due to reduced losses to the outside and therefore the ability of the walls to store much more heat due to the insulation and in that case the wall temperatures rose much faster to values even higher than that of the hot layer temperature; this also explains the lower \({\dot{q}}_{fo}\) needed for the HI case. For the CB case the wall temperatures were higher due to the burning of the cardboard on the surface of the steel which simply increased the steel sheet temperature to around 600°C, as presented in Fig. 8 and then due to the enhanced losses, the temperature of the walls decreased to 470°C up until flashover time, therefore, the cardboard flashover heated up both the walls and the fuel package which impacted the \({\dot{q}}_{fo}\) for the CB case, which meant that its value was reduced compared to the NL and LK cases.
4.7 Short Discussion
To summarize, the LK case produces a higher peak HRR as the leaks provide extra ventilation for the unburned gases to vent to the outside and burn easily, so as a first attempt of comparison, the peak HRR is higher for the LK case. However, for the top gas layer temperature, the LK case experienced lower gas layer temperatures as it vents easily the hot gases through the top leaks and therefore (due to buoyancy) extra fresh air enters and also the top gas layer is not as thick and smoky as in the NL case. Lastly, we believe these factors drive the flashover time to be the fastest for the NL case (due to the confined hot gases at the top) and the average steady state HRR to be the lowest among the four cases for the NL case. Altogether, the NL case experienced higher gas layer temperatures and therefore a faster time to flashover, with lower peak and steady state HRR values. It also seems that the combustion efficiency is not the driving factor here, comparing the oxygen concentration for both cases at the back of the compartment, as it was found that the combustion efficiency is higher in the LK case. However, the NL case still achieves higher gas layer temperatures. Therefore –in these conditions- and based on the previous discussion, it is believed that the heat losses are driving both the gas layer temperatures and the time to flashover, rather than the combustion efficiency, in these compartments.
5 Empirical Correlation of the Heat Release Rate Required for Flashover
Beshir et al. [23], showed that the main heat transfer parameter for the \({\dot{q}}_{fo}\) in compartments with thermally thin boundaries is the flow through the openings and the emissivity of the walls. It was also concluded that the empirical correlation for \({\dot{q}}_{fo}\)(e.g. MQH [24], using the updated heat transfer coefficient by Peatross and Beyler [25]) presented unrealistic values for compartment fires with thermally thin boundaries. An empirical correlation for \({\dot{q}}_{fo}\) was established for small scale compartments using a burner (ultra-fast fires) and it was found that this equation successfully describes the causation and correlation between \({\dot{q}}_{fo}\), emissivity, and ventilation factor [23]. This was a good step in studying the fire dynamics in compartments with thermally thin boundaries. However, it was established that the empirical values of this correlation did not hold in these large scale compartments with medium/fast fires (wood cribs). Therefore, an empirical correlation for estimating the \({\dot{q}}_{fo}\) for compartments with thermally thin boundaries, large scale and medium/fast growth fire is developed. The NL case was used to create an extensive parametric study based on a variety of wall emissivity and ventilation factors, as presented in Table 3 and Table 4, where the ventilation factor was increased by extending the width and the height of the door and window, respectively.
As mentioned earlier, Beshir et al. [23] showed that the \({\dot{q}}_{fo}\) could be described for each case based on the emissivity and the ventilation factor, therefore, each material was used with three different ventilation factors and the \({\dot{q}}_{fo}\) was decided as the total HRR at the time when the four corner floor TSCs will reach 20 kW/m2. The parametric study results were then used to create an empirical correlation to estimate the \({\dot{q}}_{fo}\). The new correlation was fit to predict the \({\dot{q}}_{fo}\),where the non-linear regression was conducted using a IBM-SPSS software [51] and the inputs were taken from .
Table 4 as the following:
Equation 8 was then used to estimate the \({\dot{q}}_{fo}\) for each case and compared to the numerical values from FDS. As presented in Fig. 13 and Fig. 13, it was found that the new empirical correlation fits with an accuracy ± 10% compared to the numerical results, while the empirical equations proposed by Beshir et al. [23] and MQH [24] presented unrealistic results compared to the results from FDS. This inaccuracy was expected based on the limitations of these equations as mentioned earlier, where the updated MQH was based on a constant heat transfer coefficient by Peatross and Beyler which does not consider the thermal properties of the walls with ultra-thin thickness (e.g. 0.5 mm), while the equation proposed by Beshir et al. [23] was based on small scale compartments with ultra-fast fires. The empirical correlation was then tested using three simple numerical cases with stainless steel of 0.35 emissivity and the three ventilation factors (red crosses) and it was found that the correlation has an accuracy of ± 2.5%. It was established that Eq. 8 has the same structure as the empirical correlation in [23] but with different empirical values to account for the difference in the compartments sizes and the fire type (e.g. ultra-fast fires or fast/medium fires).
6 Conclusions
Numerical CFD simulations were conducted to undertake validation of the CFD model, FDS, with four ISO-9705 steel sheet bounded dwellings fire tests. The four dwellings varied based on the walls boundary conditions as follows: no leakage dwelling (NL), normal leaky dwelling (LK), leaky dwelling with cardboard lining (CB) and no leakage dwelling with high insulated walls (HI). The experimental measurements were compared to the numerical results for six aspects of compartment fire dynamics, specifically: gas concentrations, hot gas layer temperature, wall temperature, flow field through openings, external heat fluxes and total heat release rate. For more efficient numerical simulations, the models were built on different techniques with the aim of decreasing the computational time (e.g. Time Shrink Factor and modelling the wood cribs with coarser meshes). The flashover time in this study was defined as the time when the four corners in the floor reaches 20 kW/m2. The conclusions of the study are as follows:
-
The numerical simulations reproduced the main fire dynamics and trends within these under-ventilated compartments.
-
The gas concentrations were captured with accuracy varying between ± 30%, with the highest accuracy found to be at the back of the compartment and the lowest at the front and near the openings. This might be due to the presence of high turbulence at these locations and the need of high accuracy turbulence modelling to reproduce the mixing and eventually the combustion efficiency.
-
The top gas layer temperature was well reproduced, with the lowest accuracy near the openings and the bottom gas layer temperature was found to be less accurately predicted by the model, which could be due to the ability of the model to capture the turbulence occurring at these locations.
-
The wall temperatures were overestimated by the model, this was expected as the experimental wall temperatures were measured using gas phase thermocouples attached with cement.
-
The leakage modelling was found to be effective on the end results, where the simulations overestimated the flow field at the top of the door for the LK and CB cases due to the inaccurate modelling of the leakage in these two cases. However, the flow field at the same location was well-replicated for the NL and HI cases. The same was found for the heat fluxes to the surroundings where the simulations accurately captured the heat fluxes from the door and the window for the NL and HI cases and underestimated that for the LK and CB cases.
-
18 simulations were done as a parametric study to conduct an empirical correlation to estimate the HRR required for flashover (\({\dot{q}}_{fo})\) for large scale compartments with medium and fast fires, where this empirical correlation was found to hold an accuracy of ± 10%.
-
A new flashover criteria is proposed based on lower gas layer temperatures ≈360–460 (around 30% lower compared to the used 525°C) in combination with the internal wall temperature (≈250–550°C).
Future research should be focused on enhancing the leakage modelling and further understanding the limitations of the proposed flashover criteria and the empirical correlation.
References
Rush D, Bankoff G, Cooper-Knock S-J, Gibson L, Hirst L, Jordan S, Spinardi G, Twigg J, Walls RS (2020) Fire risk reduction on the margins of an urbanizing world. Disaster Prev Manag 29(5):747–760. https://doi.org/10.1108/DPM-06-2020-0191
“Fire Incidient in Bahay Toro, Quezon City,” 2011. [Online]. Available: https://www.ndrrmc.gov.ph/index.php/20-incidents-monitored/1599-fire-incident-in-bahay-toro-quezon-city. Accessed: 13-Sep-2020.
BBC, “Valparaíso fires: Dozens of homes destroyed in Chilean city,” 2014. [Online]. Available: https://www.bbc.com/news/world-latin-america-50907976. Accessed: 13-Sep-2020.
Kahanji C, Walls RS, Cicione A (2019) Fire spread analysis for the 2017 Imizamo Yethu informal settlement con fl agration in South Africa. Int J Disaster Risk Reduct. https://doi.org/10.1016/j.ijdrr.2019.101146
BBC, “Lang’ata fire: ‘Not enough water’ to tackle Kenya blaze,” 2018. [Online]. Available: https://www.bbc.com/news/world-africa-42859032.
BBC, “Bangladesh fire: Thousands of shacks destroyed in Khaka slum,” 2018. [Online]. Available: https://www.bbc.co.uk/news/world-asia-49382682. Accessed: 30-Sep-2019.
de Koker N, Walls RS, Cicone A, Sander ZR, Loffel S, Claasen JJ, Fourie SJ, Croukamp L, Rush D (2020) 20 Dwelling large-scale experiment of fire spread in informal settlements. Fire Technol 56:599–1620. https://doi.org/10.1007/s10694-019-00945-2
Cicione A, Beshir M, Walls RS, Rush D (2020) Full-scale informal settlement dwelling fire experiments and development of numerical models. Fire Technol 56:639–672. https://doi.org/10.1007/s10694-019-00894-w
Cicione A, Walls RS, Kahanji C (2019) Experimental study of fire spread between multiple full scale informal settlement dwellings. Fire Saf J. 105:19–27. https://doi.org/10.1016/j.firesaf.2019.02.001
Wang Y, Bertrand C, Beshir M, Kahanji C, Walls R, Rush D (2020) Developing an experimental database of burning characteristics of combustible informal dwelling materials based on South African informal settlement investigation. Fire Saf J. https://doi.org/10.1016/j.firesaf.2019.102938
Wang Y, Rush D (2019) Cone calorimeter tests of combustible materials found in informal settlements. University of Edinburgh, School of Engineering. https://doi.org/10.7488/ds/2599
McGrattan K, Hostikka S, McDermott R, Floyd J, Weinschenk C, Overholt K (2015) Sixth Edition fire dynamics simulator technical reference guide volume 3: validation. NIST Spec Publ 1018(1):1–147
Walls R, Olivier G, Eksteen R (2017) Informal settlement fires in South Africa: fire engineering overview and full-scale tests on “shacks.” Fire Saf J. 91:997–1006. https://doi.org/10.1016/j.firesaf.2017.03.061
Cicione A, Walls RS (2020) Towards a simplified fire dynamic simulator model to analyse fire spread between multiple informal settlement dwellings based on full-scale experiments. Fire Mater. https://doi.org/10.1002/fam.2814pp.1-17
M. Beshir, Y. Wang, L. Gibson, S. Welch, D. Rush (2019)“A computational study on the effect of horizontal openings on fire dynamics within informal dwellings” Proc. Ninth Int. Semin. Fire Explos. Hazards, ISFEH9, St. Petersburg, pp. 512–523, https://doi.org/10.18720/spbpu/2/k19-122
M.Beshir, A.Cicione, Y.Wang, S. Welch, D. Rush (2019) “Re-visiting NIST Reduced/Full-Scale Enclosures (R/FSE),” Proc. 15th Int. Conf. and Exhibition on Fire Science & Engineering (Interflam 2019), Royal Holloway College, Nr Windsor, UK, 1–3 July.
Stevens S, Gibson L, Rush D (2020) Conceptualising a GIS-based risk quantification framework for fire spread in informal settlements: a Cape Town case study. Int J Disaster Rish Reduct. https://doi.org/10.1016/j.ijdrr.2020.101736
Cicione A, Wade C, Spearpoint M, Gibson L, Walls R, Rush D (2020) A preliminary investigation to develop a semi-probabilistic model of informal settlement fire spread using B-RISK. Fire Saf J. https://doi.org/10.1016/j.firesaf.2020.103115
Gibson L, Engelbrecht J, Rush D (2019) Detecting historic informal settlement fires with Sentinel 1 and 2 satellite data: two case studies in Cape Town. Fire Saf J 108:102828. https://doi.org/10.1016/j.firesaf.2019.102828
Y. Wang, L. Gibson, M. Beshir, D. Rush (2020), “Determination of critical separation distance between dwellings in informal settlements fire”, accepted for publication in Fire Technology.
Y. Wang, M. Beshir, L. Gibson and D. Rush (2019), “Numerical investigation of fire spread mitigation using Chinese ancient fire wall design into South African informal settlements.” International Conference on Structural Safety Under Fire and Blast.
Centenoa FR, Beshir M, Beshir D (2020) Influence of wind on the onset of flashover within small-scale compartments with thermally-thin and thermally-thick boundaries. Fire Saf J. https://doi.org/10.1016/j.firesaf.2020.103211
Beshir M, Wang Y, Centeno F, Hadden R, Welch S, Rush D (2020) Semi-empirical model for estimating the heat release rate required for flashover in compartments with thermally-thin boundaries and ultra-fast fires. Fire Saf J. https://doi.org/10.1016/j.firesaf.2020.103124
McCaffrey BJ, Quintiere JG, Harkleroad MF (1981) Estimating room temperatures and the likelihood of flashover using fire test data correlations. Fire Technol 17(2):98–119. https://doi.org/10.1007/BF02479583
Peatross M, Beyler C (1994) Thermal environment prediction in steel-bounded preflashover compartment fires. Fire Saf Sci 4:205–216. https://doi.org/10.3801/IAFSS.FSS.4-205
Wang Y, Beshir M, Cicione A, Hadden R, Krajcovic M, Rush D (2020) A full-scale experimental study on single dwelling burning behavior of informal settlement. Fire Saf J. https://doi.org/10.1016/j.firesaf.2020.103076
Hidalgo JP, Maluk C, Cowlard A, Abecassis-Empis C, Krajcovic M, Torero JL (2017) A Thin Skin Calorimeter (TSC) for quantifying irradiation during large-scale fire testing. Int J Therm Sci 112:383–394. https://doi.org/10.1016/j.ijthermalsci.2016.10.013
X. Dai, S. Welch, and D. Rush (2019), “Characterising natural fires in large compartments – revisiting an early travelling fire test (BST/FRS 1993) with CFD” Proc. 15th Int. Conf. & Exhibition on Fire Science & Engineering (Interflam 2019), Royal Holloway College, Nr Windsor, UK, 1–3 July, pp. 2111–2122
Deardorff JW (1980) Stratocumulus-capped mixed layers derived from a three-dimensional model. Boundary-Layer Meteorol 18(4):495–527. https://doi.org/10.1007/BF00119502
Nicoud F, Ducros F (1999) Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Fire Mater. https://doi.org/10.1023/A:1009995426001
Katopodes ND (2019) Free-Surface Flow, Chapter 8 - Turbulent Flow, Butterworth-Heinemann, pp 566–650. https://doi.org/10.1016/B978-0-12-815489-2.00008-3
Wilcox DC (1994) Turbulence Modelling for CFD, DCW Industries, California
Holman JP (1990) Heat transfer, 7th edn. McGraw-Hill, New York
Incropera FP, Dewitt DP (2002) Fundamentals of heat and mass transfer, 5th edn. John Wiley and Sons, Chichester
Kallada Janardhan R, Hostikka S (2019) Predictive computational fluid dynamics simulation of fire spread on wood cribs. Fire Technol 55(6):2245–2268. https://doi.org/10.1007/s10694-019-00855-3
Hansen R, Ingason H (2012) Heat release rates of multiple objects at varying distances. Fire Saf J. 52:1–10. https://doi.org/10.1016/j.firesaf.2012.03.007
R. Wills (2018), “Effect and appropriate use of Time Shrink Factor in FDS,” in The 4th Fire and Evacuation Modelling Technical Conference (FEMTC), [accessed 13/09/2020]. Available: https://www.thunderheadeng.com/files/com/FEMTC2018/files/d2-11-wills/wills-paper.pdf.
K. Mcgrattan, S. Hostikka, J. Floyd, R. McDermott and M. Vanella (2020), “Sixth Edition Fire Dynamics Simulator User ’ s Guide,”. NIST special publication 1019.
Ma TG, Quintiere JG (2003) Numerical simulation of axi-symmetric fire plumes: accuracy and limitations. Fire Saf J 38(5):467–492. https://doi.org/10.1016/S0379-7112(02)00082-6
Zhang S, Ni X, Zhao M, Feng J, Zhang R (2015) Numerical simulation of wood crib fire behavior in a confined space using cone calorimeter data. J Therm Anal Calorim 119(3):2291–2303. https://doi.org/10.1007/s10973-014-4291-4
Anderson J, Sjostrom J, Alastair T, Dai X, Welch S, Rush D (2019) FDS 891 simulations and modelling efforts of travelling fires in a large elongated compartment. Proceedings 15th International Conference Exhibition on Fire Science & Engineering (Interflam 2019), Royal Holloway College, Nr Windsor
W. prducts FI, “Fire properties of wood.” [Online]. Available: https://www.woodproducts.fi/content/wood-a-material-4. Accessed: 01-Apr-2020.
TIS, “Corrugated board.” [Online]. Available: https://www.tis-gdv.de/tis_e/ware/papier/wellpapp/wellpapp-htm/. Accessed: 01-Apr-2020.
Bartlett AI, Hadden RM, Bisby LA (2019) A review of factors affecting the burning behaviour of wood for application to tall timber construction. Fire Technol 55(1):1–49. https://doi.org/10.1007/s10694-018-0787-y
S. Hostikka, K.B. McGrattan (2001) “Large Eddy Simulation of Wood Combustion,” NIST Publication.
A. P. Robbins and C. A. Wade (2008), “Soot yield values for modelling purposes: residential occupancies,” Branz Research Report no. 185.
“The engineering tool box,” 2020. [Online]. Available: https://www.engineeringtoolbox.com/emissivity-coefficients-d_447.html. [Accessed: 01-Apr-2020].
Agarwal G, Liu G, Lattimer B (2014) Pyrolysis and Oxidation of Cardboard. Fire Safety Science 11:124–137. https://doi.org/10.3801/IAFSS.FSS.11-124
Therma-fiber, “Product infomration.” [Online]. Available: https://www.thermafiber.com/technicallibrary/productliterature/. Accessed: 22-Jun-2020.
Pilkington, “Transmission properties of windows july 85 Glaverbel, reflective glazing monsanto, solar control,” Clim United Kingdom.
“IBM SPSS software.” [Online]. Available: https://www.ibm.com/analytics/spss-statistics-software. Accessed: 01-Sep-2019.
Acknowledgements
This work is financially supported by IRIS-Fire project of UK (Engineering and Physical Sciences Research Council Grant no.: EP/P029582/1). This work used the Eddie Compute Cluster provided by the Edinburgh Compute and Data Facility (ECDF) (http://www.ecdf.ed.ac.uk/).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Beshir, M., Mohamed, M., Welch, S. et al. Modelling the Effects of Boundary Walls on the Fire Dynamics of Informal Settlement Dwellings. Fire Technol 57, 1753–1781 (2021). https://doi.org/10.1007/s10694-020-01086-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10694-020-01086-7