Abstract
Engineered timber is an innovative and sustainable construction material, but its uptake has been hindered by concerns about its performance in fire. Current building regulations measure the fire performance of timber using fire resistance tests. In these tests, the charring rate is measured under a series of heat exposures (design fires) and from this the structural performance is deduced. Charring rates are currently only properly understood for the heat exposure of a standard fire, not for other exposures, which restricts the use of performance-based design. This paper studies the charring rates under a range of design fires. We used a multiscale charring model at the microscale (mg-samples), mesoscale (g-samples), and macroscale (kg-samples) for several wood species exposed to different heating regimes and boundary conditions. At the macroscale, the model blindly predicts in-depth temperatures and char depths during standard and parametric fires with an error between 5% and 22%. Comparing simulations of charring under travelling fires, parametric fires, and the standard fire revealed two findings. Firstly, their charring rates significantly differ, with maximum char depths of 42 mm (travelling), 46 mm (parametric), and 59 mm (standard fire), and one (standard fire) to four (travelling fire) charring stages (no charring, slow growth, fast growth, steady-state). Secondly, we observed zero-strength layers (depth between the 200 °C and 300 °C isotherm) of 7 to 12 mm from the exposed surface in travelling fires compared to 5 to 11 mm in parametric fires, and 7 mm in the standard fire. Both traditional design fires and travelling fires, therefore, need to be considered in structural calculations. These results help engineers to move towards performance-based design by allowing the calculation of charring rates for a wide range of design fires. In turn, this will help engineers to build more sustainable and safe structures with timber.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Heavy timber could revolutionize the construction industry. It allows rapid, cost-efficient, and carbon-negative construction of buildings and, in particular, skyscrapers. For example, Oliver et al. [1, 2] estimated that a switch from steel and concrete to sustainable timber could reduce total carbon emissions by up 31%. Architects have already proposed skyscrapers (> 300 m high) out of timber, including the Oak tower in London (UK), the Riverside Beech tower in Chicago (USA), and the W350 tower in Tokyo (Japan). However, all timber products are flammable to a certain degree and fire engineering is a prerequisite for safe design. Practitioners often struggle to assess the safety risks of timber structures due to a lack of knowledge of the fire performance of engineered timber. Compared to steel and concrete, the research on timber is sparse [3]. This lack of knowledge is a major obstacle to unlocking the potential of timber as a construction material for medium and high-rise buildings [3].
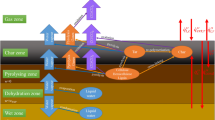
Particularly the strength decay of timber during a fire remains a major concern. A fire safety requirement of a building is its stability during and after a fire (no collapse) [4], but the determination of the strength decay of timber during a fire remains a challenge. Irrespective of the fire scenario, the strength decay of timber in a fire progresses as follows (Figure 1). The incoming heat from a fire causes timber to undergo charring which consists of three sequential sub-processes: drying, pyrolysis, and oxidation. During drying, water molecules bonded within the timber absorb the incoming heat and break, causing the water to evaporate. Once the timber is dry [5], the heat breaks the long polymer chains of the load-bearing wood into non-load-bearing char and flammable volatiles. This process is called pyrolysis and does not involve oxygen. The volatiles diffuse towards the surface [6], where they ignite and supply additional heat to the timber. This additional heat causes the char layer to propagate further into the timber until an equilibrium point is reached. At this equilibrium point either the char layer is sufficiently thick to protect the remaining load-bearing timber below (negligible charring rate) or all timber has turned into char. In the latter case, the wood has lost all its load-bearing capacity. Commonly it is assumed that only the volatiles contribute additional heat, but the oxygen can also react with the char [7]. The burning of char adds additional heat and shifts the equilibrium point towards the complete consumption of timber. Charring is therefore the complex interaction of drying, pyrolysis, char oxidation, and volatile oxidation. It remains, unsurprisingly, poorly understood [8].
Historically, the complexity of charring has led to the development of simplified methods to calculate the fire resistance of structural members made of timber. Traditionally, fire resistance has been measured by how long a structural element can withstand the standard temperature–time curve—meant to approximate the temperatures of a fire in a compartment—in a furnace, without losing its loadbearing ability [9, 10]. In this approach char is assumed to have no load-bearing capacity, while the intact timber below the char is assumed to still have most of its strength [11]. In the current Eurocode, 7 mm are added to the char depth to account for the strength loss of timber prior to its conversion to char. In other words, if one knows the depth of char at any given point, one can deduce the remaining load-bearing capacity of the timber. It follows then that the rate of charring controls the fire resistance [11]. This approach is called the reduced cross-section method and it is implemented in all major building codes [11]. Within this framework, wood is assumed to turn into char at 300 °C [11]. However, the standard temperature–time curve and furnace tests are based on convention and were not conceived with combustible structures in mind [12]. For example, when a combustible member is burning in a furnace the amount of energy has to be reduced to follow the same standard fire curve as for combustible members [13, 14]. Lately, there has been an increasing trend towards a more performance-based approach in structural fire engineering, for example, by using a range of temperature–time curves.
Temperature–time curves in a compartment are called design fires and are intended to represent the temperatures in a compartment during the reasonable worst-case fire. The standard temperature–time curve is an idealistic condition that assumes uniform temperature distribution in a compartment without any decay period, i.e. the temperature is constantly increasing. It is the same regardless of the size, geometry, or fuel load of a compartment. For example, an empty compartment and one filled with heptane, a highly flammable liquid, would be assumed to burn in the same way. Parametric fires were introduced to the Eurocode to represent post-flashover fires and address this issue by incorporating a dependence on the compartment characteristics (i.e. geometry, fuel load, opening factor, internal linings, etc.) as well as considering both the growth and decay periods of a fire. Parametric fires, however, still assume a uniform temperature distribution in the compartment with application limited to small compartments. EN 1991-1-2 limits application of parametric fires to floor areas of up to 500 m2 [15]. For the purposes of this paper, we group standard and parametric fires into the group of uniform/traditional fires following the nomenclature of [16].
A uniform fire may not always present an accurate fire behaviour in large open-plan compartments (floor area > 500 m2) common in modern buildings [17, 18]. Instead, large accidental compartment fires have been observed to travel through the room from one point to another. To incorporate this fire spread, the concept of travelling fires has been created [18, 19]. Travelling fires proposed in [18] are a function of the size, geometry, and fuel load of a compartment as well as the location of interest in the compartment. We will refer to them as non-uniform fires following the nomenclature of [16], as the room burns non-uniformly resulting in non-uniform temperature distributions within the compartment.
Except from the lack of knowledge of fire dynamics in timber framed compartments, the rate of charring under non-uniform fires is unknown. All past works only studied charring rates under uniform fires such as the standard fire [20], parametric fires [21], and some others [9, 22, 23]. No study has investigated the rate of charring under non-uniform fires. The use of charring rates derived from uniform fires for the fire safety design of compartments which will experience non-uniform fires is speculative. In fact, comparison of experiments of different uniform fires [9, 21] as well as the physical and chemical nature of charring suggests that the charring behaviour highly depends on the fire scenario.
Here, we aim to scientifically understand the charring under uniform and non-uniform fires under the same thermal and oxygen boundary conditions that are equivalent to those of a standard fire-furnace.
The paper is split into six main sections including the introduction. The second section will outline the current framework and our choice of design fires (Sect. 2). The third section (Sect. 3) will outline the development of the model of charring of wood together with the experiments for validations and design fires to be studied. All design fires originate from a non-combustible structure. The fourth section (Sect. 4) will compare the charring behaviour of uniform (standard and parametric) and non-uniform (travelling) fires. The fifth section (Sect. 5) will then discuss the applicability of multi-scale modelling to fire science and performance of current design fires to large compartments. Sect. 6 will then conclude and summarise the findings of the paper.
2 Choice of Design Fires
Within this study, we investigate the thermal response to a range of uniform and non-uniform fires in the form of applied temperature time curves as boundary conditions in a standard-fire furnace environment. As a result, all fires have the same oxygen concentration and thermal boundary conditions unlike realistic compartments where these values would differ depending on the characteristics of the compartment. These assumptions are within the current fire resistance framework—the same assumptions are taken for all other building’s materials—and they allow for a direct comparison to the outcome from a standard fire test that is the comparative metric used in building regulations. Additionally, these boundary conditions are well known in literature unlike the boundary conditions of realistic timber frame compartments where experimental evidence is lacking.
Several researchers have raised concerns that furnace fire resistance tests with a standard fire are not comparable between timber and other non-combustible building materials [13, 14, 24], which calls for a revision of the fire resistance framework for timber. Some of these authors have argued that the fire resistance framework alone is insufficient to ensure the safety of timber buildings as it decouples charring (fuel production) from the fire dynamics [3, 25]. At the same time, others provided evidence that the current framework is sufficient to ensure the stability of timber buildings [26, 27]. As this debate of the applicability of design fires, even standardised uniform fires, to timber remains yet unsolved, it was deemed reasonable to investigate timber computationally under design fires originally developed for non-combustible structures using the above-mentioned assumptions. In other words, it is reasonable to stay within the current framework of fire resistance testing and use the assumptions within that framework to investigate the effect of different design fires on charring rates.
We explore the range of design fires that were developed for a generic open plan compartment studied by Rackauskaite et al. [28]. These authors used a thermomechanical model to investigate the response of steel frames subjected to uniform and non-uniform fires. They calculated several design fires for a multi-story steel frame that was designed in line with the American Society of Civil Engineers (ASCE 7-02) standard. These design fires were chosen to study timber and not modified because of the justifications given above. Four uniform and non-uniform fires (Figure 2) were investigated. The non-uniform fires are traveling fires of four different sizes: 2.5, 10, 25, and 48%. Their size (%) quantifies the respective floor area burning at any one given time. A travelling fire is assumed to travel uniformly and across the whole width of the compartment in the longitudinal direction. Due to this nature, the temperature–time curve of a travelling fire at different locations along the fire path differs, as the fire reaches these locations at different points. Here we investigate the charring behaviour of timber slabs along the fire path every 9.1 m in a 45.5 m long compartment.
Left: Temperature-time curves of uniform fires tested in this study with ISO 834 standing for standard fire, EC-SH for a short and hot Eurocode parametric fire, EC-LC for a long and cool Eurocode parametric fire, and SFPE for the Society of Fire Protection Engineers constant temperature fire. Right: Temperature-time curves of non-uniform (travelling) fires tested in this study as measured at the centre of the compartment. All shown fires are taken from [28]
3 Methods
3.1 Computational Model
In this study, we used a multi-scale model of charring of timber integrated into Gpyro [29], that solves the physical and chemical changes of wood in the solid phase. The gas-phase was not simulated and only approximated by design fires as explained in Sect. 3.2. The model itself was developed by extending the across scale approach of Rogaume [30] by introducing uncertainty quantification as well as testing the appropriateness of the complexity of the model. The idea behind this approach is to study different chemical and physical processes in isolation across scales [31]. The assumption is that by studying them in isolation, the final model will be more robust and valid in extrapolation as it is common in engineering science [32]. The latter part is key for this study, as we will use the model to simulate the charring response of a wood sample to a design fire for which no experimental data exist. The complete development and validation of the model can be found in [33,34,35] and will be summarised here. The model consists of a physical and chemical sub-model. The chemical kinetic model was developed at the microscale [34], following a literature review that found that no appropriate heterogenous kinetic model of charring existed in the literature [34, 35]. At the microscale, the model was validated against a range of experiments with mg-samples of wood from the literature under a wide range of heating conditions, oxygen concentrations, and heating intensities. These experiments were selected according to the thresholds in [36]. Following this validation, the kinetic model was incorporated into Gpyro, which is a generalised pyrolysis solver [29], by Richter and Rein [33]. The mathematical formulation of the model can be found in [33] with the material properties described in the next section. All material properties were taken from the literature. The model itself predicts well several experiments at the mesoscale (g-samples) from the literature, as well as compares well to several other computational models of various complexities available in literature. In fact, the model reproduces the mass loss rate and in-depth temperatures of wood in different grain orientations, of different moisture content, under different oxygen concentrations, and different heat fluxes in experiments conducted by different authors. One can therefore conclude that the model is valid at both the micro-and mesoscale, and that the model can predict experiments under different heating regimes and boundary conditions. In this study, we will assess the performance of the model against macroscale experiments (> kg-samples) before using the model in extrapolation to simulate previously unstudied design fires. The results in extrapolation will be deemed valid if the model compares well at all scales as such agreement indicates that the model captures all major physical and chemical processes.
3.2 Mesh, Input Parameters, and Boundary Conditions
In this study, we simulate the response of one-dimensional wood samples to different design fires in furnace like conditions (thermal and oxygen boundary conditions), as shown in Figure 3. The wooden sample is assumed to behave as a solid block, and its depth of char can be estimated by the 300 °C isotherm. The former assumption holds for all Cross-Laminated Timber and Glulam as long as they do not delaminate. This set-up and choice of isotherm represents the experiment and choice of Konig and Wallij [21], who studied spruce under the standard (90 min) and several parametric fires. In our simulations, we will extend the heating conditions to include travelling fires. Konig and Wallij studied the charring rates of spruce using samples of 95 mm thickness by measuring the temperatures at 0,6,18, 30, 42, and 54 mm deep. All simulations assumed that each sample is 95 mm thick. In the simulations, the samples were discretised with a mesh size of 0.3 mm and a timestep of 0.09 s was used. These values were found to yield equivalent results to a mesh of 0.1 mm and 0.01 s, which was previously identified as the optimum mesh size for experiments at the mesoscale (experiments with g-samples) [37]. The material properties of spruce were assumed equal to generic wood [33], shown in Table 1, with only the density adjusted to the measured value of 430 kg/m3 [21] and the moisture content to 12%. The latter was estimated based on the experimental drying procedure [21, 38], but all simulations were also run at 5% moisture content for comparison. Our underlying assumptions and Table 1 shows that the model assumes that the thin layer of ash stays on the surface of the wood, thus creating a small resistance to mass and heat transfer. This assumes that the ash is not removed by either flow or gravity.
The boundary conditions at the front (Eq. 1) and back surface (Eq. 2) are modelled as follows:
where T is the temperature, z is the spatial coordinate, hc the heat transfer coefficient,\(\bar{\varepsilon }\) the emissivity, \(\bar{\psi }\) the porosity, \(\rho_{g}\) the gas-phase density, D the diffusivity, Y the gas-phase mass fraction, P is the pressure, and \(h_{m}\) the mass transfer coefficient. A convection coefficient of 9 W/m2-K [39] was assumed at z = 0 and the emissivity is defined in [33]. We estimated the average heat transfer coefficient as \(h_{c} = 9\frac{W}{{m^{2} - K}}\) [39] for \(z = 0\) and \(h_{c} = 0\frac{W}{{m^{2} - K}}\) for \(z = L\) due to the insulation. The emissivity of wood was estimated as 0.7 [40], while the emissivity of char and ash are estimated to be 0.95 [41]. From the heat-mass transfer analogy [42], we estimated \(h_{m0} \approx \frac{{h_{c} }}{{c_{g} }} = 9\frac{g}{{m^{2} - s}}\) for z = 0 and \(h_{m0} = 0 \frac{g}{{m^{2} - s}}\) for z = L with \(c_{g} = 1000\frac{J}{kg - K}\). No in-depth radiation is considered as it is negligible for wood [43]. The temperature \(T_{\infty }\) was assumed to follow the employed design fire at z = 0 and the ambient condition at z = L. The oxygen concentration within the furnace was assumed to be 8% as report by Schmid et al. [10]. Future research should explore the appropriate oxygen concentration and boundary conditions for realistic fires in large compartments and their impact on the charring of timber. For this work the same boundary conditions are adopted for all the design fires due to the lack of experimental evidence and understanding of fire dynamics in timber framed compartments.
3.3 Uncertainty Propagation
The boundary conditions used within this study for the furnace are uncertain, and we assess the influence of their uncertainty with Monte-Carlo simulations [44]. In the first step, we found the plausible range for each parameter of the boundary conditions as shown in Table 2. We then created an ensemble of sets of these input parameters by drawing them from a uniform distribution and combing them at random. Using a Monte-Carlo approach, we then did one simulation of the standard fire, Konig’s parametric fire C3, and Konig’s parametric fire C4 for each set of input parameters in our ensemble. These simulations gave us an ensemble of predictions which we used to derive the uncertainty of our simulations. Further details can be found in [44]. In total, we conducted 250 simulations for each design fire.
4 Results
4.1 Predictions of Furnace Tests
The developed model predicts in-depth temperatures and charring rates of timber slabs under several design fires well (Figures 4, 5, 6). The depth of char was here evaluated by the 300 °C isotherm, which in turn allowed us to calculate the charring rate. However, we focus on the final depth of char of different design fires as that value quantifies the final strength loss after a fire (the key variable). In a furnace, the boundary conditions of a sample are transient and uncertain. For example, Schmidt et al. [22] investigated the oxygen concentrations in a furnace during fire tests. They found the oxygen concentration to vary between 0 and 10%. We accounted for this uncertainty through Monte-Carlo simulations (Sect. 3.3), which are shown as the shadow region around the simulations. Regardless of the boundary conditions (standard deviation: 2.6 mm), the model predicts the experiments with an average error in the char depth of 2.1 mm in the standard fire (Figure 4), 1 mm in the parametric fire C3 (Figure 5), and 3.8 mm in the parametric fire C4 (Figure 6). The parametric fires C3 and C4 and their name are taken from [21]. Noteable, König and Walleij [21] derived his parametric fires from the works of Magnusson and Thelandersoon [21, 45].
Prediction of temperature and charring rate in a 90 min long standard fire in comparison to the experiments from [21]. The shadow bounds show the uncertainty region due to the boundary conditions. The thermocouple distances are 6, 30, and 54 mm respectively
Blind predictions of the design fire C3 from [21]. The thermocouple distances are 6, 30, and 54 mm respectively
Blind predictions of the design fire C4 from [21]. The thermocouple distances are 6, 30, and 54 mm respectively
The predictions of the charring rates are always better than the predictions of the temperature. For example, the average error in the temperatures in a standard fire is 14% (Figure 4 left), while the average error in the charring rate is 7%, excluding the first 2 min (Figure 4 right with t > 2 min). This result is unexpected as charring rates are taken as the position of the 300 °C isotherm. In other words, the char depth in the experiments and predictions are derived from the temperature profiles. The reason for this contradiction is that the predictions at low temperatures (roughly < 400 °C) are very good, but greater discrepancies are observed for higher temperatures (see Figure 6). Two discrepancies are particularly large. One is the discrepancy in predicting the temperature at 6 mm in standard fire past 50 min (Figure 4). The other is the discrepancy in predicting the temperature at 30 mm past 40 min (Figure 6). The discrepancy in Figure 4 likely stems from a discrepancy in predicting the char oxidation, which is likely caused by the transient and varying oxygen concentration in a furnace. This can be deduced from the fact that the predictions work well up until 40–50 min. Afterwards (40–45 min) the model diverges from the experiments, as the model predicts that the char oxidation front reaches 6 mm and exposes the thermocouple (heat and mass transport is only slightly limited by ash). In the experiments, however, it seems some char remained, causing the experimental temperature at 6 mm to plateau. This discrepancy is of low concern as we predict in-depth temperatures well. The discrepancy in Figure 6 is likely caused by cracking. In the experiment, the thermocouples are offset from each other. If a crack forms in the wood, it shortens the distance between one thermocouple and the surface while leaving all other thermocouple readings unaffected. For the parametric fire C4 (Figure 6), we predict the temperature readings at 6 mm and 54 mm well, so that it is unphysical to observe a discrepancy at 30 mm. Hence, a crack must have been formed to cause an unexpected rise in temperature at 30 mm. As cracking is not incorporated in the model yet, this discrepancy is of low concern. Hence, we can judge the prediction of charring rates as well, and the predictions of temperature as good despite some discrepancies.
4.2 Comparison of non-uniform and traditional design fires
The charring behaviour of timber slabs depends on the fire scenario (assuming all boundary conditions are the same between the scenarios). When comparing all uniform (Figure 7) and non-uniform (Figure 8) fires, one can conclude that char depths differ when the fire scenario differs. In a standard fire, charring only has one stage: a relative constant increase in char depth (fast growth). This is observed both numerically and experimentally (Figure 4). However, for intermediate size compartments (< 500 m2) parametric fires (Figure 7 b & c) are better suited which show a two stage charring behaviour: increase during heating (fast growth) and a plateau during the decay phase (steady-state). This finding is further supported by the experimentally measured char depths in Figures 5 and 6. For travelling fires in large-scale compartments (> 500 m2, Figure 8), one observes four stages: no-charring during the far field (T < 200–300 °C), slow increase during the arrival of the near field (T = 300–1200 °C, slow growth), fast charring during burning (T = 1200 °C, fast growth), and plateau during the decay phase (steady state). These qualitative differences in charring behaviour also result in quantitative difference with the largest char depth being observed in the SFPE (Society of Fire Protection Engineers constant temperature fire), ISO (standard fire), and EC-LC (Eurocode fire—long & cool) respectively. Hence, char depths under different fire scenarios differ significantly quantitatively and qualitatively.
Simulations of the char depth of the four uniform design fires, with a sketch of the set-up in (d). The black solid line represents the char depth with the y-axis on the left-hand side, and the red dashed line represents the gas temperature with the y-axis on the right-hand side. The Standard Fire and SFPE fire are both assumed to be 90 min long
While we said previously that charring plateau’s during the decay phase, it actually slowly continues a little into the decay phase (Figure. 7d). Wiesner and Bisby [49] found this previously experimentally. Charring continues post-heating, and sometimes even post-extinction, for three reasons. Firstly, the temperatures in the surrounding environment are still high enough to cause heating (T > 300 °C). Secondly, charring contributes to the gaseous fuel load and, therefore, potential heat release. As explained in Sect. 2, in our simulation the fire dynamics and charring are decoupled as we are using the current fire resistance framework. Secondly, the residual heat in the char will continue to advance the char front for a while. This outcome is important, as the Eurocode [15] —leading regulation in Europe to design timber buildings—offers a set of material properties to calculate charring rates in advanced heat transfer models. These parameters are only valid for heating but could benefit from extension to capture the decay phase. In our simulations charring during the decay phase is small (< 6 mm) while Wiesner and Bisby [49] observed significant charring (~ 20 mm). We attribute this discrepancy to the difference in set-up (column vs. slab, and enclosed vs. open furnace), the cooling time (2–3 min vs. 33 min), and different oxygen flow conditions (8 vs. 21% Oxygen). The above will lead to a different ratio of heat lost to heat transmitted into the solid, heat flux during the decay phase, and additional heat from char or volatile oxidation. The observed difference between the predictions and literature experiments is therefore reasonable.
Another distinction between uniform and non-uniform fires is that the latter dependent on location of the fire (or near field) in the compartment and fire size (Figure. 9). We found that independent of the fire location the maximum char depth is found after 90% (after roughly 40 m) of the fire path (Figures. 9 and 10), with the 2.5% travelling fire being the most severe. This point is unsurprising as the 2.5% travelling fire has the longest pre-heating time before the onset of charring. Hence, the sample can heat up more uniformly towards the temperature range at which pyrolysis starts, without any heating being lost due to pyrolysis. One therefore expects the smallest fire to be the most severe one. Surprisingly, the smallest fire is not the most severe one at the beginning and end of the compartment. At the beginning of the compartment (x = 0 m) there is no preheating time. The burning times of all fires in one location are relatively similar. Therefore, the fire with the highest temperature would be most severe, which is the 47% fire (Figure. 2). At the end of the compartment (x = 45.5 m), we assume the fire is extinguished instantaneously and cools within minutes to ambient temperatures. Hence, the most severe fire is the one that strikes a balance between preheating time (increases as fire size decreases) and peak temperature (decreases as fire size decreases). The fire sizes 2.5–10% strike this balance. In other words, it is important to study an ensemble of fires sizes of non-uniform fires at different location to evaluate their charring behaviour as it depends on location and fire size.
Despite the quantitative and qualitative difference between all fire scenarios, the standard fire represents the most severe heating in terms of charring after the SFPE fire. The char depth after a 90 min fire exceeds the char depth of all other fire scenarios at the end of fire exposure other than the SFPE fire. The latter is unsurprising, as the SFPE fire represents the case of a constant flame burning above the solid for an indefinite time. The char depth after a 90 min standard fire is 53.2 mm (as predicted by the computational model, which is slightly lower than the 58.5 mm given by EN 1995-1-2), while the char depths of parametric and travelling fires at the end of fire exposure are up to 46 to 42 mm respectively. In other words, travelling fires and parametric fires produce equivalent char depth up to 78 to 71 min in a standard fire (based on computational predictions). However, we assumed a fuel load of 540 MJ/m2, which in turn assumes that the timber does not contribute to the fuel load in the compartment. Taking the additional fuel load of timber into account would raise the char depth in parametric and non-uniform fires above 53 mm. In other words, a 90 min standard fire would no longer represent the most severe heating in terms of charring. However, evaluating the contribution of timber to the fire is beyond the scope of this study and we focus here on a fuel load of 540 MJ/m2. For this fuel load, the 90 min standard fire is representing the most severe heating in terms of char depth. Nevertheless, these findings suggest that the use of the standard fire adjusted for an increased duration to account for the increase in fuel load due to timber charring results in conservative calculation of the charring rate within the assumptions of the standard fire-furnace.
5 Discussion on Zero-strength Layer
The strength decay of timber slabs in a fire is calculated by the reduced cross-sectional method [11]. In this method, the char depth is subtracted from the original dimension of a timber slab with the remaining section assumed to be intact. If the remaining section can hold the load, the element is assumed safe. In this method, the char depth is assumed to be the 300 °C isotherm. However, the strength of wood decays well before 300 °C [11]. In order to account for the strength decay ahead of the char front, one adds 7 mm to the char depth in the calculation. These 7 mm are called the zero-strength layer, but the thickness of the layer has been questioned recently [49]. Implicitly, the 7 mm zero-strength layer assumes that the temperature rise beyond 7 mm from the char front is small so that the strength loss is small.
We found large temperature rises well below 7 mm from the char front in non-uniform fires (Figure. 11). If we assume, that the zero-strength layer can be defined by a 200 °C isotherm—this is the point at which at least 50% of wood’s strength in compression has decayed based on the measurements of several authors [11]. The strength of timber may start to decay below this point [49] but 200 °C was chosen as it also coincides with the onset of pyrolysis. Applying this criterion to the simulations of non-uniform fires we find the thickness of zero-strength layer to be up to 12 mm. The largest zero-strength layer are found for 2.5% travelling fire (left-hand column in Figure. 11), which is expected as the pre-heating time is the largest. In turn, the long pre-heating time should lead to the shallowest temperature gradient and the largest zero-strength layer. Also, as expected, the smallest zero-strength layer (3.6–7 mm) is observed for the 48% travelling fire. Again, this is expected as larger travelling fire represent short and intense heating, which induces large temperature gradients. These results agree with the literature. Wiesner et al. [50] exposed timber walls to a constant heat flux and found zero-strength layers between 15 and 22 mm. Schmid et al. exposed timber to the standard fire and found zero-strength layers of up 19 mm. These values are close to the value found here (12 mm). In fact, a reduction of moisture content from 12 to 5% would increase the zero-strength layer to 16 mm, which highlights the importance of considering moisture content.
Evolution of the char depth with the temperature profile behind the char front for the four different non-uniform fires and the location in the compartment. Each contour line represent a 30 K interval from 0 °C to 300 °C. The solid red line represents the char front, while the dotted line represents the location of burnout
Comparing the temperature profiles ahead of the char front for non-uniform fires (Figure. 11) and uniform fires (Figure. 12) shows that the temperature profiles are similar. The temperature gradients ahead of the char front are steeper and make that region of less interest. For example, the profiles in the standard, SFPE, and EC-LC are qualitatively similar to those of a travelling fire at 25 and 48% fire size. The zero-strength layer thicknesses (200 °C isotherm) are smaller (5 to 7 mm) for all fires except the EC-LC (11 mm). This range changed by to 4 to 12 mm, when the moisture content is reduced from 12% to 5%. Long pre-heating leads to shallow temperature gradients, which leads to a uniform strength loss across the slab that potentially exceeds the one predicted by the char depth and fixed zero-strength layer. These conditions are more likely encountered in a fire in a large compartment (non-uniform fires).
These results indicate that the commonly used value of 7 mm for the zero-strength layer might not be conservative for timber slabs. We deduce this based on the temperature profiles, but further work is needed to verify this finding structurally and for other timber elements. This recommendation agrees with the recommendation by Schmid et al. [11] to revisit the 7 mm zero-strength layer even for uniform fires. As the results agree well with those of Schmid et al., it is likely and surprising that the same zero-strength layer for uniform and non-uniform fires can be used in the future. The results (Figure. 11) show that currently the zero-strength layer in timber slabs under non-uniform fire depends on location and fire size. In general, the thickness of the zero-strength layer decreases as the fire size `increases from 12 mm at 2.5% to 7 mm at 48%. At the same time, the thickness of the zero-strength layer at one specific fire size increases with increasing char depth generally but not always. For example, for the 25% travelling fire, the maximum char depth is found 45.5 m away from the ignition location. The maximum zero-strength layer is found 36.4 m away, and the maximum strength decay of wood is 36.4 m away. This means that location of maximum char depth and maximum strength decay differ, which we also observed at 5% moisture content. In uniform fires, this behaviour is not observed. It is, therefore, important to study the char depth and zero-strength layer under non-uniform fires to correctly locate the position of maximum strength decay. The currently employed 7 mm zero-strength layer does not capture this behaviour or the magnitude of the strength decay, and we therefore recommend a revision of it.
A potential limitation of the study is that we approximated a failure of a load-bearing timber member by a thermal failure criterion (char depth). An improvement on this would be to explore both a thermal and structural failure criteria [16]. It was deemed appropriate to focus first on thermal failure in a design fire before introducing additional complexity (structural failure criteria).
6 Conclusion
We unravelled the difference in the charring behaviour of wood between uniform and non-uniform (travelling) fires using a multi-scale model. Both quantitatively and qualitatively differences were found between uniform and non-uniform design fires. Qualitatively charring under uniform fires proceeds in one or two stages, while it proceeds in four stages under non-uniform fires. Quantitatively, char depths after uniform fires are equivalent to char depths after 42 to 90 min in a furnace under the standard-temperature time curve, while for non-uniform fire that time spans only 44 to 71 min. A higher equivalent time represents a more severe fire. Therefore, when considering only the char depth, uniform fires represent a more severe heating conditions for timber under the assumption of a fire furnace test.
In addition, the impact of the thermal gradient behind the char line needs further investigation. The strength decay of wood is a combination of the char depth and the zero-strength layer. Currently, regulations assume a strength layer of 7 mm for uniform fires, but it has been recommended to re-evaluate that value to increase it up to 19 mm. In line with these previous studies, we found the zero-strength layer in travelling fires to be up to 12 mm (12% moisture content) and 16 mm (at 5% moisture content). Adding this zero-strength layer would make the strength decay in a travelling fire equal to the strength decay of timber slabs in a furnace under the standard temperature–time curve of around 80 to 90 min. Both char depth and zero-strength layer should be considered in structural calculations. In comparison to uniform fires, the location of maximum strength decay and maximum char depth differ which makes the thickness of the zero-strength layer a key parameter for timber under non-uniform fires. Hence, it is important to revisit the zero-strength layer for both uniform and non-uniform fires. based on thermal failure criteria and current design fires. Our study provides, for the first time, insight into the charring behaviour of wood under non-uniform fires, which are expected to occur in large compartments found in most modern offices. These results help engineers to move towards performance-based design by allowing the calculation of charring rates for a wide range of design fires. In turn, this will help engineers to build safely more sustainable, economical, and complex structures with timber.
References
Oliver CD, Nassar NT, Lippke BR, McCarter JB (2014) Carbon, fossil fuel, and biodiversity mitigation with wood and forests. J Sustain For 33:248–275. https://doi.org/10.1080/10549811.2013.839386
Tollefson J (2017) The wooden skyscrapers that could help to cool the planet. Nature 545:280–282. https://doi.org/10.1038/545280a
Deeny S, Hadden RM, Lawrence A, Lane B (2018) Fire safety design in modern timber buildings. Struct Eng 96:48–53
Law A, Hadden RM (2017) Burnout means Burnout. SFPE Eur Mag
Gronli MG, Melaaen MCMC, Grønli MGM, Melaaen MCMC (2000) Mathematical model for wood pyrolysis comparison of experimental measurements with model predictions. Energy Fuels 14:791–800. https://doi.org/10.1021/ef990176q
Atreya A (1983) Pyrolysis, Ignition and Fire Spread on Horizontal Surfaces of Wood. Harvard University, Harvard
Boonmee N, Quintiere JG (2005) Glowing ignition of wood: the onset of surface combustion. Proc Combust Inst 30:2303–2310. https://doi.org/10.1016/j.proci.2004.07.022
Mettler MS, Vlachos DG, Dauenhauer PJ (2012) Top ten fundamental challenges of biomass pyrolysis for biofuels. Energy Environ Sci 5:7797. https://doi.org/10.1039/c2ee21679e
Bartlett AI, Hadden RM, Bisby LA, Law A (2015) Analysis of cross-laminated timber upon exposure to non-standard heating conditions. In: 14th international conference and exhibition on fire and materials. Fire and Materials, At San Francisco, USA
Schmid J, Lange D, Sjöström J, et al (2018) The use of furnace tests to describe real fires of timber structures. World Conf Timber Eng. https://doi.org/10.4049/jimmunol.1401160
Schmid J, Just A, Klippel M, Fragiacomo M (2014) The reduced cross-section method for evaluation of the fire resistance of timber members: discussion and determination of the zero-strength layer. Fire Technol. https://doi.org/10.1007/s10694-014-0421-6
Bisby L, Gales J, Maluk C (2013) A contemporary review of large-scale non-standard structural fire testing. Fire Sci Rev 2:1. https://doi.org/10.1186/2193-0414-2-1
Lange D, Sjöström J, Schmid J, et al (2020) A comparison of the conditions in a fire resistance furnace when testing combustible and non-combustible construction. Fire Technol. https://doi.org/10.1007/s10694-020-00946-6
Węgrzyński W, Turkowski P, Roszkowski P (2020) The discrepancies in energy balance in furnace testing, a bug or a feature? Fire Mater 44:311–322. https://doi.org/10.1002/fam.2735
EC5 (1994) Eurocode 5: design of timber structures. ENV 1995-1-2: General Rules-Structural Fire Design. European Committee for Standardization, Brussels, Belgium
Rackauskaite E, Kotsovinos P, Jeffers A, Rein G (2019) Computational analysis of thermal and structural failure criteria of a multi-storey steel frame exposed to fire. Eng Struct 180:524–543. https://doi.org/10.1016/j.engstruct.2018.11.026
Stern-Gottfried J, Rein G (2012) Travelling fires for structural design–Part I: literature review. Fire Saf J 54:74–85. https://doi.org/10.1016/j.firesaf.2012.06.003
Stern-Gottfried J, Rein G (2012) Travelling fires for structural design-Part II: design methodology. Fire Saf J 54:96–112. https://doi.org/10.1016/j.firesaf.2012.06.011
Clifton CG (1996) Fire models for large fire cells
Bartlett AI, Hadden RM, Bisby LA (2018) A review of factors affecting the burning behaviour of wood for application to tall timber construction. Fire Technol 55:1–49. https://doi.org/10.1007/s10694-018-0787-y
König J, Walleij L (1999) One-dimensional charring of timber exposed to standard and parametric fires in initially unprotected and postprotection situations. Stockholm
Schmid J, Santomaso A, Brandon D, et al (2016) Timber under real fire conditions—the influence of oxygen content and gas velocity on the charring behavior. In: World conference on Timber Engineering
Schmid J, Santomaso A, Brandon D, et al (2018) Timber under real fire conditions—the influence of oxygen content and gas velocity on the charring behavior. J Struct Fire Eng 9:222–236. https://doi.org/10.1108/JSFE-01-2017-0013
Bartlett AI, McNamee R, Robert F, Bisby LA (2020) Comparative energy analysis from fire resistance tests on combustible versus noncombustible slabs. Fire Mater 44:301–310. https://doi.org/10.1002/fam.2760
Law A, Hadden R (2020) We need to talk about timber : fire safety design in tall buildings. Struct Eng 56: 967
Schmid J, Klippel M, Fahrni R, Frangi A (2018) Brandeinwirkung auf Holzbauteile im Prüfofen und bei realen Bränden. Bautechnik 95:524–534. https://doi.org/10.1002/bate.201800034
Schmid J, Brandon D, Werther N, Klippel M (2018) Technical note—thermal exposure of wood in standard fire resistance tests. Fire Saf J 107:179–185. https://doi.org/10.1016/j.firesaf.2018.02.002
Rackauskaite E, Kotsovinos P, Jeffers A, Rein G (2017) Structural analysis of multi-storey steel frames exposed to travelling fires and traditional design fires. Eng Struct 150:271–287. https://doi.org/10.1016/j.engstruct.2017.06.055
Lautenberger C, Fernandez-Pello C (2009) Generalized pyrolysis model for combustible solids. Fire Saf J 44:819–839
Rogaume T (2019) Thermal decomposition and pyrolysis of solid fuels: objectives, challenges and modelling. Fire Saf J 106:177–188. https://doi.org/10.1016/j.firesaf.2019.04.016
Torero JL (2013) Scaling-Up fire. Proc Combust Inst 34:99–124. https://doi.org/10.1016/j.proci.2012.09.007
Stoliarov SI, Li J (2016) Parameterization and validation of pyrolysis models for polymeric materials. Fire Technol 52:79–91. https://doi.org/10.1007/s10694-015-0490-1
Richter F, Rein G (2020) A multiscale model of wood pyrolysis to study the role of chemistry and heat transfer at the mesoscale. Combust Flame 216:316–325. https://doi.org/10.1016/j.combustflame.2020.02.029
Richter F, Rein G (2019) Heterogeneous kinetics of timber charring at the microscale. J Anal Appl Pyrolysis 138:1–9. https://doi.org/10.1016/j.jaap.2018.11.019
Richter F, Rein G (2020) Reduced chemical kinetics for microscale pyrolysis of softwood and hardwood. Bioresour Technol 301:122619. https://doi.org/10.1016/j.biortech.2019.122619
Richter F, Rein G (2018) The role of heat transfer limitations in polymer pyrolysis at the microscale. Front Mech Eng 4:1–13. https://doi.org/10.3389/fmech.2018.00018
Yuan H, Restuccia F, Richter F, Rein G (2019) A computational model to simulate self-heating ignition across scales, configurations, and coal origins. Fuel 236:1100–1109. https://doi.org/10.1016/j.fuel.2018.09.065
Forest Products Laboratory, Ross RJ (2010) Wood handbook: wood as an engineering material. Agriculture 72:466
Wickström U (2016) Temperature calculation in fire safety engineering. Springer, Cham
Ohlemiller TJ, Kashiwagi T, Werner K (1987) Wood gasification at fire level heat fluxes. Combust Flame 69:155–170. https://doi.org/10.1016/0010-2180(87)90028-9
Huang X, Rein G, Chen H (2015) Computational smoldering combustion: Predicting the roles of moisture and inert contents in peat wildfires. Proc Combust Inst 35:2673–2681. https://doi.org/10.1016/j.proci.2014.05.048
Lautenberger C, Fernandez-Pello C (2009) A model for the oxidative pyrolysis of wood. Combust Flame 156:1503–1513. https://doi.org/10.1016/j.combustflame.2009.04.001
Girods P, Bal H, Biteau H, et al (2011) Comparison of pyrolysis behavior results between the cone calorimeter and the fire propagation apparatus heat sources. Fire Saf Sci 98: 644
Richter F, Atreya A, Kotsovinos P, Rein G (2019) The effect of chemical composition on the charring of wood across scales. Proc Combust Inst 37:4053–4061. https://doi.org/10.1016/j.proci.2018.06.080
Magnusson S, Thelandersson S (1970) Temperature—time curves of complete process of fire development. Bull Div Struct 59: 88
Chaos M (2014) Spectral aspects of bench-scale flammability testing: application to hardwood pyrolysis. Fire Saf Sci 11:165–178. https://doi.org/10.3801/IAFSS.FSS.11-165
Miller RS, Bellan J (1997) A generalized biomass pyrolysis model based on superimposed cellulose, hemicellulos eand liqnin kinetics. Combust Sci Technol 126:97–137. https://doi.org/10.1080/00102209708935670
Ragland KW, Aerts DJ, Baker AJ (1991) Properties of wood for combustion analysis. Bioresour Technol 37:161–168. https://doi.org/10.1016/0960-8524(91)90205-X
Wiesner F, Bisby L (2018) The structural capacity of laminated timber compression elements in fire: a meta-analysis. Fire Saf J. https://doi.org/10.1016/j.firesaf.2018.04.009
Wiesner F, Randmael F, Wan W, et al (2017) Structural response of cross-laminated timber compression elements exposed to fire. Fire Saf J 91:56–67. https://doi.org/10.1016/j.firesaf.2017.05.010
Acknowledgements
This work was sponsored by the Engineering and Physical Sciences Research Council (EPSRC) (EP/M506345/1) and Ove Arup and Partners Ltd.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Richter, F., Kotsovinos, P., Rackauskaite, E. et al. Thermal Response of Timber Slabs Exposed to Travelling Fires and Traditional Design Fires. Fire Technol 57, 393–414 (2021). https://doi.org/10.1007/s10694-020-01000-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10694-020-01000-1