Abstract
Evacuation simulation has the potential to be used as part of a decision support system during large-scale incidents to provide advice to incident commanders. To be viable in these applications, it is essential that the simulation can run many times faster than real time. Parallel processing is a method of reducing run times for very large computational simulations by distributing the workload amongst a number of processors. This paper presents the development of a parallel version of the rule based evacuation simulation software buildingEXODUS using domain decomposition. Four Case Studies (CS) were tested using a cluster, consisting of 10 Intel Core 2 Duo (dual core) 3.16 GHz CPUs. CS-1 involved an idealised large geometry, with 20 exits, intended to illustrate the peak computational speed up performance of the parallel implementation, the population consisted of 100,000 agents; the peak computational speedup (PCS) was 14.6 and the peak real-time speedup (PRTS) was 4.0. CS-2 was a long area with a single exit area with a population of 100,000 agents; the PCS was 13.2 and the PRTS was 17.2. CS-3 was a 50 storey high rise building with a population of 8000/16,000 agents; the PCS was 2.48/4.49 and the PRTS was 17.9/12.9. CS-4 is a large realistic urban area with 60,000/120,000 agents; the PCS was 5.3/6.89 and the PRTS was 5.31/3.0. This type of computational performance opens evacuation simulation to a range of new innovative application areas such as real-time incident support, dynamic signage in smart buildings and virtual training environments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The use of evacuation/pedestrian modelling is well established as part of building design to ensure that buildings meet performance based safety and comfort criteria [1, 2]. Another possible use for these models is to provide data, in addition to sensor information [3, 4], to a decision support system that in turn provides live operational advice to incident commanders while disasters are actually unfolding [5]. Live decision support systems that have been suggested include: the FireGrid [6, 7] system that was designed to aid emergency responders using a combination of artificial intelligence, sensor data, and predictive computation; the EU FP7 GETAWAY project [8] developed a system where the emergency signage within a complex building can adapt to a developing hazardous environment and direct occupants to their optimal exit point using information from smoke and fire detectors, live CCTV streams, and fire and evacuation simulation. The smoke and fire detector data identifies the most closely matching scenarios from a large database of precomputed fire simulations. The GETAWAY system relies on the buildingEXODUS evacuation simulation software [9,10,11,12] to run evacuation simulations representing all the alternative evacuation strategies and identify the best route out of the structure given the evolving situation. Such a system is potentially limited by the size of the scenarios that can be simulated and the time required to perform not one, but many simulations. While there are many considerations which must be taken into account when applying such models to live incidents, one of the first concerns the speed of computation. In this case the insight that could be obtained from an evacuation model is only useful if that information can be used to affect the ongoing incident. Thus for this type of application to be useful, it is essential that the simulation can be run many times faster than real time.
Faster runtimes are also useful in the commercial environment where the modelling can be performed more quickly or to a greater level of detail than would be possible using a conventional non-parallel version of the software. In addition to faster runtimes the parallel implementation also allows the possibility of running larger problems than was previously possible. Evacuation simulation tools capable of simulating large scale events have been used to forensically analyse past tragedies such as the Love Parade in 2010 [13, 14] and the Hajj in 1990 [15, 16] and 2015 [17]. However, the large scale of these events, both in terms of area and number of people, limits the level of detail that can be represented within these evacuation simulations. The use of the parallel implementation not only results in faster runtimes but also enables the possibility of running larger problems at a higher level of detail than previously possible due to the extra memory available across the processing units. Similarly, the greater speed of computation and greater detail that can be achieved using a parallel implementation make these tools better suited to the planning of large-scale events [18].
Parallel computing techniques are one way of reducing run times for very large computational simulations. Other ways of reducing runtime can be achieved by using macroscopic models, hybrid models [19], improved algorithms and faster hardware. A typical parallel implementation distributes a simulation across a number of computers making use of the available memory and processing capabilities of all the computers in the cluster or network. There are two main benefits associated with this approach. Firstly, larger scenarios can be modelled than would be possible with an evacuation model running on a single computer. This allows the simulation of very large building complexes or potentially even large urban spaces to be modelled in far greater detail than was previously possible. Secondly, large scenarios can run more quickly than was previously possible and potentially much faster than real time.
Most pedestrian evacuation models can be described as macroscopic or microscopic although some models can be described as mesoscopic [20,21,22]. The macroscopic approach (also known as coarse network models [1, 2, 23]) do not represent individuals but treat the population more like a fluid. They can represent very large scale evacuations and compute them in short timeframes on a single PC without the need for parallel computation. However, macroscopic models cannot easily represent detailed human behaviour and the interaction of individuals [21], e.g. it is difficult to examine contra-flow. The alternative microscopic approach models the crowd as a collection of interacting agents and so potentially has the ability to represent and predict interactive behaviours. There are three commonly used approaches to representing agent behaviour within microscopic evacuation models: Cellular Automata (CA) [24], Social Forces based models [25,26,27], and rule based models [9,10,11,12, 28, 29]. CA methods have been parallelised across multiple processors [30] but CA methods are particularly well suited to parallelisation on a SIMD (Single Instruction Multiple Data) platform [31] such as a General Purpose Graphical Processing Unit (GPGPU) [30, 32, 33] or a Field Programmable Gate Array (FPGA) [32] due to each grid cell being computed in the same fashion but with different data. However if complex interactions/behaviours are to be represented involving agents utilising information obtained from beyond their immediate vicinity the effectiveness of SIMD parallelism will be affected. Parallelisation can also be applied to social forces based models [34, 35]. In evacuation models utilising the Social Forces approach the movement of agents is governed by equations representing virtual forces within a continuous spatial domain. Social Forces models appear to be very computationally intensive and so can potentially greatly benefit from a parallel implementation. For example, Steffen et al. [35] noted that an evacuation simulation of a stadium involving 20,000 occupants using a parallel implementation of a Social Forces based evacuation model could be performed approximately five times faster than real time using a parallel computer utilising 180 processors.
The work presented in this paper differs from the earlier work on parallelisation of evacuation models by exploring the parallel implementation of a rule based evacuation model. Given the differences in the formulation of rule based evacuation models and the computational costs associated with rule based models compared with CA and Social Force models, it is unclear how effective parallelisation can be for this type of model. Furthermore, most of the earlier parallel implementations were simply concerned with reducing the execution time of the simulation [30, 33, 34] but not necessarily as part of a live incident, where significantly faster than real time performance is required. Two implementations were specifically concerned with running faster than real time for use in a live incident [32, 35]. The Giitsidis et al. [32] model ran on specialist hardware (FPGA) is reported to achieve run times over 107 times faster than real time when applied to a small aircraft carrying 150 passengers. It is unclear, from the available literature, if this model could be extended to simulating larger environments. Steffen et al. [35] demonstrated their parallel social force evacuation model on a sports stadium. The simulation of the stadium evacuation involving 20,000 pedestrians could run approximately in real-time when 24 processors were used and when 180 processors were used could run approximately five times faster than real time.
Before evacuation simulation could be considered useful for real time applications, sufficient speedup over real time must be achieved in order to allow incident managers sufficient time to assess the information and suggest potential mitigation strategies. Even if the management system is automated, sufficient time must be available to implement the alternative strategies and for the alternative strategies to be effective. Thus it is suggested that speedups of at least an order of magnitude (10+ times) over real time would be required before evacuation simulation could begin to be considered useful in real time applications.
There are two potential strategies for parallelisation of the evacuation simulation; these are population decomposition and domain decomposition.
Population decomposition sub-divides the population with each processing thread responsible for a particular population sub-group i.e. an individual will always be simulated by the same processing thread. This approach is potentially attractive on a single multi-core/multi-CPU shared memory (SM) based PC using OpenMP [36] or multithreading. However, extending this approach to a distributed set of computers (i.e. a cluster) has a number of shortcomings. Each computer must accommodate the entire geometry which would restrict the maximum size geometry that could be simulated no matter how many computers were used. Also there is potentially a large amount of interaction between the agents simulated on different computers which may incur additional code complexity and high communication costs between the computers.
Domain decomposition is based on a systematic partitioning of the problem domain (geometry) onto a number of sub-domains (sub-geometries) and is the method generally used in parallelising Computational Fluid Dynamics (CFD) based simulations including fire simulations [37,38,39,40]. Each sub-domain is computed on a separate processor and runs its own copy of the evacuation simulation software. At the boundary of the domain partitions, each sub-domain must communicate with its neighbouring sub-domain to transfer agents from one sub-domain (and therefore computer) to another sub-domain (computer) as they move through the environment. Using this strategy, many computers will potentially be responsible for handling the movement of a particular agent through the environment. This was the strategy adopted in other parallel implementations [30, 32,33,34,35].
In this work a domain decomposition approach is applied to the rule based evacuation simulation software buildingEXODUS [9,10,11,12]. The parallel implementation is implemented on distributed memory cluster computer networks and a series of tests evacuation simulations are used to gauge the real time and computational speedup achieved.
2 Parallel Implementation
The implementation effort required for an advanced egress model can be substantial before considering the parallel processing. It was therefore decided to base the parallel implementation on an existing advanced egress code, buildingEXODUS. buildingEXODUS is a well validated software product and the source code was readily available to the authors.
The buildingEXODUS software has been described many times in the literature [9,10,11,12] and so only a brief description is provided here. EXODUS is a suite of software tools designed to simulate the evacuation of large numbers of people from complex enclosures. The software is a multi-agent simulation environment that utilises a two-dimensional grid of nodes to represent space. The software takes into consideration people–people, people-fire and people-structure interactions. The model tracks the trajectory of each individual as they make their way out of the enclosure, or are overcome by fire hazards such as heat, smoke and toxic gases. The behaviour and movement of each individual agent is determined by a set of heuristics or rules. The spatial grid maps out the geometry of the building, locating exits, internal compartments, obstacles, etc. The grid is made up of nodes and arcs with each node representing a small region of space and each arc representing the distance between each node. Individuals travel from node to node along the arcs.
In creating a parallel implementation of an existing serial code that has a wide international user base there are a number of core requirements that the parallel implementation must satisfy in order to make the parallel version of the software both flexible and easy to adopt by the existing user base. These include the following considerations:
-
There should be no difference between the input or output files for the serial and parallel implementations of the software. This will allow applications to be designed and the results visualised using the familiar serial components of the software.
-
The parallel implementation should work on any number of processors.
-
Minimal additional investment (in time and hardware/software) should be required by the engineer to effectively run the software. The system should work on a conventional set of PCs attached via a standard LAN as well as a dedicated cluster.
-
The parallel implementation is intended to function in a Microsoft Windows environment.
An additional requirement imposed by the software developers was that there should only be one EXODUS source code i.e. separate parallel and serial source codes would not be developed. Having a single software source code is desirable in order to minimise the effort required to maintain the product. Thus the parallel code was developed by modifying the existing serial source code.
There are a number of parallel processing technologies available that include multi-core CPUs, networked computers (e.g. specialised clusters or general office networked computers), GPGPU and FPGA.
Although GPGPU and FPGA coding looks attractive for evacuation simulation [32], due to their impressive performance compared to CPUs, it is difficult to apply to a rule based evacuation model where each agent will follow its own branching path of execution within the software making it unsuitable, at present, for a SIMD type processor [31] which can only perform a single execution branch. Another issue is the complexity of the buildingEXODUS software which has hundreds of thousands lines of code making writing a GPGPU or FPGA version a major undertaking even if it was suitable.
buildingEXODUS software is suitable for a Multiple Instruction Multiple Data (MIMD) [31] style of parallel processing as MIMD systems are able to simultaneously execute multiple execution pathways. Both multi-core CPUs and networked computers are MIMD systems. MIMD systems are able to simulate different branches of execution which is required for the rule-based movement used within buildingEXODUS.
The de-facto Application Programming Interface (API) for distributed parallel processing is MPI (Message Passing Interface) [41] and the version created by Argonne National Laboratory, MPICH2 [42] for Windows, was used to facilitate the parallel implementation. Using this API reduces the amount of programming effort required to make a parallel implementation that works on both multi-core CPUs and networked computers.
2.1 Software Parallelisation Strategy
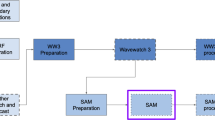
Domain decomposition was the chosen parallelisation strategy for this implementation as it favours the Distributed Memory (DM) model of parallel processing and was the strategy adopted in other parallel implementations [30, 32,33,34,35]. In PC parlance this is a network (or cluster) of PCs linked together via some form of Local Area Network (LAN). It should be further noted that the program written for a DM system would also run on a SM machine removing the need for two separate parallel versions. The decomposition concept is illustrated in Fig. 1 where the domain is simply split into two sub-domains; however the domain can be split into many sub-domains.
The code was designed using the Single Program Multiple Data (SPMD) paradigm. With this methodology only one executable is used and a copy of the executable is launched on each processor which operates on its own part of the problem domain. Typically there is one process that handles the I/O and problem distribution, this is the master process (process 0). The other processes are exactly the same as one another and only differ slightly from the master; the master process was also responsible for visualisation and collection of the results to a single output file.
2.2 Agent Transfer and Movement Across Sub-domain Boundaries
In creating the sub-domains a series of Halo nodes are added to each partition boundary of each sub-domain (see Fig. 1). Essentially, Halo nodes are an additional series of nodes that are added to the partition boundaries of a sub-domain that copy the information stored in the boundary nodes of the adjoining sub-domains. We refer to the additional series of nodes added to the partition boundary as Outer Halo nodes, while the series of nodes within the sub-domain on the partition boundary are called Inner Halo nodes. The Halo nodes are used to pass information between neighbouring sub-domains concerning the movement of individuals between the neighbouring sub-domains as illustrated in Fig. 2. Here the domain has been split into two sub-domains with each sub-domain being placed on a separate computer. Each computer is responsible for performing the computations for the evacuation simulation for the agents who are located on their assigned sub-domain. In the example shown in Fig. 2, the agent is moving from left to right and must transfer from one sub-domain to the other. The movement across sub-domain boundaries can be briefly explained as follows:
-
(a)
In Fig. 2a, the agent is approaching the sub-domain boundary but is currently controlled by the left hand sub-domain (LHSD).
-
(b)
As the agent enters the Inner Halo region of the LHSD (see Fig. 2b), the LHSD now sends a message concerning the agent stood on the Inner Halo node to the right hand sub-domain (RHSD) and the RHSD now creates a copy of the agent on its Outer halo node.
-
(c)
As the agent moves onto the Outer Halo region of the LHSD (see Fig. 2c) this information is sent to the RHSD which updates the agent on its side to move to its Inner Halo region. At this point the agent is now controlled by the RHSD.
-
(d)
In Fig. 2d, the agent now continues its journey on the RHSD and as it moves away from the boundary the LHSD is instructed to delete its copy of the agent as that copy is no longer needed.
2.2.1 Synchronisation
In the above explanation the communication model has been simplified. It is not the case that one computer can simply send a message to another. The communication needs to be arranged to ensure that the appropriate computer is ready to receive a message and the corresponding computer is sending the message. Failure to correctly orchestrate this communication can lead to deadlock. This occurs when both computers are waiting to receive a message from each other but they will wait forever as the message will not be sent until a message is received from the other computer. This was solved by using a convention based on the sub-domain numbering and using partial non-blocking communication. All sub-domains are uniquely labelled 0 to N-1, where N is the total number of sub-domains. This leads to the general case that each sub-domain will have boundaries with both lower and higher numbered sub-geometries.
These boundaries can be classified as low (neighbouring sub-domain has a lower number) and high boundaries (neighbouring sub-domain has a higher number). In order to remain synchronised every sub-domain initiates a ‘receive’ from its low boundaries and simultaneously ‘sends’ update messages to its high boundaries. All boundaries wait until they have successfully received a message from their low boundaries. Once this has been achieved the computers initiates a ‘receive’ from the high boundaries while simultaneously sending update messages to the low boundaries.
2.2.2 Parallel Movement Algorithm
Within EXODUS the overall simulation is governed by the global Simulation Clock which ticks every 1/12 s. On even ticks agents decide what their future actions will be; this is generally a movement towards the nearest exit, on odd ticks the movement is performed [9]. The population is looped over until all the PETs (Personal Elapsed Time) of each of the agents has incremented beyond the Simulation Clock due to a movement to the next node or in congested flows a decision to wait in its current position until the next tick of the global Simulation Clock. The global Simulation Clock keeps ticking until the scenario finishes.
The algorithm for the parallel implementation is essentially the same as that for the serial implementation except that the population is looped over in sub-groups related to their proximity to sub-domain boundaries. These are the high-boundary group, the low-boundary group, and the non-boundary group. The boundary groups are further sub-divided into communication groups and computation groups. A communication group consists of agents that are on the inter sub-domain boundary and consists of agents on the inner and outer halo nodes of a sub-domain. A computation group consists of agents on the inner halo nodes and the neighbouring set of nodes within the sub-domain. The non-boundary computation group consists of all the agents that are not members of a boundary computation group within the sub-domain. This arrangement ensures that agents in the non-boundary group cannot move directly into the high/low boundary communication groups when computation and communication are overlapped in steps 3 and 5 in the algorithm below. In Fig. 3, 4, 5 6 and 7 the computation groups are represented by a dashed line box, a sending communication group is represented by a continuous line box, and a receiving communication group is represented by a dash-dot line box.
Below is the logic used in the parallel movement algorithm, with the additional steps required by the parallel algorithm highlighted in italics (steps 3–7).
-
1.
Simulation Clock is incremented 1/12 s and the ticker is incremented by one tick.
-
2.
If the number of simulation ticks is even then movement options for individuals are calculated then go to 1. Else if the number of simulation ticks is odd, then the selected movement will be performed in steps 3–7, continue.
-
3.
The agents on high boundaries are sent to neighbouring sub-domains whilst at the same time other agents are received on the low boundaries. Whilst the computers wait to receive/send data from one another, members of the non-boundary group are computed for potential movement until this communication is complete. This is illustrated in Fig. 3 . In a previous iteration or time-step agents A and C had been moved to their locations. In the case of agent A this required an update to its position in the lower boundary group. In the case of agent C that moved into the high-boundary communication group a new copy of agent C is created on the j + 1 sub-domain. Agent B in the non-boundary group was computed whilst the communication was taking place.
-
4.
The agents located around the low boundaries of a sub-domain are computed for potential movement. In Fig. 4 agent D is seen to move away from the boundary and will no longer be part of the low-boundary communication group but will be part of the low-boundary computation group. Agent E crosses over to sub-domain j and leaves the low-boundary computation group of sub-domain (j + 1) although it is still a member of the low-boundary communication group of sub-domain (j + 1).
-
5.
The agents on low boundaries are sent to neighbouring sub-domains whilst at the same time the agents are received from high boundaries. Whilst the computers wait to receive/send data from one another, further members of the non-boundary group are computed for potential movement until this communication is complete. In Fig. 5 agent D’s movement is communicated to the high-boundary communication group of sub-domain (j − 1) and is deleted from sub-domain (j − 1). Agent E’s position is communicated from sub-domain (j + 1) to sub-domain j and its positon is updated on sub-domain j. Agent G and F’s movements in the non-boundary group are performed during the communication.
-
6.
The agents located around the high boundaries of a sub-domain are computed for potential movement. In Fig. 6 agent H moves from the high-boundary computation group across the boundary onto the outer halo nodes of sub-domain (j − 1).
-
7.
Any remaining members of the non-boundary group that were not processed during step 3 or step 5 are computed for potential movement. In Fig. 7 it can be seen that various agents of the non-boundary group are moved. At this point agent H has not been updated on sub-domain (j). This update will occur when step 3 of the algorithm is performed again.
-
8.
Due to movement conflicts between agents some of the agents will need to be reprocessed. Go to step 3 until all the remaining agents’ PETs have been incremented.
-
9.
Go to 1 until all the evacuation scenario has finished.
One of the important developments in the parallel implementation of EXODUS was the ability to overlap communication with calculation. This overlapping was critical to obtaining good speedups as without this development the parallel and thus runtime performance would have been significantly poorer. By overlapping the communication and computation the order in which agents are processed can be changed and due to the use of pseudo-random numbers in the software for some decision making meant that no two runs were the same due to the additional randomisation now created by the network. This change in ordering is just as valid as any other particular order but unlike the serial version of EXODUS, the simulation cannot be repeated to give exactly the same result. An exact repeat simulation could be obtained by removing the overlapping of communication and computation at the expense of run time performance; though not generally useful it was helpful to make the software run in this mode for the purposes of development and debugging.
2.3 Decomposition Strategy
The decomposition strategy determines how many sub-domains to create and how the sub-domains should be distributed to the various computers within the cluster/network. A poor decomposition, or partition, can lead to poor load balancing on the computers. This means that some of the computers utilised for parallel processing are under-utilised and therefore the wall-clock time to run the simulation is adversely effected. However, unlike CFD fire simulation, where a single domain decomposition strategy may be appropriate for virtually all fire scenarios, for evacuation simulation, the decomposition strategy is scenario specific. In the worst case scenario, at least in terms of parallel performance, it is possible that the parallel performance will be no better and possibly worse than the serial performance no matter how many computers are used if a poor decomposition is selected.
Consider a simple example involving a rectangular geometry in which there is an exit at either end of the geometry and the population is uniformly distributed throughout the environment. The population is further assumed to be smoothly flowing with no congestion. If each agent moves towards their nearest exit, half the population will move to the exit on the left and half will move to the exit on the right. In this case the ideal partition for a network of two computers would involve simply splitting the domain in half, with one half associated with the left exit and the other half associated with the right exit.
However if the scenario involved the right exit being non-viable, the simple partitioning would be inappropriate as the computer allocated the right part of the domain would have increasingly less work to do as the population progressively moves toward the only viable exit located on the left. A point would be reached when the processor handling the right domain would be idle while the processor handling the left domain would still be working hard.
A simplified analytical calculation of computational performance can be devised if communication overheads and memory access speed are ignored. It is assumed that z agents are uniformly distributed in the domain and travel with the same speed and direction. The length of the domain is l. If a single computer was used to compute the evacuation then the total work performed by that processor is, (number of agents (z)) × (average distance travelled (l/2)), zl/2. In the case of two processors using the decomposition suggested the calculation is split into 2 parts. Whilst the right hand domain is being emptied, into the left hand sub-domain, the work performed by the busy processor is, (number of agents on busy processor (z/2)) × (distance travelled (l/2)), zl/4. The second processor is now idle and the work done in emptying the remaining sub-domain is, (number of agents on busy processor (z/2)) × (average distance travelled (l/4), zl/8. The total work done by the busy processor is therefore 3zl/8. Computational Speedup (S p ) [43] is defined as the time taken to run the simulation on one processor (t 1 ) divided by the time taken to run on P processors/computers (t p ) i.e. S P = t 1 /t p . Assuming that the work done is proportional to the time taken then the maximum computational speedup of two processors over one processor for this decomposition would be 4/3 (1.33).
Another difficulty with this simple partition is that it only applies to two processors and cannot be generalised for any number of processors. If the population was not initially uniformly distributed throughout the domain this would also lead to a computational load imbalance.
These problems can be mitigated by using multiple sub-domains per computer as illustrated in Fig. 8. In this decomposition the diagonally shaded areas are computed on one processor and the crosshatched shaded areas are computed on another. Using this scheme the workload is more evenly balanced. As the population moves toward the exit both processors are generally kept busy, it is only when the geometry has emptied to the last sub-domain that the second processor becomes idle. By generalising the analysis that was performed previously the following analytical computational speedup Eqs. 1 for 2 processors can be obtained when the domain is split into N equal sized sub-domains, where N is a multiple of two.
So if the domain is split into 6 sub-domains as illustrated in Fig. 8 the analytical speedup is 12/7 (1.71) and as N tends to infinity it can be seen that the analytical speedup tends to 2.
This methodology can be extended to using any number of processors and on any arbitrary geometry using any decomposition strategy. For the above partition for two processors the partition can be represented as 121212, if three processors were being used then the partition would be represented as 123123. With this technique the computational load on each computer is kept well balanced and the load is more evenly balanced with more partitions per processor. Equation 1 can be generalised (see Fig. 9) to include any number of processors as well (Eq. 2). The derivation of Eq. 2 and Eq. 5 is described in Appendix A. Equation 2 is used to calculate the analytical computational speedups in case study 2.
where
If K = 0 then Eq. 2 simplifies to the following Eq. 5.
It can be seen from this particular example (Eq. 5) that speedup improves as the number of sub-domains increases. Equation 5 is not generally applicable but illustrates the advantage of the multiple sub-domains per processor decomposition strategy.
However the disadvantage of this technique is the increase in communications and hence communication costs associated with an increasing number of sub-domains. The increasing cost is due to the increase in the number of sub-domain boundaries which require agents to be transferred across. This communication has an overhead and there will be a point where the advantage of better computational load balance is outweighed by the extra communication cost. There is therefore an optimal number of sub-domains which will give a peak speedup performance. This balance between better load balancing that is achieved by having more sub-domains, the number of processors utilised and the communication overhead is explored later in case study 2. The general strategy used is to have multiple sub-domains per processor that are distributed in such a way as to even out the work load throughout the simulation.
3 Case Studies
To demonstrate the parallel implementation four different cases were examined (see Table 1). It is not the intention of these demonstration cases to provide any substantive analysis of evacuation behaviour but to demonstrate the performance improvements possible using the parallel implementation of buildingEXODUS. The first two cases are theoretical in nature and have been designed to gain a greater understanding of the performance of the parallel implementation. The second two cases are based on realistic scenarios; a high-rise building and a large public gathering in a large urban space. Earlier results produced by a prototype implementation of the parallel buildingEXODUS [44] have been improved using the latest version of the parallel implementation described in this paper.
The cases demonstrated here have been tested on a 64bit-Windows cluster consisting of 10× Intel Core 2 Duo (dual core) 3.16 GHz based computers connected via a 1Gbit Ethernet switch.
The software is stochastic in nature and needs to be run a number of times, generating a distribution of predicted evacuation times, which would also result in a small distribution of runtimes. However, for the purposes of this demonstration work only, the software was configured to operate in a deterministic manner. Thus, in situations where some movement decisions/conflicts are sometimes determined by random selection, they have been resolved in a deterministic manner. This was done to eliminate variability between simulations. This would further ensure that the runtimes of the simulations were consistent. Each case study configuration was run three times and it was found that there was less than a second difference in runtime for any particular configuration. The predicted evacuation time for each case study was identical across the serial and parallel configurations.
The results have been split into single core and dual core results. It has been found in previous work that better speedups are obtained on two single processors connected via a network compared to two processors (cores) on a shared memory machine [38, 39]; typically dual cores operate at a computational speedup of 1.7–1.9 compared to a single core. This effect is due to memory bus contention on the shared memory computer with both processes trying to simultaneously access the single memory bus within the computer. However, in some cases this memory bus contention is so high that the use of two processors in a shared memory computer produces little, if any, speedup compared to a single processor.
In the remainder of this paper two types of speedup will be discussed; these are computational speedup and real-time speedup. Computational speedup compares the run time of the parallel implementation against the serial or single processor run time [36]. Real-time speedup, or speed up over real time, compares the run time of the parallel or serial implementation of the software against the time required to complete the evacuation as predicted by the software. More detailed tables of results are available in Appendix B.
3.1 Case 1: Idealised Large Geometry
This test case is intended to represent an ideal case for the parallel implementation. It has been designed so that there is no sub-domain boundary interaction and that the problem is well load balanced throughout the entire simulation. This test was devised to explore the upper limits of speedup potential possible with parallel buildingEXODUS.
The geometry is 4000 m long and 25 m wide producing an area of 100,000 m2. There are twenty 5 m wide exit points located along one side of the geometry, each separated by 200 m with the first and last exits being 100 m from each end of the geometry. A population of 100,000 agents (1 person/m2) is uniformly distributed throughout the domain and move towards their nearest exit point.
In order to ensure the most optimal decomposition the domain is split into 20 equal sub-domains (each sub-domain has 5000 agents) and these are allocated to each processor by taking the modulus of the sub-domain number with the total number of processors used. Due to the layout of the geometry the population does not have to cross between processor boundaries to reach an exit point.
The following configurations were used to test the speedup potential: 1, 2, 3, 4, 5, 7 and 10 single cores; 1, 2, 3, 4, 5 and 10 dual cores. Configurations that have not been represented here would not give any speedup improvements on the configurations that have been simulated. For example with 5 (single core) computers each computer would have 4 sub-domains to process; if 6 (single core) computers were utilised then 4 computers would have 3 sub-domains but 2 computers would have 4 sub-domains and this would be limit the speedup to being the same as 5 (single core) computers. The analytical computational speedup in this instance is calculated by dividing the total number of sub-domains by the maximum number of sub-domains residing on any individual processor. The predicted evacuation time for this scenario was 14 min 26 s and was consistent across all the parallel simulations and the serial version of buildingEXODUS. The computational speedup for the various permutations are presented in Fig. 10.
An impressive computational speedup of 10.9 was achieved using 10 computers compared to a single computer. An examination of all the single core results shows that a super-linear speedup, a speedup greater than the number of processors, is achieved for all the configurations. It is difficult to say precisely why a super-linear speedup has resulted, but could be due to hardware effects [45, 46], such as the increase in overall processor cache size.
The maximum computational speedup of 13.9 achieved with 10 dual core computers is less than the analytical speedup of 20. The analytical speedup is based on the premise that doubling the processor/core count would double the speedup. This ignores the inter-processor communication cost and also the effect of cores sharing the memory bus when the computer is utilising dual cores. These speedups are good and are unlikely to be achieved for most practical scenarios. They do however demonstrate a peak performance that can be achieved from this type of application.
In a real scenario near peak performance will be achieved in the initial stages of the simulation as there is likely to be a good load balance due to the initial population distribution being reasonably uniform. However, as the simulation progresses it is expected that the parallel efficiency will decrease as the load becomes unbalanced due to the movement of people.
It is also worth noting that on a single processor the simulation was some 3.5 times slower than real time for this particular simulation i.e. on a single processor the run time was 3.5 times slower than the time required for the actual evacuation. However, using 10 dual core processors produced a real-time speedup of 4.
3.2 Case 2: Long Open Area
This scenario consists of 100,000 agents in an open rectangular geometry measuring 100 m by 1000 m producing an area of 100,000 m2 resulting in a crowd density of 1 person/m2. The crowd moves to the left to exit the geometry. The left side of the geometry is completely open, creating a 100 m wide exit. This case can be considered as a realisation of the analytical study in Sect. 2.3.
The geometry was sliced into N equally sized sub-domains in the same fashion as illustrated in Fig. 9. For this case the domain was split into 20, 50 and 100 sub-domains respectively. Each of these partitions was examined using 1–10 computers in both single and dual core processor modes and this resulted in 60 total permutations for this one case.
The predicted evacuation time for this geometry is 14 min 20 s. This predicted time was consistent across the various parallel implementations and with the serial version of buildingEXODUS.
This particular simulation was designed to represent a non-congested exit flow thus leading to a short overall predicted evacuation time with minimal computational requirements. The computational speedup for single and dual core configurations are depicted in Fig. 11. The analytical speedup is calculated using Eq. 2.
Theoretically 100 sub-partitions should give the best speedup performance for all the possible permutations due to the best load balance being maintained throughout the simulation. In practice there are other factors that influence the performance including the cost of communication, which increases with additional sub-domains, and hardware effects such as increased cache size and, in the case of multi-cores, a shared memory bus. The use of a shared memory bus and increasing communication cost both reduce the actual performance from the analytical prediction. Conversely the increased cache size made available by increasing the number of computers improves the performance beyond the analytical prediction. The actual speedup performance is therefore a combination of the load balance and these other factors. When two computers are used, either in single or dual core mode, the best partition is 20 sub-domains for this particular problem. This is due to the analytical load balance being comparable to the other partitions but the communication cost is far lower than the partitions with a higher number of sub-domains. As the number of processor/cores is increased there is a greater divergence between the analytical speedups and therefore load balances. When 10 dual core computers are used the disadvantage of increased communication for the 100 sub-domain partition compared to the 20 sub-domain partition is far outweighed by the improved load balance achieved.
The run time for a single core is 1.2 times faster than the predicted evacuation time. The real-time speedup for 10 dual core processors using the 100 sub-domain partition is 17.2. Additional processors should further improve the speedup.
3.3 Case 3: High-Rise Building
The high-rise building scenario consists of 50 floors with four emergency exit staircases and a floor area for each floor of 1800 m2. The staircases are not equally spaced within the building core leading to some of the staircases attracting more people than others. This test case was run with two population sizes of 8000 agents (160 people per floor) and 16,000 agents (320 people per floor) that were uniformly distributed throughout the building on each floor. Unlike the previous case, this scenario involves a great deal of congestion as agents attempt to gain access to the stairs and as they traverse down the stairs. The predicted evacuation time for this case was 50 min for 8000 agents and 1 h 30 min for 16,000 agents.
The partitioning strategy adopted for this high rise building was based on dividing the building into 25 sub-domains vertically i.e. two floors per sub-domain. These sub-domains are then divided horizontally into four quadrants of equal floor area with a staircase associated with each quadrant. In total there were 200 sub-domains used in the analysis.
The computational speedup obtained for both the single core and dual core processors are presented in Fig. 12. We note that the computational speedup produced for the 16,000 agent population is significantly higher than the 8000 population. Clearly, the performance of the parallel implementation improves with increasing problem size. This is a well-known phenomenon with most parallel processing problems where the speedup performance improves with increasing problem size [47]. This is due to the relative decrease of communication time with increasing computation size; this decrease is partly attributable to the fact that network communications have a fixed start-up cost in addition to the cost of sending the actual data. For this particular problem it is also related to the fact that increasing the population size by a factor of two will approximately increase the communication cost by a factor of two. However, the computational cost has increased by a factor of 4.5 due to the increased congestion.
We also note from Fig. 12 that the performance for the 8000 population has tailed off as more processors are added to the cluster, with no improvements being derived from adding more than eight processors to the cluster. However, for the 16,000 population further improvements in performance could be derived by adding additional computers (single core) to the cluster beyond 10, but the return gained from adding additional computers is diminishing.
Using 8 single core computers, the evacuation of the 8000 population can be simulated in 2 min 48 s. The predicted evacuation time is 50 min 7 s. This represents a real-time speedup of 17.9. The 16,000 population requires 1 h 30 min to evacuate and using 10 processors the evacuation can be simulated in just over 7 min, representing a real-time speedup factor of 12.9.
From Fig. 12 it is noted that the dual core simulations can return poorer performance than the single core simulations. Furthermore, unlike the single core simulations, the speedup reaches a peak for the 8000 population with 7 processors and 8 processors for the 16,000 population. Adding additional computers beyond these critical values actually diminishes performance. As noted earlier, the performance of the parallel implementation improves with increasing problem size. As the dual core computers have a greater computational performance, they require a larger problem size to make better use of the number of computers available in the cluster.
3.4 Case 4: Large Urban Space
This case study is a rough approximation of the Trafalgar Square public area in central London, UK. The usable pedestrian area measures approximately 46,000 m2 and there are 14 exit routes from the domain (see Fig. 13).
Two scenarios were created by populating the domain with 60,000 agents (1.3 p/m2) and 120,000 agents (2.6 p/m2). Unlike the other test cases the agents were assigned exit points prior to the evacuation leading to more congestion than might be expected from a more usual scenario where individuals leave via their nearest exit point. The exit allocation is roughly proportional to the size of each exit and the individuals allocated to a particular exit are randomly located in the domain. The exit allocation used in this study is not intended to be an accurate representation of actual behaviour in large urban places but is simply used to test the parallel implementation when agents will be contra-flowing and not simply exiting by their ‘nearest’ exit.
The predicted overall evacuation time for 60,000 people is 10 min 27 s, and for 120,000 people is 21 min 49 s. It should be noted due to the lack of real data and hypothetical exiting conditions for the individuals that no firm conclusions should be drawn concerning the evacuation of Trafalgar Square from these simulations. This test case is purely designed to investigate the performance of the parallel implementation on a large urban space.
For this case the Metis [48] partitioning algorithm was utilised along with multiple sub-domains per processor. Metis is generally used for partitioning computational grids used in Computational Fluid Dynamics (CFD) and Finite Element Analysis (FEA) for parallel processing. Metis divides the domain into a number of sub-domains whilst minimizing the size of the sub-domain boundaries. For this case 10, 20, and 32 sub-domains were created. An example partition is illustrated in Fig. 13, where each coloured region represents each of 20 sub-domains within the partition and each coloured sub-domain was allocated to one of five computers.
A visualisation of the evacuation of 60,000 agents is provided in Fig. 14 at 3 time slices and the congestion at a number of junctions is clearly shown. The computational speedups for parallel buildingEXODUS on this test case are depicted in Fig. 15 for a population sizes of 60,000 and 120,000 agents. Results for dual cores are limited to 10 dual core processors due to time constraints and hardware availability.
While the performance derived from using 20 partitions with single cores appears erratic it does produce the overall best single core performance for 60,000 agents returning a speedup of 4.73 from 10 processors. Clearly, as in Case 2, the performance is dependent on the number of partitions used. Using the dual core processors and 20 partitions a speedup of 5.3 from 10 processors is achieved.
It should be noted that the single processor performance is essentially equivalent to real time i.e. it takes as long to compute the evacuation as it does to actually perform the evacuation. Using 10 single core processors with 20 partitions, the run time is some 4.8 times faster than real time and runs in just over 2 min.
From Fig. 15 we note for the single core simulations, as the number of processors increases, the speedup also increases. Using 10 dual core processors with 20 partitions, the run time is some 5.31 times faster than real time and runs in just under 2 min.
Using the best partition suggested by the study involving the population of 60,000 individuals the 20 sub-domain case was re-run using a population size of 120,000 agents.
As is expected, the larger problem size produces a greater computational speedup. Using single cores, the run time on a single processor is more than twice as long as the predicted evacuation time. However, using 10 single core processors produces a speedup of 5.94 resulting in 10 single core processors running 2.6 times faster than real time. Using 10 dual core processors the speedup is a factor of 6.89 on the single core processor time. This results in the 10 dual core processors running 3 times faster than real time.
In Fig. 15 there is an uncharacteristic drop off in performance for nine processors when 20 sub-domains are used. This is due to the nature of the distribution of sub-domains on the computers. It is likely that one or two computers are substantially busier than the rest of the computers due to a poor load balance at some stage of the simulation. Although this result is notable it can be seen that the multiple sub-domains per processor is at least partially successful in maintaining speedup on this non-idealised scenario where it is not possible a priori to determine where the population load balance would exist.
4 Discussion
In all cases, the results suggest that better performance, in terms of greater speedups and reduced run times could be achieved by adding additional processors however; there is a practical limit to the improved performance that can be achieved. This limit in performance is dependent on the complexity of the problem, the domain decomposition, the problem size, the computing hardware, and the networking. More complex problems tend to perform poorly compared to simpler problems. The domain decomposition is a compromise between minimising communication, e.g. less sub-domains, and increasing load balance, e.g. more sub-domains. Larger population sizes tend to return better computational performance compared to smaller population sizes on the same domain, although smaller population sizes are more likely to return higher real-time speedups. Faster computing hardware although likely to return improved real-time speedup is likely to return a poorer computational speedup when compared to slower computing hardware. More “distributed” processors tend to perform better than the equivalent “shared” processors. Faster networking will improve both computational and real-time speedups.
Examining the cases performed it can be seen that computational speedup generally improves with larger numbers of agents. This can be seen for case 3 and 4 where that the computational speedup improves particularly for case 3 when the population size is doubled. For case 3 the load balance should be close to ideal but is not realised due to the comparatively high communication costs compared to the amount of computation. When the population is doubled the amount of computation (time taken) increases by a factor of 4.5 for case 3. This is due to the increase in congestion that needs to be resolved when there are higher population densities. The total evacuation time increases by a smaller factor, and therefore means that although the computational speedup has significantly improved, the real time speedup will be reduced in this case. For case 4 there is less of an improvement as the computational speed up highly influenced by the poor load balance in that instance.
Increasing the number of partitions will generally lead to an improved load balance when the movement of agents is ‘predictable’ as seen in case 2. When the workload is unpredictable, as in case 4 due to the high level of contra-flow, then increased partitioning will not always lead to a better load-balance. From the single core results it can be seen that no particular partition is substantively better than the others. The assignment of sub-domains to processors did not take into account the relative computational loads on the sub-domains. It was not possible a priori to determine how to optimally distribute these sub-domains amongst the processors. In addition to this the size, shape and location of the sub-domains was not optimised with regard to the load-balance.
As the number of processors increases the computational speedup generally increases although there is a diminishing return with an increased number of processors evident for case 3. It is apparent that the computational speedup increases with the number of processors but there needs to be a sufficient population size to offset the necessary communications. For case 4 there is a significant dip in computational speedup for 9 processors when 120,000 agents are simulated. As was previously mentioned the assignment of sub-domains to processors does not take into account the workload of each sub-domain and has resulted in a particularly poor load balance in this instance.
Although the strategy of multiple sub-domains per processor has been somewhat successful it can be seen that for case 4 additional work is needed on the partitioning strategy to improve the computational speedup. Apart from possibly improving the intitial partition some form of dynamic load balancing is required that can optimise the workload, per processor, whilst the scenario is running. Dynamic load balancing has been performed in parallel processing for a range of problems, e.g. fire modelling [39]. The dynamic load balancing could either be performed by: a) reassigning sub-domains from an initially defined partition dependent on population/workload distribution or b) the entire partition could be recalculated dependent on the evolving population/workload distribution.
While the computational speedup is of some interest, the most important consideration is the wall clock time or run time. How long it takes to run an evacuation simulation is one of the key considerations which will determine how practical it is to use in applications such as an advice tool for incident commanders for large building based scenarios, as part of an interactive emergency signage system, a training tool in an interactive desk top environment and as a planning tool for large scale urban applications.
The performance enhancements achieved by the parallel implementation on the various test cases are summarised in Table 2. As can be seen the performance of the parallel implementation is complex and dependent on the type of problem being addressed.
Computational speedups (parallel performance over single processor performance) ranging from 2.5× to 13.9× were achieved while real-time speedups (parallel performance over real-time) of 3.0× to 17.9× were achieved for the various problem types. Indeed, Case 3—50 floor high-rise building with 8000 agents—returned the worst computational speedup (2.5×) but returned the best speedup over real-time (17.9×).
Some of the problems represent very large cases and are extremely computationally demanding, requiring moderately long real evacuation times with single processor execution times equal to or exceeding real evacuation times. These are Case 1 (idealised large geometry case) and the Case 4 (large urban space). For these problems, it is very difficult to achieve high real-time speedups because the single processor performance is already significantly slower than real-time. For example, in Case 1, the single processor performance is 3.5× slower than real-time while in Case 4, the single processor performance is 2.3× slower than real time. These cases will produce very good computational speedups (13.9× and 6.9× for Case 1 and 4 respectively), but relatively poor real-time speedups (3.9× and 5.3× for Case 1 and 4 respectively). Thus for these applications, the parallel implementation is very useful for an engineer using the software as part of a design analysis as it reduces the time required to run the simulations but it is not very useful for real-time applications which require the software to run many times faster than real-time.
Other problems represent large real cases but are less computationally demanding, requiring very long real evacuation times with single processor execution times less than real evacuation times. These are Case 3a and Case 3b (high-rise building with 8000 and 16,000 agents). For these problems, it is easier to achieve high real-time speedups as the single processor performance is already faster than real-time. For example, the single processor performance in Case 3a is 2.3× faster than real-time while in Case 3b it is 2.9× faster than real-time. These cases produced relatively poor computational speedups (2.5× and 4.5× for Case 3a and 3b respectively), but relatively good real-time speedups (17.9× and 12.9× for Case 3a and 3b respectively). Thus these types of cases lend themselves to live applications where it is essential that computation be performed much faster than real-time e.g. dynamic signage or live incident support.
The results obtained from the idealised cases, cases 1 and 2, suggest that much better speedups could have been obtained for the case 3. Case 2 is of particular interest as it demonstrates the balance between computation vs communication. Case 2 has a high amount of communication but it does not highly impact the performance of the parallel implementation on the hardware configuration used here and is probably due to the successful overlapping of communication and computation. It also indicates that the relatively poor computational speedups seen in case 4 are due to poor load balance rather than communication cost.
While the parallel implementation has achieved significant performance gains, further gains in the real-time performance of the buildingEXODUS software are desirable and indeed achievable. These performance enhancements can be categorised into hardware and software improvements. Hardware based improvements include, using faster computers, more computers, and the possibility of using better networking technology. The networking technology used in the current implementation utilises standard equipment and as such suffers from comparatively high network latency. The use of specialist network cards and switches could improve the speedup performance by reducing the latency in the communications. Improved data transfer speeds, achieved by for example using high-speed optical fibre cables, can also enhance the parallel performance by improving the bandwidth between processors. The main disadvantage of this approach is the comparatively high price associated with the equipment compared to conventional equipment.
Software based improvements include serial algorithmic changes, utilisation of ‘hybrid discretisation’ [19], improved partitioning strategies and dynamic load balancing. It is possible that further improvements can be made to the serial version of buildingEXODUS that would increase the runtime performance of the software which would feed into the parallel implementation of buildingEXODUS.
Although this paper has focused on the buildingEXODUS evacuation software most of the technology could be utilised by other evacuation models. The multiple sub-domains per processor approach is very generalizable and the derived analytical expressions could be useful for model developers testing their own software. The concept of halo regions could be used for CA based models and continuous models. The movement algorithm and the use of boundary and non-boundary proximity groupings of agents could also be adapted.
5 Conclusion
A parallel implementation of the rule based evacuation simulation software buildingEXODUS using the technique of domain decomposition has been achieved and successfully demonstrated in a range of application cases from simple unidirectional motion to large complex buildings and open spaces. The computational speedups derived using a 10 processor system over the performance of a single processor varied from 2.5× to 13.9×, with real-time speedups varying from 3.0× to 17.9×.
In all cases examined improved performance, in terms of enhanced speedups and reduced run-times could be achieved by adding additional processors however; there is a practical limit to the improved performance that can be achieved. This limit in performance is dependent on the complexity of the problem, the domain decomposition, the problem size, the computing hardware, and the networking.
The complexity of the problem both in terms of geometry and agent behaviour will tend to have improved computational speedup with decreasing complexity. Good parallel performance seen with simpler problems may not necessarily be repeated on more complex problems.
The domain decomposition affects the parallel performance, both in terms of computational speedup and real time speedup, generally improves with the number of partitions as this generally improves the load balance across processors. However, this can be affected by the complexity of the movement behaviour of the agents. Where agent movement is not known a priori but evolves due to the nature of the simulation simply increasing the number of partitions may not necessarily lead to improved speedup.
The size of the problem affects the parallel performance, in terms of computational speedup, which generally increases with the number of agents. However, real time performance may decrease in situations where the increase in the number of agents leads to an increase in the population density.
The computing hardware will affect the performance. Generally a more “distributed” computer system will offer a higher parallel performance than an equivalent less distributed system. For example 2 networked single cores provide a greater performance than a single dual core computer. This is due to the increase in cache and memory bandwidth offered by the more distributed systems. All modern CPUs are now multicore but it would be better to have a distributed set of multicore CPUs rather than a set of multicore CPUs on a single computer.
The networking hardware is significant as communications between sub-domains is a critical factor in determining parallel performance, it is suggested that the faster the communications between CPUs the better the parallel performance. Thus the faster the networking and the lower the latency within the cluster, the better will be the parallel performance.
Unfortunately, even with good computational speedup the real-time speedup could be insufficient for real-time applications. In cases where significant real-time speedups cannot be significantly increased through enhanced hardware (more processors, faster processors and faster networking) then other methods will be required to increase the real-time speedup. This could be achieved by optimising the software and using hybrid strategies that mix coarse and fine modelling techniques.
For innovative evacuation model application areas such as dynamic signage in smart buildings, real-time incident support and virtual training environments, it is suggested that real-time speedups of at least an order of magnitude must be achieved before they can be considered viable. Parallel computing approaches demonstrated in this paper have generated up to an 18 fold real-time speedup for some problems. This approach, together with improved algorithms and improved hardware performance offers a means to address these novel applications.
Furthermore, from the cases studied in this paper (particularly case 4), it is suggested that to achieve even better parallel performance requires improving the load balancing across the processors. This would need to incorporate a dynamic load balancing algorithm as the work load is continuously varying over time.
References
Gwynne S, Galea ER, Owen M, Lawrence PJ, Filippidis L (1999) A review of the methodologies used in evacuation modeling. Fire Mater. 23(6):383–389. Doi:10.1002/(SICI)1099-1018(199911/12)23:6<383::AID-FAM715>3.0.CO;22
Kuligowski ED, Peacock RD, Hoskins B L (2010) A review of building evacuation models, 2nd edn. National Institute of Standards and Technology (NIST). Technical note 1680, November 2010.
Qureshi WS, Ekpanyapong M, Dailey MN., Rinsurongkawong, S., Malenichev, A., Krasotkina, O., “QuickBlaze: Early Fire Detection Using a Combined Video Processing Approach”, Fire Technol (2016) 52: 1293. doi:10.1007/s10694-015-0489-7
Beji T, Verstockt S, Van de Walle R, Merci B (2014) On the use of real-time video to forecast fire growth in enclosures. Fire Technol 50:1021. doi:10.1007/s10694-012-0262-0
Miller-Hooks E, Krauthammer T (2007) An intelligent evacuation, rescue and recovery concept. Fire Technol 43: 107. doi:10.1007/s10694-006-8433-5
Cowlard A, Jahn W, Abecassis-Empis C, Rein G, Torero J L (2010) Sensor assisted fire fighting. Fire Technol 46: 719. doi:10.1007/s10694-008-0069-1
Han L, Potter S, Beckett G et al (2010) FireGrid: An e-infrastructure for next-generation emergency response support. J Parallel Distrib Comput 70(11):1128–1141. doi:10.1016/j.jpdc.2010.06.005. ISSN 0743-7315
Galea ER, Xie H, Lawrence P (2016) Intelligent active dynamic signage system: bringing the humble emergency exit sign into the 21st century, SFPE Europe, Q1, Issue 3, 2016. http://www.sfpe.org/general/custom.asp?page=Issue3Feature1
Galea ER, Galparsoro JMP (1994) A computer based simulation model for the prediction of evacuation from mass transport vehicles. Fire Saf J 22:341–366. doi:10.1016/0379-7112(94)90040-X
Gwynne S, Galea ER, Lawrence PJ (2001) Filippidis L (2001) Modelling occupant interaction with fire conditions using the buildingEXODUS evacuation model. Fire Saf J 36:327–357. doi:10.1016/S0379-7112(00)00060-6
Gwynne S, Galea ER, Lawrence PJ (2006) The introduction of social adaptation within evacuation modelling. Fire Mater 30(4):285–309. doi:10.1002/fam.913
Galea ER, Sharp G, Lawrence PJ, Holden R (2008) Approximating the evacuation of the world trade center north tower using computer simulation. J Fire Prot Eng 18 (2):85–115. doi:10.1177/1042391507079343
Helbing D, Mukerji P (2012) Crowd disasters as systemic failures: analysis of the Love Parade disaster. EPJ Data Sci 1:7 1–40. doi:10.1140/epjds7
Pretorius M, Gwynne S, Galea E (2012) The collection and analysis of data from a fatal large-scale crowd incident. In: Proceedings of the 5th international symposium, human behaviour in Fire 2012, Cambridge UK, 19–21 Sept 2012, Interscience Communications Ltd., pp 263–274. ISBN: 978-0-9556548-8-6, 2012.
Helbing D, Johansson A, Al-Abideen HZ (2007) The dynamics of crowd disasters: an empirical study. Phys Rev. doi:10.1103/PhysRevE.75.046109
Gwynne SMV, Siddiqui AA (2013) Understanding and simulating large crowds. In: Traffic and granular flow ‘11, 2013, conference proceedings. Springer-Verlag Berlin Heidelberg, Berlin Heidelberg, Germany, pp. 217–239. ISBN: 9783642396687
Benedictus L (2015) Hajj crush: how crowd disasters happen, and how they can be avoided. The Guardian, 3 Oct 2015. https://www.theguardian.com/world/2015/oct/03/hajj-crush-how-crowd-disasters-happen-and-how-they-can-be-avoided. Accessed 3 Jan 2017
Lovreglio R, Ronchi E, Maragkos G, Beji T, Merci B (2016) A dynamic approach for the impact of a toxic gas dispersion hazard considering human behaviour and dispersion modelling. J Hazard Mater 318:758–771. doi: 10.1016/j.jhazmat.2016.06.015. ISSN 0304-3894
19.Chooramun, N., Lawrence, P.J., Galea, E.R., “An agent based evacuation model utilising hybrid space discretisation”, Safety Science, Vol 50, pp 1685-1694, 2012. doi:10.1016/j.ssci.2011.12.022
Hoogendoorn SP, Bovy PHL (2002) Normative pedestrian behaviour theory and modelling. In: Proceedings of the 15th international symposium on transportation and traffic theory, 2002
Lovreglio R (2016) Modelling decision-making in fire evacuation using the random utility theory. Ph.D. thesis, Politecnico di Bari, Milan and Turin (Italy)
Vassalos D, Kim H, Christiansen G, Majumder J (2001) A mesoscopic model for passenger evacuation in a virtual ship-sea environment and performance-based evaluation’, pedestrian and evacuation dynamics— 4–6 Apr 2001, Duisburg, pp 369–391. ISBN: 3-540-42690-6
Kostreva MM, Lancaster LC (1998) A comparison of two methodologies in HAZARD I fire egress analysis. Fire Technol (1998) 34:227. doi:10.1023/A:1015345923210
Kirchner A, Klüpfel H, Nishinari K, Schadschneider A, Schreckenberg M (2002) Simulation of competitive egress behaviour. Phys A 324:689–697. doi:10.1016/S0378-4371(03)00076-1
Helbing D, Molnar P (1995) Social force model for pedestrian dynamics. Phys Rev 5:4282–4286. doi:10.1103/PhysRevE.51.4282
Chraibi M, Seyfried A, Schadschneider A (2010) Generalized centrifugal-force model for pedestrian dynamics. Phys Rev E 82(4 pt 2):046111. doi:10.1103/PhysRevE.82.046111
Gao Y, Chen T, Luh PB, Zhang H (2016) Modified social force model based on predictive collision avoidance considering degree of competitiveness. Fire Technol. doi:10.1007/s10694-016-0573-7
Waterson NP, Mecca A, Wall JM (2004) Evacuation of a multilevel office building: comparison of predicted results using an agent-based model with measured data. In: Interflam 2004: 10th international fire science and engineering conference, Edinburgh, UK, 2004, pp 767–772.
Fang ZM, Song WG, Zhang J, Wu H (2012) A multi-grid model for evacuation coupling with the effects of fire products. Fire Technol 48: 91. doi:10.1007/s10694-010-0173-x
Zia K, Farrahi K, Riener A, Ferscha A (2013) An agent-based parallel geo-simulation of urban mobility during city-scale evacuation. Simulation: transactions of the society for modeling and simulation international, May 2013, pp 1–31. doi:10.1177/0037549713485468
Duncan R (1990) A survey of parallel computer architectures. Computer 23(2):5–16. doi:10.1109/2.44900
Giitsidis T, Dourvas NI, Sirakoulis GC (2015) Parallel implementation of aircraft disembarking and emergency evacuation based on cellular automata. Int J High Perform Comput Appl. doi:10.1177/1094342015584533
Chen D, Wang L, Zomaya AY, Dou M, Chen J, Deng Z, Hariri S (2015) Parallel simulation of complex evacuation scenarios with adaptive agent models. IEEE Trans Parallel Distrib Syst 26(3):847–857. doi:10.1109/TPDS.2014.2311805
Quinn MJ, Metoyer RA, Hunter-Zaworski K (2003) Parallel implementation of the social forces model. In Galea ER (ed) Proceedings of 2nd international pedestrian and evacuation dynamics conference. CMS Press, Greenwich, UK, pp 63–74. ISBN: 1904521088
Steffen B, Kemloh U, Chraibi M, Seyfried A (2011) Parallel real time computation of large scale pedestrian evacuations. In: Iványi P, Topping (BHV) (eds) Proceedings of the second international conference on parallel, distributed, grid and cloud computing for engineering, Civil-Comp Press, Stirlingshire, UK, paper 95. doi:10.4203/ccp.95.95
Dagum L, Menon R (1998) OpenMP: an industry standard API for shared-memory programming. IEEE Computat Sci Eng 5(1):46–55. doi:10.1109/99.660313
Galea ER, Ierotheou C (1992) Fire field modelling on parallel computers. Fire Saf J 19(4):251–266. doi:10.1016/0379-7112(92)90008-Z
Grandison AJ, Galea ER, Patel MK, Ewer J (2003–2004) The development of parallel implementation for a CFD based fire field model utilising conventional office based PCs. J Appl Fire Sci 12(2):137–157. doi:10.2190/AGH5-EXUR-J110-HPHE
Grandison AJ, Galea ER, Patel MK, Ewer J (2007) Parallel CFD fire modelling on office PCs with dynamic load balancing. Int J Numer Methods Fluids 55:29–39. doi:10.1002/fld.1278
McGrattan K, Hostikka S, McDermott R, Floyd J, Weinschenk C, Overholt K (XXXX) Fire Dynamics simulator user’s guide. NIST special publication 1019, 6th edn. doi: 10.6028/NIST.SP.1019
Message Passing Interface Forum (2015) MPI: a message-passing interface standard, version 3.1. High Performance Computing Centre Stuttgart, 2015, EAN: 1114444410030
Gropp W, Lusk E, Doss N, Skjellum A (1996) A high-performance, portable implementation of the MPI message passing interface standard. Parallel Comput 22:789–828. doi:10.1016/0167-8191(96)00024-5
Amdahl GM (1967) Validity of the single-processor approach to achieving large scale computing capabilities. In: Proceedings of AFIPS, pp 483–485. doi:10.1145/1465482.1465560
Grandison A, Muthu Y, Lawrence P, Galea E (2007) Simulating the evacuation of very large populations in large domains using a parallel implementation of the buildingEXODUS evacuation model. In: Proceedings of the 11th international fire science & engineering conference, Interflam 2007, 3–5th Sept 2007, Royal Holloway College, University of London, UK, vol 1, pp 259–270. ISBN: 978 0 9541216-8-6
Nagashima U, Hyugaji S, Sekiguchi S, Sato M, Hosoya H (1995) An experience with super-linear speedup achieved by parallel computing on a workstation cluster: Parallel calculation of density of states of large scale cyclic polyacenes. Parallel Comput 21(9):1491–1504. doi:10.1016/0167-8191(95)00026-K
Helmbold DP, McDowell CE (1989) Modeling speedup(n) greater than n. 1989 international conference on parallel processing proceedings, vol III, pp 219–225.
Johnson SP (1992) Mapping numerical software onto distributed memory parallel systems. Ph.D. thesis, University of Greenwich
Karypis G, Kumar V (1998) Multilevel k-way partitioning scheme for irregular graphs. J Parallel Distrib Comput 48(1):96–129. doi:10.1006/jpdc.1997.1404
Acknowledgements
The authors acknowledge the UK Home Office CBRN Science and Technology Programme for financial support enabling the development of the concept for the parallel implementation of the buildingEXODUS evacuation software.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Derivation of Analytical Speedup performance for Case Study 2 with N sub-domain and P processors
A long area with exiting on the left open side of the domain is considered. It is assumed that the domain is split into N equally sized sub-domains and are assigned to P processors as illustrated in Fig. 16. It is assumed that N ≥ P. It is assumed that all agents travel with the same speed and flow out of the left hand side with no congestion. The agents are uniformly distributed throughout the domain. There are assumed to be no communications cost involved in moving the occupants to the neighbouring sub-domain.
By considering that processor 1 (controlling the solid black sub-domains in the figure below), will always be running at 100% and assuming the processor throughput is independent of memory access patterns it is possible to calculate the amount of work performed by that processor. In this analysis let:
l = length of the domain; z = the total initial population size; N = the number of sub-domains; P = the number of processors.
1.1 Simplified Derivation
In this initial analysis it is assumed that N is an integer multiple of P to simplify the derivation. Therefore there are N/P regions consisting of P sub-domains labelled 1 to P.
The work performed by processor 1 whilst area (a) is emptied is the number of agents being computed by processor 1 × (distance travelled by an agent) this is represented by:-
Work to empty region i = 1 is:
First part of Eq. (7) is emptying from P to 2 in region i = 1 (or N to N − P + 2), the second part represents emptying sub-domain 1 (or N − P + 1) in region i = 1.
For i = 2 region a similar analysis applies but the population size being worked on by processor 1 has reduced by 1 sub-domain to
Similarly the population size worked on by processor 1 for the ith region can be expressed as
Therefore substituting Z/P in (2) with (9) yields the work done by processor 1 whilst the ith region is emptied.
Therefore the total work done by processor whilst clearing all regions is:
The work needed to empty the domain with a single serial processor (number of agents × average distance travelled) is
The work performed by a processor is assumed to be linearly related to the time taken to perform the simulation.
So the (computational) speedup over a single processor using P processors over N sub-domains can be calculated
Substituting (12) and (13) into (14) leads to (15)
Substituting the series summations
Simplifies to
From Eq. (18) it can be seen that if N ≫ P then speedup will tend to P. If N = P then then the speedup will tend to P/2.
1.2 General Derivation applicable to Any Number of Sub-domains (N)
In the more general case when N is not an integer multiple of P (see Fig. 9) the analysis is essentially the same although the first region (i = 1) needs to be given special treatment.
The work performed by processor 1 whilst area (a) is emptied is number of people being computed by processor 1 × (distance travelled by an occupant) (19).
where,
In the previous example, i = 1 region there was necessarily P sub-domains. The number of sub-domains in region 1 is now K. All other regions have P sub-domains. There are [M/P + H(K)] regions.
The work performed by processor 1 whilst region i = 1 is emptied is:
Equation (24) is analogous to (7) with the first part modified due to the number of sub-domains being reduced to K. P and H(K)P are introduced so the equation is valid when K = 0.
Equation (24) simplifies to
This equation can be generalised for the ith region (27) by substituting the population size processed by processor 1 for the ith region (26) into (25) and noting K = 0 for i > 1.
Total work (28) is the summation of emptying all the regions. The first term in (28) represents emptying the i = 1 region and the summation term represents emptying regions 2 to (M/P + H(K))
This simplifies to (29), note the change in lower summation limit to i = 1.
Introducing (30) into (29) and simplifying leads to (31).
Simplifies to
Substituting the second g in (33) with (30)
Substituting g (30) in (34) leads to
Simplifying (35) and noting that \( K \equiv H(K)K \) and \( H(K) \equiv \left( {H(K)} \right)^{2} \)
Substituting (36) and (13) into (14) gives the speedup (37)
Substituting (21) into (37) and simplifying leads to (33)
Appendix B: Additional Tables of Results for Case Studies
2.1 Case 1: Idealised Large Geometry
2.2 Case 2: Long Open Area
2.3 Case 3: High-Rise Building
2.4 Case 4: Large Urban Space
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Grandison, A., Cavanagh, Y., Lawrence, P.J. et al. Increasing the Simulation Performance of Large-Scale Evacuations Using Parallel Computing Techniques Based on Domain Decomposition. Fire Technol 53, 1399–1438 (2017). https://doi.org/10.1007/s10694-016-0645-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10694-016-0645-8