Abstract
The fire induced pressure and its influence on ventilation flows within a compartment have not been studied in detail previously. In this research work, we have investigated the development of gas pressure and the resulting flows in compartment fires first experimentally, by burning a series of heptane pool and polyurethane mattress fires inside a real, 58.6 m\(^2\) by 2.57 m high, apartment and then by carrying out numerical simulations of the experiments with the FDS code. The experiments were conducted with three different ventilation duct configurations to simulate three different airtightness conditions. The peak heat release rates were less than 1 MW and the burning times were about 180 s. The experimental results indicate that the gas pressure in relatively closed apartment can become high enough to revert the flows of the ventilation system, prevent escape through inwards-opening doors, and even break some structures. The peak gas temperatures under the ceiling of the burn room were about 300°C. The pool fires remained well-ventilated. The pressure ranges encountered in the experiments were between 100 Pa to 1650 Pa and the pressure occured within 50 s of ignition. We also report the FDS validation for this type of simulations and discuss the process of modelling the ventilation system and leakages.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In early 2014, a group of professional fire fighters from the Southwest Finland Emergency Services, city of Turku, was rehearsing a situation where they ignited a fire inside an apartment of an abandoned building, closed the door and tried to attack the fire after a moment to suppress it. To their surprise, two firemen could not open the inner door of the apartment (many Finnish apartments have double doors to the corridor) due to the high pressure inside the apartment. This led to the questions: What if there was an occupant trying to escape the burning apartment? Can the pressure be high enough to prevent escape?
Thermal expansion of gas during a fire will result in increased pressure if the fire takes place in a relatively closed compartment [1]. The phenomenon has received only little attention in the history of fire science because most studies have been performed in enclosures with large opening to ambient. This has been well-justified from the viewpoint of structural safety, as only a long-lasting fire can cause high temperatures that pose a risk to the fire resistance. Also, the need to ensure the availability of air has affected the experimental design of fire dynamics research. The smoke management calculations typically assume that pressure differences across the vents are dominated by the hydrostatic pressures, order of few tens of Pa at most.
Hägglund et al. [2, 3] have measured the pressures resulting from liquid pool fires in a compartment with only one, relatively small vent to ambient. They reported over and under pressure peaks as high as 1200 Pa and 1800 Pa respectively. By adding a mechanical ventilation to the same configuration, the over pressures were changed to 900 Pa and under pressures to \(-1200\) Pa. They observed that even the mechanically driven ventilation flows were reverted according to the direction of the pressure. Unfortunately, neither the heat release nor the mass loss rate of the fire were measured, thus limiting the possibility of quantitative analyses, such as a code validation.
More recently, the experiments within the OECD PRISME programme [4] have produced detailed information about the development of compartment pressure, ventilation flows and liquid pool fire dynamics in a very air-tight compartment, reported in numerous articles [5,6,7,8]. Prétrel et al [5, 6] investigated the influence of the enclosure airtightness on pressure using experiments and theoretical analysis. They found that closing the ventilation paths, and exhaust ducts in particular, during the fire increased the pressure significantly. The fuel mass loss rate was reduced simultaneously, though. As high as 3000 Pa over pressures were observed with fires of about 1 MW [7]. The effect of the mechanical ventilation flows on the natural flows through the multi-room compartment doorways were investigated in [8]. The results from the PRISME project cannot be directly transferred to the residential conditions due to the highly specialized construction, but they have already been used to validate the pressure and ventilation flow simulations of the Fire Dynamics Simulator [9] (FDS) software by Wahlqvist and van Hees [10]. They concluded that the airtight envelopes with small fires can create a significant positive pressure and this pressure can induce reverse flows through the ventilation networks and also threaten structural integrity. They identified the pressure to be a important issue for fire safety.
Fourneau et al. [11] used zone modelling to investigate the influence of the energy efficiency fire safety by comparing the modelling results in traditional and modern air-tight buildings (Passivhaus). They observed a significant difference in pressure rise (10 Pa vs. 450 Pa) and concluded that the high pressure can lead to a reverse flow in the supply ventilation system and possible pollution of other living areas. They did not recognize the pressure rise as a risk for the escape as such.
The main objectives of the current study were to quantify the pressures in fires taking place in closed residential compartments, to evaluate the potential risks for life and property, and to validate FDS for the simulation of such fires. Through the simulation capability, we will later evaluate the different ventilation arrangements and means for pressure management. By doing so, we want to bring more insight into the potential fire and evacuation safety issues related to the mechanically ventilated, air-tight enclosures that are currently being built due to the energy efficiency requirements and the trend of high-rise construction.
To meet the objectives we performed a series of fire experiments in a typical Finnish apartment, measuring the gas temperatures, pressures and gas species concentrations, as well as ventilation flows. The experimental setup is described in Section 2. The experiments were simulated with FDS, paying attention to the characterization of the building features that have the most influence on the pressure, such as envelope leakage. The simulation model is presented in the third section of this article, and the results reported in the fourth section. As the experiments were performed in a real apartment building, all the experimental uncertainties could not be ruled out, and they are discussed in the end of the article.
2 Experimental Study
2.1 Geometry
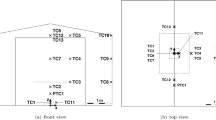
The experiments were conducted in a 1970s apartment building in the city of Kurikka, Finland. The building had three floors and a basement. The test apartment included a living room, bedroom, kitchen, bathroom, aisle and a closet, and was located in the first floor of the building. The apartment floor area was 58.6 m\(^2\) with a ceiling height of 2.57 m. The envelope area \(A_{\mathrm{env}}\) was 165 m\(^2\), including the floor and the ceiling. A floor plan is shown in Figure 1.
The concrete walls that were shared with the adjacent apartments were approximately 0.16 m thick. The walls to the exterior were around 0.20 m thick. The walls towards the outside consisted of concrete-insulation elements and three-glass windows. The wall from the living room to the balcony had a light-weight structure with wooden frame. The apartment had the typical Finnish two door system with the inner door opening inwards and outer door opening towards the staircase.
2.2 Ventilation Configuration
The apartment had three ventilation exhaust vents, one in the bathroom, one in the closet, and one in the kitchen hood. The kitchen hood was closed during the experiments. The bathroom and closet vents were connected to 160 mm diameter ducts leading to the roof of the building. The dimensions of the vertical section between the 160 mm duct and the roof are not known. There was a small replacement air vent in the living room to provide make-up air for the ventilation, but this valve was closed tightly during the experiments to enable accurate characterization of the ventilation flows. The ventilation had originally been designed to be buoyancy-driven, but a roof fan had been installed to the bathroom duct at some point during the building use.
Thirteen experiments were performed with three different configurations of two the exhaust ducts:
-
1.
open duct,
-
2.
normal configuration with the original valves installed on the ducts, and
-
3.
ducts closed with metal foil and tape.
Photographs of the duct conditions are shown in Figure 2. The ventilation configurations are summarized in Table 1. Test numbering corresponds to the order of the experiments, except for Test 12 which was in fact the last test of the campaign.
The roof fan connected to the bathroom exhaust was operating except for the tests 3, 4 and 10, where it was switched off. The solid fuel tests were performed under the normal operating conditions of the exhaust ducts with the roof fan running and the kitchen duct tightly sealed.
2.3 Leakages
The air-tightness of the apartment boundaries was measured using a Blower door test according to the standard SFS-EN 13829 [13]. A powerfull fan was attached to the door leading from the living room to the balcony, and the other vents of the apartment were closed tightly. The door from the stairway to outside was kept open so that the staircase was at the ambient pressure. The fan was used to create a pressure difference between the apartment and the ambient. The amount of air flow through the fan was measured at different pressure differences. The normal practice in the energy efficiency studies is to report the leakage at 50 Pa under-pressure in a form of a volumetric flow rate \(\dot{V}_{50}\), air permeability \(q_{50}\) or air exchange rate \(n_{50}\). The air permeability is calculated by dividing the flow rate with the envelope area (\(q_{50} = \dot{V}_{50}/A_{\mathrm{env}}\)), and the air exchange rate by dividing the flow rate with volume (\(n_{50} = \dot{V}_{50}/V\)). In this work, the leakage measurements were made at both under and over-pressures in a range \(30\ldots 70\) Pa. The measurement uncertainty for \(\dot{V}\) was ± 0.6 %, and for \(q_{50}\) it was ± 4 %. The apartment temperature at the time of the measurements was only 16\(^\circ \)C, as it had been out of use for weeks.
The measured flow rates through the apartment boundaries are shown in Table 2. The measured \(q_{50}\) values indicate that the building would comply with the requirements of the Finnish building code (Part D3, 2012) for new buildings (\(q_{50} \le \) 4 m\(^3\)/hm\(^2\)). However, the building is less air tight than the building code’s recommended level (\(q_{50} \le \) 1 m\(^3\)/hm\(^2\))
Another way of characterizing the envelope air tightness is to calculate the effective leakage area. Assuming that the leakage behaves as a flow through a sharp-edged orifice, the leakage area \(A_{leak}\) can be solved from the following equation
where \(\dot{V}\) is the leakage flow rate, \(C_d\) is the discharge coefficient, \(A_{\mathrm{leak}}\) is the leakage area, \(\rho \) is the density, and \(\Delta p\) is the pressure difference at which the leakage rate was measured. Assuming \(C_d = 0.6\), \(\rho = 1.3\) kg/m3 and \(\Delta p = 50\) Pa, for which \(\dot{V}=0.12\) m\(^3\)/s, gives \(A_{\mathrm{leak}} = 0.023\) m\(^2\). Dividing the leakage area by the apartment envelope area gives the corresponding leakage ratio of 1.4 \(\times 10^{-4}\). From the viewpoint of smoke management technologies, the building would be classified to the average class (NFPA 92, 2012, Table A.4.6.1). Comparing the leakage areas obtained at different pressures (Table 2) in the range \(-70\ldots 70\) Pa, we can observe that the leakage area is weakly dependent on the absolute value of the pressure, but the values obtained at under and over pressures were clearly different.
Before the fire experiments, the kitchen and bathroom drains were tightly sealed to avoid the situation where the over-pressure would push the water out of the water lock, thus creating an additional, uncontrolled leakage path to the apartment.
2.4 Fire Loads
The experiments were conducted in two phases based on the type of fuel: In the first phase (tests 1–10), 3.0 L (3.2 L in Test 1) of n-Heptane was burned in a 0.7 m × 0.7 m steel pan with a free height of 21 cm. The fuel was poured on a water layer to stabilize the burning and to provide uniform thickness of heptane. The position of the pan is shown in Figure 1. In the second phase, polyurethane foam (PUF) mattress were used. Test 12 was performed in the closet of the apartment, and it was the last test of the campaign.
2.5 Measurements
The quantities that were measured during the experiments were gas pressure, gas temperature, O\(_2\), CO\(_2\) and CO concentrations and the gas velocity and temperatures in the exhaust ducts. The measurement locations are shown in Figure 1. The pressure difference between the apartment gas space and ambient was measured in two locations (one in living room, other in kitchen) at height 1.8 m using Furness FCO 0508264-9 pressure transmitters and metal ducts connecting them to the measurement positions. The calibration uncertainties of the transmitters were about 1%.
For the exhaust gas velocity measurement, additional 0.5 m sections of the ventilation duct were attached in front of the exhaust vents to facilitate the placement of instruments and to improve the reliability of the velocity measurements. Although the length of the tubes was insufficient for achieving fully developed flow profiles, they were expected to make the flow more uniform at the measurement location. Flow velocities were measured using bi-directional probes with calibration uncertainty of about 2%.
Gas temperatures were measured using two trees of five K-type thermocouples (1.5 mm diameter) with 0.5 m vertical separation. One tree of thermocouples was placed in the corner of the fire room, and the other tree in the centre of the kitchen. Thermocouples were also placed in the exhaust ducts for measuring the exhaust gas temperatures.
The gas concentrations were measured through a probe placed 1.7 m from the floor in the living room corner next to the thermocouple tree. The sampling line was lead to the gas analysers outside thr apartment. The delay due to the length of the line was 16 s. In Test 13, the CO\(_2\) and CO levels exceeded the corresponding analyser ranges.
The heptane pan mass was measured using a load cell. The mass loss rate \(\dot{m}(t)\) was calculated from the mass data using by piecewise least squares fitting technique using finite interval method [12]. Second order Hermite polynomials were fitted to the mass data, thus providing the mass-loss rate as the first derivative. Heat release rate was calculated from \(\dot{m}(t)\) assuming complete combustion of flammable vapors
where \(\Delta H_{\mathrm{c}}\) is the net heat of combustion of n-Heptane (43.5 MJ/kg).
The mass measurements were not performed in the PUF fires due to the potential risk to the load cell. The HRR curve of Test 11 was estimated from the measured gas temperatures using inverse modelling. According to a classical room fire correlation [16], the temperature rise in a compartment fire is proportional to \(\dot{Q}^{2/3}\). The coefficient of proportionality was obtained from the heptane pool fires and then used to obtain a rough estimate of the PUF HRR.
The tests were recorded using video cameras placed inside the fire room and in the balcony.
2.6 Experimental Procedure
In the heptane pool fire tests (Tests 1–10), the experiment started by turning on the data loggers and closing the doors of the apartment. A fireman wearing a breathing apparatus poured the heptane into the pool, waited for a few seconds for the mass reading to stabilize, and then ignited the fire using a gas torch. The fireman stayed inside the apartment for the whole duration of the fire.
In the PUF fires, the door was kept open at the time of ignition, and the fireman left the apartment closing the doors behind, except for Test 13, where he stayed inside to test the possibility of door opening. Test 12 ended with an intentional intervention by the fire brigade.
3 Numerical Simulations
3.1 Numerical Method
FDS is a Large Eddy Simulation (LES) based Computational Fluid Dynamics sofware which solves the low mach number combustion equations on a rectilinear grid over time [9].
FDS has a dedicated module for modelling Heating, Ventilation and Air-conditioning (HVAC) systems connected to the gas space of the fire simulation. The ventilation network is described as a series of ducts and nodes. The nodes are placed at points where ducts intersect each other or the CFD computational domain. The ducts are uninterrupted domains of fluid flow which can encompass elbows, expansion/contraction fittings and various other fittings. The losses due to friction and various other duct fittings are assigned as dimensionless loss numbers to the ducts. The node losses are attached to the ducts as loss terms only appear in the duct equations [14]. The module does not presently store any mass. Therefore, mass flux into a duct is equal to the mass flux out of the duct. The nodal conservation equations for mass, energy and momentum equations are as follows:
where \(\rho \) is the density, u is the duct velocity, A is the cross sectional area of the duct, h is enthalpy of fluid in the duct, P is the pressure and K is the dimensionless loss coefficient of the duct. The subscripts j indicates the ducts in the calculation, i and k indicate the nodes of the duct [14].
3.2 Simulation Model
The simulation model is based on the apartment layout and floor area shown in Figure 1. The simulation model geometry is shown in Figure 3. Simulations were carried out with 0.05 m and 0.10 m mesh resolutions, and the results were not found to be sensitive to the resolution. Comparisons of the ceiling temperatures and peak pressures obtained with the two mesh resolutions are shown in Figures 7 and 13. The fuel pan was modelled as a 0.7 m × 0.7 m burner with a specified mass loss rate (MLR) according to the measurements. The combustion reaction was that of n-Heptane, with soot and CO yields of 3.7 % and 1 %, respectively.
Leakage modelling was one of the critical aspects of the simulation. FDS provides two different methods for the leakage modelling: The Bulk Leakage—method assigns the leakages onto large segments of the compartment boundaries. In our case, entire interior surface was used as a leakage path. The flow is driven by the difference between the background pressures inside and outside the compartment, at floor level. The Localized Leakage—method assigns the leakages to smaller locations of the boundary, and is suitable if the exact location of the leakages can be identified. The pressure difference is based on the local pressure averaged over the surface area, and includes the contribution of the perturbation pressure provided by the hydrodynamic solver. In this work, this method was also used although the exact locations of the leakages were not known. In both methods, the leakage flow is calculated by the HVAC solver. The Bulk leakage method requires a leak path to be specified, and the wall with the window was here considered as the main leak path. Similarly, the localized leakage was assigned on a 3.6 m × 2 m area around the living room window.
One challenge of the leakage modelling is that the pressure differences during fires can be an order of magnitude higher than the pressure differences used in the leakage tests. There is no guarantee that the gaps and cracks of the building envelope and the flows through them behave in a similar manner in these two situations. For example, assuming a 1 mm gap size indicates that the flow Reynolds number is less than 1000 at 50 Pa but about 2000 at 500 Pa difference, thus indicating a transition from laminar to turbulent flow. In this situation, both \(C_d\) and the exponent of the pressure in Equation 1 can be different. In addition, the high pressure differences can cause deformations in the structures, thus changing the effective leakage area.
The performance characteristics of the roof fan are not know, and the fan model parameters were estimated based on the duct velocity measurements and expected normal mode operation. A stalling pressure of 200 Pa was assumed and the flow rate at ambient conditions was set to 200 L/s. To avoid spurious pressure fluctuations the time stepping (DT_HVAC) of the HVAC network model was set to 2 seconds.
The ventilation ducts leading from the closet and bathroom to the roof were modelled as systems of two or three duct sections. The first section (length \(L_1\)) represents the additional duct fitted in front of the actual duct for measurements. It was assumed to have no flow loss. The second section represents the duct leading from the apartment to the roof. The bathroom duct was connected to a third section which contained the fan, was assumed to be 1 m long and connected to an ambient node. All the ducts had a roughness of 0.001 m. The duct lengths, areas and loss coefficients are listed in Table 3. The loss of the ventilation system was expected to be mainly due to the valve in the node connecting the duct to the room. The valves are adjustable, and the values of \(K_2\) were chosen to reproduce their expected normal-model operation. In the case of open configuration, very small losses were assumed to the system.
The thickness of the concrete walls was set to 0.20 m for external walls and 0.16 m for internal walls. The conductivity, specific heat and density of the concrete were set to 0.7 W/(m K), 0.75 kJ/(kg K) and 2200 kg/m3, respectively.
The simulations were carried out using the FDS version 6.3.2 using a single mesh and 6 OpenMP threads [14] on a personal computer with a 3.2 GHz Intel Xeon processor and 32 GB ram. The CPU time for a single simulation of 300 s was approximately 8 hours.
4 Results and Discussion
4.1 General Observations
Two main observations are of general interest:
-
1.
In few seconds after the ignition and door closing, the over-pressure inside the apartment was observed as a strong, high-pitch noise. In Test 13, the fireman who stayed inside after igniting the fire with a torch, tried to open the inwards-opening door by pulling the handle. He could not pull the door open using his own force. After a few attempts, the other firemen were able to push and bend the door from the staircase side, relieving pressure and the door opening became possible.
-
2.
In Test 12, the light-weight wall between the living room and the balcony failed structurally. The window frame was seen to move already in Test 11 and 13, after being exposed to about 1650 Pa pressure difference. In Test 12 about 60 s after the ignition, the pressure, unexpectedly, pushed the window frame out of the wall. At the moment of this structural failure, the pressure difference was about 1400 Pa. (For comparison, the typical wind loads on the envelope are of the same order of magnitude with these pressures.) The event was preceded by a low squeaky noise heard from outside for about one second. Visual inspection of the structures after the fire showed no sign of thermal damage. The pressure of the apartment was thus relieved before the fire fighters could intervene.
4.2 Heat Release Rates
The heat release rates (HRR) of the liquid pool fires were obtained from the measured mass loss rate curves. The measured HRR in the three experiments with different ventilation configurations are shown in Figure 4 as solid lines. As can be seen, the burning behaviour of the pool fire was not affected by the ventilation configuration. There were no differences between the sets of tests with nominally identical conditions, thus indicating a good repeatibility of the experiments. The measured HRR curves were prescribed HRR inputs to the FDS simulations. It has to be noted that the heat of combustion used in estimating the HRR assumed a complete combustion whereas FDS includes the production of CO and soot. The simulated HRR curves reproduce the initial transient and peak value of the experimental curves, but the decay-phase HRR is higher in the simulations. This can be partially due to the coarse estimation of the experimental HRR curve in the FDS input ramp.
As the measured HRR was not available for the PUF fire (Test 11), a rough estimate of the HRR curve was first developed using the inverse method. Then, the HRR curve was manually adjusted to reach a good agreement between measured and simulated gas temperatures. The resulting HRR curve is shown in Figure 4. These temperature results cannot be used for validating the temperature predictions. However, we will use the pressure results to supplement the heptane pool fire results, but the nature of the validation for Test 11 must be considered qualitative.
4.3 Gas Temperatures
The gas temperatures measured close to the living room ceiling are shown in Figure 5. The figure on the left shows the results for three heptane fires with different ventilation arrangements. We can observe that the repeatability of the pool fires is very good, and that the ventilation arrangement has no influence on the gas temperatures inside the burning room. The figure on the right shows the corresponding data for the three PUF fires. Here the repeatability is not observed, as the fire sources were different. In addition, the fire source of Test 12 was placed in the closet, hence showing a delay in the temperature rise.
The errobars in Figure 5 represent a combination of the statistical random component (standard deviation between the three tests) and the thermocouple measurement uncertainty of 5 %. For the errorbars in the solid fuel tests, only the measurement uncertainty is considered as the random uncertainty is very high between each test.
Experimental (solid lines) and simulated (dashed lines) temperatures at different heights are compared in Figure 6. The simulation results are shown for the 0.10 m mesh resolution. The method of leakage modelling did not have any significant influence on temperature predictions. Hence only the temperatures from the Bulk Leakage method are presented here.
The agreement between the measured and simulated temperatures in the heptane pool fires (Tests 3, 5, and 8) is within the model uncertainty estimated from other similar experiments [15]. The experimental results indicate a stronger stratification of the gas temperature profile than the FDS simulations. Underprediction of temperatures can be noticed in the three highest thermocouple positions (150 cm, 200 cm and 250 cm) and an overprediction in the two lowest thermocouples (50 cm and 100 cm). It seems that the mixing of the hot and cold gases in the smoke layer and due to the plume entrainment may be overestimated. The overall energy production seems to be reproduced well.
The results of Test 11 (PUF fire) cannot be considered validation. They are presented for the sake of comparison and to provide basis for further use in pressure validation. The errors in the simulated temperatures in Test 11 are combinations of the true model uncertainties and the HRR input uncertainty.
The sensitivity of the FDS temperature predictions on the mesh resolution was investigated by performing the simulations with both 0.05 m and 0.10 m mesh resolutions (Figure 7). The simulations with 5 cm resolution did not run into completion due to the limitations of the computing environment, but the 5 cm -results before about 80 s show a slight improvement in the temperature transient. The improvement is very modest in comparison to the large increase in computational time.
4.4 Gas Concentrations
The measured volume fraction of oxygen in the fire room is shown in Figure 8. The fires are generally well ventilated, and the heptane fire results (left figure) show a good repeatability and independence of the ventilation configuration. This indicates that the ventilation flow rates in Tests 3 and 5 are too small to influence the fire room gas concentrations within the observed time scale (Figure 9). Only Test 12 (closet fire with additional solid fuels) can be considered underventilated. However, the measurements are affected by the window breakage and fire brigade intervention. The significantly different fire development of Test 12 is visible in CO concentrations (Figure 10) as well. The peak CO concentrations are about 300 ppm in the heptane pool fires and between few hundred and 2000 ppm in the PUF fires. In Test 12, the CO concentration exceeded the analyzer range of 5000 ppm.
The comparison of measured and simulated gas concentration for O\(_2\) and CO are presented in Figures 9 and 11, respectively. The minimum O\(_2\) concentrations are predicted accurately but the experimental concentrations are found to decrease faster than the simulated ones. The CO production was simulated as a constant fraction of the fuel burning rate. During the fire, the assumed CO-yield value of 0.01 is shown to produce 50 % lower CO concentrations than what was measured, but the values after fire suppression are very close to each other. Assuming a higher yield could improve the predictions, but the post-fire results do not justify such a global adjustment. A closer investigation of the fire plume dynamics and CO kinetics may be needed to explore the reasons behind these observations.
4.5 Gas Pressures
The recorded pressures in the liquid and solid fuel tests are shown in Figure 12. The left figure shows the pressures in heptane pool fires for all the three ventilation configurations. The errorbars indicate a combined statistical and measurement uncertainty. The ventilation configuration is shown to have a significant impact on the pressure rise. As the the open ducts (Test 2–4) were changed to normal dampers (Tests 5–7), the peak over-pressures increased from about 300 Pa to 600 Pa. Closing the ducts completely increased the peak pressures further to about 900 Pa. On the other hand, the influence of the roof fan position (ON or OFF) was found to be smaller than the measurement uncertainty. After the fuel burnout at 170 s, there is an under-pressure peak of \(-200\) to \(-400\) Pa, but the difference between the normal and closed ventilation configurations cannot be observed as in the overpressures.
In the PUF fires (Figure 12, right), the over-pressures are significantly higher than in the heptane pool fires, ranging from about 1400 Pa in Test 12 to 1650 Pa or Tests 11 and 13. The pressure values follow the fuel burning behaviours and the changes in geometrical conditions. In Test 11, the fire decreased in size after about 40 s but increased again at 60 s as a pool of melt PU was formed on the floor. In Test 13, opening of the door by the firemen is seen as short reduction in pressure at about 30 s. Both tests show a negative peak after fuel burnout. In Test 12, a rapid decay of pressure is shown at 80 s when the external wall was broken, and consequently no negative pressure peak appears.
The experimental pressures and FDS predictions with the two leakage modelling methods are compared in Figure 13. The pressure predicted by FDS was smoothed over 5 datapoints using moving average method to remove some noise from the plots. For Test 3 (open ducts), FDS overpredicts the peak over-pressures, but for the normal and closed configurations (Tests 5 and 8), the experimental pressure peaks are between the predictions given by the two leakage modelling methods. This indicates that in reality, either the ventilation system of Tests 2−4 has even lower total flow loss than what is expected in the FDS model, or the effective leakage area is higher than what was found in the air-tightness tests. Allocation of the system losses between the exhaust vent valves and the other parts of the systems was based on the very limited knowledge of the system geometry and the expected fan pressure level and normal flow conditions.
The FDS predictions with the bulk leakage modelling and 0.05 m resolution are shown in Figure 13 as well. The results with 0.05 m resolution were only obtained to about 90 seconds, but the main aspects of the pressure peaks were already achieved within that duration. The effect of the resolution is found to be insignificant in comparison to other sources of uncertainty.
The localized leakage method gives lower pressure than the bulk leakage modelling method for all four tests shown in Figure 13. The result can, at least partially, be explained by the fact that the bulk leakage is calculated from the pressure difference measured at the bottom of the pressure zone formed by the simulated compartment, while the localized leakage is based on the local pressure. In local pressure, the hydrostatic effect and the perturbation components can increase the pressure difference, which results in higher leakage and lower overall pressure.
4.6 Ventilation Flows
The recorded flow velocities in Tests 3 and 5 are shown in Figures 14 and 15, respectively. The FDS predictions with the two leakage methods are also shown in the figures. The bathroom duct velocities are shown on the left and the closet duct velocities on the right. Positive direction means out of the compartment.
In both tests, the flow in the closet’s exhaust duct is shown to be initially in inwards direction. In Test 3 (Fan off), also the bathroom duct has initial inwards flow. The negative flow can be caused by three factors: First, the routes of make-up air in the original gravity-based ventilation seem to have been insufficient, and the system has been seriously unbalanced. Secondly, the cooling of the compartment, which was heated by the previous tests, before the ignition can cause an initial under-pressure. Third, the kitchen hood exhaust, although closed, may have had some leakages and small exhaust. Measurement errors may be involved as well, due to low flow speeds and the long tube lines between the bi-directional probes and the pressure transducers. The roles of these and possible other factors cannot be accurately confirmed.
The open configuration has clearly higher ventilation speeds than the normal configuration with outlet valve. FDS is shown to capture the shape and magnitude of the outwards flow, but the magnitude of reverse flow after the fire burnout is underestimated by the model.
4.7 Uncertainties and Limitations
The main sources of the experimental uncertainty are the uncertain ventilation system configuration, lack of direct HRR measurement and the problematic quantification of additional leakage. The duct sizes and the network layout of the ventilation system were not known precisely because the original HVAC drawings of the building were not available. The duct diameters were estimated from the visible sections, but the details behind the structures could not be confirmed. The model of the unknown part of the ducting was based on the standard construction practices during the 1970s. The roof fan characteristics were not known either.
The HRR was not measured directly in these experiments, but the fuel mass was measured using a load cell and used to calculate HRR. The HRR uncertainty is induced from the polynomial least squares fitting for the MLR and the assumed yields of the incomplete combustion products.
The leakage area at 30–70 Pa may not be fully representative to the leakage that occurs at fire pressures. Extrapolating the linear increase of the effective leakage area from the range 30−70 Pa (Table 2) to 1000 Pa would indicate a factor of three higher leakage area. The true leakage area corresponding to the fire peak pressures cannot be quantified without a leakage measurement system capable to significantly higher pressures. The direction of the leakage was found to have a significant effect on the leakage area.
The experiments were planned to give insight into the pressures and ventilation flows during apartment fires. The direct utilization of the results in any wider context is limited by at least two aspects of the experiments: First, both fire types increased in power very quickly after ignition. In fact, they could be classified ultra-fast fires in terms of the fire safety engineering design fires. The best way to extrapolate the results to lower growth rates is to use the simulation model which has now been validated. Second, in real fires, the high over-pressure can push out the water from the water locks of the kitchen and bathroom drains. The influence is difficult to estimate at this stage. Simulations can be used to examine this effect, but it requires hydraulic characterization of the drain systems for air flow.
Due to the observed uncertainty in the estimated leakages, we investigated the sensitivity of the peak pressure predictions to the leakage area using the bulk leakage version of the model. Table 4 compares the experimental values to the predictions using the nominal leakage area and a leakage area increased by 10 %. When the leakage area was increased, the peak pressures decreased 17 % in average, being much closer to the experimental values. However, at the same time the temperatures were reduced as well, indicating that the leakage area cannot be adjusted arbitrarily for better pressure predictions.
The model uncertainty metrics for three predicted quantities were calculated using the methods proposed in the FDS Validation Guide [15]. The data consisted of three peak values from Tests 3, 5 and 8. The resulting values for the model bias \(\delta \) and relative standard deviation \(\tilde{\sigma }_{M}\) are reported in Table 5. The table also lists the relative standard deviations of the experimental values \(\tilde{\sigma }_{E}\), both as a-priori expected values and as resulting from the current data. The expected experimental errors are combinations of the corresponding measurement errors and the propagated input uncertainty. They are higher than the values used in [15] because the HRR was not directly measured, and due to the previously mentioned leakage uncertainties. In case of gas temperature, the data indicates a similar uncertainty as what we expected. For oxygen concentration and pressure, however, the data suggest that the errors are in fact smaller than our uncertainty estimates.
Despite the small number of data points, these uncertainty metrics can be used to evaluate the quality of the validation with respect to the published FDS validation data [15]. For the peak temperatures, the model bias in the current simulations is smaller than in the large body of validation cases in [15]. For the minimum oxygen concentration, the biases are slightly greater (here 0.94 and 0.97 vs. 0.99 in [15]) but satisfactory, considering the uncertainty in HRR specification. Indeed, the low biases of temperature and oxygen concentration indicate that the HRR has been reliably estimated. For the peak pressure, the biases of the current simulations (1.21 for the bulk leakage and 0.96 for the localized leakage) are greater than in [15], where the bias of the similar simulations is only 1.02.
The two leakage methods were found to produce quite different pressures. Given the simplicity of the bulk leakage method and the fact that the predictions were in all cases equal or higher than the measured pressure, it can be considered a recommended method for this type of application. It would still be possible to model individual, known leakages such as window or door cracks using the localized method.
The conditions after the fire burnout were not in the focus of this study, and the relatiely higher uncertainties of the negative pressure peaks have not been investigated.
5 Conclusions
A set of fire experiments was conducted in an apartment building under different ventilation conditions to understand the pressure rise in compartments and its effects on the ventilation flows. The main finding was that the heptane pool and polyurethane foam fires in relatively closed compartments can lead to very high over- and under-pressures. The recorded over-pressures were between 100 Pa and 1650 Pa, and they occurred in less than 50 s from the ignition. The two experimental parameters, ventilation system configuration and fuel type, were both found to have a significant influence on the pressure magnitude. We demonstrated that during the period of high over-pressure, it is impossible to open an inwards-opening door of the apartment by pulling from inside. In addition, we observed that the pressure resulting from a polyurethane foam fire can cause structural damage to the building.
The experimental campaign was followed by the FDS simulations of the experiments to validate the predictive capability and the process of modelling the leakages and simple ventilation systems. The uncertainties of the numerical simulations in reproducing the thermal, chemical and pressure conditions within the apartment were estimated. For gas temperature and oxygen concentrations, the uncertainties were found to be close to the previously published validations under similar fire conditions. For the peak over-pressure, the simulations using the Bulk leakage method resulted in values that were 21 % too high in average. When the Localized leakage method was used, the peak pressures were underpredicted by 4 %, but the scattering of the results was more pronounced. The predicted ventilation flows were in a good qualitative agreement with the experimental results.
Based on the experimental and simulation results, we can conclude that the effect of the ventilation configuration (or effective leakage) on the pressure rise in the compartment is significant and should be taken into account during the fire safety design process. Fire-induced over-pressure must be recognized as a potential risk for evacuation because it can prevent the occupants from escaping from spaces with inward opening doors. In addition, the fire-induced pressure can cause severe structural damage and significantly modify the fire dynamics through the additional source of air. For instance, the fire spread along the building facade can be accelerated due to the envelope failures. In case of the failing internal structure, such as the wall between the burning apartment and the building’s evacuation route, the smoke spread to the evacuation route would follow and the evacuation of the whole building put in danger.
The fire simulations can be used to investigate the pressure rise and its consequences during the fire safety design or fire investigations. More work is needed to quantify the uncertainties of the ventilation flows, but the current simulations were already able to capture the qualitative flow behaviour. For performing such simulations, it is important to characterize the building air-tightness and the ventilation configuration. Moreover, the measuriments of the air-tightness of the internal structures, such as doors and wall elements, would be needed for the evaluation of the pressure effects in a wider context because the leakages are generally measured for the entire building envelope, if at all.
References
Mowrer FW (2016) Enclosure smoke filling and fire-generated environmental conditions. In: Hurley MJ (ed) SFPE Handbook of Fire Protection Engineering, 5th ed, Society of Fire Protection Engineers, Springer, Berlin, pp. 1066–1101. doi:10.1007/978-1-4939-2565-0
Hägglund B, Nireus K and Werling P (1996) Pressure rise due to fire growth in a closed room. Description of three full-scale tests. FOA Defence Research Establishment, FOA-R-96-00347-2.4-SE, p 27
Hägglund B, Nireus K and Werling P (1998) Pressure rise due to fire growth in a closed room. An experimental study of the smoke spread via ventilation ducts. FOA Defence Research Establishment, FOA-R-98-00870-311-SE, 97 p.
Audouin L, Rigollet L, Prétrel H, Le Saux W and Röwekamp M (2013) OECD PRISME project: Fires in confined and ventilated nuclear-type multi-compartments—Overview and main experimental results. Fire Safety Journal, 62: 80-101
H. Prétrel and J.M. Such. Effect of ventilation procedures on the behaviour of a fire compartment scenario, Nuclear Engineering and Design, 235, 2155-2169, 2005.
H. Prétrel, W. Le Saux and L. Andouin. Pressure variations induced by a pool fire in a well-confined and force-ventilated compartment, Fire Safety Journal, 52, 11-24, 2012.
Audouin L, Prétrel H, Le Saux W (2011) Overview of the OECD PRISME project – main experimental results. In: 21st international conference on structural mechanics in reactor technology (SMiRT 21)
H. Prétrel, A. Koched, and L. Audouin. Doorway Flows Induced by the Combined Effects of Natural and Forced Ventilation in Case of Multi-compartments Large-Scale Fire Experiments. Fire Technology 52 (2), 489-514, 2016.
McGrattan KB, McDermott R, Floyd J, Hostikka S, Forney G, and Baum H (2012) Computational fluid dynamics modelling of fire. Int J Comput Fluid Dyn 26(6–8):349–361. doi:10.1080/10618562.2012.659663
Wahlqvist J and van Hees P (2013) Validation of FDS for large-scale well-confined mechanically ventilated fire scenarios with emphasis on predicting ventilation system behavior. Fire Safety Journal 62:102-114
C. Fourneau, N. Cornil, C. Delvosalle, H. Breulet, S. Desmet and S. Brohez Comparison of fire hazards in passive and conventional houses, Chemical engineering Transactions, 26, 375-380, 2012. doi:10.3303/CET/1226063.
Baroudi D (1993) Piecewise least squares fitting technique using finite interval method with Hermite polynomials. VTT Technical Research Centre of Finland, Espoo. VTT Publications 135, p 27
SFS-EN 13829, Thermal performance of buildings. Determination of air permeability of buildings. Fan pressurization method (ISO 9972:1996, modified). Suomen standardoimisliitto SFS ry. 2000.
McGrattan K, Hostikka S, McDermott R, Floyd J, Weinschenk C, Overholt K (2015) Fire Dynamics Simulator, Technical Reference Guide, Vol 1: Mathematical Model. 6th ed, National Institute of Standards and Technology, Gaithersburg, Maryland, USA, and VTT Technical Research Centre of Finland, Espoo, Finland
McGrattan K, Hostikka S, McDermott R, Floyd J, Weinschenk C, Overholt K (November 2015) Fire Dynamics Simulator, Technical Reference Guide, Vol 3: Validation. 6th ed, National Institute of Standards and Technology, Gaithersburg, Maryland, USA, and VTT Technical Research Centre of Finland, Espoo, Finland
B.J. McCaffrey, J.G. Quintiere, M.F. Harkleroad, Estimating room fire temperatures and the likelihood of flashover using fire test data correlations. Fire Technology., 17, 2, 1981. 98-119.
Acknowledgements
We thank the experimental team for their great effort: Pasi Paloluoma and Knut Lehtinen (South-West Finland Emergency Services), Peter Biström (Stravent Oy), Tomas Fagergren (Brandskyddslaget), Jere Heikkinen and Ville Heikura (VTT). We thank Jukka Hietaniemi from Palotekninen insinööritoimisto Markku Kauriala Oy for help with the inverse modelling of PUF HRR curve. The research project was funded by the Finnish Fire Protection Fund (PSR), Ministry of Environment, Hagab AB, and the Criminal Sactions Agency of Finland. The work was also partially supported by the Academy of Finland under grant no. 289037. The authors wish to acknowledge CSC – IT Center for Science, Finland, for computational resources.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Janardhan, R.K., Hostikka, S. Experiments and Numerical Simulations of Pressure Effects in Apartment Fires. Fire Technol 53, 1353–1377 (2017). https://doi.org/10.1007/s10694-016-0641-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10694-016-0641-z