Forward-Looking Tail Risk Exposures at U.S. Bank Holding Companies

Abstract

This paper develops a simple method for quantifying banks’ exposures to large (negative) shocks in a forward-looking manner. The method is based on estimating banks’ share prices sensitivities to (market) put options and does not require the actual observation of tail risk events. We find that estimated (excess) tail risk exposures for U.S. Bank Holding Companies are negatively correlated with their share price beta, suggesting that banks which appear safer in normal periods are actually more crisis prone than their beta would suggest. We also study the determinants of banks’ tail risk exposures and find that their key drivers are uninsured deposits and non-traditional activities that leave assets on banks’ balance sheets.

1 Introduction

A systemic banking crisis—a situation in which many banks are in distress at the same time—can induce large costs for the economy. The task of supervisors and regulators is to avoid and mitigate, as far as possible, such crises. For this they need advance information about how banks are exposed to shocks to the economy. This allows them to identify weak banks and put them under increased scrutiny but also to monitor general risks in the financial system. When evaluating the exposure of banks it is also of paramount importance to distinguish between exposures to normal market shocks, and exposures to large shocks. For example, a financial institution that follows a tail risk strategy (such as writing protection in the CDS market) may appear relatively safe in normal periods as it earns steady returns but may actually be very vulnerable to significant downturns in the economy.

Supervisors and regulators obtain their information to a large extent from information generated by the bank itself, such as its accounts. While these sources are a crucial ingredient of the evaluation process they are not free from drawbacks. For example, most of this information is under the discretion of banks and may be used strategically.¹ Moreover, this data is typically backward looking and available only at relatively low frequency. Accounting information also misses important aspects such as informal knowledge (e.g., CEO reputation) or information contained in analysts’ reports.

In recent years there has been growing interest in using market-based measures of bank risk. This is on the back of evidence that market signals contain valuable information about banks’ risks (see Flannery (1998, 2001) for surveys). Some of the measures explicitly take into account systemic and tail risk aspects (e.g., Acharya et al. 2009; Adrian and Brunnermeier 2009; De Jonghe 2010). They typically use information from historical tail risk events to compute realized tail risk exposures over a certain period.

In this paper we develop a forward-looking measure of bank tail risk. We define a bank’s (systemic) tail risk as its exposure to a large negative market shock. We measure this exposure by estimating a bank’s share price sensitivity to changes in far out-of-the-money put options on the market, correcting for market movements themselves. As these options only pay out in very adverse scenarios, changes in their prices reflect changes in the perceived likelihood and severity of market crashes. Banks that show a high sensitivity to such put options are hence perceived by the market as being severely affected should such a crash materialize. As this sensitivity reflects perceived exposures to a hypothetical crash, it is truly forward-looking in nature. This property is important to the extent that bank risks change quickly and hence historical tail risk exposures become less informative. Another advantage of this method is that it does not require the actual observation of any crashes, as the method relies on changes in their perceived likelihood.

We use our methodology to estimate tail risk exposures of U.S. bank holding companies. We find that the estimated exposures are inversely related to their CAPM beta. Since our methodology estimates tail risk over and above beta risk, this implies that low beta-banks have more tail risk than their beta would suggest. Thus, banks which appear safe in normal times are actually more exposed to a crash. Conversely, of course, high beta banks have lower tail exposure than their normal risk suggests. In other words, banks’ risk exposures converge in the tails. This has interesting implications for financial regulation and we discuss various interpretations of this finding in the paper.

We also use our methodology to understand the main drivers of bank tail risk. Understanding these drivers is important for regulators as it gives them information about which activities should be encouraged and which not. There is so far very little research on this question (a notable exception is De Jonghe 2010). Our main findings are that variables which proxy for traditional banking activities (such as lending) are associated with lower perceived tail risk. Several non-traditional activities, on the other hand, are perceived to contribute to tail risk. In particular, we find that securities held for-sale, trading assets and derivatives used for trading purposes are associated with higher tail risk. These findings are consistent with the experience of the crisis of 2008 and 2009. Interestingly, securitization, asset sales and derivatives used for hedging are not associated with an increase in tail risk exposure. This suggests that a transfer of risk itself is not detrimental for tail risk, but that non-traditional activities that leave risk on the balance sheet are. On the liability side we find that leverage itself is not related to tail risk but that large time deposits (which are typically uninsured) are. We also find that perceived tail risk falls with size, which is indicative of bail-out expectations due to too-big-to-fail policies.

The remainder of this paper is structured as follows. In Section 2 we briefly review existing measures of tail risk. Section 3 develops the methodology for measuring tail risk exposure using put option sensitivities. Section 4 contains the estimation of tail risks. Section 5 studies the determinants of tail risk. Section 6 concludes.

2 Existing tail risk measures

The Value-at-Risk (VaR) has for many years been the standard measure used for risk management. VaR is defined as the worst loss over a given holding period within a fixed confidence level.² A shortcoming of the VaR is that it disregards any loss beyond the VaR level. The expected shortfall (ES) is an alternative risk measure that addresses this issue. The ES is defined as the expected loss conditional on the losses exceeding the VaR level. Another frequently used measure is Moody’s KMV. Essentially, Moody’s KMV is a distance to default measure that is turned into an expected default probability with the help of a large historical dataset on defaults.³

While these measures focus on individual bank risk, there has been a growing interest in recent years in systemic measures of bank risk. One strand of the literature focuses on tail-betas (e.g., De Jonghe 2010). This concept applies extreme value theory to derive predictions about an individual bank’s value in the event of a very large (negative) systematic shock. Loosely speaking, this method uses information from days where stock market prices have fallen heavily and considers the covariation with a bank’s share price on the same day. It thus focuses on realized covariances conditional on large share price drops. A difficulty encountered when applying this method is that tail risk observations are rarely observed, and hence a large number of observations are needed to get accurate estimates (De Jonghe (2010) suggests at least six years of daily data).

Acharya et al. (2009) develop a measure similar to the concept of market dependence, which is based on expected shortfalls instead of betas. They propose measuring the Marginal Expected Shortfall (MES), which is defined as the average loss by an institution when the market reaches a certain quantile of its left tail. Huang et al. (2010) propose a related measure focusing instead on a threshold loss for a portfolio of large banks as the tail risk event. Adrian and Brunnermeier (2009) consider a different aspect of systemic risk. They estimate the contribution of each institution to the overall system risk. A bank’s CoVaR is defined as the VaR of the whole financial sector conditional on the bank being at its own VaR level. The bank’s marginal contribution to the overall systemic risk is then measured as the difference between the bank’s CoVaR and the unconditional financial system VaR. An advantage of the CoVaR is that it is relatively simple to estimate, as it is based on quantile regressions. In terms of its informational properties it is similar to the tail risk beta in that it focuses on realized tail risk.

Our measure is most similar to the tail risk betas as we also measure bank exposures to large market swings. A difference that is important for the interpretation of the estimates, however, is that while the tail risk beta relates to large daily market drops, we estimate exposures to a large prolonged downturn in the market (e.g., several months).

There is literature on hedge funds performance which uses a methodology similar to ours. This literature estimates tail exposures for various styles of hedge funds with a non-linear market factor that takes the shape of an out-of-the-money put option (see, for example, Agarwal and Naik 2004). However, the focus of this literature is different. While we are interested in estimated tail risk exposures per se (i.e., regulators want to know which banks are more exposed to tail risk), the hedge fund literature looks at whether tail risk exposures can be used to forecast fund performance.

3 Measuring tail risk using put option sensitivities

In this section we present our methodology for measuring banks’ tail risk exposures. We define the latter to be the bank’s exposure to a general market crash (that is, a severe downturn in the economy). If the market crashes, a bank may suffer large, simultaneous losses on its assets, which may push it close to or into bankruptcy. Crucially, the extent to which it is exposed to crashes may differ from its normal market sensitivity. Consider two banks, A and B. Bank A invests mostly in traditional banking assets such as, for example, loans to businesses and households. Moreover, it invests in assets that are mainly exposed to normal period risk, such as, for example, junior tranches of securitization products (which lose value for modest increases in defaults, but are insensitive to defaults that go beyond the first loss level). In addition to these assets, bank A insures itself against default by buying protection on its assets (such as by buying credit default swaps on its loans). Bank A’s equity value will thus depend less on the market in times of crisis, compared to normal times.

Bank B follows a different business strategy. It invests in traditional assets as well. However, in addition, it also follows investment strategies that return a small and steady payoff in normal periods but incur large losses when the market crashes. Examples of such a strategy is selling protection in the credit default swap (CDS) market or buying senior tranches of securitization products (which lose value only when all other tranches have already incurred a total loss). Thus, even though bank B’s equity value may behave similarly to bank A’s in normal periods, it tends to fall relatively more when the market crashes.

We next describe our method. For this we consider the economy’s representative firm (the “market”). We suppose the firm exists for one period only and that its (stochastic) next period equity value is denoted with x. Similarly, we consider a bank with next period equity value y. We assume for the relationship between the equity values of the bank and the market:

$$ y(x)=\left \{ \begin{tabular}{@{}cc} $x^{\beta }$ & if $x\geq \overline{x}$ \\\\ $\dfrac{x^{\beta }}{\left(\frac{\overline{x}-x}{\overline{x}}+1\right)^{\gamma }}$ & if $ x<\overline{x}$ \end{tabular} \right. $$

(1)

When $x\geq \overline{x}$, the bank’s equity value has thus a market dependence equal to the one of a firm with a beta of β (that is, the bank’s return is β times the market return). However, for $x< \overline{x}$, the bank’s equity value additionally depends on the relative shortfall of the market to $\overline{x}$, $\frac{\overline{x}-x}{\overline{x }}$ (∈ [0, 1]). For γ > 0 its equity value will be more sensitive to the market, hence the bank has tail risk over and above the normal period exposure (as expected for Bank B), while for γ < 0 we have the opposite case (Bank A). Only in the case of γ = 0 does the bank’s tail not differ from its normal period risk.

Since tail risk realizations ($x<\overline{x}$) are rarely observed, our estimation relies on changes in perceived tail risk, which we will measure through changes in put options prices. For this consider a put option with strike price $\overline{x}$ that is deep out-of-the-money ($\overline{x}$ is hence a tail risk realization). We have for the pay-off from this put

$$ p(x)=\left \{ \begin{tabular}{@{}cc} $0$ & if $x\geq \overline{x}$ \\ $\overline{x}-x$ & if $x<\overline{x}$ \end{tabular} \right. $$

(2)

Inserting into Eq. 1, totally differentiating with respect to y and dividing by y yields

$$ \frac{dy(x)}{y}=\beta \frac{dx}{x}-\gamma \frac{dp}{p+\overline{x}}. $$

(3)

Percentage changes in the bank’s equity values ($\frac{dy(x)}{y}$) thus relate to percentage changes in the market ($\frac{dx}{x}$), giving the standard β-effect. Additionally, they also relate to relative changes in the value of the option, $\frac{dp}{p+\overline{x}}$,⁴ arising from tail risk exposure.

In our empirical implementation we will identify tail risk sensitivities (γ in Eq. 3) by adding a put option (on the market) to a standard market regression and interpreting the sign of the put option coefficient. Tail risk sensitivities will thus be estimated through changes in put option prices, which (loosely speaking) arise from changes in either the likelihood of a market crash or its severity.⁵

3.1 A discussion of the methodology

We believe that this method has several attractive features. First, the method is forward-looking in nature, that is, it captures expected tail risk exposure at banks. This contrasts with other popular methods for measuring tail risk, such as tail risk betas or the CoVAR. These methods essentially compute correlations (or covariation) of banks with the market (or other banks) at days of large share price drops. They thus draw inferences from historical tail risk distributions and hence measure realized tail risk. The difference between forward and backward-looking measures is likely to be limited when banks only undergo small changes in their risks over time, but is potentially important in a dynamically evolving financial system.

Second, our measure identifies banks’ tail risk exposure through changes in expected market tail risk, as measured by put option prices. This has the advantage that for our estimation we do not need tail risk events to materialize. Such events, by definition, occur only very infrequently and hence it is difficult to estimate their properties. Existing measures that rely on the historical distribution of tail risk events reduce this problem by relying on a large time series and by looking at modest tail risk realizations that occur more frequently. Our method allows the measurement of exposure to extreme forms of tail risk (for this one simply includes a very far out-of-the-money put option).

Since we estimate exposures to market crashes, our measure captures system tail risk exposure. This is desirable since externalities from banking failures are typically associated with system events, and not isolated bank failures. It should, however, be kept in mind that a bank that has a low estimated systematic tail risk may still be individually very risky to the extent that it pursues activities that are uncorrelated with the market. In addition, one should also keep in mind that market risk is not identical to banking sector risk. Even though banks’ market exposures have probably increased in recent decades, credit risk is still the major source of risk for banks. However, market and credit exposures are highly correlated in practice: when economic conditions deteriorate, the default risk of firms increases and stock values decline at the same time. For example, during our sample period the correlation between the S&P 500 and the CDX crossover index was − 0.77. Due to this high correlation, our estimates will (indirectly) also capture credit risks at banks.⁶

In our empirical implementation of Eq. 3 we measure tail risk exposures by the (negative) coefficient of a put-option return ( γ) in a regression on bank stock returns. This, however, is in a regression where we also separately control for the market return. Conditional on the market, a key driver of put-option returns is market volatility. We can thus expect the γ to give us similar information as the (negative) coefficient in a regression of bank returns on market volatility.⁷ This provides us with an alternative interpretation of the γ. If a bank is symmetrically exposed to upwards and downwards movements in the market, an increase in volatility will not affect its value and the γ should be zero. However, if a bank is more exposed to downward than to upward movements (e.g., Bank B), its value will decrease when volatility increases. It then obtains a positive γ. The tail-risk estimate can thus also be interpreted as a measure of how much more a bank is exposed to downturns than to upturns. Total tail risk is then a combination of the symmetric dependence on the market (given by the standard β-risk) and the asymmetric sensitivity to downturns (the γ-risk).

It should be noted that our measure, like other market-based measures, is net of any bailout expectations. If, for example, markets anticipate that governments may bail out certain banks (for example because they are too-big-to-fail) then these banks may have a low perceived tail risk even if their underlying activities are relatively risky (Kane (1985), for example, shows that the expected value of these bail-out subsidies can be significant). Thus, while our estimates are important for regulators and supervisors in that they quantify a bank’s effective failure risk, there are less suitable for being used as a base for regulation that aims at reducing risk-shifting (for example, by conditioning capital requirements on tail risk exposures).

4 Empirical analysis

4.1 Data

We collect daily data on bank share prices and the S&P 500 (our proxy for the market) for the period 4 October 2005 until 26 September 2008 from Datastream. Put option data on the S&P 500 for the same period is from IVolatility.⁸ In addition, various balance sheet data are collected from the FR Y-9C Consolidated Financial Statements for Bank Holding Companies (BHCs). We focus on U.S. BHCs which are classified as commercial banks and for which data is fully available. We focus on the BHC instead of the commercial bank itself, as typically it is the BHC that is listed on the stock exchange. Excluded are those banks whose share price change is zero in more than 10% of the cases in order to mitigate problems arising from illiquidity. Foreign banks (even when listed in the U.S.) and pure investment banks are also excluded. The final sample contains 209 Bank Holding Companies.

An important question is the choice of the option strike price. Ideally we would choose an option such that on each day it represents the same crash probability. Simply taking an option with a constant strike price is hence not appropriate as market prices change over time and hence the moneyness of the option will change. Taking the strike price to be a (fixed) fraction of the S&P500 is also not desirable as this ignores that the likelihood of tail risk realizations is also driven by the volatility. We hence decided to construct a series of options such that their option price does not vary. Specifically, each day we adjust the strike of the option such that the previous day price of the options is fixed over time.

For this we use an option price of 0.5$, which translates into an implied strike that was on average 33% below the S&P 500 during our sample period.⁹ We have checked the S&P500 over the last 25 years and have found three periods with stock market declines of this magnitude: the 1987 stock market crash (maximum decline: 32%), the burst of the dotcom bubble (maximum decline: 23%) and the subprime crisis (maximum decline: 41%). Thus, such a decline materialized about once every eight years.

In order to compute the option price change for, say day 1, we proceed as follows. We first identify among all traded options the two strike prices that give day 0 prices closest to 0.5. We then calculate the weight that makes their average price 0.5. Given this weight, we calculate the weighted average of their prices at day 1 and calculate from this the change of the price, dP, from day 0 to day 1. Effectively, we compute price changes of options whose (hypothetical) strike price varies from day to day.

We initially considered all out-of-the-money puts. A first inspection, however, revealed that the 100er strikes (i.e. 500, 600, 700 etc.) are much more liquid than put options with other strike prices. We therefore use only these puts. For each day an option’s strike price and its price change are then calculated according to the procedure described above. In order to mitigate the influence of changes in the remaining time to maturity on our analysis, we use for this an “on-the-run” series, where each quarter we jump to more recently issued options with longer maturity. As a result, the remaining time to maturity is limited to an interval of between three and six months.

4.2 Estimated tail risk exposures

We estimate Eq. 3 for each bank using the following specification:

$$ \frac{\Delta y_{t}}{y_{t}}=\alpha _{0}+\alpha _{1}\frac{\Delta x_{t}}{x_{t}} +\alpha _{2}\frac{\Delta p_{t}}{p_{t}+\overline{x}_{t}}+\varepsilon _{t}. $$

(4)

In Eq. 4 the subindix t indicates time. The market value of the bank and the S&P500 index are denoted by y _t and x _t , respectively ($\frac{\Delta y_{t}}{y_{t}}$ and $\frac{\Delta x_{t}}{x_{t}}~$ are hence the returns on the bank and the market). The term p _t denotes the price of a put-option on the S&P 500 index with a strike price $\overline{x}_{t}$ that is set such that its previous-day-price is a constant over time (as described in the previous section), $\overline{x}_{t}$ denotes the (time-varying) strike price of the option, and ε _t is an error term that fulfills the classical OLS-assumptions.

We expect α ₁ in Eq. 4 to be close to one in case banks display similar properties as other firms in the market. We do not hold any priors about the sign of α ₂ (note that γ in the model (3) relates to − α ₂ in the estimation; high α ₂ thus indicates less tail risk). If a bank is similar to the average firm in the market, its γ should be zero. This is because the bank will then react one-to-one to market movements. Its market dependence in the tail is then not dif/ferent from its market dependence in normal times and hence gamma is zero. The existence of systemic risk in the financial system may suggests that banks display excess market dependence in the tail, that is, γ is positive (negative α ₂). However, bail-out expectation may also limit the perceived exposures of the stocks of banks to a market downturn, in which case we obtain a negative γ (positive α ₂).

We estimate Eq. 4 using OLS on daily data. For this we winsorize the dependent variables at the 2.5% level. Table 1 reports summary statistics for the coefficients on the 209 bank-level regressions. We can see that the betas are reasonably distributed. The mean beta is 1.56; banks are thus on average riskier than the market. The 25th and the 75th percentiles are 1.39 and 1.93, respectively. The γ (= − α ₂) is only significant in 16.3% of the cases, which is not surprising considering that the γ of an average firm in the market should be zero. However, we can see that there is substantial cross-sectional variation in the γ: the 25th and 75th percentiles are − 12.2 and − 2.8. The mean γ is negative (− 7.8), suggesting that that overall factors that reduce tail risk (relative to the market) dominate.

Table 1 Summary statistics for 2-factor model. The table summarizes the coefficients from the 209 bank-level 2-factor regressions given by Eq. 4

What can be said about the economic significance of the γ-estimates? For the β-estimates it is straightforward to interpret their value since a drop in the market by x% translates into a drop in the stock price by βx%. Such a simple relationship does not exist for the γ because the return on a put-option is not proportional to the return on the market. However, in order to get a sense of the economic significance of the γ-estimates one can do the following exercise. We can consider different scenarios for (instantaneous) drops in the market index of, say 5, 10, 15, 20%. For these drops, we can calculate implied put-option price changes (using an option price formula). We can then use Eq. 3 to calculate the share price return for the average gamma implied by the put-option change, which is given by the term $-\gamma \frac{dp}{p+\overline{x}} (=\alpha _{2}\frac{dp}{p+\overline{ x}})$. Finally, we can compare this return to the share price return implied by the average beta.

Some caveats apply to this method. First, when we compute the implied option price change we keep constant all the other determinants of the option price, while in reality a significant drop in the index value, for example, is likely to be associated with a change in volatility as well (most likely an increase in the volatility). Thus, our calculations may over- or underestimate the real impact on the put-option price. Second, the OLS coefficients for beta and gamma relate to small changes in the explanatory variables, while we simulate large changes in these variables. For the beta-coefficient this issue may be relatively innocent—as it only requires the relationship between the bank and stock return to be linear over a wide range of index returns. However, for the gamma this assumption is more problematic. This is because the price of an out-of-the-money put-option responds non-linearly to changes in the market. In particular, it becomes more sensitive to the market as the market gets closer to the strike price (less out-of-the money). Our OLS estimates of the gamma are based on the less sensitive range (where the index value is far away from the strike) but for the simulations we make inferences about the more sensitive range (where the put-option is less out-of-the-money). This may introduce an additional source of error in our exercise.

We proceed as follows. In order to calculate the expression $-\gamma \frac{dp }{p+\overline{x}}$, we assume an index value equal to the average of the S&P 500 during our sample period. From this we calculate the strike of the option using the average discount used in our analysis. We then calculate the implied volatility (using the Black–Scholes formula) which makes the option price equal to 0.5 (the price used in our regressions). Holding this volatility constant we can then compute the option price change if the market drops by a certain amount. Using the sample mean γ, we can then calculate the term $-\gamma \frac{dp}{p+\overline{x}}$, which gives us the share price return induced by the γ-risk. The share price return induced by the β-risk of the average bank is simply given by the (mean) β times the drop in the market.

Table 2 summarizes the results for the various scenarios about index drops. The first column shows the stock return implied by the β-risk, the second column the return implied by the γ-risk. The third column shows the total implied return. We can see that for modest index drops, the γ-exposure does not matter a lot. For example, for an index drop of 5%, the average share price change implied by the gamma is only 0.6%, compared to an average share price change implied by the beta of − 7.8% (recall that the average beta in our sample is larger than one). However, for larger index drops the importance of the gamma raises. For example, for an index drop of 20%, the change implied by the gamma is 10.2%, while the beta-implied change is − 31.2%. The increasing importance of the γ-exposure for larger index drops reflects the non-linear dependence of the put-option price on the underlying: as we get closer to the strike, the sensitivity (delta) of the (out-of-the money) put increases.

Table 2 Economic significance of γ-estimates. The table calculates the share price reaction to various market crash scenarios. The first column gives the share price reaction implied by the average beta (= 1.56). The second column gives the share price reaction implied by the average gamma (= − 7.82). The third column gives the combined share price reaction. The last column gives the difference in the share price response of a bank at the 25% quantile and at the 75% quantile of the gamma-distribution

Besides this exercise (which compares the average γ-risk with the average β-risk), it is also informative to study how important the cross-sectional variations in γ-risk are in economic terms. This matters for a regulator who wants to know whether a bank that has a high γ-risk relative to its peers really has much more tail risk. For this we have calculated in the last column of the table the difference in the implied share price return for a bank that has a gamma equal to the 25% quantile of the distribution with the one of a bank at the 75% quantile of the distribution. As before, it turns out that for smaller index drops the gamma does not matter a lot (for a 5% drop the difference in the return is about 0.7% between the two banks). However, for larger drops, the difference becomes important. For example, when the market drops by 20%, a bank with a gamma at the 75% quantile of the γ-distribution drops by 12% more than a bank at the 25% quantile.

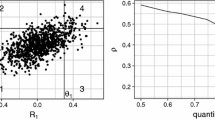
Figure 1 shows next the gammas plotted against bank size. It can be seen that there is considerable variation. There also seems to be a pattern of large banks having lower tail risk.

Fig. 1

Gamma and bank size

An important question is whether our tail risk measure really adds anything in terms of informational content to the normal beta. For example, it may simply be that the banks with large tail risk are also banks that have a large beta. In this case, estimating the tail risk beta separately is of little value. To shed light on this question we study how gammas relate to betas. In order to avoid potential interdependencies between beta and gamma arising when they are estimated in the same regression, we estimate for this betas that are obtained from a standard one-factor model (that is, without put-options) of the following form:

$$ \frac{\Delta y_{t}}{y_{t}}=\alpha _{0}+\alpha _{1}\frac{\Delta x_{t}}{x_{t}} +\varepsilon _{t}. $$

(5)

Table 3 provides summary statistics for β’s estimated from this 1-factor model, showing that although the mean beta is now somewhat smaller (1.48 instead of 1.56), the overall distribution is similar to the one from the 2-factor model.

Table 3 Summary statistics for 1-factor model. The table summarizes the coefficients from the 209 bank-level 1-factor regressions given by Eq. 5

Figure 2 plots the banks’ gammas against market betas. The scatter plot shows that higher gammas cannot simply explained by higher betas. In fact, there is a strong negative relationship between beta and gamma.

Fig. 2

Gamma vs. beta

This negative relationship has the following interpretation. Since the gamma is estimated from a regression that also includes the market, it measures tail risks over and above the tail-dependence implied by the beta. In other words: a positive gamma implies that a bank has more tail risk than its beta would suggest. A negative relationship between beta and gamma thus means that low beta banks have more tail risk than their beta would indicate (and vice versa for high beta banks). Thus, there is convergence in the tail: banks’ risk exposures in the tail are more similar than the ones in normal times.

A potential explanation for the negative relationship is so-called tail risk strategies, which produce steady returns in normal periods but actually expose the banks to severe downturns. For example, an institution that writes protection in the CDS market receives in normal periods a relatively safe stream of insurance premia. However, in a large recession many exposures will simultaneously default and large losses may materialize for this institution. Many trading strategies, such as the ones exploiting apparent arbitrage relations, create similar pay-off distributions. If banks that have low beta (and hence also low tail risk) tend to source additional tail-risk through such means, this could explain our finding. Another explanation for this negative correlation is that highly profitable institutions that operate in risky environments protect their franchise, for example by buying protection in the CDS market or by imposing a less fragile capital structure. Yet another interpretation is that it is simply difficult for banks to avoid exposure to systemic events. Thus while banks may differ substantially in their normal business risk, their tail exposure may be rather similar.

We can classify banks into different risk profiles using the two dimensions of Fig. 2. Specifically, we allocate banks to four groups relative to a benchmark bank with β = 1 and γ = 0. This creates the following categorization in Fig. 2:

• 1. Upper-right quadrant (Quadrant I): Banks with high normal times ( β > 1) and high tail risk (γ > 0).

• 2. Upper-left quadrant (Quadrant II): Banks with high normal times ( β > 1) and low tail risk (γ < 0).

• 3. Lower-left quadrant (Quadrant III): Banks with low normal times ( β < 1) and low tail risk (γ < 0).

• 4. Lower-right quadrant (Quadrant IV): Banks with low normal times ( β < 1) and high tail risk (γ > 0).

Table 4 lists the top-10 banks (in terms of their average asset size during the sample period) for each of the four risk profiles. We can see that all the very large banks are in Quadrant II (high beta − low gamma). This is good news to the extent that it suggests that many of the large banks have tail-risks that do not exceed their normal times risk. In addition, due to their high-normal times risk these banks are likely to be already on the radar screen of regulators. We can also see that some of large banks are in Quadrant I (high beta − high gamma). These banks have excess tail-risk, but are probably under (well-deserved) regulatory scrutiny because they also have large betas. The probably most interesting quadrant—from a regulatory perspective—is Quadrant IV (low beta − high gamma). These are the banks were normal times risk understates their tail risk and which may hence fall through the cracks. Regulators should pay more attention to these banks. It is, however, comforting that the largest banks do not belong to these category. In fact, the banks in this category tend be much smaller than in the previous two quadrants. Finally, in Quadrant III (low beta − low gamma) we have the relatively unproblematic banks. These banks tend to be also small in size.

Table 4 Classification of banks according to their risk profiles. The table lists the ten largest banks for each quadrant in Fig. 2

5 Determinants of bank tail risk

In this section we study whether and how a bank’s business activities relate to its tail risk. The most obvious way to do this is by regressing (estimated) gammas upon a number of balance sheet variables that represent various banking activities. This two step method, however, has the disadvantage that the estimation is not efficient as information from the first step (estimating the gammas) is not used in the second step.

For this reason we estimate the relationship in one step.¹⁰ We amend Eq. 3 to allow a bank’s put option sensitivity to vary with a certain bank activity, say B, relative to its sample mean ($\hat{B}$). In addition, we also interact the S&P 500 return with the balance sheet variable B to take into account that general market sensitivities may also differ depending on bank activities. We obtain the modified equation:

$$ \frac{dy(x)}{y}=\alpha +(\beta +\theta (B-\hat{B}))\frac{dx}{x}-(\gamma +\delta (B-\hat{B}))\frac{dp}{p+\overline{x}}. $$

(6)

The coefficient δ in this equation gives us the relationship between a bank’s gamma and activity B (the equivalent of the coefficient of a regression of estimated gammas on B), evaluated at the mean. Since we are interested in several determinants of bank tail risk, we estimate a multivariate variant of Eq. 6:

$$ \frac{\Delta y_{i,t}}{y_{i,t}}\!=\alpha _{0}\!+\left(\alpha _{1}\!+\displaystyle\sum\limits_{j}\alpha _{2}^{j}\left(B_{i}^{j}-\hat{B}_{i}^{j}\right)\right)\frac{\Delta x_{t}}{x_{t}}\!+\left(\alpha _{3}+\displaystyle\sum\limits_{j}\alpha _{4}^{j}\left(B_{i}^{j}-\hat{B}_{i}^{j}\right)\right)\frac{\Delta p_{t}}{ p_{t}+\overline{x}_{t}}+\varepsilon _{i,t}\text{.} $$

(7)

where j denotes a bank activity. Our coefficients of interest in this estimation are the $\alpha _{4}^{j}$. A positive $\alpha _{4}^{j}$ implies that balance activity j decreases tail risk, while a negative coefficient implies that it increases tail risk.

We estimate Eq. 7 by means of pooled OLS. Table 5 presents the implied coefficients for the determinants of gamma, δ ^j ($=-\alpha _{4}^{j}$). Note that a positive coefficient in the table implies that the activity increases tail risk.¹¹ The first column contains the results from a regression with some basic bank characteristics: size (measured by the log of total assets), the loan-to-asset ratio and the leverage ratio (measured by the debt-to-asset ratio). Size is negatively related to tail risk exposure. This may indicate that markets perceive large banks as being too-big-to-fail (TBTF). The loan-to-asset ratio is also negatively related to a bank’s tail risk exposure. This finding is in line with other recent findings: both De Jonghe (2010) and Demirgüç-Kunt and Huizinga (2010) find that traditional banking activities are less risky than non-traditional activities. The last variable considered is the leverage ratio. Although a higher leverage ratio is often associated with more default risk, it does not come out significant here (we return to this later).

Table 5 Relationship between gamma and bank characteristics. This table reports the negative coefficients of the interaction terms between the adjusted put option and the respective balance sheet variables. It represents the effect of the respective balance sheet item on a bank’s tail risk exposure where a positive value implies a larger exposure to tail risk

Column two focuses on banks’ lending activities by including proxies for loan quality and profitability. Among the loan quality proxies only the loan growth variable is significant, indicating a positive relationship with tail risk. This is consistent with the idea that a bank may only grow faster at the cost of lowering lending quality, and hence may become more exposed in a downturn.¹² We also find that a higher interest rate on the loans is associated with less tail risk, which can be explained by the fact that this indicates a higher profitability of banks, thus exposing them less to a crash in the market. Additionally, we include the return of assets (ROA) to capture the returns from other (partly non-traditional) asset activities. We find a positive relationship with tail risk, which is consistent with other recent findings (e.g., Demirgüç-Kunt and Huizinga 2010).¹³

Next, we turn to the influence of other assets. In column three we include held-to-maturity securities, for-sale securities and trading assets (all scaled by total assets). Only trading assets turn out significant, and only at the 10% level. At this point, one has to keep in mind that non-traditional activities are likely to be negatively correlated with traditional activities (banks may specialize in either), which may create multicollinearity problems and hence affect the estimates. Therefore, in column four we use the ratio of commercial and industrial loans to total assets (C&I Loans/TA) instead of the loan-to-asset ratio (the traditional activity) as it is less correlated with the non-traditional activities. The result is that trading assets and for-sale securities now contribute very significantly to tail risk. Held-to-maturity securities have a positive coefficient as well, but its magnitude and significance is lower. The C&I-loans-to-asset ratio is insignificant, similar to the loan-to-asset ratio in column three.

It is often argued that non-traditional activities increase (tail) risk exposure. In columns five and six, we will analyze which role financial innovations play among the non-traditional activities. First, we investigate securitization and asset sales activities. In addition to the total value of securitization and asset sales (both scaled by total assets) we also include the internal and external credit exposure arising from these activities. The internal credit exposure arises from a bank’s own securitization or asset sale activities via recourse and other credit enhancing agreements between the bank and its special purpose vehicle (SPV). An external credit exposure can arise if a bank provides credit enhancements to other banks’ securitization structures.

Column five shows that only the external credit exposure variable is significant and positive. This is in line with our prior findings as external credit exposure is new credit exposure taken on in addition to existing exposure. Moreover, such exposure (for example, from credit enhancements) only materializes under relatively adverse scenarios, and hence should be related to tail risk. The insignificance of a bank’s own securitization and asset sale activities may indicate that opposing forces are at work. On the one hand, securitization and asset sales are, by themselves, of course a mean of off-loading risk to other market participants, making a bank less risky.¹⁴ In particular, if the bank keeps the equity tranche but sells senior tranches it sheds tail risk relative to normal period risk. On the other hand, recent experience has shown that these activities induced banks to take on more risk.¹⁵ In addition, although the credit exposure seemingly disappeared from the balance sheet to the SPV (which is legally independent), the market might expect that this separation does not survive if the SPV encounters large losses. A bank might buy back assets from its SPV in order to protect its reputation and customer base (as happened in the case of Bear Stearns). Therefore, the credit exposure (which is mostly tail risk exposure) may not be effectively removed by securitization.

Column six focuses on banks’ derivatives activities. Based on the available data, we can make the distinction between derivatives that are held for trading purposes and derivatives that are held for other purposes (most likely hedging). A priori one would expect that the latter would reduce tail risk. The expected effect for derivative trading is less clear cut. Resulting counterparty risk (which tends to materialize in tail risk scenarios) may, for example, create an increase in tail risk exposure. The results in column six show that derivatives held for trading contribute to tail risk, while the other derivatives do not seem to affect it. The latter is somewhat surprising but may be explained by the fact that only some of these derivatives are used for hedging and that they create counterparty risk as well.

The last column takes a closer look at the importance of capital structure for tail risk. In column one we found that the leverage ratio does not contribute to tail risk exposure. We now include information on the share of deposits and the composition of deposits. In the last column of Table 5, in addition to the variables from column one, we consider the deposit-to-liabilities ratio and the ratio of time deposits above $100,000 to domestic deposits.¹⁶ Time deposits above $100,000 were not insured during our sample period, which makes them similar to wholesale funding, as both funding sources might be prone to runs. The results in column seven show that the leverage ratio is again not significant. Insignificance also obtains for the deposit-to-liabilities ratio. However, the time deposits above $100,000 do contribute positively and significantly to tail risk. Since these deposits are subject to withdrawal risks similar to wholesale funding, this result is consistent with Demirgüç-Kunt and Huizinga (2010) who find that wholesale funding increases bank risk.¹⁷

6 Conclusion

In this paper we propose a forward-looking method to measure tail risk exposures at banks. Tail risk is defined as a bank’s exposure to a large negative market shock and it is measured by estimating a bank’s share price sensitivity to changes in far out-of-the-money put options on the market, correcting for market movements themselves. Because far out-of-the-money put options on the market only pay out if the market crashes, changes in their prices reflect changes in the perceived likelihood and severity of a crash. The estimated sensitivities, in turn, represent the market’s perception of exposures to a hypothetical crash, making them a truly forward-looking measure. Another attractive feature of this measure is that it does not require the actual observation of tail risk events since it identifies banks’ tail risk exposure through changes in expected market tail risk. Our measure is also relatively easy to estimate as it basically comes from an amended market regression.

The application to U.S. bank holding companies yields several interesting facts about their tail risk exposures. For example, (excess) tail risk seems to be negatively correlated with the CAPM share price beta. This suggests that banks which appear relatively safe in normal times (that is, have a low beta) are actually riskier than their beta would suggest. We also find that the impact of non-traditional activities on tail risk depends on whether they leave assets on the balance sheets or not. In the former case they increase tail risk, while in the latter they do not. Our results also suggest that leverage itself does not increase tail risk, but will do so if it comes through uninsured deposits.