Plasma-neutral gas interactions in various space environments: Assessment beyond simplified approximations as a Voyage 2050 theme

Abstract

In the White Paper, submitted in response to the European Space Agency (ESA) Voyage 2050 Call, we present the importance of advancing our knowledge of plasma-neutral gas interactions, and of deepening our understanding of the partially ionized environments that are ubiquitous in the upper atmospheres of planets and moons, and elsewhere in space. In future space missions, the above task requires addressing the following fundamental questions: (A) How and by how much do plasma-neutral gas interactions influence the re-distribution of externally provided energy to the composing species? (B) How and by how much do plasma-neutral gas interactions contribute toward the growth of heavy complex molecules and biomolecules? Answering these questions is an absolute prerequisite for addressing the long-standing questions of atmospheric escape, the origin of biomolecules, and their role in the evolution of planets, moons, or comets, under the influence of energy sources in the form of electromagnetic and corpuscular radiation, because low-energy ion-neutral cross-sections in space cannot be reproduced quantitatively in laboratories for conditions of satisfying, particularly, (1) low-temperatures, (2) tenuous or strong gradients or layered media, and (3) in low-gravity plasma. Measurements with a minimum core instrument package (< 15 kg) can be used to perform such investigations in many different conditions and should be included in all deep-space missions. These investigations, if specific ranges of background parameters are considered, can also be pursued for Earth, Mars, and Venus.

1 Introduction

One of the fundamental questions regarding the Universe is how the different types of matter interact and shape stellar systems, planetary environments, and specific environments that allow life forms to emerge. The small-scale limit of such an interaction is between quarks and photons, and belongs to high-energy physics. The large-scale limit includes dark matter and dark energy, and belongs to cosmology.

For the habitable part of the Universe such as planetary and exoplanetary systems, their evolution is driven by interactions between visible (baryonic) matter through radiation, collisions, and collective forces such as electric and magnetic forces, in addition to gravity. For example, the lifetime of a comet is strongly affected by the solar radiation, the solar wind plasma interaction, and the tidal forces near perihelion. Chemical interactions start forming complicated molecules including biomolecules from a mixture of low-energy (< 1 keV) ions and neutrals (both in the gas phase and the condensed phase) that are exposed to strong external energy sources (such as cosmic rays and extreme ultraviolet radiation), particularly at low temperature such as in the interstellar medium [1] and the upper atmosphere of planets and satellites. For example, the thermosphere and mesosphere of the Earth contain complicated molecules and even aerosols such as ion-water cluster molecules [2,3,4] and noctilucent clouds [5, 6]. Considering the fact that the habitable part of the Universe is composed of low-temperature ions and neutral species (T < 0.04 eV) and that the heavy molecules are exposed to extremely low-temperature space plasma before being trapped by ice or dust in interstellar space, understanding the actual plasma-neutral gas interaction at low energy through in-situ observations is very important.

If the organic matter is formed in the low-temperature plasma, a similar process that involves plasma-neutral gas interactions might take place during the formation of the Solar System, which should have had its effect on comets in, e.g., the Oort Cloud. By looking back to 4.6 billion years ago, the formation of the Solar System might have undergone a period when the plasma-neutral gas interactions played a critical role, which is not only relevant for the formation of heavier materials but also for re-distributing (partitioning) the energy among all components, or even degrading the material. On the other hand, plasma-neutral gas interactions in the thermosphere and ionosphere have substantially influenced planetary evolution through atmospheric escape [7,8,9,10].

However, our knowledge of the actual plasma-neutral gas interactions in tenuous space plasmas with some neutral particle content – either gaseous or in the form of icy grains – is still incomplete. The chemical pathways to forming heavy (organic) molecules are only partially understood. This is partly because low-energy ion-neutral and electron-neutral interactions in low-temperature plasma vary across different environments, depending on the external DC and AC electric and magnetic fields, as described in Section 3 below. Although the cross section of a single interaction between a simple ion and a neutral particle in the gaseous phase without complicated force or energy is known from both theory and laboratory experiments [11], a substantial change in the plasma conditions (composition and velocity distribution of the ions and neutrals) or in the ambient energy (electric and magnetic fields, radiation, and temperature) can cause a significant change in the ion-neutral particle and electron-neutral particle interactions, particularly in a tenuous plasma. Also, the electron impact ionization properties [12] are not well understood at distant environments and for different neutral species, although they provide a dominant source of ionization, especially far from the Sun, where photo-ionization is subdominant because of significantly low solar UV flux.

With such a variety of environments and ambient energy distributions, it is not easy to pinpoint the exact conditions for relevant laboratory experiments without in-situ measurements in space. This makes the plasma-neutral gas interactions in actual space environments less well understood when compared to the present knowledge on the dynamics and interactions in fully ionized space plasma. Consequently, our knowledge on the interaction between low-energy ions and neutral species is far from complete (cf. Section 5).

In this paper, based on a White Paper prepared for the ESA Voyage 2050 Call, we show that our knowledge of the plasma-neutral gas interactions and of the partially ionized environments is far from sufficient, although they are ubiquitous in the upper atmospheres of planets and moons, and elsewhere in space. In order to advance such knowledge, we advocate for measurements addressing the following fundamental questions in future space missions:

• (A) How and by how much do plasma-neutral gas interactions influence the re-distribution of externally provided energy to the composing species?

• (B) How and by how much do plasma-neutral gas interactions contribute toward the growth of heavy complex molecules and biomolecules?

Sections 2 and 3 present an overview of current knowledge of plasma-neutral gas interactions in different environments. Section 4 proposes specific science questions to be addressed. Here, we do not include the cases when either the neutral part or the ion plasma part are in the solid form, because such interaction problems open up another world of fundamental questions. For instance, electrostatic charging of icy grains under the influence of cosmic ray or UV radiation may grow or dismantle the grains [13, 14], thus controlling the grain size distribution and also the total grain surface area available for chemical reactions. Inversely the plasma is also affected by the charged grain and dusty plasma behavior, which is the case at Saturn's rings [15]. Although in this paper we do not discuss such science themes relevant to dust and grain (which belongs to the "dusty plasma science"), they should also involve the plasma-neutral gas interaction. In Section 5 we propose a strategy for obtaining measurements needed to address these questions, with a specific terrestrial mission case elaborated in Section 6. Technology challenges are discussed in Section 7

2 Low-energy plasma-neutral gas interaction in space: knowledge and limitations

2.1 Present-day knowledge

The low-energy plasma-neutral gas interaction in partially and weakly ionized plasmas has long been studied as one of the central themes of ionospheric physics and aeronomy. Plasma-neutral gas interactions include both the direct collisional interaction and indirect interaction through electric, magnetic, and radiation fields. Unlike ion-ion, ion–electron, and electron–electron interactions, the role of the indirect interaction between ions and neutral species is generally ignored in standard formulations to describe the dynamics of a gas state, such as the Boltzmann equation (or Vlasov equation when the collisional term is ignored). In these equations, all the external forces are separated from collisional effects [16]. Unless the actual force at each location is not significantly different from locally averaged forces, such as radiation with wavelengths less than the inter-particle distance (which can be treated in a chemical manner like UV-induced reactions), such equations provide a good description of the plasma dynamics.

However, solving the Boltzmann equation for the velocity distributions requires vast computational resources in numerical modeling, and therefore, fluid equations derived from integrals of the Boltzmann equation are normally used to solve the large-scale dynamics. The most complex model currently used for the dynamics and chemistry in the partially ionized plasma of the ionosphere-thermosphere system (with collective plasma-neutral gas interactions) is the set of 13-moment multi-fluid equations (mass, 3 elements of velocity, temperature, 5 elements of stress tensor, and 3 elements of heat flow) with Boltzmann collision integrals under the assumption that each species has a smooth distribution (Maxwellian, bi-Maxwellian, tri-Maxwellian, and toroidal, including the anisotropic case) so that a truncated expansion can be applied to the collision terms [16, 17]. This assumption works well for a small net energy loss (using a sort of linear approximation) such as Coulomb collisions, elastic plasma-neutral gas collisions, collisions between different neutral species, and a resonant charge exchange interaction between an ion and its corresponding neutral particle, which is pseudo-elastic.

Models are further simplified in various manners. For the Earth's upper atmosphere there are many models: TGCM (Thermosphere General Circulation Model); GITM (Global Ionosphere Thermosphere Model); WACCM (Whole Atmosphere Community Climate Model); TIE-GCM (Thermosphere Ionosphere Electrodynamics General Circulation Model); TIME-GCM (Thermosphere Ionosphere Mesosphere Electrodynamics General Circulation Model); CTIM (Coupled Thermosphere Ionosphere Model); CTIP (Coupled Thermosphere Ionosphere Plasmasphere Model); and CMAT (Coupled Middle Atmosphere Thermosphere Mode), see Bougher et al. [17] and references therein. All these models are designed under the assumptions of (a) a Maxwellian-type distribution, (b) no minor components except WACCM, which is specialized for climate change, (c) well-defined boundary conditions, (d) a specified energy input, and other conditions.

On the other hand, collisions play a fundamental role in the dynamics and energetics of ionospheres. They are responsible for the production of ions, diffusion of plasma from high to low density regions, conduction of heat from hot to cold regions, and exchange of energy between different species, among other processes. The collisional processes can be either elastic or inelastic. Some interactions lead to chemical reactions. All these processes wait for future investigations.

As we have mentioned earlier, it is difficult to learn from the interaction when the neutral particles are in the form of grains, which deserves its own study field of dusty plasma. The plasma-grain interactions, often taking place at the grain surfaces, are an important ingredient. The interstellar medium embodies this situation, where equilibrium is assumed between the ambient interstellar gas and dust grain condensation nuclei. However, modeling the composition depends on the condensation temperature, ambient UV flux, cosmic ray radiation field, charging, and surface area during the growth of the grain. The UV flux may also lead to grain charging and dusty plasma effects. Regarding protoplanetary discs for which such interaction is under the influence of a young star, significant progress has been made in view of the growing body of observational data (e.g. with ALMA), but more can also be learned from the study of comets and asteroids as relics of Solar System formation that have undergone limited alteration since then. Even minor species can play a major dynamic role, as they may behave as catalysts, changing the surface albedo or the sublimation temperature of ices. Thus, plasma-grain interactions or the ion-neutral problem constitute fundamental questions that are still unsolved, and hence they motivate us to tackle the ion-neutral gas interaction in the gas form (including heavy molecules) as a separate problem.

2.2 Limitations

The exact nature of the collision process depends both on the relative kinetic energy of the colliding particles and on the type of particles. In general, elastic collisions dominate at low energies, but as the relative kinetic energy increases, inelastic collisions become progressively more important. The excess energy during inelastic collisions is normally converted into, in the order of rotational, vibrational, electronic excitation, and ionization, as the relative kinetic energy increases. However, the different collision processes can affect the continuity, momentum, and energy equations in several different ways.

This complicates the plasma dynamics and chemistry especially when the externally provided variable energy density exceeds the pre-existing energy density under quasi-static state because collisions take place under the influence of short-range external fields and adding an AC electric field further alters the collision configuration. In such cases, it is difficult to evaluate the external force terms in the multi-fluid equations and the collective effects on the collisional term. Even the derived distribution can already violate the Maxwellian assumption. Since the relative energy between the variable external energy and pre-existing energy must play an important role, unexpected plasma behaviors can arise in low-energy density plasma, with low density and low temperature.

By contrast, if the external field is not strong, its (collective) effects on the collision process also cannot be ignored. Such forces are formulated with, e.g., quasi-linear approximation to describe the ion dynamics. However, quantitative verification of the Boltzmann collision integrals in the real space environment is not easy even if the distribution function is known. What makes space environments special are the unique combinations of phenomena and their interplay. Studying plasma-neutral gas interactions becomes more challenging when some of the neutral particles condense to form clouds or heavy molecules, but not as heavy as grains or dust.

3 Observation-model discrepancy

For high-density collisional regions such as the lower thermosphere, existing models provide a good estimate of the bulk ion properties from bulk neutral properties when compared with ionospheric and thermospheric observations. However, when the partially ionized plasma becomes tenuous with very low collision rates both for neutral species and ions, such as at altitudes above 300 km for the Earth's case, observations start to depart from what we expect from combinations of empirical and theoretical models and from laboratory experiments because the assumptions of Maxwellian distributions are no longer valid, particularly near the exobase.

3.1 Earth: neutral particle behavior in the upper thermosphere and exosphere

Ultraviolet observations of N₂ and O in the Earth's upper thermospheric density and temperature profile by NASA's TIMED satellite [18] found a significant discrepancy with the empirical NRLMSIS model [19]. Even the scale height for density is not yet clear: for hydrogen, the UV observations of the exosphere beyond 3 R_E indicate a scale height of about 20000 km for one order of magnitude decrease [20] as shown in Fig. 1a, whereas it is only 3000 km for the thermospheric model based on outdated in-situ measurements [21].

Fig. 1

a Average exospheric hydrogen density profile that is model-fitted from Lyman-alpha line-of-sight observations by the two TWINS spacecraft [20]. b Example altitude profile by the International MSIS model (https://ccmc.gsfc.nasa.gov/modelweb/models/nrlmsise00.php). The smoothness of the profile (nearly exponential above 200 km for neutral species) comes from the lack of observations beyond the 1960's [21]

For the range between 500 km and 3 R_E, where the exospheric profiles are basically obtained from the hydrostatic assumption as shown in Fig. 1b, there is no reliable information. This comes partly from insufficient observational knowledge on the energy re-distribution in that region, and partly from the lack of sufficient in-situ observations of neutral species and ions in the upper thermosphere and above [22]. Modern spacecraft that carry accelerometers for total density measurements do not cover that altitude range, and we still rely on measurements from the 1960's–1970's that are already 50 years old (except DE-2, from 1981).

The discrepancy or unexpected dynamics becomes more significant when a massive energy input is provided from space, e.g., near the cusp and during geomagnetic storms. Figure 2 shows the cusp case. Narrow channels with a density increase of neutral particles are observed near the cusp by CHAMP satellite [22]. Since strong field-aligned currents, both DC and AC, are continuously providing electromagnetic energy to the ionosphere in a narrow region in the cusp, such a density enhancement is conventionally considered to be the result of upward neutral wind sustained by the Joule heating at 120–130 km altitude [22]. However, simulations of neutral wind in a narrow channel [23] do not reproduce simple upward flow but require downward flow at the sides. The strong structuring of density and temperature has also been found by TIMED, which showed the structure within 5° in latitude during geomagnetic storms, while models predict essentially constant density (less than a factor of 2 change, [18].

Fig. 2

a CHAMP observation of density (using accelerometer) and fine-scale field-aligned current derived from magnetic field at above 400 km altitude [22]. b Simulation of neutral wind in narrow channel [23]

During geomagnetic storms, when the energy flow from the magnetosphere to the thermosphere is enhanced, neutral properties deviate over an area that is wider than the local cusp where the energy input is locally high. The TIMED satellite [18, 24,25,26] showed large variability of neutral temperature and density of O and N₂, responding to both the solar EUV flux and the magnetospheric activity, which are significantly different from the model predictions for average conditions [19, 27, 28]. For example, during geomagnetic storm periods, the temperature nearly doubled and the N₂ density increased by one order of magnitude within 10 days. Figure 3 shows observations of neutral density during major geomagnetic storms by GRACE the satellite [29] and the TWINS satellites [30]. The enhancement of the neutral density in response to major geomagnetic storms (black line in Fig. 3a) is much more than it was predicted by the empirical model (red line in Fig. 3a) during similar but stable conditions. This also indicates that the enhanced energy inflow caused an unexpected response of the neutral atmosphere [31].

Fig. 3

a Neutral densities from GRACE measurements (black) and the empirical thermosphere JB08 model (red) using average daily indices in November 2004 [29]. The sudden increase due to the X2.0 solar flare is marked as 1, whereas the impact of an interplanetary coronal mass ejection (ICME) a few hours later is marked as 2. b TWINS Lyman-alpha observations of relative variation in the column density of exospheric H that is represented by total solar Lyman-alpha flux (%) when a large geomagnetic storm took place [30]

In summary, our knowledge is not sufficient to even understand the basic behavior of the terrestrial upper ionosphere and upper thermosphere. This equally applies to ion-neutral phenomena in the mesosphere, such as polar mesospheric summer and winter echoes that seem to be partially influenced by solar activity [32]. ESA's candidate Earth Explorer 10 mission Daedalus [33] would have contributed to improving our understanding of the plasma-neutral gas interactions in the lower thermosphere and ionosphere in view of its special orbit (with perigee between 120 and 150 km altitude) and with its instrument suite that consists of ion, neutral, and electromagnetic field instruments. In February 2021, unfortunately, Daedalus was not selected to go forward to Phase A studies.

3.2 Venus and Titan: super-rotation and fast ion flow

The cause of the super-rotation of Venus' atmosphere [34] is a long-standing mystery. Such a large-scale atmospheric convection, much faster than the surface rotation, was also found on Titan [35], suggesting that this might be a common feature of atmospheric dynamics on planets or moons with sufficient atmosphere and slow solid rotation. There were two fundamentally different ideas regarding the driver: (i) the momentum of the extremely slow surface motion keeps transferring a massive total momentum to the upper atmosphere so that it flows 100 times faster than the ground, and (ii) plasma transfers a sufficient amount of momentum to the neutral atmosphere despite the plasma density being much smaller than the neutral density. The amount of the transferred energy does not have to be very large (unlike terrestrial global circulation) because intrinsic modes of planetary convection might exist, such that a very small momentum transfer from either below (the ground) or above (space) may maintain the mode. The Japanese Venus mission Akatsuki (https://akatsuki.isas.jaxa.jp/en/mission/) is dedicated to this problem by examining details of the atmospheric convection to evaluate the energy transfer from smaller-scale to larger-scale convection. Akatsuki's observations indicated a strong third candidate scenario: (iii) the thermal tide at the cloud layer can play a major role (like a piston), leaving the relation to and contribution from the ionospheric convection as an unsolved problem.

While Akatsuki did not include the instrumentation to examine the second scenario due to mass limitations, both Venus Express [36, 37] and Pioneer Venus Orbiter [38] showed strong ion convection in the super-rotation direction, with velocity 10 times faster in the Venus Express observations, as shown in Fig. 4. The observations suggest that the ionospheric super-rotation and atmospheric super-rotation are related [39], raising a possibility of a much more effective momentum transfer than predicted by any model of plasma-neutral gas interaction.

Fig. 4

Ion convection directions observed by Venus Express [36]

In addition to super-rotation, Titan has several other mysteries that are relevant to the plasma-neutral gas interaction. One is the cause of the massive cold ion outflow from Titan's ionosphere, which is believed to be too cold to produce such an outflow. Unexpectedly high-density cold ions in Titan's upper ionosphere and high escape rates with ~ 100 km/s velocity were found by Cassini spacecraft [40, 41], as shown in Fig. 5. If the ion velocity is maintained by the magnetospheric convection of Saturn or by other plasma processes, scenario (ii) for the super-rotation may apply here because thermal tides at Tidan far away from the Sun are very small. However, the momentum may still be transferred from neutral atmosphere's super-rotation (which is much slower than the observed ion flow) to the ion flow. In both cases, the observations suggest a momentum transfer that is higher than predicted in any model of plasma-neutral gas interaction.

Fig. 5

a Cassini observations of density and velocity of cold (thermal) ions above the Titan ionosphere [41]. b Summary of cold ion escape observed by Cassini [40]

3.3 Cold environments such as interstellar space: formation of organic matter

Another important issue relevant to the plasma-neutral gas interaction at Titan is the formation of heavy molecules, including organic matter [42]. The process is more chemistry-led in a collisional atmosphere rather than being controlled by collective effects of external forces. In the terrestrial middle atmosphere, cold environments are known to enhance certain types of chemical reactions such as the ozone depletion [43] and the formation of noctilucent clouds and heavier particles causing specific radar echoes near the mesopause [44]. Similarly, the enhanced plasma-neutral gas chemistry in Titan's upper atmosphere is expected to behave as a purely chemical system [45]. However, this chemistry is initiated by external energy provided by the solar UV, high-energy photons, electrons, and ions, through ionization of the major neutral species like nitrogen and methane.

The Cassini mission confirmed that Titan has one of the most compositionally complex ionospheres in the Solar System, with roughly 50 molecular ions at or above the detection threshold, most of which are composed of C, H, and N, as shown in Fig. 6 [46]. Unlike terrestrial atmospheric chemistry, where heavy molecules imply water compounds [2, 47], the observed composition at Titan naturally should lead to the formation of amino acids [48] although Cassini's instruments were not capable of identifying them. It appears that much of the interesting chemistry, even that forming heavy species, occurs in the upper atmosphere rather than at lower altitudes, which indicates that energetic particles from above may be one of the key elements in addition to the UV irradiation.

Fig. 6

Cassini observation of ionospheric heavy ions [46]

The formation of organic matter, including amino acids, in cold tenuous environments may also occur in the formation region of comets (such as the Kuiper belt and the Oort cloud) and in interstellar space where the environment is very cold [49]. Figure 7 shows observations of a cometary amino acid by the Rosetta spacecraft [50]. Because of the intimate relationship between the condensed and gas phases in molecular clouds and their exposure to strong UV from young OB stars in star-forming regions, and also due to their long-duration immersion in the cosmic ray background, the formation pathways leading to organic matter can be multiple and complex, beyond what we can model so far. Such cold environments make the situation more favorable, when  an external one-time energy deposit exceeds the background energy density in non-thermal processes (e.g., cosmic ray energy deposition inside an icy dust grain triggering the formation of chemical radicals), but interaction mechanisms in such environments are impossible to examine in a laboratory experiment [51].

Fig. 7

Rosetta observations of volatile Glycine (C₂H₅NO₂) and other amino acids [50]

3.4 Comet: unexpected structures in plasma-neutral gas mixed plasma

Comets are fascinating laboratories for studying plasma-neutral gas interactions, both for the formation of heavy molecules and for the solar wind interaction with the outgassing of neutral species. Rosetta was able to explore the diamagnetic cavity, a completely field-free region, at comet 67P/Churyumov-Gerasimenko. Figure 8 shows an example of these measurements [52]. The boundary normal direction is variable which implies that the structure is not spherical in shape. Henri et al., [53] found that the boundary location can be organized by the electron-neutral collision rate, but the formation mechanism has not been elucidated yet. At high activity comets, like 1P/Halley, the ion-neutral collisions are an important mechanism of energy transfer in the inner coma. There, the ions are efficiently cooled and remain coupled to the neutral species. Then the influence of collisions with neutral species is deemed important in forming these diamagnetic cavities at comets. Indeed, the neutral particle density and their composition determines the amount of ionization and thus the mass-loading of the solar wind plasma, which then affects the size of the diamagnetic cavity. The role of charged dust in the coma remains largely unexplored.

Fig. 8

a Rosetta observations of magnetic cavity; b The observed location and the boundary normal direction (bar direction); c Zoom up of (b), illustrating the temporal boundary of the cavity (solid line) that is rippled from the average boundary (dashed line) but its physics is still unclear [52]. X-axis points sunward, z-axis points northward in the orbital plane

3.5 Meteor: air burst

Meteors are known to produce a shock front leading to an enhanced ionization of the ambient atmosphere (because of intense heating at the shock) and of ablated meteor material (through high-speed collisions with air) [54]. The Chelyabinsk meteor burst in 2013 produced more energy than the traditional models predicted. A large part of its kinetic energy was unexpectedly consumed in the atmosphere rather than at ground impact, causing various effects in the geomagnetic field, lithosphere, and atmosphere. Most of the energy was emitted as a result of disruption (airburst) at around 27–30 km altitudes, affecting the ionospheric electron density in a wide area, as illustrated in Fig. 9 [55]. This indicates that energy conversion from the meteor motion to the atmosphere through the plasma around the meteoroid was more effective in terms of the plasma-neutral gas interaction than our present-day knowledge suggests.

Fig. 9

Illustration of how the Chelyabinsk meteoroid airburst affected the ionosphere [55]

3.6 Past climate change: solar influence

The role of the Sun's plasma and magnetic activity in the paleoclimate (4 billion years ago) and climate change over the past millennia and longer (but prior to major anthropogenic impact on climate) is the subject of a long-standing debate for nearly 30 years after the introduction of non-linear methods to correlate the solar activity (length of the solar cycle, length of solar minimum, or strength of solar dipole magnetic field, instead of simple sunspot number or solar irradiance) with the terrestrial climate (not only the average temperature but also the regional pressure such as north Atlantic oscillation or cloud coverage) [56,57,58,59,60,61]. Figure 10 shows the correlation study by Stauning [60]. The reason that the solar impacts have been ignored in climate models is an lack of established understanding of a physical link between the solar activity and tropospheric temperature or meteorological phenomena [62].

Fig. 10

Northern hemisphere average temperature (red line) and length of sunspot cycle (blue line). Before the human effect took over during the 1980's, they are strongly correlated [60]

In the upper thermosphere the ion density and neutral density are comparable. If the plasma-neutral gas interactions are strongly intensified when the external energy source grows, as has been suggested from observational discrepancies (cf. §3.1 above), the neutral atmosphere could be affected too via the vertical coupling of the energy in the atmosphere through, e.g., gravity waves. Thus, the influence of the Sun or of other external sources (e.g., galactic cosmic rays) on atmospheric chemistry that shapes the past climate variability cannot be evaluated unless we understand the interaction between the plasma and the neutral atmosphere.

4 Science questions related to the plasma-neutral gas interactions

As discussed above, there are many unexplained observations related to the plasma-neutral gas interactions. The above examples are mainly focused on ion-neutral interactions, but our understanding of electron-neutral interactions also needs to be updated.

4.1 First fundamental question: dynamics aspect

The behavior of comet atmospheres and magnetospheres, including diamagnetic cavities (§3.4), indicates that the plasma-neutral gas interactions can play an important role in the dynamics. The terrestrial examples (§3.1, §3.5, and §3.6) illustrate the importance of the plasma-neutral gas interactions on the energy re-distribution between energized ions and neutral species and how the ambient environment has often been overlooked, i.e., how external energy feeds into the energization of ions, of neutral species, or of the background populations (acceleration and thermalization). Either ions or neutral species could depend more sensitively on the external drivers than what the present models predict. This problem is formulated as the first fundamental question:

• (A) How and by how much do plasma-neutral gas interactions influence the re-distribution of externally provided energy to the composing species?

  The plasma-neutral gas interaction and subsequent energy re-distribution is expected to be largely modified when the external energy (characterized by energy flux density) is large compared to the background energy (characterized by pressure), which is more readily the case in the upper ionosphere near the exobase. Although the most affected region has a limited extent, the consequences of the enhanced energy re-distribution through the plasma-neutral gas interaction can be far-reaching. They are classified into the following four major topics.

• (A1) Impact of atmospheric particle energization on long-term large-scale evolution:

  A more extreme energy re-distribution, such as focusing the energy into specific form, causes more atmospheric heating for both ions and neutral species directly in the upper thermosphere in addition to the Joule heating in the lower thermosphere. This is important for understanding the origin of certain types of ion escape that require neutral species reaching to altitudes from which adiabatic acceleration and ion acceleration through ambipolar and/or auroral electric fields become effective, for assessing the present-day atmospheric escape rate and its effects on magnetospheric circulation and dynamics, and for understanding atmospheric escape over geological time [62]. This is related to the question whether a magnetic field protects an atmosphere against escape, or not [63, 64]. The problem can be generalized to the Solar System size, e.g., in the interaction region between the heliosphere and the interstellar medium.

• (A2) Structures and variability in the upper thermosphere and exosphere:

  Since the external energy that is provided from space to the upper thermosphere is localized in the dayside cusp or very variable in the auroral oval, the energy re-distribution in the upper thermosphere through the ion-neutral interaction there should be enhanced locally in space and/or variable globally (§3.1), causing a structure and variability near the exobase and in the exosphere. The exobase altitude and temperature and scale height of the exosphere determine a large part of neutral escape from Mars and the ancient Earth. Hence, local anomalies and/or temporal changes in this region significantly modify the neutral escape and the related neutral dynamics from the lower part of the atmosphere. Through the vertical coupling via gravity waves and other mechanisms, such variability may influence even the lower thermosphere and the mesosphere as well as the local plasma-neutral gas interactions, particularly during severe magnetospheric activities such as magnetic storms. An improved understanding of the thermosphere will have immediate benefits for technological applications such as satellite drag in low Earth orbits, space debris management, and spacecraft re-entry. The anomaly of the exobase altitude is a natural feature of comets that have localized outgassing regions, and the same argument applies to the moons with plumes. A non-uniform neutral density is even expected at the heliospheric boundary.

• (A3) The turbulent energy cascade and the Kolmogorov scale in partially ionized plasma:

  Different interactions imply different scale sizes (in both space and time) in the energy transfer. In the small-scale limit of the turbulent energy cascade, an enhanced energy re-distribution through the plasma-neutral gas interaction will change the scale size of the energy cascade, influencing even the Kolmogorov scale. This cascade will become even more complex in the layered region where the ionization rate and the collision frequency rapidly change, like in a comet and the ionosphere. Since the turbulence energy is small, such a modification through the plasma-neutral interaction is expected to be substantial.

• (A4) Roles of ions in the transfer of angular momentum and energy to neutrals:

  The possibility that the dawn-dusk asymmetric plasma motion helps to maintain the super-rotation of the atmosphere of Venus (§3.2) indicates the possibility of more effective momentum and energy transfer from the Sun or protoplanetary disc to the protoplanets, with more significant roles of the plasma and the electromagnetic fields in the formation of the Solar System than so far understood. A higher energy transfer from the protoplanetary disc to the protoplanets may even heat the protoplanets more during their formation when the Sun was colder than at present. For example, strong solar flares are expected to have taken place during the ancient Earth [10, 65], and may even provide extra heat to solve the faint Sun paradox. Since the effect is expected to be of large scale but slow, it is also relevant to the plasma effects on the upper atmosphere on the time scale of climate variability. A more effective energy re-distribution also means a larger plasma energy input to the neutral atmosphere, which particularly affects the mesospheric climate, with a possible long-term influence on the stratosphere and even on the tropopause.

4.2 Second fundamental question: chemistry aspect

The observations of organic matter in Titan, comets, and the interstellar medium (§3.3) indicate that the plasma-neutral gas interactions in low-density and low-temperature environments might contribute to chemistry and changes in composition, including the formation of heavy molecules and organic matter such as biomolecules and amino acids. Also, sputtering chemistry by ion-atmosphere interaction is another candidate in forming heavy particles as an analogy of the surface sputtering chemistry. These indications lead to the second fundamental question:

• (B) How and by how much did plasma-neutral gas interactions contribute toward the growth of heavy complex molecules and biomolecules?

  Here, the interaction includes both the chemical reactions and plasma physical interaction, but excludes surface interaction which has its own important science as mentioned in Section 1. Both types of reaction offer major topics of scientific study.

• (B1) Favorable conditions of plasma and external energy in enhancing the chemical reaction:

  Since the basic elements of organic matter (N₂, NH₃, NO, CH₄, CO₂, CO, H₂, H₂O, O₂) have very low condensation temperatures, low-temperature conditions are considered favorable for developing organic molecules in space. However, the conditions in space where organic matter is most likely formed (interstellar medium, Oort cloud, and Titan's ionosphere) are impossible to reproduce in the laboratory without in-situ measurements that provide the exact parameters, although some of the pure chemical interactions or reaction efficiencies have been determined pretty well with laboratory experiments and quantum chemistry modeling (cf. §5.1).

• (B2) Formation of plasma structures that may work as catalysts in tenuous environments:

  The terrestrial stratospheric chemistry is enhanced when the stratospheric thin clouds (i.e., layers of condensed molecules) are formed through rarefaction that is sustained by horizontal wind [66]. Thus, density structures sustained by the neutral dynamics (e.g., rarefied layers) may work as catalysts for the condensation and chemistry resulting from photolysis and electron-impact, and identifying such structures in the Solar System (as mentioned in A2) and examining their relation to the chemical reactions and to the roles of neutral species provide fundamental information about chemistry in space. Thus this is not limited to the Earth. For example, the organic matter in Titan is found at altitudes where vertical convection is weak, while we have no knowledge about structures in the formation regions of comets or interstellar space. Since energy density is very low and the plasma is collocated with substantial amounts of neutral species, a small amount of external energy may cause large modifications in the plasma-neutral gas interactions, and such interactions may complicate the reactions significantly.

5 Measurement strategy

As listed in the examples in Section 3, our current knowledge regarding plasma-neutral gas interactions is not sufficient, particularly for cold and low-density environments. This comes partly from a lack of missions to such environments, but mainly from a lack of appropriate instrumentation in all missions up to now, including those to the Earth's upper atmosphere and Venus. To improve our knowledge on the plasma-neutral gas interaction at low energy (< 1 keV), the most fundamental observations are those of velocity and density distributions of ions and neutral species. In addition, at least we need certain information for the composition.

The most dramatic lack of observations is that of ions and neutral species at energies below 10 eV, which for ion energy spectrometers corresponds to the + 1 eV limit of controlling the spacecraft potential by the existing methods. As a reference, a spacecraft velocity of 7.6 km/s (circular orbital velocity at the terrestrial exobase) corresponds to a ram energy of only 0.3 eV for H, 1.2 eV for He, 5 eV for O, much lower than 10 eV, so that these species have remained largely undetected. Moreover, in-situ detections need a trade-off between mass resolution and energy resolution. Even for the Earth, past neutral particle measurements are limited to bulk (moment) information such as density, bulk velocity, and temperature. Using the Doppler shift in optical remote sensing measurements to derive velocity and temperature requires high enough density in the target region such that emission or absorption is intense, but the regions we consider are low density regions. Also, the optical (emission and absorption) method cannot reveal the dynamics much below the exobase.

Recent developments in the in-situ instrumentation can solve some of what was impossible in past and on-going missions. A trade-off should also be considered when combining the remote sensing and in-situ observations, and between single- and multi-point measurements. This means that we must define mandatory measurements for each major topic outlined in points (A1) to (B2).

5.1 Why do we need in-situ observations in space in addition to the laboratory experiments?

The ion-neutral interaction problem is in principle reduced to the cross-section problem, which belongs to the field of fundamental microphysics and should first be determined by laboratory experiments with the aid of collision models. However, the microphysics process of collisions in a plasma is affected by the local magnetic and electric fields. These electric and magnetic fields are set by the macroscopic plasma environment, and their parameters are eventually measured through macroscopic quantities. Such influences are more significant for lower energy particles and under larger gradients in the environment. Therefore, the laboratory experiments may not fully represent real space environments with large-scale gradients and many external parameters (cf. Figure 11). In fact, space observations show notable discrepancies between model predictions and observations at higher altitudes in Earth's geospace (larger discrepancy at higher altitudes) as described in Section 3, and our knowledge of these cross-sections is not sufficient for evaluating the effects of ion-neutral and electron-neutral interactions in many space plasma environments ranging from the Earth to the interplanetary cloud.

Fig. 11

Illustration of complicated background conditions in space that are difficult to reproduce in a terrestrial laboratory

Some of these fundamental processes in space can be qualitatively reproduced and studied in the laboratory, but not quantitatively. For example, the field-aligned potential drop (double layer), which is a fundamental process in space, was first demonstrated in laboratory experiments [67] before it was found in space [68], and the laboratory experiments were improved after finding the parallel electric field in space. However, many space missions were still needed to study double layers in space because it is not possible to reproduce the space environment in a quantitatively representative manner in the laboratory.

Thus, the theme of "Plasma-neutral gas interactions in various space environments" must be addressed by space missions in various environments in terms of macroscopic plasma conditions related to collisions.

5.2 Required measurements for ions and neutral species

For (A1): To examine the role of plasma-neutral gas interactions on atmospheric escape, we must know the density profile and the velocity distributions at different altitudes for the most relevant species near the exobase and in the exosphere (H, He, N, N₂, NO, O, O₂, CO, CO₂ for the Earth's case), both for the thermal ion and neutral background components and for the non-thermal escaping components of ions and neutral particles. Here we note that the current empirical models of the exosphere and upper thermosphere, such as the MSIS model, are outdated [18] and not suitable for modeling the thermal escape. The TIMED results are even different from the estimates from ground-based observations of airglow [69].

Even the baseline densities of the most abundant species (O and N₂) are observed to be 20–30% below those of the empirical model, while the temperature is not directly measured so far, but estimated from the density gradient (scale height). The model cannot be tuned for the best fit because the discrepancy changes from year to year. To explain the mismatch, a higher cross-section to produce low energy Energetic Neutral Atoms (ENA; < 100 eV) than the current estimate for different solar conditions has been suggested as one possibility [18]. In this respect, covering H, He, N, N₂, and O, could already be sufficient for the Earth's case. Separation of N and O for the non-thermal component, which was difficult before but now becomes technically possible for < 100 eV, is needed to estimate the efficiency of nitrogen-related chemical and photochemical reactions, for which no good observational knowledge exists near the exobase and above. On the other hand, N–O separation is not required for the background velocity in the thermal energy range.

For (A2): To reveal the structures of these regions, the spatial distribution of bulk quantities (density, bulk drift velocity, and ideally temperatures of thermal and non-thermal components) becomes more important than their velocity distributions. To obtain data from different altitudes simultaneously, we need to combine the optical "snapshot" from line-of-sight integrated measurements with "in-situ" observations. This is possible with even a single spacecraft if the target region of the optical observation is along the spacecraft trajectory (we assume no significant change during this traversal) or is conjugate with the spacecraft during its traverse, like for the Reimei satellite, when conjugacy along the geomagnetic field can be assumed [70, 71]. A more standard method is a combination of two spacecraft or a combination with ground-based optical and radar measurements. To estimate the dynamics, isotope fractionation above the homopause can also be used. Therefore, very high accuracy ion composition measurements are recommended with mass resolution of m/∆m > 1000. This applies to both the Earth and extraterrestrial environments.

For (A3): To examine the small-scale limit, we need multi-point measurements of ions and neutral species with high-time resolution. Since this does not require fine composition information, small sub-satellites can provide the necessary information.

For (A4): To measure the momentum transfer from ions to neutral species through tangential stress, altitude profiles of velocity distribution for both ions and neutral species are needed. Since the composition information for such measurements can be at the minimum level, the requirement for (A1) and (A2) is sufficient.

For (B1): To diagnose the conditions favourable for growing heavy molecules, bulk properties of ions and neutral species (density, bulk velocity, and temperature) need to be known. Here, the temperature can be common for the cold backgrounds, and velocity can be measured only as an average over a long integration time. However, the separation of different species is needed in the density distribution measurements for H, N₂, NO, NH₃, O, H₂O, CH₄, CO, and CO₂. These requirements are covered by the measurements required for (A1) and (A2). In addition, detection of heavy molecules and organic molecules are needed. This means that we need a mass spectrometer of high mass resolution (m/∆m > 1000) that has very high mass limit such as m > 100 and a high sensitivity (supported by extensive ground-based efforts) for determination of fragmentation patterns, since untangling the contributions of the neutral species to the recorded fragment intensities is a major puzzle for heavy species. High mass resolution is also required to obtain the isotope ratio of simple molecules because this gives essential information on the location and process of molecular formation [72,73,74].

For (B2): The extra requirement from (B1) is measuring differential velocities between species, for at least two major species (e.g., O and N₂). Such instruments are more difficult to build than what is required for (A2) because the velocity is expected to be very slow. Therefore, they have not been used in the past and present space observations but are under development.

5.3 Required measurements of the background plasma

In addition to the background magnetic field that is mandatory in describing the plasma, electron temperature and the DC electric field are needed. Ideally, electromagnetic or electrostatic waves with slow group velocities should also be known, but most of them do not influence the plasma-neutral gas interactions unless the energy density of the waves is very high, causing any type of resonance with the ions. In this sense, low sensitivity wave measurements at low frequencies (below 100 Hz) could be sufficient, although high frequency measurements can be useful as well, particularly for the Earth. The gravity field must be also considered but it will be anyway known before any mission.

5.4 Required measurements for the external energy source

Obvious energy sources are non-thermal ions and energetic neutral species. Each target environment is characterized by energy sources with its characteristic energies, such as the solar wind for comets and for the Earth, magnetospheric particles (keV–MeV) for the Earth and for moons, and cosmic rays including solar energetic particles for the Earth, planets, and interstellar space. Another obvious energy source is the radiation that directly triggers photochemistry for short wavelengths (UV and soft X-ray) and absorption and scattering for long wavelengths (infrared and mm waves). The solar source and a large fraction of cosmic sources can be monitored by other spacecraft and space weather monitoring, while planetary and galactic source fluxes in the outer Solar System might need local measurements (i.e., by the same space mission). However, the energy flux is probably low, and therefore such measurements might be optional. Electromagnetic waves from local sources might be more important to measure, for which the energy flux is very high, as mentioned in §5.3.

5.5 Summary of relevant measurements

Table 1 summarizes mandatory and optional measurement requirements, in which we also specified minimum measurement requirements: (i) neutral and ion density for major species (which include composition and ionization rate), (ii) neutral velocity distribution for major species (which may also provide the average neutral temperature depending to design), (iii) cold ion (< 10 eV) energy spectra for major species, and (iv) approximate direction of background DC magnetic field (the Venus Express level of electromagnetic cleanness is sufficient). The other instrumentation required to study the problems of plasma-neutral gas (including ion-neutral) interactions, depends on how many of the sub-themes are to be studied. They include (v) gravity, (vi) internal energy such as velocity differences between different species, (vii) external free energy such as radiation, cosmic rays, and large-scale electric, and (viii) the existence of catalysts such as the surfaces of the dust grains, cloud (layer of condensed molecules), or catalytic structures such as non-mixing layers.

Table 1 Required and useful measurements for both in-situ and remote sensing (RS) methods

Not all the measurements in Table 1 have been possible in the past and present missions. Even the minimum mandatory measurements (i)-(vi) are not yet available: instruments for (i) and (iv) are mature, whereas the instrumentation for (iii) needs improvements, and instruments for (ii) are still under development (present Technology Readiness Level is 3). Here, "mature" does not necessarily mean that the size is optimized for missions with severe mass and power limitations.

However, instrument technology has significantly improved (for optical remote sensing, plasma spectrometers, mass spectrometers, and electric and magnetic field instruments) for near future missions. The highest-rank ("1" in Table 1, or (i)-(iv) above) in-situ measurements can constitute a small plasma package with total payload mass of < 20 kg at present and will become < 15 kg within a decade. With such a minimum package, a large part of the important questions on the plasma-neutral gas interactions (A1)–(B2) can be studied at planets or moons with an atmosphere, by orbiting through the upper ionospheres or exospheres. The detailed description of how these measurements answer the questions in the listed topics (A1)–(B2) is given in Section 6 where a mission for terrestrial observations is presented as an example.

Recent and future improvements are also needed for the spacecraft technology, such as the automated operation of multiple spacecraft including low-cost sub-spacecraft of less than 50 kg (the Swedish Innosat platform already achieved this for 15 kg payload). The improvements are also needed for  methods combining in-situ and remote sensing measurements, and for the upgraded ground infrastructure. These technologies have rapidly improved in the recent decade. For example, in the middle of 2010's, Comet Interceptor [75] was not possible even as an ESA's M-class mission. We expect further improvements within a decade.

5.6 Destinations of relevant missions: almost all Solar System objectives

Possible parameters that influence the ion-neutral interactions (cf. (i)-(viii) in §5.5) can be also summarized as: (1) temperature, (2) density and degree of ionization, (3) gravity, (4) external free energy, (5) internal energy, and (6) the existence of catalysts. While there is room to improve the knowledge on (6) and a part of (4) and (5) through laboratory experiments, extreme environments of (1)–(3), e.g., low value extremes are difficult to achieve inside ground laboratory experiments (cf. §5.1).

Limiting the discussion just to parameters (1)–(3), the Solar System is full of different environments. Table 2 summarizes a number of possible missions that may contribute to the plasma-neutral gas interaction theme. Most of these are self-explanatory. The "artificial comet" mission refers to a massive release of water or other "light materials" in the solar wind. The "planetary L2 composition" mission aims at measuring the composition of pick-up ions of planetary origin near planetary L2 points, since there might be several piggy-back opportunities for Earth L2 telescopes or for Martian missions in the 2040's. Other destinations have been under discussion by other space agencies. For each destination, temperature (T), density (n), and gravity (g) are classified from extremely low to extremely high. Therefore, each mission can address the topics only in that range.

Table 2 Possible destinations

Considering the wide range of environments to be investigated, this theme is better pursued as just one of the science objectives in as many missions to Solar System objects as possible, including comets, all planets (except Mercury), and moons with substantial atmosphere (e.g., Titan, Enceladus, Europa, Triton). Such an approach enhances the mission science for all Solar System missions (except solar missions). This is not limited to atmospheric and plasma missions, but also to surface missions and sample return missions if the spacecraft (orbiter) traverses the upper ionosphere or exosphere.

The most comprehensive knowledge can be obtained with a comet rendezvous mission for aphelion reaching the Kuiper belt so that the spacecraft can measure both the comet environment and the space plasma in the Kuiper belt. The advantage such a comet target lies in the extremely large range of temperature and UV environments along the highly elliptic orbit. This produces various levels of outgassing that also lead to various levels of density and gradients. Therefore, we can examine the plasma-neutral gas interactions in various space environments with a single mission in terms of (1)–(6) mentioned above. Such a mission is also useful as a step toward the Halley comet rendezvous in the 2060's, and in fact at least two such missions are proposed in White Papers in this issue (a cryogenic comet sample return mission by D. Bockelée-Morvan and a comet plasma mission by C. Goetz). Since the required measurements can be performed with a suite of small instruments (~ 15 kg) as described in §5.5, this theme can easily be added even to a sample return mission from a comet.

On the other hand, other missions can also contribute to improving our knowledge on the plasma-neutral gas interactions to answer many of the fundamental questions on topics (A1)–(B2). By combining different targets (e.g., Earth and Venus with the same instrumentation, like Mars Express and Venus Express), even missions to study a high temperature or high-density environment also help understanding the solar energy conversion, which has different roles in the evolution of the Solar System, and even help understanding if low-temperature stars with neutral species possibly exist.

6 Terrestrial mission case

Since the plasma-neutral gas interaction problem is very fundamental, a mission in the terrestrial environment has a large advantage because of strong support from remote sensing measurements by ground-based instruments, including EISCAT_3D. The mandatory altitude range to cover is 500–3000 km, i.e., upper thermosphere and lower exosphere, where our knowledge of even the ground state is poor for both neutral species and cold thermal ions (except hydrogen atoms) as described in §3.1, and is an important subject even for the ground-based observation community. Here, the apogee of > 3000 km comes from the requirement to obtain the scale height for H. Since ion and neutral mass spectrometers have a dynamic range of six orders of magnitude, tuning the instruments for the exosphere can provide unprecedented new information.

6.1 Observation strategy using multiple spacecraft

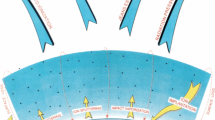
Figure 12 shows one example of such a mission design. The apogee altitude is 1.5 R_E (about 10000 km) in the figure but this is flexible between 3000 km and 30000 km (below the forbidden region for geosynchronous orbits and preferably avoiding the radiation belts). To combine the optical and in-situ measurements and to address topic (A3), a multi-spacecraft mission with three or more spacecraft is ideal. For both options in Fig. 12, the mission is composed of a main spinning spacecraft for in-situ observation (payload 100–120 kg), a 3-axis stabilized sub-spacecraft just for optical remote sensing observation (payload 10–15 kg), and one or two sub-spacecraft (the attitude control can be either spinning and 3-axis stabilized) for multi-point in-situ measurements flying with separation in the ion scale to fluid scale from the main spacecraft (payload 5–10 kg). A spinning platform is preferable for the main spacecraft to cover 3D for particle instruments, for which a substantial portion of the field-of-view (FOV) would otherwise be blocked by the spacecraft body on a 3-axis stabilized platform, and to have good coverage of DC electric field measurements.

Fig. 12

Orbits for the M-class or smaller class mission for the Earth and Venus

The difference between the left and right in Fig. 12 is where to locate the remote sensing observation spacecraft: (a) It can be placed in a completely different orbit than the in-situ spacecraft so that the camera's FOV includes the in-situ spacecraft for real-time comparison, or (b) fly together with the main spacecraft and look along the orbit so that the camera's FOV covers the region of in-situ observation with some time delay. The first option has the advantage of not looking at the high-density region, whereas the second option has the advantage of avoiding conjugacy problems. In the first option, the in-situ spacecraft is not always in good conjugacy with the remote sensing spacecraft even though the spacecraft inclination is adjusted such that the longitudinal drift velocity matches.

The telemetry for the in-situ sub-spacecraft is through the main spacecraft, both for downlink and uplink, so that the cost for ground operations can be minimized. In this sense, the second option reduces the cost because the telemetry for the remote sensing spacecraft can go through the main spacecraft. Using a despun platform could be less expensive than having a separate spacecraft for remote sensing, but by 2030 the cost for building and operating very small (< 50 kg) sub-satellites will be significantly reduced, so that the trade-off has to be re-evaluated. The telemetry link through the main spacecraft also opens up the possibility of having nearly identical platforms (with some difference in thermal design, the radiation protection, the antenna design, and numbers of payload or sub-spacecraft).

The other requirements for the orbit and spacecraft are:

• The 3-year radiation dose shall not be excessive so that it would require an unreasonable amount of shielding.

• Orbital parameters must be designed to require as few maneuvers as possible (e.g., free drift) to avoid contamination of composition measurements from (chemical) propulsion exhaust.

• To be able to study ion-neutral interactions properly, the spacecraft should cover the auroral regions, and thus the inclination must be as close to 90° as possible. This automatically facilitates conjugate observations with ground-based radar (e.g., EISCAT_3D) and optical instruments (e.g., Fabry–Pérot interferometer for airglow) that are mainly located in the polar region.

• At mission completion all spacecraft can be de-orbited.

6.2 Payload

Tables 3 and 4 summarizes a model payload. Compared to the Cluster mission, measurements of the neutral gas have to be added, ion spectrometers with sufficient mass separation ability have to be used, and the detection of low-energy ions has to be improved, whereas we do not require a very wide frequency range for waves. Still, most of the instruments are already available with acceptable masses and sensitivities. And developments for further miniaturisation of neutral gas mass spectrometers are ongoing, to use them on a cubesat platform [76]. As of 2020, instruments for neutral gas velocity and temperature with sufficient sensitivity are not ready. However, a miniature prototype with very low sensitivity has already flown on the Dellingr cubesat in 2017 [77, 78], and another design was also proposed by Shimoyama (private communication, 2019) as shown in Fig. 13. Therefore, this challenge can be most likely solved in the near future.

Table 3 Model payload elements with their technological heritage (last two columns): mandatory measurements

Table 4 Model payload elements with their technological heritage (last two columns): important measurements

Fig. 13

Preliminary design of NIVA instrument (Shimoyama, private communication, 2019) (https://www.irf.se/~yamau/future/2019N_enc3.pdf): (a) principle of measurement, and (b) an example of ion optical simulations. Particle trajectories are shown as coloured lines, with equipotential lines in the background

The addition of a strong suite for neutral gas and composition measurements makes this mission unique compared to the past missions. The last mission that obtained density profiles of the thermosphere and exosphere is 40 years old (Dynamics Explorer 2) and did not cover a very high altitude range (309 km × 1012 km). All recent missions to study the density profiles are using the line-of-sight integrated measurements, which strongly rely on the model (for example, the temperature of the exosphere is derived from the scale height with an assumption of nearly constant temperature). By combining in-situ measurements and remote sensing measurements, we can construct density profiles without the assumptions that are inevitable for line-of-sight observations. In addition, no systematic measurements of isotope ratios have been made in the terrestrial exosphere, although that has been done for Mars (MAVEN, https://www.nasa.gov/mission_pages/maven/overview/index.html) and comets (Rosetta, https://www.esa.int/Science_Exploration/Space_Science/Rosetta).

6.3 Support from the ground-based observations

In Tables 3 and 4, the ground-based observations will be included for many measurements. In principle, the mission is closed without such support, but accuracy and particularly the three dimensional (3D) spatial coverage improves significantly with the ground-based conjugate observations. The relevant facilities that already exist or are planned to be installed in the near future are:

• Incoherent scatter (IS) radars: located in different regions (e.g., Europe, North America, and Asia), these radars at 200–1000 MHz range can measure some key parameters described in §5.3 (electron temperature, electron density, ion temperature, and line-of-sight ion velocity) at different altitudes nearly simultaneously.

• EISCAT_3D (https://eiscat.se): the next generation IS radar will be able to cover a large 3D volume of space in very short time thanks to phased-array antenna arrays as opposed to a large parabolic dish, which can scan through a volume of space only very slowly. With high-power 5–10 MW transmitting and receiving antennas at the core site and 10,000 high-sensitivity receiving antennas at remote sites, EISCAT_3D covers a very wide area (> 300 km diameter at 500 km altitude with three sites), and is under construction toward operation in 2023 for the first three sites, and additional two sites are planned afterward. Even with a spacecraft velocity of 10 km/s (perigee velocity of a highly elliptic orbit), the spacecraft is continuously within this volume over 30 s for the diameter traversals (instead of passing at some distance from the radar line of sight in current systems). Since the Earth is magnetized, only the geomagnetic conjugacy is often required, which allows a much longer time sequence of continuous conjugate observations.

• SuperDARN: With much lower power than IS radars, and optimizing the array direction nearly horizontal, HF radars (8–22 MHz) can provide ion line-of-site velocity in a wide region in Earth's upper atmosphere and ionosphere. SuperDARN is a network of such HF radars from more than 30 sites, and continuously provides ionospheric convection. Although the detection altitude is lower than 150 km altitude, this gives important information on the plasma motion.

• Fabry–Pérot interferometer: The mid thermosphere (around 240 km altitude) is the region where the airglow intensity is maximum. Optical interferometry measurement of the Doppler spectrum is a standard method to obtain the neutral motion and temperature at the altitude where the airglow emission is maximized [79]. Although this altitude is lower than the spacecraft perigee, this gives another important piece of information on the momentum transfer and convection in the upper thermosphere. A scanning Doppler imager (SDI) is capable of measuring 2D wind and temperature fields from a snapshot of the all-sky image. The wide field-of-view can increase the opportunity to obtain simultaneous measurements with satellites. An international team is working to deploy multiple SDIs in the Northern Scandinavia.

• Magnetometers: Global and regional networks of the magnetometers are the most traditional ground-based support to indicate the ionospheric dynamics and electric currents that are important in evaluating the external energy, although there is no altitude resolution and the estimate is not perfect [80, 81]. In recent years, Iridium satellites also provide extra information about geomagnetic activity, improving the accuracy of the estimation of the electric current system obtained by the ground geomagnetic data.

• OH airglow imager: The upper mesosphere-lower thermosphere temperature can be permanently monitored based on OH airglow measurements around the globe. This will provide input data on temperature variations due to plasma-neutral gas interactions in the upper atmosphere.

6.4 Science Closure

By covering the energy distribution of both background neutrals and ions, together with their macroscopic parameters (n, v, T), energy transfer can be measured on the distribution function level, e.g., whether a double-peak distribution is formed or not when the velocity is different between ions and neutrals under low collision frequency. Thus, the effect of the external energy can be examined at the distribution function level, i.e., in wide energy range. This addresses (A1) and (A4). By adding extra measurement points using small sub-satellites, such measurements can even address (A3). A combination of the in-situ and remote sensing measurements (remote sensing measurements from both the spacecraft and from the ground) will reveal the layer structure in the global context, addressing (A2). The composition data can give the chemical interaction including photochemistry, addressing (B1). Combining with the observations of layer structure, this also addresses (B2).

6.5 Requirements for the spacecraft

For Earth missions, power and telemetry are not a major issue. Since the mission is oriented to neutral species and ions rather than waves and fields, the magnetic cleanliness and EMC requirements do not exceed the Cluster level, e.g., a linear regulated power system, and distributed single-point-ground power system. The other requirements for the orbit and spacecraft are:

• Cold Xenon propulsion is preferable for orbit maneuvers or attitude control instead of ordinary propulsion that contains nitrogen (N) because atomic nitrogen and nitrogen ion are the major components in the thermosphere and exosphere and any nitrogen contamination should be avoided. Similarly, propane (C₃H₈) should be avoided because it is easily dissociated into C₂H₃⁺, C₂H₄⁺ and C₂H₄⁺, covering the mass range of ¹⁴N₂ (mass 28) and ¹⁴N¹⁵N (mass 29).

• External conductive surfaces are needed to keep the spacecraft potential as constant and as low as possible, together with active spacecraft potential control.

• The required pointing accuracy is 1° (0.1° knowledge) for both the main spacecraft and the remote sensing sub-spacecraft.

• A Sun-pointing constant attitude is preferable to maintain a constant spacecraft surface exposure to sunlight. This helps to avoid evaporation of eventual condensed volatiles on the night side of the spacecraft, i.e., outgassing from the spacecraft associated with attitude change (lessons from Rosetta; [82, 83].

• All particle instruments shall be placed with unobstructed FOV so as not to harm the 3D observations.

With these requirements, a spacecraft with a dry mass of 350 kg is sufficient for the main spacecraft when the required power for payloads is less than 200 W (reasonable requirement). For the sub-spacecraft, a dry mass of 50–60 kg for remote sensing and a dry mass of 20–30 kg each for multipoint measurements is feasible. This means that total launch mass for all spacecraft would be < 700 kg for the Earth mission.

A similar mission could be devised for Venus. In that case, some on-board processing of the data before sending to the Earth would be needed. Such processing could be done by each science payload. The requirement on the spacecraft would be that it has sufficient mass memory (> 10 GByte). A main spacecraft dry mass of < 900 kg would be sufficient.

7 Technological challenges

As described in Section 6, new developments of or improvements toward light-weight instruments and low-cost small spacecraft are required to make the proposed observations feasible. For the instrument, the following developments and improvements are the technological challenges that must be solved for both the terrestrial mission and the Solar System missions:

• Develop a new instrument to measure the temperature of the background neutral gas for at least two major components except H. For the exobases of the Earth and Venus, it should be able to measure N₂ and O with an accuracy for 10 s integration that should correspond to the largest variation of temperature: ∆T = 300 K (or 30% for heated events with > 1000 K). For velocity, an accelerometer can give an accuracy up to tens m/s.

• Develop a new instrument to measure the 2D-velocity distribution of background neutral particles for at least two major components except H, with 10% sensitivity compared to the Maxwellian peak. The need for this measurement arises from the extraordinary interaction out of the theoretical prediction resulting in multiple-peaks in the velocity distribution.

• Improve the old instrument or newly develop an instrument to measure the velocity and energy distribution of the background cold ions.

• Improve the low energy ENA for < 100 eV toward high angular resolution. This improves significantly the estimate of the substantial cross-section that produces ENA at an energy range of 10–100 eV, for which our knowledge even in the laboratory is poor.

These challenges are being addressed at many places, and the design shown in Fig. 13 is one such attempt. In addition, the spacecraft and operation side have some technological issues to address for reliability and cost, to make the proposed multi-spacecraft missions as mentioned in Section 6 possible. As well as the requirement of further optimization for the inter-spacecraft telemetry and the low-cost manufacturing (including managing cost) of small sub-satellites, we have another challenge:

• The Sun-pointing constant attitude requirement means frequent maneuver operations because a maximum off-pointing from the solar direction cannot be kept due to Earth's rotation around the Sun (1% per day). Therefore, autonomous maneuvers using a Sun-sensor should be developed to keep the cost low. If not, as an alternative, a cold trap should be developed for the controlled condensation and re-evaporation of volatiles. This will avoid interference from the spacecraft background.

• Another autonomous system to be developed is for radiation belt detection so that all instruments can be turned on/off automatically. This is possible by using the on-board data (energetic particle detector and background noise in particle instruments that use a microchannel plate) combined with a radiation belt model and space weather predictions.

8 Summary

In this White Paper, prepared in response to the European Space Agency (ESA) Voyage 2050 Call, we advocated for the importance of advancing our knowledge of plasma-neutral gas interactions, and of deepening our understanding of the partially ionized environments that are ubiquitous in the upper atmospheres of planets and moons, and elsewhere in space. In future space missions, the above task requires addressing the following fundamental questions:

• (A) How and by how much do plasma-neutral gas interactions influence the re-distribution of externally provided energy to the composing species?

• (B) How and by how much do plasma-neutral gas interactions contribute toward the growth of heavy complex molecules and biomolecules?

Most matter in stars and interstellar space is composed of free ions and electrons, whereas the majority of planets, satellites, small bodies, and their envelopes are composed of neutral species. Given our very limited understanding of plasma-neutral gas interactions, the small amount of neutral species in space above the exobase and the effects of electric charges on neutrals have been underestimated in considering plasma dynamics and the formation of planets, exoplanets, satellites, small bodies, and their atmospheres.

However, recent space observations in the upper thermosphere and exosphere where plasma-neutral gas collisions become important compared to neutral–neutral interactions suggest that this lack of knowledge of the plasma-neutral gas interactions is a serious drawback when trying to describe neutral behavior in a tenuous plasma such as the upper thermosphere and exosphere. This raises the first question (A).

Furthermore, the finding of organic matter, including amino acids and other building blocks of life in comets and in interstellar space, indicates that they are formed in low-temperature environments where neutral-ion interactions cannot be neglected with respect to neutral–neutral interactions. This is the chemical aspect of the energy re-distribution problem. Since the amount and types of the required energy is different from physical energy re-distribution, the chemical aspect raises its own question (B).

Answering these questions is an absolute prerequisite for addressing the long-standing question of atmospheric escape and the origin of biomolecules, and their roles in the evolution of planets, moons, or comets under the influence of energy sources in the form of electromagnetic and corpuscular radiation.

Study of the ion-neutral and electron-neutral interactions requires accurate measurements of plasma and neutral species in relevant partially ionized media, including composition of the neutral and ion species, velocity distribution of ions and electrons, as well as ambient energy that is characterized by electric and magnetic fields, radiation, and temperature. Since such complicated environments, particularly under the influence of various electromagnetic fields and with complicated composition, temperature, and radiation fluxes, cannot easily be reproduced in a laboratory, the only way to understand the plasma-neutral gas interactions in space is through in-situ observations in various environments in space, a task suitable for space missions. In particular, observations in low-density environments with substantial neutral particle content are needed, for example, in the upper ionosphere near the exobase of a planet or natural satellite, in comets, or in interstellar space.

Ideally, measurements should be performed in partially ionized plasmas under diverse thermal conditions, for example, from extremely low to moderately high temperatures. Doing so in a long-period comet is one obvious candidate because it covers wide density and temperature ranges. The diversity of the target environments can also be achieved through several different missions in collaboration with other space agencies. In this respect, we can start with a mission at a nearby planet (Earth or Venus) as a small- or medium-class mission, while we can also contribute relevant instrumentation to possible large-class Solar System missions (e.g., interstellar probe, an ice giant mission, or a long-period comet mission). In this article, we have described one possible mission scenario for the Earth's upper atmosphere, which can be copied for Venus, while the space physics community is simultaneously submitting White Papers devoted to the other relevant environments.