1 Introduction

Metis is the first solar coronagraph designed for a space mission, the Solar Orbiter ESA-NASA observatory [21], capable of performing simultaneous imaging of the off-limb solar corona both in the visible and in the ultraviolet. This mission will reach the inner heliosphere to observe the Sun from elliptical orbits with perihelion distances as small as 0.28 AU and aphelion distances of about 0.8 AU. Metis has been conceived to perform imaging of the off-limb solar corona simultaneously in visible (580–640 nm) and ultraviolet (centered at HI Lyman-α 121.6 nm line, 15 nm FWHM) spectral bands. This will allow to diagnose, with unprecedented temporal coverage and spatial resolution, the structures and dynamics of the solar corona in the 1.6°-2.9° field of view (FoV), which corresponds to 1.7 to 3.1 solar radii (R☉) at the minimum 0.28 AU perihelion distance. Metis will image the linearly polarized broad-band visible-light emission and the narrow-band ultraviolet (UV) HI Lyman-α line emission of the full corona will be imaged by Metis with a nominal spatial resolution (2-pixel element) of 40 arcsec. These measurements will allow for the first time a simultaneous characterization of the main physical parameters (i.e., density, temperature and outflow velocities) of the electron and hydrogen plasma components of the full corona and of the solar wind in the region where the acceleration process takes place [3, 13, 23].

The most commonly used optical design for visible-light (VL) solar coronagraphs is based on the traditional design proposed by Bernard Lyot who first introduced a stop along the optical path to block the light diffraction off the entrance pupil [20]. This solution is highly effective to allow the visibility of the very weak solar corona, while masking at the same time the solar disk, even if only at small distances from the disk limb. In order to include also the extended corona, a modified design has then been introduced adopting external occultation [10, 22]. This allows the observation of the fainter outer corona, reducing the Sun disk stray light to levels as low as 10−9 inside the coronagraph, and reduces the intrinsic need of a very high dynamic range thanks to the pupil vignetting at the brighter coronal regions close to the solar disk. Metis has been designed starting from these very consolidated concepts, but adapting them to two fundamental requirements of this project: the maintenance of the instrument stability in very variable thermal conditions, and the observability of the corona in both VL and UV spectral bands.

The Solar Orbiter mission profile is quite challenging because of the dramatic variation of the distance from the Sun: this forced instrument designs not only able to sustain the extremely high thermal flux at the perihelion, but also capable to maintain operational the instruments during the whole orbit, independent of the large variability of the satellite temperature and heat flow. This poses important constraints to the overall thermal design of the instrument: in fact, the thermo-elastic structural deformations associated to these variable thermal conditions have to be controlled to minimize their impact on the optical performance of the instrument. Actually, the work done in order to satisfy this requirement has driven the main innovative idea at the basis of the Metis optical design. Moreover, Solar Orbiter being, de-facto, an interplanetary mission, there are also very stringent constraints on the mass, volume and telemetry available to the scientific payload. This puts serious limitations on the Metis design, which in some cases are very difficult to cope with. At the same time, the requirement of being able to simultaneously observe the solar corona in two different spectral bands with very different “optical” characteristics has forced the search of suitable dichroic materials, and of optimized coatings for all the Metis optical elements. The goodness of the proposed solution was tested with the Sounding Rocket Coronagraphic Experiment (SCORE) onboard the HERSCHEL suborbital mission (e.g., [11]). All this has led to the realization of very innovative solutions and at the end to a very peculiar solar coronagraph optical design.

The Metis optical design and its characteristics are described in the following. In section 2 the expected instrument scientific performance is provided. Then, the optical design is described in detail in section 3, for both the channels, as well its nominal optical performance; a subsection is also dedicated to the instrument tolerance analysis. Section 4 is a short one, dedicated to a brief description of the Metis detectors. Finally, section 5 is dedicated to the very critical issue of stray light suppression. Being this paper specifically dedicated to the description of Metis optical design, not many details are provided about the instrument hardware implementation (that can be found in ref. [3]), and no information is provided about the actual measured performance of Metis, that will be the topic of a future paper.

2 Instrument required scientific performance

The scientific objectives coupled to the mission profile define the Metis observational requirements, and as a consequence the instrument performance. To briefly summarize [3, 13], Metis has to provide maps of the solar corona in an annular FoV of 1.6° - 2.9°, corresponding to imaging the off-limb corona from 1.7 R☉ to ~9 R☉ depending on the Sun-spacecraft distance, in the following spectral ranges:

  • HI Ly-α (121.6 nm), to look at the coronal emission;

  • 580–640 nm, to investigate the polarized coronal emission VL component (NB a linearly polarized brightness (pB) sequence consists of four VL images taken at different polarization modulations).

Table 1 summarizes the Metis top-level instrument optical performance aimed at satisfying these main observational requirements. To be noted in the Metis requirements that the optical quality is specified considering the presence of both diffraction, which strongly limits the optical performance of the innermost FoVs for both the VL and UV channels, and geometrical aberrations (mainly coma and astigmatism) which limit the performance of the outer FoVs for the UV channel.

Table 1 Metis instrument nominal optical performance
Full size table

3 Metis optical design

Metis optical design can be simply schematized as a wide field telescope with an external occultation system to mask the solar disk. The major difficulty to face when designing a solar coronagraph is to drastically dump the residual stray-light scattered by the occulter edge, in order to have an acceptable signal-to-noise ratio when imaging the solar corona at the FoV extremes. To this end, suitable masks/diaphragms have to be inserted in the proper position.

3.1 Metis telescope and UV channel

With reference to Fig. 1, the first optical element encountered by sun/coronal light is the “inverted” external occulter (IEO): this is a small circular aperture (∅ 40 mm) acting as the system input pupil and aperture stop. This is a very critical element for the whole system. First, in terms of cleanliness: in fact, for example even a single 10 μm dust grain located on its edge could act as an “intense” source of stray light for the coronagraph [17], and for this reason the highest cleanliness requirements for the whole instrument lifetime have to be satisfied. Second, still to avoid any possible unwanted light entering the instrument, nothing that could possibly deviate light inside this aperture should be present between the IEO and the Sun. This forces the IEO to be located outside the spacecraft heat shield, and so to be also subject to the highest spacecraft temperatures (more than 400 °C). This implies not only thermal control issues on the IEO (and on the entire instrument), but also the need to find a suitable mechanical solution to hold the IEO in its nominal position at 80 cm from the first following optical element. For this, the IEO is supported by a suitable boom which protrudes from the spacecraft instrument bay through the protective heat shield. Thus, as part of the Metis structure reaches such high temperatures, thermal control has played a particularly important role in the design of the instrument.

Fig. 1
figure 1

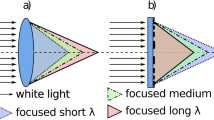
Schematic views of Metis coronagraph ray-tracings: a) UV channel; b) VL channel. In a) the optical path of coronal light is shown; in b) also the optical path of the light from a sun disk edge back rejected by M0 is shown. IEO: inverted external occulter; M0, M1 and M2 are the mirrors along the Metis optical path; LS: Lyot Stop; IO: Internal Occulter; FS: Field Stop; IF: Interference Filter; UV/VL FP: UltraViolet / Visible Light Focal Plane; CD: Collimating Doublet; BP: Band Pass filter; QW: Quarter Wave plate; PMP: Polarization Module Package; LP: Linear Polarizer; FLS: Focusing Lens System

Full size image

Light from the solar disk directly passing through the IEO aperture is back-rejected by a small (∅ 71 mm) spherical mirror (M0) located 800 mm behind IEO along the telescope optical axis. This is a fundamental requirement for a solar coronagraph, because direct disk light possibly entering the optical path could create a huge amount of stray light, largely reducing the capability of observing the very weak solar corona. M0 has been designed to collect all the radiation up to 1.1° from the system optical axis (i.e., 1.17 R☉ at 0.28 AU, the minimum distance from the Sun), and to refocus it on the IEO plane. To maximize the back-reflected Sun radiation over the whole spectrum, M0 has an Al + SiO2 coating.

As previously said, the main motivation of adopting this original occultation scheme, i.e. a circular aperture coupled to a circular back-rejection mirror, has been the need to reduce the thermal load inside the instrument during perihelion operations. For a better understanding, let us consider the most classical externally occulted coronagraph design: in this case, an annular aperture is used as occulter, with the central circular mask acting as occulter to shadow the direct solar disk light to the following optical train. Such a standard design with the same collecting area of Metis would have required a much larger aperture at the heat shield plane (for example, assuming the same distance between external occulter and first mirror, the occulter area for a classical coronagraph would be about 1.4 dm2, with respect the 0.13 dm2 of Metis one), and an (annular) solar disk light back-rejecting mirror much larger than the used small (circular) one. In practice, this innovative design, in which the occulter has been “inverted” with respect to the classical configuration (a circular aperture instead of an opaque disk) has allowed to reduce by more than one order of magnitude the thermal load on the back-rejection mirror, and in general inside the Metis structure: this has been a great advantage in terms of the instrument structure thermal stability with respect to a more classical coronagraph design.

Radiation from the solar corona at FoV larger than 1.1° and passing through the IEO overcomes M0 (with a partial vignetting that decreases as the FoV increases), and reaches the Metis telescope. The latter has been designed as an on-axis aplanatic Gregorian one, with both primary and secondary mirrors, M1 and M2 respectively, elliptical. In order to optimize the telescope reflectivity at both VL and UV, the two mirrors have been coated with an optimized Al + MgF2 layer structure. Since M0 back reflects the central portion of the beam of light entering the telescope, the section of the radiation beam propagating after M0 is annular. So the telescope mirrors also have been shaped in this way, that is circular with a large central hole, to minimize the needed mass resources but still collecting all the passing radiation.

In between these two mirrors there is an optical subsystem with the very critical task of suppressing the residual stray light inside the instrument (see section 5). It consists of three optical elements: the field stop (FS), the internal occulter (IO), and the Lyot stop (LS). The first is a “large” circular aperture located on the focal plane of M1 which defines the Metis FoV and blocks the out-of-field radiation that could possibly enter the instrument. The IO is circular aperture conjugated with the IEO, and is meant to block the light diffracted by the IEO edge. In fact, the latter is extremely bright, as the IEO is the first element to be hit by direct solar disk light, and acts as a stray light “ring” source; this is then imaged by M1 on a plane where the IO is mounted. The IO is sized to block the image of this stray light ring source. Finally, the LS is a circular stop conjugated to M0 edge which blocks the residual light diffracted by this edge and then imaged by M1.

The solar corona light reflected by M1 and passing through this subsystem is then collected by M2, which focuses the beam light behind M1. Before reaching the UV focal plane on the rear of M1, the coronal light reflected by M2 is intercepted by a dichroic beam splitter. The latter is actually a multilayer interference filter (IF), tilted at 12° with respect to the optical axis, optimized to transmit a 15 nm FWHM spectral band centred at 121.6 nm (UV channel) and to reflect the visible portion of the spectrum towards a dedicated optical path (VL channel). This filter has been designed with a small wedge (0.15°) between the two flat surfaces, to minimize possible internal ghost effects and residual astigmatism in the UV channel.

The UV light transmitted by the IF reaches the ultraviolet sensor without encountering any other optical element. The visible light, reflected by the IF, instead passes through a collimating system, a suitable polarizing device, and a focusing system before reaching the dedicated detector.

Table 2 summarizes the main optical characteristics of the Metis telescope and UV channel, and Table 3 more specifically those of the dichroic beam splitter.

Table 2 Metis telescope main optical parameters and characteristics
Full size table
Table 3 Dichroic beam splitter optical characteristics
Full size table

3.2 Visible light channel optical path

The Metis visible light path branches out from the dichroic filter as the reflected beam, “returning” back along the optical path with an inclination of 24° with respect to the telescope optical axis. To satisfy the scientific requirements for observing the broad-band visible-light K-corona emission which is linearly polarized by Thomson scattering of the photospheric light with coronal electrons, it is necessary to realize the coronal imaging in the 580–640 nm spectral range, measuring the polarization of the light with an accuracy better than or equal to 1% [7, 12].

For this, the VL path has been conceived as an optical subsystem, the “polarimeter”, located on a side of the telescope: it collects the light after the telescope focus, makes a polarization measurement, and then refocuses it on the VL detector [4]. The polarimeter realizes a paraxial demagnification of 0.67 with respect to the telescope focal plane, so optimizing the Metis VL channel spatial resolution performance considering the VL detector pixel size, and works with an f/4.2 aperture ratio.

With reference to Fig. 2, the polarimeter comprises first a collimating doublet (CD) followed by a bandpass filter (BP) to limit the spectral band to the range of interest. Then there is a quarter wave plate (QWP) retarder, a pair of liquid crystal variable retarders (LCVR) also named “polarization module package” (PMP), and a linear polarizer (LP) acting as analyser. Finally, a focusing three lens system (FLS) projects the polarized coronal image on the visible detector.

Fig. 2
figure 2

Ray tracing view of the Metis polarimeter (VL channel)

Full size image

The measurement of coronal light polarization is realized by the analysis of four images acquired with different setups of the PMP. The PMP in fact is the key and most innovative optical element of the polarimeter. Its assembly includes two nematic LCVRs, that are active optical elements that can change the orientation of the LC molecules by application of a suitable low voltage (< 10 V) [2]; thus it is possible to vary in a controlled way the optical retardance of the PMP without the need of any mechanism, which is a clear advantage for space applications. This property is used for the polarimetric analysis, thanks to the adopted de Sénarmont configuration [9] for the polarimeter. In its classical configuration, the de Sénarmont compensator couples a QWP with a 180° rotating analyser: here, the analyser function is realized by the combination of LCVR and LP in a suitable relative orientation. Considering a right-handed reference frame with the z axis oriented along the light propagation direction and the x axis parallel to the LP polarization axis, the fast axis of the QWP is parallel to the y axis, and the fast axis of the LCVR is tilted by −45° with respect to the x axis (see Fig. 3).

Fig. 3
figure 3

Schematic view of the Metis polarimeter optical elements relative orientations. The arrows in the optical elements represent, respectively: the fast axes for both the QWP and the PMP, and the polarization axis for the PMP

Full size image

By the analysis of four images of the corona obtained by setting the PMP optical retardance at 90°, 180°, 270°, and 360° it is possible to obtain the Stokes vector of the incoming radiation. This is simply done [5, 6] by solving the linear system S = X+M, where

$$ {X}^{+}=\frac{1}{2}\left(\begin{array}{c}1\\ {}0\\ {}-2\end{array}\begin{array}{c}\kern0.5em 1\\ {}-2\\ {}\kern0.5em 0\end{array}\begin{array}{c}\kern0.5em 1\\ {}\kern0.5em 0\\ {}\kern0.5em 2\end{array}\begin{array}{c}\kern0.5em 1\\ {}\kern0.5em 2\\ {}\kern0.5em 0\end{array}\right) $$

is the theoretical demodulation matrix associated to the above indicate PMP optical retardances, and M = (m0, m1, m2, m3) is a vector whose elements are the intensities measured for the four images.

Table 4 summarizes the main polarimeter characteristics.

Table 4 Main characteristics of Metis polarimeter
Full size table

3.3 Optical performance

The main optical performance of Metis design, as provided by both geometrical ray-tracing and diffraction estimation, is summarized in this section.

One of the main characteristics of a solar coronagraph is the obscuration of the central portion of the telescope field of view to mask the solar disk. The obvious consequence is a vignetting function which depends on the angular radial distance from the system axis. In particular, the telescope vignetting function cannot be an “ideal” step function, completely masking the solar disk light and fully transmitting the solar corona one; rather, it is a continuous function with a linear increase from the central fully masked FoVs to the most external ones (see Fig. 4). Actually, since the coronal radiance strongly depends on the radial distance from the solar disk center, with the inner corona much brighter than the outer one, a vignetting function with such a profile is a convenient situation. In fact, with such a vignetting the very intense inner corona is much more attenuated than the very weak outer, so reducing the need of a large dynamical range at the detector level.

Fig. 4
figure 4

Dependence of the Metis vignetting function on the radial field of view. (a): Gray scale representation of the bidimensional vignetting function, as obtained by ray-tracing; overlapped dashed circles represent 1° (red), 2° (orange), and 3° (blue) FoVs. (b): plots of the vignetting function along the radial directions shown in (a) as a function of the different colours

Full size image

Figure 4 shows that the unobscured portion of the FoV is for angles slightly larger than 1.5°, so respecting the requirement of being able to observe the lowest FoV of 1.6°, even if strongly vignetted. The fraction of unvignetted rays grows roughly linearly way up to 3°, so fully covering the nominal Metis FoV. A couple of further considerations have to be done to properly describe this function. First, along the optical path there are spiders masking a portion of the beam light: in fact, four 7 mm diameter spiders hold the M0 + LS opto-mechanical sub-system; then, other four cylindrical rods of 5 mm diameter hold the IO+FS sub-system in its position. The two sets of spiders are oriented along the sensor diagonals, with the IO+FS (smaller) spider set in the shadow of the M0 + LS (larger) one. These spiders locally shadow the telescope FoV, providing a decrease of intensity along the directions corresponding to the detector diagonals. For this, the percentage of vignetting in the spider shadows is about 20% larger than along the open path. Of negligible impact, but it has to be mentioned also a further local vignetting of some FoVs of the visible channel only, due to a minor interference of M1 with the beam of light after its reflection at the dichroic IF. Second, at the level of the focal plane, also the detectors contribute as field stops and limit the FoV. In particular, with the Sun center projected at the center of the detector, and considering the detector central row and column directions, the FoV is limited at 2.9° (see red and green plots in Fig. 4b); along the detector diagonal directions, instead, the FoV is larger and arrives up to 3.5° (pink and cyan lines in Fig. 4b).

Figure 5 shows the geometrical spot diagrams at the UV channel focal plane (at 121.6 nm) for four fields of view along a radial direction (because of the radial symmetry of the optical design, they are representative of the whole FoV of the Metis UV channel). By the analysis of these spots it is also possible to estimate the Metis vignetted telescope performance. From this figure we can easily calculate the plate scale of this channel, which is about 690 arcsec/mm; considering the UV detector pixel size of 30 μm (see section 4), we obtain a pixel scale factor of 20.7 arcsec/pixel, substantially in line with the relative requirement. It is also evident from Fig. 5 that even if the geometrical spot diagrams for the innermost Metis FoVs are minimal, with rms radius of the order of few microns, the diffraction contribution is here rather significant, actually limiting the channel optical performance. In fact, as an example, at 1.6° FoV the vignetting is so large that just very tiny portions of the mirrors are illuminated, and only about 1% of the whole beam is passing through. As shown in Fig. 5 by the diffraction curve first minimum, the theoretical spot in this case has an ellipsoidal shape, as a consequence of the vignetted beam shape; the diffracted light has an Airy-like distribution with the peak at the position of the geometrical spot and decreasing intensity along the radial direction. For FoVs between 1.9° and 2.2°, the calculated diffraction and geometrical aberration contribution becomes smaller than the pixel size, and the Metis UV channel is here detector limited. This behaviour is evident also in Fig. 6, which shows the percentage of the diffraction ensquared energy (EE) for several FoVs including diffraction. From these plots we can also see that the requirements about the point source energy distribution is fully satisfied. In fact, for FoV larger than 1.6° the EE had to be nominally larger than 50% within one pixel (30 μm pixel size, see Section 4), and for FoVs larger than 2.4° the EE had to be larger than 60% in 2 × 2 pixels. Finally, for large FoVs, astigmatism increases and becomes the dominant aberration, even if also some coma is present: at the largest FoV the geometrical aberrations are larger than the resolution element (two pixels) along the tangential direction, arriving up to about 20 × 90 μm2 (full width zero height). This is evident also by Fig. 7, which shows the telescope field curvature: since the focal plane is close to the tangential focus surface, the spots have the shortest size along the radial direction, and the longest one tangentially oriented, providing the typical astigmatic images shown in Fig. 5. Figure 7 shows also the extremely low image distortion for the UV channel, which has a maximum of less than 0.4% at the largest FoV. In any case, we can confirm that the requirements listed in Table 1 for the UV channel relative to the point source energy distribution are all satisfied.

Fig. 5
figure 5

Spot diagrams of the UV channel at the detector focal plane for four radial FoVs. The drawn square box is 90 μm side, the same in all cases. The given coordinates correspond to the position of the chief ray in the detector reference frame. The drawn ellipses, evident for the two inner fields, represent the size of the calculated first diffraction minimum

Full size image
Fig. 6
figure 6

Diffraction ensquared energy percentage as a function of the distance from the chief ray for the 1.6°, 1.8°, and 2.0° FoVs (a), and for 2.4°, and 2.9° FoVs (b) in the Metis UV channel

Full size image
Fig. 7
figure 7

Left: field curvature (T: tangential focus; S: sagittal focus) for Metis UV channel. Right: relative distortion. In both cases, the considered field (+Y axis) ranges from 0° to 2.9°, that is the nominal largest Metis field of view

Full size image

Figure 8 shows the geometrical spot diagrams on the VL channel focal plane for four fields of view and three wavelengths within the bandpass. With respect to the UV channel, these spots include not only the telescope aberrations, but also the effect of the polarimeter optical train, which shortens the telescope focal length (from 300 mm to 200 mm), makes this channel faster (f/5, to be compared to the f/7.5 of the UV channel), and largely compensates the residual telescope aberrations. Calculating the plate scale of this channel, we obtain about 1030 arcsec/mm; considering the VL detector pixel size of 10 μm (see section 4), we obtain a pixel scale factor of 10.3 arcsec/pixel, in line with the associated requirement. The geometrical spot diagrams are rms micron-size for all the Metis FoV. However, we have not to forget the vignetting effect: in fact, because of the small section of the light beam, mainly at the innermost FoVs, the actual optical performance of Metis VL channel is limited by diffraction. This is represented in Fig. 8 by means of the drawn ellipses, which correspond to the first minimum of the calculated diffraction figure.

Fig. 8
figure 8

Spot diagrams of the VL channel at the detector focal plane for four radial FoVs. The drawn square box side is 400 μm for the innermost FoV, and 40 μm in all the other cases. The given coordinates correspond to the position of the chief ray in the detector reference frame. The legend identifies the spots for three different wavelengths. The drawn ellipses represent the size of the calculated first diffraction minimum

Full size image

As examples of calculations of energy distribution within the spots including diffraction, Fig. 9 shows the percentage of the diffraction EE for several FoVs. It is possible to see from these plots that the expected performance requirements concerning the point source energy distribution are not fully satisfied. In particular for FoVs larger than 1.6° the EE had to be nominally larger than 60% within 6 × 6 pixels (10 μm pixel size, see Section 4), while this is verified only for FoVs larger than 1.65°; and for FoVs larger than 1.8° the EE had to be larger than 80% in 4 × 4 pixels, while at 1.8° it is 74%. Unfortunately, this lower performance was expected: in fact, during the instrument design phase, the pointing accuracy of the spacecraft had to be redefined, with the consequence that we had to increase the stop sizes for instrument safety. As a result, the innermost FoVs are now more vignetted than what was initially foreseen, and the diffraction has increased with respect to the expectations.

Fig. 9
figure 9

Diffraction ensquared energy percentage as a function of the distance from the chief ray for the 1.6°, 1.66°, and 1.8° FoVs (a), and for 2.0°, 2.4°, and 2.9° FoVs (b) in the Metis visible channel

Full size image

3.4 Tolerance analysis

In this section we are going to summarize the main results of the error budget analysis that has been done to determine the opto-mechanical tolerances of Metis optical design [8]. The aim of this analysis has been the determination of the tolerances at three different stages: a) tolerances for instrument manufacturing and alignment phases; b) long term stability tolerances, related to the whole mission lifetime; c) short term stability tolerances, associated to the in-flight tolerances the instrument has to sustain during a standard acquisition time. Concerning tolerances a), we have assumed as a goal a maximum degradation of the spot diagram rms radius at the end of Metis integration equal to 30% with respect to the nominal ideal case. For tolerances b), we considered as acceptable a further degradation of 30% of the rms spot diagram with respect to the nominal case, so bringing the maximum degradation of the image quality at the end of the mission to about 40% (quadratic sum). Finally, for tolerances c) we considered as figure of merit an instrumental maximum shift of the Metis boresight (i.e. not considering possible spacecraft jitter) equivalent to one third of a detector pixel during a standard time of integration. These tolerance values have been assumed as a reasonable compromise between the need of not worsening too much the instrument scientific results, and the technical difficulties for reaching them.

Since the telescope optical path is common to both the Metis channels, and substantially coincident with the UV channel, the tolerance analysis has been performed on this sub-system first, thus in practice providing the tolerances for the UV channel; then, the polarimeter tolerances have been studied independently, providing also the information about the VL channel tolerances. Finally, since along the optical path there are also other elements, M0, IO, LS and FS, whose alignment is not relevant to the quality of the image but very critical for stray light suppression, a tolerance analysis has been dedicated to these items only, to define the constraints on their manufacturing and positioning.

3.4.1 Telescope tolerance analysis

To provide the right estimates of the tolerance values to consider in the Metis telescope error budget, the quality of the image at both the UV channel focal plane position and at the intermediate focus along the VL optical path, after the reflection by the IF, has been checked by means of MonteCarlo analysis. In this way, we include in this section also the tolerances of the IF, that is the element which splits the incoming radiation beam along the two optical paths, and of the UV detector. The fraction of the simulated designs which fulfils the requirement we set on the image quality is larger than 80% in all the cases.

Table 5 shows the results of the telescope tolerance analysis for manufacturing (including also possible effects associated to mounting holders, e.g. induced surface deformation) and alignment. We found that an error on the curvature radius of the mirrors of ±200 μm can be tolerated, as well as an error of the order of 1% in the conic constant, and a surface quality of λ/2 P-V (λ = 633 nm). Thanks to the possibility of using the telescope back focal length, i.e. the distance between M2 and the intermediate focus, as an alignment compensator within the range ± 1 mm (UV detector), a tilt of 0.01° and a decenter of 40 μm on the mirrors can be tolerated, as well as a misplacement of 150 μm on the axial distance between M1 and M2.

Table 5 Telescope manufacturing and alignment tolerances
Full size table

Table 6 shows the results of the telescope tolerance analysis for long and short term stability; the latter has been considered independently for each channel. The short term stability for the VL channel corresponds to the time necessary to acquire four exposures, i.e. when polarimetric measurements have to be performed. In this case, the polarimeter optical train is not included, since it is described in the following section. When there is no indication, the short term stability is equivalent to the long term one. The long term stability tolerances correspond to the maximum acceptable shift/rotation of each optical element over the whole mission lifetime. The reported values have been obtained by means of an inverse sensitivity analysis with MonteCarlo runs.

Table 6 Telescope stability tolerances
Full size table

These results show that the distance between the two mirrors, that has to remain constant within 15 μm during the whole mission lifetime, is the most critical tolerance to satisfy. In fact, this distance, together with the curvature of the mirrors, determines the telescope focal length and hence the focal plane position which has to remain extremely stable. For what concerns the short term tolerances, the most critical items are the stability of the mirrors and of the IF (the latter, for the visible channel only).

3.4.2 Visible light path tolerances

As described in section 3.2, the VL channel comprises a collimating doublet (CD), a polarization system, and finally a focusing lens system (FLS). The tolerances have been calculated first at the level of each surface of these optical elements, and then at the sub-system level, that is considering each lens as a single element. In all the cases, a maximum degradation of 30% of the RMS spot radius at the VL channel focal plane has been assumed to be acceptable.

For all the surfaces of the various lenses, we found as maximum acceptable manufacturing tolerances a variation of ±0.2 mm on the nominal surface curvature radii, a tilt of ±0.05° between the surface on-axis normals, a decenter of ±0.05 mm with respect to the optical axis, a ± 0.2 mm in the lens on-axis thickness, and a λ/4 P-V (λ = 633 nm) standard quality surface. For all the plane elements of the polarization system, we estimated a maximum acceptable manufacturing tolerance of ±0.05° parallelism between the two surfaces of each element. Moreover, the analysis of long and short term stabilities, provided similar values in both cases. To summarize, the acceptable stability tolerances for both long and short term for the lens surfaces are: ±50 μm and ± 100 μm for the radii of curvature respectively for the CD and the FLS; are ±0.026° for the relative surface tilt; are ±25 μm on decenter, and ± 50 μm on the thickness. The stability tolerance on the parallelism between the surfaces of the polarizer elements is equal to ±0.02°.

Concerning the alignment and long/short term stability tolerances of the VL path optical elements, we can refer to Table 7, where again the reported values have been obtained by means of an inverse sensitivity analysis and MonteCarlo runs. The alignment values have been obtained considering a 1 mm compensation at the focal plane position. As can be seen from these values, the most critical issue for the VL channel is the positional stability of the lenses, that have to be maintained within 50 μm for the whole mission. Even if not evident from this analysis, another issue for the VL channel tolerances is the tilt of the IF. In fact, even if a small tilt of the IF does not affect the image quality, it may increase the vignetting at the previously mentioned interference of the beam with M1 after the reflection by IF. We evaluated an increase of about 1% vignetting at the largest FoV for a tilt of 2.5 arcmin.

Table 7 VL path alignment and long/short term tolerances
Full size table

3.4.3 Tolerance analysis of optical elements associated to stray light reduction

In the tolerance analysis of a coronagraphic instrument, also the maintenance of the instrument capability to minimize the stray-light inside the instrument has to be considered. On this respect, let us remind that the relevant optical elements for this are: the IEO, that is the instrument aperture stop; M0, which rejects the direct solar disk light through the IEO; the IO, conjugated with IEO, which blocks the stray-light produced by the IEO edge and reflected by M1; the LS, conjugated with M0, which blocks the stray-light produced by M0 edge and reflected by M1.

For the tolerances associated to these optical elements, we can refer to Table 8. For this analysis, we had to consider the conjugation between IEO and IO, and M0 and LS through the mirror M1, and it has been assumed that the tolerances for the imaging mirror M1 reported in Table 6 are respected. In practice, point sources have been simulated at either the IEO or M0 edges, and their images at the IO or LS plane, respectively, have been analysed assuming both the alignment and manufacturing tolerances of all the optical elements along this optical path. To be not so stringent with M1 tolerances, it has been assumed the positions of IO and of LS along the optical axis as possible compensators; also an oversizing of LS has been taken under possible consideration if needed. Only geometrical ray tracing has been considered for this analysis, as diffraction effect is negligible in this case.

Table 8 Tolerances of optical elements associated to stray light reduction
Full size table

Since IO has the task to block the largest contribution of stray-light and its correct positioning is crucial to the success of the instrument, a dedicated translation mechanism has been foreseen. The LS instead is less critical on this respect, since it has to block a second order scattered light, so an appropriate oversizing (0.4 mm) with respect to the minimal size is sufficient to avoid problems.

Concerning M0 and its function of back-rejecting the direct solar disk light, it has been oversized by 2 mm on the radius, so there is no risk of not collecting all this light; on the other hand, possible tilts of the mirror with respect to its nominal axis orientation have to be limited to less than 13 arcmin to avoid to send the solar disk image on the internal part of the IEO.

4 Metis detection system

Metis has two independent detectors, the Visible Light Detector Assembly (VLDA) and the Ultraviolet Detector Assembly (UVDA), each of them located at the end of the respective optical path [3]. The specifications of these detectors have been derived by both the different scientific requirements for the two channels and the need not to exceed the foreseen cost cap.

The VLDA is a cooled visible camera equipped with a complementary metal oxide semiconductor (CMOS) active pixel sensor (APS) (2048 × 2048 format, 10-μm square pixel). The front side illuminated (FSI) custom made CMOS-APS sensor was developed by CMOSIS Imaging Sensors (now AMS) in Belgium for application on the Polarimetric and Helioseismic Imager (SO/PHI) on Solar Orbiter [26]. It shows a full well of about 90 ke− and a quantum efficiency (QE) inclusive of the pixel’s filling factor (FF) of about 55% in the 580–640 nm Metis science range. The UVDA is an intensified sensor that consists of three main elements: a) a single stage microchannel plate intensifier with KBr photocathode accelerating the electrons extracted by the UV photons against a phosphor screen output in optical contact with b) a fiber optics 2:1 de-magnifying coupler connected to c) a CMOS APS STAR1000 (1024 × 1024 format, 15-μm square pixel) FSI sensor; given the CMOS pixel size and the fiber optics demagnifier, the effective pixel size of the UVDA is 30-μm square. The APS has a QE × FF of about 20% in the green (phosphor screen output) and a full well of about 100 ke−. The MgF2 entrance window of the intensifier provides a vacuum tight environment that protects the photocathode and allows a much easier handling of the camera during the alignment, integration and test activities. Its 4 mm thickness ensures good resistance against air pressure by a wide margin. On the other hand, since it collects a converging beam, has the effect of moving the focus backward by about 1.2 mm. The UVDA can operate either in analog or photon counting mode by suitably changing the intensifier gain.

5 Stray light suppression

The most important source of stray light is the solar disk light that either directly enters the IEO or that is diffracted (scattered) by the IEO aperture. As previously described, direct disk light passing through IEO is blocked by M0 and back-rejected out of the instrument through the same IEO aperture. Because of M0 surface microroughness, some light will be inevitably scattered; so not all the solar disk light will be back-rejected, and part of it will hit the walls of Metis external baffle (Metis is enclosed by a suitable cover system, and the portion of the instrument between IEO and M0 is enveloped in a truncated cone, that is the Metis external baffle) [18]. To limit as much as possible that also small amounts of scattered light pass through the instrument, the baffle walls are blackened.

What is however more critical, and that has to be carefully controlled is the light scattered by the IEO aperture edge. In fact, a good portion of this light is not going to be stopped by M0, and enters the instrument essentially along the optical path. In order to minimize this stray light contribution, an optimal shape of the IEO has been considered and suitable stops (FS, IO and LS) have been positioned along the optical path, as described in the following. For more detailed information, a thorough analysis of Metis stray light optimization process can be found in Landini et al. [17], Fineschi et al. [14], Romoli et al. [24], Landini et al. [19], Sandri et al. [25].

5.1 Suppression of reflected stray light component

Radiation from the solar disk arriving at the entrance aperture of a coronagraph is going to be diffracted by the edge of the aperture itself: this makes the edge a bright ring-like source of light entering the instrument. In several configurations, as in Metis, this first optical element is the so-called external occulter [10], and great care is taken in finding the shape which minimizes the amount of diffracted light. For example, a simple circular stop cannot be used when looking at the extended corona, because the light diffracted by its edge is brighter than the coronal signal itself; as an alternative, a technique called apodization [1, 15] can be used to optimize the occulter shape and so reduce this diffracted light contribution. In the Metis design, analysis coupled to a series of laboratory measurements [17, 19] brought to configure the IEO as the on-axis inner surface of a truncated cone with the smallest radius towards the sun (see Fig. 10 and next section). The extension of this cone intercepts the M0 surface, so the large majority of the diffracted light is blocked by M0 and does not enter the telescope. However, a minor portion of light passes on the sides of M0 and reaches M1.

Fig. 10
figure 10

Section sketch showing the profile of the adopted apodized Metis IEO

Full size image

A first action which has been considered in the Metis optical design is to block the light diffracted by IEO edge, and then collected and focused by M1, by means of a suitable stop. For this, the IO stop has been located on the conjugate plane of IEO with respect to M1, that is where M1 makes the image of IEO (see Fig. 11). A second action taken under consideration has been to block also a secondary stray light effect, associated to the illumination of M0 edge by the light diffracted by IEO. In fact, now also this edge behaves like a second order light emitter; and even if this is clearly a much less critical source of stray light, in a coronagraph also this much smaller contribution can significantly reduce the signal to noise ratio, mainly at large radial distances from the sun where the corona is weaker. Thus, in order to block also this stray light contribution, a LS is placed in the conjugate plane of M0 with respect to M1, that is where M1 makes the image of the M0 edge (see Fig. 12).

Fig. 11
figure 11

The edge of IEO illuminated by the sun behaves as a ring-like light source. The primary mirror M1 collects a portion of this light and creates an image that is blocked by the IO stop

Full size image
Fig. 12
figure 12

The edge of M0, illuminated by light diffracted by IEO, acts as a ring-like source of light. M1 makes an image of this source that is blocked by the Lyot stop

Full size image

5.2 Suppression of the non-reflected stray light component

Both IO and LS take care of the IEO diffracted light component that is reflected by M1. But there is another residual component of stray light that has to be minimized: it is the part of light diffracted by IEO and collected by M1 which is not going to be reflected but scattered because of the residual microroughness of the mirror surface. Unfortunately, this non-reflected component cannot be blocked or somehow separated from the corona radiation, and can arrive on M2 and then on the instrument sensors. Two are the possible solutions to reduce as much as possible also this stray light component: a) to work on the source side, minimizing the amount of light diffracted by IEO towards M1; b) to work on the M1 side, polishing its surface to the minimum possible value of microroughness, avoiding surface defects, and maintaining its particle contamination at the lowest possible level.

Point a) is actually the main motivation of the apodization technique previously mentioned: to find the best shape of the coronagraph entrance aperture, in order to reduce the amount of diffracted light going to be collected by the telescope as much as possible. To find the best shape for the IEO, both theoretical analysis and laboratory measurements have been performed. As described in Landini et al. [17], the optimal IEO was found to have the characteristics reported in Table 9. As an example of the amount of scattered light as a function of the cone angle, it is possible to look at Fig. 13, where some of many experimental results are shown.

Table 9 Optimal characteristics of Metis IEO to minimize the diffracted stray light
Full size table
Fig. 13
figure 13

Experimental measurements showing the normalized radial flux scattered by the IEO as a function of different IEO shapes: either a simple circular knife edge or 30 mm long cones with different surface angles with respect to the instrument optical axis

Full size image

Concerning point b), considering that the M1 ellipsoidal surface is not the simplest to be superpolished, we set a requirement of 0.3 nm rms microroughness, with a goal of 0.2 nm rms, for obtaining a total integrated scatter (TIS) smaller than 5·10−5. Under these assumptions for M1 surface roughness, the expected visible stray-light level at the Metis focal plane for different Sun-spacecraft distances corresponds to the one shown in Fig. 14. These plots have been determined by a two steps process: first, by means of a suitable algorithm based on the Fresnel-Kirchhoff diffraction integral [16], the amount of diffracted light arriving on M1 has been defined; then, by using a BRDF model derived by the measured M1 surface power spectral density, the amount of light scattered on the detector has been estimated. Moreover, calculations of stray light contribution by particulate contamination of Metis mirrors have been conducted using the bi-directional scattering distribution function (BSDF) for various surface cleanliness classes [14, 25]. This analysis showed that, given the selected shape of the IEO, with the assumed values of microroughness, considering a 20–10 high precision quality for S/D, and an M1 particle contamination equivalent to Class 300 at end-of-life, the attainable ratios between the stray light radiance, Bstray (photons cm−2 s−1) at the telescope focal plane and the solar disk mean radiance, Bsun, for the two Metis channels is:

  • Visible channel: (Bstray/Bsun)VL analysis < 3·10−10

  • Ultraviolet channel: (Bstray/Bsun)UV analysis < 9·10−9

Fig. 14
figure 14

Expected visible stray-light level versus FoV at the Metis focal plane for different Sun-spacecraft distances

Full size image

This analysis confirms that Metis has been properly designed also concerning the minimization of the stray light at the focal plane, with a nominal stray light level lower than the minimum required, (Bstray/Bsun) VL requirement = 10−9 (see Fig. 14) and (Bstray/Bsun) UV requirement = 10−7.

6 Conclusions

With this paper we have described the optical design of the Metis coronagraph for the Solar Orbiter ESA-NASA mission. The Metis optical design has been challenging under several points of view. A first issue has been the ability of compacting in a single instrument two channels with very different optical needs, one dedicated to far ultraviolet and one to visible. Then, a novel optical configuration with “inverted” external occultation has been adopted for reducing the extremely high thermal load on the instrument. Moreover, the capability of minimizing the internal stray light, to allow the observation of the very weak solar corona having the extremely bright solar disk at the center of the instrument field of view, has also been obtained. Finally, all these issues had to be coupled with the standard constraints related to the realization of a remotely controlled space instrument.

We have been able to obtain an instrument design able to satisfy all the technical requirements set by the need of obtaining an excellent scientific return. On the basis of this design, Metis has been realized, integrated and tested, demonstrating its excellent performance.