Abstract
The past decade has seen the advent of various radio astronomy arrays, particularly for low-frequency observations below 100 MHz. These developments have been primarily driven by interesting and fundamental scientific questions, such as studying the dark ages and epoch of re-ionization, by detecting the highly red-shifted 21 cm line emission. However, Earth-based radio astronomy observations at frequencies below 30 MHz are severely restricted due to man-made interference, ionospheric distortion and almost complete non-transparency of the ionosphere below 10 MHz. Therefore, this narrow spectral band remains possibly the last unexplored frequency range in radio astronomy. A straightforward solution to study the universe at these frequencies is to deploy a space-based antenna array far away from Earths’ ionosphere. In the past, such space-based radio astronomy studies were principally limited by technology and computing resources, however current processing and communication trends indicate otherwise. Furthermore, successful space-based missions which mapped the sky in this frequency regime, such as the lunar orbiter RAE-2, were restricted by very poor spatial resolution. Recently concluded studies, such as DARIS (Disturbuted Aperture Array for Radio Astronomy In Space) have shown the ready feasibility of a 9 satellite constellation using off the shelf components. The aim of this article is to discuss the current trends and technologies towards the feasibility of a space-based aperture array for astronomical observations in the Ultra-Long Wavelength (ULW) regime of greater than 10 m i.e., below 30 MHz. We briefly present the achievable science cases, and discuss the system design for selected scenarios such as extra-galactic surveys. An extensive discussion is presented on various sub-systems of the potential satellite array, such as radio astronomical antenna design, the on-board signal processing, communication architectures and joint space-time estimation of the satellite network. In light of a scalable array and to avert single point of failure, we propose both centralized and distributed solutions for the ULW space-based array. We highlight the benefits of various deployment locations and summarize the technological challenges for future space-based radio arrays.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The success of Earth-based radio astronomy in the frequencies between 30 MHz and 3 GHz is jointly credited to Earth’s transparent ionosphere and the steady technological advancements during the past few decades. In recent times, radio astronomy has seen the advent of a large suite of radio telescopes, particularly towards the longer observational wavelengths, i.e., ≥3 m. These arrays include the Murchison Widefield Array (MWA) [47], LOw Frequency ARray (LOFAR) [74] and the Long Wavelength Array (LWA) [27] to name a few. However, Earth-based astronomical observations at these ultra-long wavelengths are severely restricted [37]. Due to ionospheric distortion, especially during the solar maximum period, when scintillation occurs, the celestial signals suffer from de-correlation among the elements of a ground based telescope array [39]. Currently, advanced calibration and mitigation techniques are employed in the LOFAR telescope array, which can be used to remove these distortions, provided the time scale of disturbances is much longer than the time needed for calibration [77]. Furthermore, at frequencies below 10 MHz the ionosphere is completely non-transparent which impede observations by ground-based instruments. In addition to ionospheric interference, man-made transmitter signals below 30 MHz also impede terrestrial based astronomical observations. This terrestrial interference was even observed as far as ∼400,000 km away from Earth by the RAE-2 lunar orbiter, which was limited by very poor spatial resolution at these wavelengths, e.g., 37∘ at 9.18 MHz [3]. Due to the above mentioned reasons, the very low frequency range of 0.3−30 MHz remains one of the last unexplored frontier in astronomy. An unequivocal solution to observe the radio sky at ULW with the desired resolution and sensitivity is to deploy a dedicated satellite array in outer-space. Such a space-based array must be deployed sufficiently far away from Earths’ ionosphere, to avoid terrestrial interference and offer stable conditions for calibration during scientific observations.
1.1 Science at ultra-long wavelengths
A space-based low frequency radio instrument would open up the virtually unexplored ULW domain and as such addresses a wealth of science cases that undoubtedly will lead to new exciting scientific discoveries, similar to the uncovering of other wavelength domains has revealed in the past. For most of these science cases such an array would add information to the existing radio, optical, infrared, sub-mm or high frequency X-ray or gamma-ray instrumentation, and thereby provide insight into the processes that take place at the lowest energies and largest physical scales. As explained in [34] and [41] science topics include the study of the solar activity and space weather providing important clues on the effect of solar flares and bursts on the Earth to much larger distances from the solar surface. Investigating the magnetospheric emission from large planets such as Jupiter and Saturn (see Zarka et al. [79]) reveals information on the spin period of these planets. Other key science cases include the study of large-scale structures from galaxy clusters (and radio galaxies) and the detection of Jupiter-like flares and Crab-like pulses from (extra-)galactic sources.
The greatest advance in science is expected in the study of the very early universe in a period referred to as the cosmological Dark Ages [62]. The Dark Ages is the period between the epoch of recombination when the universe became transparent and the cosmic (microwave) background was emitted, and the epoch of reionisation (EoR) when the first stars started to reionise the neutral hydrogen. The global Dark Ages signal, essentially the redshifted 21-cm line absorption feature, is expected to peak around 30-40 MHz and is weak, ∼106 below the foreground signal.
Jester and Falcke [34] show that with a single antenna placed at an ideal location on the moon (i.e. under low RFI and stable temperature and gain conditions), the global signal can be detected at a 5 σ level for one year of integration. In order to trace the variations in the hydrogen at arc-minute or even arc second scale resolution a larger sensitivity and thus a larger collecting area is required. For instance, [34] show that up to 10 5 individual antenna elements are required corresponding to 0.5 km 2 in order to reach 10′ spatial resolution (see Loeb and Zaldarriaga [45]). So, in addition to a low-RFI, low-temperature and stable gain location, a ULW radio interferometer that aims at detecting the arcmin variations in the mass distribution of the Dark Ages and the EoR, must have a large collecting area (in the order of km 2). Ideal locations for such an array include the farside of the moon, an eternally dark crater on the lunar south or north pole, space-based solutions for instance in a Sun-leading or trailing orbit, at the Sun-Earth L2 point or in Lunar orbit.
1.2 Previous studies
The proposition for a space-based radio astronomy instrument is not novel [9, 10, 37, 76]. One of the first such proposals was made by [29], who discussed the benefits of a moon-based radio interferometer. In 1968 and 1973, the RAE-1 [75] and RAE-2 [3] spacecrafts were launched respectively. The RAE-1 covered a frequency range of 0.2 MHz to 9.2 MHz using two 229 meter V-antennas and one 37 meter electric dipole, while the RAE-2 mapped the non-thermal galactic emission in the frequency range of 25 kHz to 13 MHz using a single 37m dipole antenna, achieving a resolution of 37 ∘. These explorers were the first dedicated missions exclusively for ULW radio astronomy. Science at the ultra-long wavelengths was revived in the 1990s with a particular focus on Lunar based arrays [21, 23]. The Lunar surface on the far-side presents a large and stable platform for antennas and shields unwanted interference from Earth and the Sun [5, 43, 69, 78], which motivated studies such as VLFA [66], MERIT [36] and more recently DEX [42]. Along similar lines, lunar orbiting single-satellite missions dedicated for radio astronomy such as LORAE [22] and DARE [24] were also investigated to map bright sources and to facilitate relatively easier Earth-based down-link of science data. Furthermore, the pursuit of higher angular resolutions has led to Earth-orbiting single-satellite missions such as HALCA [32] and Radio Astron [38] which enable Earth-space very long baseline interferometry [31].
However, the concept of space-based array for ULW radio astronomy has received considerably less attention and has been explored inadequately, which is our primary focus in this article. The successful single-satellite RAE missions motivated the first space-based array proposal to NASA i.e., the Low Frequency Space Array (LFSA) [76]. Another notable NASA funded study in this regard was the ALFA concept, which proposed an array of 10−16 satellites in a distant retrograde orbit [35]. More recently, two ESA funded studies namely FIRST [12] and DARIS [15] investigated passive-formation flying missions for space-based satellite arrays (see Table 1). The FIRST study proposed a constellation of 7 satellites deployed at the second Earth-Moon Lagrange (L2) point, sufficiently far enough from Earth to avert interference and allowed for a low-drift orbit. On the other hand, the DARIS study primarily investigated the feasible ULW science cases and showed ready feasibility of 9 satellites using existing off the shelf technologies. The benefits of both these studies were combined in the SURO concept, which proposed a mission at Sun-Earth L2. In all these studies, a dedicated centralized mothership managed the processing and communication. However, futuristic arrays such as OLFAR [11, 59] with ≥10 satellites will operate cooperatively and employ distributed architectures for both processing and communication.
1.3 Overview
The purpose of this article is to discuss the current technological advances towards the feasibility of space-based array for radio astronomy at ultra-long wavelengths. To this end, we elaborate on the system design for a space-based array in Section 2. We address various subsystems of the potential satellite array in the Sections 3 – 6, including the astronomy antenna design in Section 3. While current technologies limits us to ≤10 nodes, we foresee next generation arrays will contain larger number of satellites and operate as a co-operative wireless network. Hence, a dominant theme of the article is to investigate the extension of the proposed centralized solutions to distributed scenarios, particularly for processing (Section 4), communication (Section 5) and joint space-time estimation of the satellites in the network (Section 6). We summarize the article with a brief overview of the potential deployment locations (Section 7) and the fundamental challenges ahead for a space-based ULW array (Section 8).
2 Ultra-long wavelength interferometry
2.1 Aperture synthesis
Radio astronomy imaging is achieved by aperture synthesis, wherein the cosmic signals received at a large number of time-varying antenna positions, are coherently combined to produce high quality sky maps. For a N−antenna array, each antenna pair forms a baseline of an aperture synthesis interferometer, contributing \(\bar {N} \triangleq \ 0.5N(N-1)\) unique sampling points at a given time instant. Let x i (t) and x j (t) be two arbitrary antenna position vectors at time t forming a baseline, then the corresponding uvw point is defined as
where λ is the observed wavelength. Figure 1a shows the uvw points (in blue) for a N = 9 satellite cluster which is arbitrarily deployed with a maximum distance separation of d = 50km and an observational frequency of 10 MHz. The effective synthesized aperture is then obtained by projecting the uvw points onto a 2-D plane which is orthogonal to the source direction. As an illustration, Fig. 1a shows 3 such projections (in black) for sources orthogonal to the uv, uw and wv planes. The minimum distance between the satellites is only constrained by practical safety requirements and the maximum distance d between the satellites defines the resolution of the interferometric array as
Baseline and sky map simulations: Aperture filling of a 9-satellite ULW array for an Earth leading orbit around the Sun, to illustrate the effect of the sampling space on the normalized Point Spread Function (PSF). The uvw coverage for the 3-D array of satellites at ν = 10 MHz (a) for a single snapshot N t = 1 along with (b) corresponding PSF. Bandwidth synthesis is illustrated in (c) which shows the uvw coverage of single snapshot using 10 frequency bins uniformly distributed in the range 1 - 10 MHz with (d) the resultant PSF. The subfigures (e) and (f) show the UVW and corresponding PSF, for an entire orbit around the sun at 10 MHz with a single observation each day, i.e., 365 snapshots
The Van Cittert-Zernike theorem relates the spatial correlation of these antenna pairs directly to the source brightness distribution by a Fourier transform [71]. Hence for radio imaging, each antenna pair output is cross-correlated to measure the coherence function which is subsequently converted to a sky map, conventionally by an inverse Fourier transform. Figure 1b shows the normalized Point Spread Function (PSF) corresponding to the aperture coverage in Fig. 1a, for a single point source along the w direction. A densely sampled aperture plane lowers the spatial side-lobes of the sky image. The filling factor of the synthesized aperture can be increased by either using bandwidth synthesis or by populating sufficient baselines. In bandwidth synthesis, different frequency channels can be used to scale λ. As shown in Fig. 1c and d, using only 10 frequency bins uniformly distributed across 1−10 MHz, the aperture filling and the PSF is significantly improved as compared to Fig. 1b. A first-order simulation of an array of N = 9 satellites in Earth-leading orbit around Fig. 1e and the corresponding PSF in Fig. 1f, where one snapshot each day is assumed at a single observation frequency of 10 MHz. The number of uvw points are directly related to the unique number of baselines and the observational frequency. To achieve the confusion limit and resolve the sources individually, the total number of unique uvw points over the observational time period must be larger than the total number of detected sources.
2.2 Ultra-long wavelength sky
The dominant foreground in the low frequency radio sky is the galactic synchrotron radiation, which is due to synchrotron emission from electrons moving in the Galactic magnetic field. This emission causes the brightness temperature to rise from ∼10 4K at 30 MHz, to as high as ∼10 7K around 2 MHz [54]. At frequencies below 2 MHz, the Galactic plane is nearly completely opaque and the extra-galactic sources cannot be observed. More explicitly, for frequencies above 2 MHz, the sky temperature can be approximated as [34]
where ν is the observation frequency. For Earth-based observations at higher frequencies (>100 MHz), the overall system noise temperature T s y s plaguing the cosmic signal is typically dominated by the noise from receiver electronics T r e c . However, at lower frequencies (≤30 MHz), the intense galactic background implies that T s k y will be at least an order of magnitude larger than T r e c , and hence the overall noise temperature T s k y ≫T s y s . The immediate effect of this extremely high sky noise is the poor sensitivity of the interferometric array. The 1- σ RMS sensitivity for an antenna array of N nodes is [25]
where Δν is the bandwidth, t o b s is the observation time period over which the signal is integrated and the total number of estimated sources above this sensitivity is given by
Furthermore, the scattering in the interplanetary media (IPM) and interstellar media (ISM) also hinder observational frequencies less than 30 MHz, which limit the maximum baseline between the satellites to
For very long baseline interferometry, [44] noted that angular broadening of radio sources due to interstellar scattering will cause interplanetary scattering to be greatly reduced. Finally, the lower limit of the achievable noise is not the RMS sensitivity of the array, but the confusion limit. The presence of unresolved sources with individual flux densities below the detection limit leads to a constant noise floor, that is reached after a certain observation time t o b s [34]. For extra-galactic observations, under certain nominal assumptions, this anticipated confusion limit due to background sources is
where θ is the effective resolution for which the flux is below the confusion limit. The confusion limit is the lower limit to the achievable noise floor and thus is an upper limit to the useful collective area of the array. In other words, adding more antennas only decreases the time in which the confusion limit is reached, but not the overall array sensitivity (4). The time necessary for an array to reach this confusion limited sensitivity is given by the “survey equation”
Using these elementary and yet fundamental equations, a preliminary design for a space-based array can be proposed for desired science cases. For a more detailed study, refer to [34].
2.3 System definition
The science cases for an ULW array broadly span cosmology, galactic surveys, transients from solar and planetary bursts and even the study of Ultra-High Energy particles. Although a single satellite mission would suffice to detect the global dark-ages signal, over 104 antennas are required to investigate the radio emission from Extrasolar planets (see Jester and Falcke [34], Table 1). For a first space-based ULW array however, with possibly only a few satellite nodes, extra-galactic surveys and study of transients are among the best suited science cases [14], which we present as case studies. The proposed space-based array design can be readily extended to cater to other science cases, e.g., detection of the global dark-ages signal.
The expected signal strength for the extra-galactic surveys is in the order of 65 mJy with a desired spatial resolution of ∼1′. In Table 2, we present different scenarios to investigate the effects of varying observational frequencies, bandwidth and observation time, on the number of antennas to achieve 65 mJy. It is evident that increasing the observation time (1 day, 1 month, 1 year) steadily reduces the required number of antennas. Secondly, increasing the bandwidth (1 MHz to 3 MHz) is also an alternative to achieve the desired resolution for a small array. However, the increase in bandwidth has little effect on the confusion limit. We note that the confusion limit is a bottleneck for shorter integration times and lower observing frequencies. The maximum baseline is in general confusion limited for frequencies ≥10 MHz, however at <10 MHz, the ISM and IPM scattering limits the maximum baseline and subsequently the resolution. At 10 MHz, we require at least one year of observation time with more than 7 antennas for an observational bandwidth of 3 MHz to achieve the 65 mJy sensitivity. However, in the last column of the Table 2, we see that at 30 MHz, only 4 antennas are sufficient. Such a configuration is estimated to detect over a million sources using (5). These small array of antennas are adequate if arbitrarily long observations are possible, which may be limited by rapid, strong radio bursts from the Sun and Jupiter, and possibly high relative satellite motion. In such scenarios, quasi-snapshot imaging may be necessary, and consequentially a larger number of antennas may be needed.
A similar investigation was conducted for Jupiter-like flares and Giant crab-like pulses, which are bright events with order of MJy and kJy respectively, with typical time scales of milliseconds. The desired resolution for these transient radio systems are ∼1′ at ≤30 MHz. Since these events are extremely bright, even a single antenna with a nominal bandwidth of 10 % of observational frequency would meet the desired requirements. However, unlike the extragalactic surveys the observations are not confusion limited but possibly by the number of baselines for short integration timescales of milliseconds. The number of unique uvw points will depend on the deployment location and the relative velocities of the antennas. However, in general this limitation can be overcome by increasing the integration times in both these cases by over a minute.
In general, higher bandwidth, higher observing frequencies and longer integration times require less antennas to reach the same sensitivity level. In this article we choose the DARIS mission specifications as a reference to illustrate various sub-systems. To this end, we particularly focus on an array of N = 9 satellites, with a maximum satellite separation of 100km and capable of observing the skies at 0.1−10 MHz. This particular setup meets the requirements for the extra-galactic survey and transient radio system science cases. Moreover, all the proposed techniques and technologies (in the following sections) can be readily extended to for observation frequencies up to 30 MHz and more generally, for larger arrays.
3 Radio astronomy antenna design
We begin our discussion with the design of the observational antenna, which is a critical component for the space-based array. The system model of the observation antenna (connected to a LNA) is shown in Fig. 2a, wherein the antenna is modeled as an ideal lossless antenna, followed by an attenuator representative of the antenna losses. For the observation frequencies of 0.3−30 MHz, this front end must be sky noise limited i.e., T r e c <0.1T s k y , where T r e c is the receiver noise and T s k y is the sky noise temperatures which are defined at the interface between the lossless antenna and attenuator. The LNA noise temperature T L N A defined at the input of the LNA is equal to (1−η)T 0, where η is the radiation efficiency and T 0 is the physical temperature of the antenna (chosen as 290 K). Without loss of generality, we assume that the LNA noise is dominant over the noise contribution of subsequent electronics of the receiver. Under these assumptions, the prerequisite on the LNA noise temperature is derived as
where Γ is the reflection coefficient of the antenna [6]. A straightforward candidate for the observation antenna is a dipole (e.g., Fig. 2b), which can be realized by rolling out metallic strips from the satellite [49]. The observational wavelengths are much larger compared to the dimensions of the satellites and hence due to practical limitations, the realized dipole will be short compared to the wavelength. For instance, the classic half-wave dipole for 10 MHz and 30 MHz observation frequencies yields a dipole length of 15 m and 10 m respectively. For lower frequencies, this dipole length beegg,ets a directional pattern similar but with less directivity. Consequentially, the radiation resistance of the small antenna would be low and the thermal noise will significantly dominate the total antenna noise.
Space-based antenna model, configurations and simulations: (a) System model for an LNA connected to the Antenna (b) Configuration of a dipole antenna on a cubesat (c) Configuration of a tripole antenna in a cubesat (d) four monopoles (e) A dipole antenna placed on the opposite ends of a 3U-cubesat (f) Required T L N A as a function of frequency for non-matched dipoles of varying lengths. (g) Real part of input impedance and (h) Absolute value of imaginary part of input impedance for two monopoles placed on a satellite compared to a dipole (i) Ratio of gain of two monopoles placed on a satellite and a dipole
To maximize the received power at the antenna, matched dipoles can be used, in which case Γ≈ 0. However, the combination of antenna and matching network becomes highly resonant with a high quality factor, significantly limiting the achievable bandwidth of the system, in particular for shorter dipoles. Hence, we propose the use of a non-matched dipole [6]. Using (9), we have the Fig. 2f, which shows the T L N A for varying lengths of non-matched dipole lengths. We use a LNA with input impedance of 2K Ω, which is a realistic value for an LNA using a bipolar transistor. While the T L N A is above 100 K for 10 m and 15 m antennas, the required noise temperature for shorter dipole lengths are significantly lower, especially for lower frequencies.
In practice, a dipole is implemented on a satellite using two monopoles. To verify the validity of the proposed model, impedances of two monopoles on a satellite body is compared to that of the dipole. The satellite body under simulation is modeled as a cube of 40×40×40 cm , with perfect conducting surfaces. Furthermore, since the impedance of the monopole above a perfect ground plane is half the impedance of a dipole, the impedance of the monopole is multiplied by a factor 2 in the simulations for a fair comparison. Figure 2g and h show the real component of the impedance and absolute value of the imaginary component of the impedance respectively, for 1m dipole versus 0.5 m monopoles and 15 m dipole versus 7.5 m monopoles respectively. As seen in these figures, there is negligible difference between the dipole and the two monopole configuration. A step further, we compare the ratio of gains between a pair of monopoles against the 1 meter and 15 meter dipoles at 1 and 10 MHz. The investigated antenna lengths the ratio of gain are almost flat across for varying angles as seen in Fig. 2i, which indicates the element pattern does not change if a configuration of two monopoles is used instead of a dipole.
Two orthogonal dipoles (Fig. 2b) are in principle sufficient to get all the polarization information of the cosmic signal, however a tripole (i.e., three dipoles, see Fig. 2c) can be used to obtain information of all 3 components. The third dipole improves the directivity of the antenna system, thereby increasing the field of view. Along similar direction, an equiangular four monopole configuration can also be considered, as shown in Fig. 2d. However, the number of correlations is much higher and consequentially demanding more signal processing hardware for each antenna. In the OLFAR study where a 3U-cubesat (30×10×10 cm) is utilized, the monopoles are deployed in groups of three at the opposite ends of the satellite, as seen in Fig. 2e. The asymmetric design changes the properties of the monopoles and reduces the purity of the independent components, which is studied by [65] and experimentally evaluated on a smaller scale by [56].
4 Digital signal processing
Sky images in radio astronomy are made by calculating the Fourier transform of the measured coherence function [70]. The coherence function is the cross correlation product between two antenna signals located at the two spatial positions, averaged over a period of the integration time τ i n t . One way to implement such a system is using the traditional XF correlator i.e., cross correlation first and Fourier transform later and the more recent FX correlator which measures directly the cross-power spectrum between the two antenna signals [20]. Although the XF architecture is beneficial because bandwidth can be traded for spectral resolution, the FX architecture offers computational efficiency. The processing factor for XF vs FX is given by
where N s i g = N p o l N and N b i n s = Δν/Δν r e s [58]. Observe that the multiplicands in the XF mode are additive in the FX mode, besides the log2 reduction on the number of frequency bins. Thus, although for lower number of nodes the XF is comparable to FX mode, for large scalable architectures the FX mode is computationally cost effective. Since we prefer a scalable space-based array the FX architecture is chosen as the preferred architecture. Table 3 shows data rates for a cluster of N = 9 nodes, with an instantaneous bandwidth of Δν = 1 MHz and τ = 1 second integration time.
A typical pre-processing unit at each satellite node is shown in Fig. 3, where each satellite generates D o b s = 2Δν N p o l N b i t s bps. Observe that with N p o l = 3, for a signal with nominal instantaneous bandwidth of Δν = 1 MHz sampled with N b i t = 1bit resolution, the output data rate is 6Mbps. Given a far away deployment location, such as Lunar orbit (∼400,000 km) or Earth leading/trailing (∼2 × 10 6 to ∼4 × 10 6 km), this down-link data rate levies heavy prerequisites on the limited resources of a small satellite using current techonology. Hence, the satellite cluster must not only employ on-board pre-processing of astronomical signals, but also on-board correlation to minimize down-link data rate back to Earth. To this end, either a centralized or a distributed correlator can be employed as illustrated in Fig. 4.
Node level signal processing: Given the low observational bandwidth, the N p o l = 3 polarized astronomical signals received by each antenna will be signal conditioned and Nyquist sampled with a 14-bit (or more) Analog to Digital Converter (ADC) as shown in Fig. 3. A coarse Poly-phase Filter Bank (PFB) is used to selectively choose the desired instantaneous bandwidth of Δν = 1 MHz. After successful RFI Mitigation (RFIM), only N b i t s = 1−2bits will be used in further processing stages [4]. The total data generated for N p o l signal paths in each satellite is D o b s = 6Δν N b i t s bps, which is transported to the Inter-satellite communication layer
Correlator architectures: An illustration of two potential correlator architectures for space-based radio interferometric array, where the tags ‘X’ and ‘T’ on the nodes indicate Correlation and Transmission to Earth capabilities respectively. In the (a) Centralized correlator architecture a centralized mother ship receives data from all observational satellites, correlates and down-links data to Earth. On the contrary, in the (b) Distributed correlator framework, the observed data is evenly distributed between all nodes. Post correlation, all satellite nodes down-link their respective correlated data to Earth
4.1 Centralized architecture
In the centralized FX correlator framework each satellite node transmits D o b s = 2Δν N p o l N b i t s bps to the centralized mothership, which in turn receives \(D^{c}_{in} =\ D_{obs}(N-1)\)bps in total, excluding the data collected from the antenna on the mothership itself. The input data from all satellites is then correlated and the output is then transmitted down to Earth at the rate \(D^{c}_{out} =\ (2N^{2}_{sig}N_{bins}/ \tau )\)bps, where N b i n s = Δν/Δν r e s . A significant drawback of the centralized correlation is that it depends heavily on the healthy operation of a single correlation station, which introduces a Single Point Of Failure (SPOF) for large array of satellites in space.
4.2 Distributed architecture
To alleviate SPOF, a Frequency distributed correlator is proposed where each node is pre-assigned a specific sub-band Δν s b of the observed instantaneous bandwidth Δν s b for cross correlations [58]. Hence, in addition to the node pre-processing (Fig. 3), a secondary fine Polyphase Filter Bank (PFB) is implemented to further split the instantaneous bandwidth Δν into N s b sub bands, each of bandwidth Δν s b = Δν/N s b . Each satellite is assigned a specific sub-band for processing and the other (N s b −1) sub-bands are transmitted to corresponding satellites via the intra-satellite communication layer. Furthermore, for even distribution of data and to ensure scalability, we enforce the number of sub-bands equal to the number of satellite nodes, i.e., N s b = N. Subsequently, in the distributed framework, each node receives a specific sub-band of the observed data, i.e., (D o b s /N s b ) from N−1 other satellites in the network which yields a total input of \(D^{d}_{in}= (D_{obs}/N_{sb}) (N-1) = (D^{c}_{in}/N)\)bps, and down-links \(D^{d}_{out}= (D^{c}_{out}/N)\)bps respectively.
Thus, the Frequency distributed correlator reduces the inter-satellite communication by a factor N. Furthermore, at the cost of equipping all observational satellite nodes with communication capability (both inter-satellite and down-link to Earth), SPOF is averted and scalability is ensured. In the context of the projects discussed earlier, DARIS, FIRST and SURO-LC implement a centralized architecture, whereas OLFAR employed the distributed architecture. Given that the system frequency is typically an order of magnitude or more than the processing instantaneous bandwidth, computing requirements are negligibly small, which has been duly noted by all these studies.
4.3 Clocks
The choice of the on-board clock on each satellite has a significant impact on the signal processing system . The short-term clock stability i.e., t≪1 second is dominated by the clock jitter, which limits the Effective Number Of Bits (ENOB) for a given input frequency ν. Although 1−bit resolution suffices, the potential array will digitize the observed signal at a higher data rate ≥12 bits, to ensure functionality in (possible) high-RFI deployment locations Fig. 3. For instance, to facilitate 14-bit sampling of the observation frequency ν, the chosen clock must have δ t j i t t e r <1ps, as seen in the Fig. 5a. Secondly, to evaluate clock stability over long durations i.e., t≫1 seconds, we use Allan variance, which is a measure of nominal fractional frequency drift [8]. Following [71, 73], the stability requirement on the clock and define the coherence time τ c , such that the RMS phase error of the clock remains less than 1 radian
where ν is the observational frequency and σ ζ (τ c ) is the Allan deviation as a function of τ c [57]. The product σ ζ (τ c )τ c can be visualized as the time drift due to non-linear components of the clock after τ c seconds. Furthermore, the linear parameters of the clock i.e., frequency and phase offsets can be eliminated by exploiting the affine clock model, which is discussed in Section 6. Figure 5 shows expected Allan deviations of potential clocks versus the coherence time as per (11) for various input frequencies ν. Among the presented choices in Fig. 5, the ASTRIUM RAFS (3.3 kg, 30 W) and Airbus OCXO-F (220 g, 2 W) are space qualified Rubidium and Oven controlled oscillators respectively. A particular clock of interest is the Chip-Scale Atomic Clock (CSAC) SA.45s, which is a Rubidium clock weighing less than 35 grams, consuming <0.125 watts and offers an coherence time of up to 15 minutes. Although the SA.45s is not space qualified, more recently, similar CSACs are available for space-based applications e.g., Airbus OCXO-H [2].
Clock stability: (Left) Short term: The plot shows limiting cases of the Signal to Noise Ratio (SNR) and corresponding Effective Number of Bits (ENOB) due to jitter t jitter versus input frequency ν . Three demarkation lines shows the maximum input frequency of ν = 10 MHz, ν = 30 MHz and ν = 50 MHz. (Right) Long term: Desired Allan deviations of free running clocks are plotted versus the coherence time (in green) for various input frequencies ν. The map is overlayed with Allan deviations of potential clocks (in blue) for potential space-based low frequency arrays namely PRS-10 Rubidium [68], ASTRIUM RAFS [26], GPS 1pps [46], Airbus OCXO-F [1], SA.45s [51] and Space Hydrogen Maser (SHM) [30]
5 Communications
The potential communication scenarios for the envisioned space-based array are shown in Fig. 6, which follow directly from the correlator architectures discussed in the previous section. A centralized architecture, as shown in Fig. 6a, comprises of a mothership collecting raw observed data from a cluster of daughter satellites and down-links the processed data to an Earth-based ground station. Alternatively, in case of the distributed scenario shown in Fig. 6b, all satellites are capable of both exchanging data and correlating them, before down-linking back to Earth. In addition to the science data, housekeeping information is also exchanged between the satellites via tele-commands and telemetry, which is expected to be relatively small (≾100 kbps) in comparison to the astronomical data of 6 Mbps. The housekeeping information is critical for control, timing and synchronization of the satellite, and to maintain coherence within the satellite network.
Communication architectures: An illustration of a (a) Centralized communication architecture and (b) single pairwise-link of a Distributed communication architecture for a space-based radio interferometric array. The Inter-satellite link is indicated in blue and the Earth-downlink by red. Telemetry and Tele-commands are exchanged between the satellites and with Earth in both scenarios. In case of the centralized scenario, we assume that the mothership is in the center of the array with a maximum mothership-node distance of 50km
5.1 Inter-satellite link (ISL)
Implementing the ISL using high-frequency optical communication has many advantages as compared to radio communication, such as reduced mass and volume of equipment, higher data rates and no regulatory restrictions as experienced for Radio Frequency (RF) bands [67, 72]. However, this would also require extremely accurate alignment of the satellites, robust synchronization and more power than what could potentially be available for a small satellite. In the RF domain, Orthogonal Frequency-Division Multiplexing (OFDM) is an efficient modulation scheme for the ISL, in particular for a scalable antenna array with limited available bandwidth [53]. OFDM is well suited to frequency selective channels and offers potentially a good spectral efficiency. The signals from each satellite node which form individual channels will be modulated using a form of Phased Shift Keying (PSK), Amplitude Shift Keying (ASK), or a combination Quadrature Amplitude Modulation (QAM). In this article, we consider an ISL transmission frequency of 2.45 GHz, although other frequency bands can also be used.
One of the possible solutions to implement the ISL is to use patch antennas on each face of a satellite node, such that the combined implementation yields a full coverage of the sky. All the satellites will have patch antennas on all six faces for both uplink and downlink. In addition, a diplexer will be used to separate the receiving and transmitting channels. Using a coaxial switch (controlled by the CPU) this signal is selected, amplified and finally detected in the node. The desired antenna must have a bandwidth of 100 MHz around 2.4 GHz with the reflection coefficient less than −10 dB between 2.35 GHz and 2.45 GHz, and the half-power beam-width must be at least 90∘. Figure 7a shows the simulated patch antenna, where all dimensions are in millimeters. The patch is fed by a coaxial probe located 7.5 mm from the center of the patch. It was observed that in case of a linearly polarised patch antenna, the given setup yields a −3 dB beamwidth less than 90 ∘ for the radiation pattern in the ϕ = 90∘ plane, which is less than our desired requirement. Thus, to improve the radiation pattern we implemented a circularly polarized patch antenna. Moreover, an added advantage is that the polarization of both transmit and receive antenna is independent of the orientation of the antennas with respect to each other. The circular polarization is realized by adding a second co-axial probe to the patch, shown in red in Fig. 7a. As seen in the Fig. 7b, the reflection coefficient is better than −10 dB in the frequency range 2.35−2.8 GHz. Additionally, the radiation patterns in Fig. 7c show the half-power beam width is more than 3 dB for both the ϕ = 0∘ and ϕ = 90∘ planes.
5.2 ISL link margin
Table 4 shows the ISL Link budget for the centralized and distributed scenarios. In case of the centralized scenario, we assume that the mothership is in the center of the array with a maximum mothership-node distance of 50 km. To estimate the link margin for a centralized scenario, we assume that the mothership can transmit with a power of 1W i.e., 30 dBm. Now, using the patch antenna gain of 3 dBi and nominal losses (at the diplexer, transmitting cable and coaxial switch loss) of 2.6 dB, the EIRP (Equivalent Isotropically Radiated Power) of each satellite is 30.4 dBm. For both centralized and distributed scenarios, the ISL channel in space is in principle free space loss, where Multi-path, atmospheric losses, absorption losses and even Doppler effects can be ignored. Hence, the Friis free space loss for 2.4 GHz transmission frequency and 50 km is 134.7 dB. Hence, the effective received power for an EIRP of 30.4 dB and a pointing loss of 0.5 dB is −104.80 dB. The received C/N0 is estimated at 67.66 dB/Hz, for a G/T ratio of −26.14 dB/K (see Table 4). The transmission data rate mothership to node is 100 kbps (50 dB/Hz), which yields an Eb/No of 17.66 dB. For a typical receiver, an Eb/No of 2.5 dB is needed. Now, including a implementation loss of 2dB, the link margin for uplink with transmit power of 1 W is 13.16 dB. The downlink from the node satellite to the mothership, includes the 6 Mbps data (see Table 3) and the housekeeping data of 100 kbps, which amounts to 6.10Mbps. This downlink can be achieved with a link margin of 2.29 with a transmission power of 5 W.
Extending the link margin estimates of the centralized ISL architecture to a distributed scenario has two fundamental challenges. Firstly, the transmission data rate is now 5.44 Mbps, which includes 5.34 Mbps of science data (see Table 3) and 100 kbps of housekeeping data. Secondly, in the absence of a centralized correlator, the maximum distance between the satellites is 100 km, a factor 2 compared to the centralized scenario. Hence, to achieve the same link margin of 2.29 dB as the node to mothership downlink, the transmission power of each satellite in the distributed architecture must be 4 times that of the centralized scenario, i.e., 20 W. Although 15 W suffices to achieve a positive link margin for the distributed architecture. This requirement is a bottle neck for scalable array of small satellites with limited transmission power. One possibility is to use clustering schemes and multi-hop approaches to reduces the communication distances between the satellites [19], which is a research area currently being explored [52].
5.3 Space to earth downlink
The total downlink data rate \(D^{c}_{out}\) after correlation quadratically increases with the number of nodes in the cluster and reduces linearly with the integration time (see Table 3). For a cluster of 9 satellites, with 1 second integration interval this rate is ≥1.46Mbps. In the DARIS study, the space to earth downlink was achieved using an X-band Downlink Unit (XDU). Figure 8 shows the X-Band transmit chain which consists of a modulator and a 60 W Traveling Wave Tube Amplifiers (TWTA) with 60 % efficiency. In the nominal operation case the data is directly BPSK modulated on the X-band carrier at 4.3 Mbps, amplified, filtered at the diplexer and transmitted via the high gain antenna (40 dBi). During launch and early orbit phase and in contingency cases the tranmission rate is reduced to 100 bps, BPSK-modulated onto a subcarrier with low frequency (e.g., 8 kHz) which itself PM-modulates the carrier. In order to enable full coverage two adversely polarized low gain antennas are transmitting into the two hemispheres. The receiver downconverts and demodulates the X-band data and feeds them to the OBC via RS422 link. In the nominal mode the command rate is 400 kbps, BPSK-modulated on a 16 kHz subcarrier and PM modulated onto the carrier. The estimated power consumption of the transceiver is 110 W operational and 30 W in standby. The HGA, covering both up- and downlink band, could be realized as a parabolic antenna similar to the one of Mars Express. With a 40 dBi design, the 3 dB beamwidth would be around 1.7 ∘ posing no big challenge to the pointing mechanism. The LGA s a conventional helix antenna design covering also both transmit and receive band.
DARIS mothership-Earth Link X-band Downlink Unit (XDU): The XDU unit consists of a complete redundant transmit and receive subsystem, the X-band antennas and the interconnecting waveguide links. The X-Band downlink transceivers are directly interfaced to the Onboard Computer (OBC) via RS422. Two different modes are available for the communication link (a) Nominal link via High Gain Antenna (HGA) for science telemetry and commanding (b) Emergency link via low gain antennas (LGA) with full coverage and reduced data rates for telemetry and command
The number of ground stations on Earth are limited and are therefore almost always in high demand. However, a 35 m ground station with access for 8 hours per day suffices to meet the downlink data rate of upto 4.5 Mbps for 9 nodes in Earth Leading/Trailing or Lunar Orbit. This requires a 1.5 m diameter parabolic antenna on board, with a one axis pointing mechanism to ensure the antenna can always point at the Earth as the satellite remains Sun pointed [14]. For arrays larger than 50 satellites with minimal power, it is difficult to establish Earth-based downlink with current off the shelf technology. However, these challenges and possible distributed downlink scenarios are currently being investigated [18].
6 Synchronization, localization and attitude determination
To maintain coherence between satellites, all the satellites must be synchronized, and their positions known up to sub-meter accuracies. These requirements on space-time accuracies at ULWs are considerably lower in comparison to other space-based array missions, such as LISA [13]. Almost all Earth-based antenna arrays synchronize using GPS-aided atomic clocks, where fixed antenna positions are known up to millimeter accuracies, cf e.g., LOFAR [74]. However, the envisioned space-based array will be deployed far-away from Earth-based GPS satellites and unlike Earth-based antennas, these satellites will be mobile. In addition, given the large number of satellites and limited ground segment capability, tracking each satellite independently is infeasible. Moreover, in certain deployment locations such as the Lunar orbit, the satellite array will be partially or even completely disconnected from Earth-based ground stations during eclipse periods.
Hence, the satellite array must be an anchorless network, cooperatively synchronizing the clocks and estimating time-varying relative positions, in the absence of absolute reference on time and position. The estimated relative positions, which are identical to the absolute positions upto a rotation, are sufficient for inter-satellite communication, collision avoidance and on-board correlation of observed data. However, for radio astronomy imaging, to ensure the desired orientation of the projected baselines (see Fig. 1), an external reference may be required occasionally to map the relative spacecraft positions on an inertial reference frame. Such an absolute reference can be obtained by tracking a few satellites, during intermittent Earth-based communication.
In this section we briefly discuss a dynamic ranging based solution to estimate the clock parameters and the time-varying distances of the network. Given these time-varying distance estimates, the relative positions over time can be estimated from distances via MDS-like algorithms [16, 60]. We are primarily interested in solutions for cold start scenarios, when no prior information is known. For longer time scales, when the orbital dynamics of the deployment location is well known, the estimated space-time parameters can be tracked and improved using recursive filters, e.g., Kalman Filter [40]. In the end, attitude control for a satellite array is discussed.
6.1 Joint ranging and synchronization
All clocks are inherently non-linear w.r.t. the ideal time t. However, a given clock can be approximated to a linear model provided the Allan-deviation of the clock is relatively low for a small coherence time (see Section 4.3). More generally, let t i , t j denote the local times at i, j respectively, then the ideal time t is
where (ψ i , ψ j ) and \((\dot {\psi }_{i}, \dot {\psi }_{j})\) are the phase and frequency offsets of a satellite pair (i, j) and, \(\mathcal {C}(\cdot )\) represents a linear function of the local clock parameters. However, in case of a satellite network, the pairwise distances are time-varying, which can be expanded as
where d i j (t) is the time-varying distance between the satellite pair (i, j) and \((r_{ij},\dot {r}_{ij},\ddot {r}_{ij}, \hdots )\) are range parameters of the Taylor expansion at ideal time t = 0 [61]. More specifically, r i j is the initial pairwise distance, \(\dot {r}_{ij}\) is the range rate and \(\ddot {r}_{ij}\) denotes the rate of range rate between the satellites. Given these pairwise distances, the relative positions of the satellites can be estimated using MDS-like algorithms [16]. Our aim is to jointly estimate the clock parameters and the time-varying pairwise distances between the satellite nodes. The joint synchronization and ranging problem can be formulated as shown in Fig. 9, which shows a pair of asynchronous mobile satellite nodes. The mobile satellites transmit messages asymmetrically between each other, during which K time-markers are recorded at each end. Let T i j, k and T j i, k be the kth time-markers recorded at the ith and jth satellite nodes respectively, and E i j, k ∈{+1,−1} indicates the transmit and receive direction of the message. For any kth time instant, the Generalized Two-Way Ranging (GTWR) equation [61] is
where without loss of generality the ideal time t of the time-varying distance d i j (t) is replaced with the clock model at satellite i (12). The unknown frequency offsets, phase offsets and the pairwise distances over K time instances can be estimated using the iterative Mobile Pairwise Least Squares (iMPLS) and iterative Mobile Global Least Squares (iMGLS). The iMPLS algorithm is applicable when the daughter satellite nodes communicate only with a centralized Mother-ship (i.e., Star network topology, see Fig. 4a, whereby only the clocks of the satellites can be corrected. For a full mesh network, when all satellites communicate with each other (i.e., Full mesh topology, see Fig. 4b both the clock parameters and the distances can be estimated, which is achieved by the iMGLS algorithm.
Dynamic ranging: A generalized Two Way Ranging (TWR) scenario between a pair of asynchronous mobile satellite nodes where the asynchronous nodes transmit and receive asymmetrically, during which K time stamps are recorded at respective nodes. Unlike classical TWR [33] where the transmission and reception is alternating, the proposed setup imposes no pre-requisites on the sequence or number of two way communications. Consequently, this framework and proposed solutions for joint ranging and synchronization [61] can be readily extended to a plethora of TWR ranging protocols, including broadcasting and passive listening [64]
6.2 Simulations
To illustrate the algorithms, we consider a cluster of N = 9 mobile nodes in a 3−dimensional Euclidean space. The initial frequency offsets \(\dot {\psi }=[\dot {\psi }_{1}, \dot {\psi }_{2}, \hdots , \dot {\psi }_{9}]\) and phase offsets ψ = [ψ 1, ψ 2,…, ψ 9] of the nodes are arbitrarily chosen in the range [−10−4,10−4] and [−1,1] seconds respectively, where without loss of generality satellite node 1 is chosen as the reference node with \([\dot {\psi }_{1}, \psi _{1}]= [0,0]\). Secondly, the initial positions X and initial velocities Y, whose values are arbitrary chosen as
For these assumed positions, the initial pairwise distance \(\dot {\mathbf {r}}\) is in the range [0,10] km. Secondly, for these values the range rates \(\dot {r}\) are distributed in the period [−100,100] m/s and the rate of range rate \(\ddot {r}\) are distributed over [−10,10]m2/s. These values are typically for worst case scenarios, assumed to evaluate the performance of the proposed algorithms. The mobile satellites communicate K messages with each other within a time interval of [−1.5,1.5] seconds, and the time-markers T i j, k ∀ i, j≤N,∀ K are generated accordingly. We assume alternating communication between the nodes and a Gaussian noise of σ = 10−8 seconds(∼ 3.3 meters) plaguing the time-markers. Figure 10 shows the performance of the proposed algorithms for phase offset, frequency offset and pairwise distance estimation. The Root Mean Square Errors are plotted (in blue) againstvarying pairwise communications, from K = 10 to K = 100, where the clock parameters are averaged over N nodes and, the distances and range parameters are averaged over \(N \choose 2\) unique links. In addition, the Cramér Rao Lower Bounds for the corresponding estimates are also plotted (in red), which is achieved asymptotically by the proposed estimators. To show the performance of the prevalent solutions, we also plot the Low Complexity Least Squares (LCLS) which synchronizes the clocks for immobile network of satellite nodes. The iMGLS algorithm outperforms the iMPLS estimator since it exploits the full mesh communication network between the nodes. More significantly, the iMGLS estimator achieves clock accuracies upto nanoseconds and distance errors up to meter accuracies at cold start.
Joint ranging and synchronization: A simulation showing the Root Mean Square Errors (RMSEs) of the estimated frequency offset (\(\hat {\dot {\phi }}\)), phase offset (\(\hat {\phi }\)), range parameters (\(\hat {\mathbf {r}}, \hat {\dot {\mathbf {r}}}, \hat {\ddot {\mathbf {r}}}\)) and distance \(\hat {\mathbf {d}}\) using the MGLS algorithm for joint ranging and synchronization
An added advantage of using dynamic ranging is that the timestamps can potentially piggyback on the housekeeping data exchanged between the satellite nodes, which mitigates the need for a dedicated ranging system. However, if a ranging system is employed, then the achievable lower bound on the standard deviation for Time Of Arrival in multipath-free channels is given by
where F c denotes the carrier frequency, B≪F c is the bandwidth of the signal, T is the signal duration in seconds [55]. The assumed noise variance on the time-markers in the simulation is σ = 10−8 (shown in green in Fig. 10), which can be adequately achieved by a wireless node communicating at F c = 2. GHz with a nominal bandwidth of 1 kHz transmitting and SNR=10 dB for a signal duration of T∼1ms.
6.3 Attitude determination
For estimating the spacecraft orientation, two-vector attitude determination can be employed where these vectors are either (a) the unit-vectors to the Sun and the Earths’ magnetic field vector or (b) unit vectors to two stars. The pointing direction for the satellites can be provided by commercially available sun and star trackers, which typically form an integral part of the Attitude and Orbit Control System (AOCS) of the satellites. Using these measurements, methods such as TRIAD or a solution to Wahbas’ problem would yield the attitude determination (see [??], chap. 5).
7 Deployment locations
The deployment location of the space-based array must be chosen to ensure the following conditions.
-
Minimize RFI during scientific observation cycles.
-
Offer maximum possible down-link data rate.
-
Provide sufficient positional stability during integration time τ.
-
Remain within a sphere of ∼100 km.
In addition, each satellite must offer low noise conditions with minimal EMC and stable temperature (and gain) conditions. To alleviate the high complexity of active control to keep all the satellites within a cluster, passive formation flying could be employed. In passive formation flying paradigm, the satellites are allowed to drift, during which the relative positions and orientations of the satellites are constantly monitored. This approach eliminates the need for excess propulsion and heavy orbital maintenance equipment on all satellites. Additionally, the naturally varying position vectors of the satellites produce unique uvw sampling points, which consequentially improve the PSF.
In order to avoid interference either the cluster must be located far from Earth-based RFI and ionospheric distortions, such as Earth leading/trailing orbits and Sun-Earth Lagrangian points. However, by increasing the distance to the Earth, the communication with the Earth becomes more difficult. Alternatively, RFI shielding can be achieved by positioning the array on the far side of the moon. The Radio Astronomy Explorer RAE-2 showed that interference at very low frequencies is reduced by 2 orders of magnitude behind the moon, making it an ideal location for radio astronomy observations [3]. However, during the eclipse behind the moon the cluster has no communication with Earth. The following section discusses the quest to find an optimum balance between down-link data rates and maximizing observation time, emphasizing the challenges in various deployment locations.
7.1 Lagrange points and moon-farside
The relative velocities of the satellites are minimal at Lagrange points and hence these locations offer increased positional stability for longer time intervals. Therefore, the Lagrange points are an optimal choice to increase the integration time of the observations and also the mission lifetime. The Earth-Moon L4 and L5 are much closer for Earth based communication, however are suspected to be less radio quiet relative to the Earth-Moon L2. The Earth-Moon L2 located at ∼61347 km away from the Moon, is still in the cone of radio-silence and is sufficiently shielded from RFI. However, this Lagrange point may not be a favorable deployment location, since transmission in this radio quiet zone may affect future missions [48]. The Sun-Earth L4 and L5 points are too far and subsequently limit downlink rates. In contrast, the Sun-Earth L2 liberation point at ∼1.5 Million km away from Earth, is a tradeoff between downlink data rate, RFI avoidance and increasing τ i n t . Although this is a stationary point, in practice a satellite operating at L2 will experience a gravity gradient with a slow and steady outward drift. Such a scenario is preferred by the FIRST [12] and SURO-LC [7] studies. The SURO-LC proposes a array of 8 daughter satellites drifting slowly in Lissajous orbit and a mothership at a fixed distance of 10 km from the cluster. While such a mission will provide enhanced imaging performance with improved uvw coverage and longer integration times, the downlink data rate is estimated to be 2−3 orders of magnitude less than a Moon based array using prevalent technology [59].
7.2 Orbiting the moon
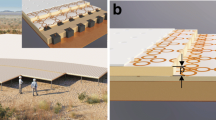
An equatorial orbit around the Moon presents a relatively easier down-link to Earth and sufficiently long eclipse times behind the Moon w.r.t. Earth. The long eclipse time periods shield against radio noise from Earth and enable the science observations. In the DARIS study, to increase the predictability of the relative positioning, the reference orbit around the Moon was chosen to be circular which additionally also decreases the chance of collisions [63]. The array formation is build up from different relative orbits with a different relative inclination around a reference orbit (Fig. 11a), where each of these relative orbits contain several node spacecrafts (Fig. 11b). The reference orbit determines the duration of the eclipse time and subsequently the science duty cycle, which is increased by aligning an orbit with the Earth-Moon plane and/or by lowering the altitude [14]. As seen in Fig. 12, the Eclipse time period can be increased by decreasing the orbital altitude, however consequently the percentage of the orbit in the shade increases and thereby reducing the science duty-cycle. In addition, by decreasing the orbital altitude, the relative range rates of the satellites also increase, which in turn affects the baseline stability. Hence, a balance between the relative velocity and the eclipse time must be found. When including the perturbations of the Earths’ gravity field, the irregularities in the lunar gravity field, the solar gravity field and the solar pressure, a constant drift of the relative orbits occurs. Coincidentally, this drift is mainly along the in-track direction of the reference orbit which can be compensated by adjusting the semi-major axis of the spacecraft node. In essence, a circular orbit in the Lunar equatorial plane offers a stable orbit, provided a trade-off is achieved between eclipse time and the satellite range rates.
Altitude vs Orbital period in Lunar orbit: A satellite cluster orbiting the moon over the far-side enters a “cone of silence” behind the moon, once every orbit. During this phase, the moon shields the satellite cluster from Earth-based and solar interference and subsequently permitting relatively noise-free scientific observations. These eclipse periods can be extended by inserting the satellite network at a higher altitude, which also offers more orbital stability [59]. However, a longer eclipse period behind the moon severly limits the communications with Earth
7.3 Orbiting the sun
A potential reference orbit for formation flying around the Sun is the Earth orbit itself. However, if the satellites are too close to Earth, then the terrestrial interference is a major disturbance to science observations. Alternatively, an orbit around the Sun with a different eccentricity than the Earth orbit keeps the satellite array at 4 to 10 million km from Earth, which is far enough to offer both stability and also reduce radio noise from Earth. The large distance separation severely limits the available down-link bandwidth by at least an order magnitude compared to the Lunar orbits. In view of an optimal balance between increased data-downlink and RFI free science observation, we choose the Earth orbit as a reference orbit with the satellite nodes orbiting at a distance of 4 to 10 million km from Earth. Hence, even though the constellation orbits the Sun as a central body, the reference orbit does go around the Earth, from leading to trailing. One of the many benefits of this particular orbit is that it is relatively stable for 10 years and allows continuous scientific observations. However unlike the lunar orbital design, this reference orbit is eccentric and highly sensitive to small changes due to large difference between the semi-major axis and the relative pairwise distances of the satellites [14, 63]. Furthermore, the time period of the reference orbit is equal to the period of the relative orbits, which causes the formation to drift in all directions. With reference to the reference orbit, the cluster will slowly expand with time and hence offers unique sampling points for interferometry. One of the key advantages of this orbit is the low relative range rates which facilitates longer integration period. In addition, the relative range rates of the satellites in this orbit are less than 20cm/s for 3 years. Despite this advantage, the solar orbit is sensitive to small errors in velocity and the relative orbits are stable only for change in injection velocities upto 0.1mm/s, which can be compensated using minor corrections [63].
8 Summary and discussion
A satellite cluster of less than 10 nodes is scientifically very interesting and meets the requirements for the extra-galactic survey science cases in terms of resolution and sensitivity. At least 4 antennas observing at 30 MHz for more than a year is sufficient to achieve the confusion limit of 65 mJy with 1′ resolution, in which case over a million sources can be detected (Section 2.3). Moreover, even with fewer antennas, transient science cases such as bright Jupiter-like flares and Crab-like pulses can be addressed. All the satellites will be equipped with 2 (or 3) 5m dipole antennas (or two 2.5 monopoles) to observe the ≤ 30MHz spectrum (Section 3).
For a nominal observational bandwidth of ≥1MHz, each satellite is estimated to generate ≥6 Mbits/s, which must be correlated in space to minimize downlink data rate to Earth. In both centralized and distributed scenarios, the processing requirements for filtering and correlation are negligibly small for up to 50 satellites and can be readily incorporated into the On Board Computer (OBC) (Section 4). To establish the inter-satellite link, the satellites will be equipped with patch antennas to transmit the desired ≥6 Mbps data rate. The ISL budget analysis shows that in the Centralized scenario using 2.45 GHz ISM band, the node to mothership link can be established with 5 W over 50 km distance with a positive link margin. However, in the distributed scenario upto 15 W is desired to establish a link over 100 km, which could be improved using clustering schemes and multi-hop communication (Section 5). Nonetheless, the proposed distributed framework is indispensable for large and scalable array of ≥10 satellites, where SPOF must be avoided.
The on-board clock on all satellites must have an Allan-deviation of ≤10−12, which can be met by a Rubidium or OCXO clock (Section 4.3). The current bulky space-qualified clocks, such as Airbus OCXO-F, will potentially be replaced by light-weight and low-power on-chip atomic clocks e.g., the chip-scale SA.45s or Airbus OCXO-H. In inaccessible (e.g., Moon-farside) or far-away deployment scenarios (e.g., Lagrange points), the satellites can be synchronized and localized using MGLS like algorithms, which enable the satellite network to be a co-operative network with minimum dependence on Earth-based ground stations (Section 6). In addition, the orientation of the satellites can be estimated using the sensors in the Attitude and Orbit Control System (AOCS) which include the sun sensor and star trackers. All satellites will also be equipped with sufficient propulsion to ensure precise deployment and to maintain the maximum baseline separation of 100 km (Section 7).
8.1 Technological challenges for ULW arrays
The actual satellite implementation is intricately connected to specific mission requirements, the number of satellites, the active choices in network architecture and the deployment location. However, recent studies which investigated centralized scenarios for an ULW array give insights into the current state-of-the-art space technology. Figure 13 shows the mass and power breakdown for the DARIS mission, where all subsystems use only existing and tested off the shelf components [14]. The power consumption for the daughter node and the mothership was estimated at 160W and 502W respectively. Reliable and highly efficient solar panels based on triple junction GaAs cells were employed on both the mothership and Daughter nodes to meet the power requirements. Furthermore, the dry mass of each daughter node was estimated at ∼100kg and the mothership at ∼550 kg.
In comparison to DARIS, futuristic missions such as OLFAR are expected to be lighter by two orders of magnitude and consuming an order of magnitude less power (see Table 1). The reduced mass and power requirements will not only enable a larger array of antennas for radio astronomy, but can potentially enable the system to piggy-back on other missions, without the need for a dedicated launch vehicle. Thus, future missions will possibly consist of relatively cheaper nano-satellites with miniaturized and power-efficient subsystems.
The intra-satellite communication between the satellite nodes is a fundamental bottleneck, which limits the bandwidth of observation and possibly the achievable baseline for radio astronomy imaging (see Section 5.2). In addition to limiting the feasibility of the science cases, the power consumption of existing technologies is also high. The DARIS project indicates >25 % of the power consumption for communication for both the daughter node and mothership respectively (Fig. 13). The satellite network to Earth communication limits the possible number of satellites in the cluster. Moreover, one of the limiting factors for the number of satellites is the downlink data rate of the satellite network, such as the HBA XDU for the centralized architecture (see Section 5.3). In case of a distributed architecture, the satellite swarm will employ diversity schemes to cooperatively downlink data to earth [18].
Further potential research areas identified during the study include the antenna design for observation frequencies below 10 MHz, development of efficient imaging techniques for radio astronomy, high speed and robust RF Inter-satellite communications techniques [17] and investigating control and reliability of large satellite arrays [28]. In addition, observability challenges such as the unknown RFI environment at the desired deployment location must also be investigated, possibly by a ≥2 satellite interferometer via a precursor mission.
8.2 Conclusion
The frequency window of ≤30 MHz opens a new realm of interesting science cases and yet remains one of the last unexplored frequency regime in astronomy. To achieve the science objectives at these wavelengths with desired resolution and sensitivity, a dedicated space-based ULW array is necessary. Recent advances in technology and computing resources have improved both the feasibility and scientific desirability of such a space-based array. In this article, we justified the need for a space-based antenna array for ultra-long wavelength radio astronomy and discussed various subsystems needed to achieve the desired science cases. More recently concluded projects such as DARIS, FIRST, SURO have shown feasibility of such an array. In particular, the DARIS project showed that a cluster of less than 10 satellites can be launched using current off the shelf technology. An expanded set of science cases can be targeted by scaling the number of satellite nodes, extending the frequency range of observation and increasing the instantaneous bandwidth. However, this would significantly increase the mass, power consumption and eventually the cost of the mission. The on-going work on miniaturized nano-satellites may overcome this bottleneck and could pave the way for feasible and affordable missions in the future.
References
Airbus Defense and Space: Quartz crystal oscillators OCXO-F. Technical report, Airbus Defense and Space. http://www.space-airbusds.com/en/equipment/quartz-crystal-oscillators-ocxo-f.html (2012)
Airbus Defense and Space: Quartz crystal oscillators OCXO-H. Technical report, Airbus Defense and Space. http://www.space-airbusds.com/en/equipment/quartz-crystal-oscillators-ocxo-h.html (2015)
Alexander, J., Kaiser, M., Novaco, J., Grena, F., Weber, R.: Scientific instrumentation of the Radio-Astronomy-Explorer-2 satellite. NASA STI/Recon Tech. Rep. N 75, 18284 (1974)
Altunin, V.: Protecting Space-Based Radio Astronomy. In: Cohen, R.J., Sullivan, W.T. (eds.) Preserving the astronomical sky, vol. 196 of IAU symposium, p 324 (2001)
Aminaei, A., Wolt, M.K., Chen, L., Bronzwaer, T., Pourshaghaghi, H.R., Bentum, M.J., Falcke, H.: Basic radio interferometry for future lunar missions. In: IEEE Aerospace Conference, pp. 1–19. IEEE (2014)
Arts, M., van der Wal, E., Boonstra, A.-J.: Antenna concepts for a space-based low-frequency radio telescope. In: ESA Antenna Workshop on Antennas for Space Applications, Noordwijk, pp. 5–8 (2010)
Baan, W.: SURO-LC: A space-based ultra-long wavelength radio observatory. In: Proceedings of the meeting from Antikythera to the Square Kilometre Array: Lessons from the Ancients (Antikythera & SKA). Kerastari, Greece,vol. 1, p. 45, 12–15 June 2012
Barnes, J.A., Chi, A.R., Cutler, L.S., Healey, D.J., Leeson, D.B., McGunigal, T.E., Mullen, J.A., Smith, W.L., Sydnor, R.L., Vessot, R.F.C., Winkler, G.M.R.: Characterization of frequency stability. IEEE Trans. Instrum. Meas. IM-20(2), 105–120 (1971)
Basart, J., Burns, J., Dennison, B., Weiler, K., Kassim, N., Castillo, S., McCune, B.: Directions for space-based low frequency radio astronomy: 1. System considerations. Radio Sci. 32(1), 251–263 (1997)
Basart, J., Burns, J., Dennison, B., Weiler, K., Kassim, N., Castillo, S., McCune, B.: Directions for space-based low-frequency radio astronomy: 2. Telescopes. Radio Sci. 32(1), 265–275 (1997)
Bentum, M., Verhoeven, C., Boonstra, A.-J., van der Veen, A.-J., Gill, E.: A novel astronomical application for formation flying small satellites. In: 60th International Astronautical Congress: IAC 2009, 12–16 October 2009, Daejeon, Republic of Korea. http://doc.utwente.nl/68514 (2009)
Bergman, J.E.S., Blott, R.J., Forbes, A.B., Humphreys, D.A., Robinson, D.W., Stavrinidis, C.: FIRST Explorer – An innovative low-cost passive formation-flying system (2009). arXiv:0911.0991
Bik, J., Visser, P., Jennrich, O.: LISA satellite formation control. Adv. Space Res. 40(1), 25–34 (2007)
Boonstra, A.-J., Bentum, M., Rajan, R.T., Wijnholds, S.J., van Cappellen, W., Saks, N., Falcke, H., Klein-Wolt, M.: DARIS: Distributed aperture array for radio astronomy in space. Technical Report 08, ASTRON, Dwingeloo (2011)
Boonstra, A.-J., Saks, N., Bentum, M., van’t Klooster, K., Falcke, H.: DARIS, A low-frequency distributed aperture array for radio astronomy in space. In: 61st International Astronautical Congress. IAC, IAC (2010)
Borg, I., Groenen, P.J.F.: Modern Multidimensional Scaling: Theory and Applications (Springer Series in Statistics) Springer, 2nd edition (2005)
Budianu, A., Castro, T.J.W., Meijerink, A., Bentum, M.: Inter-satellite links for cubesats. In: IEEE Aerospace Conference, pp. 1–10 (2013)
Budianu, A., Meijerink, A., Bentum, M.: Swarm-to-earth communication in OLFAR. Acta Astronaut 107(0), 14–19 (2015)
Budianu, A., Rajan, R.T., Engelen, S., Meijerink, A., Verhoeven, C., Bentum, M.: OLFAR: Adaptive topology for satellite swarms. In: International Astronautical Congress, pp. 3–7, Cape Town (2011)
Bunton, J.: SKA correlator advances. Exp. Astron. 17, 251–259 (2004)
Burke, B.F.: Astrophysics from the moon. Science 250(4986), 1365–1370 (1990)
Burns, J.: The lunar observer radio astronomy experiment (LORAE), pp. 19–28. Low frequency astrophysics from space (1990)
Burns, J.O., Duric, N., Taylor, G.J., Johnson, S.W.: Observatories on the moon. Sci. Am. 262, 42–49 (1990)
Burns, J.O., Lazio, J., Bale, S., Bowman, J., Bradley, R., Carilli, C., Furlanetto, S., Harker, G., Loeb, A., Pritchard, J.: Probing the first stars and black holes in the early universe with the dark ages radio explorer (DARE). Adv. Space Res. 49(3), 433–450 (2012)
Cohen, A.: Estimates of the classical confusion limit for the LWA. Long Wavelength Array Memo Series, vol. 17, p 20375. Naval Research Laboratory, Washington (2004)
Droz, F., Barmaverain, G., Wang, Q., Rochat, P., Emma, F., Waller, P.: Galileo rubidium standard - lifetime data and GIOVE-A related telemetries. In: 21st European Frequency and Time Forum, pp. 1122–1126. IEEE (2007)
Ellingson, S.W., Clarke, T.E., Cohen, A., Craig, J., Kassim, N.E., Pihlstrom, Y., Rickard, L.J., Taylor, G.B.: The long wavelength array. IEEE Proc 97(8), 1421–1430 (2009)
Engelen, S., Gill, E., Verhoeven, C.: On the reliability, availability, and throughput of satellite swarms. IEEE Trans. Aerosp. Electron. Syst. 50(2), 1027–1037 (2014)
Gorgolewski, S.: The advantages of a lunar radio astronomy observatory. Astronaut. Acta New Ser. 11(2), 130–131 (1965)
Goujon, D., Rochat, P., Mosset, P., Boving, D., Perri, A., Rochat, J., Ramanan, N., Simonet, D., Vernez, X., Froidevaux, S.: Development of the space active hydrogen maser for the aces mission. In: EFTF-2010 24th European frequency and time forum. IEEE, pp. 1–6 (2010)
Gurvits, L.: Space radio astronomy in the next 1000001 (binary) years. In: Resolving the sky-radio interferometry: past, present and future, vol. 1, p 45 (2012)
Hirabayashi, H., Hirosawa, H., Kobayashi, H., Murata, Y., Asaki, Y., Avruch, I.M., Edwards, P.G., Fomalont, E.B., Ichikawa, T., Kii, T.: The VLBI space observatory programme and the radio-astronomical satellite halca. Publ Astron Soc Jpn 52(6), 955–965 (2000)
IEEE 2007: Part 15.4: Wireless medium access control (MAC) and physical layer (PHY) specifications for low-rate wireless personal area networks (WPANs). Technical report, IEEE Working Group 802.15.4 (2007)
Jester, S., Falcke, H.: Science with a lunar low-frequency array: From the dark ages of the Universe to nearby exoplanets. New Astron. Rev. 53, 1–26 (2009)
Jones, D., Allen, R., Basart, J., Bastian, T., Blume, W., Bougeret, J.-L., Dennison, B., Desch, M., Dwarakanath, K., Erickson, W.: The alfa medium explorer mission. Adv. Space Res. 26(4), 743–746 (2000)
Jones, D.L., Lazio, J., MacDowall, R., Weiler, K., Burns, J.: Towards a lunar epoch of reionization telescope. In: Bulletin of the American Astronomical Society, vol. 39, p. 196 (2007)
Kaiser, M.L., Weiler, K.W.: The current status of low frequency radio astronomy from space. Geophys. Monogr. 119, 1–11 (2000)
Kardashev, N., Khartov, V., Abramov, V., Avdeev, V.Y., Alakoz, A., Aleksandrov, Y.A., Ananthakrishnan, S., Andreyanov, V., Andrianov, A., Antonov, N.: RadioAstron-a telescope with a size of 300 000 km: Main parameters and first observational results. Astron. Rep. 57(3), 153–194 (2013)
Kassim, N.E., Perley, R.A., Erickson, W.C., Dwarakanath, K.S.: Subarcminute resolution imaging of radio sources at 74 MHz with the Very Large Array. Astron. J. 106, 2218–2228 (1993)
Kay, S.M.: Fundamentals of statistical signal processing: estimation theory. Prentice-Hall, Inc., NJ (1993)
Klein-Wolt, M., Aminaei, A., Zarka, P., Schrader, J.-R., Boonstra, A.-J., Falcke, H.: Radio astronomy with the european lunar lander: Opening up the last unexplored frequency regime. Planet. Space Sci. 74(1), 167–178 (2012). Scientific Preparations For Lunar Exploration
Klein-Wolt M., et al.: Dark ages explorer, DEX, a white paper for a low frequency radio interferometer mission to explore the cosmological dark ages for the L2. L3 ESA Cosmic Vision Program (2013)
Kuiper, T., Jones, D.: Lunar surface arrays. Radio Astronomy at Long Wavelengths, pp.. 351–357 (2000)
Linfield, R., Keihm, S., Teitelbaum, L., Walter, S., Mahoney, M., Treuhaft, R., Skjerve, L.: A test of water vapor radiometer-based troposphere calibration using very long baseline interferometry observations on a 21-km baseline. Radio Sci. 31(1), 129–146 (1996)
Loeb, A., Zaldarriaga, M.: Measuring the small-scale power spectrum of cosmic density fluctuations through 21 cm tomography prior to the epoch of structure formation. Phys. Rev. Lett. 92(21), 211301 (2004)
Lombardi, M.A., Nelson, L.M., Novick, A.N., Zhang, V.S.: Time and frequency measurements using the global positioning system. Cal Lab: International Journal of Metrology 8(3), 26–33 (2001)
Lonsdale, C., et al.: The murchison widefield array: Design overview. Proc. IEEE 97(8), 1497–1506 (2009)
Maccone, C.: NASA gateways at L1 and L2 and the radio-quiet moon farside imperative. In: Selected Proceedings of the 55th International Astronautical Federation Congress, Vancouver, Canada, 4-8 October 2004, vol. 57, pp. 145–155 (2005)
Manning, R.: Instrumentation for space-based low frequency radio astronomy. Geophysical Monograph Series 119, 329–337 (2000)
Markley, F.L., Crassidis, J.L.: Fundamentals of Spacecraft Attitude Determination and Control, vol. 33. Springer (2014)
Microsemi: SA.45sCSAC- Chip Scale Atomic Clock datasheet. Technical report, Microsemi. http://www.microsemi.com/products/timing-synchronization-systems/embedded-timing-solutions/components/sa-45s-chip-scale-atomic-clock (2011)
Naghshvar, M., Zhuang, H., Javidi, T.: A general class of throughput optimal routing policies in multi-hop wireless networks. IEEE Trans. Inf. Theory 58 (4), 2175–2193 (2012)
Nee, R. v., Prasad, R.: OFDM for wireless multimedia communications. Artech House, Inc (2000)
Oberoi, D., Pinçon, J.-L.: A new design for a very low frequency spaceborne radio interferometer. Radio Sci. 40(4) (2005)
Patwari, N., Ash, J., Kyperountas, S., Hero, A.O.I., Moses, R., Correal, N: Locating the nodes: Cooperative localization in wireless sensor networks. IEEE Signal Process. Mag. 22(4), 54–69 (2005)
Quillien, K., Engelen, S., Gill, E., Smith, D., Arts, M., Boonsta, A.-J.: Astronomical antenna for a space based low frequency radio telescope. In: 27th Conference on Small Satellites, pp. 1–4 (2013)
Rajan, R.T., Bentum, M., Boonstra, A.-J.: Synchronization for space based ultra low frequency interferometry, pp. 1–8 (2013)
Rajan, R.T., Bentum, M., Gunst, A., Boonstra, A.-J.: Distributed correlators for interferometry in space. In: IEEE Aerospace Conference, pp. 1–9 (2013)
Rajan, R.T., Engelen, S., Bentum, M., Verhoeven, C.: Orbiting Low Frequency Array for Radio astronomy. In: IEEE Aerospace Conference, pp.. 1 –11 (2011)
Rajan, R.T., Leus, G., van der Veen, A.-J.: Joint relative position and velocity estimation for an anchorless network of mobile nodes. Signal Process. 115 (0), 66–78 (2015)
Rajan, R.T., van der Veen, A.-J.: Joint ranging and synchronization for an anchorless network of mobile nodes. IEEE Trans. Signal Process. 63(8), 1925–1940 (2015)
Rees, M.J.: The End of the ‘Dark Age’. In: Holt, S., Smith, E. (eds.) After the Dark Ages: When Galaxies were Young (the Universe at 2<z<5), volume 470 of American Institute of Physics Conference Series, pages 13–23. AIP Publishing (1999)
Saks, N., Boonstra, A.-J., Rajan, R.T., Bentum, M.J., Beilen, F., van’t Klooster, K.: DARIS, a fleet of passive formation flying small satellites for low frequency radio astronomy. In: The 4S Symposium (Small Satellites Systems & Services Symposium), Madeira, Portugal,(ESA and CNES conference), 31 May - 4 June 2010
Serpedin, E., Chaudhari, Q.M.: Synchronization in Wireless Sensor Networks: Parameter Estimation, Peformance Benchmarks, and Protocols, 1st edition. Cambridge University Press, New York (2009)
Smith, D., Arts, M.: Characterization of astronomical antenna for space based low frequency radio telescope. In: IEEE Aerospace Conference, Big Sky, Montana US, 2-9 March 2013
Smith, H.J.: Very low frequency radio astronomy from the moon. In: Low Frequency Astrophysics from Space, pp.. 29–33. Springer (1990)
Sodnik, Z., Furch, B., Lutz, H.: Free-space laser communication activities in Europe: SILEX and beyond. In: 19th Annual Meeting of the IEEE Lasers and Electro-Optics Society (LEOS), pp. 78–79 (2006)
Stanford: PRS10-rubidium frequency standard, Technical report, Stanford. http://www.leapsecond.com/museum/prs10/ (2006)
Takahashi, Y.D.: A concept for a simple radio observatory at the lunar south pole. Adv. Space Res. 31(11), 2473–2478 (2003)
Taylor, G.B., Carilli, C.L., Perley, R.A. (eds.): Synthesis Imaging in Radio Astronomy II, volume 180 of Astronomical Society of the Pacific Conference Series, Astronomical Society of the Pacific, San Francisco (1999)
Thompson, A.R., Moran, J.M., Swenson Jr, G.W.: Interferometry and synthesis in radio astronomy. Wiley (2008)
Toyoshima, M.: Trends in satellite communications and the role of optical free-space communications. J. Opt. Netw. 4(6), 300–311 (2005)
Ulvestad, J.S., Edwards, C.D., Linfield, R.P.: Very long baseline interferometry using a radio telescope in earth orbit. Technical Report 42–88, JPL (1986)
van Haarlem, M. P., et al.: LOFAR: The LOw-Frequency ARray. Astron. Astrophys. 556, A2 (2013)
Weber, R., Alexander, J., Stone, R.: The radio astronomy explorer satellite, a low-frequency observatory. Radio Sci. 6(12), 1085–1097 (1971)
Weiler, K., Johnston, K., Simon, R., Dennison, B., Erickson, W., Kaiser, M., Cane, H., Desch, M.: A low frequency radio array for space. Astron. Astrophys. 195, 372–379 (1988)
Wijnholds, S.J., van der Tol, S., Nijboer, R., van der Veen, A.-J.: Calibration challenges for future radio telescopes. IEEE Signal Process. Mag. 27(1), 30–42 (2010)
Woan, G.: A very low frequency radio telescope on the far side of the moon. In: Measuring the Size of Things in the Universe: HBT Interferometry and Heavy Ion Physics, vol. 1, p 347 (1999)
Zarka, P., Bougeret, J.-L., Briand, C., Cecconi, B., Falcke, H., Girard, J., Griemeier, J.-M., Hess, S., Klein-Wolt, M., Konovalenko, A., Lamy, L., Mimoun, D., Aminaei, A: Planetary and exoplanetary low frequency radio observations from the moon. Planet. Space Sci. 74(1), 156–166 (2012). Scientific Preparations For Lunar Exploration
Acknowledgments
The authors would like to thank all the project members of DARIS, OLFAR and SURO for discussions, in particular Willem Baan, Heino Falcke and Kees van’t Klooster. We also thank our reviewers for their insightful comments, which helped improve the quality of the manuscript.
This research was funded in part by two projects namely, the STW-OLFAR study (Contract Number: 10556) within the Dutch ASSYS perspectief program and secondly the ESA-funded DARIS Study “Feasibility of Very Large Effective Receiving Antenna Aperture in Space” (Contract Number: 22108/08/NL/ST).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rajan, R.T., Boonstra, AJ., Bentum, M. et al. Space-based aperture array for ultra-long wavelength radio astronomy. Exp Astron 41, 271–306 (2016). https://doi.org/10.1007/s10686-015-9486-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10686-015-9486-6