Compression of intensity interferometry signals

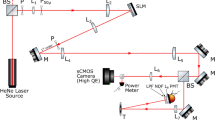
Abstract

Correlations between photon currents from separate light-collectors provide information on the shape of the source. When the light-collectors are well separated, for example in space, transmission of these currents to a central correlator is limited by band-width. We study the possibility of compression of the photon fluxes and find that traditional compression methods have a similar chance of achieving this goal compared to compressed sensing.

Appendices

Appendix A

We examine the case of a star of magnitude m _v at zenith, a collector area A, and detection efficiency η, for which the power is P (m _v  = 0) = 5°10⁻⁵ s⁻¹ m⁻¹Hz⁻¹ [5]. Let x ₁[n] and x ₂[n] be the numbers of photons arriving at each detector during time n which is an integral over the interval T. Then the mean flux is

$$ \overline{x}\kern3pt \equiv \kern3pt E\left({x}_i\left[n\right]\right)={2.5}^{-{m}_v}P\eta A\frac{T}{\tau_c}, $$

(A1)

Since the two fluxes have the same mean and variance, their correlation variance is

$$ \begin{array}{l}\operatorname{var}\left({x}_1\left[n\right]{x}_2\left[m\right]\right)=E\left\{{\left[{x}_1\left[n\right]{x}_2\left[m\right]-E\left({x}_1\left[n\right]{x}_2\left[m\right]\right)\right]}^2\right\}=E\left({x}_1{\left[n\right]}^2{x}_2{\left[m\right]}^2\right)\hfill \\ {}\kern7.62em =E\left({x}_1{\left[n\right]}^2\right)E\left({x}_2{\left[m\right]}^2\right)=\operatorname{var}{\left({x}_1\left[n\right]\right)}^2\hfill \end{array}. $$

(A2)

The covariance of the two photon fluxes is different from zero only for matching times, and the correlation expectation includes the sought coherence function,

$$ \mathrm{c}\mathrm{o}\mathrm{v}\left({x}_1\left[n\right],{x}_2\left[m\right]\right)=\left(\frac{\tau_c}{T}{\overline{x}}^2+\overline{x}\right)\delta \left[n-m-{n}_0\right]=\frac{\tau_c}{T}\overline{x}{\gamma}_b\delta \left[n-m-{n}_0\right], $$

(A3)

which does not average to zero only at time difference n ₀. The correlation of the mean-subtracted fluxes over a signal of length N is

$$ y\left[n\right]=\frac{1}{N}{\displaystyle \sum_{k=1}^N\left({x}_1\left[m-n\right]-\overline{x}\right)\left({x}_2\left[m\right]-\overline{x}\right).} $$

(A4)

Thus y [n] can be thought of a mean of N random, zero-mean variables of the same variance. Since N is large (10^~12), the mean of the sum will be the same, but the variance will be scaled down by 1/N,

$$ var\left(y\left[n\right]\right)=\frac{\operatorname{var}{\left({x}_i\left[n\right]\right)}^2}{N}=\frac{{\left({\overline{x}}^2{\tau}_c/T+\overline{x}\right)}^2}{N}. $$

(A5)

For n ≠ n ₀ we get E [y (n)] = 0, but for n = n ₀

$$ E\left(y\left[{n}_0\right]\right)=\operatorname{cov}\left({x}_1\left[{n}_0+n\right],{x}_2\left[n\right]\right)={\overline{x}}^2\frac{\tau_c}{T}{\gamma}_b, $$

(A6)

which is a random gaussian function with known mean and variance. However, the position of n ₀ is unknown, although it must be close to zero delay. In other words, we can write the correlation as

$$ y\left[n\right]=\alpha \delta \left[n-{n}_0\right]+\beta z\left[n\right];\kern1em \alpha ={\overline{x}}^2\frac{\tau_c}{T}{\gamma}_b;\kern1em \beta =\frac{{\overline{x}}^2{\tau}_c/T+\overline{x}}{\sqrt{N}}. $$

(A7)

Here z [n] is a random gaussian vector with zero mean and variance of 1, the result of averaging N ≫ 1 random processes. We have two degrees of freedom, the delay n ₀ and the correlation signal α. Experimentally we try to overcome the noise by increasing the signal x and the number of measurements N.

The correlation of the two signals of length N (Eq. A3) can be described as the product of the two Fourier transforms of these signals,

$$ Y\left[k\right]=\mathfrak{F}\left[\frac{1}{N}{\displaystyle \sum_{m=1}^N\left({x}_1\left[m-n\right]-\overline{x}\right)\left({x}_2\left[m\right]-\overline{x}\right)}\right]=\frac{1}{N}\left({\widehat{x}}_1\left[k\right]-\overline{x}\right)\left({\widehat{x}}_2\left[-k\right]-\overline{x}\right). $$

(A8)

If we wish to sample them in only a few frequencies, we must do that at the same frequencies, then multiply them and transform back to the time domain, to obtain their correlation (Fig. 2). We express the Fourier correlation as Y = Y _s   + Y _n , namely the signal and noise components. The signal correlation will be

$$ {Y}_s\left[k\right]=\mathfrak{F}{\left\{\alpha \delta \left[n-{n}_0\right]\right\}}_{\left[k\right]}=\alpha \exp \left(i2\pi k{n}_0/N\right) $$

(A9)

We choose L Fourier terms, κ ⊆ {1, 2,,,N}, |κ| = L ≪ N, the sampling vector will be C [k] which is a subset of Y _s [k]. Here k is an index, mapping each of the group κ [k] arbitrarily into the matching index,

$$ C\left[k\right]={\displaystyle \sum_{n=1}^Ny\left[n\right] \exp \left[i2\pi \kappa (k)n/N\right]}\equiv Dy\left[n\right], $$

(A10)

where the elements of matrix D (also called the dictionary matrix) are given by D _kn  = exp [i2πκ(k)n/N]. We are seeking a solution giving a δ function, which means that it is of very low sparsity. We find it through minimization of ‖y‖₀ subject to Dy = C, which is a typical compressed sensing problem with known solutions such as projection, matching pursuit, orthogonal matching pursuit, and other variations [3]. They all converge to the same solution when we only have to identify a single coefficient, by requiring the amplitude to provide the least error

$$ {\tilde{y}}_n=\underset{y_n}{ \arg \min }{\left\Vert {D}_n{y}_n-C\right\Vert}_2^2. $$

(A11)

D _n is the nth column vector (of length L) in matrix D. The solution is

$$ {\tilde{y}}_n=\frac{{D_n}^TC}{{\left\Vert {D}_n\right\Vert}^2}, $$

(A12)

whose maximum value is L α ², found at index

$$ \tilde{n}=\underset{n}{ \min }{\left\Vert \left(C-{D}_n{\tilde{y}}_n\right)\right\Vert}^2=\underset{n}{ \min}\left({\left\Vert C\right\Vert}_2^2-\frac{{\left({D_n}^TC\right)}^2}{{\left\Vert {D}_n\right\Vert}_2^2}\right)=\underset{n}{ \max}\frac{{\left({D_n}^TC\right)}^2}{{\left\Vert {D}_n\right\Vert}_2^2}. $$

(A13)

We now turn to the noise, represented by β z [n] (Eq. A7) with a Fourier transform β Z [k]. The variance at each frequency is

$$ \operatorname{var}\left(Z\left[k\right]\right)=E\left(Z{Z}^{*}\right)=E\left({\displaystyle \sum_{n=1}^N\beta z\left[n\right]{e}^{\frac{i2\pi kn}{N}}{\displaystyle \sum_{m=1}^N\beta z\left[m\right]{e}^{\frac{-i2\pi km}{N}}}}\right)={\beta}^2{\displaystyle \sum_{n=1}^NE\left(z{\left[n\right]}^2\right)}=N{\beta}^2, $$

(A14)

independent of frequency. Returning to the Fourier correlation, we have

$$ E\left(Y\left[k\right]\right)=C\left[k\right]\le L{\alpha}^2;\kern1em \operatorname{var}\left(Y\left[k\right]\right)=N{\beta}^2. $$

(A15)

The variance is a random variable made of a sum of N random complex gaussian variables. These variables can be written as

$$ W\left[k\right]\equiv \beta {\displaystyle \sum_{n=1}^Nx\left[n\right]{e}^{i2\pi \kappa (k)n/N}}\kern0.36em =\beta \sqrt{\frac{N}{2}}\left(u+iv\right), $$

(A16)

where u and v are zero-mean real gaussian variables with unity variance. The combined signal Y[k] is shown in Fig. 3.

Appendix B

The expectation of the number of bits of distribution k is

$$ \left\langle b\right\rangle ={\displaystyle \sum_{k=0}^{\infty }b(k)p(k)}, $$

(B1)

where for k = 0, the number of bits is 2, and for every other value it follows the ceiling (next integer) of the logarithm of k

$$ b(k)=2\left\lceil { \log}_2\left(k+1\right)\right\rceil . $$

(B2)

If $P = \overline{n}$ is the probability to have one photon during a time slot and Q is the probability to have no photon (P + Q = 1), then the expectation of each k is p (k) = QkP. Thus

$$ \left\langle b\right\rangle ={\displaystyle \sum_{k=0}^{\infty }b(k)p(k)}=2\overline{n}+{\displaystyle \sum_{k=1}^{\infty }2\left\lceil { \log}_2\left(k+1\right)\right\rceil {Q}^kP}. $$

(B3)

Notice that the RHS summation starts at k = 1. If we define k = 2 l – 1, we get for that summation

$$ {\displaystyle \sum_{k=1}^{\infty }2\left\lceil { \log}_2\left(k+1\right)\right\rceil {Q}^kP}={\displaystyle \sum_{k=1}^{\infty}\left\lceil l\right\rceil {Q}^kP}. $$

(B4)

Thus we can divide this sum into sub-sums where each is an addition from one power of two to the next. Thus the number of bits in each such sub-sum is constant and can be taken out of the total,

$$ \left\langle b\right\rangle =2P+2P{\displaystyle \sum_{l=0}^{\infty }l{\displaystyle \sum_{k={2}^l-1}^{2^{l+1}}{Q}^k}}. $$

(B5)

Each separate sum is an algebraic. Thus

$$ \left\langle b\right\rangle =2P+2P{\displaystyle \sum_{l=1}^{\infty }l{\displaystyle \sum_{k={2}^l-1}^{2^{l+1}}{Q}^k}}=2P+2P{\displaystyle \sum_{l=1}^{\infty }l\frac{\left({Q}^{2^{l+1}}-{Q}^{2^l-1}\right)}{P}=}2P+2{\displaystyle \sum_{l=1}^{\infty }l\left({Q}^{2^{l+1}}-{Q}^{2^l-1}\right)}. $$

(B6)

As the number of consecutive zeros, k, grows at lower flux, the sum approaches very fast (−log₂ P) and the approximate expectation of the number of bits will be

$$ \left\langle b\right\rangle =2\left[P-{ \log}_2(P)\right]\cong 2\left[\frac{1}{k}+{ \log}_2(k)\right]. $$

(B7)