Abstract
The primary scientific goal of the GRIPS mission is to revolutionize our understanding of the early universe using γ-ray bursts. We propose a new generation gamma-ray observatory capable of unprecedented spectroscopy over a wide range of γ-ray energies (200 keV–50 MeV) and of polarimetry (200–1000 keV). The γ-ray sensitivity to nuclear absorption features enables the measurement of column densities as high as 1028cm − 2. Secondary goals achievable by this mission include direct measurements of all types of supernova interiors through γ-rays from radioactive decays, nuclear astrophysics with massive stars and novae, and studies of particle acceleration near compact stars, interstellar shocks, and clusters of galaxies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction: Stepping beyond classical limits
Gamma-ray bursts (GRB) are the most luminous sources in the sky, and thus act as signposts throughout the Universe. The long-duration sub-group is produced by the explosion of massive stars, while short-duration GRBs likely originate during the merging of compact objects. Both types are intense neutrino sources, and being stellar sized objects at cosmological scales, they connect different branches of research and thus have a broad impact on present-day astrophysics.
Identifying objects at redshift \(\gtrsim\)6.5 has become one of the main goals of modern observational cosmology, but turned out to be difficult. GRBs offer a promising opportunity to identify high-z objects, and moreover even allow us to investigate the host galaxies at these redshifts. GRBs are a factor 105 − 7 brighter than quasars during the first hour after explosion, and a favourable relativistic k-correction implies that they do not get fainter beyond z ~3. Yet, present and near-future ground- and space-based sensitivity limits the measurement of redshifts at z ~13 (as H-band drop-outs), because GRB afterglows above 2.5 \(\upmu\)m are too faint by many magnitudes for 8–10 m telescopes. Thus, a completely different strategy is needed to step beyond redshift 13 to measure when the first stars formed.
Fortunately, nuclear physics offers such a new strategy. Similar to X-ray and optical absorption lines due to transitions between electronic levels, resonant absorption processes in the nuclei exist which leave narrow absorption lines in the γ-ray range. The most prominent and astrophysically relevant are the nuclear excitation and Pygmy resonances (element-specific narrow lines between 5–9 MeV), the Giant Dipole resonance (GDR; proton versus neutron fluid oscillations; ~25 MeV; two nucleons and more) and the Delta-resonance (individual-nucleon excitations, 325 MeV; all nucleons, including H!). Such resonant absorption only depends on the presence of the nucleonic species, and not on ionization state and isotope ratio. They imprint well-defined spectral features in the otherwise featureless continuum spectra of GRBs (and other sources). This is completely new territory [26], but with the great promise to measure redshifts directly from the gamma-ray spectrum, i.e. without the need for optical/near infrared (NIR) identification!
Technically, this new strategy requires sensitive spectroscopy in the 0.2–50 MeV band. The detection of GRBs requires a large field of view. Therefore, the logical detection principle is a Compton telescope. In addition, such detectors can be tailored to have a high polarisation sensitivity. Polarimetry is the last property of high-energy electromagnetic radiation which has not been utilized in its full extent, and promises to uniquely determine the emission processes in GRBs, as well as many other astrophysical sources. With its large field of view, such a detector will not only scan 80% of the sky within one satellite orbital period of 96 min, but also provide enormous grasp for measuring the diffuse emission of nucleosynthesis products and cosmic-ray acceleration.
2 Scientific goals
2.1 Main mission goal
We aim at a detection of GRBs at redshifts above 13. This will allow us to explore rather directly the universe in the epoch where first stars formed.
2.1.1 When did the first stars form?
High-redshift GRBs GRB afterglows are bright enough to be used as pathfinders to the very early universe. Since long-duration GRBs are related to the death of massive stars, it is likely that high-z GRBs exist. Theoretical predictions range between few up to 50% of all GRBs being at z > 5 [9, 35], and stellar evolution models suggest that 50% of all GRBs occur at z > 4 [71]. The polarisation data of the Wilkinson Microwave Anisotropy Probe (WMAP) indicate a high electron scattering optical depth, hinting that the first stars formed in the range 20\(\lesssim\) z \(\lesssim\) 60 [10, 33, 42]. GRIPS is designed to measure GRBs from the death of these first stars and probe the universe up to the highest redshifts after matter-photon decoupling.
Redshift determination via resonance absorption The observational use of nuclear resonance absorption for GRB redshift determination depends on two critical questions: “Is there enough matter along the sight lines to GRBs?”, and “Is the resulting absorption detectable?”.
Is there enough matter along the sight lines to GRBs?
Apart from galactic foreground extinction, relatively little intrinsic extinction has been found in the afterglow sepctral energy distributions of GRBs, both at X-rays and at optical/NIR wavelengths. A recent combined analysis of Swift XRT and UVOT data shows that the absorbers associated with the GRB host galaxy have column densities (assuming solar abundances) in the range (1–8)×1021 cm − 2 [52]. Yet, there is evidence, both theoretical as well as observational, that there is substantial amount of matter along the line of sights to GRBs. This applies to the local GRB surrounding as well as to the larger environment of the host galaxy in which the GRB explodes. Temporally variable optical absorptions lines of fine-structure transitions indicate that (i) all material at distances within a few kpc is ionized, most likely by the strong UV photon flux accompanying the emission front of the GRB, and (ii) beyond this ionized region the absorbing column is still at a level of 1021 cm − 2 [65]. Thus, present-day measurement capabilities in the optical/NIR as well as X-rays are not adequate to determine the density of local matter around GRBs. However, at γ-rays this matter will be measurable through nuclear resonance absorption even though this matter is simultaneously being ionized: the GRB gamma-ray radiation has to pass through it - and it will suffer resonance absorption independent on whether this material is ionized or not.
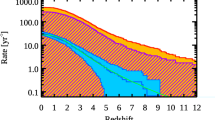
A variety of theoretical simulations of GRB progenitors have been made (e.g. Yoshida et al. [72]; Abel et al. [1]; Gao et al. [14]), pertaining to the formation of the first stars, the fragmentation rate, and density structure around the first star. The first stars are thought to form inside halos of mas 105...10\(^6 \ M_{\odot}\) at redshifts 10–60. It is generally accepted that most of the 105...10\(^6 \ M_{\odot}\) halo mass remains in the surroundings of the forming proto-star, with about the original dimensions of the proto-cloud. The resulting mass of the star as well as the density structure are difficult to predict because they depend on the collapse conditions (merger or not, strength of winds, etc). However, it is important to realize that some simulations in fact predict column densities of up to 1029 cm − 2 around the first stars [55, 72]; see also Fig. 1)! These simulations have been done independent of the knowledge of nuclear resonance absorption. It remains to be demonstrated (preferentially observationally) whether the conditions modelled in these simulations are realized. Yet, the existence of what one “normally” would refer to as “unbelievably high” column densities is plausible – note that even pristine and fully-ionized hydrogen imprints resonant absorption! GRBs are the best and possibly only tool to measure such conditions.
Radial density around a GRB progenitor at a redshift z=19. The density profile is close to a power law ∝R − 2.2 (dashed line). It contains about 1028 cm − 2 column density within the inner 1-2 AU, and further 1028 cm − 2 in each shell from 2–10, 10–100, 100–1000 AU! (From Yoshida et al. [72])
Is the resulting absorption detectable?
This question can be subdivided into two issues: Firstly, are there astrophysical conditions which favour large line of sight columns, but not excessively large densities? If the density is too high, multiple-scattering of higher energy photons could partly fill the energy window of a resonance, thus smearing the absorption trough. This may happen via Compton scattering or the cascading of high-energy photons. While the total pair production or Compton scattering cross sections are about a factor of 30-40 larger than the peak cross section of the Giant Dipole or Delta Resonance, the jet geometry in both, GRBs as well as blazars, over-compensates for this statistical measure: it is the differential cross section which matters. At the Dipole Resonance energy, the Compton-scattered photon beam has a full-width-half-maximum of 16°, or 0.05 sr. For a 1° opening angle of the jet, the resulting GDR absorption is a factor ~12 more efficient than the Compton re-scattering of higher energy continuum photons into the beam. In addition, Compton scattering changes the energy of the scattered photon by arbitrary large values, much greater than the width of the resonance - this adds another factor of E/ΔE (\(\gtrsim 3\) for the GDR) in favor of the resonance absorption. For pair production, only the latter effect comes into play. Furthermore, even in high-density environments, there are two possibilities which allevate the problem of re-filling: (i) the transverse dimension of the absorber is less than ~1.5 attenuation lengths at the energy of the highest attenuation value [63] or (ii) the absorber consists of many clumps (clouds) of matter, a solution which has been proposed to explain the UV and X-ray [4, 5] or IR emission [13] in optically thick absorbers around AGN. First hints for resonance absorption in AGN (Fig. 2, left panel; [26]), and GRBs (Fig. 2, right panel) at the 2σ level have been found based on COMPTEL and EGRET data.
Left: 3C 279 spectrum during the January 1996 flare as measured by COMPTEL (diamonds) and EGRET (squares), which includes the Δ resonance absorption in the circumnuclear environment (red line) in addition to a cut-off power law (black line). The best-fit energy for the Δ resonance is 208±25 MeV, implying a redshift 0.57 ± 0.12, close to the optically determined z=0.536. Right: Fit to the combined COMPTEL/EGRET spectrum of GRB 930131. The throughs at 5–8 and 100–200 MeV are compatible with the Giant Dipole and Delta resonance, respectively, at a redshift of z~1 [28]
Secondly, how narrow/broad will the resonant absorption features be at different redshifts, and what is the required energy resolution and sensitivity to detect them? Figure 3 shows the rest-frame resonance absorption lines for two different metallicities which clearly illustrate their starkly different relative intensity ratios. The GDR around 25 MeV has a FWHM ~ 10 MeV, thus GRIPS’ ~300 keV resolution at 10 MeV is fully sufficient to properly resolve the feature. The goal of GRIPS is to measure those resonance absorptions at redshifts z ~13 − 30. A simulated GRB spectrum at z = 25 is also shown in Fig. 3. Full simulations for the γ-ray instrument on GRIPS show that column densities of 1026...1027 cm − 2 will be detectable for ~ 30–40% of all GRBs seen in spectroscopy mode, and those with as little as 1025 cm − 2 for the 10% brightest GRBs (see Section 4.2.4).
Resonance absorption lines for two different redshifts (black: z = 25; color: z = 0) and different metallicities: Z = 0.1 (green) and Z = 1 (red) solar metallicity. Note the obvious difference in the relative strengths of the absorptions. The solid vertical lines bracket the energy band of GRIPS from 200 keV to 50 MeV. A total column of 1028 cm − 2 has been assumed to clearly visualise the effect, and a density smaller than 105 cm − 3 to avoid refilling of the lines due to scattering. The detectability of these resonance lines with the proposed instrument is achieved down to column densities of 1025 cm − 2 (Fig. 12)
These features have not been seen before in EGRET TASC, BATSE SD, or COMPTEL (D2) data due to the combination of insufficient sensitivity, poor energy resolution and pre-canned response matrices for fixed energy bins. GRIPS will move γ-ray astronomy into a new era combining sensitivity, energy resolution and a large FOV in one instrument that will detect nuclear resonance troughs in the spectra of a large number of sources.
If the GRB environment contains total (neutral plus ionized) column densities of 1025 cm − 2 or higher, GRIPS will be able to measure redshifts via the nuclear resonance absorption directly from the γ-ray spectrum, and thus be sensitive well beyond z~13.
2.1.2 What are the energetics of GRBs?
There is increasing evidence, both observational [56] and from theory [70] that a GRB may launch two jets: one highly relativistic (Γ > 200, kinetic energy of 1051 erg), central jet with an opening angle of a few degrees, and a broader jet with sub-relativistic ejecta (0.1c, kinetic energy 1052 erg) spread over 1 radian. The underlying physical basis of the correlation between the isotropic equivalent energy emitted in the prompt radiation phase and the peak energy (Epeak) of the measured spectrum [2, 15] is mysterious. Measuring the Lorentz factor Γ from the γ-ray emission itself with GRIPS would provide a major step in understanding the cause of this correlation and in determining the energetics of GRBs.
Numerical models of the prompt emission due to internal shocks in an expanding relativistic wind exist in many different variants. In most of these, the spectrum is expected to significantly deviate from an optically thin synchrotron spectrum. A time-dependent calculation which includes cyclo-synchrotron emission and absorption, inverse and direct Compton scattering, and e + e − pair production and annihilation has shown [45] that (i) (in-flight) annihilation emission lines are expected at surprising strength (Fig. 4), and (ii) thermal Comptonization leads to emission peaking at \(\gtrsim\)30 MeV, possibly explaining the additional MeV component seen in GRB 941017 [16]. The annihilation line will be boosted by Γ into the \(\gtrsim\)100 MeV range, but adiabatic energy losses as well as GRB cosmological redshift lowers the observed photon energy back into the few MeV band. Thus, once the redshift is determined by the resonance lines (or ground-based optical/NIR telescopes for z<13), the measured energy of the annihilation line allows a direct determination of the Lorentz factor from the prompt gamma-ray emission spectrum. GRIPS will allow us to measure the Lorentz factor of the prompt γ-ray burst emission via the predicted annihilation line, and thus directly measure the total energy of the explosion for at least 15% of all GRBs. Since the measured annihilation line energy is proportional to the ratio Γ/z, GRIPS can detect the line in the range (0.5 \(\gtrsim \Gamma\)/(1 + z) \(\gtrsim\) 100), thus covering the full predicted range of Γ (50–1000) and z (0.5 − 60).
Spectra averaged over the GRB duration, obtained for high compactness l. The two models assume Γ = 300, L = 1052 erg, z = 1, and differ in the variability timescale of δt = 10 − 4 s, (blue solid line; implied l = 250); and δt = 10 − 5 s (dashed line; l = 2500) at which the Lorentz factor Γ varies. The scattering optical depth at the end of the dynamical time is 13 and 56, respectively. The peaks observed at ~80 MeV result from pair annihilation which is larger for larger compactness. (From Pe’er and Waxmann [45])
2.1.3 What is the emission mechanism?
Spectra Based on the knowledge gained from observation in the keV–MeV range several possible radiation mechanisms exist, all of which produce characteristic spectra in the super-MeV range. Two main classes of models (see Mészáros 2006) have been discussed. (1) Synchrotron/inverse Compton emission of electrons and protons: It is very probable that particles are accelerated to very high energies close to the emission site. This could either be in shock waves, where the Fermi mechanisms or other plasma instabilities act, or in magnetic reconnection sites. Therefore, it is likely that the observed emission in the keV range scatters on these relativistic electrons, which will result in inverse Compton emission in the super-MeV domain. This occurs in both internal and external shock scenarios. Furthermore, most of the outflow energy, transported by the protons will predominantly be in the super-MeV range. (2) Hadron related emission via pion production and cascades: High-energy, neutral pions (π0) can be created as shock-accelerated, relativistic protons scatter inelastically off ambient photons (pγ interactions). These later decay into γ-rays. This is, e.g., suggested to occur in GRB 941017 [16]. Similarly, if the neutrons in the outflow decouple from protons, inelastic collisions between neutrons and protons can produce pions and subsequent high-energy emission.
The spectra of some GRBs alternatively have been well fit by both the Band model and a combination of a black body plus power law model [40, 51]. Rees [50] suggested that the E peak in the γ–ray spectrum is due to a Comptonised thermal component from the photosphere, where the comoving optical depth falls to unity. The thermal emission from a laminar jet when viewed head–on would give rise to a thermal spectrum peaking in the X-ray or γ-ray band. The resulting spectrum would be the superposition of the Comptonised thermal component and the power law from synchrotron emission. Thus, from theory there is no indication that GRB spectra should deviate from a smooth continuum, and thus can be used as reliable background light sources for nuclear absorption features.
GRIPS will measure the broad-band spectra of ~660 GRBs/year from 100 keV–50 MeV with 3% energy resolution. GRIPS will distinguish between the various, contradictory mechanisms by covering the transition from the classical keV and the tens of MeV regime.
Polarisation as a diagnostic of the GRB emission mechanism The link between the γ-ray production mechanism in GRBs and the degree of linear polarisation can constrain models. A significant level of polarisation can be produced in GRBs by either synchrotron emission or by inverse Compton scattering. The fractional polarisation produced by synchrotron emission in a perfectly aligned magnetic field can be as high as 70–75%. An ordered magnetic field of this type would not be produced in shocks but could be advected from the central engine [17, 18, 38]. It should be possible to distinguish between Synchrotron radiation from an ordered magnetic field advected from the central engine and Compton Drag. Only a small fraction of GRBs should be highly polarised from Compton Drag because they have narrower jets, whereas the synchrotron radiation from an ordered magnetic field should be a general feature of all GRBs.
GRIPS will allow us to measure the polarisation of the prompt γ-ray burst emission to a few percent accuracy for about 10% of all detected GRBs. Moreover, the superior polarisation sensitivity will even securely measure whether or not the percentage polarisation varies with energy, angle and/or time over the burst duration of a dozen brightest GRBs.
2.2 Other mission goals
GRIPS will address other, non-GRB science topics, and lead to guaranteed science returns. Major science topics are (a) to unveil the physics of stellar explosions, and (b) to illuminate the physical processes which lead to particle accelerations from thermal up to relativistic (cosmic-ray) energies.
With the imminent launch of NASA’s GLAST Observatory (30 MeV–100 GeV) and the long-term continuation of ESA’s INTEGRAL Observatory (20 keV - few MeV) there will be a dramatic lack of coverage of the gamma-ray sky in the1–30 MeV range. GLAST will detect thousands of new sources, while the only existing MeV data (from GRO/COMPTEL) is for a handful of very bright ones. The discovery potential is clearly enormous. At present, multiwavelength spectra of the majority of sources have a notable absence of data at MeV energies, although often the main power is expected there. Without a mission like GRIPS, the MeV sky with its wealth of astrophysics will be less well known even than the TeV sky (via the new Cerenkov observatories), which is a quite disillusioning prospect.
2.2.1 Nuclear astrophysics
Supernovae of Type Ia (SNIa) are considered on purely empirical grounds to be standardizable candles; no physical explanation could be established for the homogeneity of thermonuclear disruptions of white dwarf stars, which is the widely-accepted model. In view of the far-reaching cosmological implications of the apparent dimming of SNIa in the distant universe, this remains a major concern for supernova scientists [8, 36]. Phrased at an extreme: dark energy might not exist at all, if our estimates of SNIa properties across cosmic times or selection biases are inadequate! Already a 7% Ibc contamination level is sufficient to produce Ω λ = 0.7 from no effect [23]. Thus, understanding the physics of SNIa is of utmost importance. GRIPS will provide the data for a physical understanding of the Phillips relation and the related errors. Due to the huge dynamic scales in time and space of the relevant physical processes, numerical simulations must make use of approximations. Guidance from observations is essential in building a physical model. Most direct access to isotope information would be through nuclear lines emitted from radioactive decays, which even can provide kinematic information from partially-embedded freshly-synthesized species. Penetrating γ-rays are expected to escape from the supernova as early as a few days after the explosion. 56Ni decays to 56Co within ~8 days, which then decays to stable 56Fe within ~111 days, producing γ-ray lines at 158 keV (56Ni, early and probably occulted) and at 847, 1238, 1771 and 2598 keV. Line shape and centroids reflect the original 56Ni kinematics, line ratios are a key diagnostic of the explosion morphology and hence model types (Fig. 5). In the period before full γ-ray transparency is reached (~100 days), γ-rays from 56Co decay provide the key information; the GRIPS band is designed to include these lines. Recent SNIa surveys record >10 nearby events (<50 Mpc; Isern, priv.comm.), which will be detected by GRIPS in the energy range of the (direct and scattered) 56Ni decay γ-ray range up to ~2.5 MeV at ~100 days after explosion, when the SN is transparent to gamma-rays (see Sim and Mazzali [54]). In addition to an absolute determination of the 56Ni amount from the γ-ray line flux, due to its broad energy range, line ratio diagnostics will be provided by GRIPS, thus significantly enhancing the sample of SNIa with meaningful γ-ray constraints.
SNIa model light curves in the 0.1–3.5 MeV band for a 1 Mpc distance, and time since explosion (left), as well as ratios of gamma-ray lines from 56Ni decay (middle and right) which provide an important diagnostics of the inner supernova and the explosion mechanism. Shown are spherically-symmetric models as well as two cases of asphericities (AO and AE) which represent the extremes with respect to viewing angle. The high-energy lines provide a sensitive diagnostics to asphericities of the SN. (From Sim and Mazzali [54])
GRIPS will at least measure one SNIa per year in one or more of the 56Ni decay gamma-ray lines, to constrain explosion models through energy-dependent transparency and the absolute 56Ni radioactivity.
Massive-star nucleosynthesis is responsible for most of the intermediate-mass elements from oxygen through iron [20, 69]. Different burning episodes from hydrogen through silicon burning in shells of the rapidly-evolving star after its core-hydrogen burning phase (main sequence), plus nucleosynthesis in the supernova following the final gravitational collapse of the star, are responsible for this element production. The complexities of stellar-structure evolution and active nuclear-reaction networks are difficult to model. Beyond the (precise and abundant, but rather indirect) observations of elemental abundances through atomic lines, measurements of the key isotopes through their radioactive decays provide calibrators of those models.
A key isotope for supernova-interior nucleosynthesis is 44Ti with a decay time of ~85 years, a γ-ray line at 1156 keV and X-ray lines at 68 and 78 keV. This radioactive decay has been observed from the Cas A supernova remnant [25, 64]. Its abundance and kinematics directly arises from the processes of accretion and fall-back onto the central remnant. This otherwise unaccessible inner region of a core collapse is at the origin of GRB formation by massive stars [61]. GRIPS will deepen surveys for 44Ti gamma-ray sources (1.16 MeV) in the Galaxy within a 5-year mission down to 6×10 − 7 ph cm − 2 s − 1, and should detect 10–15 sources if 44Ti ejection is typical for core-collapse supernovae (see The et al. [60, 61]). Furthermore, detection of MeV continuum in core-collapse SNe, and especially in the Ib/c class, would indicate that a fraction of the relevant kinetic energies liberated in these explosions is conveyed to the acceleration of electrons to very high energies and to the re-emission through the synchrotron process, illuminating our understanding of the GRB-powering mechanisms in SNe. Moreover, if the high energy spectrum were polarized, we would get unique insights into the geometry of the magnetic fields. For a sufficiently closeby (less than 100 Mpc) SN associated with a GRB, prompt gamma-ray spectroscopy of possible early 56Ni lines at 158 keV and 812 keV would be another unique opportunity, according to the predicted gamma-ray flux near the time of transparency (~50–100 days) (see Sim and Mazzali [54]). GRIPS would be the only monitor for such continuum and radioactivity MeV gamma-rays from nearby core-collapse supernovae, with these unique signatures.
The 60Fe isotope is produced in late burning stages of massive stars, and only ejected by the terminal supernova. 60Fe decays with ~2.2 My, hence cumulative production over My time scales is observed in the γ-ray lines. INTEGRAL detected the γ-ray lines from this isotope in the larger region of the inner Galaxy [66]. Yet, spatial information is insufficient to be able to conclude on an origin from core collapse SN. With a 5-year survey sensitivity of ~6×10 − 7 ph cm − 2 s− 1, GRIPS will map the Galaxy in 60Fe radioactivity gamma-rays for the first time at several degrees spatial resolution. This will allow detailed tests of massive-star nucleosynthesis models for massive-star regions of different ages along the plane of the Galaxy.
The 26Al isotope is predominantly produced by massive stars [48], although not only by supernovae, but with nucleosynthesis in early stages of core hydrogen burning and in late shell burning stages plus supernova nucleosynthesis [37]. With a 1.04 My decay time, its cumulative emission in the 1808.65 keV γ-ray line provides a diagnostic of massive-star nucleosynthesis in the Galaxy [12]. The 26Al production in nearby massive-star clusters with correspondingly-low surface brightness are within reach with the sensitivity of GRIPS. This is a key ingredient of chemical-evolution models of galaxies [39]. GRIPS will deepen the Galactic surveys for these key isotopes of massive-star nucleosynthesis, and provide significant improvement on the Galactic distribution of massive-star radioactivities.
Novae are understood as explosive Hydrogen burning on the surface of a white dwarf (WD), igniting once a sufficient amount of matter has been accreted from the WD’s companion star. Nuclear burning is dominated by rapid proton capture (rp-process) on light elements, and the main theoretical issue is up to which heavy isotopes the rp-process proceeds. Many proton-rich isotopes are produced, which undergo β + -decay at their characteristic decay times, most important contributions being from 13N (τ~14 min) and 18F (τ~2.5 h) [21, 22]. Therefore, a bright flash of positron annihilation emission with a characteristic line at 511 keV and a bright lower-energy continuum occurs right after the thermonuclear runaway, well before the envelope expands and lights up as a nova in optical emission. Alongside the rp-process, radioactive 7Be is produced and is expected to be the brightest γ-ray line source, with a decay time of 78 days (E γ =478 keV).
GRIPS will detect several Galactic novae through annihilation emission, and combine positron annihilation with 7Be and 22Na diagnostics to understand the nova ignition and burning process.
2.2.2 Positron astrophysics
Imaging of the γ-ray emission from the annihilation of positrons with INTEGRAL/SPI [32] has revealed a new major puzzle: The expected sources of positrons in the Galaxy are predominantly located in the disk of the Galaxy, while the Galactic bulge is by far the brightest observed feature in annihilation γ-rays. This initiated a quest for new types of candidate positron producers, such as the annihilation of dark matter particles accumulated by the Galaxy’s gravitational field [24]. An alternative hypothesis could be the large-scale transport of positrons from their disk sources through the Galactic halo into the central bulge before their annihilation [47], or significant diffusion of positrons generated by past activity and energetic proton ejection from the central black hole in our Galaxy [11].
GRIPS will help to clarify the validity of such extreme models, as it will be sensitive to the full spectral range of annihilation emission ( 300→511 keV, and above, for annihilations-in-flight). With its angular resolution of \(\sim 3^\circ \!\! .5\) at 511 keV, GRIPS will map the bright bulge emission of positron annihilation and its merging with the disk component; the latter can be mapped with GRIPS along the bright regions of the disk such as the inner ridge and Cygnus, as inferred from 26Al gamma-rays and its associated positron production (see Zoglauer et al. [75]).
2.2.3 Other γ-ray sources
Blazars Recent Swift/BAT observations find many blazars with very flat (photon index 1.6–1.8) spectra in the 20–150 keV range, and extrapolations indicate that all of those will be securely detectable by GRIPS. The measurement of the resonance absorption will substantially help in the identification process, since the redshift will be known from the gamma-ray spectra [26, 27]. Gamma-ray polarization can be measured for the flare states. Comparing with radio polarization and multi-wavelength light-curves, this will pin down the origin of the γ-ray flares [30, 67].
Pulsars, anomalous X-ray Pulsars, and soft gamma-ray repeaters Pulsars are an excellent laboratory for the study of particle acceleration, radiation processes and fundamental physics in environments characterized by strong gravity, strong magnetic fields, high densities and relativity. Above ~50 MeV EGRET has detected 6–10 pulsars and candidates. Thompson et al. [62] and Schönfelder et al. [53] reported for the COMPTEL survey 4–5 pulsars corresponding to EGRET detections and one high-magnetic field pulsar (PSR B1509-58) with emission up to 30 MeV. Estimates for the number of possible pulsar detections by future, more sensitive, gamma-ray instruments are based on our empirical knowledge of pulsar efficiencies and spectra, new radio surveys that now contain about 2000 pulsar detections, and on the extrapolations afforded by theories of high-energy emission from rotating, magnetized neutron stars. These theories are still quite disparate. For energies above several 10 MeV and for the sensitivity of the Large Area Telescope on GLAST, predictions range from ~60 detections [19] to about 800 [29], with several predictions between 120 and 260 pulsars. Many of these pulsars are so-called ‘radio-quiet’ objects comparable to the Geminga pulsar. Additional predictions for about 100 millisecond-pulsars have been published for GLAST by Story et al. [58]. GRIPS’ sensitivity for wide band spectra above ~10 MeV (normal pulsars) and below 1 MeV [high B-field pulsars and anomalous X-ray Pulsars (AXPs)] exceeds the COMPTEL sensitivity by a similar factor that holds when going from EGRET to GLAST. From the EGRET/COMPTEL relation we therefore estimate the number of GRIPS pulsars to be about 50–70% of the GLAST pulsars and expect to detect 60–70 pulsars in the GRIPS energy range > 10 MeV. GRIPS-determined light curves and phase-resolved spectra in the 1–50 MeV range will provide decisive insights into the pulsar magnetosphere and the acceleration processes located there. Polarisation is a unique characteristic of particles radiating in strong magnetic fields. Pulsars and their surrounding pulsar wind nebulae are highly polarised. GRIPS will be sensitive enough to measure polarisation below a few MeV from several pulsars.
‘Magnetars’ appear to observers in the forms of ‘AXPs’ or, possibly related, ‘soft gamma-ray repeaters’. Pulsed radiation with a thermal spectrum at soft X-rays (1–10 keV) and an extremely hard power-law up to nearly 1 MeV has been observed from 6–8 AXPs [34]. The continuous all-sky survey of GRIPS promises to capture unique data for high-energy neutron star astrophysics.
Superbubbles Massive stars in the Galaxy appear in groups (e.g. OB associations), such that their strong wind and supernova activity overlaps and generates large superbubbles (SBs). Interacting shocks within the SB thus provides a natural environment for cosmic ray accerelation (GCRs). GRIPS has sufficient sensitivity to test the theory of galactic cosmic ray acceleration in the SB environment by observing galactic SBs as well as 30 Dorado in the LMC in gamma-ray line emission. Lines of 12C* and of 16O* at 4.44 MeV, and 6.1 MeV, 6.97 MeV, and 7.17 MeV, respectively, would be the best indicators of the CR acceleration in the SB.
Diffuse continuum MeV gamma-ray emission from the interstellar medium arises from the interactions of cosmic-ray electrons with interstellar matter and radiation fields. Bremsstrahlung on atomic and molecular hydrogen produces gamma-rays with energies typically half of the electron energy, so that gamma-rays in the GRIPS range trace electrons in the 1–100 MeV ranges. At these energies direct cosmic-ray measurements are virtually impossible because of the large solar modulation; synchrotron radiation occurs at frequencies too low to be observable. Hence GRIPS gamma-ray observations are our only window to interstellar electrons at MeV energies. Inverse-Compton scattering of 100–1000 MeV electrons and positrons on interstellar radiation is an important component of continuum gamma-rays, and dominates at low energies. In fact, recently this component has been shown to explain most of the diffuse emission from the Galactic ridge observed by INTEGRAL [46]. Both primary and secondary cosmic-ray electrons and positrons contribute to this emission, and hence observations in this part of the spectrum give valuable information on high-energy particles in the Galaxy. On the other hand this process fails to explain all of the diffuse emission observed by COMPTEL [46, 59], suggesting there could be a contribution from populations of unresolved hard gamma-ray sources, like AXPs and radio pulsars. GRIPS can trace and disentangle those components towards higher energies.
Solar flares accelerate ions to tens of GeV and electrons to tens of MeV. GRIPS would obtain high-statistics time-resolved spectra, permitting precise measurements of the hard-X ray continuum from accelerated electrons, of tens of strong nuclear lines and of the high-energy emission from π0 decay and π±-decay leptons. This, for the first time, would allow detailed studies of the evolution of the energy spectra and composition of the accelerated particles which are the key properties for the understanding of the acceleration mechanism and the transport of energetic particles in solar flares. In particular, it will be possible to determine the accelerated 3He/4He ratio and the heavy-ion content of the interacting particles and compare them with observations of solar energetic particles in interplanetary space, where large overabundances of 3He (≈ 100 – 1000) and of low-FIP elements (≈ 10–30) are found after impulsive-type flares. Additional information would come from polarization measurements of the bremsstrahlung continuum and of some nuclear lines and the detection of delayed X- and γ-ray line emission from solar active regions that are following the production of relatively long-lived radio-isotopes during strong flares [60].
3 Mission profile
For the GRIPS mission, a mass of 3.5 t needs to be delivered to a circular equatorial low-Earth orbit (LEO), with an altitude of about 500 km. The Soyuz Fregat 2B is capable of launching this payload (capacity of 5.3 t) and with its fairing of diameter 3.8 m and height of 7.7 m readily accommodates GRIPS with the science instruments, the Gamma-Ray (GRM) and X-Ray Monitors (XRM).
GRIPS will generally be operated in a continuous zenith pointed scanning mode. The field of view (diameter 160°) will cover most of the sky over the course of one orbit. A similar strategy is planned for the all-sky survey of the high-energy telescope LAT on the forthcoming GLAST mission. Pointing the XRT to a selected source will not disturb the scanning coverage of the GRM, since the detector response is nearly invariant under rotation around the axis.
3.1 Orbit requirements
The orbit was selected to optimize for low background, high science data fraction per orbit, good coverage of the orbit by ground stations, and high probability of the mission to remain at the chosen orbit for a mission life-time of ≈10 years. This implies, without any serious alternative, a LEO, at a typical altitude of 500 km below the radiation belts seeking a balance between orbital lifetime (5 years should be guaranteed) and accumulated radiation dose. A previous study concluded that from a launch altitude of 500 km the satellite remains above 400 km for at least 5 years without active orbit control. While background considerations would argue for an orbit even lower than 500 km, a compromise has to be made with respect to the size of the propulsion system to compensate the orbit-decay, in particular since our lifetime goal is 10 years.
The requirement for a low background means low inclination, preferably 0° to avoid the radiation belts and the South Atlantic Anomaly. It is now well established that the background in hard X-ray and gamma-ray instruments in a LEO can be a factor of 100 lower than a Highly Eccentric Orbit, such as that of INTEGRAL.
3.2 Special requirements
The telemetry down-link must have the capability of rapid transmission of the GRB alerts to the MOC for ground-based as well as satellite-based far-IR (e.g. JWST) follow-up of very high redshift GRBs to start as soon as possible. This approach should be adopted also for the dissemination of some main properties of sources observed in target-of-opportunity mode. Feeding of this information to ATELs, IAU Circulars, and GCN is foreseen. The strategy of the GRIPS mission is very similar to that adopted for BSAX and Swift, i.e. to slew the X-ray telescopes to each new GRB and follow the afterglow as long as it is visible. To observe the earliest phase of the afterglow, new gamma-ray monitor positions will trigger an autonomous spacecraft rotation and telescope slew, followed by a possible programmed sequence of observations at later times.
The initial GRB position is normally determined by the GRM, but uploading positions of GRBs or other transients from other satellites or ground-based facilities should also be possible. Either case will trigger the spacecraft software to plan and execute an autonomous rotation/slew. All calculations of the slew path and pointing constraints have to be done on-board.
4 Payload
4.1 Overview of instruments
GRIPS will carry two major telescopes (Fig. 6): the GRM and the XRM. The GRM is a combined Compton scattering and Pair creation telescope for the energy range 0.2–50 MeV. It will thus follow the successful concepts of imaging high-energy photons used in COMPTEL (0.7–30 MeV) and EGRET (>30 MeV) but combines them into one instrument. New detector technology and a design that is highly focused on the rejection of instrumental background will provide greatly improved capabilities. Over an extended energy range the sensitivity will be improved by at least an order of magnitude with respect to previous missions (Fig. 9) and the large field of view, better angular and spectroscopic resolution of GRM allows the scientific goals outlined in this project to be addressed. The XRM is based on the mature concept and components of the eROSITA X-ray telescope, which is scheduled for a space mission on the Russian platform Spektrum-XG [44, 49].
A possible flight configuration of the GRIPS payload. The GRM is located atop the spacecraft bus and the XRT is shown with a slight offset pointing. The XRM is mounted on a hinge, and can be offset with respect to the GRM axis by up to 90°. A rotation of the whole satellite around the GRM axis then allows the XRM to reach any point on the sky in the short time needed for rapid GRB follow-up observations but maintaining at the same time the zenith pointing of GRM
4.2 Gamma-ray monitor
4.2.1 Key characteristics
Two physical processes dominate the interaction of photons with matter in the γ-ray energy band from 200 keV to ~50 MeV: Compton scattering at low energies, and electron-positron pair production at high energies, with the changeover at ~ 8 MeV for most detector materials. In both cases the primary interaction produces long-range secondaries whose directions and energies must be determined in order to reconstruct the incident photon. The GRM, like previous Compton and pair creation telescopes, will employ two separate detectors to accomplish this task: a tracker (D1), in which the initial Compton scatter or pair conversion takes place, and a calorimeter (D2), which absorbs and measures the energy of the secondaries. In the case of Compton interactions, the incident photon scatters off an electron in the tracker. The interaction position and the energy imparted to the electron are measured. The scattered photon interaction point and energy are recorded in the calorimeter. From the positions and energies of the two interactions the incident photon angle is computed from the Compton equation. The primary-photon incident direction is then constrained to an event circle on the sky. For incident energies above about 2 MeV the recoil electron usually receives enough energy to penetrate several layers, allowing it to be tracked. This further constrains the incident direction of the photon to a short arc on the event circle. GRM will determine GRB locations to better than 1° (radius, 3σ).
The differential Klein-Nishina cross-section for Compton scattering contains a strong dependence on the polarization of the incident γ-ray photon. Scattered photons are emitted preferentially perpendicular to the direction of the electric field vector of the incoming photon. The strongest azimuthal modulation in the distribution of scattered photons will be achieved for low gamma-ray energies and Compton scatter angles around 90°. This will make a Compton telescope with a calorimeter covering a large solid angle a unique polarimeter. In the case of pair production, the incident photon converts into an electron-positron pair in the tracker. These two particles are tracked and determine the incident photon direction. The total energy is then measured through the deposits absorbed in the tracker and/or the calorimeter.
In addition to the ‘telescope-mode’ described above, the D2 detectors can also be read out in the so-called ‘spectroscopy-mode’ i.e. recording interactions that deposit energy only in the calorimeter. Using the side walls and the bottom of D2 as separate units a coarse localization and high-quality spectra of GRB events can be obtained. This mode of operation follows the example of BATSE and the EGRET-TASC on CGRO, the lateral shields of the Phoswich Detector System on Beppo-SAX, and the GBM on GLAST.
4.2.2 GRM design and simulations
The design of a new high-energy γ-ray telescope must be based on numerical simulations as well as experimental detector developments. The baseline design and input to the Monte-Carlo simulations of the GRM is shown in Fig. 7. The top part shows the detector head with the central stack of double-sided Si-strip detectors (tracker D1) surrounded by the pixellated calorimeter (D2) and an anticoincidence system (ACS) made of plastic scintillator. The simulations were carried out with the MGGPOD suite [68], which allows for a detailed simulation of the primary and secondary (activation) background in the chosen LEO. The modeling of the instrument functions, the reconstruction of the Compton and pair data, and the final performance calculations were carried out with the MEGAlib software suite [74] which had been developed in the course of the MEGA prototype development (Fig. 8, [3]).
The GEANT models for the MEGA satellite version (right), prototype (middle) and a photograph (left) of the actual prototype detector (open to show the DSSD and CsI detectors). (From Kanbach et al. [31])
Below the γ-ray detector is the GRM electronics and a generic spacecraft bus. In the simulations the bus of the Advanced Compton Telescope study was used [7].
The D1 detector consists of 64 layers each containing a mosaic of 8×8 double-sided Si strip detectors of area 10×10 cm2. The layers are spaced with 5 mm distance. The D2 calorimeter is made of LaBr3 prisms (5×5 mm2 cross-section) which are read out with Si Drift Diode (SDD) photodetectors. The upper half of the D2 side walls feature scintillators of 2 cm length and the lower half has 4 cm thick walls. The side wall crystals are read out by one SDD each. The bottom calorimeter is 8 cm thick and is read out on both ends of the crystals to achieve a depth resolution of the energy deposits.
The whole detector is surrounded by a plastic scintillator counter that acts as an anti-coincidence shield (ACS) against charged particles. Read out of the scintillation light, which is collected with embedded wavelength-shifting fibers to ensure the ACS uniformity, will be done with Si APD detectors.
Most of the structural material that holds the detector elements will be fabricated with carbon-fiber compounds in order to reduce the background of activation radioactivity produced by cosmic-rays in aluminum. Table 1 lists the parameters and properties of the detector subsystems that were used in the simulations.
4.2.3 GRM electronics design
The subsystems provide with their internal front-end (FEE) and front-end control (FEC) electronics essentially three types of output: the trigger signals, indicating the deposit of energy in suitable groups of detector units (e.g. one layer in D1, or a section of D2) are constantly flowing onto the common trigger bus system. The Trigger Processing Unit (TPU) screens the flow of trigger signals for coincidences and checks the signature of a coincidence against the stored patterns of valid events. If a potentially useful event is found, the Master Event Trigger (MET) is issued, the FEEs are instructed to sample, hold and digitize the signal amplitudes, and the Event Builder starts to collect the available measurements, attaches time and attitude tags to the event and supplies it to the Telemetry Builder (TB) to be assembled into telemetry packets. Housekeeping data are also collected by the TB at regular time intervals and included into the packets. GRBs are detected in two ways from the data stream: a ‘rate trigger’ can be derived from a suitably selected stream of trigger signals, e.g. D2 events that have not been vetoed by an ACS signal. Also, the raw event data can be analyzed on-board in a cursory way to derive the incidence direction of the GRB with sufficient accuracy to allow pointing at the source with the X-ray telescope. This is called an ‘image trigger’. The consistent detection of rate- and image-trigger lead to a short burst alert message via the real-time telemetry link and to the commanding of an XRT slew.
4.2.4 Performance
The performance of the GRM on GRIPS in an equatorial low Earth orbit was extensively simulated with the MGGPOD suite and analyzed with the MEGAlib package. MEGAlib contains a geometry and detector description tool that was used to set up the detailed modelling of the GRM with its detector types and characteristics. The geometry file is then used by the MGGPOD simulation tool to generate artificial events. The event reconstruction algorithms for the various interactions are implemented in different approaches (Chi-square and Bayesian). The high level data analysis tools allow response matrix calculation, image reconstruction (list-mode likelihood algorithm), detector resolution and sensitivity determination, spectra retrieval, polarization modulation determination etc. Based on many billions of simulated events we have now derived a good understanding of the properties of GRIPS.
Various source and spectral scenarios have been simulated: a series of GRB spectra and intensities which span the range of burst properties known from BATSE as well as time constant line and continuum sources were simulated and analyzed. In all cases the environmental orbital radiation background and the instrumental activation were taken into account. The small intrinsic radioactivity of the proposed scintillator material LaBr3 (0.8–2.0 cts/s/cm3 depending on the compound) is negligible compared to other background components and has been ignored in the simulations.
Continuum sensitivity GRIPS will achieve a major improvement in sensitivity over previous and presently active missions, such as a factor 40 improvement over COMPTEL around 1 MeV, or a factor of >20 over IBIS above 200 keV. Also, GRIPS will be more sensitive than NASA’s planned EXIST-mission above 250 keV (Fig. 9). The FOV, simulated for a typical GRB spectrum (Fig. 10, left panel) extends to large off-axis angles: in ‘telescope-mode’ up to ~50° incidence angle for the 50% level, or all-sky in ‘spectroscopy-mode’.
Left: Field of view of the GRM. Right: Polarisation sensitivity of GRM. Various models of GRB spectra are shown which differ in their break energy and their high-energy powerlaw slope; see legend for the parameter pair for each model. Note that at the bright end the minimal detectable polarization changes much more slowly than the fluence
Line sensitivity The narrow-line point-source sensitivity of the GRM for three astrophysically important γ-ray lines is given in Table 2. The exposure time is 106 s in all cases. For the standard operation mode, the all-sky scan, the resulting sensitivity is slightly worse than in pointing mode since the exposure is distributed over most of the sky and not concentrated into a small FOV like for INTEGRAL. This reduction is, however, offset by the large geometrical factor (effective area × solid angle), the uniformity of the scan, and the permanent accumulation of exposure. As consequence, after 5 years in orbit, GRIPS will achieve a factor 40 sensitivity improvement over COMPTEL (in 9 years) in e.g. the 1809 keV line.
Polarisation The dominant mode of interaction for photons in Silicon in the energy range from a few hundred keV to about 8 MeV is Compton scattering. Linearly polarised γ–rays preferentially scatter perpendicular to the incident polarisation vector, resulting in an azimuthal scatter angle distribution (ASAD) which is modulated relative to the distribution for unpolarised photons. The sensitivity of an instrument to polarisation is given by the ratio of the amplitude of the ASAD and its average, which is called the modulation factor μ. The modulation is a function of incident photon energy, E, and the Compton scatter angle, θ, between the incident and scattered photon directions (see Fig. 11 for the MEGA calibration).
Measured polarisation response of the MEGA prototype for two different energies. Within measurement errors and statistics, all values are in agreement with GEANT4 simulations: the polarisation angle of 90° is reproduced to 82%±24% (0.7 MeV) and 86%±11% (2.0 MeV), respectively. The measured modulation is 0.17±0.04 and 0.13±0.03 as compared to the simulated values 0.19 (at 0.7 MeV) and 0.14 (2.0 MeV). (From Zoglauer [73])
GRIPS is a nearly perfect polarimeter (Fig. 10, lower panel): The well-type geometry allows the detection of Compton events with large scatter angles which carry most of the polarisation information. GRIPS’ polarisation sensitivity will be best at 200–400 keV where the polarisation information of the photons is best preserved through the Compton scatter process.
GRBs We have created model spectra (Fig. 12) with parameters for Epeak, high-energy power law slope β and peak flux, which cover the distribution of these parameters as observed with BATSE (4th BATSE catalog; [43]). The faintest BATSE GRBs are clearly ‘detected’ by GRIPS with spectra extending from 100 keV up to 2 MeV and having more than 7 energy bins with 3σ each. From these simulations we estimate that GRIPS will be a factor of 3 more sensitive than BATSE below 1 MeV and detect about a factor of 2.5 more GRBs than BATSE. Folding in the smaller field of view of GRIPS compared to BATSE, we find that GRIPS will detect 665 GRBs/year. For GRBs at an off-axis angle of >70°, only poor localizations, if any, will be possible, so we expect 440 GRBs/year with good positions and XRM follow-up.
Residuals of a simulated power law spectrum with resonance absorption and the model fit with a straight power law. The GRB was chosen among the 3% brightest BATSE bursts, with 10 s duration, and an intervening rest-frame column of 5×1026 cm − 2. The spectrum has been sent through the full GRM detector model. The power law slope is reproduced to within 0.1, and the resonance lines (marked) are detected at overwhelming significance
The present Swift sample of GRBs contains 5% GRBs at z>5. This is a lower limit, since only 50% have a redshift. There are two ways to extrapolate: (i) If the remaining 50% have the same z-distribution as the identified ones, and are just fainter, then 10% of all GRBs would be at z>5. (ii) If the remaining 50% are predominantly high-z, i.e. missed in the identification because of Ly-α break, then slightly above 50% of all GRBs would be at z > 5. This translates into a fraction of 1%–10% of all GRBs located at z>10, or 0.1%–1% of all GRBs at z > 20. Here, the lower value is based on the assumption that the comoving GRB density distribution (often referred to as the star formation rate based on the expectation that GRBs originate from massive stars) remains constant beyond z = 2 (based on Steidel et al. [57]), while the higher value assumes the GRB density distribution to continue to rise beyond z = 2 which reflects the possibility of observational biases like an extinction underestimate [6]. With 665 GRBs per year, and a nominal lifetime of 5 years (goal 10 years) we would expect 33–330 (goal 66–660) GRBs at z>10, and 3–33 GRBs (goal 6–66) at z > 20. Of these, 67% would be detected with an accurate (<25 arcsec) position. This estimate includes a duty cycle of the instrument similar to that of BATSE and a detection rate of the X-ray afterglows of 98%, as for Swift/XRT. (We note for comparison that Naoz and Bromberg [42] predict 1% of GRBs at z > 20 in their pessimistic case and 5% and 15% for their optimistic cases.) This implies that (1) the detection frequency of GRBs at z > 20 is high enough to achieve at least one detection during the mission lifetime, and (2) that GRIPS will clearly detect the cut-off in the z-distribution IF star formation starts at a certain redshift (below ~25) throughout the Universe. (Even if this cut-off were to happen at z < 13, it would be a very important measurement.) Measuring this cut-off, or no cut-off up to z~25, would in turn be a limit to the earliest time when stars formed and re-ionization might have happened.
4.3 X-ray telescope
The main driver for the design of the XRM is the positional accuracy of GRBs, so that their full error circle can be covered by the XRM. GRM will determine GRB positions to better than 1° (radius, 3σ) down to off-axis angles of 60°. We add a 50% margin, and require a field of view of the XRM of 3° diameter.
The second requirement is for sensitivity which should be at least a factor 3 larger than that of Swift’s XRT, since GRIPS will cover more distant GRBs, and thus likely fainter afterglows. Such sensitivity requirement (of order >300 cm2) excludes coded mask systems, and even single-telescope Wolter-I optics are problematic.
The easiest and probably most cost-effective option is to adopt the eROSITA scheme of 7 Wolter-I telescopes and adjust their orientation on the sky such that they fill the required FOV (Fig. 6). eROSITA (for extended ROentgen Survey with an Imaging Telescope Array) shall perform the first imaging sky survey in the medium X-ray range, i.e. between 0.2 and 12 keV.
It is relevant to mention a number of improvements of the eROSITA detector over the XMM EPIC/PN detector: (i) lower noise and very homogeneous over detector pixels, (ii) smaller charge transfer losses, (iii) higher energy resolution, especially for low X-ray energies (<1 keV), (iv) smaller number of out-of-time events due to frame-store technique, (v) higher time resolution of 50 ms. As with the XMM EPIC/PN, the eROSITA detectors will share the high quantum efficiency (>90% over 0.2–10 keV band), the high radiation hardness against high energy protons including self-shielding against the low energy protons focused by the Wolter telescope, The effective area of the eROSITA telescope, even after placing all 7 telescopes at different sky positions, well matches the GRIPS requirements.
For some fraction of the mission, the XRM would perform follow-up observations of GRB afterglows. Over one year of mission time, about 10% of the sky would be covered with an exposure time of typically 20 ksec, thus reaching about 4×10 − 15 erg/cm2/s. Within the envisaged 10 years mission life time, the whole sky would be covered to that depth. Alternatively, one could reduce the length of pointed observations of GRB afterglows in later phases of the mission, and perform a sky-survey every 6 months.
4.4 Nice-to-have additions
Three additional instruments may enhance the versatility of the mission:
-
(1)
Optical/Near-Infrared telescope: For localizing GRBs up to z~8–9, an optical telescope would be optimal. For even higher redshifts, cooled NIR detectors are necessary, and given the complicated thermal balance of GRIPS, this would need a concept study.
-
(2)
Neutron-Monitor: The neutron flux in a LEO varies with time, and induced γ-radiation in the telescope is a source of background. A small neutron detector would act as monitor of the general radiation field, and thus substantially help in fighting the background radiation.
-
(3)
Lobster XRM: The Lobster camera principle is ideal for an all-sky monitor at soft X-rays with a spatial resolution in the few-arcmin range. It would allow detection of the prompt X-rays which are connected to the GRB prompt emission. A Lobster system, properly adapted to the GRIPS needs (ring-like FOV), would allow the localization of (i) the additional 220 GRBs for which the GRM will not be able to measure a position and (ii) those GRBs for which Earth or Sun constraints would prohibit slewing the XRT.
5 Spacecraft details
GRIPS should be 3-axis stabilized with closed loop attitude control, and follows the tradition of many recent astronomical space missions. It presents no new problems in the control of the dynamics of the spacecraft. GRIPS will have, however, two distinct features:
-
1.
GRIPS will do zenith-pointing all the time, thus the standard few re-pointings per orbit around the Earth will not occur.
-
2.
For each detected and localized GRB, GRIPS should autonomously respond with a rotation around its z-axis such that the hinge-mounted X-ray telescope can point towards the GRB location. This satellite rotation is expected to occur about twice per day, in rare cases up to 10 per day.
The orientation of the spacecraft around the zenith axis is free during all periods of the mission except when follow-up observations with the narrow-field of view instruments are being performed.
For the launch mass estimate (Table 3), we have applied 5% margins to the GRM detectors (scintillators), 10% margin to the bus, and 20% system margin. This results in a launch mass of 3.5 t comparable to earlier γ-ray missions such as CGRO and INTEGRAL, well within the capabilities of the SF launcher of 5.3 t.
The seven X-ray telescopes have a length which is comparable to the total height of satellite bus, and GRM instrument and electronics. The X-ray telescope should be mounted such that it does not obstruct the field of view of the gamma-ray instrument (160°!). Thus, the hinge mechanism should be placed at the very bottom of the satellite bus (see Fig. 13 for a first design study).
References
Abel, T., Wise, J.H., Bryan, G.L.: The HII region of a primordial star. ApJ 659, L87 (2007)
Amati, L., et al.: Intrinsic spectra and energetics of BeppoSAX gamma-ray bursts with known redhsifts. A&A 390, 81 (2002)
Andritschke, R.: The Compton and pair creation telescope MEGA. Exp. Astron. 20, 395 (2005)
Arav, N., Kaastra, J., Steenbrugge, K., et al.: Contrasting the ultraviolet and XRay O VI column density inferred for the outflow in NGC 5548. ApJ 590, 174 (2003)
Arav, N., Kaastra, J., Kriss, G.A., et al.: X-Ray/Ultraviolet campaign on the MRK 279 AGN outflow: constraining inhomogeneous absorber models. ApJ 620, 665 (2005)
Blaine, A.W., Kneib, J.P., Ivison, R.J., Smail, I.: Deep counts of submillimeter galaxies. ApJ 512, L87 (1999)
Boggs, S.E., Coburn, W., Kalemci, E.: Gamma-ray polarimetry of two X-class solar flares. ApJ 638, 1129 (2006)
Branch, D., Nomoto, K.: Supernovae: answers and questions. Nature 447, 393 (2007)
Bromm, V., Loeb, A.: The expected redshift distribution of gamma-ray bursts. ApJ 575, 111 (2002)
Bromm, V., Loeb, A.: High-redshift gamma-ray bursts from population III progenitors. ApJ 642, 382 (2006)
Cheng, K.S., Chernyshov, D.O., Dogiel, V.A.: Annihilation emission from the galactic black hole. ApJ 645, 1138 (2006)
Diehl, R., et al.: Radioactive26 Al from massive stars in the galaxy. Nature 439, 45 (2006)
Elitzur, M., Nenkova, M., Ivecic, Z.: In: Aalto, S., Huttemeister, S., Pedlar, A. (eds.) The Neutral ISM in Starburst Galaxies, ASP 320, p. 242. Astronomical Society of the Pacific, San Francisco (2004)
Gao, L., Yoshida, N., Abel, T., Frenk, C.S., Jenkins, A., Springel, V.: The first generation of stars in the A cold dark matter cosmology. MNRAS 378, 449 (2007)
Ghirlanda, G., Ghisellini, G., Lazzati, D.: The collimation-corrected gamma-ray burst energies correlate with the peak energy of their νF ν spectrum. ApJ 616, 331 (2004)
González, M.M., Dingus, B.L., Kaneko, Y., Preece, R.D., Dermer, C.D., Briggs, M.S.: A gamma-ray burst with a high-energy spectral component inconsistent with the synchrotron shock model. Nature 424, 749 (2003)
Granot, J., Königl, A.: Linear polarization in gamma-ray bursts: the case for an ordered magnetic field. ApJ 594, L83 (2003)
Granot, J.: The most probable cause for the high gamma-ray polarization in GRB 021206. ApJ 596, L17 (2003)
Harding, A.K., Grenier, I.A., Gonthier, P.L.: The Geminga fraction. Astrophys. Space Sci., 309, 221 (2007)
Heger, A., et al.: How massive single stars end their life. ApJ 591, 288 (2003)
Hernanz, M., José, J.: Radioactivities from novae. New Astron. Rev. 50, 504 (2006)
Hernanz, M., Gomez-Gomar, J., Jose, J.: The prompt gamma-ray emission of novae. New Astron. Rev. 46, 559 (2002)
Homeier, N.L.: The effect of type Ibc contamination in cosmological supernova samples. ApJ 620, 12 (2005)
Hooper, D., Wang, L.: Possible evidence for axino dark matter in the galactic bulge. Phys. Rev. D70, 063506 (2004)
Iyudin, A.F., Diehl, R., Bloemen, H., et al.: COMPTEL observations of Ti-44 gamma-ray line emission from CAS A. A&A 284, L1 (1994)
Iyudin, A.F., Reimer, O., Burwitz, V., Greiner, J., Reimer, A.: Resonant absorption troughs in the gamma-ray spectra of QSO. A&A 436, 763 (2005)
Iyudin, A.F., Burwitz, V., Greiner, J., Larsson, S., Küpcü Yoldas, A.: Gamma-ray absorption method (GRAM) application to the identification of EGRET unidentified sources. A&A 468, 919 (2007)
Iyudin, A.F., Greiner, J., Larsson, S., Ryde, F.: Gamma-ray bursts: prospects for GLAST. In: Axelsson, M., Ryde, F. (eds.) AIP Conf. 906, Sept. 2006, p. 89. AIP, College Park (2007)
Jiang, Z.J., Zhang, L.: Statistical properties of high-energy radiation from young pulsars. ApJ 643, 1130 (2006)
Jorstad, S.G., Marscher, A.P., Lister, M.L., et al.: Jet kinematics of AGNs at high radio frequencies. ASP CS-350, 149 (2006)
Kanbach, G., et al.: Development and calibration of the tracking Compton/Pair telescope MEGA. NIM-A 541, 310 (2005)
Knödlseder, J., Jean, P., Lonjou, V., et al.: The all-sky distribution of 511 keV electron-positron annihilation emission. A&A 441, 513 (2005)
Kogut, A., Spergel, D.N., Barnes, C., et al.: First-year Wilkinson microwave anisotropy probe (WMAP) observations: temperature- polarization correlation. ApJS 148, 161 (2003)
Kuiper, L., Hermsen, W., den Hartog, P.R., Collmar, W.: Discovery of luminous pulsed hard X-ray emission from anomalous X-ray pulsars 1RXS J1708-4009, 4U 0142+61, and 1E 2259+586 by INTEGRAL and RXTE. ApJ 645, 556 (2006)
Lamb, D.Q., Reichart, D.E.: In: Costa, E., et al. (eds.) GRBs in the afterglow era, p. 226. ESO-Springer, Heidelberg (2001)
Leibundgut, B.: Cosmological implications from observations of type Ia supernovae. ARA&A 39, 67 (2001)
Limongi, M., Chieffi, A.: The nucleosynthesis of 26Al and 60Fe in solar metallicity stars extending in mass from 11 to 120 Msolar: the hydrostatic and explosive contributions. ApJ 647, 483 (2006)
Lyutikov, M., Pariev, V.I., Blandford, R.D.: Polarization of prompt gamma-ray burst emission: evidence for electromagnetically dominated outflow. ApJ 597, 998 (2003)
MacLow, M.M., Klessen, R.S.: Control of star formation by supersonic turbulence. Rev. Mod. Phys. 76, 125 (2004)
McBreen, S., Hanlon, L., McGlynn, S., et al.: Observations of the intense and ultra-long burst GRB 041219a with the Germanium spectrometer on INTEGRAL. A&A 455, 433 (2006)
Mészáros P.: Gamma-ray bursts. Rep. Prog. Phys. 69, 2259 (2006)
Naoz, S., Bromberg, O.: MN 385, L63. Detecting early galaxies through their 21-cm signature. Mon. Not. R. Astron. Soc. Lett. 385, L63–L67 (2008)
Paciesas, W.S., Meegan, C.A., Pendleton, G.N., et al.: The fourth BATSE gamma-ray burst catalog (revised). ApJS 122, 465 (1999)
Pavlinsky, M., Hasinger, G., Parmar, A., Fraser, G., Churazov, E., et al.: Spectrum-RG/eROSITA/Lobster astrophysical mission. SPIE 6266, 18 (2006)
Pe’er, A., Waxman, E.: Prompt gamma-ray burst spectra: detailed calculations and the effect of pair production. ApJ 613, 448 (2004)
Porter, T.A., Moskalenko, I.V., Strong, A.W., et al.: Inverse compton origin of the hard X-ray and soft gamma-ray emission from the galactic ridge. ApJ (2008, in press) (arXiv:0804.1774)
Prantzos, N.: Radioactive 26Al and 60Fe in the Milky Way: implications of the RHESSI detection of 60Fe. A&A 420, 1033 (2004)
Prantzos, N., Diehl, R.: Radioactive 26Al in the galaxy: observations versus theory. Phys. Rep. 267, 1 (1996)
Predehl, P., Hasinger, G., Böhringer, H., Briel, U., Brunner, H., et al.: eROSITA. SPIE 6266, 19 (2006)
Rees, M.J., Mészáros, P.: Dissipative photosphere models of gamma-ray bursts and x-ray flashes. ApJ 628, 847 (2005)
Ryde, F.: Is thermal emission in gamma-ray bursts ubiquitous? ApJ 625, L95 (2005)
Schady, P., Mason, K.O., Page, K., et al.: Dust and gas in the local environments of gamma-ray bursts. MN 377, 273 (2007)
Schönfelder, V., Bennett, K., Blom, J.J., et al.: The first COMPTEL source catalogue. AAS 143, 145 (2000)
Sim, S.A., Mazzali, P.A.: On the gamma-ray emission of type Ia supernovae. MNRAS 385, 1681 (2008)
Spolyar, D., Freese, K., Gondolo, P.: Dark matter and the first stars: a new phase of stellar evolution. PRL 100, 051101 (2008)
Starling, R.L.C., Wijers, R.A.M.J., Hughes, M.A., et al.: Spectroscopy of the gamma-ray burst GRB 021004: a structured jet ploughing through a massive stellar wind. MN 360, 305 (2005)
Steidel, C.C., et al.: Lyman-break galaxies at z> ~4 and the evolution of the ultraviolet luminosity density at high redshift. ApJ 519, 1 (1999)
Story, S.A., Gonthier, P.L., Harding, A.K.: Population synthesis of radio and -ray millisecond pulsars from the Galactic Disk. ApJ 671, 713 (2007)
Strong, A.W., et al.: Gamma-ray continuum from the inner Galactic region as observed with INTEGRAL/SPI. A&A 444, 495 (2005)
Tatischeff, V., Kozlovsky, B., Kiener, J., Murphy, R.J.: Delayed X- and gamma-ray line emission from solar flare radioactivity. ApJS 165, 606 (2006)
The, L.-S., Clayton, D.D., Diehl, R., et al.: Are 44Ti-producing supernovae exceptional? A&A 450, 1037 (2006)
Thompson, D.J., Bailes, M., Bertsch, D.L., et al.: Gamma radiation from PSR B1055-52. ApJ 516, 297 (1999)
Varier, K.M., Nasiruddeen Kunju M.A., Madhusudanan, K.: Effect of finite absorber dimensions on gamma-ray attenuation measurements. Phys. Rev. A33, 2378 (1986)
Vink, J., Laming, J.M., Kaastra, J.S., et al.: Detection of the 67.9 and 78.4 keV lines associated with the radioactive decay of 44Ti in cassiopeia A. ApJ 560, 79 (2001)
Vreeswijk, P.M., Ledoux, C., Smette, A., et al.: Rapid-response mode VLT/UVES spectroscopy of GRB 060418. Conclusive evidence for UV pumping from the time evolution of FeII and NiII excited- and metastable-level populations. A&A 468, 83 (2007)
Wang, W., et al.: SPI observations of the diffuse 60Fe emission in the galaxy. A&A 469, 1005 (2007)
Wehrle, A.E., Piner, B.G., Unwin, S.C., et al.: Kinematics of the parsec-scale relativistic jet in Quasar 3C 279: 1991–1997. ApJS 133, 297 (2001)
Weidenspointner, G., Harris, M.J., Sturner, S., Teegarden, B. J., Ferguson, C.: MGGPOD: a Monte Carlo suite for modeling instrumental line and continuum backgrounds in gamma-ray astronomy. ApJS 156, 69 (2005)
Woosley, S.E., Weaver, T.A.: The evolution and explosion of massive stars. II. Explosive hydrodynamics and nucleosynthesis. ApJS 101, 181 (1995)
Woosley, S., et al.: The supernova gamma-ray burst connection. AIP 836, 398 (2006)
Yoon, S.-C., Langer, N., Norman, C.A.: Single star progenitors of long gamma-ray bursts. I. Model grids and redshift dependent GRB rate. A&A 460, 199 (2006)
Yoshida, N., Omukai, K., Hernquist, L., Abel, T.: Formation of primordial stars in a CDM universe. ApJ 652, 6 (2006)
Zoglauer, A.: Expected line sensitivity of the MEGA telescope. PhD thesis, TU Munich (2005)
Zoglauer, A., Andritschke, R., Schopper, F.: MEGAlib the medium energy gamma-ray astronomy library. New Astron. Rev. 50(7/8), 629 (2006)
Zoglauer, A., et al.: Nuclear astrophysics capabilities of the GRIPS telescope. New Astron. Rev. (2008). doi:10.1016/j.newar.2008.05.009
Author information
Authors and Affiliations
Corresponding author
Additional information
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Excerpt of a proposal submitted in response to the ESA Cosmic Vision Call in June 2007, invited for an audition on October 9 at ESA headquarters, but not selected for further consideration in mid-October 2007.
See www.grips-mission.eu for the authors’ affiliations.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Greiner, J., Iyudin, A., Kanbach, G. et al. Gamma-ray burst investigation via polarimetry and spectroscopy (GRIPS). Exp Astron 23, 91–120 (2009). https://doi.org/10.1007/s10686-008-9102-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10686-008-9102-0