1 Introduction

A large number of retail transactions occur on centralized online platforms which allow sellers and buyers to seamlessly exchange goods and services. These transactions are easily recorded, often in real time, and offer sellers rich data on consumer preferences. In turn, these data can be used by sellers to forecast future demand with greater precision. Typically, the production decision involves the question of how much to produce, or the intensive margin, and whether to produce, or the extensive margin. The latter is also known as a market entry decision. In this paper, we conduct a laboratory experiment to study how different payoff information affects the market entry decision.

Understanding how subjects respond to information is important for maximizing the profit of market participants, including buyers, sellers, and the designer of the market platform. Profit is often tied to the spell or length of market participation, which is state-dependent. Our experiment allows us to study both components: (i) market entry/exit and (ii) the length of market participation. In the field, studying market entry (or exit) decisions under different information sets may be costly, if not impossible when researchers cannot alter market characteristics. A laboratory experiment can overcome these difficulties by providing complete control over the information available to market participants. In this paper, we present a novel experiment in which the market participants have access to counterfactual information in one environment, but not the other, and in which this decision is reversible. Our primary research question is how the information provided to a subject affects their entry decision. While market transparency for buyers is an actively developing field,Footnote 1 our experiment allows us to study the impact of transparency on the market’s supply side.

In our environment, market participants can switch between IN and OUT decisions at any time. The payoff to IN follows a stationary AR(1) process, which reflects market conditions. A participant does not have any market power, and therefore takes prices as given. The payoff to OUT is less than the expected payoff to IN. For simplicity, we assume zero transaction costs for switching between IN and OUT and provide subjects with information about the risky payoff generation process. In the private information treatment, which is a typical bandit problem, participants select between a safe arm (OUT), and a risky arm (IN), where the platform provides information in almost real-time. If a participant selects OUT, then the participant will not be able to observe the risky payoff. In order to observe the return to the risky arm, this option must be selected. In the public information treatment, we provide information on the risky payoff regardless of whether the participant is IN or OUT.

To draw predictions for IN and OUT decisions across both treatments, we assume that agents forecast their future revenues under two different rules: (i) rational expectations, and (ii) behavioral expectations which allow for the well-known forecasting biases such as extrapolation and stickiness (Landier et al., 2019). While both rules suggest that IN should be observed more often under public information, we find that subjects select IN more often when information is private. This result suggests that there is a demand for information, and that participants do not exhibit a high degree of risk aversion since they are willing to explore the risky option. These results are also supported by other bandit experiments in the lab (Hoelzemann & Klein, 2021).Footnote 2

Our experimental design is motivated by the market entry decisions when information flows rapidly. We modify the standard bandit problem found in economics and finance (Bergemann & Välimäki, 2008) to study reversible entry decisions under different disclosure rules. In a related experiment, Grosskopf et al. (2006) find that providing counterfactual information in a bandit problem can increase risky behavior. However, this result disappears with more experience, suggesting that subjects become less sensitive to additional information over time. Yechiam and Busemeyer (2006) show that counterfactual information can increase risk taking when the negative outcome is rare and large. Biele et al. (2009) employ a Markov process with two states for the risky option, H and L, which are unknown to subjects. They find that players do not learn to become risk averse. In our experiment, we enrich the set of possible outcomes by providing more opportunities for the subjects to familiarize themselves with the payoff realization process due to the nearly continuous environment.Footnote 3

To formulate our predictions, we draw from literature on expectation formation when the predicted variable is exogenous.Footnote 4 According to Assenza et al. (2014) and Mokhtarzadeh and Petersen (2020), having access to historical data in forecasting experiments can encourage more adaptive and trend-chasing expectations. Landier et al. (2019) asked subjects to forecast 40 realizations of a risky asset and found evidence of both sticky (Coibion & Gorodnichenko, 2015; Bouchaud et al., 2019), and extrapolative (Bordalo et al., 2018) expectations.Footnote 5 We simplify the forecasting tasks by focusing on the binary decision of IN or OUT, which indirectly measures market expectations. Our findings complement existing experimental literature on switching behavior (Anufriev et al., 2016, 2018 and Anufriev et al., 2019). In these experiments, participants were offered an opportunity to switch between investment alternatives. In contrast to our paper, participants in these studies (i) were not informed about the payoff generating process, and (ii) were evaluated only in a public information environment.

2 Environment

For each \(t=\{1\dots , T\}\), a player seeks to maximize profit \(\pi _{t}\), by choosing between two actions; IN (\(a=1\)) and OUT (\(a=0\)). Choosing \(a=1\) yields a stochastic payoff \(\pi _t = x_t+100\), in which \(x_t\) is driven by an autoregressive process of order one AR(1) as specified in Eq. (2), and \(\epsilon\) follows a standard normal distribution, while OUT, the outside option, yields a constant payoff \(r+100\), such that

$$\begin{aligned} \pi _{_{t}}= {\left\{ \begin{array}{ll} x_{_{t}}+100 &{} \text {if} \quad a=1, \\ r +100 &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$
(1)

where

$$\begin{aligned} x_{_{t+1}} = \rho x_{_{t}} + \sigma \cdot \epsilon _{_{t}}. \end{aligned}$$
(2)

The payoff structure that we employ has two important features. First, the payoff for IN, \(x_{t}\), incorporates a risk premium, and therefore \(r< E(x_{t})\). Second, to avoid negative payoffs we add a constant component equal to 100 to both alternatives. We study two environments with different information disclosure rules: public information and private information. In the private information treatment, the subject does not observe the payoff to IN if they choose OUT. In the public information treatment, we provide counterfactual information on the foregone payoff when the subject selects OUT. In both environments, the subject’s decision between IN and OUT at every t is driven by the subject’s beliefs regarding the one period ahead value \(x_{_{t+1}}\), denoted as \(F_{_{t}} x_{_{t+1}}\). Consequently,

$$\begin{aligned} a= {\left\{ \begin{array}{ll} 1 &{} \text {if} \quad F_{_{t}} x_{_{t+1}} > r, \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$
(3)

We allow beliefs \(F_{_{t}} x_{_{t+1}}\) to accommodate a large family of expectations, from Rational Expectations (RE) with \(F_{_{t}} x_{_{t+1}} = E_{_{t}} x_{t+1}=\rho x_{t}\), to Sticky and Extrapolative Expectations (SEE) which capture the belief formation for AR(1) processes (Landier et al., 2019). Under SEE, the belief \(F_{_{t}} x_{_{t+1}}\) combines extrapolative expectations, in which subjects overreact to unexpected innovations (Bordalo et al., 2018), and sticky expectations (Coibion & Gorodnichenko, 2015, Bouchaud et al., 2019), in which subjects demonstrate inertia in updating expectations. We use a nonrecursive specification for the one period ahead forecast, which depends on current and past RE, denoted as \(\sum ^n_{k=0} E_{_{t-k}} x_{_{t+1}}\), as well as the history of x,

$$\begin{aligned} F_{_{t}} x_{_{t+1}} = (1-\lambda )\sum ^n_{k=0}\lambda ^k E_{_{t-k}} x_{_{t+1}}+\gamma \sum ^n_{k=0}\lambda ^k (x_{_{t-k}}-E_{_{t-k-1}}x_{_{t-k}})\cdot \mathbbm{1}_{_{t-k}}, \end{aligned}$$
(4)

where \(\lambda \in [0,1]\) is the degree of stickiness, \(\gamma >0\) captures the importance of extrapolative beliefs, and \({\mathbbm{1}}_{t-k}\) takes the value of one when either (i) the environment is public information, and therefore \(x_{_{t-k}}\) is always observed, or (ii) the environment is private, and the subject selected IN for \(t-k\). If there is no stickiness to belief updating (\(\lambda =0\)), and no trend extrapolation (\(\gamma =0\)), then the SEE belief is exactly RE, \(F_{_{t}} x_{_{t+1}}=E_{_{t}} x_{_{t+1}}\).

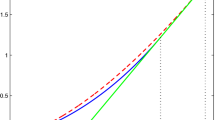
Figure 1 shows examples of RE and SEE belief formations using a series of actual x realizations observed by participants in the public and private information treatments with \(\{\rho , \sigma , T, r, \lambda ,\gamma \}=\{0.85, 12, 160, -8, 0.21, 0.41 \}\). We employ such parameter values for the following reasons. The value of \(\rho\) has to be high enough to create an important half-life for innovations \(\epsilon\). However, it should not be too close to one in order to avoid a random walk. The value of \(\sigma\) follows the empirical work of Landier et al. (2019), though we assume a smaller value to mitigate fatigue from facing very volatile series. The value for OUT, r, is obtained from simulations, which create meaningful OUT spells. A smaller value of r incentivizes subjects to stay IN, and therefore limits the ticks in which we can observe players selecting OUT. The last two parameters (\(\lambda\) and \(\gamma\)) are the estimates of behavioral expectations parameters reported by Landier et al. (2019).Footnote 6 The solid black line in Fig. 1 shows the value of IN, the RED line represents an agent’s belief under RE, and the blue line represents the belief under SEE. We assume that the simulated player makes a decision according to Eqs. (3) and (4), and does not have information on the risky payoff when selecting OUT. The beliefs of the player evolve upwards after choosing OUT, because the value of IN follows a mean reversion process centered around zero plus the constant of 100.

Fig. 1
figure 1

Payoff from choosing IN and the evolution of belief under rational expectations (RE) and sticky and extrapolative expectations (SEE). The left panel depicts an example of public information treatment. The right panel depicts an example of private information treatment. The horizontal dashed line represents the value of OUT option and the solid line represents the value of IN option

Full size image

Hypothesis

Under both behavioral rules, RE and SEE, the frequency of OUT will be lower in the public information treatment than in the private information treatment.

We perform numerical simulations using the observed values of \(x_{_t}\) (a total of 160-ticks per round) from our experimental sessions to formulate our Hypothesis. We simulate the RE- and SEE-type behavior for all treatments and report the average values of the statistics of interest in Table 1, which include the frequency of staying OUT, the payoff as a fraction of ex-post optimal payoffs, and the switching values of \(x_{_t}\).Footnote 7 The predictions show that OUT frequency is smaller in the public information treatment. This is due to the mean reversion process of \(x_t\) and the lower payoff to OUT. This prediction is consistent across the forecasting rules.

We analyze the drivers of behavioral differences across treatments according to the value of x with respect to the payoff to OUT. Conditional on \(x<r\), the simulated player behaves similarly, on average, under both rules, choosing the outside option approximately 70 percent of the time under RE, and opting OUT a bit more frequently under SEE. The main difference arises when \(x \ge r\), where the frequency of IN is smaller in the private information treatment (0.77 under SEE and 0.82 under RE) compared to the public information treatment (0.85 in SEE and 0.88 under RE).

Table 1 Predictions under sticky and extrapolative expectations (SEE) and rational expectations (RE)
Full size table

In the second section of Table 1, we calculate how the simulated choices perform in terms of the ex-post optimal (maximum) payoff. The predicted behavior is close to optimal under both treatments, and under both forecasting rules. The next section of Table 1 shows the values of x when simulated players switch to OUT and IN. We find that players switch OUT, for both first and all switching decisions, when the value of OUT is below 92, which is in line with our expectations. Regarding the value of x that triggers the switch to IN, we observe it to be slightly higher with public information than with private information. However, the difference is not statistically significant. The predicted comparative statics in the Hypothesis are robust to increasing risk aversion.Footnote 8

Alternatively, we may also find that subjects opt IN more often in the private information treatment due to informational demand. Thus, to obtain information on the payoff to x, subjects may (i) delay their decision to switch from IN to OUT, and/or (ii) shorten the OUT spells by re-entering prematurely to gain information about the risky payoff. This alternative hypothesis implies that the value of x that triggers the decision to switch from IN to OUT may be higher in the public information treatment, where players do not gain anything from delaying the decision to switch from IN to OUT. To accurately identify the value of x that triggers switching and separate the effect of exploration, we present summary statistics for the first switching decision, when the information sets are comparable across treatments.

3 Laboratory procedures

The experiments were conducted at the MonLee laboratory in Monash University using oTree software (Chen, 2016). Subjects were recruited online via SONA software and included undergraduate students across all fields. We assigned all participants to one of the two possible treatments: (i) public information, where the information on the foregone payoff is always available, or (ii) private information, where the risky payoff (IN) is unknown when the player opts OUT, and earns a constant payoff.Footnote 9

In the instructions, we present the subjects with the underlying AR(1) process and the parameters used. After reading the instructions, subjects answered four control multiple-choice questions.Footnote 10 If a subject answered a question incorrectly, then the experimenter privately discussed with the participant the relevant section of the instructions.

Each session included two practice rounds, followed by 20 paid rounds. The risky asset payoff was updated every half a second, for 80 s (160 ticks) per round. The value of the risky asset was the same within a session, but all realizations of AR(1) were different between sessions. In total, 83 subjects participated in the experiment. Forty-one subjects participated in the public information treatment, and 42 participated in the private information treatment. Table 2 presents an overview of all laboratory sessions, and an Online Appendix provides dynamic graphs for all experimental sessions.

Table 2 Overview of sessions
Full size table

Figure 2 shows the user interface (UI) in the public information treatment for two different decisions. The left panel of Fig. 2 shows the UI as seen by the subjects when they select IN, and the right panel shows the UI when they select OUT. The UI for the private information treatment is similar to the public information treatment, except that when the player selects OUT, they no longer observe the payoff to IN. The value of IN, \(x+100\), is depicted as a blue line while the value of OUT appears as a horizontal line at the ordinate value of \(r+100 = 92\). For each subject, the default initial state is IN. If the current strategy is IN, subjects can switch OUT by clicking the “GET OUT" button located at the bottom of the interface, and if the current strategy is OUT, subjects can switch IN by clicking the “GET IN" button also located at the bottom of the interface. Players can switch between IN and OUT each tick, which lasts half a second, for \(T-1\) ticks. The green shaded area represents the accumulated payoffs. When a subject selects OUT, the payoffs accumulate at the constant rate of 92 points per tick (see right panel of Fig. 2).

Fig. 2
figure 2

User interface in the public information treatment: (i) left panel shows the payoff (in green) for staying IN up to tick 30, and (ii) right panel shows the payoff (in green) if a subjected switched OUT at tick 30. (Color figure online)

Full size image

After each round ends, we show subjects the points accrued in that round, and the cumulative points earned from all non-practice rounds. The experimental sessions lasted about 50 minutes. At the end of the session, the points earned across all rounds were added and converted to cash at the exchange rate of $.003125 per 100 points. Excluding the show-up fee of $10, subjects received on average $10.12 in the public information treatment and $10.01 in the private information treatment (see Table 2). The two treatments have similar payoffs, which is consistent with our predictions, due to the mean reversion process that governs the evolution of the value of IN. Despite the similarities in average values, we observe important differences in behavior when the value of x goes below the outside option payoff.

4 Results

We begin our discussion of results with Fig. 3, which shows an example of a round from each treatment.Footnote 11

Fig. 3
figure 3

Evolution of x (blue) and fraction of players (red) in a session selecting IN for the public (left) and private (right) treatments. The black dotted line is the outside option payoff. (Color figure online)

Full size image

The left panel of Fig. 3 presents the results for the public information treatment, while the right panel presents the results for the private information treatment. The blue line depicts the value of \(x+100\), measured against the left y-axis, while the red line shows the fraction of subjects who choose IN, measured against the right y-axis, at time t. The black line is the outside option payoff. We observe that subjects actively move IN and OUT of the market throughout the round. When the value of IN is high, more players select the risky option (such that the fraction of subject IN approaches 1), and when the value of IN is low, more players choose the outside option.

Figure 4 provides a summary of the observed frequency of OUT spells and the duration of the median OUT spell for both treatments. The black bar shows the results for the public information treatment, while the grey bar shows the results for the private information treatment. According to the left panel, subjects stay OUT more frequently in the public information treatment. Similarly, the median OUT spell duration is also longer in the public information treatment.

Fig. 4
figure 4

Summary of results (pooled data): (i) frequency of OUT (left panel), and (ii) median spell OUT (right panel). Under RE, the frequency of OUT is 0.31 and 0.33 for public and private treatments, respectively, while the median OUT spell is 2 and 4 for public and private treatments, respectively

Full size image

Next, we study the cumulative distribution function (CDF) in Fig. 5 which shows the fraction of ticks when subjects select OUT. The CDF for the public information treatment first order stochastically dominates the distribution for the private information treatment, which is consistent with the larger mean frequency of OUT in Fig. 4.

Fig. 5
figure 5

CDF of the fraction of OUT choices in the private versus public information treatments (pooled data)

Full size image

To study subject behavior over time, we present summary statistics in Table 3 using data from (i) all rounds, and (ii) rounds 11 through 20. We find that experience does not affect subject behavior, with both data samples showing similar outcomes for each treatment. To better understand the observed behavior, we compute the frequency of IN conditional on the value of x being equal to or greater than the outside option payoff (IN \(\mid\) \(x\ge r\)), and the frequency of OUT conditional on the value of x being below the outside option payoff (OUT \(\mid\) \(x<r\)). When IN is more profitable, subjects select IN 72 percent of the time in the public information treatment and 79 percent of the time in the private information treatment. When OUT is more profitable, subjects play OUT 60 percent of the time in the public information treatment and 41 percent of the time in the private information treatment. The second section of Table 3 calculates the relative payoff as a fraction of the ex-post optimal payoff. Overall, players perform slightly worse than the predicted payoff of 0.97 under both forecasting rules.

Table 3 Summary statistics
Full size table

In the third section of Table 3, we compute the mean value of x that triggers players to switch from IN to OUT. For the public information treatment, the value is close to the outside option payoff of 92. For the private information treatment, players wait until \(x+100\) drops to 85 to switch from IN to OUT. The observed value of x is sightly above the RE prediction of 86 in the public information treatment, and close to the RE prediction of 84 in the private information treatment.Footnote 12

The last section of Table 3 presents the value of \(x+100\) that triggers the decision to select IN. In the public information treatment, subjects require approximately 104 points to select IN again. In the private information treatment, where subjects do not observe the value of IN while OUT, subject require a lower payoff of 96 to re-enter the market. A lower trigger value in the private information treatment is consistent with the shorter OUT duration in the private information treatment, where subjects switch sooner due to the lack of information.

Result 1

Subjects select OUT more often in the public information treatment.

According to the linear probability model presented in Table 4, subjects are more likely to select OUT in the public information treatment, contrary to the hypothesis.Footnote 13 The dependent variable takes the value of one when the subject selects OUT, and zero when the subject selects IN for all specifications except (III), where the definition is reversed. Further, in specifications (III) and (IV), the probability is conditional on the value of x. The dummy variable Private is the treatment effect, which equals one if the subject is in the private information treatment and zero otherwise. The dummy variable Round is the trend effect, which controls for learning. We find that, on average, the frequency of OUT in the private information treatment is 10 percentage points lower than in public information treatment.

Table 4 Linear probability model
Full size table

Specification (III), which restricts the sample to when the risky option outperforms the outside option, suggests that players in the private information treatment stay IN more often than players in the public information treatment. The largest difference in behavior is observed in specification (IV), which restricts the sample to observations where the risky option under-performs the outside option. In this subsample, the frequency of OUT in the private information treatment is 18 percentage points lower. If information had no value, then we would not observe OUT more often in the private information treatment (see Table 1). Thus, specification (IV) suggests that subjects in the private information treatment value information because they are willing to stay IN. To confirm that these results are robust, Table 9 in Appendix A presents the linear regression results for rounds in which the value of IN is below 80 for at least 40 ticks. We conclude that the treatment differences are robust to when players are in markets with a low rate of return.

Result 2

Duration of an OUT spell, or uninterrupted time spent OUT without switching, is longer in the public information treatment.

To analyze the duration of an OUT spell, we use a Weibull survival function,

$$\begin{aligned} S(t;p, z{_{j}} \beta ) =\exp (-\lambda _{_{j}} t^p_{_{j}}), \end{aligned}$$

where t is the number of ticks that a player chooses OUT, p is the shape parameter and \(\lambda _{_{j}}=\exp (z_j \beta )\), which includes the regressors (\(z_{_{j}}\)) and the coefficient (\(\beta\)). The hazard rate is computed as

$$\begin{aligned} h(t)=f(t)/S(t)= -\frac{d \ln S}{d t}. \end{aligned}$$

The estimated parameters of the hazard function are presented in Table 5, and the survival function S(t) is shown in Fig. 6. The standard errors in the parametric estimation are clustered at the subject level. We find that \(p<1\), which indicates that h(t) is a decreasing function. Note that in each round, we observe multiple OUT spells.

The survival function confirms that subjects in the public information treatment stay out longer (solid black line) than in the private information treatment (dashed green line). We estimate the survival function using the parameters from Table 5 and find that the coefficient for Private is 0.36, and the hazard rate is \(1.43 \ (=\exp (0.36))\) in the private information treatment relative to public information treatment. Shorter OUT spells in the private information treatment confirm that information has value– subjects choose IN to determine and evaluate the payoff of x relative to the outside option OUT. In the public information treatment, subjects know the value of x and can evaluate the relative payoff without switching prematurely. Hence, subjects are willing to opt OUT of the risky option more often in the public information treatment because they do not lose access to information.

Fig. 6
figure 6

Weibull survival function: \(OUT\rightarrow\) IN

Full size image
Table 5 Hazard function
Full size table

Result 3

Subjects select OUT faster in the public information treatment.

To determine when subjects switch from IN to OUT, we use a Tobit regression. Since we are interested in a point estimate rather than the duration of an event, a Tobit regression can provide a more precise estimate than a Weibull survival analysis. The decision to switch OUT is dependent on observing a sufficiently low value of x. Therefore, we address possible censoring issues by using the Tobit regression.

Table 6 summarizes the results of the Tobit regressions for the value of x when subjects switch from \(IN\rightarrow\) OUT in specifications (I) and (II). Specification (I) analyzes all IN/OUT decisions, while specification (II) focuses only on the first IN/OUT switch. In the public information treatment, subjects switch when \(x+100\) is around 90. In the private information treatment, subjects switch when x is about 3.94 points lower. In other words, subjects in the public information treatment do not wait as long to exit (select OUT). This difference can be explained by the fact that the value of x is always available in the public information treatment, and therefore, the payoff to each strategy is clear. In the private information treatment selecting OUT reduces the information available. Thus, waiting to select OUT suggests that subjects demand information on the relative payoff.

Table 6 Switching value of \(x+100\)
Full size table

Result 4

Subjects wait longer to select IN in the public information treatment.

Specification (III) in Table 6 shows the value of x when subjects switch from OUT\(\rightarrow\) IN. We find that in the public information treatment subjects wait longer to re-enter, and that when subjects switch, the value of x is close to 105. In the private information treatment, the subject is uninformed about x and therefore its particular value is not as meaningful. In this environment, subjects switch IN to learn the payoff to x, while in the public information environment subjects react to the value of x. The shorter duration of the OUT spell is consistent with a lower value of x observed in the OUT\(\rightarrow\) IN decision in the private information treatment.

5 Discussion

In this paper, we study market entry decisions, where the payoff to entry is governed by a stationary AR(1) process, while market exit guarantees a constant payoff, under alternative information disclosure policies. In the public information treatment, we provide information on forgone payoffs to market entry, while in the private information treatment the subjects learn about market payoffs only if they enter the market. We introduce a nearly continuous environment where the risky payoff is updated every 0.5 s,Footnote 14 and omit point forecast elicitation.

Our results show that market entry is higher by about 10 percentage points when we omit information about foregone payoffs. While we observe strong treatment differences, the payoffs under both public and private information treatments are quite similar. The small difference may be due to the mean reversion process which governs the evolution of the risky payoff.Footnote 15 It would be interesting to study whether a process other than mean reversion leads to a different conclusion. However, we hypothesize that the behavior will be consistent due to demand for information in the private information treatment, but with larger payoff differences.

The analysis presented in this paper is motivated by the modern online retail platforms. In these markets, information flows continuously, and profit of market participants might depend on the time spent on the platform. We show that information about the state of the market is important for participation, and that the extent of information disclosure has consequences for market entry, and exit decisions. We also believe that our results are applicable to other settings. For example, managers can potentially increase participation rates in investment ventures by selectively disclosing payoff information to clients. Furthermore, one can extend our design to analyze how the decisions of others affect individual entry decisions. In a related bandit experiment, Hanaki et al. (2018) show that providing information about the decisions of others can help maximize profit, while in an exponential bandit problem, Hoelzemann and Klein (2021) find an increase in free-riding on the information produced by partners. Alternatively, one can also study how almost continuous-time affects the evolution of prices in learning-to-forecast experiments (Hommes, 2005, and recently Arifovic and Petersen, 2017 and Kopányi, 2019). We leave these ideas for future research.