Attention and salience in preference reversals

Abstract

We investigate the implications of Salience Theory for the classical preference reversal phenomenon, where monetary valuations contradict risky choices. It has been stated that one factor behind reversals is that monetary valuations of lotteries are inflated when elicited in isolation, and that they should be reduced if an alternative lottery is present and draws attention. We conducted two preregistered experiments, an online choice study ($N=256$) and an eye-tracking study ($N=64$), in which we investigated salience and attention in preference reversals, manipulating salience through the presence or absence of an alternative lottery during evaluations. We find that the alternative lottery draws attention, and that fixations on that lottery influence the evaluation of the target lottery as predicted by Salience Theory. The effect, however, is of a modest magnitude and fails to translate into an effect on preference reversal rates in either experiment. We also use transitions (eye movements) across outcomes of different lotteries to study attention on the states of the world underlying Salience Theory, but we find no evidence that larger salience results in more transitions.

1 Introduction

Uncovering individual preferences is fundamental for applied economics, and it is essential to allow for policy recommendations and positive analysis. In practice, different methods are used, some relying on actual choices and others on the elicitation of monetary equivalents (see Bateman et al., 2002, for an overview of elicitation methods and how they are used in applied work). It is well-known, however, that different elicitation methods might contradict each other. This is illustrated by one of the most important anomalies in decision making under risk, namely the classical preference reversal phenomenon (Lichtenstein and Slovic, 1971; Grether and Plott, 1979; see Seidl, 2002 for a detailed survey). This phenomenon refers to an empirically-robust pattern of decisions under risk where decision makers provide monetary values for long-shot lotteries which are above those of more moderate ones but then choose the latter. Such a pattern is in contradiction with any value-based theory as Expected Utility Theory or (Cumulative) Prospect Theory.

A large literature has demonstrated the robustness of the preference reversal phenomenon and postulated different, sometimes competing, explanations (e.g., Tversky et al., 1988, 1990; Tversky and Thaler, 1990; Casey, 1994; Fischer et al., 1999; Cubitt et al., 2004; Schmidt and Hey, 2004; Butler and Loomes, 2007). The phenomenon is typically demonstrated in paradigms involving pairs of lotteries consisting of a riskier option (Fig. 1; left-hand side) offering a larger prize (a long shot), called the $ -bet and a relatively safe one (a moderate lottery; Fig. 1, right-hand side), called the P-bet (for “probability”). Individual preferences over such pairs are then elicited both through a choice task involving pairwise choices and by comparing valuations obtained separately for each lottery in an evaluation task eliciting (typically) stated minimal selling prices (Willingness To Accept, WTA). The anomalous pattern is that decision makers often choose the P-bet in the choice task but explicitly value the $ -bet above the P-bet in the evaluation task. This yields a contradiction since a decision maker should be indifferent between a lottery and its certainty equivalent. In contrast, the opposite pattern of choices and evaluations occurs much more rarely.

A recent, prominent argument on the origins of the classical preference reversal phenomenon arises from Salience Theory (Bordalo et al., 2012, 2013). Essentially, it states that decision makers’ attention is drawn to salient payoff comparisons, and, as a consequence, true probabilities are replaced by decision weights distorted in favor of the corresponding states of the world. For this argument, it is essential that salience is determined by the visible outcomes. In the choice task both lotteries are present, while in the evaluation task employed in classical preference reversal experiments only the target lottery is present. Bordalo et al. (2012) assume that during evaluation the decision maker compares the lottery to an alternative of not having it with probability one (“a natural way to model the elicitation of minimum selling prices,” Bordalo et al., 2012, p. 1271). This results in a distortion of the decision weights, which in turn leads to an overpricing of both lotteries. That overpricing is particularly strong for $-bets, because the high outcomes generate more salient states. Salience Theory suggests that reversals should be more frequent when lotteries are evaluated in isolation compared to when they are evaluated in the context of another lottery.

Fig. 1

Two lotteries. The left lottery yields a large monetary amount with relatively low probability ($-bet) while the right lottery yields a moderate monetary amount with relatively high probability (P-bet)

We conducted two preregistered preference reversal experiments, an online experiment ($N=256$) and an eye-tracking experiment ($N=64$), with two different treatments (varying the “salience” of lotteries) to provide direct evidence on the role of attention and salience on the classical preference reversal phenomenon. In the online study, we test the hypothesis that preference reversals should be reduced when evaluation of a target lottery happens while an alternative lottery is present. In the eye-tracking study, we additionally examine gaze data and test the hypotheses that the alternative lottery attracts attention and that this attention influences both the evaluation of the target lottery and the resulting preference reversal rates. We also make use of the fact that in Salience Theory the states of the world correspond to comparisons between the outcomes of the two lotteries in a choice pair, and hence we can link them to measurable transitions (eye movements). This allows us to use the latter to test the hypothesis that more salient states attract more attention.

The results fail to support Salience Theory. Neither the online nor the eye-tracking experiment revealed any effect of the presence or absence of an alternative lottery during evaluations on the preference reversal rates or on the monetary valuations of the target lotteries. Additionally, our eye-tracking experiment included the exact lottery pair used in Bordalo et al. (2012) to illustrate the predictions of Salience Theory, and we also failed to detect an effect for this pair. A more detailed regression analysis of the effect of fixations revealed that attention on the alternative lottery reduced both the monetary valuation of the target lottery and the likelihood of a preference reversal when the target lottery was a long shot. This is a confirmation of the implications of Salience Theory, and in particular the prediction that evaluations in the presence of an alternative lottery should reduce overpricing. However, this effect failed to translate into a measurable difference in preference reversal rates and also failed to be significant when the target was a moderate lottery instead of a long shot.

Our analysis suggests two possible reasons for the failure of the effect on valuations to translate into a difference in reversal rates. On the one hand, the effects are modest. The alternative lottery receives a relatively small number of fixations, and the effect of a fixation on the valuation of the target lottery is of a small magnitude. On the other hand, there might be countervailing effects. Bordalo et al. (2012) argued that salience should indeed impact monetary valuations of both types of lotteries but that the impact on long shots should be proportionally larger. When the target lottery is a moderate one (P-bet) instead of a long shot, attention to the alternative lottery should also decrease the monetary valuation of the target, which in this case should increase the likelihood of preference reversals. Although this effect failed to reach significance in our data, linear combination tests taking both channels into account show that they cancel out and overall there is no effect of attention on the alternative lottery on standard reversal rates. Thus, our data suggests that the relative difference in overpricing across lottery types is too small to have a large impact on reversal rates.

Conceptually, our studies contribute to the literature examining the consequences and implications of attention and salience for economic decisions, and in particular Salience Theory as put forward by Bordalo et al., (2012, 2013). Methodologically, we add to the small but growing literature directly examining eye-tracking measurements in economics and related fields. For example, Glöckner and Herbold (2011), Ludwig et al. (2020), and Alós-Ferrer et al. (2021b) use eye-tracking to study decisions under risk, while Reutskaja et al. (2011) concentrates on consumer choice. Alós-Ferrer et al. (2021c) relied on pupil dilation to study effort allocation in a belief-updating task. Further, a growing number of contributions uses eye-tracking to examine decision making in games (Knoepfle et al., 2009; Polonio et al., 2015; Devetag et al., 2016; Polonio and Coricelli 2019; Fiedler and Hillenbrand 2020; Marchiori et al., 2021; Zonca et al., 2019). This category also includes Hausfeld et al. (2021), who gave their subjects eye-tracking information about another player that they competed against or cooperated with to analyze how subjects used that information, and Avoyan et al. (2021), who used eye-tracking to analyze how participants plan to allocate attention in a matrix-game setting introduced in Avoyan and Schotter (2020).

This paper is structured as follows. Section 2 briefly reviews Salience Theory. Section 3 presents the design and results of the online experiment. Section 4 presents the design and results of the eye-tracking experiment. Section 5 presents the analysis of the lottery pair used in Bordalo et al. (2012). Section 6 concludes. The online supplementary materials discuss additional exploratory analyses, present detailed analyses of transitions, fixation durations, and individual heterogeneity. They also contain a transcript of the original experimental instructions.

2 Salience theory

Bordalo et al. (2012, 2013) proposed a theory of context-dependent choice where salient outcomes draw more attention than others, resulting in distorted decision weights. For simplicity, in this manuscript, we will refer to it as Salience Theory. Unlike other theories relying on distorted weights, as e.g. Prospect Theory (Kahneman and Tversky 1979; Tversky and Kahneman 1992), Salience Theory makes those dependent on the outcomes themselves, and, specifically, on their salience relative to the outcomes of other available alternatives.

For binary choices under risk as those considered here, Salience Theory can be summarized as follows. There is a finite set of states of the world, S. Each state $s\in S$ has an objective probability $\pi _s\in [0,1]$, so that $\sum _{s\in S} \pi _s=1$. The decision maker chooses among two lotteries $L_a$, $L_b$, where each lottery $i=a,b$ gives a payoff $x^i_s\in \mathbb {R}$ in state s. Assume for simplicity that, for each i, $x^i_s\ne x^i_{s'}$ for all $s,s'\in S$, that is, lotteries are non-degenerate in the sense that different states result in different payoffs. Then, every state $s\in S$ is associated with one and only one pair of payoffs $(x^a_s,x^b_s)$. That is, the set of states can be identified with the Cartesian product of the sets of outcomes of the lotteries. This is highly consequential for our purposes, because it creates a one-to-one mapping between the underlying states of the world that Salience Theory is built upon, and comparisons between outcomes of different lotteries (and thus eye movements). Consider, for instance, the binary choice depicted in Fig. 2, which is based on the actual representation used in our experiments. The left lottery $L_a$ pays $ 4.0 with probability 0.77 and $ 14.0 with probability 0.23. The right lottery $L_b$ pays $ 3.0 with probability 0.1 and $ 6.5 with probability 0.9. Lotteries are independent. In Salience Theory, this corresponds to a set of four states $s_1,s_2,s_3,s_4$, with probabilities $\pi _1= 0.077$, $\pi _2= 0.693$, $\pi _3= 0.023$, and $\pi _4= 0.207$, respectively. State $s_1$ corresponds to the payoff vector $(x^a_{s_1},x^b_{s_1})=(4,3)$, and so on. As seen in the figure, each state is uniquely identified by a comparison of two outcomes, one for each lottery, and thus one could write, abusing notation, $s_1=(4,3)$, $s_2=(4,6.5)$, $s_3=(14,3)$, and $s_4=(14,6.5)$.

Fig. 2

Schematic representation of binary choice. Salience theory’s states are one-to-one with the possible transitions comparing particular outcomes across lotteries. In the classical preference reversal phenomenon, decision makers choose lottery $L_b$ (a moderate lottery or P-bet) over lottery $L_a$ (a long shot or $-bet) in direct binary choice but then provide a larger monetary valuation for $L_a$ than for $L_b$

Salience Theory predicts that choices reflect maximization of a value function

$$\begin{aligned} V^{ST}(L_i)=\sum _{s\in S} \frac{\delta ^{k^i_s}\pi _s}{\sum _{r\in S}\delta ^{k^i_r}_r\pi _r}v\left( x_s^i\right) , \end{aligned}$$

where $v(\cdot )$ is a utility of money (typically assumed to be linear in Bordalo et al., 2012), and $\delta \in (0,1]$ is a parameter indicating the degree of distortion ($\delta =1$ would mean no distortion). The key element capturing salience considerations are the natural numbers $k^i_s\in \{1,\ldots ,|S|\}$, which indicate the salience ranking of the states, from most to least salient (that is, each state is assigned a different salience ranking).¹

The salience ranking is determined through a salience function $\sigma$ which assigns a real number (the salience) to each state s and lottery $L_i$, $\sigma (x^i_s,x^{-i}_s)$, depending also on the outcome of the other lottery $-i$ in that state. The key axiomatic assumptions on $\sigma$ are ordering, meaning that a state should be more salient than another one if the outcomes of the former cover a larger range than those of the latter, and diminishing sensitivity, meaning that the salience of a state with positive outcomes should decrease if the outcomes of both lotteries are increased by the same constant (so that they become closer in relative terms; this reflects the well-known Weber’s Law).² For instance, in the example depicted in Fig. 2, the first property implies that state $s_3=(14,3)$ is more salient than each of the other three states.

Bordalo et al. (2012) further assume $\sigma$ to be a continuous and bounded function, and suggest using the particular functional form

$$\begin{aligned} \sigma (x_s^i,x_s^{-i})=\frac{|x_s^{i}-x_s^{-i}|}{|x_s^{i}|+|x_s^{-i}|+0.1}, \end{aligned}$$

(1)

which we will also rely on for some aspects of our experimental design.³ For instance, using this function for the example in Fig. 2 yields the salience ranking $k^i_{s_1}= 4, k^i_{s_2}= 3, k^i_{s_3}= 1, k^i_{s_4}= 2$.

To understand the implications of Salience Theory for the classical preference reversal phenomenon, remember that this phenomenon involves a specific, contradictory pattern of choices and evaluations (Fig. 2). In Salience Theory, the value $V^{ST}(L_i)$ for a lottery can only be computed with reference to an alternative lottery. This is straightforward for the direct choices in a preference reversal experiment, where two lotteries are present. For the monetary valuation embedded in such experiments, where lotteries are presented in isolation, Bordalo et al. (2012) assume that the “natural way to model the elicitation” is to assume that the actually-presented lottery is compared to the alternative of not having the lottery, i.e. a virtual lottery yielding zero with probability one. By the ordering property, this results in a higher salience for the resulting states compared to the ones involved in direct choices, since the (typically strictly positive) outcomes of the other lottery in a pair are replaced with zero, leading to a larger range. For instance, evaluation of $L_b$ in Fig. 2 would involve the state (14, 0) rather than states (14, 3) and (14, 6.5). However, since by definition the $-bets involve a higher outcome, this results in a relatively more salient state for the high outcome of the $-bet compared to the one of the P-bet ((14, 0) compared to (6.5, 0) in Fig. 2), resulting in a particularly strong overpricing which might lead to a preference reversal. As pointed out by Bordalo et al., (2012), one could shut down this effect by conducting the monetary valuation of each lottery while the second lottery in the corresponding choice pair is actually present (instead of presenting the former in isolation). In this way, the salience ranking should be the same during choices and evaluations, preventing reversals. In other words, Salience Theory predicts that the classical preference reversal phenomenon should occur if lotteries are evaluated in isolation, but not if they are evaluated in the context of another lottery while keeping the salience of states constant. Bordalo et al. (2012) reported data from a particular choice pair, where the monetary valuation of the $-bet decreased when conducted immediately after seeing it next to another lottery, compared to its evaluation when presented later and in isolation. That is, the authors used timing to compare evaluation in isolation and evaluation in reference to an alternative lottery. Their argument was that, if a lottery is evaluated immediately after seeing it as part of a choice, the evaluation will be made in reference to the alternative lottery in the choice pair. In contrast, if a lottery is evaluated immediately after an unrelated task, it will be evaluated in isolation. In the first case, the relevant states of the world should be the combination of outcomes of the two lotteries in the choice pair. In the second case, as explained above, the states will refer to the comparison with not having an alternative lottery, i.e. an outcome of zero with probability one. This hence creates different evaluations in terms of Salience Theory.

In our experiments, we test for differences between evaluation in the actual presence of another lottery (that is, concurrently presented on screen) and in its absence. In this way, we can test for the predictions of Salience Theory, which also include a conceptual replication of the test in Bordalo et al. (2012). Our eye-tracking experiment additionally allows us to test for the implicit assumptions of Salience Theory on attentional processes. For instance, there could be no difference between evaluations in isolation and in the presence of an alternative lottery if the latter did not attract actual attention.

3 Online experiment

3.1 Design and procedures

We conducted an online experiment using Qualtrics (preregistered at the AEA RCT Registry; see next subsection). The sample size of $N=256$ was determined by a power analysis expecting a small-to-moderate effect size (Cohen’s $d=.35$) for a one-sided non-parametric test for a between-subject design. The average earnings were $\pounds ~4.21$ and the experiment took on average 11.5 minutes. Participants were recruited through Prolific (Palan and Schitter 2018).

To ensure enough variance in choices and avoid effects arising from particular lotteries, we designed a set of 32 lottery pairs, each containing a $-bet and a P-bet (Lotteries 1–32 in Table 4, Appendix lotteries). The outcomes were given in experimental currency units (ECU) which were then exchanged into $\pounds$ (1 ECU=$\pounds ~0.4$). Each $-bet consisted of a high monetary outcome ($>10$ ECU) with a low probability ($<45\%$) and a second, low monetary outcome, while the P-bet consisted of a moderate monetary outcome ($<10$ ECU) with a high probability ($>60\%$) and a second, lower monetary outcome. In any given lottery pair, the high outcomes of the $-bet and the P-bet were always the highest and second-highest of the four outcomes presented in the pair, respectively. The outcome ranking for the low outcomes of the P/$-bets varied. The construction of lottery pairs was such that the most salient state according to Salience Theory always corresponded to the comparison between the high outcome of the $-bet and the low outcome of the P-bet (using the salience ranking derived from (1)), and the least salient state corresponded to the comparison between the low outcomes of both lotteries.⁴

To keep the length of the online experiment within Prolific’s standards, we divided the set of lottery pairs in four subsets of 8 pairs each, and each participant in the online experiment was randomly assigned to one of the subsets. That is, each participant in the online experiment faced 8 binary lottery choices and 16 evaluations (for the 16 lotteries involved in the binary choices). Choices and evaluations were interspersed.

Fig. 3

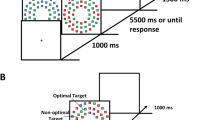
Representation of lotteries during the Choice task (left panel) and the Evaluation task of the left lottery for both treatments (center panel: Joint Treatment; right panel: Separate Treatment). This example shows a $-bet on the left side and a P-bet on the right side of the circle, but the actual position was counterbalanced

In binary choices, the participant selected the lottery she preferred. Lotteries were presented in a circle format (see Fig. 3, left panel, for an example) with outcomes and probabilities at equal distance from the center. Outcomes were always close to the horizontal axis to facilitate transitions (eye movements) between outcomes, because those correspond to the underlying states in Salience Theory (recall Sect. 2; this is particularly important for the subsequent eye-tracking experiment). The exact position of the high outcomes (top vs. bottom) was counterbalanced independently for each $-bet/P-bet. The position of the $-bets (left vs. right) was also counterbalanced, yielding a total of 8 different counterbalance situations for a lottery pair. In particular, this means that, for each individual participant, most-salient states corresponded to horizontal transitions for half of the observations, and to diagonal transitions for the other half, and analogously for least-salient states. This counterbalancing is crucial because, as shown by Arieli et al. (2011), horizontal transitions are more frequent than diagonal ones. The set-up (top-bottom and left-right) for a specific lottery pair was kept constant across the different tasks (choice vs. evaluation).

The experiment was incentivized according to a standard procedure. Specifically, one randomly-selected decision was implemented and paid. If that decision was a choice, then the chosen lottery was played out. If that decision was an evaluation, a random selling price between the low and high outcome of the lottery was drawn. In case the price was above the stated minimum selling price, the participant sold the lottery and received the price, otherwise the lottery was played out.

We implemented two different treatments between subjects, which differed only in the evaluation phase. In the Joint Treatment, participants saw the lottery they were asked to evaluate while another lottery was also present (Fig. 3, center panel). The lottery that had to be evaluated was always one of the lotteries in the choice pairs. The other lottery shown was a slightly perturbed version of the one offered in that choice pair (here a perturbed P-bet). The perturbation was such that the salience ranking remained the same as in the choice pair where the lottery was also present. The non-evaluated lottery was perturbed to avoid the exact repetition of choice pairs, which could have led to participants recognizing them and artificially enforcing consistency. In the Separate Treatment, participants saw the lottery that they had to evaluate but saw black circles as placeholders where the other lottery would have been during the choice task (Fig. 3, right panel).⁵

3.2 Hypothesis and result

The two treatments (Joint vs. Separate) allow to directly test the claim derived from Salience Theory that reversals should not occur when lotteries are evaluated while another lottery is present (and the salience ranking is unaltered with respect to the choice pair). The intuition is that overpricing arises because, if a second lottery is not present, the salience ranking is altered and the high outcome is then associated with a much more salient state (e.g., because it is implicitly compared to an outcome of zero for sure). The reduction in overpricing when another lottery is present during the evaluation phase should then lead to fewer reversals. Hence, we preregistered the following hypothesis (AEA RCT, Registry ID: AEARCTR-0005988):

• H: Standard reversal rates should be lower in the Joint Treatment compared to the Separate Treatment (between subjects).

The standard reversal rate for a given participant is defined as the rate of $-bets being evaluated higher than P-bets conditional on the P-bet being chosen over the $-bet during the choice task. Since Hypothesis H is directional, we preregistered a one-sided Mann-Whitney-Wilcoxon test.

Figure 4 displays violin plots for the distribution of reversal rates for both treatments. For completeness, the figure also displays the non-standard reversal rates (rate of P-bets evaluated higher than $-bets conditional on the $-bet being chosen).⁶ In the Joint Treatment, the average standard reversal rate was $70.28\%$, compared to $67.49\%$ in the Separate Treatment. Those rates are comparable to the ones observed in the literature (Grether and Plott 1979; Tversky et al. 1990; Cubitt et al. 2004), and in particular we reproduce the classical preference reversal phenomenon. However, contrary to Hypothesis H, we did not find lower reversal rates in the Joint Treatment than in the Separate Treatment according to the preregistered Mann-Whitney-Wilcoxon test ($N=245$, $z=-.539$, $p=.7050$).⁷

Fig. 4

Reversal rates in the Online Experiment. Violin plots depict the median, interquartile range, and kernel density plot. One-sided non-parametric test was not significant for Hypothesis H ($p>.05$)

4 Eye-tracking experiment

The online (purely behavioral) experiment did not find evidence for Salience Theory’s prediction that changes in attention due to treatment differences should translate into differences in preference reversal rates. However, attention cannot be directly observed with just choice data. For this purpose, we turn to eye-tracking data, which allows us to infer how attention is actually distributed.

4.1 Design and procedures

We conducted an eye-tracking experiment at the Laboratory for Social and Neural Systems Research (SNS Lab) of the University of Zurich (preregistered at the AEA RCT Registry; see next subsection). The sample size of $N=64$ was determined by a power analysis expecting a small-to-moderate effect size (Cohen’s $d=.35$) for a one-sided non-parametric test for a within-subject design. The data was collected in $N=64$ individual sessions, each lasting around 48 minutes. Average earnings were 27.66 CHF. Lottery outcomes were given in experimental currency units (ECU) which were then exchanged into Swiss Francs (1 ECU = CHF 2.5).

The design built upon the online experiment, with a few modifications. First, each participant faced a total of 32 binary lottery choices and 64 evaluations (32 $-bets and 32 P-bets), instead of the reduced subsets used in the shorter online experiment. Second, the two treatments were implemented within subjects, counterbalancing the lottery pairs evaluated jointly and separately across participants. That is, each subject conducted both evaluations in isolation and evaluations in the presence of an alternative lottery but no subject evaluated the same lottery twice.⁸ Third, since we did not find the reduction in standard reversals between treatments predicted by Salience Theory in the online experiment, we replaced half of the lottery pairs. Specifically, in the online experiment, lottery pairs with higher outcomes for $-bets (pairs 17–32 in Table 4, Appendix lotteries) displayed a larger standard reversal rate in the Joint Treatment than in the Separate Treatment (difference of $3.11\%$), contrary to the prediction, while the difference was in the predicted direction ($-3.13\%$) for the remaining lotteries. Hence, in the eye-tracking experiment, we replaced the former set of lottery pairs with pairs displaying lower outcomes for the $-bets (pairs 33–48 in Table 4, Appendix lotteries). Further, one of the new pairs (nr. 47) was the exact pair used by Bordalo et al. (2012).⁹

Visual fixations were measured using an EyeLink 1000 Plus produced by SR Research (Ontario, Canada). Participants were placed 55 cm in front of a $22''$ screen which showed the stimuli with a resolution of $1920\times 1080$ pixels, and placed their heads on a chin-rest to reduce random movements. Eye movement was recorded at 500 Hz and fixations were calculated by SR Research’s proprietary software. The eye tracker was calibrated at the beginning of the task (after instructions) using a 9-point calibration routine. The calibration was repeated until the average deviation was below 0.5$^\circ$ during validation. The median eye tracking recording lasted 25 minutes. Pre-defined non-overlapping Areas of Interest (AOIs) were defined around every piece of information ($160\times 90$ pixels per AOI).

4.2 Hypotheses and results

The eye-tracking experiment and all hypotheses and tests reported below were preregistered at AEA RCT, Registry ID: AEARCTR-0005985. We refer the interested reader to the Supplementary Materials available online for a brief overview of average number of fixations, decision times, and type of transitions. Salience Theory implies that the presence of the other lottery changes attention and hence affects overpricing. With eye-movement data, the first natural test to conduct concerns whether the participants actually look at the other lottery. For the other lottery to affect evaluation, one would expect that participants direct some attention to it. This can be tested by comparing how often they look at that lottery in the Joint Treatment, compared to how often they look at the placeholder black circles in the Separate Treatment. Hence, we test the following hypothesis:

Fig. 5

Heatmap of fixations. Fixations when evaluating the left lottery in the Joint (left-hand side) and Separate (right-hand side) Treatments, averaged over all subjects. The “warmer” the colors the more fixations in the same area. Solid frames indicate Areas of Interest used for calculating the number of fixations and were not visible to participants. In the experiment, the lottery to be evaluated could be on either side

H1

There should be more fixations on the other lottery in the Joint Treatment than fixations on the black circles in the Separate Treatment.

Figure 5 displays a heatmap of the fixations during the evaluation task in both treatments. The “warmer” the colors, the more fixations are in a certain area. The solid frames indicate the non-overlapping AOIs used for calculating the number of fixations and were not visible to participants. We found that participants had on average 2.16 fixations on the other lottery in the Joint Treatment and only 0.08 fixations on average on the black circles in the Separate Treatment. This difference is statistically significant according to a Wilcoxon Signed-Rank test (WSR; $N=64$, $z=6.935$, $p<.0001$) and confirmed that, although the number of fixations is modest, participants indeed looked at the other lottery present during evaluation.

We now turn to behavior in the experiment. In accordance with Salience Theory, and analogously to Hypothesis H in the online experiment, the first hypothesis concerns reversal rates:

H2a

Standard reversal rates should be lower in the Joint Treatment compared to the Separate Treatment (within subjects).

The difference between (H2a) of the eye-tracking experiment and (H) of the online study is that, in the eye-tracking experiment, we can conduct this test within subjects. Further, the test includes a different set of lotteries. Figure 6 illustrates the reversal rates in both treatments. In the Joint Treatment the standard reversal rate was $62.55\%$, compared to $60.47\%$ in the Separate Treatment. As in the online experiment, those reversal rates are as commonly observed in the literature and we reproduce the classical preference reversal phenomenon. However, again as in the online experiment, and contrary to Salience Theory’s prediction, we did not find lower standard reversal rates in the Joint compared to the Separate Treatment according to a Wilcoxon Signed-Rank test (WSR; $N=63$, $z=0.722$, $p=.7650$).

Fig. 6

Reversal rates in the Eye-tracking Experiment. Violin plots depict the median, interquartile range, and kernel density plot. One-sided non-parametric test was not significant: n.s. $p>.05$

In addition to reversal rates, for the eye-tracking experiment we also preregistered hypotheses about monetary valuations. According to Salience Theory, evaluating a lottery in the context of another lottery should reduce overpricing. Following Salience Theory, we preregistered the following hypotheses:

H2b

The evaluations of $-bets should be lower in the Joint Treatment compared to the Separate Treatment, when P-bets were chosen, and

H2c

The differences in lottery evaluations ($-bets minus P-bets) should be smaller in the Joint Treatment compared to the Separate Treatment, when P-bets were chosen.

Fig. 7

Evaluations in the Eye-tracking Experiment. Left-hand side: Evaluation of $-bets. Right-hand side: Evaluation difference between $- and P-bets. One-sided non-parametric tests were not significant(n.s.)

The hypotheses were conditional on pairs in which the P-bet was chosen because the standard reversal rate refers to those pairs. Figure 7 displays the evaluations of $-bets (left-hand side) and the difference in evaluations between $- and P-bets (right-hand side) for both treatments. The average evaluation of the $-bet when the P-bet was chosen was 6.52 in the Joint Treatment and 6.44 in the Separate Treatment. That is, contrary to Salience Theory’s prediction (H2b), $-bets were not evaluated lower in the Joint compared to the Separate Treatment (WSR, $N=63$, $z=1.486$, $p=.9313$). In fact, if anything, our experiment found a trend in the opposite direction. That is, data suggests that $-bets were evaluated higher in the Joint than in the Separate Treatment, although the opposite test missed statistical significance at the 5%-level ($p=.0687$).¹⁰

The right-hand side of Fig. 7 displays the differences in evaluations between $- and P-bets, when the P-bet was chosen. The average difference in evaluations was .691 ECU in the Joint Treatment and .598 ECU in the Separate Treatment. That is, the difference between $- and P-bets was not smaller in the Joint compared to the Separate Treatment (WSR, $N=63$, $z=1.308$, $p=.9045$), contrary to Salience Theory’s prediction (H2c). Again, our experiment found a trend in the opposite direction, with a larger difference in evaluations between $- and P-bets in the Joint compared to the Separate Treatment (but the comparison is not significant at the 5% level, $p=.0955$).

Behavioral data thus again failed to provide evidence for Salience Theory’s predictions. The non-parametric analysis, however, does not use the additional information borne by the eye-tracking data. Rather, it simply aggregates over all observations. In the next step, we look at evaluations and preference reversals again but control for the number of fixations on the other lottery in panel regressions. According to Salience Theory, overpricing should be reduced when a lottery is evaluated in the presence of another lottery. Eye-tracking allows to explore whether the other lottery is looked at and how often. Thus, in the following analyses we can control for the fixations on the other lottery. We thus preregistered the following hypotheses:

H3a

More fixations on the other lottery should reduce the minimum selling price.

H3b

More fixations on the other lottery should reduce (standard) preference reversals.

Table 1 Random effects panel regression on evaluations in the Joint Treatment

Table 1 presents a random effects panel regression on monetary valuations in the Joint Treatment for pairs such that the P-bet was chosen in the choice phase. The coefficient of interest is “# Fix. on other lottery” in the first row, which measures the number of fixations on the other lottery (the one not being evaluated) during the evaluation phase. This coefficient thus reflects the impact of attention on the other lottery on the actual monetary valuation. According to Salience Theory, this coefficient should be negative. In the first two models, we did not find a significant coefficient. Those models, however, do not distinguish whether the evaluated lottery is a P-bet or a $-bet. The coefficient becomes (weakly) significant when introducing a dummy taking the value one when the evaluated lottery was a P-bet (Model 3). Model 4 includes the interaction between the number of fixations on the other lottery and the dummy. Models 5–6 add further controls and Model 7 adds lottery-pair fixed effects as a robustness check. In models 4–7, the coefficient “# Fix. on other lottery” concerns the evaluation of $-bets only. This coefficient is (highly) significant¹¹ and negative, showing that fixations on the other lottery significantly reduce the evaluation of the $-bets, as predicted by Salience Theory, by approximately 4 ECU cents per fixation (equivalent to 0.1 CHF) relying on Model 6, or 3 ECU cents ($\approx 0.08$ CHF) relying on Model 7. In contrast, linear combination tests (bottom of the table, second to last row) show that fixations on the other lottery did not significantly affect the evaluation of P-bets.

We conclude that, in the Joint Treatment, fixations on the other lottery did reduce the monetary valuation of $-bets but the actual effect was small (about 0.1 CHF per fixation). Taking into account that the average number of fixations on the other lottery was just 2.16, the impact on monetary valuations can be seen to be rather modest. It is thus unclear whether this effect can translate into a measurable impact on preference reversals. Thus we turn to a panel probit regression with Standard Reversals as the dependent variable (Table 2), again for the Joint Treatment and pairs such that the P-bet was chosen in the choice phase. That is, the dependent variable is a dummy taking the value one if the choice was in favor of the P-bet and the monetary valuation of the $-bet was higher than that of the P-bet, and zero otherwise.¹² In this regression, an observation is a choice pair, which is hence associated with two different evaluations (for the $-bet and for the P-bet in the pair), and for each of those evaluations two lotteries were displayed (Joint Treatment). Thus there are four different kinds of fixations, depending on whether they are on the actually-evaluated lottery (in turn either a $-bet or a P-bet) or on the other, alternative lottery (which is hence either a P-bet or a $-bet itself).

Table 2 Panel probit regression on preference reversals for lotteries jointly evaluated

In all models in Table 2, the coefficient # Fix. on other P-bet is negative and highly significant. That is, standard reversals were less likely when, during evaluation of the $-bet, the alternative lottery (hence a P-bet) was fixated more. This is aligned with the previous result that overpricing of $-bets decreased with the number of fixations on the alternative lottery, and suggests that this indeed has an overall impact on the likelihood of reversals.

If fixating the alternative lottery reduces overpricing of the P-bet (and although the regression in Table 1 did not detect this effect), the result should be a reduction in the monetary valuation of this lottery. Since standard preference reversals involve the evaluation of the P-bet being lower than that of the $-bet, this effect should translate into an increase in the likelihood of standard reversals. This means that the coefficient # Fix. on other $-bet in Table 2 should be positive, i.e. standard reversals should be more likely with additional fixations on the alternative lottery (a $-bet) during evaluation of the P-bet. Although this coefficient is indeed positive in Models 1–3, it misses significance (Model 1: $p=.0847$; Model 2: $p=.0797$; Model 3: $p=.0869$).

Even if one concedes that there might be a positive effect of fixations on the other lottery when the evaluated lottery is a P-bet, linear combination tests (bottom of Table 2) show that this effect cancels out with the negative effect of fixations on the other lottery when the evaluated lottery is a $-bet, and overall there is no effect on the likelihood of standard reversals.¹³ This is interesting, because the intuition derived from Bordalo et al. (2012) is that salience impacts monetary valuations of both types of lotteries when conducted in isolation. However, the impact on $-bets should be proportionally larger than on P-bets and the overall effect should result in fewer preference reversals. In contrast, our data suggests that the effects are relatively modest and not large enough for the relative difference in overpricing across different lottery types accruing to salience effects to actually have a large impact on reversal rates.¹⁴

For the next hypothesis, recall that Salience Theory is built upon the concept of state of the world and specifically the assumption that more salient states receive more attention. Since a state corresponds to a comparison between outcomes across the two lotteries (recall Sect. 2), attention to this state should be reflected by the number of transitions (eye movements) between the two outcomes that the state consists of. Thus, we calculated the number of transitions for each state in each round of choice and joint evaluation.¹⁵ Thus, the difference in attention should be the largest when comparing the most salient and least salient state for each given pair. Hence, we preregistered the following hypothesis (separately for choices and for joint evaluations):

H4

There should be more transitions between the outcomes in the most-salient state than between the outcomes in the least-salient state.

Fig. 8

Example of lotteries and transitions between outcomes corresponding to states. Transitions between outcomes encircled in green ($14.0\leftrightarrow 3.0$) represent attention on the most salient state and transitions between outcomes encircled in red ($4.0\leftrightarrow 3.0$) attention on the least salient state. Horizontal and diagonal transitions were counterbalanced for the most and least salient states, i.e. most salient states corresponded to diagonal transitions in half of the occasions, and to horizontal transitions in the other half

By design, in our choice pairs the most salient state was always the one corresponding to the comparison between the high outcome of the $-bet and the low outcome of the P-bet, while the least salient state was always the one corresponding to the comparison between the low outcome of the $-bet and the low outcome of the P-bet (see Fig. 8).¹⁶ During choice rounds, there were on average 0.61 transitions between outcomes in the most salient state and 0.75 transitions between outcomes in the least salient state. There was no statistically significant evidence in favor of Salience Theory’s prediction (WSR, $N=64$, $z=-2.231$, $p=.9872$) and in fact, we find significant evidence that the least salient state received more attention than the most salient state ($p=.0128$). The same conclusion is obtained for transitions during the joint evaluation rounds. Recall that there were few fixations on the alternative lottery, thus there are even fewer average transitions. There were on average 0.13 and 0.12 transitions for most-salient and least-salient states, respectively, with no significant differences (WSR, $N=64$, $z=0.859$, $p=.1953$).

As a robustness check, we considered transitions not only between outcomes but enlarged the area of interest to the whole quadrant (containing both the outcome and its probability). We confirm the previous findings for both types of rounds. Overall, there were more transitions during choice rounds. However, the most salient state (1.59) received significantly less attention than the least salient state (1.74), contrary to Salience Theory’s prediction (WSR, $N=64$, $z=-1.963$, $p=.0248$). In joint evaluation rounds, there were no significant differences in attention between most-salient (0.32) and least-salient (.31) states (WSR, $N=64$, $z=1.197$, $p=.1156$).¹⁷

Our results regarding hypothesis (H4) go clearly against the predictions of Salience Theory. There is, however, an alternative explanation for the attention pattern that we actually observe. Overwhelming evidence from psychology and neuroscience (e.g., Dashiell 1937; Moyer and Landauer 1967) shows that stimuli that are closer (e.g., in terms of outcomes) are harder to differentiate and require more attention and longer response times (see also Alós-Ferrer et al., 2021a, for an application in economics). The transitions in our data are compatible with this effect. By definition, the least-salient states have the smallest differences across outcomes and should hence receive more attention, which is what we observe.¹⁸

Alternatively, one could speculate that some people process decisions in an option-wise manner, leading to different predictions which would depend on the layout. However, since we counterbalanced whether most/least salient states corresponded to horizontal or diagonal transitions, one should then predict no differences between most and least salient states. This is contrary to what we obtain.

Of course, one could also hypothesize that some participants followed certain heuristics which might predict specific transition patterns. For instance, the priority heuristic would expect an attention pattern first examining the minimum gain, then the probability of the minimum gain, and finally the maximum gain (Brandstätter et al., 2006). The minimax heuristic prescribes to choose the lottery with the highest minimum outcome while the maximax prescribes to choose the lottery with the highest outcome (see Fiedler and Glöckner 2012, for an overview of several attention heuristics). These heuristics yield distinct attention patterns one could analyze using fixations and transitions. For instance, Glöckner and Herbold (2011) found evidence contrary to the fixation pattern predicted by the priority heuristic (see also Ludwig et al., 2020, for a related eye-tracking experiment). Our work, however, targeted the predictions of Salience Theory. While we conclude that the attention patterns we find do not agree with those predicted by Salience Theory, exploring possible heuristics is beyond the scope of this work.

Fig. 9

Evaluation of the lottery pair from Bordalo et al. (2012). Left and center panels, evaluations in the two surveys in Bordalo et al. (2012). Right panel, evaluations of the same lotteries in our eye-tracking experiment. One-sided non-parametric tests were not significant (n.s.)

5 The lottery pair in Bordalo et al. (2012)

Our results, following our preregistered hypotheses and tests, deliver mixed evidence for the postulated implications of Salience Theory. We do find a connection between fixations and evaluations but overall we do not find the predicted reduction of reversal rates when lotteries are evaluated in the context of another one as suggested by Bordalo et al. (2012). That work included a survey where each participant chose between two lotteries and immediately afterwards priced one of them (price in choice context) and after filler questions priced the other lottery in isolation. That is, the manipulation is whether the evaluation took place right after seeing both lotteries or later. Reversals conditional on the manipulation were not actually observable within subjects, since each subject priced only one of the lotteries in the pair under each manipulation. The survey employed only one lottery pair, which was one of the 32 lottery pairs we used in our eye-tracking experiment: $L_{\$}=[.31,16;.69,0]$, $L_{P}=[.97,4;.03,0]$. A second survey using the same lottery pair followed a similar evaluation procedure but did not include an actual choice.

Figure 9 illustrates the evaluations of the lottery pair in different treatments and experiments. Bordalo et al. (2012) observed lower evaluations in the Joint Treatment than in the Separate Treatment. We, however, do not find such a difference in the evaluation for the exact same lotteries. Since the manipulations differ (actual presence of the other lottery in our case, in contrast with temporal distance in Bordalo et al. 2012), we cannot discard that the effect in Bordalo et al. (2012) might be due to a different mechanism than whether evaluation is driven by the salience of states as derived from the comparison with another lottery.

6 Discussion

In this work, we investigated the predictions of Salience Theory in an online experiment and an eye-tracking experiment where attention could be measured directly. We implemented two treatments which according to Salience Theory should result in differences in preference reversals.

The predictions and our results are summarized in Table 3. Contrary to the predictions of Salience Theory, whether the monetary valuation for a lottery was elicited in isolation or in the presence of an alternative one failed to have any effect on the preference reversal rates or on the monetary valuations themselves. However, an analysis of the effect of fixations revealed that attention on the alternative (not evaluated) lottery reduced the monetary valuation of the target lottery, but only if the latter was a long shot ($-bet), in agreement with the view that the overpricing of long shots which is associated with the preference reversal phenomenon should be reduced if evaluations do not happen in isolation. This particular result is hence a conceptual confirmation of the implications of Salience Theory. However, the effects were small, both in terms of the attention attracted by the alternative lottery and in terms of the monetary reduction in the valuation per fixation on the other lottery. This might explain why the documented effect fails to translate into a reduction in reversal rates.

Table 3 Summary of predictions according to Salience Theory and our results

A further result in line with Salience Theory is the fact that, in a regression analysis, the number of fixations on the alternative lottery when the target lottery was a $-bet significantly reduced the probability of a reversal. Following Salience Theory, however, the number of fixations on the alternative lottery when the target lottery was a P-bet should have a negative effect on overpricing for the latter lottery and increase the probability of a reversal. Although this effect did not reach significance in our data, taking both possible channels into account results in an overall null effect, suggesting another possible reason for the absence of an effect of attention (as measured by fixations) on preference reversal rates, namely that both postulated effects cancel out. This echoes the discussion in Bordalo et al. (2012), which argued that salience impacts monetary valuations of both types of lotteries when conducted in isolation but that the impact on $-bets should be proportionally larger, resulting in an effect on preference reversals. Our results suggest that the effects are modest and the relative difference in overpricing across different lottery types is too small to have an impact on reversal rates.

Overall, we do not find strong evidence for Salience Theory’s predictions in the context of the classical preference reversal phenomenon. Other authors have previously looked at Salience Theory in different contexts. Frydman and Mormann (2018) found behavioral evidence supporting Salience Theory in the context of the Allais’ Paradox. Specifically, by changing the correlation structure among lotteries in a pair, they change the salience of the corresponding states and find that the Allais’ Paradox is strengthened in the direction predicted by Salience Theory. Dertwinkel-Kalt and Köster (2020) investigated preferences for skewed risks for choices under risk and found effects compatible with Salience Theory. However, these results have been challenged by Ostermair (2021) and Loewenfeld and Zheng (2021), who argue that results supporting Salience Theory are largely driven by event-splitting effects. A similar point was previously made by Starmer and Sugden (1993) for the case of generalized regret theory, which has been shown to encompass Salience Theory (Herweg and Müller 2021).

Adding to this literature, we conclude that, although the evidence confirms effects of attention on monetary valuations as predicted by Salience Theory, those might be too weak to result in measurable behavioral effects, at least for the case of the classical preference reversal phenomenon.

Appendix lotteries

See Tables 4 and 5.

Table 4 Lottery pairs: Online (1–32) and Eye-tracking (1–16, 33–48) experiment

Table 5 Descriptive information about lottery pairs