Abstract
We study the emergence of bubbles in a laboratory experiment with large groups of individuals. The realized price is the aggregation of the forecasts of a group of individuals, with positive expectations feedback through speculative demand. When prices deviate from fundamental value, a random selection of participants receives news about overvaluation. Our findings are: (i) large asset bubbles are robust in large groups, (ii) information contagion through news affects behaviour and may break the coordination on a bubble, (iii) time varying heterogeneity provides an explanation of bubble formation and crashes, and (iv) bubbles are strongly amplified by coordination on trend-extrapolation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Expectations play an important role for intertemporal decisions in everyday economic life. Based on their expectations about the future, agents decide on what actions to take today. For example, traders and firms form price forecasts and based on these forecasts they buy or sell assets or decide on how many goods to produce. The subsequent actions that all individual agents then execute determine the realised market price and aggregate behaviour. To understand markets we have to understand how groups of individuals form and coordinate their expectations. Since Muth (1961) and Lucas (1972) the traditional approach has become the Rational Expectations (RE) hypothesis, which states that the expectations of all agents are the same and consistent with their model of the economy. While the RE hypothesis may be a natural benchmark, as a realistic description of real world behavior it faces challenges both theoretically and empirically. For example, many studies show that survey data on expectations are inconsistent with RE, see e.g. the recent survey of Coibion et al. (2018). Alternative models of expectations assume that agents are boundedly rational (Sargent 1993), are prone to behavioral biases (Barberis and Thaler 2003), form expectations through an adaptive learning process (Evans and Honkapohja 2001; Branch and Evans 2010) or use simple, but ‘smart’ heuristics (Anufriev et al. 2019).
Speculative asset markets are probably the best example where price movements are amplified by expectations (‘animal spirits’) leading to long-lasting bubbles followed by sudden market crashes. Recent examples of bubbles include the dot com stock market bubble in the late 1990s, the U.S. housing market bubble in the early 2000s and the recent bitcoin bubble in 2017 (and crash in 2018). It has been argued that non-rational, trend-extrapolating expectations, have amplified these movements in asset prices. For example, Case et al. (2012) study surveys of household expectations about changes in home values and show the prevalence of trend-extrapolation, while Barberis et al. (2018) argue that trend-extrapolation explains bubbles in the stock market, the housing market and commodity markets.
A complementary method to simultaneously study expectation formation of a group of individuals and the emergence of bubbles is a controlled laboratory experiment. Bubbles have been extensively studied in the lab, for example in the seminal work of Smith et al. (1988) and follow-up papers (see Noussair and Tucker 2013; Palan 2013; Powell and Shestakova 2016 or Nuzzo and Morone 2017 for a review). Almost all of these bubble experiments, however, use small groups of 6–10 subjects. The main goal of the current paper is to study whether bubble formation is robust to increasing the group size. Will a large group of individuals coordinate expectations on trend-extrapolating rules and cause an asset market bubble? To address this question, we conduct asset market experiments with large groups of up to 100 subjects, to our best knowledge the largest groups of paid human subjects in bubble experiments.Footnote 1
Our experimental design is based on the learning-to-forecast asset pricing experiment of Hommes et al. (2005, 2008).Footnote 2 Subjects need to forecast the future price of a risky asset for 50 periods. The average forecast of the group will determine the realised market price with a positive feedback between expectations and realisations: higher (lower) expected prices lead to higher (lower) market prices.Footnote 3 Subjects know this qualitative relationship, but they do not know the exact law of motion for the prices. The market price is determined as an equilibrium price using mean-variance optimisation of asset trade, which is computerised, and subjects do not need to carry out the trades themselves. Subjects are paid according to their forecasting performance. In Hommes et al. (2008) very large bubbles in 5 out of the 6 groups have been observed. In their setup the market price depended on the average forecast of a group of six individuals, so that the influence of one subject was relatively high. Bubbles may then arise because of one “irrational” individual. The natural question is whether bubbles would still arise in large markets, where each individual only has a small weight in determining the market price. In our experiment about 100 subjects form a large market. In order to have a valid comparison between different group sizes under the same circumstances we also run small markets. In total we have 6 large groups, ranging from 92 to 104 subjects and 13 small groups of 6. Such large groups do not fit in a single laboratory and we coupled the CREED lab at UvA and the LINEEX lab in Valencia. A large group thus consists of about 50 subjects in Amsterdam and 50 in Valencia and their overall average price forecast determines the realized market price.Footnote 4
It is important to note that a priori theory cannot decide whether large groups are more or less stable than small groups. One could argue that large markets are more stable, as each individual has a smaller effect on the market, and individual errors are more likely to cancel out (Muth 1961). Furthermore, in small groups, even a small probability of a mistake in forecasting can hugely affect the market price. Each individual has a much larger market power in small groups than in large groups, thus a single mistake can drive prices up or down very easily. This possibility is mitigated in large groups, where such a mistake has a much smaller effect on the realised market price. On the other hand, once a bubble arises in a large group, e.g. due to a few positive shocks and coordination of a majority on trend-following behaviour, it may be hard to break the coordination on a bubble in a large group. This suggests that large groups may be more unstable. Hence, theory does not provide a unique answer, and it becomes an empirical question, well suited for a laboratory test, whether large markets are more or less stable.
Beyond the large group size and the coupling of two different labs, we introduce another new experimental design feature in LtF experiments, namely the role of “news” elements and its effect on individual and aggregate behavior.Footnote 5 In the real world, when markets are (far) out of equilibrium, investors are likely to read in the news discussions about whether the market is in a bubble or not, which may influence their expectations about future prices. We introduce news announcements when prices are too high or too low compared to the fundamental value. These news elements are short messages that can appear on a subjects’ screen: “Experts say the stock market is overvalued (undervalued).” It is common knowledge that these messages do not have a direct effect on the price realisation, but might have an effect on subjects’ beliefs.Footnote 6 Because these messages are received only with a fixed probability we can compare the difference in expectations of participants in the same market who did or did not receive the message.Footnote 7 A key question then is whether information contagion arises, that is, whether news about fundamental price can break the coordination on a bubble in small or large groups. In order to prevent prices diverging forever, we also kept an (unknown) upper bound on the forecasts, but it is high enough to leave room for the news to have an effect before prices reach the upper bound.
Our main results are threefold. First, and most importantly, we do not find group size differences in bubble formation across small and large groups. We observe both stable and unstable markets for both group sizes. Two out of six large groups and two out of the 13 small groups exhibit very large bubbles of more than ten times fundamental price until they reach the exogenously set upper bound. Bubbles are therefore a robust phenomenon in large groups. Three other large groups and 5 other small groups are rather stable with small fluctuations around the fundamental price. Second, we find information contagion at the individual and the aggregate level. At the individual level subjects who receive news that the market is overvalued have a significantly lower increase in their relative forecasts compared to those who did not receive the news. At the aggregate level news that the market is overvalued has an effect on the price in some (six out of eight) of the small groups and in one (out of three) large groups. In these groups the news breaks the coordination on the bubble before reaching the upper bound and leads to a market crash. Third, analysis of the individual and aggregate data of the large groups provides a more detailed explanation of the bubbles and crashes. At the initial stage of the experiment expectations heterogeneity is high, but quickly subjects coordinate their expectations, often on a non-fundamental price. Due to small random shocks and coordination on a trend-extrapolating forecasting rule the asset price starts increasing slowly. Strong coordination of expectations amplifies the bubble. As the bubble forms, expectations heterogeneity gradually increases and eventually the market crashes. Heterogeneity then peaks and remains high suggesting a state of confusion after the market crash. This pattern clearly emerges for the large bubbles in the large groups. The same pattern seems to occur in small groups, but it is noisier.
In experimental economics it is not yet common to run large-scale experiments. Usual labs are simply not large enough for such an experiment, and also it is costly to pay the standard amount for such a large number of subjects. However, we are not the first to run incentivised large-scale experiments. For example, Isaac et al. (1994), and Weimann et al. (2019) investigated group size effect for public good games. Isaac et al. (1994) considered groups of 4, 10, 40 and 100 in multiple sessions for extra credits rather than cash. They found that large groups provide the public good more efficiently than small groups. Weimann et al. (2019) found similar results by comparing groups of 60 and 100. Gracia-Lázaro et al. (2012) looked at the prisoner’s dilemma game on large networks of about 600 people each. They do not find substantial differences between network types in terms of cooperation rate. Williams and Walker (1993) examined how traders behave in a single large-scale double auction asset market with more than 300 traders. In their experiment student subjects were incentivised by extra credits. Bossaerts and Plott (2004) investigated asset markets with about 40 subjects per market. Their main focus was not on group-size however. A related paper to our study is Bao et al. (2020), who investigated a similar setup in 7 groups, with size ranging from 21 to 32 subjects, without adding news to the economy. In their experiment 6 out of the 7 groups exhibit large bubbles, and these bubbles arise faster than in the small groups of Hommes et al. (2008). We add to their work by larger group size (a size that does not fit a single lab), thus obtaining a more accurate picture of individual and aggregate behavior in bubble formation, and by studying information contagion of news about fundamental price in both small and large groups.
The remainder of this paper is organised as follows. Section 2 describes the experimental economy and procedures. In Sect. 3 we present the experimental results. Section 4 concludes.
2 Experimental design
2.1 Experimental market
The lab environment is based on an asset pricing model with heterogeneous beliefs following Brock and Hommes (1998); for a textbook treatment see Campbell et al. (1997). Consider an asset market with heterogeneous beliefs where agents need to allocate their wealth between a risk-free bond (that pays gross return of \(R=1+r\)) and a risky asset that pays an uncertain dividend with an average dividend of \({\bar{y}}\). Based on this allocation decision, the wealth of agent i in period \(t+1\) is given by
where \(z_{i,t}\) is the position of the risky asset by agent i in period t (positive or negative) and \(p_t\) and \(p_{t+1}\) are the prices of the risky asset in periods t and \(t+1\) respectively. We assume that agents maximize a simple myopic mean-variance utility function, that is, they solve the following problem:
where \(E_{i,t}\) and \(V_{i,t}\) are the individual expectations about wealth and variance. Note that these might not be perfectly rational. Furthermore, a is a parameter for risk aversion, and \(\rho _{t+1}\) is the excess return defined as \(\rho _{t+1}\equiv p_{t+1}+y_{t+1}-Rp_t\). For simplicity we assume that the expected variance of excess return is constant and homogeneous across agents, i.e. \(V_{i,t}(\rho _{t+1})=\sigma ^2\). Given these assumptions the optimal demand of agent i is given by
where \(p^e_{i,t+1}=E_{i,t}(p_{t+1})\) is the individual forecast by agent i of the price in period \(t+1\) and \({\bar{y}}=E_t[y_t]\) is the forecast of the exogenous dividend process \(y_t\), assumed to be correct for all agents. The market price for the risky asset is set by market clearing, that is demand equals supply:
where \(Z^S_t\) is the exogenous supply. For simplicity, we assume that this exogenous supply is 0. Furthermore we assume a small fraction of noise traders. Their position is incorporated in the equilibrium pricing equation as a small IID noise term, \(\varepsilon _t\sim N(0,0.5)\). This results in an equilibrium pricing equation
or equivalently
where \({\overline{p}}^e_{t+1}\) is the average forecast for period \(t+1\) across all individuals.
Note that the realized price \(p_t\) in period t depends on the average prediction \({\bar{p}}_{t+1}^e\) for period \(t+1\) and agents use information up to period \(t-1\) when predicting the price of \(t+1\), so all forecasts are two periods ahead. Also note that the rational expectation equilibrium is that agents expect the price to be equal to the fundamental price, \(p^f={\bar{y}}/r\). In that case, the law of motion for the price becomes \(p_t=p^f+\varepsilon _t\), so that expectations are self-fulfilling. In the experiment, we use the following parameters: \({\bar{y}}=3.3\) and \(R=1.05\). This implies that the fundamental price is 66.
Notice also that the price equation (5) has rational bubble solutions, where the deviation from the fundamental price \(x_t=p_t-p^f\) grows at the risk-free rate r. In theory, these rational bubbles are often excluded by a transversality condition.
2.2 Implementation
In the experiment subjects are playing the role of a financial advisor of a pension fund. They are informed that they have to forecast the price of a risky asset, and that based on their forecast, the pension funds will have a certain demand of the asset. They are not explicitly told the law of motion (5), but they know that there is positive feedback in the market (i.e., the higher their forecast is, the higher the realized price will be ceteris paribus). The market lasts 50 periods.
Subjects are only paid according to their forecasting performance. Their payoff is determined by the following formula:Footnote 8
where \(p^e_{i,t+1}\) denotes the forecast of the price at period \(t+1\) formulated by subject i in period t without knowing \(p_t\), and \(p_{t+1}\) is the realised asset price at period \(t+1\). Subjects were informed about this payoff function, and they were also provided a payoff table showing earnings corresponding to given forecast errors. Subjects accumulated their payoffs during the experiment, which was converted to euros at the end. They received 0.5 euro for each 1300 points they earned.
During the experiment subjects could see past prices, their own actions and whether they received news in a given period, but not others’ decisions. As in previous experiments (see e.g. Hommes et al. 2008), we did not explicitly tell subjects the fundamental price, but they are informed about the average dividend, \({\bar{y}}\) and the risk free interest rate r, thus they would have been able to calculate the fundamental price as \(p^f={\bar{y}}/r\).
In order to control huge deviations from the fundamental price, we imposed an upper limit of 1000 on the forecasts. Subjects became only aware of this once they tried to submit a forecast higher than 1000.Footnote 9 They would receive an error message in that case and had to reenter a forecast \(\le\) 1000. As a new experimental design feature, we introduced news announcements which stated either “Experts say the stock market is overvalued” or “Experts say the stock market is undervalued”. When the price was more than 3 times the fundamental price, or when it was lower than \(\frac{1}{3}\) of the fundamental price, the news announcement appeared on screen with 25% probability for each subject (independently drawn). Subjects were told that “When there is news, on average only 1 out of 4 subjects will receive news.” This procedure was employed in all periods, so when the price was far from fundamental price for several periods in a row, it could be that a subject did not get the news in one of the first periods but only later (or never), and it could be that a subject did receive news in a period but not in the subsequent one although the price was even farther away from the fundamental price. This way the direct effect of the news on individual behaviour can be measured, as in each round when the news was depicted, there were some subjects receiving it, and others not.Footnote 10 For an example of the news, see Supplementary material online Appendix. Finally, in order to prevent huge variation in initial predictions, subjects were told that the price in the first period is very likely to be between 0 and 100.
2.3 Treatments and experimental procedure
Large groups around 100 do not fit into a single lab. Therefore, the experiment was conducted by connecting the experimental CREED-lab in Amsterdam and the LINEEX-lab in Valencia via internet. All participants knew this and they could choose between English and Spanish at the beginning of the session. The experiment was programmed in php. In the first 6 sessions all subjects formed one large market, whereas in the \(7^{\text {th}}\) session subjects were grouped in markets of 6. This results in total in 6 large markets and 13 small markets.Footnote 11 In total 676 (370 in Valencia and 306 in Amsterdam) subjects participated, mainly students with various backgrounds.
In order to keep the length of the experiment within a reasonable time span, a time limit on the decisions was imposed. Subjects had 2 min to make a decision in the first 10 periods, and 1 minute in later periods. If subjects did not submit a decision on time, they would not earn anything that period, and the average forecast was determined based only on the other forecasts.Footnote 12 Before the experiment, subjects had the opportunity to read the instructions at their own pace from the computer screen, which took on average 40 min until everyone completed. The experimental market took on average 1 hour per session. The English instructions are presented in Supplementary material online Appendix (the Spanish instructions are available upon request). Subjects earned on average 8.3 euros from the forecasting task (with a minimum of 0 and a maximum of 21.84 euros out of 25 euros) plus a show-up fee, plus additional earnings from an unrelated, surprise one-shot volunteer’s dilemma after the experimental asset market (Kopányi-Peuker 2019).Footnote 13
3 Experimental results
In this section we present the results of the experimental asset markets. Section 3.1 describes how the market price evolved in the different markets, and Sect. 3.2 investigates how individuals coordinated their price forecasts. In Sect. 3.3 the effect of news on individual behaviour and the market price are analyzed. Unless otherwise stated all statistical tests are carried out by a two-sided nonparametric test (Mann-Whitney ranksum test or Wilcoxon signrank test).
Before we discuss the experimental results, we make a few remarks about the implementation of the large-scale experiments. In each session two labs were connected, one in Amsterdam and one in Valencia. The experiment was bilingual (English and Spanish), which meant that the original English instructions and screens had to be translated. The translation was checked by another native Spanish speaker. This made the experiment costlier, compared with an experiment in only one language. The communication with the team in Valencia was by chat, and no technical problems were encountered. We have no indication that subjects didn’t believe the existence of the subjects in the other location (it may have helped that both labs have strict rules of no-deception and the subjects know this or could know this). The subject pools were also quite comparable in terms of gender (52% males in Amsterdam and 48% males in Valencia) and age (mean age was 22.1 in Amsterdam and 23.8 in Valencia). Markets were randomly formed from subjects from both locations.
3.1 Market behaviour
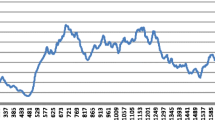
Figure 1 shows the market price for each market in the 13 small groups (left panel) and the 6 large groups (right panel).Footnote 14 The time evolution of the market price is very heterogeneous across groups for both the Small and the Large treatments. We distinguish three different qualitative market behaviours:
-
(i)
markets which are stable or exhibit small oscillations around the fundamental price;
-
(ii)
markets with moderately large bubbles, with a peak at about 3-4 times the fundamental price, so that some subjects receive news, but the bubble does not reach the exogenous upper bound; and
-
(iii)
markets with very large bubbles, with a peak of more than 10 times fundamental price, and a crash because some subjects reached the highest possible forecast of 1000.
Table 1 contains descriptive statistics about each market by presenting the median and mean market price, the standard deviation and the relative (absolute) deviation from the fundamental price. The markets are ranked according to their median price. For the small group size there are five stable markets (the first five groups in Table 1), six markets with moderately large bubbles (groups 6 to 13 in Table 1) and two markets with very large bubbles (groups 10 and 11). For the large group size there are three stable markets (groups 92, 103 and 100-1), one with a moderately large bubble (group 99) and two with very large bubbles (groups 100-2 and 104). Markets which have a relative low average/mean price also have a relative low standard deviation and are thus more stable. Other markets are heavily overpriced, and they also have rather high standard deviation due to the observed bubbles and crashes.
The overall average market price over the 50 periods per treatment is 139.38 for the Large groups and 153.41 for the Small groups (this difference is not statistically significant, \(p = 0.93\)).Footnote 15 Furthermore, in the Small treatment the average price is significantly higher than the fundamental price of 66 (\(p = 0.02\) according to the Wilcoxon signrank test), whereas the average price is not significantly higher than 66 for the Large groups (\(p = 0.17\); n = 6).Footnote 16 All markets’ standard deviations are significantly higher than the standard deviation predicted by the rational expectation model, that is, the \(SD=0.5\) of the noise term \(\varepsilon _t\) in (5), so all markets exhibit significant excess volatility.
Table 1 also reports the Relative Absolute Deviation (RAD) and the Relative Deviation (RD) from the fundamental price.Footnote 17 Most markets are overpriced, but there is no market in which the price never goes under the fundamental price. There is one market in which the price is constantly under the fundamental price: group 5 in the Small treatment (group 8 shows almost the same pattern). The most stable groups 92, 103 and 8 (in terms of SD) stay quite close to the fundamental price (with relatively low RAD and RD), but the stable group 100-1 oscillates around \(p^f\) (with relatively high RAD compared to RD). In markets with bubbles both RAD and RD are relatively high. To sum up, based on the qualitative market price behaviour and these summary statistics, no striking differences between the aggregate behaviour in small and large groups can be observed.Footnote 18
3.2 Coordination of expectations
Do subjects manage to coordinate their expectations in a market or does heterogeneity prevail? Figure 2 shows time series plots of the coefficient of variation of individual forecasts, that is, the standard deviation divided by the mean, for the small and the large markets. A low (high) value of the coefficient of variation corresponds to a high (low) degree of coordination of forecasts. Heterogeneity strongly fluctuates over time with many high peaks. In the small groups, the time variation seems somewhat noisier, with many sudden high peaks perhaps due to individual experimentation. In the large groups heterogeneity seems to vary more smoothly and gradually, although there are still some sudden high peaks. In any case, we do not observe stronger coordination towards the end of the experiment, but for most markets heterogeneity continues to fluctuate over time.
To study the time-varying heterogeneity in more detail, Figs. 3, 4 and 5 plot typical examples of the three different types of market behavior for both small and large markets. These figures show the market price together with the coefficient of variation of individual predictions. Figure 3 illustrates a typical example of a stable market; Fig. 4 of moderately large bubbles, and Fig. 5 of very large bubbles.Footnote 19 The blue solid lines correspond to the market price and are depicted on the left vertical axis; the red dashed lines correspond to the coefficient of variation of individual forecasts and are measured on the right vertical axis.
In the stable markets (Fig. 3) after an initial phase of high heterogeneity and some initial fluctuations, the heterogeneity drops almost to zero after about 15 periods. Subjects thus learn to coordinate their expectations within 15 periods and in both the small and large markets the price exhibits small fluctuations close to the fundamental value. Compared to the other markets, coordination of expectations is the strongest in the stable markets.
In the markets with moderately large bubbles (Fig. 4) heterogeneity is initially high, but quickly drops to lower levels. The market price is above fundamental value, however, and starts to increase further. In the small market (left panel in Fig. 4) the price starts following a strong upward trend and heterogeneity gradually increases. The market price increases and peaks around 400 in period 15, after which the market crashes and heterogeneity increases rapidly and sharply. The pattern in the large market is somewhat different (right panel in Fig. 4), where first a small bubble with a peak around 100 at period 10 occurs, followed by a decline to very low prices around period 20, followed by a larger bubble with a peak around 200 in period 30. After the first small bubble and crash, heterogeneity increases substantially and remains high during the second bubble and crash.
Figure 5 illustrates the time variation of heterogeneity in markets with very large bubbles. Initially heterogeneity is high, but quickly drops to low levels within 5 periods, after which heterogeneity gradually increases along the large bubbles. After the market crash heterogeneity peaks and remains high illustrating a state of confusion among subjects. This pattern of time variation of heterogeneity and coordination is particularly clear and smooth in the large market (right panel in Fig. 5), but it also occurs in the small market, although the pattern is noisier there due to more individual uncertainty in small groups. We conclude from this pattern that strong coordination of expectations amplifies the large bubbles and that after a market crash heterogeneity (confusion) remains high. In Supplementary material online Appendix we fit the behavioural heuristics switching model (HSM) of Anufriev and Hommes (2012) to the experimental data and show that coordination on a trend-following heuristic amplifies bubbles in small and in large markets.
To further quantify the coordination between subjects, we have calculated the average quadratic individual error (IE), the dispersion error (DE) and the common error (CE) for each market. IE is calculated by taking all individual quadratic forecast errors for each period in which a forecast was submitted, and then taking the average of all these forecasts over individuals and periods for each market (\(\text {IE}=\frac{1}{K}\sum _{t,i}(p^e_{i,t}-p_t)^2\), where K is the number of individual forecasts in a group in all 50 periods). This error measures how well subjects predict the market price. The dispersion error is calculated by taking the average of the quadratic difference of the individual forecasts and the average forecast of the given period over all individuals and periods for each market (\(\text {DE}=\frac{1}{K}\sum _{t,i}(p^e_{i,t}-{\bar{p}}^e_t)^2\), where K is the same as before). DE measures how well subjects coordinate with each other. Finally, the common error (CE) is calculated by taking the average quadratic error of the mean forecast compared to the realized price (\(\text {CE}=\frac{1}{50}\sum _t({\bar{p}}^e_t-p_t)^2\)). The common error measures the quality of the average expectations. Table 1 presents IE, DE and CE for each market. By definition \(IE=DE+CE\). Because of this it is easy to see that DE and CE cannot easily be interpreted in absolute terms, but only relative to IE. This is because in a more stable market IE tends to be much smaller than in less stable markets. There is a huge variation across markets whether the common or the dispersion errors are relatively large within the individual errors. However, a relatively small common error is more common in the more stable groups. The correlation between the standard deviation of the marketprice and the percentage of CE compared to IE is 0.71 (\(p=0.00\) according to the Spearman rank correlation test). This means that in these more stable markets individual errors tend to cancel out (although of course not perfectly). This happens both in small and large groups. The percentage of CE compared to IE is not significantly different in small and large groups (\(p=0.66\) according to the ranksum test). This finding is in line with Muth (1961), who stated that even though individuals make prediction errors, on average they make rational decisions when individual errors are likely to cancel out. In markets with large bubbles CE is much larger than DE. Thus, in these markets aggregate expectations are not rational in the sense of Muth (1961).
3.3 News announcements
Does news about the over- or undervaluation affect individual expectations and aggregate behaviour? In particular, can news break the coordination on a bubble? News appeared with probability 25% when the last price was sufficiently far away from the fundamental price, either below 1/3 or above 3 times fundamental value. For practical reasons, our analysis focuses only on overvaluation.Footnote 20
News of overvaluation was observed in 8 small groups (from Group 6 onwards in Table 1) and in 3 large groups (from Group 99 onwards in Table 1). Table 2 shows the average relative increase in individual predictions after the first news element is seen in a group, for each bubble separately for those who have seen the news, and those who have not seen the news.Footnote 21 The data is pooled for small and large markets. In all bubbles the participants who received the news increase their prediction less than those who did not receive the news. We first test the statistical significance in a quite conservative way in which the level of observation is the individual group, and the data is the average relative change in prediction of the participants who did or did not receive the news. This means that we have only few data-points and thus a low statistical power. Nevertheless, a Wilcoxon test shows (two-sided) p-values of \(p<0.01\) for bubble 1 and \(p=0.05\) for bubble 2 and 3. Note that in this analysis small and large groups are pooled. To study a treatment effect and possible interaction effects we run regressions, as shown in Table 3. We find significant effect for the news, and no effects for the treatment small/large. These results are the same for all three bubbles combined, or the first two separate bubbles. For bubble 3, with relatively few observations, the effect of the news is not statistically significant.
Another striking feature of Tables 2 and 3 is that the average increase in predictions substantially grows from the first to the second bubble. It looks as if the first bubble is generally slower than later bubbles when subjects already gained experience with bubbles, crashes, and the news element. However, these differences are not statistically significant at conventional levels.
News of overvaluation thus has a significant effect on individual expectations: it leads to significantly lower increase in forecasts along the first bubble. Does this effect of news on individual behaviour translate into an aggregate effect and stabilize the bubble? We compare our markets with earlier LtF markets that did not have a news- element in their design. We focus only on groups that have received news in our experiment (8 small and 3 large groups) and the markets in three earlier LtF experiments in which participants would have received news in our setup. All these markets have bubbles, and we define a bubble to be extreme if the market price almost hits the upper bound. In the present experiment 4/11 bubbles are extreme (2 small and 2 large market). In Hommes et al. (2008) 5/6 bubbles are extreme; in Bao et al. (2020) 6/7 bubbles are extreme; and in Kopányi-Peuker and Weber (2019) 5/8 bubbles are extreme. Combining these no-news markets we get a 16/21 proportion of extreme markets, which is statistically significant more than the 4/11 proportion in the present experiment (one-sided proportion test \(p=0.014\)). This is not the most elegant way to compare the effect of news on market stability (future research could direct compare markets with and without news), but this data suggests strongly that news did have an effect, not only at an individual level but also at the aggregate level of markets.
4 Conclusion
A common objection to financial market and macroeconomic experiments is that laboratory markets are (too) small and therefore individual decisions may have a stronger influence on aggregate outcomes than in real markets. In this paper we study expectation formation and coordination on asset bubbles in large (about 100 participants) and small (6 participants) experimental markets. We add further realism to the markets by allowing for information contagion, that is, providing news from experts about market fundamental price. When the price moves far away from its fundamental value, we randomly choose some of the market participants to receive news about the market being either over- or undervalued. An important question then is whether in small and large groups these news incidents will spread and be successful in breaking the coordination on a bubble and drive prices back to the fundamental price.
Our experiment reveals that coordination on bubbles is not sensitive to group size. In fact, our experiment reveals no substantial difference between small and large groups in the asset pricing experimental framework. For both small and large groups three different types of aggregate behaviour emerge: relatively stable markets, markets with moderately large bubbles and markets with very large bubbles. Bubbles are robust in large groups. The news did not stabilize prices in all markets, as some bubbles only crashed after reaching an artificial upper bound imposed on prices. However, subjects reacted significantly to news: those exposed to the news of overvaluation predict lower prices compared to those who have not seen the news. These individual effects may lead to information contagion. For some, but not all, markets, both for small and large groups, news seem to break the coordination on bubbles and trigger market crashes. Compared to earlier LtF experiments contagion of news about overvaluation has a significant stabilizing effect on markets.
We study the degree in which the subjects within a market tend to agree on their predictions (coordinate) as opposed to disagree (and have heterogeneous beliefs). In the first periods, expectations are typically heterogeneous, but subjects quickly coordinate expectations. This may lead to above fundamental prices and subjects coordinating expectations on an initially weak, but increasingly stronger trend. As the bubble continues to grow, heterogeneity in expectations gradually increases and the bubble eventually crashes, either due to the contagion of the news or by reaching an exogenous upper bound. After a market crash heterogeneity peaks to very high levels and continues to stay high representing a state of confusion. This pattern of bubble formation and market crash is similar in large and small markets, but appears somewhat noisier in small markets and smoother in large markets due to averaging over many individuals.
To sum up, in learning-to-forecast asset pricing experiments the results for small groups, such as coordination on bubbles, carry over to large groups. This lends support to the many learning-to-forecast experiments with small groups in the literature. However, this robustness result cannot be extrapolated to all macroeconomic or financial market experiments. In other environments aggregate behaviour in large groups may or may not differ from small group behaviour. Designing large group experiments in macro and finance is an important area of research to test the robustness of small group behaviour and/or the emergence of new phenomena arising in large macro-financial systems.
Notes
Duffy (2016) gives an overview of the progress in the related field of experimental macroeconomics. A common critique to these macroeconomic experiments is the limited group size. In the real macro economy many agents are interacting with each other and, therefore the findings in small group experiments might not be directly applicable outside the lab. Our study contributes to the important issue of how group size may affect individual and aggregate behavior. Williams and Walker (1993) examined how traders behave in a single large-scale double auction asset market with more than 300 traders, with student subjects incentivised by extra credits.
Learning-to-Forecast Experiments (LtFE) were pioneered by Marimon and Sunder (1993); Marimon et al. (1993); Marimon and Sunder (1994). In a LtFE, subjects’ only task is to form expectations about the future (e.g. to predict prices, output gap, inflation), and all actions based on the expectations are computerised based on optimal decision making. In this way clean data on expectations are obtained, as subjects are only rewarded based on their forecasting performance. A large literature on LtFEs in different economic environments has developed, see Hommes (2011) for an overview.
Earlier work has shown that it is much more difficult to coordinate on the unique rational expectations equilibrium under positive than under negative feedback, especially if the system exhibits a near unit root process. For experimental evidence see Heemeijer et al. (2009), Sonnemans and Tuinstra (2010) and Hanaki et al. (2019).
LtFEs are related to repeated number guessing games or beauty contest games, introduced by Nagel (1995). In number guessing games subjects predict a number between 0 and 100 and the winner is she whose guess is closest to 2/3 of the average. The Nash equilibrium of this guessing game is 0, but in the laboratory experiment first- and second order rationality (where the subject guesses \(2/3\cdot 50\) respectively \((2/3)^2\cdot 50\)) are most common. These games differ in several aspects from LtFE: (i) In number guessing games the Nash Equilibrium is at the border (so undershooting is not possible), while in LtFE the equilibrium price is strictly positive; (ii) number guessing games are competitive and only the subject whose guess is closest to the target (the winner) earns a positive payoff, while in LtFE payoff is determined by the individual size of the error in the prediction, (iii) the feedback parameter in number guessing games (e.g. 2/3) is typically much farther away from 1 than in LtFE (in this experiment 0.95). See Sonnemans and Tuinstra (2010) for an overview and an experimental comparison of these two games. See Mauersberger and Nagel (2018) for an extensive overview of experimental coordination games and their relevance for macro and finance.
Corgnet et al. (2010) also study news in a market setting, but their study differs in two important aspect from ours. First, Corgnet et al. study double auctions in a Smith et al. (1988) setup (assets with a fixed duration and probabilistic dividends) while our setup is a LtF experiment. Second, in Corgnet et al. the periods in which news was provided was determined beforehand, and did thus not depend on the current market prices. In contrast, in our design news could be provided in any period, and depended only on the current price.
In an individual experiment, Andreassen (1987) showed that subjects’ trading behaviour is affected by reading news about the market. Furthermore, news can also cause excitement or other emotions which has been shown to affect trading behavior in experimental asset markets (Andrade et al. 2015; Breaban and Noussair 2017). Even though we do not directly manipulate emotions, we cannot disentangle the effect of emotions and beliefs about others in our experiment, as it is not designed for it.
In a different context (monetary policy in a macroeconomic liquidity trap experiment) Hommes et al. (2019) provide all participants with (bad) news in specific pre-determined periods. In our setup news announcements arise endogenously depending only on the price and only for a randomly chosen subset of participants.
The payoff function is the same as in Hommes et al. (2005, 2008) with groups of six. Bao et al. (2017) compare Learning-to-Forecast versus Learning-to-Optimize treatments where the payoff is based on realized utility. Large bubbles also arise in the Learning-to-Optimize experiments with groups of six subjects.
Note that this limit is more than 15 times the fundamental price, which allows large bubbles to form.
It would have been possible to run separate markets with and without news, but that would have made it hard to measure the precise effect of a news announcement, because expectations in a market are very much path-dependent. In our setup, the participants in a specific market have faced exactly the same history, which makes it possible to compare directly the reaction of the participants who did and did not receive the message. So, the comparison is within-markets, but between-subjects, and thus controlling for all market specific peculiarities. Future research may compare markets with and without news, to see whether the fact that participants know that they may receive news, already influences the stability of the market.
In the session for the small markets, we had 78 subjects. Additionally we have run 2 pilot sessions in Amsterdam. As here we did not connect the two labs, the procedures of the experimental sessions and pilot sessions differ. Therefore we do not consider these pilot data in the analysis.
Fortunately, this time constraint is rarely executed: only 0.7% of the decisions were not made within the time limit. There is no clear pattern over the rounds. The percentage is slighter higher in the rounds within a bubble, about 1.35%. This number is the same for participants who did or did not receive news in that round (1.28% vs. 1.37%, respectively).
The total expenses (including payment for the volunteer’s dilemma, and laboratory expenses) were about 18K euros.
For one of the large groups, Group 104, the market price was incorrectly saved, leading to small errors in round 30, for 22 of the 104 subjects, who saw a price of 202.1 instead of the realized market price of 204.1. Note that this difference is small in absolute terms (about 1%) as well as compared to the distance from the fundamental price 66. For the data analysis we used the market price of 204.1 in that round for all subjects.
All statistical tests are at the group level (\(n = 13\) for the small groups and \(n = 6\) for the large groups), using nonparametric tests.
For both treatments the median prices are significantly higher than the fundamental price (\(p=0.046\) for the Large, and \(p=0.03\) for the Small markets).
These measures are calculated following Stöckl et al. (2010): \(\text {RAD}=\frac{1}{50}\sum ^{50}_{t=1}{|p_t-p^f| /p^f}\), and \(\text {RD}=\frac{1}{50}\sum ^{50}_{t=1}{(p_t-p^f) /p^f}\).
Comparing small and large markets in Fig. 1 suggests that along the very large bubbles the price increases with a higher growth rate in the large markets. Following Hüsler et al. (2013) we estimate the growth rate of the bubbles, but do not find clear evidence for treatment differences. If anything, the growth rate seems to be faster in the large groups than in the small groups when looking at anchoring on the price. Note however, that we only have 2 small and 2 large markets with very large bubbles, thus our results can only give suggestive evidence on this issue. This analysis is relegated to Supplementary material online Appendix.
The markets have been chosen to illustrate the typical behavioural patterns. Plots for other markets and plots showing individual predictions as well as market prices per market are relegated to Supplementary material online Appendix.
News of undervaluation was observed 9/20 times only in total (in large and small groups, resp.), whereas news of overvaluation was observed 48/136 times (in large and small groups, resp.).
Only the first period in which news was displayed for at least one member of the group, is included in the analysis, because differences in later periods might be influenced by potential views of the news in earlier periods. There was only one market with 5 repeated bubbles, these last two bubbles are excluded from the analysis because of insufficient observations.
References
Andrade, E. B., Odean, T., & Lin, S. (2015). Bubbling with excitement: An experiment. Review of Finance, 20(2), 447–466.
Andreassen, P. B. (1987). On the social psychology of the stock market: Aggregate attributional effects and the regressiveness of prediction. Journal of Personality and Social Psychology, 53(3), 490.
Anufriev, M., & Hommes, C. (2012). Evolutionary selection of individual expectations and aggregate outcomes in asset pricing experiments. American Economic Journal: Microeconomics, 4(4), 35–64.
Anufriev, M., Hommes, C. H., & Makarewicz, T. (2019). Simple forecasting heuristics that make us smart: Evidence from different market experiments. Journal of the European Economic Association, 17(5), 1538–1584.
Arifovic, J., & Duffy, J. (2018). Heterogeneous agent modeling: Experimental evidence. In C. Hommes & B. LeBaron (Eds.), Handbook of computational economics, volume 4: Heterogeneous agent modelling (pp. 491–540). Amsterdam: Elsevier.
Bao, T., Hennequin, M., Hommes, C., & Massaro, D. (2020). Coordination on bubbles in large-group asset pricing experiments. Journal of Economic Dynamics and Control, 110, 103702.
Bao, T., Hommes, C., & Makarewicz, T. (2017). Bubble formation and (in) efficient markets in learning-to-forecast and optimise experiments. The Economic Journal, 127(605), F581–F609.
Barberis, N., Greenwood, R., Jin, L., & Shleifer, A. (2018). Extrapolation and bubbles. Journal of Financial Economics, 129, 203–227.
Barberis, N., & Thaler, R. (2003). A survey of behavioral finance. Handbook of the Economics of Finance, 1, 1053–1128.
Bossaerts, P., & Plott, C. (2004). Basic principles of asset pricing theory: Evidence from large-scale experimental financial markets. Review of Finance, 8(2), 135–169.
Boswijk, H. P., Hommes, C. H., & Manzan, S. (2007). Behavioral heterogeneity in stock prices. Journal of Economic Dynamics and Control, 31(6), 1938–1970.
Branch, W. A., & Evans, G. W. (2010). Asset return dynamics and learning. The Review of Financial Studies, 23(4), 1651–1680.
Breaban, A., & Noussair, C. N. (2017). Emotional state and market behavior. Review of Finance, 22(1), 279–309.
Brock, W. A., & Hommes, C. H. (1997). A rational route to randomness. Econometrica, 65(5), 1059–1095.
Brock, W. A., & Hommes, C. H. (1998). Heterogeneous beliefs and routes to chaos in a simple asset pricing model. Journal of Economic Dynamics and Control, 22(8), 1235–1274.
Campbell, J. Y., Lo, A. W., MacKinlay, A. C., et al. (1997). The econometrics of financial markets (Vol. 2). Princeton, NJ: Princeton University Press.
Case, K. E., Shiller, R. J., & Thompson, A. K. (2012). What have they been thinking? Homebuyer behavior in hot and cold markets. Brookings Papers on Economic Activity, 2012(Fall), 265–298.
Coibion, O., Gorodnichenko, Y., & Kamdar, R. (2018). The formation of expectations, inflation, and the phillips curve. Journal of Economic Literature, 56, 1447–1491.
Corgnet, B., Kujal, P., & Porter, D. (2010). The effect of reliability, content and timing of public announcements on asset trading behavior. Journal of Economic Behavior & Organization, 76(2), 254–266.
Cornea-Madeira, A., Hommes, C., & Massaro, D. (2017). Behavioral heterogeneity in us inflation dynamics. Journal of Business & Economic Statistics, 1–13.
Duffy, J. (2016). Macroeconomics: A survey of laboratory research. Handbook of Experimental Economics (Vol. 2, pp. 1–90). Princeton: Princeton University Press.
Evans, G. W., & Honkapohja, S. (2001). Learning and expectations in macroeconomics. Princeton: Princeton University Press.
Gracia-Lázaro, C., Ferrer, A., Ruiz, G., Tarancón, A., Cuesta, J. A., Sánchez, A., et al. (2012). Heterogeneous networks do not promote cooperation when humans play a prisoner’s dilemma. Proceedings of the National Academy of Sciences, 109(32), 12922–12926.
Hanaki, N., Koriyama, Y., Sutan, A., & Willinger, M. (2019). The strategic environment effect in beauty contest games. Games and Economic Behavior, 113, 587–610.
Heemeijer, P., Hommes, C., Sonnemans, J., & Tuinstra, J. (2009). Price stability and volatility in markets with positive and negative expectations feedback: An experimental investigation. Journal of Economic Dynamics and Control, 33(5), 1052–1072.
Hommes, C. (2011). The heterogeneous expectations hypothesis: Some evidence from the lab. Journal of Economic Dynamics and Control, 35(1), 1–24.
Hommes, C., Massaro, D., & Salle, I. (2019). Monetary and fiscal policy design at the zero lower bound: Evidence from the lab. Economic Inquiry, 57(2), 1120–1140.
Hommes, C., Sonnemans, J., Tuinstra, J., & Van de Velden, H. (2005). Coordination of expectations in asset pricing experiments. Review of Financial Studies, 18(3), 955–980.
Hommes, C., Sonnemans, J., Tuinstra, J., & van de Velden, H. (2008). Expectations and bubbles in asset pricing experiments. Journal of Economic Behavior & Organization, 67, 116–133.
Hüsler, A., Sornette, D., & Hommes, C. H. (2013). Super-exponential bubbles in lab experiments: evidence for anchoring over-optimistic expectations on price. Journal of Economic Behavior & Organization, 92, 304–316.
Isaac, R. M., Walker, J. M., & Williams, A. W. (1994). Group size and the voluntary provision of public goods: Experimental evidence utilizing large groups. Journal of Public Economics, 54(1), 1–36.
Kopányi-Peuker, A. (2019). Yes, I’ll do it: A large-scale experiment on the volunteer’s dilemma. Journal of Behavioral and Experimental Economics, 80, 211–218.
Kopányi-Peuker, A., & Weber, M. (2019). Experience does not eliminate bubbles: Experimental evidence. University of St. Gallen, School of Finance Research Paper, (2018/22).
Lucas, R. E. (1972). Econometric testing of the natural rate hypothesis. In Eckstein, O., (Ed.), The econometrics of price determination [Conference)] (pp. 50–59). Washington DC: Board of Governors of the Federal Reserve System and Social Science Research Council.
Marimon, R., Spear, S. E., & Sunder, S. (1993). Expectationally driven market volatility: An experimental study. Journal of Economic Theory, 61(1), 74–103.
Marimon, R., & Sunder, S. (1993). Indeterminacy of equilibria in a hyperinflationary world: Experimental evidence. Econometrica, 61, 1073–1107.
Marimon, R., & Sunder, S. (1994). Expectations and learning under alternative monetary regimes: An experimental approach. Economic Theory, 4(1), 131–162.
Mauersberger, F., & Nagel, R. (2018). Heterogeneity in (micro) experiments or experimental games. In C. Hommes & B. LeBaron (Eds.), Handbook of Computational Economics, Volume 4: Heterogeneous agents models (pp. 541–634). Amsterdam: Elsevier.
Muth, J. F. (1961). Rational expectations and the theory of price movements. Econometrica, 29(3), 315–335.
Nagel, R. (1995). Unraveling in guessing games: An experimental study. American Economic Review, 85(5), 1313–1326.
Noussair, C. N., & Tucker, S. (2013). Experimental research on asset pricing. Journal of Economic Surveys, 27(3), 554–569.
Nuzzo, S., & Morone, A. (2017). Asset markets in the lab: A literature review. Journal of Behavioral and Experimental Finance, 13, 42–50.
Palan, S. (2013). A review of bubbles and crashes in experimental asset markets. Journal of Economic Surveys, 27(3), 570–588.
Powell, O., & Shestakova, N. (2016). Experimental asset markets: A survey of recent developments. Journal of Behavioral and Experimental Finance, 12, 14–22.
Sargent, T. J. (1993). Bounded rationality in macroeconomics. Oxford: Oxford University Press.
Smith, V. L., Suchanek, G. L., & Williams, A. W. (1988). Bubbles, crashes, and endogenous expectations in experimental spot asset markets. Econometrica, 56(5), 1119–1151.
Sonnemans, J., & Tuinstra, J. (2010). Positive expectations feedback experiments and number guessing games as models of financial markets. Journal of Economic Psychology, 31(6), 964–984.
Stöckl, T., Huber, J., & Kirchler, M. (2010). Bubble measures in experimental asset markets. Experimental Economics, 13(3), 284–298.
Weimann, J., Brosig-Koch, J., Heinrich, T., Hennig-Schmidt, H., & Keser, C. (2019). Public good provision by large groups-the logic of collective action revisited. European Economic Review (in press).
Williams, A. W., & Walker, J. M. (1993). Computerized laboratory exercises for microeconomics education: Three applications motivated by experimental economics. The Journal of Economic Education, 24(4), 291–315.
Acknowledgements
The authors are grateful for the support of the experimental team at the University of Valencia. We are also grateful for the discussions with members of the H2020- IBSEN project, seminar participants at the University of Zurich and conference participants at ABEE 2016, EF 2016, CEF 2016, CCS 2016, ESA 2016, EEA-ESEM 2018, BEAM-ABEE 2018. Financial support of the H2020 grant of the IBSEN project (“Bridging the gap: from Individual Behavior to the Socio-Technical Man”) is gratefully acknowledged (Grant Number: 662725). The views expressed in the paper are those of the authors and do not necessarily reflect those of the Bank of Canada.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
\Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hommes, C., Kopányi-Peuker, A. & Sonnemans, J. Bubbles, crashes and information contagion in large-group asset market experiments. Exp Econ 24, 414–433 (2021). https://doi.org/10.1007/s10683-020-09664-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10683-020-09664-w