Nash versus coarse correlation

Abstract

We run a laboratory experiment to test the concept of coarse correlated equilibrium (Moulin and Vial in Int J Game Theory 7:201–221, 1978), with a two-person game with unique pure Nash equilibrium which is also the solution of iterative elimination of strictly dominated strategies. The subjects are asked to commit to a device that randomly picks one of three symmetric outcomes (including the Nash point) with higher ex-ante expected payoff than the Nash equilibrium payoff. We find that the subjects do not accept this lottery (which is a coarse correlated equilibrium); instead, they choose to play the game and coordinate on the Nash equilibrium. However, given an individual choice between a lottery with equal probabilities of the same outcomes and the sure payoff as in the Nash point, the lottery is chosen by the subjects. This result is robust against a few variations. We explain our result as selecting risk-dominance over payoff dominance in equilibrium.

Introduction

The problem of multiple equilibria and coordination in games, even in a 2 $\times$ 2 game, has been one of the major themes of research in experimental economics (Cooper et al. 1989, 1990, 1992; Van Huyck et al. 1990, 1991, 1992; Straub 1995). Experimental research suggests that players are able to coordinate if they are helped to do so (see Devetag and Ortmann 2007 for a survey) or by using features such as, risk-dominance (Cabrales et al. 2000), pre-play non-binding communication (Crawford 1998; Costa-Gomes 2002; Camerer 2003; Burton et al. 2005; Cabrales et al. 2018). On the other side, there may be a different problem in a game where there is no issue of coordination at all as the game may have a clear unique pure Nash equilibrium; however, this equilibrium may be improved upon by using a lottery involving several other outcomes if the players agree to commit to such a plan.

Committing to a lottery in a game has been captured in the notion of coarse correlation. In a coarse correlated equilibrium (Moulin and Vial 1978), a mediator first asks the players to either commit to a device (and thereby get the outcome that the device would select using a given probability distribution) or to reject the device (and subsequently play any strategy of their own in the game, without learning anything about the outcome from the device).

The equilibrium concept, coarse correlated equilibrium, has many merits; it is computationally tractable, and hence it is also useful in bounding the set of Nash equilibria, for instance in congestion games (see Roughgarden 2016). Coarse correlation may improve upon the Nash equilibrium payoff for oligopolies (Gerard-Varet and Moulin 1978) and other potential games that correlated equilibrium cannot (see Ray and Sen Gupta 2013; Moulin et al. 2014 and Dokka et al. 2019 for details). The notion of coarse correlation has a natural interpretation in many economic situations, such as the abatement game (Barrett 1994) in environmental economics (see Forgó et al. 2005 and Forgó 2011 who used notions of correlation in other environmental games as well). This equilibrium concept has received a lot of attention recently in algorithmic game theory literature (for example, Feldman et al. 2016 who studied the correlated and coarse correlated equilibria in a full information first-price auction of a single item). Reischmann and Oechssler (2018) suggested a new simple mechanism called the Binary Conditional Contribution Mechanism (BCCM) that implements a coarse correlated outcome of a repeated public good provision and found strong support for such a mechanism in their experiments. Awaya and Krishna (2019, 2020) studied the role of in-play communication in repeated games and linked the Nash equilibrium to the coarse correlated equilibrium payoffs of the single-shot game due to the computational ease of the latter. This kind of structure is common to many economic situations of interest, such as, expending effort (Fleckinger 2012; Deb et al. 2016), contributing towards public good (Moulin et al. 2014), gathering information (Gromb and Martimort 2007).

There is a literature on experiments with correlated devices that recommend strategies to the players according to a probability distribution (see Moreno and Wooders 1998; Cason and Sharma 2007; Duffy and Feltovich 2010; Bone et al. 2013; Duffy et al. 2017; Anbarci et al. 2018), to test the validity of the concept of correlated equilibrium (Aumann 1974, 1987); however, to the best of our knowledge, there has been no attempt to understand the notion of coarse correlation in an experimental set-up. The purpose of this paper is to understand, using a laboratory experiment, whether individuals are willing to commit to a device that improves upon the pure Nash outcome in a game or not.

We use a two-person game (introduced by Moulin and Vial 1978) with unique pure Nash equilibrium which is also the solution of the iterative elimination of strictly dominated strategies (and therefore, the unique correlated equilibrium). We then take a lottery with equal probabilities of three symmetric outcomes (including the Nash equilibrium), which is a coarse correlated equilibrium with ex-ante expected payoff higher than the unique Nash equilibrium payoff. The question we ask is simple: which prevails—playing the unique Nash or accepting the coarse correlation device? We also contrast the choice of committing to the device for the game with an individual problem of choosing between a lottery with equal probabilities of these three payoffs and the sure payoff as in the Nash equilibrium of the game.

Our main result is that at the individual choice level, the lottery is chosen; however, in a game, we find that the subjects do not accept this lottery (the coarse correlation device). Instead, they play the game and choose the Nash equilibrium. We also find that the proportion of the Nash equilibrium outcome is the highest in the treatment without any correlation. Thus, the answer to our question is: Nash prevails!

We addressed three different types of robustness checks for our main result. First of all, admittedly, one may find a lack of comparability between an individual lottery and the coarse correlation device. The results in these two are different from each other perhaps due to “other regarding” preferences. We have thus checked our result using a lottery for a pair which is considerably closer to the coarse correlated equilibrium in the game and found very similar result. Second, one may ask whether committing to the device (to get higher expected payoffs) increases if the players’ relationship were repeated, as each player is then likely to get the higher payoff sometimes (as in Kaplan and Ruffle 2012). We however find no such indication from fixed-match pairs. Finally, we checked the robustness by varying payoffs using three other similar games, however we found results analogous to the main result.

How do we interpret our main result? One possible implication of our work is that our subjects are averse to random devices (as in Keren and Teigen 2010) and favour ex-post equality in outcomes (as in Cappelen et al. 2013). Our result is in line with Andreoni et al. (2002) who found that the equilibrium prediction may fail when the equilibrium outcome consists of unequal payoffs. In our set-up, the device used is procedurally fair, however the outcomes generated by the device are not fair (similar in nature to different strands of work such as Bolton et al. 2005; Krawczyk 2011; Trautmann and Vieider 2012; Trautmann and van de Kuilen 2016). The socially preferred outcome here is indeed the Nash equilibrium outcome.

We may explain the observed phenomenon of not committing to the device as an equilibrium behaviour. Accepting the device is a Nash equilibrium of the extended game, extended by the (coarse correlation) device; however, this equilibrium may not be unique and there may be other (Nash) equilibria of the extended game. Indeed, rejecting the correlation device and playing the unique Nash equilibrium of the game is a risk-dominant equilibrium in a modified version of the extended game. It is well-known in the literature that in such games (Aumann 1990) risk-dominant outcomes are observed (Cabrales et al. 2000; Charness 2000). Cason and Sharma (2007) also provide evidence consistent with our result; in their experiment on correlated equilibrium, if an agent does not follow recommendations from a correlated equilibrium, it is because she believes that her opponent will not follow the recommendation.

Related literature

As it is well-known now, a correlated equilibrium (Aumann 1974, 1987) can be interpreted as a mediator who selects and sends to each player a private recommendation to play a strategy in a game that each player finds optimal to follow. A fairly well-established experimental literature analyses the use of correlation devices in normal form games to understand this issue of following a mediator and thereby coordinating in a game. The main message of this literature (see Moreno and Wooders 1998; Cason and Sharma 2007; Duffy and Feltovich 2010; Bone et al. 2013; Duffy et al. 2017; Anbarci et al. 2018) is that the subjects do follow recommendations from a correlation device when the device is indeed a correlated equilibrium. Duffy and Feltovich (2010) also showed that the subjects learn to ignore the recommendations which are not based on a correlated equilibrium.

Our current work lies within the above research agenda. In this paper as well, we found very similar results using a treatment on correlated equilibrium for the specific game and device we used. However, our specific correlation device can also be used to test the issue of commitment to a device and thereby to analyse the notion of coarse correlated equilibrium (Moulin and Vial 1978). This paper provides a new result and insight: our subjects do not commit to a (coarse) correlation device that picks, with equal probability, the pure Nash outcome and other symmetric outcomes around Nash point of the game; however, they do accept a lottery, mimicking the device, as an individual choice.

To the best of our knowledge, our paper is the first such attempt to analyse commitment to a (coarse) correlation device. There are of course related papers in the literature. Any convex combination over pure Nash equilibrium outcomes (thus a public lottery) can also be viewed as a correlated equilibrium. Indeed, Cason and Sharma (2007), Duffy and Feltovich (2010) and Bone et al. (2013) used a (public) correlated equilibrium that randomly selects one of the two pure Nash equilibria in symmetric 2 $\times$ 2 games like Battle of the Sexes (BoS) and showed that the subjects do play the recommended strategies. Anbarci et al. (2018) provided a design to test how correlated equilibrium performs in BoS type games with different sets of payoffs. The main message of their paper is that the subjects do not like recommendations that lead to unequal payoffs, which is similar in nature to our main result in this paper.

Duffy et al. (2017) studied normal form games with multiple Nash equilibrium; the main question addressed there is how the subjects coordinate on any equilibrium, particularly when there are ex-ante symmetric equilibria to choose from. Their paper used a version of BoS and considered different treatments to study coordination using perfectly correlated signals. In addition, their paper also asked how, if at all, players use different coded language (in terms of indirect messages that are not directly related to actions in the game) to achieve coordination. The device we have used in this paper is a randomisation involving non-Nash outcomes, and thus is not a correlated equilibrium; our experimental results in this paper does confirm the findings of Cason and Sharma (2007), Duffy and Feltovich (2010) and Duffy et al. (2017) in the literature.

The specific type of correlation device used in this paper also relates to “sunspots”; thus, the experimental literature on public information (McKelvey and Page 1990; Marimon et al. 1993; McCabe et al. 2000; Anctil et al. 2004; Heinemann et al. 2004) and that on sunspot equilibrium become relevant to our study and to the results we found in this paper. Duffy and Fisher (2005) introduced sunspots as coordination devices using randomisation over equilibria and provided a direct evidence of sunspot equilibria in markets. Stahl (2013) and Camera et al. (2013) used randomised messages for cooperation in Prisoners’ Dilemma; Brandts and Macleod (1995) and Seely et al. (2005) analysed public recommendations while Fehr et al. (2019) and Arifovic et al. (2013) studied sunspot-driven strategies. Arifovic and Jiang (2014) studied the simple bank-run game by Diamond and Dybvig (1983) and analysed situations in which sunspots matter through a laboratory study. Kaplan and Ruffle (2012) investigated models of cooperation through a class of two-player games that requires the players to coordinate on which player cooperates and who gets to defect, so as to achieve the socially efficient outcome. Our paper fits well within this literature as well.

In our set-up, the (coarse) correlation device is not accepted perhaps because accepting the device implies that an individual does not “win” in two out of three possible outcomes. This interpretation is similar in nature to the findings of Keren and Teigen (2010) who have shown aversion to use random devices and of Cappelen et al. (2013) who have demonstrated that most individuals favour some redistribution ex-post. Our main result can possibly be derived from the notion of strategic uncertainty as well which may relate to the work by Van Huyck et al. (1990) who have provided experimental evidence on how subjects behave in case of strategic uncertainty. Their paper studied a class of pure coordination games with multiple equilibria that are Pareto ranked; it showed coordination-failure may resulting from strategic uncertainty as some subjects conclude that it was too “risky” to choose the payoff-dominant action and most subjects focused on outcomes in earlier periods.

Our result is also connected to the work by Andreoni et al. (2002) who found that the equilibrium prediction may fail when the equilibrium results in unequal distributions of payoffs, and there are alternative outcomes involving equality. It is also analogous to Machina’s (1989) parental example where the child (among the two children) who loses the toss and does not like the outcome ex-post. Finally, our paper is related to a literature (Bolton et al. 2005; Krawczyk 2011; Trautmann and Vieider 2012; Trautmann and van de Kuilen 2016) that distinguishes between preferences for outcome fairness (where the agent is concerned about the actual distribution of payoffs) and preferences for process fairness (where the agent is concerned about the random process by which outcomes are created, but not what these outcomes actually are).

Theoretical framework

We first briefly recall some theoretical concepts behind our experiment. Here, we closely follow the notations and definitions of a few notions from Moulin et al. (2014), Ray and Sen Gupta (2013) and Kar et al. (2010), where more details can be found.

Consider any fixed finite normal form game, $G=[N,\{S_{i}\}_{i\in N},\{u_{i}\}_{i\in N}]$, with set of players, $N=\{1,\ldots ,n\}$, finite pure strategy sets, $S_{1},\ldots ,S_{n}$ with $S=\prod _{i\in N}S_{i}$, and payoff functions, $u_{1},\ldots ,u_{n}$, $u_{i}:S\rightarrow {\mathfrak {R}}$, for all i. A direct correlation device, $\mu$, for such a game G, is simply a probability distribution over S. In this paper, we will consider direct correlation devices only and therefore in what follows, we will call such a device just a correlation device, or a device, in short, for convenience. G can be extended by using a device $\mu$. An extended game $G_{\mu }$ is the game where the device selects a strategy profile s ($=(s_{1},\ldots ,s_{n})$) according to the probability distribution and sends private recommendation $s_{i}$ to each player i, and then the players play the original game G. $\mu$ is called a correlated equilibrium (Aumann 1974, 1987) of the game G if following the recommendations form a Nash equilibrium in the extended game $G_{\mu }$, that is, following the recommendations is the best response for each player when all others are also following.

One may use a device, $\mu$, in a different way for a finite normal form game to get a coarser notion of correlation. A game G may be extended to a game $G_{\mu }^{\prime }$ in which the strategies of a player are to commit to the correlation device $\mu$, or to play any strategy in G. If all the players commit to the device, an outcome is chosen by the device according to the probability distribution $\mu$. If one of the players unilaterally deviates, while the others commit to the device, the deviant faces the marginal probability distribution $\mu _{i}^{\prime }$ over $s_{-i}\in S_{-i}$ which is given by $\mu _{i}^{\prime }(s_{-i})= \sum _{s_{i}\in S_{i}}\mu (s_{i},s_{-i})$. $\mu$ is called a coarse correlated equilibrium of the game G if committing to the device forms a Nash equilibrium in the extended game $G_{\mu }^{\prime }$, that is, accepting the device is the best response for each player when all others are also accepting.¹

We can think of one specific type of correlation device, for which recommendations are “public”. Given a correlation device $\mu$, a strategy profile s ($=(s_{1},\ldots ,s_{n})$), is called a public recommendation, if $\mu (s)>0$ and the conditional probability of $(s_{-i})$ given $s_{i}$ is 1, for all i. A correlation device $\mu$ is called a public device if for all $s\in S$, either $\mu (s)=0$ or s is a public recommendation. A public device may even be considered as a “sunspot” device (Ray 2002; Polemarchakis and Ray 2006; Ray and Sen Gupta 2013), as players may “coordinate” using such public recommendations as sunspots. Clearly, a public device is a correlated equilibrium if and only if all the public recommendations in the device are (pure) Nash equilibria.

In this paper, we consider the two-person game, $G_{0}$, in which each player has three pure strategies (player 1’s pure strategies are A, B and C while player 2’s are X, Y and Z) (Table 1).

Table 1 The game $G_{0}$

(A, X) is the unique Nash equilibrium of $G_{0}$, with payoffs (3, 3). Also note that the strategies C and Y are strictly dominated (by A and X for player 1 and 2 respectively). One can thus analyse this game by iterative elimination of dominated strategies and get the profile (A, X) as the unique outcome (having eliminated C and Y, in the reduced game A dominates B and X dominates Z). We modify the payoffs in $G_{0}$ to get other similar games labelled respectively as $G_{1}$, $G_{2}$ and $G_{3}$ and use them for our purpose (Table 2).

Table 2 Three further games

The structure of the above games is clearly very similar to that of the original game $G_{0}$; in all these games, strategies C and Y are strictly dominated and (A, X) is the unique Nash and correlated equilibrium.

We consider a specific correlation device which is an equally-weighted lottery of three outcomes including the Nash equilibrium, as in Table 3. This device is a public device as the probabilities are positive only for the outcomes (A, X), (B, Y) and (C, Z) that are public recommendations.

Table 3 The public correlation device

The public device in Table 3 is not a correlated equilibrium (for the games $G_{0}$, $G_{1}$, $G_{2}$ and $G_{3}$) as not all three public recommendations in the device are Nash equilibria of the game. For example, if the outcome (B, Y) is selected by the device and players 1 and 2 are recommended to play B and Y respectively, then player 2 will not follow the recommendation Y (and play X instead); similarly, if the outcome (C, Z) is selected by the device, then player 1 will not follow the recommendation C (and play A instead). The Nash outcome (A, X), that is, the device with probability 1 on (A, X), is the only correlated equilibrium of these games.

The device however is indeed a coarse correlated equilibrium for $G_{0}$ (and similarly for games $G_{1}$, $G_{2}$ and $G_{3}$), that is, committing to the device is the best response of a player when the other player is committing as well. Given that player 2 commits to the device, in $G_{0}$, player 1 gets an expected payoff of $\frac{10}{3}$ ($=\frac{1}{3}(3+5+2)$) from committing; however, if player 1 decides not to commit and instead plays the game, player 1 gets an expected payoff of $\frac{8}{3}$ ($= \frac{1}{3}(3+1+4)$) from choosing the pure strategy A, gets 2 ($= \frac{1}{3}(1+5+0)$) from B and 1 ($=\frac{1}{3}(1+0+2)$) from C.

It should be also noted that the device in Table 3 is not the unique coarse correlated equilibrium for our games; a (public) device which is a lottery with probability $\frac{1}{2}$ each over the outcomes (B, Y) and (C, Z) is also a coarse correlated equilibrium for these games, giving an even higher payoff (3.5 to each of the two players in $G_{0}$). The chosen device (in Table 3) includes the Nash equilibrium; also, it picks outcomes that are either Nash or symmetric around the Nash point and thus is similar to a Nash-centric device.² The device in Table 3 is a coarse correlated equilibrium for each of the games $G_{1}$, $G_{2}$ and $G_{3}$ with an expected payoff to each player of $\frac{7}{3}$, $\frac{16}{3}$ and $\frac{22 }{3}$, respectively improving upon the respective Nash payoff of 2, 4 and 5.

In a coarse correlated equilibrium, committing to the device is a Nash equilibrium of the extended game; however, this equilibrium may not be unique and there may be other (Nash) equilibria of the extended game.³ Indeed for the game $G_{0}$ (and similarly for $G_{1}$, $G_{2}$ and $G_{3}$), the strategy profile of not committing to the device by both players and subsequently playing (A, X) in the game is also a Nash equilibrium. To see this, consider player 1(2) in $G_{0}$ and assume that player 2(1) is not committing to the device and is playing X (A); if now player 1(2) commits to the device, the device will pick any strategy for player 1(2) with probability $\frac{1}{3}$ each and thus the expected payoff of player 1(2) is $\frac{5}{3}$ ($=\frac{1}{3}(3+1+1)$) from committing to the device when player 2(1) is playing X(A), which is less than 3 that player 1(2) would have got by not committing to the device and playing A(X). We formally analyse the induced 2 $\times$ 2 game(s), $G_{0}$ (and similarly for $G_{1}$, $G_{2}$ and $G_{3}$) as shown in Table 4 in each of which there are only two strategies for the players, namely, “commit to the device (Com)” and “do not commit and then play A (X)”. There are two Nash equilibria in each game. The first equilibrium, (Com, Com), is payoff-dominant; the second Nash equilibrium (of not committing to the device) is ex-ante sub-optimal with the payoff (3 in $G_{0}$) for either player and is less than the expected payoff from the coarse correlated equilibrium ($\frac{10}{3}$ in $G_{0}$). However, note that the Nash equilibrium (A, X) is risk-dominant (Harsanyi and Selten 1988; Harsanyi 1995) in the induced game.

Table 4 The induced 2 $\times$ 2 games from $G_{0}$, $G_{1}$, $G_{2}$ and $G_{3}$

Experimental design

Following the theoretical notions presented earlier, we first present our treatments and our own hypotheses, some of which are already confirmed in the existing literature. Our main purpose is to test the concept of coarse correlated equilibrium in our game(s). However, as a baseline, we first have two treatments in which we analyse the game $G_{0}$ with the notions of Nash and correlation. In the first of these treatments, namely, the Nash treatment, we just use the game $G_{0}$ without any kind of correlation device. We expect to find evidence from our Nash treatment in favour of our Hypothesis 1 as it is fairly well-established in the existing literature for such games with unique equilibrium outcomes.

Hypothesis 1

In the Nash treatment (for the game $G_{0}$), subjects do not play the dominated strategies, $C$ and $Y$, and play the unique Nash equilibrium $(A,X)$.

In our second treatment, the correlated treatment, we use the device in Table 3 to send non-binding recommendations to the subjects to test whether these recommendations are followed or not, with the following hypothesis in mind, as the Nash point (A, X) is the only correlated equilibrium for the game $G_{0}$.

Hypothesis 2

In the correlated treatment (for the game $G_{0}$), subjects follow the recommendation $(A,X)$ ; however, they do not follow the recommendations of $(B,Y)$ and $(C,Z)$ and instead play the unique Nash equilibrium of the game, $(A,X)$, in those cases.

This behaviour is based on the results in the literature on correlated equilibrium (see Cason and Sharma 2007; Duffy and Feltovich 2010; Bone et al. 2013; Duffy et al. 2017; Anbarci et al. 2018).

Finally, in the third treatment with the game $G_{0}$, the coarse correlated treatment, we use the same device (as in Table 3) as a commitment device, rather than for sending recommendations, to test the concept of coarse correlation. One could perhaps expect, as in the existing literature on correlated equilibrium, the theoretical prediction to be observed here, that is, the device will be accepted.

Hypothesis 3

In the coarse correlated treatment, subjects commit to the device for the game $G_{0}$.

There could be a couple of justifications behind Hypothesis 3. One may expect individuals to accept the device with higher expected payoffs (than the Nash payoff). Also, as the structure of our device is similar to that of “sunspots” (Ray 2002; Polemarchakis and Ray 2006), following the well-known experimental literature on sunspots (initiated by Duffy and Fisher 2005), one may hypothesise that the theoretical notion of coarse correlation will be validated by our experiment as well. However, an alternative hypothesis can also be put forward here.

Hypothesis 3a

In the coarse correlated treatment, subjects reject the device and then play $(A,X)$ in the game $G_{0}$.

As we explained earlier, rejecting the device and playing (A, X) is the risk-dominant equilibrium in the induced game. Further, Hypothesis 3a can be justified as the coarse correlated equilibrium results in unequal payoffs while the outcome (A, X) in the game may appear to be fair to the subjects. Along with this issue of fairness (Fehr and Schmidt 1999), one may also note that although the expected payoff for an individual from accepting the device is higher than that from the Nash equilibrium of the game, however, the outcomes chosen by the device have consequences (Hammond 1988); two of these three outcomes involve some inequality, in each of which a player, randomly chosen, gets more payoff than the other. Another motivation for our Hypothesis 3a could be how subjects behave in case of strategic uncertainty (see the literature on two-player coordination games with multiple equilibria that are Pareto ranked, e.g., Van Huyck et al. 1990).

The main result in this paper therefore will tell us which of the above two is more sustained. Moreover, as a robustness check for the coarse correlated treatment, we run two additional treatments. As it will be described more clearly below, in all our treatments, subjects interacted for a few rounds. The first robustness check aims to test whether behaviour changes when the interaction is repeated instead of an approximated one-shot interaction. To this end we run our fixed-match coarse correlated treatment, which follows the exact same structure as in the coarse correlated treatment, with the only difference being that the pair-matching remains fixed through all rounds. The multi-game coarse correlated treatment aims to test the validity of coarse correlation when the subjects face different games; here, subjects face the games $G_{1}$, $G_{2}$ and$\ G_{3}$ as well as the original game $G_{0}$. In support of the robustness of our design, we expect both our fixed-match coarse correlated treatment and the multi-game coarse correlated treatment to have similar levels of accepting the device as in the coarse correlated treatment.

On top of these treatments involving games, we also run a couple of treatments in which we considered just the lottery part of the device. As a fair comparison, we study the differences, if any, between the choices made in the coarse correlated treatment with a lottery treatment that we call the paired lottery treatment. In this treatment, subjects have to choose between a safe option that yields payoffs $\pounds 3$ for both individuals in the pair, or a lottery which yields either ($\pounds 3$, $\pounds 3$) or ($\pounds 5$, $\pounds 2$) or ($\pounds 2$, $\pounds 5$), with equal chances, for the two paired individuals respectively.

In the second, namely, the individual lottery treatment, the subjects are asked to choose among a sure outcome and a lottery to contrast with the coarse correlated treatment. In this choice problem, a participant has to choose between the lottery that picks one of three outcomes $\pounds 2$, $\pounds 3$ and $\pounds 5$ each with probability $\frac{1}{3}$ and the sure (with probability 1) outcome of $\pounds 3$. We have designed two very similar individual choice problems that mirror the outcomes chosen by the device in the game $G_{0}$ for two players; the only difference between these two choice problems used is the framing (the order) of the outcomes in the lottery ($\pounds 2$, $\pounds 3$ and $\pounds 5$ as opposed to $\pounds 5$, $\pounds 3$ and $\pounds 2$). Note that those who do accept the lottery (over the sure outcome of $\pounds 3$) are not necessarily risk-averse or risk-seeking; conversely, risk-neutral or risk-seeking individuals and even some risk-averse individuals (for whom the certainty equivalent is between $\pounds 3$ and $\pounds \frac{10}{3}$) would accept the lottery. It is thus not designed to measure subjects’ risk preferences. Indeed, choosing the lottery for an individual in our individual lottery treatment can be viewed as similar to accepting the device for a player in the coarse correlated treatment, whatever be their risk-attitude. The choices for the subjects in our lottery treatments and in the coarse correlated treatment are the same; moreover, the paired lottery treatment takes into consideration the interactive nature of payoffs. Therefore, one may assume ex-ante the following hypothesis.

Hypothesis 4

The level of accepting the lottery and committing to the device in (two) lottery treatments and (three) coarse correlated treatments are similar.

Design

In the Nash, correlated, coarse correlated, fixed-match coarse correlated and multi-game coarse correlated treatments involving the game(s), each subject was first assigned to a role of either a row or a column player, as the game(s) under investigation is (are) not symmetric. These roles were held fixed throughout the experiment. We labelled the row and column players as Red and Blue individuals respectively. In the paired lottery treatment, subjects were also split in two groups: Red and Blue and formed pairs; both individuals submitted their choices and the choice of one of the two was implemented; the subjects knew that for every round there was a $50\%$ chance that their choice would be implemented. In the individual lottery treatment as well, subjects were split in two groups: Red and Blue. Red individuals could see the outcomes of the lottery in the order $\pounds 3$, $\pounds 5$, $\pounds 2$ while Blue individuals could see it in the form $\pounds 3$, $\pounds 2$, $\pounds 5$. In both these lottery treatments, the subjects’ type (Blue or Red) was fixed between rounds.

In all our treatments, subjects interacted for a total of 20 rounds. In every treatment, except obviously in the fixed-match coarse correlated treatment, there was a new random matching of pairs in every round; participants interacted in groups of 6 (6 are assigned as Blue individuals and 6 as Red individuals). This was implemented, following the common practice, in order to create an environment as close as possible to a one-shot interaction between subjects. In addition, there was no way for a participant to identify the opponent with whom they were matched. In the multi-game coarse correlated treatment, each game was played for 5 rounds and the games appeared in random order in an effort to mitigate potential order effects. In our study, we have collected data from several sessions, with one matching group consisting of 12 subjects in each session. Each subject participated in only one treatment. As the groups remain fixed during the experiment, each matching group represents an independent observation, except of course in the fixed-match coarse correlated treatment in which there are in total 12 independent observations.

Table 5 Experimental design

The overview of the experimental sessions is summarised in Table 5 above.

Procedure

The experiment was conducted at the Lancaster Experimental Economics Lab (LExEL). In total, 264 subjects (out of which $53\%$ were females) participated in seven treatments. The participants were mostly undergraduate students from the Lancaster University, from various fields of studies and were invited using the ORSEE recruitment system (Greiner 2015). The experiment was computerised and the experimental software was developed in Python.

All sessions followed identical protocol. Upon arrival at the lab, participants were randomly allocated to computer terminals. At the beginning of a session, subjects were seated and given a set of printed experimental instructions (see the Online Appendix) which were also read aloud so as to ensure common knowledge. After the instructions phase, the participants were asked to complete a brief questionnaire (see the Online Appendix) to confirm that there were no misunderstandings regarding the game, the matching procedure, the correlation device and the payoffs. When the subjects had completed the questionnaire, we made sure that they had all the answers correct. The experiment did not proceed until every subject had the correct answers to these questions. Subjects could not communicate with each other, neither could they observe the choices of other participants during the experiment.

Effort was made to use neutral language in the instructions for the experiment, to avoid any potential connotations. The actions in the games were represented as choices A, B and C (X, Y and Z) for the row (column) player; the opponent player was labelled as the counterpart. Any recommendation in the correlated treatment was given in a format so that the subjects are not influenced (to follow the recommendations). Similarly, in the coarse correlated, fixed-match coarse correlated and the multi-game coarse correlated treatments, the commitment choice was framed as whether a participant would like the computer to choose according to the device; it was made clear that the choice is entirely up to the participants.

For each round, subjects had 1.5 min (2.5 min in the coarse correlated, fixed-match coarse correlated and the multi-game coarse correlated treatments) for the first 10 rounds to confirm their choices and 1 min (1.5 min in coarse correlated, fixed-match coarse correlated and the multi-game coarse correlated treatments) for the remaining 10 rounds. If no decision was made by that time, the software was programmed to randomly pick one of the choices in the corresponding treatment.⁴

In the individual lottery, paired lottery and Nash treatments, subjects simply clicked on their preferred choice and when ready, they could confirm their choice by clicking the “OK” button. The framework in the correlated treatment was the same as in the Nash treatment with the difference that now an individual recommendation was made to the pair on what action to choose. The software was programmed to generate i.i.d. recommendations for each pair, based on a uniform distribution over the three possible outcomes. The recommendations were uniquely generated for each session in the correlated treatment. In the correlated, coarse correlated, fixed-match coarse correlated and the multi-game coarse correlated treatments, the device was commonly known to the players and was implemented using a random number generator programmed to create recommendations or actions based on the probability distribution of the device.

In the coarse correlated, fixed-match coarse correlated and the multi-game coarse correlated treatments, the choice was made in one or two stages, depending on whether subjects were willing to commit to the correlation device or not. During the first stage, the subjects could see the correlation device and were asked whether they would like to allow the computer to make a choice for them (equivalent to committing to the device). There are three possible cases: (1) if both members of the pair did not want to commit, then the second stage appeared on their screens, identical to the framework of the Nash treatment (the corresponding game without any correlation device or recommendations), in which the subjects could choose their preferred action; (2) in the case where both members of the pair were willing to commit to the device, there was no second stage, the computer was randomly choosing one of the possible three outcomes and the subjects were receiving the corresponding payoff; (3) finally, if a member of the pair wanted to commit and the other did not, then the latter could see the second stage of the game and indicate her choice while for the former, the choice was randomly made by the computer based on the correlation device; the payoff was then determined by the combination of the randomly chosen action by the computer and the action that the other individual picked. Note that in the various coarse correlated treatments, when a subject chooses to reject the device, the subject is not informed (before own action choice) whether or not the opponent chose also to reject the device.

At the end of each round, after the subjects have made and confirmed their choices, they were given the relevant feedback. In the individual and paired lottery treatments, the subjects were informed about their payoffs in that round; in the paired lottery treatment, the pair was also informed of whose choice was implemented by the computer. In the Nash, correlated, coarse correlated, fixed-match coarse correlated and the multi-game coarse correlated treatments, the subjects were informed of own and opponent’s choice, own and opponent’s payoff, plus, own and opponent’s recommendation (in the correlated treatment), own and opponent’s commitment choice (in the coarse correlated, fixed-match coarse correlated and the multi-game coarse correlated treatments).

After 20 rounds, the experimental session ended and the subjects were privately paid, according to their point earnings. In all the treatments, we used an exchange rate of 1 : 1 ($\pounds 1$ per point).⁵ For the payment, the random incentive mechanism was implemented; two rounds out of the total 20 were randomly selected for all the participants. The payments were made in private and in cash, directly after the end of the experiment. The average payment was $\pounds 9.94$ including a show-up fee of $\pounds 3.00$ and the experimental sessions lasted less than 45 min that correspond to an approximate hourly rate of $\pounds 13.25$ ($17.23) which is considerably higher than usual student-jobs in the UK that offer about $\pounds 8.00$ ($10.40) per hour.

Results and analysis

We first provide a descriptive analysis of our results from our experimental sessions.

Nash and correlated treatments

(A, X), which is the unique outcome of the iterative elimination of strictly dominated strategies and thus the unique Nash equilibrium outcome, is played in our Nash treatment; overall, 433 out of 480 ($90.2\%$) of the outcomes played is the Nash equilibrium outcome, (A, X). We also note that the two strictly dominated strategies in the game, C (for row players) and Y (for column players) have been chosen only in 10 ($2.1\%$) and 5 ($1.1\%$) cases, respectively. In line with the existing literature, our Hypothesis 1 thus finds support in the observed data from this treatment.

To check whether the frequency of the Nash outcome (A, X) played is increasing (over time) or not, we formally compared the frequency of the outcome (A, X) and the individual choices of A and X in the first 5 rounds with that in the final 5 rounds using a suitable parametric z -test and found that the difference is indeed statistically significant.⁶

Finding 1

The dominated strategies, $C$ and $Y$, have not been chosen by the subjects in the Nash treatment. The Nash equilibrium, $(A,X)$, is played, with an increasing trend over time.

We then look at the correlation device used for the game in the correlated treatment and check whether the individuals followed the recommendations from the device or not. In theory, the correlation device first selects one of the three possible outcomes, (A, X), (B, Y) and (C, Z) with probability $\frac{1}{3}$ each; indeed, the actual frequencies of these recommendations in our correlated treatment were 163 ($34\%$), 149 ($31\%$) and 168 ($35\%$), respectively. We do find that the Nash equilibrium outcome (A, X), when recommended, is followed in 145 (out of 163) times; furthermore, (A, X) is the most frequently chosen outcome given the other two recommendations, respectively, 101 (out of 149) and 111 (out of 168) times. We also note that overall in this treatment, A is chosen by row players (426 times; $88.8\%$) and X by column players (395 times; $82.3\%$). One may be interested in checking whether following or playing (A, X) increased over time or not; we do observe an increasing trend of playing (A, X) over time.⁷

Finding 2

The outcome $(A,X)$ has been played when recommended, however the recommendations $(B,Y)$ and $(C,Z)$ have not been followed and instead $(A,X)$ has been played; in all these three cases, the strategy profile $(A,X)$ has been played with an increasing trend over time.

Based on Finding 2 above, we can say our experimental data support Hypothesis 2 that the individuals play (A, X), either by following the (good) recommendation of playing (A, X) or not following other recommendations and instead playing the unique Nash equilibrium of the game. As already mentioned, results similar to our Finding 2 are well-established in the experimental literature on correlated equilibrium (see Cason and Sharma 2007; Duffy and Feltovich 2010; Bone et al. 2013; Duffy et al. 2017; Anbarci et al. 2018).

Coarse correlated treatments

In our coarse correlated treatment, only 31 out of 480 ($6.5\%$) pairs (that is, both individuals in a pair) committed to the device to get the expected payoff of $\frac{10}{3}$.⁸ On the other hand, in 305 pairs ($63.5\%$), both players did not commit to the correlation device. The frequencies (and the percentages) of individually committing to the device over 20 rounds (that is, out of 480 observations each, for row and for column players) are 119 ($24.8\%$) and 92 ($19.2\%$), respectively. This difference between the row and column players’ committing is not significant ($p=0.482$); however, we do note a statistically significant decreasing time-trend for the individual players committing to the device ($p=0.000$).⁹

We summarise our finding for the coarse correlated treatment which turns out to be robust against both variations, the fixed-match coarse correlated treatment and the multi-game coarse correlated treatment.

Finding 3

A low proportion of subjects committed to the device in the coarse correlated treatment, less so over time.

Based on Finding 3 above, we can say that our Hypothesis 3a finds support in our data.

In the fixed-match coarse correlated treatment, only 22 out of 240 ($9.2\%$) pairs committed to the device which is not significantly ($p=0.190$) different from that ($6.5\%$) in the main coarse correlated treatment, as reported above. The frequencies (and the percentages) of individually committing to the device in this treatment are 41 out of 240 ($17.1\%$) and in 42 out of 240 ($17.5\%$) respectively for row and column players; these percentages clearly are not significantly different ($p=0.903$).

In our multi-game coarse correlated treatment, only 11 out of 240 ($4.6\%$) pairs committed to the device, which is also not significantly different ($p=0.312$) from the main coarse correlated treatment. The frequencies (and the percentages) of individually committing to the device in this treatment are 58 out of 240 ($24.2\%$) and in 43 out of 240 ($17.9\%$) respectively for row and column players; unlike the fixed-match coarse correlated treatment, these percentages are however indeed significantly different at $10\%$ level ($p=0.093$).

Playing Nash

We first focus on how individual behaviour in our baseline game varied in different treatments, in particular, on the choice of A and X (over B, C and Y,  Z) in the games in our Nash, correlated and coarse correlated treatments and see if there is any important differences across these series.

As already noted, in our correlated treatment, having received recommendations of either (B, Y) or (C, Z), the individuals chose the outcome (A, X) in 212 out of 317 cases ($66.88\%$). We also observed in our coarse correlated treatment, in 305 pairs out of 480 ($63.5\%$), both players did not commit to the correlation device; having rejected the device, these pairs played the game (as in the Nash treatment) and they chose the outcome (A, X) in 238 out of these 305 cases ($78\%$). In the fixed-match coarse correlated treatment, we found both players did not commit to the device in 179 pairs out of 240 ($74.6\%$); having rejected the device, these pairs played the outcome (A, X) in 138 out of 179 cases ($77.1\%$). Finally, in our multi-game coarse correlated treatment, we found both players did not commit to the device in 150 pairs out of 240 ( $62.5\%$); having rejected the device, these pairs played the outcome (A, X) in 127 cases ($84.6\%$). Also, we can report that the percentage of playing (A, X) in our Nash treatment ($90.2\%$, as reported above) is significantly different from those in the correlated ($p=0.000$) and borderline significant from those in the coarse correlated ($p=0.059$) treatments.

Fig. 1

Playing (A, X) in different scenarios

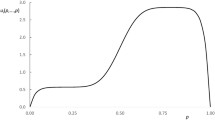
We now display these findings in one figure to compare the frequencies of playing (A, X) in our different treatments. Figure 1 above presents in six different scenarios from our treatments, the proportions of (A, X) played respectively in (1) the Nash treatment, (2) the correlated treatment, conditional on the recommendation of (A, X) only, (3) the correlated treatment, conditional on the recommendations of either (B, Y) or (C, Z), (4) the coarse correlated treatment conditional on rejecting the device, (5) the fixed-match coarse correlated treatment conditional on rejecting the device and (6) the multi-game coarse correlated treatment conditional on rejecting the device.

In Fig. 1, the average percentages are shown in 5-period blocks, as they are quite noisy. The multi-game coarse correlated treatment data includes all the games.¹⁰ We here note that all the plots in Fig. 1 follow the same pattern with an increasing trend to play (A, X). We have indeed performed necessary tests to check if there is any significant difference in the proportions of playing (A, X) among these cases, involving 15 pairwise comparisons and have found no significant differences.

Lottery treatments: paired and individual

In contrast with the different coarse correlated treatments, we observe that 317 out of 480 ($66\%$) individuals accepted our paired lottery and thereby asked the computer to make the choice for them and their counterparts. The frequencies (and the percentages) of accepting the paired lottery by the two different types of individuals are 166 out of 240 ($69.2\%$) and 152 out of 240 ($63.3\%$), respectively for the Red and Blue individuals; these percentages are not significantly different.¹¹ Also, we find that there is no significant difference between the percentages in the first and the last five rounds for either types ($p=0.439$ for Red and $p=0.456$ for Blue), indicating no time-trend in accepting the paired lottery.

We then observe in our individual lottery treatment that$\ 681$ out of 960 ($70.9\%$) individual choices accepted the lottery, in comparison to 317 out of 480 ($66\%$) in the paired lottery, as reported above; this difference (between these two percentages) is indeed not statistically significant ($p=0.057$). 345 out of 480 ($71.9\%$) individual choices of the Red type and 336 out of 480 ($70\%$) Blue individual choices accepted the computerised lottery.¹² As in the paired lottery treatment, we find that these percentages of accepting the lottery are not statistically different between the two types ($p=0.522$).

We thus conclude that the findings from the paired lottery treatment are very similar to those in the individual lottery treatment. Our conclusion in this subsection therefore is that most (about 7 out of 10) individuals preferred the given lottery with an expected payoff of $\frac{10}{3}$ to the sure outcome of 3 which indicates that they are either risk-neutral or risk-seeking or at best mildly risk averse; we also confirm that there is no framing effect in this case as the individuals of Blue type did not find the lottery less attractive than the individuals of Red type did.

Finding 4

A high proportion of individuals accepted the lottery in the paired and individual lottery treatment.

Finding 4 above is in direct contrast with our finding from the coarse correlated treatment (Finding 3) in which a very low proportion of subjects committed to the correlation device, less so over time; based on Finding 4, one can say that our Hypothesis 4 does not find support in our data.

Accepting the device/lottery

Fig. 2

Accepting the correlation device or the lottery

We now show in one figure the frequencies of accepting the correlation device and choosing the lottery in our different treatments. Figure 2 above presents in five different scenarios from our treatments, the proportions of accepting the device or the lottery respectively in (1) the coarse correlated treatment, (2) the fixed-match coarse correlated treatment (3) the multi-game coarse correlated treatment conditional on rejecting the device (4) paired lottery treatment, and (5) individual lottery treatment. As in Fig. 1, the average percentages are shown in 5-period blocks in Fig. 2; the multi-game coarse correlated treatment data includes all the games.¹³

Figure 2 clearly shows that choosing the lottery is very common in our (paired and individual) lottery treatments, whereas accepting the device is fairly rare in various coarse correlated treatments. We can thus reject Hypothesis 3 and instead conclude that Hypothesis 3a finds support in our experiment. As explained earlier, this observed phenomenon of not committing to the device can be explained as an equilibrium behaviour as well. We also conclude that the findings for the coarse correlated treatment are robust against a change of our design to a fixed-match and also when we change the payoffs in the game suitably.

We now report our findings from Probit regressions to assess the choice of committing to the device or accepting the lottery (that serves as our dependent variable). The independent variables used are Round that takes integer values from 2 to 20 for different rounds, Row (takes value 1 when the individual is a row player), PastCommit (takes value 1 when the device or the lottery was committed to in the previous round) and PastOppoCommit (takes value 1 when the device was committed to by the opponent in the previous round).

Table 6 Probit regression on accepting the device in different coarse correlated treatments

We first estimate the model using the pooled data from the coarse correlated, the multi-game coarse correlated and the fixed-match coarse correlated treatments. Dummies are used for the fixed-match treatment and for the three different games played in the multi-game treatment ($G_{0}$ being the baseline). Table 6 above presents the marginal effects from this Probit regression.¹⁴

From Table 6, we conclude that not committing to the coarse correlation device significantly increases with time; a subject is more likely not to commit in a round if the subject or the opponent has not committed in the previous round.¹⁵

Table 7 Probit regression on accepting the lottery in different lottery treatments

We then estimate a model based on the pooled data from the paired and the individual lottery treatments. Accepting the lottery now is our dependent variable; we use the same independent variables as above (Round, Row and PastCommit) except the PastOppoCommit as it is not available for the individual lottery treatment. An appropriate dummy variable is used for the paired lottery treatment (individual lottery treatment being the baseline). Table 7 above presents the marginal effects from this Probit regression.

From Table 7, we note that subjects are more likely to accept the lottery in a round if they have accepted in the previous round. Significant marginal effects presented in Tables 6 and 7 highlight the difference between subjects’ accepting the lottery and their rejecting the coarse correlation device in our treatments. Marginal effects of Round number in the various treatments are either negative or insignificant which indicate that subjects do not learn to accept the device.

Our Findings 1–4 along with the Figs. 1 and 2 are sufficient to address all of our hypotheses; the regression analysis in Tables 6 and 7 additionally addresses some of the potential explanations for our main result which is summarised below.

Main Result 1

Although subjects accept the lottery in our lottery treatments, they do not commit to the device; moreover, having rejected the coarse correlation device, subjects played the Nash equilibrium $(A,X)$ in the game.

Concluding remarks

In this paper, we report the observations from an experiment comparing the level of the Nash equilibrium outcome played by the subjects in a game with unique pure Nash equilibrium, with and without the help of a specific correlation device. Our results from different treatments involving Nash equilibrium and correlated equilibrium are in line with the existing literature. However, the main treatment in this paper suggests that subjects do not commit to a public randomisation device that selects a few symmetric outcomes (including and around the Nash equilibrium) of the game with equal probabilities and instead play the game and choose the Nash equilibrium outcome; thereby, the paper raises a question about selecting an equilibrium under the concept of coarse correlation in this simple set-up. We also find that the choice of Nash equilibrium outcome is the highest in the treatment without any correlation device. We contrast our main result about not accepting the randomisation device in a game with an individual choice of accepting a lottery over the same outcomes. We run two versions of this lottery treatment—paired and individual—and observe that the subjects accept the lottery over a sure outcome in both the treatments.

What do these various treatments contribute to our understanding of correlated and coarse correlated equilibria? How can we interpret our findings? Our multi-game coarse correlated treatment shows that moderate changes to the incentives do not change our main finding. The fixed-match coarse correlated treatment indicates that giving both players a chance to get the fair share of higher payoff doesn’t matter, though one could also conclude that reducing strategic uncertainty doesn’t matter. The treatments on individual lottery and the coarse correlated equilibrium suggest that the rejection of the correlation device is not due to subjects’ risk attitudes; combined with the finding from our paired lottery treatment, one can perhaps rule out the so-called “other-regarding preferences” in this context. Another plausible reason why the subjects rejected the device could be the issue of fairness (Fehr and Schmidt 1999); however, one may argue that the inequity aversion argument has been, to a large extent, controlled for in our paired lottery treatment. One could thus explain this behaviour in the game as selecting a risk-dominant equilibrium. It can just be an example of risk dominance beating payoff dominance (in which case, arguably perhaps, a very large change to incentives might change the subjects’ behaviour); other explanations such as strategic uncertainty may also be possible (as in Van Huyck et al. 1990, in which coordination-failure results from strategic uncertainty).

Table 8 Another game

One may wonder whether our main finding depends on the choice of the specific device; admittedly, the concept of coarse correlation here requires a lot of trust in the device in order to be implemented, although, our chosen public device is similar to a Nash-centric device (Ray and Sen Gupta 2013; Moulin et al. 2014). In our set-up, it is clear that the deterministic Nash equilibrium in the game has a strong incumbent advantage. Probably, coarse correlated equilibrium would fare better when the Nash outcome is completely mixed as in the above game (Table 8).¹⁶

In the above game, there is no pure Nash equilibrium (none of the diagonal elements in the payoff matrix with payoffs (3, 2) is a Nash equilibrium). The only Nash outcome is the completely mixed equilibrium in which the players play each strategy with probability $\frac{1}{3}$, with payoffs $(\frac{5}{3},\frac{5}{3})$. For this game, our public device (as in Table 3) is clearly not a correlated equilibrium but it is indeed a coarse correlated equilibrium with payoffs (3, 2) which improves upon the Nash payoffs for both players (although player 1 gets more than player 2). One may run such an experiment in future.

Appendix

We provide the instructions for our experiments as an Online Appendix.

Here, we present two figures that correspond to our Figs. 1 and 2 respectively in this paper. Figures 3 and 4 below provide specific information about how behaviour varied across games in our multi-game coarse correlated treatment; as already mentioned in Footnotes 10 and 13, we find, from Figs. 3 and 4, no systematic differences in different games in this treatment.

In Fig. 3 below, we present the percentages of (A, X) played conditional on rejection of the device by both players, for each game (each played only 5 times), separately within the multi-game coarse correlated treatment.

Fig. 3

Playing (A, X) in different games in the multi-game treatment

Figure 4 below shows the percentages of subjects accepting the correlation device within the multi-game coarse correlated treatment, for each game separately.

Fig. 4

Accepting the correlation device for different games